A New Data-Driven Control System for MEMSs Gyroscopes: Dynamics Estimation by Type-3 Fuzzy Systems
Abstract
:1. Introduction
2. Problem Formulation
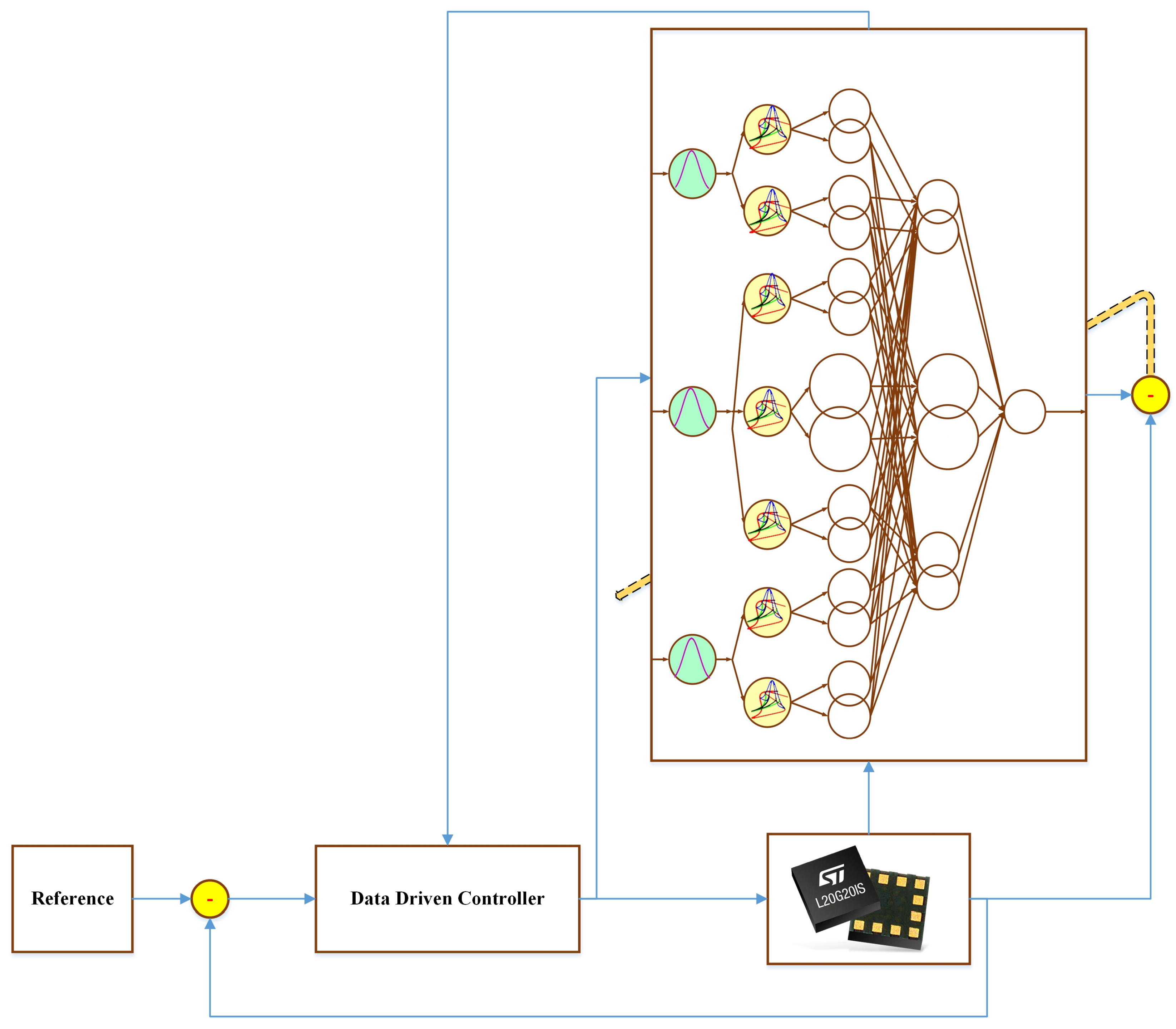
3. Type-3 FLS
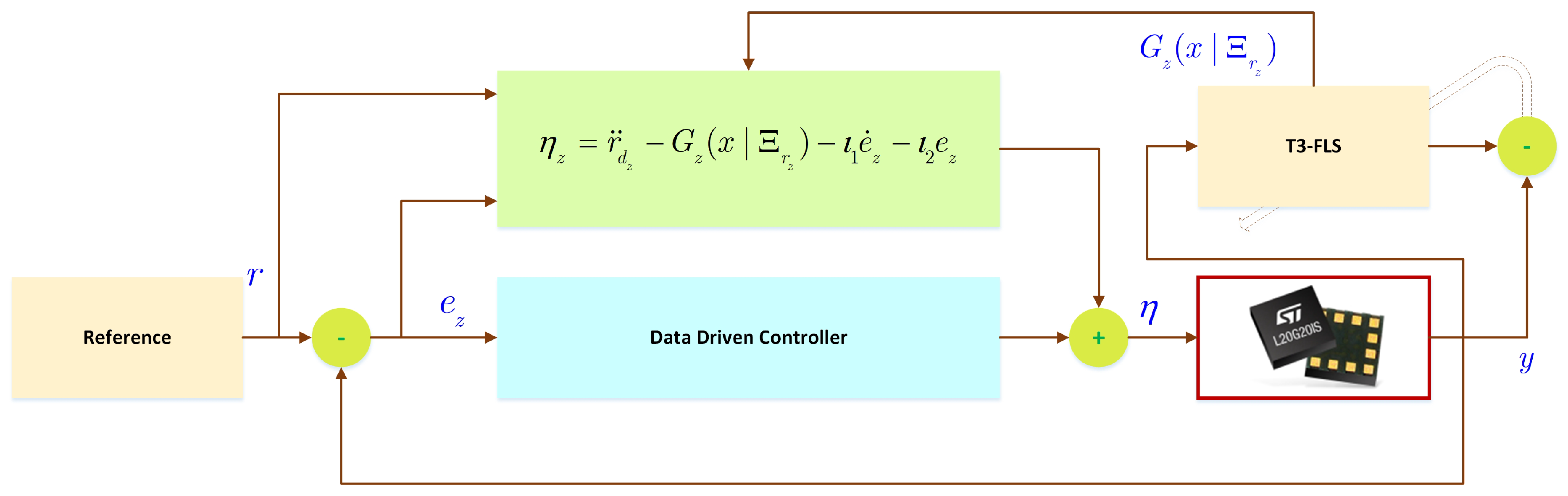
4. Data Driven Control System
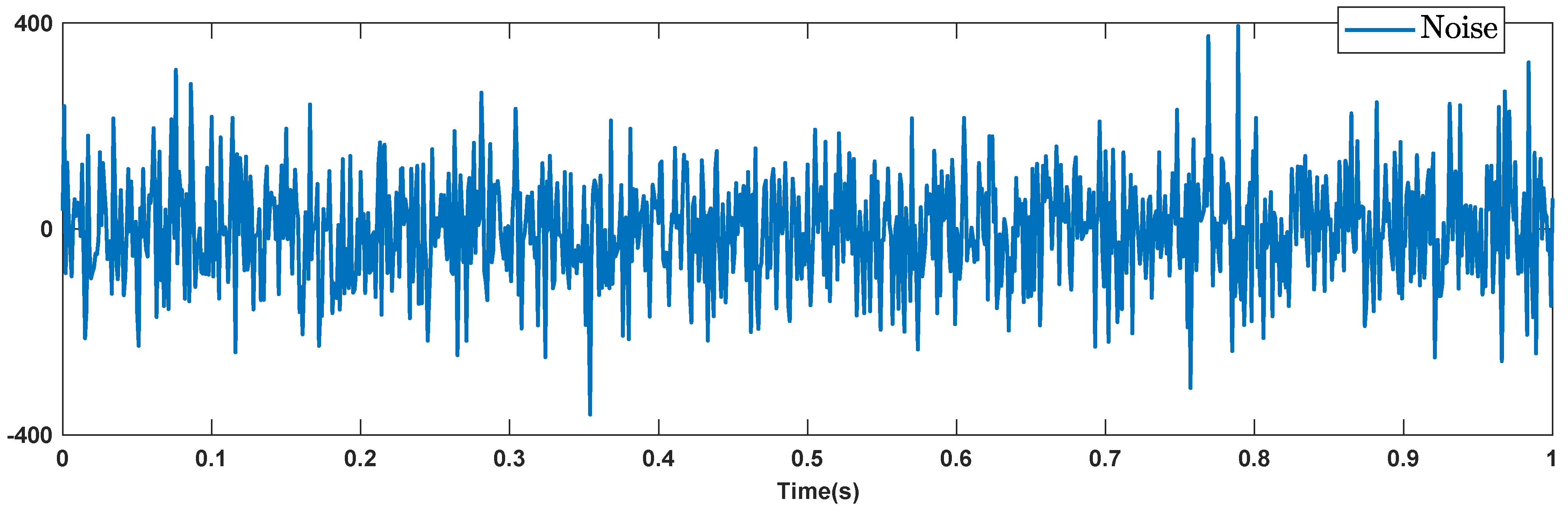
5. Stabilization with Noisy Data
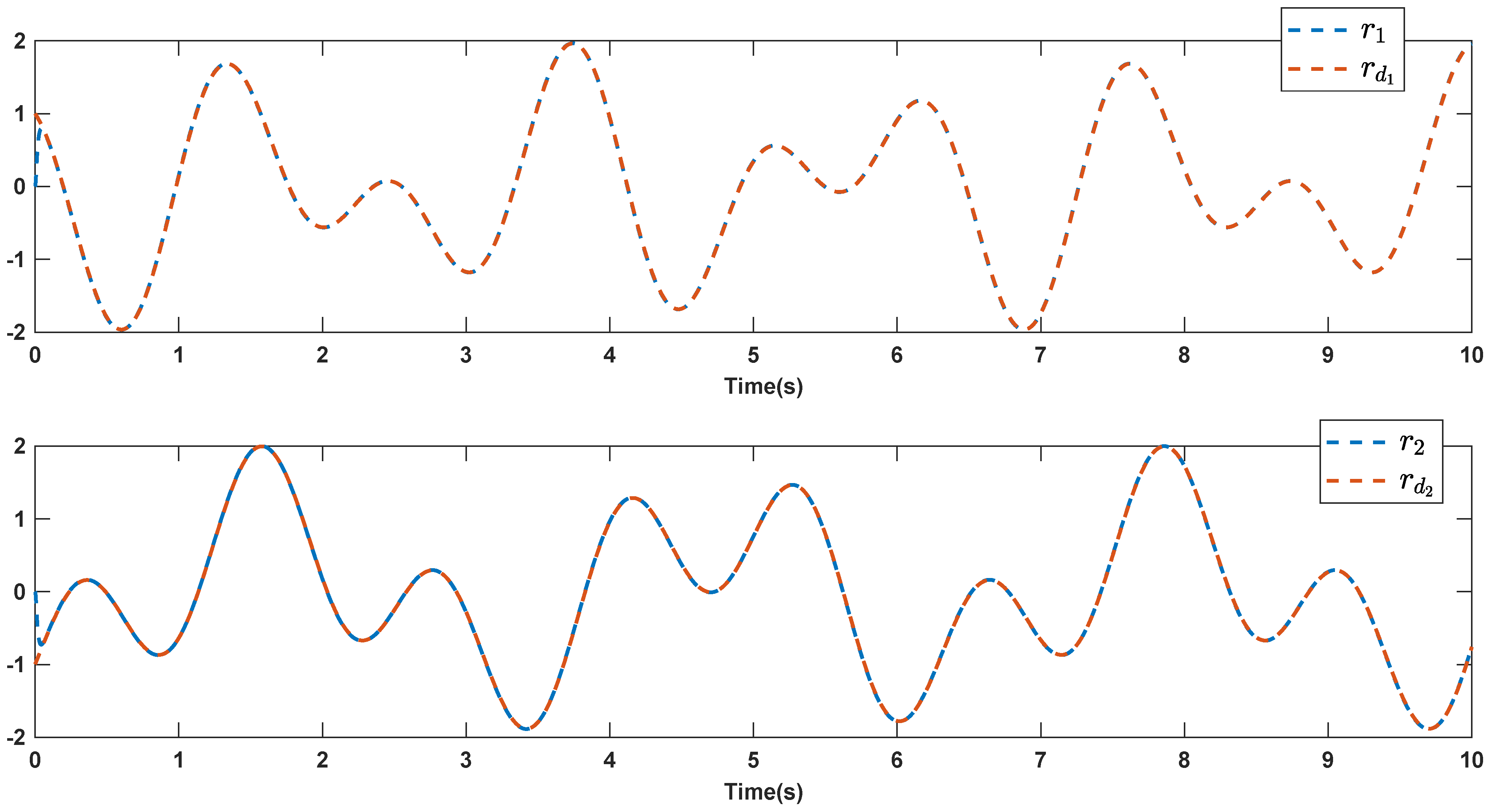
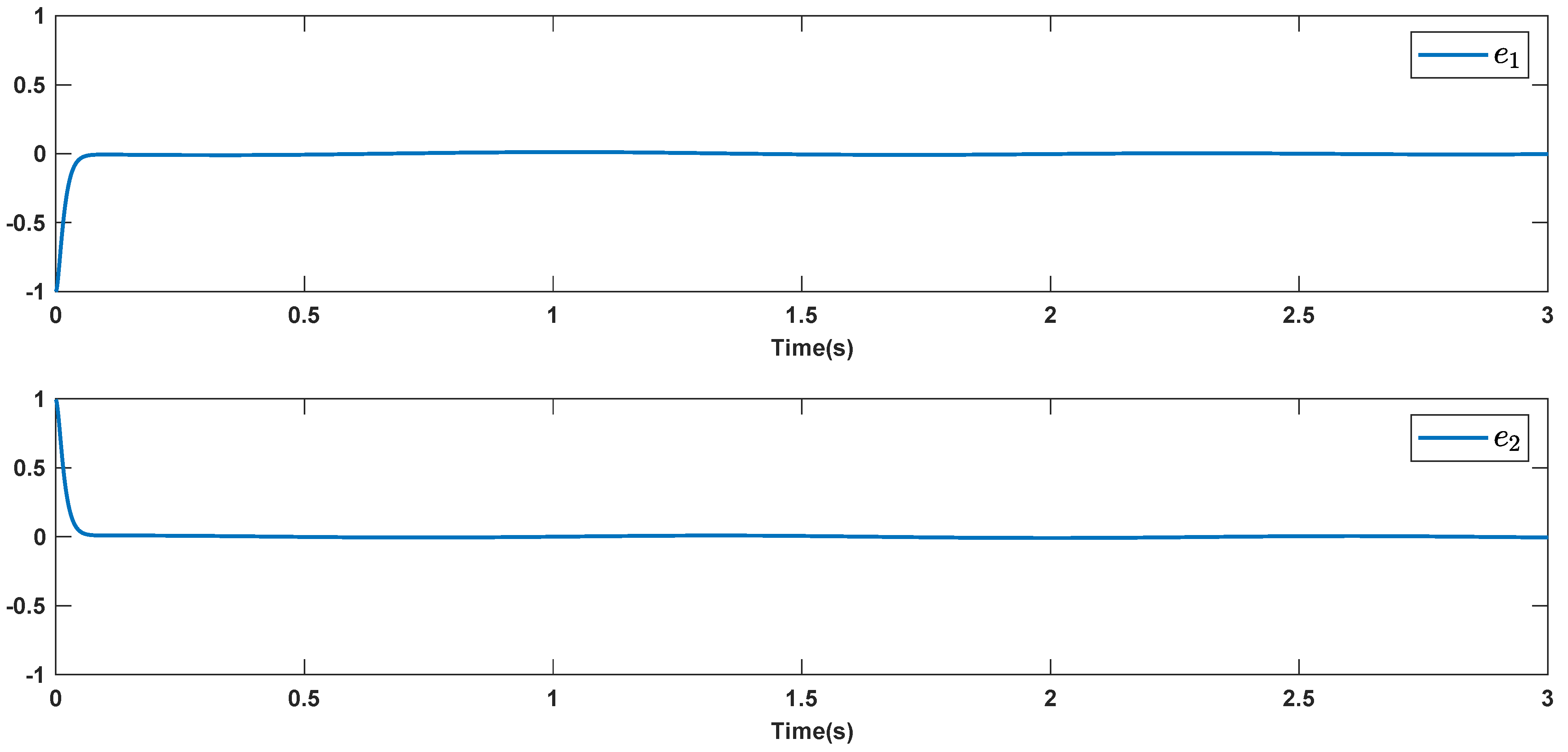
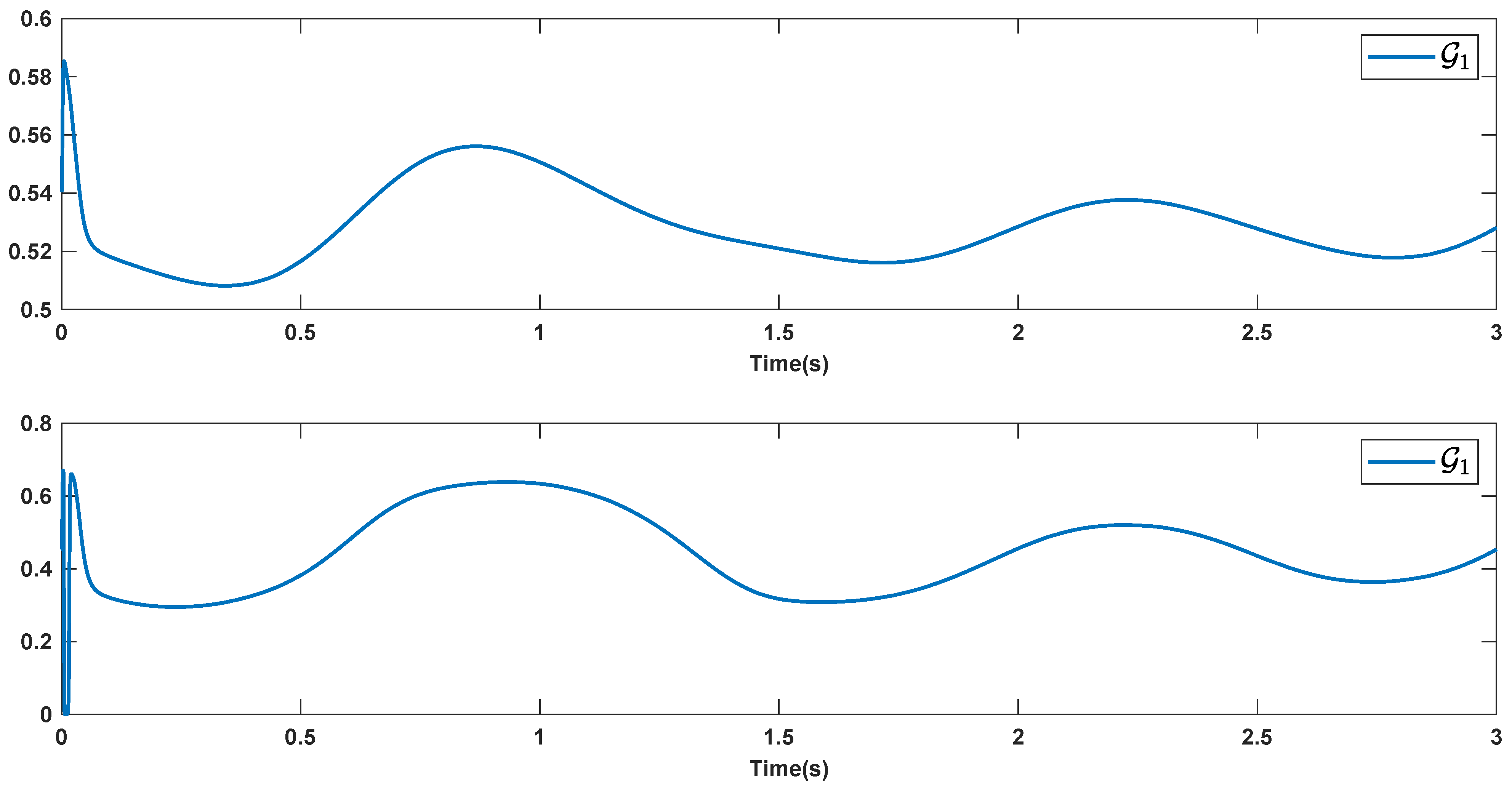
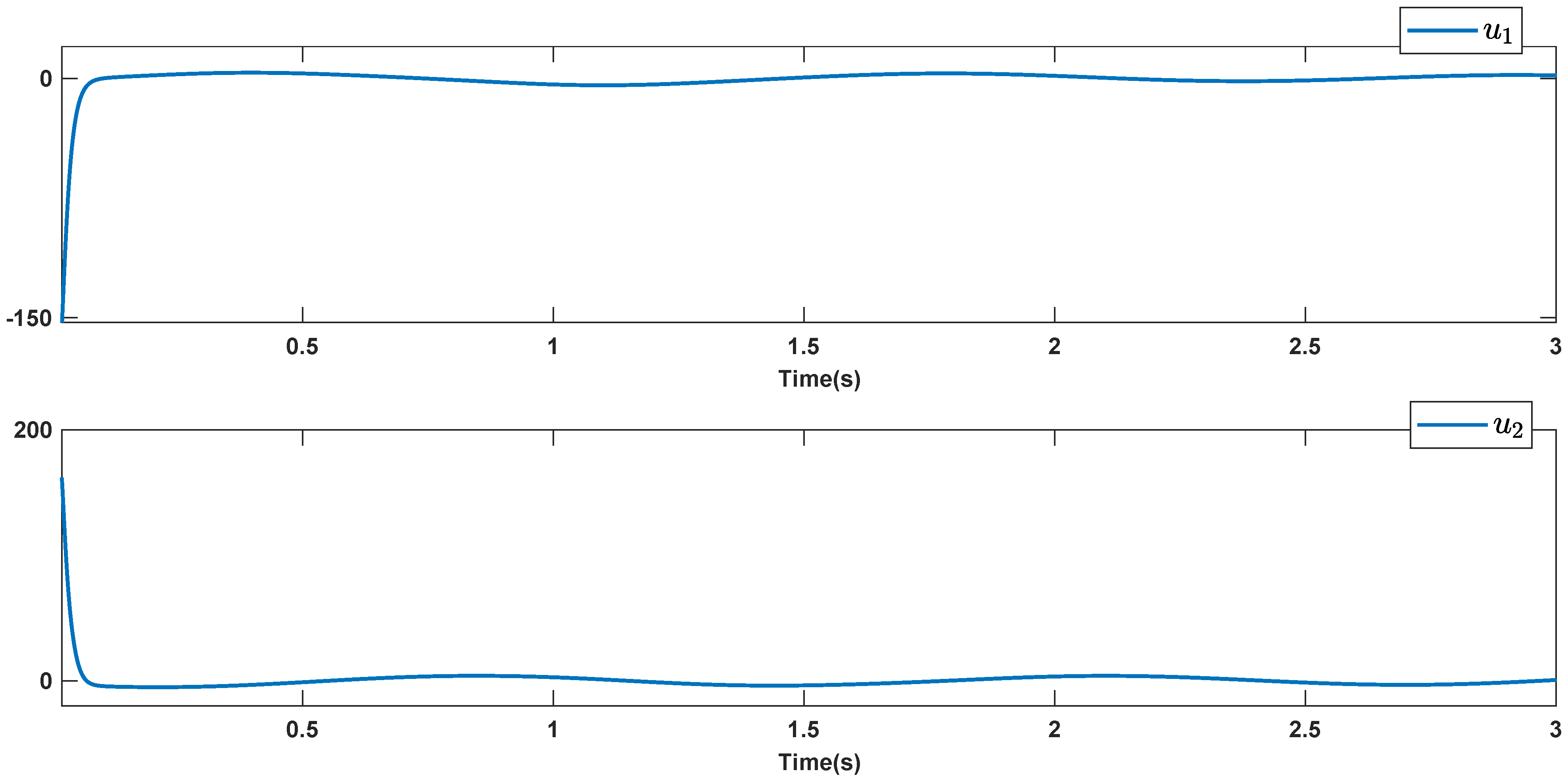
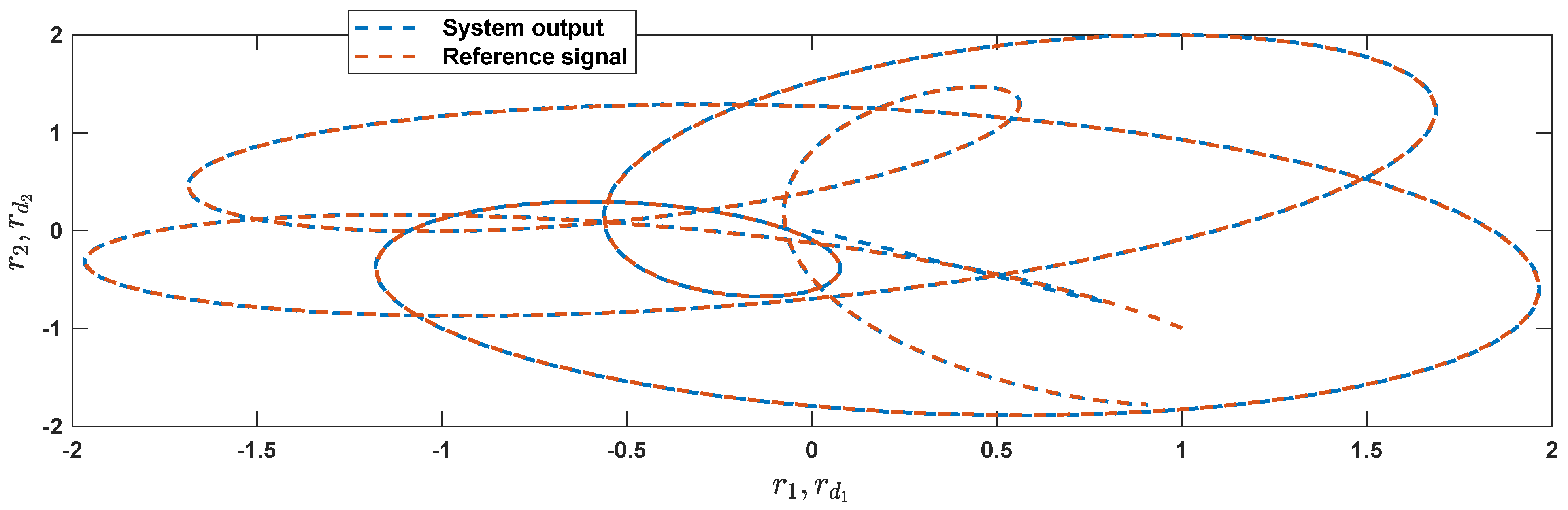
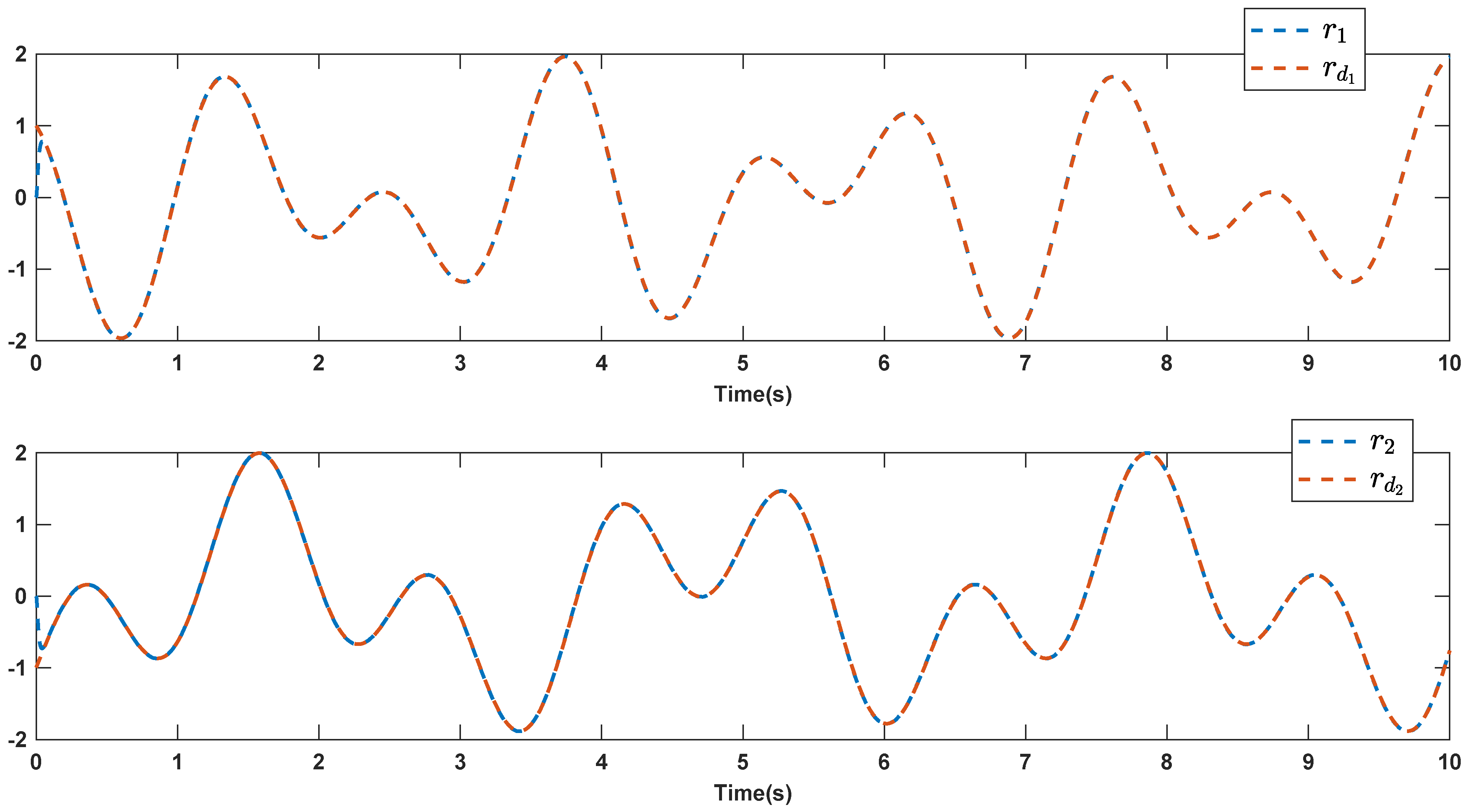
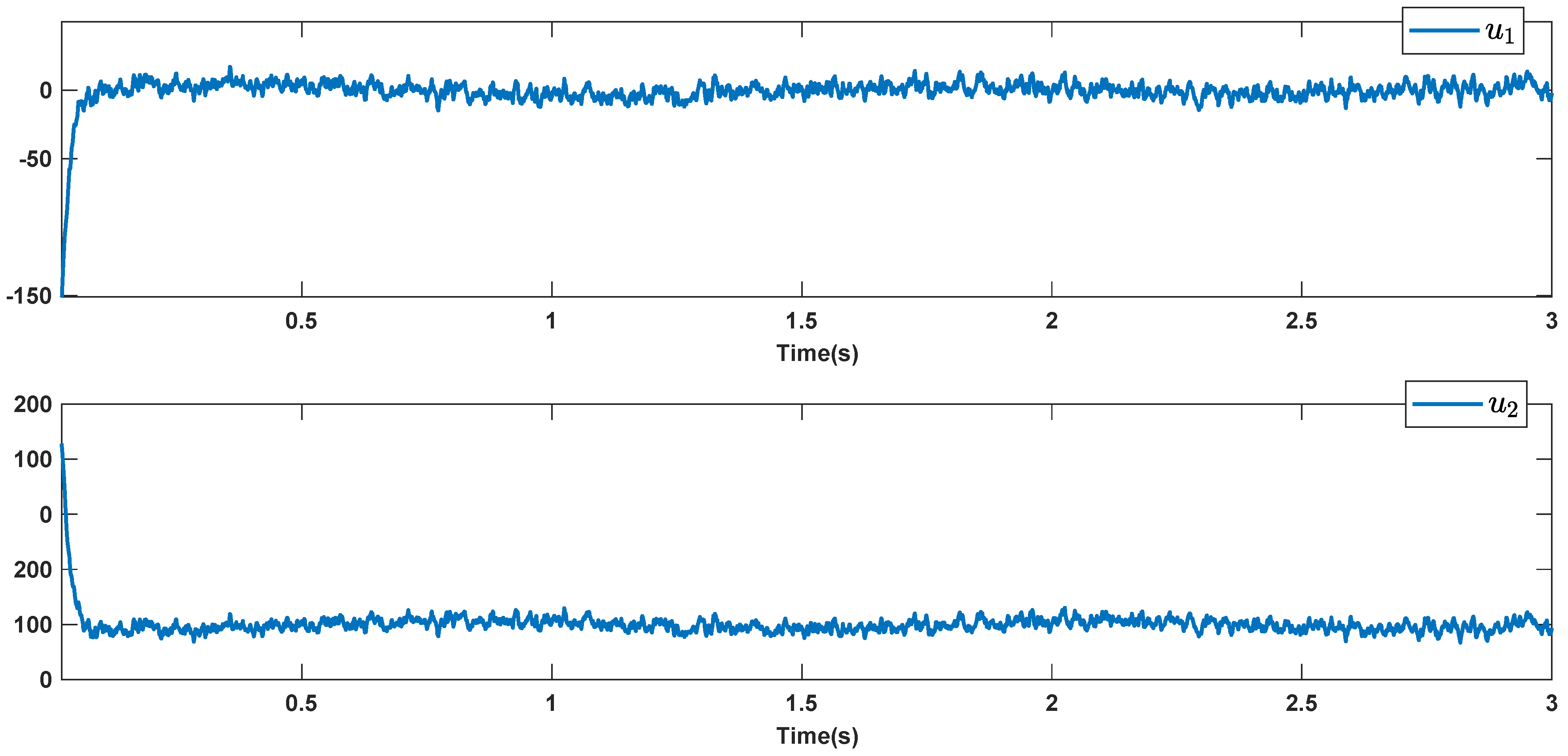
6. Simulations
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fang, Y.; Fu, W.; An, C.; Yuan, Z.; Fei, J. Modelling, simulation and dynamic sliding mode control of a mems gyroscope. Micromachines 2021, 12, 190. [Google Scholar] [CrossRef]
- Fang, Y.; Chen, F.; Fei, J. Multiple Loop Fuzzy Neural Network Fractional Order Sliding Mode Control of Micro Gyroscope. Mathematics 2021, 9, 2124. [Google Scholar] [CrossRef]
- Chang, L.; Cao, H.; Shen, C. Dual-Mass MEMS Gyroscope Parallel Denoising and Temperature Compensation Processing Based on WLMP and CS-SVR. Micromachines 2020, 11, 586. [Google Scholar] [CrossRef]
- Shen, C. Temperature Drift Modeling and Compensation for Gyroscope. In Intelligent Information Processing for Inertial-Based Navigation Systems; Springer: Berlin/Heidelberg, Germany, 2021; pp. 49–67. [Google Scholar]
- Fang, Y.; Fei, J.; Yang, Y. Adaptive backstepping design of a microgyroscope. Micromachines 2018, 9, 338. [Google Scholar] [CrossRef] [Green Version]
- Ma, T.; Cao, H.; Shen, C. A temperature error parallel processing model for MEMS gyroscope based on a novel fusion algorithm. Electronics 2020, 9, 499. [Google Scholar] [CrossRef] [Green Version]
- Rahmani, M. MEMS gyroscope control using a novel compound robust control. Isa Trans. 2018, 72, 37–43. [Google Scholar] [CrossRef]
- Rahmani, M.; Rahman, M.H.; Nosonovsky, M. A new hybrid robust control of MEMS gyroscope. Microsyst. Technol. 2020, 26, 853–860. [Google Scholar] [CrossRef]
- Wang, H.; Hua, L.; Guo, Y.; Lu, C. Control of Z-Axis MEMS Gyroscope Using Adaptive Fractional Order Dynamic Sliding Mode Approach. IEEE Access 2019, 7, 133008–133016. [Google Scholar] [CrossRef]
- Fei, J.; Fang, Y.; Yuan, Z. Adaptive Fuzzy Sliding Mode Control for a Micro Gyroscope with Backstepping Controller. Micromachines 2020, 11, 968. [Google Scholar] [CrossRef] [PubMed]
- Jafari, M.; Mobayen, S.; Roth, H.; Bayat, F. Nonsingular terminal sliding mode control for micro-electro-mechanical gyroscope based on disturbance observer: Linear matrix inequality approach. J. Vib. Control. 2021, 1077546320988192. [Google Scholar] [CrossRef]
- Lu, C.; Fei, J. Adaptive prescribed performance sliding mode control of MEMS gyroscope. Trans. Inst. Meas. Control 2018, 40, 400–412. [Google Scholar] [CrossRef]
- Fei, J.; Yan, W.; Yang, Y. Adaptive nonsingular terminal sliding mode control of MEMS gyroscope based on backstepping design. Int. J. Adapt. Control Signal Process. 2015, 29, 1099–1115. [Google Scholar] [CrossRef]
- Ma, T.; Li, Z.; Cao, H.; Shen, C.; Wang, Z. A parallel denoising model for dual-mass MEMS gyroscope based on PE-ITD and SA-ELM. IEEE Access 2019, 7, 169979–169991. [Google Scholar] [CrossRef]
- Tran, H.K.; Chiou, J.S. PSO-based algorithm applied to quadcopter micro air vehicle controller design. Micromachines 2016, 7, 168. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chao, C.T.; Sutarna, N.; Chiou, J.S.; Wang, C.J. An optimal fuzzy PID controller design based on conventional PID control and nonlinear factors. Appl. Sci. 2019, 9, 1224. [Google Scholar] [CrossRef] [Green Version]
- Mohammadzadeh, A.; Sabzalian, M.H.; Ahmadian, A.; Nabipour, N. A dynamic general type-2 fuzzy system with optimized secondary membership for online frequency regulation. Isa Trans. 2021, 112, 150–160. [Google Scholar] [CrossRef]
- Sabzalian, M.H.; Mohammadzadeh, A.; Zhang, W.; Jermsittiparsert, K. General type-2 fuzzy multi-switching synchronization of fractional-order chaotic systems. Eng. Appl. Artif. Intell. 2021, 100, 104163. [Google Scholar] [CrossRef]
- Mohammadzadeh, A.; Zhang, W. Dynamic programming strategy based on a type-2 fuzzy wavelet neural network. Nonlinear Dyn. 2019, 95, 1661–1672. [Google Scholar] [CrossRef]
- Wang, J.W.; Zhang, Q.Y. Using Parallel Algorithm to Speedup the Rules Learning Process of a Type-2 Fuzzy Logic System. In Proceedings of the 2021 Chinese Intelligent Systems Conference, Fuzhou, China, 16–17 October 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 141–151. [Google Scholar]
- Melin, P.; Sánchez, D. Optimal design of type-2 fuzzy systems for diabetes classification based on genetic algorithms. Int. J. Hybrid Intell. Syst. 2021, 17, 15–32. [Google Scholar] [CrossRef]
- Qin, B.; Fan, Y.; Xiao, T.; Li, Z. Distributed type-2 fuzzy adaptive control for heterogeneous nonlinear multiagent systems. Asian J. Control 2021, 2020, 4081904. [Google Scholar] [CrossRef]
- Mohammadzadeh, A.; Sabzalian, M.H.; Zhang, W. An Interval Type-3 Fuzzy System and a New Online Fractional-Order Learning Algorithm: Theory and Practice. IEEE Trans. Fuzzy Syst. 2020, 28, 1940–1950. [Google Scholar] [CrossRef]
- Qasem, S.N.; Ahmadian, A.; Mohammadzadeh, A.; Rathinasamy, S.; Pahlevanzadeh, B. A type-3 logic fuzzy system: Optimized by a correntropy based Kalman filter with adaptive fuzzy kernel size. Inf. Sci. 2021, 572, 424–443. [Google Scholar] [CrossRef]
- Precup, R.E.; Preitl, S.; Petriu, E.; Bojan-Dragos, C.A.; Szedlak-Stinean, A.I.; Roman, R.C.; Hedrea, E.L. Model-based fuzzy control results for networked control systems. Rep. Mech. Eng. 2020, 1, 10–25. [Google Scholar] [CrossRef]
- Teodora Milošević, T.; Pamučar, D.; Chatterjee, P. Model for selecting a route for the transport of hazardous materials using a fuzzy logic system. Vojnotehnički Glasnik 2021, 69, 355–390. [Google Scholar] [CrossRef]
- Fei, J.; Feng, Z. Fractional-Order Finite-Time Super-Twisting Sliding Mode Control of Micro Gyroscope Based on Double-Loop Fuzzy Neural Network. IEEE Trans. Syst. Man Cybern. Syst. 2020, 1–15. [Google Scholar] [CrossRef]
- Rahmani, M.; Komijani, H.; Ghanbari, A.; Ettefagh, M.M. Optimal novel super-twisting PID sliding mode control of a MEMS gyroscope based on multi-objective bat algorithm. Microsyst. Technol. 2018, 24, 2835–2846. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, R.; Li, S.; He, W.; Shi, Z. Composite Neural Learning-Based Nonsingular Terminal Sliding Mode Control of MEMS Gyroscopes. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 1375–1386. [Google Scholar] [CrossRef]
- Shao, X.; Shi, Y. Neural Adaptive Control for MEMS Gyroscope with Full-State Constraints and Quantized Input. IEEE Trans. Ind. Inform. 2020, 16, 6444–6454. [Google Scholar] [CrossRef]
- Zhang, R.; Xu, B.; Wei, Q.; Yang, T.; Zhao, W.; Zhang, P. Serial-Parallel Estimation Model-Based Sliding Mode Control of MEMS Gyroscopes. IEEE Trans. Syst. Man Cybern. Syst. 2020, 1–12. [Google Scholar] [CrossRef]
- Guo, Y.; Xu, B.; Zhang, R. Terminal Sliding Mode Control of MEMS Gyroscopes With Finite-Time Learning. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4490–4498. [Google Scholar] [CrossRef]
- Zhang, R.; Xu, B.; Shi, P. Output Feedback Control of Micromechanical Gyroscopes Using Neural Networks and Disturbance Observer. IEEE Trans. Neural Netw. Learn. Syst. 2020, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Shao, X.; Shi, Y. Neural-Network-Based Constrained Output-Feedback Control for MEMS Gyroscopes Considering Scarce Transmission Bandwidth. IEEE Trans. Cybern. 2021, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Vafaie, R.H.; Mohammadzadeh, A.; Piran, M.J. A new type-3 fuzzy predictive controller for MEMS gyroscopes. Nonlinear Dyn. 2021, 106, 381–403. [Google Scholar] [CrossRef]
- Mohammadzadeh, A.; Vafaie, R.H. A deep learned fuzzy control for inertial sensing: Micro electro mechanical systems. Appl. Soft Comput. 2021, 109, 107597. [Google Scholar] [CrossRef]
- Van Waarde, H.J.; De Persis, C.; Camlibel, M.K.; Tesi, P. Willems’ Fundamental Lemma for State-Space Systems and Its Extension to Multiple Datasets. IEEE Control. Syst. Lett. 2020, 4, 602–607. [Google Scholar] [CrossRef] [Green Version]
- De Persis, C.; Tesi, P. Formulas for Data-Driven Control: Stabilization, Optimality, and Robustness. IEEE Trans. Autom. Control 2020, 65, 909–924. [Google Scholar] [CrossRef] [Green Version]
- Van Waarde, H.J.; Eising, J.; Trentelman, H.L.; Camlibel, M.K. Data Informativity: A New Perspective on Data-Driven Analysis and Control. IEEE Trans. Autom. Control 2020, 65, 4753–4768. [Google Scholar] [CrossRef] [Green Version]
- Berberich, J.; Köhler, J.; Müller, M.A.; Allgöwer, F. Data-Driven Model Predictive Control With Stability and Robustness Guarantees. IEEE Trans. Autom. Control 2021, 66, 1702–1717. [Google Scholar] [CrossRef]
- Guo, M.; De Persis, C.; Tesi, P. Data-driven stabilization of nonlinear polynomial systems with noisy data. IEEE Trans. Autom. Control. 2021. [Google Scholar] [CrossRef]
- van Waarde, H.J.; Camlibel, M.K.; Mesbahi, M. From noisy data to feedback controllers: Non-conservative design via a matrix S-lemma. IEEE Trans. Autom. Control. 2020, 1. [Google Scholar] [CrossRef]
- De Persis, C.; Tesi, P. Low-complexity learning of Linear Quadratic Regulators from noisy data. Automatica 2021, 128, 109548. [Google Scholar] [CrossRef]
- Liu, H.; Li, X.J.; Deng, C.; Ahn, C.K. Fault Estimation and Control for Unknown Discrete-Time Systems Based on Data-Driven Parameterization Approach. IEEE Trans. Cybern. 2021, 1–12. [Google Scholar] [CrossRef]
- Bisoffi, A.; De Persis, C.; Tesi, P. Data-based stabilization of unknown bilinear systems with guaranteed basin of attraction. Syst. Control. Lett. 2020, 145, 104788. [Google Scholar] [CrossRef]
- Chu, Y.; Fei, J.; Hou, S. Adaptive neural backstepping PID global sliding mode fuzzy control of MEMS gyroscope. IEEE Access 2019, 7, 37918–37926. [Google Scholar] [CrossRef]
- Fei, J.; Yan, W. Adaptive control of MEMS gyroscope using global fast terminal sliding mode control and fuzzy-neural-network. Nonlinear Dyn. 2014, 78, 103–116. [Google Scholar] [CrossRef]
- Fei, J.; Chen, F. Dynamic Fractional Order Sliding Mode Control Method of Micro Gyroscope Using Double Feedback Fuzzy Neural Network. IEEE Access 2020, 8, 125097–125108. [Google Scholar] [CrossRef]



| Parameters | Values | Equations |
|---|---|---|
| 0.5 0.8 1 | (12) and (13) | |
| 0 0.3 0.7 | (14) and (15) | |
| −1 | (12)–(15) | |
| 1 | (12)–(15) | |
| −1 | (12)–(15) | |
| 1 | (12)–(15) | |
| 100 | (27) | |
| 20 | (27) |
| Controller | ||
|---|---|---|
| BSMC | 7.4207 | 11.1113 |
| FSMC | 5.3741 | 10.3440 |
| FNC | 6.1931 | 7.0221 |
| Proposed Controller | 3.4442 | 3.4373 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alattas, K.A.; Mohammadzadeh, A.; Mobayen, S.; Aly, A.A.; Felemban, B.F.; Vu, M.T. A New Data-Driven Control System for MEMSs Gyroscopes: Dynamics Estimation by Type-3 Fuzzy Systems. Micromachines 2021, 12, 1390. https://doi.org/10.3390/mi12111390
Alattas KA, Mohammadzadeh A, Mobayen S, Aly AA, Felemban BF, Vu MT. A New Data-Driven Control System for MEMSs Gyroscopes: Dynamics Estimation by Type-3 Fuzzy Systems. Micromachines. 2021; 12(11):1390. https://doi.org/10.3390/mi12111390
Chicago/Turabian StyleAlattas, Khalid A., Ardashir Mohammadzadeh, Saleh Mobayen, Ayman A. Aly, Bassem F. Felemban, and Mai The Vu. 2021. "A New Data-Driven Control System for MEMSs Gyroscopes: Dynamics Estimation by Type-3 Fuzzy Systems" Micromachines 12, no. 11: 1390. https://doi.org/10.3390/mi12111390
APA StyleAlattas, K. A., Mohammadzadeh, A., Mobayen, S., Aly, A. A., Felemban, B. F., & Vu, M. T. (2021). A New Data-Driven Control System for MEMSs Gyroscopes: Dynamics Estimation by Type-3 Fuzzy Systems. Micromachines, 12(11), 1390. https://doi.org/10.3390/mi12111390










