Theoretical Study of Field-Free Switching in PMA-MTJ Using Combined Injection of STT and SOT Currents
Abstract
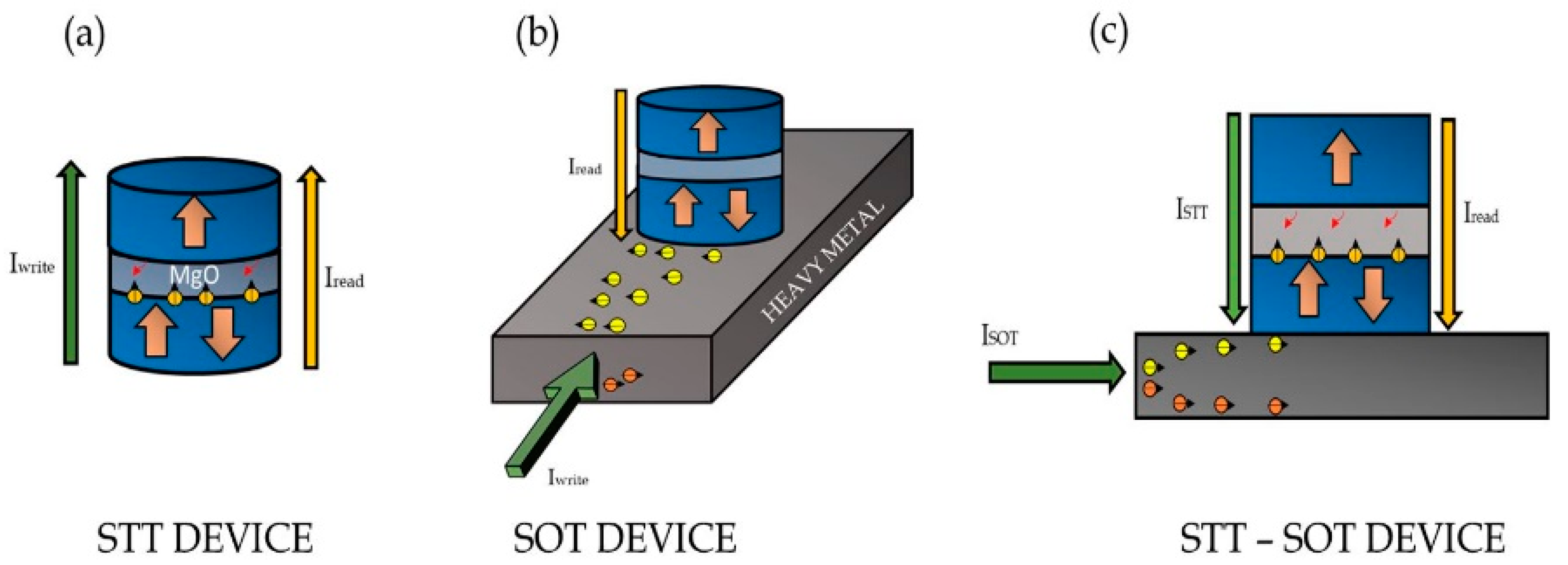
1. Introduction
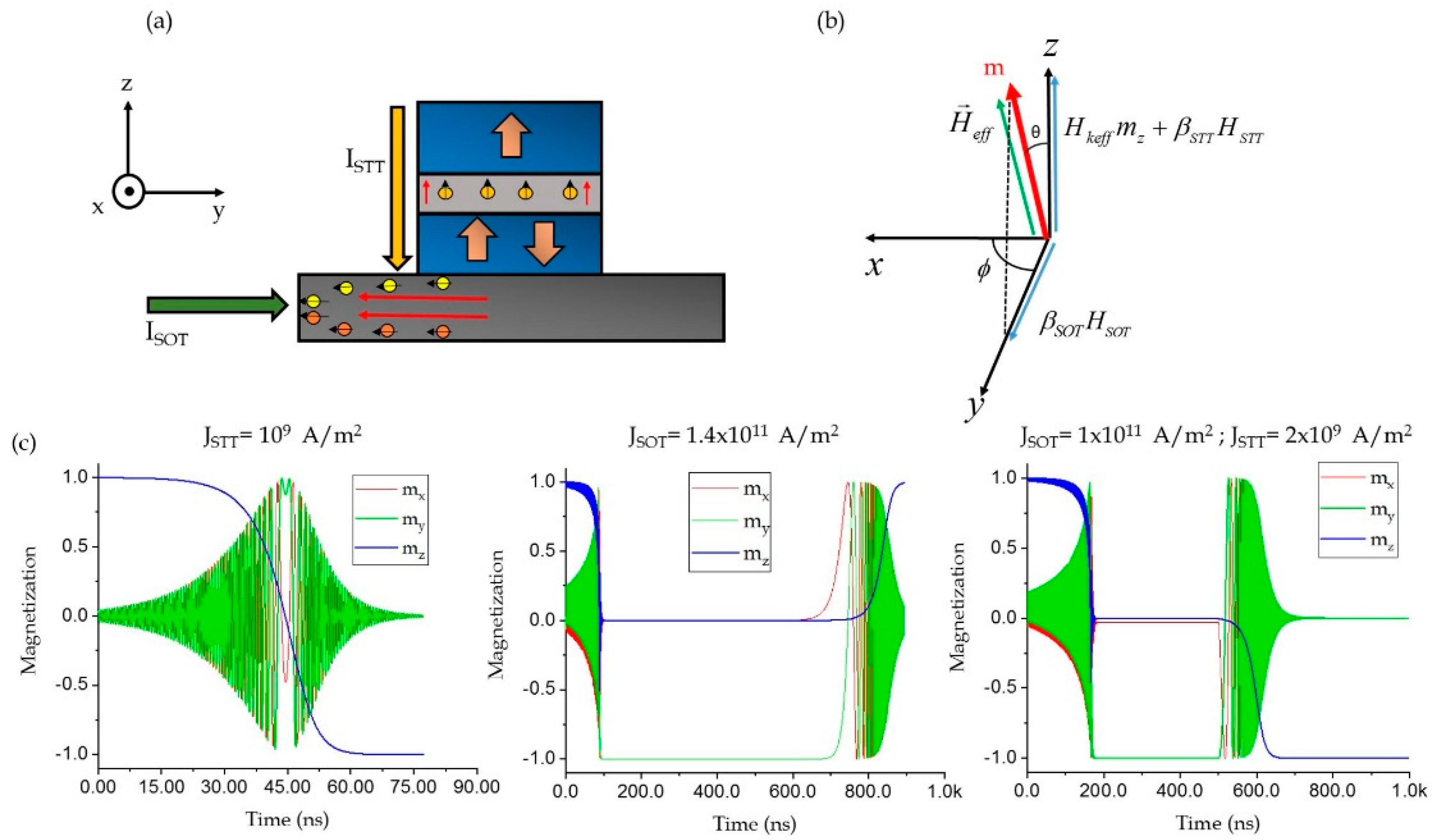
2. Landau–Lifshitz–Gilbert Equation with Spin-Transfer Torque (STT) and Spin-Orbit Torque (SOT) Terms
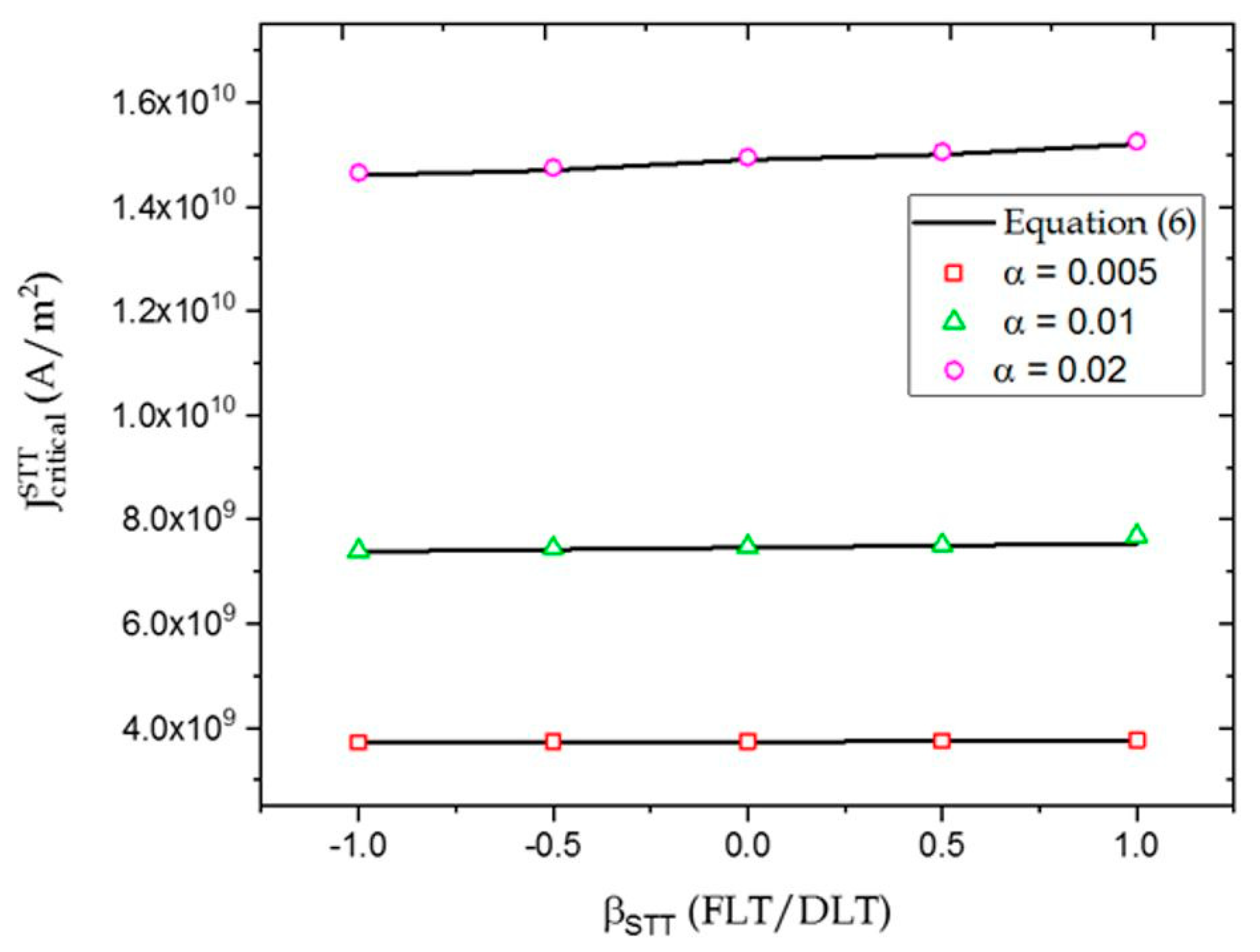
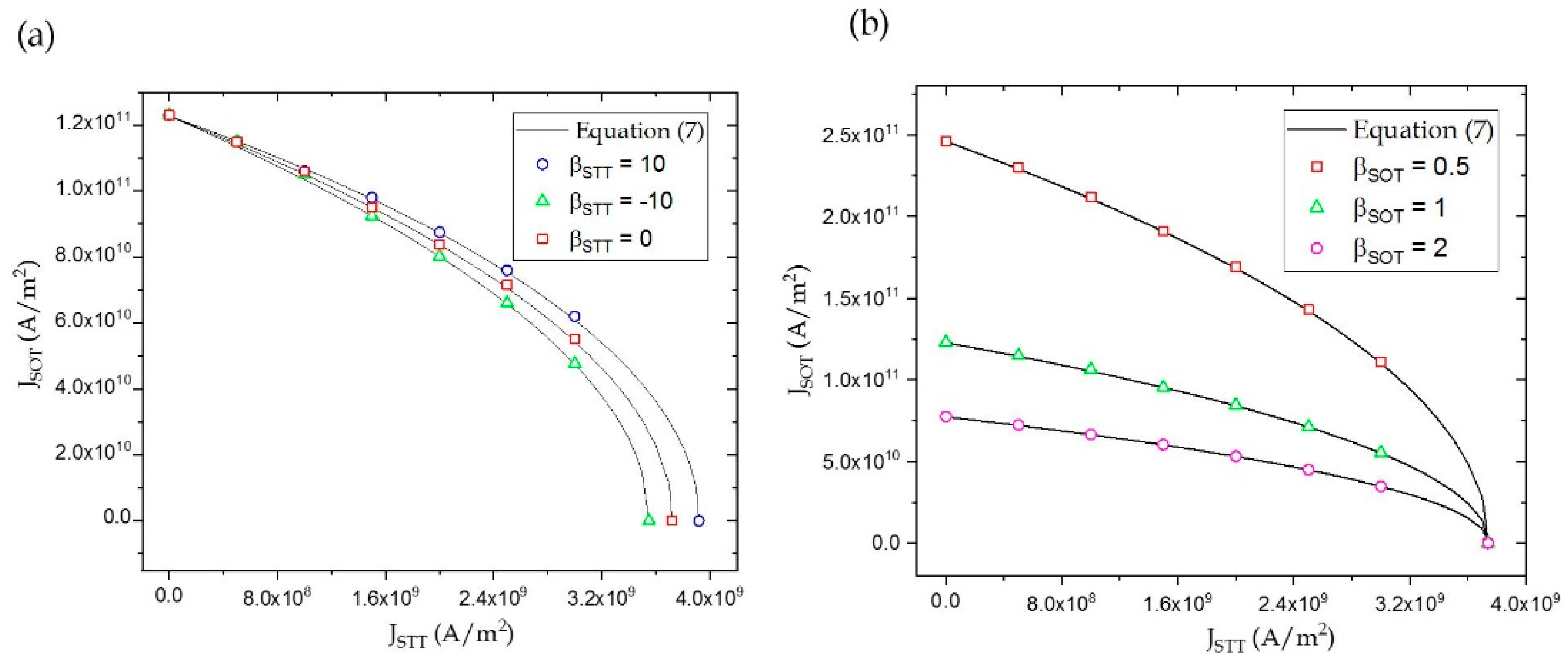
3. Results
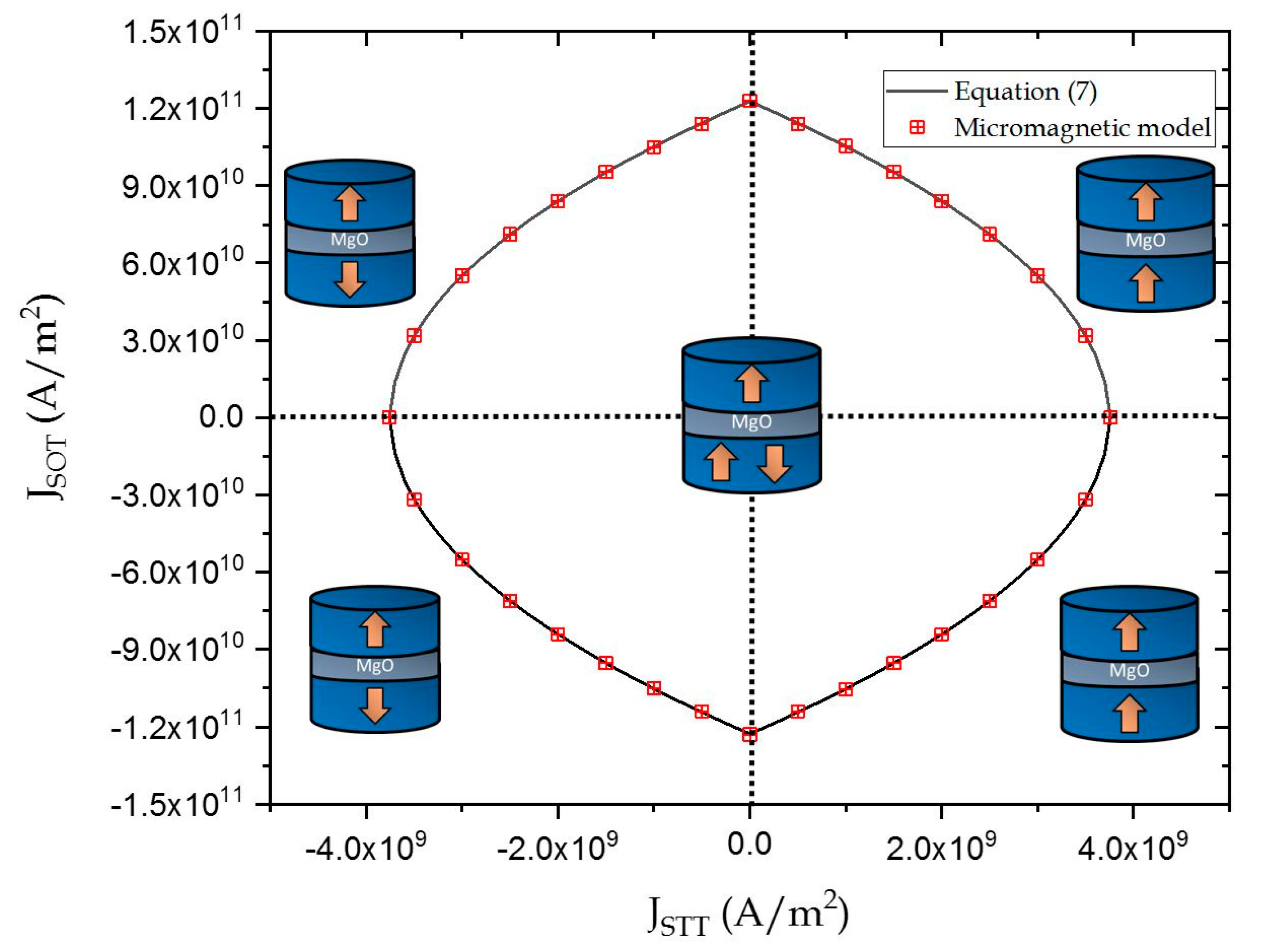
COMBINED STT-SOT Induced Switching in PMA-MTJ
4. Conclusions
5. Methods
Micromagnetic Model
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Hu, G.; Lee, J.H.; Nowak, J.J.; Sun, J.Z.; Harms, J.; Annunziata, A.; Brown, S.; Chen, W.; Kim, Y.H.; Lauer, G.; et al. STT-MRAM with double magnetic tunnel junctions. In Proceedings of the IEEE 2015 Internaional Electron Devices Meeting (IEDM), Washington, DC, USA, 7–9 December 2015. [Google Scholar]
- Ikeda, S.; Sato, H.; Honjo, H.; Enobio, E.C.I.; Ishikawa, S.; Yamanouchi, M.; Fukami, S.; Kanai, S.; Matsukura, F.; Endoh, T.; et al. Perpendicular-anisotropy CoFeB-MgO based magnetic tunnel junctions scaling down to 1X nm. In Proceedings of the 2014 IEEE International Electron Devices Meeting, San Francisco, CA, USA, 15–17 December 2014. [Google Scholar]
- Slonczewski, J.C. Current-driven excitation of magnetic multilayers. J. Magn. Magn. Mater. 1996, 159, L1–L7. [Google Scholar] [CrossRef]
- Liu, L.; Pai, C.-F.; Li, Y.; Tseng, H.W.; Ralph, D.C.; Buhrman, R.A. Spin-torque switching with the giant spin Hall effect of tantalum. Science 2012, 336, 555–558. [Google Scholar] [CrossRef]
- Miron, I.M.; Gaudin, G.; Auffret, S.; Rodmacq, B.; Schuhl, A.; Pizzini, S.; Vogel, J.; Gambardella, P. Current-driven spin torque induced by the Rashba effect in a ferromagnetic metal layer. Nat. Mater. 2010, 9, 230–234. [Google Scholar] [CrossRef]
- Miron, I.M.; Garello, K.; Gaudin, G.; Zermatten, P.-J.; Costache, M.V.; Auffret, S.; Bandiera, S.; Rodmacq, B.; Schuhl, A.; Gambardella, P. Perpendicular switching of a single ferromagnetic layer induced by in-plane current injection. Nature 2011, 476, 189–193. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Levy, P.M.; Fert, A. Mechanisms of Spin-Polarized Current-Driven Magnetization Switching. Phys. Rev. Lett. 2002, 88, 236601. [Google Scholar] [CrossRef] [PubMed]
- Heinonen, O.G.; Stokes, S.W.; Yi, J.Y. Perpendicular spin torque in magnetic tunnel junctions. Phys. Rev. Lett. 2010, 105, 066602. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Sinha, J.; Hayashi, M.; Yamanouchi, M.; Fukami, S.; Suzuki, T.; Mitani, S.; Ohno, H. Layer thickness dependence of the current-induced effective field vector in Ta/CoFeB/MgO. Nat. Mater. 2012, 12, 240–245. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Yamanouchi, M.; Sato, H.; Fukami, S.; Ikeda, S.; Matsukura, F.; Ohno, H. Magnetotransport measurements of current induced effective fields in Ta/CoFeB/MgO. Appl. Phys. Lett. 2013, 103, 262407. [Google Scholar] [CrossRef]
- Zhou, Y. Effect of the field-like spin torque on the switching current and switching speed of magnetic tunnel junction with perpendicularly magnetized free layers. J. Appl. Phys. 2011, 109, 023916. [Google Scholar] [CrossRef]
- Taniguchi, T.; Mitani, S.; Hayashi, M. Critical current destabilizing perpendicular magnetization by the spin Hall effect. Phys. Rev. B 2015, 92, 024428. [Google Scholar] [CrossRef]
- Chun, K.C.; Zhao, H.; Harms, J.D.; Kim, T.H.; Wang, J.-P.; Kim, C.H. A scaling roadmap and performance evaluation of in-plane and perpendicular MTJ based STT-MRAMs for high-density cache memory. IEEE J. Solid-State Circuits 2013, 48, 598–610. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, Y.; Devolder, T.; Klein, J.-O.; Ravelosona, D.; Chappert, C.; Mazoyer, P. Failure and reliability analysis of STT-MRAM. Microelectron. Reliab. 2012, 52, 1848–1852. [Google Scholar] [CrossRef]
- Garello, K.; Avci, C.O.; Miron, I.M.; Baumgartner, M.; Ghosh, A.; Auffret, S.; Boulle, O.; Gaudin, G.; Gambardella, P. Ultrafast magnetization switching by spin-orbit torques. Appl. Phys. Lett. 2014, 105, 212402. [Google Scholar] [CrossRef]
- Garello, K.; Avci, C.O.; Miron, I.M.; Baumgartner, M.; Ghosh, A.; Auffret, S.; Boulle, O.; Gaudin, G.; Gambardella, P. Spin–orbit torque magnetization switching of a three-terminal perpendicular magnetic tunnel junction. Appl. Phys. Lett. 2014, 104, 042406. [Google Scholar]
- Wang, M.; Cai, W.; Zhu, D.; Wang, Z.; Kan, J.; Zhao, Z.; Cao, K.; Wang, Z.; Zhang, Y.; Zhang, T.; et al. Field-free switching of a perpendicular magnetic tunnel junction through the interplay of spin–orbit and spin-transfer torques. Nat. Electron. 2018, 1, 582–588. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, W.; Deng, E.; Zhang, Y.; Klein, J.O. Magnetic non-volatile flip-flop with spin-Hall assistance. Phys. Status Solidi-Rapid Res. Lett. 2015, 9, 375–378. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, W.; Deng, E.; Klein, J.; Chappert, C. Perpendicular anisotropy magnetic tunnel junction switched by spin-Hall-assisted spin-transfer torque. J. Phys. D 2015, 48, 065001. [Google Scholar] [CrossRef]
- Brink, A.A.V.D.; Cosemans, S.; Cornelissen, S.; Manfrini, M.; Vaysset, A.; Van Roy, W.; Min, T.; Swagten, H.J.M.; Koopmans, B.B. Spin-Hall-assisted magnetic random access memory. Appl. Phys. Lett. 2014, 104, 012403. [Google Scholar] [CrossRef]
- Donahue, M.J.; Porter, D.G. (Eds.) OOMMF User’s Guide, Version 1.0; Interagency Report NISTIR 6376; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1999. [Google Scholar]
- You, C.-Y. Micromagnetic Simulations for Spin Transfer Torque in Magnetic Multilayers. J. Magn. 2012, 17, 73–77. [Google Scholar] [CrossRef][Green Version]
- Liu, L.; Lee, O.J.; Gudmundsen, T.J.; Ralph, D.C.; Buhrman, R.A. Current-Induced switching of perpendicularly magnetized magnetic layers using spin torque from the spin Hall effect. Phys. Rev. Lett. 2012, 109, 096602. [Google Scholar] [CrossRef]
- Siracusano, G.; Tomasello, R.; d’Aquino, M.; Puliafito, V.; Giordano, A.; Azzerboni, B.; Braganca, P.; Finocchio, G.; Carpentieri, M. Description of statistical switching in perpendicular STT-MRAM within an analytical and numerical micromagnetic framework. IEEE Trans. Magn. 2018, 54, 1400210. [Google Scholar] [CrossRef]
- Zwierzycki, M.; Tserkovnyak, Y.; Kelly, P.J.; Brataas, A.; Bauer, G.E.W. First-principles study of magnetization relaxation enhancement and spin transfer in thin magnetic films. Phys. Rev. B 2005, 71, 064420. [Google Scholar] [CrossRef]
- Theodonis; Kioussis, N.; Kalitsov, A.; Chshiev, M.; Butler, W.H. Anomalous bias dependence of spin torque in magnetic tunnel junctions. Phys. Rev. Lett. 2006, 97, 237205. [Google Scholar] [CrossRef] [PubMed]
- Xiao, J.; Bauer, G.E.W. Spin-transfer torque in magnetic tunnel junctions: Scattering theory. Phys. Rev. B 2008, 77, 224419. [Google Scholar] [CrossRef]
- Tulapurkar, A.A.; Suzuki, Y.; Fukushima, A.; Kubota, H.; Maehara, H.; Tsunekawa, K.; Djayaprawira, D.D.; Watanabe, N.; Yuasa, S. Spin-torque diode effect in magnetic tunnel junctions. Nature 2005, 438, 339. [Google Scholar] [CrossRef]
- Kubota, H.; Fukushima, A.; Yakushiji, K.; Nagahama, T.; Yuasa, S.; Ando, K.; Maehara, H.; Nagamine, Y.; Tsunekawa, K.; Djayaprawira, D.D.; et al. Quantitative measurement of voltage dependence of spin-transfer torque in MgO-based magnetic tunnel junctions. Nat. Phys. 2008, 4, 37. [Google Scholar] [CrossRef]
- Sankey, J.C.; Cui, Y.-T.; Sun, J.Z.; Slonczewski, J.C.; Buhrman, R.A.; Ralph, D.C. Measurement of the spin-transfer-torque vector in magnetic tunnel junctions. Nat. Phys. 2008, 4, 67. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wasef, S.; Fariborzi, H. Theoretical Study of Field-Free Switching in PMA-MTJ Using Combined Injection of STT and SOT Currents. Micromachines 2021, 12, 1345. https://doi.org/10.3390/mi12111345
Wasef S, Fariborzi H. Theoretical Study of Field-Free Switching in PMA-MTJ Using Combined Injection of STT and SOT Currents. Micromachines. 2021; 12(11):1345. https://doi.org/10.3390/mi12111345
Chicago/Turabian StyleWasef, Shaik, and Hossein Fariborzi. 2021. "Theoretical Study of Field-Free Switching in PMA-MTJ Using Combined Injection of STT and SOT Currents" Micromachines 12, no. 11: 1345. https://doi.org/10.3390/mi12111345
APA StyleWasef, S., & Fariborzi, H. (2021). Theoretical Study of Field-Free Switching in PMA-MTJ Using Combined Injection of STT and SOT Currents. Micromachines, 12(11), 1345. https://doi.org/10.3390/mi12111345






