A Hardware Pseudo-Random Number Generator Using Stochastic Computing and Logistic Map
Abstract
1. Introduction
2. Background
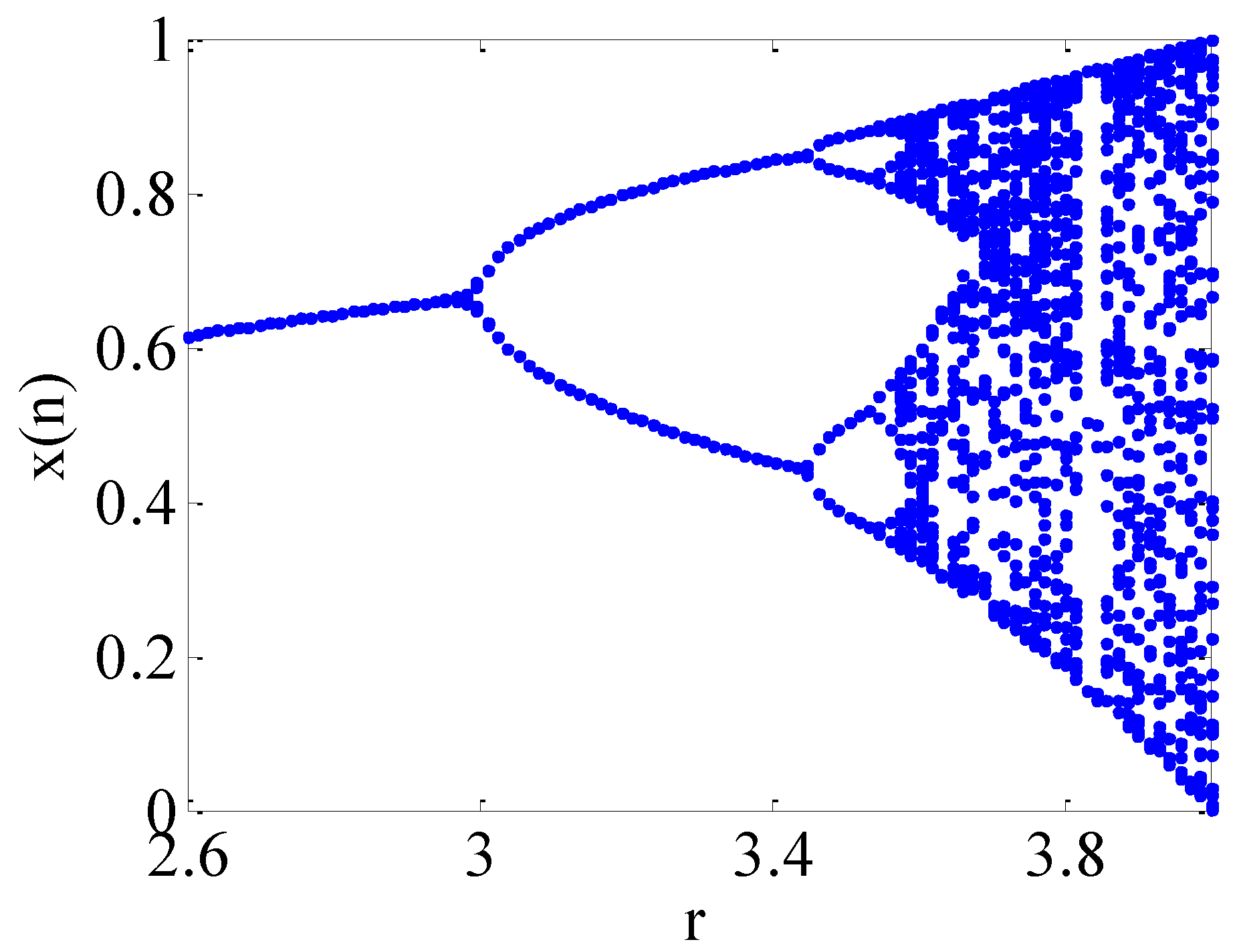
2.1. Logistic Map
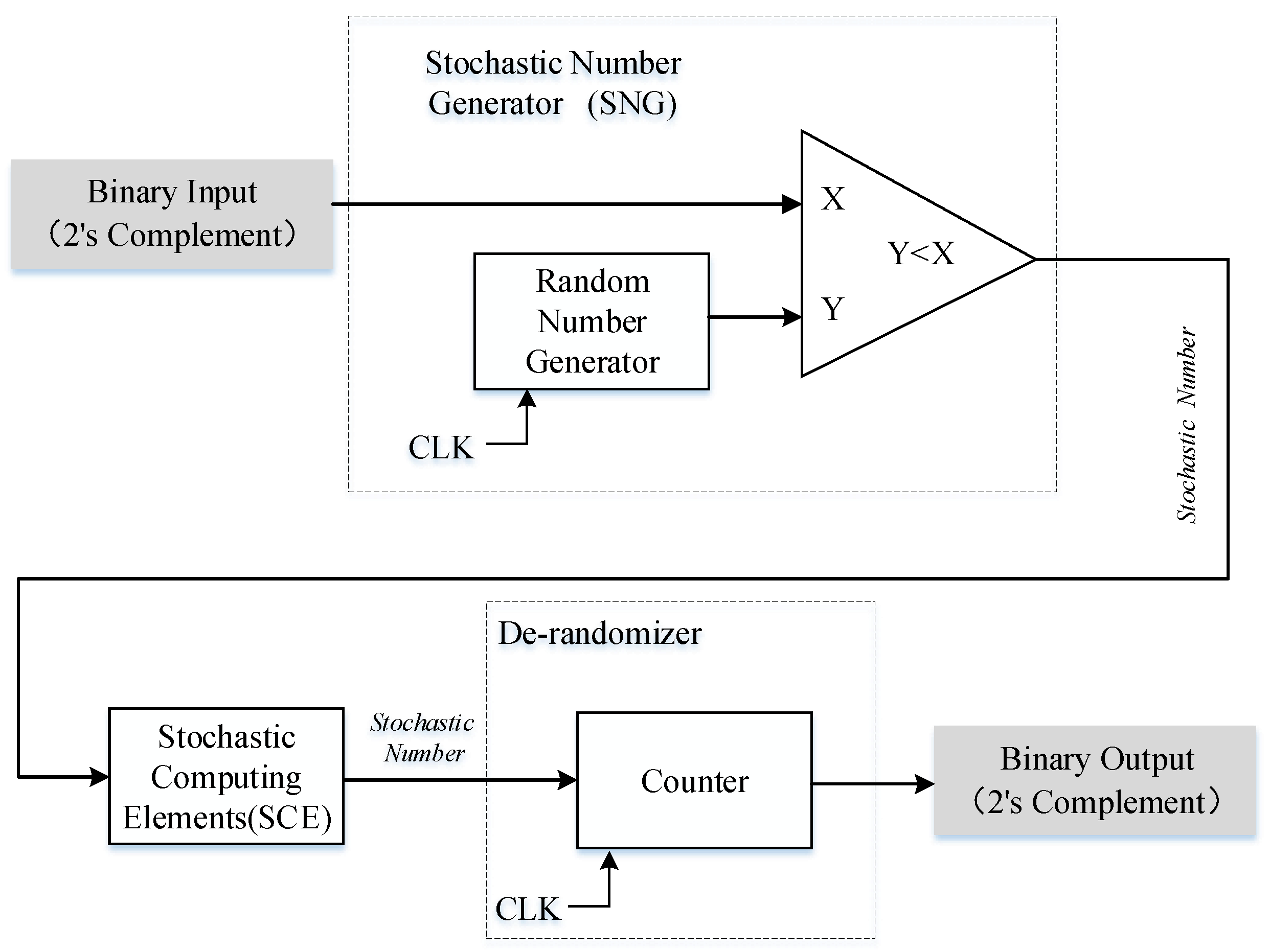
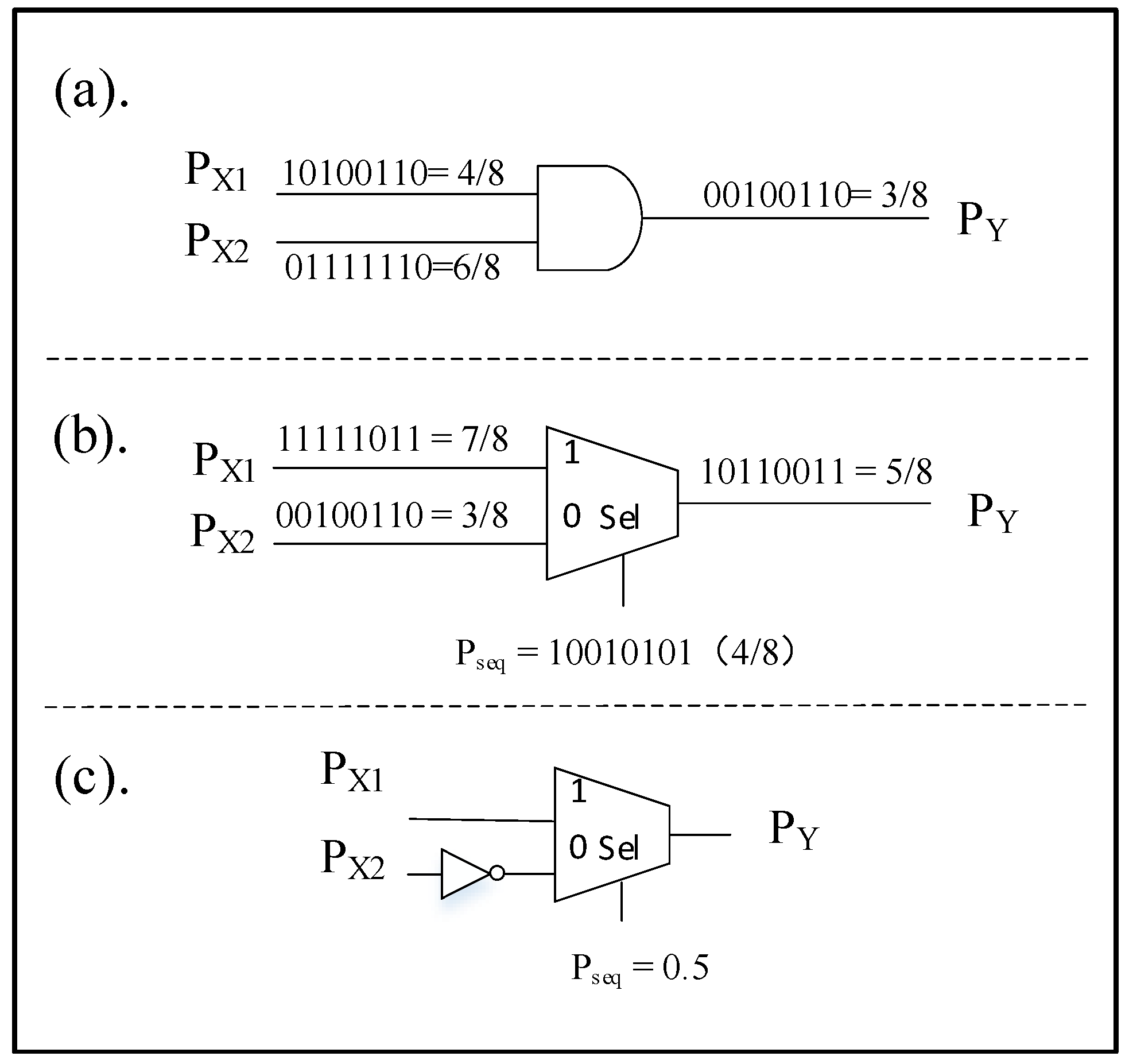
2.2. Stochastic Computing
3. Enhanced Digital Logistic Map and Hardware Implementation
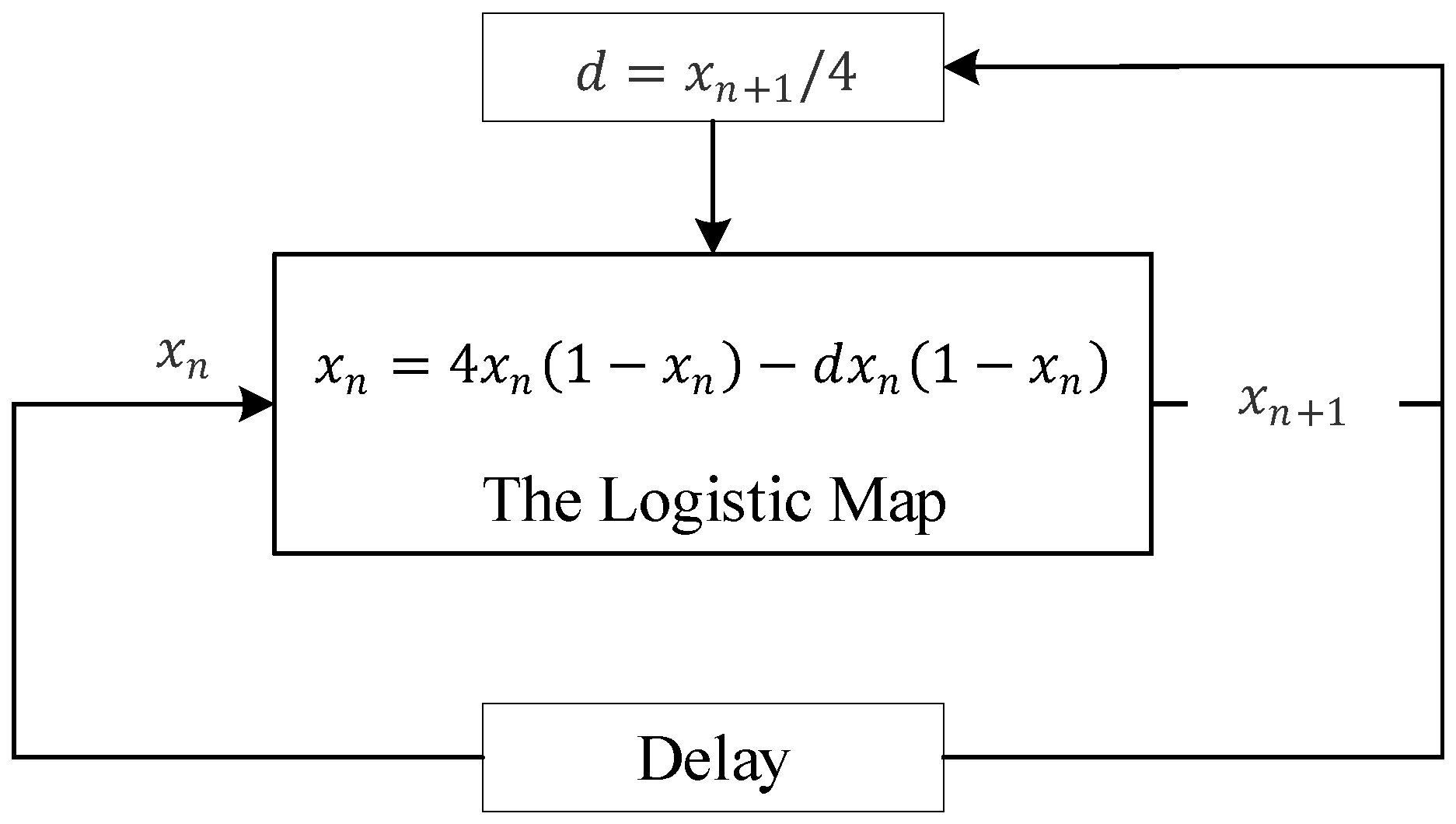
3.1. Enhanced Digital Logistic Map
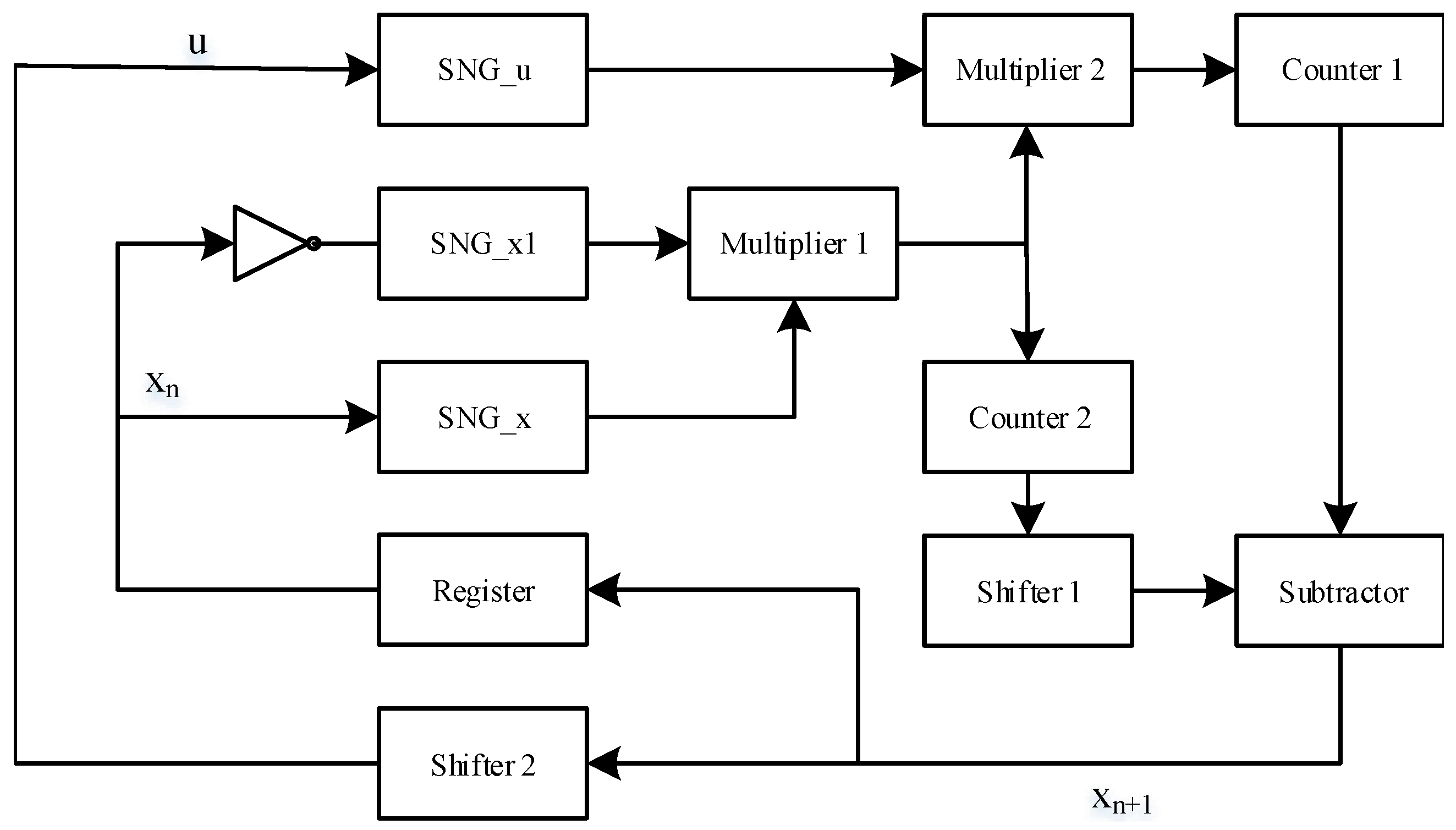
3.2. Hardware Implementation of PRNG
4. Performance Analysis
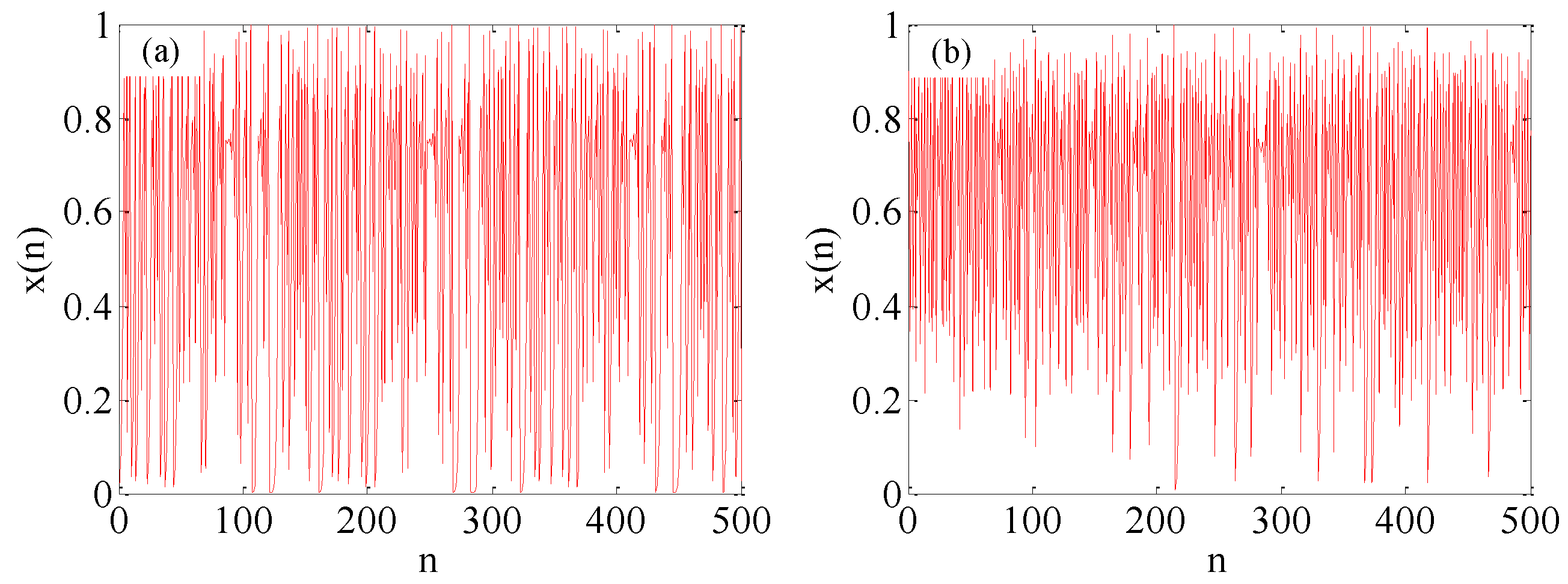
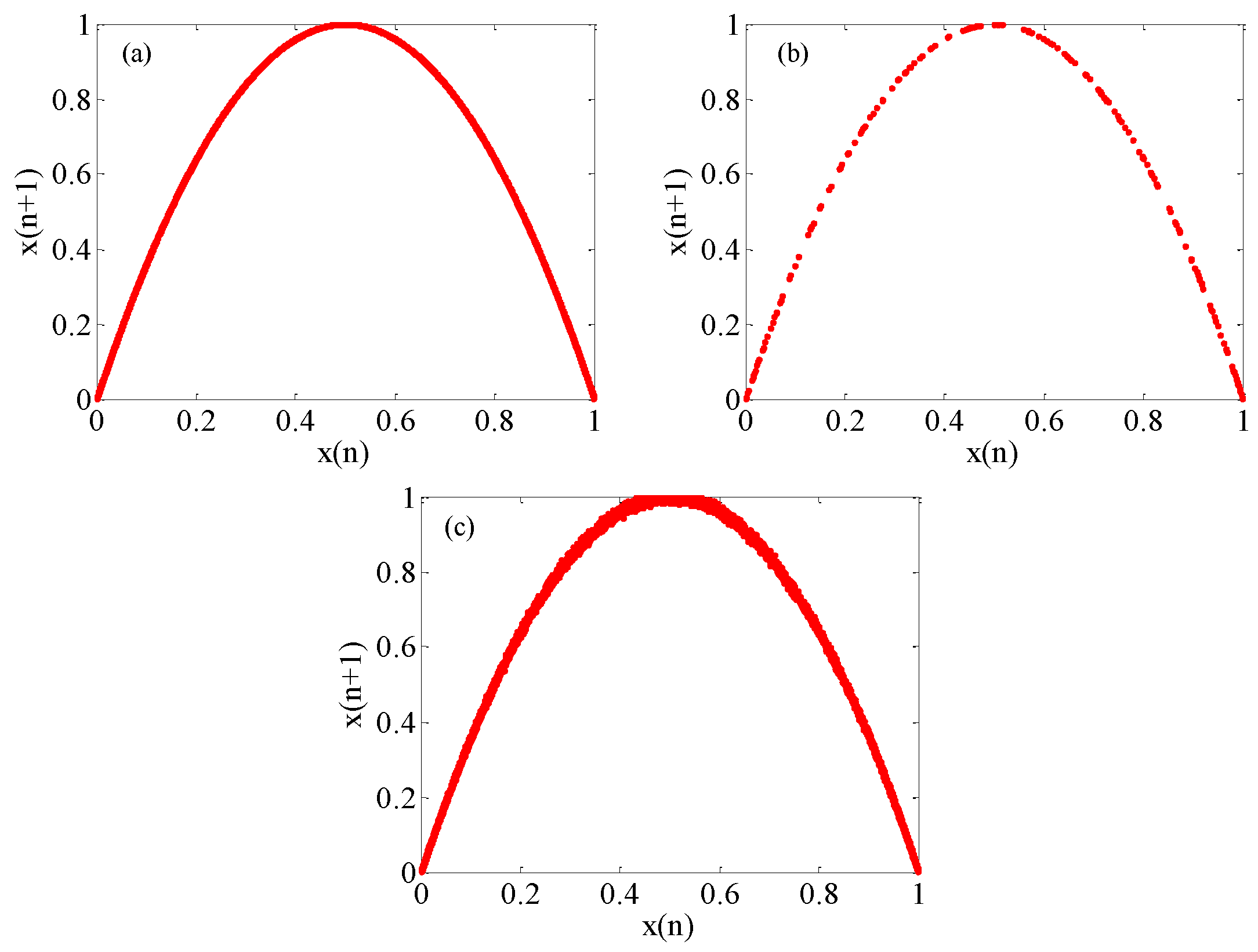
4.1. Performance Improvement of Digital Chaotic System
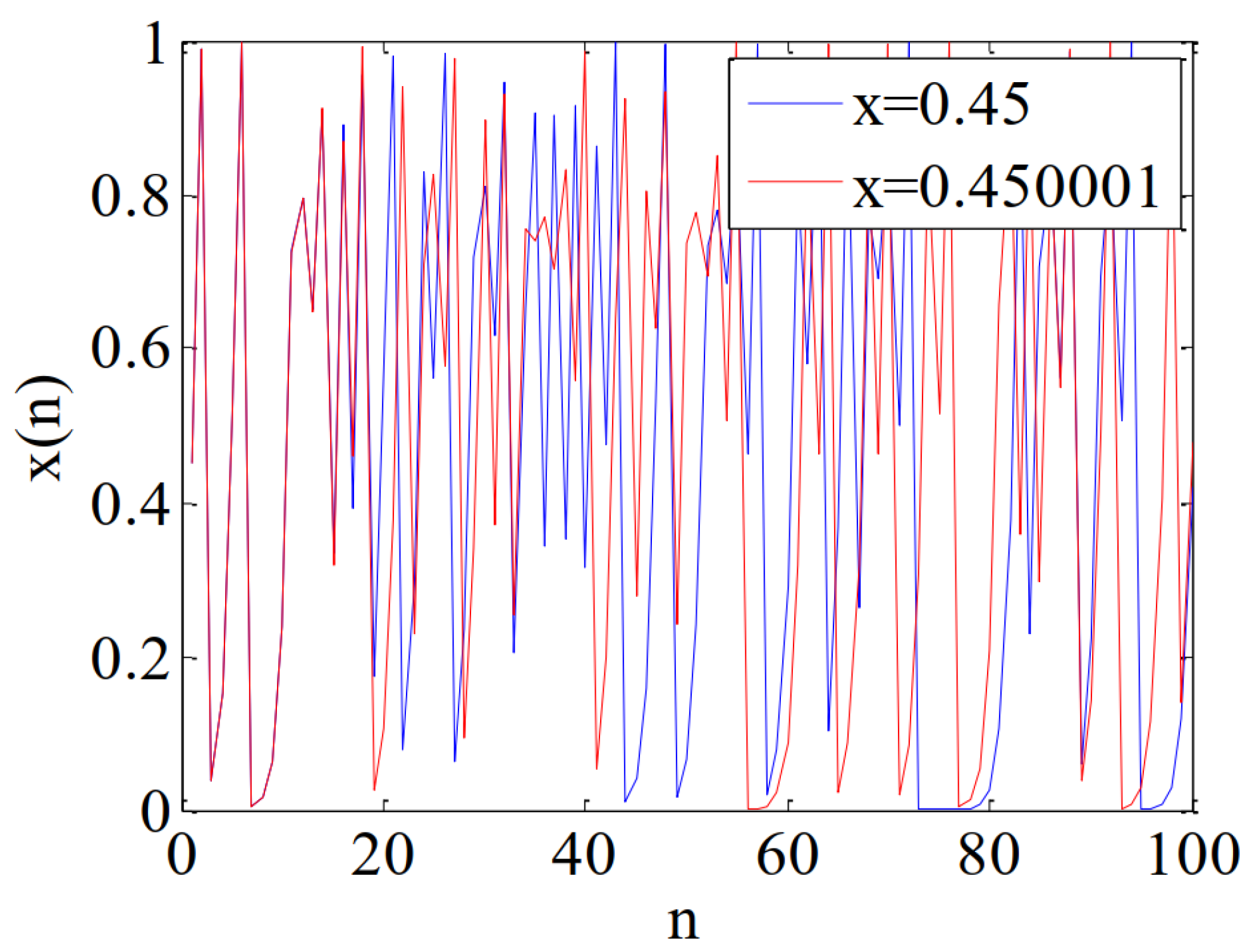
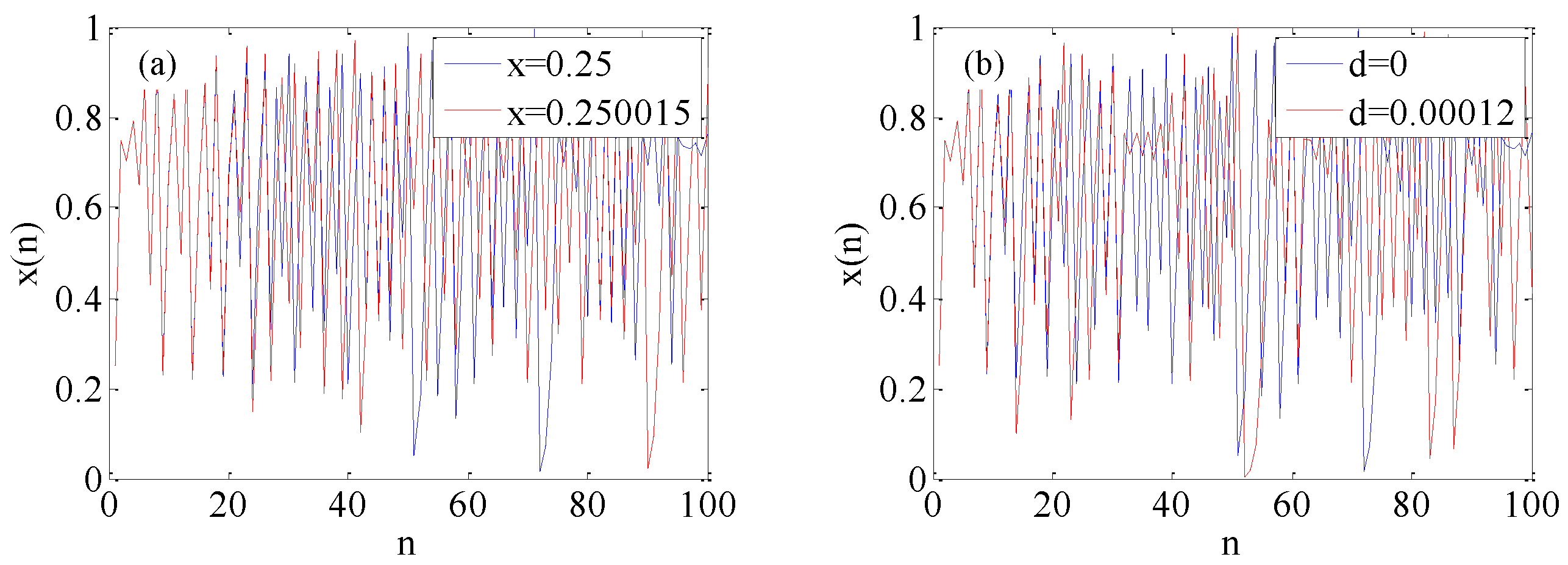
4.2. Initial Value Sensitivity
4.3. Chaotic Attractor
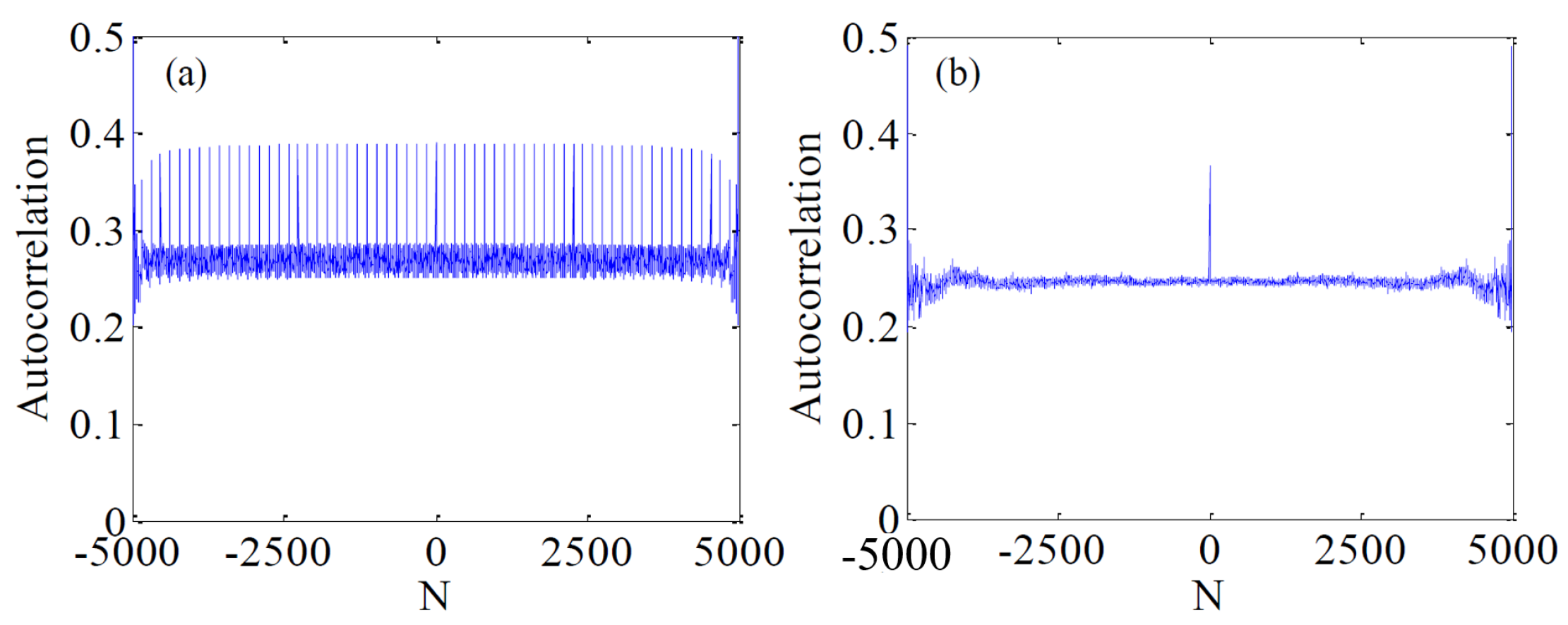
4.4. Autocorrelation
4.5. Approximate Entropy
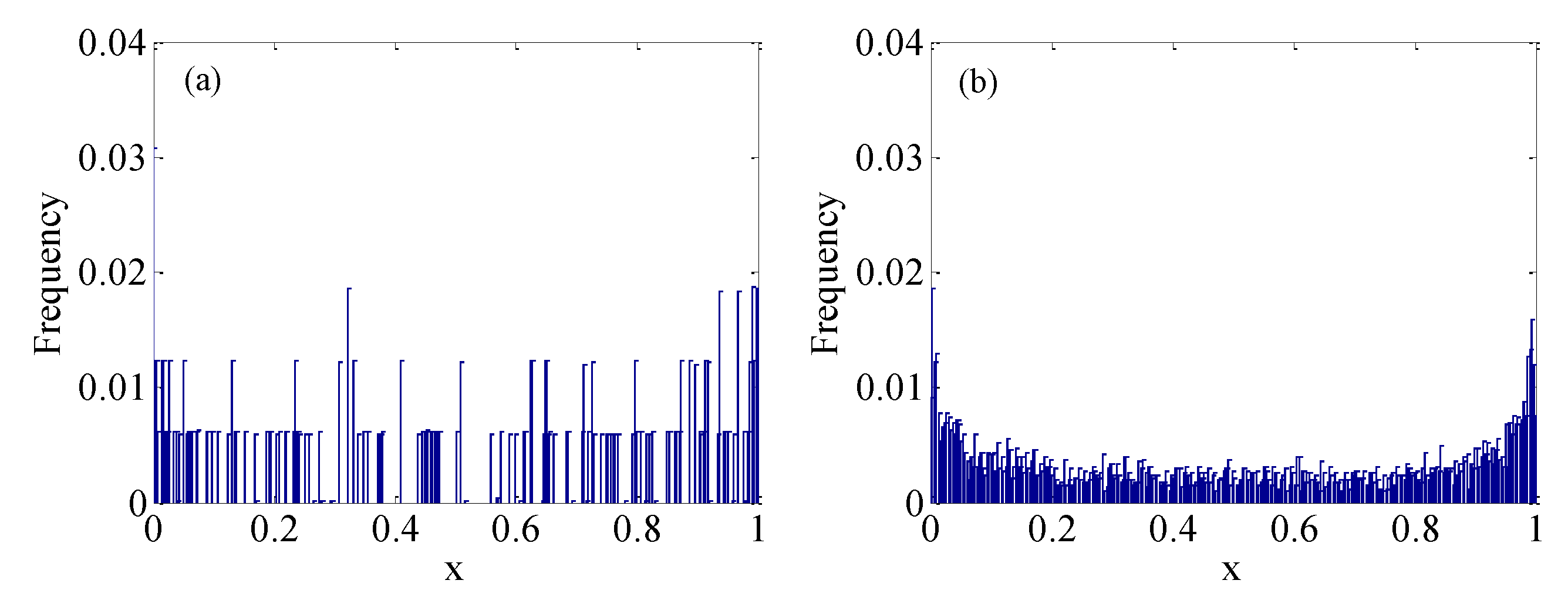
4.6. Histogram of Frequency Distribution
4.7. NIST SP 800-22 Analyses
4.8. TestU01 Test
4.9. Area Overhead
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, L.; Miao, S.; Hu, H.; Deng, Y. Pseudorandom bit generator based on non-stationary logistic maps. IET Inf. Secur. 2016, 10, 87–94. [Google Scholar] [CrossRef]
- Oishi, S.; Inoue, H. Pseudo-random number generators and chaos. Trans. Inst. Electron. Commun. Eng. Jpn. 1982, 65, 534–541. [Google Scholar]
- Andrecut, M. Logistic map as a random number generator. Int. J. Mod. Phys. B 1998, 12, 921–930. [Google Scholar] [CrossRef]
- Shujun, L.; Xuanqin, M.; Yuanlong, C. Pseudo-random bit generator based on couple chaotic systems and its applications in stream-cipher cryptography. In Progress in Cryptology—INDOCRYPT 2001, Proceedings of the International Conference on Cryptology in India, Calcutta, India, 10–13 December 2001; Springer: Berlin, Germany, 2001; pp. 316–329. [Google Scholar]
- Meng, F.S.; Yang, C.Z.; An, Z.Y. Chaos-Based Random Number Generators. J. Comput. Res. Dev. 2004, 4, 1–23. [Google Scholar]
- Li, P.; Li, Z.; Halang, W.A.; Chen, G. A novel multiple pseudo random bits generator based on spatiotemporal chaos. IFAC Proc. Vol. 2005, 38, 1085–1089. [Google Scholar] [CrossRef]
- Pellicer-Lostao, C.; López-Ruiz, R. Pseudo-random bit generation based on 2D chaotic maps of logistic type and its applications in chaotic cryptography. In Proceedings of the International Conference on Computational Science and Its Applications, Perugia, Italy, 30 June–3 July 2008; pp. 784–796. [Google Scholar]
- Patidar, V.; Sud, K.K.; Pareek, N.K. A pseudo random bit generator based on chaotic logistic map and its statistical testing. Informatica 2009, 33, 441–452. [Google Scholar]
- Cristina, D.A.; Radu, B.; Ciprian, R. A new pseudorandom bit generator using compounded chaotic tent maps. In Proceedings of the International Conference on Communications (COMM), Bucharest, Romania, 21–23 June 2012; pp. 339–342. [Google Scholar]
- Wang, X.Y.; Yang, L. Design of pseudo-random bit generator based on chaotic maps. Int. J. Mod. Phys. B 2012, 26, 1250208–1250217. [Google Scholar] [CrossRef]
- Hu, H.; Liu, L.; Ding, N. Pseudorandom sequence generator based on the Chen chaotic system. Comput. Phys. Commun. 2013, 184, 765–768. [Google Scholar] [CrossRef]
- Francois, M.; Grosges, T.; Barchiesi, D.; Erra, R. A new pseudo-random number generator based on two chaotic maps. Informatica 2013, 24, 181–197. [Google Scholar] [CrossRef]
- Yang, H.T.; Huang, J.R.; Chang, T.Y. A chaos-based fully digital 120 MHz pseudo random number generator. In Proceedings of the IEEE Asia-Pacific Conference on Circuits and Systems, Tainan, Taiwan, 6–9 December 2004; pp. 357–360. [Google Scholar]
- Mao, Y.; Cao, L.; Liu, W. Design and FPGA implementation of a pseudo-random bit sequence generator using spatiotemporal chaos. In Proceedings of the International Conference on Communications, Circuits and Systems, Guilin, China, 25–28 June 2006; pp. 2114–2118. [Google Scholar]
- Mansingka, A.S.; Radwan, A.G.; Salama, K.N. Fully digital 1-D, 2-D and 3-D multiscroll chaos as hardware pseudo random number generators. In Proceedings of the International Midwest Symposium on Circuits and Systems (MWSCAS), Boise, ID, USA, 5–8 August 2012; pp. 1180–1183. [Google Scholar]
- Barakat, M.L.; Mansingka, A.S.; Radwan, A.G.; Salama, K.N. Generalized Hardware Post-processing Technique for Chaos-Based Pseudorandom Number Generators. ETRI J. 2013, 35, 448–458. [Google Scholar] [CrossRef]
- de la Fraga, L.G.; Torres-Pérez, E.; Tlelo-Cuautle, E.; Mancillas-López, C. Hardware implementation of pseudo-random number generators based on chaotic maps. Nonlinear Dyn. 2017, 90, 1661–1670. [Google Scholar] [CrossRef]
- Dastgheib, M.A.; Farhang, M. A digital pseudo-random number generator based on sawtooth chaotic map with a guaranteed enhanced period. Nonlinear Dyn. 2017, 89, 2957–2966. [Google Scholar] [CrossRef]
- Brown, B.D.; Card, H.C. Stochastic neural computation. I. Computational elements. IEEE Trans. Comput. 2001, 50, 891–905. [Google Scholar] [CrossRef]
- Boeing, G. Visual analysis of nonlinear dynamical systems: Chaos, fractals, self-similarity and the limits of prediction. Systems 2016, 4, 37. [Google Scholar] [CrossRef]
- Luo, Y.; Ouyang, X.; Liu, J.; Cao, L. An image encryption method based on elliptic curve elgamal encryption and chaotic systems. IEEE Access 2019, 7, 38507–38522. [Google Scholar] [CrossRef]
- Alaghi, A.; Hayes, J.P. Survey of stochastic computing. ACM Trans. Embed. Comput. Syst. TECS 2013, 12, 1–19. [Google Scholar] [CrossRef]
- Wong, M.M.; Wong, D.M.L. Stochastic computing with spiking neural P systems. J. Univ. Comput. Sci. 2017, 7, 589–602. [Google Scholar]
- Ouyang, X.; Luo, Y.; Liu, J.; Liu, Y.; Bi, J.; Qiu, S. Period analysis of chaotic systems under finite precisions. In Proceedings of the International Conference on Systems Engineering (ICSEng), Nevada, LV, USA, 18–20 December 2018; pp. 1–5. [Google Scholar]
- Wheeler, D.D.; Matthews, R.A. Supercomputer investigations of a chaotic encryption algorithm. Cryptologia 1991, 15, 140–152. [Google Scholar] [CrossRef]
- Heidari-Bateni, G.; McGillem, C.D. A chaotic direct-sequence spread-spectrum communication system. IEEE Trans. Commun. 1994, 42, 1524–1527. [Google Scholar] [CrossRef]
- Wong, K.W.; Kwok, B.S.H.; Law, W.S. A fast image encryption scheme based on chaotic standard map. Phys. Lett. A 2008, 372, 2645–2652. [Google Scholar] [CrossRef]
- Hu, H.; Xu, Y.; Zhu, Z. A method of improving the properties of digital chaotic system. Chaos Solitons Fractals 2008, 38, 439–446. [Google Scholar] [CrossRef]
- Xing-Yuan, W.; Lin-Lin, W. A new perturbation method to the Tent map and its application. Chin. Phys. B 2011, 20, 50509–50517. [Google Scholar]
- Yoshioka, D.; Tsuneda, A. Design of pseudochaotic maximum length sequences with prescribed autocorrelation obtained from discretized chaos maps. In Proceedings of the International Symposium on Spread Spectrum Techniques and Applications, Bologna, Italy, 25–28 August 2008; pp. 161–165. [Google Scholar]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Bassham, L.E., III; Rukhin, A.L.; Soto, J.; Nechvatal, J.R.; Smid, M.E.; Barker, E.B.; Leigh, S.D.; Levenson, M.; Vangel, M.; Banks, D.L.; et al. Sp 800-22 rev. 1a. a Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; National Institute of Standards & Technology: Gaithersburg, MD, USA, 2010. [Google Scholar]
- L’Ecuyer, P.; Simard, R. TestU01: AC library for empirical testing of random number generators. ACM Trans. Math. Softw. TOMS 2007, 33, 1–40. [Google Scholar] [CrossRef]
- Hue, T.T.K.; Van Lam, C.; Hoang, T.M.; Al Assad, S. Implementation of secure SPN chaos-based cryptosystem on FPGA. In Proceedings of the International Symposium on Signal Processing and Information Technology (ISSPIT), Ho Chi Minh City, Vietnam, 12–15 December 2012; pp. 129–134. [Google Scholar]
- Mansingka, A.S.; Radwan, A.G.; Salama, K.N. Design, implementation and analysis of fully digital 1-D controllable multiscroll chaos. In Proceedings of the ICM 2011 Proceeding, Istanbul, Turkey, 13–14 June 2011; pp. 1–5. [Google Scholar]
- Giard, P.; Kaddoum, G.; Gagnon, F.; Thibeault, C. FPGA implementation and evaluation of discrete-time chaotic generators circuits. In Proceedings of the Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 3221–3224. [Google Scholar]
- Chung, H.; Miri, A. On the hardware design and implementation of a chaos-based RFID authentication and watermarking scheme. In Proceedings of the International Conference on Information Science, Signal Processing and their Applications (ISSPA), Montreal, QC, Canada, 2–5 July 2012; pp. 460–465. [Google Scholar]
- Cao, L.; Luo, Y.; Bi, J.; Qiu, S.; Lu, Z.; Harkin, J.; McDaid, L. An authentication strategy based on spatiotemporal chaos for software copyright protection. Secur. Commun. Netw. 2015, 8, 4073–4086. [Google Scholar] [CrossRef]

| Chaotic System | Tent Map | Logistic Map | The Proposed System |
|---|---|---|---|
| Approximate entropy | 0.5170 | 0.6506 | 0.7112 |
| Sub-Tests | p-Value | Result |
|---|---|---|
| Frequency | 0.213309 | Pass |
| Universal | 0.554405 | Pass |
| Serial | 0.739918 | Pass |
| Rank | 0.441376 | Pass |
| FFT | 0.902014 | Pass |
| Runs | 0.350485 | Pass |
| Longest Run | 0.911413 | Pass |
| Block Frequency | 0.565945 | Pass |
| Cumulative Sums | 0.534146 | Pass |
| Overlapping Template | 0.395130 | Pass |
| Non-overlapping Template | 0.066882 | Pass |
| Approximate Entropy | 0.122325 | Pass |
| Linear Complexity | 0.911413 | Pass |
| Random Excursions | 0.652391 | Pass |
| Random Excursions Variant | 0.381832 | Pass |
| PRNGs | Rabbit | Alphabit |
|---|---|---|
| Original logistic map | 35/38 | 15/17 |
| Enhanced logistic map | 38/38 | 17/17 |
| Approaches | Chaotic Generators | LUTs | Registers | DSP Blocks | Frequency (MHz) | Device |
|---|---|---|---|---|---|---|
| [35] | Jerk | 716 | 130 | 16 | 50.46 | Virtex 4 |
| [36] | Cubic map | 387 | N/A | 24 | 100 | Virtex 6 |
| [34] | Logistic map | 3711 | 1176 | N/A | 50 | Cyclone II |
| [37] | Loren | 3476 | N/A | N/A | 100 | Virtex 6 |
| [38] | Coupled map lattices | 2548 | 2429 | 32 | 100 | Stratix IV |
| This work | Logistic map | 373 | 445 | 0 | 100 | ZedBoard |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Liang, Z.; Luo, Y.; Cao, L.; Zhang, S.; Wang, Y.; Yang, S. A Hardware Pseudo-Random Number Generator Using Stochastic Computing and Logistic Map. Micromachines 2021, 12, 31. https://doi.org/10.3390/mi12010031
Liu J, Liang Z, Luo Y, Cao L, Zhang S, Wang Y, Yang S. A Hardware Pseudo-Random Number Generator Using Stochastic Computing and Logistic Map. Micromachines. 2021; 12(1):31. https://doi.org/10.3390/mi12010031
Chicago/Turabian StyleLiu, Junxiu, Zhewei Liang, Yuling Luo, Lvchen Cao, Shunsheng Zhang, Yanhu Wang, and Su Yang. 2021. "A Hardware Pseudo-Random Number Generator Using Stochastic Computing and Logistic Map" Micromachines 12, no. 1: 31. https://doi.org/10.3390/mi12010031
APA StyleLiu, J., Liang, Z., Luo, Y., Cao, L., Zhang, S., Wang, Y., & Yang, S. (2021). A Hardware Pseudo-Random Number Generator Using Stochastic Computing and Logistic Map. Micromachines, 12(1), 31. https://doi.org/10.3390/mi12010031





