Fundamental Definitions for Axially-Strained Piezo-Semiconductive Nanostructures
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Depletion Piezopotential (ΔVPZ-DEPL) and Enhancement Piezopotential (ΔVPZ-ENHANC)
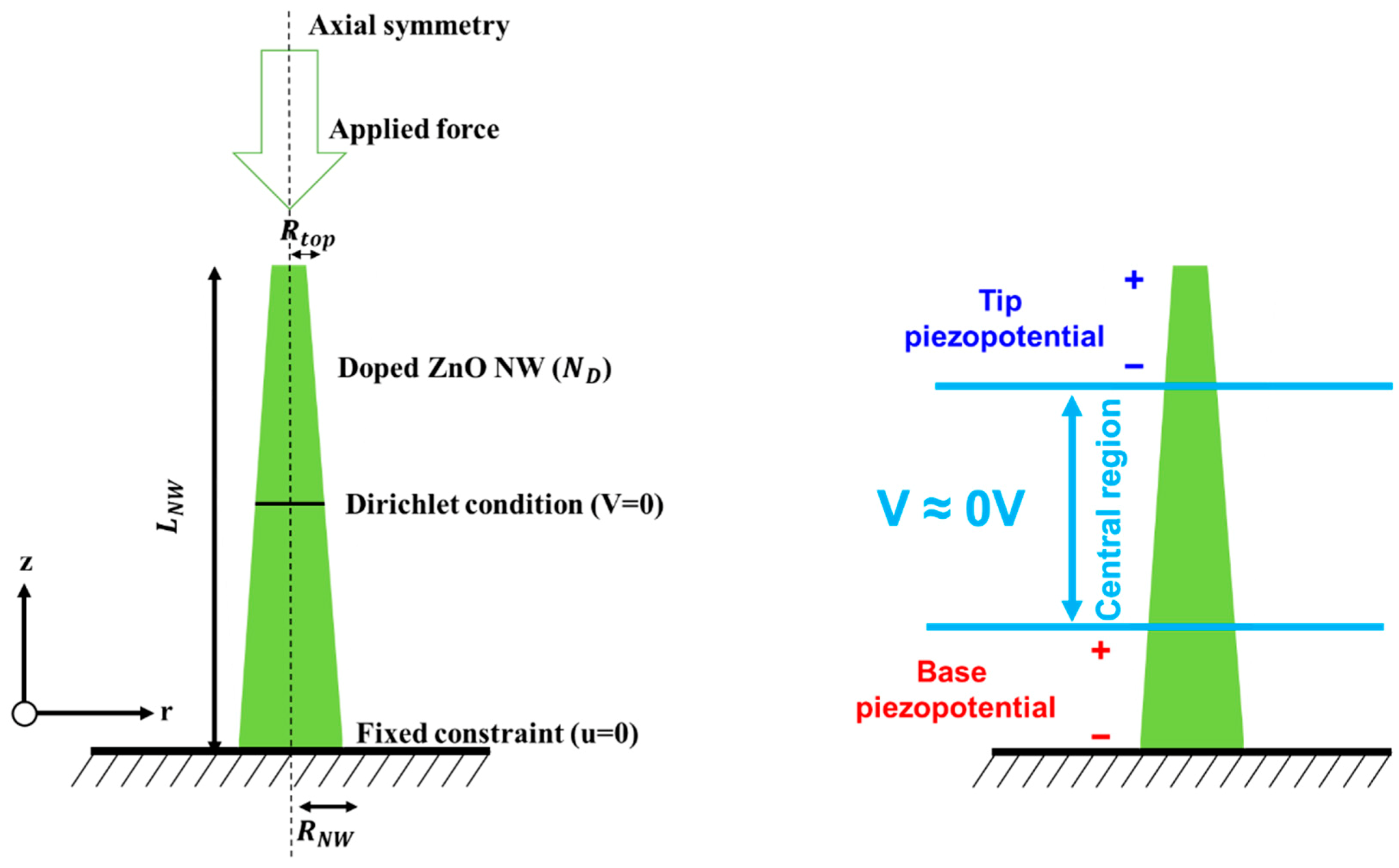
3.2. Tip Piezopotential (ΔVPZ-TIP) and Base Piezopotential (ΔVPZ-BASE)
3.3. Characteristic Lengths of the Piezopotentials (Tip, Base, Depletion or Enhancement Piezopotential)
3.4. Depletion-to-Enhancement Piezopotential Ratio (rPZ,DEPL-TO-ENHANC)
3.5. Tip-to-Base Piezopotential Ratio (rPZ,TIP-TO-BASE)
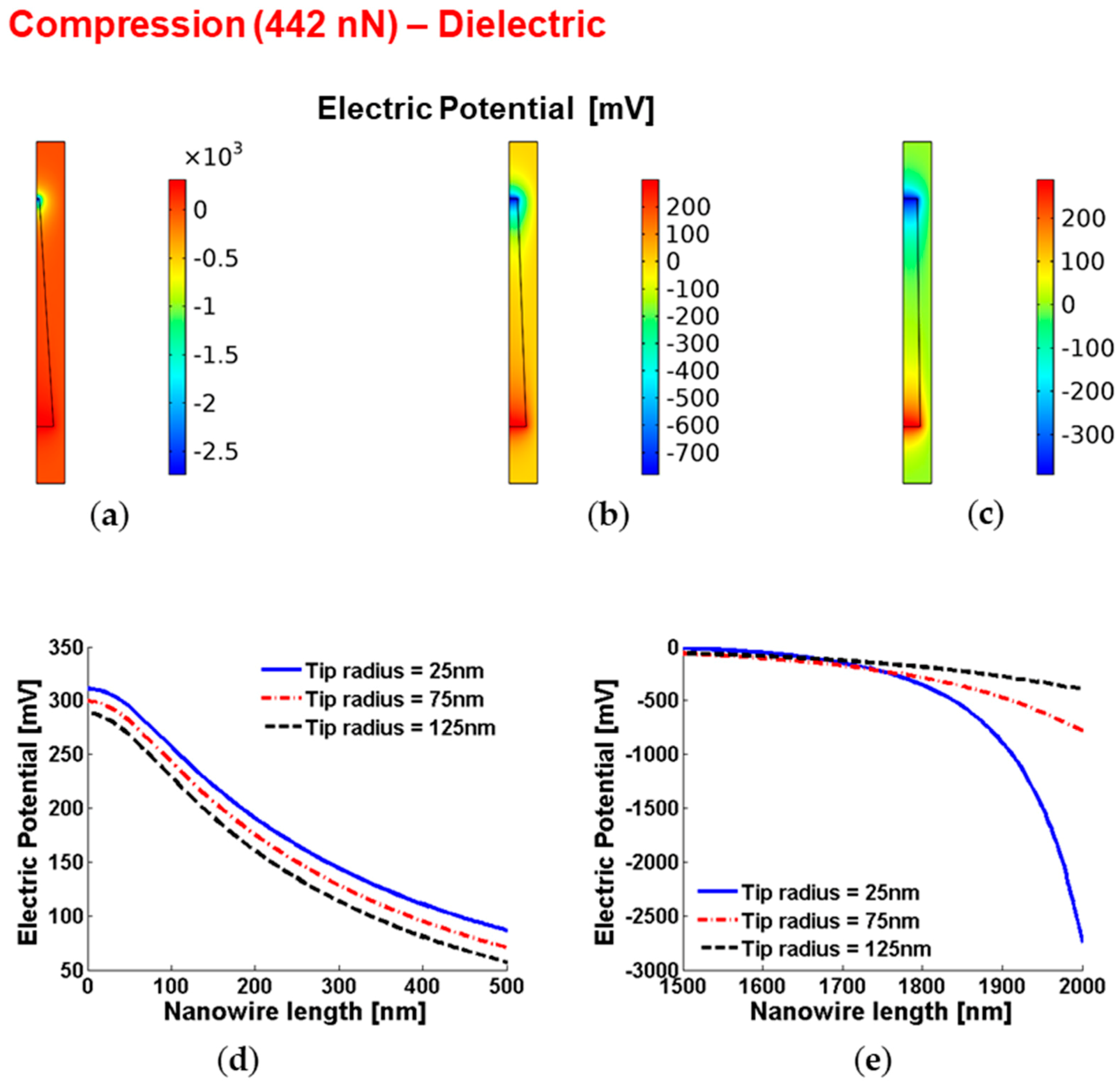
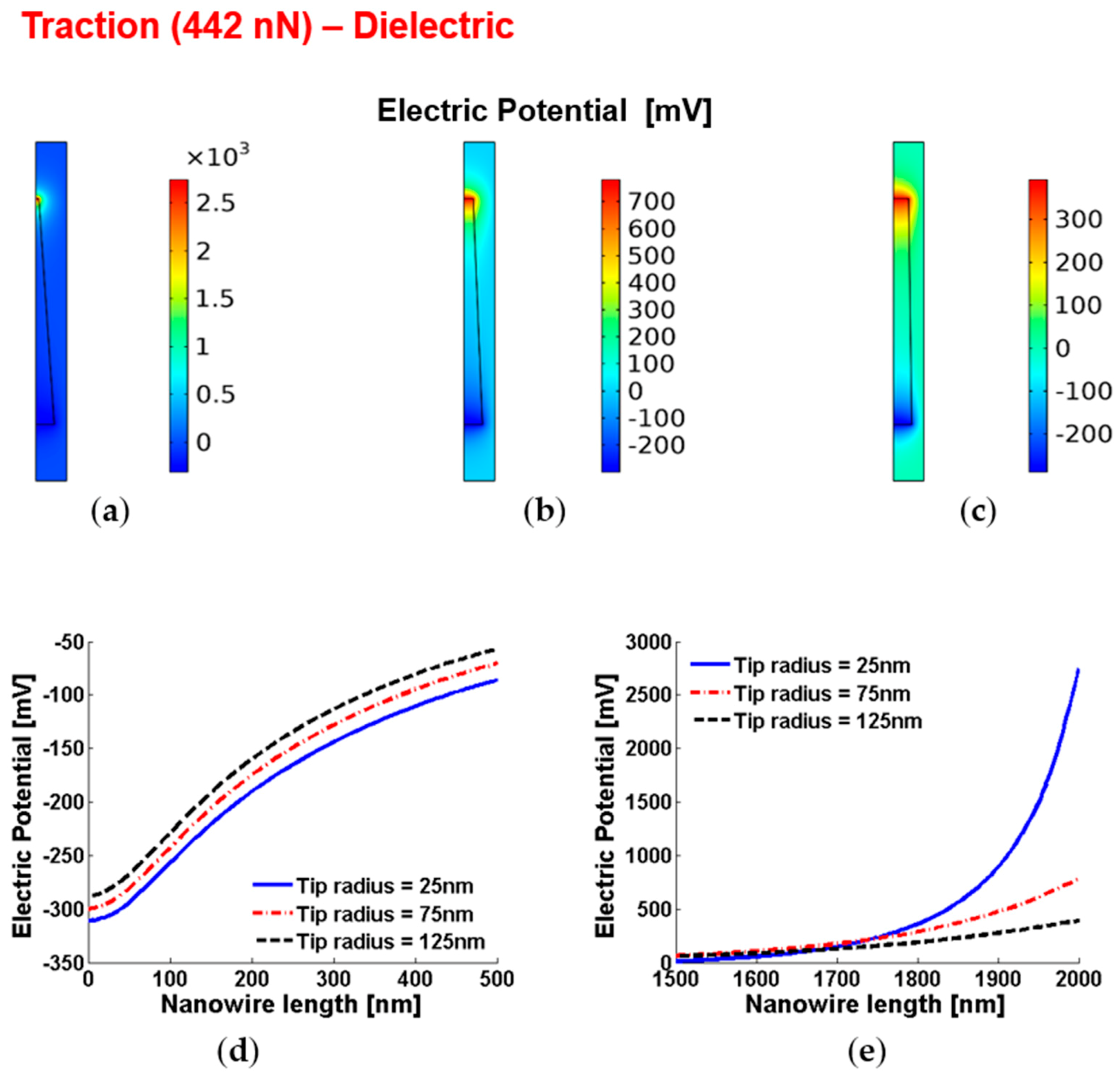
3.6. Piezopotential in Truncated Conical Dielectric Nanowires under Vertical Compression or Traction
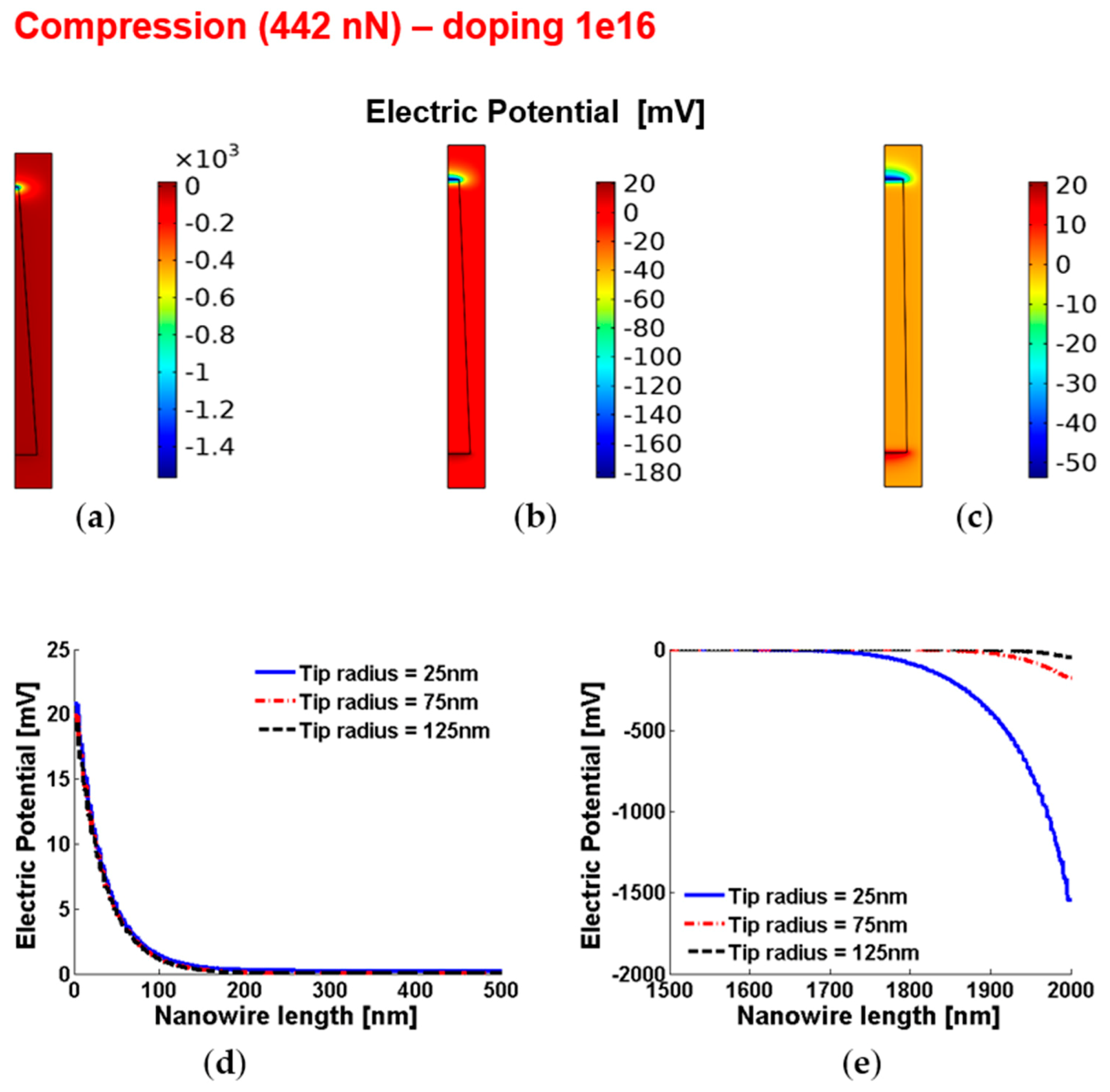
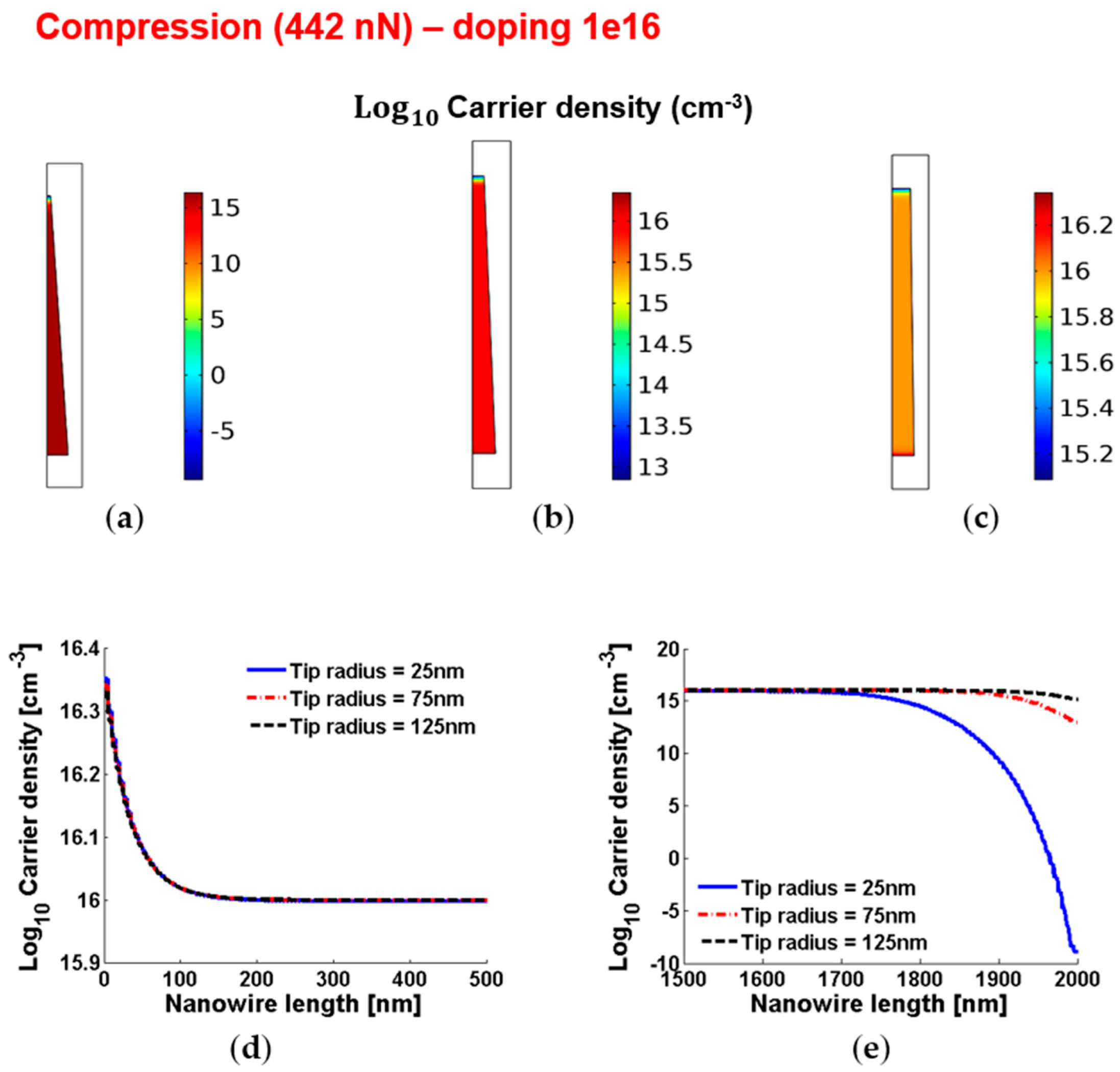
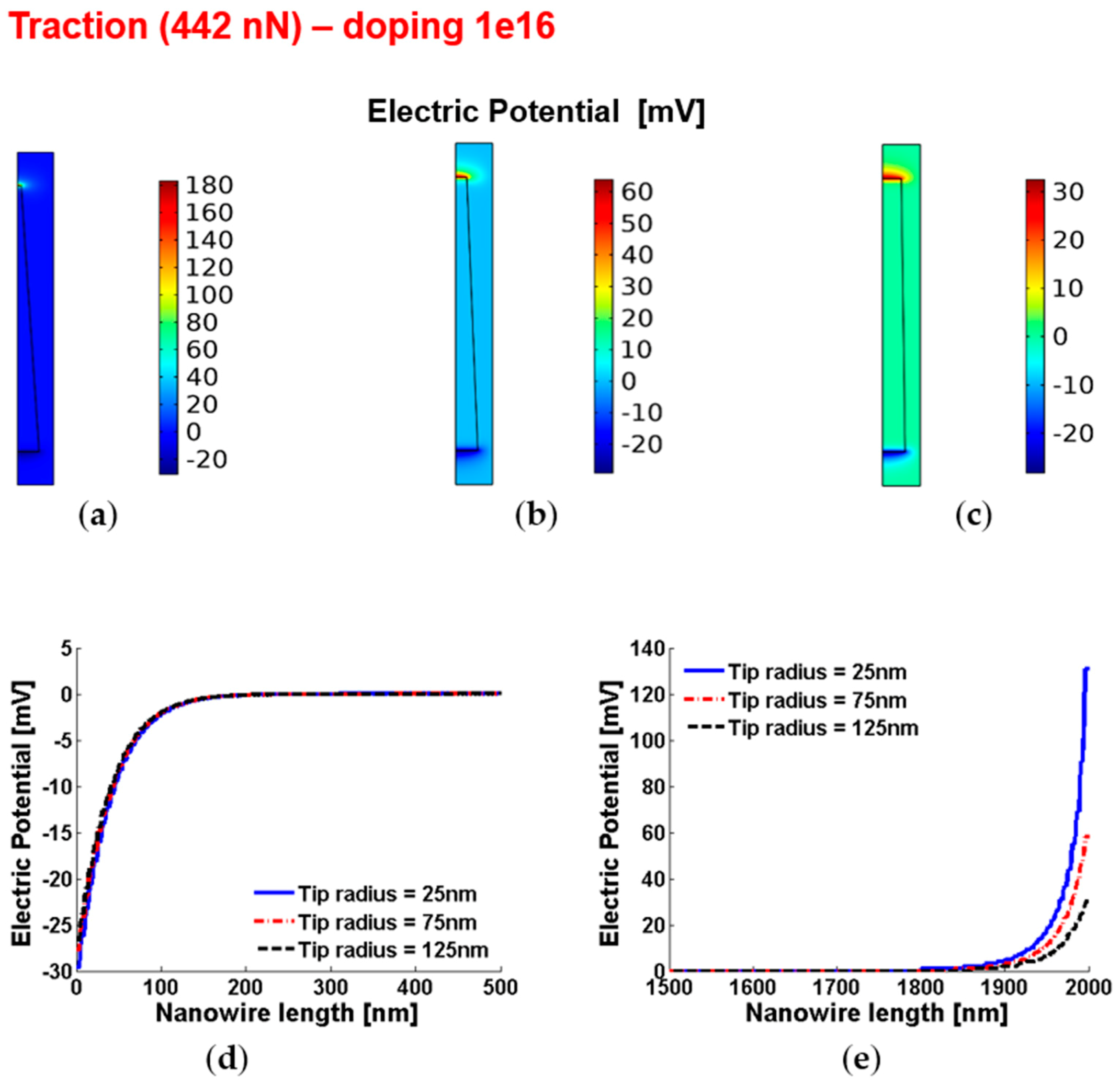
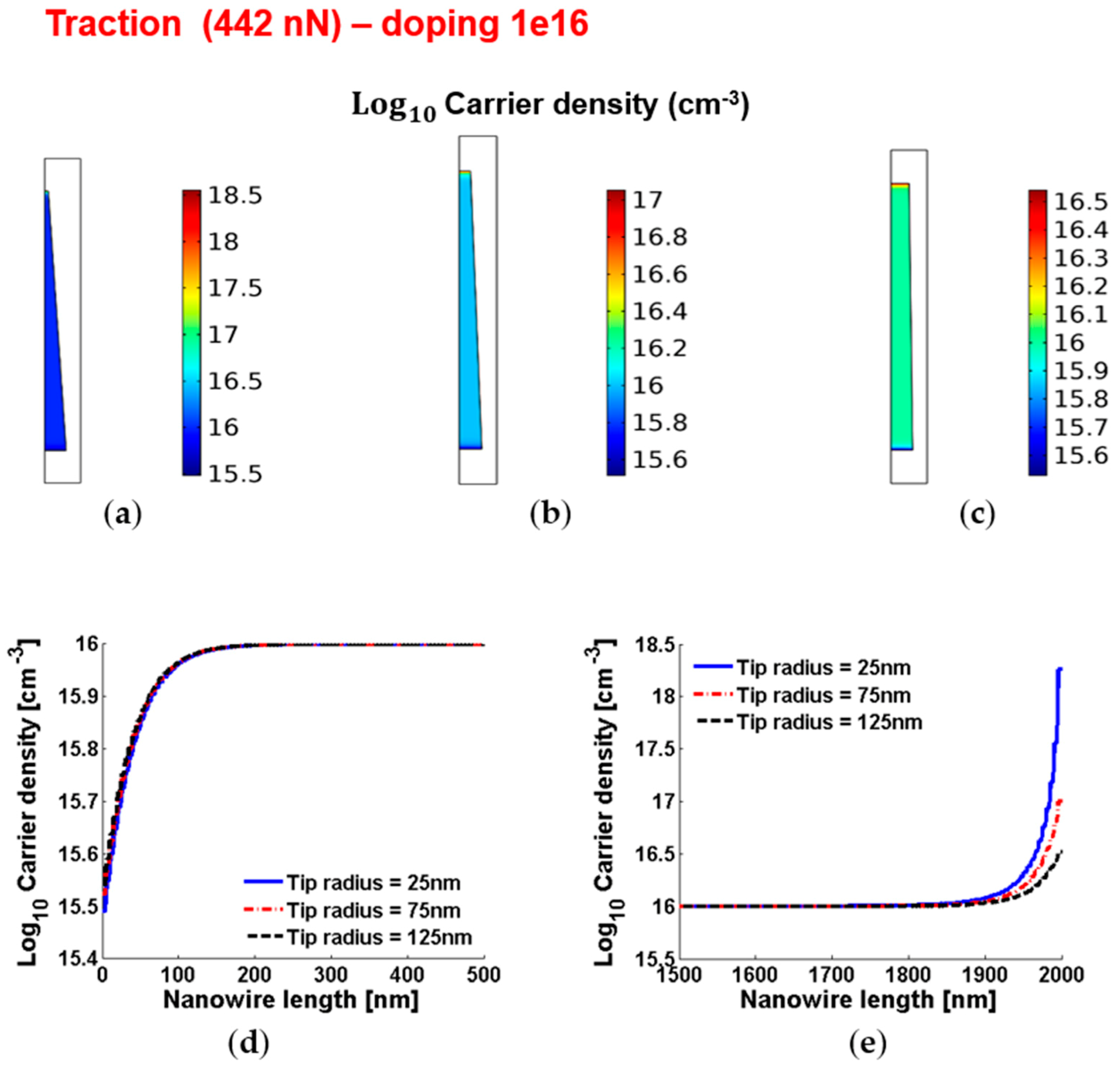
3.7. Piezopotentials, Free Carrier Concentrations, Piezopotential Ratios and Characteristic Lengths of the Piezopotentials in Truncated Conical Nanowires with 1016 cm−3 Doping under Vertical Compression or Traction
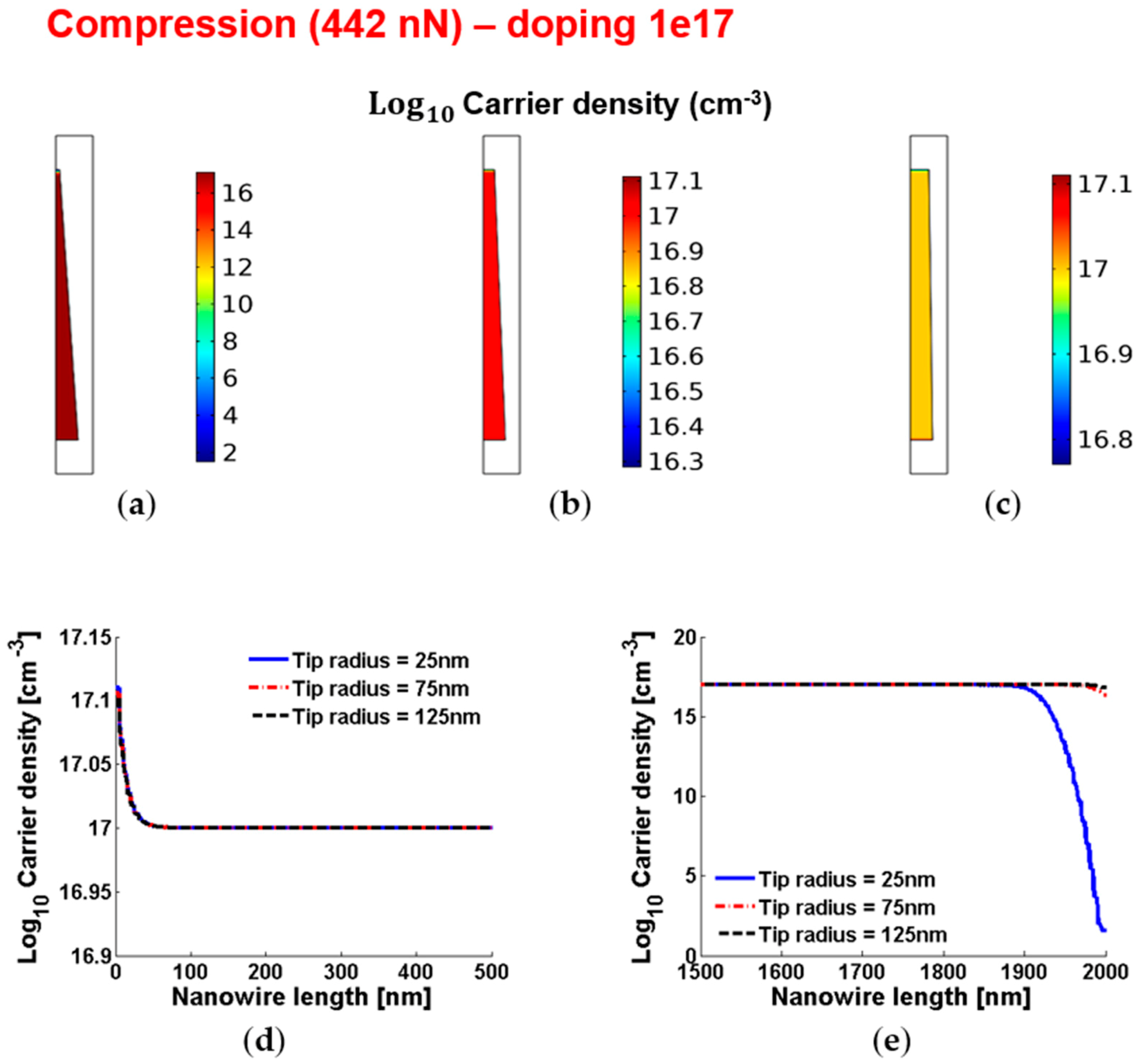
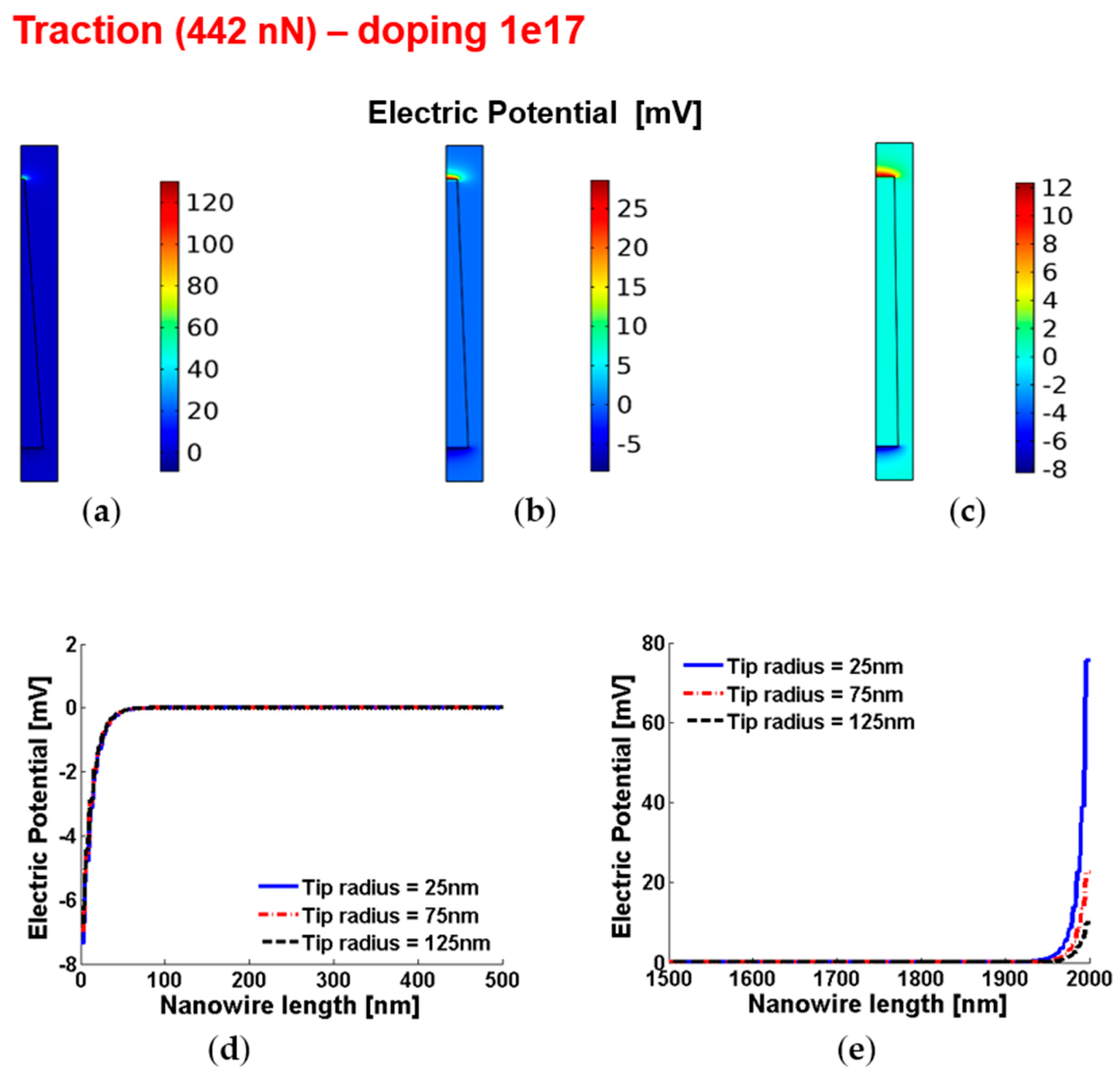
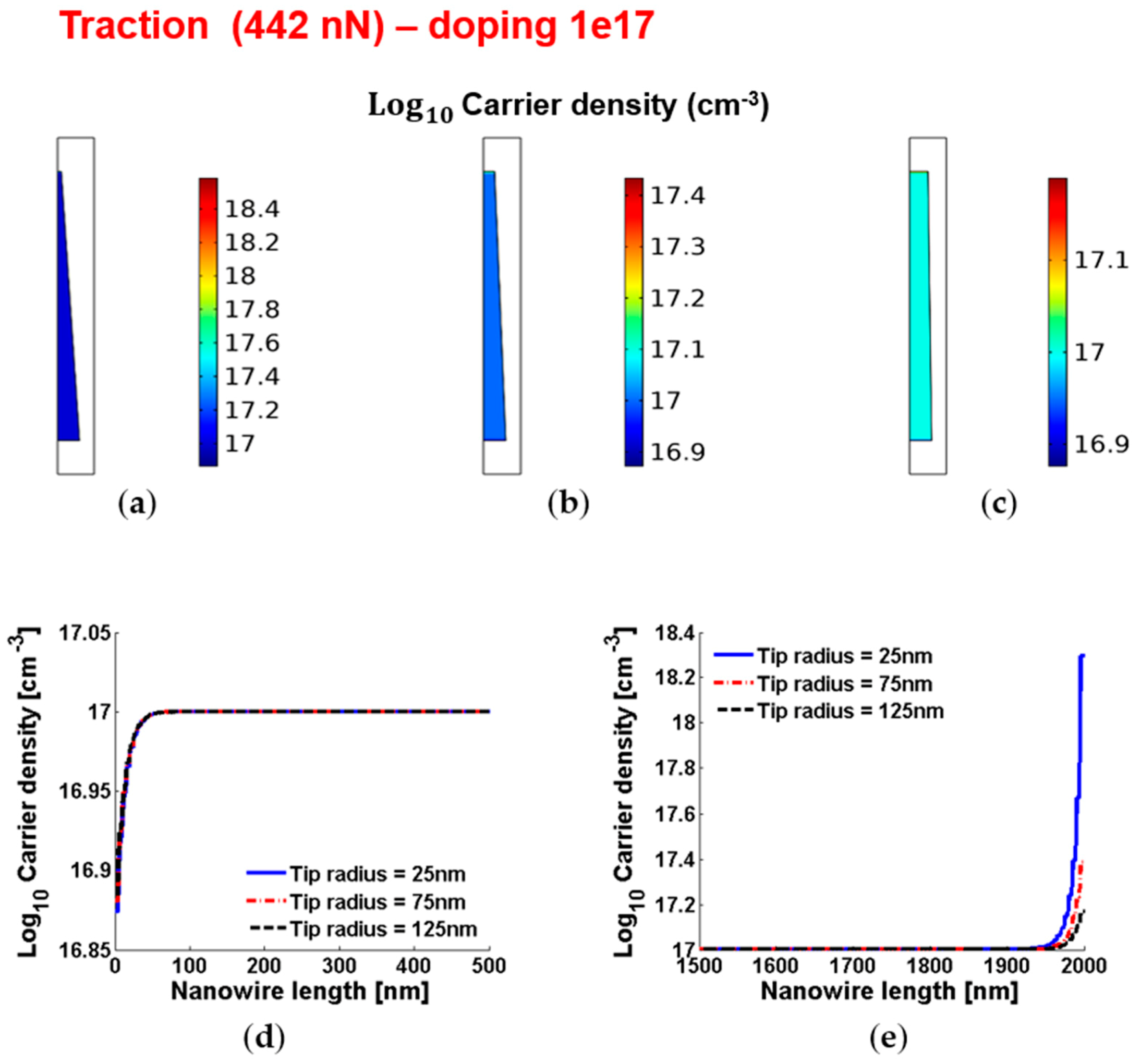
3.8. Piezopotentials, Free Carrier Concentrations, Piezopotential Ratios and Characteristic Lengths of the Piezopotentials in Truncated Conical Nanowires with 1017 cm−3 Doping under Vertical Compression or Traction
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Falconi, C. Piezoelectric nanotransducers. Nano Energy 2019, 59, 730–744. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, J.; Song, J.; Liu, J.; Xu, N.; Wang, Z.L. Piezoelectric field effect transistor and nanoforce sensor based on a single ZnO nanowire. Nano Lett. 2006, 6, 2768–2772. [Google Scholar] [CrossRef] [PubMed]
- Koka, A.; Sodano, H.A. High-sensitivity accelerometer composed of ultra-long vertically aligned barium titanate nanowire arrays. Nat. Commun. 2013, 4. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.D.; Deshmukh, N.; Nagarah, J.M.; Kramer, T.; Purohit, P.K.; Berry, M.J.; McAlpine, M.C. Piezoelectric nanoribbons for monitoring cellular deformations. Nat. Nanotechnol. 2012, 7, 587–593. [Google Scholar] [CrossRef] [PubMed]
- Zhu, G.; Wang, A.C.; Liu, Y.; Zhou, Y.; Wang, Z.L. Functional electrical stimulation by nanogenerator with 58 v output voltage. Nano Lett. 2012, 12, 3086–3090. [Google Scholar] [CrossRef] [PubMed]
- Yang, R.; Qin, Y.; Li, C.; Zhu, G.; Wang, Z.L. Converting Biomechanical Energy into Electricity by a Muscle-Movement-Driven Nanogenerator. Nano Lett. 2009, 9, 1201–1205. [Google Scholar] [CrossRef]
- Li, Z.; Zhu, G.; Yang, R.; Wang, A.C.; Wang, Z.L. Muscle-driven in vivo nanogenerator. Adv. Mater. 2010, 22, 2534–2537. [Google Scholar] [CrossRef]
- Shi, B.; Li, Z.; Fan, Y. Implantable Energy-Harvesting Devices. Adv. Mater. 2018, 30, 1801511. [Google Scholar] [CrossRef]
- Zheng, Q.; Shi, B.; Li, Z.; Wang, Z.L. Recent Progress on Piezoelectric and Triboelectric Energy Harvesters in Biomedical Systems. Adv. Sci. 2017, 4, 1–23. [Google Scholar] [CrossRef]
- Dagdeviren, C.; Li, Z.; Wang, Z.L. Energy Harvesting from the Animal/Human Body for Self-Powered Electronics. Annu. Rev. Biomed. Eng. 2017, 19, 85–108. [Google Scholar] [CrossRef]
- Wang, Z.L. Piezotronic and Piezophototronic Effects. J. Phys. Chem. Lett. 2010, 1, 1388–1393. [Google Scholar] [CrossRef]
- Starr, M.B.; Shi, J.; Wang, X. Piezopotential-driven redox reactions at the surface of piezoelectric materials. Angew. Chem. Int. Ed. 2012, 51, 5962–5966. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Ma, C.; Wang, Z.L. Self-Catalysis and Phase Transformation in the Formation of CdSe Nanosaws. Adv. Mater. 2004, 16, 1740–1743. [Google Scholar] [CrossRef]
- Xue, X.; Nie, Y.; He, B.; Xing, L.; Zhang, Y.; Wang, Z.L. Surface free-carrier screening effect on the output of a ZnO nanowire nanogenerator and its potential as a self-powered active gas sensor. Nanotechnology 2013, 24, 225501. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Klein, B.D.B.; Su, Y.; Niu, S.; Liu, Y.; Wang, Z.L. Temperature dependence of the piezotronic effect in ZnO nanowires. Nano Lett. 2013, 13, 5026–5032. [Google Scholar] [CrossRef] [PubMed]
- Xue, F.; Zhang, L.; Tang, W.; Zhang, C.; Du, W.; Wang, Z.L. Piezotronic effect on ZnO nanowire film based temperature sensor. ACS Appl. Mater. Interfaces 2014, 6, 5955–5961. [Google Scholar] [CrossRef] [PubMed]
- Falconi, C.; D’Amico, A.; Wang, Z.L. Wireless nanosensors and nanoactuators for in-vivo biomedical applications. In Proceedings of the Eurosensors, Göteborg, Sweden, 17–20 September 2006. [Google Scholar]
- Falconi, C.; D’Amico, A.; Wang, Z.L. Wireless Joule nanoheaters. Sens. Actuators B Chem. 2007, 127, 54–62. [Google Scholar] [CrossRef]
- Ciofani, G.; Danti, S.; D’Alessandro, D.; Ricotti, L.; Moscato, S.; Bertoni, G.; Falqui, A.; Berrettini, S.; Petrini, M.; Mattoli, V.; et al. Enhancement of Neurite Outgrowth in Neuronal-Like Cells following Boron Nitride Nanotube-Mediated Stimulation. ACS Nano 2010, 4, 6267–6277. [Google Scholar] [CrossRef]
- Wang, A.; Liu, Z.; Hu, M.; Wang, C.; Zhang, X.; Shi, B.; Fan, Y.; Cui, Y.; Li, Z.; Ren, K. Piezoelectric nanofibrous scaffolds as in vivo energy harvesters for modifying fibroblast alignment and proliferation in wound healing. Nano Energy 2018, 43, 63–71. [Google Scholar] [CrossRef]
- Falconi, C.; Mantini, G.; D’Amico, A.; Wang, Z.L. Studying piezoelectric nanowires and nanowalls for energy harvesting. Sensors Actuators B Chem. 2009, 139, 511–519. [Google Scholar] [CrossRef]
- Araneo, R.; Lovat, G.; Burghignoli, P.; Falconi, C. Piezo-semiconductive quasi-1D nanodevices with or without anti-symmetry. Adv. Mater. 2012, 24, 4719–4724. [Google Scholar] [CrossRef] [PubMed]
- Araneo, R.; Falconi, C. Lateral bending of tapered piezo-semiconductive nanostructures for ultra-sensitive mechanical force to voltage conversion. Nanotechnology 2013, 24, 265707. [Google Scholar] [CrossRef] [PubMed]
- Hao, H.; Jenkins, K.; Huang, X.; Xu, Y.; Huang, J.; Yang, R. Piezoelectric potential in single-crystalline ZnO nanohelices based on finite element analysis. Nanomaterials 2017, 7, 430. [Google Scholar] [CrossRef] [PubMed]
- Han, J.H.; Park, K.I.; Jeong, C.K. Dual-structured flexible piezoelectric film energy harvesters for effectively integrated performance. Sensors 2019, 19, 1444. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Zhao, L.; Jiang, Z.; Luo, G.; Yang, P.; Han, X.; Li, X.; Maeda, R. High accuracy comsol simulation method of bimorph cantilever for piezoelectric vibration energy harvesting. AIP Adv. 2019, 9. [Google Scholar] [CrossRef]
- Wang, Z.L.; Song, J. Piezoelectric nanogenerators based on zinc oxide nanowire arrays. Science 2006, 312, 242–246. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Wang, Z.L. Electrostatic potential in a bent piezoelectric nanowire. The fundamental theory of nanogenerator and nanopiezotronics. Nano Lett. 2007, 7, 2499–2505. [Google Scholar] [CrossRef]
- Xu, S.; Wang, Z.L. One-dimensional ZnO nanostructures: Solution growth and functional properties. Nano Res. 2011, 4, 1013–1098. [Google Scholar] [CrossRef]
- Xia, B.Y.; Yang, P.; Sun, Y.; Wu, Y.; Mayers, B.; Gates, B.; Yin, Y.; Kim, F.; Yan, H.; Xia, Y.; et al. One-Dimensional Nanostructures: Synthesis, Characterization, and Applications. Adv. Mater. 2003, 15, 353–389. [Google Scholar] [CrossRef]
- Arrabito, G.; Errico, V.; Zhang, Z.; Han, W.; Falconi, C. Nanotransducers on printed circuit boards by rational design of high-density, long, thin and untapered ZnO nanowires. Nano Energy 2018, 46, 54–62. [Google Scholar] [CrossRef]
- Özgür, Ü.; Alivov, Y.I.; Liu, C.; Teke, A.; Reshchikov, M.A.; Doǧan, S.; Avrutin, V.; Cho, S.J.; Morko̧, H. A comprehensive review of ZnO materials and devices. J. Appl. Phys. 2005, 98, 1–103. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, Z.L. Equilibrium Potential of Free Charge Carriers in a Bent Piezoelectric Semiconductive Nanowire. Nano Lett. 2009, 9, 1103–1110. [Google Scholar] [CrossRef] [PubMed]
- Romano, G.; Mantini, G.; Di Carlo, A.; D’Amico, A.; Falconi, C.; Wang, Z.L. Piezoelectric potential in vertically aligned nanowires for high output nanogenerators. Nanotechnology 2011, 22, 465401. [Google Scholar] [CrossRef] [PubMed]
- Araneo, R.; Lovat, G.; Falconi, C.; Notargiacomo, A.; Rinaldi, A. Accurate analysis of the piezopotential and the stored energies in laterally bent piezo-semiconductive NWs. In Proceedings of the Materials Research Society Symposium Proceedings, Boston, MA, USA, 25–30 November 2012; Volume 1556, pp. 89–94. [Google Scholar]
- Araneo, R.; Lovat, G.; Falconi, C.; Notargiacomo, A.; Rinaldi, A. Accurate models for the current-voltage characteristics of vertically compressed piezo-semiconductive quasi-1D NWs. Mater. Res. Soc. Symp. Proc. 2013, 1556, 11–16. [Google Scholar] [CrossRef]
- Tao, R.; Mouis, M.; Ardila, G. Unveiling the Influence of Surface Fermi Level Pinning on the Piezoelectric Response of Semiconducting Nanowires. Adv. Electron. Mater. 2018, 4, 1–9. [Google Scholar] [CrossRef]
- Min Kim, S.; Kim, H.; Nam, Y.; Kim, S. Effects of external surface charges on the enhanced piezoelectric potential of ZnO and AlN nanowires and nanotubes. AIP Adv. 2012, 2, 42174. [Google Scholar] [CrossRef]
- Fathi, S.; Sheikholeslami, T.F. Investigation of external charges effects on piezoelectric ZnO nanogenerator. J. Nano Electron. Phys. 2016, 8, 6–11. [Google Scholar] [CrossRef]

| Young’s Modulus | Poisson’s Ratio | Piezoelectric Coefficients (e33) |
|---|---|---|
| 129 GPa | v = 0.349 | 1.22 C m−2 |
| ND = 1016 cm−3, Compression (442 nN) | |||
|---|---|---|---|
| RTIP | 25 nm | 75 nm | 125 nm |
| ΔVPZ-DEPL = ΔVPZ-TIP | −1540 mV | −180 mV | −52 mV |
| ΔVPZ-ENHANC = ΔVPZ-BASE | −21 mV | −20 mV | −19 mV |
| rPZ,DEPL-TO-ENHANC = rPZ,TIP-TO-BASE | 73 | 9 | 2.7 |
| Characteristic length (ΔVPZ-DEPL = ΔVPZ-TIP) | 165 nm | 115 nm | 94 nm |
| Characteristic length (ΔVPZ-ENHANC = ΔVPZ-BASE) | 83 nm | 80 nm | 80 nm |
| ND = 1016 cm−3, Traction (442 nN) | |||
|---|---|---|---|
| RTIP | 25 nm | 75 nm | 125 nm |
| ΔVPZ-DEPL = ΔVPZ-BASE | 131 mV | 58 mV | 30 mV |
| ΔVPZ-ENHANC = ΔVPZ-TIP | 30 mV | 28 mV | 27 mV |
| rPZ,DEPL-TO-ENHANC = 1/rPZ,TIP-TO-BASE | 4.4 | 2.1 | 1.1 |
| rPZ,TIP-TO-BASE = 1/rPZ,DEPL-TO-ENHANC | 0.23 | 0.48 | 0.9 |
| Characteristic length (ΔVPZ-ENHANC = ΔVPZ-TIP) | 60 nm | 74 nm | 79 nm |
| Characteristic length (ΔVPZ-DEPL = ΔVPZ-BASE) | 90 nm | 89 nm | 89 nm |
| ND = 1017 cm−3, Compression (442 nN) | |||
|---|---|---|---|
| RTIP | 25 nm | 75 nm | 125 nm |
| ΔVPZ-DEPL = ΔVPZ-TIP | −1028 mV | −38 mV | −12 mV |
| ΔVPZ-ENHANC = ΔVPZ-BASE | −6 mV | −6 mV | −6 mV |
| rPZ,DEPL-TO-ENHANC = rPZ,TIP-TO-BASE | 170 | 6.3 | 2 |
| Characteristic length (ΔVPZ-DEPL = ΔVPZ-TIP) | 66 nm | 31 nm | 30 nm |
| Characteristic length (ΔVPZ-ENHANC = ΔVPZ-BASE) | 29 nm | 29 nm | 29 nm |
| ND = 1017 cm−3, Traction (442 nN) | |||
|---|---|---|---|
| RTIP | 25 nm | 75 nm | 125 nm |
| ΔVPZ-DEPL = ΔVPZ-BASE | 75 mV | 22 mV | 10 mV |
| ΔVPZ-ENHANC = ΔVPZ-TIP | 7 mV | 7 mV | 7 mV |
| rPZ,DEPL-TO-ENHANC = 1/rPZ,TIP-TO-BASE | 10.7 | 3.2 | 1.4 |
| rPZ,TIP-TO-BASE = 1/rPZ,DEPL-TO-ENHANC | 0.093 | 0.32 | 0.7 |
| Characteristic length (ΔVPZ-ENHANC = ΔVPZ-TIP) | 25 nm | 26 nm | 29 nm |
| Characteristic length (ΔVPZ-DEPL = ΔVPZ-BASE) | 30 nm | 30 nm | 30 nm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amiri, P.; Falconi, C. Fundamental Definitions for Axially-Strained Piezo-Semiconductive Nanostructures. Micromachines 2021, 12, 20. https://doi.org/10.3390/mi12010020
Amiri P, Falconi C. Fundamental Definitions for Axially-Strained Piezo-Semiconductive Nanostructures. Micromachines. 2021; 12(1):20. https://doi.org/10.3390/mi12010020
Chicago/Turabian StyleAmiri, Peyman, and Christian Falconi. 2021. "Fundamental Definitions for Axially-Strained Piezo-Semiconductive Nanostructures" Micromachines 12, no. 1: 20. https://doi.org/10.3390/mi12010020
APA StyleAmiri, P., & Falconi, C. (2021). Fundamental Definitions for Axially-Strained Piezo-Semiconductive Nanostructures. Micromachines, 12(1), 20. https://doi.org/10.3390/mi12010020






