High-Performance Pure Sine Wave Inverter with Robust Intelligent Sliding Mode Maximum Power Point Tracking for Photovoltaic Applications
Abstract
1. Introduction
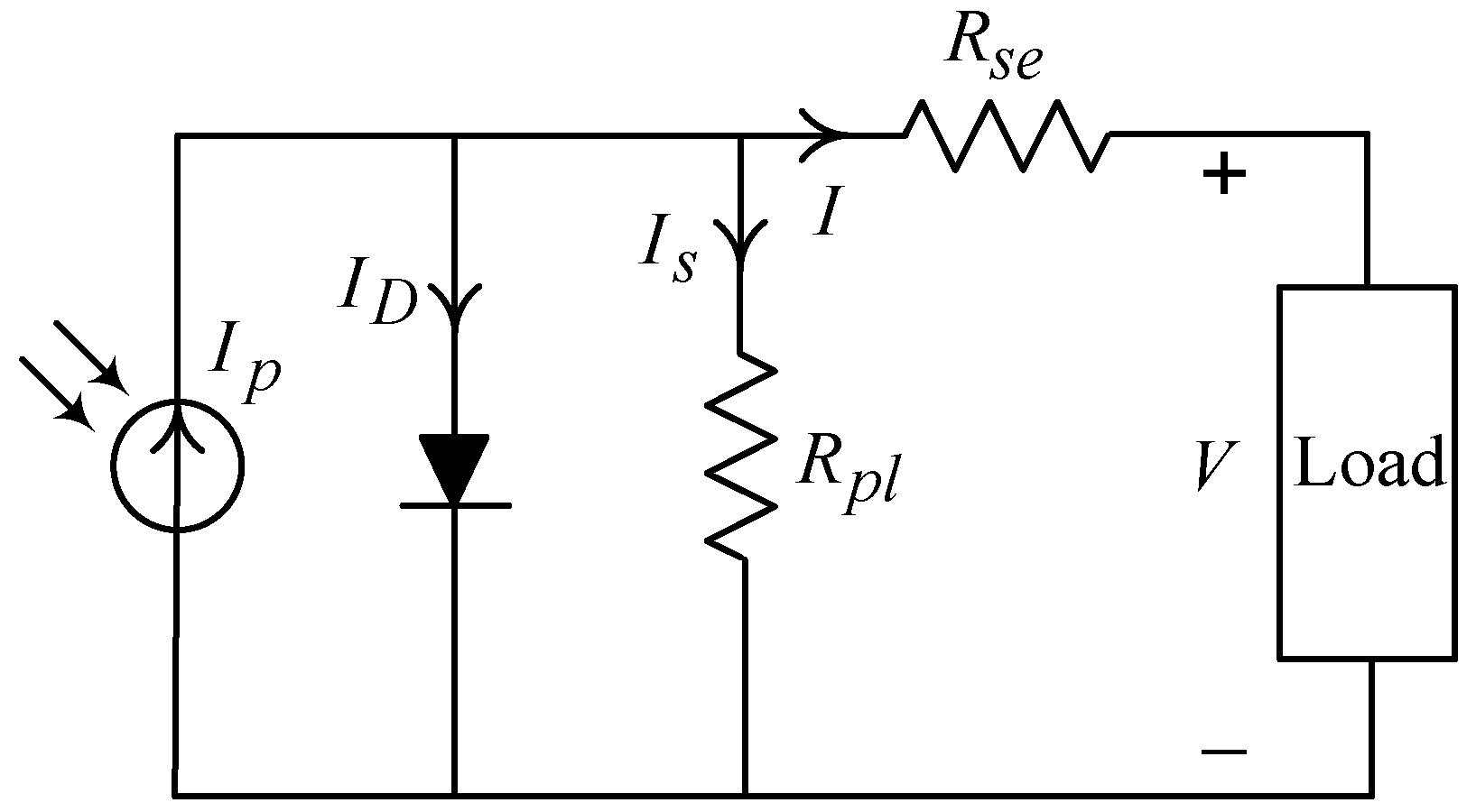
2. Dynamic Modeling of MPPT-Based Pure Sine Wave Inverter
3. Proposed Controller
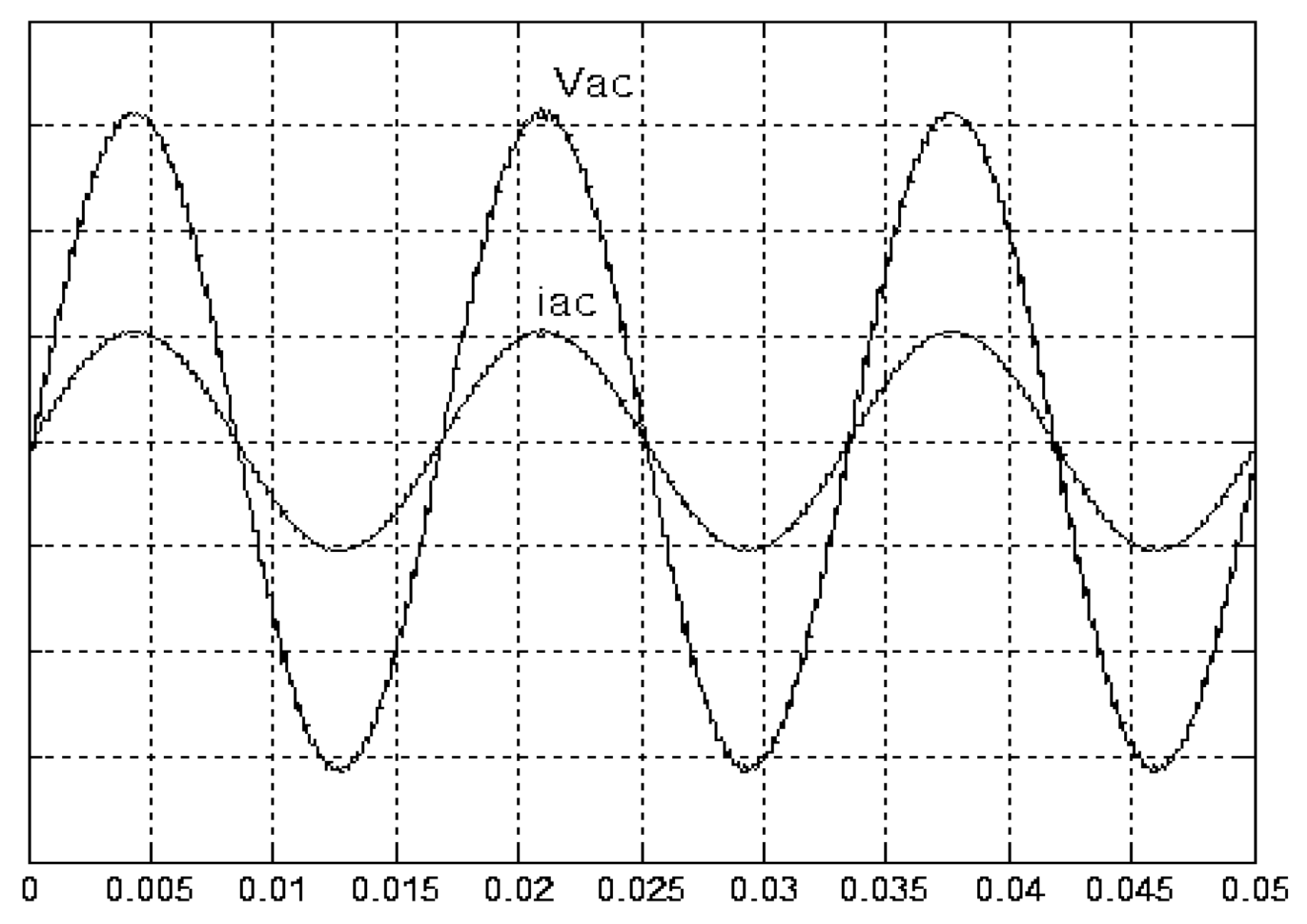
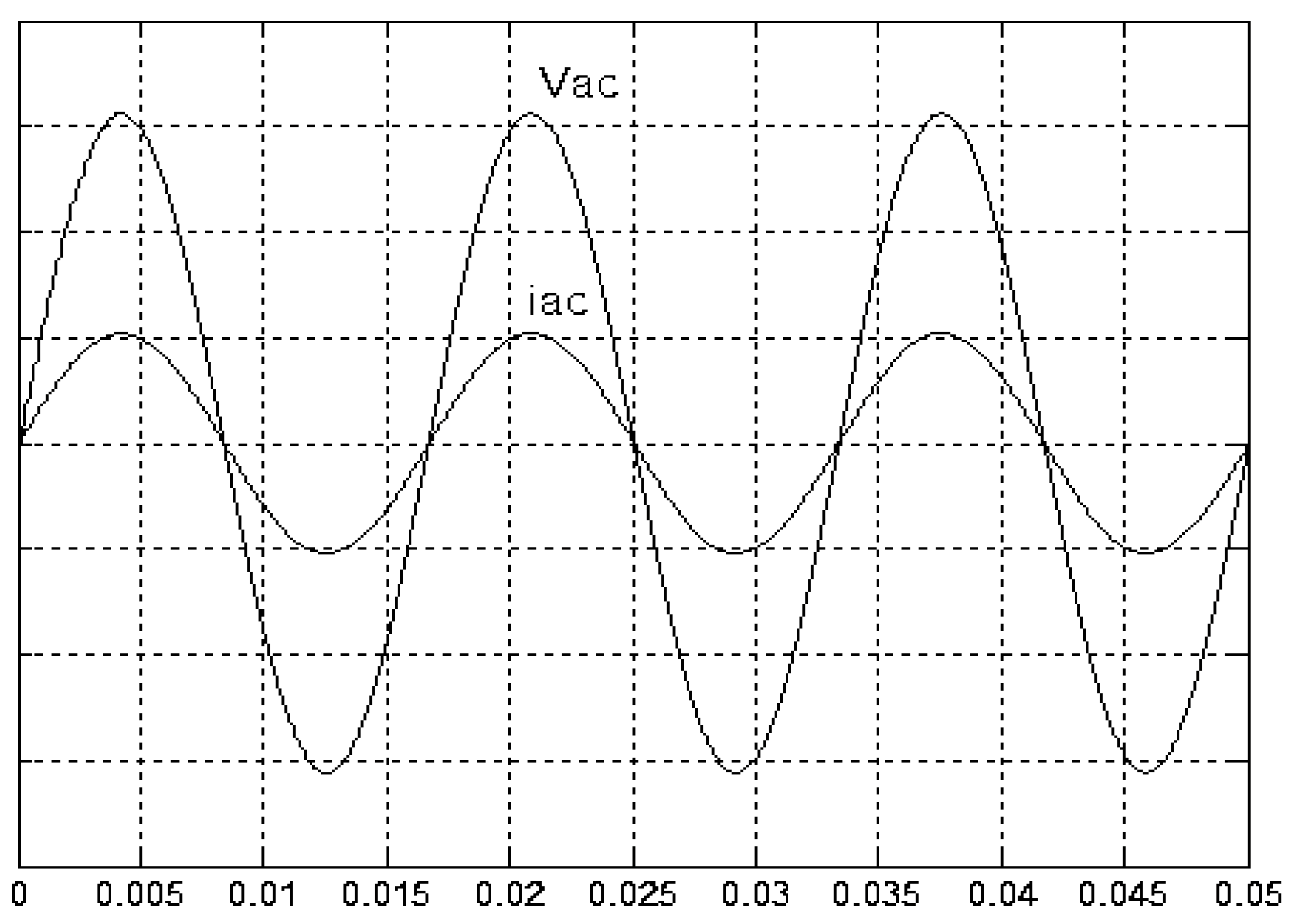
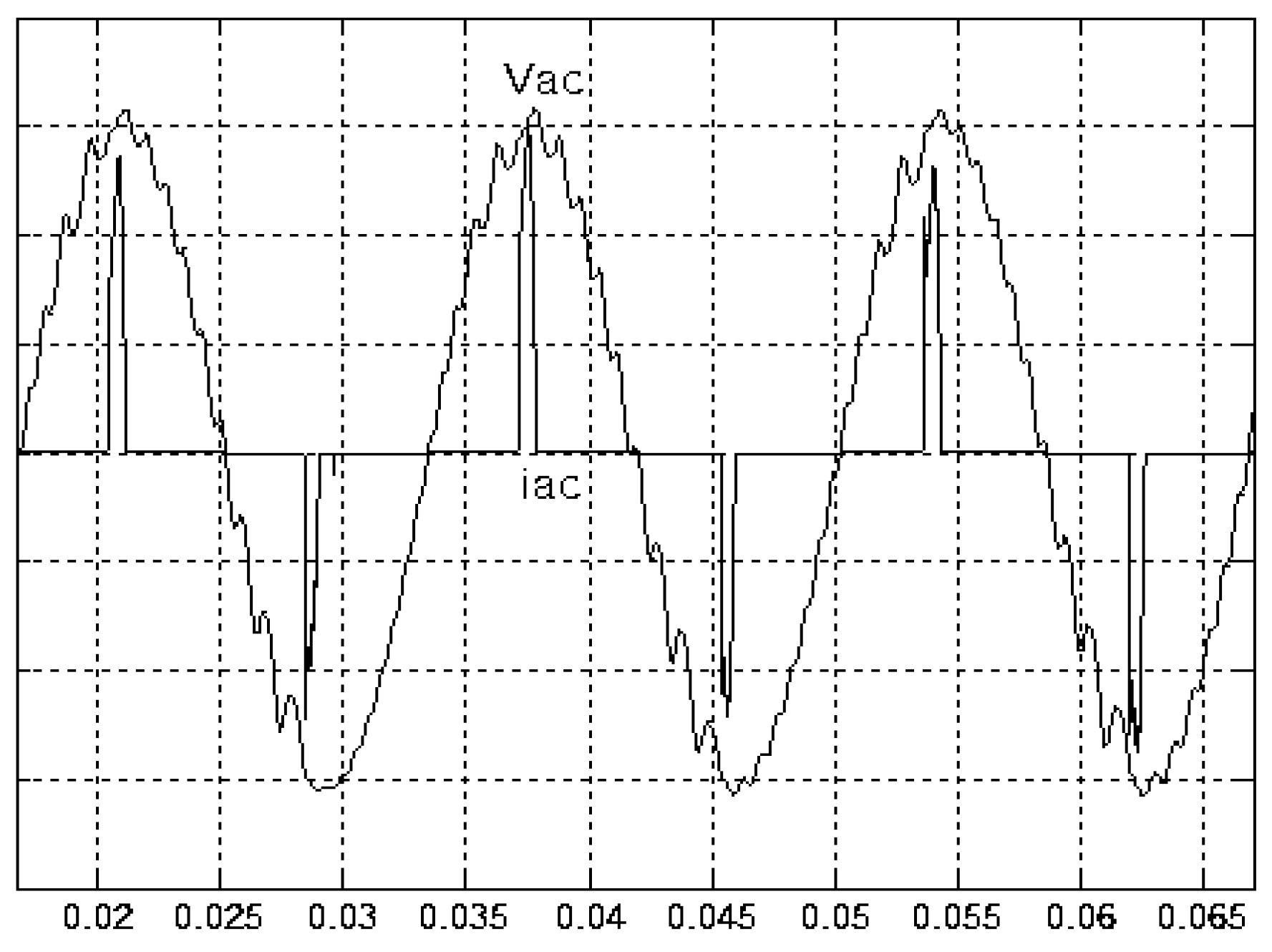
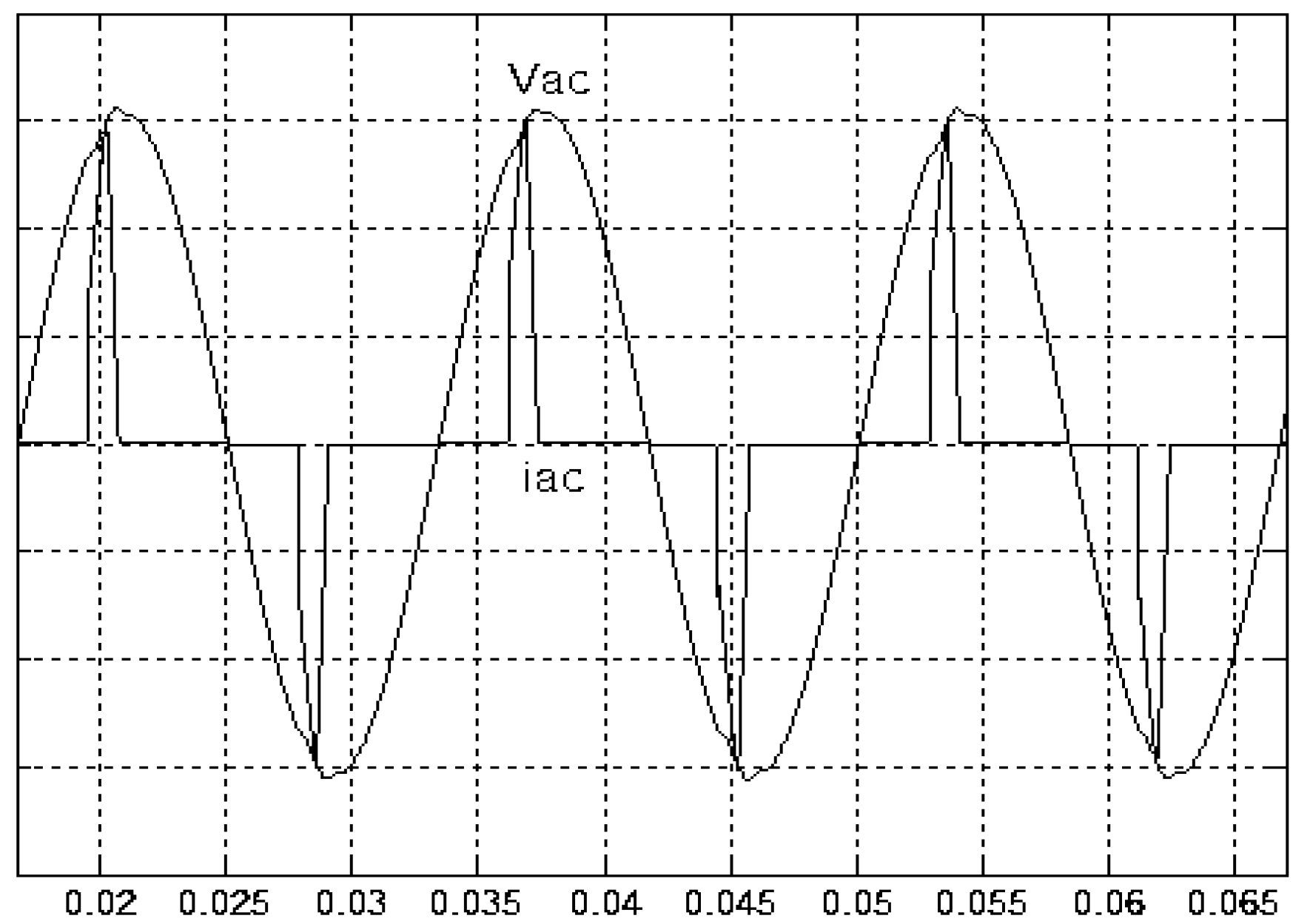
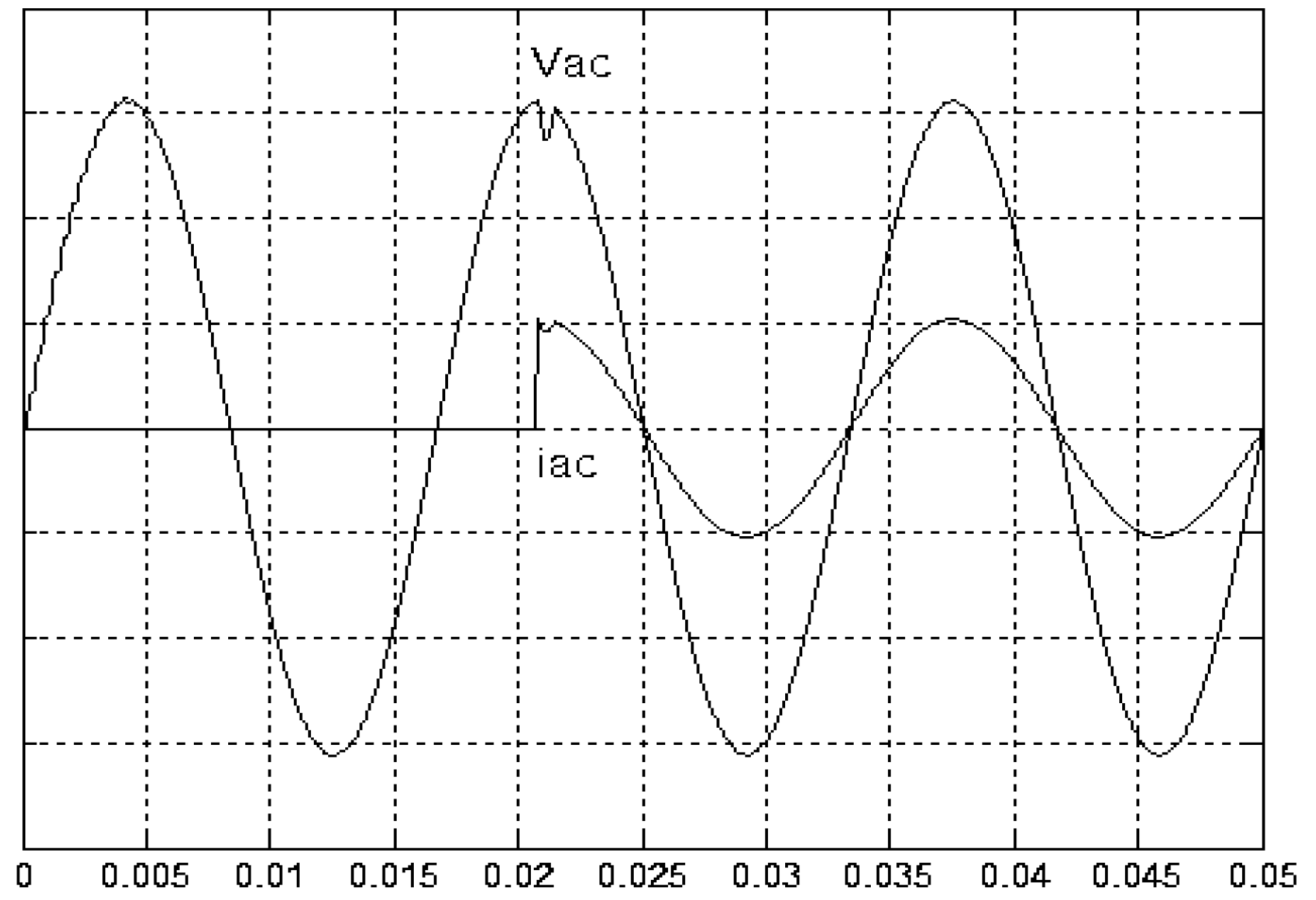
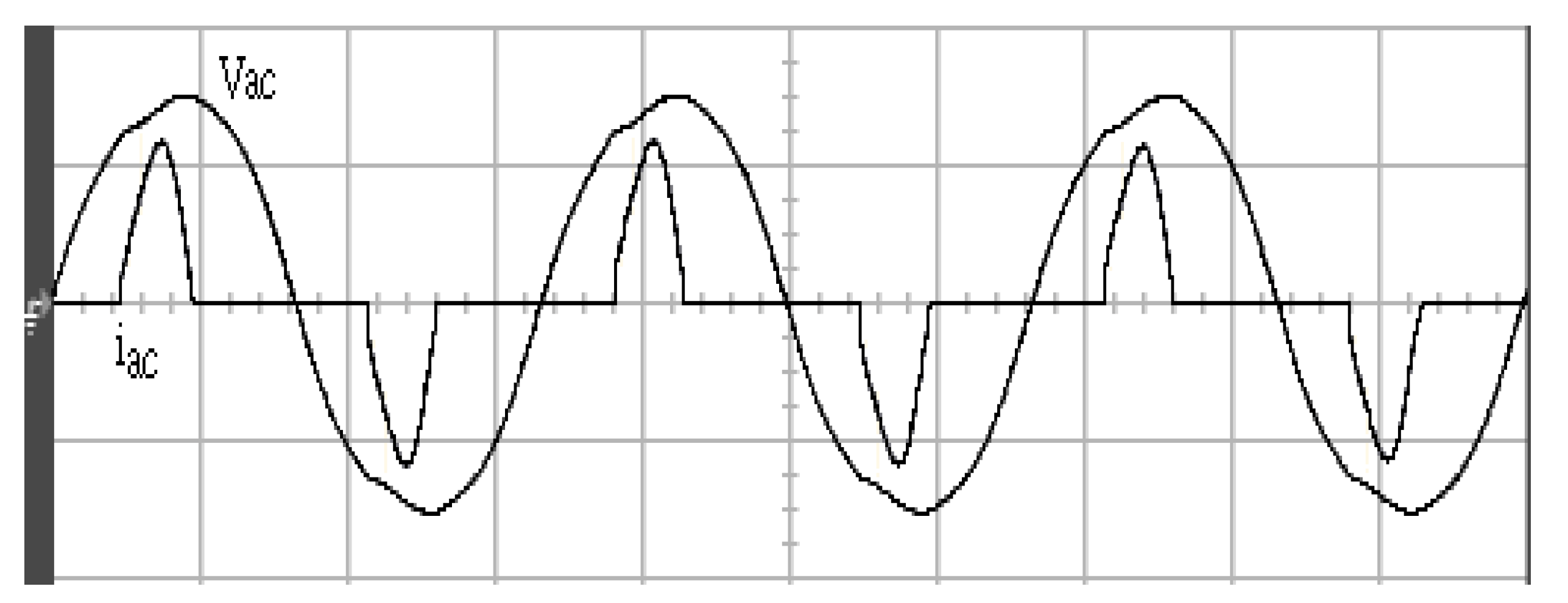
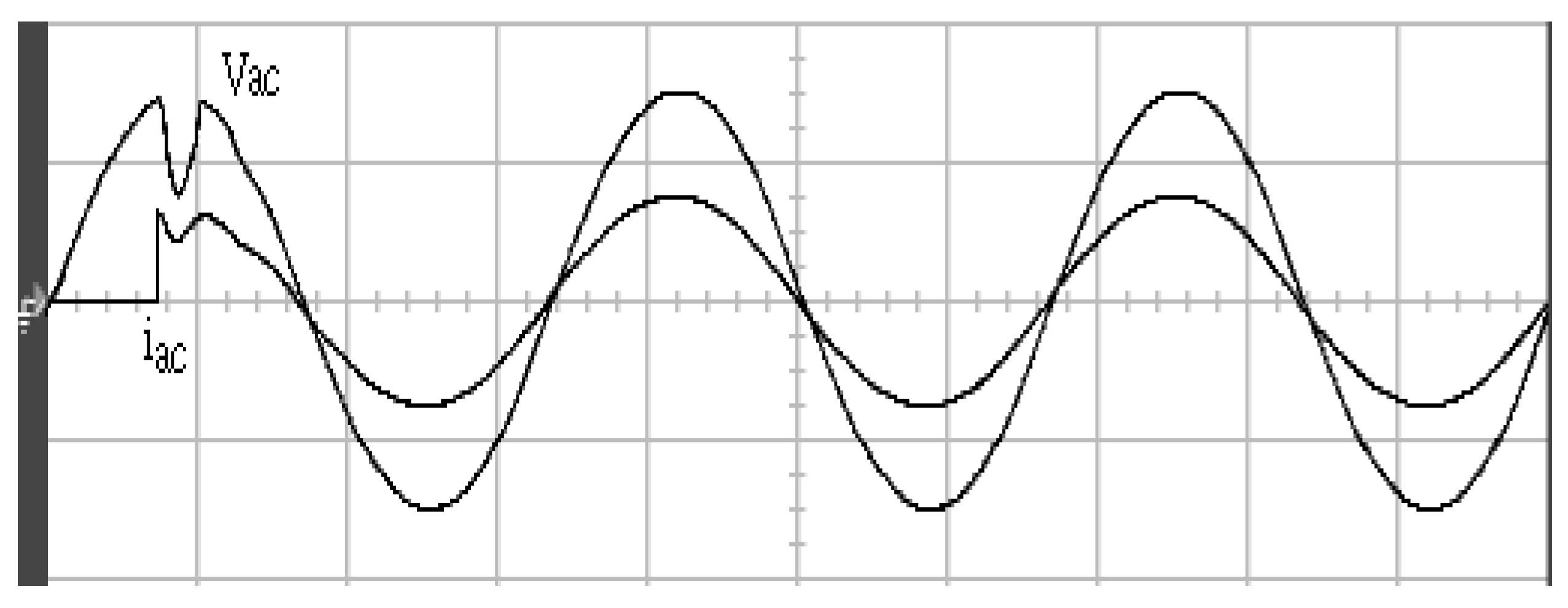
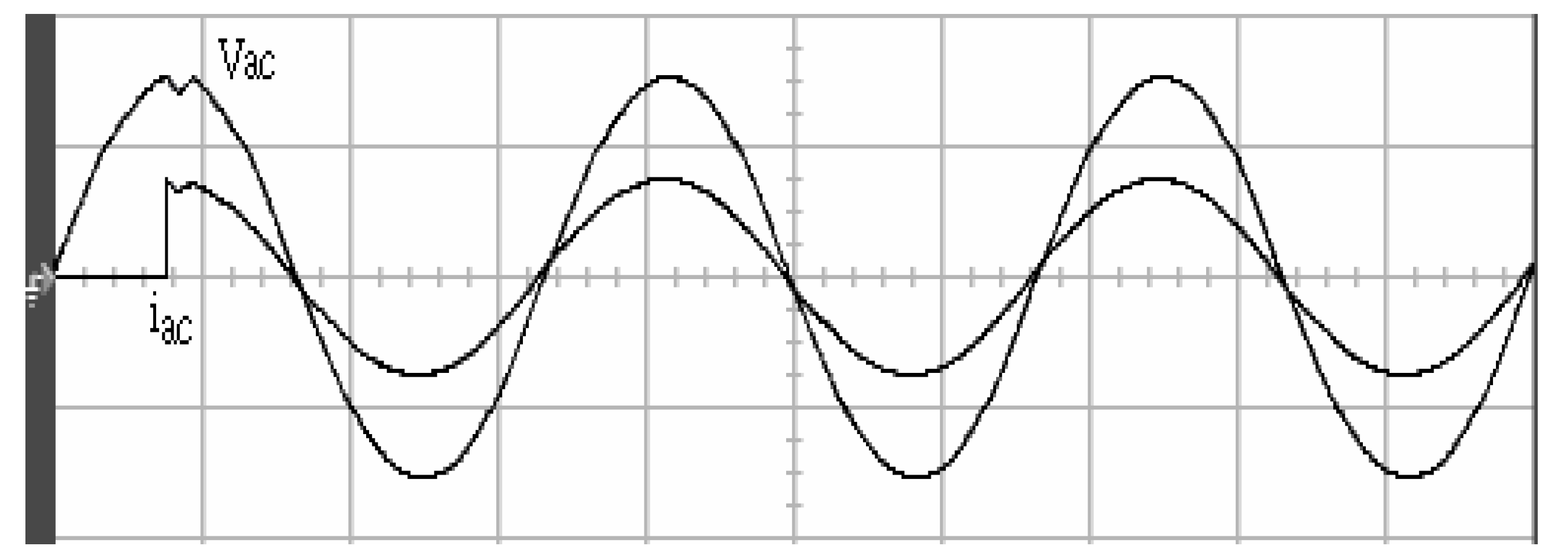
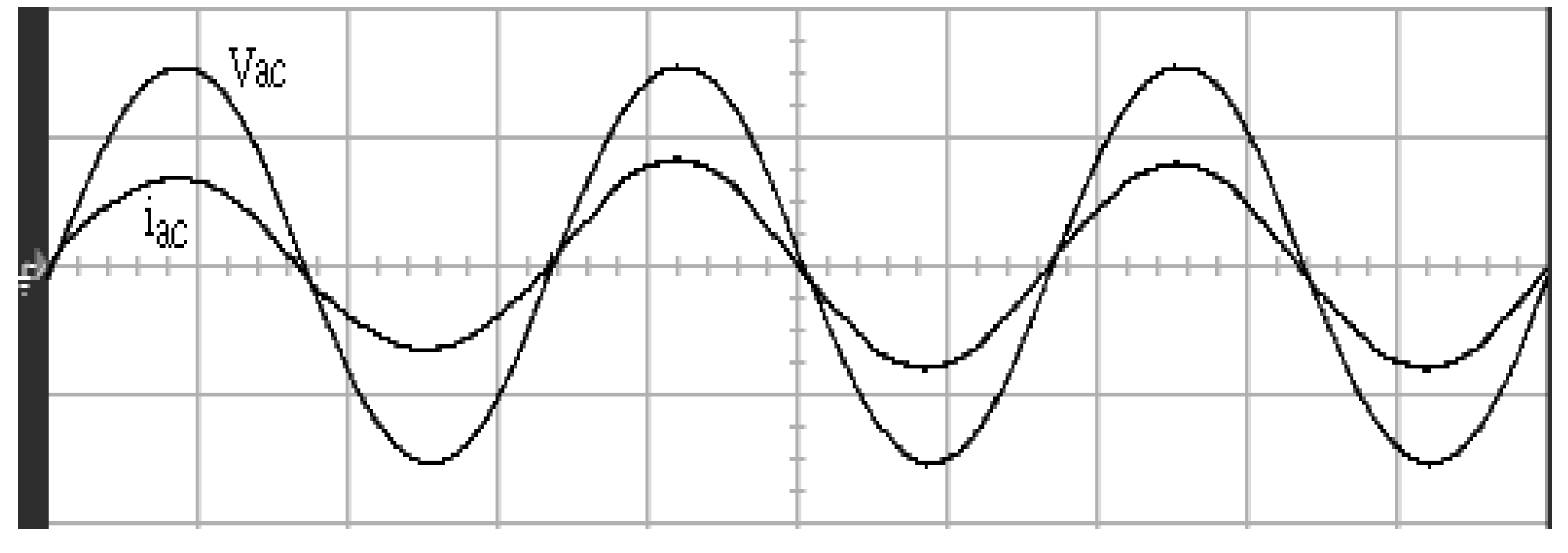
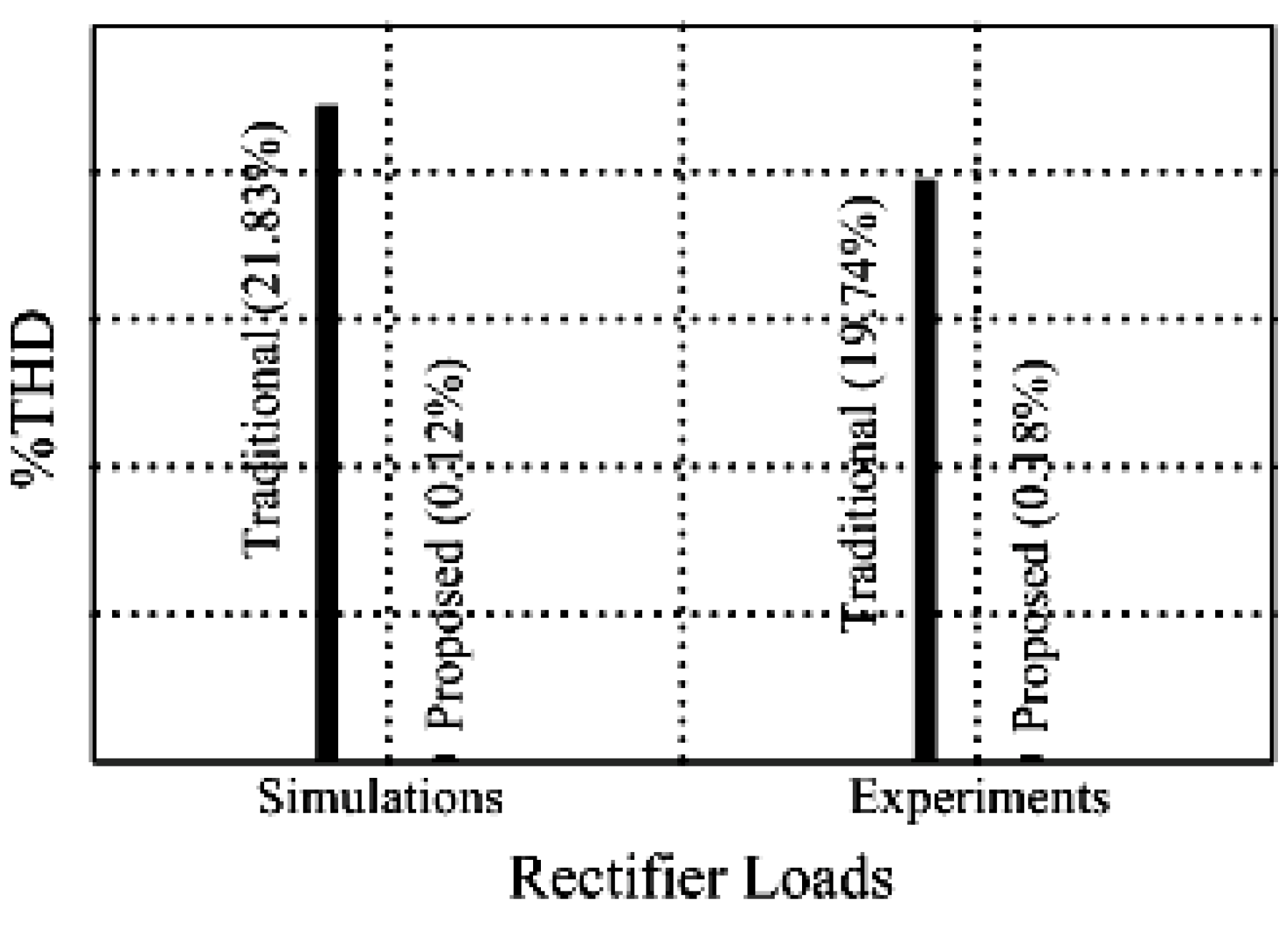
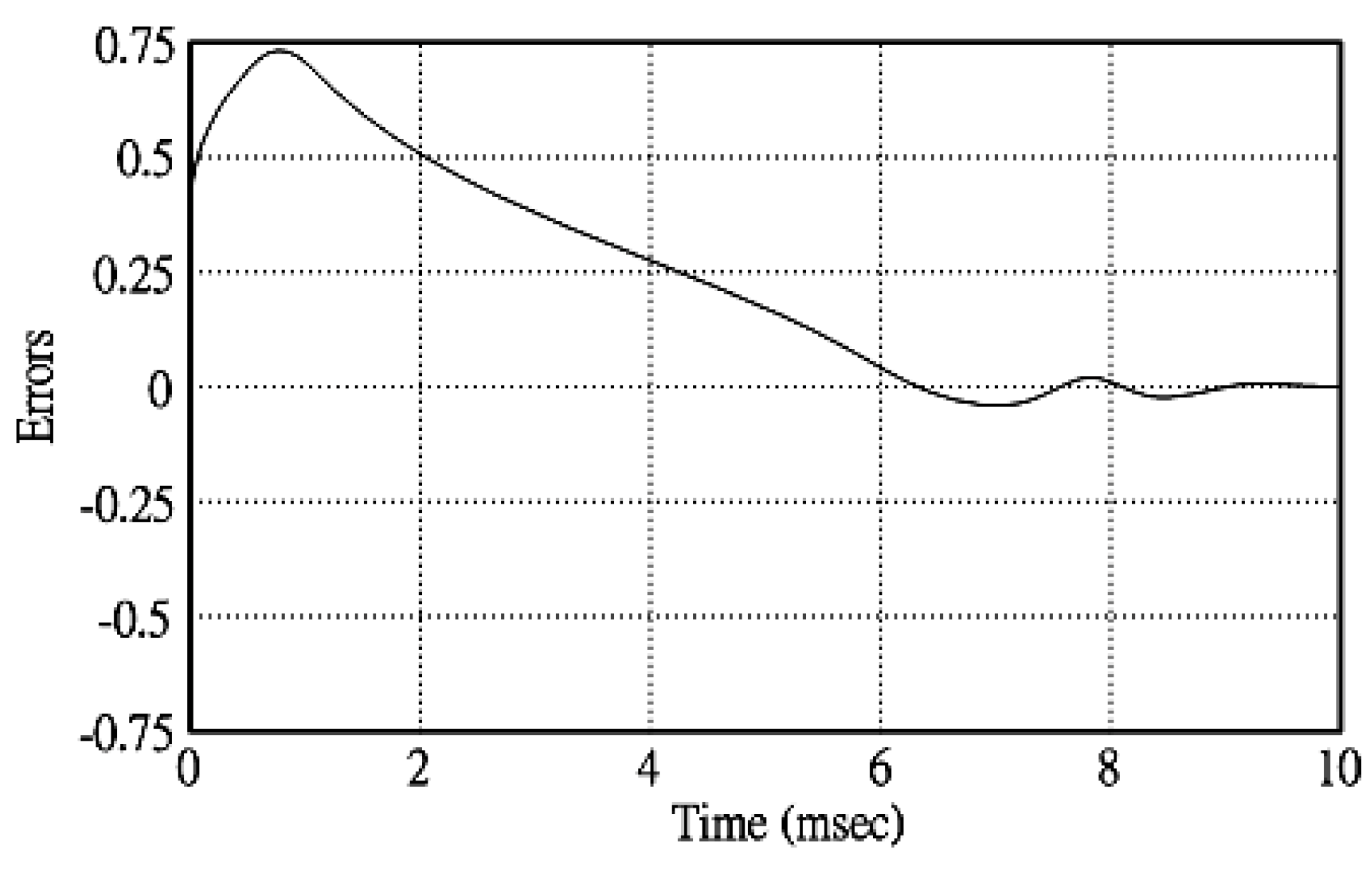
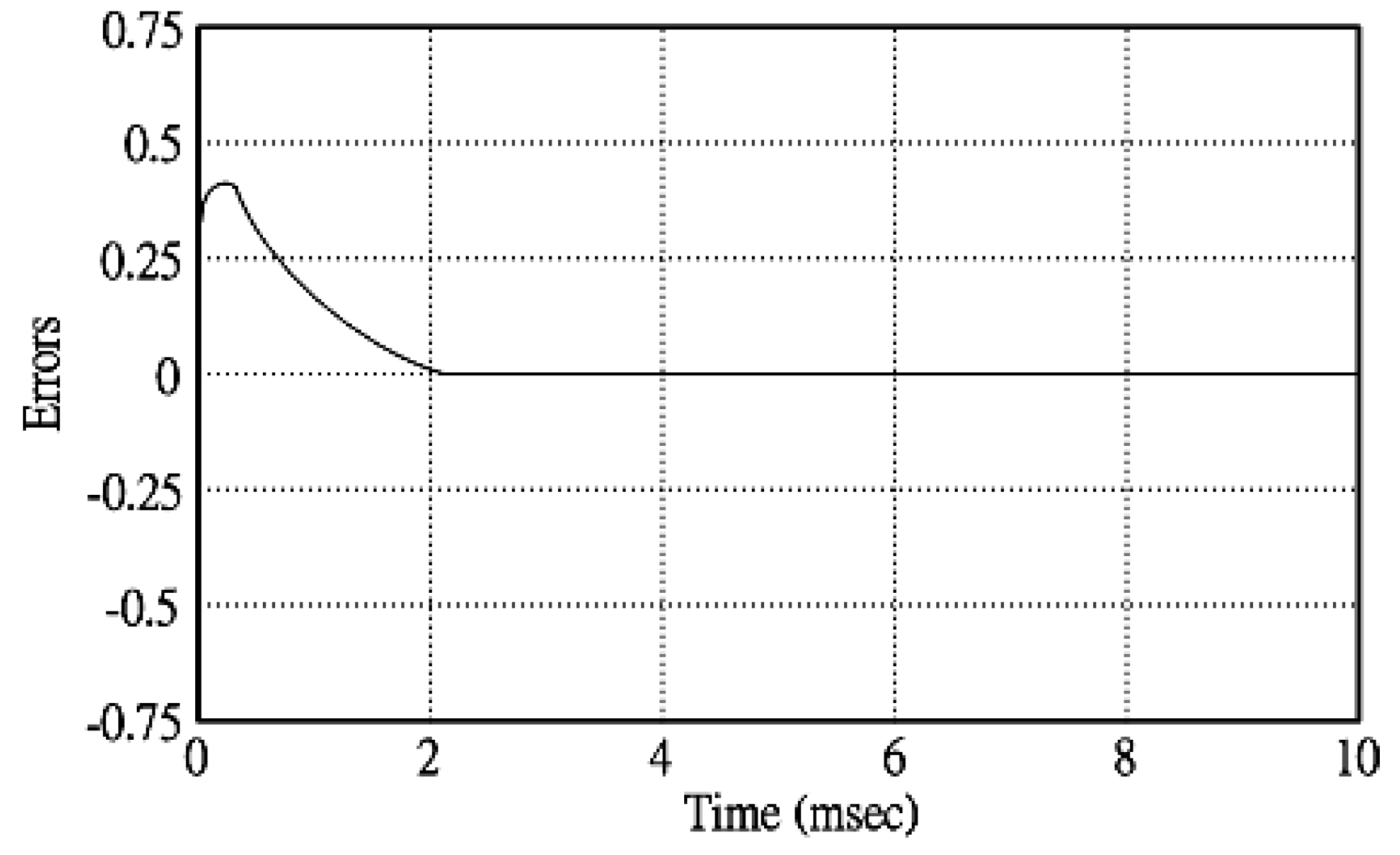
4. Results and Analysis
5. Conclusions
Funding
Conflicts of Interest
References
- Baliga, B.J. Wide Bandgap Semiconductor Power Devices; Woodhead Publishing: Cambridge, UK, 2019. [Google Scholar]
- Wang, F.; Zhang, Z.Y.; Jones, E.A. Characterization of Wide Bandgap Power Semiconductor Devices; Institution of Engineering and Technology: Stevenage, UK, 2018. [Google Scholar]
- Hatti, M. Renewable Energy for Smart and Sustainable Cities; Springer International Publishing: New York, NY, USA, 2018. [Google Scholar]
- Mohamed, M.A.; Eltamaly, A.M. Modeling and Simulation of Smart Grid Integrated with Hybrid Renewable Energy Systems; Springer International Publishing: New York, NY, USA, 2018. [Google Scholar]
- Mamatha, G. Perturb and Observe MPPT Algorithm Implementation for PV Applications. Int. J. Comput. Sci. Inf. Technol. 2015, 6, 1884–1887. [Google Scholar]
- Zhang, Q.; Hu, C.S.; Chen, L.; Amirahmadi, A.; Kutkut, N.; Shen, Z.J.; Batarseh, I. A Center Point Iteration MPPT Method With Application on the Frequency-Modulated LLC Microinverter. IEEE Trans. Power Electron. 2014, 29, 1262–1274. [Google Scholar] [CrossRef]
- Benhalima, S.; Chandra, A.; Rezkallah, M. Real-time experimental implementation of an LMS-adaline-based ANFIS controller to drive PV interfacing power system. IET Renew. Power Gener. 2019, 13, 1142–1152. [Google Scholar] [CrossRef]
- Fannakh, M.; Elhafyani, M.L.; Zouggar, S. Hardware implementation of the fuzzy logic MPPT in an Arduino card using a Simulink support package for PV application. IET Renew. Power Gener. 2019, 13, 510–518. [Google Scholar] [CrossRef]
- Steinberger, M.; Horn, M.; Fridman, L. Variable-Structure Systems and Sliding-Mode Control; Springer International Publishing: New York, NY, USA, 2020. [Google Scholar]
- Bartoszewicz, A. Recent Developments in Sliding Mode Control; IntechOpen: London, UK, 2017. [Google Scholar]
- Liu, J.K. Sliding Mode Control Using MATLAB; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Chinnappan, R.; Logamani, P.; Ramasubbu, R. Fixed frequency integral sliding-mode current-controlled MPPT boost converter for two-stage PV generation system. IET Circuits Devices Syst. 2019, 13, 793–805. [Google Scholar] [CrossRef]
- Feshara, H.F.; Ibrahim, A.M.; El-Amary, N.H.; Sharaf, S.M. Performance Evaluation of Variable Structure Controller Based on Sliding Mode Technique for a Grid-Connected Solar Network. IEEE Access 2019, 7, 84349–84359. [Google Scholar] [CrossRef]
- Pahari, O.P.; Subudhi, B. Integral sliding mode-improved adaptive MPPT control scheme for suppressing grid current harmonics for PV system. IET Renew. Power Gener. 2018, 12, 1904–1914. [Google Scholar] [CrossRef]
- Haq, I.U.; Khan, Q.; Khan, I.; Akmeliawati, R.; Nisar, K.S.; Khan, I. Maximum power extraction strategy for variable speed wind turbine system via neuro-adaptive generalized global sliding mode controller. IEEE Access 2020. [Google Scholar] [CrossRef]
- Alsumiri, M. Residual Incremental Conductance Based Nonparametric MPPT Control for Solar Photovoltaic Energy Conversion System Performance Evaluation of Variable Structure Controller Based on Sliding Mode Technique for a Grid-Connected Solar Network. IEEE Access 2019, 7, 87901–87906. [Google Scholar] [CrossRef]
- Zhu, Y.K.; Fei, J.T. Adaptive Global Fast Terminal Sliding Mode Control of Grid-connected Photovoltaic System Using Fuzzy Neural Network Approach. IEEE Access 2017, 5, 9476–94849. [Google Scholar] [CrossRef]
- Ma, H.F.; Li, Y.M. Multi-Power Reaching Law Based Discrete-Time Sliding-Mode Control. IEEE Access 2019, 7, 49822–49829. [Google Scholar] [CrossRef]
- Mojallal, A.; Lotfifard, S. Enhancement of Grid Connected PV Arrays Fault Ride Through and Post Fault Recovery Performance. IEEE Trans. Smart Grid. 2019, 10, 546–555. [Google Scholar] [CrossRef]
- Mishra, J.; Wang, L.P.; Zhu, Y.K.; Yu, X.H.; Jalili, M. A Novel Mixed Cascade Finite-Time Switching Control Design for Induction Motor. IEEE Trans. Ind. Electron. 2019, 66, 1172–1181. [Google Scholar] [CrossRef]
- Pradhan, S.; Singh, B.; Panigrahi, B.K.; Murshid, S. A Composite Sliding Mode Controller for Wind Power Extraction in Remotely Located Solar PV–Wind Hybrid System. IEEE Trans. Ind. Electron. 2019, 66, 5321–5331. [Google Scholar] [CrossRef]
- Yazıcı, İ.; Yaylacı, E.K. Discrete-time integral terminal sliding mode based maximum power point controller for the PMSG-based wind energy system. IET Power Electron. 2019, 12, 3688–3696. [Google Scholar] [CrossRef]
- Mojallizadeh, M.R.; Badamchizadeh, M.; Khanmohammadi, S.; Sabahi, M. Chattering free full-order terminal sliding-mode control for maximum power point tracking of photovoltaic cells. IET Renew. Power Gener. 2017, 11, 85–91. [Google Scholar] [CrossRef]
- Yang, B.; Zhong, L.; Yu, T.; Shu, H.C.; Cao, P.L.; An, N.; Sang, Y.Y.; Jiang, L. PCSMC design of permanent magnetic synchronous generator for maximum power point tracking. IET Gener. Transm. Distrib. 2019, 13, 3115–3126. [Google Scholar] [CrossRef]
- Wang, S.Y.; Li, S.Q.; Gu, R.J.; Ma, L.Y.; Li, M.J. Adaptive sliding mode based active disturbance rejection control method for a direct-driven wind power conversion system. J. Eng. 2019, 2019, 8365–8369. [Google Scholar] [CrossRef]
- Zolfaghari, M.; Hosseinian, S.H.; Fathi, S.H.; Abedi, M.; Gharehpetian, G.B. A New Power Management Scheme for Parallel-Connected PV Systems in Microgrids. IEEE Trans. Sustain. Energy 2018, 9, 1605–1617. [Google Scholar] [CrossRef]
- Bag, A.; Subudhi, B.; Ray, P.K. A combined reinforcement learning and sliding mode control scheme for grid integration of a PV system. CSEE J. Power Energy Syst. 2019, 5, 498–506. [Google Scholar]
- Yang, X.S.; Deb, S. Cuckoo search: Recent advances and applications. Neural Comput. Appl. 2014, 24, 169–174. [Google Scholar] [CrossRef]
- Huang, X.L.; Xie, Z.Y.; Huang, X.Y. Fault Location of Distribution Network Base on Improved Cuckoo Search Algorithm. IEEE Access 2020, 8, 2272–2283. [Google Scholar] [CrossRef]
- Zhang, Z.C.; Hong, W.C.; Li, J.C. Electric Load Forecasting by Hybrid Self-Recurrent Support Vector Regression Model With Variational Mode Decomposition and Improved Cuckoo Search Algorithm. IEEE Access 2020, 8, 14642–14658. [Google Scholar] [CrossRef]
- Wang, D.Y.; Zhou, L.J.; Dai, C.J.; Guo, L.; Liao, W. Insulation Defect Diagnostic Method for OIP Bushing Based on Multiclass LS-SVM and Cuckoo Search. IEEE Trans. Instrum. Meas. 2020, 69, 163–172. [Google Scholar] [CrossRef]
- Wang, R.Q.; Jiao, Y.C. Synthesis of Sparse Linear Arrays With Reduced Excitation Control Numbers Using a Hybrid Cuckoo Search Algorithm With Convex Programming. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 428–432. [Google Scholar] [CrossRef]
- Gao, S.Z.; Gao, Y.; Zhang, Y.M.; Xu, L.T. Multi-Strategy Adaptive Cuckoo Search Algorithm. IEEE Access 2019, 7, 137642–137655. [Google Scholar] [CrossRef]
- Ji, J.C.; Pang, W.; Li, Z.R.; He, F.; Feng, G.Z.; Zhao, X.W. Clustering Mixed Numeric and Categorical Data With Cuckoo Search. IEEE Access 2020, 8, 30988–31003. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, J.Y.; Zhang, X.D.; Kurniawan, A.; Juhana, T.; Ai, B. Tabu-Search-Based Pilot Assignment for Cell-Free Massive MIMO Systems. IEEE Trans. Veh. Technol. 2020, 69, 2286–2290. [Google Scholar] [CrossRef]
- Lai, X.J.; Fu, Z.H. A Tabu Search Approach With Dynamical Neighborhood Size for Solving the Maximum Min-Sum Dispersion Problem. IEEE Access 2019, 7, 181357–181368. [Google Scholar] [CrossRef]
- Zhang, W.F.; Feng, W.Q.; Zhao, H.B.; Zhao, Q.A. Rapidly Learning Bayesian Networks for Complex System Diagnosis: A Reinforcement Learning Directed Greedy Search Approach. IEEE Access 2020, 8, 2813–2823. [Google Scholar] [CrossRef]
- Zhou, J.; Zhao, X.Z.; Zhang, X.P.; Zhao, D.D.; Li, H.H. Task Allocation for Multi-Agent Systems Based on Distributed Many-Objective Evolutionary Algorithm and Greedy Algorithm. IEEE Access 2020, 8, 19306–19318. [Google Scholar] [CrossRef]
- Musiał, K.; Kotowska, J.; Górnicka, D.; Burduk, A. Tabu Search and Greedy Algorithm Adaptation to Logistic Task. In Proceedings of the 16th International Conference on Computer Information Systems and Industrial Management Applications (CISIM 2017), Bialystok, Poland, 16–18 June 2017; pp. 39–49. [Google Scholar]
- Gokhale, S.S.; Kale, V.S. Time overcurrent relay coordination using the Levy flight Cuckoo search algorithm. In Proceedings of the 2015 IEEE Region 10 Conference (TENCON 2015), Macau, China, 1–4 November 2015; pp. 1–6. [Google Scholar]
- Gálvez, A.; Iglesias, A.; Cabellos, L. Cuckoo Search with Lévy Flights for Weighted Bayesian Energy Functional Optimization in Global-Support Curve Data Fitting. Sci. World J. 2014, 2014, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.S.; He, X.S. Mathematical Foundations of Nature-Inspired Algorithms; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Wang, J.; Zhou, B.H.; Zhou, S.D. An Improved Cuckoo Search Optimization Algorithm for the Problem of Chaotic Systems Parameter Estimation. Comput. Intell. Neurosci. 2016, 2016, 1–8. [Google Scholar] [CrossRef] [PubMed]
- El Gmili, N.; Mjahed, M.; El Kari, A.; Ayad, H. Particle Swarm Optimization and Cuckoo Search-Based Approaches for Quadrotor Control and Trajectory Tracking. Appl. Sci. 2019, 9, 1719. [Google Scholar] [CrossRef]
- Iglesias, A.; Gálvez, A.; Suárez, P.; Shinya, M.; Yoshida, N.; Otero, C.; Manchado, C.; Gomez-Jauregui, V. Cuckoo Search Algorithm with Lévy Flights for Global-Support Parametric Surface Approximation in Reverse Engineering. Symmetry 2018, 10, 58. [Google Scholar] [CrossRef]
- Huang, L.B.; Xin, H.H.; Dörfler, F. H∞-Control of Grid-Connected Converters: Design, Objectives and Decentralized Stability Certificates. IEEE Trans. Smart Grid 2020, 1. [Google Scholar] [CrossRef]
- Jamil, M.; Waris, A.; Gilani, S.O.; Khawaja, B.A.; Khan, M.N.; Raza, A. Design of Robust Higher-Order Repetitive Controller Using Phase Lead Compensator. IEEE Access 2020, 8, 30603–31614. [Google Scholar] [CrossRef]
- Wang, B.F.; Manandhar, U.; Zhang, X.N.; Gooi, H.B.; Ukil, A. Deadbeat Control for Hybrid Energy Storage Systems in DC Microgrids. IEEE Trans. Sustain. Energy 2019, 10, 1867–1877. [Google Scholar] [CrossRef]
- Ghafouri, M.; Karaagac, U.; Karimi, H.; Mahseredjian, J. Robust subsynchronous interaction damping controller for DFIG-based wind farms. J. Mod. Power Syst. Clean Energy 2019, 7, 1663–1674. [Google Scholar] [CrossRef]
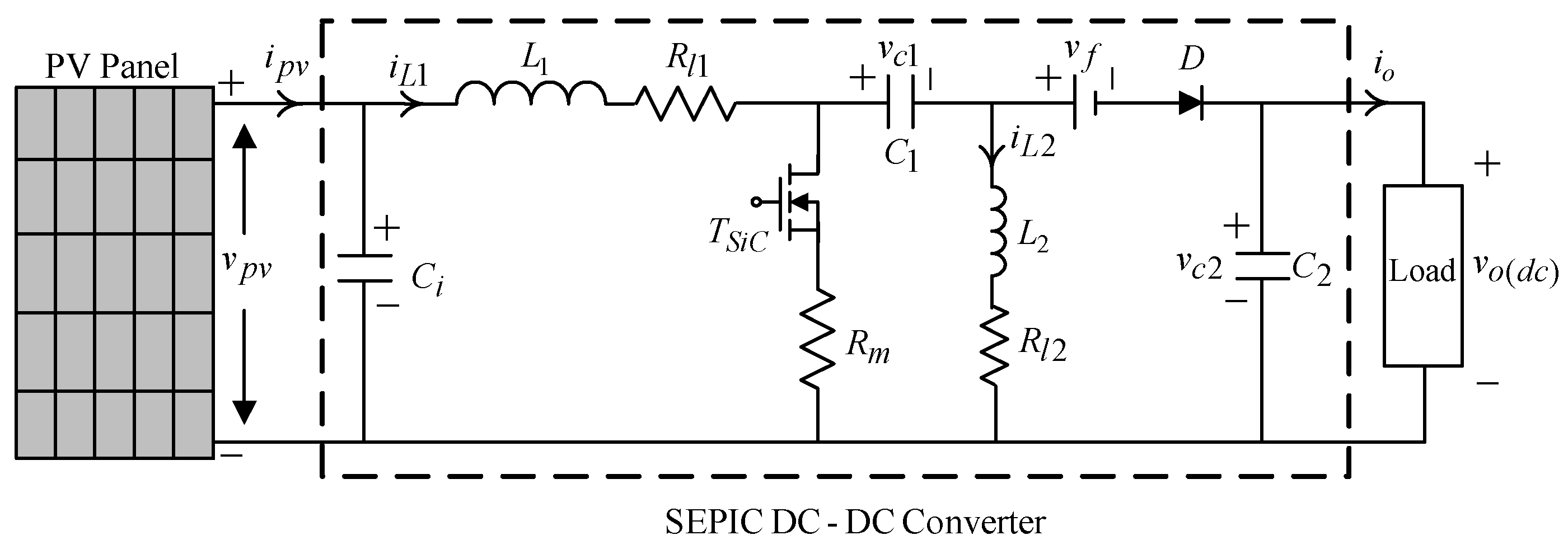
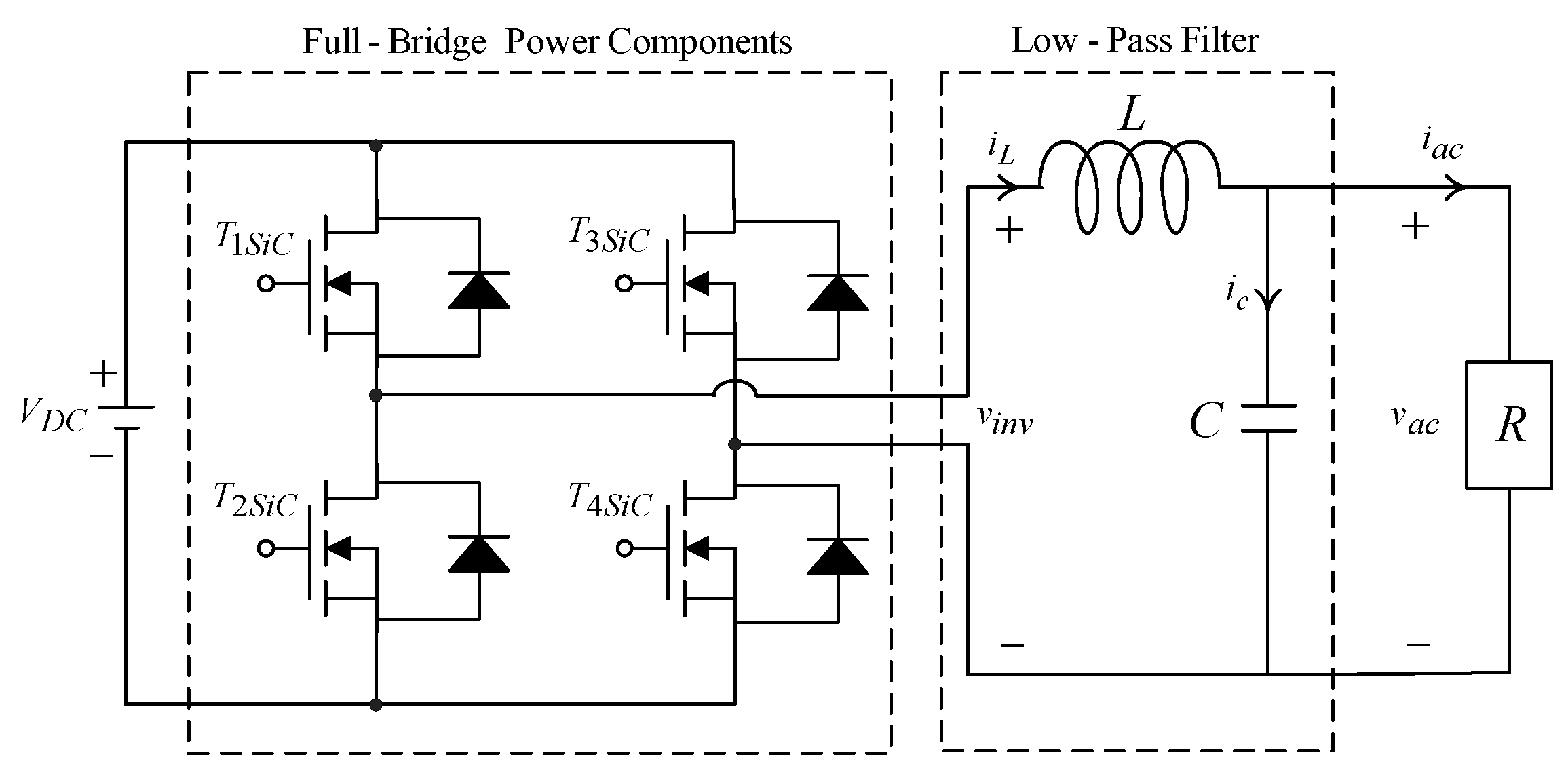



| SEPIC DC-DC Converter | |
| Inductance | 50 μH |
| Internal resistance | 136 mΩ |
| Input capacitance | 330 μF |
| Output capacitance | 1000 μF |
| Single-phase DC-AC Inverter | |
| Filter inductor | 0.2 mH |
| Filter capacitor | 5 μF |
| Resistive load | 12 Ω |
| DC-link voltage | 200 V |
| AC output voltage | 110 Vrms |
| AC output-voltage frequency | 60 Hz |
| Switching frequency | 24 kHz |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, E.-C. High-Performance Pure Sine Wave Inverter with Robust Intelligent Sliding Mode Maximum Power Point Tracking for Photovoltaic Applications. Micromachines 2020, 11, 585. https://doi.org/10.3390/mi11060585
Chang E-C. High-Performance Pure Sine Wave Inverter with Robust Intelligent Sliding Mode Maximum Power Point Tracking for Photovoltaic Applications. Micromachines. 2020; 11(6):585. https://doi.org/10.3390/mi11060585
Chicago/Turabian StyleChang, En-Chih. 2020. "High-Performance Pure Sine Wave Inverter with Robust Intelligent Sliding Mode Maximum Power Point Tracking for Photovoltaic Applications" Micromachines 11, no. 6: 585. https://doi.org/10.3390/mi11060585
APA StyleChang, E.-C. (2020). High-Performance Pure Sine Wave Inverter with Robust Intelligent Sliding Mode Maximum Power Point Tracking for Photovoltaic Applications. Micromachines, 11(6), 585. https://doi.org/10.3390/mi11060585




