AC/DC Fields Demodulation Methods of Resonant Electric Field Microsensor
Abstract
1. Introduction
2. Resonant EFM with Coplanar Electrodes
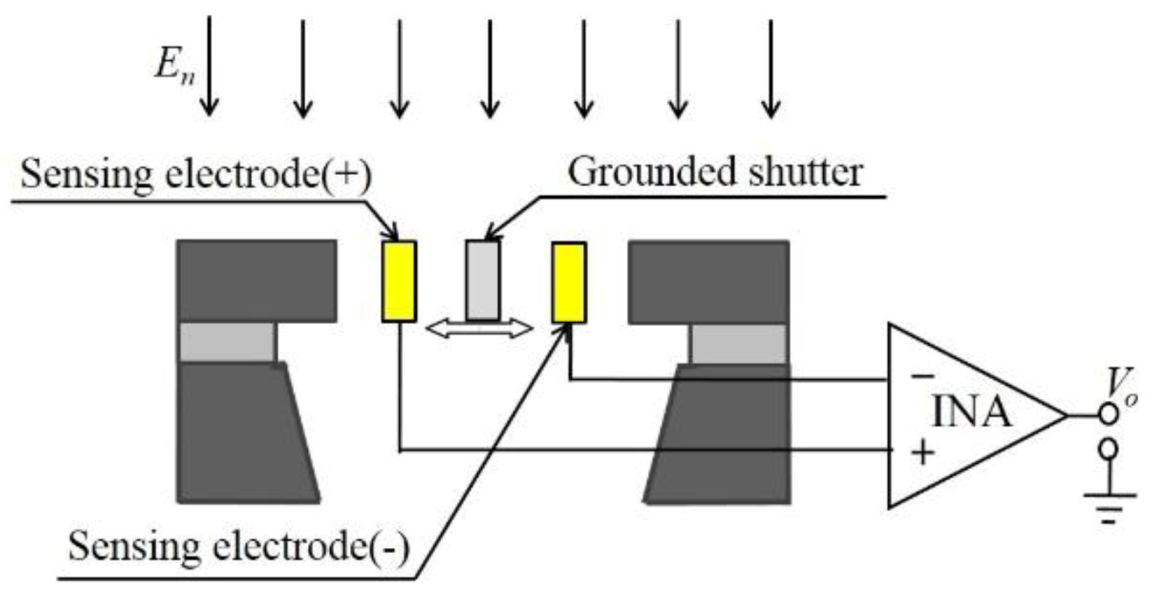
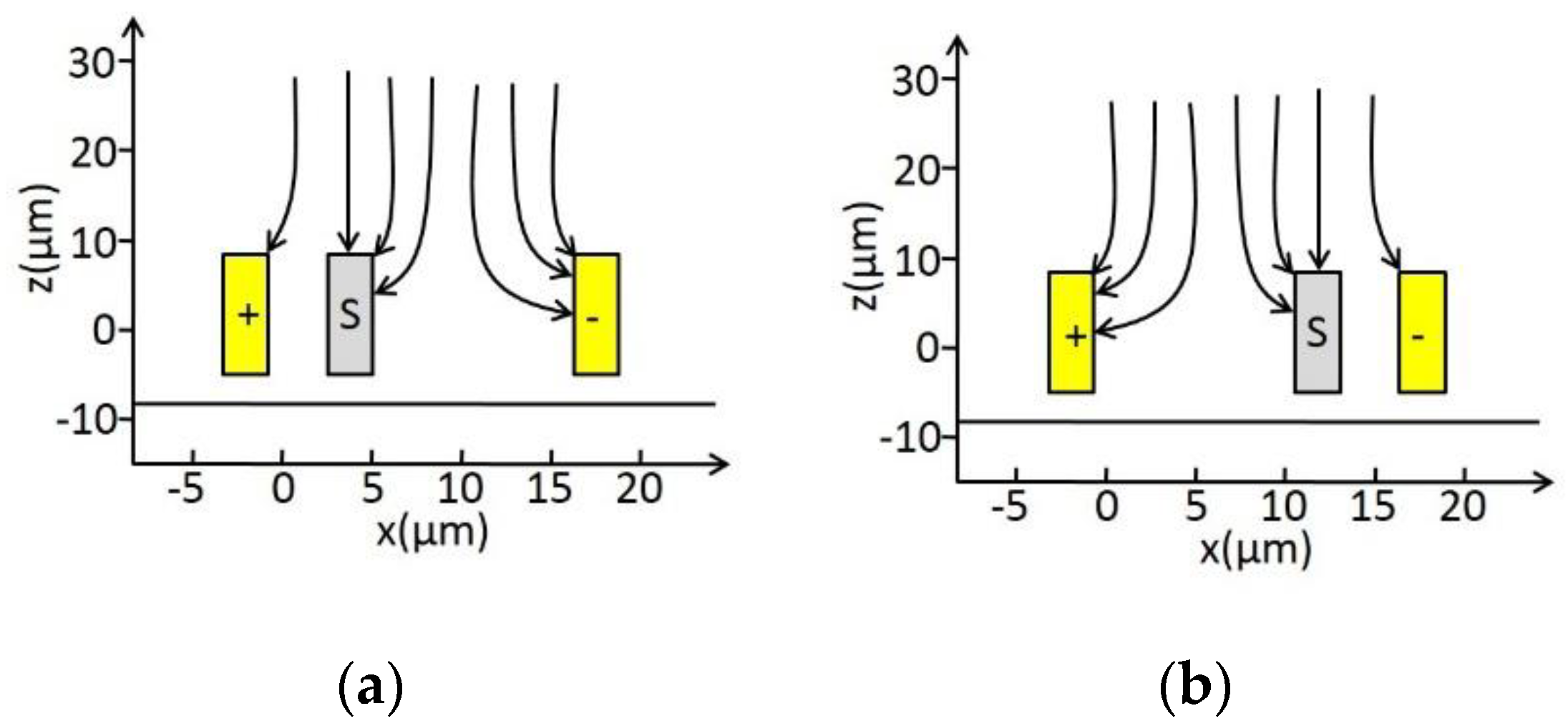
2.1. Operating Principle
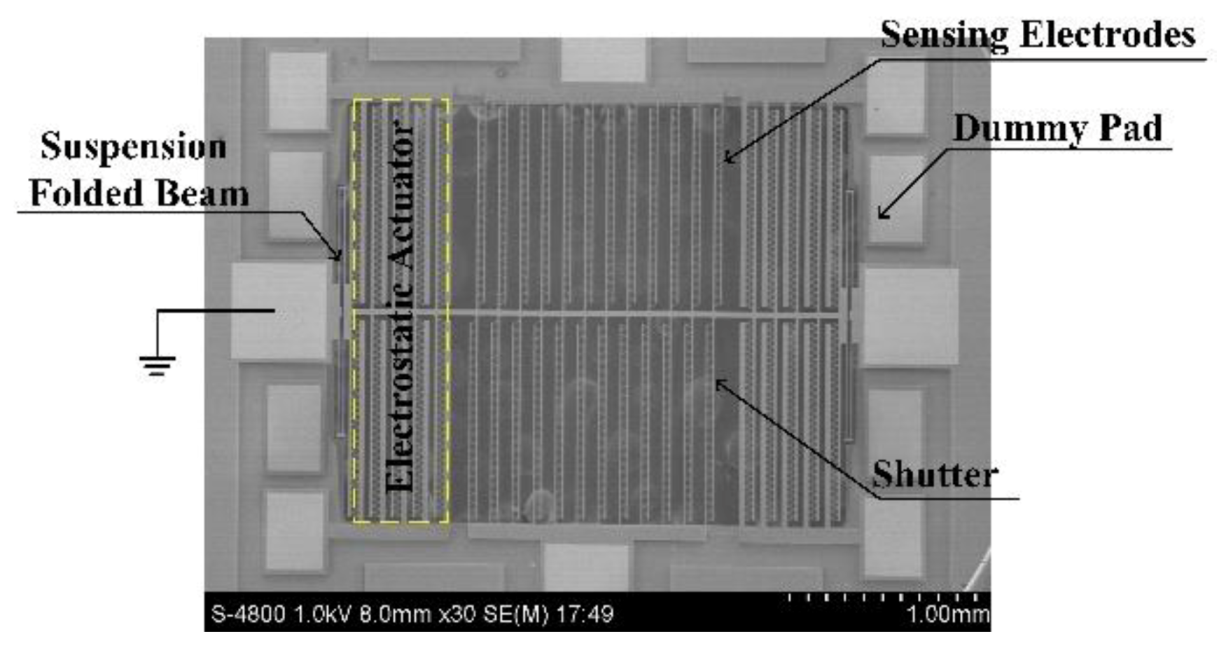
2.2. Structure and Fabrication
2.3. Differential Induced Charge and Output Signal
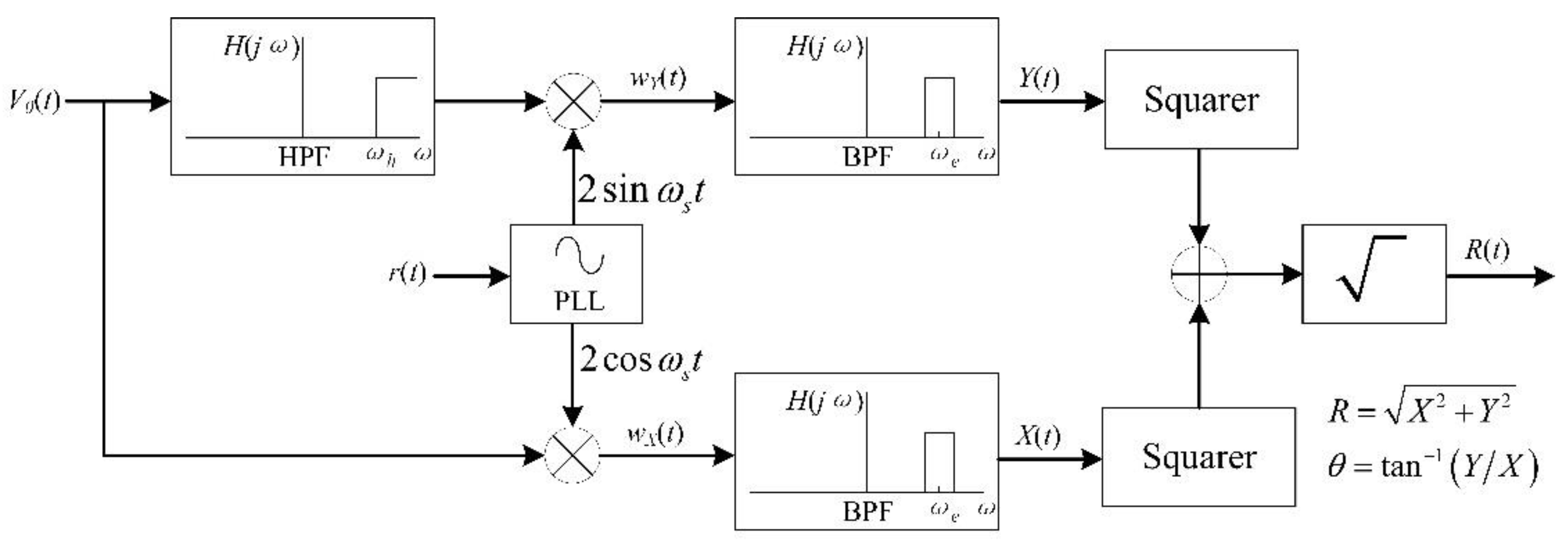
3. Demodulation Methods
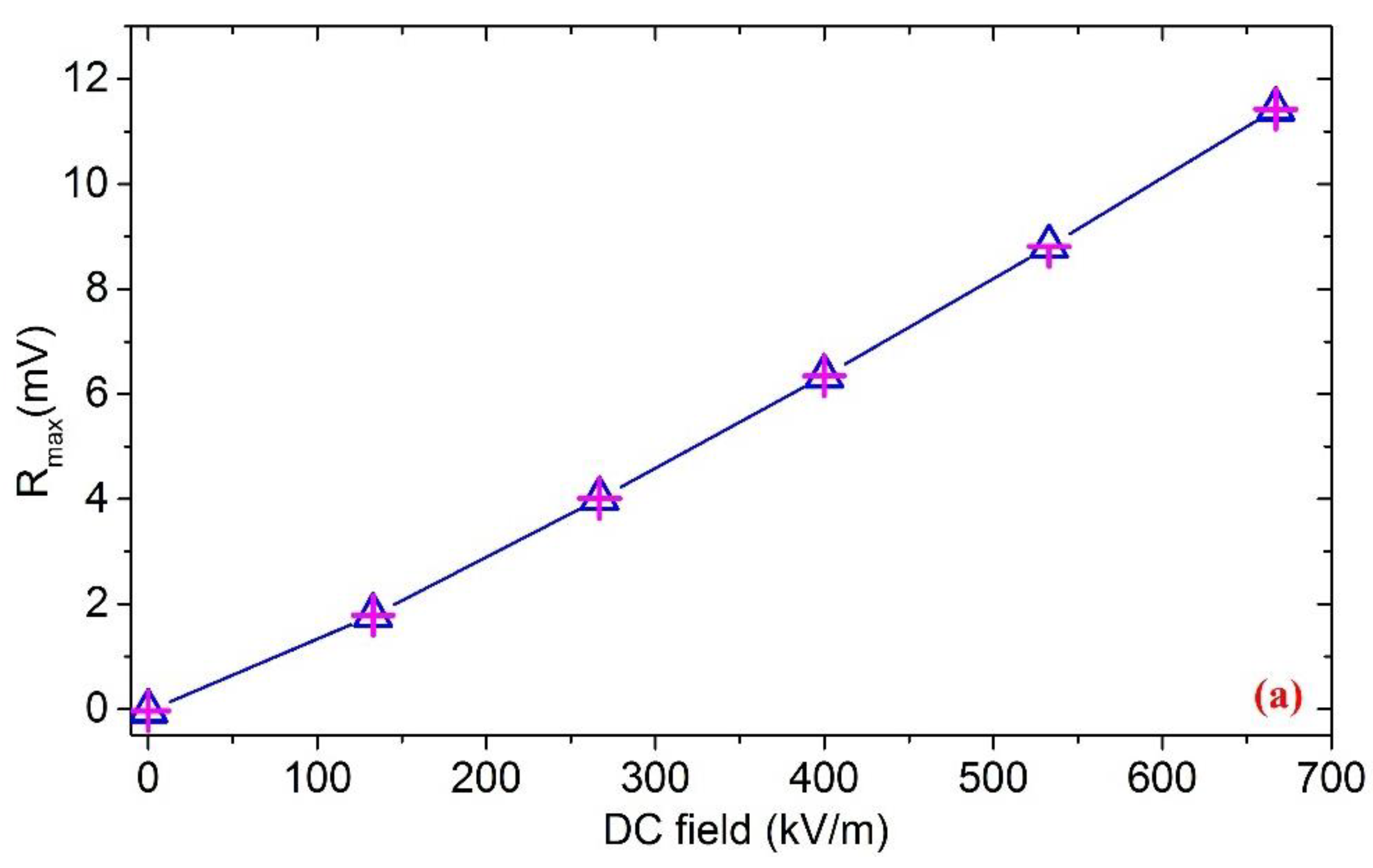
3.1. DC Electric Field Demodulation
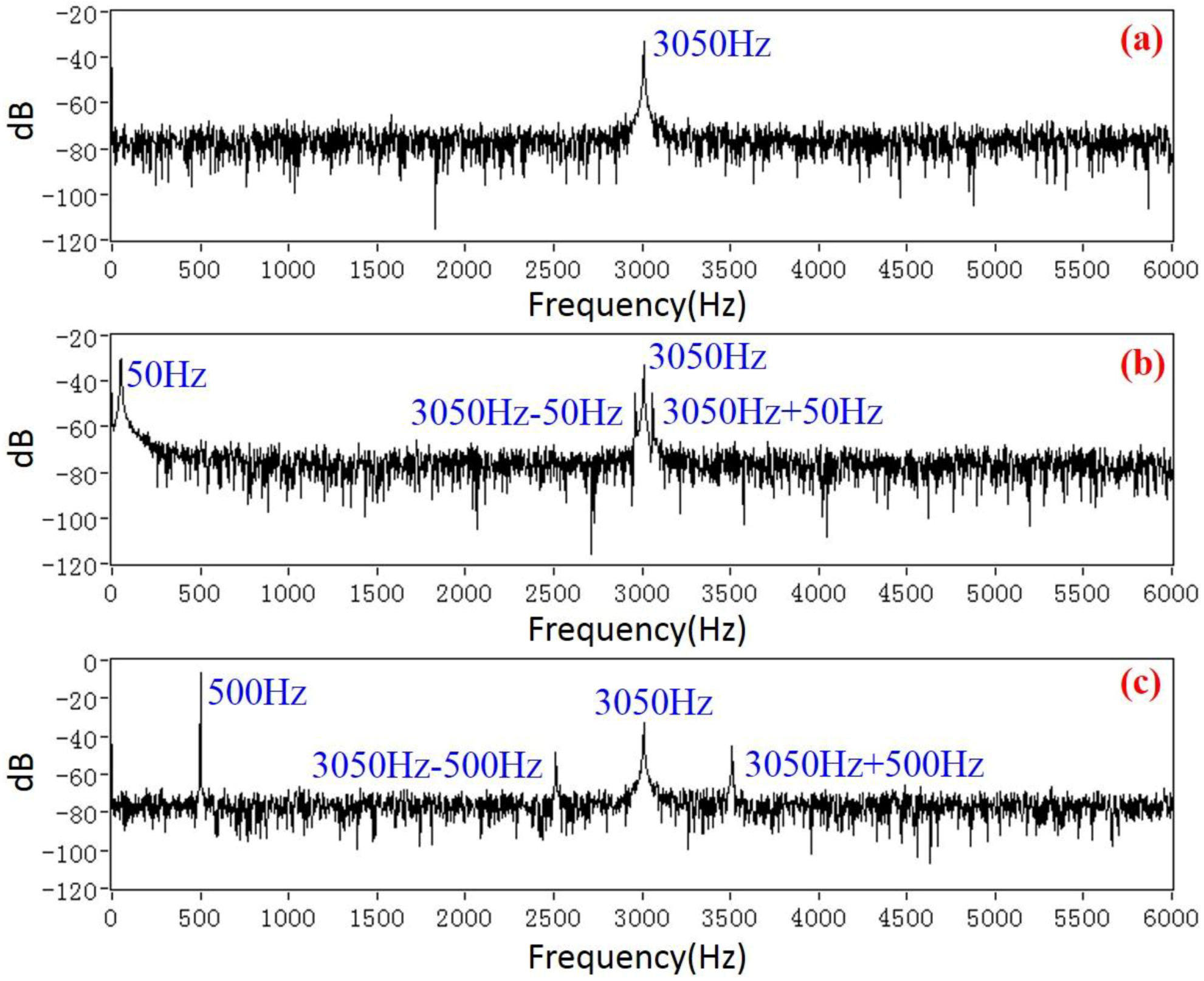
3.2. Power Frequency Electric Field Demodulation
- Because the microsensor output first passes a high-pass filter, the influence of power frequency interference and its harmonic components on the electric field measurements is suppressed.
- Unlike the synchronous demodulation of the DC electric field using a low-pass filter, band-pass filters are used to obtain the power frequency electric field signal, which inhibits the impact of the AC drive-signal feedthrough of the EFM.
- Unlike the synchronous demodulation of the DC electric field, using the HOCBM to finally extract the peak value of R (t) can avoid the change of the microsensor sensitivity caused by the θ variation.
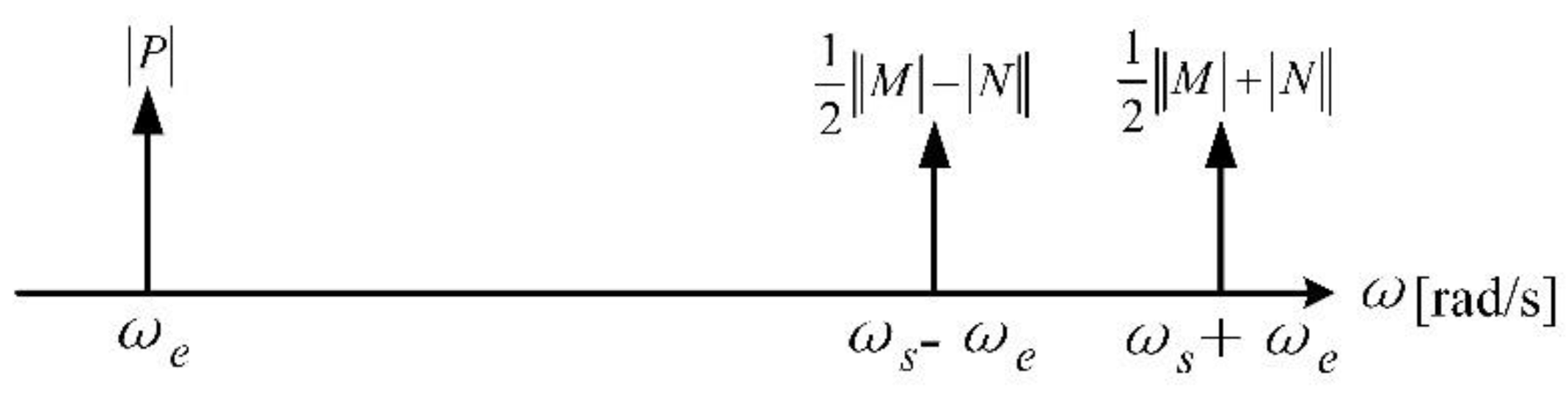
3.3. AC/DC Hybrid Electric Fields Demodulation
4. Experimental Results and Discussion
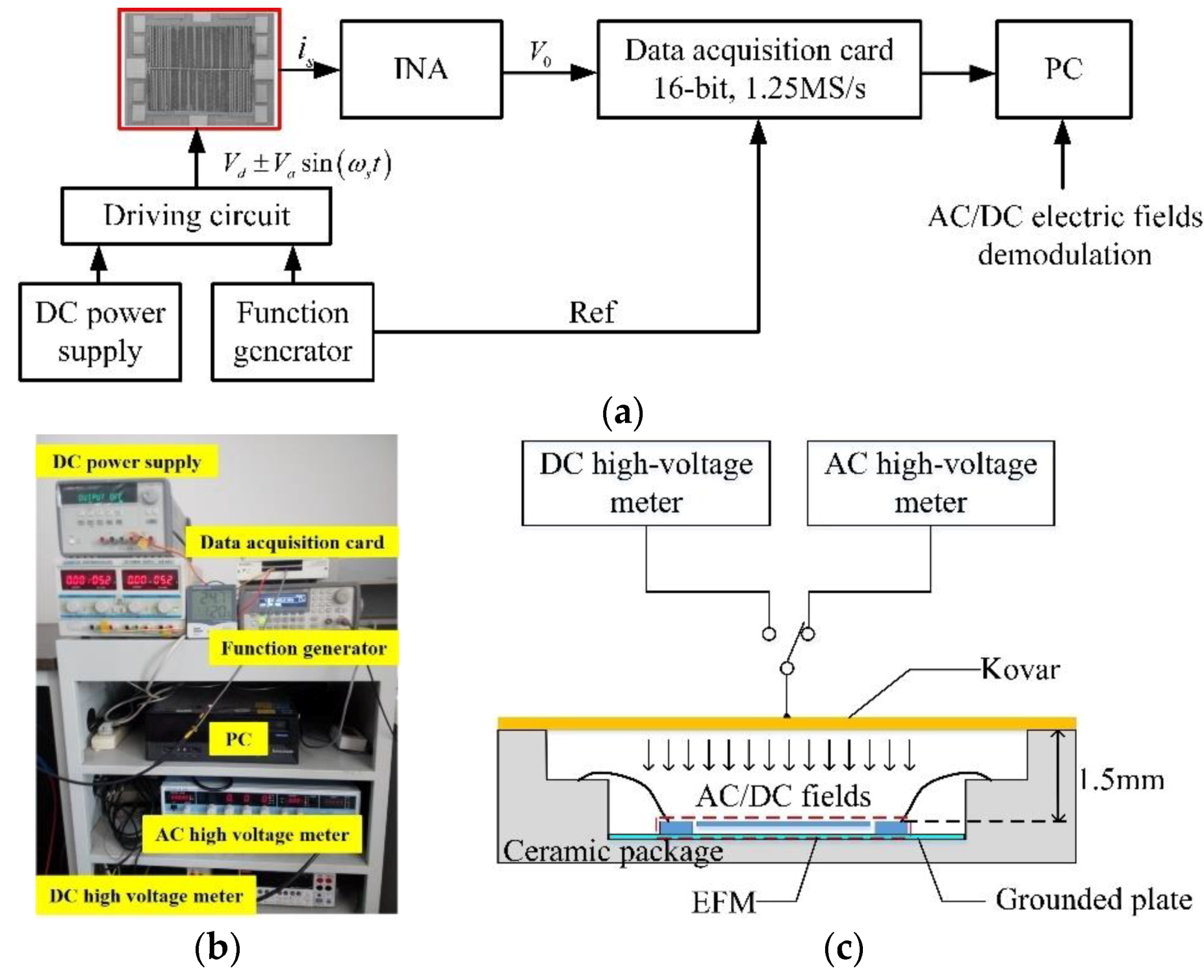
4.1. AC/DC Electric Fields Demodulation Verification Test System
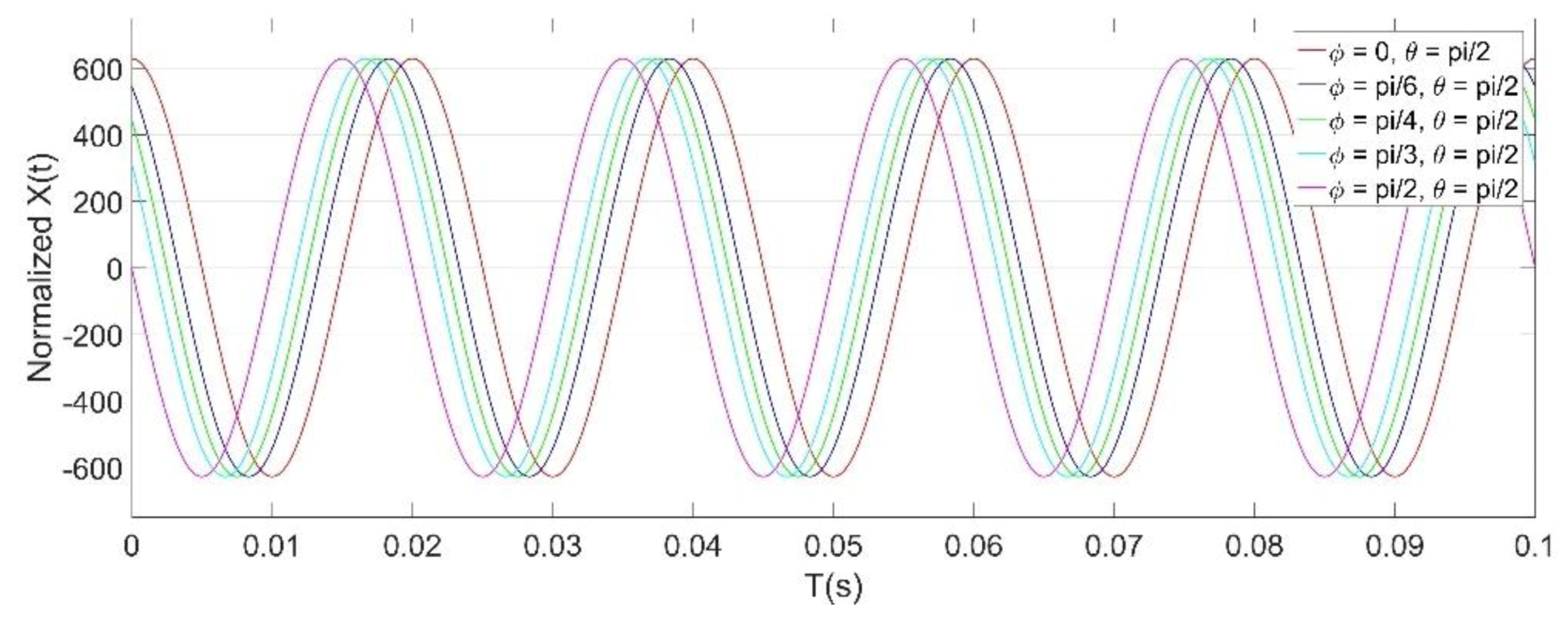
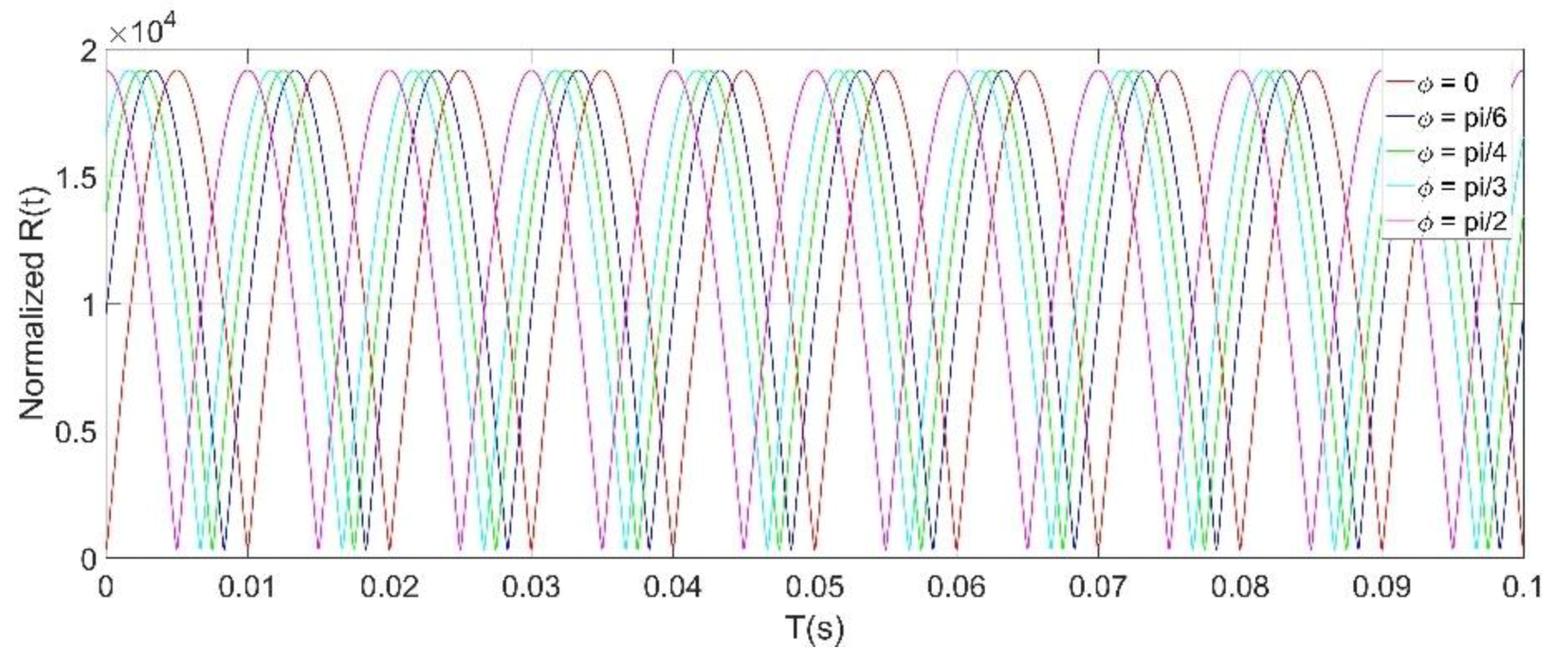
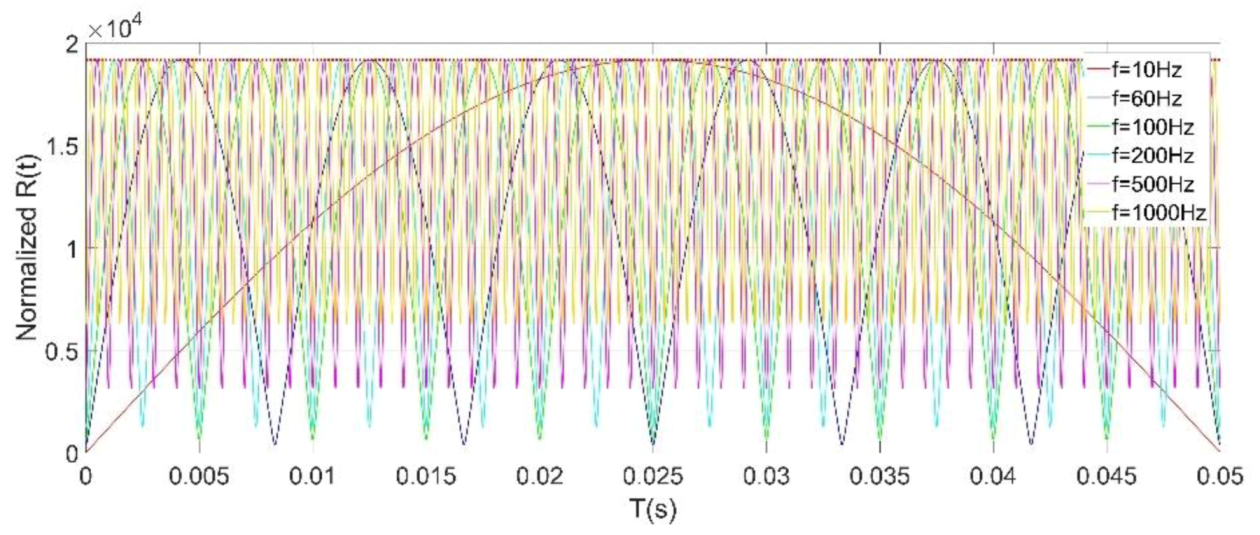
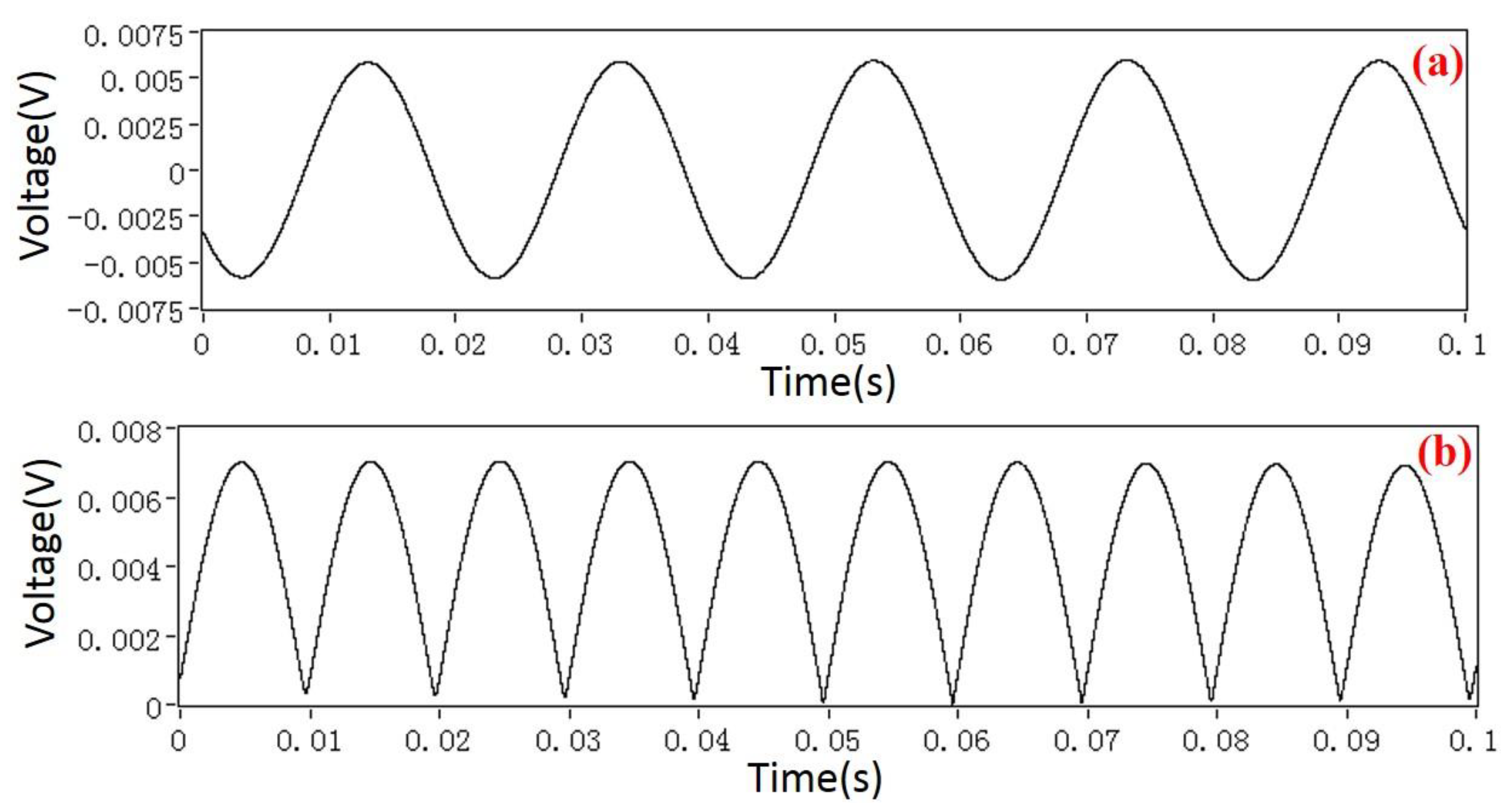
4.2. Testing and Analysis of Signal Characteristics
4.3. Demodulation Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Wijeweera, G.; Bahreyni, B.; Shafai, C.; Rajapakse, A.; Swatek, A.D. Micromachined electric-field sensor to Measure AC and DC fields in power systems. IEEE Trans. Power Deliv. 2009, 24, 988–995. [Google Scholar] [CrossRef]
- Vaillancourt, G.H.; Bellerive, J.P.; St-Jean, M.; Jean, C. New live line tester for porcelain suspension insulators on high-voltage power lines. IEEE Trans. Power Deliv. 1994, 9, 208–219. [Google Scholar] [CrossRef]
- Vaillancourt, G.H.; Carignan, S.; Jean, C. Experience with the detection of faulty composite insulators on high-voltage power lines by the electric field measurement method. IEEE Trans. Power Deliv. 1998, 13, 661–666. [Google Scholar] [CrossRef]
- Wei, S.; Zhang, L.; Gao, W.; Cao, Z. Non-contact voltage measurement based on electric-field effect. Procedia Eng. 2011, 15, 1973–1977. [Google Scholar] [CrossRef]
- Gerrard, C.A.; Gibson, J.R.; Jones, G.R.; Holt, L.; Simkin, D. Measurements of power system voltages using remote electric field monitoring. IEE Proc. Gener. Transm. Distrib. 1998, 145, 217–224. [Google Scholar] [CrossRef]
- Williams, K.R.; Bruyker, D.P.H.; Limb, S.J.; Amendt, E.M.; Overland, D.A. Vacuum steered-electron electric-field sensor. J. Microelectromech. Syst. 2014, 23, 157–167. [Google Scholar] [CrossRef]
- Barthod, C.; Passard, M.; Bouillot, J.; Galez, C.; Farzaneh, M. High electric field measurement and ice detection using a safe probe near power installations. Sens. Actuators A 2004, 113, 140–146. [Google Scholar] [CrossRef]
- Wang, H.; Zeng, R.; Zhuang, C.; Gang, L.; Yu, J.; Niu, B.; Li, C. Measuring AC/DC hybrid electric field using an integrated optical electric field sensor. Electr. Power Syst. Res. 2020, 179, 106087. [Google Scholar] [CrossRef]
- Frank, C.M. HVDC circuit breakers: A review identifying future research needs. IEEE Trans. Power Deliv. 2011, 26, 998–1007. [Google Scholar] [CrossRef]
- Ma, Q.; Huang, K.; Yu, Z.; Wang, Z. A MEMS-based electric field sensor for measurement of high-voltage DC synthetic fields in Air. IEEE Sens. J. 2017, 17, 7866–7876. [Google Scholar] [CrossRef]
- Tabib-Azar, M.; Sutapun, B.; Srikhirin, T.; Lando, J.; Adamovsky, G. Fiber optic electric field sensors using polymer-dispersed liquid crystal coatings and evanescent field interactions. Sens. Actuators A 2000, 84, 134–139. [Google Scholar] [CrossRef]
- Zeng, R.; Wang, B.; Yu, Z.; Chen, W. Design and application of an integrated electro-optic sensor for intensive electric field measurement. IEEE Trans. Dielectr. Electr. Insul. 2011, 18, 312–319. [Google Scholar] [CrossRef]
- Maruvada, P.S.; Dallaire, R.D.; Pedneault, R. Development of field-mill instruments for ground-level and above-ground electric field measurement under HVDC transmission lines. IEEE Trans. Power Appar. Syst. 1983, PAS-102, 738–744. [Google Scholar] [CrossRef]
- Hornfeldt, S.P. DC-probes for electric field distribution measurements. IEEE Tans. Power Deliv. 1991, 6, 524–528. [Google Scholar] [CrossRef]
- Tant, P.; Bolsens, B.; Sels, T.; Dommelen, D.V.; Driesen, J.; Belmans, R. Design and application of a field mill as a high-voltage DC meter. IEEE Trans. Instrum. Meas. 2007, 56, 1459–1464. [Google Scholar] [CrossRef]
- Kainz, A.; Steiner, H.; Schalko, J.; Jachimowicz, A.; Kohl, F.; Stifter, M.; Beigelbeck, R.; Keplinger, F.; Hortschitz, W. Distortion-free measurement of electric field strength with a MEMS sensor. Nat. Electron. 2018, 1, 68–73. [Google Scholar] [CrossRef]
- Huang, J.; Wu, X.; Wang, X.; Yan, X.; Lin, L. A novel high-sensitivity electrostatic biased electric field sensor. J. Micromech. Microeng. 2015, 25, 095008. [Google Scholar] [CrossRef]
- Horenstein, M.N.; Stone, P.R. A micro-aperture electrostatic field mill based on MEMS technology. J. Electrost. 2001, 51, 515–521. [Google Scholar] [CrossRef]
- Riehl, P.S.; Scott, K.L.; Muller, R.S.; Howe, R.T.; Yasaitis, J.A. Electrostatic charge and field sensors based on micromechanical resonators. J. Microelectromech. Syst. 2003, 12, 577–589. [Google Scholar] [CrossRef]
- Denison, T.; Kuang, J.; Shanfran, J.; Judy, M.; Lundberg, K. A self-resonant MEMS-based electrostatic field sensor with 4V/m/√Hz sensitivity. In Proceedings of the 2006 IEEE International Solid State Circuits Conference, San Francisco, CA, USA, 6–9 February 2006. [Google Scholar]
- Peng, C.; Chen, X.; Ye, C.; Tao, H.; Cui, G.; Bai, Q.; Chen, S.; Xia, S. Design and testing of a micromechanical resonant electrostatic field sensor. J. Micromech. Microeng. 2006, 16, 914–919. [Google Scholar] [CrossRef]
- Chen, X.; Peng, C.; Tao, H.; Ye, C.; Bai, Q.; Chen, S.; Xia, S. Thermally driven micro-electrostatic fieldmeter. Sens. Actuators A 2006, 132, 677–682. [Google Scholar] [CrossRef]
- Bahreyni, B.; Wijeweera, G.; Shafai, C.; Rajapakse, A. Analysis and design of a micromachined electric-field sensor. J. Microelectromech. Syst. 2008, 17, 31–36. [Google Scholar] [CrossRef]
- Konbayashi, T.; Oyama, S.; Takahashi, M.; Maeda, R.; Itoh, T. Microelectromichanical systems-based electrostatic field sensor using Pb (Zr, Ti)O3 thin films. Jpn. J. Appl. Phys. 2008, 47, 7533–7536. [Google Scholar] [CrossRef]
- Kobayashi, T.; Oyama, S.; Makimoto, N.; Okada, H.; Itoh, T.; Maeda, R. An electrostatic field sensor operated by self-excited vibration of MEMS-based self-sensitive piezoelectric microcantilevers. Sens. Actuators A 2013, 198, 87–90. [Google Scholar] [CrossRef]
- Yang, P.; Peng, C.; Zhang, H.; Liu, S.; Fang, D.; Xia, S. A high sensitivity SOI electric-field sensor with novel comb-shaped microelectrodes. In Proceedings of the Transducers’11, Beijing, China, 5–9 June 2011. [Google Scholar]
- Chen, T.; Shafai, C.; Rajapakse, A.; Liyanage, J.S.H.; Neusitzer, T.D. Micromachined AC/DC electric field sensor with modulated sensitivity. Sens. Actuators A 2016, 245, 76–84. [Google Scholar] [CrossRef]
- Ghionea, S.; Smith, G.; Pulskamp, J.; Bedair, S.; Meyer, C.; Hull, D. MEMS electric-field sensor with lead zirconate titanate (PZT)-actuated electrodes. In Proceedings of the IEEE Sensors 2013, Baltimore, MD, USA, 3–6 November 2013. [Google Scholar]
- Wang, Y.; Fang, D.; Feng, K.; Ren, R.; Chen, B.; Peng, C.; Xia, S. A novel micro electric field sensor with X–Y dual axis sensitive differential structure. Sens. Actuators A 2015, 229, 1–7. [Google Scholar] [CrossRef]
- Chu, Z.; Peng, C.; Ren, R.; Ling, B.; Zhang, Z.; Lei, H.; Xia, S. A high sensitivity electric field microsensor based on torsional resonance. Sensors 2018, 18, 286. [Google Scholar] [CrossRef]
- Makihata, M.; Matsushita, K.; Pisano, A.P. MEMS-based non-contact voltage sensor with multi-mode resonance shutter. Sens. Actuators A 2019, 294, 25–36. [Google Scholar] [CrossRef]
- Yang, P.; Peng, C.; Fang, D.; Wen, X.; Xia, S. Design, fabrication and application of an SOI-based resonant electric field microsensor with coplanar comb-shaped electrodes. J. Micromech. Microeng. 2013, 23, 055002. [Google Scholar] [CrossRef]
- Park, H.W.; Kim, Y.K.; Jeong, H.G.; Song, J.W.; Kim, J.M. Feed-through capacitance reduction for a micro-resonator with push–pull configuration based on electrical characteristic analysis of resonator with direct drive. Sens. Actuators A 2011, 170, 131–138. [Google Scholar] [CrossRef]
- SOIMUMPs Design Rules. Available online: http://www.memscap.com/products/mumps/soimumps/reference-material (accessed on 1 April 2020).
- Abdolvand, R.; Bahreyni, B.; Lee, J.E.Y.; Nabki, F. Micromachined resonators: A review. Micromachines 2016, 7, 160. [Google Scholar] [CrossRef] [PubMed]
- National Standard of the People’s Republic of China: GB/T 35086-2018, General Specification for MEMS Electric Field Sensor. Available online: http://www.gov.cn/fuwu/bzxxcx/bzh.htm (accessed on 1 April 2020).


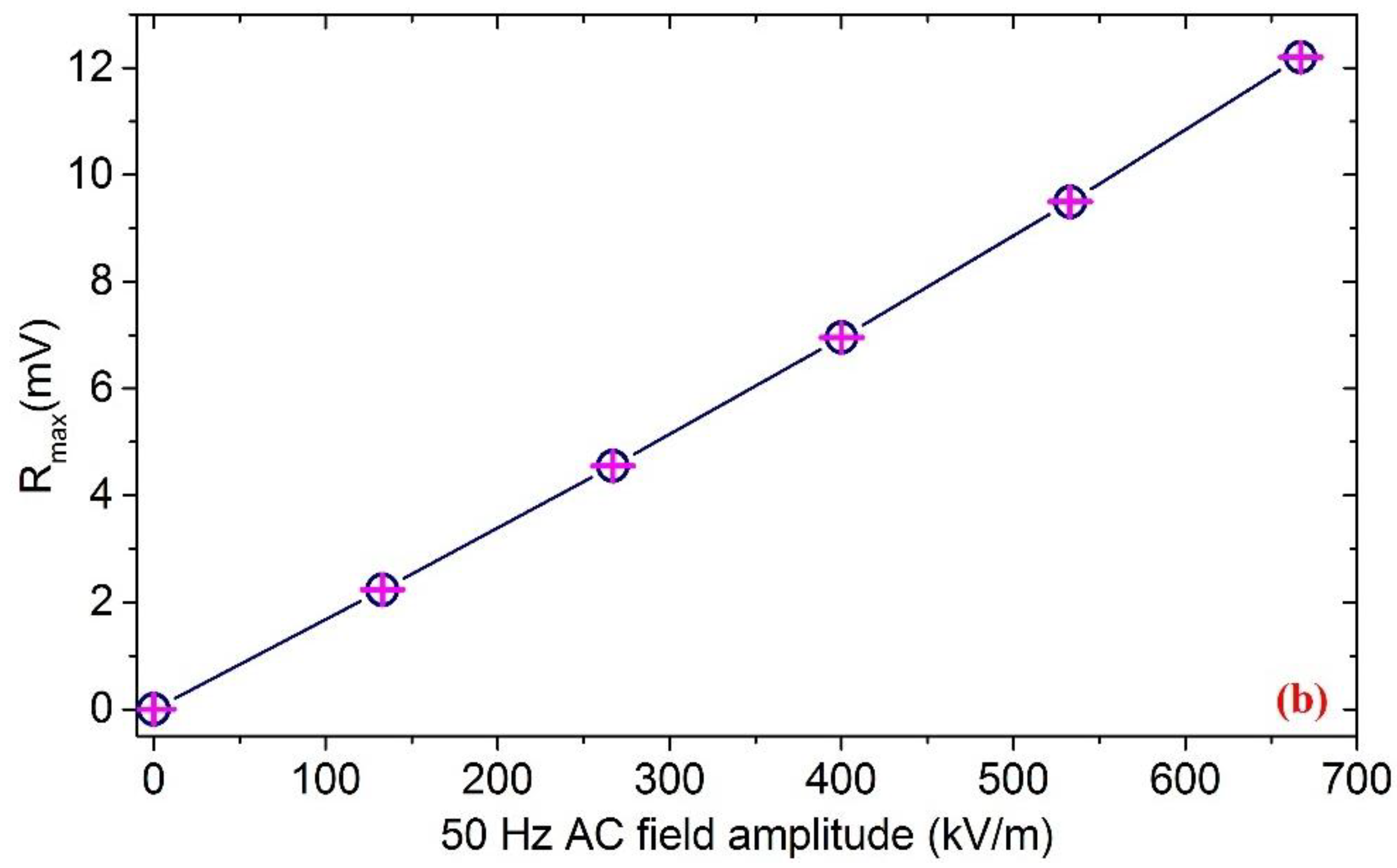
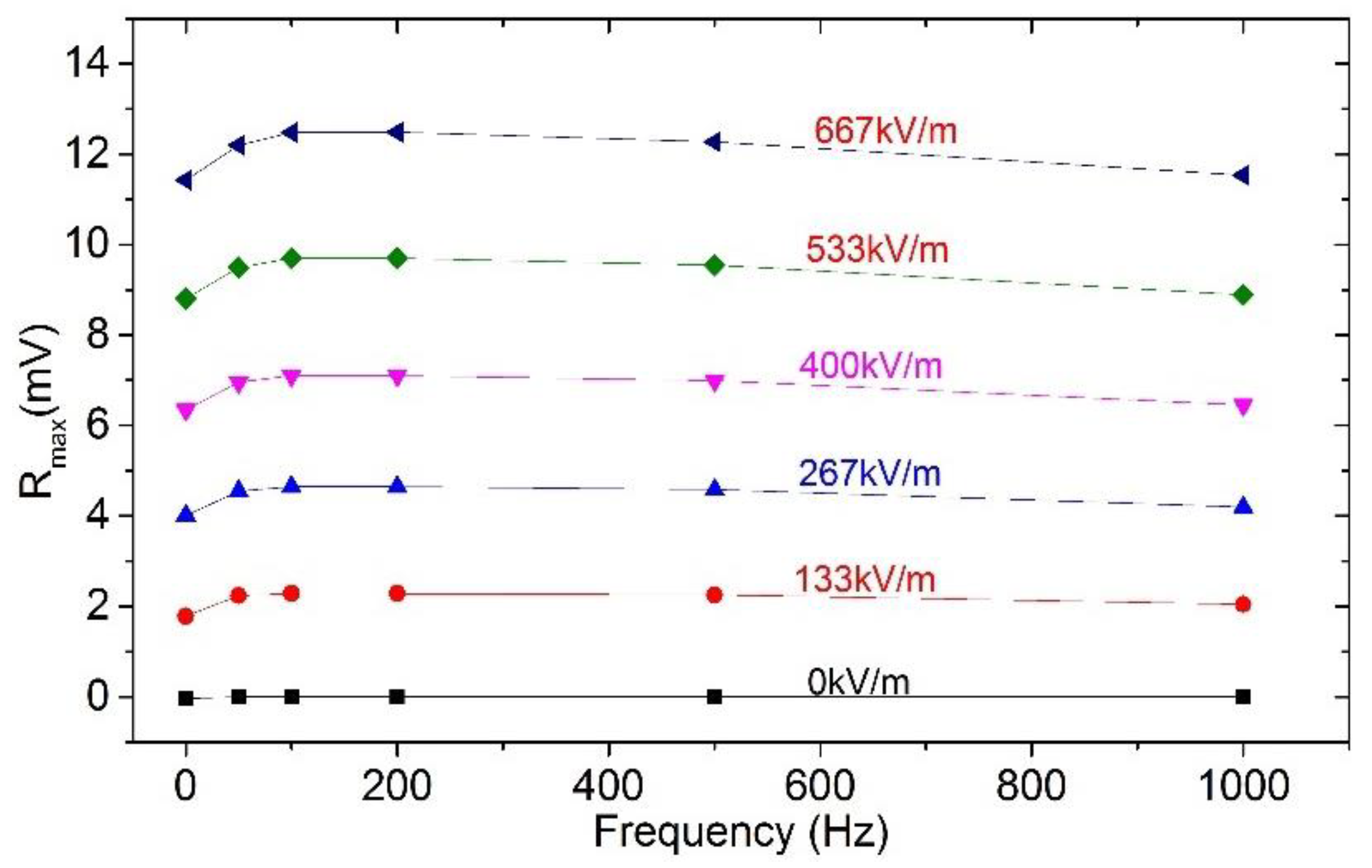
| Roundtrip | 0 kV/m | 133 kV/m | 267 kV/m | 400 kV/m | 533 kV/m | 667 kV/m |
|---|---|---|---|---|---|---|
| 1st direct journey | −0.034 mV | 1.785 mV | 4.011 mV | 6.344 mV | 8.808 mV | 11.432 mV |
| 1st reverse journey | −0.035 mV | 1.783 mV | 4.006 mV | 6.342 mV | 8.810 mV | 11.426 mV |
| 2nd direct journey | −0.031 mV | 1.785 mV | 4.011 mV | 6.346 mV | 8.809 mV | 11.426 mV |
| 2nd reverse journey | −0.031 mV | 1.788 mV | 4.008 mV | 6.344 mV | 8.809 mV | 11.422 mV |
| 3rd direct journey | −0.035 mV | 1.781 mV | 4.010 mV | 6.343 mV | 8.809 mV | 11.427 mV |
| 3rd reverse journey | −0.036 mV | 1.789 mV | 4.010 mV | 6.343 mV | 8.810 mV | 11.422 mV |
| Roundtrip | 0 kV/m | 133 kV/m | 267 kV/m | 400 kV/m | 533 kV/m | 667 kV/m |
|---|---|---|---|---|---|---|
| 1st direct journey | 0.003 mV | 2.233 mV | 4.550 mV | 6.952 mV | 9.487 mV | 12.200 mV |
| 1st reverse journey | 0 mV | 2.236 mV | 4.550 mV | 6.954 mV | 9.494 mV | 12.196 mV |
| 2nd direct journey | 0.001 mV | 2.236 mV | 4.543 mV | 6.955 mV | 9.495 mV | 12.202 mV |
| 2nd reverse journey | 0.002 mV | 2.236 mV | 4.553 mV | 6.953 mV | 9.488 mV | 12.198 mV |
| 3rd direct journey | 0.001 mV | 2.238 mV | 4.550 mV | 6.954 mV | 9.494 mV | 12.204 mV |
| 3rd reverse journey | 0.001 mV | 2.241 mV | 4.551 mV | 6.952 mV | 9.492 mV | 12.199 mV |
| Frequency (Hz) | 0 kV/m | 133 kV/m | 267 kV/m | 400 kV/m | 533 kV/m | 667 kV/m |
|---|---|---|---|---|---|---|
| 0 | −0.03 mV | 1.79 mV | 4.01 mV | 6.34 mV | 8.81 mV | 11.43 mV |
| 50 | 0 | 2.24 mV | 4.55 mV | 6.95 mV | 9.49 mV | 12.20 mV |
| 100 | 0 | 2.28 mV | 4.65 mV | 7.10 mV | 9.70 mV | 12.48 mV |
| 200 | 0 | 2.27 mV | 4.65 mV | 7.10 mV | 9.70 mV | 12.49 mV |
| 500 | 0 | 2.25 mV | 4.58 mV | 6.99 mV | 9.54 mV | 12.27 mV |
| 1000 | 0 | 2.05 mV | 4.19 mV | 6.46 mV | 8.89 mV | 11.53 mV |
| Absolute error | 0.03 mV | 0.5 mV | 0.63 mV | 0.75 mV | 0.89 mV | 1.06 mV |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, P.; Wen, X.; Chu, Z.; Ni, X.; Peng, C. AC/DC Fields Demodulation Methods of Resonant Electric Field Microsensor. Micromachines 2020, 11, 511. https://doi.org/10.3390/mi11050511
Yang P, Wen X, Chu Z, Ni X, Peng C. AC/DC Fields Demodulation Methods of Resonant Electric Field Microsensor. Micromachines. 2020; 11(5):511. https://doi.org/10.3390/mi11050511
Chicago/Turabian StyleYang, Pengfei, Xiaolong Wen, Zhaozhi Chu, Xiaoming Ni, and Chunrong Peng. 2020. "AC/DC Fields Demodulation Methods of Resonant Electric Field Microsensor" Micromachines 11, no. 5: 511. https://doi.org/10.3390/mi11050511
APA StyleYang, P., Wen, X., Chu, Z., Ni, X., & Peng, C. (2020). AC/DC Fields Demodulation Methods of Resonant Electric Field Microsensor. Micromachines, 11(5), 511. https://doi.org/10.3390/mi11050511





