Development of a Piezo-Driven Liquid Jet Dispenser with Hinge-Lever Amplification Mechanism
Abstract
1. Introduction
2. Motivation for Research
3. Needle-Type Dispenser Simulation and Modelling
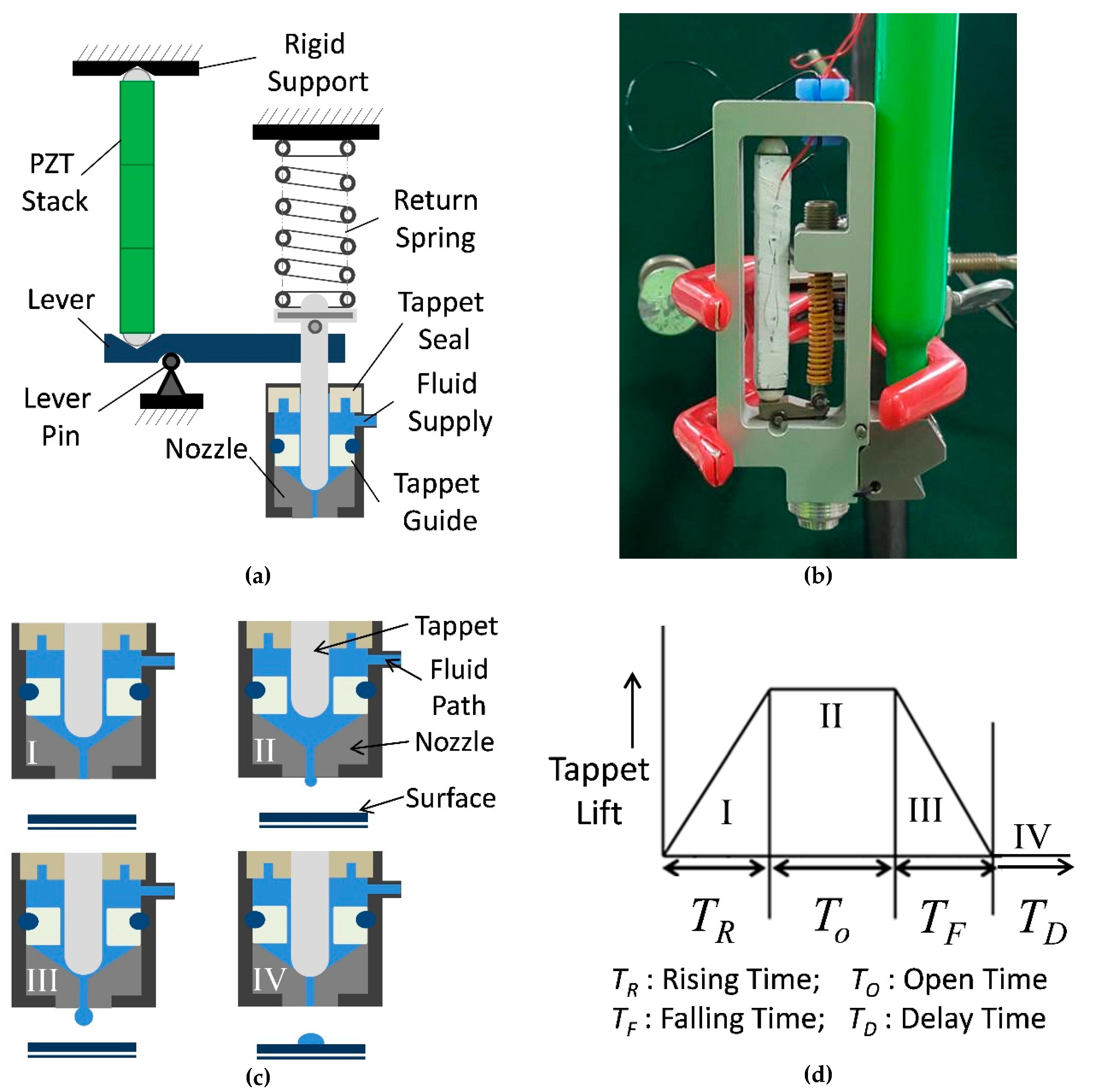
3.1. Dispensing System Overview and Working Principle
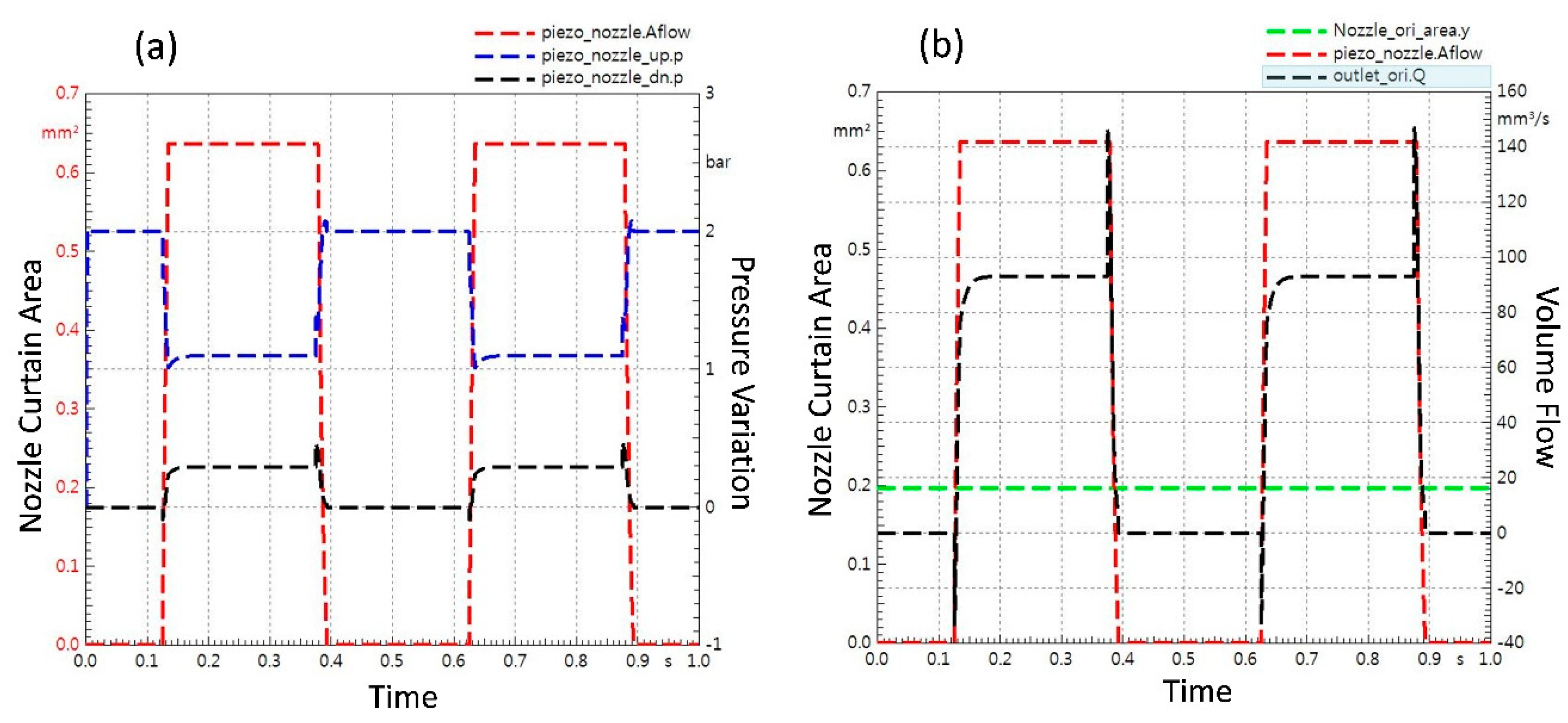
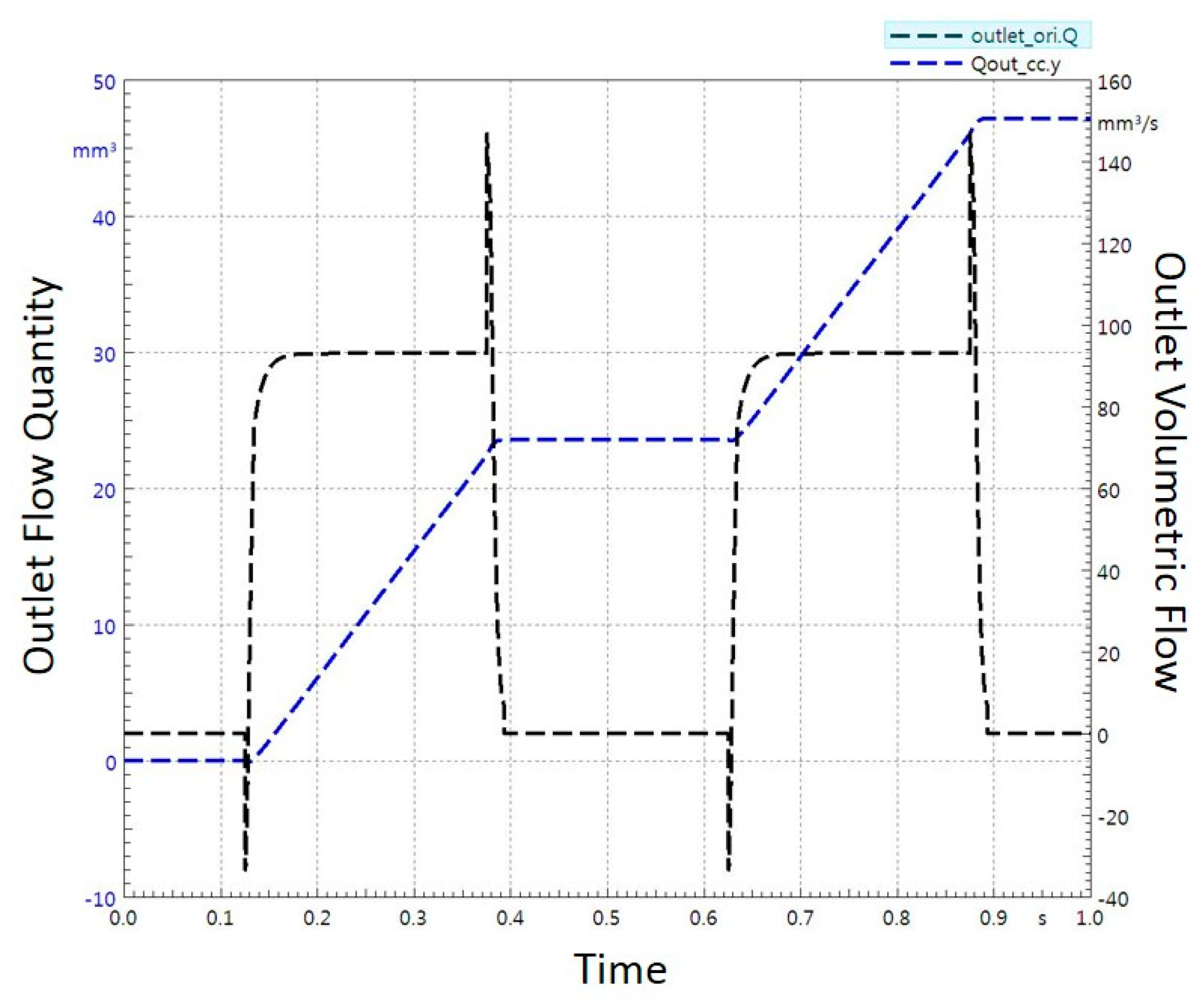
3.2. Governing Equations for Jet Dispenser Modelling
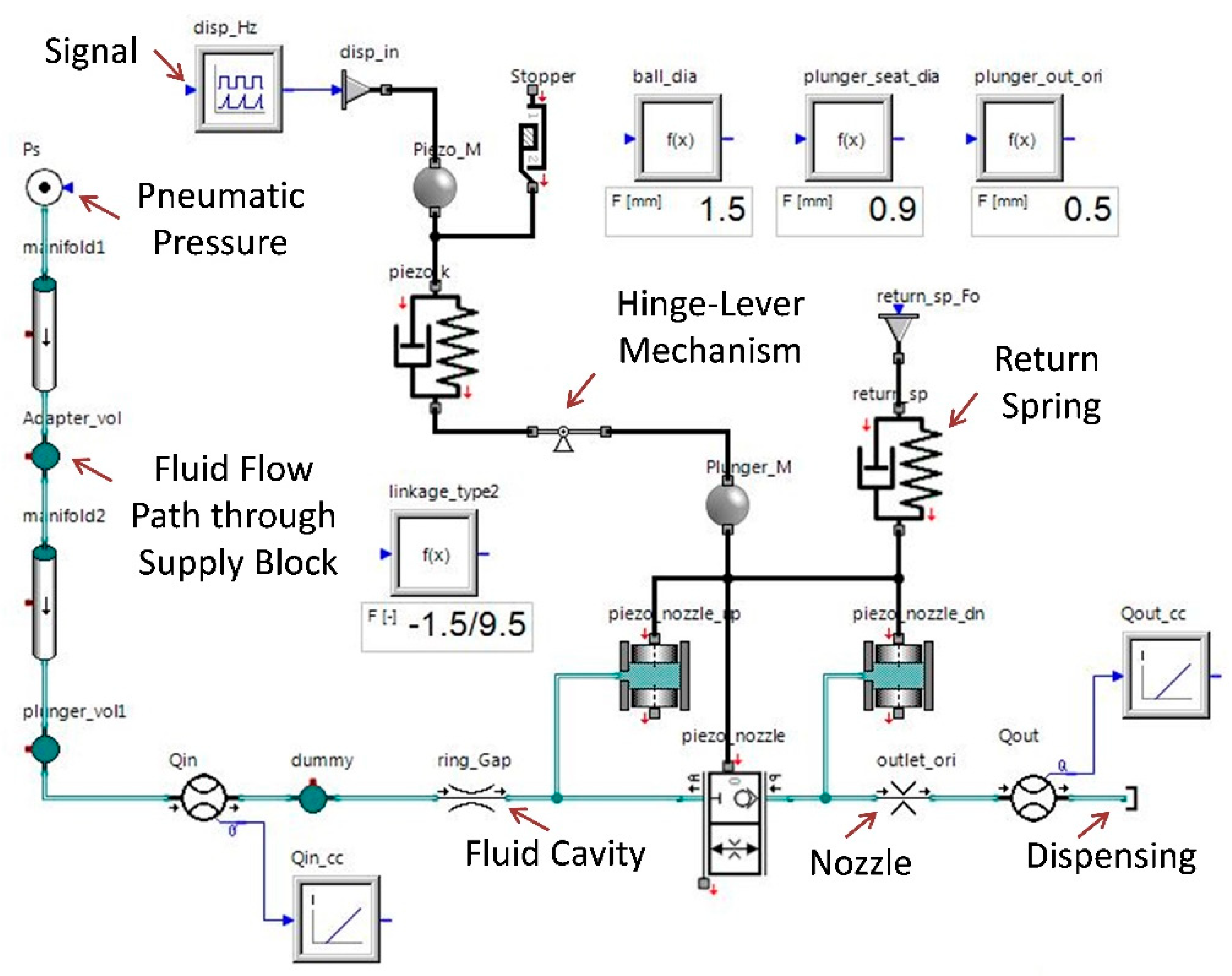
3.3. Geometry Based Modelling of Dispenser
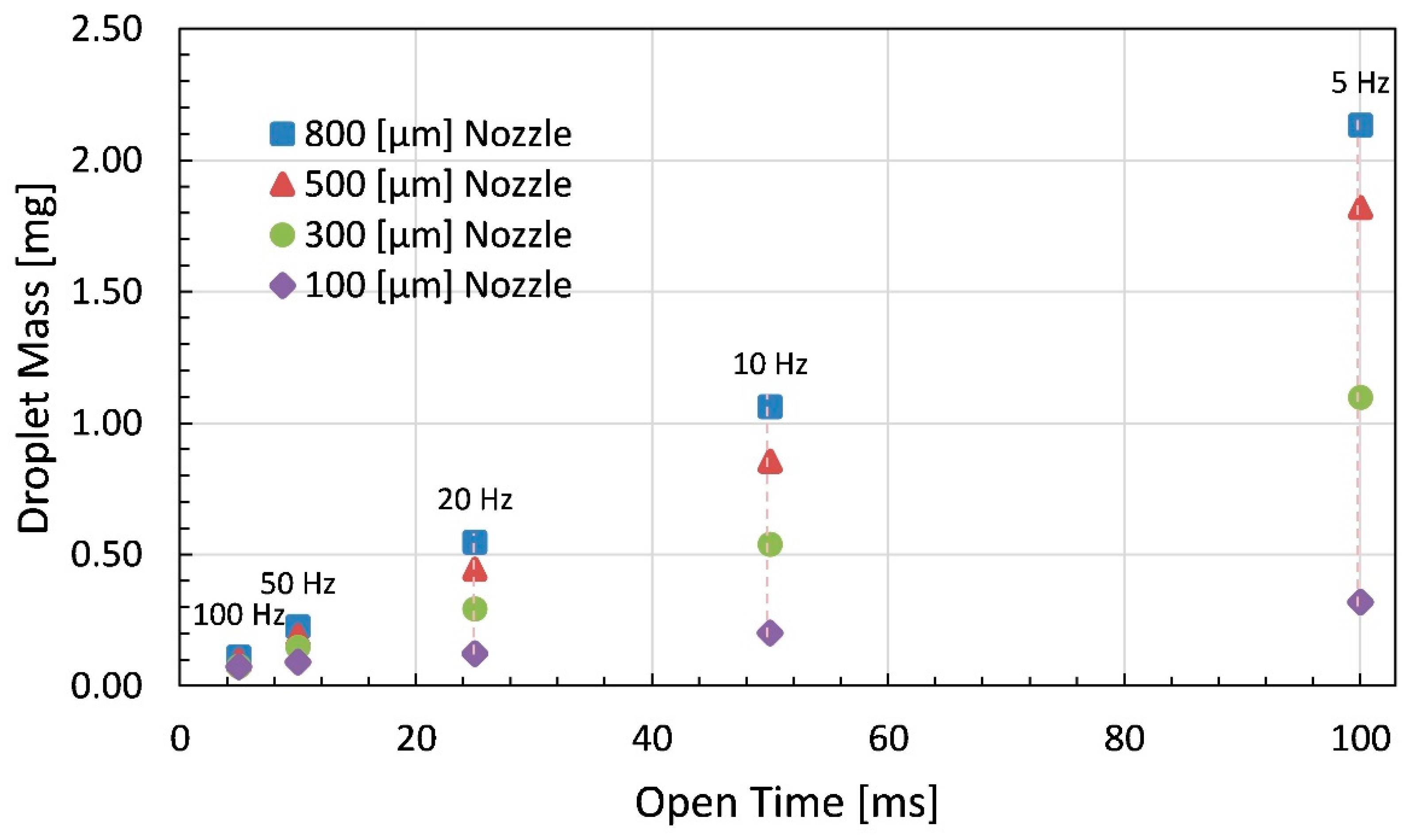
4. Experimental Results and Analysis
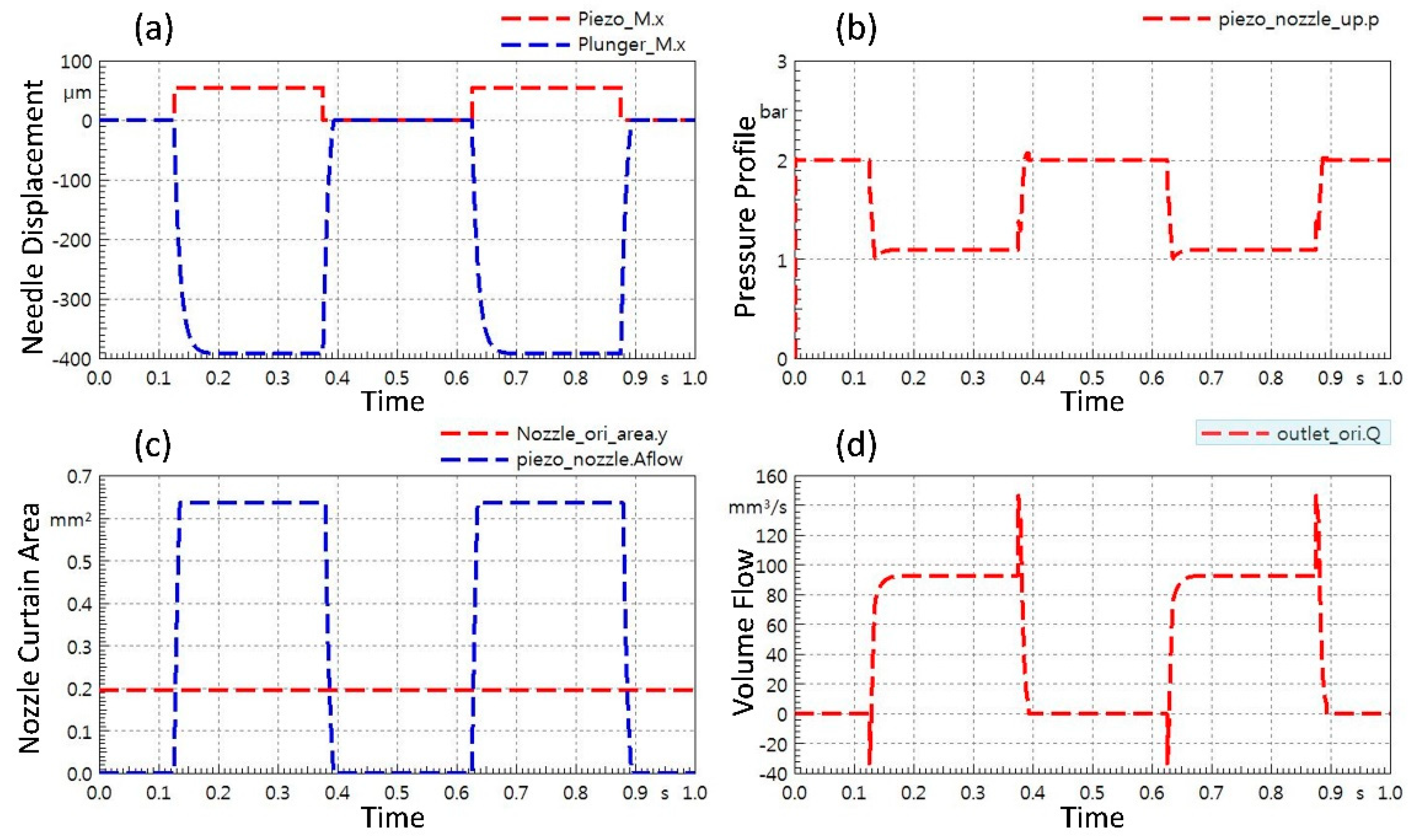
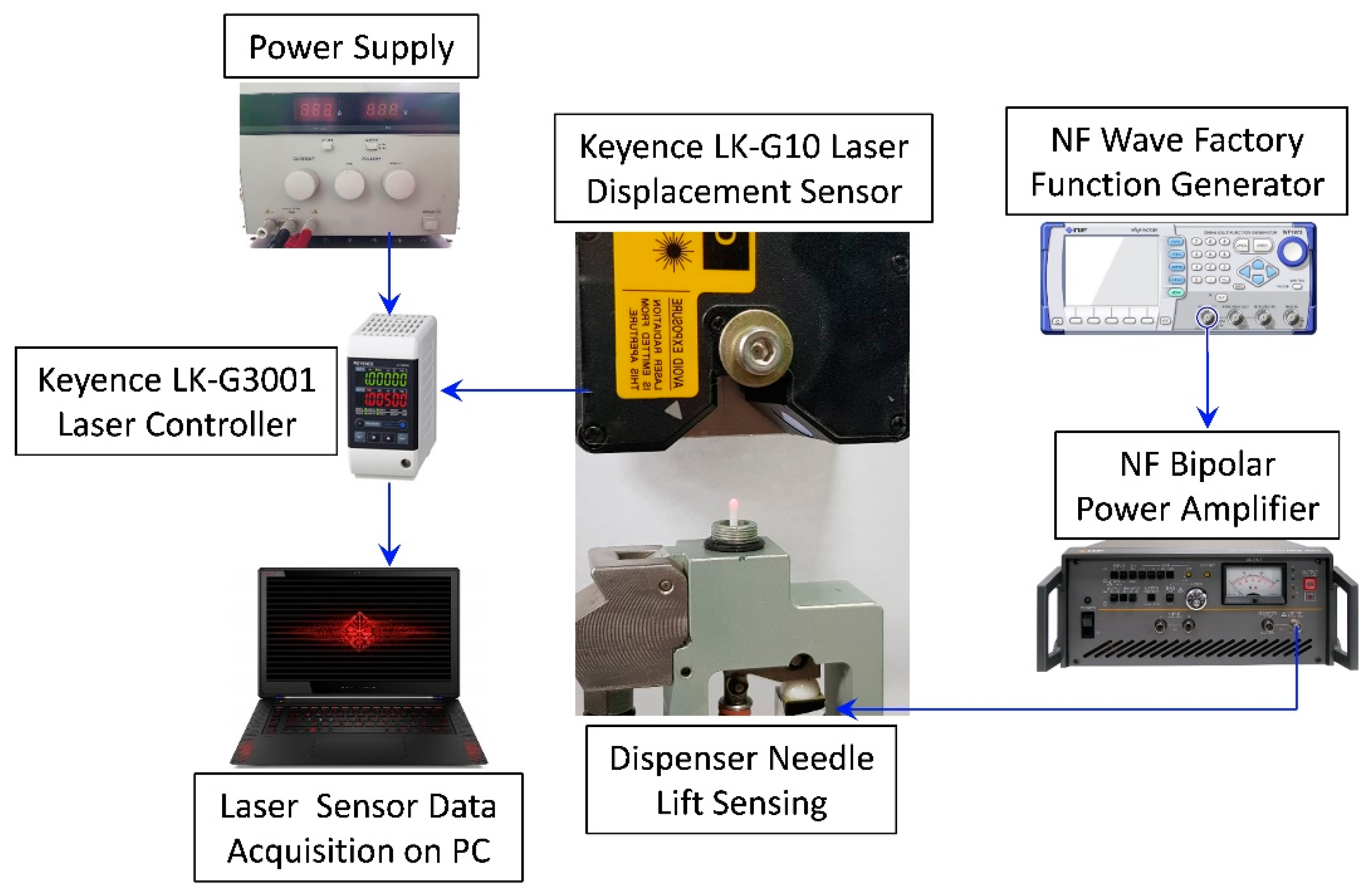
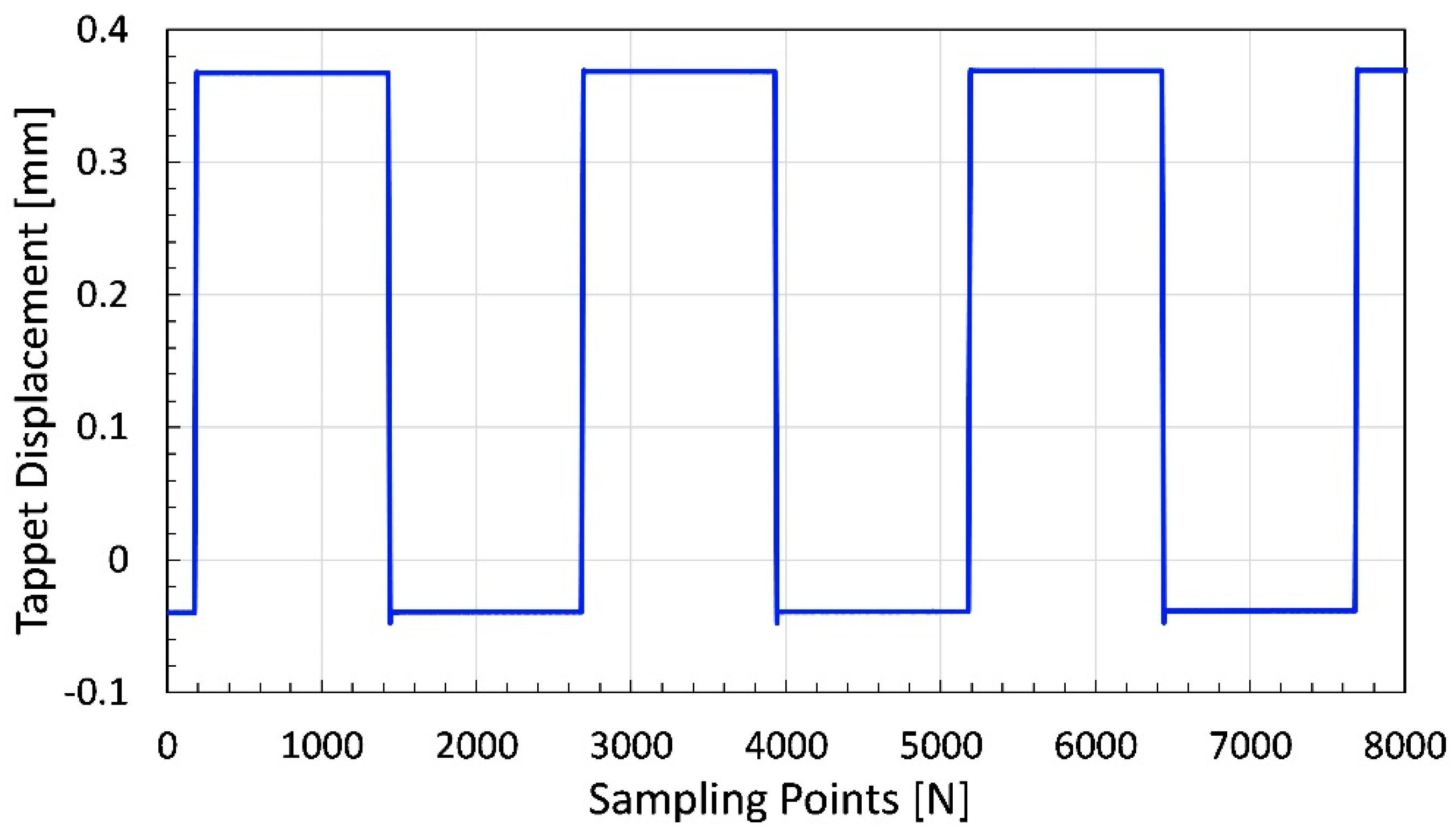
4.1. Laser Displacement Sensing Experiment
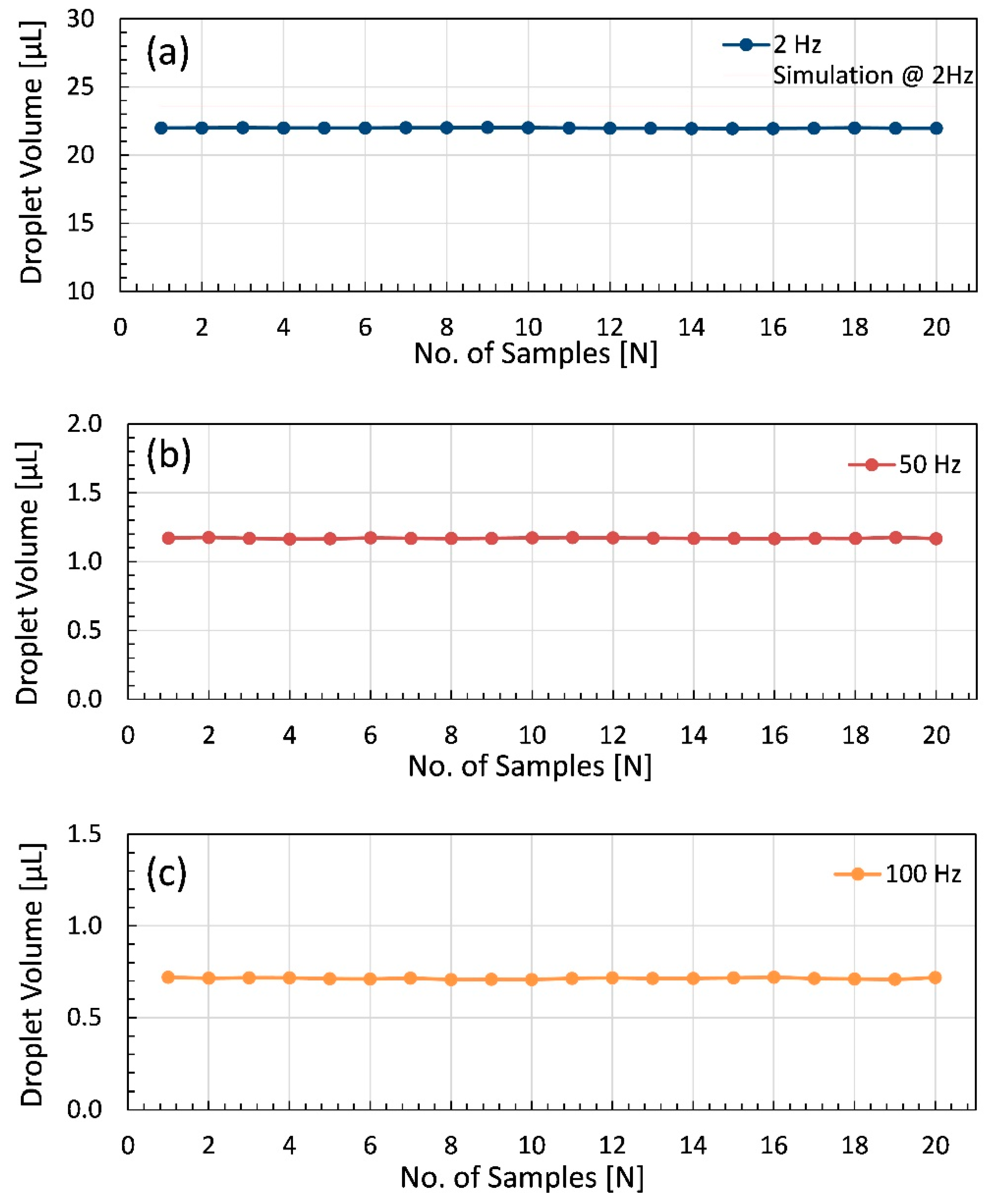
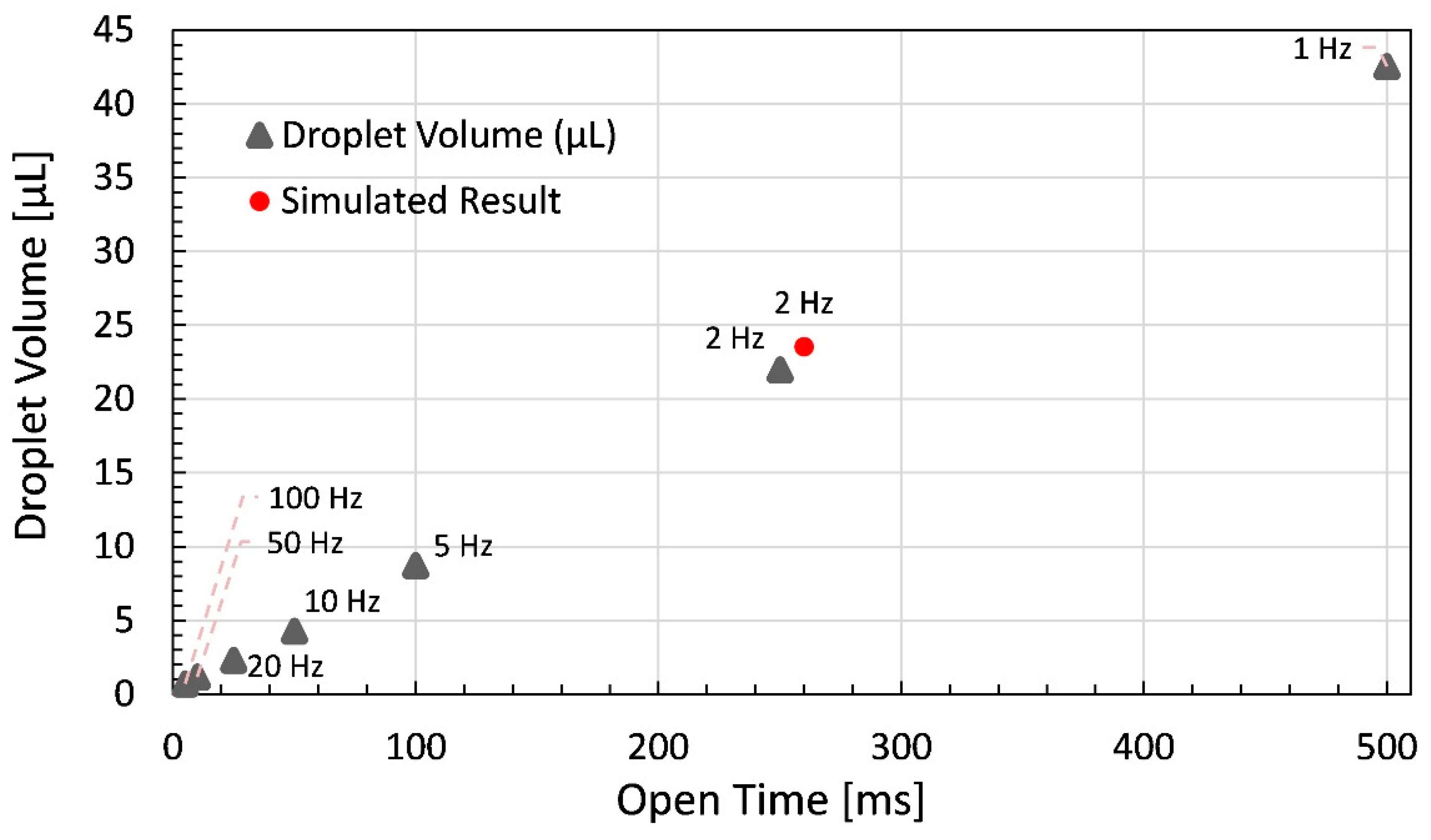
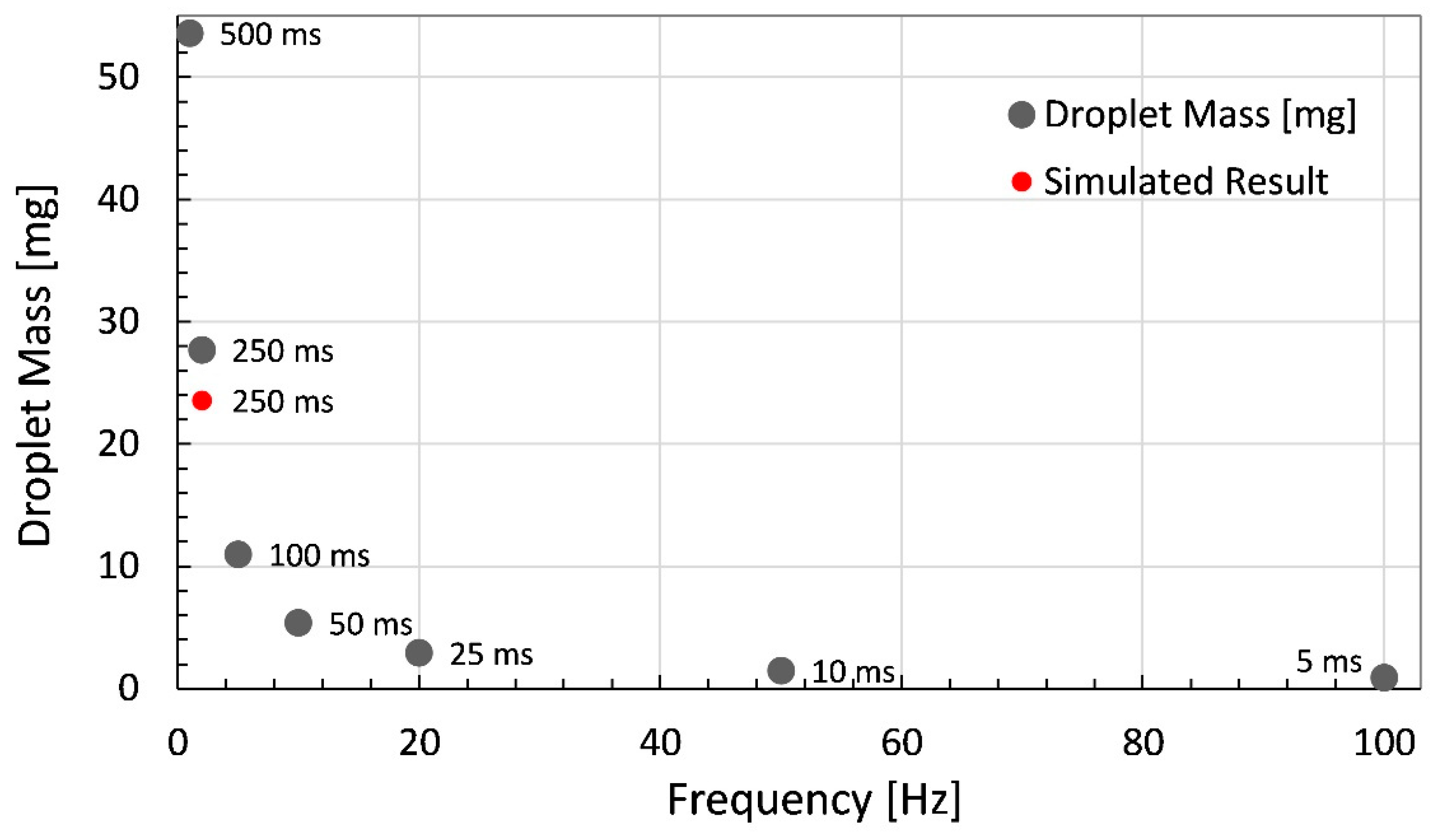
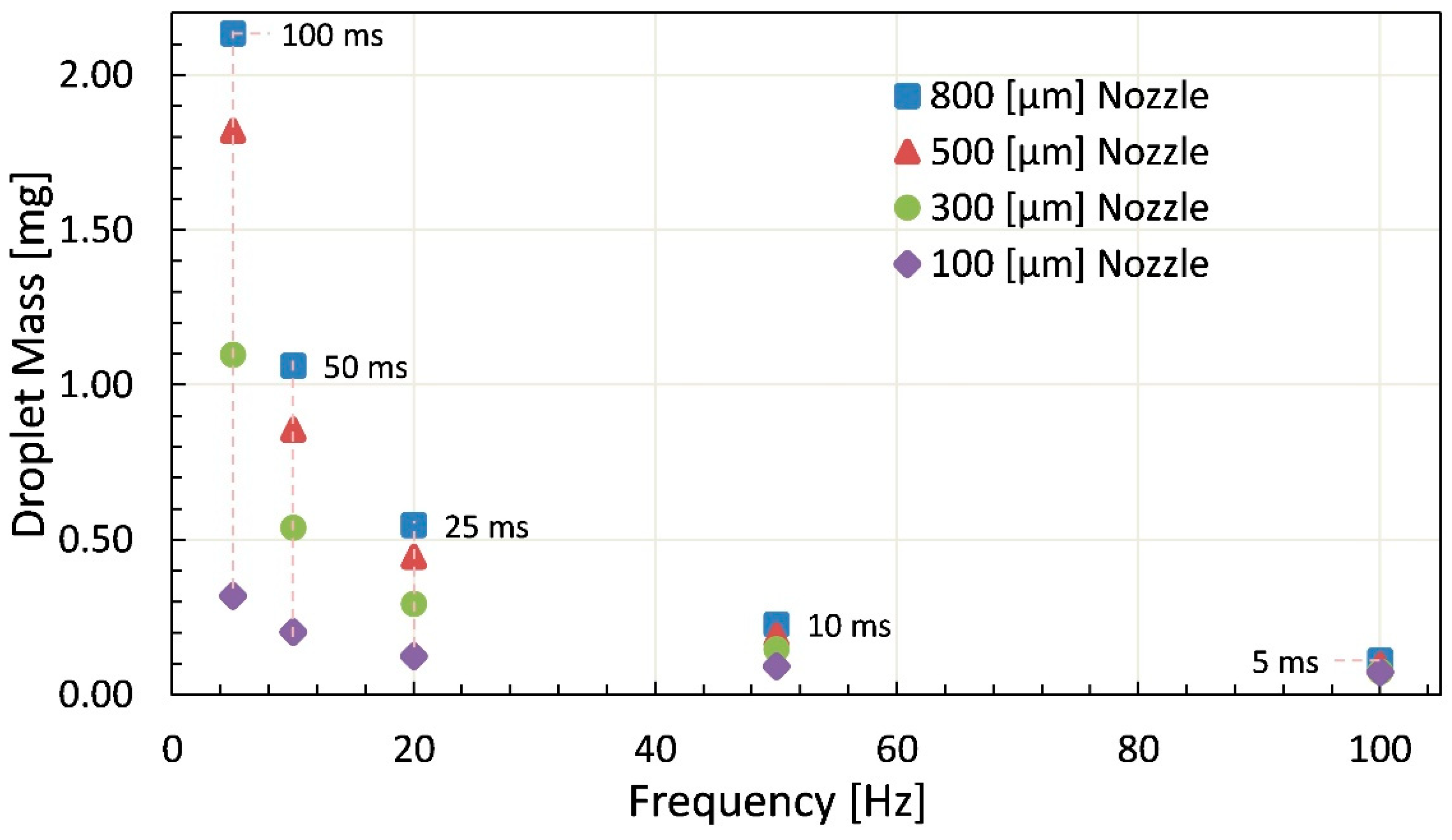
4.2. Fluid Dispensing Experimentation
4.2.1. Dispensing of Glycerin
4.2.2. Dispensing of Liquid Silicone
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Urano, M.; Sakata, T.; Shimamura, T.; Ishii, H.; Chino, M.; Shimada, T.; Tazawa, H.; Machida, K. Novel Packaging Technology for Microelectromechanical-System Devices. Jpn. J. Appl. Phys. 2005, 44, 8177–8181. [Google Scholar] [CrossRef]
- Kumagai, K.; Fuchiwaki, O. A Development of Dispenser for High-Viscosity Liquid and Pick and Place of Micro Objects Using Capillary Force. Key Eng. Mater. 2012, 516, 48–53. [Google Scholar] [CrossRef]
- Kim, K.Y.; Lee, Y.C.; Chang, H.; Lee, R.F.; Wu, H.W. Jetting Dispenser Height Effect on the Accuracy of Test Strip for Blood Glucose. J. Med. Biol. Eng. 2019, 39, 109–116. [Google Scholar] [CrossRef]
- Zhou, C.; Duan, J.; Deng, G.; Li, J. A Novel High-Speed Jet Dispenser Driven by Double Piezoelectric Stacks. IEEE Trans. Ind. Electron. 2017, 64, 412–419. [Google Scholar] [CrossRef]
- Shan, X.; Li, H.; Si, H.; Chen, Y. Integrated Sensing-/Model-Based Online Estimation of Jet Dispensing. IEEE Trans. Compon. Packag. Manuf. Technol. 2018, 8, 300–309. [Google Scholar] [CrossRef]
- Nguyen, Q.H.; Choi, S.B. Performance Evaluation of a High-Speed Jetting Dispenser Actuated by a Ring-Type Piezostack. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2009, 223, 1401–1413. [Google Scholar] [CrossRef]
- Ham, Y.B.; Jang, S.K.; Oh, S.J.; Jeon, E.C.; Park, J.H.; Yun, S.N.; Choi, S.G. Piezoelectrically Driven Dispensing Head for Encapsulation of Light Emitting Diode Chip. Jpn. J. Appl. Phys. 2012, 51. [Google Scholar] [CrossRef]
- Zhou, C.; Du, P.; Feng, Z.; Cui, W.; Deng, G. Influence of Bi-Piezoelectric Micro-Valve’s Parameters on Jet Performance. Optik 2018, 167, 129–135. [Google Scholar] [CrossRef]
- Jeon, J.; Hong, S.M.; Choi, M.; Choi, S.B. Design and Performance Evaluation of a New Jetting Dispenser System Using Two Piezostack Actuators. Smart Mater. Struct. 2015, 24. [Google Scholar] [CrossRef]
- Ahamed, M.J.; Ben-Mrad, R.; Sullivan, P. A Drop-on-Demand-Based Electrostatically Actuated Microdispenser. J. Microelectromech. Syst. 2013, 22, 177–185. [Google Scholar] [CrossRef]
- Lu, S.; Yao, Y.; Liu, Y.; Zhao, Y. Design and Experiment of a Needle-Type Piezostack-Driven Jetting Dispenser Based on Lumped Parameter Method. J. Adhes. Sci. Technol. 2015, 29, 716–730. [Google Scholar] [CrossRef]
- Bu, Z.; Lin, S.; Huang, X.; Li, A.; Wu, D.; Zhao, Y.; Luo, Z.; Wang, L. A Novel Piezostack-Driven Jetting Dispenser with Corner-Filleted Flexure Hinge and High-Frequency Performance. J. Micromech. Microeng. 2018, 28. [Google Scholar] [CrossRef]
- Han, H.; Lee, J.S.; Kim, H.; Shin, S.; Lee, J.; Kim, J.; Hou, X.; Cho, S.W.; Seo, J.; Lee, T. Single-Droplet Multiplex Bioassay on a Robust and Stretchable Extreme Wetting Substrate through Vacuum-Based Droplet Manipulation. ACS Nano 2018, 12, 932–941. [Google Scholar] [CrossRef]
- Nguyen, Q.H.; Han, Y.M.; Choi, S.B.; Hong, S.M. Design of a New Mechanism for Jetting Dispenser Featuring Piezoactuator. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2008, 222, 711–722. [Google Scholar] [CrossRef]
- Liu, S.Z.; Zhang, Y.B.; Chen, X.B. Experiment and Dynamic Model of Motor for Rotary-Screw-Driven Dispensing System. Appl. Mech. Mater. 2012, 220, 1071–1076. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, Y.; Chen, H.; He, N. Research on Micro-Liquid Dispensing Anomaly Monitoring System Based on Pressure Sensor. Nanosci. Nanotechnol. Lett. 2017, 9, 859–866. [Google Scholar] [CrossRef]
- Trimzi, M.A.; Ham, Y.-B.; An, B.-C.; Park, J.-H.; Yun, S.-N. Numerical Analysis and Simulation of an Impulse Driven Piezoelectric Needle-Free Jet Injector. J. Mech. Sci. Technol. 2019. [Google Scholar] [CrossRef]
- Satkoski, C.A.; Ruikar, N.S.; Biggs, S.D.; Shaver, G.M. Piezoelectric Fuel Injection: Cycle-to-Cycle Control of Tightly Spaced Injections. Control Eng. Pract. 2012, 20, 1175–1182. [Google Scholar] [CrossRef]
- Stachowiak, J.C.; von Muhlen, M.G.; Li, T.H.; Jalilian, L.; Parekh, S.H.; Fletcher, D.A. Piezoelectric Control of Needle-Free Transdermal Drug Delivery. J. Control. Release 2007, 124, 88–97. [Google Scholar] [CrossRef]
- Ham, Y.-B.; An, B.-C.; Trimzi, M.A.; Park, J.-H.; Yun, S.-N. Numerical Analysis on Piezoelectrically Driven Jet Dispensing Mechanism for Nanoliter Droplet of High Viscosity Liquid. J. Nanosci. Nanotechnol. 2019, 19, 1843–1847. [Google Scholar] [CrossRef]
- Ham, Y.B.; An, B.C.; Trimzi, M.A.; Kim, J.D.; Lee, G.T.; Park, J.H.; Yun, S.N. Experiments of Micro Jet Injection for Bio-Medical Application. Trans. Korean Soc. Mech. Eng. B 2016, 40, 681–687. [Google Scholar] [CrossRef]
- Shah, M.A.; Lee, D.G.; Hur, S. Design and Characteristic Analysis of a MEMS Piezo-Driven Recirculating Inkjet Printhead Using Lumped Element Modeling. Micromachines 2019, 10, 757. [Google Scholar] [CrossRef] [PubMed]
- Piezoelectric Transducers & Actuators. Available online: https://www.physikinstrumente.com/en/products/piezoelectric-transducers-actuators/ (accessed on 20 December 2019).
- Yong, Y.K.; Lu, T.F.; Handley, D.C. Review of Circular Flexure Hinge Design Equations and Derivation of Empirical Formulations. Precis. Eng. 2008, 32, 63–70. [Google Scholar] [CrossRef]
- Ueda, J.; Secord, T.W.; Asada, H.H. Large Effective-Strain Piezoelectric Actuators Using Nested Cellular Architecture With Exponential Strain Amplification Mechanisms. IEEE/ASME Trans. Mechatron. 2010, 15, 770–782. [Google Scholar] [CrossRef]
- Newnham, R.E.; Dogan, A.; Xu, Q.C.; Onitsuka, K.; Tressler, J.; Yoshikawa, S. Flextensional “Moonie” Actuators. In Proceedings of the 1993 Proceedings IEEE Ultrasonics Symposium, Baltimore, MD, USA, 31 October–3 November 1993; Volume 1, pp. 509–513. [Google Scholar] [CrossRef]
- Lam, K.H.; Wang, X.X.; Chan, H.L.W. Lead-Free Piezoceramic Cymbal Actuator. Sens. Actuators A Phys. 2006, 125, 393–397. [Google Scholar] [CrossRef]
- Kim, J.H.; Kim, S.H.; Kwaka, Y.K. Development of a Piezoelectric Actuator Using a Three-Dimensional Bridge-Type Hinge Mechanism. Rev. Sci. Instrum. 2003, 74, 2918–2924. [Google Scholar] [CrossRef]
- Haertling, G.H. Compositional Study of PLZT Rainbow Ceramics for Piezo Actuators. In Proceedings of the 1994 IEEE International Symposium on Applications of Ferroelectrics, University Park, PA, USA, 7–10 August 1994; pp. 313–318. [Google Scholar] [CrossRef]
- Ling, M.; Cao, J.; Zeng, M.; Lin, J.; Inman, D.J. Enhanced Mathematical Modeling of the Displacement Amplification Ratio for Piezoelectric Compliant Mechanisms. Smart Mater. Struct. 2016, 25. [Google Scholar] [CrossRef]
- Zhou, C.; Li, J.; Duan, J.A.; Deng, G. Direct-Acting Piezoelectric Jet Dispenser with Rhombic Mechanical Amplifier. IEEE Trans. Compon. Packag. Manuf. Technol. 2018, 8, 910–913. [Google Scholar] [CrossRef]
- Liu, R.; Cross, L.E.; Knowles, G.; Bower, B.; Childers, B. A Stackable Bonding-Free Flextensional Piezoelectric Actuator. J. Electroceram. 2000, 4, 201–206. [Google Scholar] [CrossRef]
- Lu, S.; Chen, X.; Zheng, H.; Zhao, Y.; Long, Y. Simulation and Experiment on Droplet Volume for the Needle-Type Piezoelectric Jetting Dispenser. Micromachines 2019, 10, 623. [Google Scholar] [CrossRef]
- Lu, S.; Cao, G.; Zheng, H.; Li, D.; Shi, M.; Qi, J. Simulation and Experiment on Droplet Formation and Separation for Needle-Type Micro-Liquid Jetting Dispenser. Micromachines 2018, 9, 330. [Google Scholar] [CrossRef] [PubMed]
- Uchino, K. Piezoelectric Actuators 2006: EEExpansion from IT/Robotics to Ecological/Energy Applications. J. Electroceram. 2008, 20, 301–311. [Google Scholar] [CrossRef]
- Wen, Y.; Deng, G.; Zhou, C. Simulation Analysis of Jet Dispenser Based on Piezoelectric Actuators. In Proceedings of the 2014 15th International Conference on Electronic Packaging Technology, Chengdu, China, 12–15 August 2014; pp. 680–683. [Google Scholar] [CrossRef]
- Huang, X.; Lin, X.; Jin, H.; Lin, S.; Bu, Z.; He, G.; Sun, D.; Wang, L. Effect of Enhanced Squeezing Needle Structure on the Jetting Performance of a Piezostack-Driven Dispenser. Micromachines 2019, 10, 850. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Cross, L.E.; Knowles, G.; Bower, B.; Childers, B.; Mawatari, K.; Sameshima, K.; Miyai, M.; Matsuda, S.; Wassink, G.; et al. Piezoelectric Actuators 2006: EEExpansion from IT/Robotics to Ecological/Energy Applications. J. Electroceram. 2008, 20, 301–311. [Google Scholar] [CrossRef]
- Amemiya, I.; Nomura, Y.; Mori, K.; Yoda, M.; Takasu, I.; Uchikoga, S. LED Packaging by Ink-Jet Microdeposition of High-Viscosity Resin and Phosphor Dispersion. J. Soc. Inf. Disp. 2008, 16, 475. [Google Scholar] [CrossRef]
- Choi, K.-H.; Rahman, K.; Malik, N.; Khan, A.; Kwon, K.-R.; Doh, Y.-H.; Kim, H.-C. Electrohydrodynamic Inkjet–Micro Pattern Fabrication for Printed Electronics Applications. Recent Adv. Nanofabr. Tech. Appl. 2012. [Google Scholar] [CrossRef]
- Hutchings, I.M.; Martin, G.D. (Eds.) Inkjet Technology for Digital Fabrication; A John Wiley & Sons, Ltd.: Chichester, UK, 2013; Volume 2a. [Google Scholar]
- Mawatari, K.; Sameshima, K.; Miyai, M.; Matsuda, S. Development of New Inkjet Head Applying MEMS Technology and Thin Film Actuator. Int. Conf. Digit. Print. Technol. 2014, 2014, 11–14. [Google Scholar]
- Wassink, G. Inkjet Printhead Performance Enhancement by Feedforward Input Design Based on Two-Port Modeling. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2007. [Google Scholar]
- Simulation in Mechanical Engineering | ESI ITI. Available online: https://www.simulationx.com/industries/simulation-machinery.html (accessed on 20 December 2019).
- Piezomechanik GmbH: Products. Available online: https://www.piezomechanik.com/en/products/ (accessed on 20 December 2019).
- Micro Dispensing Valve -MDV 3200A: VERMES Microdispensing GmbH. Available online: https://www.vermes.com/en/micro-dispensing-systems/mds-micro-dispensing-systems/micro-dispensing-system-mds-3200-series/micro-dispensing-valve-mdv-3200a/ (accessed on 20 December 2019).
- WAVE FACTORY:WF1973/WF1974. Available online: http://www.nfcorp.co.jp/english/pro/mi/sig/f_gen/wave/index.html (accessed on 20 December 2019).
- Positioning Sensors | KEYENCE America. Available online: https://www.keyence.com/products/sensor/positioning/index.jsp (accessed on 20 December 2019).
- Ham, Y.B.; An, B.C.; Trimzi, M.A.; Lee, G.T.; Park, J.H.; Yun, S.N. An Experimental Study on the Displacement Amplification Mechanism Driven by Piezoelectric Actuators for Jet Dispenser. In Proceedings of the 2016 International Conference on Manipulation, Automation and Robotics at Small Scales, MARSS 2016, Paris, France, 18–22 July 2016. [Google Scholar] [CrossRef]
- Physical Properties of Glycerine and Its Solutions; Gulf Publishing Company: Houston, TX, USA, 1967.
- Sheely, M.L. Glycerol Viscosity Tables. Ind. Eng. Chem. 1932, 24, 1060–1064. [Google Scholar] [CrossRef]
- General Purpose Silicone. Available online: https://www.brookfieldengineering.com/products/viscosity-standards/general-purpose-silicone (accessed on 20 December 2019).
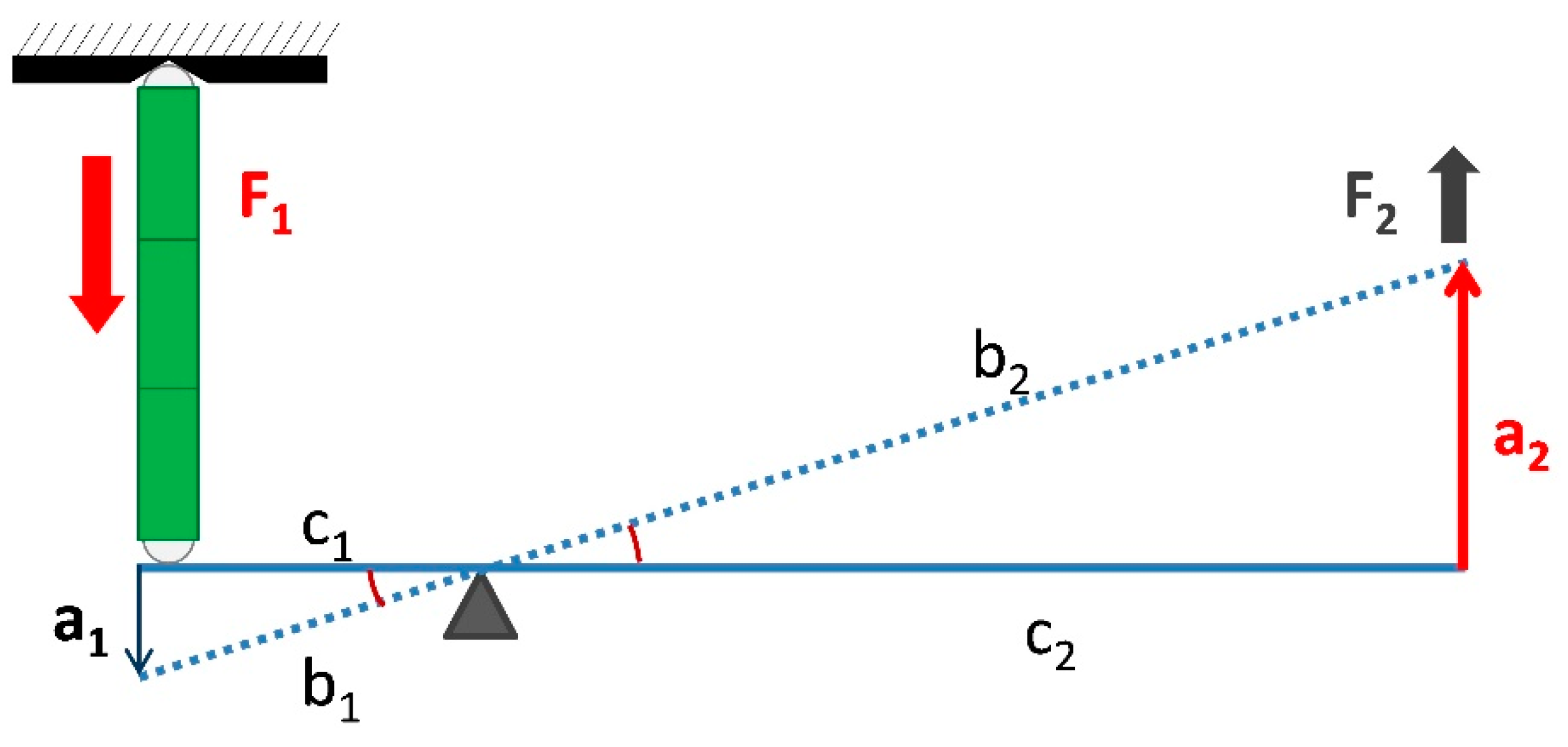

| c1 (mm) | c2 (mm) | R = c1/c2 | a1 (μm) | a2 (μm) | F1 (N) | F2 (N) |
|---|---|---|---|---|---|---|
| 1.5 | 9.5 | 6.34 | 60.0 | 380.0 | 3500.0 | 552.6 |
| Parameter | Value |
|---|---|
| Density of Fluid | 0.8916 g/cm3 |
| Dynamic Viscosity | 1328.0 mPa·s |
| Temperature | 0 °C |
| Nozzle Diameter | 300 μm |
| Feed Pressure | 0.2 MPa |
| Amplification Ratio | 6.34 |
| Piezo Stroke | 55 μm |
| Spring Stiffness | 25.3 N/mm |
| Maximum Displacement | Minimum Displacement | Overall Displacement | Overall Displacement | Sampling Points |
|---|---|---|---|---|
| −0.0478 mm | 0.3766 mm | 0.4244 mm | 424.4 μm | 0–8000 N |
| Rising Time (RT) | Open Time (OT) | Falling Time (FT) | Frequency Range | Voltage |
|---|---|---|---|---|
| 0.5 ms | 5–500 ms | 0.1 ms | 1–100 Hz | 130 V |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trimzi, M.A.; Ham, Y.B.; An, B.C.; Choi, Y.M.; Park, J.H.; Yun, S.N. Development of a Piezo-Driven Liquid Jet Dispenser with Hinge-Lever Amplification Mechanism. Micromachines 2020, 11, 117. https://doi.org/10.3390/mi11020117
Trimzi MA, Ham YB, An BC, Choi YM, Park JH, Yun SN. Development of a Piezo-Driven Liquid Jet Dispenser with Hinge-Lever Amplification Mechanism. Micromachines. 2020; 11(2):117. https://doi.org/10.3390/mi11020117
Chicago/Turabian StyleTrimzi, Mojiz Abbas, Young Bog Ham, Byeung Cheol An, Young Min Choi, Jung Ho Park, and So Nam Yun. 2020. "Development of a Piezo-Driven Liquid Jet Dispenser with Hinge-Lever Amplification Mechanism" Micromachines 11, no. 2: 117. https://doi.org/10.3390/mi11020117
APA StyleTrimzi, M. A., Ham, Y. B., An, B. C., Choi, Y. M., Park, J. H., & Yun, S. N. (2020). Development of a Piezo-Driven Liquid Jet Dispenser with Hinge-Lever Amplification Mechanism. Micromachines, 11(2), 117. https://doi.org/10.3390/mi11020117







