Analysis of the Failure and Performance Variation Mechanism of MEMS Suspended Inductors with Auxiliary Pillars under High-g Shock
Abstract
:1. Introduction
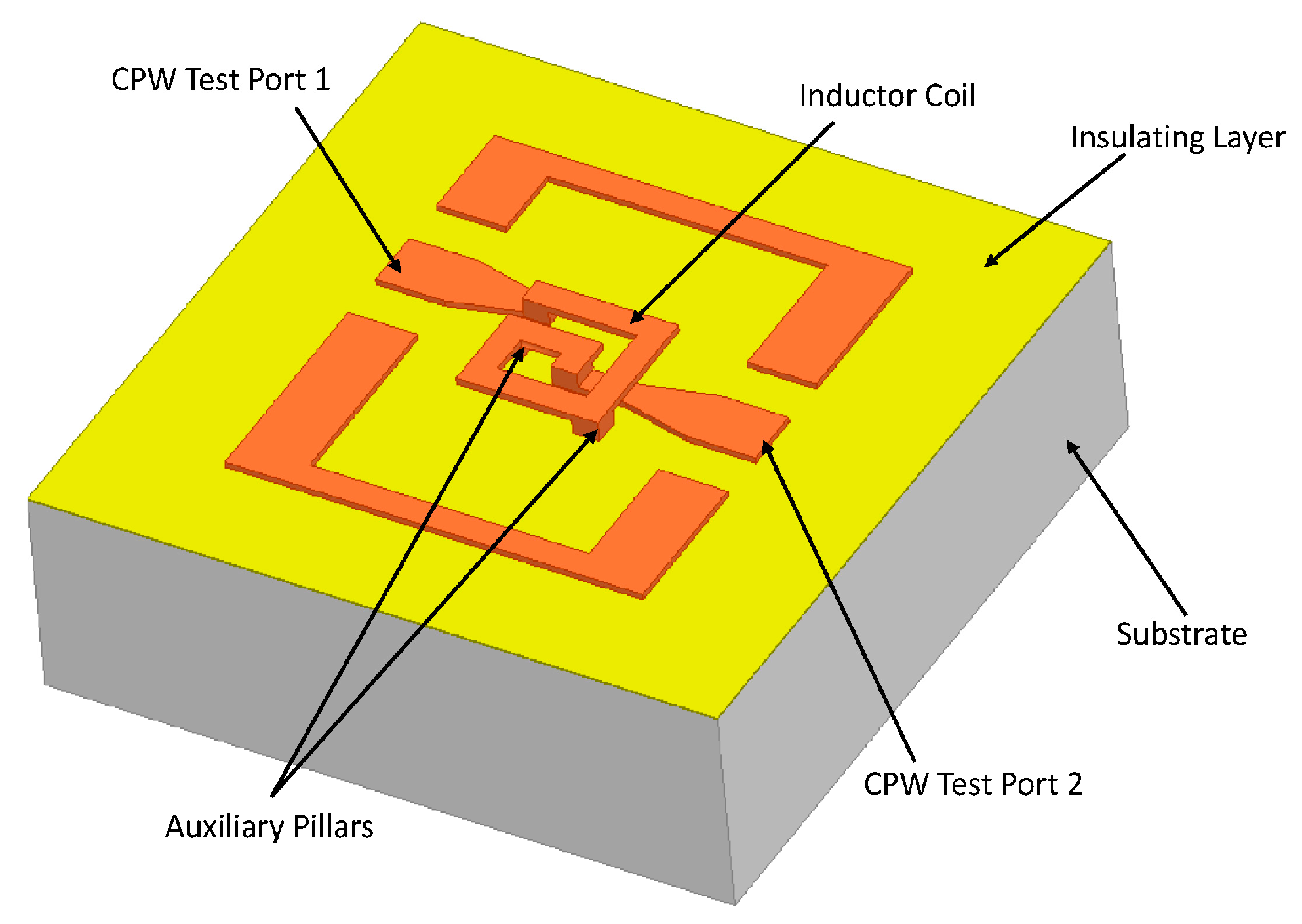
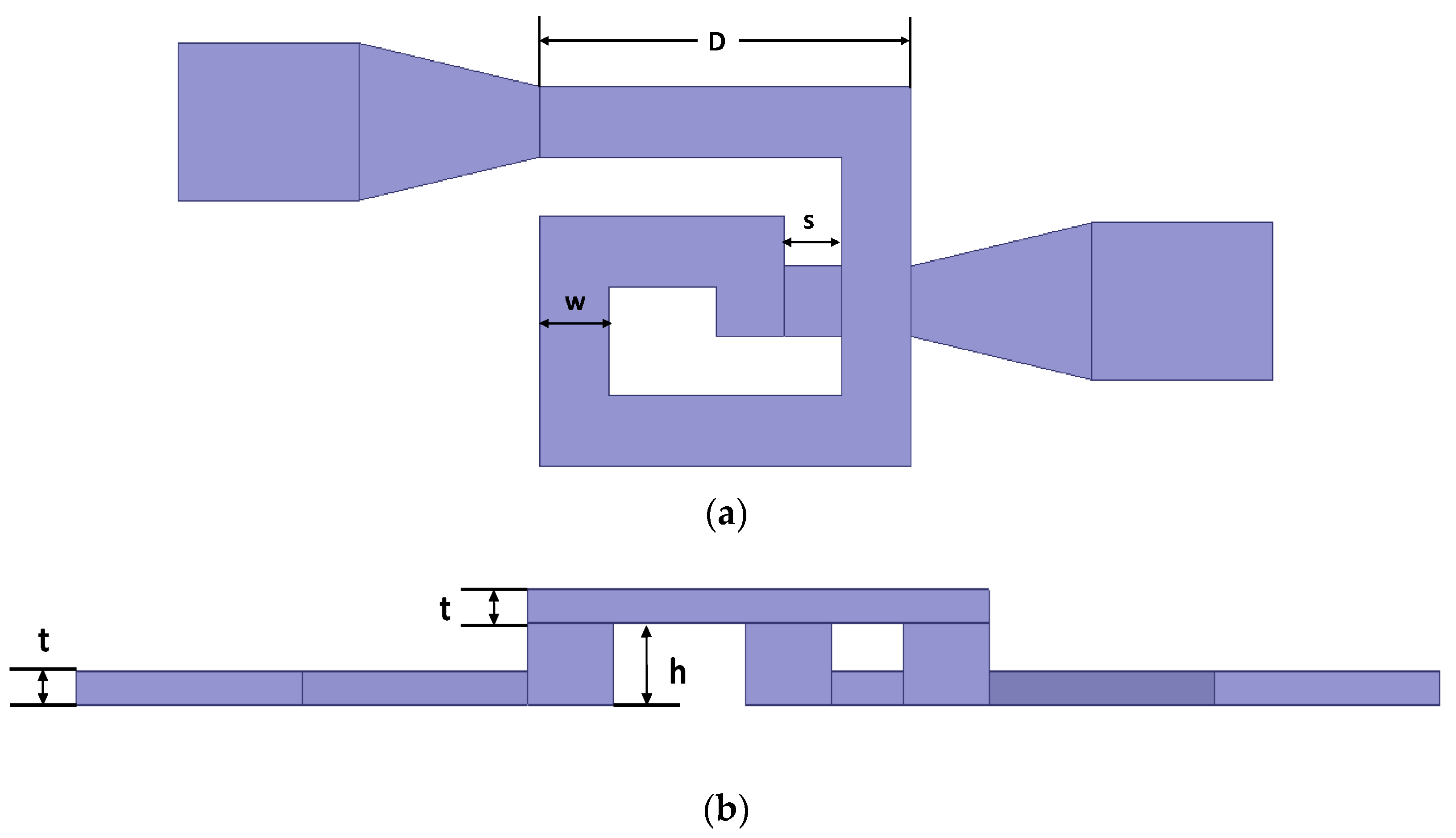
2. MEMS Suspended Inductor Sample and Fabrication
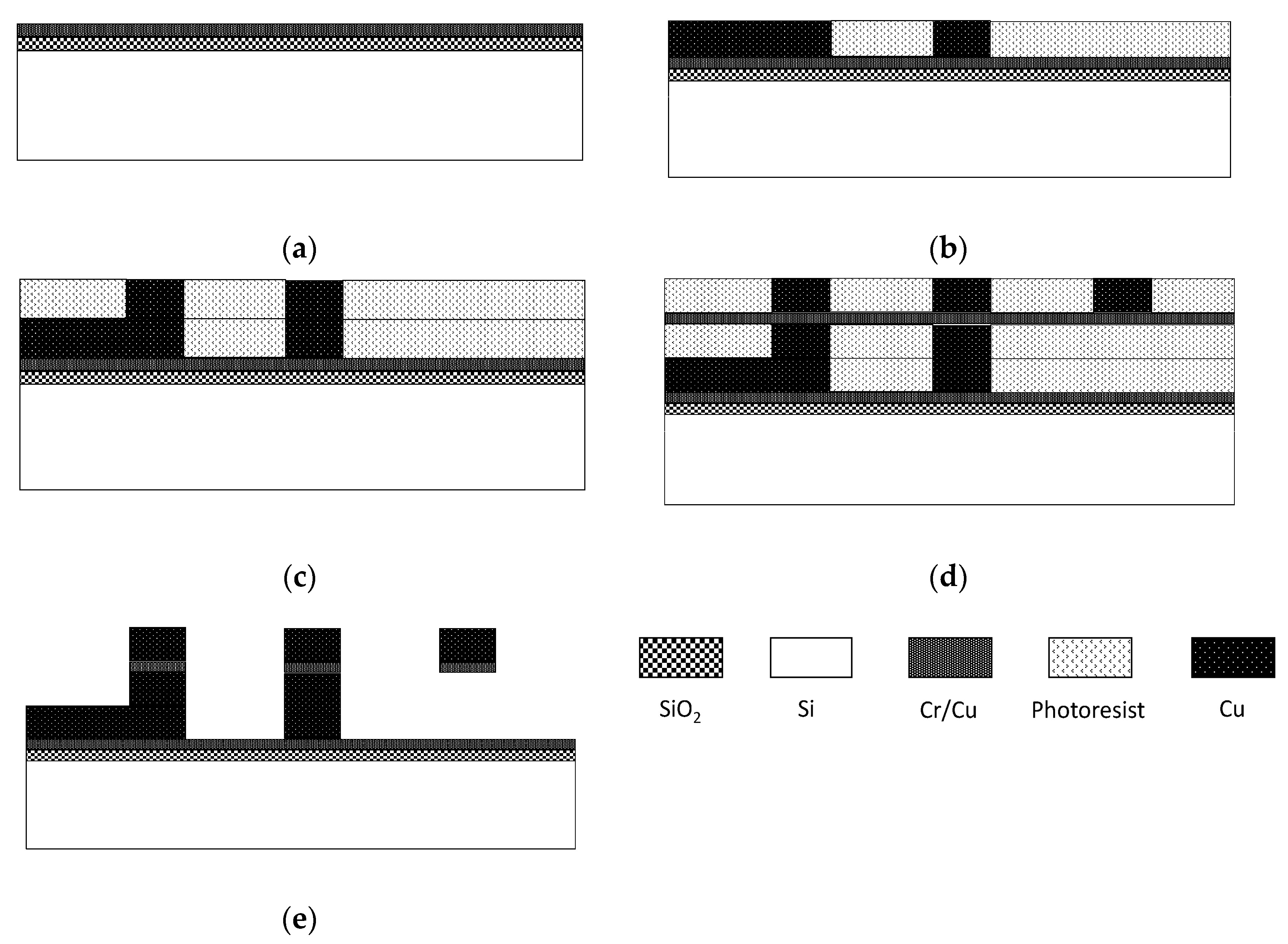
- As Figure 4a shows, a 1.5 μm thick silicon oxide insulating layer is first deposited using a plasma enhanced chemical vapor deposition method. Then wash the wafer with mixture of concentrated sulfuric acid and hydrogen peroxide. A chromium/copper (Cr/Cu) seed layer is then deposited on the wafer by a magnetron sputtering process, the thickness of Cr and Cu are 200 Å and 1000 Å respectively.
- As Figure 4b shows, a 10 μm AZ4620 positive photoresist is spin coated and patterned with the first mask after treating the wafer with Hexamethyldisilazane (HDMS) to remove moisture on it. Then the underpass lines and the test ports are electroplated in the molds; electroplating thickness is 10 μm. A mixture of copper sulfate and sulfuric acid is chosen as the electroplating bath in all electroplating process steps.
- As Figure 4c shows, a 10 μm AZ4620 photoresist is spin coated and patterned with the second mask. Then, the pillars of the suspended inductor are electroplated.
- As Figure 4d shows, a Cr/Cu seed layer is deposited on the wafer by magnetron sputtering and the thickness of Cr and Cu are also 200 Å and 1000 Å respectively. Then a 10 μm AZ4903 photoresist is spin coated and patterned with the third mask, the spiral coil of the suspended inductor is finally electroplated.
- As Figure 4e shows, all photoresist and seed layers are removed in sequence to release the suspended structure. The photoresist is removed by sodium hydroxide and acetone, the remaining acetone is dissolved with anhydrous alcohol, the copper seed layer is removed by mixture of ammonia and hydrogen peroxide, and the chromium seed layer is removed by mixture of potassium ferricyanide and sodium hydroxide.
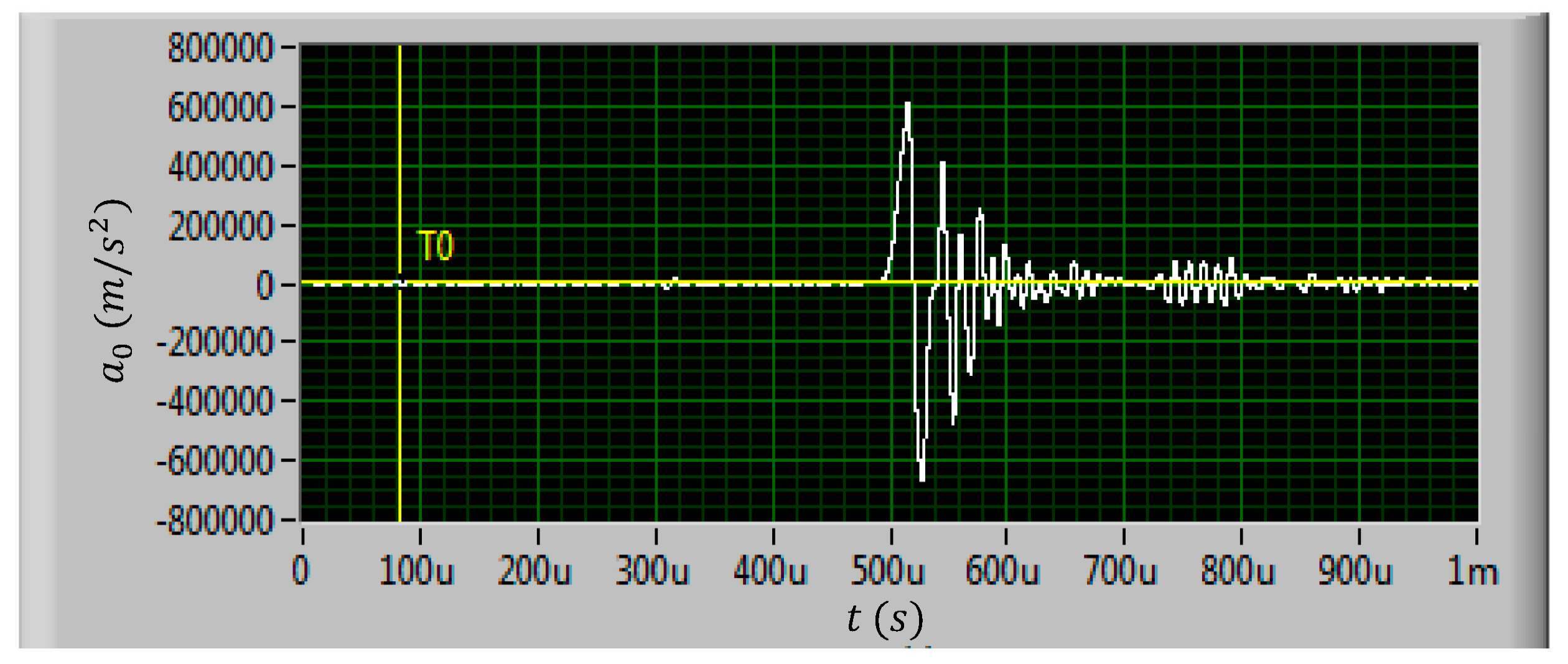
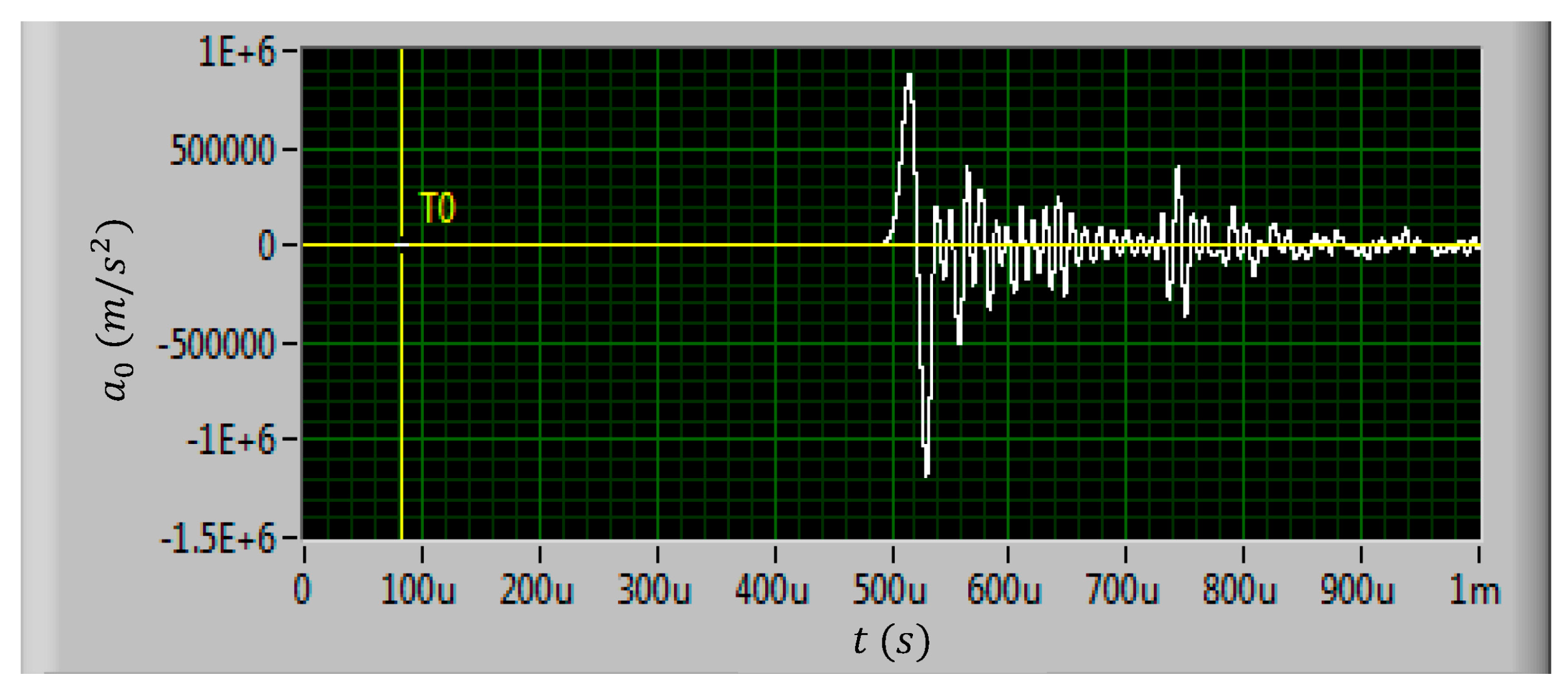
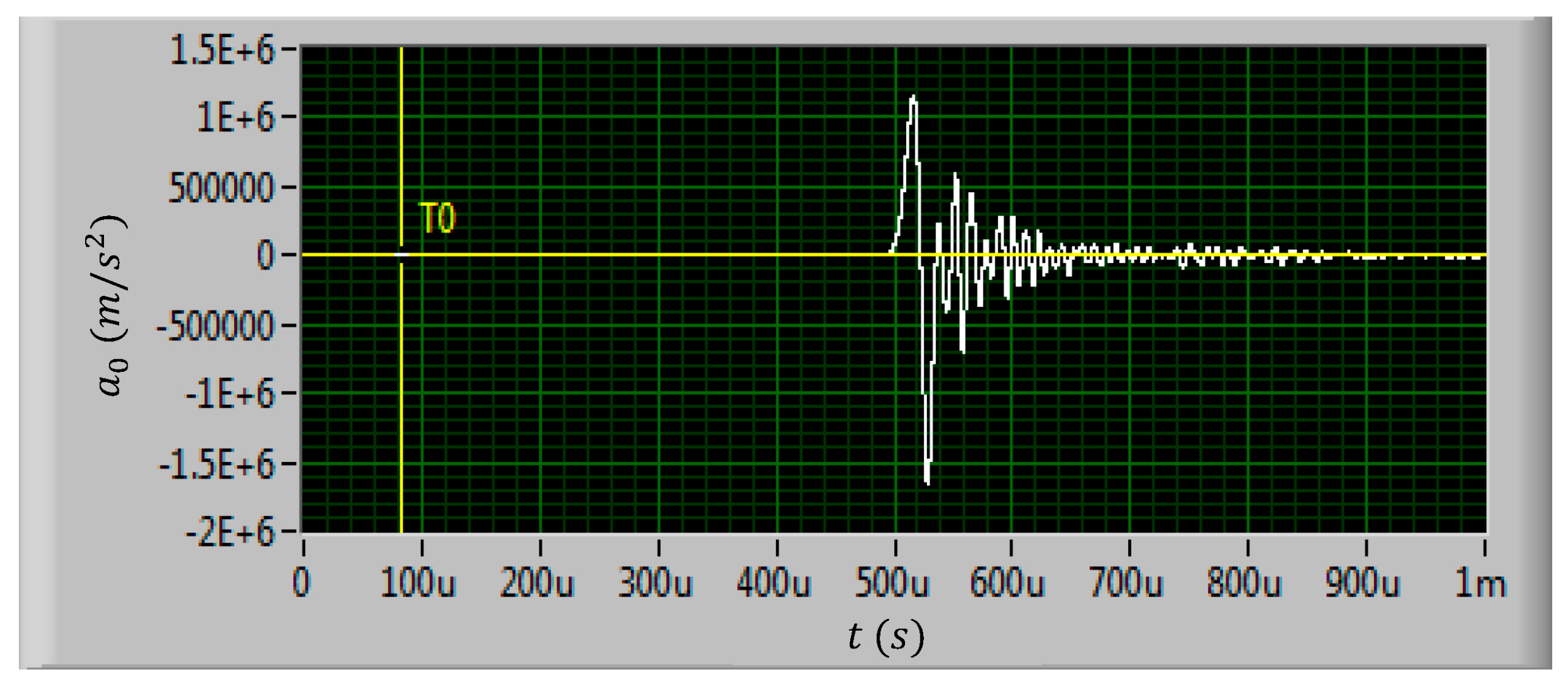
3. Shock Test of MEMS Suspended Inductors
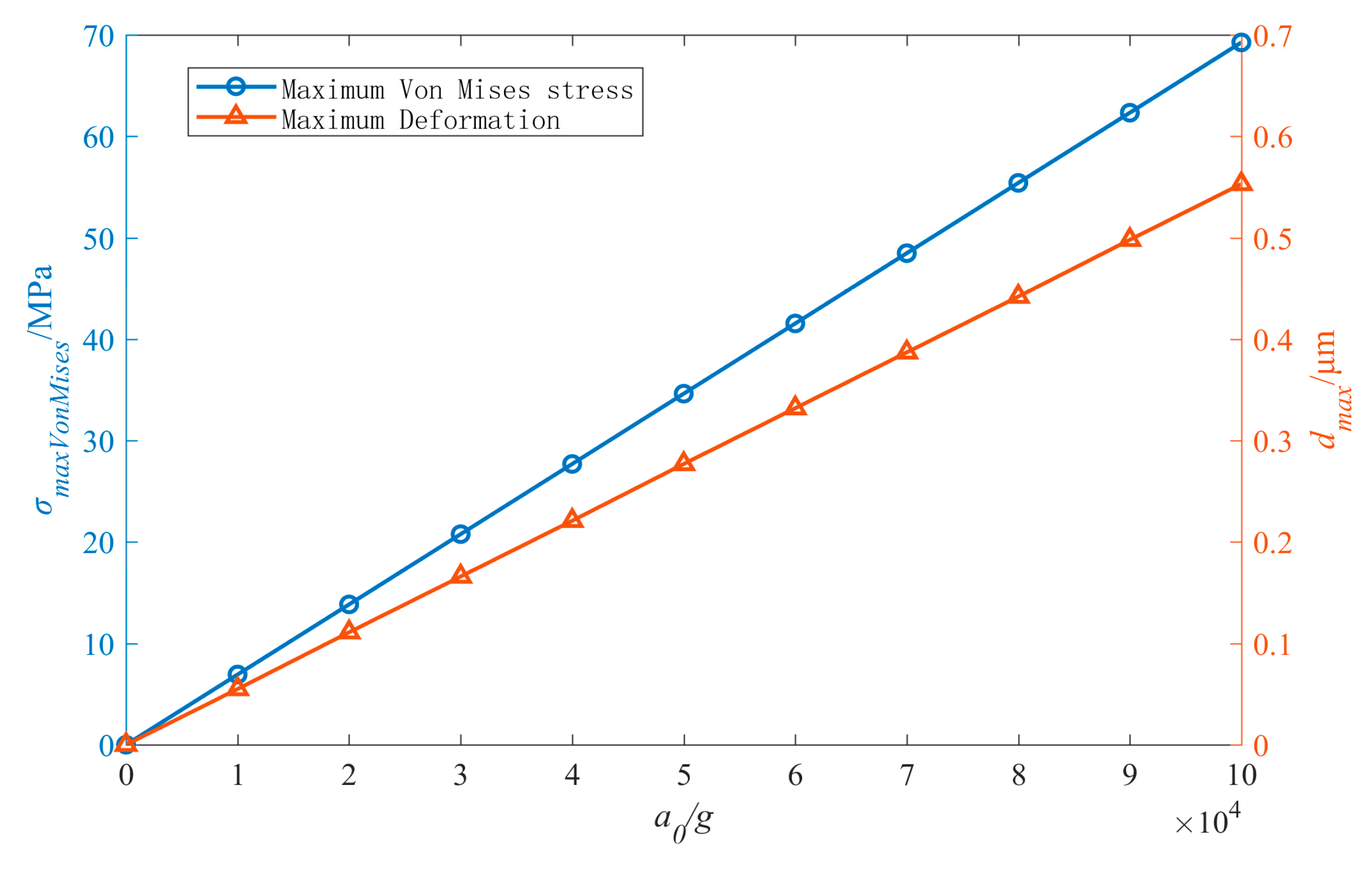
4. Results and Discussion
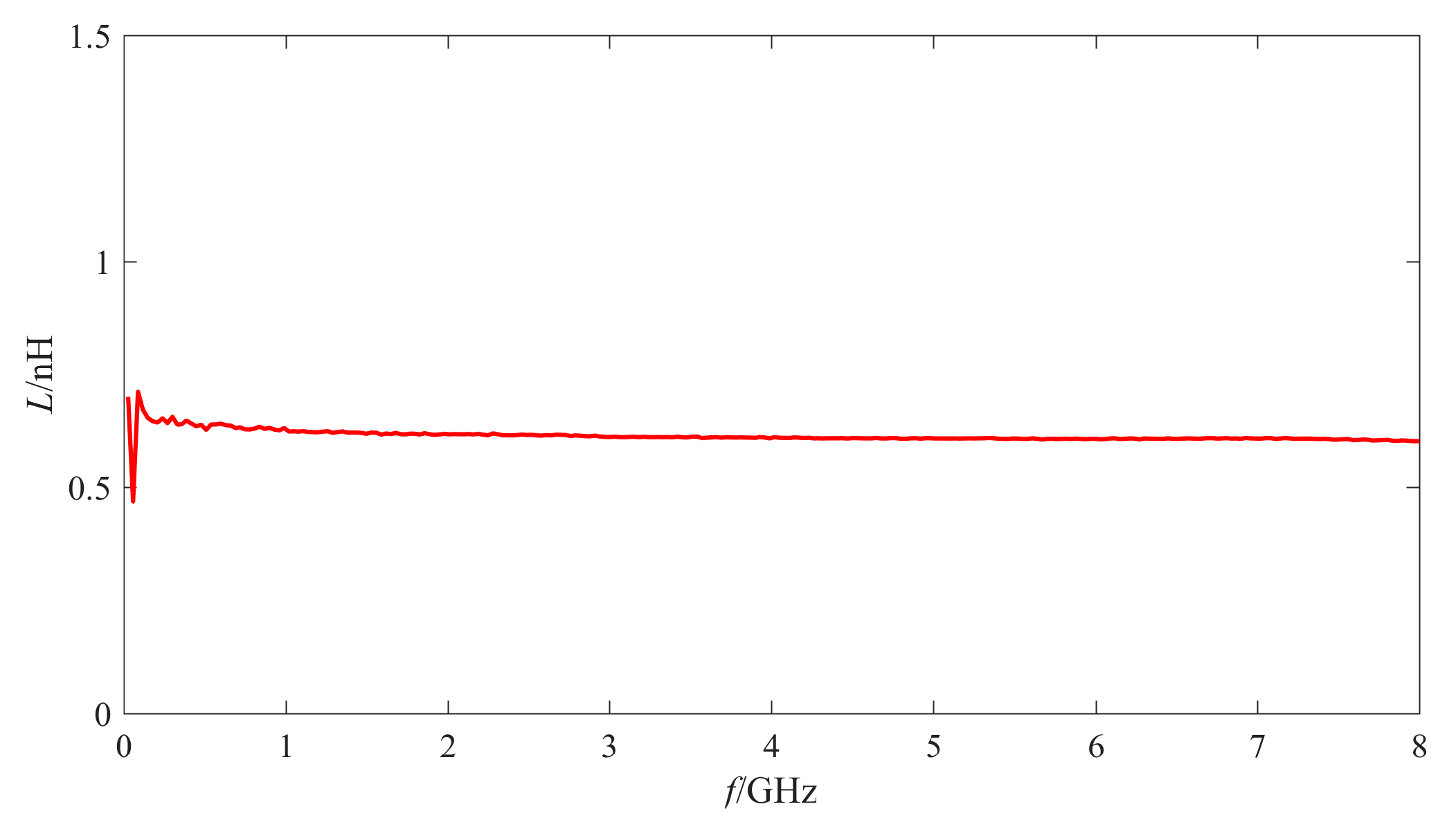
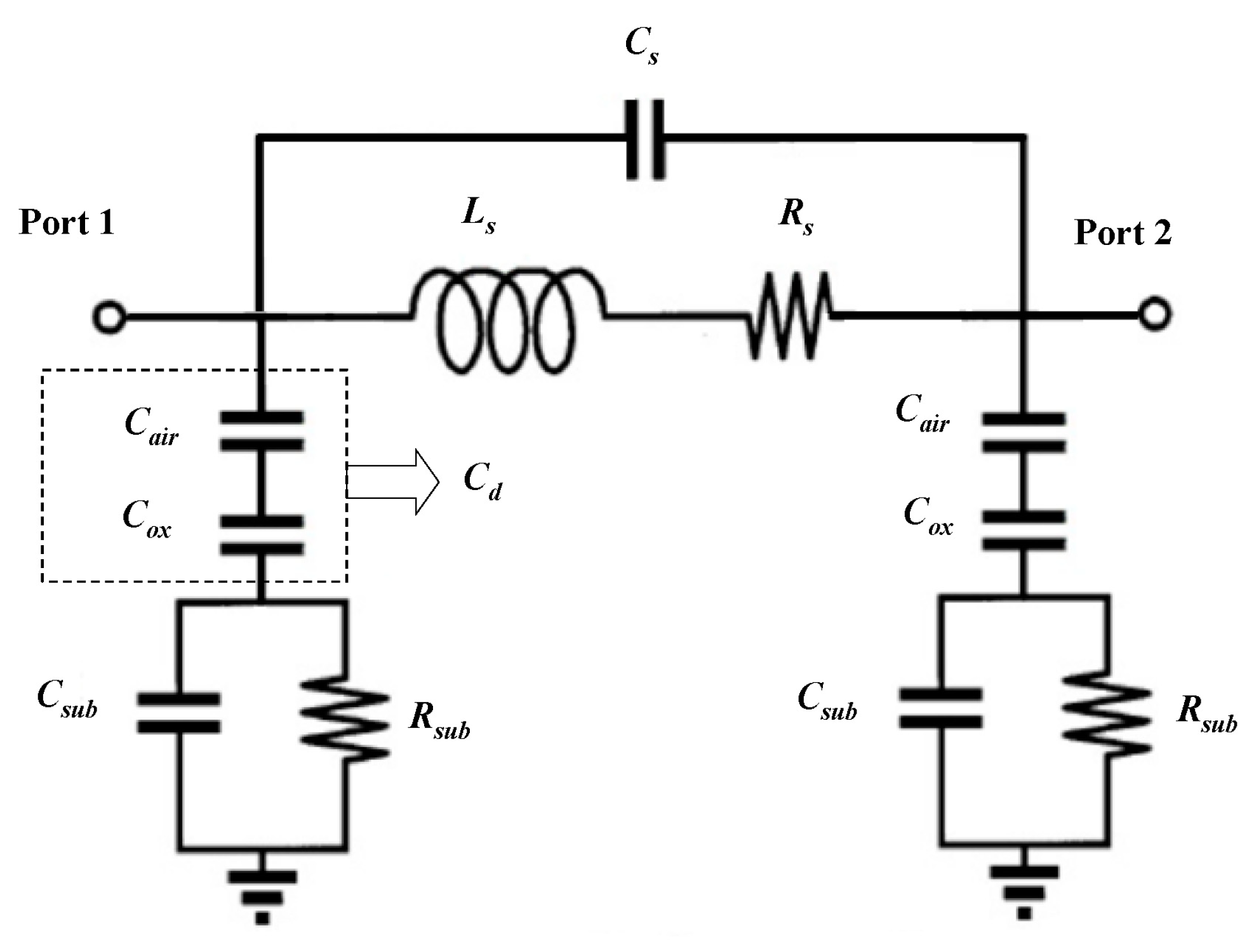
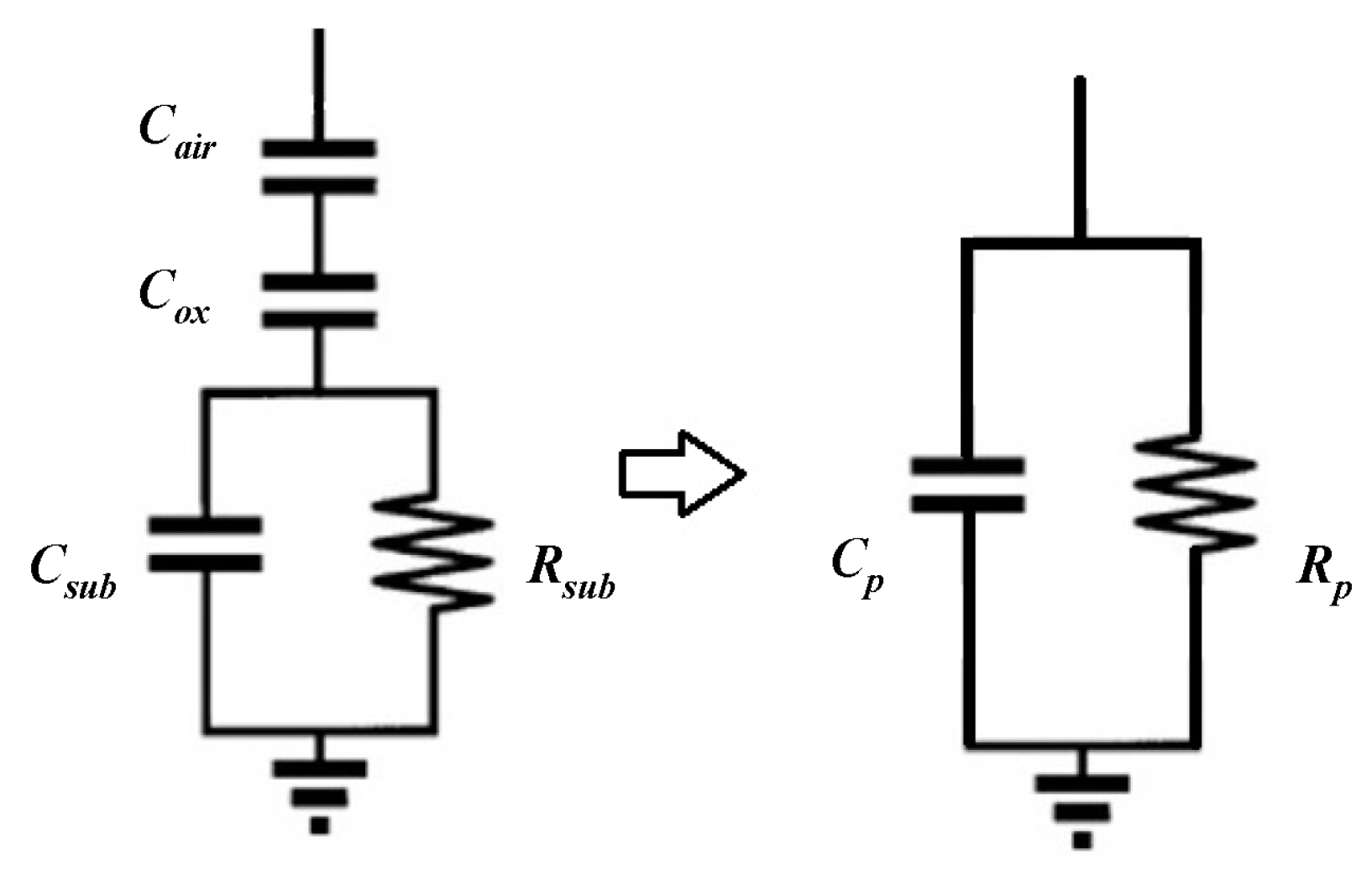
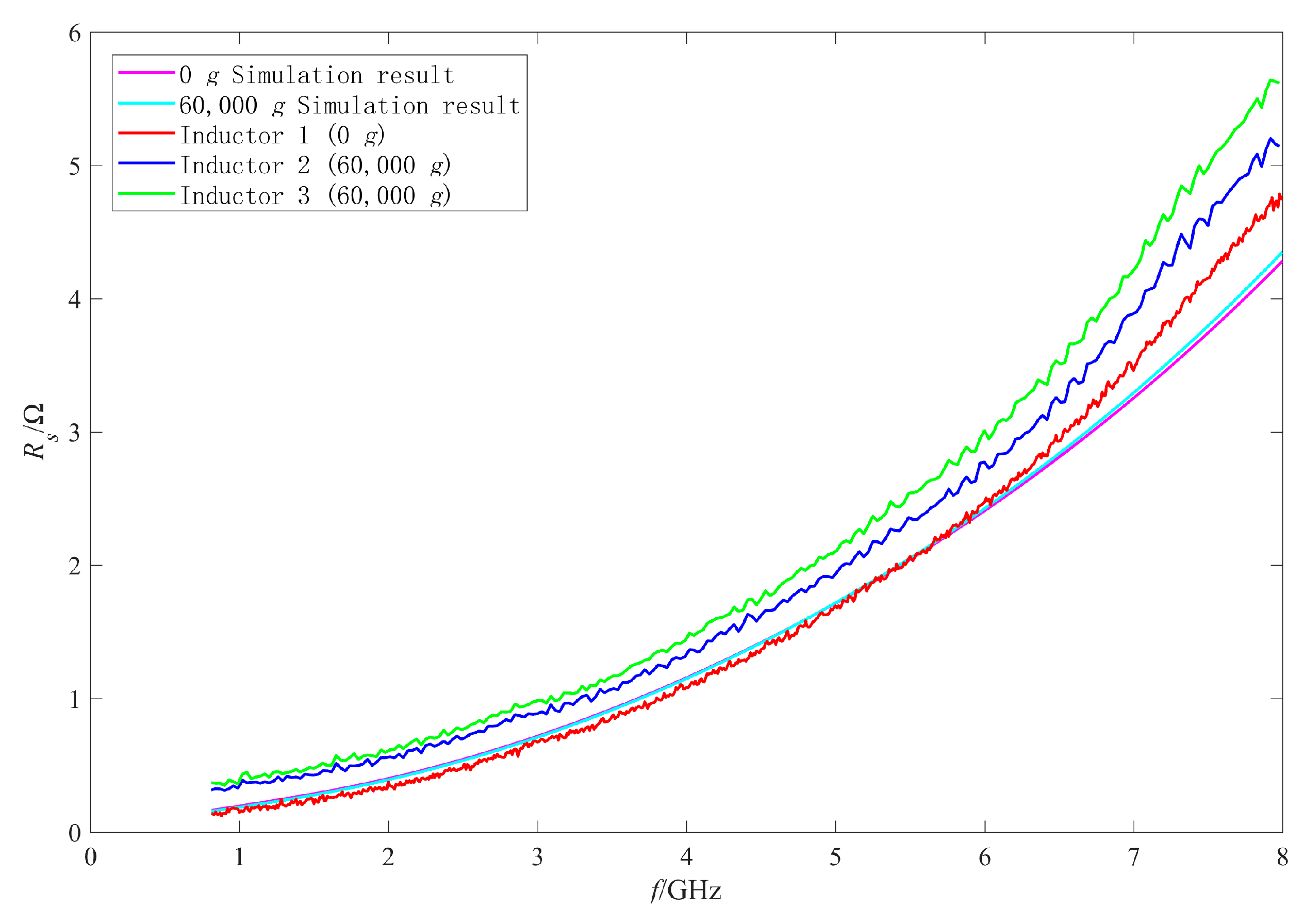
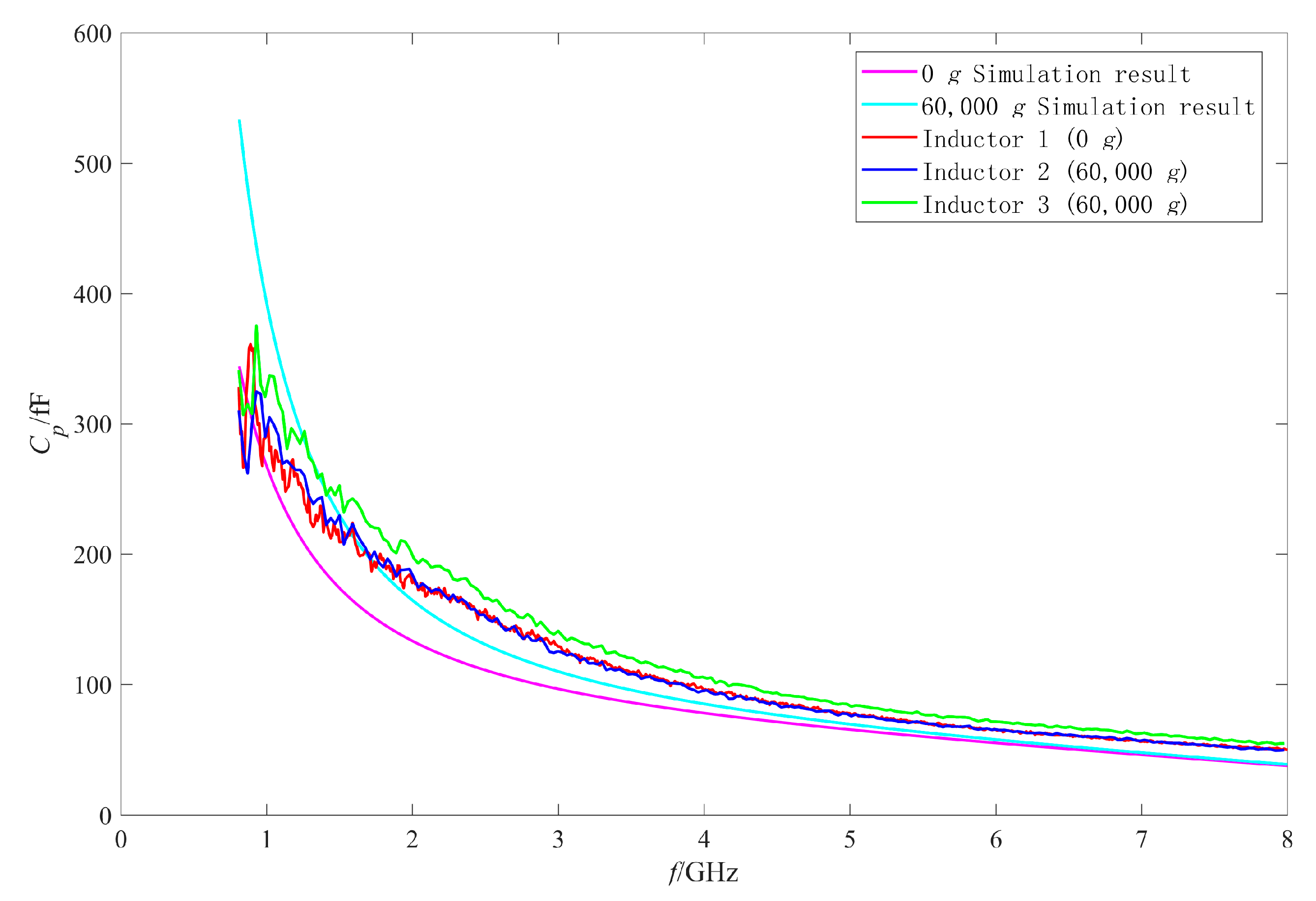
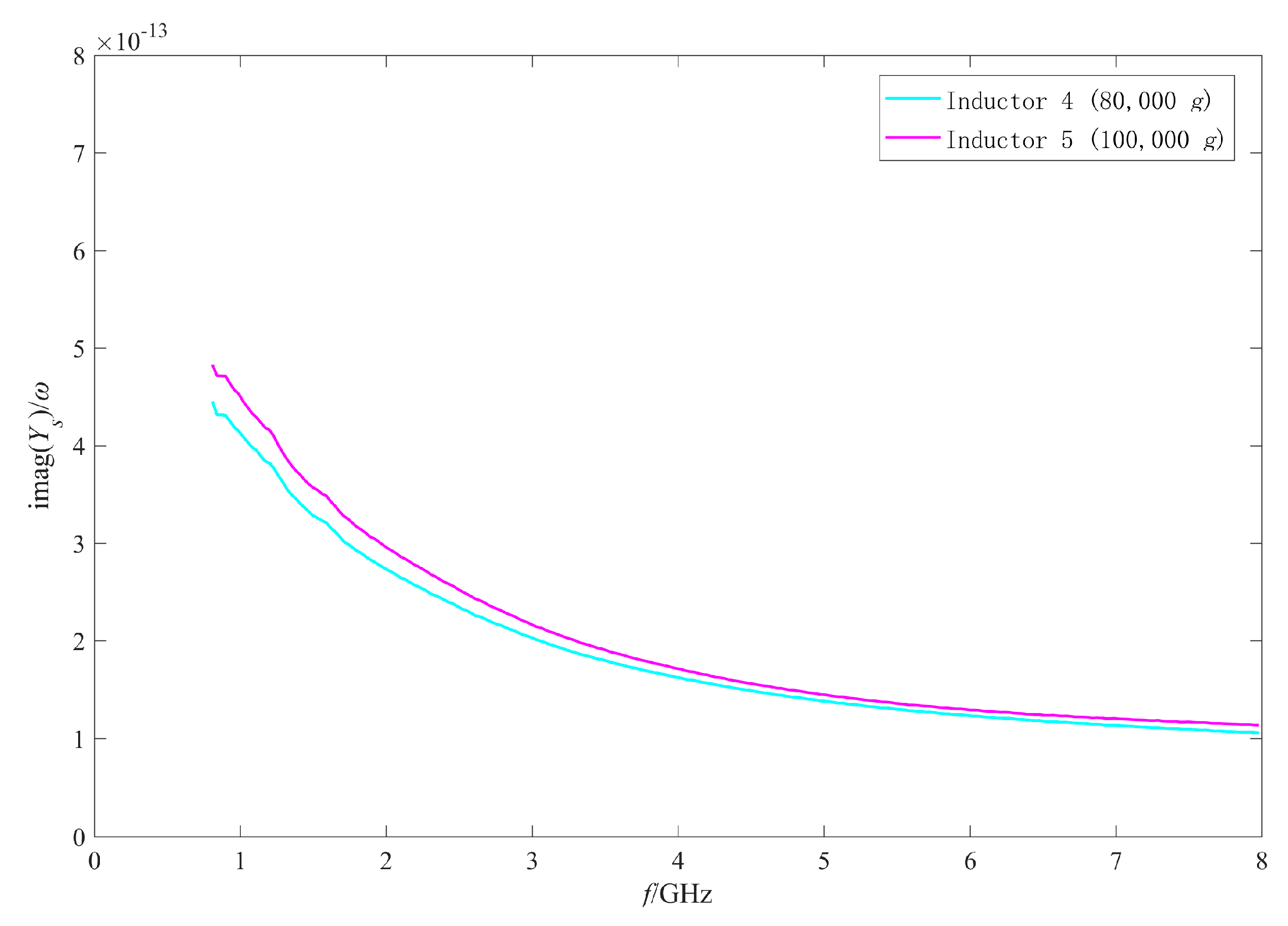
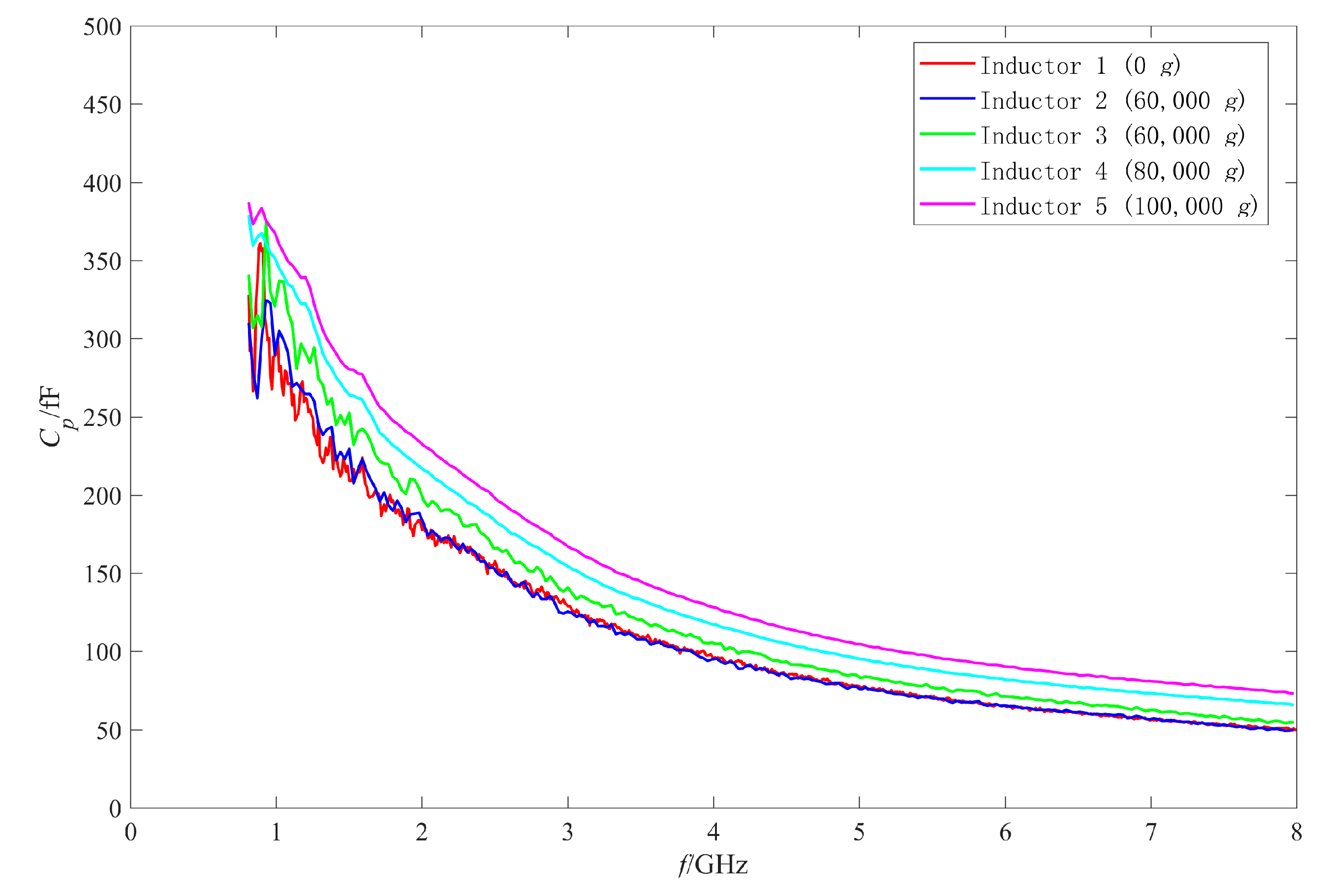
4.1. Analysis of the RF Performance Variation Mechanism of the Intact Inductors
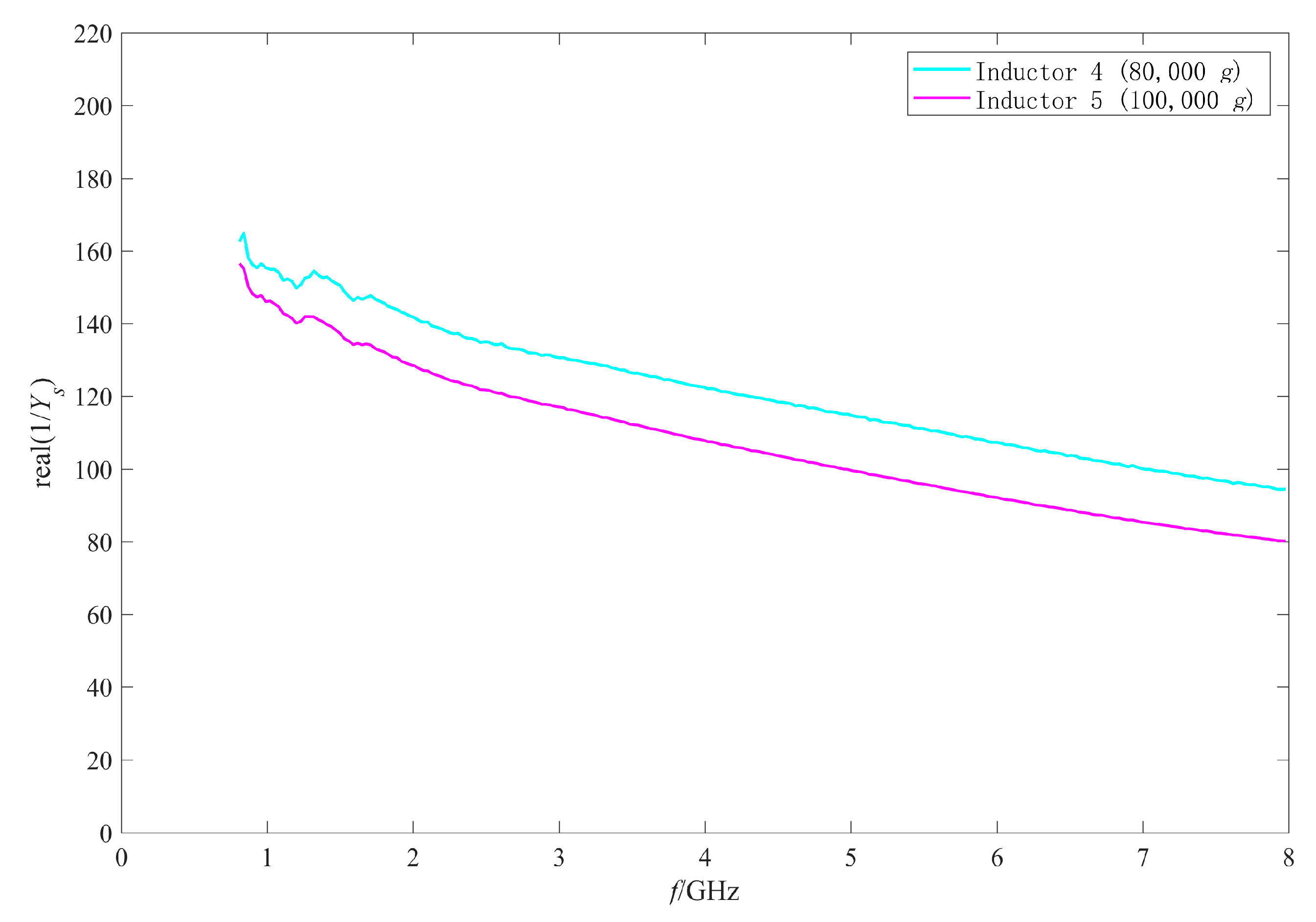
4.2. Analysis of the Failure Mechanism of the Failed Inductors
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shi, J.; Yin, W.-Y.; Liao, H.; Mao, J.-F. The enhancement of Q factor for patterned ground shield inductors at high temperatures. IEEE Trans. Magn. 2006, 42, 1873–1875. [Google Scholar]
- Lin, Y.-S.; Chen, C.-Z.; Liang, H.-B.; Chen, C.-C. High-performance on-chip transformers with partial polysilicon patterned ground shields (PGS). IEEE Trans. Electron Devices 2007, 54, 157–160. [Google Scholar] [CrossRef]
- Wang, Y.F.; Liao, X.P.; Huang, Q.A. Research and Progress of RF MEMS Inductors. Chin. J. Electron. Dev. 2004, 27, 354–359. [Google Scholar]
- Yoon, J.B.; Han, C.H.; Yoon, E.; Kim, C.K. Monolithic high-Q overhang inductors fabricated on silicon and glass substrates. In Proceedings of the IEEE International Electron Devices Meeting, Washington, DC, USA, 5–8 December 1999; pp. 753–756. [Google Scholar]
- Yoon, J.B.; Han, C.H.; Yoon, E.; Kim, C.K. High-performance three-dimensional on-chip inductors fabricated by novel micromachining technology for RF MMIC. In Proceedings of the IEEE international Microwave Symposium Digest, Anaheim, CA, USA, 13–19 June 1999; pp. 1523–1526. [Google Scholar]
- Ding, Y.; Liu, Z.; Liu, L.; Li, Z. A surface micromachining process for suspended RF-MEMS applications using porous silicon. Microsyst. Technol. 2003, 9, 470–473. [Google Scholar] [CrossRef]
- Wang, X.N.; Zhao, X.L.; Zhou, Y.; Dai, X.H.; Cai, B.C. Fabrication and performance of a novel suspended RF spiral inductor. IEEE Trans. Electron Devices 2004, 51, 814–816. [Google Scholar] [CrossRef]
- Tai, C.M.; Liao, C.N. Multilevel suspended thin-film inductors on silicon wafers. IEEE Trans. Electron Devices 2007, 54, 1510–1514. [Google Scholar]
- Zheng, T.; Xu, G.; Luo, L. High performance suspended spiral inductor and band-pass filter by wafer level packaging technology. Microsyst. Technol. 2017, 23, 2107–2111. [Google Scholar] [CrossRef]
- Li, L.; Ma, K.; Mou, S. A Novel High Q Inductor Based on Double-sided Substrate Integrated Suspended Line Technology with Patterned Substrate. In Proceedings of the IEEE MTT-S International Microwave Symposium (IMS), Honololu, HI, USA, 4–9 June 2017; pp. 480–482. [Google Scholar]
- Stojanović, G.; Živanov, L.; Damnjanović, M. Novel efficient methods for inductance calculation of meander inductor. COMPEL Int. J. Comput. Math. Electr. Eng. 2006, 25, 916–928. [Google Scholar] [CrossRef]
- Wang, T.P.; Li, Z.W.; Tsai, H.Y. Performance Improvement of a 0.18-μm CMOS Microwave Amplifier Using Micromachined Suspended Inductors: Theory and Experiment. IEEE Trans. Electron Devices 2013, 60, 1738–1744. [Google Scholar] [CrossRef]
- Park, E.-C.; Choi, Y.-S.; Yoon, J.-B.; Hong, S.; Yoon, E. Fully integrated low phase-noise VCOs with on-chip MEMS inductors. IEEE Trans. Microw. Theory Tech. 2003, 51, 289–296. [Google Scholar] [CrossRef] [Green Version]
- Mohammadi, A.; Karmakar, N.C. High Quality MEMS Inductors for Chipless RFID in Harsh Environment. In Proceedings of the 2016 IEEE 2nd Australian Microwave Symposium, Adelaide, SA, Australia, 11–12 February 2016; pp. 43–44. [Google Scholar]
- Brown, T.G.; Davis, B.; Hepner, D.; Faust, J.; Myers, C.; Muller, C.; Harkins, T.; Holis, M.; Placzankis, B. Strap-down microelectromechanical (MEMS) sensors for high-g munition applications. IEEE Trans. Magn. 2001, 37, 336–342. [Google Scholar] [CrossRef]
- Le, H.T.; Mizushima, I.; Nour, Y.; Torben Tang, P.; Knott, A.; Ouyang, Z.; Jensen, F.; Han, A. Fabrication of 3D air-core MEMS inductors for very-high-frequency power conversions. Microsyst. Nanoeng. 2017, 3, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.W.; Chen, C.C.; Cheng, Y.T. A robust high-Q micromachined RF inductor for RFIC applications. IEEE Trans. Electron Devices 2005, 52, 1489–1496. [Google Scholar] [CrossRef]
- Chiu, Y.; Hong, H.C.; Wu, P.C. Development and Characterization of a CMOS-MEMS Accelerometer with Differential LC-Tank Oscillators. J. Microelectromech. Syst. 2013, 22, 1285–1295. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.C.; Zaghloul, M.E. CMOS Micromachined Inductors with Structure Supports for RF Mixer Matching Networks. IEEE Electron Devices Lett. 2008, 29, 1209–1211. [Google Scholar] [CrossRef]
- Li, Y.Y.; Xu, L.X.; Li, J.H. Analysis of the Performance Variation Mechanism of MEMS Suspended Inductors under Mechanical Shock. Micromachines 2019, 10, 686. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Srikar, V.T.; Senturia, S.D. The reliability of microelectromechanical systems (MEMS) in shock environments. J. Microelectromech. Syst. 2002, 11, 206–214. [Google Scholar] [CrossRef]
- Xu, L.; Li, Y.; Li, J.; Lu, C. Mechanical Response of MEMS Inductor with Auxiliary Pillar under High-g Shock. Micromachines 2018, 9, 176. [Google Scholar] [CrossRef] [Green Version]
- Hikmat, O.F.; Ali, M.S.M. RF MEMS Inductors and Their Applications—A Review. J. Microelectromech. Syst. 2017, 26, 17–44. [Google Scholar] [CrossRef]
- Yue, C.P.; Ryu, C.; Lau, J.; Lee, T.H.; Wong, S.S. A Psysical Model for Planar Spiral Inductors on Silicon. In Proceedings of the International Electron Devices Meeting Technical Digest, San Francisco, CA, USA, 8–11 December 1996; pp. 155–158. [Google Scholar]
- Yue, C.P.; Wong, S.S. On-Chip Spiral Inductors with Patterned Ground Shields for Si-Based RF IC’s. IEEE J. Solid State Circuits 1998, 33, 743–752. [Google Scholar] [CrossRef]
- Yue, C.P.; Wong, S.S. Psysical Modeling of Spiral Inductors on Silicon. IEEE Trans. Electron Devices 2000, 47, 560–568. [Google Scholar] [CrossRef] [Green Version]
- Huang, F.Y.; Jiang, N.; Bian, E.L. Modeling of single-π equivalent circuit for on-chip spiral inductors. Solid State Electron. 2005, 49, 473–478. [Google Scholar] [CrossRef]
- Huang, F.Y.; Lu, J.X.; Jiang, D.M.; Wang, X.C.; Jiang, N. A novel analytical approach to parameter extraction for on-chip spiral inductors taking into account high-order parasitic effect. Solid State Electron. 2006, 50, 1557–1562. [Google Scholar] [CrossRef]
- Kuhn, W.B.; Ibrahim, N.M. Analysis of Current Crowding Effects in Multiturn Spiral Inductors. IEEE Trans. Microw. Theory Tech. 2001, 49, 31–38. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.D.; Shang, D.G.; Liu, H.; Xu, M.H.; Xu, J.; Liu, T.L. Study of Fatigue Property for Electroplated Copper Thin Film by Pulsed Laser Shock Peening. J. Mech. Strength 2012, 34, 751–756. [Google Scholar]





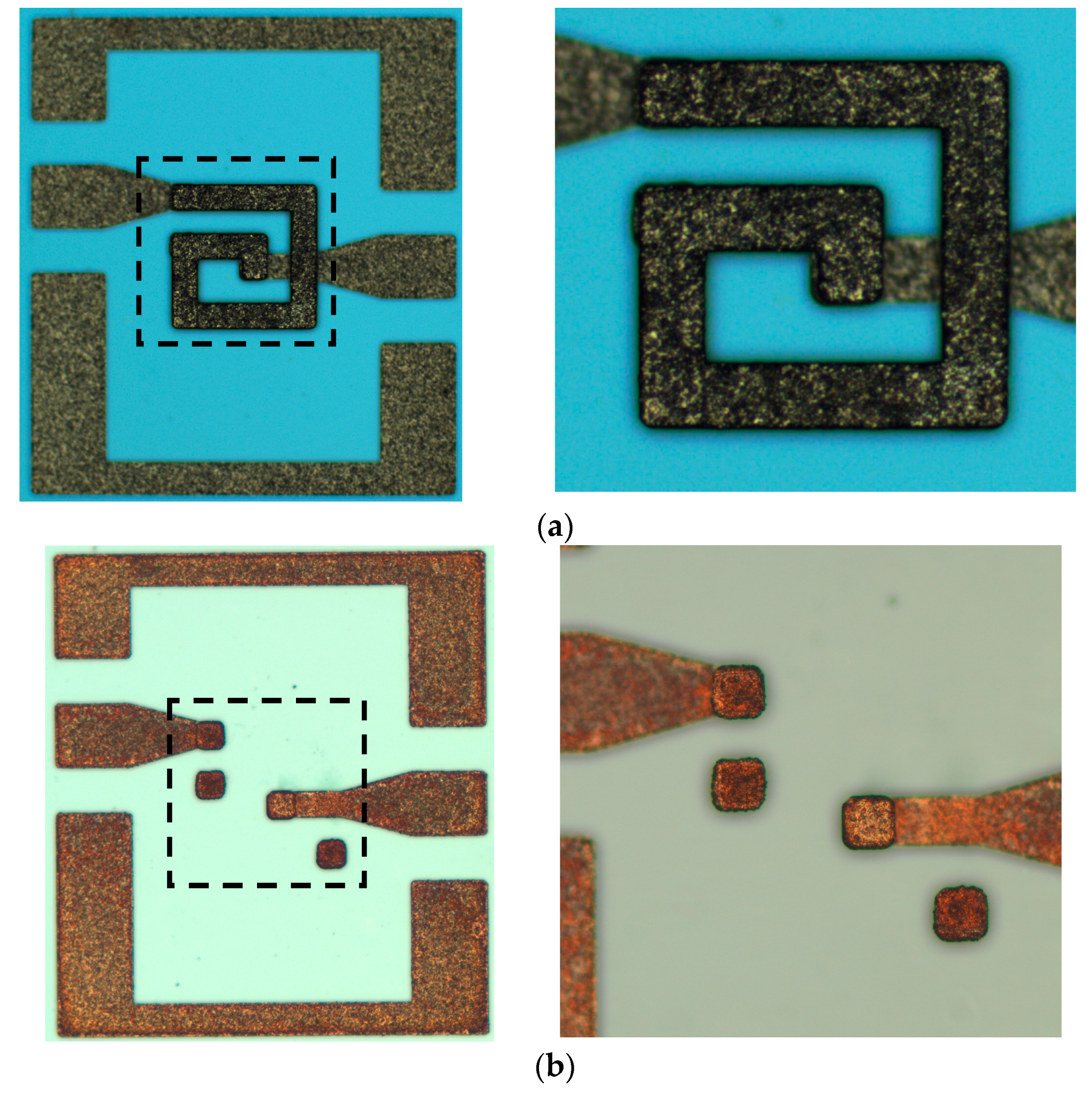
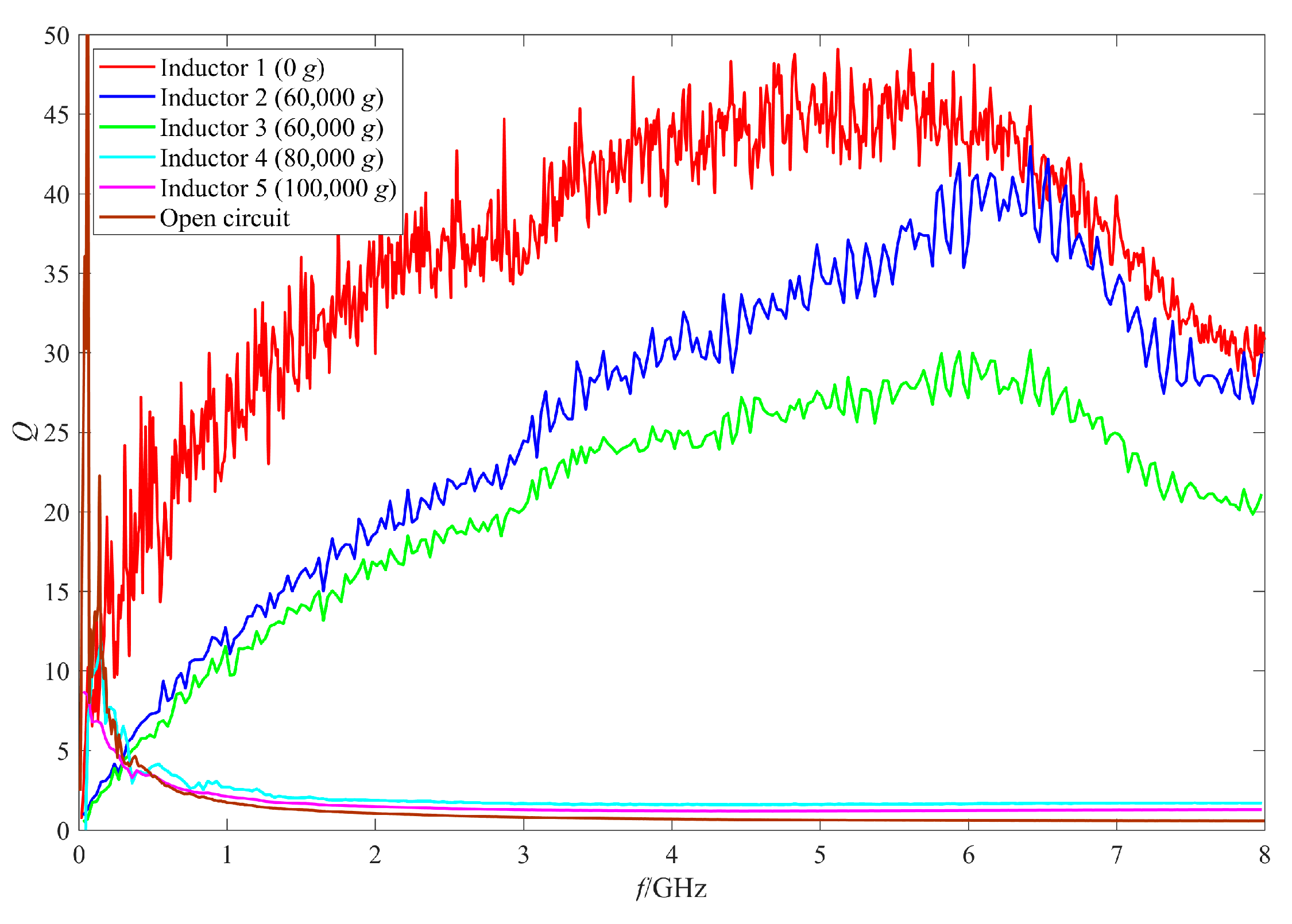
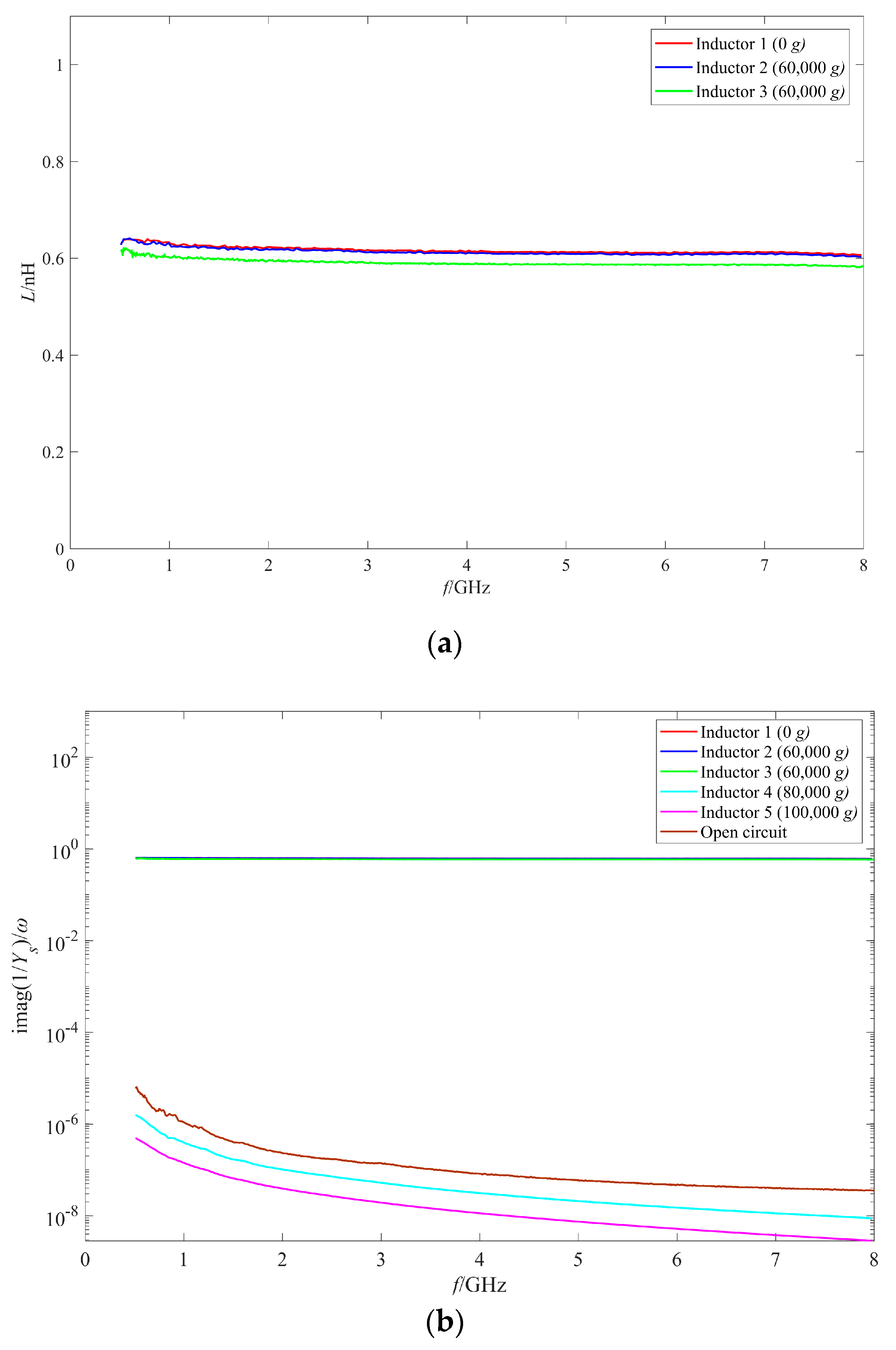



| Shock Amplitude | Shell Number | Number of Inductor Samples | Number of Intact Inductors | Intact Rate of the Inductors After Shock |
|---|---|---|---|---|
| 100,000 g | 1 2 3 | 5 4 5 | 0 3 2 | 35% |
| 80,000 g | 4 5 6 | 3 3 4 | 1 1 1 | 30% |
| 60,000 g | 7 8 | 4 4 | 3 3 | 75% |
| Shock Amplitude | The Measured /fF | The Simulated /fF |
|---|---|---|
| 0 g | 1.5275 (Inductor 1) | 1.4722 |
| 60,000 g | 1.5513 (Inductor 2) | 1.5497 |
| 1.7230 (Inductor 3) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Li, Y.; Li, J. Analysis of the Failure and Performance Variation Mechanism of MEMS Suspended Inductors with Auxiliary Pillars under High-g Shock. Micromachines 2020, 11, 957. https://doi.org/10.3390/mi11110957
Xu L, Li Y, Li J. Analysis of the Failure and Performance Variation Mechanism of MEMS Suspended Inductors with Auxiliary Pillars under High-g Shock. Micromachines. 2020; 11(11):957. https://doi.org/10.3390/mi11110957
Chicago/Turabian StyleXu, Lixin, Yiyuan Li, and Jianhua Li. 2020. "Analysis of the Failure and Performance Variation Mechanism of MEMS Suspended Inductors with Auxiliary Pillars under High-g Shock" Micromachines 11, no. 11: 957. https://doi.org/10.3390/mi11110957
APA StyleXu, L., Li, Y., & Li, J. (2020). Analysis of the Failure and Performance Variation Mechanism of MEMS Suspended Inductors with Auxiliary Pillars under High-g Shock. Micromachines, 11(11), 957. https://doi.org/10.3390/mi11110957





