Investigation of a Liquid-Phase Electrode for Micro-Electro-Discharge Machining
Abstract
1. Introduction
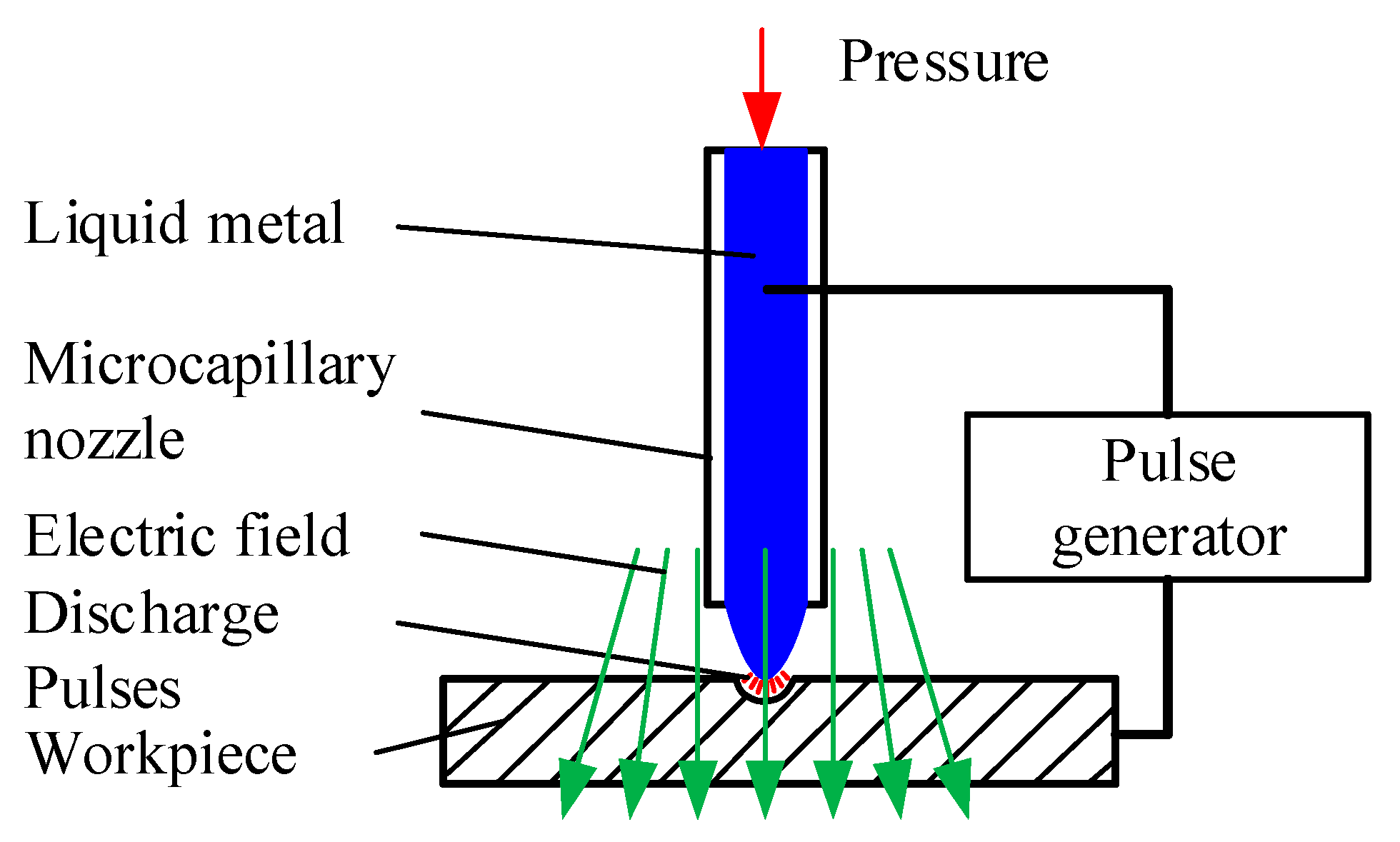
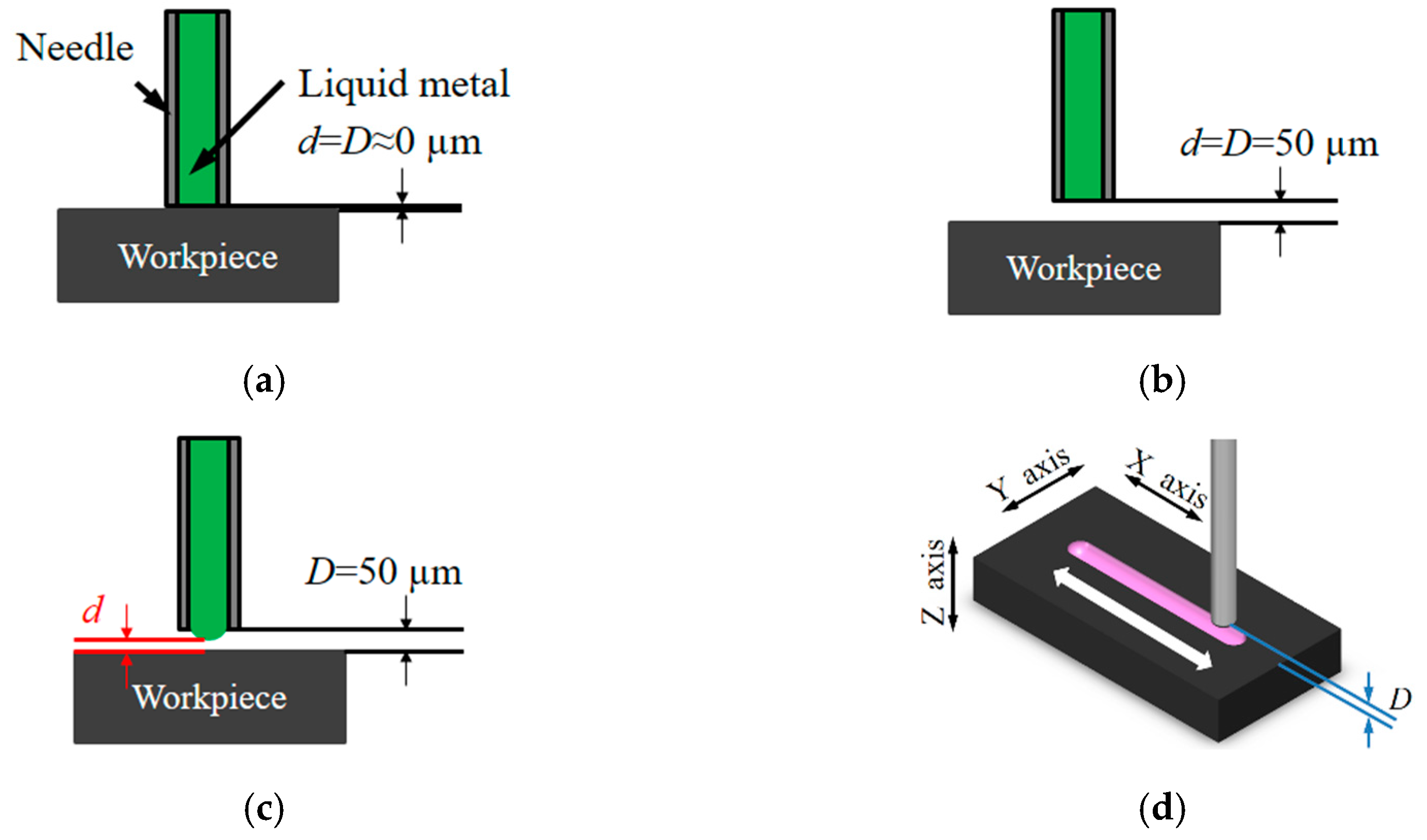
2. Method
3. Shape of the Liquid-Phase Electrode
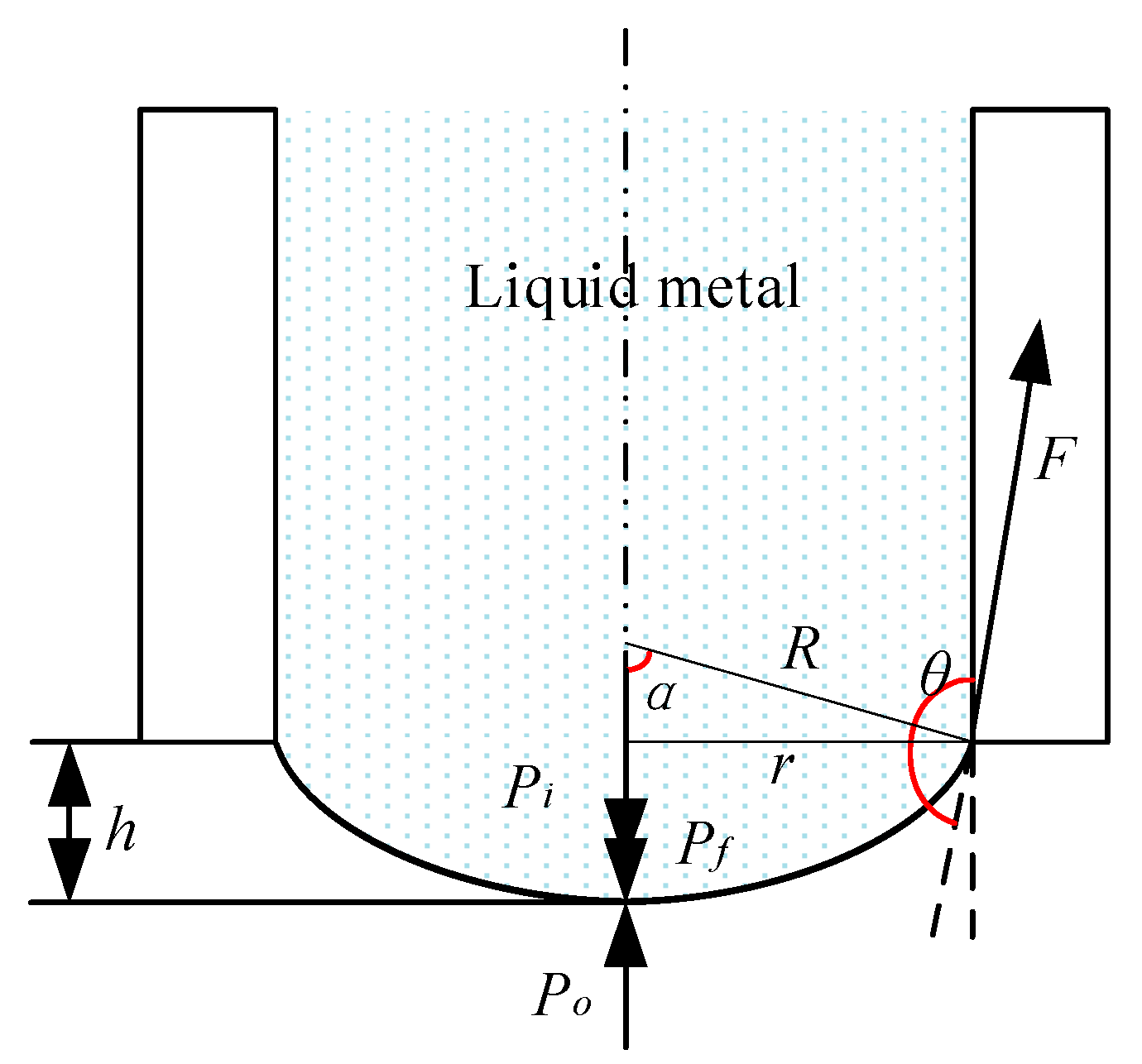
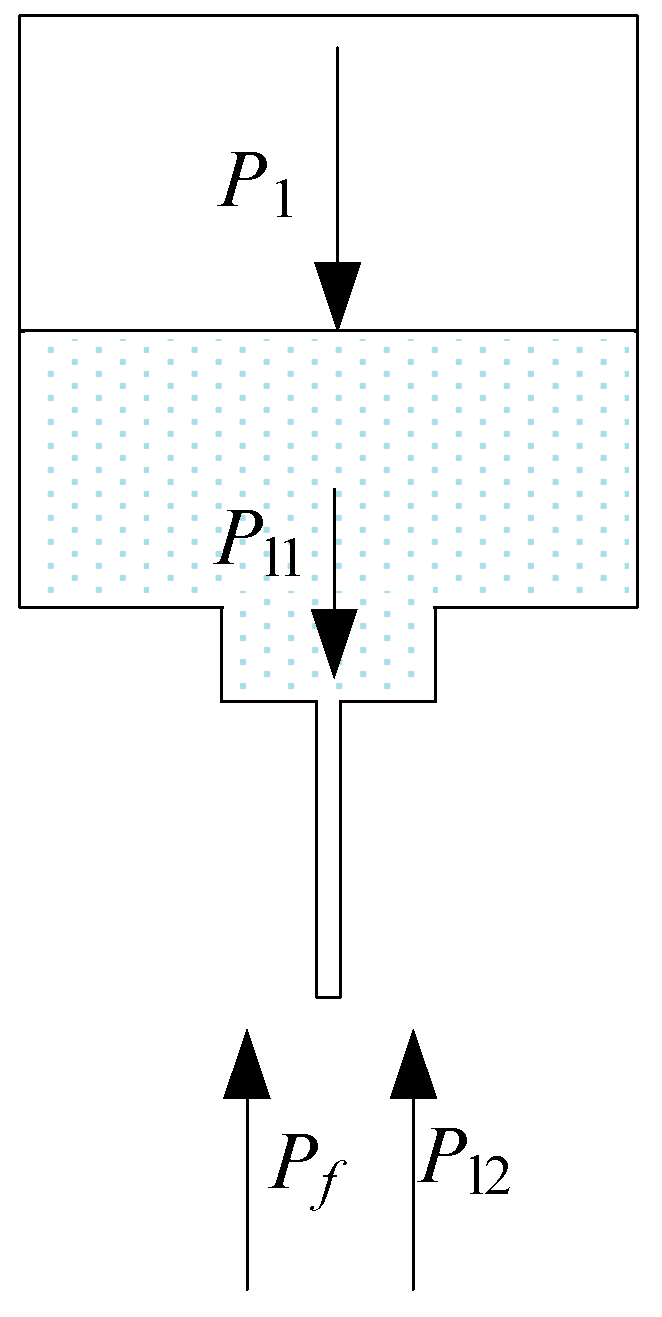
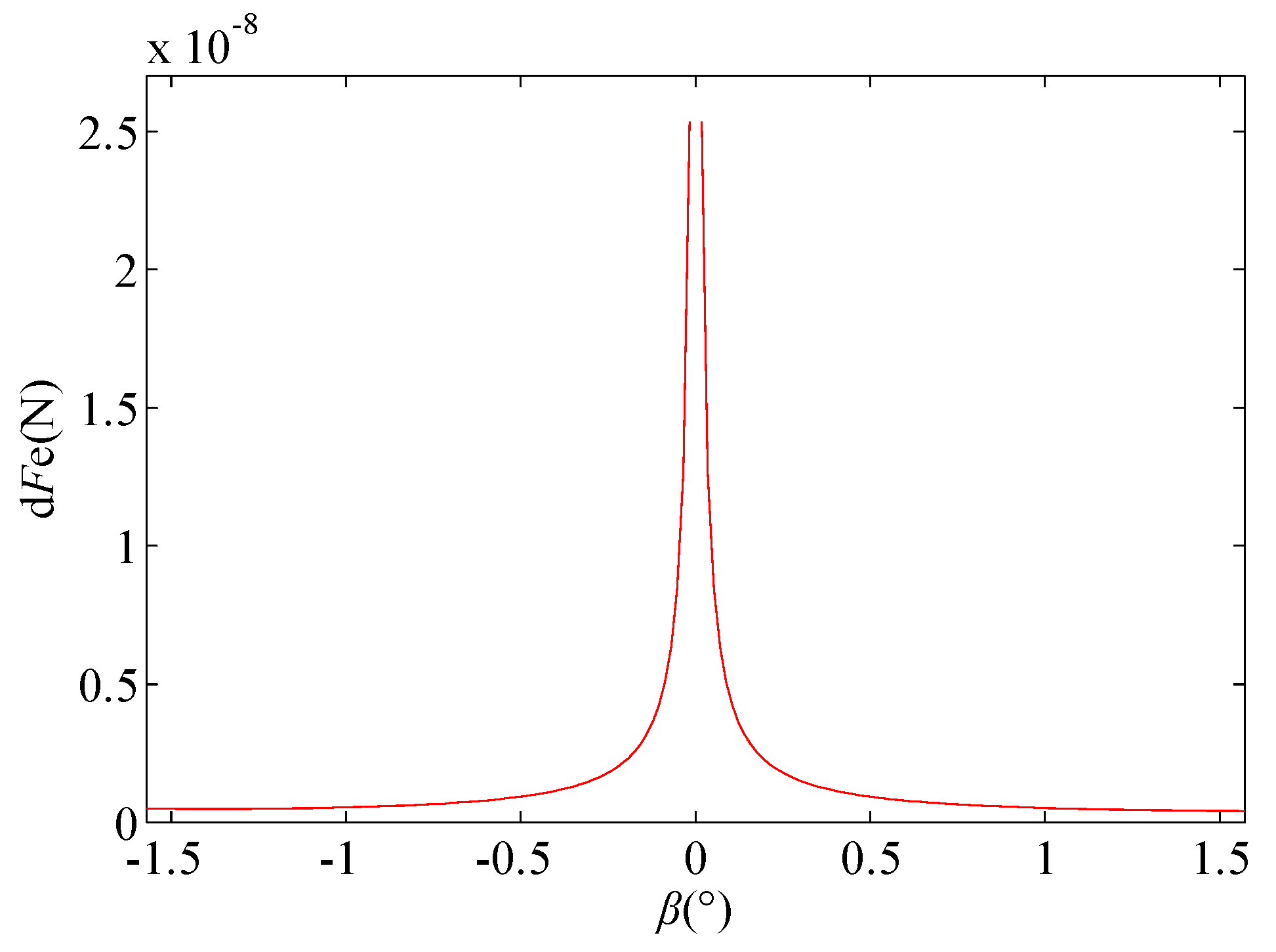
3.1. Mathematical Model
3.2. Simulation
3.2.1. Geometric Model and Boundary Condition
3.2.2. Tip Shape of the Liquid Electrode at Different Extra Pressures
3.2.3. Tip Shape of the Liquid Electrode at Different Voltages
4. Experimental Set-Up and Procedure
5. Experimental Results and Discussion
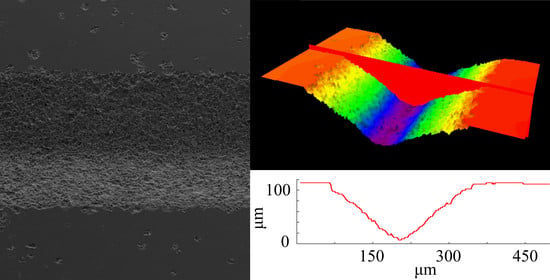
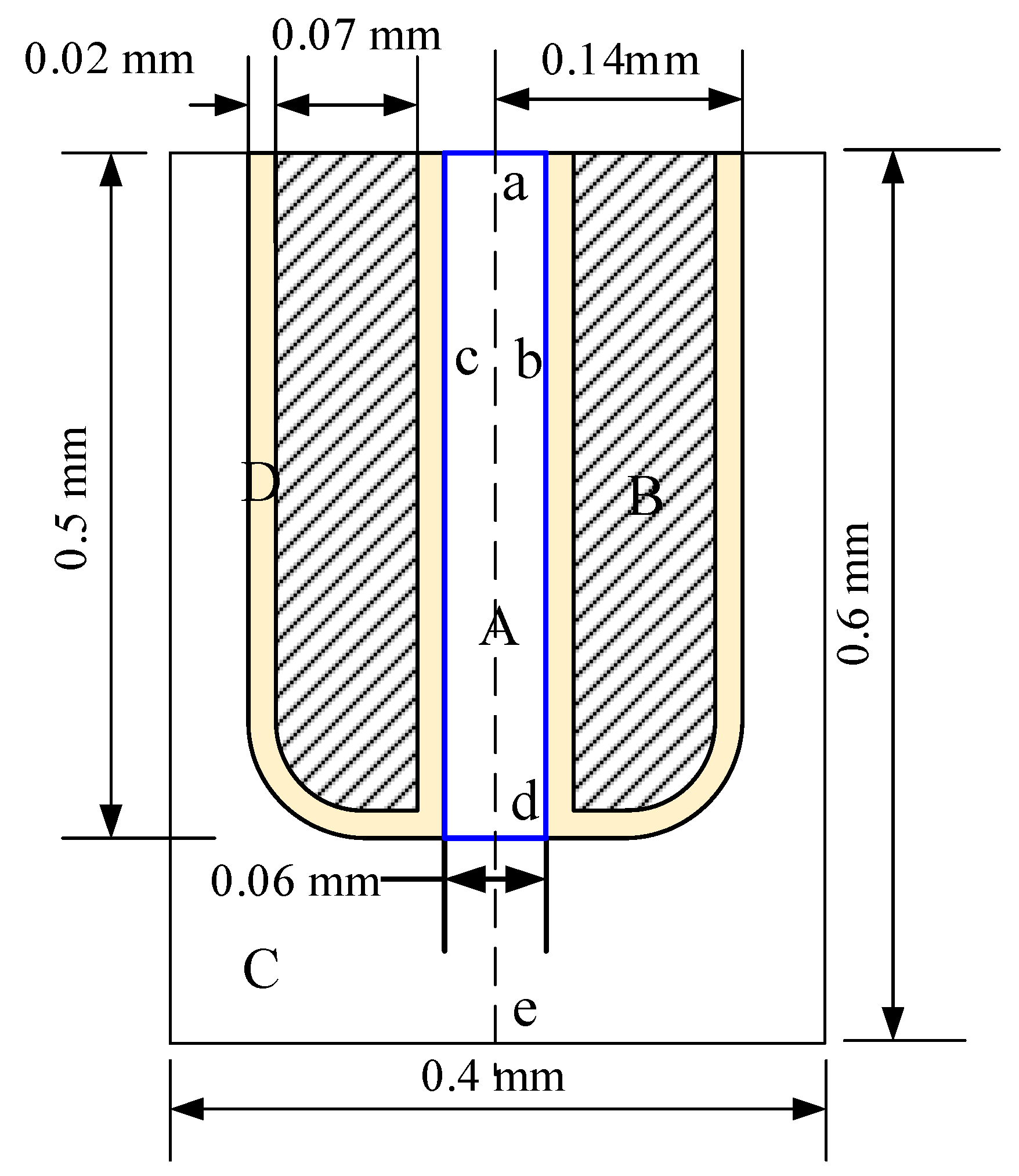
5.1. Microgroove and Arbitrary Patterning
5.2. Process Characterizations
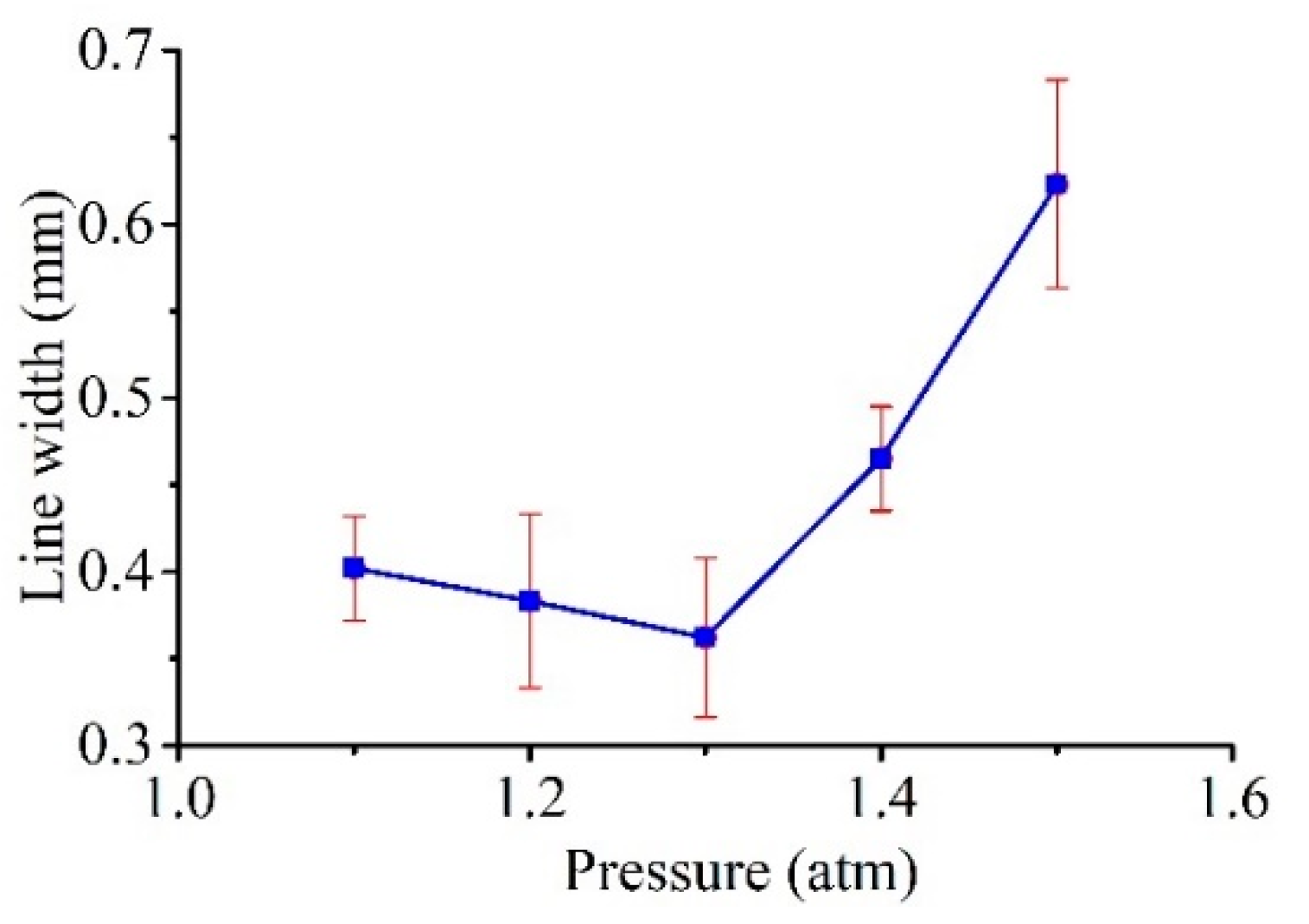
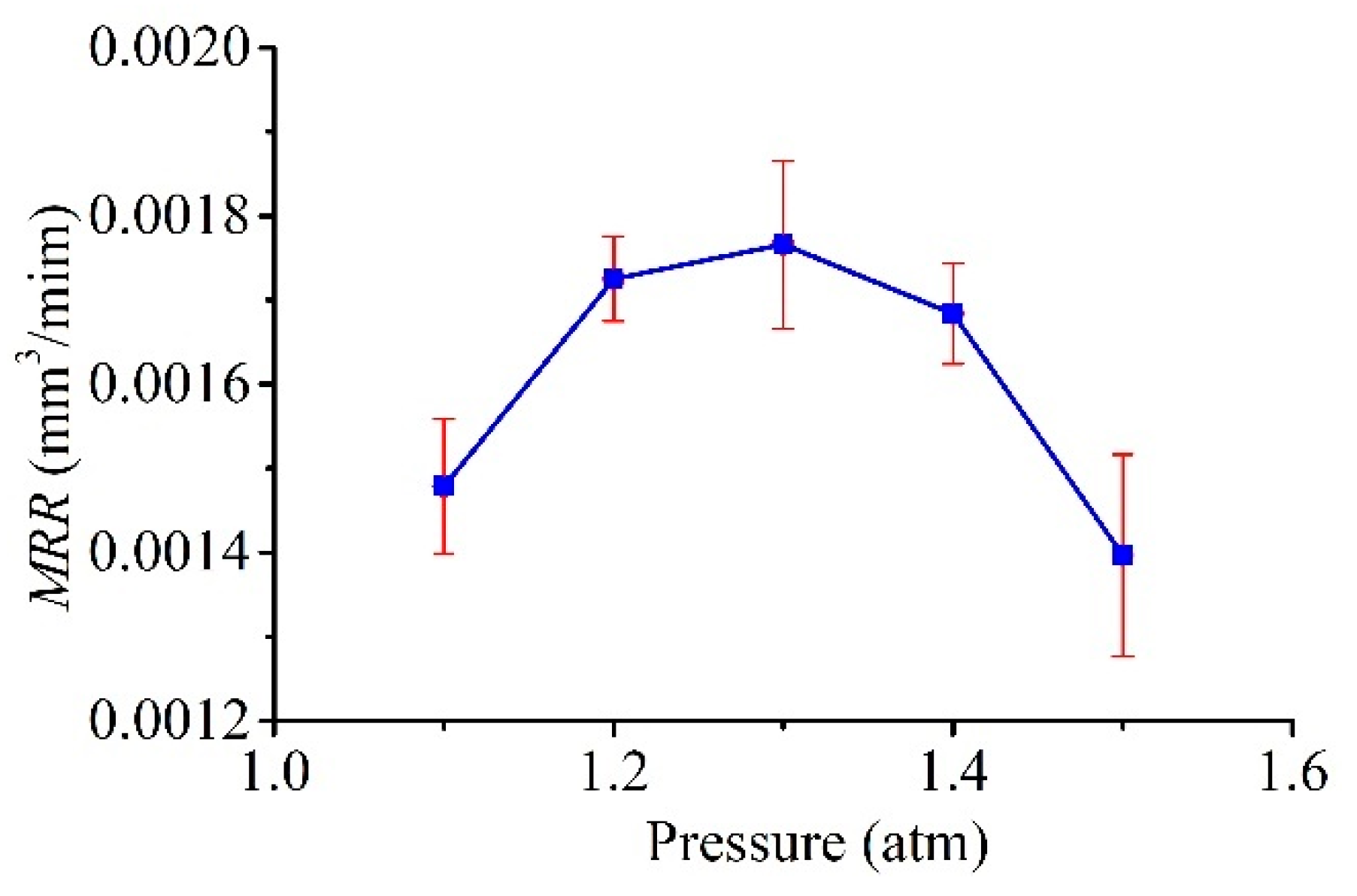
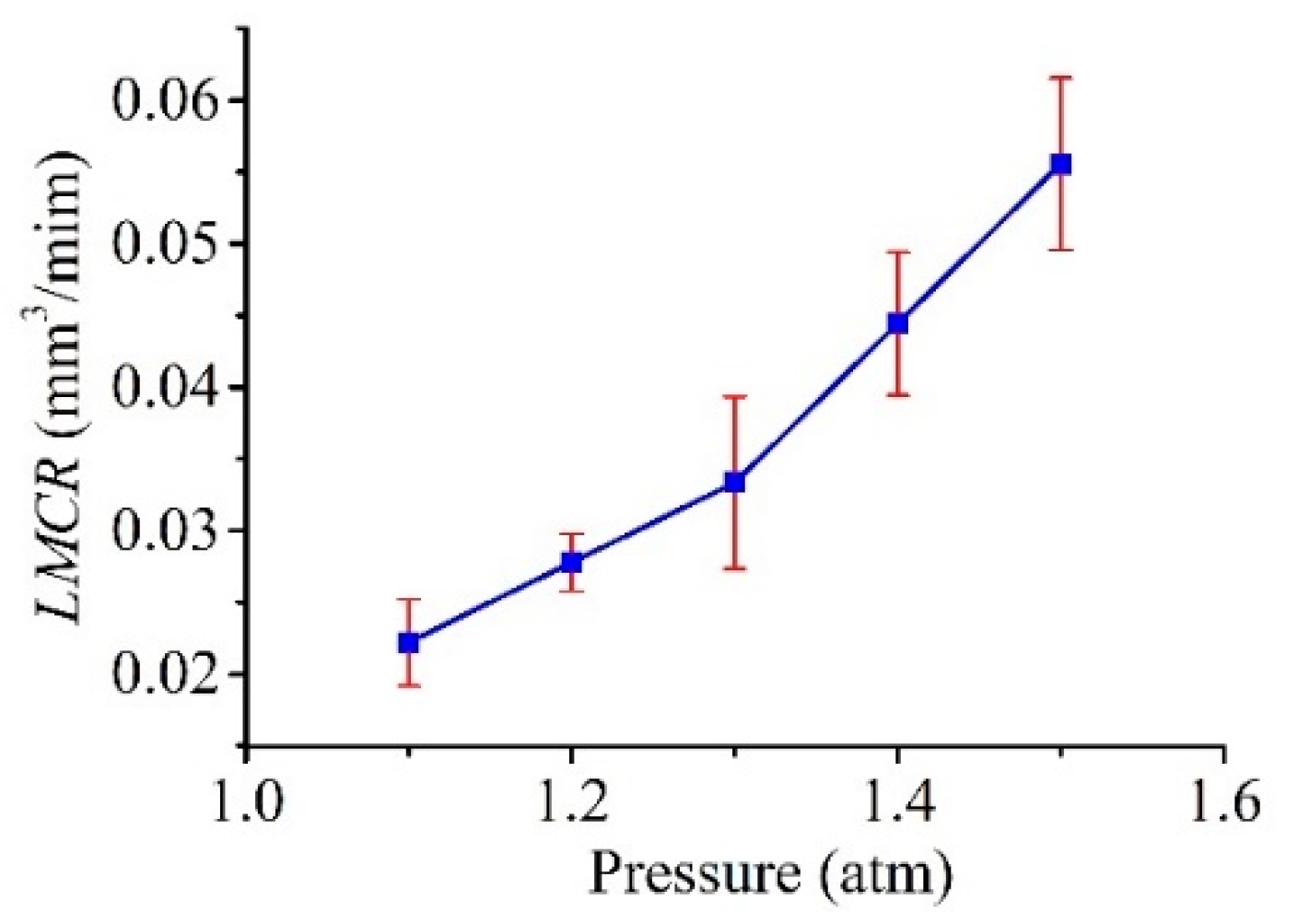
5.2.1. Dependence of Machining Characteristics on the Pressure
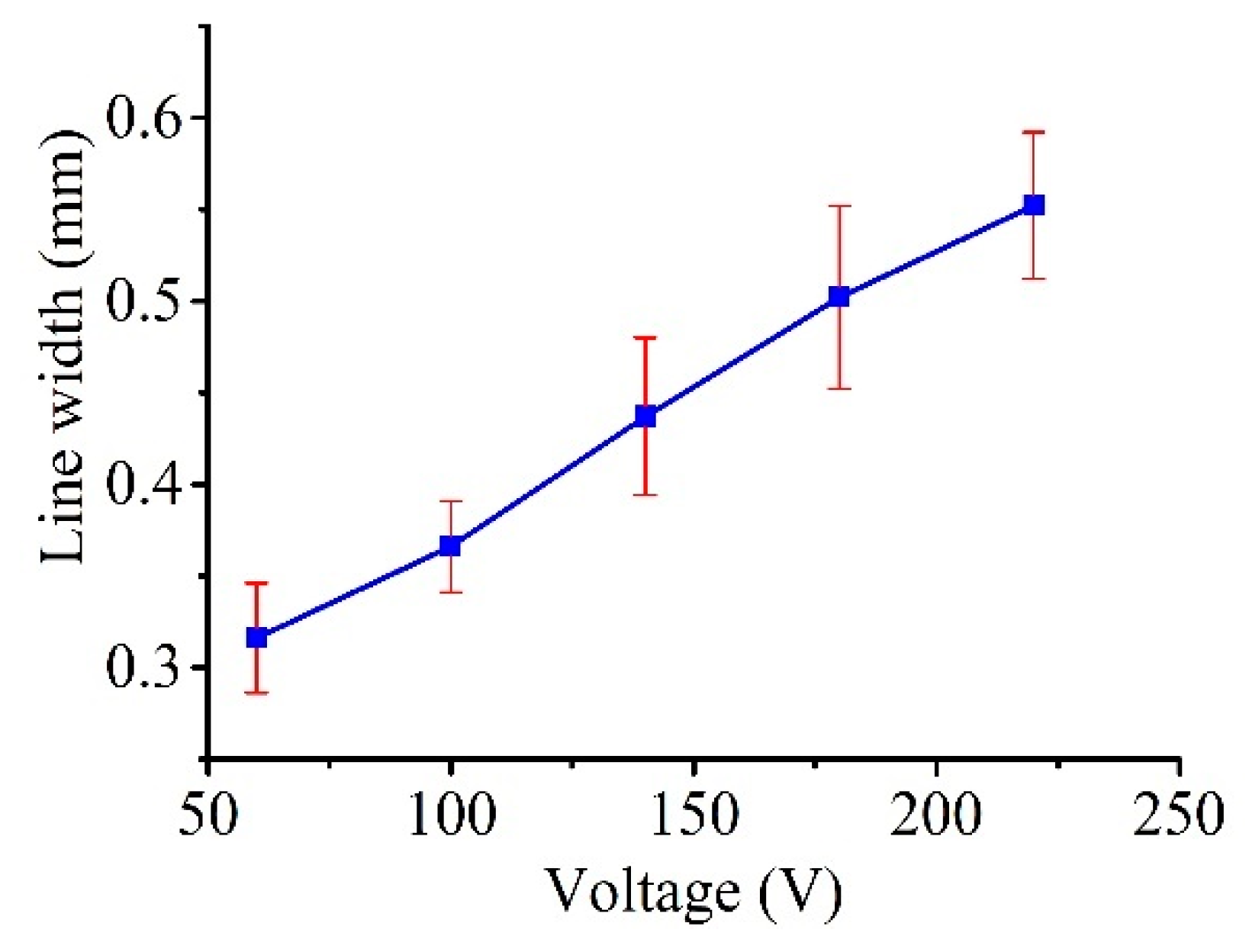
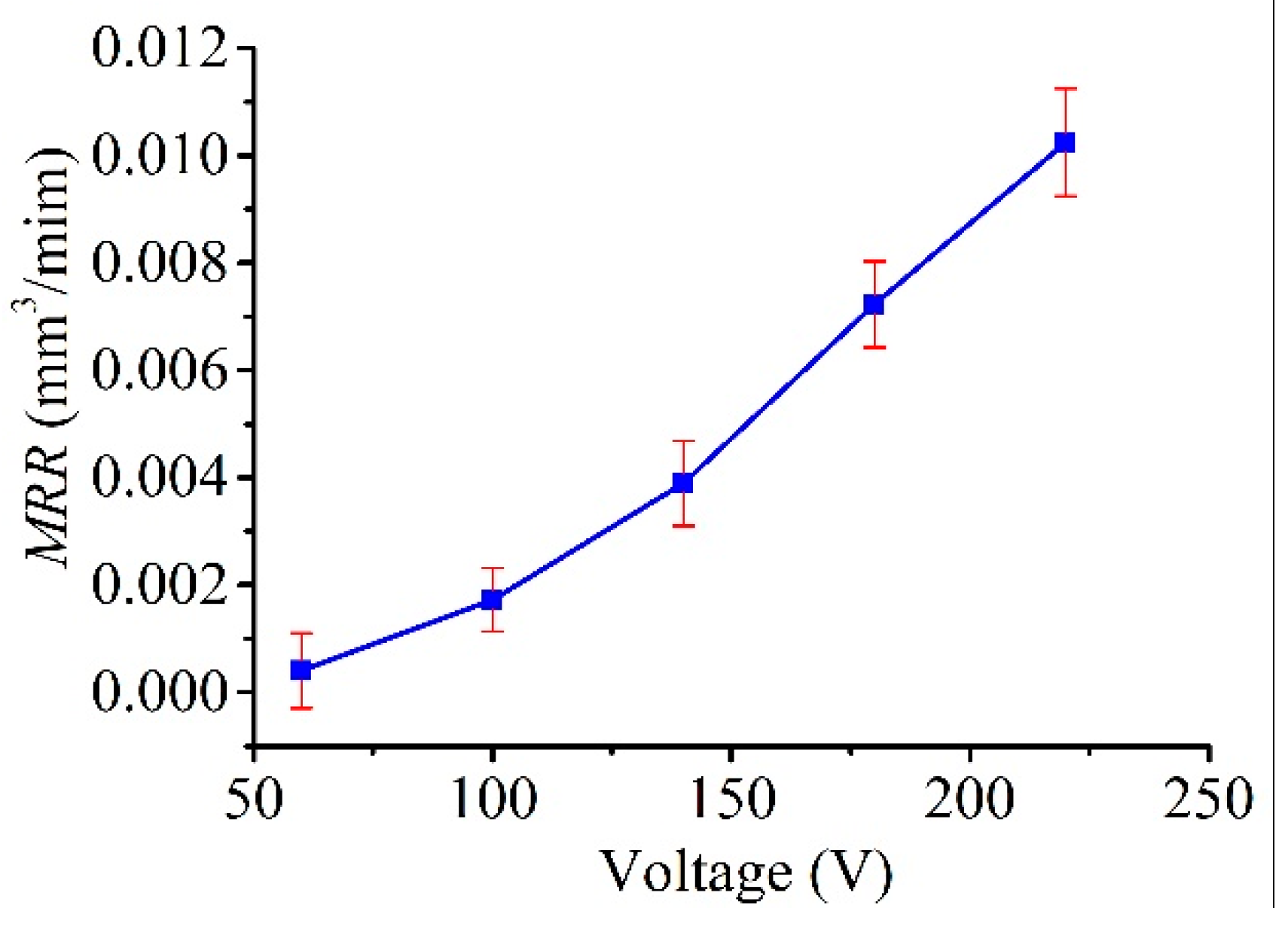
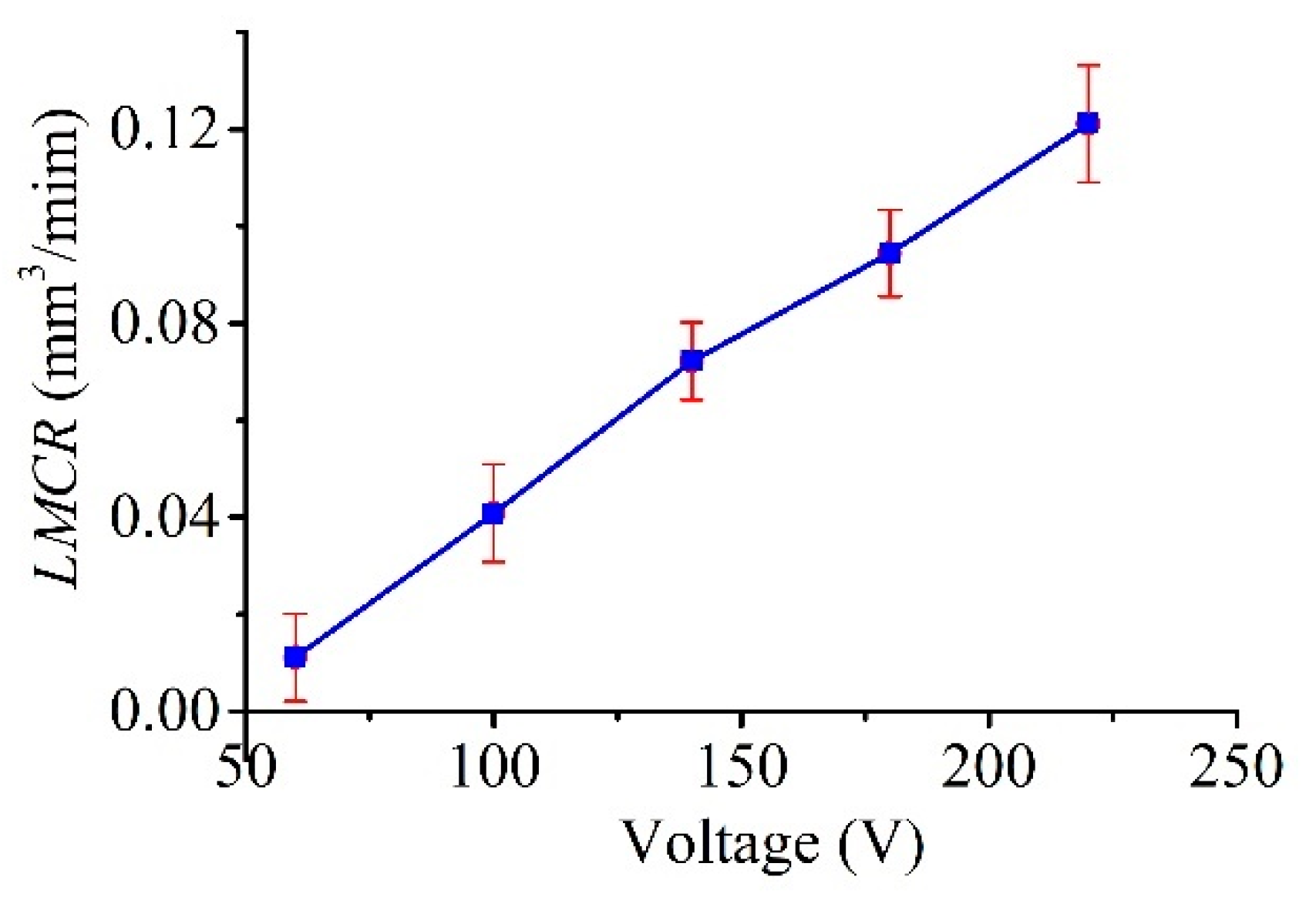
5.2.2. Dependence of Machining Characteristics on the Voltage
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bilal, A.; Jahan, M.P.; Talamona, D.; Perveen, A. Electro-Discharge Machining of Ceramics: A Review. Micromachines 2019, 10, 10. [Google Scholar] [CrossRef] [PubMed]
- Chavoshi, S.Z.; Luo, X.C. Hybrid Micro-machining Processes: A Review. Precis. Eng. 2015, 41, 1–23. [Google Scholar] [CrossRef]
- Raju, L.; Hiremath, S.S. A State-of-the-art Review on Micro Electro-Discharge Machining. Procedia Technol. 2016, 25, 1281–1288. [Google Scholar] [CrossRef]
- Oliaei, S.N.B.; Karpat, Y.; Paulo Davim, J.; Preveen, A. Micro Tool Design and Fabrication: A review. J. Manuf. Process. 2018, 36, 496–519. [Google Scholar] [CrossRef]
- Masuzawa, T.; Fujino, M.; Kobayashi, K.; Suzuki, T.; Kinoshita, N. Wire Electro-Discharge Grinding for Micro-Machining. CIRP Ann. Manuf. Technol. 1985, 34, 431–434. [Google Scholar] [CrossRef]
- Egashira, K.; Morita, Y.; Hattori, Y. Electrical Discharge Machining of Submicron Holes Using Ultrasmall-diameter Electrodes. Precs. Eng. 2010, 34, 139–144. [Google Scholar] [CrossRef]
- Zhang, L.; Tong, H.; Li, Y. Precision Machining of Micro Tool Electrodes in Micro EDM for Drilling Array Micro Holes. Precis. Eng. 2015, 39, 100–106. [Google Scholar] [CrossRef]
- Lim, H.S.; Wong, Y.S.; Rahman, M.; Lee, M.K.E. A Study on the Machining of High Aspect Ratio Micro-structures Using micro-EDM. J. Mater. Process. Technol. 2003, 140, 318–325. [Google Scholar] [CrossRef]
- Zhao, W.S.; Jia, B.X.; Wang, Z.L.; Hu, F.Q. Study on Block Electrode Discharge Grinding of Micro Rods. Key Eng. Mater. 2006, 304–305, 21. [Google Scholar] [CrossRef]
- Yin, Q.F.; Wang, X.Q.; Wang, P.; Qian, Z.Q.; Zhou, L.; Zhang, Y.B. Fabrication of Micro Rod Electrode by Electrical Discharge Grinding Using Two Block Electrodes. J. Mater. Process. Technol. 2016, 234, 143–149. [Google Scholar] [CrossRef]
- Mohri, N.; Tani, T. Micro-pin Electrodes Formation by Micro-Scanning EDM Process. CIRP Ann. Manuf. Technol. 2006, 55, 175–178. [Google Scholar] [CrossRef]
- Liu, Y.; Cai, H.T.; Li, H.S. Fabrication of Micro Spherical Electrode by One Pulse EDM and Their Application in Electrochemical Micromachining. J. Manuf. Process. 2015, 17, 162–170. [Google Scholar] [CrossRef]
- Singh, A.K.; Patowari, P.K.; Deshpande, N.V. Analysis of Micro-rods Machined Using Reverse Micro-EDM. J. Braz. Soc. Mech. Sci. 2019, 41, 15. [Google Scholar] [CrossRef]
- Ming, P.M.; Zhu, D.; Zeng, Y.B.; Hu, Y.Y. Wear Resistance of Copper EDM Tool Electrode Electroformed from Copper Sulfate Baths and Pyrophosphate Baths. Int. J. Adv. Manuf. Technol. 2010, 50, 635–641. [Google Scholar] [CrossRef]
- Hu, Y.Y.; Zhu, D.; Qu, N.S.; Zeng, Y.B.; Ming, P.M. Fabrication of High-aspect-ratio Electrode Array by Combining UV-LIGA with Micro Electro Discharge Machining. Microsyst. Technol. 2009, 15, 519–525. [Google Scholar] [CrossRef]
- Zhang, Y.O.; Zhao, W.S.; Kang, X.M. Intensive Study on the Electrostatic Field Induced Electrolyte Jet Micro Electrical Discharge Machining. Procedia CIRP 2018, 68, 599–603. [Google Scholar] [CrossRef]
- Huang, R.N.; Yi, Y.; Yu, W.B.; Takahata, K. Liquid-phase Alloy as a Microfluidic Electrode for Micro-electro-discharge patterning. J. Mater. Process. Technol. 2018, 258, 1–8. [Google Scholar] [CrossRef]
- Bissacco, G.; Valentincic, J.; Hansen, H.N. Towards the Effective Tool Wear Control in Micro-EDM Milling. Int. J. Adv. Manuf. Technol. 2010, 47, 3–9. [Google Scholar] [CrossRef]
- Wang, J.; Ferraris, E.; Galbiati, M.; Qian, J.; Reynaerts, D. Simultaneously Counting of Positive and Negative Pulse Parts to Predict Tool Wear in Micro-EDM Milling. In Proceedings of the 9th International Conference on Micromanufacturing, Singapore, 25–28 March 2014; Available online: https://lirias.kuleuven.be/handle/123456789/445665 (accessed on 25 March 2014).
- Tsai, Y.Y.; Masuzawa, T. An Index to Evaluate the Wear Resistance of the Electrode in Micro-EDM. J. Mater. Process. Technol. 2004, 149, 304–309. [Google Scholar] [CrossRef]
- Chiou, H.; Tsao, C.C.; Hsu, C.Y. A Study of the Machining Characteristics of Micro EDM Milling and its Improvement by Electrode Coating. Int. J. Adv. Manuf. Technol. 2015, 78, 1857–1864. [Google Scholar] [CrossRef]
- Tsai, H.C.; Yan, B.H.; Huang, F.Y. EDM Performance of Cr/Cu-based Composite Electrodes. Int. J. Mach. Tool. Manuf. 2003, 43, 245–252. [Google Scholar] [CrossRef]
- Zou, R.M.; Yu, Z.Y.; Yan, C.Y.; Li, J.Z.; Liu, X.; Xu, W.J. Micro Electrical Discharge Machining in Nitrogen Plasma Jet. Precs. Eng. 2018, 51, 198–207. [Google Scholar] [CrossRef]
- Wang, J.; Qian, J.; Ferraris, E.; Reynaerts, D. In-situ Process Monitoring and Adaptive Control for Precision Micro-EDM Cavity Milling. Precs. Eng. 2017, 47, 261–275. [Google Scholar] [CrossRef]
- Zhang, L.N.; Du, J.Y.; Zhuang, X.S.; Wang, Z.L.; Pei, J.Y. Geometric Prediction of Conic Tool in Micro-EDM Milling with Fix-length Compensation Using Simulation. Int. J. Mach. Tool. Manuf. 2015, 89, 86–94. [Google Scholar] [CrossRef]
- Nirala, C.K.; Saha, P. Precise μEDM-drilling Using Real-time Indirect Tool Wear Compensation. J. Mater. Process. Technol. 2017, 240, 176–189. [Google Scholar] [CrossRef]
- Lee, C.S.; Heo, E.Y.; Kim, J.M.; Choi, I.H.; Kim, D.W. Electrode Wear Estimation Model for EDM drilling. Robot. Cim-Int. Manuf. 2015, 36, 70–75. [Google Scholar] [CrossRef]
- Huang, R.N.; Xiong, X.G.; Yi, Y.; Zhu, E.L. Liquid alloy electrode for no-wear micro electrical discharge machining. Int. J. Adv. Manuf. Technol. 2020, 106, 1281–1290. [Google Scholar] [CrossRef]
- Liu, Y.C.; Wang, Y. Analysis and Discussion on Related Problems of Surface Tension. Chin. J. Chem. Educ. 2018, 39, 12–15. [Google Scholar] [CrossRef]






| Boundary | Fluid Field | Electrostatic Field |
|---|---|---|
| a | Entrance, extra pressure P1 | E |
| b,c | No slip wall | E |
| d | Initial interface | E |
| e | Export | 0 |
| Parameters | Conditions |
|---|---|
| Workpiece | Doped silicon (p type) |
| Voltage (Vs) | 60–220 V |
| Resistance (R) | 0.2–10 kΩ |
| Capacitance (C) | 10–470 nF |
| Pressure (P1) | 1.1–1.5 atm |
| Working medium | Kerosene |
| Lateral scan speed | 0.5 mm/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, R.; Yi, Y.; Zhu, E.; Xiong, X. Investigation of a Liquid-Phase Electrode for Micro-Electro-Discharge Machining. Micromachines 2020, 11, 935. https://doi.org/10.3390/mi11100935
Huang R, Yi Y, Zhu E, Xiong X. Investigation of a Liquid-Phase Electrode for Micro-Electro-Discharge Machining. Micromachines. 2020; 11(10):935. https://doi.org/10.3390/mi11100935
Chicago/Turabian StyleHuang, Ruining, Ying Yi, Erlei Zhu, and Xiaogang Xiong. 2020. "Investigation of a Liquid-Phase Electrode for Micro-Electro-Discharge Machining" Micromachines 11, no. 10: 935. https://doi.org/10.3390/mi11100935
APA StyleHuang, R., Yi, Y., Zhu, E., & Xiong, X. (2020). Investigation of a Liquid-Phase Electrode for Micro-Electro-Discharge Machining. Micromachines, 11(10), 935. https://doi.org/10.3390/mi11100935