Spin Injection and Transport in Organic Materials
Abstract
1. Introduction
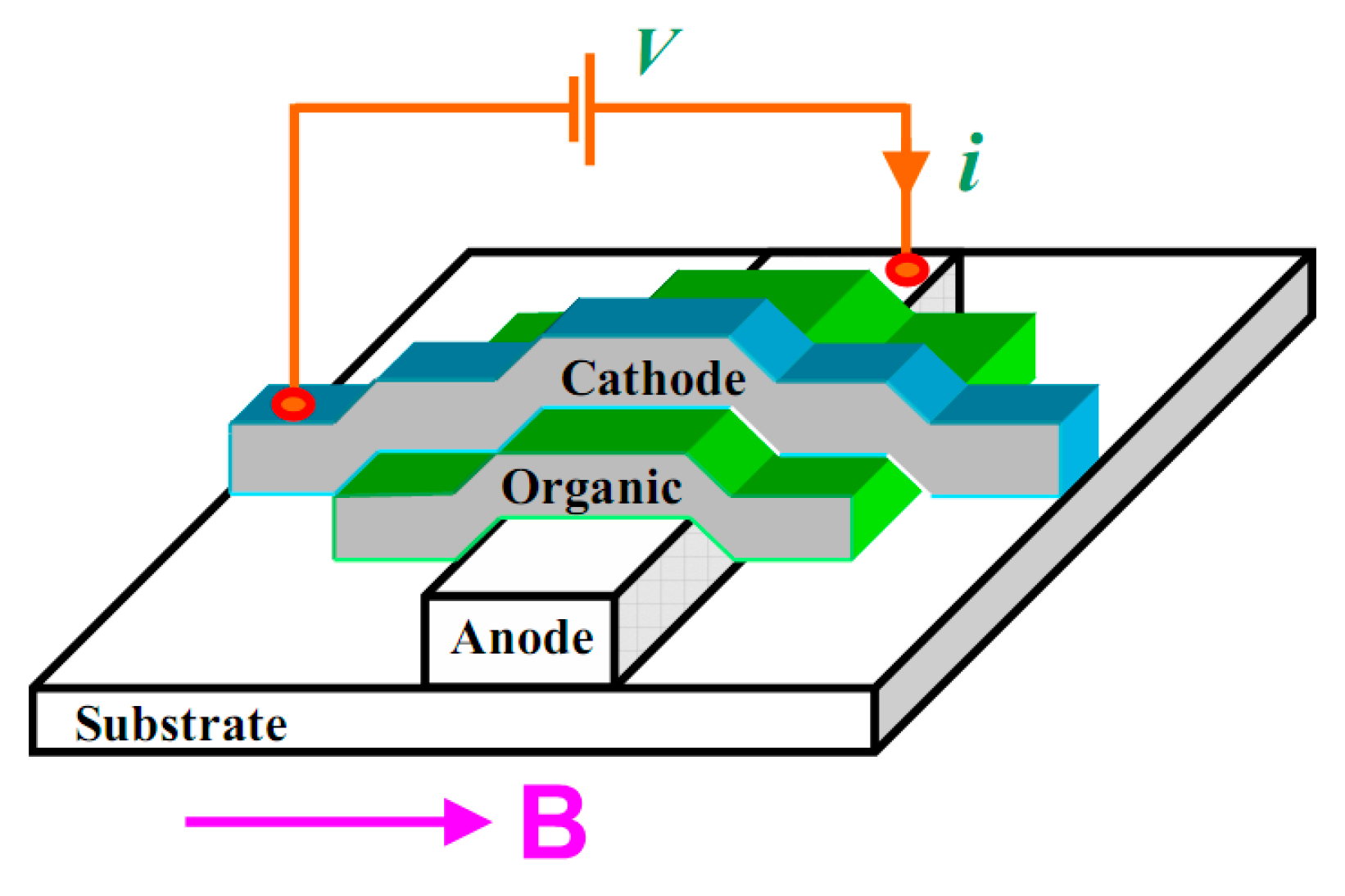
2. Organic Spin Valve
2.1. Organic Spin Valve
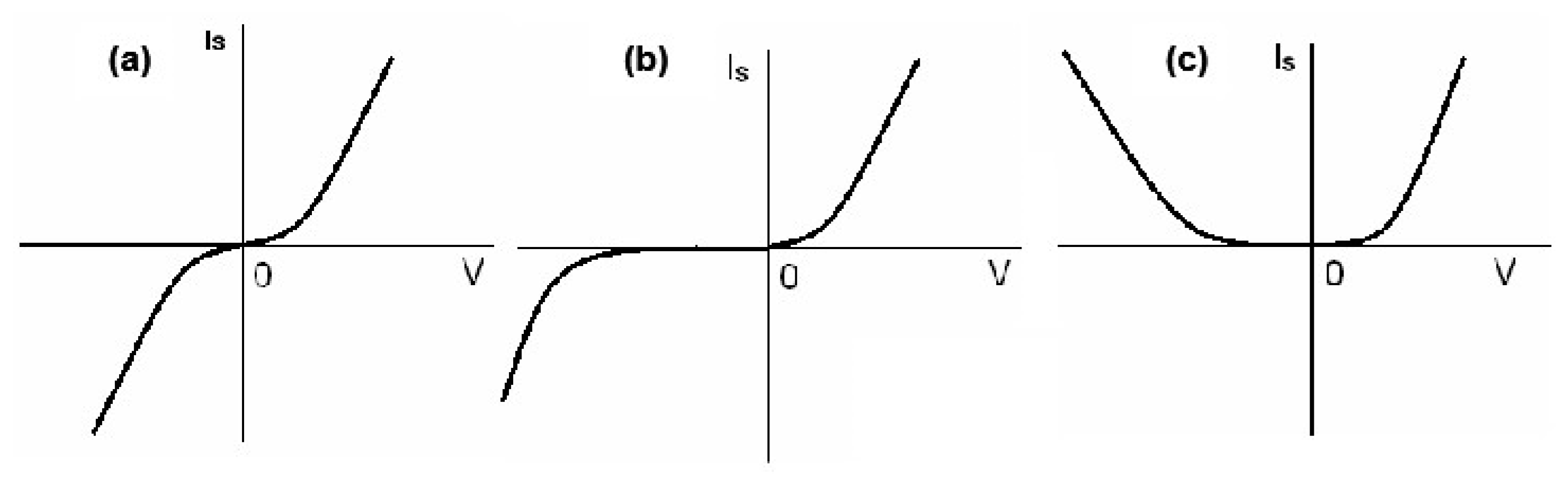
2.2. Tunneling Theory of OMAR
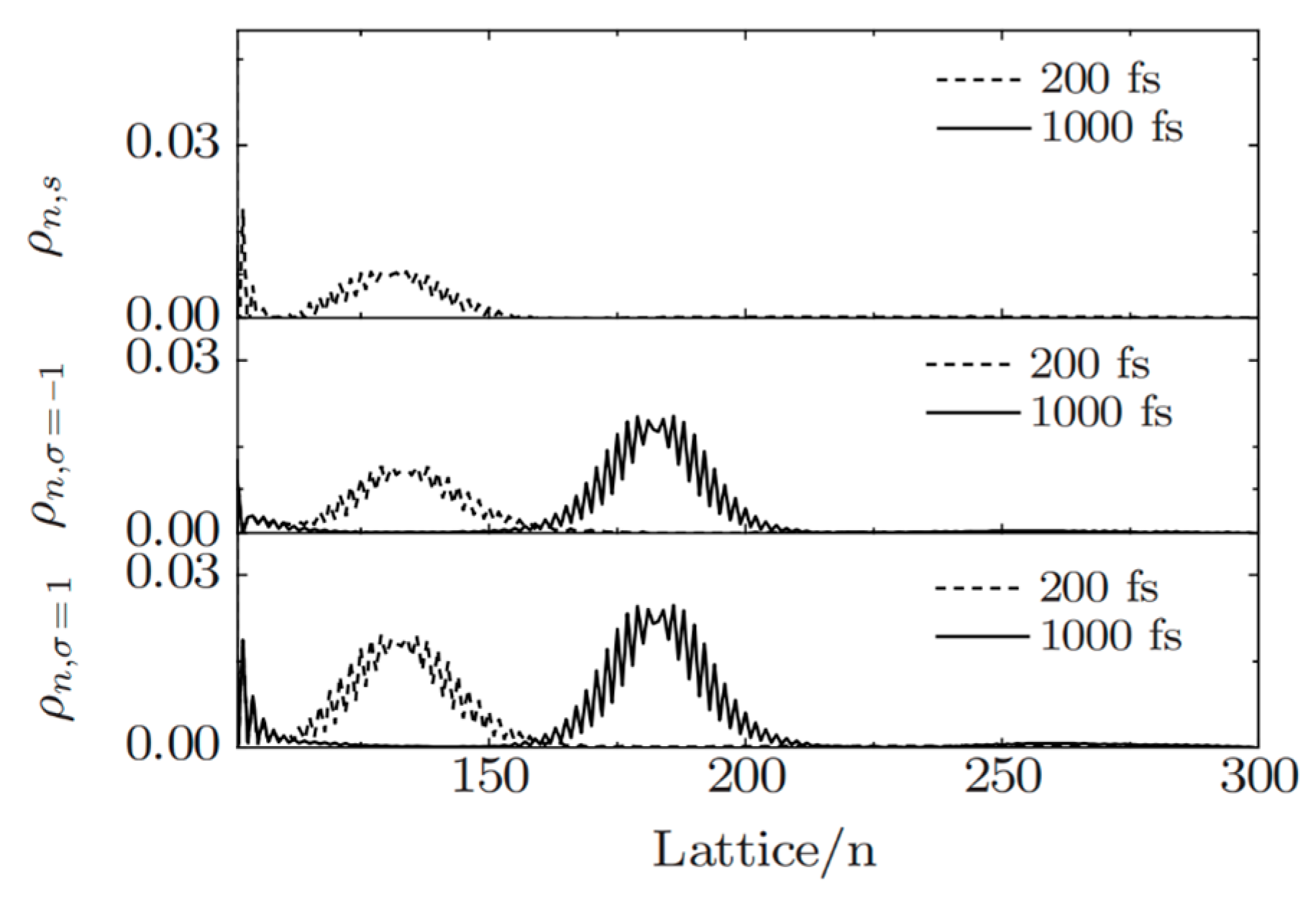
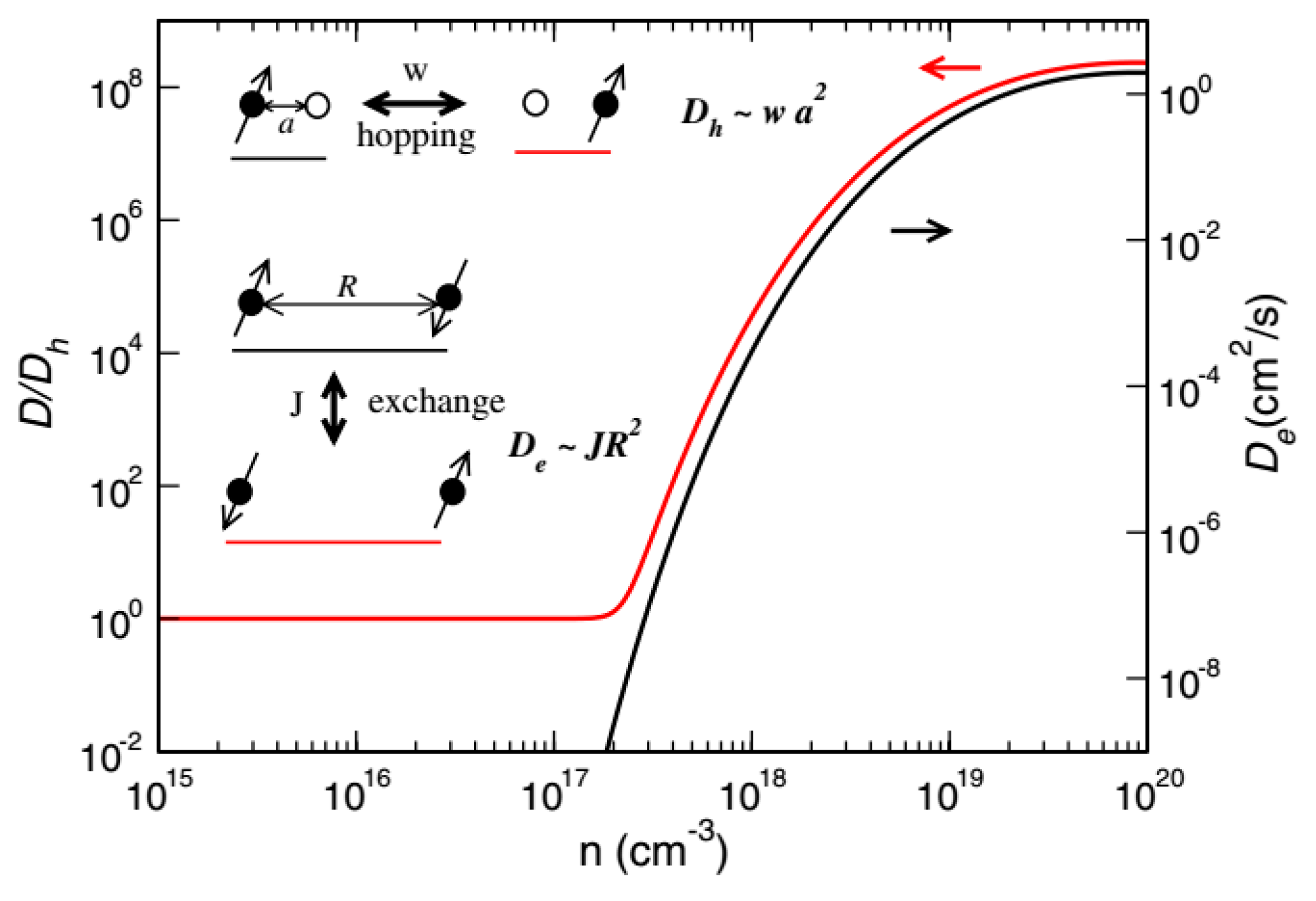
2.3. Organic Spin Injection and Transport Theory
3. Organic Magnetic Field Effect
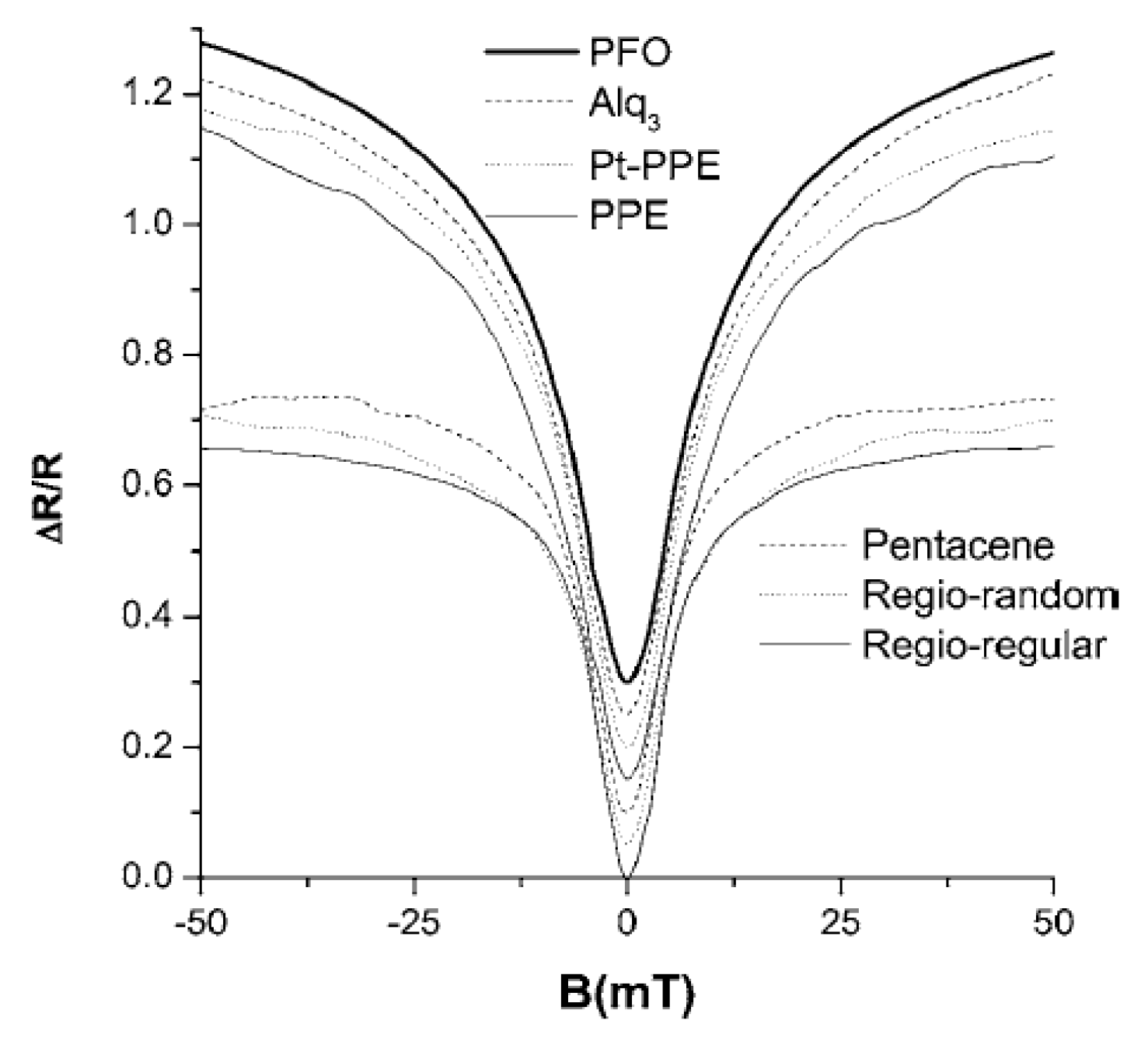
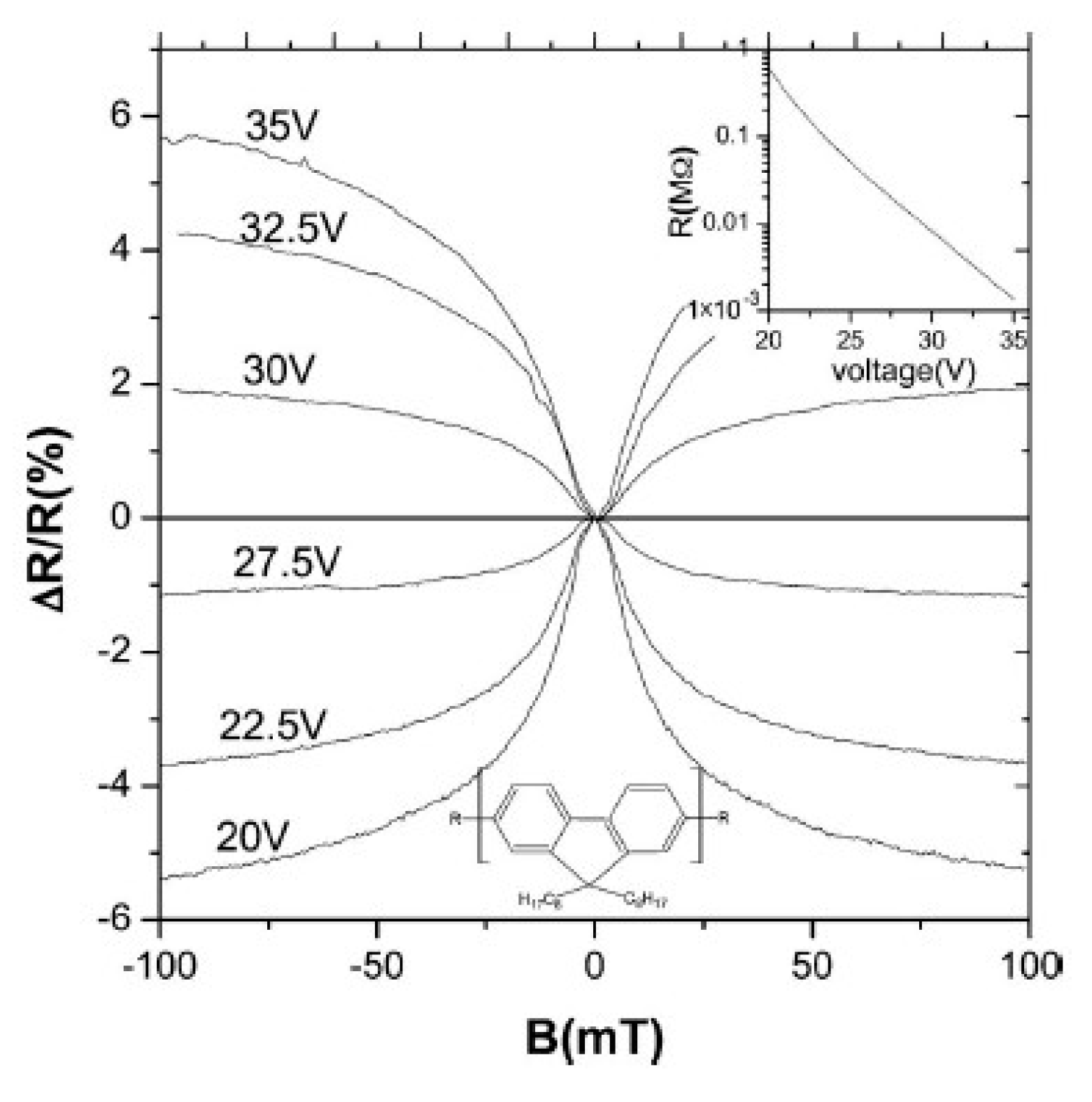
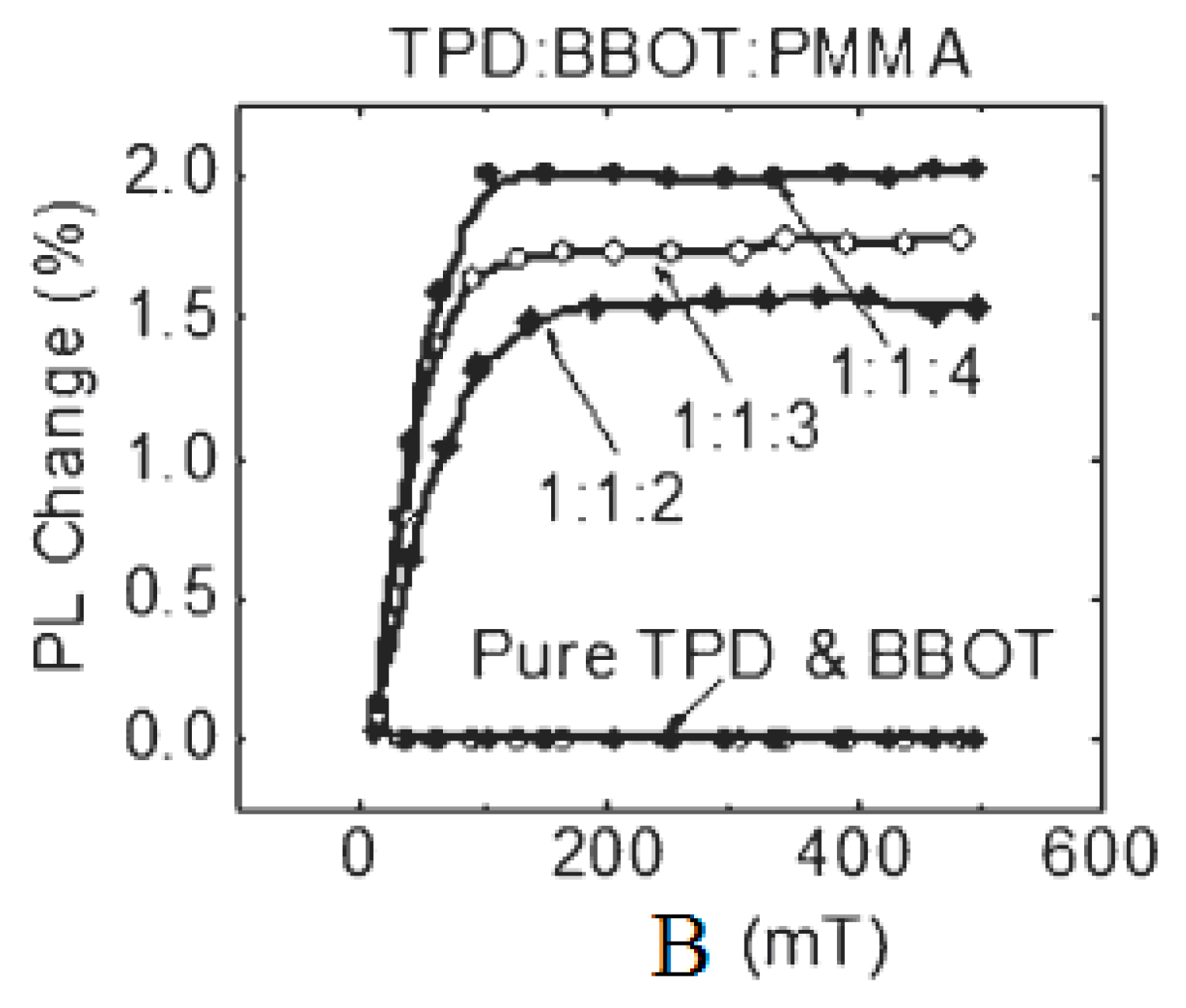
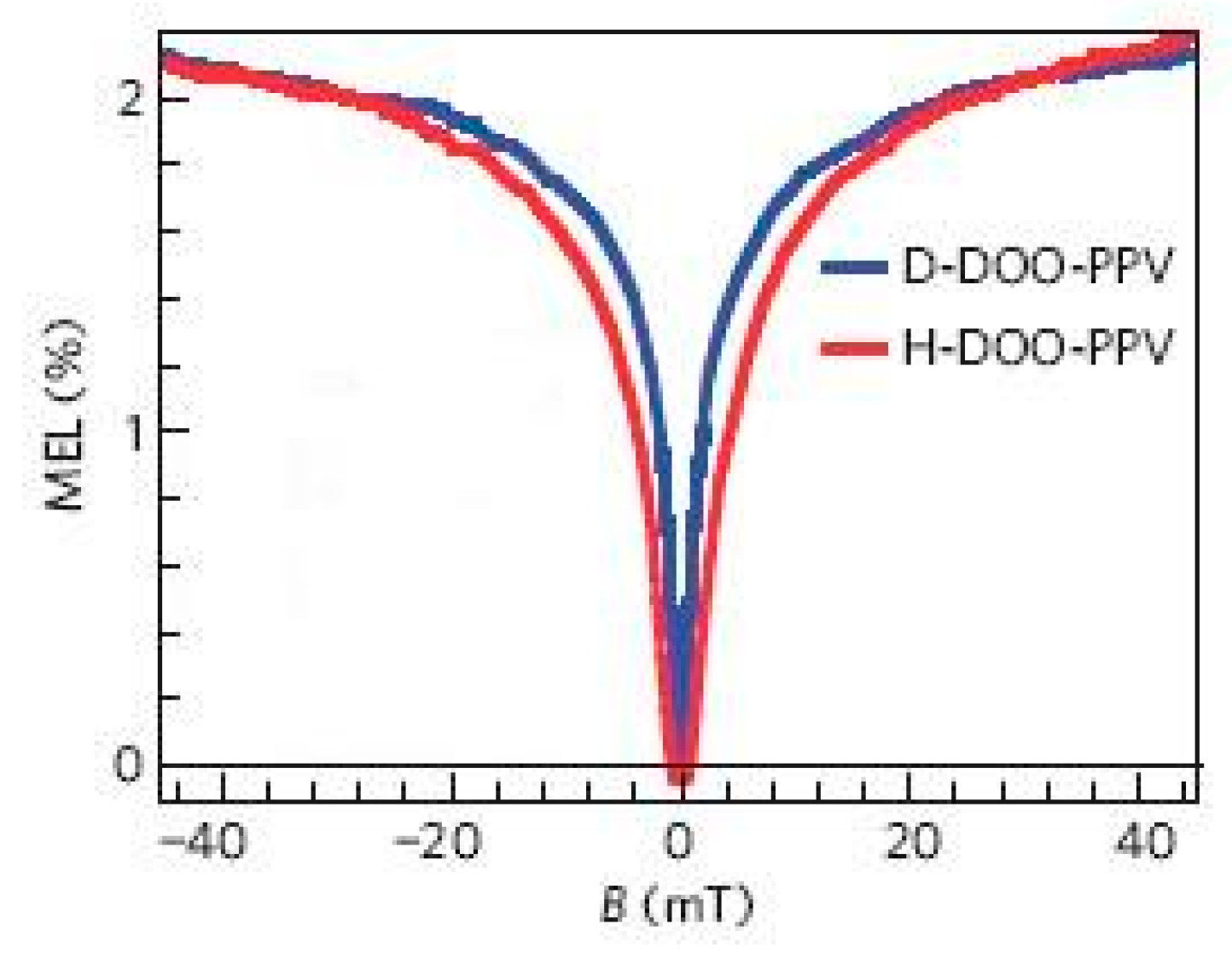
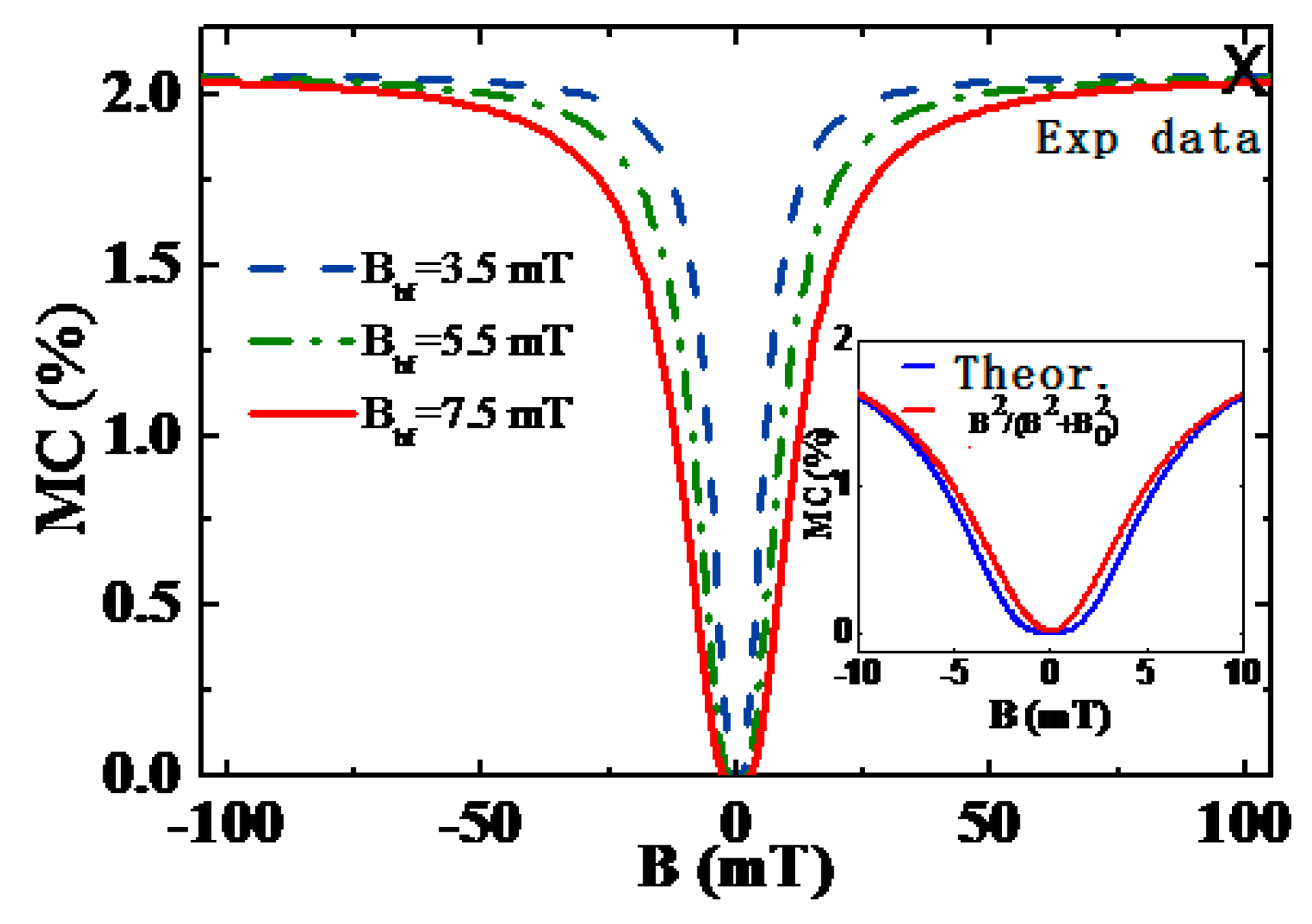
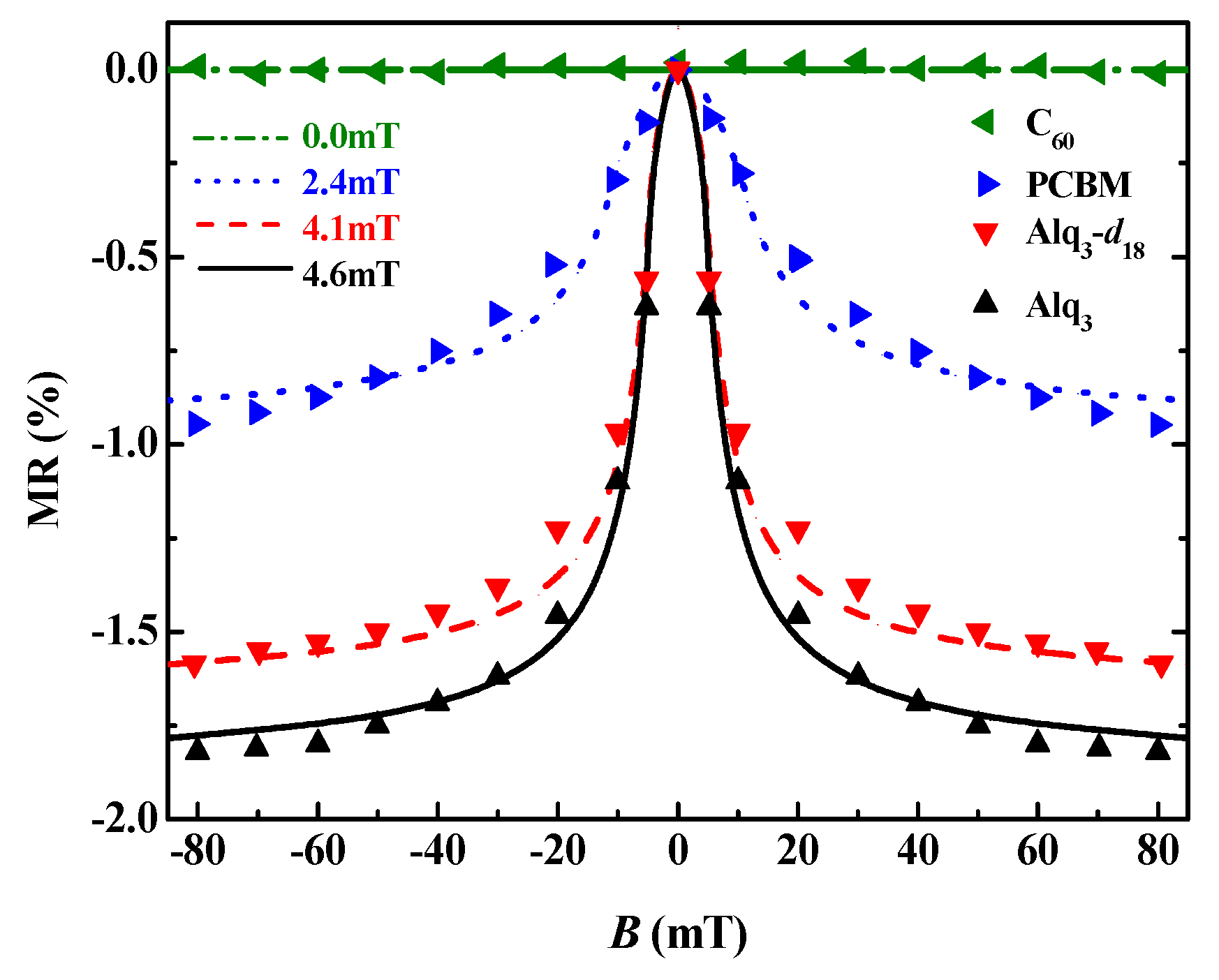
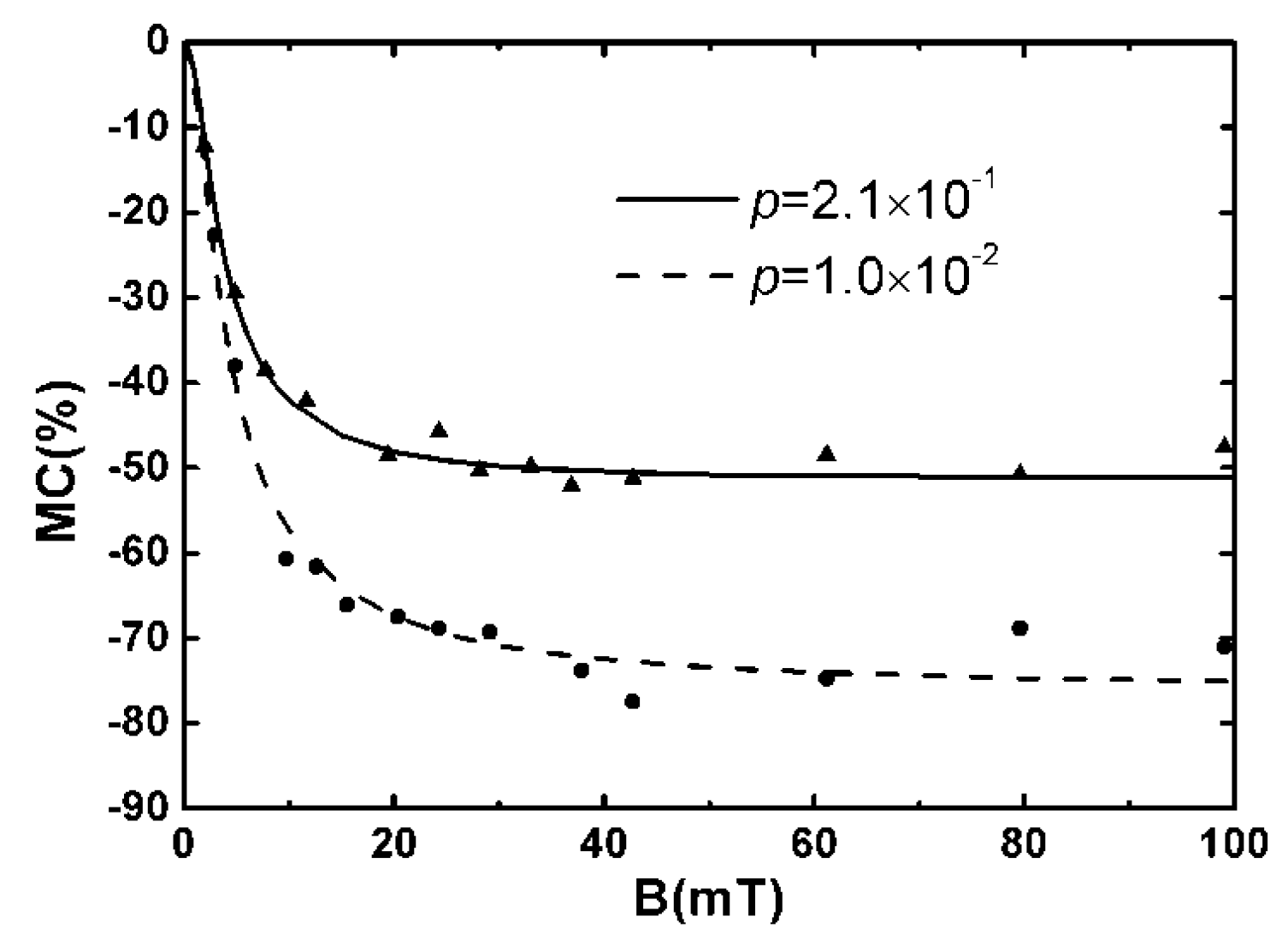
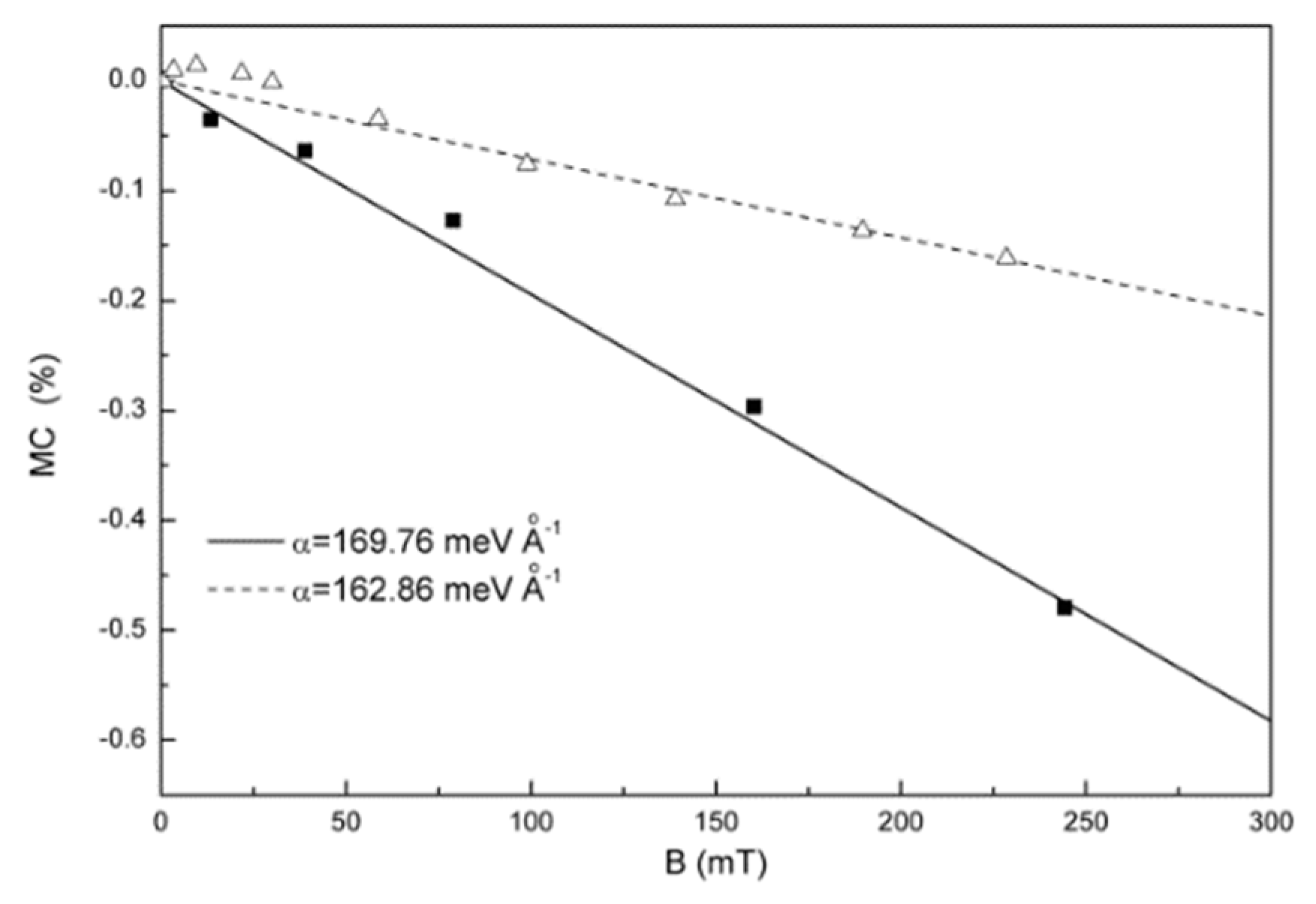
3.1. Organic Magnetic Field Effect Experiment
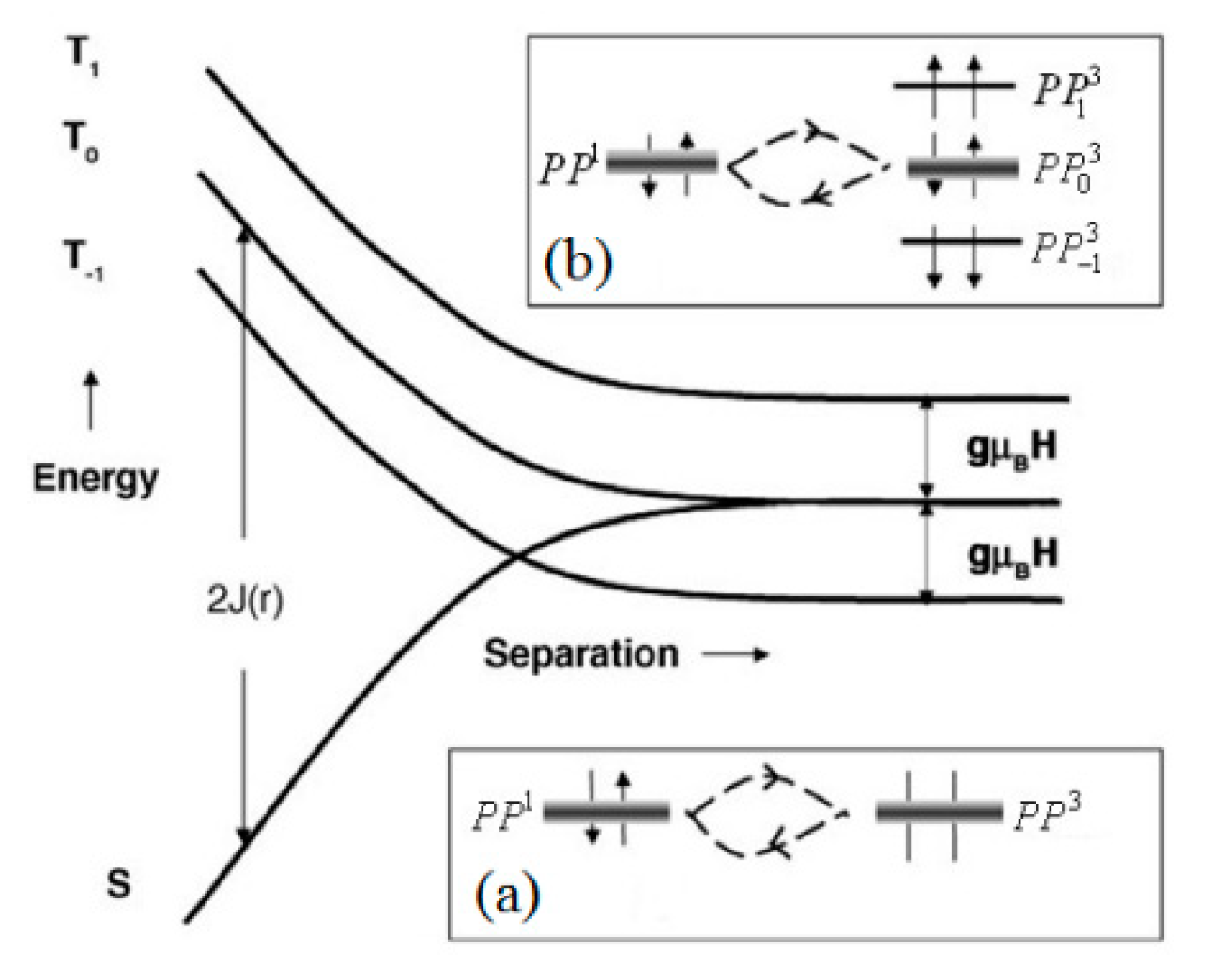
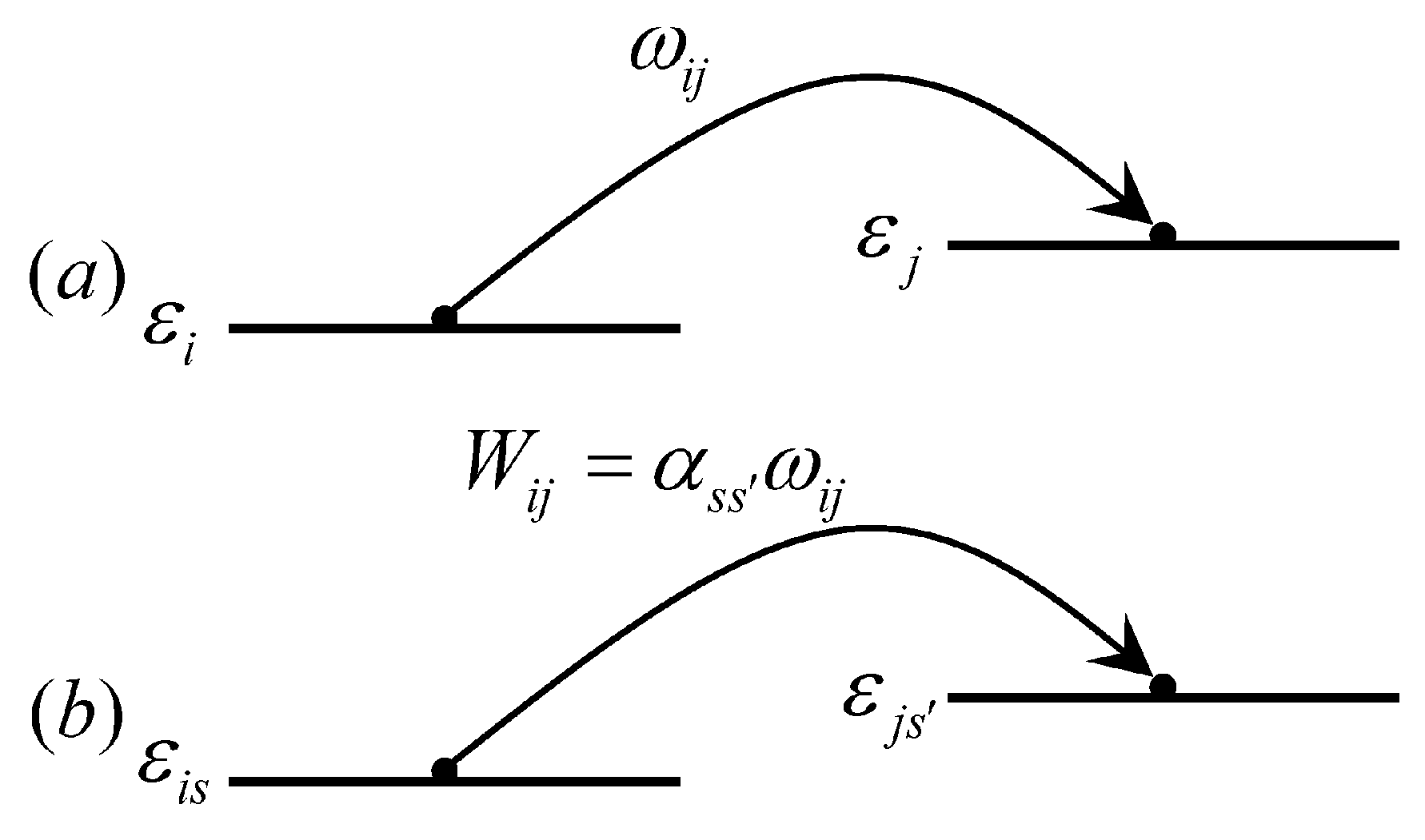
3.2. Organic Magnetic Field Effect Theory
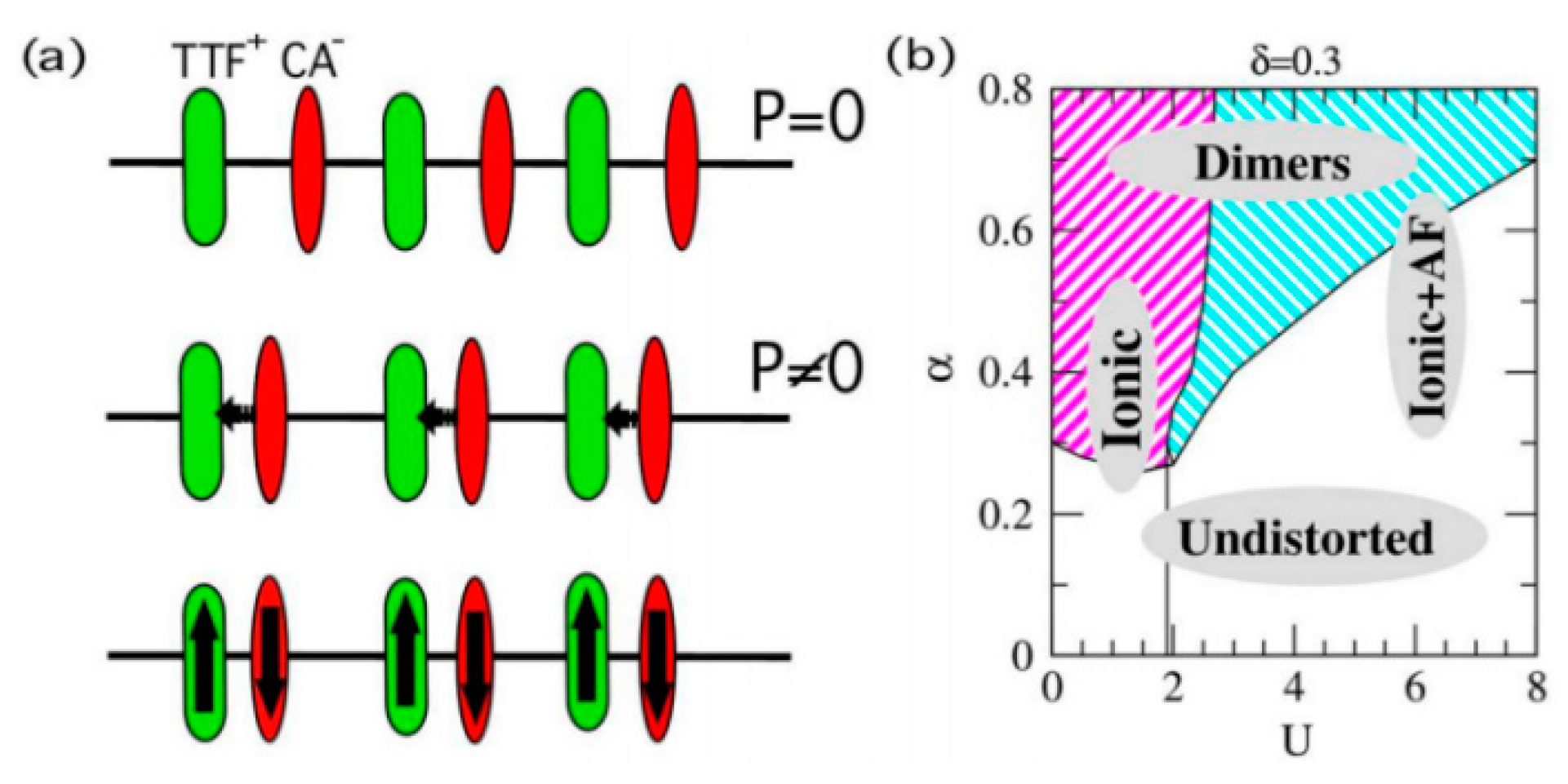
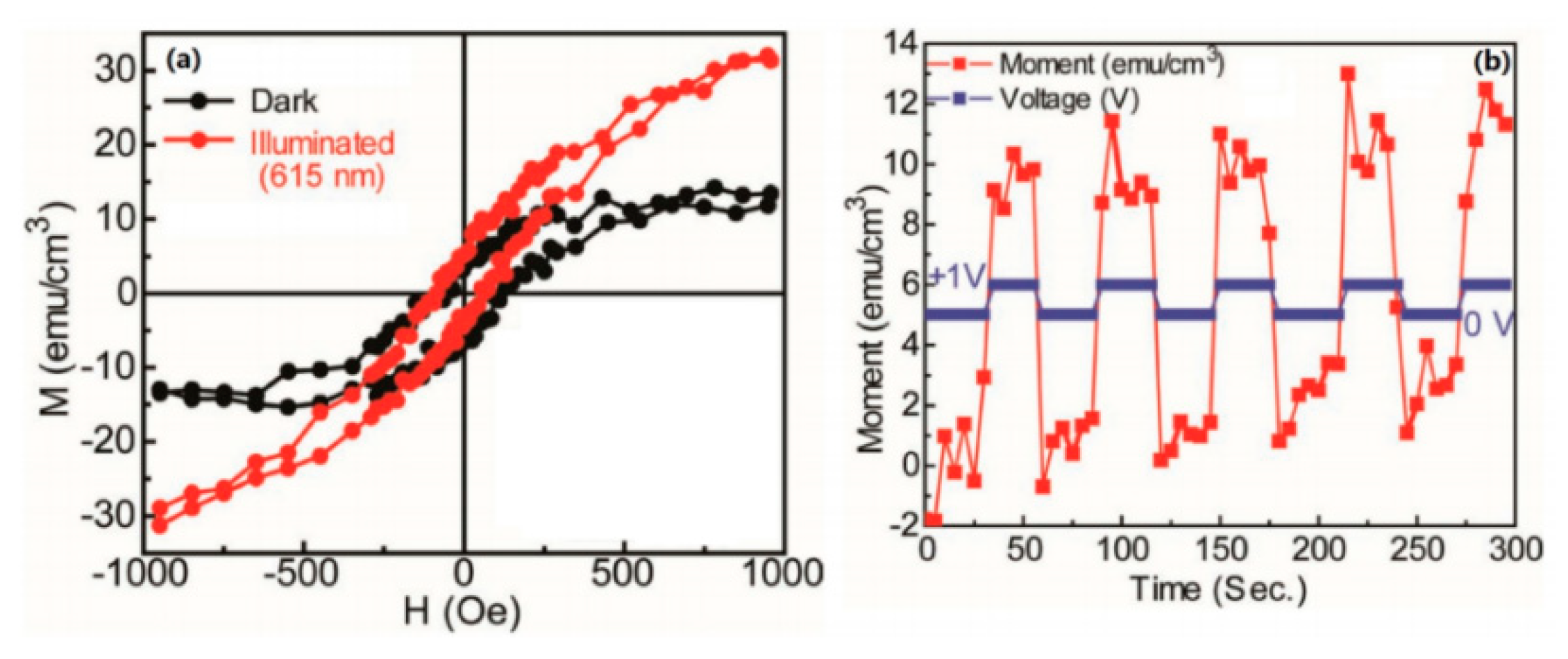
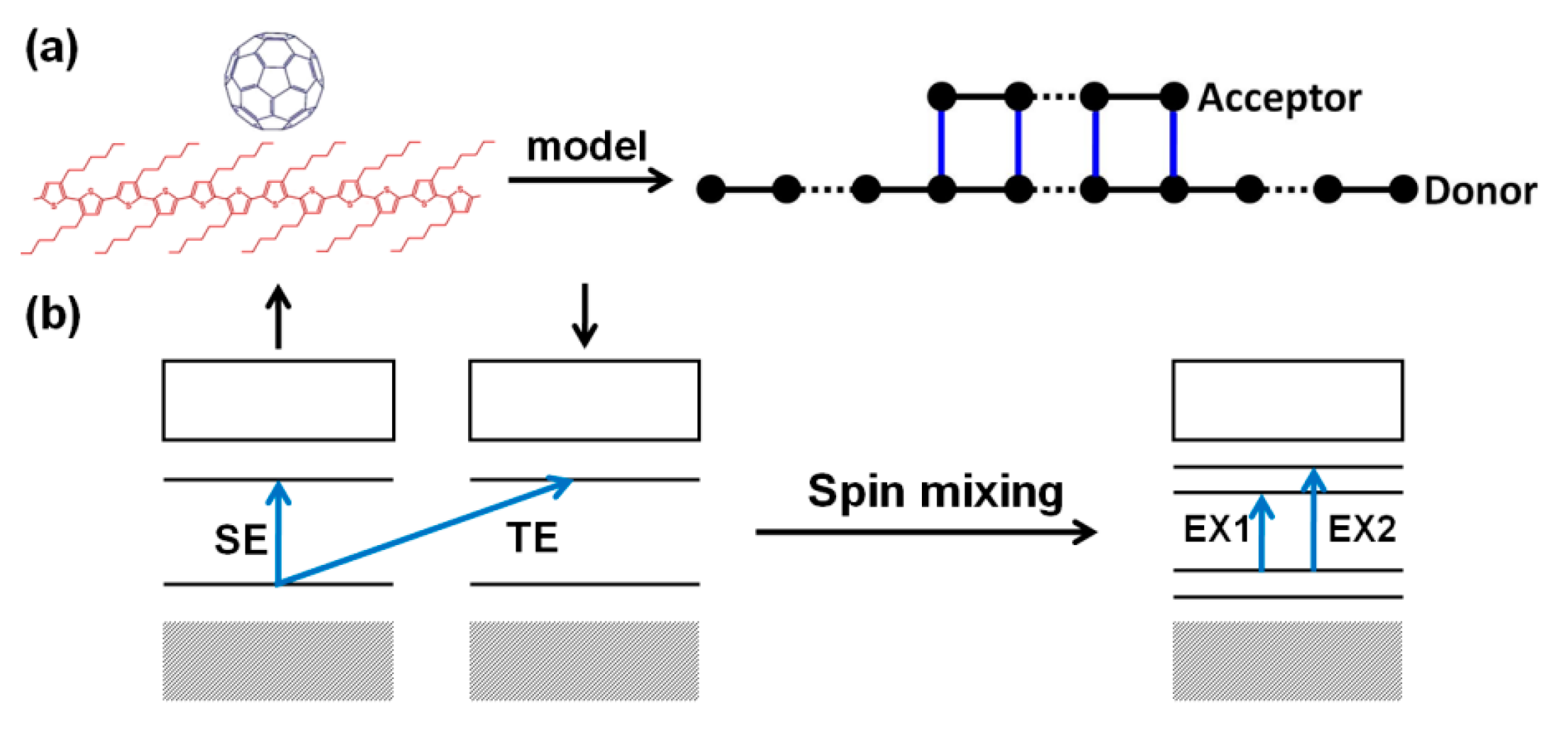
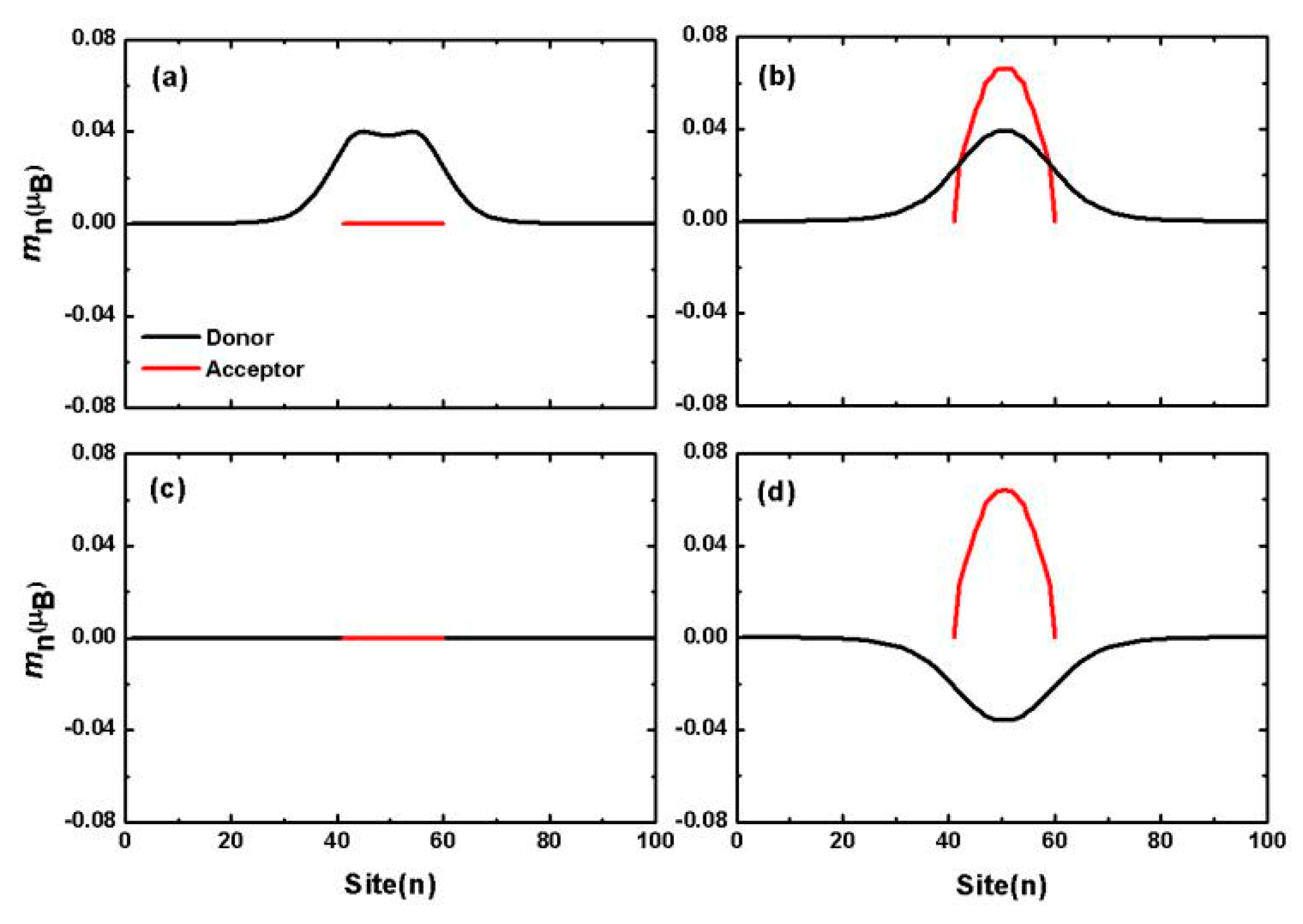
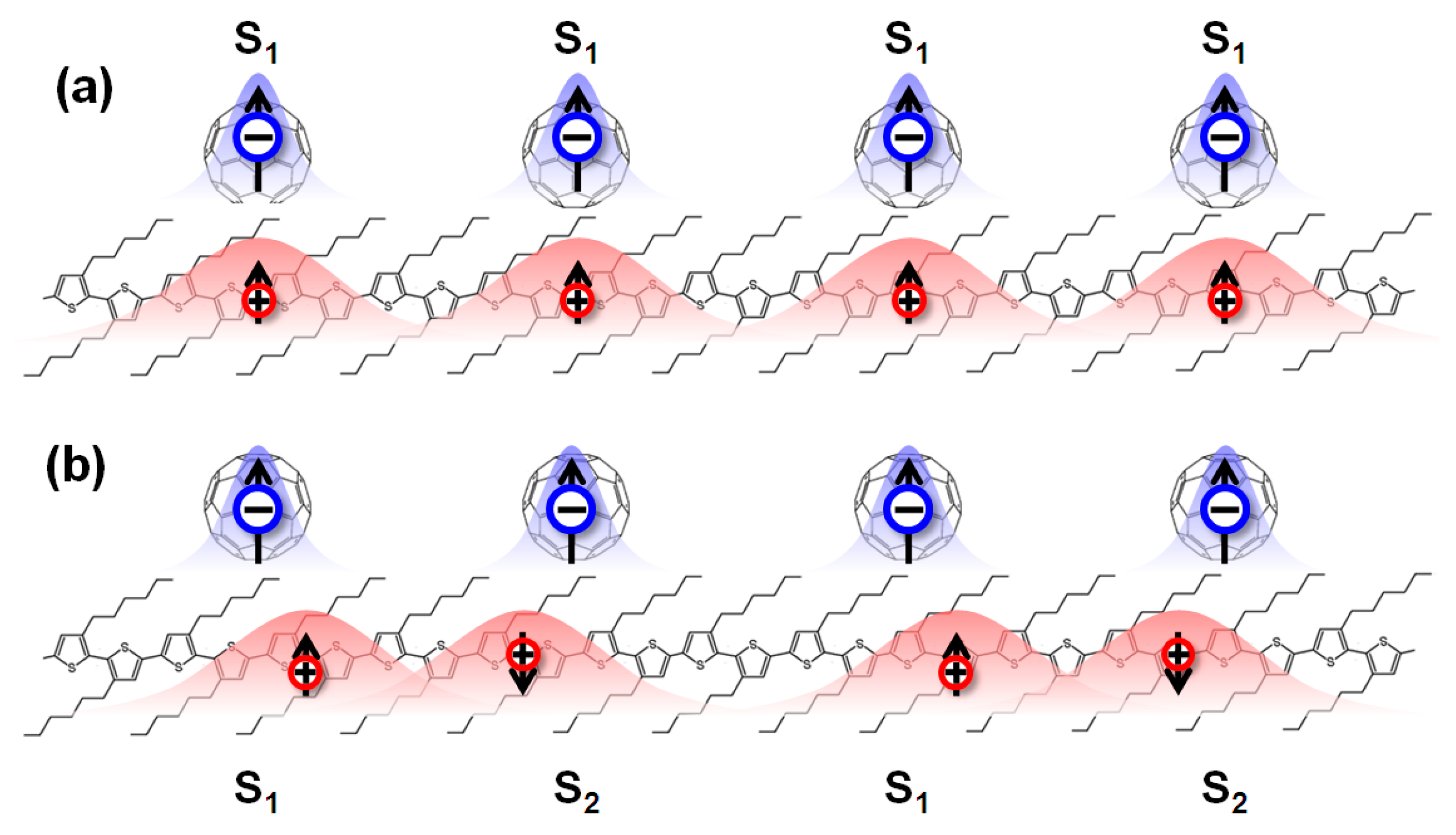
4. Organic Excited Ferromagnetism
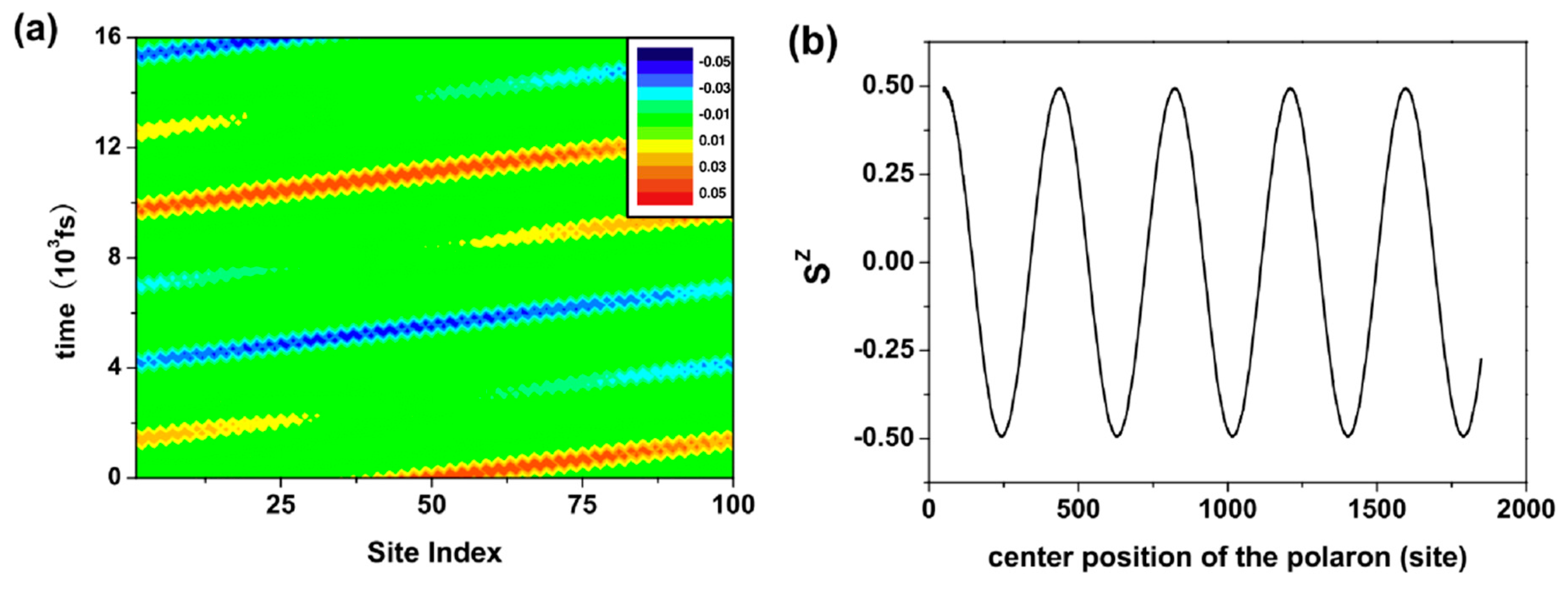
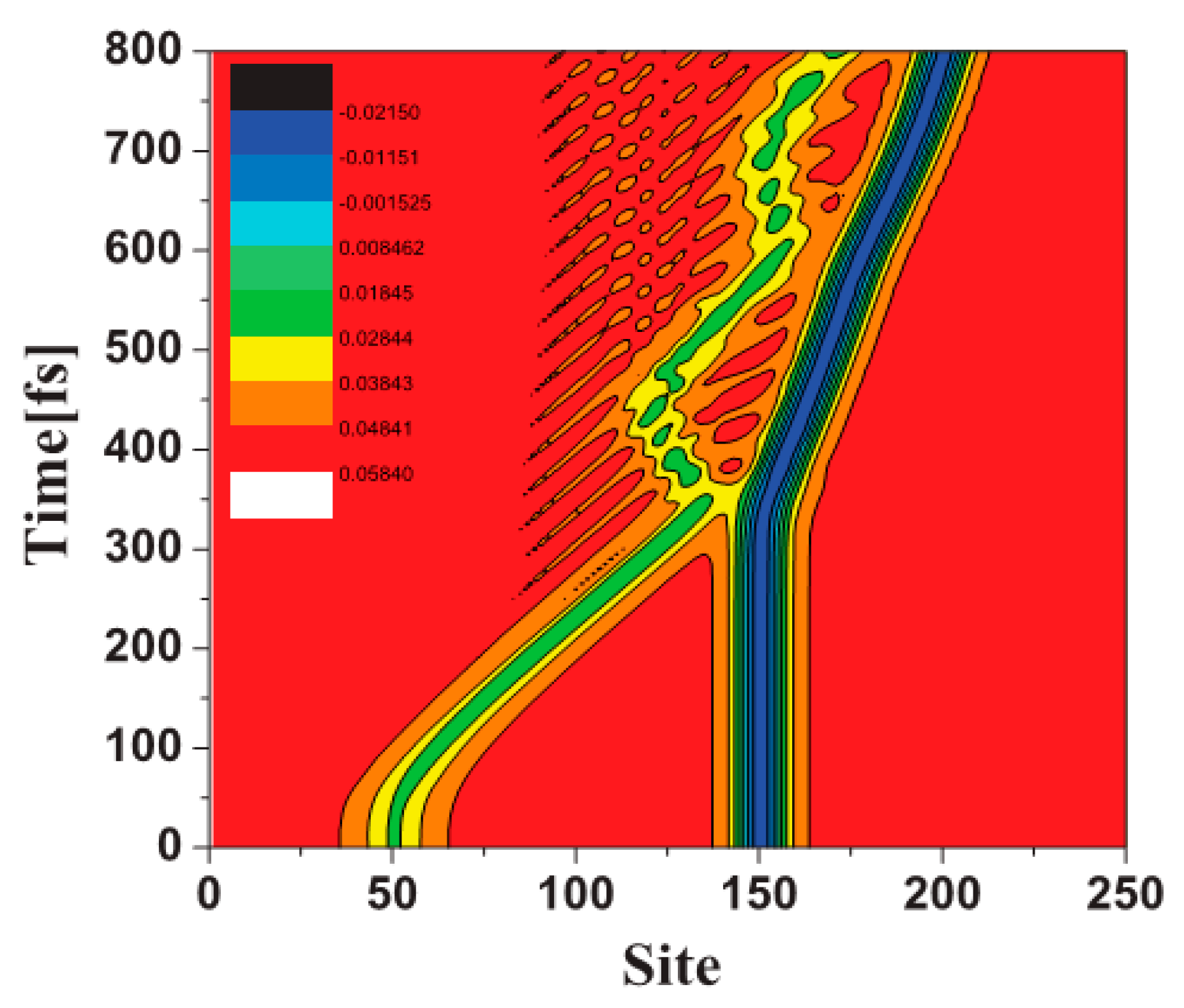
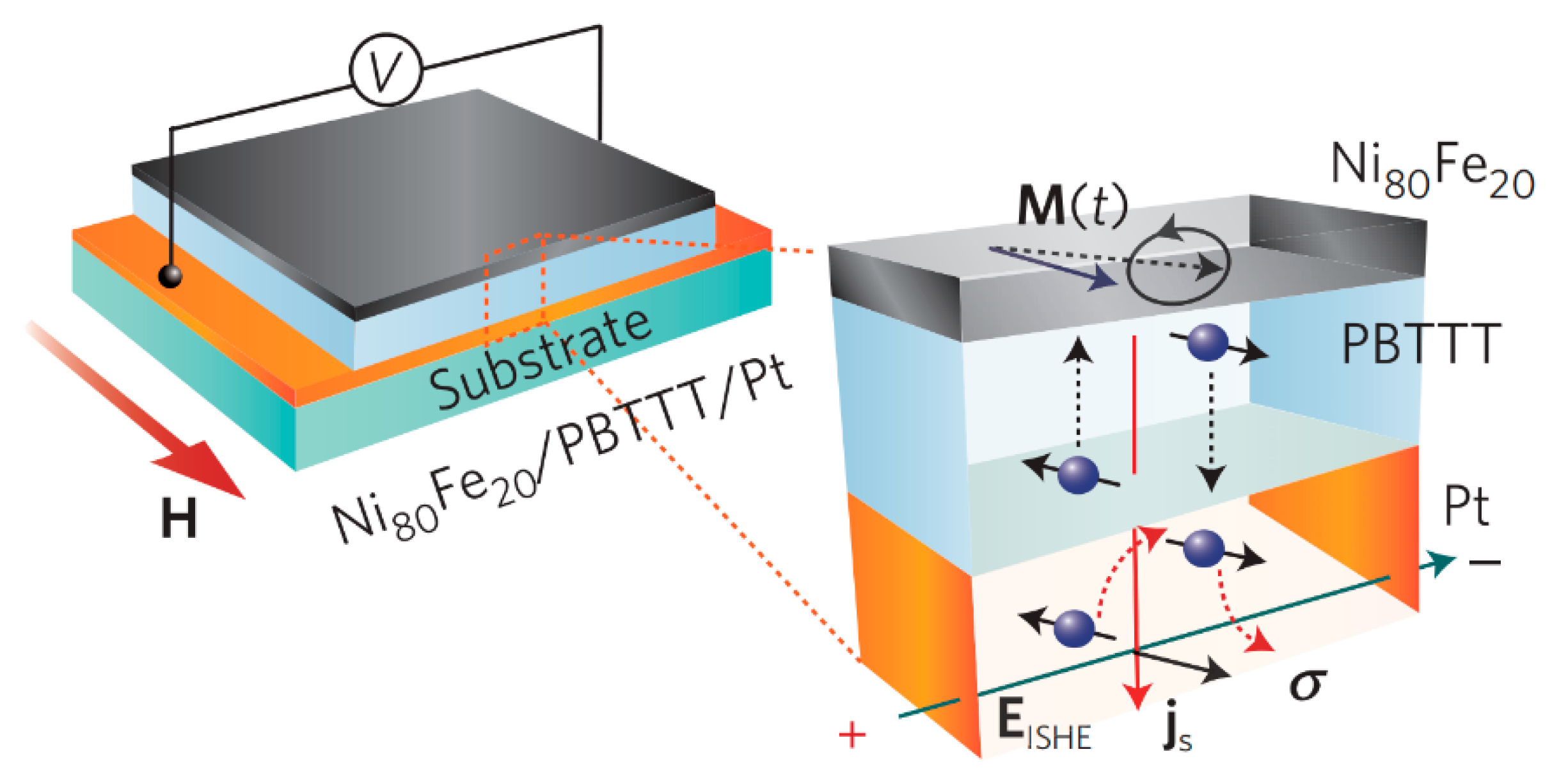
5. Organic Spin Current
6. Organic Spin Device Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Baibich, M.N.; Broto, J.M.; Fert, A.; Nguyen Van Dau, F.; Petroff, F.; Etienne, P.; Creuzet, G.; Friederich, A.; Chazelas, J. Giant magnetoresistance of (001)Fe/(001)Cr magnetic superlattices. Phys. Rev. Lett. 1988, 61, 2472–2475. [Google Scholar] [CrossRef] [PubMed]
- Binasch, G.; Grunberg, P.; Saurenbach, F.; Zinn, W. Enhanced magnetoresistance in layered magnetic structures with antiferromagnetic interlayer exchange. Phys. Rev. B Condens. Matter 1989, 39, 4828–4830. [Google Scholar] [CrossRef] [PubMed]
- Slonczewski, J.C. Current-driven excitation of magnetic multilayers. J. Magn. Magn. Mater. 1996, 159, L1–L7. [Google Scholar] [CrossRef]
- Berger, L. Emission of spin waves by a magnetic multilayer traversed by a current. Phys. Rev. B 1996, 54, 9353–9358. [Google Scholar] [CrossRef] [PubMed]
- Tsoi, M.; Jansen, A.G.M.; Bass, J.; Chiang, W.C.; Seck, M.; Tsoi, V.; Wyder, P. Excitation of a Magnetic Multilayer by an Electric Current. Phys. Rev. Lett. 1998, 80, 4281–4284. [Google Scholar] [CrossRef]
- Myers, E.B.; Ralph, D.C.; Katine, J.A.; Louie, R.N.; Buhrman, R.A. Current-Induced Switching of Domains in Magnetic Multilayer Devices. Science 1999, 285, 867. [Google Scholar] [CrossRef] [PubMed]
- Wolf, S.A.; Awschalom, D.D.; Buhrman, R.A.; Daughton, J.M.; von Molnár, S.; Roukes, M.L.; Chtchelkanova, A.Y.; Treger, D.M. Spintronics: A Spin-Based Electronics Vision for the Future. Science 2001, 294, 1488. [Google Scholar] [CrossRef] [PubMed]
- Dediu, V.; Murgia, M.; Matacotta, F.C.; Taliani, C.; Barbanera, S. Room temperature spin polarized injection in organic semiconductor. Solid State Commun. 2002, 122, 181–184. [Google Scholar] [CrossRef]
- Xiong, Z.H.; Wu, D.; Valy Vardeny, Z.; Shi, J. Giant magnetoresistance in organic spin-valves. Nature 2004, 427, 821–824. [Google Scholar] [CrossRef] [PubMed]
- Francis, T.L.; Mermer, Ö.; Veeraraghavan, G.; Wohlgenannt, M. Large magnetoresistance at room temperature in semiconducting polymer sandwich devices. New J. Phys. 2004, 6, 185. [Google Scholar] [CrossRef]
- Mermer, Ö.; Veeraraghavan, G.; Francis, T.L.; Sheng, Y.; Nguyen, D.T.; Wohlgenannt, M.; Köhler, A.; Al-Suti, M.K.; Khan, M.S. Large magnetoresistance in nonmagneticπ-conjugated semiconductor thin film devices. Phys. Rev. B 2005, 72, 205202. [Google Scholar] [CrossRef]
- Giovannetti, G.; Kumar, S.; Stroppa, A.; van den Brink, J.; Picozzi, S. Multiferroicity in TTF-CA organic molecular crystals predicted through ab initio calculations. Phys. Rev. Lett. 2009, 103, 266401. [Google Scholar] [CrossRef] [PubMed]
- Kagawa, F.; Horiuchi, S.; Tokunaga, M.; Fujioka, J.; Tokura, Y. Ferroelectricity in a one-dimensional organic quantum magnet. Nat. Phys. 2010, 6, 169–172. [Google Scholar] [CrossRef]
- Ren, S.; Wuttig, M. Organic exciton multiferroics. Adv. Mater. 2012, 24, 724–727. [Google Scholar] [CrossRef] [PubMed]
- Qin, W.; Gong, M.; Chen, X.; Shastry, T.A.; Sakidja, R.; Yuan, G.; Hersam, M.C.; Wuttig, M.; Ren, S. Multiferroicity of carbon-based charge-transfer magnets. Adv. Mater. 2015, 27, 734–739. [Google Scholar] [CrossRef]
- Qin, W.; Chen, X.; Li, H.; Gong, M.; Yuan, G.; Grossman, J.C.; Wuttig, M.; Ren, S. Room Temperature Multiferroicity of Charge Transfer Crystals. ACS Nano 2015, 9, 9373–9379. [Google Scholar] [CrossRef]
- Ando, K.; Watanabe, S.; Mooser, S.; Saitoh, E.; Sirringhaus, H. Solution-processed organic spin-charge converter. Nat. Mater. 2013, 12, 622–627. [Google Scholar] [CrossRef]
- Watanabe, S.; Ando, K.; Kang, K.; Mooser, S.; Vaynzof, Y.; Kurebayashi, H.; Saitoh, E.; Sirringhaus, H. Polaron spin current transport in organic semiconductors. Nat. Phys. 2014, 10, 308–313. [Google Scholar] [CrossRef]
- Anderson, P.W. Antiferromagnetism. Theory of Superexchange Interaction. Phys. Rev. 1950, 79, 350–356. [Google Scholar] [CrossRef]
- Sun, Q.-F.; Wang, J.; Guo, H. Quantum transport theory for nanostructures with Rashba spin-orbital interaction. Phys. Rev. B 2005, 71, 165310. [Google Scholar] [CrossRef]
- Tarafder, K.; Sanyal, B.; Oppeneer, P.M. Charge-induced spin polarization in nonmagnetic organic moleculeAlq3. Phys. Rev. B 2010, 82, 060413. [Google Scholar] [CrossRef]
- Hou, D.; Qiu, J.; Xie, S.; Saxena, A. Charge-induced spin polarization in thiophene oligomers. New J. Phys. 2013, 15, 073044. [Google Scholar] [CrossRef][Green Version]
- Han, S.; Jiang, H.; Li, X.; Xie, S. Spontaneous spin polarization in organic thiophene oligomers. Org. Electron. 2014, 15, 240–244. [Google Scholar] [CrossRef]
- Sakurai, J.J.; Napolitano, J. Modern Quantum Mechanics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Majumdar, S.; Majumdar, H.S.; Laiho, R.; Österbacka, R. Comparing small molecules and polymer for future organic spin-valves. J. Alloy. Compd. 2006, 423, 169–171. [Google Scholar] [CrossRef]
- Wang, F.J.; Xiong, Z.H.; Wu, D.; Shi, J.; Vardeny, Z.V. Organic spintronics: The case of Fe/Alq3/Co spin-valve devices. Synth. Met. 2005, 155, 172–175. [Google Scholar] [CrossRef]
- Pramanik, S.; Stefanita, C.G.; Patibandla, S.; Bandyopadhyay, S.; Garre, K.; Harth, N.; Cahay, M. Observation of extremely long spin relaxation times in an organic nanowire spin valve. Nat. Nanotechnol. 2007, 2, 216–219. [Google Scholar] [CrossRef]
- Dediu, V.; Hueso, L.E.; Bergenti, I.; Riminucci, A.; Borgatti, F.; Graziosi, P.; Newby, C.; Casoli, F.; De Jong, M.P.; Taliani, C.; et al. Room-temperature spintronic effects inAlq3-based hybrid devices. Phys. Rev. B 2008, 78, 115203. [Google Scholar] [CrossRef]
- Hill, E.W.; Geim, A.K.; Novoselov, K.; Schedin, F.; Blake, P. Graphene Spin Valve Devices. IEEE Trans. Magn. 2006, 42, 2694–2696. [Google Scholar] [CrossRef]
- Tsukagoshi, K.; Alphenaar, B.W.; Ago, H. Coherent transport of electron spin in a ferromagnetically contacted carbon nanotube. Nature 1999, 401, 572–574. [Google Scholar] [CrossRef]
- Julliere, M. Tunneling between ferromagnetic films. Phys. Lett. A 1975, 54, 225–226. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Hukic-Markosian, G.; Wang, F.; Wojcik, L.; Li, X.G.; Ehrenfreund, E.; Vardeny, Z.V. Isotope effect in spin response of pi-conjugated polymer films and devices. Nat. Mater. 2010, 9, 345–352. [Google Scholar] [CrossRef] [PubMed]
- Lei, J.; Li, H.; Yin, S.; Xie, S.-J. Spin precession of a polaron induced by a gate voltage in one-dimensional organic polymers. J. Phys. Condens. Matter 2008, 20, 095201. [Google Scholar] [CrossRef]
- Qin, W.; Yin, S.; Gao, K.; Xie, S.J. Investigation on organic magnetoconductance based on polaron-bipolaron transition. Appl. Phys. Lett. 2012, 100, 124. [Google Scholar] [CrossRef]
- Zwolak, M.; Di Ventra, M. DNA spintronics. Appl. Phys. Lett. 2002, 81, 925–927. [Google Scholar] [CrossRef]
- Li, K.-S.; Chang, Y.-M.; Agilan, S.; Hong, J.-Y.; Tai, J.-C.; Chiang, W.-C.; Fukutani, K.; Dowben, P.A.; Lin, M.-T. Organic spin valves with inelastic tunneling characteristics. Phys. Rev. B 2011, 83, 172404. [Google Scholar] [CrossRef]
- Yu, Z.G. Spin-orbit coupling, spin relaxation, and spin diffusion in organic solids. Phys. Rev. Lett. 2011, 106, 106602. [Google Scholar] [CrossRef] [PubMed]
- Xie, S.J.; Ahn, K.H.; Smith, D.L.; Bishop, A.R.; Saxena, A. Ground-state properties of ferromagnetic metal/conjugated polymer interfaces. Phys. Rev. B 2003, 67, 125202. [Google Scholar] [CrossRef]
- Fu, J.-Y.; Ren, J.-F.; Liu, X.-J.; Liu, D.-S.; Xie, S.-J. Dynamics of charge injection into an open conjugated polymer: A nonadiabatic approach. Phys. Rev. B 2006, 73, 195401. [Google Scholar] [CrossRef]
- Dalgleish, H.; Kirczenow, G. Spin-current rectification in molecular wires. Phys. Rev. B 2006, 73, 235436. [Google Scholar] [CrossRef]
- Gallagher, N.M.; Olankitwanit, A.; Rajca, A. High-spin organic molecules. J. Org. Chem. 2015, 80, 1291–1298. [Google Scholar] [CrossRef]
- Ruden, P.P.; Smith, D.L. Theory of spin injection into conjugated organic semiconductors. J. Appl. Phys. 2004, 95, 4898–4904. [Google Scholar] [CrossRef]
- Bergenti, I.; Borgatti, F.; Calbucci, M.; Riminucci, A.; Cecchini, R.; Graziosi, P.; MacLaren, D.A.; Giglia, A.; Rueff, J.P.; Céolin, D.; et al. Oxygen Impurities Link Bistability and Magnetoresistance in Organic Spin Valves. ACS Appl. Mater. Interfaces 2018, 10, 8132–8140. [Google Scholar] [CrossRef] [PubMed]
- Riminucci, A.; Yu, Z.-G.; Prezioso, M.; Cecchini, R.; Bergenti, I.; Graziosi, P.; Dediu, V.A. Controlling Magnetoresistance by Oxygen Impurities in Mq3-Based Molecular Spin Valves. ACS Appl. Mater. Interfaces 2019, 11, 8319–8326. [Google Scholar] [CrossRef] [PubMed]
- Tsurumi, J.; Matsui, H.; Kubo, T.; Häusermann, R.; Mitsui, C.; Okamoto, T.; Watanabe, S.; Takeya, J. Coexistence of ultra-long spin relaxation time and coherent charge transport in organic single-crystal semiconductors. Nat. Phys. 2017, 13, 994. [Google Scholar] [CrossRef]
- Wang, C.; Dong, H.; Jiang, L.; Hu, W. Organic semiconductor crystals. Chem. Soc. Rev. 2018, 47, 422–500. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Dong, H.; Hu, W. Organic Semiconductor Single Crystals for Electronics and Photonics. Adv. Mater. 2018, 30, 1801048. [Google Scholar] [CrossRef] [PubMed]
- Guo, L.; Qin, Y.; Gu, X.; Zhu, X.; Zhou, Q.; Sun, X. Spin Transport in Organic Molecules. Front. Chem. 2019, 7, 428. [Google Scholar] [CrossRef] [PubMed]
- Hu, B.; Yan, L.; Shao, M. Magnetic-Field Effects in Organic Semiconducting Materials and Devices. Adv. Mater. 2009, 21, 1500–1516. [Google Scholar] [CrossRef]
- Davis, A.H.; Bussmann, K. Large magnetic field effects in organic light emitting diodes based on tris(8-hydroxyquinoline aluminum) (Alq3)/N,N′-Di(naphthalen-1-yl)-N,N′diphenyl-benzidine (NPB) bilayers. J. Vac. Sci. Technol. A 2004, 22, 1885–1891. [Google Scholar] [CrossRef]
- Shakya, P.; Desai, P.; Somerton, M.; Gannaway, G.; Kreouzis, T.; Gillin, W.P. The magnetic field effect on the transport and efficiency of group III tris(8-hydroxyquinoline) organic light emitting diodes. J. Appl. Phys. 2008, 103, 103715. [Google Scholar] [CrossRef]
- Martin, J.L.; Bergeson, J.D.; Prigodin, V.N.; Epstein, A.J. Magnetoresistance for organic semiconductors: Small molecule, oligomer, conjugated polymer, and non-conjugated polymer. Synth. Met. 2010, 160, 291–296. [Google Scholar] [CrossRef]
- Kang, H.; Park, C.H.; Lim, J.; Lee, C.; Kang, W.; Yoon, C.S. Power law behavior of magnetoresistance in tris(8-hydroxyquinolinato)aluminum-based organic light-emitting diodes. Org. Electron. 2012, 13, 1012–1017. [Google Scholar] [CrossRef]
- Frankevich, E.; Zakhidov, A.; Yoshino, K.; Maruyama, Y.; Yakushi, K. Photoconductivity of poly(2,5-diheptyloxy-p-phenylene vinylene) in the air atmosphere: Magnetic-field effect and mechanism of generation and recombination of charge carriers. Phys. Rev. B 1996, 53, 4498–4508. [Google Scholar] [CrossRef] [PubMed]
- Kalinowski, J.; Cocchi, M.; Virgili, D.; Di Marco, P.; Fattori, V. Magnetic field effects on emission and current in Alq3-based electroluminescent diodes. Chem. Phys. Lett. 2003, 380, 710–715. [Google Scholar] [CrossRef]
- Zhang, Y.; Ren, J.; Lei, J.; Xie, S. Effect of Co permeation on spin polarized transport in a Co/organic semiconductor (OSC) structure. Org. Electron. 2009, 10, 568–572. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Sheng, Y.; Rybicki, J.; Veeraraghavan, G.; Wohlgenannt, M. Device-spectroscopy of magnetic field effects in several different polymer organic light-emitting diodes. Synth. Met. 2010, 160, 320–324. [Google Scholar] [CrossRef]
- Veeraraghavan, G.; Nguyen, T.D.; Sheng, Y.; Mermer, O.; Wohlgenannt, M. Magnetic field effects on current, electroluminescence and photocurrent in organic light-emitting diodes. J. Phys. Condens. Matter 2007, 19, 036209. [Google Scholar] [CrossRef]
- Ding, B.F.; Yao, Y.; Sun, Z.Y.; Wu, C.Q.; Gao, X.D.; Wang, Z.J.; Ding, X.M.; Choy, W.C.H.; Hou, X.Y. Magnetic field effects on the electroluminescence of organic light emitting devices: A tool to indicate the carrier mobility. Appl. Phys. Lett. 2010, 97, 228. [Google Scholar] [CrossRef]
- Majumdar, S.; Majumdar, H.S.; Aarnio, H.; Vanderzande, D.; Laiho, R.; Österbacka, R. Role of electron-hole pair formation in organic magnetoresistance. Phys. Rev. B 2009, 79, 201202. [Google Scholar] [CrossRef]
- Prigodin, V.N.; Bergeson, J.D.; Lincoln, D.M.; Epstein, A.J. Anomalous room temperature magnetoresistance in organic semiconductors. Synth. Met. 2006, 156, 757–761. [Google Scholar] [CrossRef]
- Obolda, A.; Peng, Q.; He, C.; Zhang, T.; Ren, J.; Ma, H.; Shuai, Z.; Li, F. Triplet-Polaron-Interaction-Induced Upconversion from Triplet to Singlet: A Possible Way to Obtain Highly Efficient OLEDs. Adv. Mater. 2016, 28, 4740–4746. [Google Scholar] [CrossRef] [PubMed]
- Wallikewitz, B.H.; Kabra, D.; Gélinas, S.; Friend, R.H. Triplet dynamics in fluorescent polymer light-emitting diodes. Phys. Rev. B 2012, 85, 045209. [Google Scholar] [CrossRef]
- Sun, Z.; Liu, D.; Stafstrom, S.; An, Z. Scattering process between polaron and exciton in conjugated polymers. J. Chem. Phys. 2011, 134, 044906. [Google Scholar] [CrossRef] [PubMed]
- Troisi, A.; Orlandi, G. Charge-transport regime of crystalline organic semiconductors: Diffusion limited by thermal off-diagonal electronic disorder. Phys. Rev. Lett. 2006, 96, 086601. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.D.; Sheng, Y.; Wohlgenannt, M.; Anthopoulos, T.D. On the role of hydrogen in organic magnetoresistance: A study of C60 devices. Synth. Met. 2007, 157, 930–934. [Google Scholar] [CrossRef]
- Rolfe, N.J.; Heeney, M.; Wyatt, P.B.; Drew, A.J.; Kreouzis, T.; Gillin, W.P. Elucidating the role of hyperfine interactions on organic magnetoresistance using deuterated aluminium tris(8-hydroxyquinoline). Phys. Rev. B 2009, 80, 241201. [Google Scholar] [CrossRef]
- Yang, F.J.; Qin, W.; Xie, S.J. Investigation of giant magnetoconductance in organic devices based on hopping mechanism. J. Chem. Phys. 2014, 140, 144110. [Google Scholar] [CrossRef]
- Desai, P.; Shakya, P.; Kreouzis, T.; Gillin, W.P. Magnetoresistance in organic light-emitting diode structures under illumination. Phys. Rev. B 2007, 76, 235202. [Google Scholar] [CrossRef]
- Wang, X.R.; Xie, S.J. A theory for magnetic-field effects of nonmagnetic organic semiconducting materials. EPL (Europhys. Lett.) 2010, 92, 57031. [Google Scholar] [CrossRef][Green Version]
- Li, S.; Dong, X.; Yi, D.; Xie, S. Theoretical investigation on magnetic field effect in organic devices with asymmetrical molecules. Org. Electron. 2013, 14, 2216–2222. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Sheng, Y.; Rybicki, J.; Veeraraghavan, G.; Wohlgenannt, M. Magnetoresistance in π-conjugated organic sandwich devices with varying hyperfine and spin–orbit coupling strengths, and varying dopant concentrations. J. Mater. Chem. 2007, 17, 1995–2001. [Google Scholar] [CrossRef]
- Sheng, Y.; Nguyen, T.D.; Veeraraghavan, G.; Mermer, Ö.; Wohlgenannt, M. Effect of spin-orbit coupling on magnetoresistance in organic semiconductors. Phys. Rev. B 2007, 75, 035202. [Google Scholar] [CrossRef]
- Kimura, T.; Goto, T.; Shintani, H.; Ishizaka, K.; Arima, T.; Tokura, Y. Magnetic control of ferroelectric polarization. Nature 2003, 426, 55–58. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Neaton, J.B.; Zheng, H.; Nagarajan, V.; Ogale, S.B.; Liu, B.; Viehland, D.; Vaithyanathan, V.; Schlom, D.G.; Waghmare, U.V.; et al. Epitaxial BiFeO3 Multiferroic Thin Film Heterostructures. Science 2003, 299, 1719. [Google Scholar] [CrossRef] [PubMed]
- Ishihara, S. Electronic ferroelectricity in molecular organic crystals. J. Phys. Condens. Matter 2014, 26, 493201. [Google Scholar] [CrossRef] [PubMed]
- Qin, W.; Xu, B.; Ren, S. An organic approach for nanostructured multiferroics. Nanoscale 2015, 7, 9122–9132. [Google Scholar] [CrossRef] [PubMed]
- Bauer, G.E.; Saitoh, E.; van Wees, B.J. Spin caloritronics. Nat. Mater. 2012, 11, 391–399. [Google Scholar] [CrossRef]
- Han, S.; Yang, L.; Gao, K.; Xie, S.; Qin, W.; Ren, S. Spin polarization of excitons in organic multiferroic composites. Sci. Rep. 2016, 6, 28656. [Google Scholar] [CrossRef]
- Fang, Z.; Liu, Z.L.; Yao, K.L.; Li, Z.G. Spin configurations of pi electrons in quasi-one-dimensional organic ferromagnets. Phys. Rev. B Condens. Matter 1995, 51, 1304–1307. [Google Scholar] [CrossRef]
- Xie, S.J.; Zhao, J.Q.; Wei, J.H.; Wang, S.G.; Mei, L.M.; Han, S.H. Effect of boundary conditions on SDW and CDW in organic ferromagnetic chains. Europhys. Lett. (EPL) 2000, 50, 635–641. [Google Scholar] [CrossRef]
- Hu, G.; Guo, Y.; Wei, J.; Xie, S. Spin filtering through a metal/organic-ferromagnet/metal structure. Phys. Rev. B 2007, 75, 165321. [Google Scholar] [CrossRef]
- Wang, Z.; Gao, M.; Wei, M.; Ren, S.; Hao, X.-T.; Qin, W. Organic Chiral Charge Transfer Magnets. ACS Nano 2019, 13, 4705–4711. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Liu, G.; Liu, J.; Wei, M.; Wang, Z.; Hao, X.; Maheswar Repaka, D.V.; Ramanujan, R.V.; Tao, X.; Qin, W.; et al. Anisotropic Magnetoelectric Coupling and Cotton–Mouton Effects in the Organic Magnetic Charge-Transfer Complex Pyrene–F4TCNQ. ACS Appl. Mater. Interfaces 2018, 10, 44654–44659. [Google Scholar] [CrossRef] [PubMed]
- Ando, K.; Saitoh, E. Observation of the inverse spin Hall effect in silicon. Nat. Commun. 2012, 3, 629. [Google Scholar] [CrossRef] [PubMed]
- Sun, D.; van Schooten, K.J.; Kavand, M.; Malissa, H.; Zhang, C.; Groesbeck, M.; Boehme, C.; Valy Vardeny, Z. Inverse spin Hall effect from pulsed spin current in organic semiconductors with tunable spin-orbit coupling. Nat. Mater. 2016, 15, 863–869. [Google Scholar] [CrossRef] [PubMed]
- Ohshima, R.; Sakai, A.; Ando, Y.; Shinjo, T.; Kawahara, K.; Ago, H.; Shiraishi, M. Observation of spin-charge conversion in chemical-vapor-deposition-grown single-layer graphene. Appl. Phys. Lett. 2014, 105, 162410. [Google Scholar] [CrossRef]
- Yu, Z.G. Suppression of the Hanle effect in organic spintronic devices. Phys. Rev. Lett. 2013, 111, 016601. [Google Scholar] [CrossRef]
- Bandyopadhyay, S. Dominant spin relaxation mechanism in compound organic semiconductors. Phys. Rev. B 2010, 81, 153202. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Z.F.; Mei, J.W.; Wu, Y.S.; Liu, F. Flat Chern band in a two-dimensional organometallic framework. Phys. Rev. Lett. 2013, 110, 106804. [Google Scholar] [CrossRef]
- Beljonne, D.; Shuai, Z.; Pourtois, G.; Bredas, J.L. Spin−Orbit Coupling and Intersystem Crossing in Conjugated Polymers: A Configuration Interaction Description. J. Phys. Chem. A 2001, 105, 3899–3907. [Google Scholar] [CrossRef]
- Yu, Z.-G. Spin relaxation and diffusion in disordered organic solids. J. Photonics Energy 2018, 8, 032213. [Google Scholar] [CrossRef]
- Castro Neto, A.H.; Guinea, F. Impurity-Induced Spin-Orbit Coupling in Graphene. Phys. Rev. Lett. 2009, 103, 026804. [Google Scholar] [CrossRef] [PubMed]
- Ray, S.G.; Daube, S.S.; Leitus, G.; Vager, Z.; Naaman, R. Chirality-induced spin-selective properties of self-assembled monolayers of DNA on gold. Phys. Rev. Lett. 2006, 96, 036101. [Google Scholar] [CrossRef] [PubMed]
- Göhler, B.; Hamelbeck, V.; Markus, T.Z.; Kettner, M.; Hanne, G.F.; Vager, Z.; Naaman, R.; Zacharias, H. Spin Selectivity in Electron Transmission Through Self-Assembled Monolayers of Double-Stranded DNA. Science 2011, 331, 894. [Google Scholar] [CrossRef] [PubMed]
- Eremko, A.A.; Loktev, V.M. Spin sensitive electron transmission through helical potentials. Phys. Rev. B 2013, 88, 165409. [Google Scholar] [CrossRef]
- Einati, H.; Mishra, D.; Friedman, N.; Sheves, M.; Naaman, R. Light-controlled spin filtering in bacteriorhodopsin. Nano Lett. 2015, 15, 1052–1056. [Google Scholar] [CrossRef] [PubMed]
- Di Nuzzo, D.; Kulkarni, C.; Zhao, B.; Smolinsky, E.; Tassinari, F.; Meskers, S.C.J.; Naaman, R.; Meijer, E.W.; Friend, R.H. High Circular Polarization of Electroluminescence Achieved via Self-Assembly of a Light-Emitting Chiral Conjugated Polymer into Multidomain Cholesteric Films. ACS Nano 2017, 11, 12713–12722. [Google Scholar] [CrossRef] [PubMed]
- Naaman, R.; Paltiel, Y.; Waldeck, D.H. Chirality and Spin: A Different Perspective on Enantioselective Interactions. Chimia (Aarau) 2018, 72, 394–398. [Google Scholar] [CrossRef] [PubMed]
- Tassinari, F.; Jayarathna, D.R.; Kantor-Uriel, N.; Davis, K.L.; Varade, V.; Achim, C.; Naaman, R. Chirality Dependent Charge Transfer Rate in Oligopeptides. Adv. Mater. 2018, 30, e1706423. [Google Scholar] [CrossRef]
- Varade, V.; Markus, T.; Vankayala, K.; Friedman, N.; Sheves, M.; Waldeck, D.H.; Naaman, R. Bacteriorhodopsin based non-magnetic spin filters for biomolecular spintronics. Phys. Chem. Chem. Phys. 2018, 20, 1091–1097. [Google Scholar] [CrossRef]
- Naaman, R.; Waldeck, D.H. The Chiral Induced Spin Selectivity (CISS) Effect. In World Scientific Reference on Spin in Organics; World Scientific: Singpore, 2018; pp. 235–270. [Google Scholar] [CrossRef]
- Al-Bustami, H.; Koplovitz, G.; Primc, D.; Yochelis, S.; Capua, E.; Porath, D.; Naaman, R.; Paltiel, Y. Single Nanoparticle Magnetic Spin Memristor. Small 2018, 14, e1801249. [Google Scholar] [CrossRef] [PubMed]
- Koplovitz, G.; Leitus, G.; Ghosh, S.; Bloom, B.P.; Yochelis, S.; Rotem, D.; Vischio, F.; Striccoli, M.; Fanizza, E.; Naaman, R.; et al. Single Domain 10 nm Ferromagnetism Imprinted on Superparamagnetic Nanoparticles Using Chiral Molecules. Small 2019, 15, e1804557. [Google Scholar] [CrossRef] [PubMed]
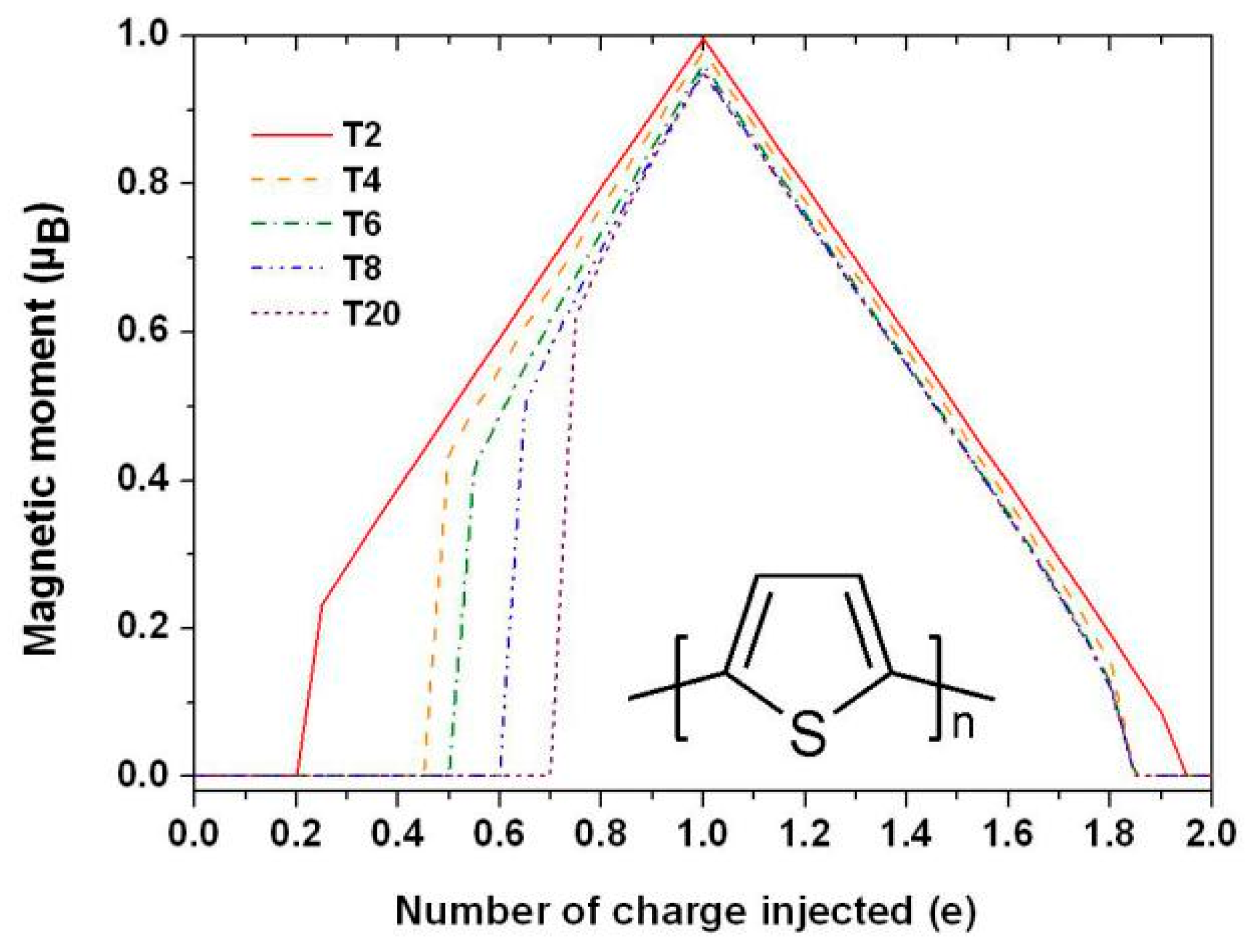
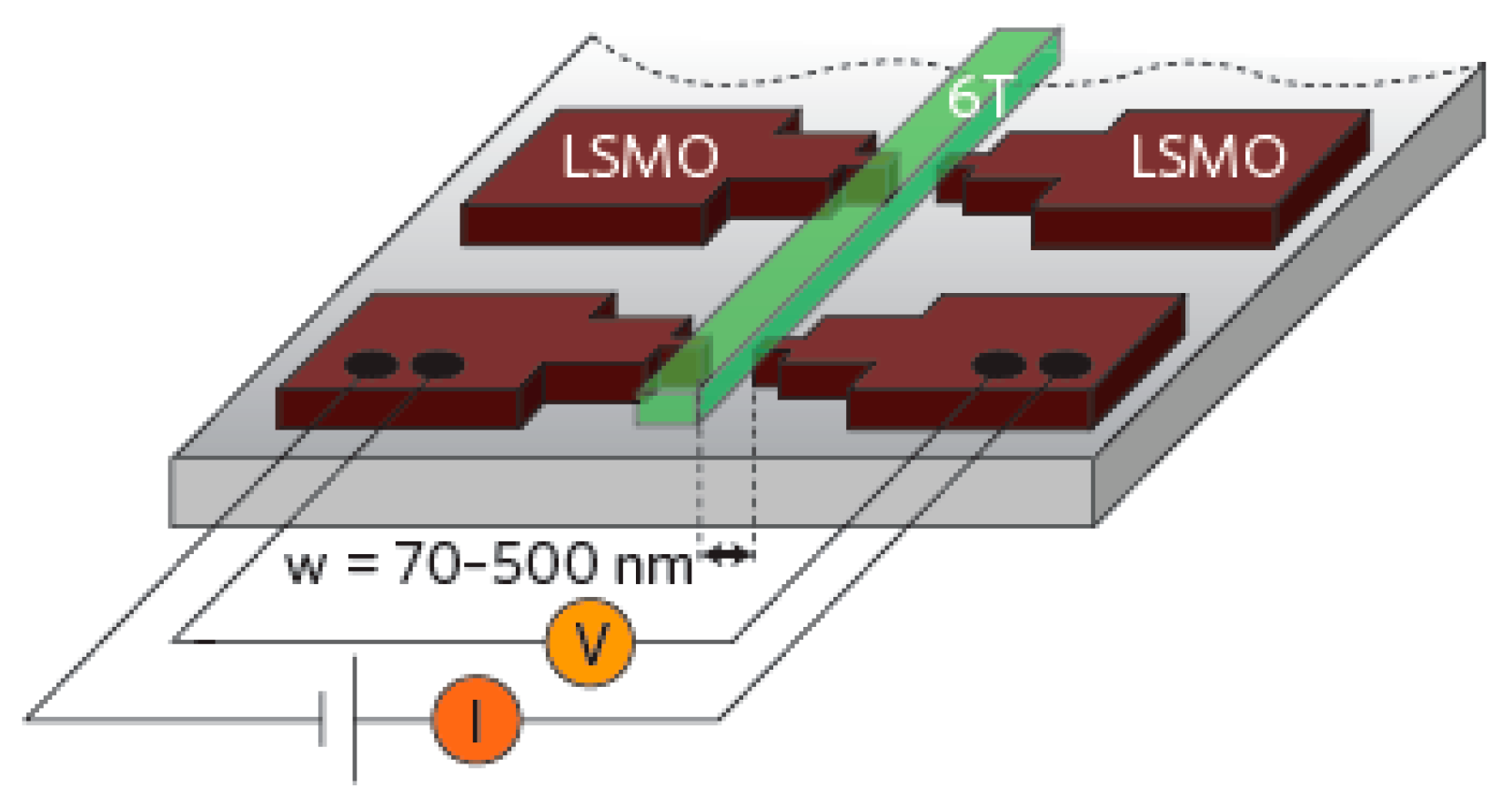
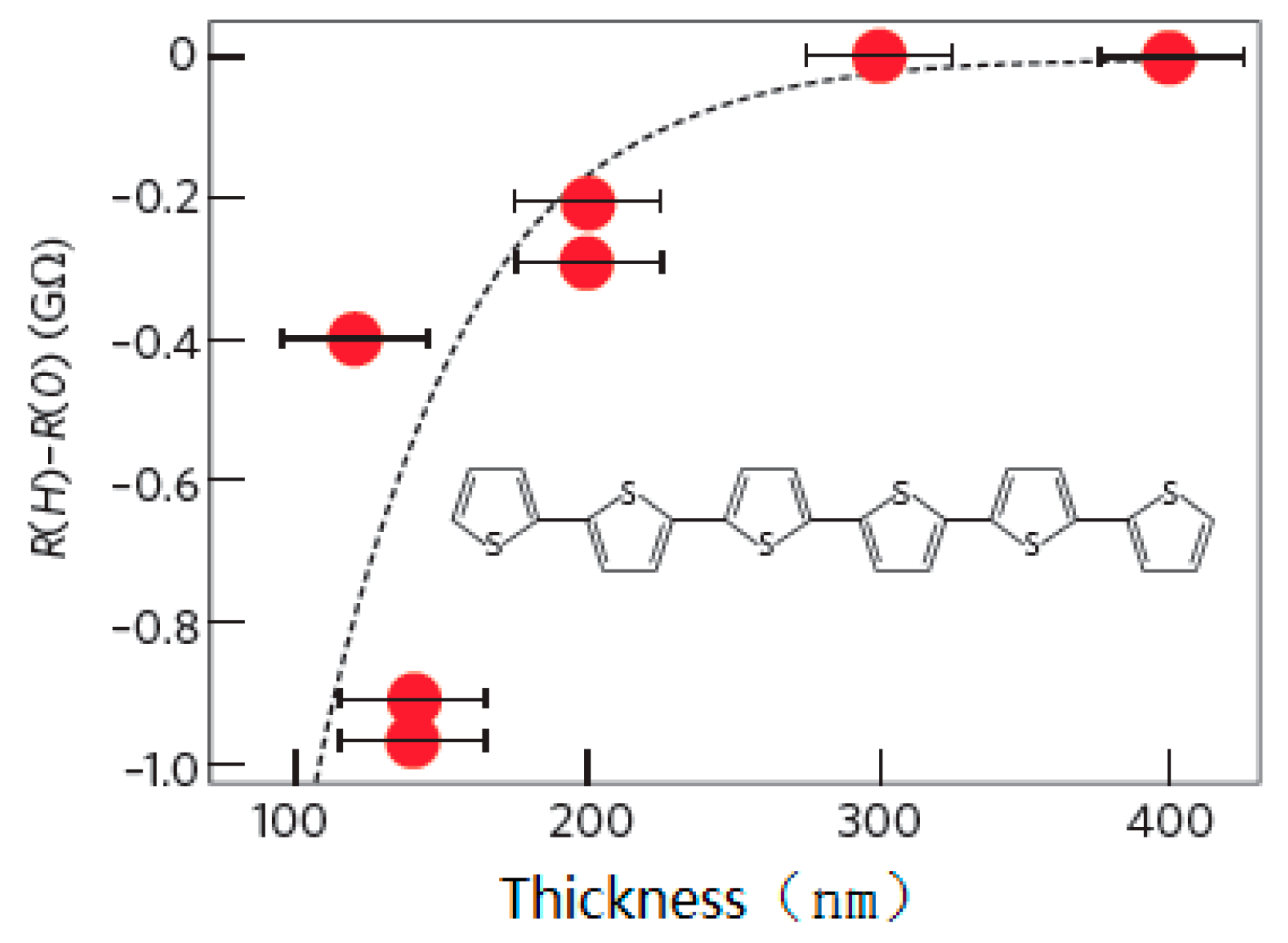
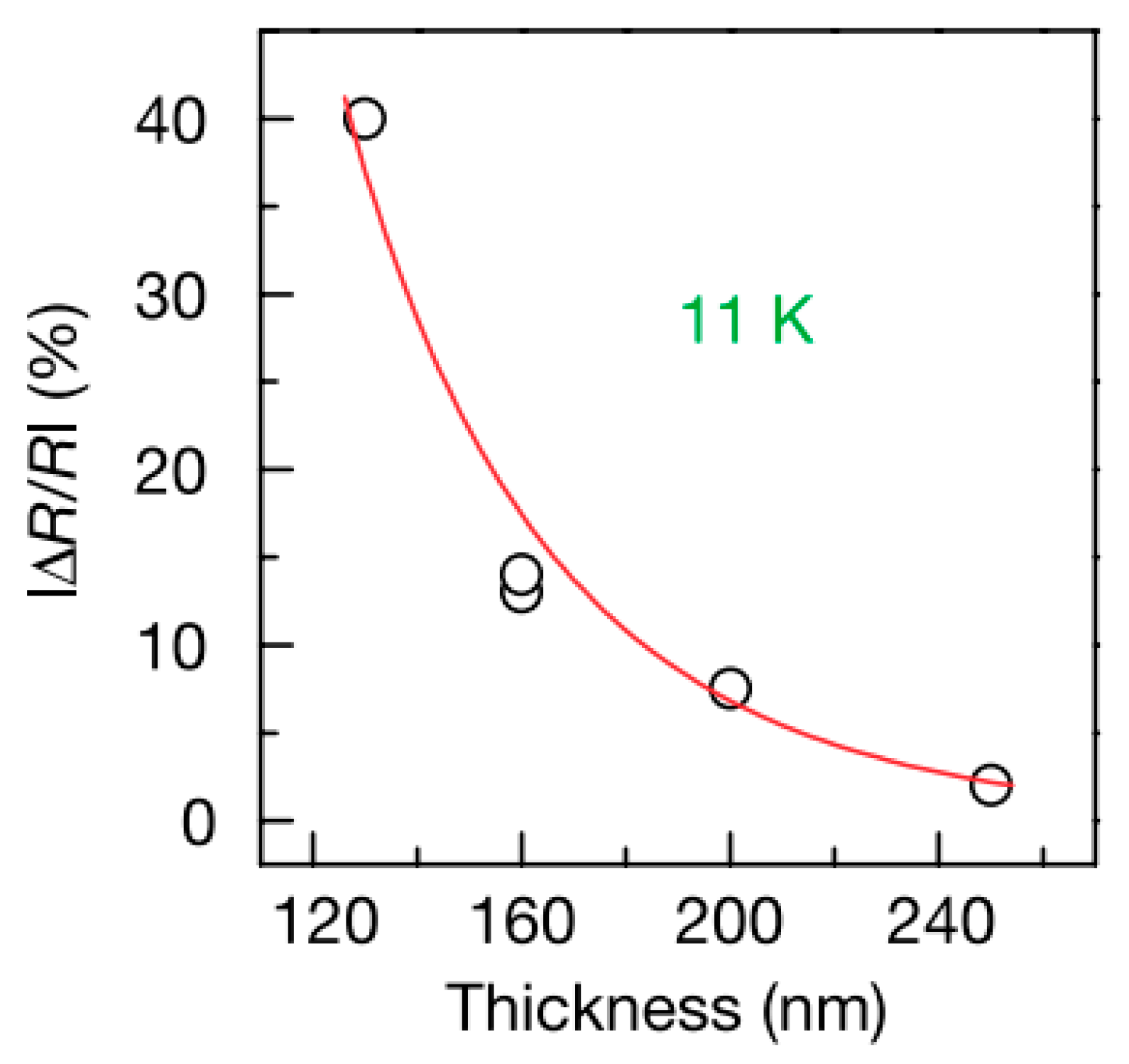
| Carrier | Charge (e) | Spin (ħ) | Degeneracy |
|---|---|---|---|
| Neutral soliton | 0 | 1/2 | Degenerate |
| Charged soliton | ±1 | 0 | Degenerate |
| Polaron | ±1 | 1/2 | Degenerate, Non-degenerate |
| Bipolaron | ±2 | 0 | Non-degenerate |
| Singlet exciton | 0 | 0 | Non-degenerate |
| Triplet exciton | 0 | 1 | Non-degenerate |
| Biexciton | 0 | 0 | Non-degenerate |
| Trion | ±1 | 1/2 | Non-degenerate |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Q.; Xie, S. Spin Injection and Transport in Organic Materials. Micromachines 2019, 10, 596. https://doi.org/10.3390/mi10090596
Tian Q, Xie S. Spin Injection and Transport in Organic Materials. Micromachines. 2019; 10(9):596. https://doi.org/10.3390/mi10090596
Chicago/Turabian StyleTian, Qipeng, and Shijie Xie. 2019. "Spin Injection and Transport in Organic Materials" Micromachines 10, no. 9: 596. https://doi.org/10.3390/mi10090596
APA StyleTian, Q., & Xie, S. (2019). Spin Injection and Transport in Organic Materials. Micromachines, 10(9), 596. https://doi.org/10.3390/mi10090596




