Analytical Investigation of the Micro Groove Surface Topography by Micro-Milling
Abstract
:1. Introduction
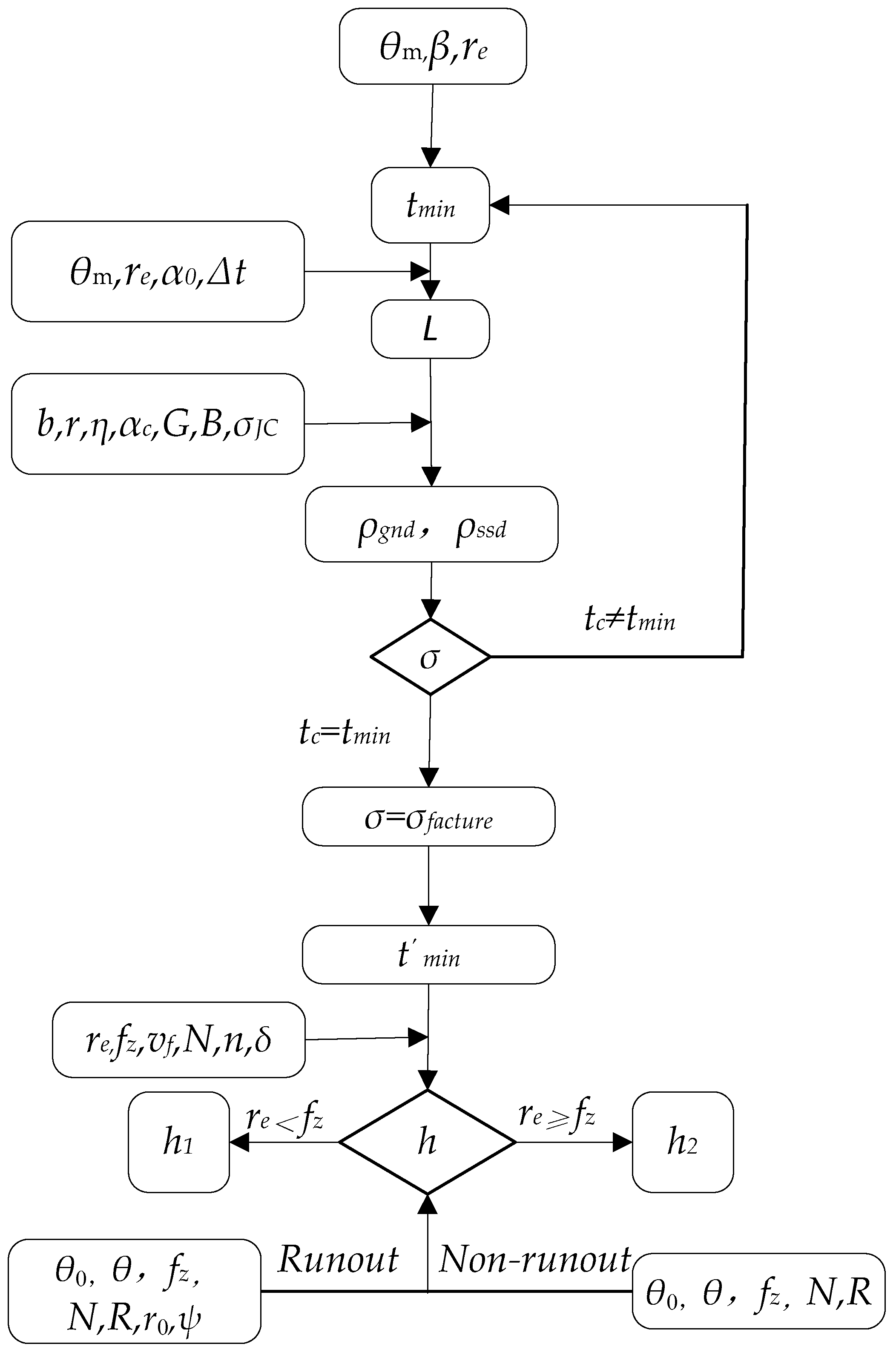
2. Theoretical Model Analysis
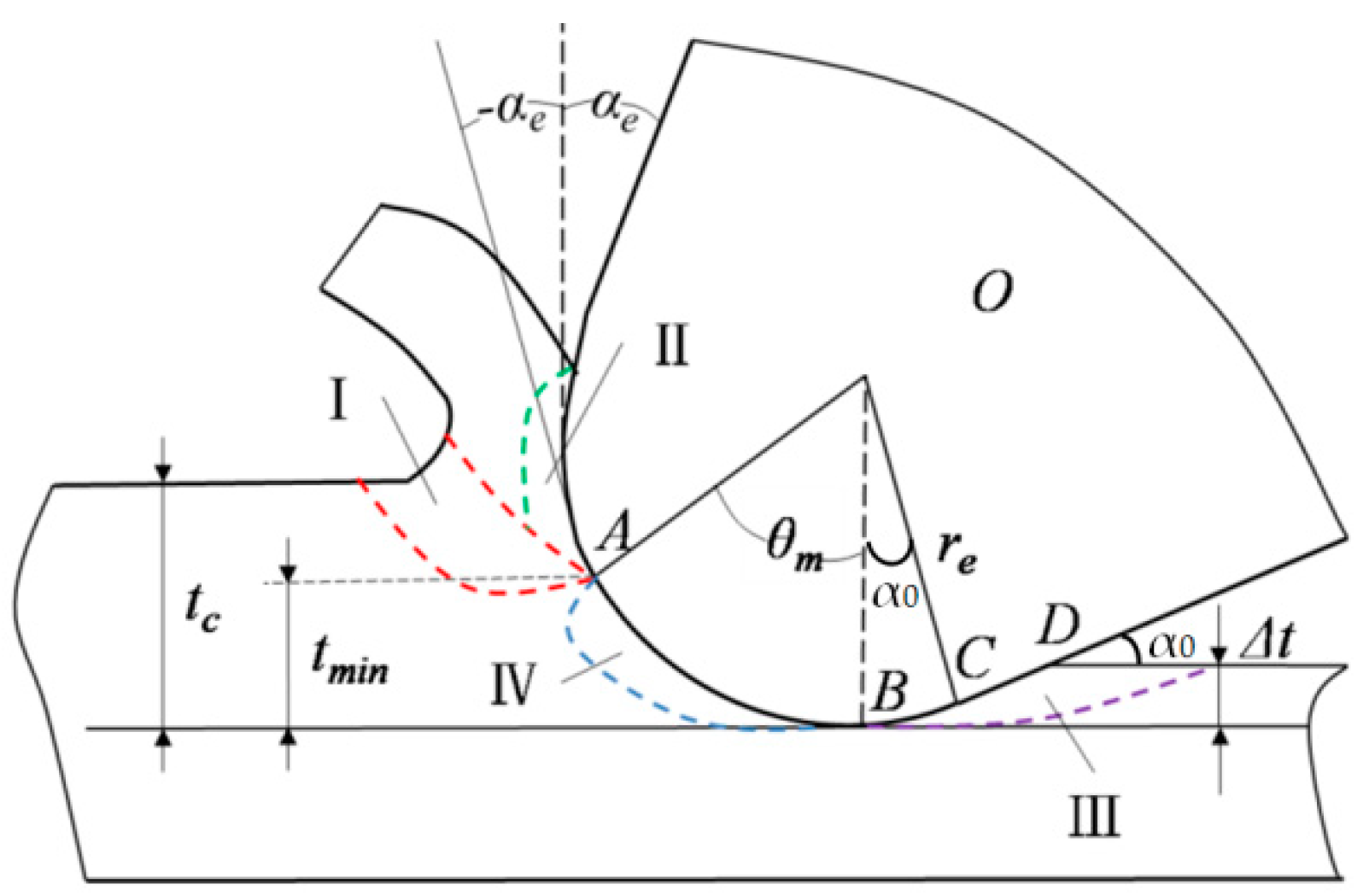
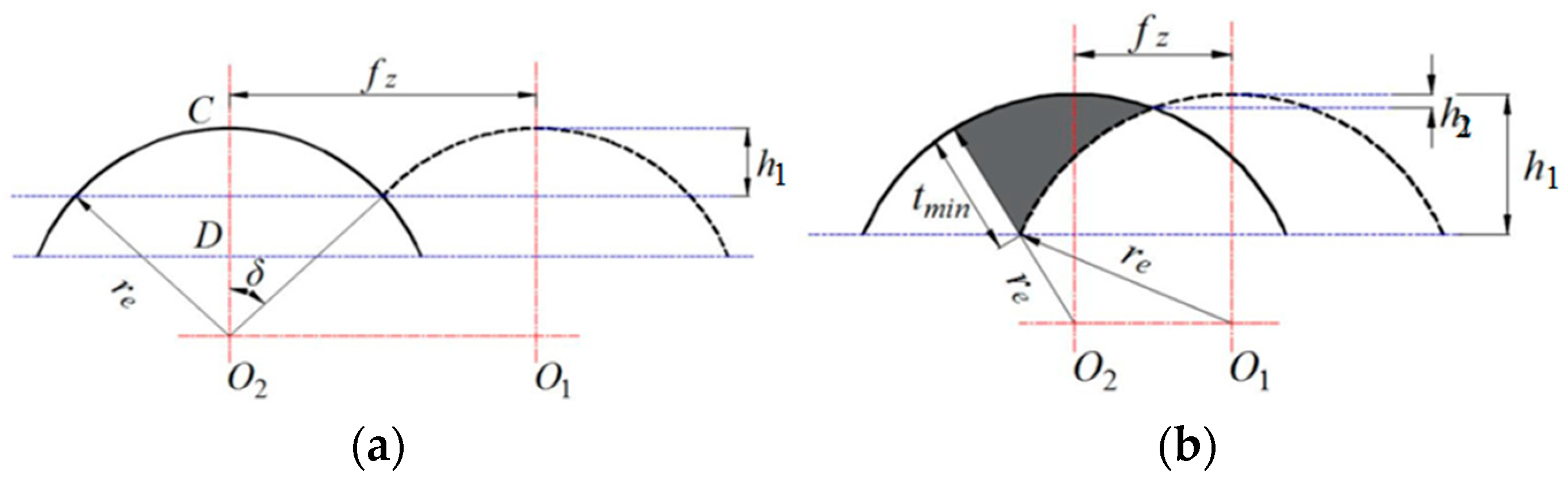
2.1. Micro Surface Formation Models
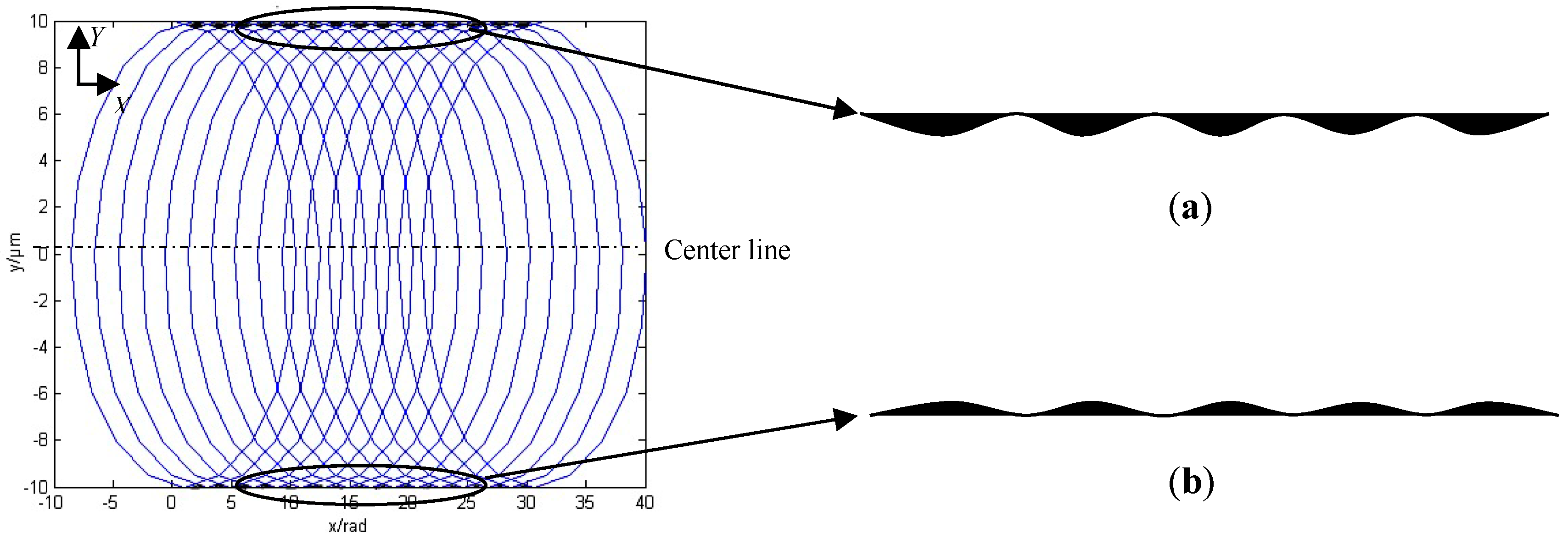
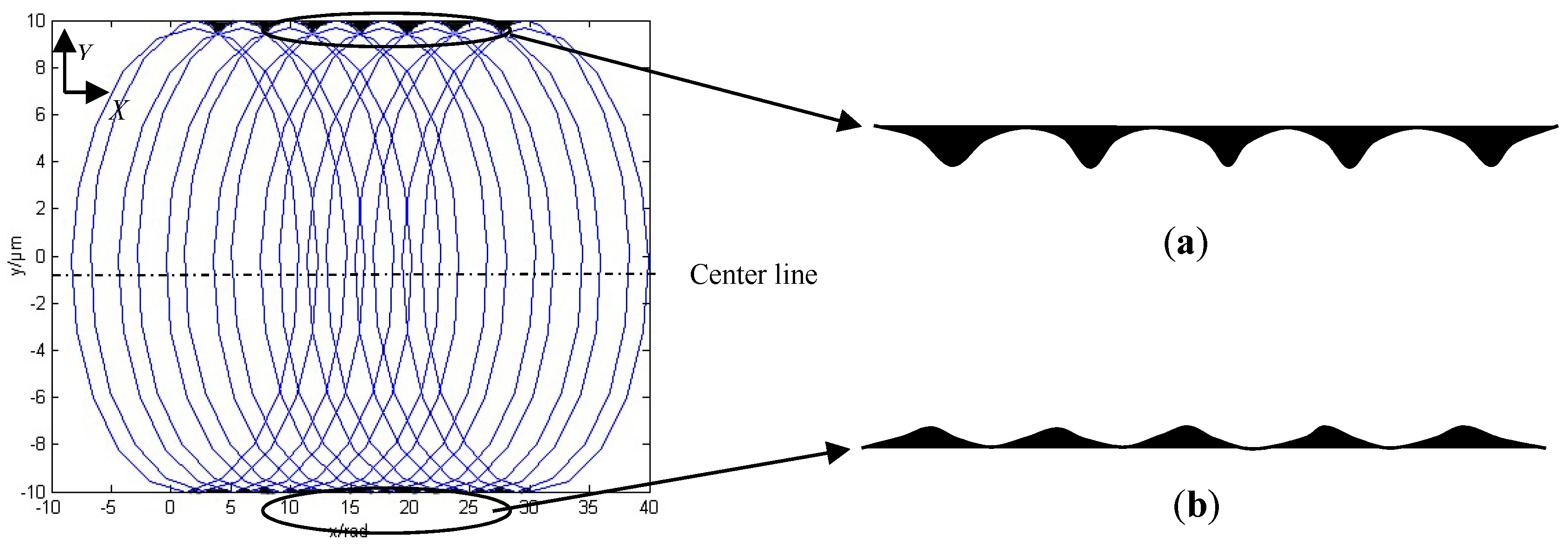
2.2. Micro Machined Surface Roughness
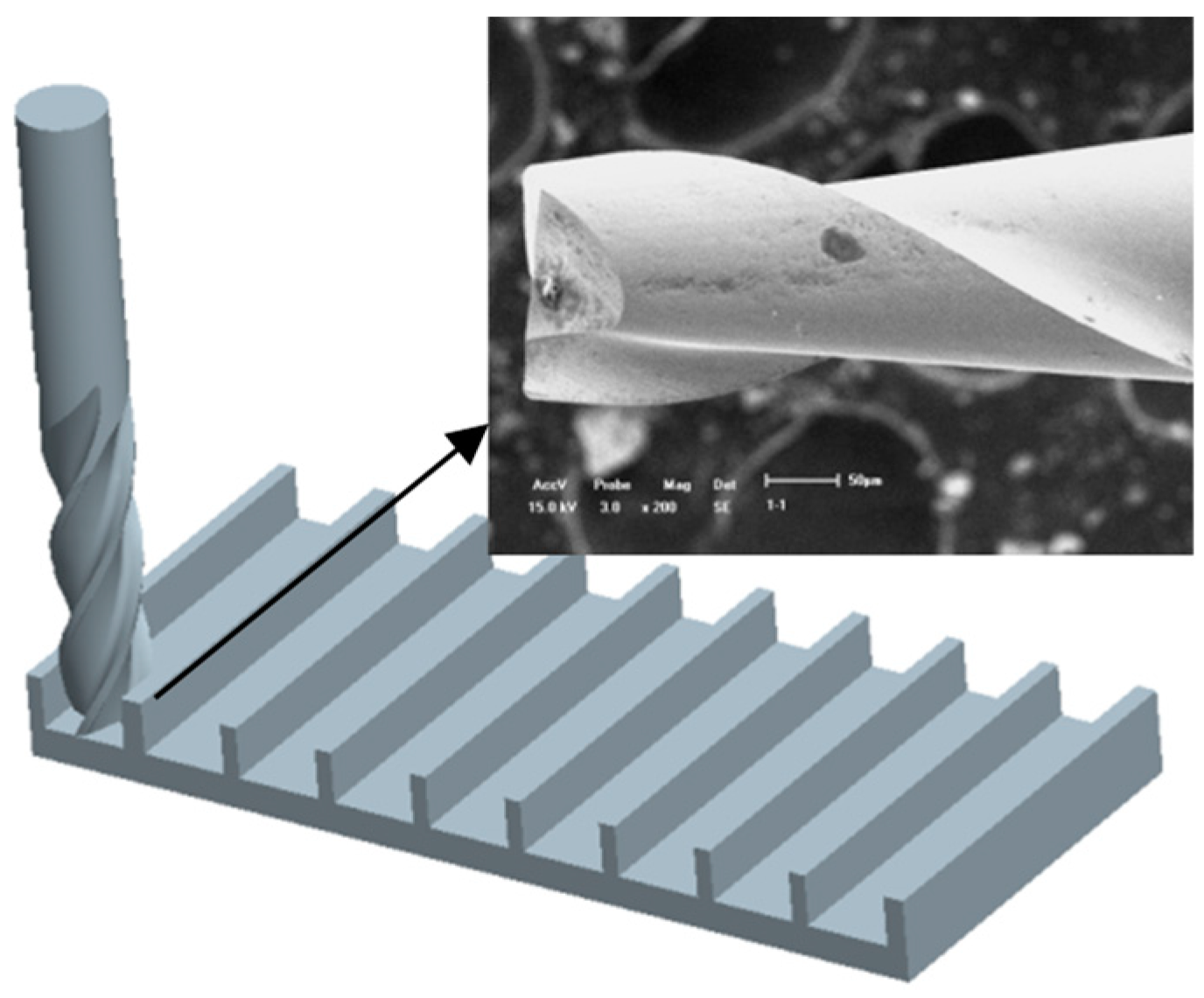
3. Experimental Details
3.1. Setup for Experiments
3.2. Materials Behaviors
3.3. Approach Design
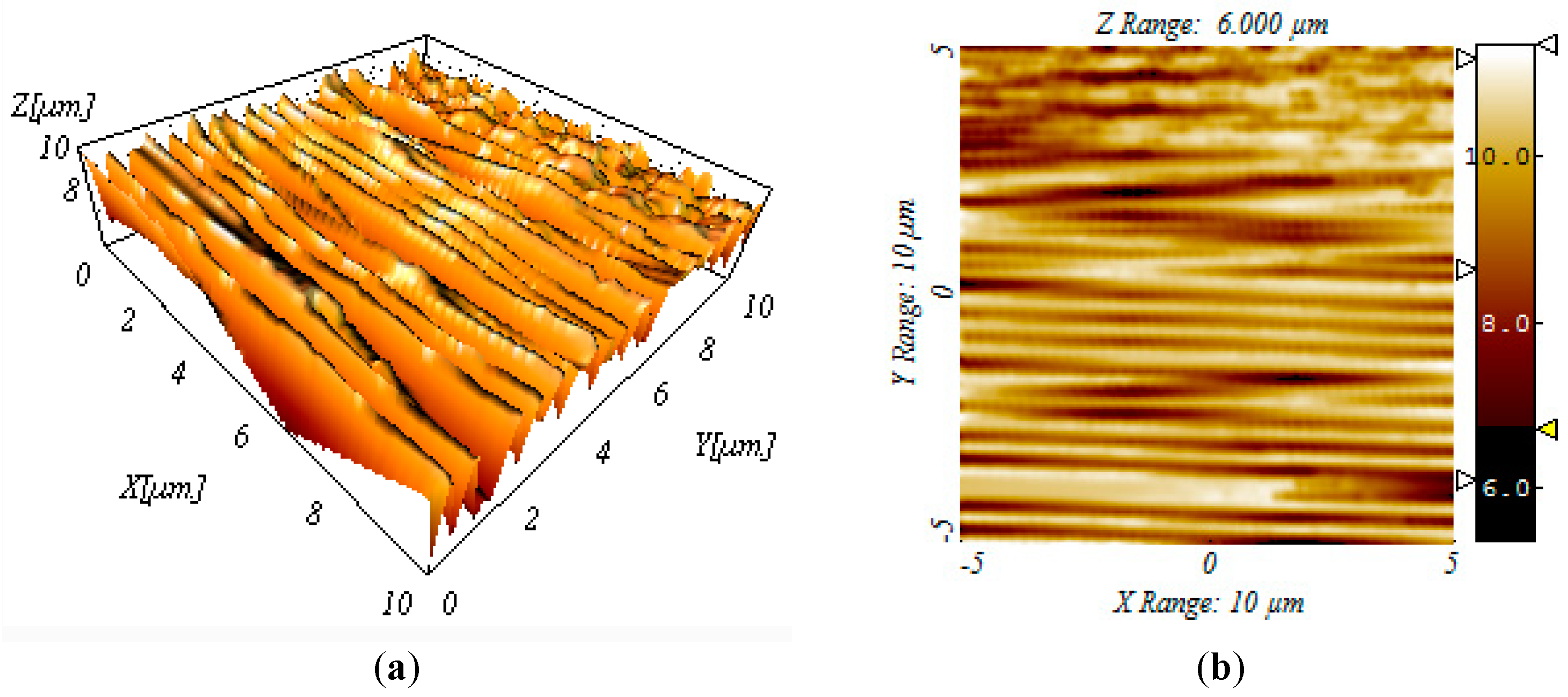
4. Experimental Results
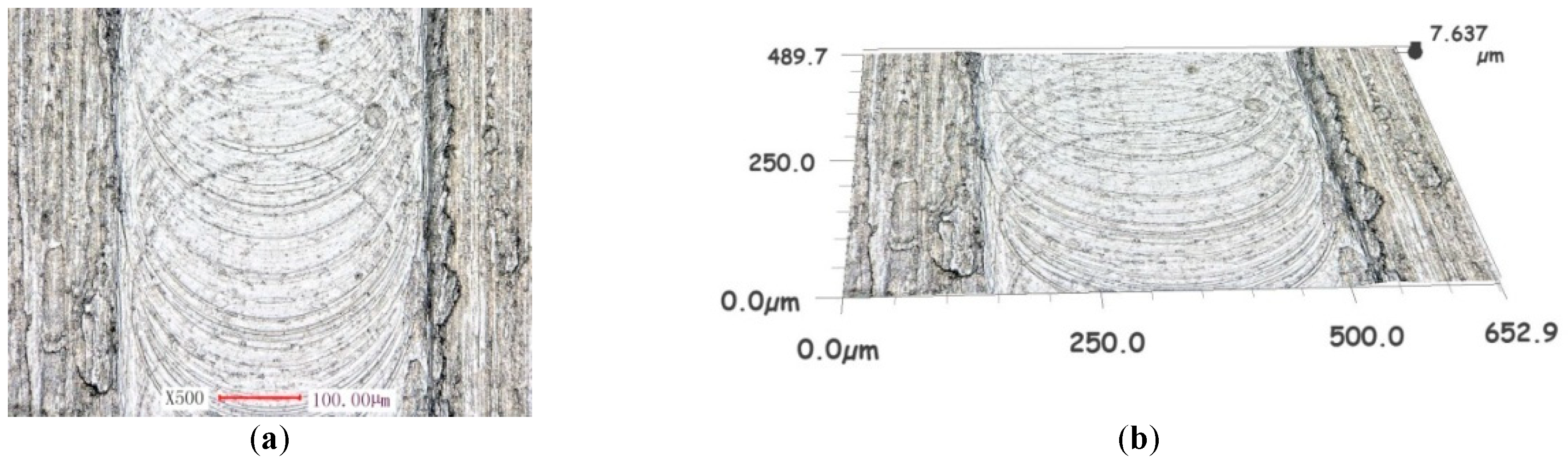
5. Discussion and Analysis
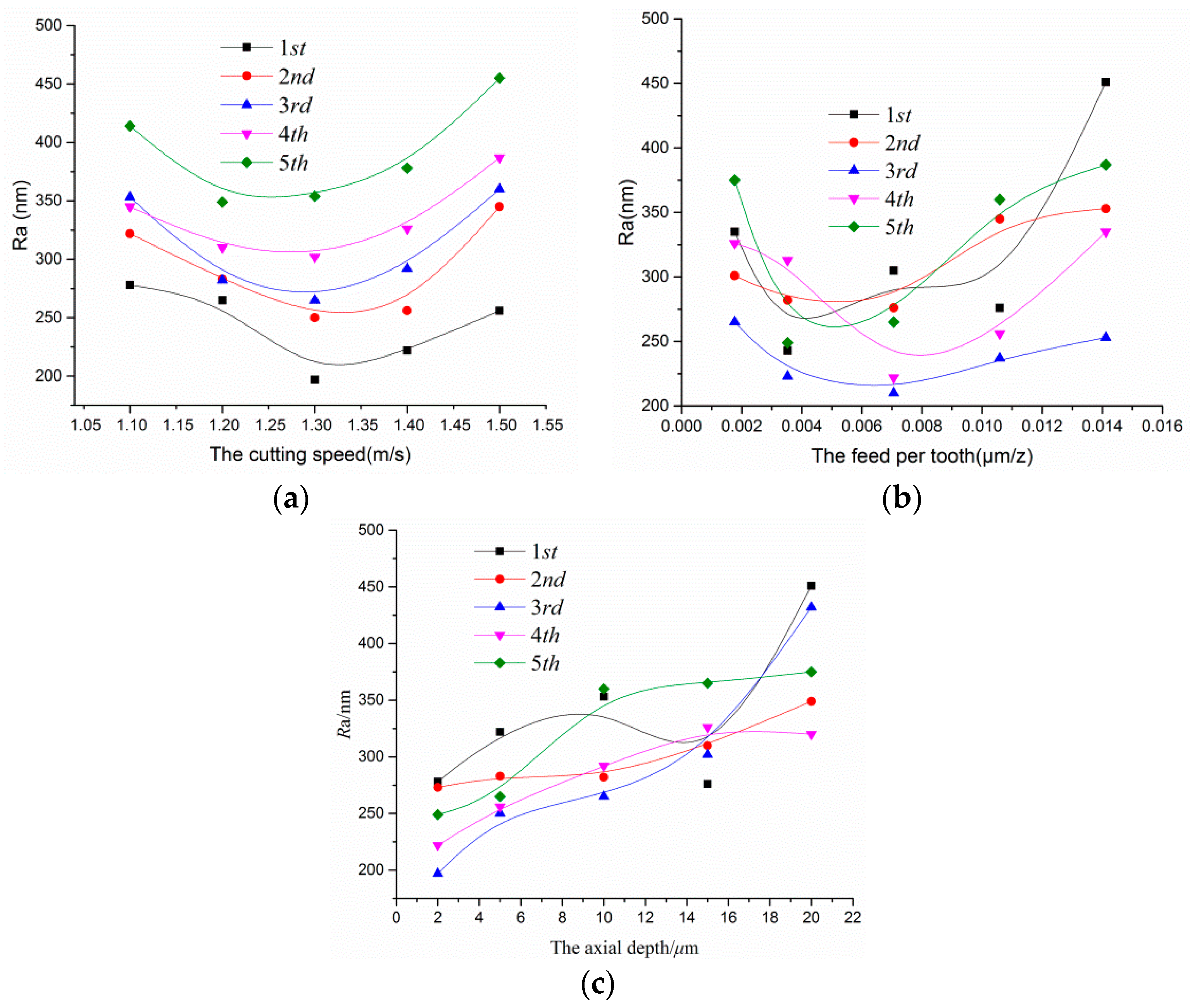
5.1. The Cutting Speed for the Surface Roughness
5.2. The Feed Per Tooth for the Surface Roughness
5.3. The Axial Cutting Depth for the Surface Roughness
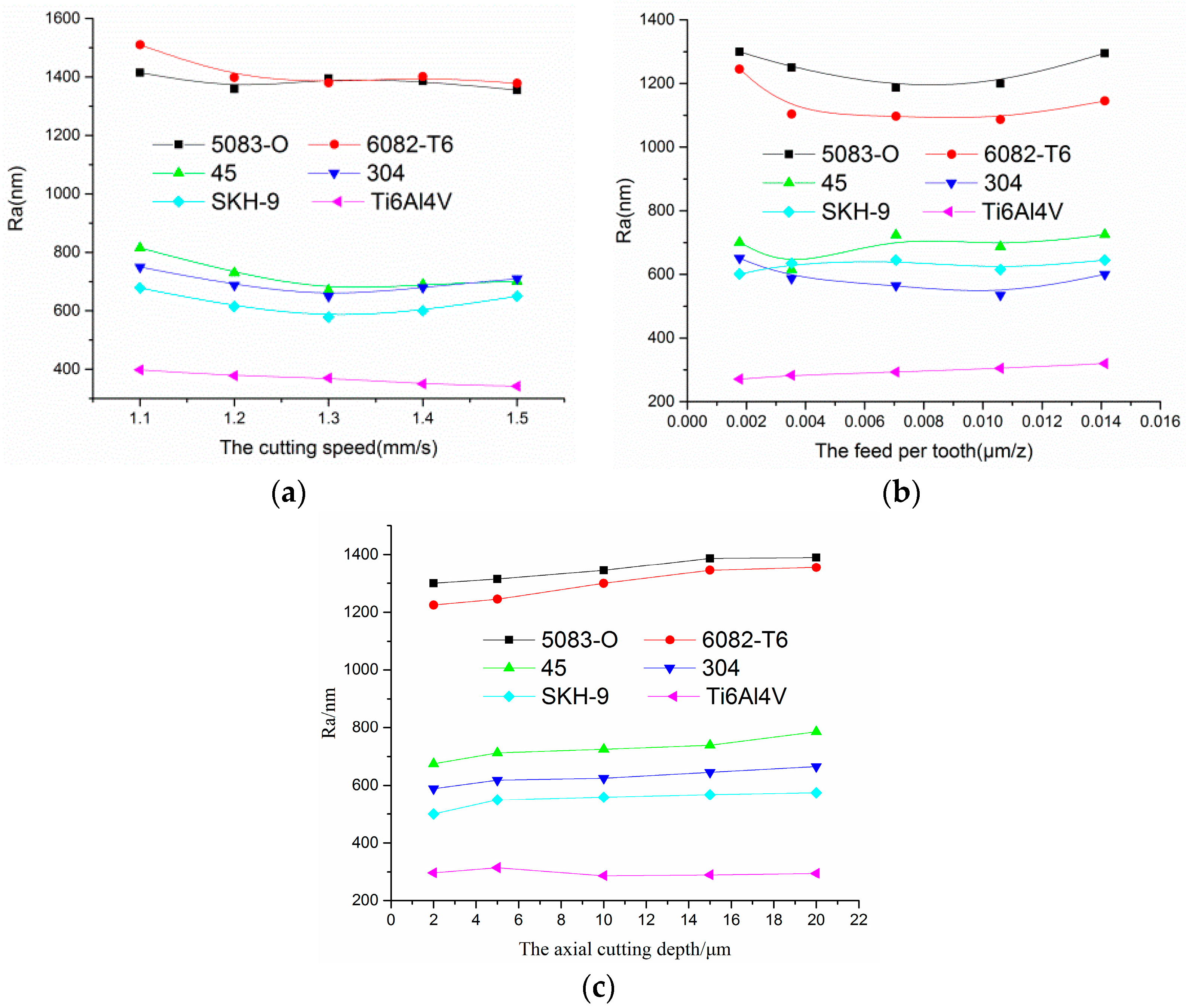
5.4. The Structural Material for the Surface Roughness
5.5. The Run Out for the Surface Roughness
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Takacs, M.; Vero, B.; Meszaros, I. Micro milling of metallic materials. J. Mater. Process. Technol. 2003, 138, 152–155. [Google Scholar] [CrossRef]
- Lai, X.; Li, H.; Li, C.; Lin, Z.; Ni, J. Modelling and analysis of micro scale milling considering size effect, micro cutter edge radius and minimum chip thickness. Int. J. Mach. Tools Manuf. 2008, 48, 1–14. [Google Scholar] [CrossRef]
- Shi, W.T. Micro Cutting Technology; China Machine Press: Beijing, China, 2011. [Google Scholar]
- Michael, P.V.; Richard, E.D.; Shiv, G.K. On the modeling and nalysis of machining performance in micro-endmilling. Part I: Surface generation. ASME J. Manuf. Sci. Eng. 2004, 126, 685–694. [Google Scholar]
- Yao, Y.; Zhu, H.T.; Huang, C.Z.; Wang, J.; Zhang, P.; Yao, P. Investigation on chip formation and surface integrity in micro end milling of maraging steel. Int. J. Adv. Manuf. Technol. 2019, 102, 1973–1984. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhou, M.; Dong, S. Effect of diamond tool sharpness on minimum cutting thickness and cutting surface integrity in ultraprecision machining. J. Mater. Process. Technol. 1996, 62, 327–330. [Google Scholar] [CrossRef]
- Liu, X.; Devor, R.E.; Kapoor, S.G. An Analytical model for the prediction of minimum chip thickness in micromachining. ASME J. Manuf. Sci. Eng. 2006, 128, 474–481. [Google Scholar] [CrossRef]
- Weule, H.H.; Tritschler, H. Micro-cutting of steel to meet new reuirements in miniaturization. CIRP Ann. Manuf. Technol. 2001, 50, 61–64. [Google Scholar] [CrossRef]
- Wu, J.H.; Liu, Z.Q. Modeling of flow stress in orthogonal micro-cutting process based on strain gradient plasticity theory. Int. J. Adv. Manuf. Technol. 2010, 46, 143–149. [Google Scholar] [CrossRef]
- Sun, Z.; To, S.; Zhang, S.; Zhang, G. Theoretical and experimental investigation into non-uniformity of surface generation in micro-milling. Int. J. Mech. Sci. 2018, 140, 313–324. [Google Scholar] [CrossRef]
- Sun, Z.W.; To, S. Effect of Machining Parameters and Tool Wear on Surface Uniformity in Micro-Milling. Micromachines 2018, 9, 268. [Google Scholar] [CrossRef]
- Jin, X.; Altintas, Y. Slip-line field model of micro-cutting process with round tool edge effect. J. Mater. Process. Technol. 2011, 211, 339–355. [Google Scholar] [CrossRef]
- Dornfeld, D.; Min, S.; Takeuchi, Y. Recent advances in mechanical micro-machining. CIRP Ann. Manuf. Technol. 2006, 55, 745–768. [Google Scholar] [CrossRef]
- Wang, W.; Kweon, S.H.; Yang, S.H. A study on roughness of the micro-end-milled surface produced by a miniatured machine tool. J. Mater. Process. Technol. 2005, 162, 702–708. [Google Scholar] [CrossRef]
- He, N.; Cao, Z.Y.; Li, L. Experimental study of the surface roughness in micro-milling. Mech. Sci. Tech. Aerosp. Eng. 2011, 30, 785–788. [Google Scholar]
- Gong, Y.D.; Zhang, J.F.; Zhang, Y.Z.; Liu, Y.M. Experimental research on surface quality in the process of high-speed and micro-scale milling. J. Mech. Eng. 2013, 49, 190–198. [Google Scholar] [CrossRef]
- Duan, C.Z.; Hao, Q.L. Surface roughness prediction of end milling process based on IPSO-LSSVM. J. Adv. Mech. Des. Syst. Manuf. 2014, 8, 1–12. [Google Scholar] [CrossRef]
- Duan, C.Z.; Hao, Q.L. Surface roughness prediction in high speed milling of 45 Steel. J. Harbin Eng. Univ. 2015, 36, 1229–1233. [Google Scholar]
- Liu, T.; Xu, Z.W.; Cao, K.X.; Wu, W. Experimental research on cutting force characteristics and surface quality in micro-milling. Nano Tech. Precis. Eng. 2015, 13, 258–263. [Google Scholar]
- Shi, Z.Y.; Liu, Z.Q.; Li, Y.C.; Qiao, Y. Swept Mechanism of Micro-Milling Tool Geometry Effect on Machined Oxygen Free High Conductivity Copper (OFHC) Surface Roughness. Materials 2017, 10, 120. [Google Scholar] [CrossRef]
- Wang, H.; To, S.; Chan, C.; Cheung, C.; Lee, W.B. A theoretical and experimental investigation of the tool-tip vibration and its influence upon surface generation in single-point diamond turning. Int. J. Mach. Tools Manuf. 2010, 50, 241–252. [Google Scholar] [CrossRef]
- Biondani, F.; Bissacco, G. Effect of cutting edge micro geometry on surface generation in ball end milling. CIRP Ann. 2019, 68, 571–574. [Google Scholar] [CrossRef]
- Lu, X.H.; Hu, X.C.; Jia, Z.Y.; Liu, M.Y.; Gao, S.; Qu, C.L.; Liang, S.Y. Model for the prediction of 3D surface topography and surface roughness in micro-milling Inconel 718. Int J. Adv Manuf. Technol. 2018, 94, 2043–2056. [Google Scholar] [CrossRef]
- Yuan, Y.J.; Jing, X.B.; Ehmann, K.F.; Zhang, D.W. Surface roughness modeling in micro end-milling. Int. J. Adv. Manuf. Technol. 2018, 95, 1655–1664. [Google Scholar] [CrossRef]
- Malekian, M.; Mostofa, M.; Park, S.; Jun, M. Modeling of minimum uncut chip thickness in micro machining of aluminum. J. Mater. Process. Technol. 2012, 212, 553–559. [Google Scholar] [CrossRef]
- Lu, X.L.; Jia, Z.Y.; Wang, X.X.; Li, G.J.; Ren, Z.J. Three-dimentioanl dynamic cutting forces prediction model during micro-milling nickel-based superalloy. Int. J. Adv. Manuf. Technol. 2015, 81, 2067–2086. [Google Scholar] [CrossRef]
- Johmson, G.R.; Cook, W.H. A constitutive model and data for metals subjected to large strain, high strain rates and high temperatures. In Proceedings of the 7th International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983; pp. 541–547. [Google Scholar]
- Yang, Z.C.; Zhang, D.H.; Yao, C.F.; Ren, J.X.; Du, S.G. Effect of high speed milling parameters on surface integrity of TC4 titanium alloy. J. Northwestern Polytech. Univ. 2009, 27, 538–543. [Google Scholar]
- Joshi, S.S. An explanation for the size-effect in machining using strain gradient plasticity. J. Manuf. Sci. Eng. 2004, 126, 679–685. [Google Scholar] [CrossRef]
- Subbiah, S. Some investigations of scaling effects in microcutting. Ph.D. Thesis, Georgia Institute of technology, Atlanta, GA, USA, 2006. [Google Scholar]
- Zhang, X.X.; Yu, H.D.; Xu, J.K.; Yang, S. The research on milling force and surface roughness of high speed micro-milling aluminum alloy. Modul. Mach. Tool Autom. Manuf. Tech. 2015, 7, 46–49. [Google Scholar]
- Li, H.; Liu, K.; Li, X. A new method for determining the undeformed chip thickness in milling. J. Mater. Process. Technol. 2001, 113, 378–384. [Google Scholar] [CrossRef]
- Liu, S.X. Handbook of Practical Metal Materials, 2nd ed.; China Machine Press: Beijing, China, 2007. [Google Scholar]
- Thepsonthi, T.; Özel, T. An integrated toolpath and process parameter optimization for high performance micro-milling process of Ti-6Al-4V titanium alloy. Int. J. Adv. Manuf. Technol. 2014, 75, 57–75. [Google Scholar] [CrossRef]
- Wan, Y.L.; Zhang, X.R.; Yu, H.D.; Xu, J.K.; Zhang, L.X. An multi–index orthogonal test study of aluminum alloy surface roughness using high speed micro-milling process. J. China Mech. Eng. 2013, 24, 3278–3288. [Google Scholar]
- Kang, X.J. Research on milling force and surface quality of high speed milling of 45 steel. Master’s Thesis, Hunan University of Science and Technology, Xiangtan, China, 2012. [Google Scholar]
- Yang, S.; Xu, J.K.; Li, X.Z.; Yu, H.D.; Zhang, X.H.; Zhao, Z.L. Experimental study on process parameters of high-speed micro-milling Al2O3 engineering ceramics. Modul. Mach. Tool Autom. Manuf. Tech. 2014, 9, 123–126. [Google Scholar]
- Wu, J.H.; Shi, Z.Y. Minimum of thickness in orthogonal micro-cutting based on plasticity strain gradient theory. J. China Mech. Eng. 2009, 20, 2227–2247. [Google Scholar]



| Materials | ρ [kg/m3] × 10−3 | HB [N/m2] × 10−4 | σb [Pa] × 109 | δ5 [%] × 102 | E [Pa] × 1011 | K [W/m·k] × 10 |
|---|---|---|---|---|---|---|
| 5083-O | 2.70 | 0.852 | ≥0.270 | ≥0.12 | 0.720 | 8.876 |
| 6082-T6 | 2.70 | 1.05 | ≥0.205 | ≥0.14 | 0.725 | 8.878 |
| Ti6Al4V | 4.40 | 1.95 | 0.539 | ≥0.10 | 1.100 | 0.795 |
| 45 | 7.85 | 2.29 | ≤0.355 | ≥0.16 | 2.100 | 4.768 |
| 304 | 7.93 | ≤1.87 | ≥0.520 | ≥0.40 | 1.985 | 1.540 |
| SKH-9 | 8.61 | ≤2.62 | 3.430 | – | 2.180 | 1.675 |
| Factor | n [rpm] × 104 | fs [μm/s] | ap [μm] |
|---|---|---|---|
| 1 | 7.04 | 5 | 2 |
| 2 | 7.68 | 10 | 5 |
| 3 | 8.32 | 20 | 10 |
| 4 | 8.96 | 30 | 15 |
| 5 | 9.60 | 40 | 20 |
| n (rpm) | 70,400 | 76,800 | 83,200 | 89,600 | 96,000 |
| v (m/s) | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 |
| N | n/rpm | fs/μm/s | ap/μm | fz/10−3 μm/z | Ra/nm |
|---|---|---|---|---|---|
| 1 | 70,400 | 5 | 2 | 2.13 | 278 |
| 2 | 70,400 | 10 | 5 | 4.26 | 322 |
| 3 | 70,400 | 20 | 10 | 8.52 | 353 |
| 4 | 70,400 | 30 | 15 | 12.8 | 276 |
| 5 | 70,400 | 40 | 20 | 17.1 | 451 |
| 6 | 76,800 | 5 | 20 | 1.95 | 305 |
| 7 | 76,800 | 10 | 2 | 3.91 | 283 |
| 8 | 76,800 | 20 | 5 | 7.81 | 282 |
| 9 | 76,800 | 30 | 10 | 11.7 | 310 |
| 10 | 76,800 | 40 | 15 | 15.6 | 349 |
| 11 | 83,200 | 5 | 15 | 1.80 | 197 |
| 12 | 83,200 | 10 | 20 | 3.60 | 250 |
| 13 | 83,200 | 20 | 2 | 7.21 | 265 |
| 14 | 83,200 | 30 | 5 | 10.8 | 302 |
| 15 | 83,200 | 40 | 10 | 14.4 | 445 |
| 16 | 89,600 | 5 | 10 | 1.67 | 222 |
| 17 | 89,600 | 10 | 15 | 3.35 | 256 |
| 18 | 89,600 | 20 | 20 | 6.70 | 292 |
| 19 | 89,600 | 30 | 2 | 10.0 | 326 |
| 20 | 89,600 | 40 | 5 | 13.4 | 243 |
| 21 | 96,000 | 5 | 5 | 1.56 | 249 |
| 22 | 96,000 | 10 | 10 | 3.13 | 213 |
| 23 | 96,000 | 20 | 15 | 6.25 | 360 |
| 24 | 96,000 | 30 | 20 | 9.38 | 387 |
| 25 | 96,000 | 40 | 2 | 12.5 | 335 |
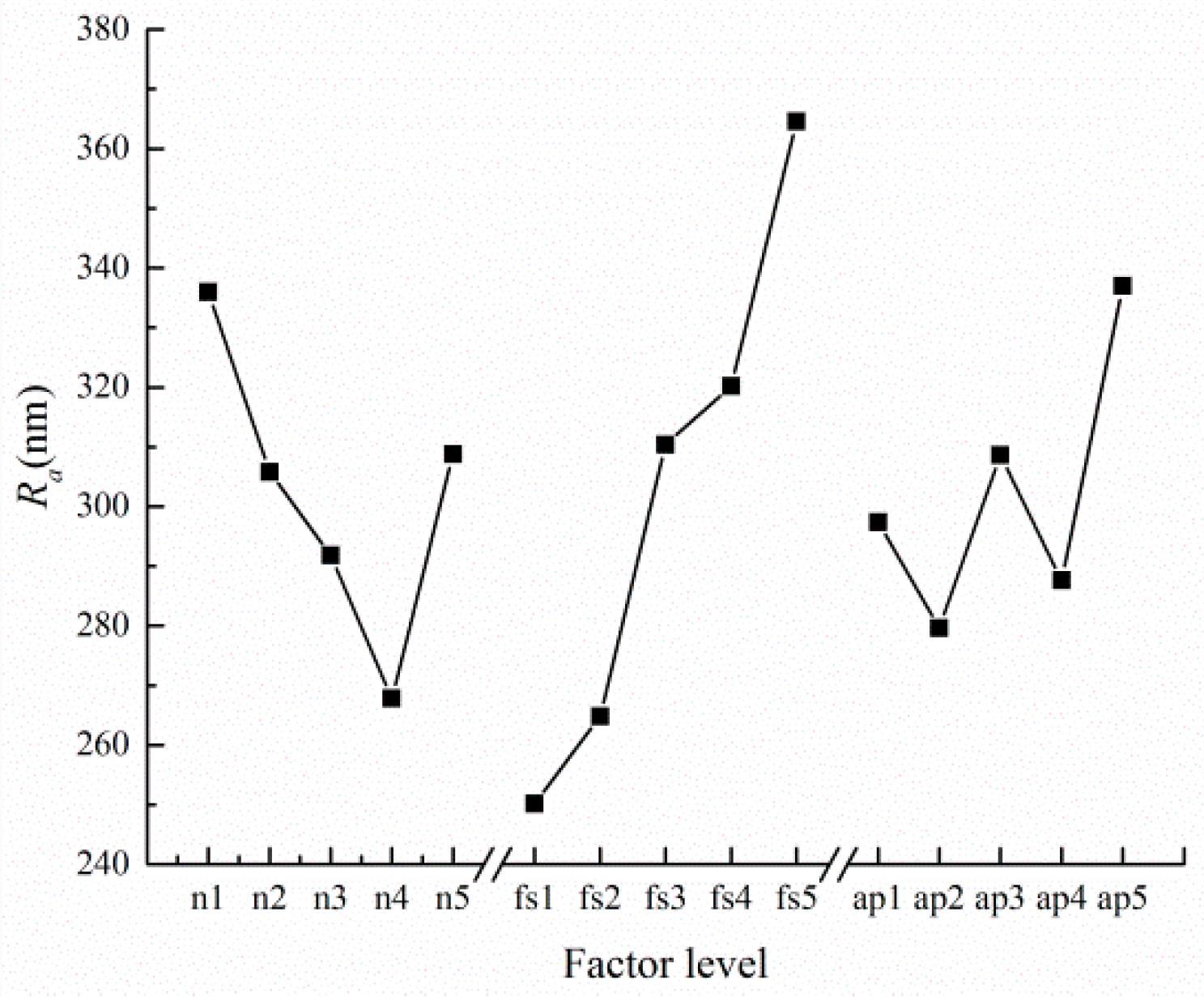
| K1 | 1680 | 1251 | 1487 | ||
| K2 | 1529 | 1324 | 1398 | ||
| K3 | 1459 | 1552 | 1543 | ||
| K4 | 1339 | 1601 | 1438 | ||
| K5 | 1544 | 1823 | 1685 | ||
| 336 | 250.2 | 297.4 | |||
| 305.8 | 264.8 | 279.6 | |||
| 291.8 | 310.4 | 308.6 | |||
| 267.8 | 320.2 | 287.6 | |||
| 308.8 | 364.6 | 337 | |||
| Rj | 68.2 | 114.4 | 57.4 | ||
| Sequence | fs > n > ap | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Feng, C.; Wang, H.; Gong, Y. Analytical Investigation of the Micro Groove Surface Topography by Micro-Milling. Micromachines 2019, 10, 582. https://doi.org/10.3390/mi10090582
Zhang J, Feng C, Wang H, Gong Y. Analytical Investigation of the Micro Groove Surface Topography by Micro-Milling. Micromachines. 2019; 10(9):582. https://doi.org/10.3390/mi10090582
Chicago/Turabian StyleZhang, Jinfeng, Chao Feng, Hao Wang, and Yadong Gong. 2019. "Analytical Investigation of the Micro Groove Surface Topography by Micro-Milling" Micromachines 10, no. 9: 582. https://doi.org/10.3390/mi10090582
APA StyleZhang, J., Feng, C., Wang, H., & Gong, Y. (2019). Analytical Investigation of the Micro Groove Surface Topography by Micro-Milling. Micromachines, 10(9), 582. https://doi.org/10.3390/mi10090582






