Design, Modeling, and Testing of a Novel XY Piezo-Actuated Compliant Micro-Positioning Stage
Abstract
1. Introduction
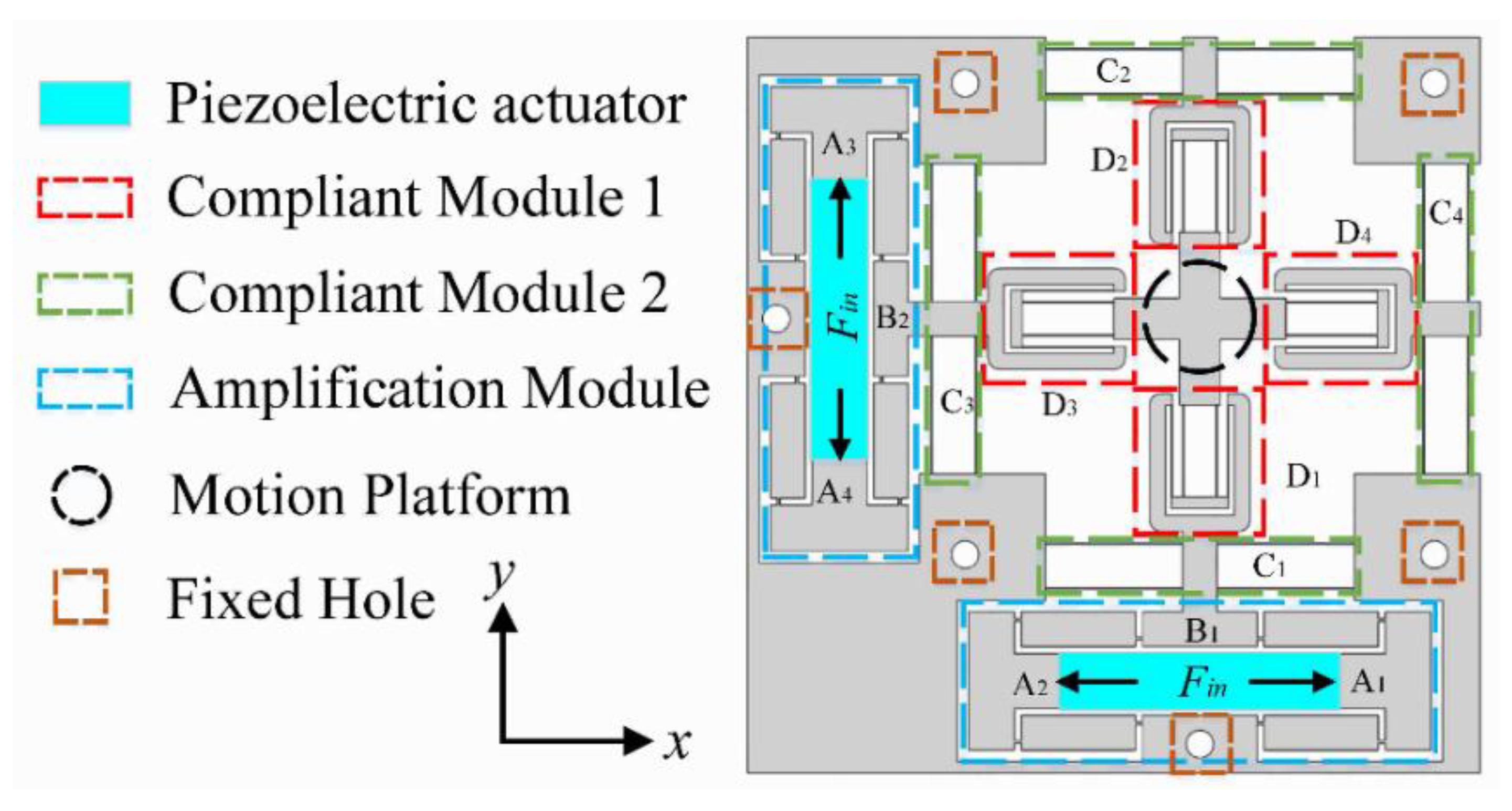
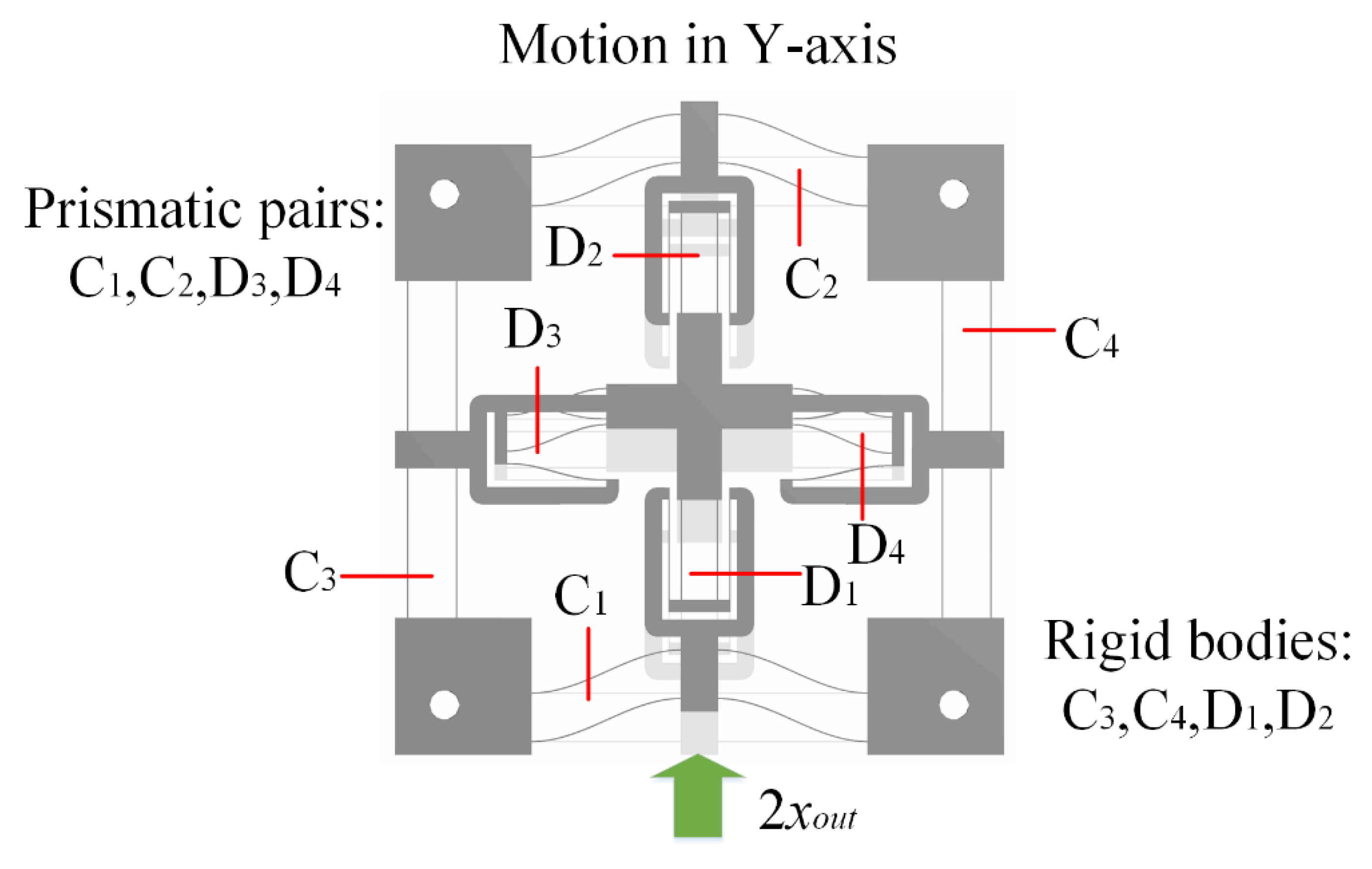
2. Mechanical Design and Working Principle of Compliant Positioning Stage
3. Mathematical Model of the Positioning Stage
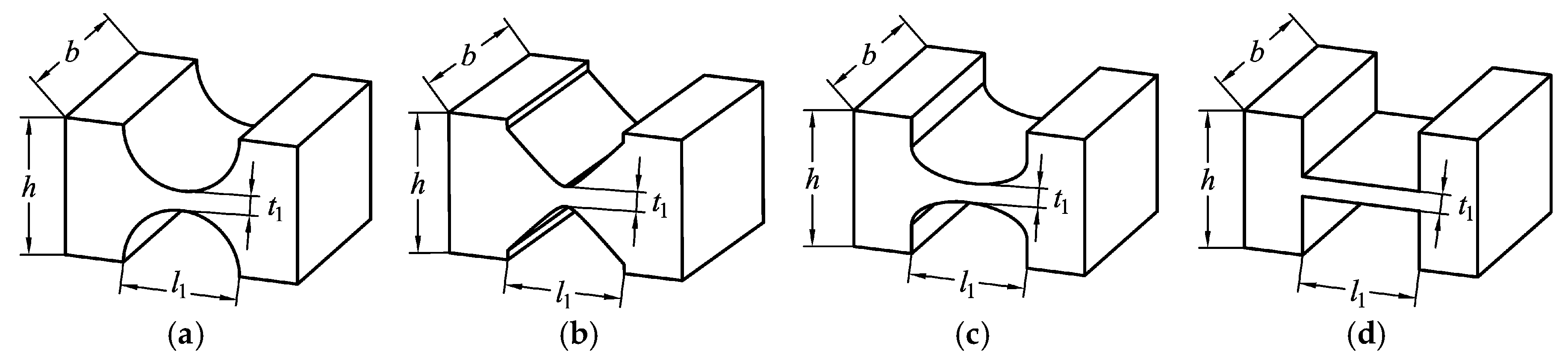
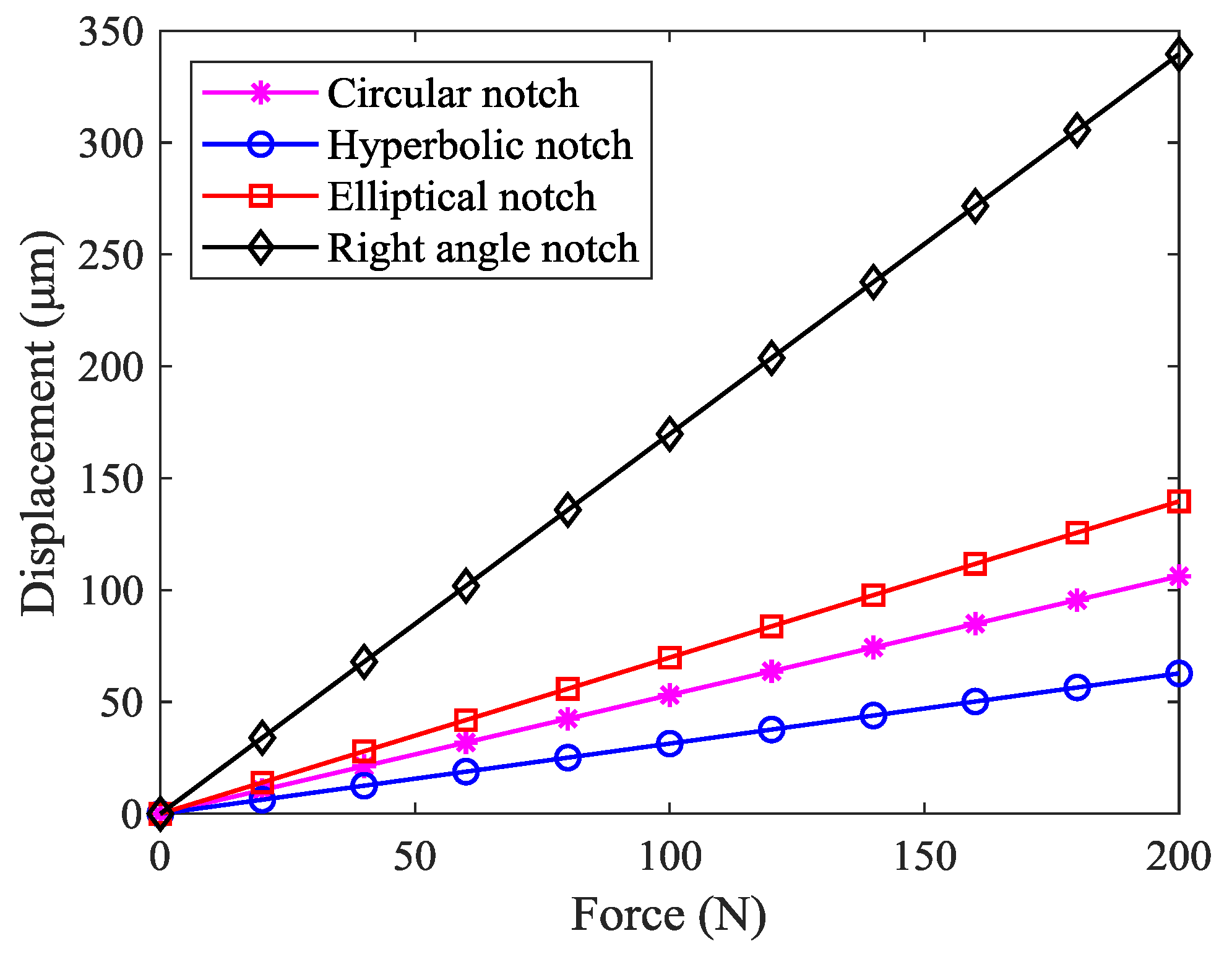
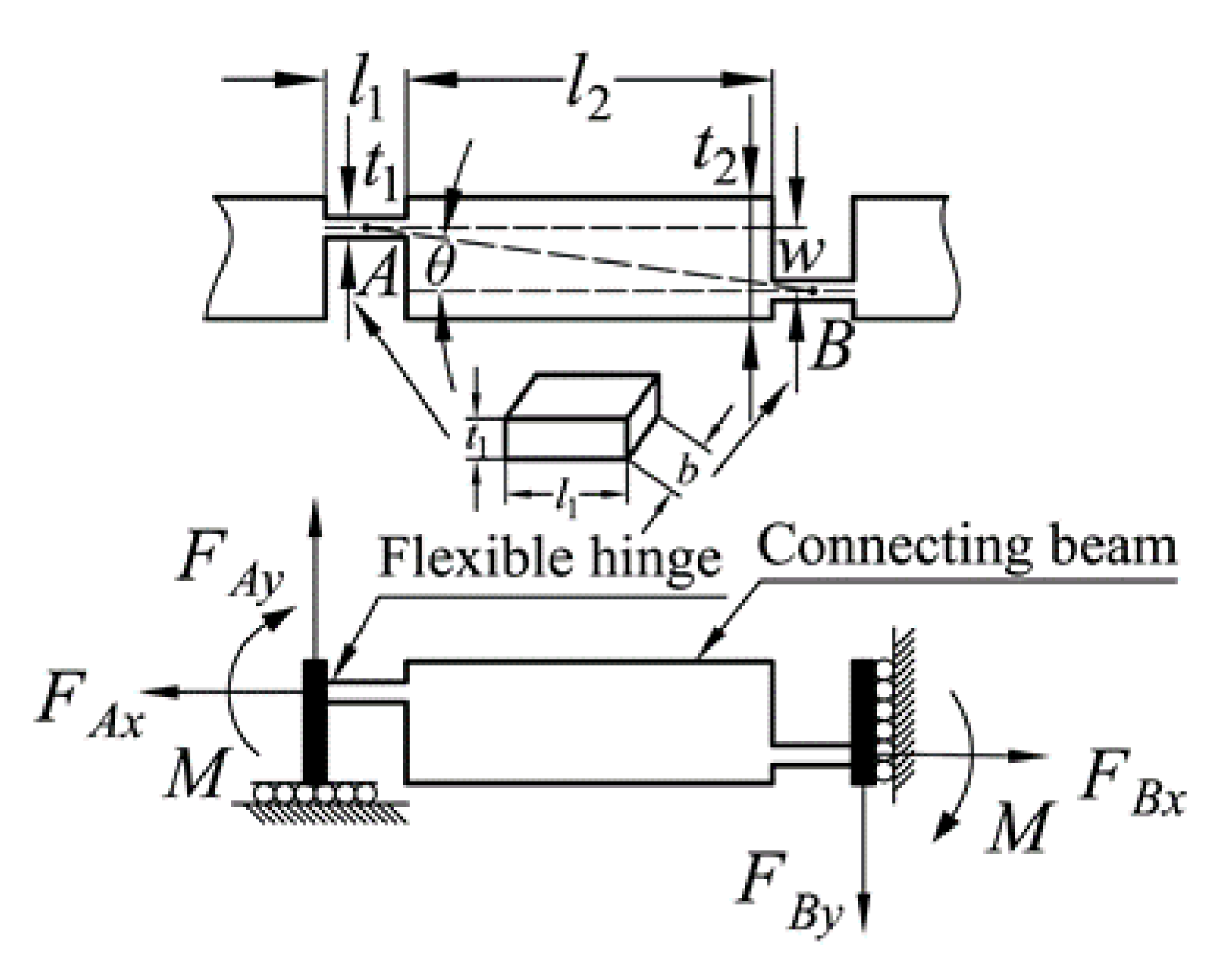
3.1. Stiffness Model of the Parallelogram Mechanism
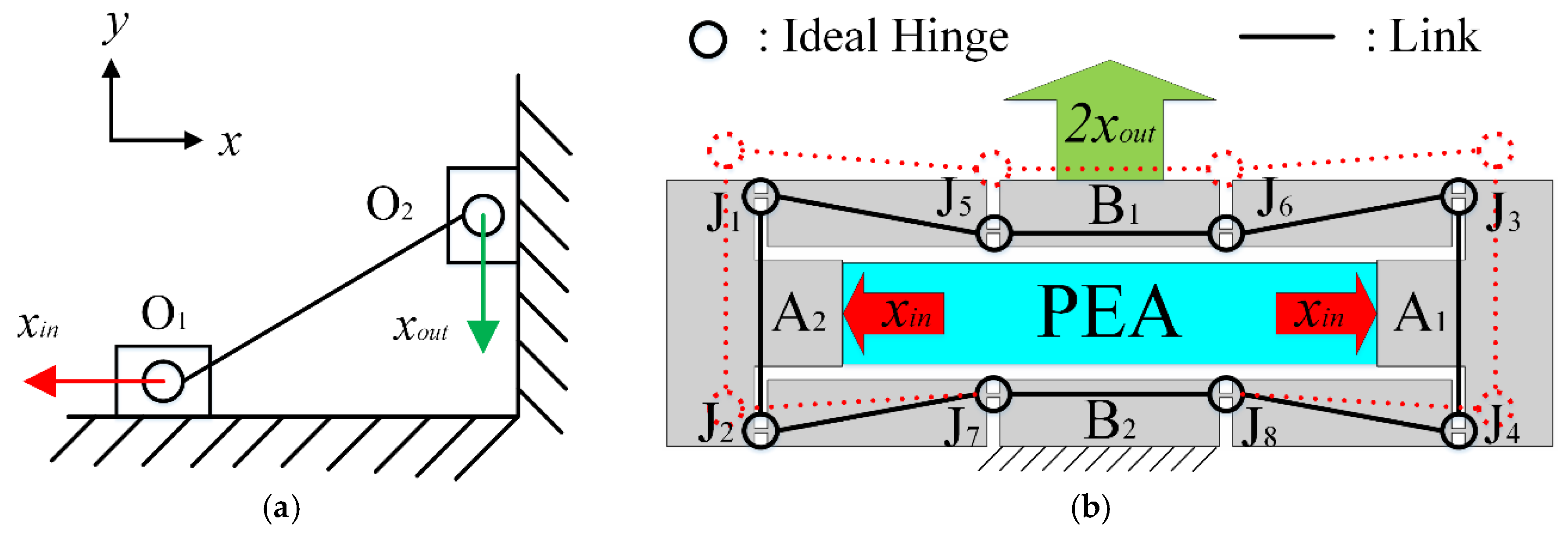
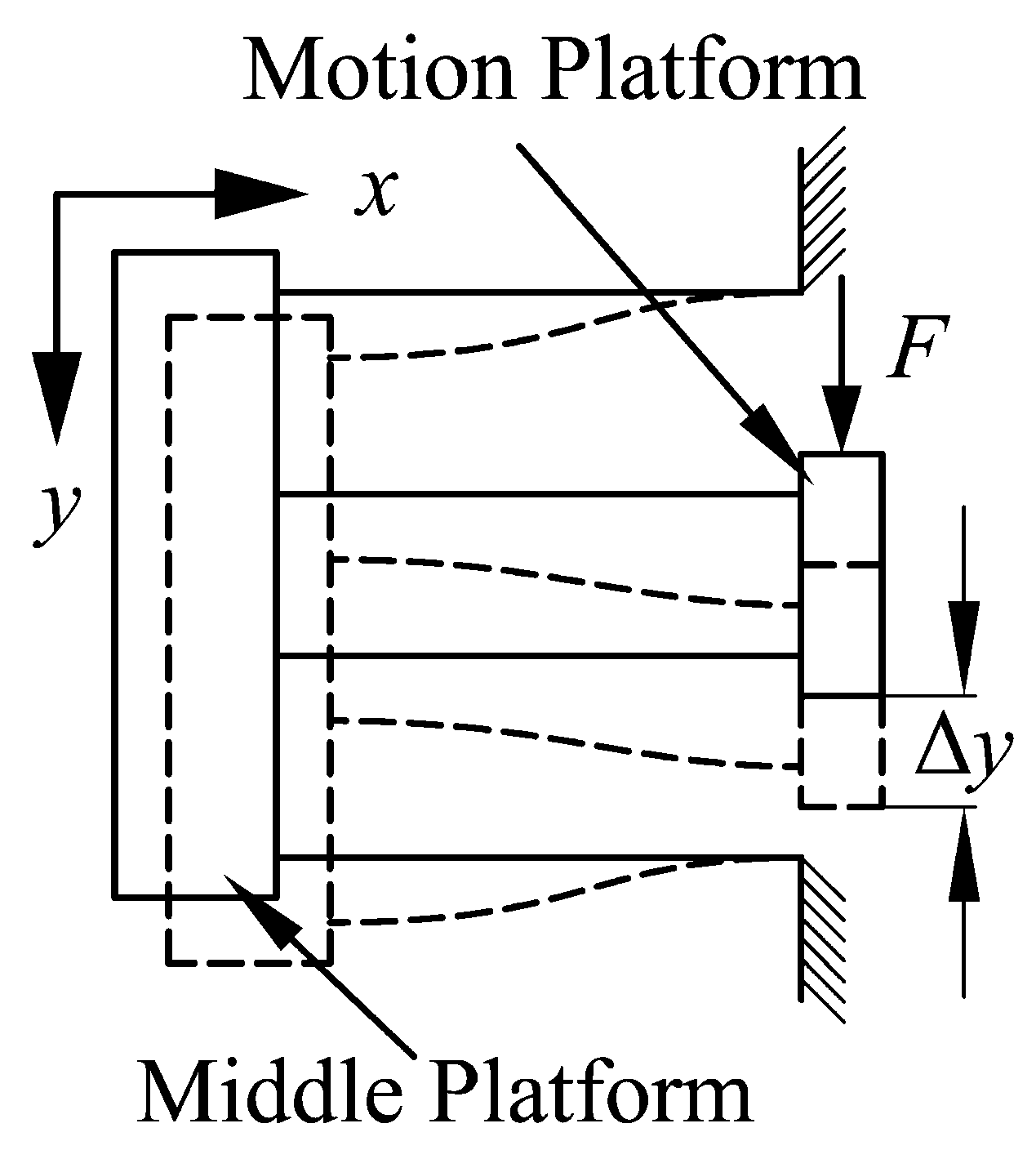
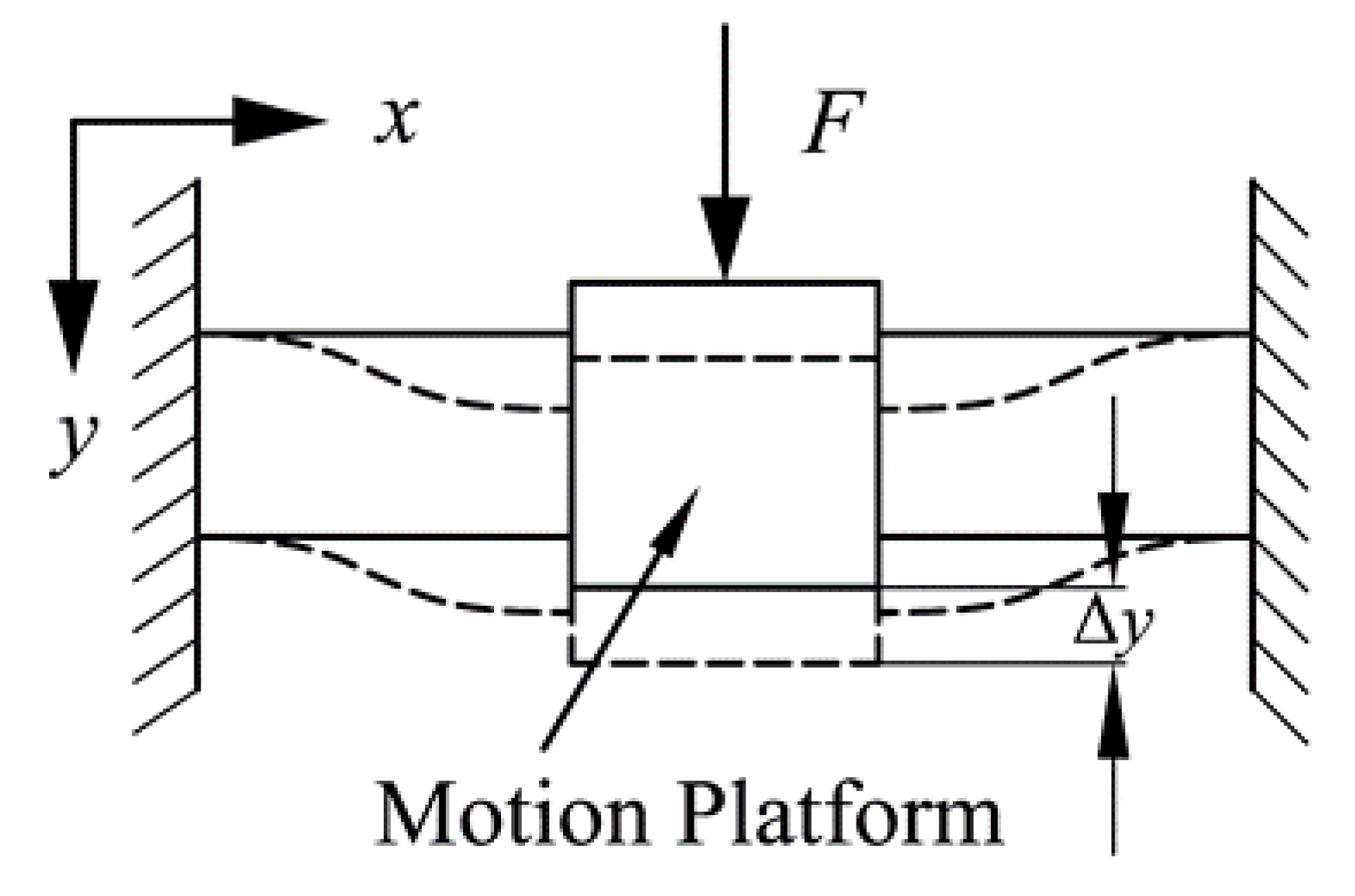
3.2. Model of Bridge-type Amplification Mechanism
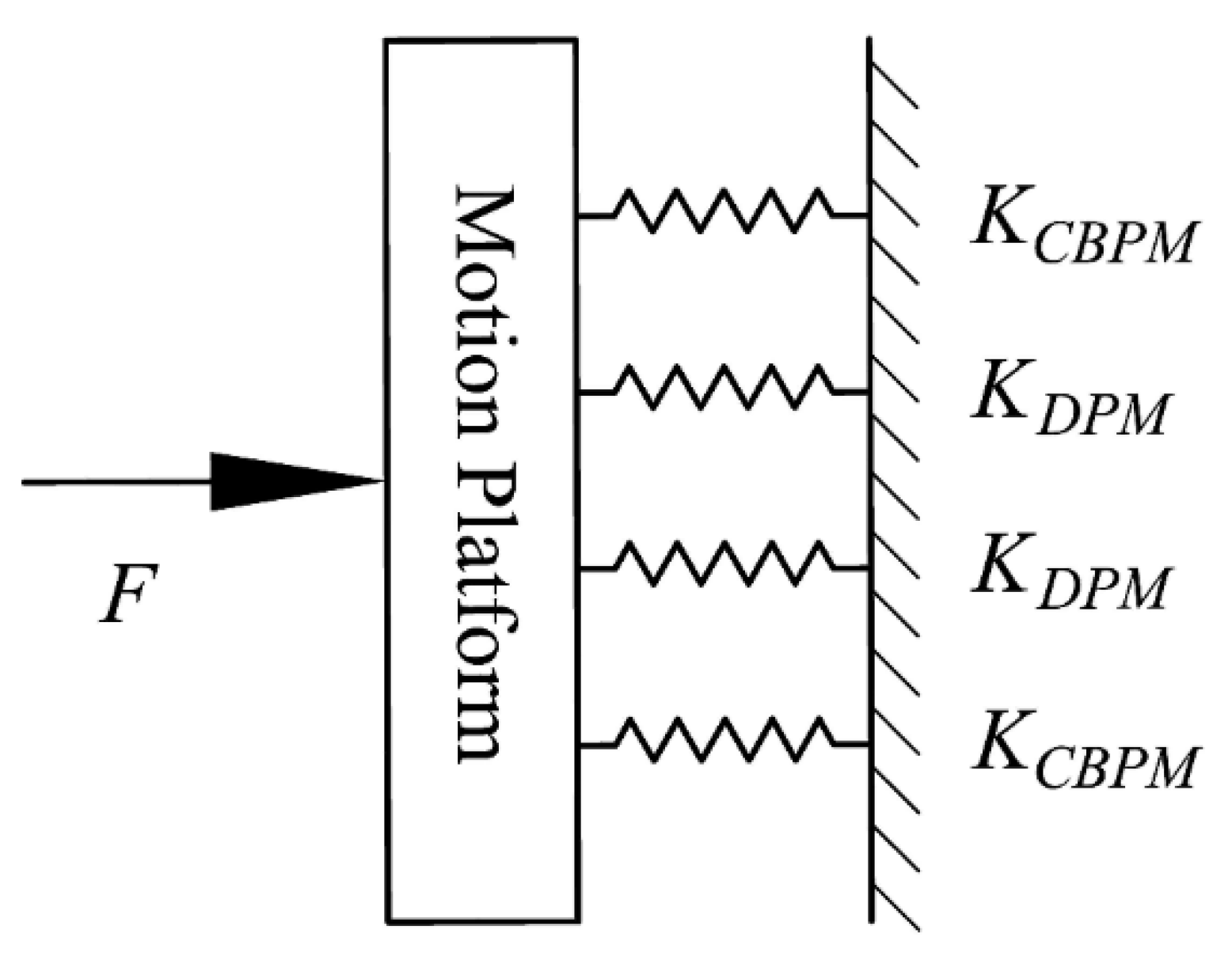
3.3. Stiffness Model of the Positioning Stage
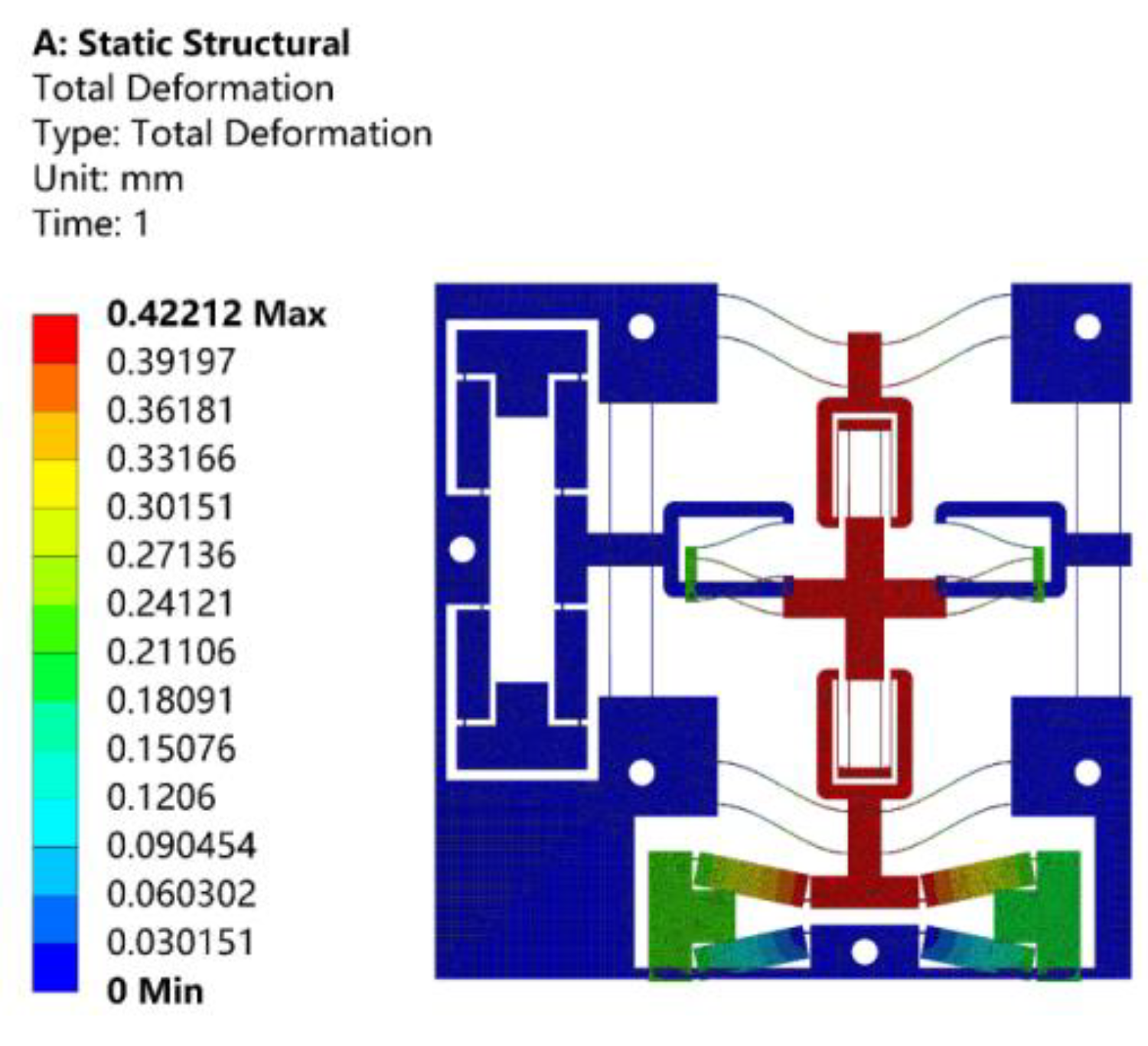
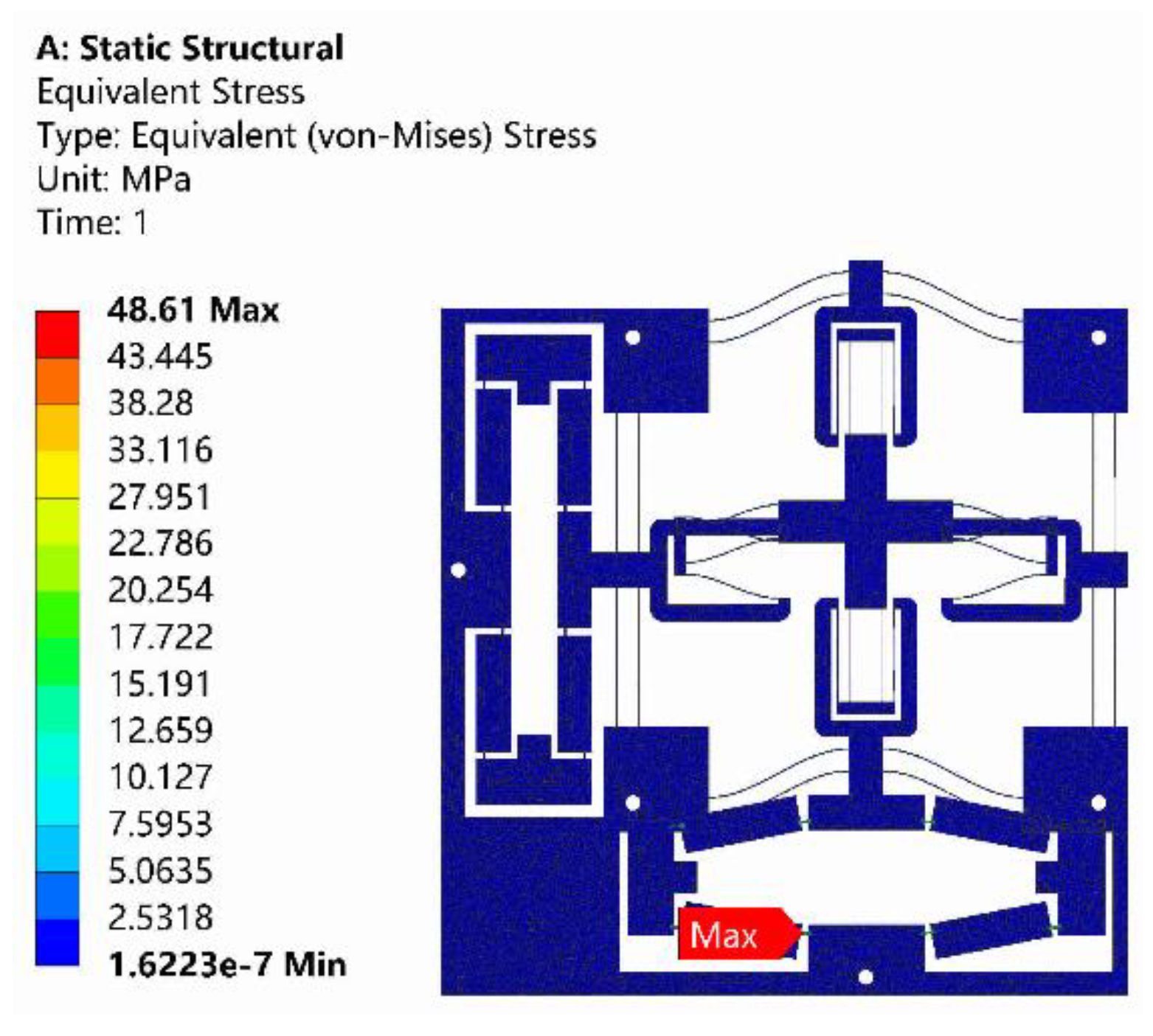
4. Finite Element Simulation
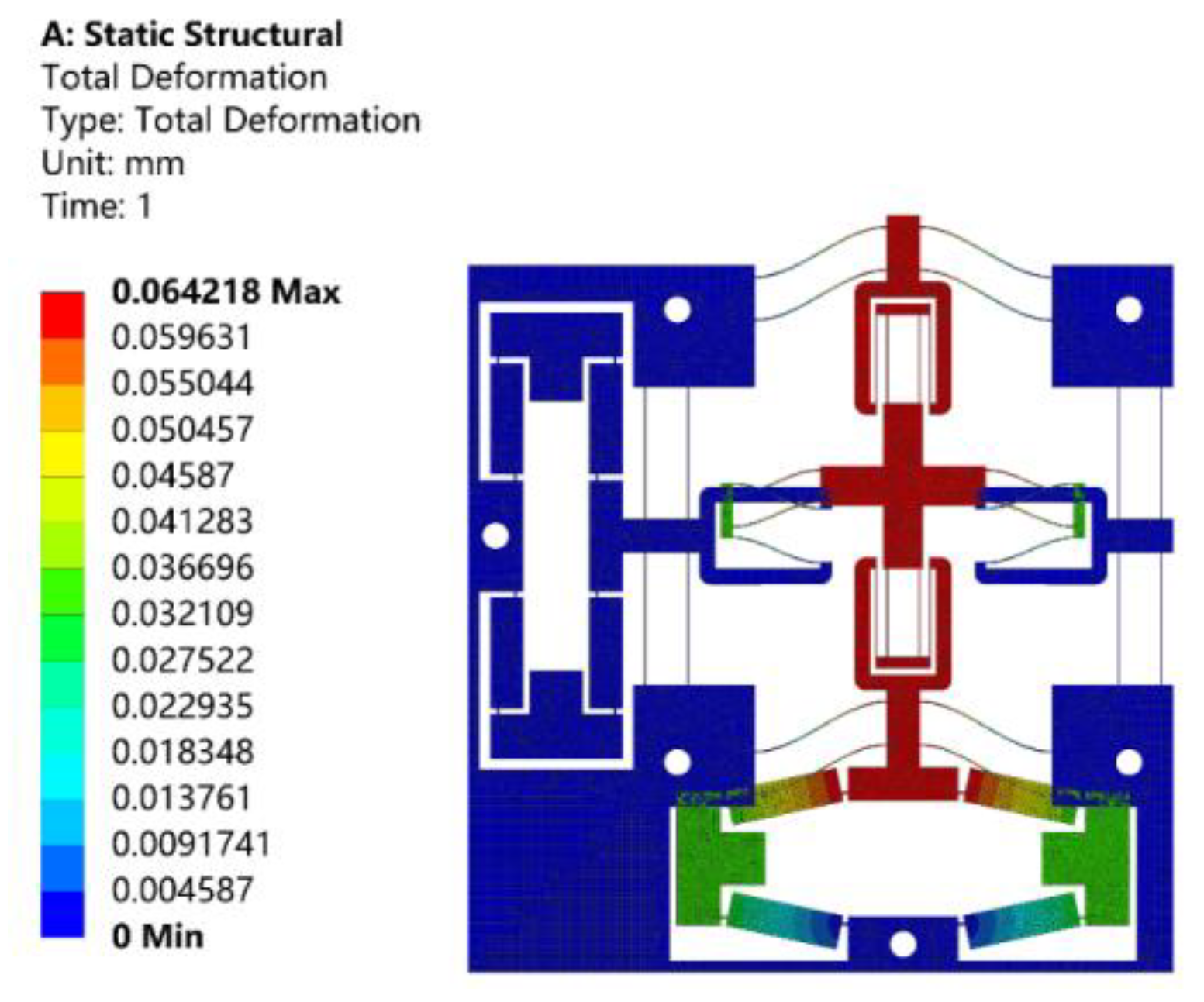
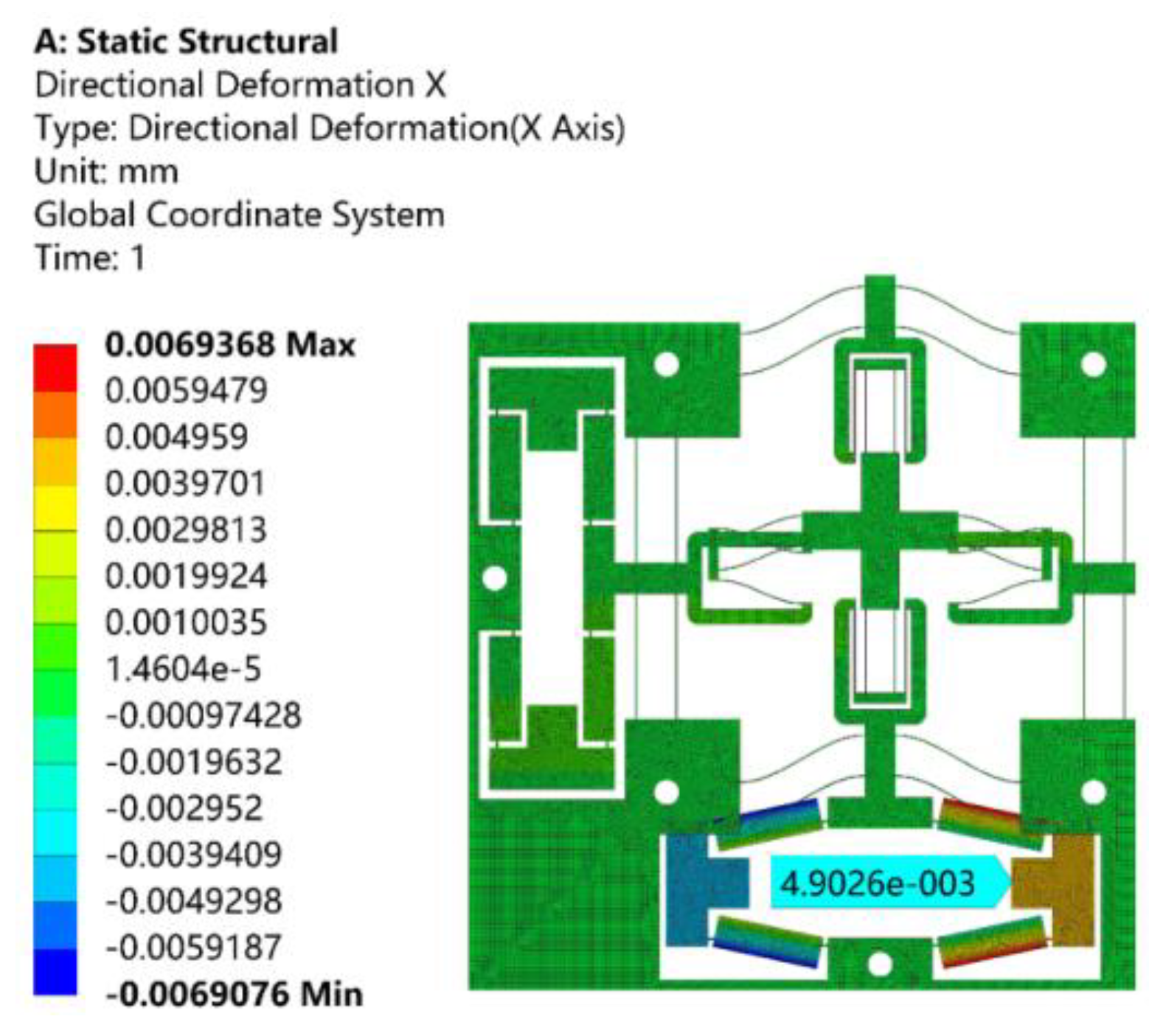
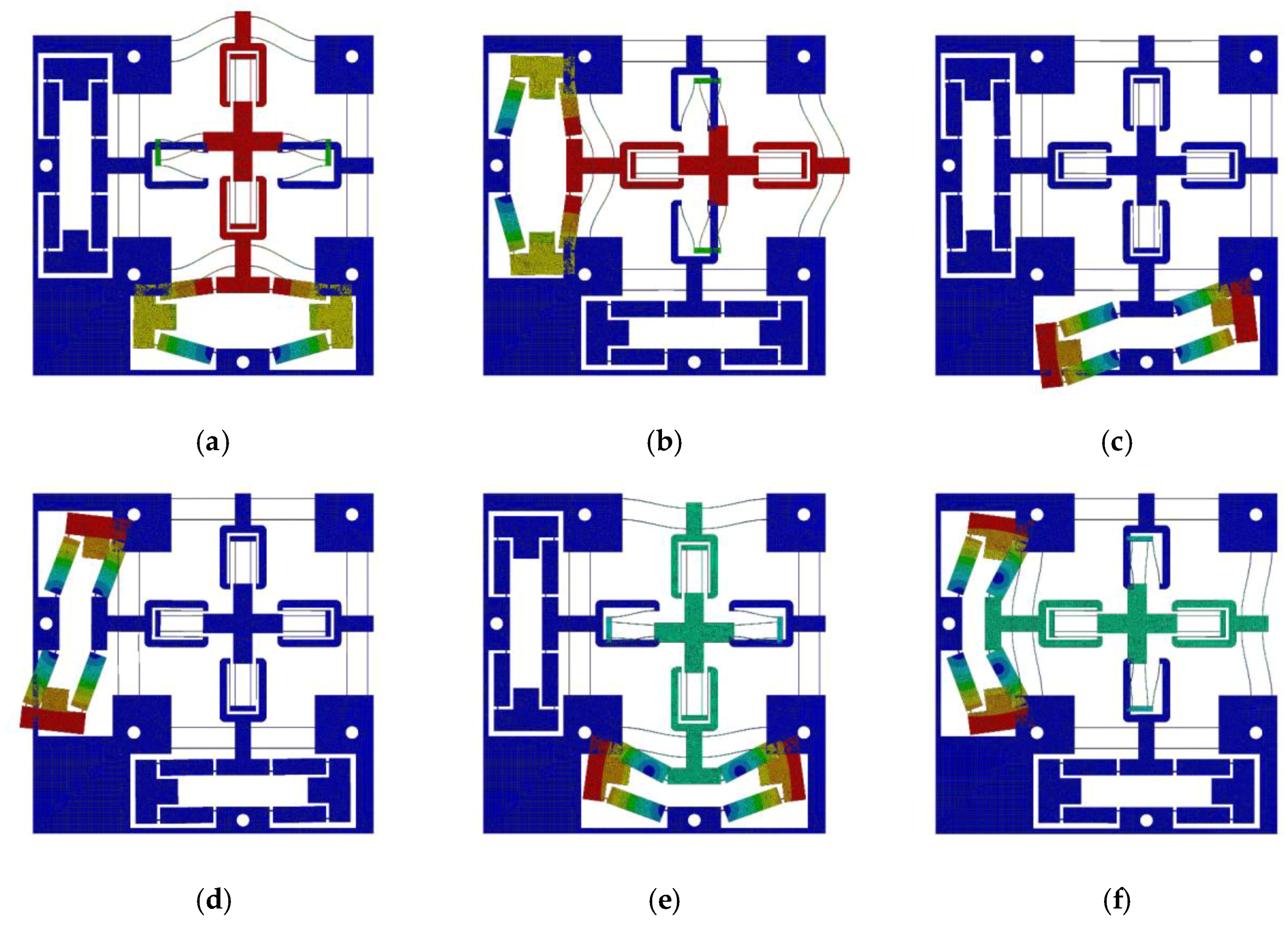
4.1. Static Analysis
4.2. Dynamic Analysis
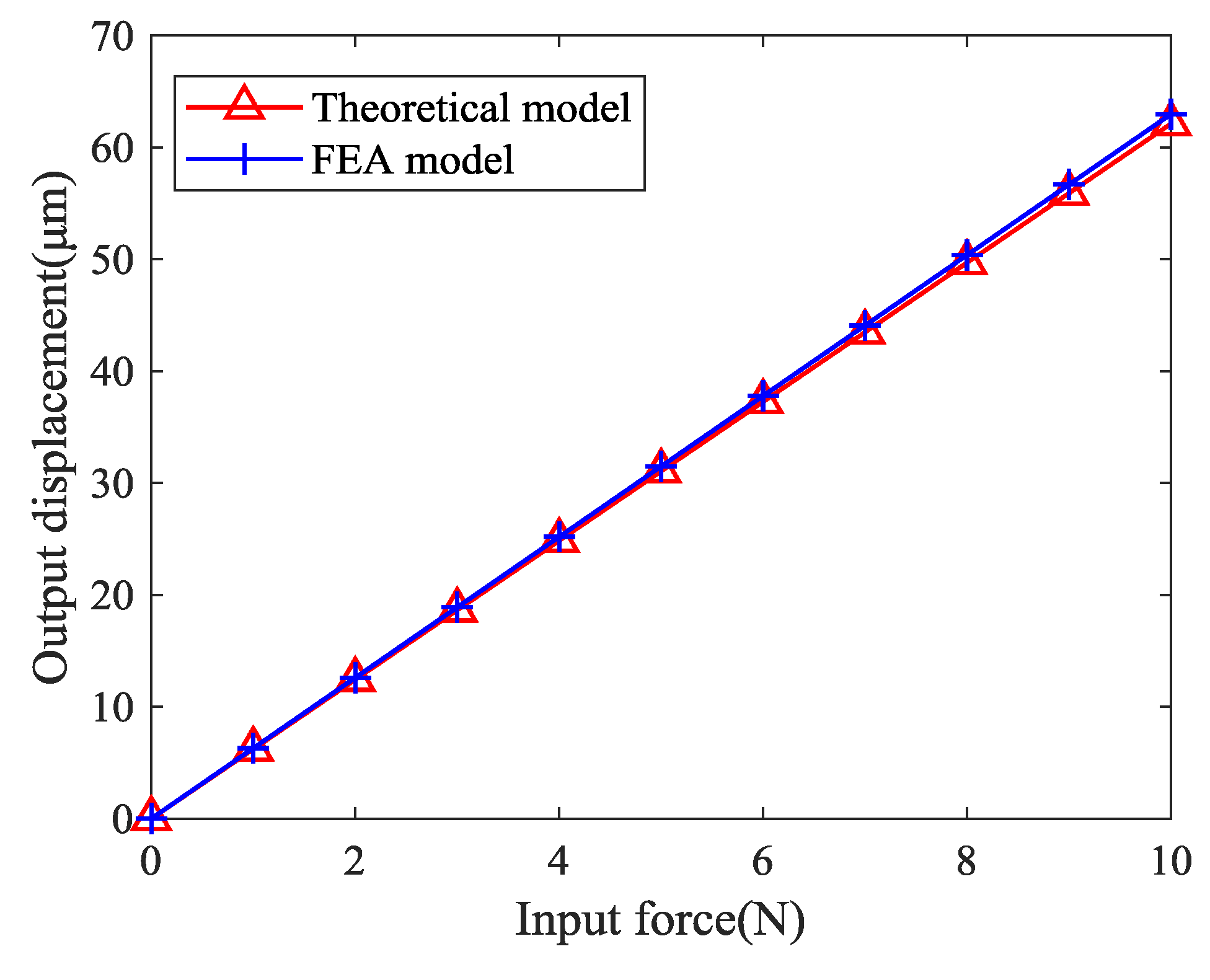
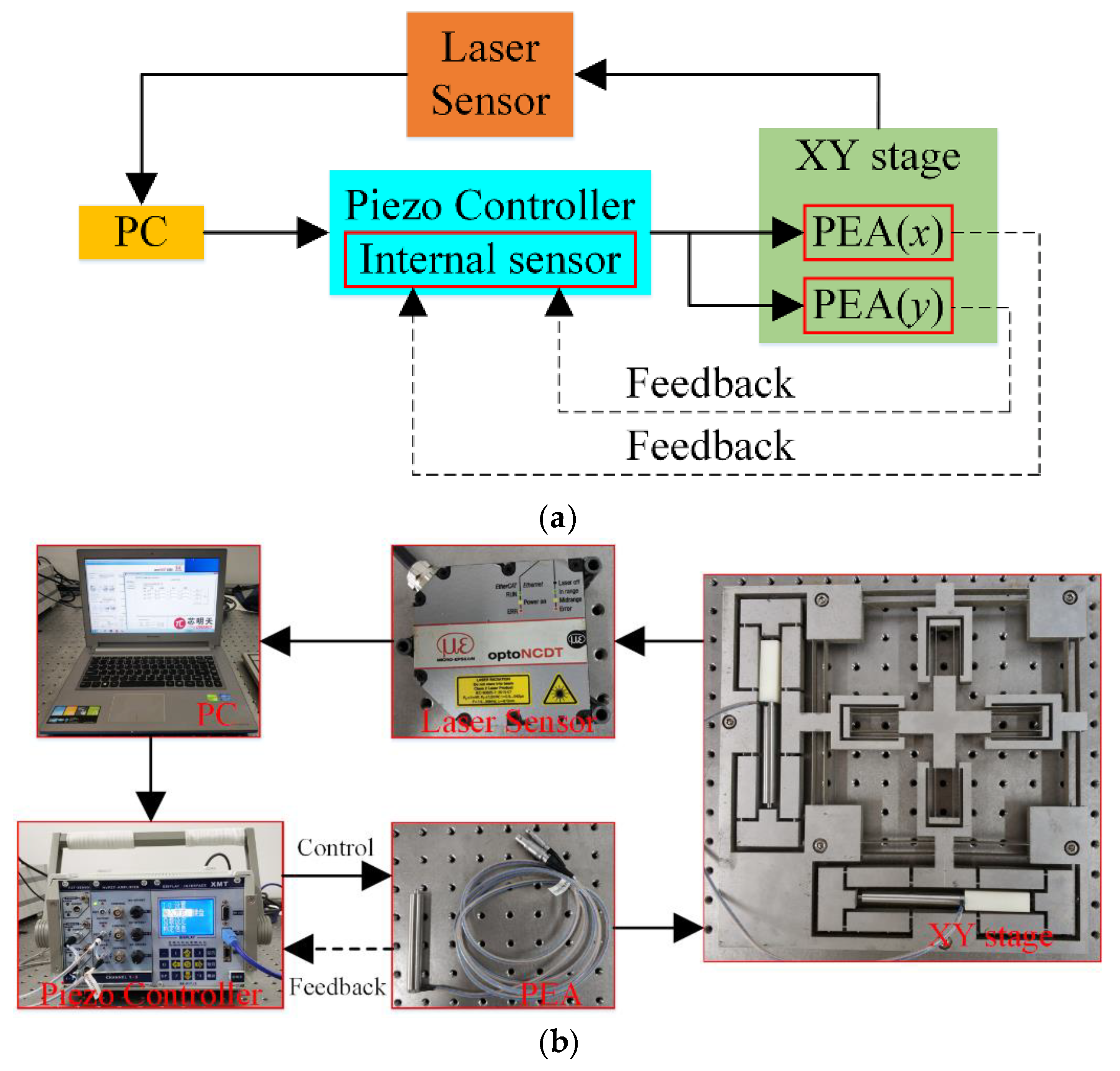
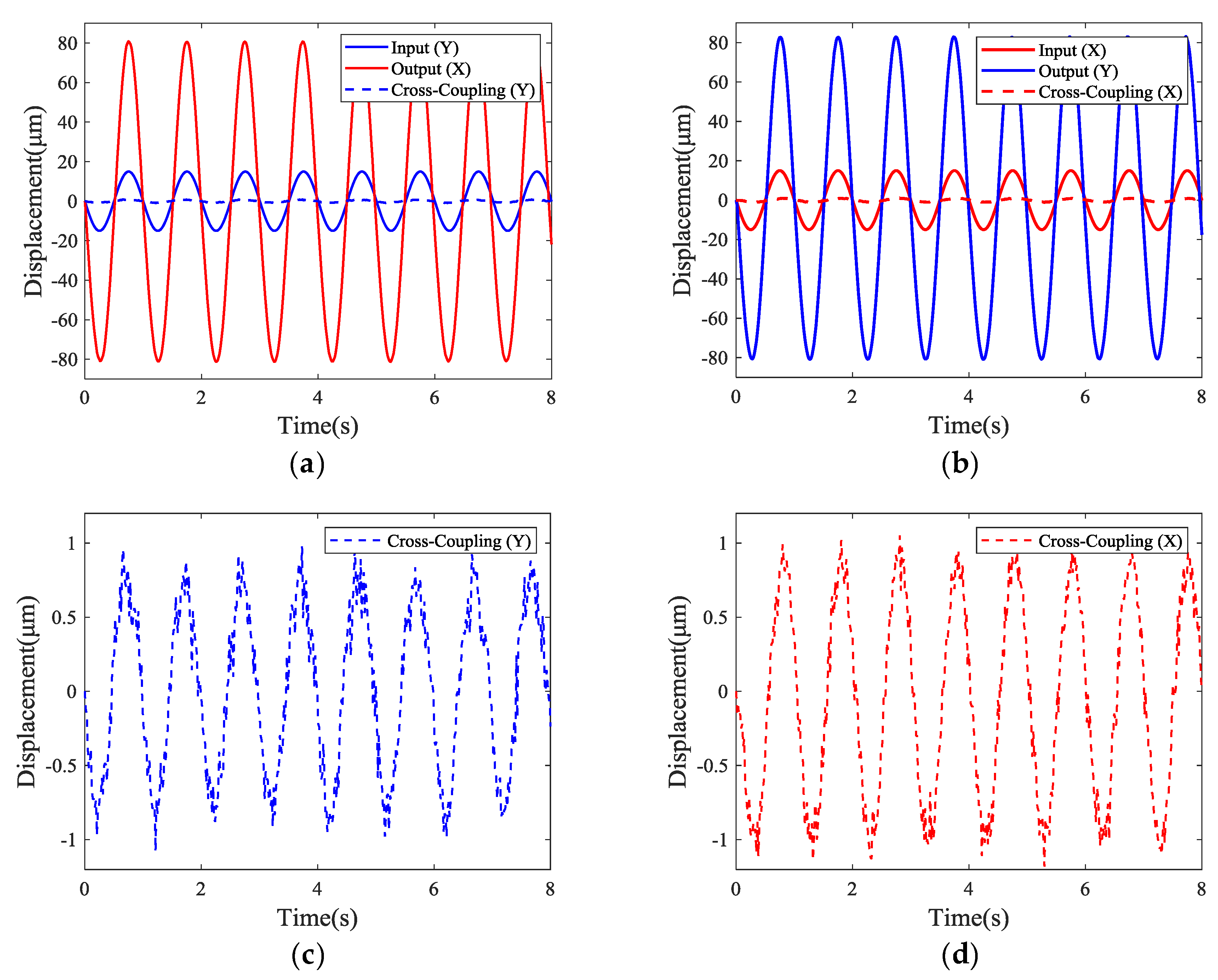
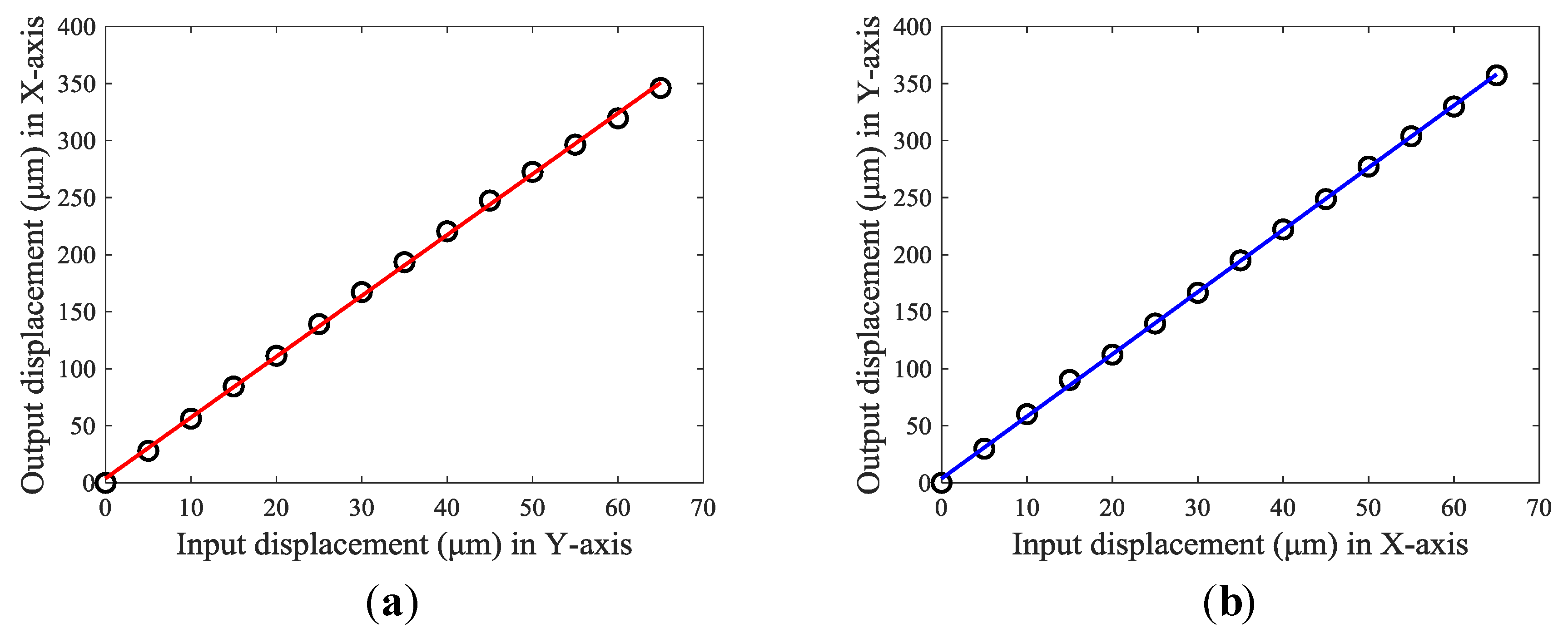
5. Experiment Setup
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Wang, F.; Huo, Z.; Liang, C.; Shi, B.; Tian, Y.; Zhao, X.; Zhang, D. A Novel Actuator-Internal Micro/Nano Positioning Stage with an Arch-Shape Bridge Type Amplifier. IEEE Trans. Ind. Electron. 2018, 66, 9161–91721. [Google Scholar] [CrossRef]
- Bell, D.J.; Lu, T.J.; Fleck, N.A.; Spearing, S.M. MEMS actuators and sensors: observations on their performance and selection for purpose. J. Micromech. Microeng. 2005, 15, S153–S164. [Google Scholar] [CrossRef]
- Thielicke, E.; Obermeier, E. Microactuators and their technologies. Mechatronics 2000, 10, 431–455. [Google Scholar] [CrossRef]
- Fleming, A.J. A review of nanometer resolution position sensors: Operation and performance. Sens. Actuators A 2013, 190, 106–126. [Google Scholar] [CrossRef]
- Dochshanov, A.; Verotti, M.; Belfiore, N.P. A Comprehensive Survey on Modern Microgrippers Design: Operational Strategy. J. Mech. Des. 2017, 139, 070801. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, Q. Survey on Recent Designs of Compliant Micro-/Nano-Positioning Stages. Actuators 2018, 7, 5. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, C.; Zhang, J.; Zhang, X. Synchronized motion control and precision positioning compensation of a 3-DOFs macro-micro parallel manipulator fully actuated by piezoelectric actuators. Smart Mater. Struct. 2017, 26, 115001. [Google Scholar] [CrossRef]
- Herpe, X.; Walker, R.; Dunnigan, M.; Kong, X. On a simplified nonlinear analytical model for the characterisation and design optimisation of a compliant XY micro-motion stage. Rob. Comput. Integr. Manuf. 2018, 49, 66–76. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Q. Design, fabrication and testing of a novel symmetrical 3-DOF large-stroke parallel micro/nano-positioning stage. Rob. Comput. Integr. Manuf. 2018, 54, 162–172. [Google Scholar] [CrossRef]
- Tang, C.; Zhang, M.; Cao, G. Design and testing of a novel flexure-based 3-degree-of-freedom elliptical micro/nano-positioning motion stage. Adv. Mech. Eng. 2017, 9. [Google Scholar] [CrossRef]
- Peng, Y.; Zhang, L.L.; Liu, P.B. Flexure-based XY micro-positioning stage with large stroke and coupling compensation. Opt. Precis. Eng. 2016, 24, 804–811. [Google Scholar] [CrossRef]
- Ling, M.; Cao, J.; Jiang, Z.; Zeng, M.; Li, Q. Optimal design of a piezo-actuated 2-DOF millimeter-range monolithic flexure mechanism with a pseudo-static model. Mech. Syst. Sig. Process. 2019, 115, 120–131. [Google Scholar] [CrossRef]
- Zhang, Q.; Dong, Y.; Peng, Y.; Luo, J.; Xie, S.; Pu, H. Asymmetric Bouc-Wen hysteresis modeling and inverse compensation for piezoelectric actuator via a genetic algorithm-based particle swarm optimization identification algorithm. J. Intell. Mater. Syst. Struct. 2019, 30, 1263–1275. [Google Scholar] [CrossRef]
- Xu, Q. New Flexure Parallel-Kinematic Micropositioning System With Large Workspace. IEEE Trans. Rob. 2012, 28, 478–491. [Google Scholar] [CrossRef]
- Zhang, Q.; Mills, J.K.; Cleghorn, W.L.; Jin, J.; Zhao, C. Trajectory tracking and vibration suppression of a 3-PRR parallel manipulator with flexible links. Multibody Sys. Dyn. 2015, 33, 27–60. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, C.; Zhang, J.; Zhang, J. Smooth adaptive sliding mode vibration control of a flexible parallel manipulator with multiple smart linkages in modal space. J. Sound Vib. 2017, 411, 1–19. [Google Scholar] [CrossRef]
- Bhagat, U.; Shirinzadeh, B.; Clark, L.; Qin, Y.; Tian, Y.; Zhang, D. Experimental Investigation of Robust Motion Tracking Control for a 2-DOF Flexure-Based Mechanism. IEEE/ASME Trans. Mechatron. 2014, 19, 1737–1745. [Google Scholar] [CrossRef]
- Tang, H.; Gao, J.; Chen, X.; Yu, K.-M.; To, S.; He, Y.; Chen, X.; Zeng, Z.; He, S.; Chen, C.; et al. Development and Repetitive-Compensated PID Control of a Nanopositioning Stage With Large-Stroke and Decoupling Property. IEEE Trans. Ind. Electron. 2018, 65, 3995–4005. [Google Scholar] [CrossRef]
- Liu, P.; Yan, P.; Özbay, H. Design and trajectory tracking control of a piezoelectric nano-manipulator with actuator saturations. Mech. Syst. Sig. Process. 2018, 111, 529–544. [Google Scholar] [CrossRef]
- Gu, Y.; Chen, X.; Lin, J.; Lu, M.; Lu, F.; Zhang, Z.; Yang, H. Vibration-Assisted Roll-Type Polishing System Based on Compliant Micro-Motion Stage. Micromachines 2018, 9, 499. [Google Scholar] [CrossRef]
- Tian, Y.; Shirinzadeh, B.; Zhang, D.; Alici, G. Development and dynamic modelling of a flexure-based Scott-Russell mechanism for nano-manipulation. Mech. Syst. Sig. Process. 2009, 23, 957–978. [Google Scholar] [CrossRef]
- Hwang, D.; Byun, J.; Jeong, J.; Lee, M.G. Robust Design and Performance Verification of an In-Plane XYθ Micropositioning Stage. IEEE Trans. Nanotechnol. 2011, 10, 1412–1423. [Google Scholar] [CrossRef]
- Awtar, S.; Slocum, A.H. Design of parallel kinematic XY flexure mechanisms. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, California, CA, USA, 24–28 September 2005; pp. 89–99. [Google Scholar]
- Wang, N.; Zhang, Z.; Zhang, X.; Cui, C. Optimization of a 2-DOF micro-positioning stage using corrugated flexure units. Mech. Mach. Theory 2018, 121, 683–696. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, Q. Design, Fabrication, and Testing of a New Compact Piezo-Driven Flexure Stage for Vertical Micro/Nanopositioning. IEEE Trans. Autom. Sci. Eng. 2019, 16, 908–918. [Google Scholar] [CrossRef]
- Tang, H.; Li, Y.; Huang, J. Design and Analysis of a Dual-Mode Driven Parallel XY Micromanipulator for MicroNano Manipulations. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2012, 226, 3043–3057. [Google Scholar] [CrossRef]
- Li, Y.; Xiao, S.; Xi, L.; Wu, Z. Design, modeling, control and experiment for a 2-DOF compliant micro-motion stage. Int. J. Precis. Eng. Manuf. 2014, 15, 735–744. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, Q. Design, optimization and testing of a compact XY parallel nanopositioning stage with stacked structure. Mech. Mach. Theory 2018, 126, 171–188. [Google Scholar] [CrossRef]
- Lin, C.; Shen, Z.; Yu, J.; Li, P.; Huo, D. Modelling and Analysis of Characteristics of a Piezoelectric-Actuated Micro-/Nano Compliant Platform Using Bond Graph Approach. Micromachines 2018, 9, 498. [Google Scholar] [CrossRef]
- Qin, Y.; Shirinzadeh, B.; Zhang, D.; Tian, Y. Design and Kinematics Modeling of a Novel 3-DOF Monolithic Manipulator Featuring Improved Scott-Russell Mechanisms. J. Mech. Des. 2013, 135, 101004. [Google Scholar] [CrossRef]
- Zhu, W.-L.; Zhu, Z.; Guo, P.; Ju, B.-F. A novel hybrid actuation mechanism based XY nanopositioning stage with totally decoupled kinematics. Mech. Syst. Sig. Process. 2018, 99, 747–759. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y. Design and Analysis of a New High Precision Decoupled XY Compact Parallel Micromanipulator. Micromachines 2017, 8, 82. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Q. Design and testing of a new 3-DOF spatial flexure parallel micropositioning stage. Int. J. Precis. Eng. Manuf. 2018, 19, 109–118. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Y.; Xu, Q. Design and control of a novel piezo-driven XY parallel nanopositioning stage. Microsyst. Technol. 2016, 23, 1067–1080. [Google Scholar] [CrossRef]
- Smith, S.T.; Badami, V.G.; Dale, J.S.; Ying, X. Elliptical flexure hinges. Rev. Sci. Instrum. 1997, 68, 1474–1483. [Google Scholar] [CrossRef]
- Lobontiu, N.; Cullin, M. In-plane elastic response of two-segment circular-axis symmetric notch flexure hinges: The right circular design. Precis. Eng. 2013, 37, 542–555. [Google Scholar] [CrossRef]
- Lobontiu, N.; Cullin, M.; Petersen, T.; Alcazar, J.A.; Noveanu, S. Planar Compliances of Symmetric Notch Flexure Hinges: The Right Circularly Corner-Filleted Parabolic Design. IEEE Trans. Autom. Sci. Eng. 2014, 11, 169–176. [Google Scholar] [CrossRef]
- Lobontiu, N.; Cullin, M.; Ali, M.; Hoffman, J. Planar Compliances of Thin Circular-Axis Notch Flexure Hinges with Midpoint Radial Symmetry. Mech. Based Des. Struct. Mach. 2013, 41, 202–221. [Google Scholar] [CrossRef]
- Verotti, M.; Dochshanov, A.; Belfiore, N.P. A Comprehensive Survey on Modern Microgrippers Design: Mechanical Structure. J. Mech. Des. 2017, 139, 060801. [Google Scholar] [CrossRef]
- Yang, Y.; Wei, Y.; Lou, J.; Xie, F. Design and analysis of a new flexure-based XY stage. J. Intell. Mater. Syst. Struct. 2017, 28, 2388–2402. [Google Scholar] [CrossRef]
- Su, H.J. A Pseudorigid-Body 3R Model for Detmining Large Deflection of Cantilever Beams Subject to Tip Loads. J. Mech. Rob. 2009, 1, 795–810. [Google Scholar]
- Chen, G.; Xiong, B.; Huang, X. Finding the optimal characteristic parameters for 3R pseudo-rigid-body model using an improved particle swarm optimizer. Precis. Eng. 2011, 35, 505–511. [Google Scholar] [CrossRef]
- Xu, P.; Yu, J.; Zong, G.; Bi, S. An effective pseudo-rigid-body method for beam-based compliant mechanisms. Precis. Eng. 2010, 34, 634–639. [Google Scholar]
- Awtar, S.; Slocum, A.H.; Sevincer, E. Characteristics of Beam-Based Flexure Modules. J. Mech. Des. 2007, 129, 625–639. [Google Scholar] [CrossRef]
- Awtar, S.; Slocum, A.H. Constraint-based Design of Parallel Kinematic XY Flexure Mechanisms. J. Mech. Des. 2007, 129, 816–830. [Google Scholar] [CrossRef]
- Verotti, M. Analysis of the center of rotation in primitive flexures: Uniform cantilever beams with constant curvature. Mech. Mach. Theory 2016, 97, 29–50. [Google Scholar] [CrossRef]
- Verotti, M. Effect of initial curvature in uniform flexures on position accuracy. Mech. Mach. Theory 2018, 119, 106–118. [Google Scholar] [CrossRef]
- Ling, M.; Cao, J.; Zeng, M.; Lin, J.; Inman, D.J. Enhanced mathematical modeling of the displacement amplification ratio for piezoelectric compliant mechanisms. Smart Mater. Struct. 2016, 25, 075022. [Google Scholar] [CrossRef]
- Lobontiu, N.; Paine, J.S.; Garcia, E.; Goldfarb, M. Corner-Filleted Flexure Hinges. J. Mech. Des. 2001, 123, 346–352. [Google Scholar] [CrossRef]
- Ling, M.; Cao, J.; Jiang, Z.; Lin, J. Modular kinematics and statics modeling for precision positioning stage. Mech. Mach. Theory 2017, 107, 274–282. [Google Scholar] [CrossRef]
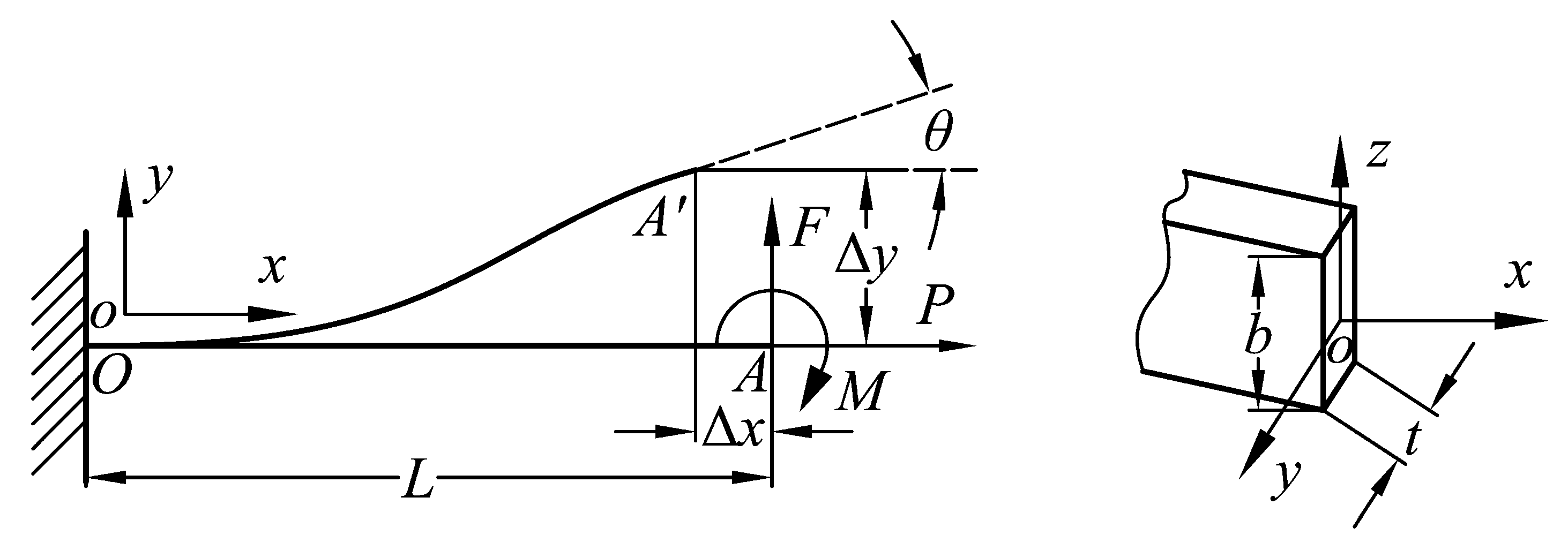
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| a | 12 | i | −0.6 |
| b | 4 | j | −1/15 |
| c | −6 | k | 1/20 |
| e | 1.2 | r | 1/700 |
| g | 2/15 | s | 11/6300 |
| h | −0.1 | q | −1/1400 |
| Parameters | Values | Parameters | Values | Parameters | Values |
|---|---|---|---|---|---|
| t | 0.5 | l1 | 3 | LCBPM | 60 |
| t1 | 1 | l2 | 50 | w | 8 |
| t2 | 15 | LDPM | 40 | b | 12 |
| Model | Ramp | ||
|---|---|---|---|
| Analytical | 6.57 | 2.118 | 24.32 |
| FEA | 6.42 | 2.039 | 23.69 |
| Error | 2.34% | 3.87% | 2.66% |
| Properties | Values |
|---|---|
| Nominal displacement (μm) | 76 ± 10% |
| Stiffness (N/μm) | 12 ± 20% |
| Blocked force (N) | 1200 |
| Capacitance (μF) | 7.2 ± 20% |
| Resonant frequency (kHz) | 12 |
| Dimensions (mm) | Φ 12 × 87.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Zhao, J.; Shen, X.; Xiao, Q.; Huang, J.; Wang, Y. Design, Modeling, and Testing of a Novel XY Piezo-Actuated Compliant Micro-Positioning Stage. Micromachines 2019, 10, 581. https://doi.org/10.3390/mi10090581
Zhang Q, Zhao J, Shen X, Xiao Q, Huang J, Wang Y. Design, Modeling, and Testing of a Novel XY Piezo-Actuated Compliant Micro-Positioning Stage. Micromachines. 2019; 10(9):581. https://doi.org/10.3390/mi10090581
Chicago/Turabian StyleZhang, Quan, Jianguo Zhao, Xin Shen, Qing Xiao, Jun Huang, and Yuan Wang. 2019. "Design, Modeling, and Testing of a Novel XY Piezo-Actuated Compliant Micro-Positioning Stage" Micromachines 10, no. 9: 581. https://doi.org/10.3390/mi10090581
APA StyleZhang, Q., Zhao, J., Shen, X., Xiao, Q., Huang, J., & Wang, Y. (2019). Design, Modeling, and Testing of a Novel XY Piezo-Actuated Compliant Micro-Positioning Stage. Micromachines, 10(9), 581. https://doi.org/10.3390/mi10090581







