1. Introduction
Cancer has always been a significant threat to human beings. The global rate of deaths associated with this fatal disease is alarming. In 2016, 17.2 million people were estimated to live with cancer, and cancer accounted for 8.9 million deaths worldwide [
1], which elucidates that it is a critical issue to be concerned about. Therefore, evaluating the characteristics of tumors and their growth process is of paramount importance and is useful for obtaining successful treatment.
Avascular growth phase is the common phase between both benign and malignant tumors and can be better experimentally simulated using in vitro platforms. In this phase, the growth rate is limited to diffusion and consumption of the nutrients [
2]. Studies in avascular tumor growth by means of diffusion have been extensively conducted over the past decades, and many models have been presented. In early models, the process of the diffusion of the dissolved substance through tissues as well as their consumption by metabolic processes was studied [
3]. Subsequently, a few experimental studies—both in vitro and in vivo—focused on radiotherapy and the effects of radiation on the tumor growth [
4,
5]. Thomlinson and Gray [
6] extensively examined the effects of radiations on hypoxic tumor cells, which were proved to be radio-sensitive and less vulnerable to X- and γ-radiations.
In 1966, Burton [
7] established a new mathematical model which examined oxygen distribution inside a tumor spheroid. The model was capable of determining the radius of the central zone of a tumor, and the growth curve obtained by the model could fit a well-known mathematical function, the Gompertzian function. Thereafter, Greenspan [
8] presented a model by considering the living cell adhesion, which results in an inward pressure in spheroids. The author also assumed the disintegration of necrotic cellular debris into permeable, simpler compounds whose volume loss was compensated by some cells that were pushed inward due to the surface tension and adhesion. The authors concluded that the inhibitory chemicals were produced in the necrotic core. These chemicals could retard the tumor growth by preventing cells from mitosis, without causing the death of cells. Depending on whether the inhibitory chemicals were produced due to the insufficient nutrient supply and a necrosis product or by the metabolic process of living cells, the model would predict two utterly different growth patterns.
McElwain and Morris [
9] developed a new mathematical model for tumor growth. The tumor passes through three different phases according to their model. During the first phase, cells are supplied with a sufficient amount of nutrient (oxygen) and cell mitosis proceeds ordinarily. In the second phase, the growth rate decreases until the nutrient reaches its critical value, and in the third phase, the growth rate further decreases, and the cell mitosis rate is in balance with tumor volume loss. The authors adopted in their model Greenspan’s assumption for cell loss mechanism—the disintegration of living cells after being forced inward by surface tension and adhesion. In a later study [
10], the same group improved their model by considering apoptosis as a cell loss mechanism in the tumor. Using the general approach developed in their previous paper, they applied the apoptosis mechanism to all the cells except those in the necrotic core. The authors concluded that the tumor might reach a dormant state in the second phase, as the apoptosis rate may balance the cell mitosis rate; and otherwise, the growth proceeds to the third phase. Inspired by McElwain and Morris’s model, Lakshminarayanan et al. developed a model for tumor growth based on nutrient diffusion as well as apoptosis and necrosis as cell loss mechanisms [
11].
Casciari et al. introduced a model for the growth of multicellular tumor spheroids based on oxygen and glucose concentrations, as well as the culture medium pH [
12]. The authors investigated the shedding of mitotic cells from the surface of the tumor spheroid as a cell loss mechanism. The team also defined a maximum growth rate fraction, which was a function of glucose and oxygen concentrations as well as the culture medium pH, whose multiplication in the tumor volume would be the growth rate. They also conducted some experiments regarding culturing and observing the tumor growth and utilized their experimental data to verify their model [
13]. In the later experiments, Freyer and Sutherland [
14] cultured multicellular spheroids in dishes with various oxygen and glucose concentrations for more than three weeks. Long enough culture time in their study allowed the tumors to pass through different stages of growth; accordingly, their experimental data are appropriate for evaluating models of tumor growth.
As a precise simulation of in vitro process, mathematical models of tumor growth can be employed to investigate tumor growth procedure in microfluidic devices. In fact, microfluidic approaches are widely used for examining a diverse range of phenomena [
15,
16,
17,
18], and using microfluidic devices is a common approach to study different characteristics of cancerous tumors [
19,
20,
21,
22,
23,
24,
25]. Hu and Li [
21] simulated tumor growth in a microchannel bioreactor. They used Casciari’s model as well as Navier-Stokes equations to investigate the growth of the tumor exposed to the culture medium flow. By repeating the simulations for different inlet velocity of the culture medium, the authors concluded that the tumors grow faster under high inflow velocity, because of the fast nutrient supply to the tumor. They monitored tumor growth for fewer than 80 h. Given the nutrient concentrations and their simulation time, it can be concluded that the tumors in their simulations do not develop the necrotic zone.
Herein, we modify Lakshminarayanan’s model [
11] for better agreement with experimental data [
14]. Even though our modified model is still based on the nutrient diffusion and considers apoptosis as well as necrosis as the main cell loss mechanisms, the tumor growth kinetics is modified in such a way that the nutrient consumption rate of the cells in the quiescent zone is half of that in the proliferative zone, according to Jiang et al. [
26]. With the employed modifications, the proposed modified model can better predict the experimental results in the literature [
14]. We further investigate the effects of the concentrations of the essential nutrients and the initial spheroid radius on the tumor growth. As the next step, we include the effect of dynamic perfusion of the culture medium into the model and examine the tumor growth in microfluidic devices. Despite previous studies which simulated the tumor growth for a short duration, we simulate the tumor growth in a microfluidic device containing U-shaped barrier for 300 h. This approach enables time-dependent investigation of the different stages of the tumor growth and quantifies dynamic necrotic as well as quiescent zones in the tumor. Moreover, we evaluate the effect of the flow velocity of the culture medium on the tumor growth rate. Finally, to investigate how the geometry of the trap may affect the spheroidal tumor growth, we simulate the tumor behavior in a microchip with a microwell trap and compare the results to those obtained in the U-shaped barrier.
2. Materials and Methods
2.1. Tumor Growth Model
The equations used for the tumor growth are based on the analytical model of Lakshminarayanan et al. [
11]; however, some reasonable modifications have been applied to the proposed model so as to make it more compatible with the experimental data. In this model, two main cell-loss mechanisms are considered, namely apoptosis and necrosis. Moreover, the growth of the tumor is directly affected by the concentration distributions of oxygen and glucose, which are the two essential components for cancerous tumors to thrive. As such, the whole tumor volume is divided into three main regions, i.e., proliferative, quiescent and necrotic zones. In the proliferative zone, adequate nutrients are available for all the cells. Accordingly, the cells grow at the maximum rate in this zone. As the tumor grows, however, the quiescent zone appears and the concentration of one of the nutrients falls off below its critical value. Hence, according to Jiang et al. [
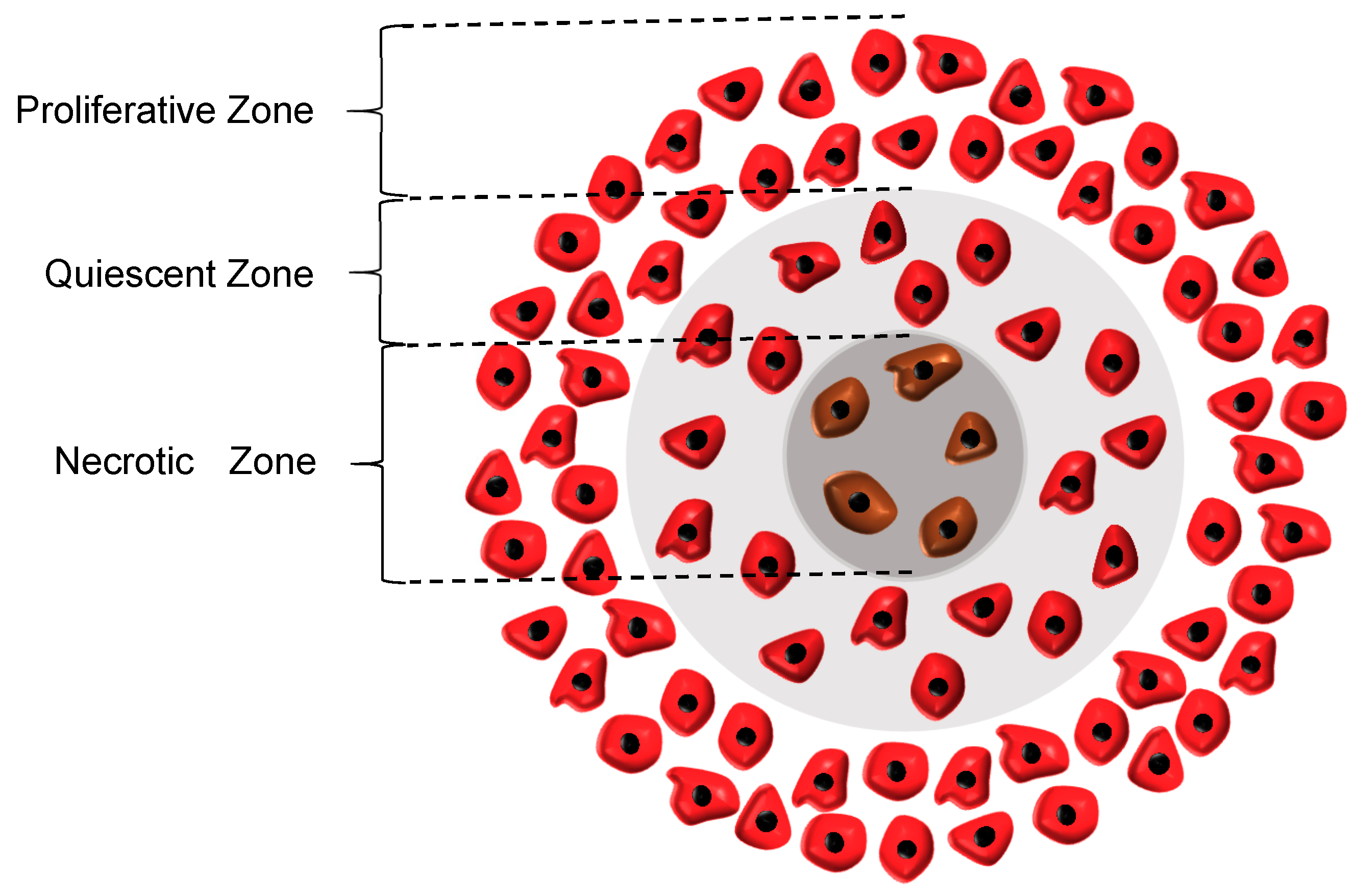
26], the rate of cell growth in this zone declines to half of its initial rate. Although the cells in the quiescent zone are not dead yet and still take up some nutrients, they are regarded as non-dividing cells. Subsequently, the necrotic region appears when the concentrations of both oxygen and glucose are below their critical values, causing all the cells in this zone to die. As a result, the growth rate in this zone is zero and the necrosis mechanism retards the tumor growth. It also should be noted that in the whole tumor volume except the necrotic area, the apoptosis mechanism acts as an inhibitory factor against the tumor growth. The three main regions in a tumor are graphically displayed in
Figure 1.
2.1.1. Nutrient Concentrations
The concentrations of nutrients can be obtained using the general form of convection-diffusion-reaction equation:
where
,
and
are the concentration, diffusion coefficient and reaction rate of a nutrient, respectively. Since the velocity of nutrients inside the tumor is negligible, a simplified yet logical assumption is to neglect the convection term in the left-hand side of Equation (1). In addition, by considering a constant value for the diffusion coefficient, Equation (1) can be simplified for the three regions mentioned above.
Equations (2)–(4) are related to the nutrient consumption in proliferative, quiescent and necrotic zones, respectively.
In the above equations,
r is the radial position in the tumor; the last term on the right-hand side of Equation (2) is the Michaelis-Menten reaction term;
i = 1, 2 identifies glucose and oxygen, respectively;
is the maximum reaction rate of the nutrients, and
K is the Michaelis constant of the nutrients. Moreover, in contrast to the Lakshminarayanan’s model [
11], where the authors considered no nutrient consumption in the quiescent zone, here we consider the fact that the consumption rate of nutrients is half in the quiescent zone compare to that in the proliferative zone [
26]. In addition, due to the lack of sufficient nutrients, the cells in the quiescent region are assumed not to proliferate.
2.1.2. Growth Equation
Based on what was mentioned in the model definition, during the growth process, tumor passes through three phases. The tumor is in the first phase of its growth until the quiescent zone comes into existence. The second phase begins with the appearance of the quiescent zone and lasts until the necrotic zone appears. The onset of the necrotic zone is the beginning of the third phase: the last phase of the growth. The rate of volumetric change of tumor follows different patterns in the three phases. The general growth equation with radial growth assumption is as follows:
where
,
and
are the volume of the spheroidal tumor, quiescent and necrotic zones, respectively. Additionally,
,
and
are respectively the proliferative, apoptosis and necrosis constants. It is noteworthy that
is zero during the first phase. Moreover, since the necrotic core appears in the third phase,
is zero in the first two phases. Using the above equations, the tumor radius can be determined as a function of time.
2.1.3. Initial and Boundary Conditions
As an initial condition, we assume that at the beginning of the growth, the concentrations of both nutrients are equal to that of the culture medium:
In the model, the tumor spheroid is exposed to an unlimited, static culture medium. Thus, as a boundary condition, the concentrations of both nutrients are equal to that of the culture medium at the tumor surface:
2.1.4. Applying the Modified Model to Tumor Spheroid in Microfluidic Devices
By assuming that the tumor grows radially [
21], the model introduced above can be employed for simulating the growth of the tumor in microfluidic devices. Additionally, for modeling tumor growth in microfluidic devices, continuity and momentum equations which are related to the nutrient flow through the microchannel must be considered:
where
ρ,
μ,
and
are the fluid density and viscosity, velocity vector, and pressure gradient, respectively.
As it is further discussed in
Section 4, we assume steady-state culture medium flow for the tumor growth. Also, for the diffusion of the nutrients through the culture medium, since there is no consumption of the nutrients outside the tumor spheroid, Equation (1) is simplified as follows:
Accordingly, Equations (8)–(10) are coupled and solved numerically in order to find the nutrient concentrations in the culture medium. The parameters of the equations are listed in
Table 1.
2.2. Geometry
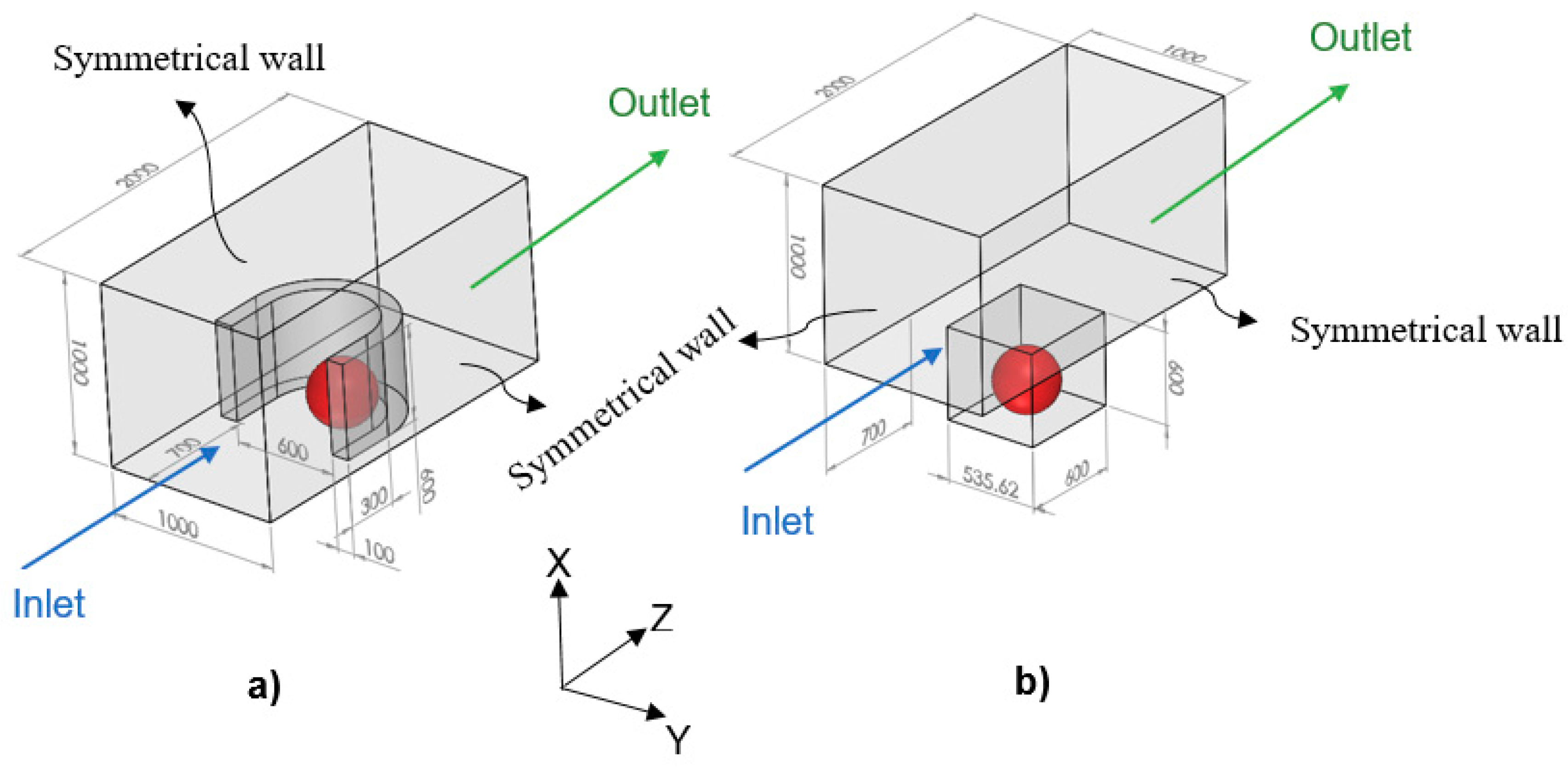
In the model, since the tumor is exposed to the static, unlimited culture medium and nutrient concentrations at the tumor surface are constant, the distributions of the nutrient concentrations are spherically symmetric. Therefore, the nutrient concentrations change only in the radial direction, and accordingly, we consider the tumor geometry an axially symmetric semicircle. Since the spherical symmetry is assumed, there is no difference between the results obtained by a sphere or a semicircle as the tumor geometry; however, considering the tumor as a semicircle will be more numerically efficient (this issue will be further discussed in the numerical method section). Inspired by Barisam et al. [
27], the microfluidic devices studied in this research contain traps in the form of a microwell or a U-shaped barrier. Due to the symmetry condition of the side surfaces of the microchannels, only one trap has been considered in the geometry of each one. Also, all of the surfaces in both types of microchannels are impermeable to the nutrients. As shown in
Figure 2, the traps have the same length, height and cross-section area. Moreover, the centers of both types of traps superpose the center of the lower surface of the microchannel.
2.3. Numerical Method
The first five equations, which are related to the growth and the concentration distributions, are solved numerically for achieving an approximate solution. As mentioned in the geometry section, for the condition of static, unlimited culture medium, the tumor is assumed as an axially symmetric semicircle, the revolution of which around its axis will be the actual 3D tumor in the model. Since the tumor assumes the shape of a hemisphere, it requires much fewer computational cells for a numerical solution than a sphere and can be solved more easily, without making any difference in the results.
Tessellation method is utilized to mesh the tumor exposed to the unlimited, static culture medium, and unstructured triangular grids with initial sizes between 9.71 up to 4.85 are generated. Finite element approach is used with a residual value less than for growth as well as diffusion-reaction equations. For the tumor placed in a microfluidic device, unstructured tetrahedral grids are generated which are between 4 up to 1.2 for the tumor domain and between 5.06 up to 1.64 for the microchannel zone. In this case, mesh refinement has been employed to the boundaries as well as interface surfaces. Convergence criteria to solve the equations of continuity, momentum, concentration distribution, and tumor growth are selected as residual values less than , , , , respectively.
For a specific flow rate and tumor radius, the flow equations (i.e., Equations (8) and (9)) along with the convection-diffusion equation (Equation (10)) need to be solved only once in order to obtain the distributions of the nutrient concentration in the culture medium. The time required for the concentrations of the nutrients to reach a steady-state, both inside the tumor and in the microchannel, is far much shorter than the growth time of the cells. Once the nutrients concentrations are determined, for a given tumor radius, the growth rate of the tumor is calculated using the growth equations (by calculating the volume occupied by the whole tumor, quiescent, and necrotic zones and employing Equation (5). After 20 h, the tumor radius is updated using the growth rate obtained. The same procedure is repeated for the new tumor radius.
It is noteworthy that the conditions and the distribution of the nutrients within a tumor in the microfluidic device is asymmetric. However, this cannot affect the accuracy of applying the present model to tumor growth in a microfluid device because in the proposed model, the growth equation is simply influenced by the volume of different regions of the tumor, not by its geometrical distribution.
2.4. Model Validation
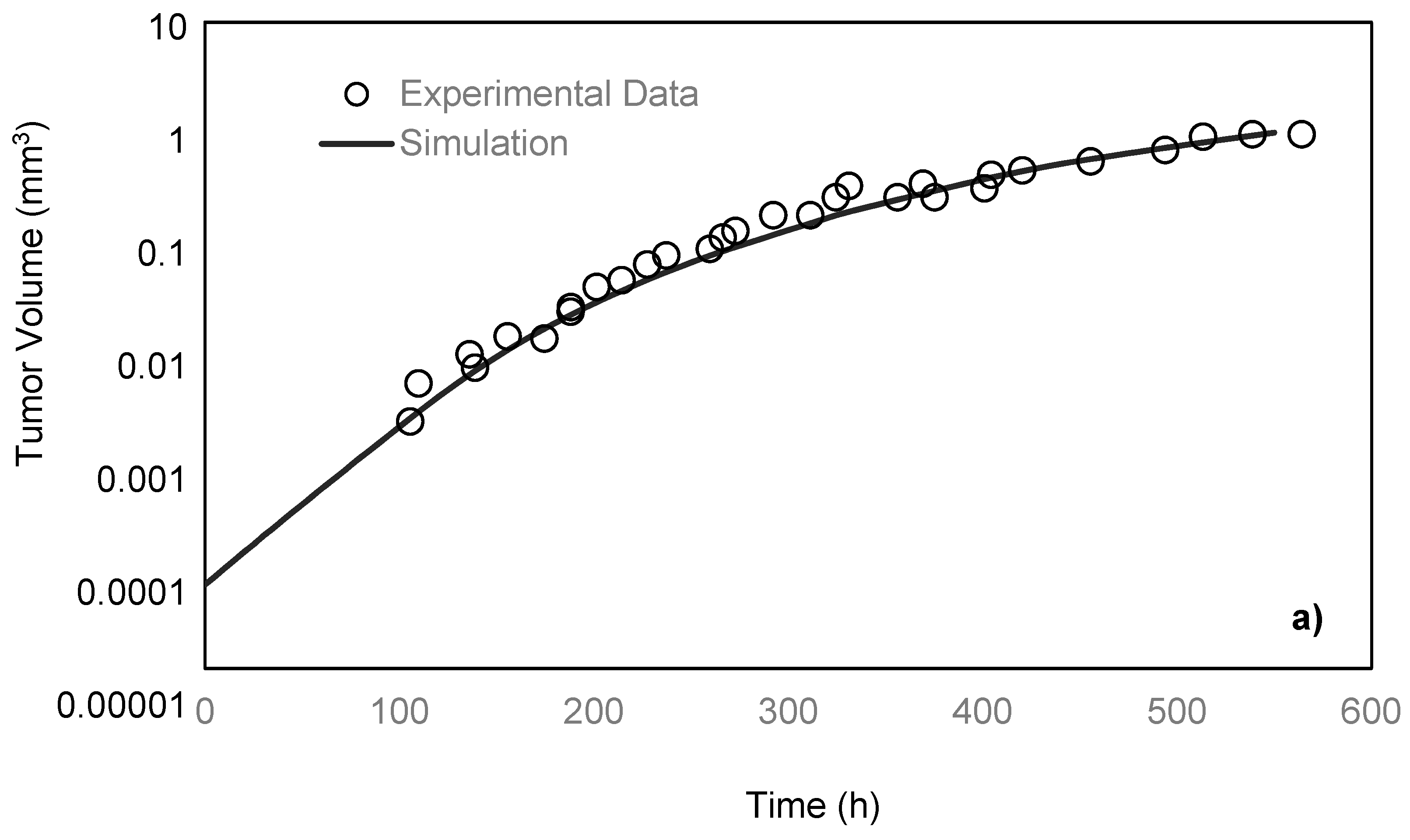
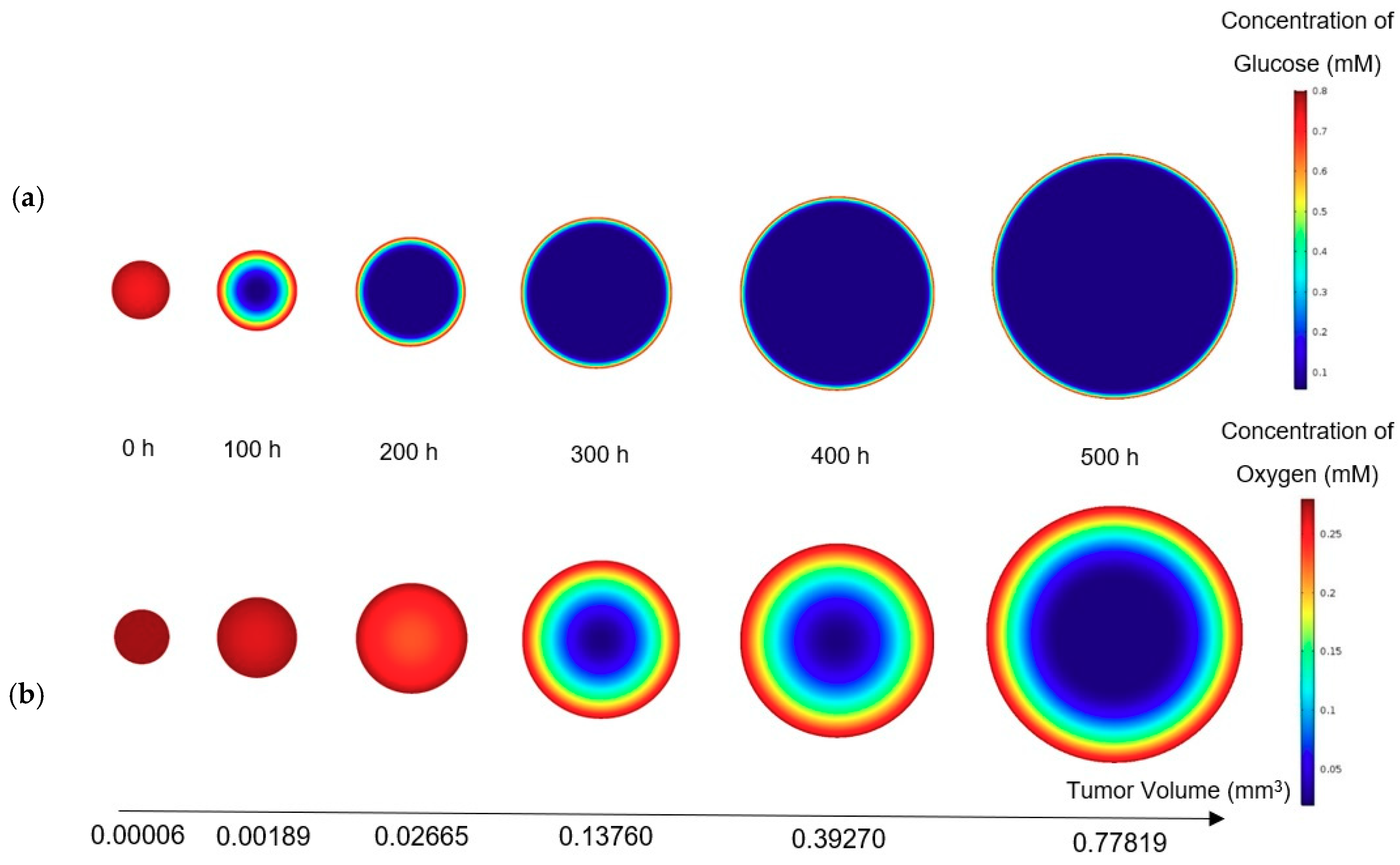
Freyer and Sutherland [
14] cultured mouse mammary carcinoma spheroids in different concentrations of glucose and oxygen and studied how the nutrient concentrations affect the tumor size. To maintain a steady-state and constant-concentration medium, the authors replenished the spinner flask, in which the tumors were placed every 10–14 h. To measure the spheroid size, they measured two orthogonal diameters of the spheroids by means of an inverted microscope, which was fitted with a calibrated eyepiece reticule. After monitoring the tumors for 28 days, the team reported the growth rate of the tumor by obtaining the values of its volume over time. In the present paper, the simulation results are compared with their experimental data under 0.8 mM glucose and 0.28 mM oxygen medium concentrations. As previously discussed, a spherically symmetric tumor is exposed to the static, unlimited culture medium, and its growth kinematics has been monitored. It is assumed that the concentrations of the nutrients are constant in the culture medium since it is unlimited. The growth starts with a single cell, which will develop into a tumor spheroid containing proliferative, quiescent and necrotic zones [
26]. Using the proposed model, the simulation curve is obtained, which is in a good agreement with the experimental data of the EMT6/Ro spheroid, compared to the previous studies (
Figure 3a).
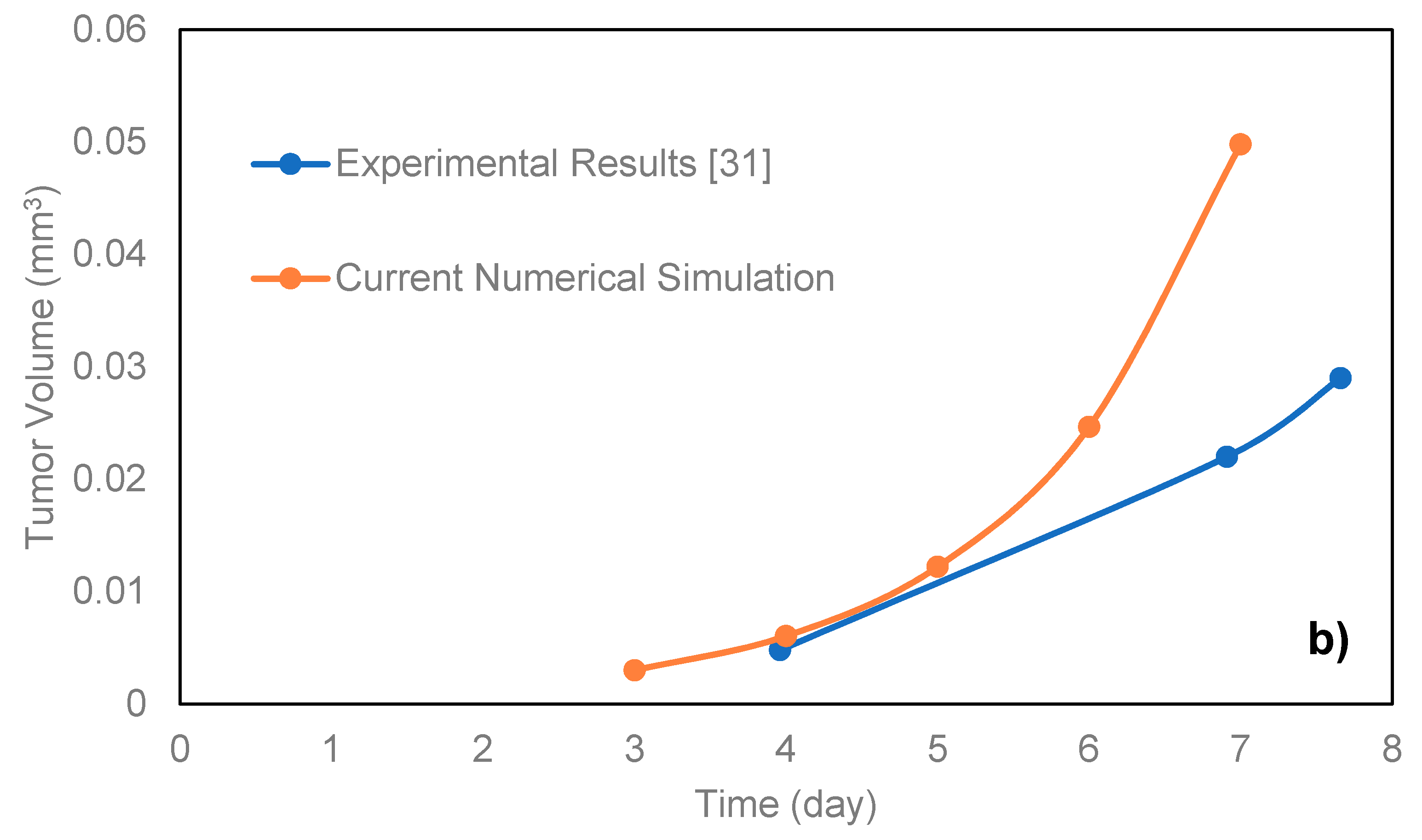
For the comparison of the proposed model with microfluidic systems, the exact relevant values of various parameters should be experimentally measured. As on-chip measurements of such parameters in a microfluidic platform require integration of related biosensors with the chip, there are very limited numbers of studies in this field. Here, the model was compared with the data of the microfluidic platforms proposed by Ziółkowska et al. [
31]. In that work, the authors used HT-29 human carcinoma cells cultured in a microfluidic system with microwell arrays in the form of multicellular spheroids with a cell density of 1.5 × 10
6 cells/mL. The authors only provided the exact value of the proliferation rate constant of HT-29. Here, we applied the model for the proliferating phase of the HT-29 tumor spheroids in the dynamic microwells,
Figure 3b. Although the general trend is achieved, there are some disagreements between the experimental and simulation results. This is directly due to the lack of knowledge about some necessary parameters of HT-29 cell line, such as the necrosis and apoptosis rates, the diffusion coefficient of the nutrients to the HT-29 tumor spheroids, as well as Michaelis-Menten parameters of the nutrients. The only known parameter was the proliferation rate constant, and the rest of the parameters were adopted from EMT6/Ro cell line. The better agreement could be achieved in future studies by replacing the exact parameters of HT-29.
4. Limitations and Suggestions
In the present study, the effect of extracellular matrix on tumor growth has not been considered. Actually spheroids in this examination are matrix-free. Certainly, the presence of extracellular matrix affects the distribution of oxygen and glucose [
34,
35] by changing the rate of diffusion and consumption. It is also a physical barrier to cell growth [
36]. This model can be developed to be used for such problem if the information on nutrients diffusion and consumption and growth parameters under this condition is available.
Another limitation is that only one cell type was examined in this study because the mentioned information on the other cell types is very limited. Therefore, experimental studies are necessary to obtain the required parameters for the simulation.
Tumor growth is divided into two stages, avascular and vascular growth [
37]. The present study, considering that it merely focused on avascular tumor growth, is only able to be used as a tool in designing drug therapies for patients with this stage of the disease. To this end, the drug concentration distribution equation in the tumor and the effect of drug concentration on the growth of cancer cells need to be added to the model. Such a model can also be used in combination with angiogenesis models to evaluate vascular tumor growth. It also can be utilized to study the growth of multicellular spheroids in other microfluidic systems containing concentration gradient generators and a variety of cell traps.
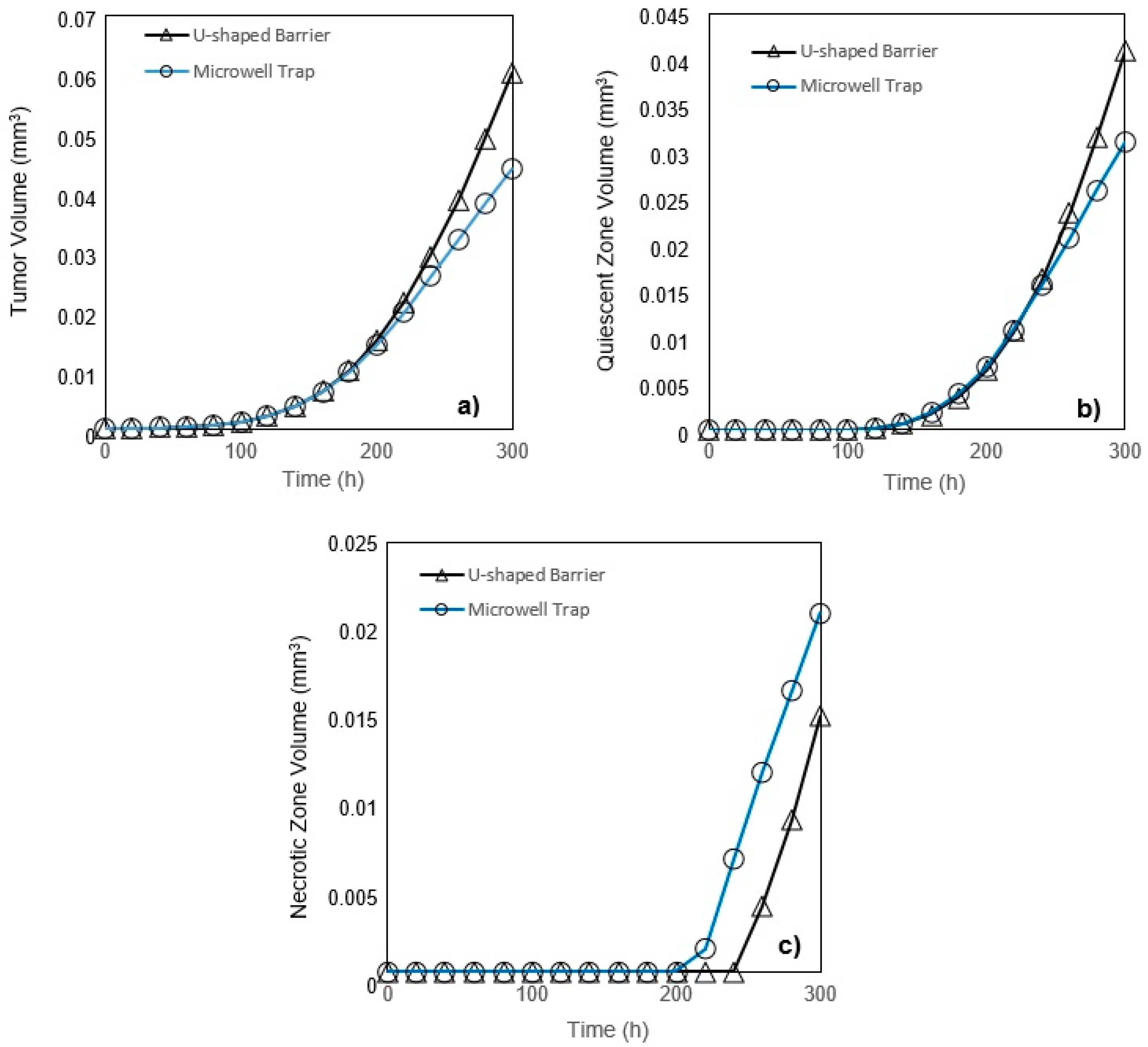
5. Conclusions
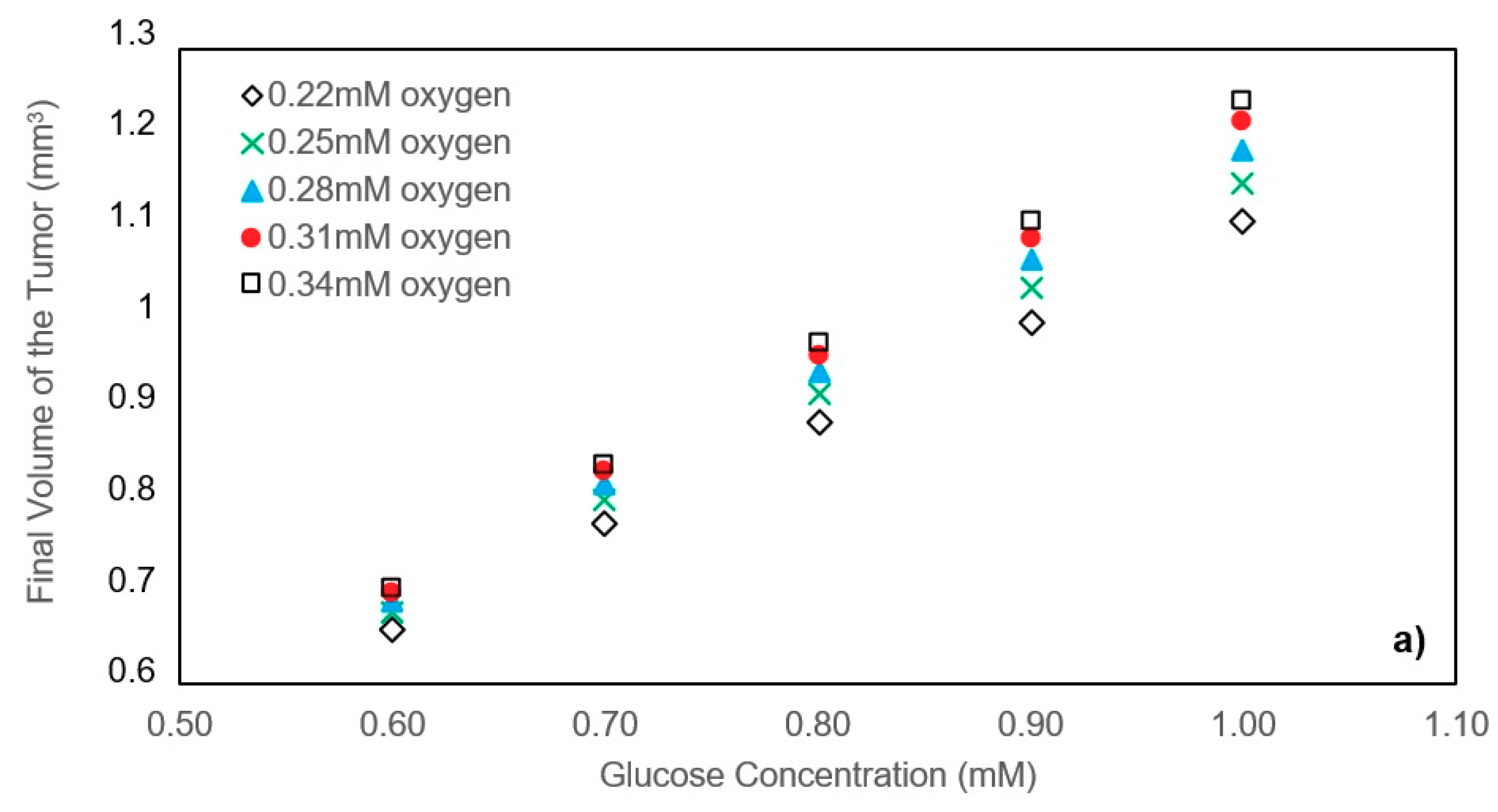
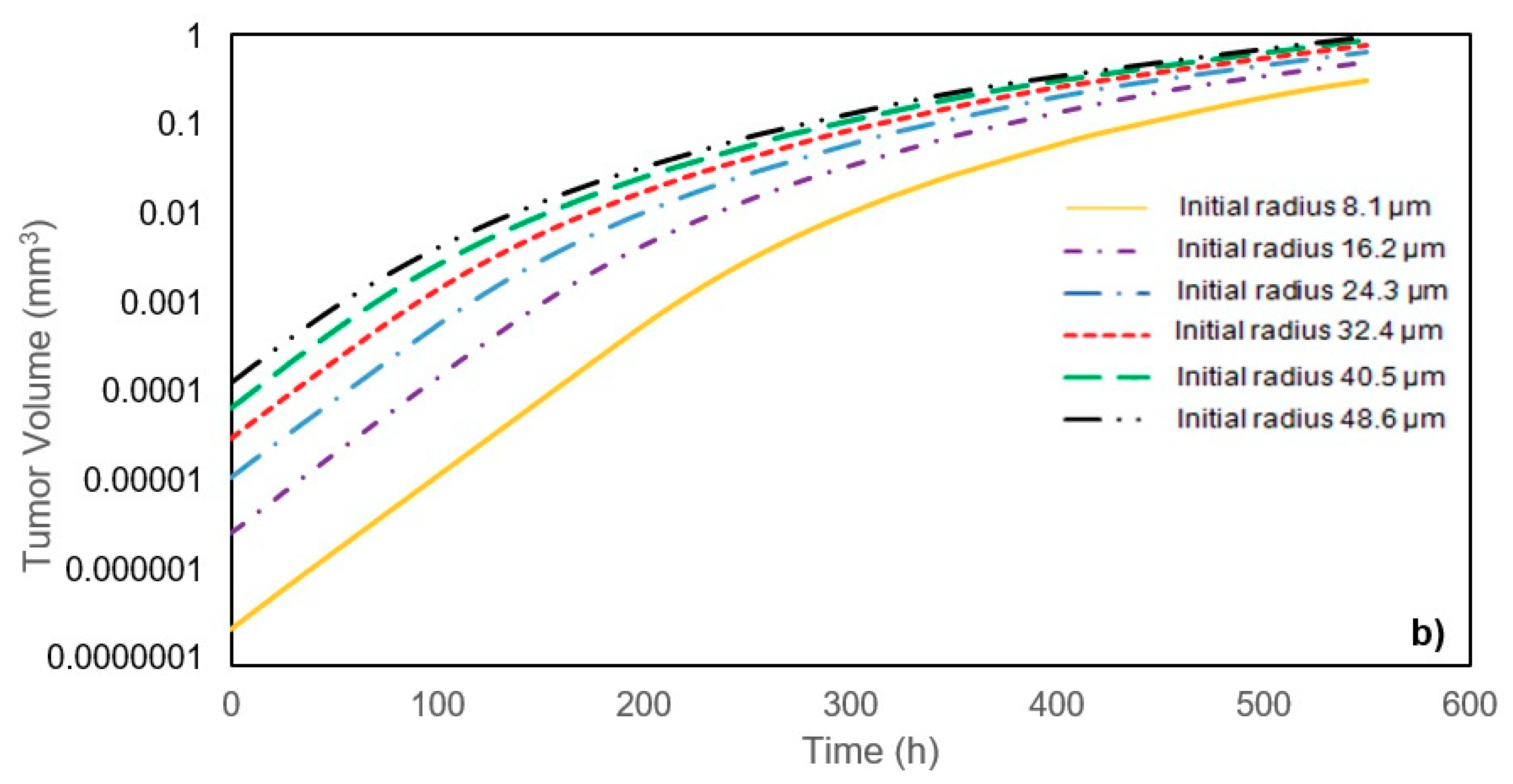
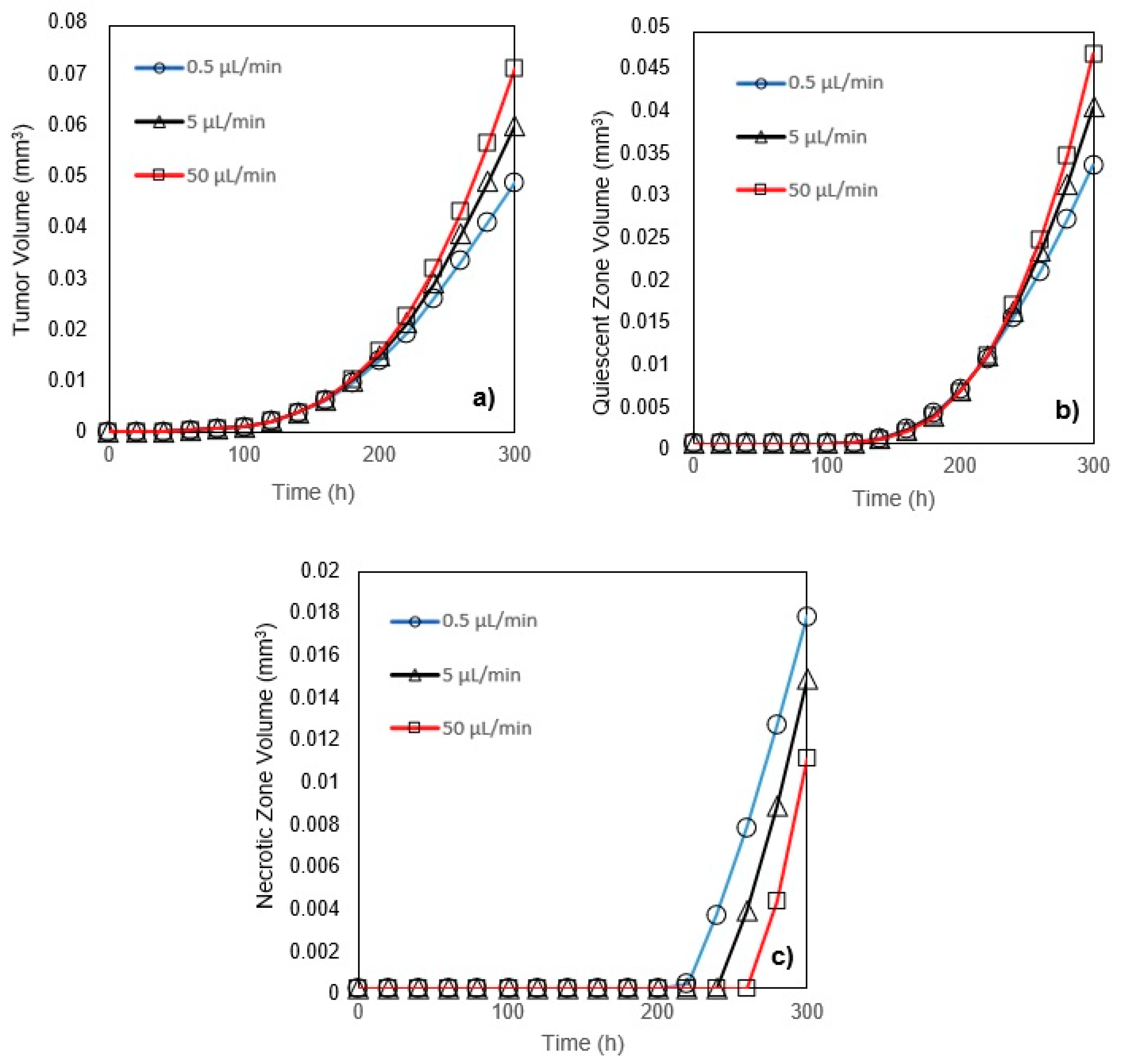
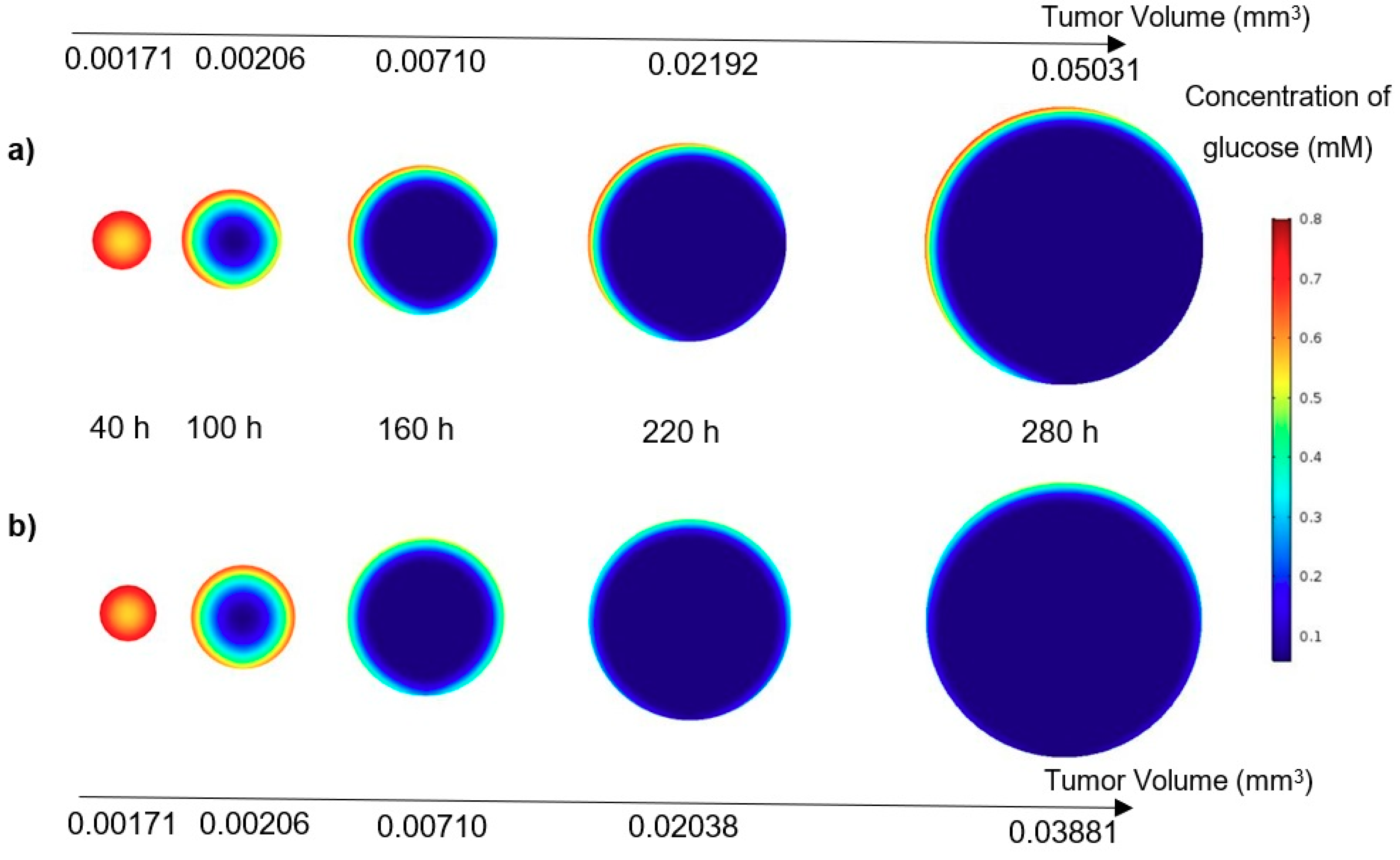
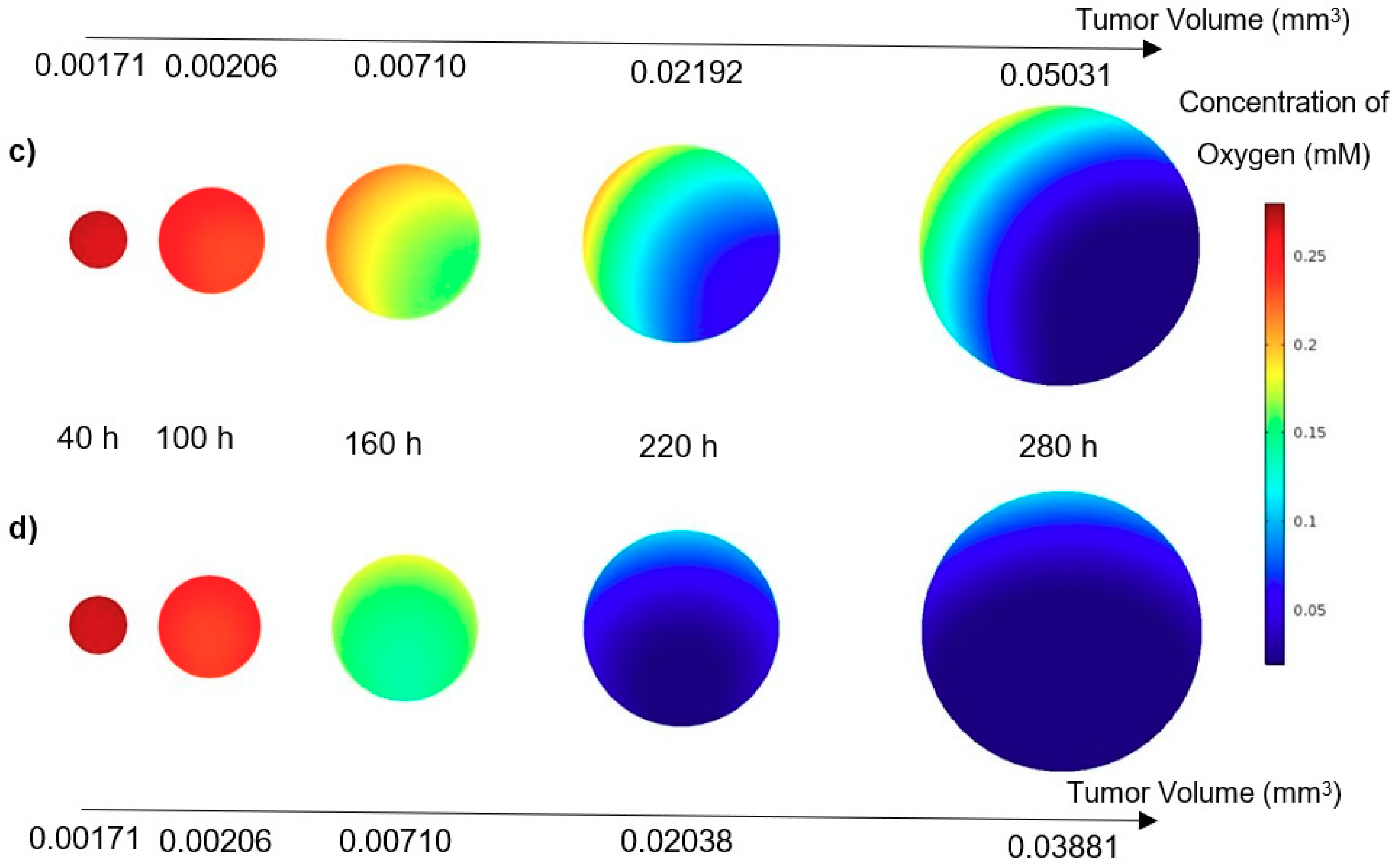
In this study, a modified mathematical model for tumor growth was first presented. In the modified model, it was considered that cells in the quiescent zone consume nutrients at the half rate of the proliferative zone consumption rate. Using the model for static, unlimited culture medium, the model was validated with the experimental data in the literature and was in an excellent agreement. By inspecting the effect of the nutrient concentrations on the growth of a tumor exposed to the static, unlimited culture medium, it was concluded that the determinative nutrient in retarding the tumor growth was glucose and that the concentrations of glucose and oxygen within the tumor respectively specify the volume of the quiescent and necrotic zones. In addition, by studying the growths of the tumors with different initial radii in the static, unlimited culture medium, we observed that the initial tumor radius does not significantly affect the final volume of the tumor. Then, by employing the equations concerned with the culture medium flow, the model was applied to the 3D growth of the tumor in the microfluidic system. The tumor growth in a microfluidic device containing a U-shaped barrier for three flow rates of the culture medium was investigated. The tumors developed faster when the inflow rate was increased, and nutrient delivery to the tumor surface was more difficult in microchannels with low inflow rate. Subsequently, the tumor growth in a microfluidic device containing a microwell trap was investigated. The results revealed that in equal inflow rate, the tumor grows slower in the microwell trap in comparison to the U-shaped barrier. The results also showed that the reduced velocity of the nutrient delivery to the tumor surface in the microwell trap was the reason of its slower growth rate, in comparison with the one in the U-shaped barrier. The approach of this study can be useful for further research on the growth of other tumor types in microfluidic devices. Furthermore, the proposed model can be helpful for experimental investigations in the growth of avascular tumor growth.