Efficient Fabrication Process of Ordered Metal Nanodot Arrays for Infrared Plasmonic Sensor
Abstract
1. Introduction
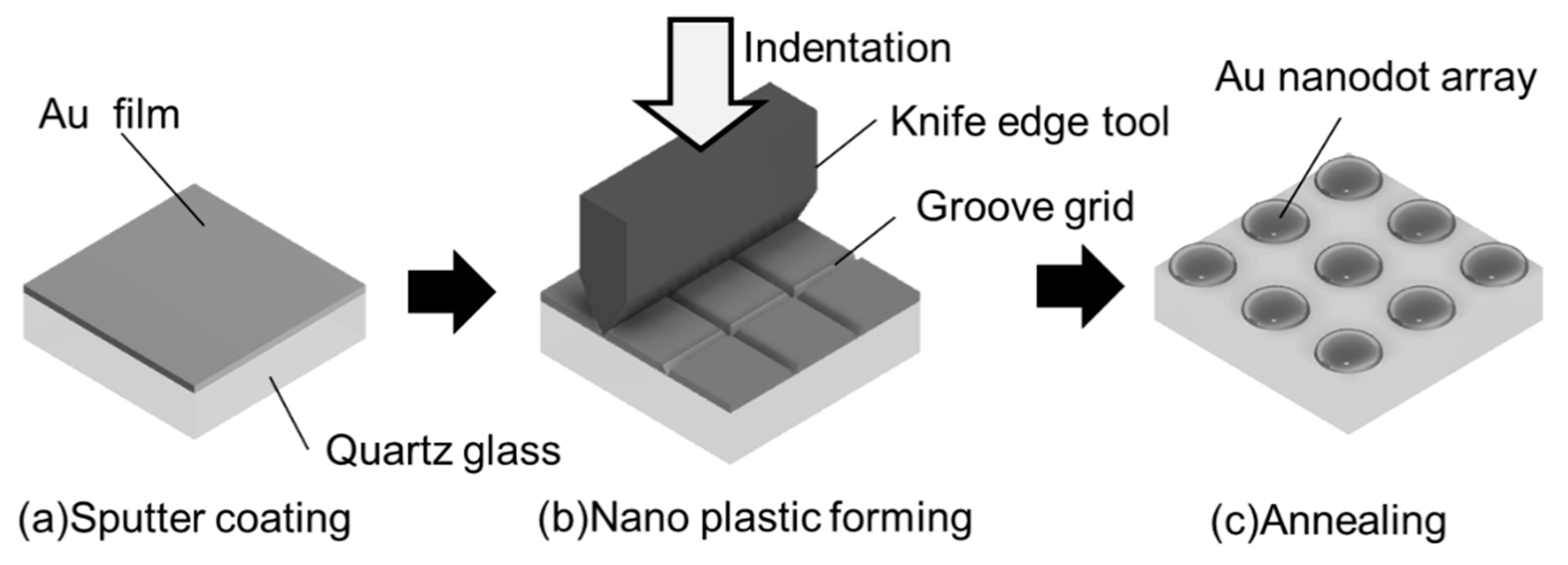
2. Fabrication Process for Metal Nanodot Array
3. Experimental Results and Agglomeration Mechanism by Thermal Dewetting
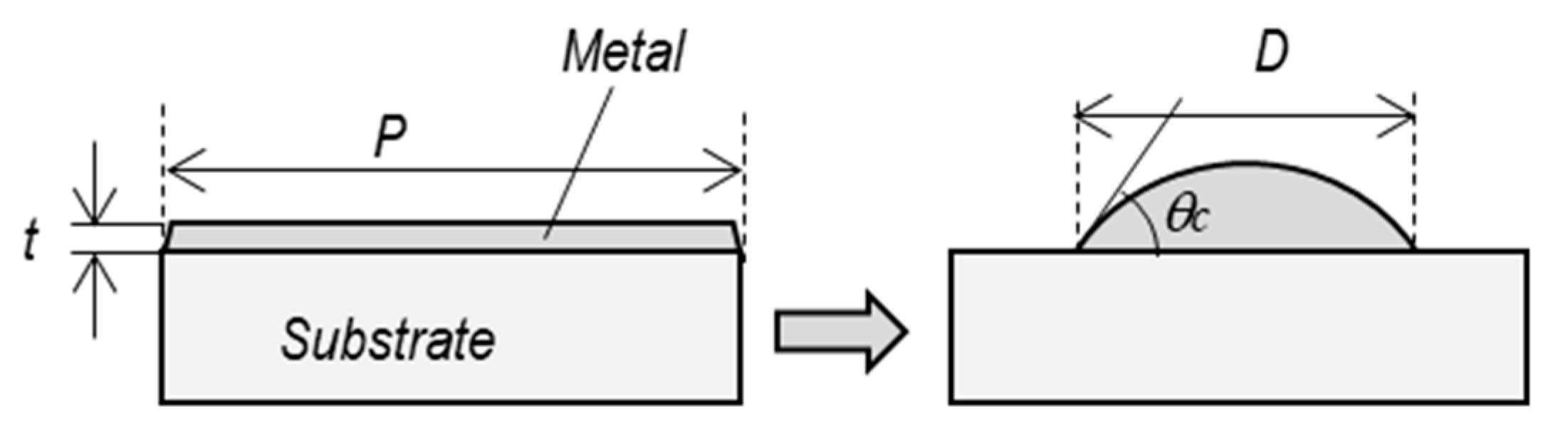
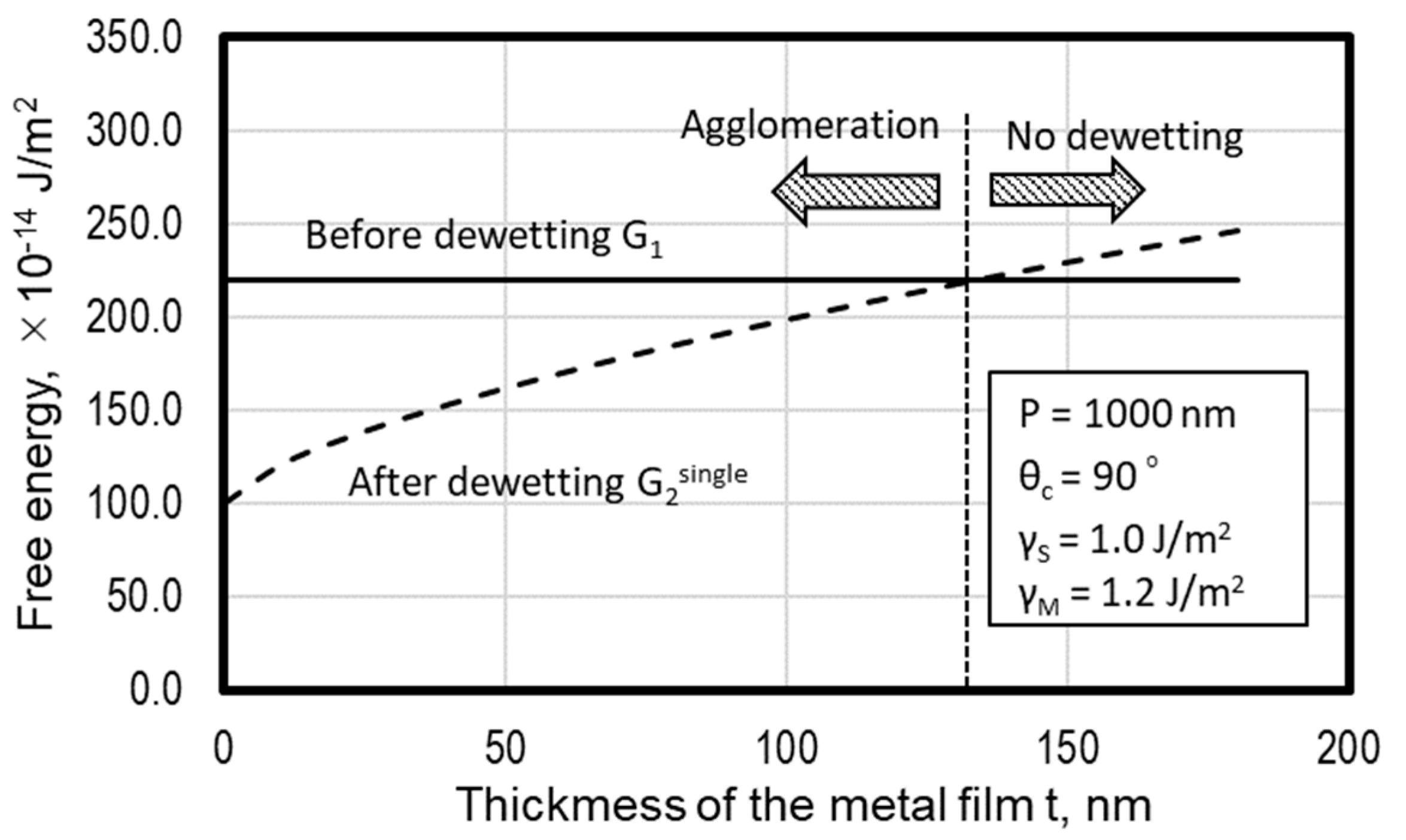
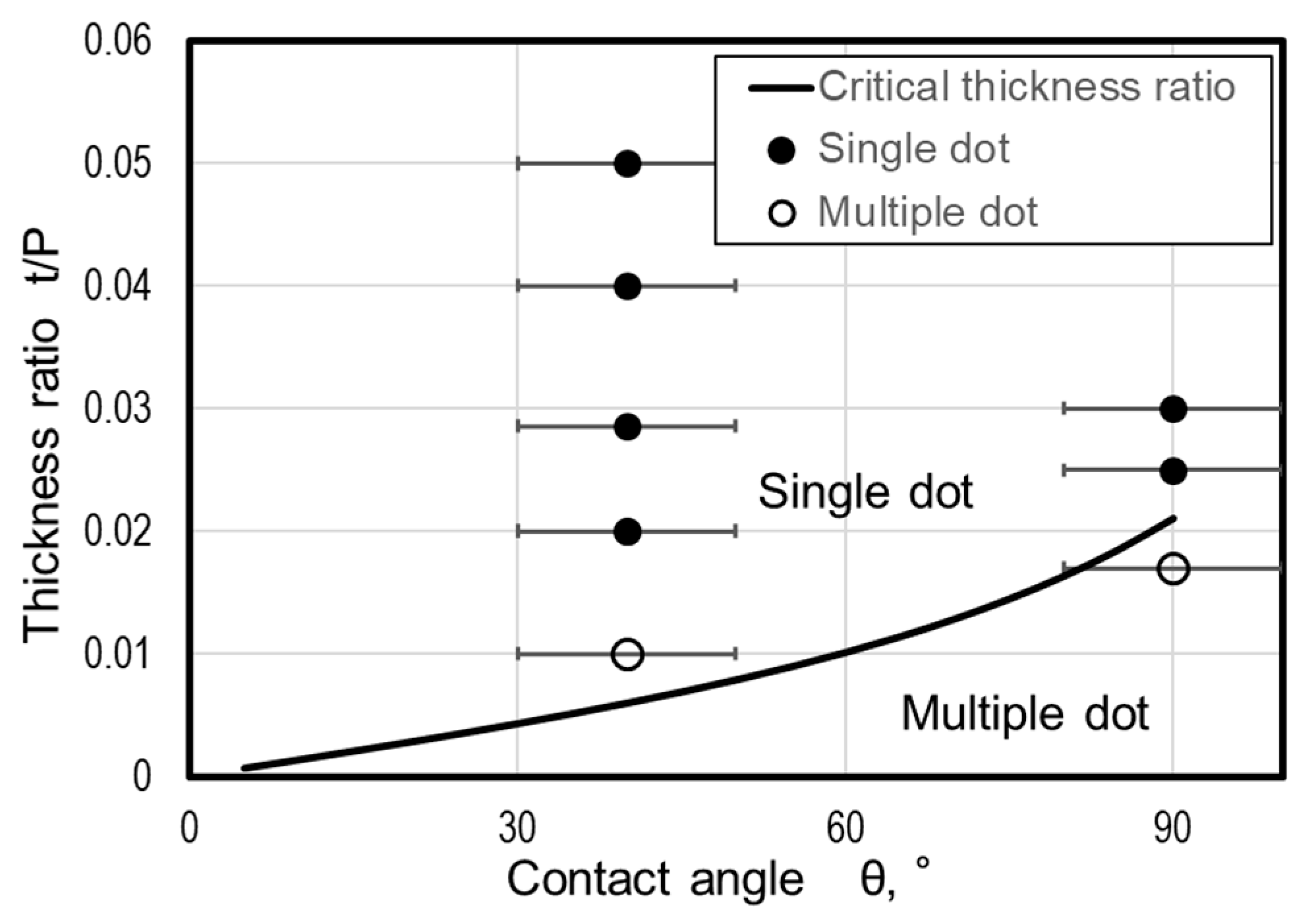
3.1. Agglomeration of a Single Nanodot
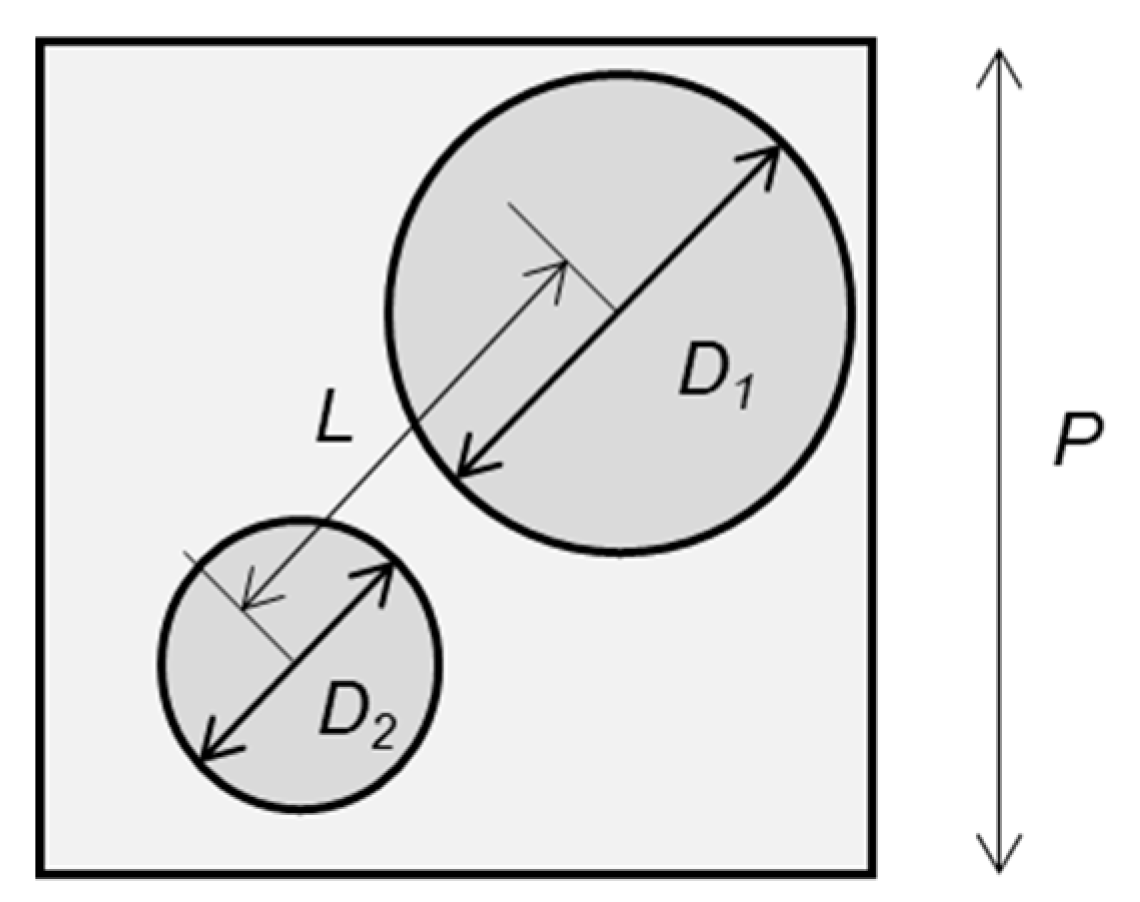
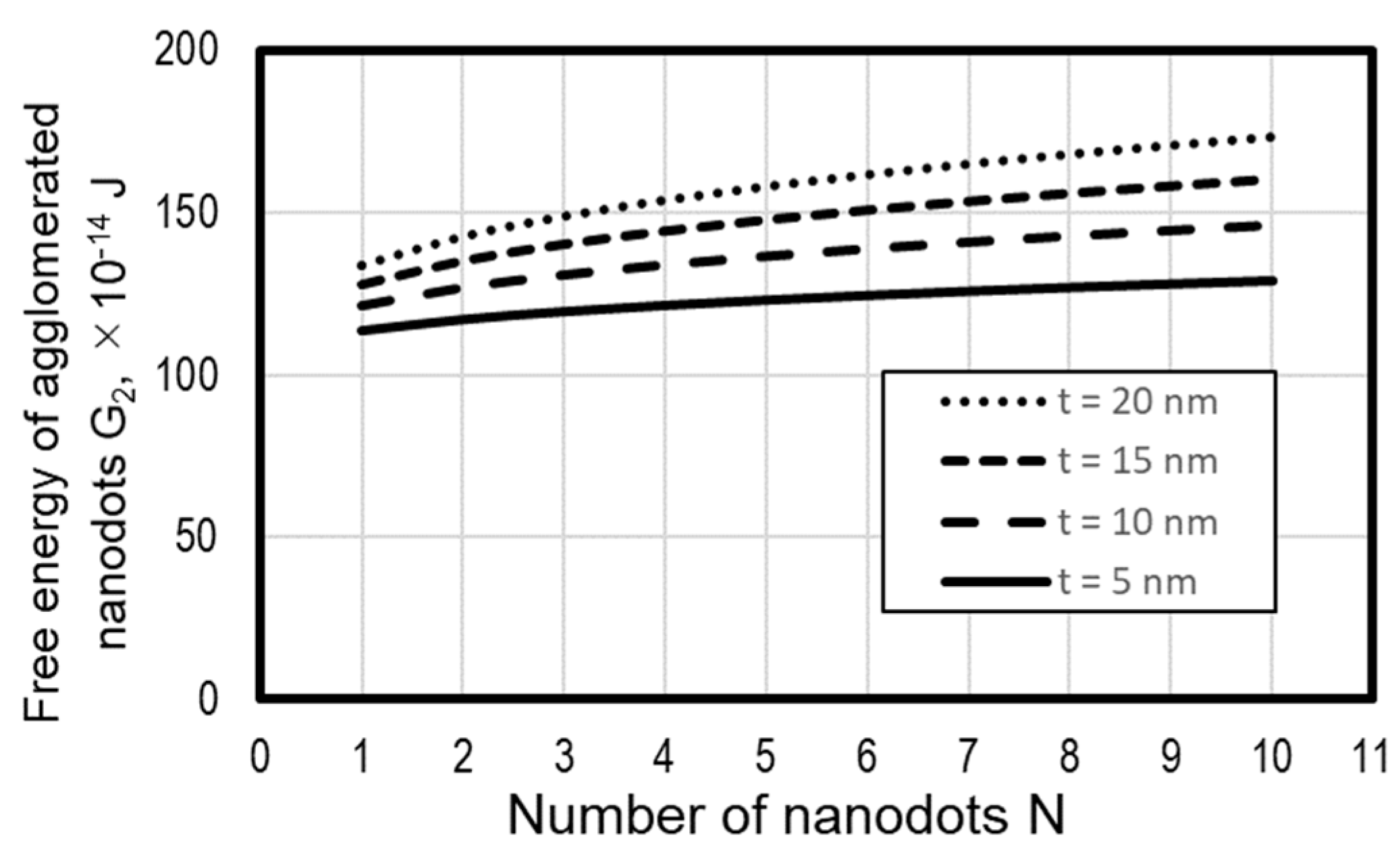
3.2. Agglomeration Mechanism of Multiple Nanodots
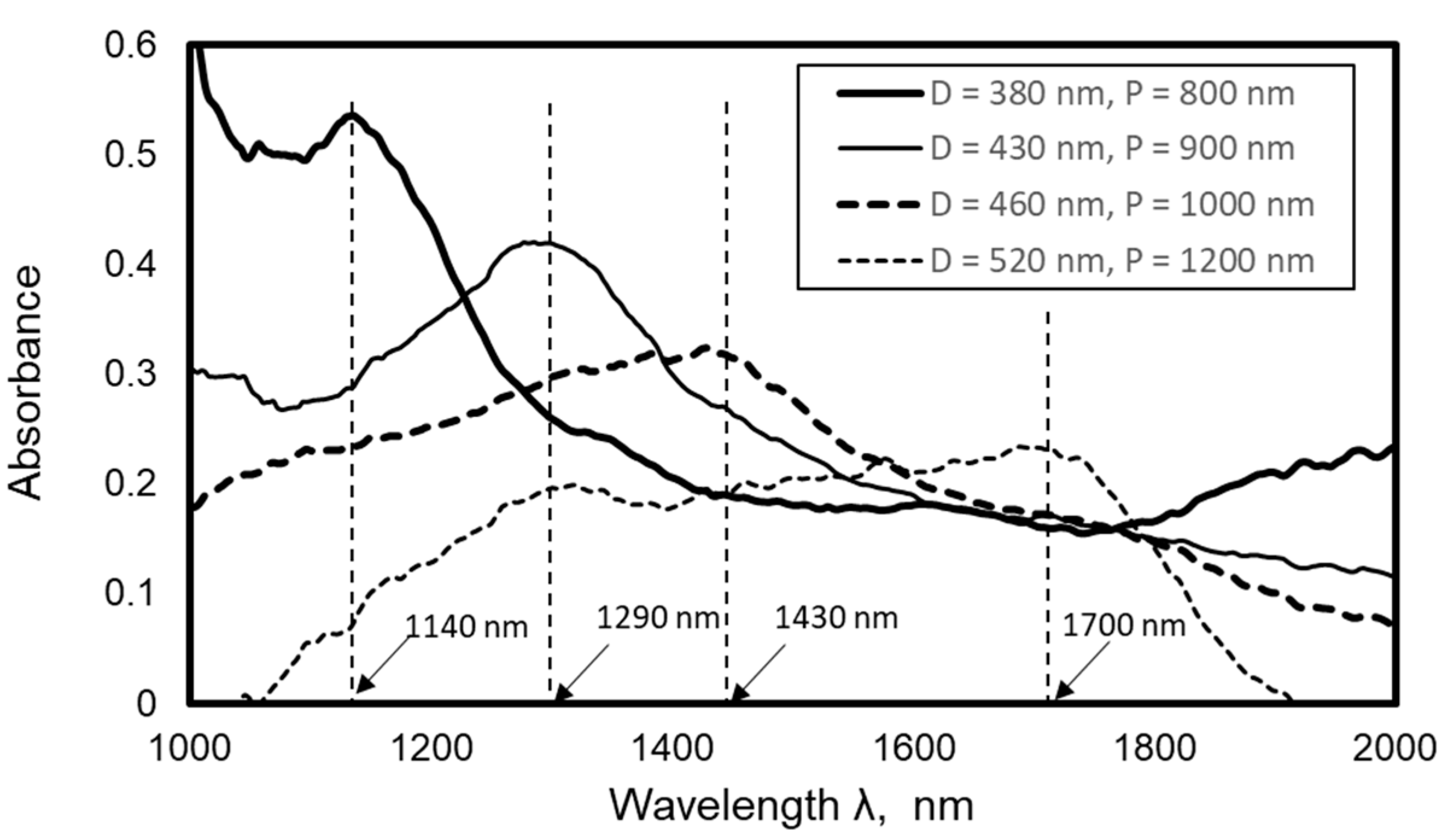
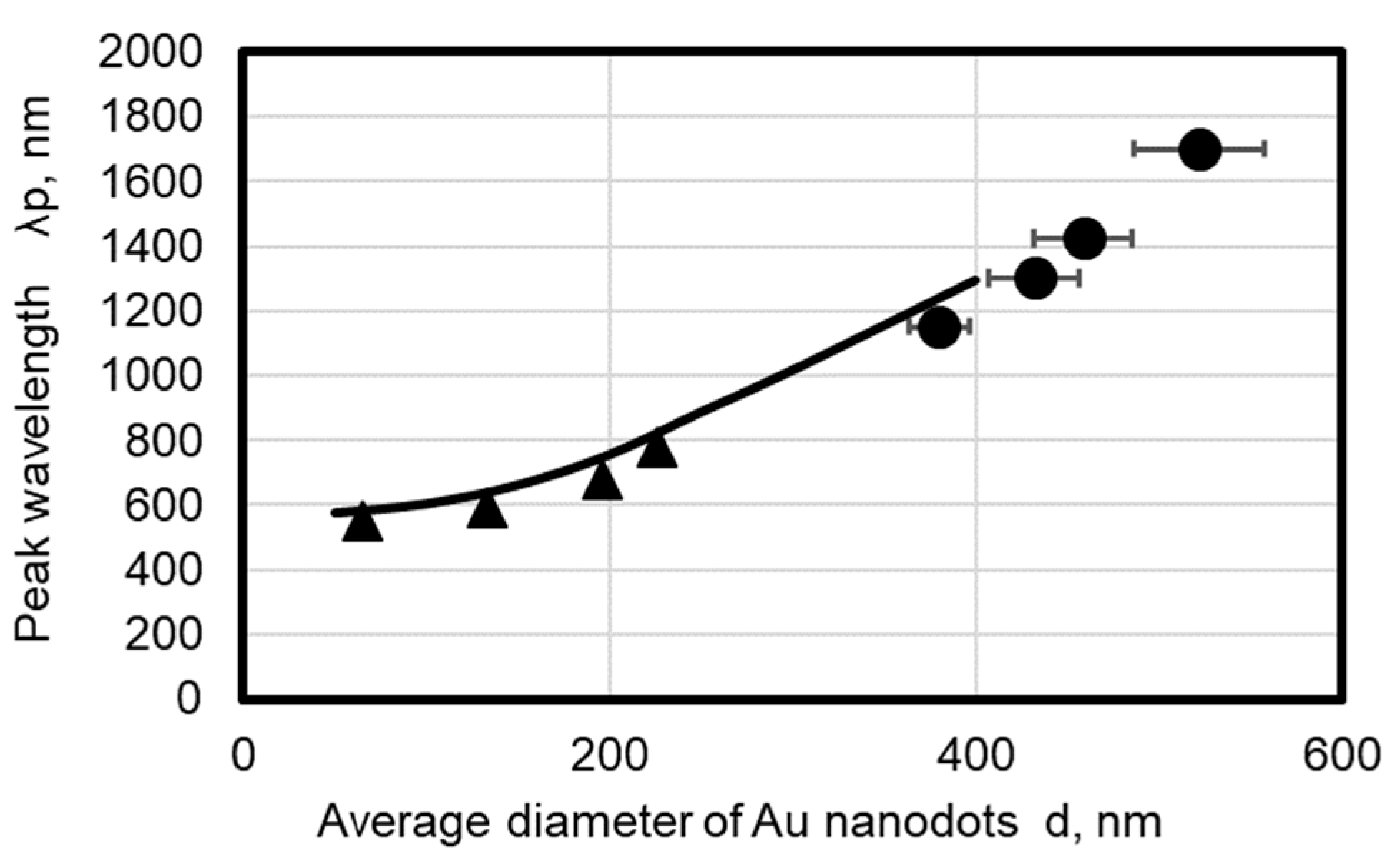
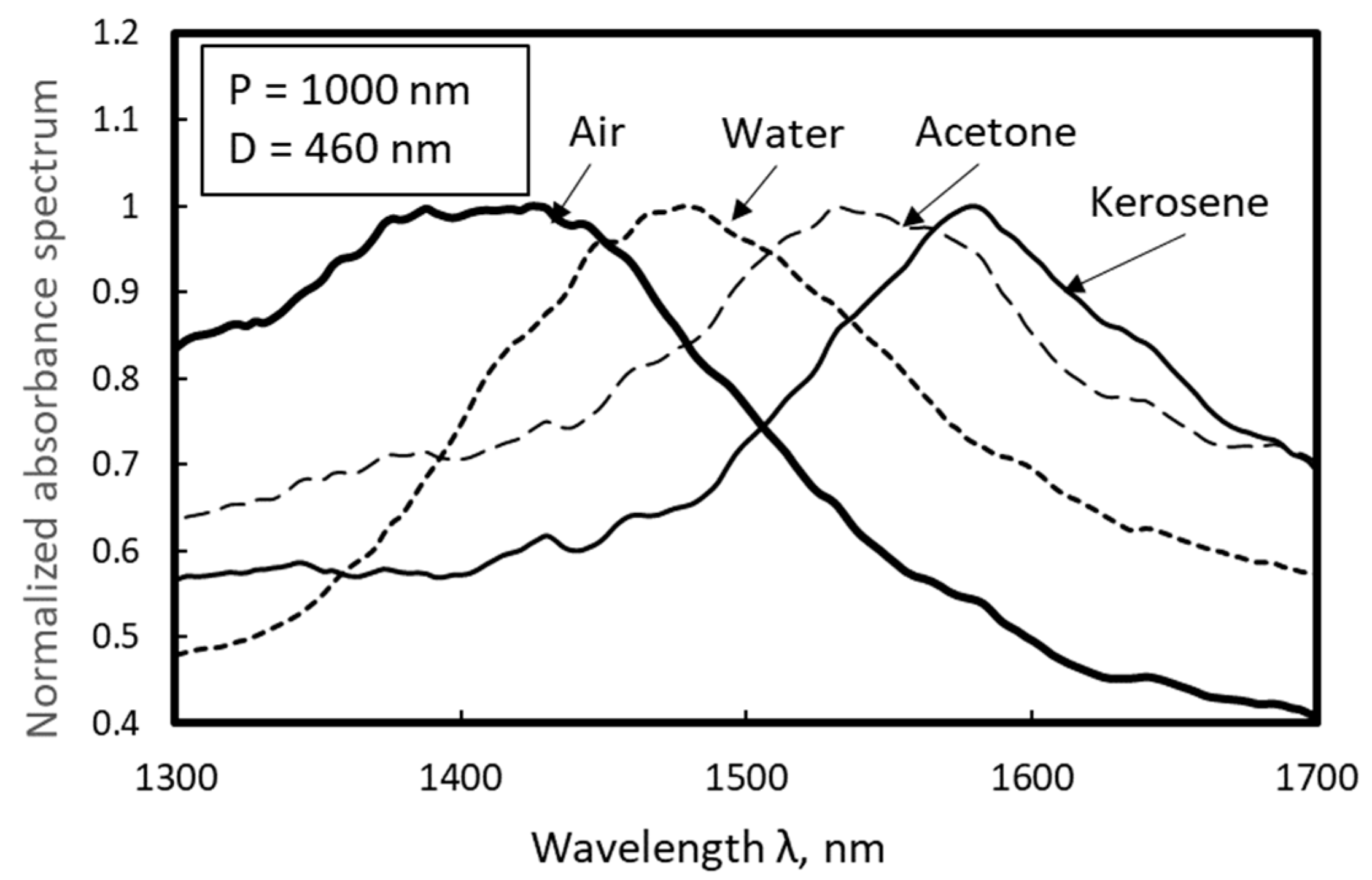
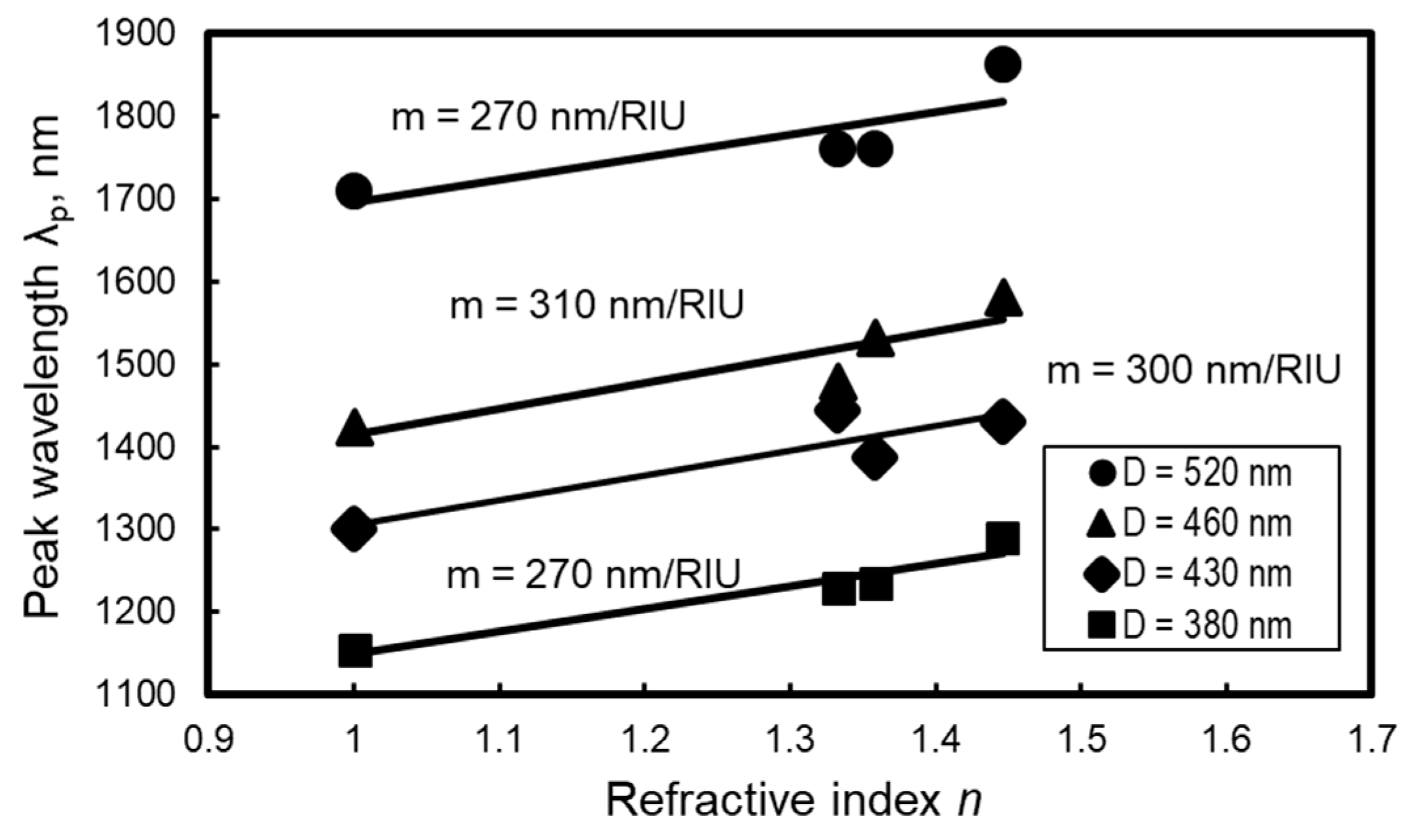
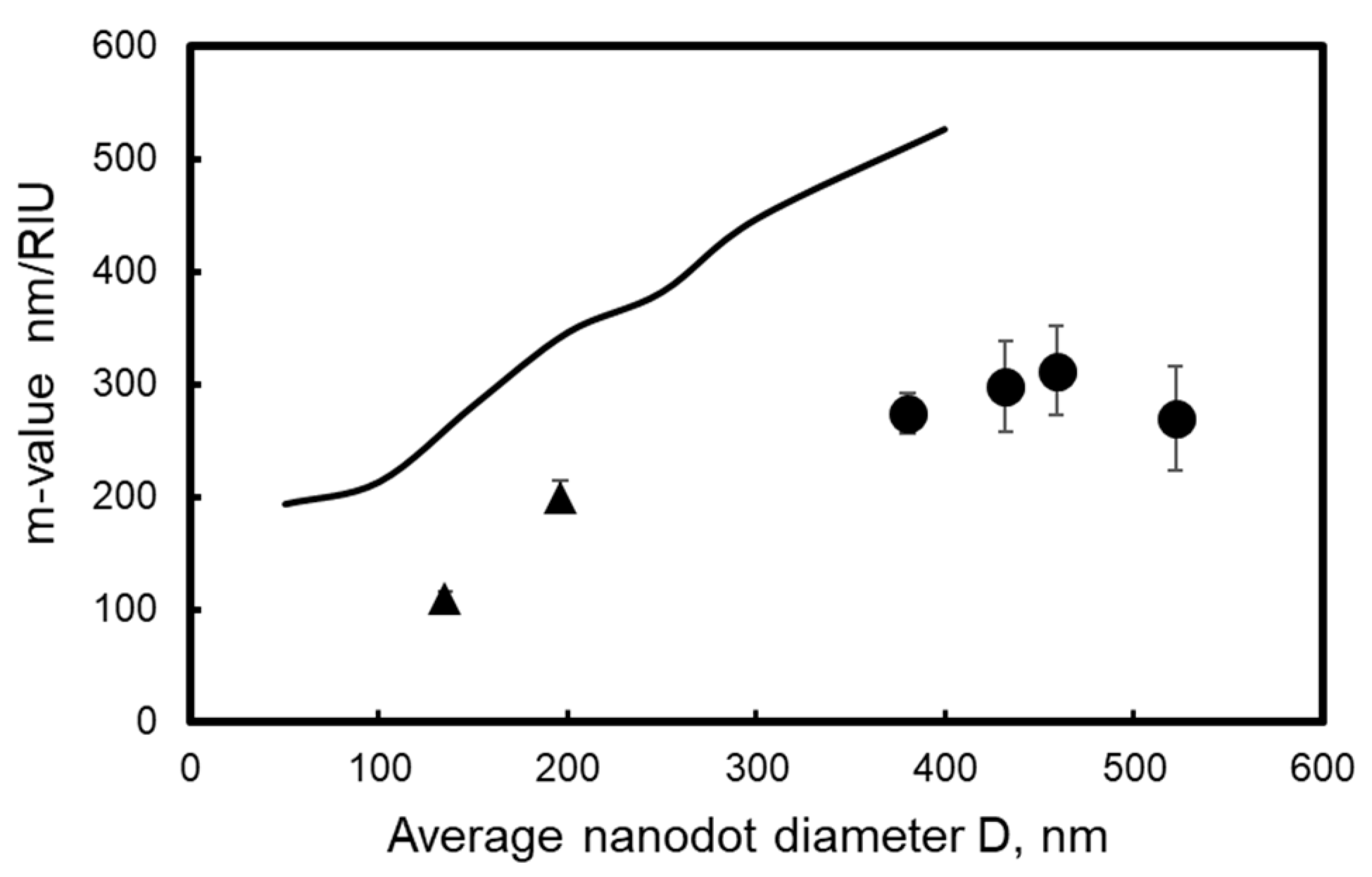
4. Optical Properties of Au Nanodot Arrays
5. Conclusion
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Number of Points | Average of Minimum Distance | Standard Deviation |
|---|---|---|
| 2 | 0.52106 | 0.24783 |
| 3 | 0.30556 | 0.16004 |
| 4 | 0.21179 | 0.10976 |
| 5 | 0.16233 | 0.08362 |
| 6 | 0.13189 | 0.06816 |
| 7 | 0.11103 | 0.05737 |
| 8 | 0.09583 | 0.04959 |
| 9 | 0.08436 | 0.04367 |
| 10 | 0.07538 | 0.03904 |
References
- Hossain, M.K.; Huang, G.G.; Kaneko, T. Characteristics of surface-enhanced Raman scattering and surface-enhanced fluorescence using a single and a double layer gold nanostructure. Phys. Chem. Chem. Phys. 2001, 11, 7484–7490. [Google Scholar] [CrossRef] [PubMed]
- Lahav, M.; Vaskevich, A.; Rubinstein, I. Biological sensing using transmission surface plasmon resonance spectroscopy. Langmuir 2004, 20, 7365–7367. [Google Scholar] [CrossRef] [PubMed]
- Leebeeck, A.D.; Kumar, L.K.S.; Lange, V.; Sinton, D.; Gordon, R.; Brolo, A.G. On-chip surface-based detection with nanohole arrays. Anal. Chem. 2007, 79, 4094–4100. [Google Scholar] [CrossRef] [PubMed]
- Gupta, G.; Tanaka, D.; Ito, Y.; Shibata, D.; Shimojo, M.; Furuya, K.; Mitsui, K.; Kajikawa, K. Absorption spectroscopy of gold nanoisland films: Optical and structural characterization. Nanotechnology 2009, 20, 025703. [Google Scholar] [CrossRef] [PubMed]
- Mader, M.; Perlt, S.; Höche, T.; Hilmer, H.; Grundmann, M.; Rauschenbach, B. Gold nanostructure matrices by diffraction mask-projection laser ablation: Extension to previously inaccessible substrates. Nanotechnology 2010, 21, 175304. [Google Scholar] [CrossRef]
- Yang, S.; Xu, F.; Ostendorp, S.; Wilde, C.; Zhao, H.; Lei, Y. Template-confined dewetting process to surface nanopatterns: Fabrication, structural tunability, and structure-related properties. Adv. Funct. Mater. 2011, 21, 2446–2455. [Google Scholar] [CrossRef]
- Smitha, S.L.; Gopchandran, K.G.; Ravindran, T.R.; Prasad, V.S. Gold nanorods with finely tunable longitudinal surface plasmon resonance as SERS substrates. Nanotechnology 2011, 22, 265705. [Google Scholar] [CrossRef]
- Hong, Y.; Huh, Y.M.; Yoon, D.S.; Yang, J. Nanobiosensors based on localized surface plasmon resonance for biomarker detection. J. Nanomater. 2013, 2012, 759830. [Google Scholar] [CrossRef]
- Jiang, R.; Chen, H.; Shao, L.; Li, Q.; Wang, J. Unraveling the evolution and nature of the plasmons in (au core)–(ag shell) nanorods. Adv. Opt. Mater. 2012, 24, 200–207. [Google Scholar] [CrossRef]
- Li, M.; Cushing, S.K.; Zhang, J.; Lankford, J.; Aguilar, Z.P.; Ma, D.; Wu, N. Shape-dependent surface-enhanced Raman scattering in gold–Raman-probe–silica sandwiched nanoparticles for biocompatible applications. Nanotechnology 2012, 23, 115501. [Google Scholar] [CrossRef]
- Sun, H.; Yu, M.; Wang, G.; Sun, X.; Lian, J. Temperature-Dependent Morphology Evolution and Surface Plasmon Absorption of Ultrathin Gold Island Films. J. Phys. Chem. C 2012, 116, 9000–9008. [Google Scholar] [CrossRef]
- Pinhas, H.; Malka, D.; Danan, Y.; Sinvani, M.; Zalevsky, Z. Design of fiber-integrated tunable thermo-optic C-band filter based on coated silicon slab. J. Eur. Opt. Soc.-Rapid Publ. 2017, 13. [Google Scholar] [CrossRef]
- Zhang, B.; Zhao, Y.; Hao, Q.; Kiraly, B.; Khoo, I.-C.; Chen, S.; Huang, T.J. Polarization-independent dual-band infrared perfect absorber based on a metal-dielectric-metal elliptical nanodisk array. Opt. Express 2011, 19, 15221–15228. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Mesch, M.; Weiss, T.; Hentschel, M.; Giessen, H. Infrared Perfect Absorber and Its Application As Plasmonic Sensor. NANO Lett. 2010, 10, 2342–2348. [Google Scholar] [CrossRef] [PubMed]
- Rodrigo, D.; Limaj, O.; Janner, D.; Etezadi, D.; Javier de Abajo, F.; Pruneri, V.; Altug, H. Mid-infrared plasmonic biosensing with graphene. Science 2015, 349, 165–168. [Google Scholar] [CrossRef] [PubMed]
- Diem, M.; Koschny, T.; Soukoulis, C.M. Wide-angle perfect absorber/thermal emitter in the terahertz regime. Phys. Rev. B 2009, 79, 033101. [Google Scholar] [CrossRef]
- Zheng, B.Y.; Huang, T.J.; Desai, A.Y.; Wang, S.J.; Tan, L.K.; Gao, H.; Huan, A.C.H. Thermal behavior of localized surface plasmon resonance of Au/TiO2 core/shell nanoparticle arrays. Appl. Phys. Lett. 2007, 90, 183117. [Google Scholar] [CrossRef]
- Chen, A.; Cua, S.J.; Chen, P.; Chen, X.Y.; Jian, L.K. Fabrication of sub-100-nm patterns in SiO2 templates by electron-beam lithography for the growth of periodic III-V semiconductor nanostructures. Nanotechnology 2006, 17, 3903–3908. [Google Scholar] [CrossRef]
- Dolling, G.; Enkrich, C.; Wegener, M. Low-loss negative-index metamaterial at telecommunication wavelengths. Opt. Lett. 2006, 31, 1800–1802. [Google Scholar] [CrossRef]
- Valentine, J.; Zhang, S.; Zentgraf, T.; Ulin-Avila1, E.; Genov, D.A.; Bartal, G.; Zhang, X. Three-dimensional optical metamaterial with a negative refractive index. Nature 2008, 455, 376–380. [Google Scholar] [CrossRef]
- Zin, M.T.; Leong, K.; Wong, N.Y.; Ma, H.; Sarikawa, M.; Jen, A.K.Y. Surface-plasmon-enhanced fluorescence from periodic quantum dot arrays through distance control using biomolecular linkers. Nanotechnology 2009, 20, 015305. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y.; Xu, J.; Fung, K.H.; Jin, Y.; Kumar, A.; He, S.; Fang, N.X. A thin film broadband absorber based on multi-sized nanoantennas. Appl. Phys. Lett. 2011, 99, 253101. [Google Scholar] [CrossRef]
- Chou, S.Y.; Krauss, P.R.; Renstrom, P.J. Imprint of sub-25 nm vias and trenches in polymers. Science 1996, 272, 85–87. [Google Scholar] [CrossRef]
- Chou, S.Y.; Keimel, C.; Gu, J. Ultrafast and direct imprint of nanostructures in silicon. Nature 2002, 417, 835–837. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.C.; Wang, C.K.; Huang, J.B.; Hong, L.S. A nanoporus AlN layer patterned by anodic aluminum oxide and its application as a buffer layer in a GaN-based light-emitting diode. Nanotechnology 2009, 20, 085303. [Google Scholar] [CrossRef] [PubMed]
- Yanagisita, T.; Nishio, K.; Masuda, H. Anti-Reflection structures on lenses by nanoimprinting using ordered anodic poruous alumina. Appl. Phys. Express 2009, 2, 022001. [Google Scholar] [CrossRef]
- Reilly, T.H., III; van de Lagemaat, J.; Tenent, R.C.; Morfa, A.J.; Rowlen, K.L. Surface-plasmon enhanced transparent electrodes in organic photovoltaics. Appl. Phys. Lett. 2008, 92, 243304. [Google Scholar] [CrossRef]
- Ren, Z.; Zhang, X.; Zhang, J.; Li, Z.; Yang, B. Building cavities in microspheres and nanospheres. Nanotechnology 2009, 20, 065305. [Google Scholar] [CrossRef]
- Huang, C.H.; Igarashi, M.; Wone, M.; Uraoka, Y.; Fuyuki, T.; Takeguchi, M.; Yamashita, I.; Samukawa, S. Two-dimensional si-nanodisk array fabricated using bio-nano-process and neutral beam etching for realistic quantum effect devices. Jpn. J. Appl. Phys. 2009, 48, 04C187. [Google Scholar] [CrossRef]
- Chang, C.H.; Tian, L.; Hesse, W.R.; Gal, H.; Choi, H.J.; Kim, J.G.; Siddiqui, M.; Barbastathis, G. From two-dimensional colloidal self-assembly to three-dimensional nanolithography. Nano Lett. 2011, 11, 2533–2537. [Google Scholar] [CrossRef]
- Yoshino, M.; Ohsawa, H.; Yamanaka, A. Rapid fabrication of an ordered nano-dot array by the combination of nano plastic forming and annealing method. J. Micromech. Microeng. 2011, 21, 125017. [Google Scholar] [CrossRef]
- Li, Z.; Yoshino, M.; Yamanaka, A. Fabrication of three dimensional ordered nanodot array structures by thermal dewetting method. Nanotechnology 2012, 23, 485303. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Yoshino, M.; Yamanaka, A. Regularly-formed three-dimensional gold nanodot array with controllable optical properties. J. Micromech. Microeng. 2014, 24, 045011. [Google Scholar] [CrossRef]
- Yoshino, M.; Nagamatsu, A.; Li, Z.; Yamanaka, A.; Yamamoto, T. Optical property of metallic nanodot arrays fabricated by combination of nano plastic forming and thermal dewetting method. Trans. JSME 2014, 80, 1–13. [Google Scholar]
- Yoshino, M.; Li, Z.; Terano, M. Theoretical and experimental study of metallic dot agglomeration induced by thermal dewetting. ASME J. Micro Nano-Manuf. 2015, 3, 021004. [Google Scholar] [CrossRef]
- Li, Z.; Dao, T.D.; Nagao, T.; Yoshino, M. Optical properties of ordered dot-on-plate nano-sandwich arrays. Microelectron. Eng. 2014, 127, 34–39. [Google Scholar] [CrossRef]
- Li, Z.; Dao, T.D.; Nagao, T.; Terano, M.; Yoshino, M. Fabrication of plasmonic nanopillar arrays based on nanoforming. Microelectron. Eng. 2015, 139, 7–12. [Google Scholar] [CrossRef]
- Mullins, W.W. Theory of Thermal Grooving. J. Appl. Phys. 1957, 28, 333–339. [Google Scholar] [CrossRef]
- Jiran, E.; Thompson, C.V. Capillary instabilities in thin films. J. Electron. Mater. 1990, 19, 1153–1160. [Google Scholar] [CrossRef]
- McCallum, M.S.; Voorhees, P.W.; Miksis, M.J.; Davis, S.H.; Wong, H. Capillary instabilities in solid thin films: Lines. J. Appl. Phys. 1996, 79, 7604–7611. [Google Scholar] [CrossRef]
- Danielson, D.T.; Sparacin, D.K.; Michel, J.; Kimerling, L.C. Surface-energy-driven dewetting theory of silicon-on-insulator agglomeration. J. Appl. Phys. 2006, 100, 083507. [Google Scholar] [CrossRef]
- Young, T. An essay on the cohesion of fluids. Philos. Trans. R. Soc. Lond. 1805, 95, 65–87. [Google Scholar] [CrossRef]
- Cheynis, F.; Bussmann, E.; Leroy, F.; Passanante, T.; Muller, P. Dewetting dynamics of silicon-on-insulator thin films. Phys. Rev. B 2011, 84, 245439. [Google Scholar] [CrossRef]
- Rayleigh, L. On the instability of jets. Proc. Lond. Math. Soc. 1878, S1–10, 4–13. [Google Scholar] [CrossRef]
- Zhigal’skii, G.P.; Jones, B.K. The Physical Properties of Thin Metal Films; Taylor & Francis: London, UK, 2003. [Google Scholar]
- Kuwata, H.; Tamaru, H.; Esumi, K.; Miyano, K. Resonant light scattering from metal nanoparticles: Practical analysis beyond Rayleigh approximation. Appl. Phys. Lett. 2003, 83, 4625–4627. [Google Scholar] [CrossRef]
- Hanarp, P.; Kall, M.; Sutherland, D.S. Optical properties of short range ordered arrays of nanometer gold disks prepared by colloidal lithography. J. Phys. Chem. B 2003, 107, 5768–5772. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical constants of the noble metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: New York, NY, USA, 1983; pp. 136–148. [Google Scholar]



| Thickness of Gold Film t, nm | Grid Size P, nm | Annealing Temperature T, °C | Annealing Time, min |
|---|---|---|---|
| 5 | 50, 75, 100, 175, 250 | 700 | 10 |
| 10 | 250, 500, 1000 | 700 | 10 |
| 30 | 800, 900 | 1000 | 10 |
| 40 | 1000, 1200 | 1000 | 10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoshino, M.; Kubota, Y.; Nakagawa, Y.; Terano, M. Efficient Fabrication Process of Ordered Metal Nanodot Arrays for Infrared Plasmonic Sensor. Micromachines 2019, 10, 385. https://doi.org/10.3390/mi10060385
Yoshino M, Kubota Y, Nakagawa Y, Terano M. Efficient Fabrication Process of Ordered Metal Nanodot Arrays for Infrared Plasmonic Sensor. Micromachines. 2019; 10(6):385. https://doi.org/10.3390/mi10060385
Chicago/Turabian StyleYoshino, Masahiko, Yusuke Kubota, Yuki Nakagawa, and Motoki Terano. 2019. "Efficient Fabrication Process of Ordered Metal Nanodot Arrays for Infrared Plasmonic Sensor" Micromachines 10, no. 6: 385. https://doi.org/10.3390/mi10060385
APA StyleYoshino, M., Kubota, Y., Nakagawa, Y., & Terano, M. (2019). Efficient Fabrication Process of Ordered Metal Nanodot Arrays for Infrared Plasmonic Sensor. Micromachines, 10(6), 385. https://doi.org/10.3390/mi10060385





