1. Introduction
With the increasing importance of conventional ammunition guidance in modern war, developing technology to realize the navigation control and trajectory real-time correction of conventional ammunition is key [
1]. Accurate measurement of attitude information of the guided projectile is the basis for precise guidance and control. The inertial navigation system (INS) is a fully autonomous navigation system based on Newton’s law of inertia, and can provide attitude, velocity, and position information without the influence of terrain, weather, and time [
2], therefore, INS plays an irreplaceable role in conventional weapon guidance. At present, microelectromechanical system (MEMS) sensors are suitable for projectile-borne applications in terms of size, cost, consumption, and anti-overload ability [
3]. When a MEMS strapdown inertial measurement system is used to measure the attitudes of high-spinning projectiles, the large dynamic range of MEMS inertial sensor is required, meanwhile, the high precision of MEMS inertial sensors is very important [
4]. However, the fact that the noise properties of a typical MEMS gyroscope lead to large accumulative errors makes it difficult for the strapdown INS (SINS) to accurately measure the roll angle. Due to many factors, such as the manufacturing level of MEMS inertial devices, integrated design of high-performance detection circuits, and high-reliability packaging, improving the accuracy of MEMS sensors in a short time is difficult [
5].
In practice, due to factors such as the application environment and sensor error, the system usually exhibits nonlinear and non-Gaussian problems, and the common filtering method is no longer applicable. Instead, an advanced filtering algorithm plays the central role. Gustafsson et al. explored the relationship between extended Kalman filter (EKF) and unscented Kalman filter (UKF). For nonlinear filtering problems where the nonlinearity is severe compared to the prior state information, the performance of UKF is significantly better than EKF [
6]. Another good way to deal with nonlinear filtering problems is particle filter (PF), which is a sequential Monte Carlo methodology where the basic idea is the recursive computation of relevant probability distributions using the concepts of importance sampling and approximation of probability distributions with discrete random measures, and good anti-noise and stability [
7]. Martino et al. designed a sequential Monte Carlo scheme for the dual purpose of Bayesian inference and model selection, and used interacting parallel particle filters, each one addressing a different model. The robustness is greatly improved [
8].
At the same time, the high accuracy measurement of high-spinning projectile attitude has attracted a lot of attention in recent years. Schuler et al. proposed the method of measuring the rotational motion of the carrier with the accelerometers in 1967, which was also known as gyro-free SINS (GF-SINS) [
9]. In theory, GF-SINS requires a minimum of 6 sensors. However, it has been shown in various works of literature that at least nine accelerometers, or even twelve, are required to improve the stability and accuracy of the system. Moreover, due to the precession and nutation of the projectile during high-dynamic flight, its normal acceleration will be affected by the aerodynamic lift, which affects the accuracy of the speed measurement.
With the development of control and guided technology, many new foreign weapons adopt the GPS/INS in recent years. Fairfax et al. proposed an algorithm for estimating the position and velocity of projectiles, which established the point mass (PM) flight dynamics model in the EKF model using the inertial measurement unit (IMU), attitude, and global positioning system (GPS) information. Measurement parameters are estimated in flight with a moving average filter (MAF) using GPS/INS loose coupling [
10]. However, the method of GPS/INS integrated navigation still relies on external information and cannot achieve complete autonomous navigation. Similarly, the solar azimuth measurement method can also be used to measure the attitude of the projectile, and has the ability to resist high overload, but it is susceptible to the weather.
Above all, we still choose the MEMS-IMU (MIMU) to measure the velocity, position, and attitude information. To solve the contradiction between high range and high precision, the concept of semi-strapdown inertial navigation system (SSINS) was proposed by the Key Laboratory of Instrumentation Science and Dynamic Measurement [
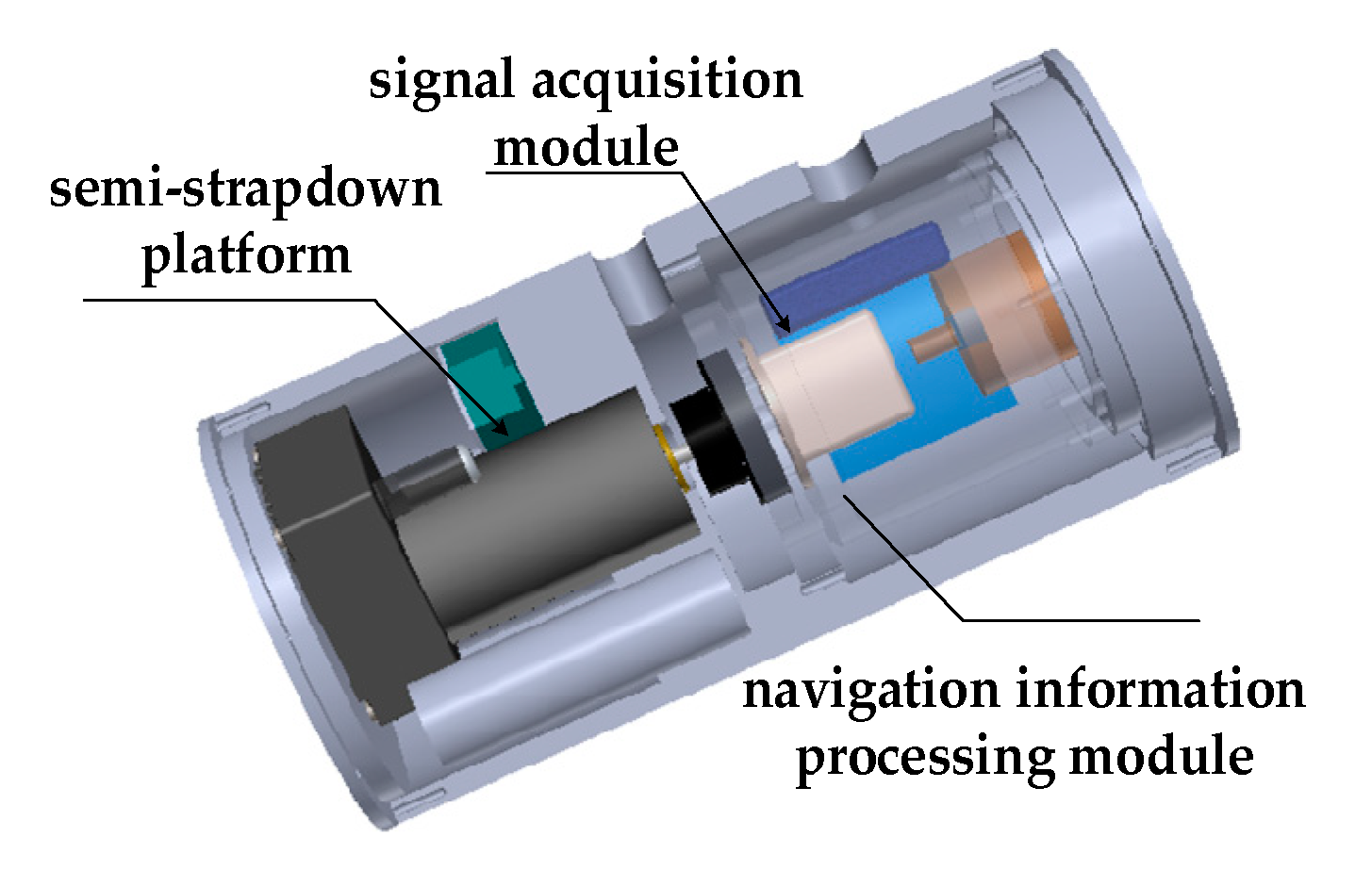
11]. The structure of the system is shown as
Figure 1, which is mainly composed of semi-strapdown platform, signal acquisition module, and navigation information processing module.
In contrast to SINS, the signal acquisition module is not rigidly attached to the carrier but, rather, is connected to the carrier via the servo motor. The main function of the semi-strapdown platform is to realize roll isolation between MEMS-IMU(MIMU) and carrier, which makes the MIMU work in the low-dynamic environment, so that the gyroscope with smaller range and higher accuracy can be utilized to measure rolling angular rate. However, SINS is still prone to sensor error accumulation with time, resulting in deterioration of the navigation solution [
12]. Fortunately, the rotation modulation technique can serve as an alternative way to reduce navigation errors, which uses its own rotating mechanism to rotate in a certain order, and the constant bias of the inertial devices are modulated into the zero mean form [
13,
14,
15]. Therefore, on the basis of reducing rotation in SSINS, the motor drives the MIMU to rotate at the appropriate angular rate to complete the single-axis rotation modulation, called rotary semi-strapdown inertial navigation system (RSSINS).
Reference [
16] shows that the faster the modulation angular rate is, the better the constant error suppression effect is. Nevertheless, the symmetry scale factor error and installation error of the gyroscope can not only be modulated, but also generate instantaneous velocity errors related to the modulation angular rate [
17,
18]. For MEMS-based rotary inertial navigation system, due to the low accuracy of MEMS gyros, a faster modulation angular rate is required for error suppression [
19]. However, in practical applications, the faster rotation speed will introduce rotation speed errors in the rotating mechanism, resulting in the modulation effect being destroyed [
20]. As a result, the design of the rotation modulation angular rate has become a hotspot of rotation modulation. Che deduced the influence of IMU motion change process on navigation precision in detail, and analyzed the error characteristics of the forward and reverse rotation scheme, but did not propose a method for designing the optimal modulation angular rate [
21]. Combined with the error characteristics of fiber optic gyro, Yu proposed a method based on Laplace transform and its inverse transform to design the optimal angular rate [
22].
However, due to the application characteristics of short-endurance and semi-strapdown, the rotating mechanism is required to follow the high-dynamic changes of the projectile in real-time, which inevitably generates rotating mechanism errors, thus destroying the modulation effect and even causing greater errors. Until now, have been few studies on the optimal design of modulation angular rate for MEMS-based rotation inertial navigation system (RINS). Therefore, the setting of the modulation angular rate as one of the key technologies for the rotation modulation scheme cannot be avoided. In this article, combined with factors such as the measurement environment, motor performance, carrier movement, device error characteristic, and others, a novel modulation angular rate design method was proposed.
In this study, combined with the characteristics of MEMS sensor and rotation speed error of rotating mechanism, we propose a design method for optimal modulation angular rate suitable for missile-borne navigation systems. The rest of this paper is organized as follows.
Section 2 introduces the system working principle and systematic error model. Combined with the measurement environment, motor performance, and device error characteristic, the method to obtain optimal modulation angular rate is presented in
Section 3. The optimal modulation angular rate is obtained, and the tests are given to verify error suppression performance in
Section 4.
Section 5 is the conclusion.
2. System Working Principle
2.1. The Principle behind the Rotary Semi-Strapdown Inertial Navigation System (RSSINS)
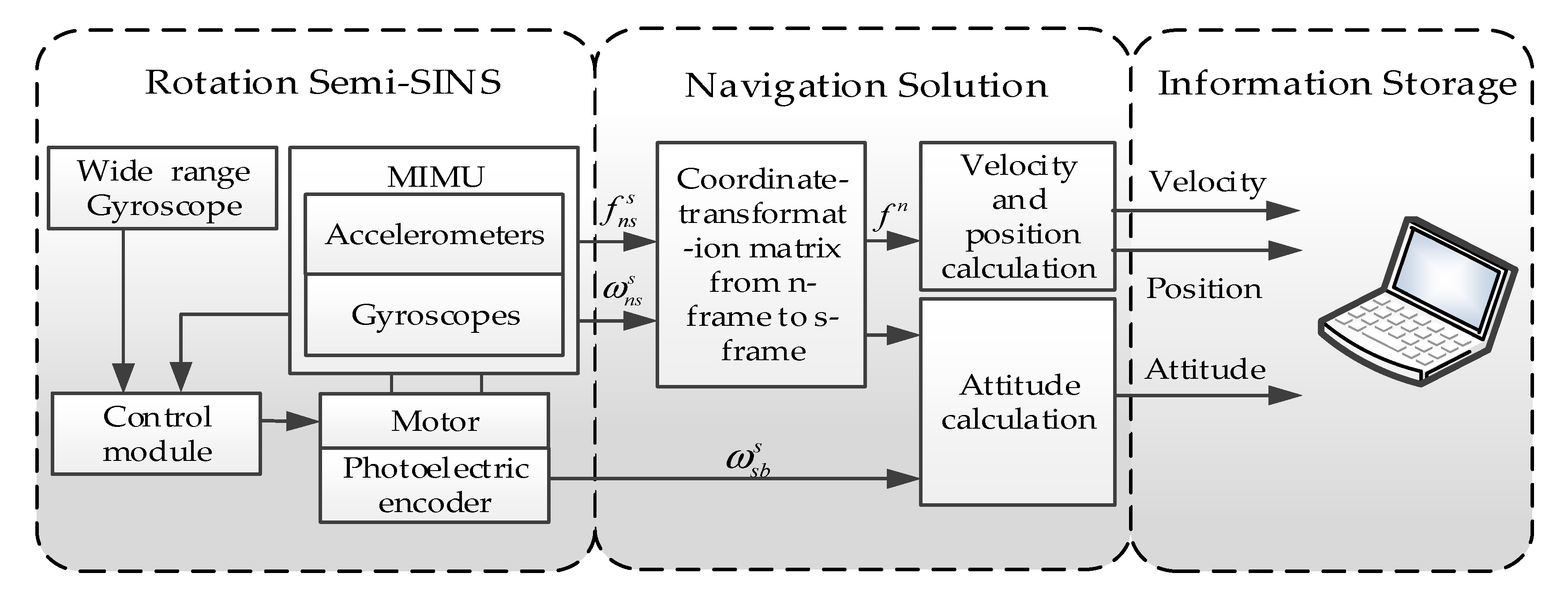
Differently from SINS, a gyro with wide range is mounted on the roll axis to measure carrier spin rate in RSSINS and, then, the information measured by it is processed and converted into a control signal to drive the motor to rotate in an opposite direction to the carrier, so as to provide a low-dynamic environment for the MIMU.
On the basis of “spin reduction”, due to the low precision of the wide-range gyro, the MIMU installed on the signal acquisition module can be sensitive to the residual angular rate, and it is fed back to the control module for adjusting the motor output in real-time, to drive the MIMU to complete the rotation modulation. At the same time, the photoelectric encoder is used to measure the relative rotation angle between the carrier and the MIMU, thus realizing the solution of carrier navigation parameters. The principle behind the RSSINS is shown in
Figure 2. In this case, isolation of the MIMU and the high-spinning of the carrier’s roll axis is implemented by the mechanical structure and control method.
In general, the mechanization algorithm of RSSINS is similar to the one of conventional SINS. Gyro and accelerometer are used to measure the angular motion information and line motion information of the carrier, respectively, and then calculate the attitude, speed, and position information. Differently from the solution algorithm of SINS, the measurement information of the encoder shall be introduced into the navigation solution loop. Since there is no relative displacement between the IMU and the carrier, the MIMU’s position is the carrier’s position. Therefore, the angular rate and specific force measured by the MIMU are directly introduced into the solution algorithm, such that the attitude matrix between the MIMU coordinate system and navigation coordinate system is obtained, from which the attitude of MIMU can be obtained. Then, the carrier attitude needs to be calculated according to the relative rotation of the carrier and the MIMU measured by the encoder. In this navigation solution loop, the measurement error of the relative rotation angle will result in roll angle error, but the relative rotation angle error will not be introduced into the solution loop and have no effect on the velocity and position accuracy [
23].
2.2. Error Model
In order to analyze the error propagation characteristic of the RSSINS, the frames are defined as follows.
(1) s-frame: MIMU frame, with X—Forward, Y—Up, and Z—Right pointing orientations;
(2) b-frame: carrier’s body frame, with X—Roll, Y—Yaw, and Z—Pitch pointing orientations;
(3) n-frame: navigation reference frame, with N–U–E (North–Up–East) pointing orientations;
(4) b′-frame: for the convenience of description, in addition, -frame is defined as a virtual coordinate system, which refers to the s-frame before rotation modulation is introduced.
For MIMU, the influence of the variation of the gravitational field and the curvature radius of the Earth’s surface on the inertial navigation system error is negligible when the carrier is working for a short time [
24]. Since the sensors selected by this system cannot sense the Earth’s rotation speed, the cross-coupling term generated by it can be ignored. Consequently, the error propagation equations of RSSINS have been derived as follows.
where
represents the carrier velocity error in n-frame; represents the carrier velocity in n-frame; , , and represent the attitude errors between n-frame and mathematical platform frame; and represent the carrier’s specific force in n-frame and s-frame, respectively; and represent the scale factor error and the installation error of accelerometers; and represent the scale factor error and the installation error of gyroscopes; and represent the constant bias of accelerometers and gyroscopes, respectively; is the transformation matrix from A-frame to B-frame; , , and represent the error of the local latitude, longitude, and height; and L represents the local latitude.
4. Test and Results Analysis
The optimal design method of the modulation angular rate is proposed in
Section 3. The theoretical optimal modulation angular rate is obtained in terms of this method. In order to verify the correctness of the former conclusions, experiments are implemented by using a high-precision three-axis flight simulator, the technical parameters of which are shown in
Table 2.
The RSSINS is installed on the high-precision three-axis flight simulator as shown in
Figure 5, which is used to simulate the carrier’s attitude change. With the sensitive axes of MIMU defined as the
x-axis pointing forward, the
z-axis pointing right, and the
y-axis pointing up, the rotation of the inner frame rotates the system about its
x-axis.
At the same time, the characteristics of the MIMU in the system is shown in
Table 3.
In
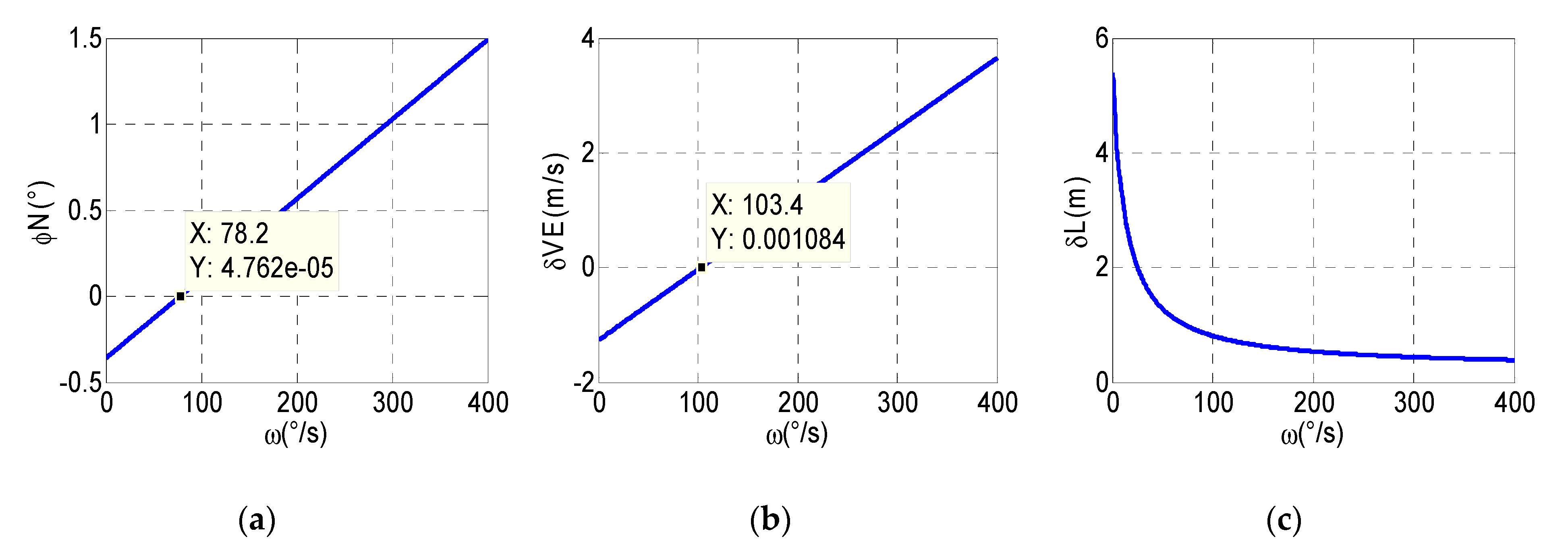
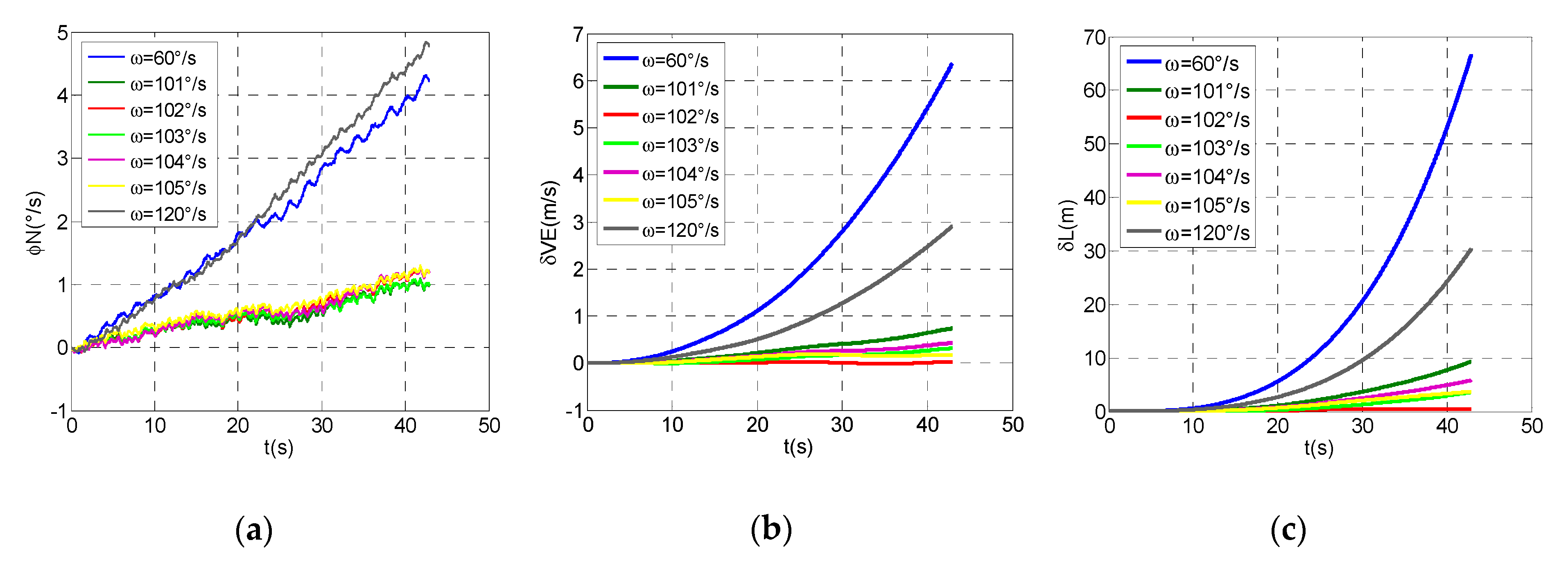
Section 3.2, the average value of motor rotation speed error is used to analyze the impact on modulation effect. In order to more accurately obtain the optimal modulation angular rate, in addition to the theoretical optimal modulation angular rate of 103°/s, the angular rates of 101°/s, 102°/s, 104°/s, and 105°/s were also selected as the modulation angular rate for testing, and compared with the testing results. Furthermore, two groups were added to the test, with 60°/s and 120°/s as the modulation angular rates, respectively, to analyze the error suppression effect.
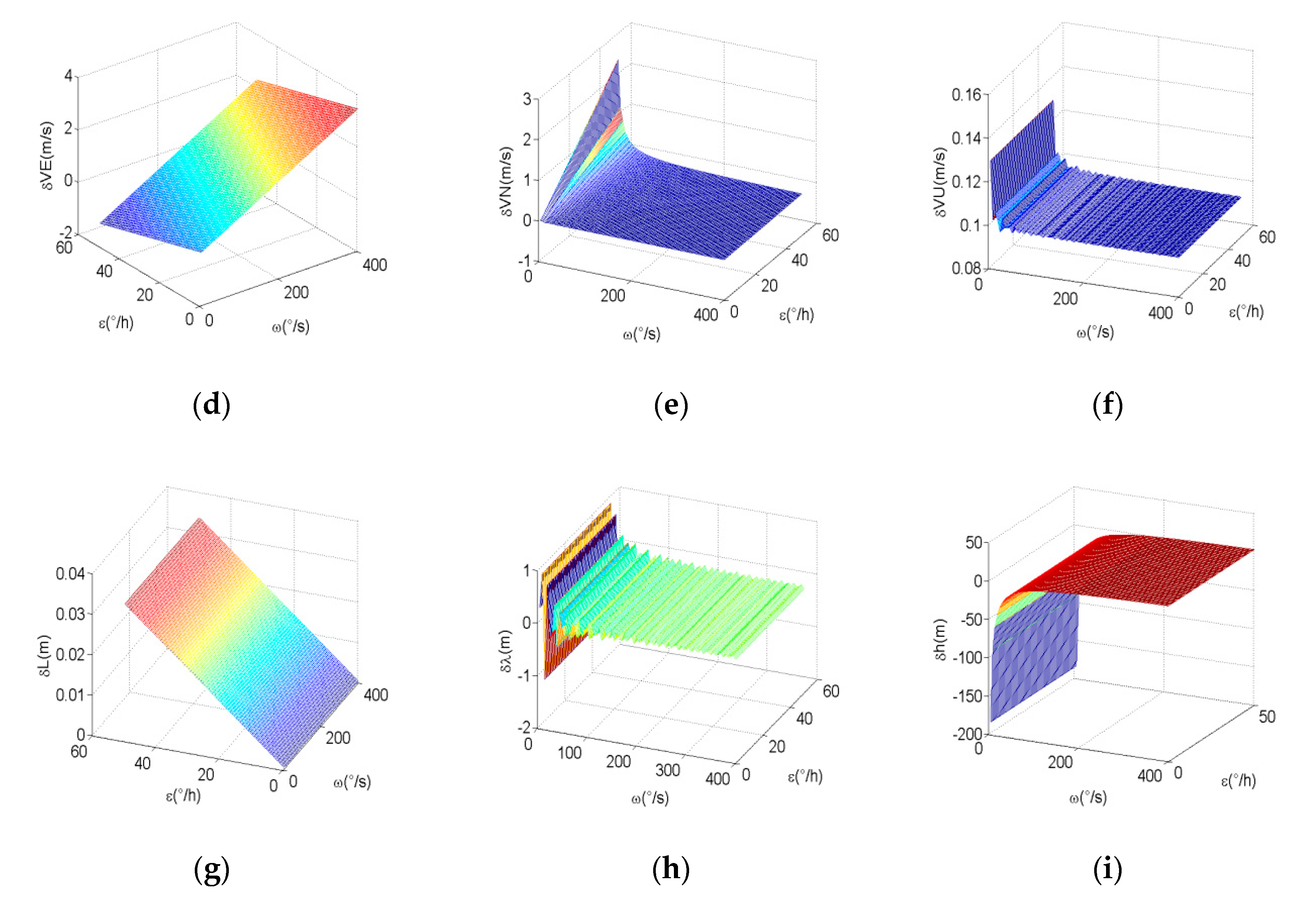
In all the experiments, the inner frame of three-axis flight simulator simulates the carrier rolling motion with the speed of 5400°/s; the mid-frame simulates the carrier’s pitching motion, with the range between +45° and −45°; the modulation time is 40 s, and the reciprocating rotation scheme is employed. Comparing the navigation information measured by RSSINS with the standard information provided by the three-axis flight simulator, the navigation parameter measurement errors of the system at different modulation angular rates can be obtained to analyze the error suppression performance. Though the analysis of experimental results, the errors of north attitude, east velocity, and latitude at different modulation angular rates are shown in
Figure 6, and the maximum values of each error are shown in
Table 4.
Compared with the modulation angular rate of 60°/s and 120°/s, we can observe that the error suppression effect is better when the modulation angular rates are between 101°/s and 105°/s, but it is not the best, which proves the validity of the analysis in
Section 3.2, that is, 102°/s is not the best angular rate of the attitude error suppression effect. Meanwhile, the modulation angular rate error results in the constant bias of gyro not being completely eliminated, so that the residual error accumulates with time, which is one of the reasons for the divergence of the attitude error. In addition, the attitude accuracy can be improved by compensating the rotation speed error. Given the limited space available, it will not be described in detail here. Similarly, through analyzing the characteristics of east velocity error and latitude error, the navigation performance is optimal when the modulation angular rate is 102°/s, which is different from the modulation angular rate obtained by the method mentioned in the
Section 3. The difference between them is mainly caused by the accuracy of the motor rotation speed error model, whereas the accurate modeling of rotation speed error makes it more difficult to analyze and calculate. Hence, the method proposed in this paper can be used to determine the optimal angular rate simply by theoretical calculation and experimental verification, and it is suitable for rotary navigation systems with different types of motors as the rotating mechanism.