Modeling the AC Electrokinetic Behavior of Semiconducting Spheres
Abstract
:1. Introduction
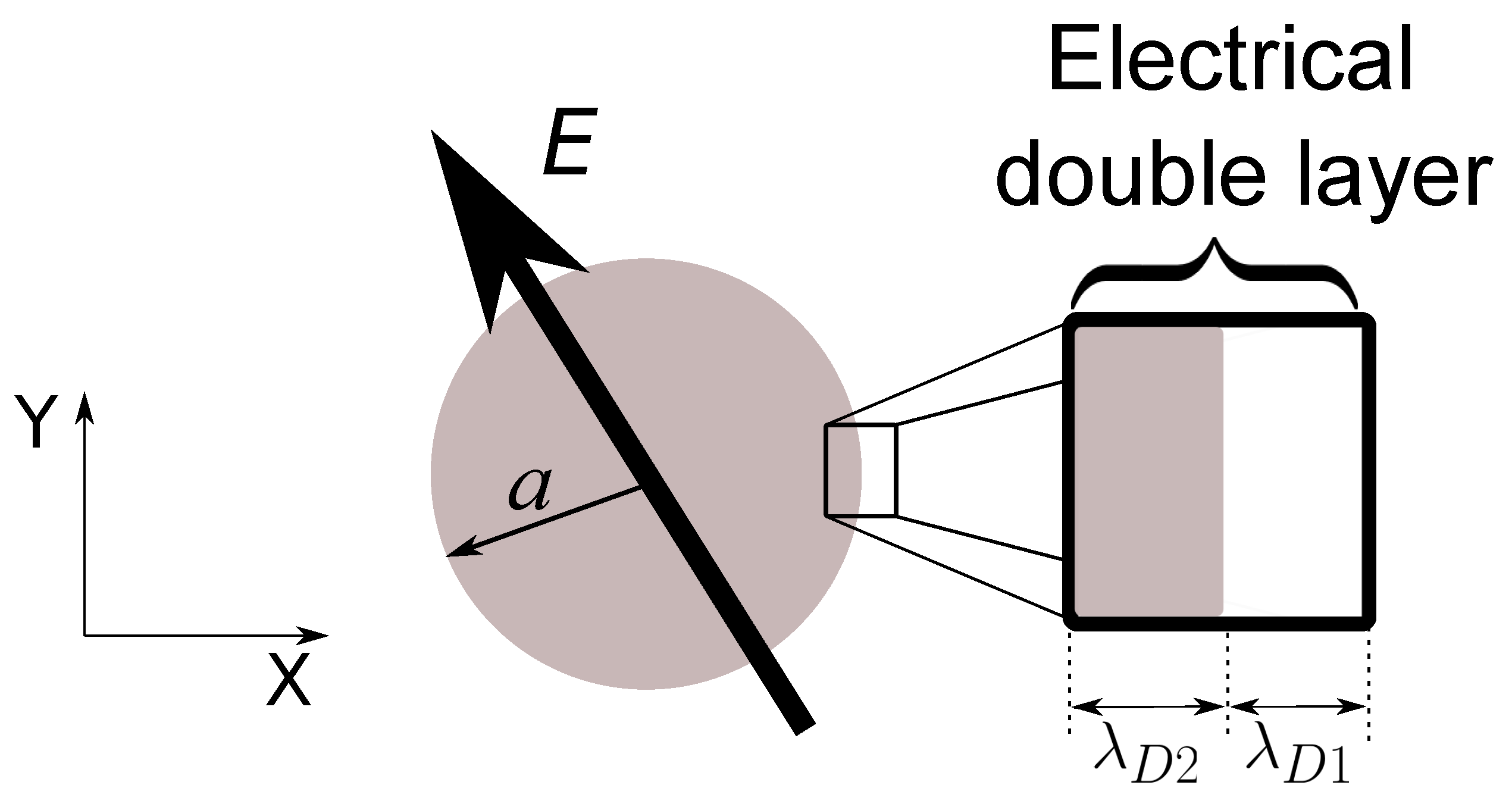
2. Theory
2.1. Particle Polarizability
2.2. Limit of Thin Electrical Double Layers
3. Results
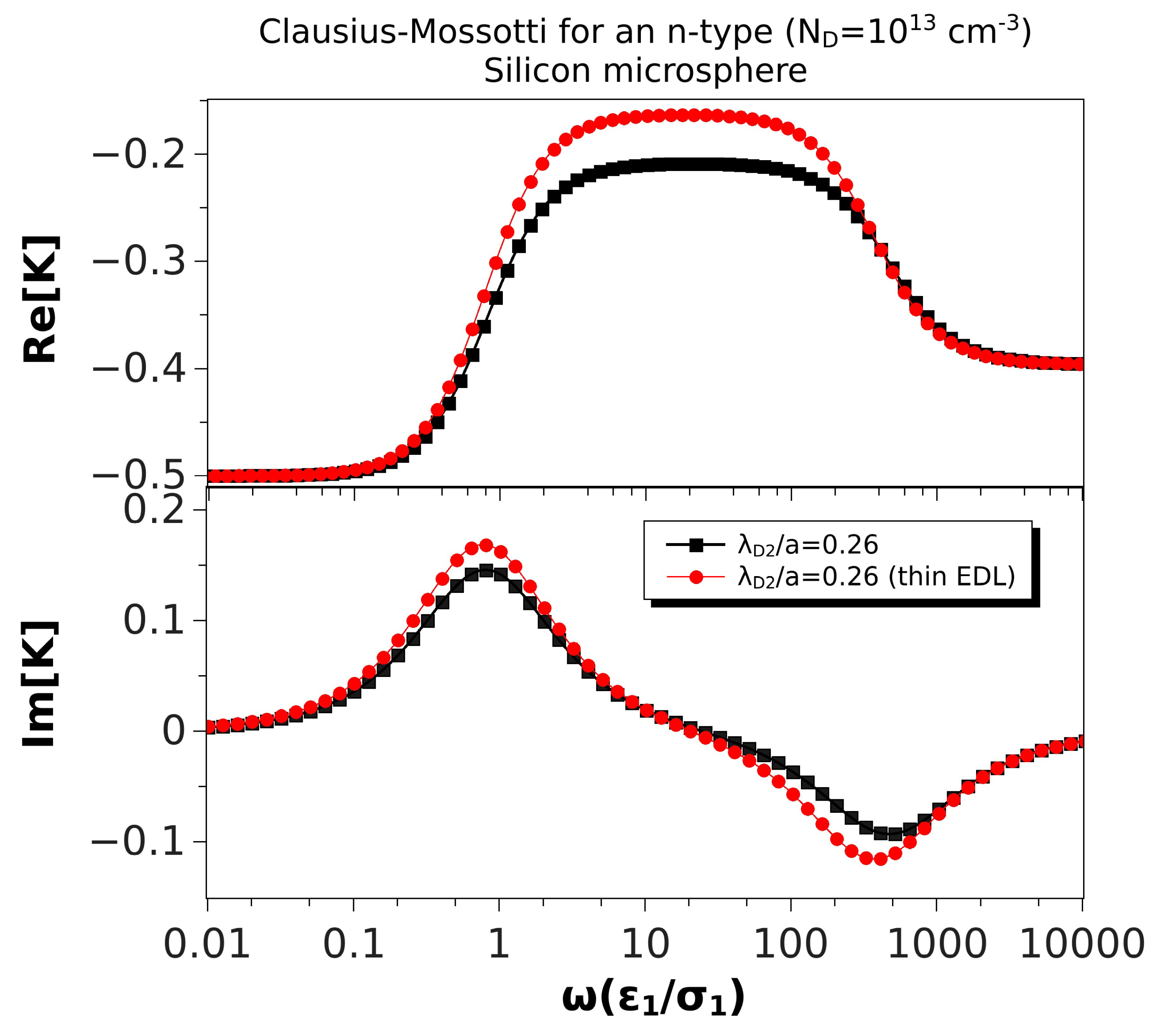
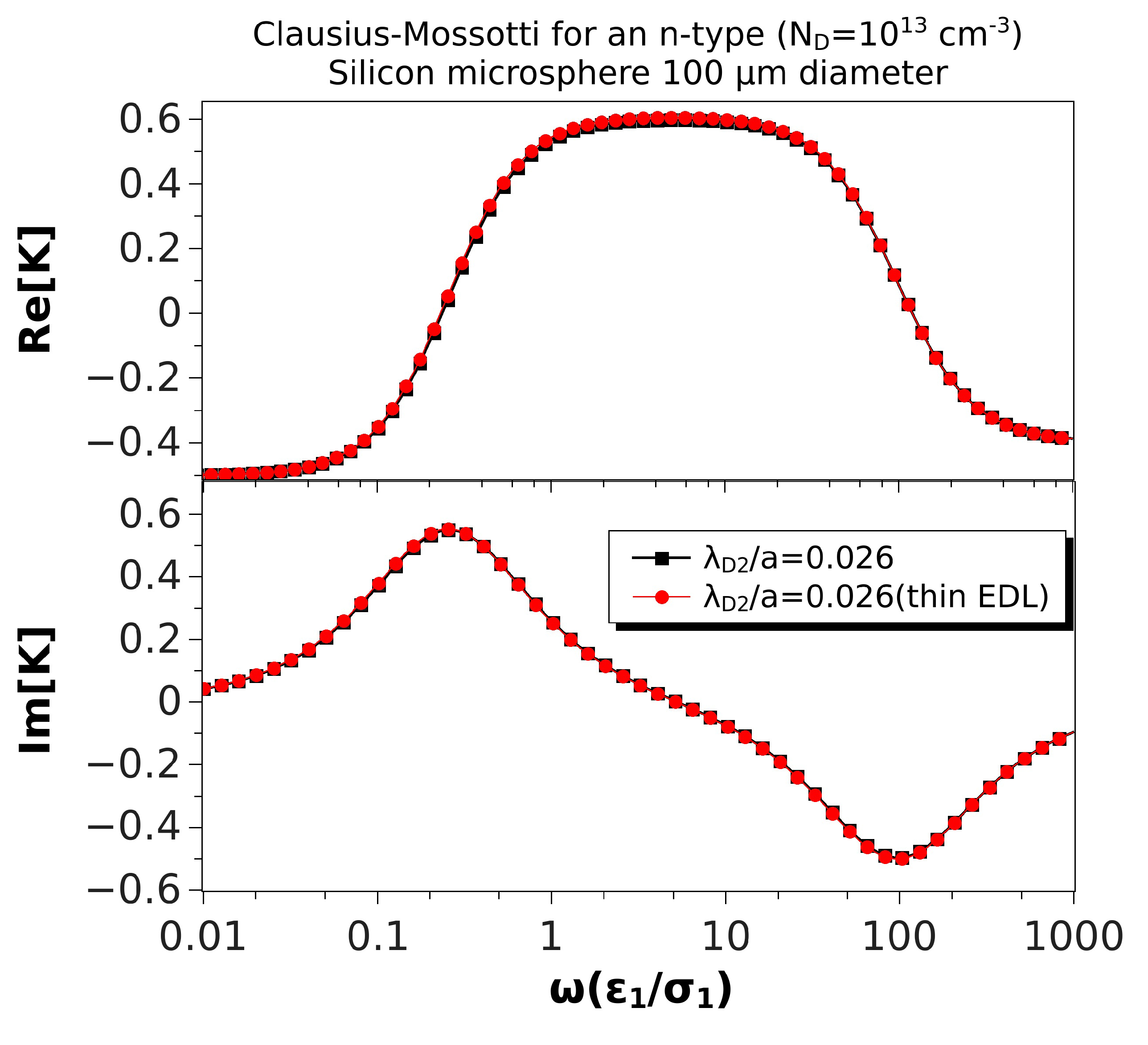
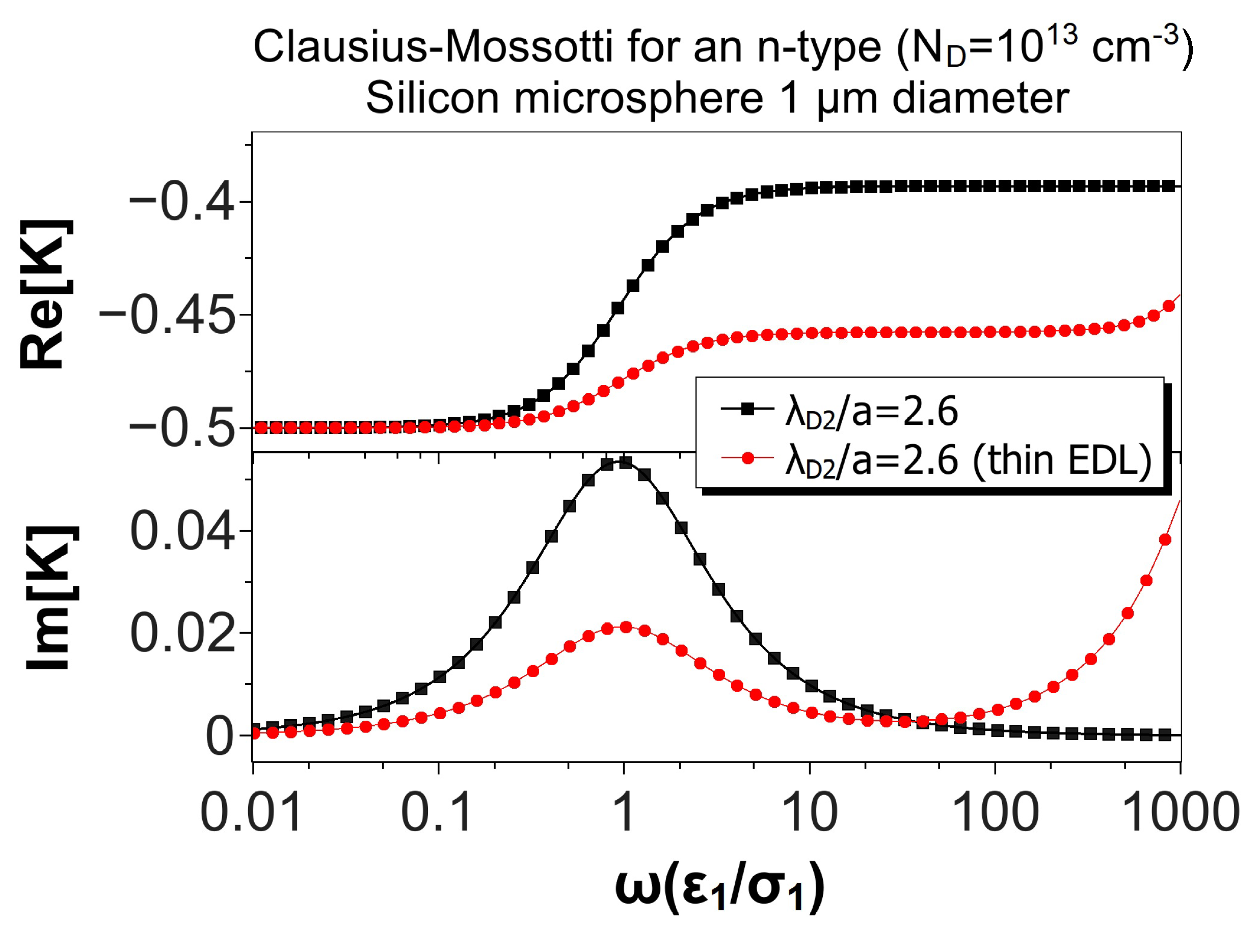
Comparisons with the Results for a Thin Electrical Double Layer
4. Conclusions
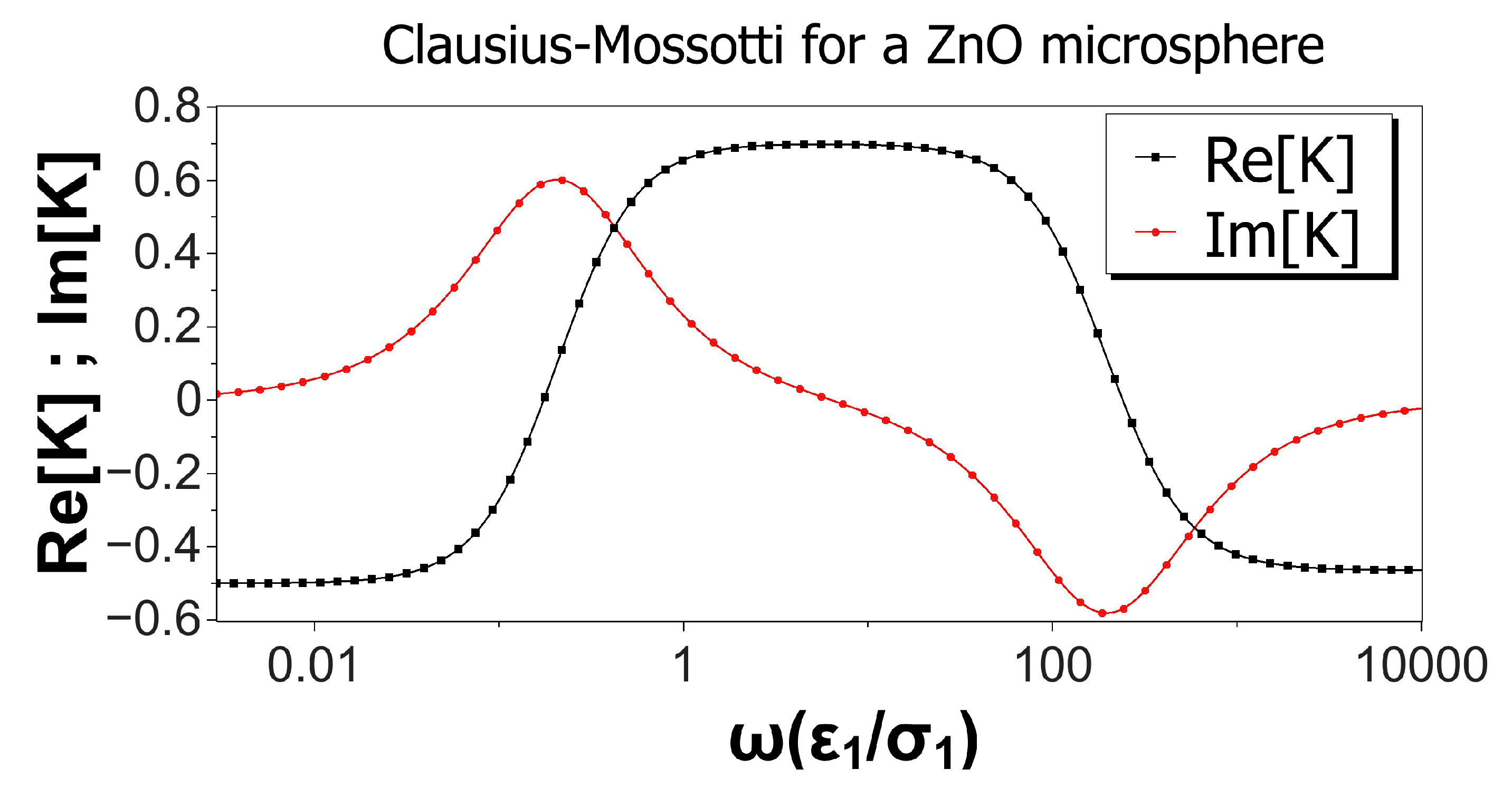
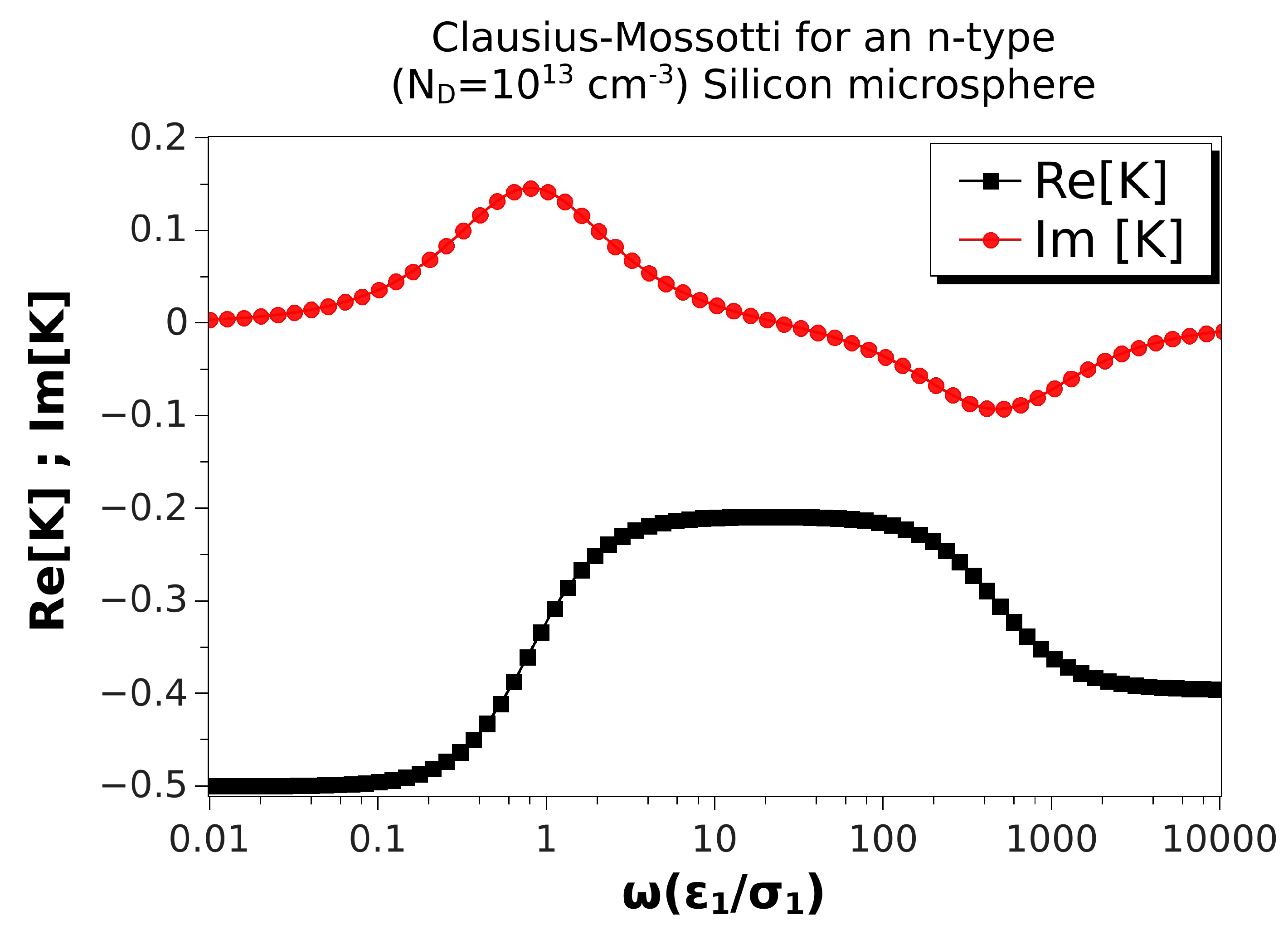
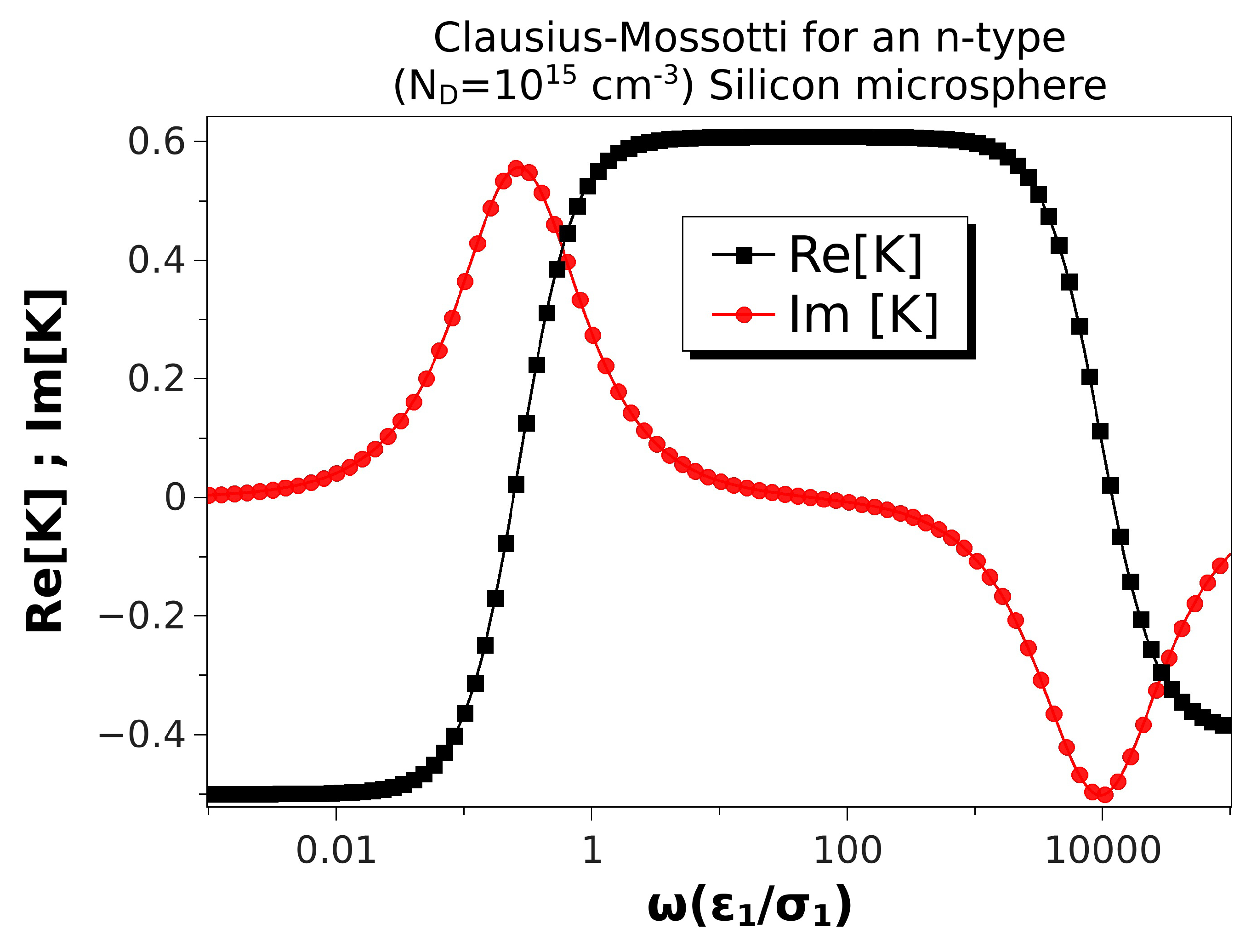
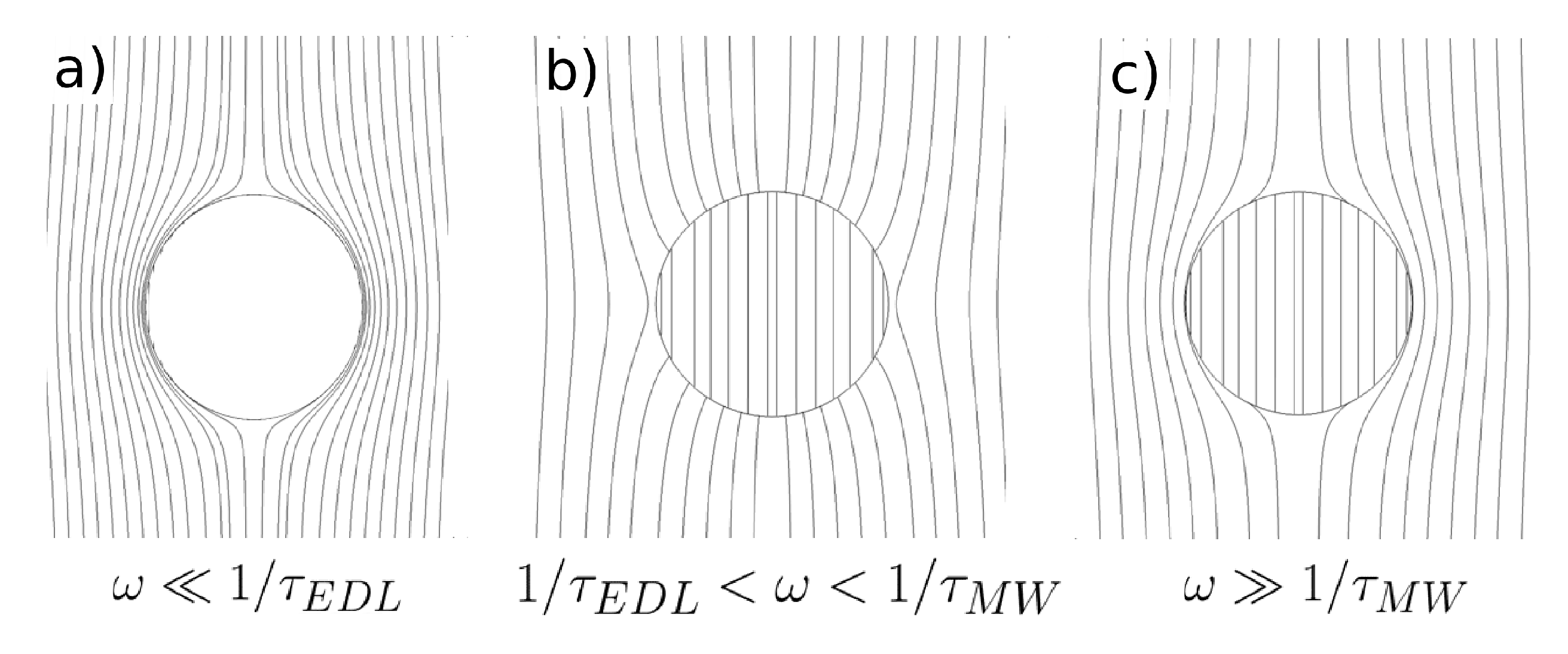
- The model predicts negative dielectrophoresis at very low frequencies: the Clausius–Mossotti factor with real part equal to . This is the minimum value attainable for the Clausius–Mossotti factor of a sphere, and it arises when the electric field in the liquid surrounds the particle, as if the sphere were a perfectly insulating material; see Figure 8a. The reason for this is that the electrical double layer (EDL) is fully charged.
- As the signal frequency increases, there is not sufficient time for complete charging of the EDL by the electrical currents coming from the liquid bulk. The real part of the Clausius–Mossotti factor increases, leading to a weaker negative DEP and, eventually, to positive DEP behavior if the sphere conductivity is high enough; see Figure 8b.
- The Clausius–Mossotti factor shows a new relaxation for higher frequencies of the AC field; and the value of its real part decreases until a negative value that depends on the ratio of solid to liquid dielectric constants. This is the well-known Maxwell–Wagner relaxation, and negative dielectrophoresis occurs since the permittivity for the liquid is higher than for the solid; see Figure 8c.
- The imaginary part of the Clausius–Mossotti factor mirrors the behavior of the real part. As mentioned above, the EDL relaxation leads to an increase in the value of with frequency, and consequently, a positive peak for the imaginary part appears. This peak corresponds to a prediction of counterfield electrorotation in experiments. Likewise, the decrease of the real part at higher frequencies predicts a cofield electrorotation.
Author Contributions
Acknowledgments
Conflicts of Interest
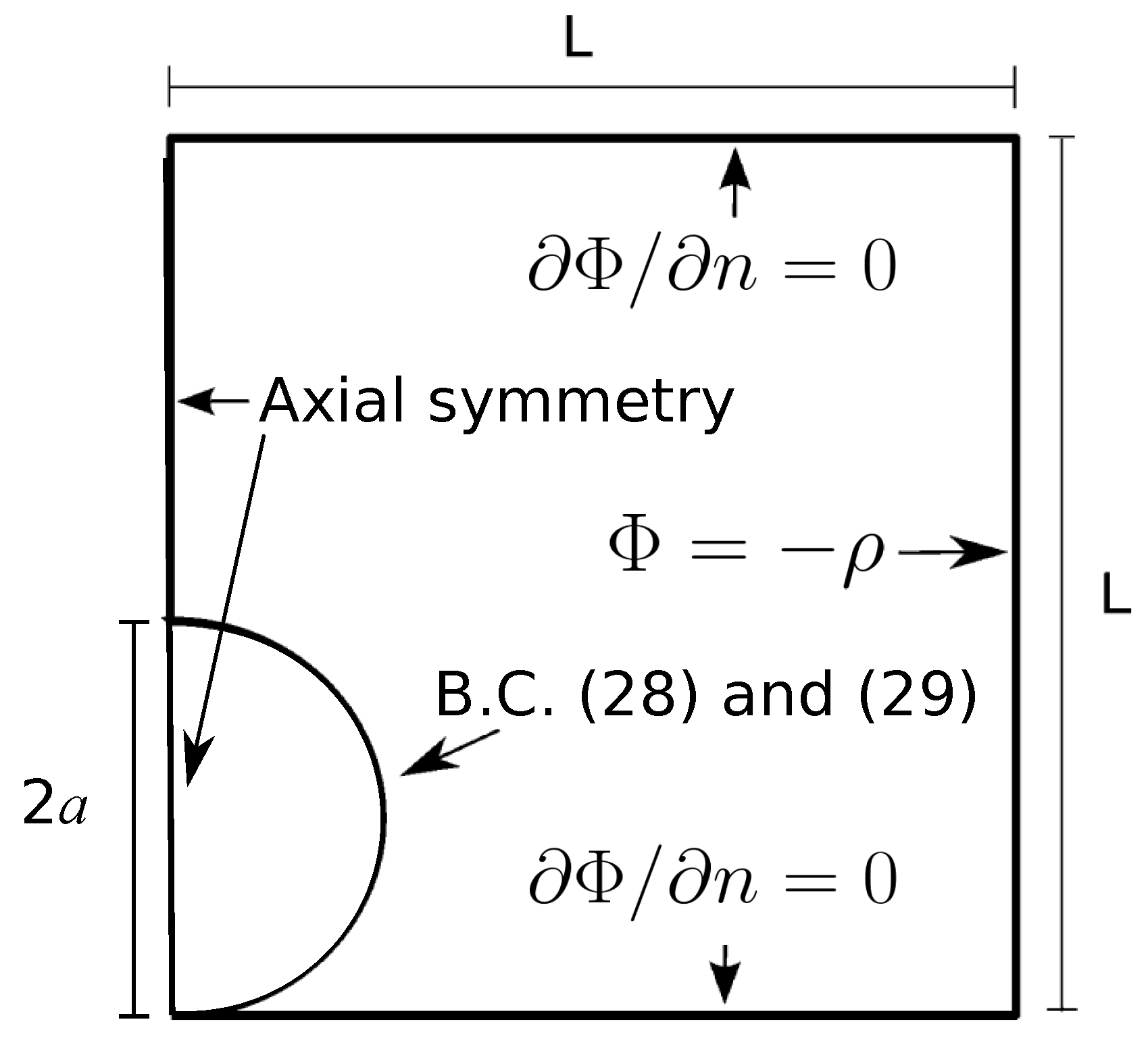
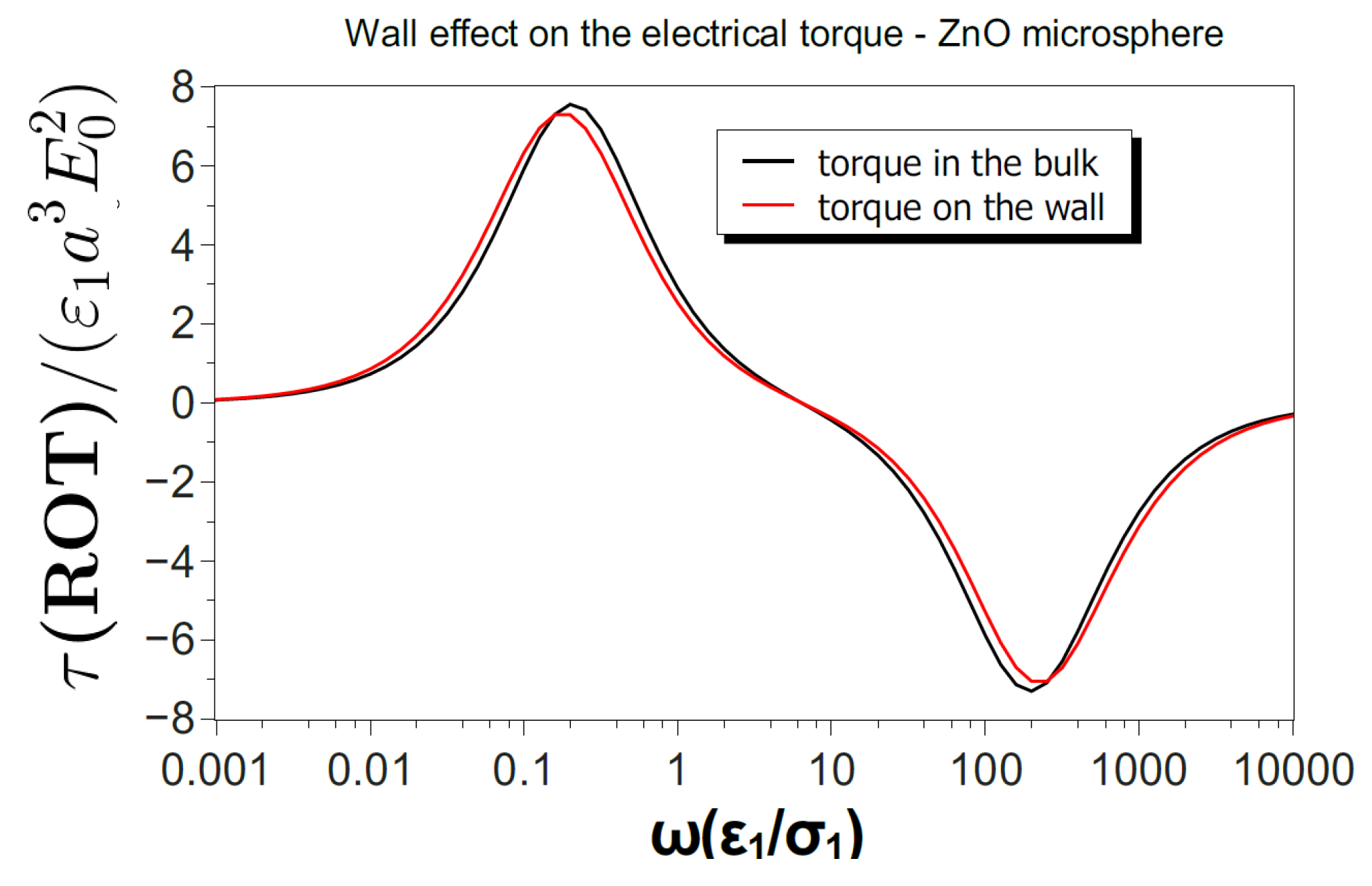
Appendix A. Wall Effects in the Electrorotation of a Semiconducting Sphere
References
- Jones, T.B. Electromechanics of Particles; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Morgan, H.; Green, N.G. AC Electrokinetics: Colloids and Nanoparticles; Research Studies Press Ltd.: Oxford, UK, 2003. [Google Scholar]
- Yu, K.; Yi, J.; Shan, J.W. Automated characterization and assembly of individual nanowires for device fabrication. Lab Chip 2018, 18, 1494–1503. [Google Scholar] [CrossRef] [PubMed]
- Fan, D.; Cammarata, R.; Chien, C. Precision transport and assembling of nanowires in suspension by electric fields. Appl. Phys. Lett. 2008, 92, 093115. [Google Scholar] [CrossRef]
- Fan, D.; Zhu, F.Q.; Xu, X.; Cammarata, R.C.; Chien, C. Electronic properties of nanoentities revealed by electrically driven rotation. Proc. Natl. Acad. Sci. USA 2012, 109, 9309–9313. [Google Scholar] [CrossRef] [Green Version]
- Ren, Y.; Morganti, D.; Jiang, H.Y.; Ramos, A.; Morgan, H. Electrorotation of Metallic Microspheres. Langmuir 2011, 27, 2128–2131. [Google Scholar] [CrossRef] [PubMed]
- García-Sánchez, P.; Ren, Y.; Arcenegui, J.J.; Morgan, H.; Ramos, A. Alternating Current Electrokinetic Properties of Gold-Coated Microspheres. Langmuir 2012, 28, 13861–13870. [Google Scholar] [CrossRef] [PubMed]
- Arcenegui, J.J.; García-Sánchez, P.; Morgan, H.; Ramos, A. Electrorotation of titanium microspheres. Electrophoresis 2013, 34, 979–986. [Google Scholar] [CrossRef]
- Fan, D.L.; Zhu, F.Q.; Cammarata, R.C.; Chien, C.L. Controllable High-Speed Rotation of Nanowires. Phys. Rev. Lett. 2005, 94, 247208. [Google Scholar] [CrossRef] [Green Version]
- Arcenegui, J.J.; García-Sánchez, P.; Morgan, H.; Ramos, A. Electric-field-induced rotation of Brownian metal nanowires. Phys. Rev. E 2013, 88, 033025. [Google Scholar] [CrossRef]
- Arcenegui, J.J.; García-Sánchez, P.; Morgan, H.; Ramos, A. Electro-orientation and electrorotation of metal nanowires. Phys. Rev. E 2013, 88, 063018. [Google Scholar] [CrossRef]
- Smith, P.A.; Nordquist, C.D.; Jackson, T.N.; Mayer, T.S.; Martin, B.R.; Mbindyo, J.; Mallouk, T.E. Electric-field assisted assembly and alignment of metallic nanowires. Appl. Phys. Lett. 2000, 77, 1399–1401. [Google Scholar] [CrossRef]
- Saintillan, D.; Darvel, E.; Shaqfeh, E. Hydrodynamic interactions in the induced-charge electrophoresis of colloidal rod dispersionss. J. Fluid Mech. 2006, 563, 223–259. [Google Scholar] [CrossRef]
- Rose, K.A.; Meier, J.A.; Dougherty, G.M.; Santiago, J.G. Rotational electrophoresis of striped metallic microrods. Phys. Rev. E 2007, 75, 011503. [Google Scholar] [CrossRef] [PubMed]
- Arcenegui, J.J.; García-Sánchez, P.; Morgan, H.; Ramos, A. Electro-orientation of a metal nanowire counterbalanced by thermal torques. Phys. Rev. E 2014, 89, 062306. [Google Scholar] [CrossRef] [PubMed]
- Liang, Z.; Fan, D. Visible light–gated reconfigurable rotary actuation of electric nanomotors. Sci. Adv. 2018, 4, 0981. [Google Scholar] [CrossRef] [PubMed]
- Akin, C.; Feldman, L.C.; Durand, C.; Hus, S.M.; Li, A.P.; Hui, H.Y.; Filler, M.A.; Yi, J.; Shan, J.W. High-throughput electrical measurement and microfluidic sorting of semiconductor nanowires. Lab Chip 2016, 16, 2126–2134. [Google Scholar] [CrossRef] [PubMed]
- Akin, C.; Yi, J.; Feldman, L.C.; Durand, C.; Hus, S.M.; Li, A.P.; Filler, M.A.; Shan, J.W. Contactless Determination of Electrical Conductivity of One-Dimensional Nanomaterials by Solution-Based Electro-orientation Spectroscopy. ACS Nano 2015, 9, 5405–5412. [Google Scholar] [CrossRef] [PubMed]
- Hermanson, K.D.; Lumsdon, S.O.; Williams, J.P.; Kaler, E.W.; Velev, O.D. Dielectrophoretic assembly of electrically functional microwires from nanoparticle suspensions. Science 2001, 294, 1082–1086. [Google Scholar] [CrossRef]
- García-Sánchez, P.; Arcenegui, J.J.; Morgan, H.; Ramos, A. Self-assembly of metal nanowires induced by alternating current electric fields. Appl. Phys. Lett. 2015, 106, 023110. [Google Scholar] [CrossRef] [Green Version]
- Gangwal, S.; Cayre, O.J.; Bazant, M.Z.; Velev, O.D. Induced-charge electrophoresis of metallodielectric particles. Phys. Rev. Lett. 2008, 100, 058302. [Google Scholar] [CrossRef]
- Gangwal, S.; Cayre, O.J.; Velev, O.D. Dielectrophoretic assembly of metallodielectric Janus particles in AC electric fields. Langmuir 2008, 24, 13312–13320. [Google Scholar] [CrossRef]
- Boymelgreen, A.; Yossifon, G.; Park, S.; Miloh, T. Spinning Janus doublets driven in uniform AC electric fields. Phys. Rev. E 2014, 89, 011003. [Google Scholar] [CrossRef] [PubMed]
- Boymelgreen, A.; Yossifon, G.; Miloh, T. Propulsion of active colloids by self-induced field gradients. Langmuir 2016, 32, 9540–9547. [Google Scholar] [CrossRef] [PubMed]
- Boymelgreen, A.M.; Balli, T.; Miloh, T.; Yossifon, G. Active colloids as mobile microelectrodes for unified label-free selective cargo transport. Nat. Commun. 2018, 9, 760. [Google Scholar] [CrossRef] [PubMed]
- Miloh, T. A unified theory of dipolophoresis for nanoparticles. Phys. Fluids 2008, 20, 107105. [Google Scholar] [CrossRef]
- Miloh, T. Dipolophoresis of nanoparticles. Phys. Fluids 2008, 20, 063303. [Google Scholar] [CrossRef]
- Ramos, A.; García-Sánchez, P.; Morgan, H. AC electrokinetics of conducting microparticles: A review. Curr. Opin. Colloid Interface Sci. 2016, 24, 79–90. [Google Scholar] [CrossRef] [Green Version]
- García-Sánchez, P.; Ramos, A. Electrorotation of a metal sphere immersed in an electrolyte of finite Debye length. Phys. Rev. E 2015, 92, 052313. [Google Scholar] [CrossRef]
- Bazant, M.Z.; Squires, T.M. Induced-charge electrokinetic phenomena: theory and microfluidic applications. Phys. Rev. Lett. 2004, 92, 066101. [Google Scholar] [CrossRef]
- Bazant, M.Z.; Thornton, K.; Ajdari, A. Diffuse-charge dynamics in electrochemical systems. Phys. Rev. E 2004, 70, 021506. [Google Scholar] [CrossRef]
- García-Sánchez, P.; Ramos, A. Electrorotation and Electroorientation of semiconductor nanowires. Langmuir 2017, 33, 8553–8561. [Google Scholar] [CrossRef]
- Lyklema, J. Fundamentals of Interface and Colloid Science; Academic Press Limited: New York, NY, USA, 1995. [Google Scholar]
- Macdonald, J.R. Theory of AC space-charge polarization effects in photoconductors, semiconductors, and electrolytes. Phys. Rev. 1953, 92, 4. [Google Scholar] [CrossRef]
- Hunter, R. Introduction to Modern Colloid Science; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Sze, S.M.; Ng, K.K. Physics of Semiconductor Devices; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- González, A.; Ramos, A.; Green, N.; Castellanos, A.; Morgan, H. Fluid Flow Induced By Nonuniform AC Electric Fields in Electrolytes on Microelectrodes. II. A Linear Double-Layer Analysis. Phys. Rev. E 2000, 61, 4019–4028. [Google Scholar] [CrossRef]
- Zhao, C.; Yang, C. AC electrokinetic phenomena over semiconductive surfaces: Effective electric boundary conditions and their applications. Phys. Rev. E 2011, 83, 066304. [Google Scholar] [CrossRef]
- Goldberger, J.; Sirbuly, D.J.; Law, M.; Yang, P. ZnO nanowire transistors. J. Phys. Chem. B 2005, 109, 9–14. [Google Scholar] [CrossRef] [PubMed]
- Shilov, V.; Simonova, T. Polarization of electric double-layer of disperse particles and dipolophoresis in a steady (DC) field. Colloid J. USSR 1981, 43, 90–96. [Google Scholar]
- Bazant, M.Z.; Kilic, M.S.; Storey, B.D.; Ajdari, A. Towards an understanding of induced-charge electrokinetics at large applied voltages in concentrated solutions. Adv. Colloid Interface Sci. 2009, 152, 48–88. [Google Scholar] [CrossRef] [Green Version]
- Messinger, R.; Squires, T. Suppression of Electro-Osmotic Flow by Surface Roughness. Phys. Rev. Lett. 2010, 105, 144503. [Google Scholar] [CrossRef] [PubMed]
- Ramos, A.; González, A.; García-Sánchez, P.; Castellanos, A. A linear analysis of the effect of Faradaic currents on traveling-wave electroosmosis. J. Colloid Interface Sci. 2007, 309, 323–331. [Google Scholar] [CrossRef]
- García-Sánchez, P.; Ramos, A.; González, A. Effects of Faradaic currents on AC electroosmotic flows with coplanar symmetric electrodes. Colloids Surf. A Physicochem. Eng. Asp. 2011, 376, 47–52. [Google Scholar] [CrossRef]
- Jeffery, G. On the Steady Rotation of a Solid of Revolution in a Viscous Fluid. Proc. Lond. Math. Soc. 1915, 14, 327–338. [Google Scholar] [CrossRef]
| — | |||
|---|---|---|---|
| Semiconductor (ZnO) | 30 nm | 480 mS/m | 3.9 |
| Electrolyte (KCl in water) | 30 nm | 1.5 mS/m | 80 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Sánchez, P.; Flores-Mena, J.E.; Ramos, A. Modeling the AC Electrokinetic Behavior of Semiconducting Spheres. Micromachines 2019, 10, 100. https://doi.org/10.3390/mi10020100
García-Sánchez P, Flores-Mena JE, Ramos A. Modeling the AC Electrokinetic Behavior of Semiconducting Spheres. Micromachines. 2019; 10(2):100. https://doi.org/10.3390/mi10020100
Chicago/Turabian StyleGarcía-Sánchez, Pablo, Jose Eladio Flores-Mena, and Antonio Ramos. 2019. "Modeling the AC Electrokinetic Behavior of Semiconducting Spheres" Micromachines 10, no. 2: 100. https://doi.org/10.3390/mi10020100
APA StyleGarcía-Sánchez, P., Flores-Mena, J. E., & Ramos, A. (2019). Modeling the AC Electrokinetic Behavior of Semiconducting Spheres. Micromachines, 10(2), 100. https://doi.org/10.3390/mi10020100






