Recent Advances in Continuous-Flow Particle Manipulations Using Magnetic Fluids
Abstract
:1. Introduction
1.1. Magnetic Particles
1.2. Magnetic Fluids
2. Theoretical Background
2.1. Magnetic Force and Translation
2.2. Magnetic Torque and Rotation
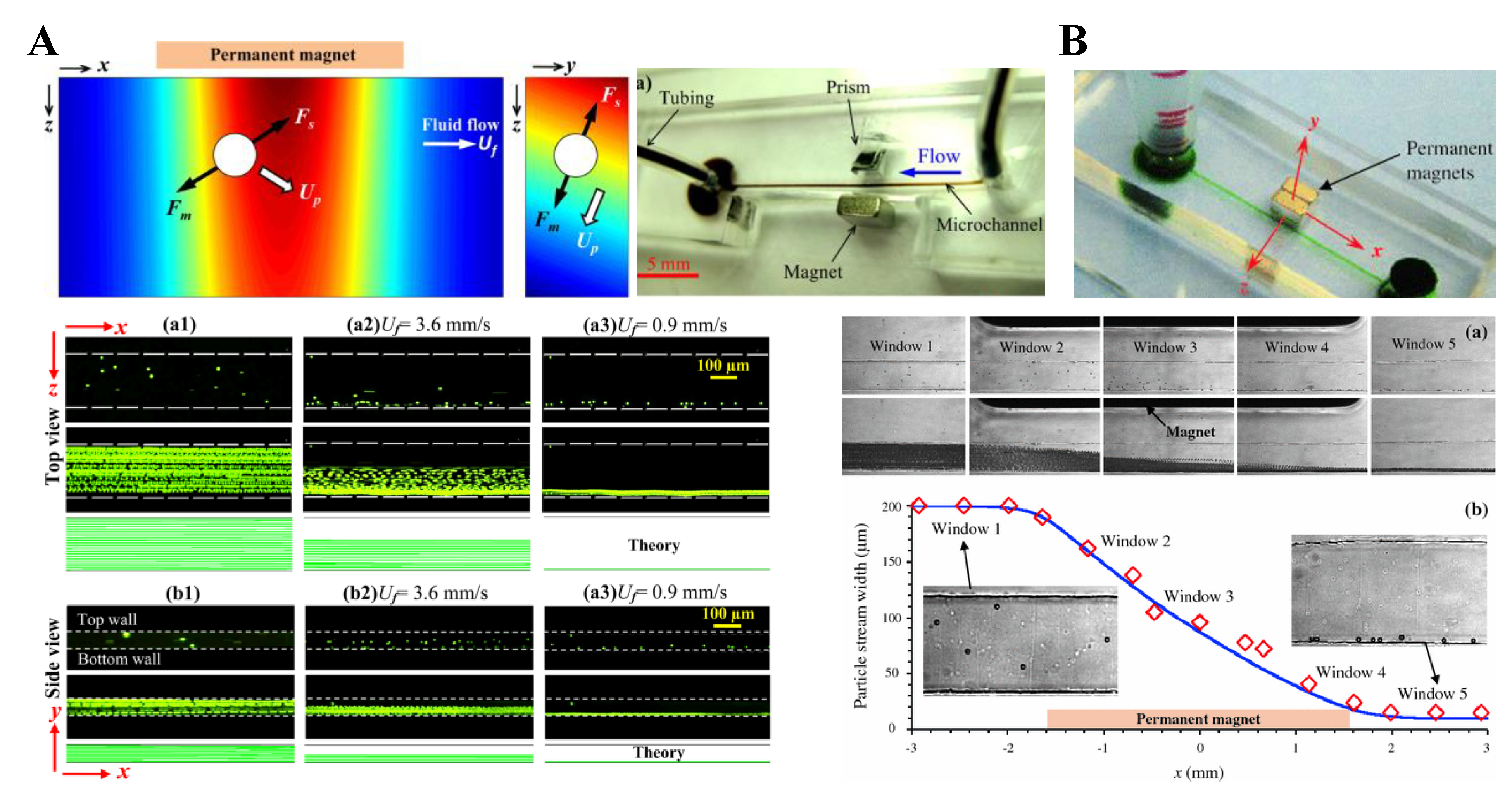
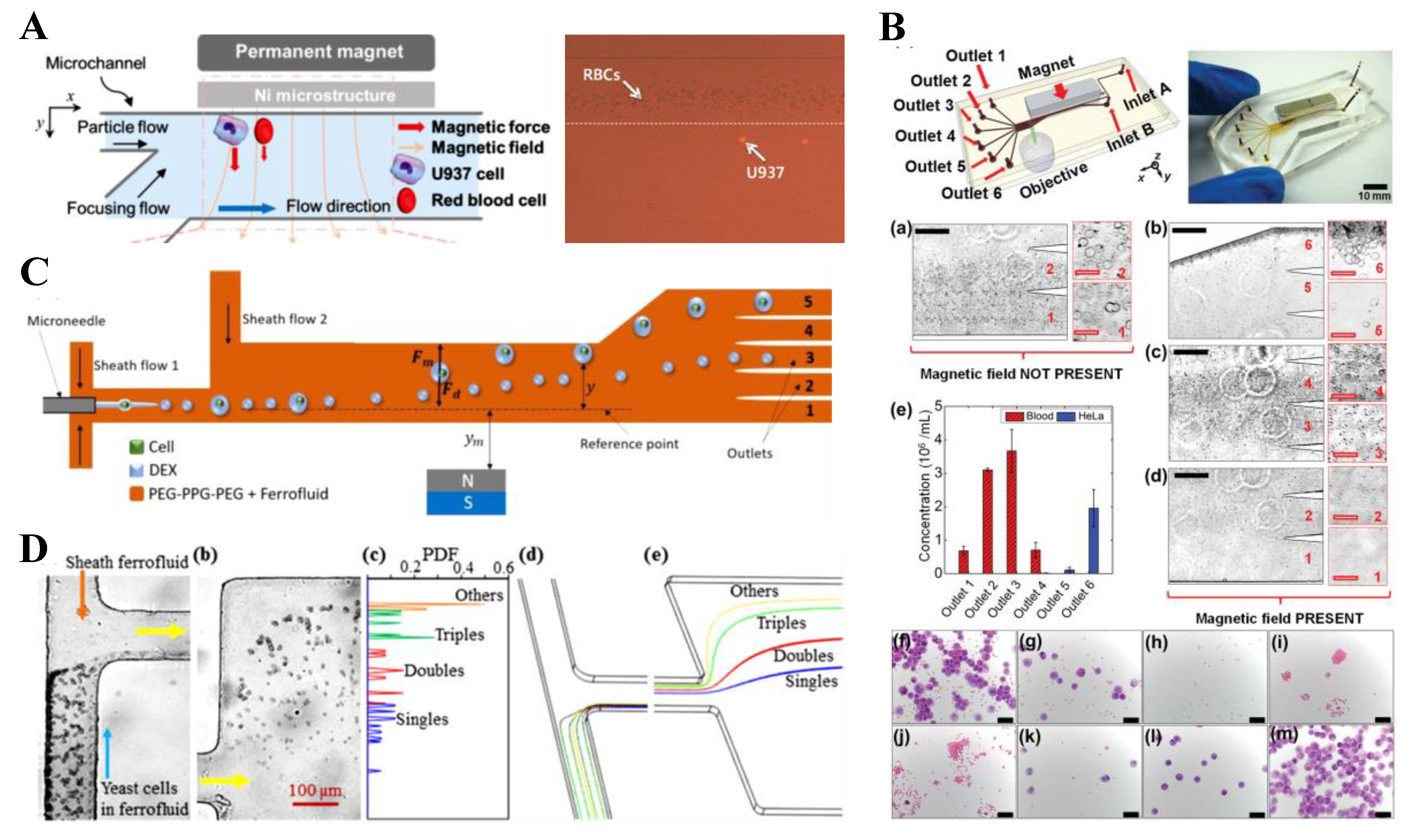
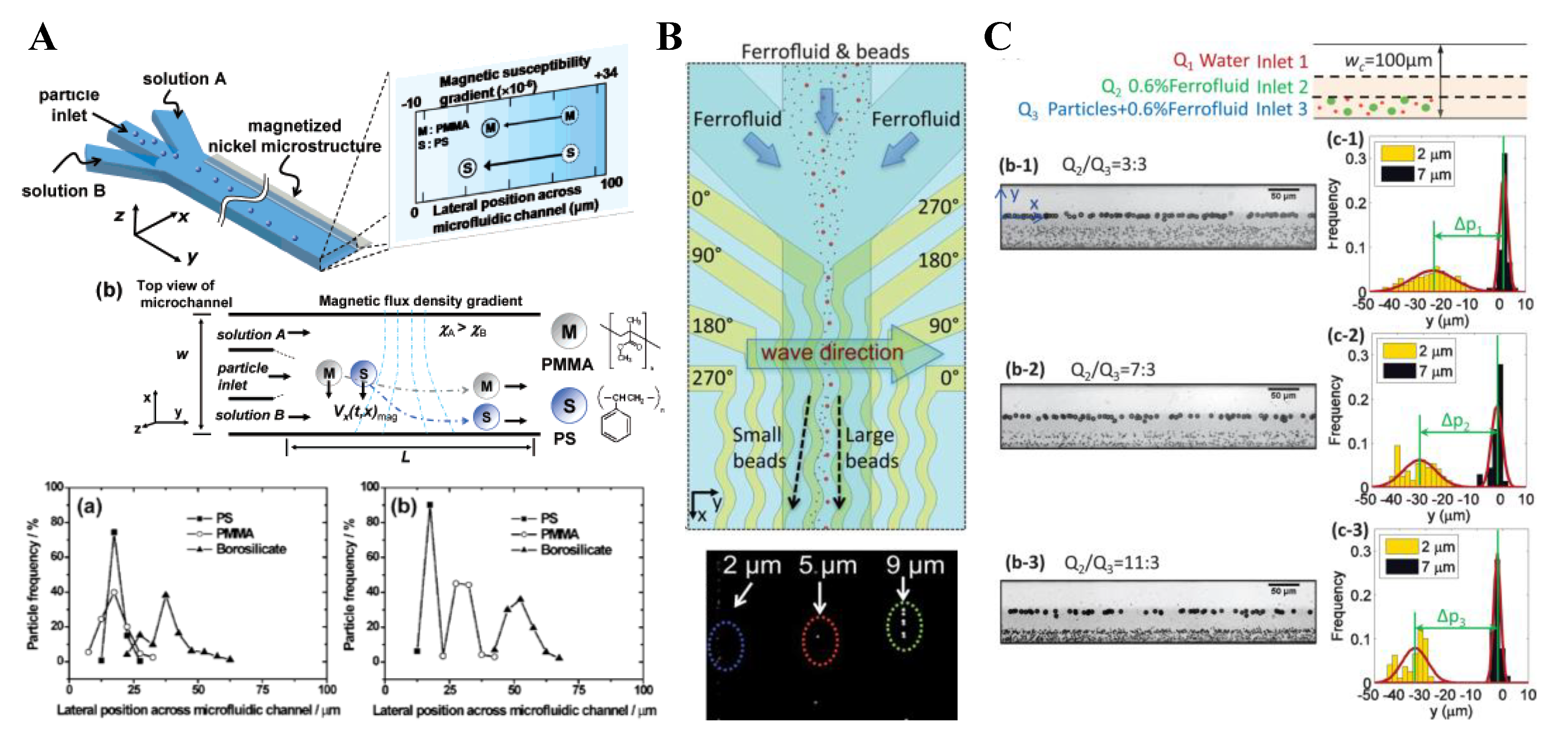
3. Particle Deflection
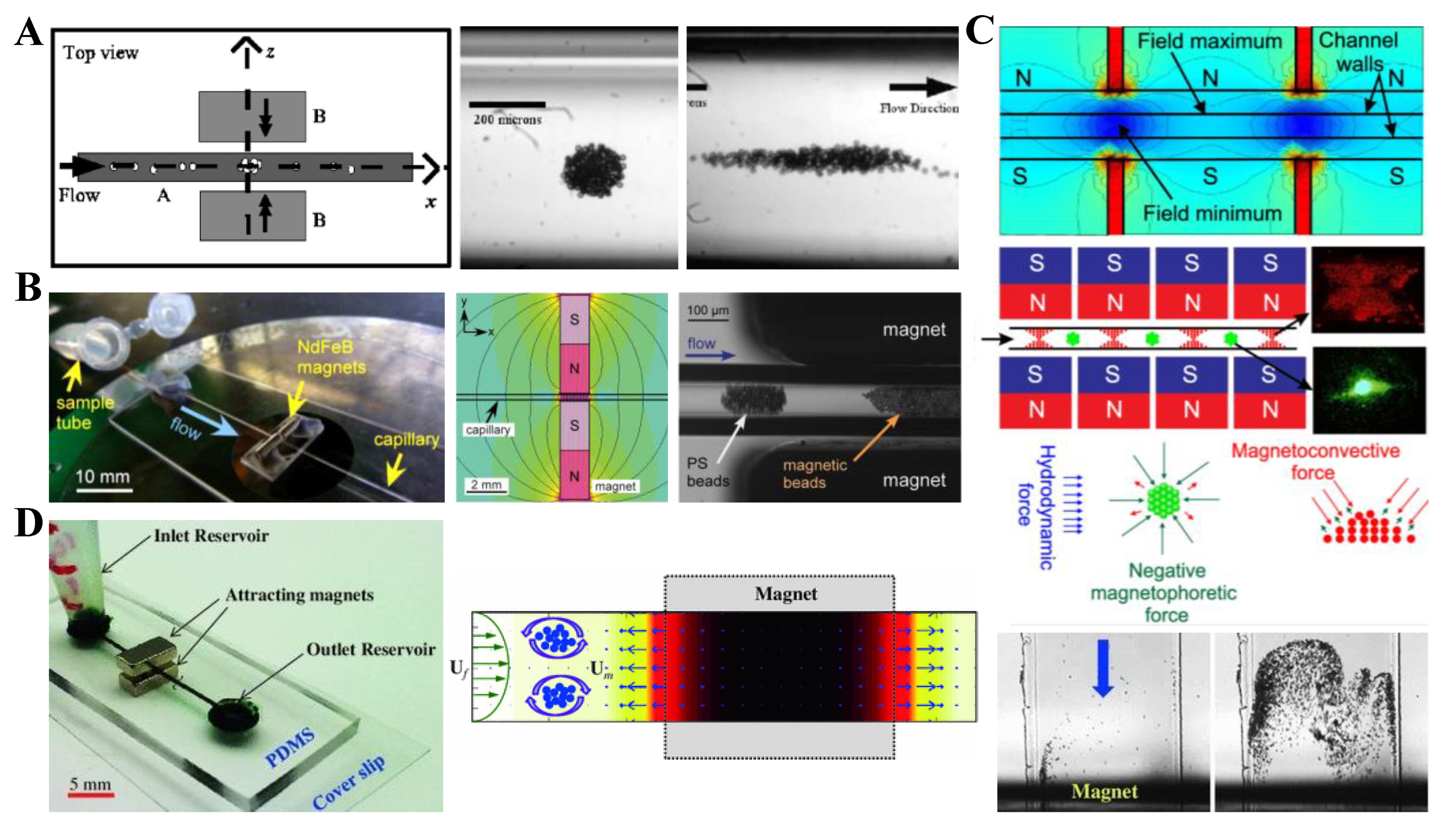
3.1. Non-Uniform Magnetic Field
3.2. Uniform Magnetic Field
3.3. Summary
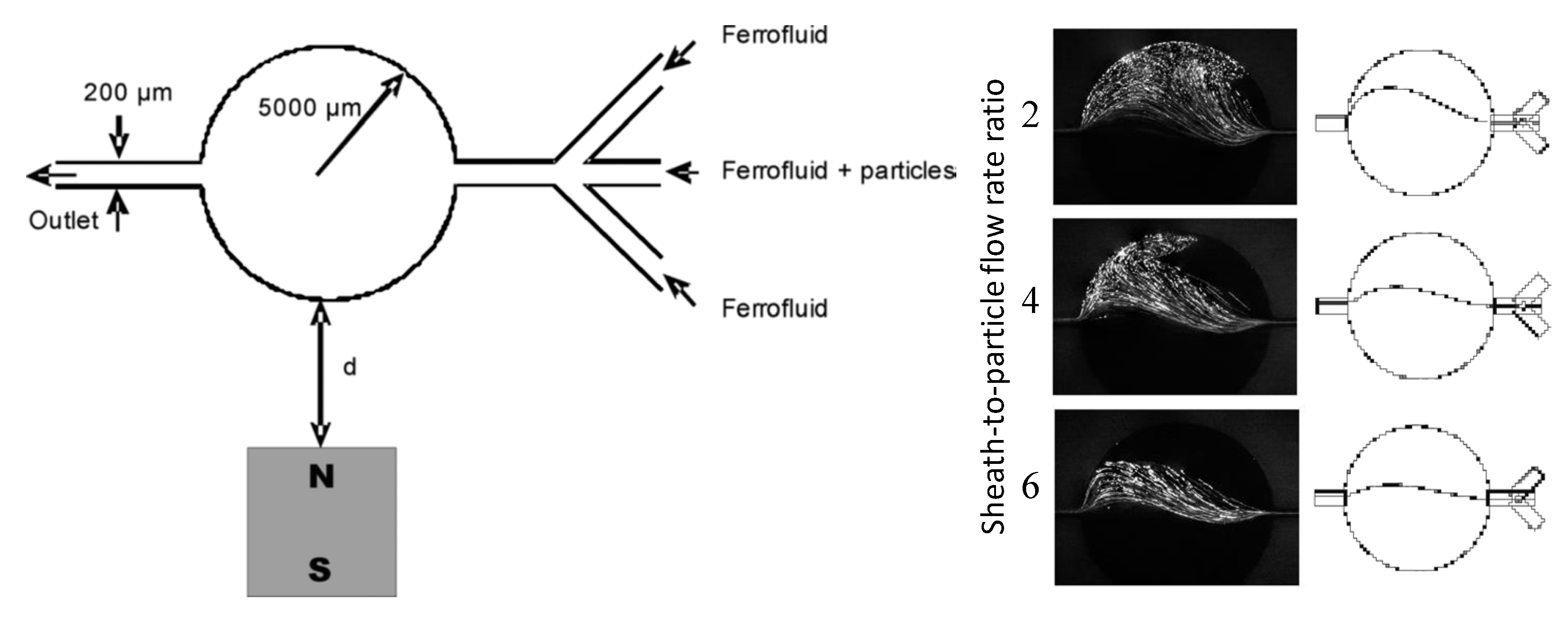
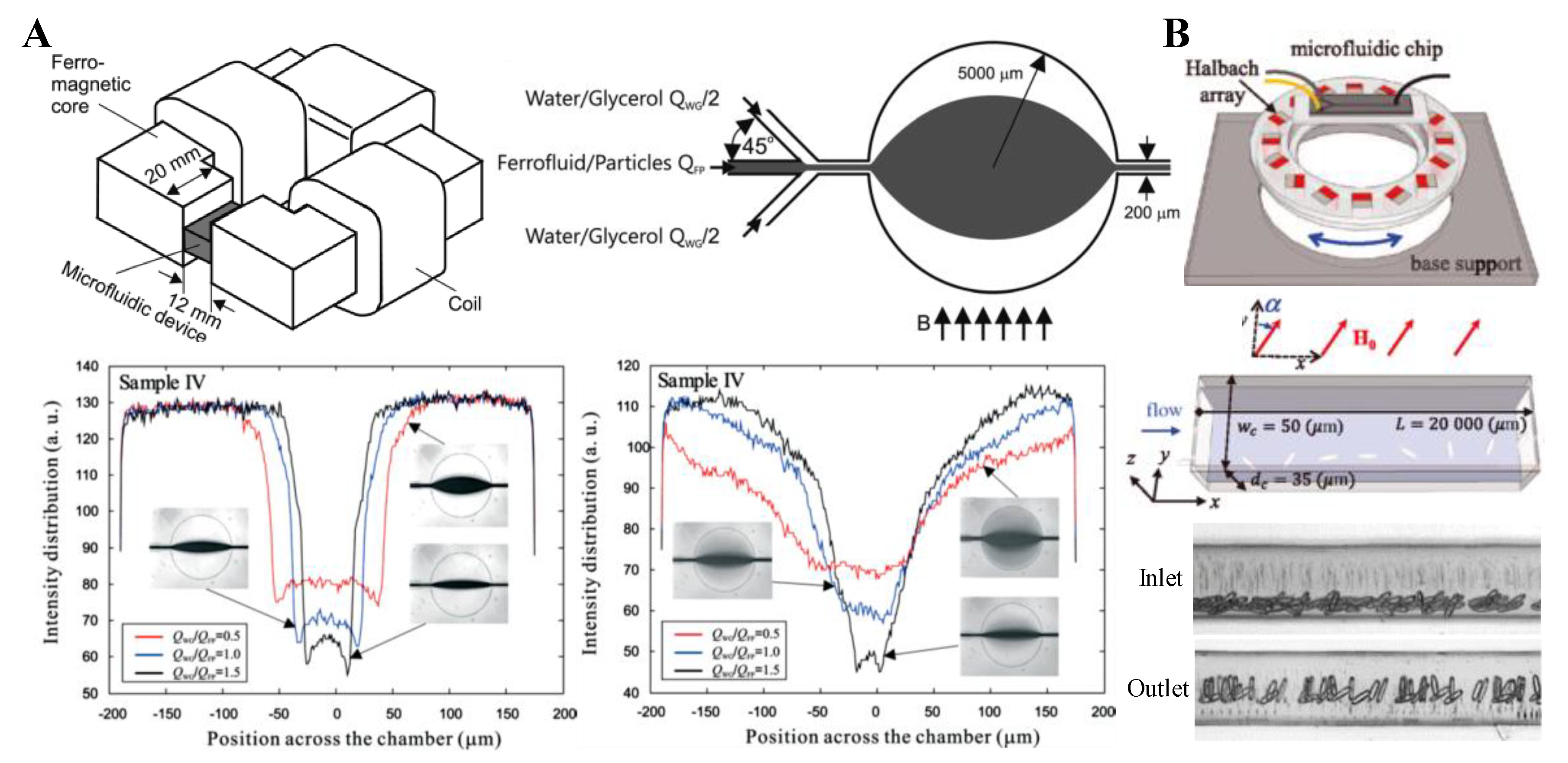
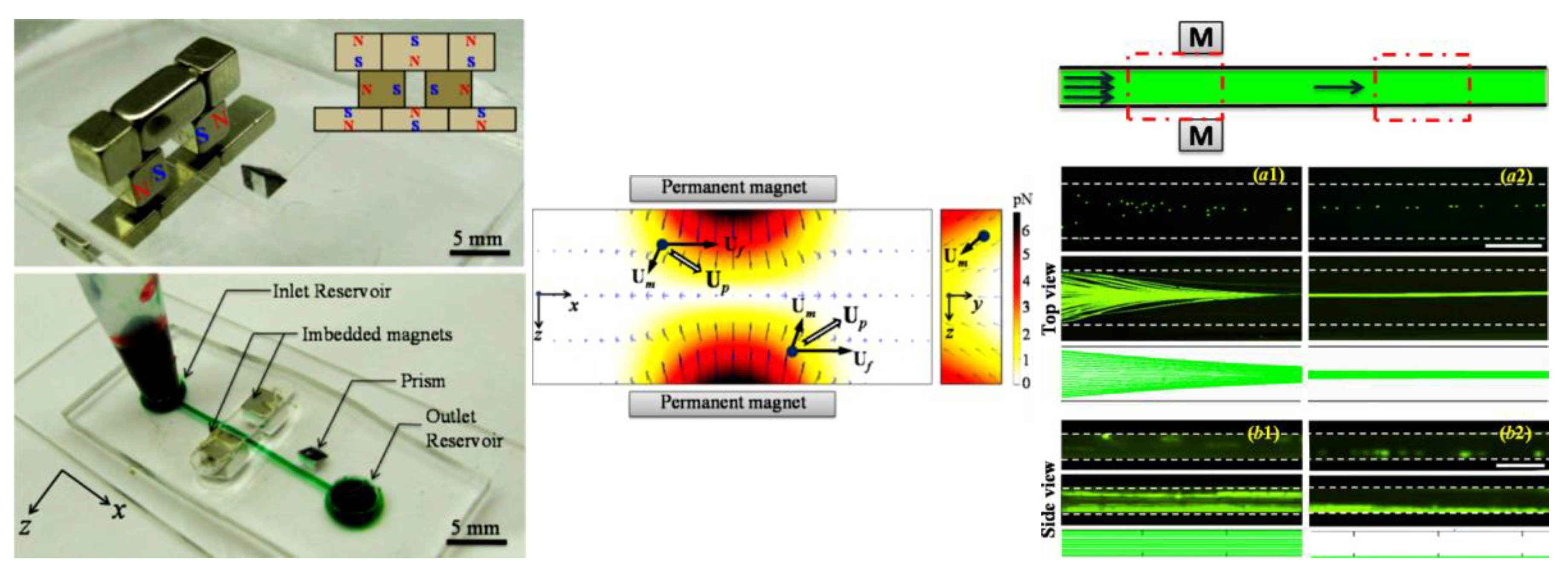
4. Particle Focusing
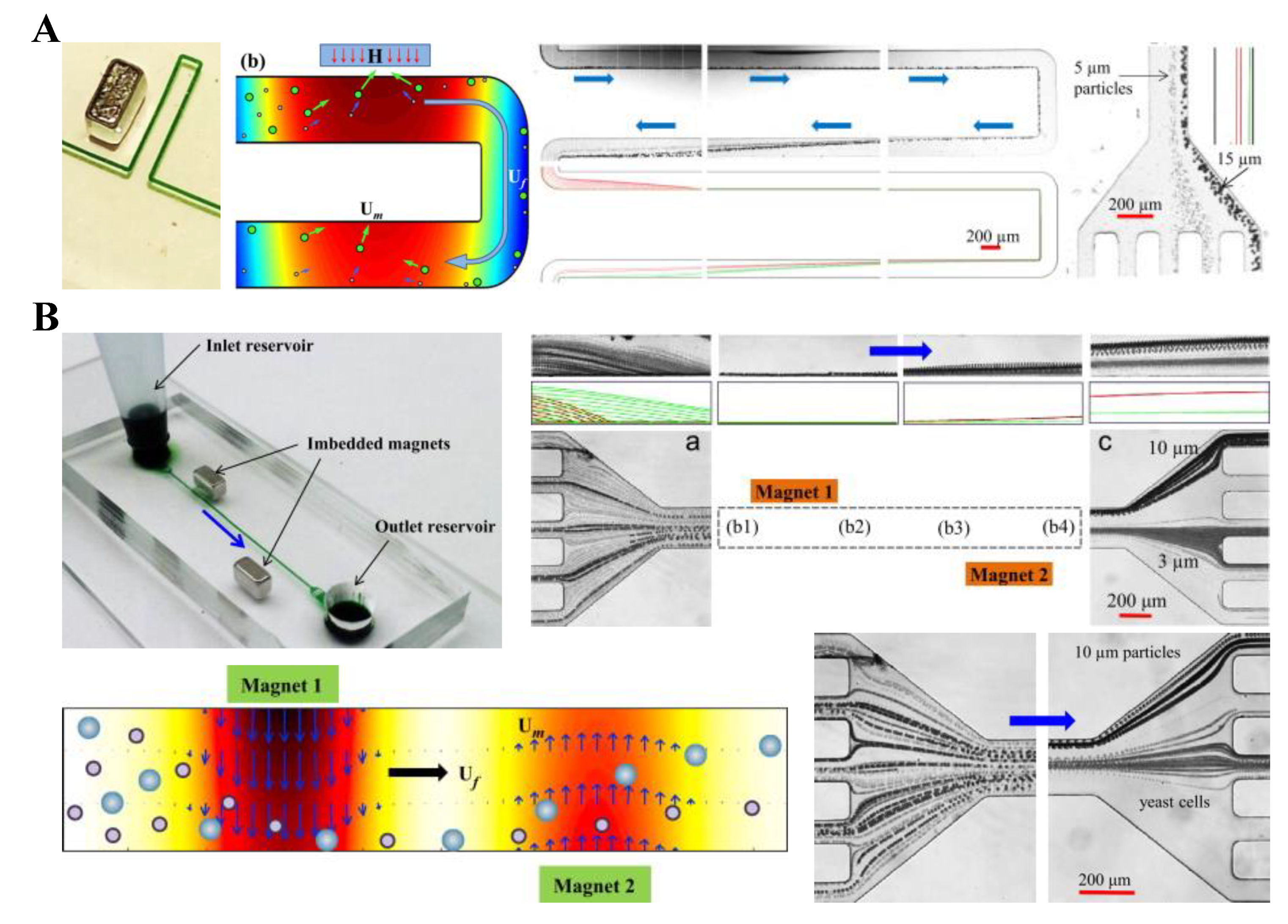
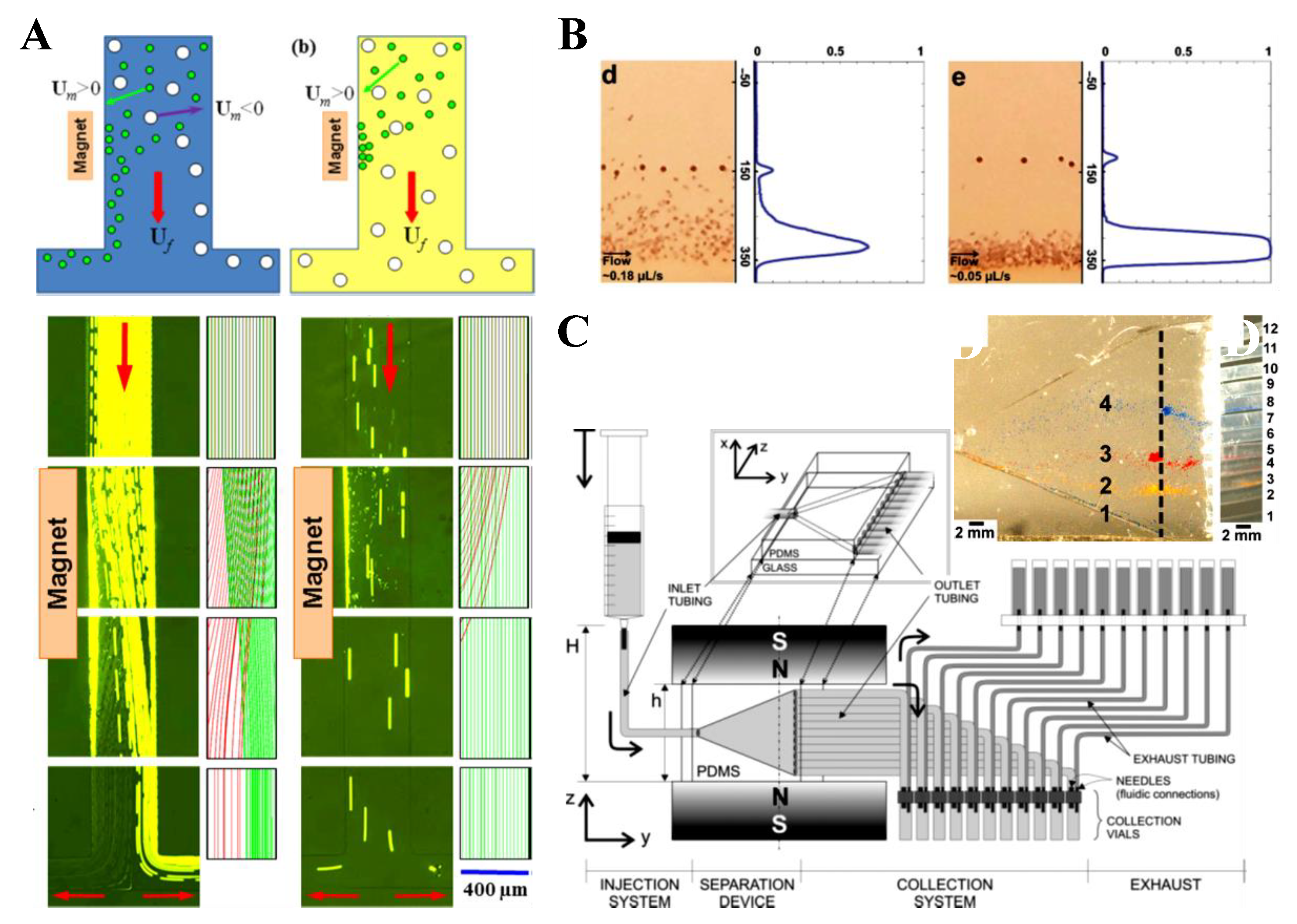
4.1. Repulsing Magnet Pair
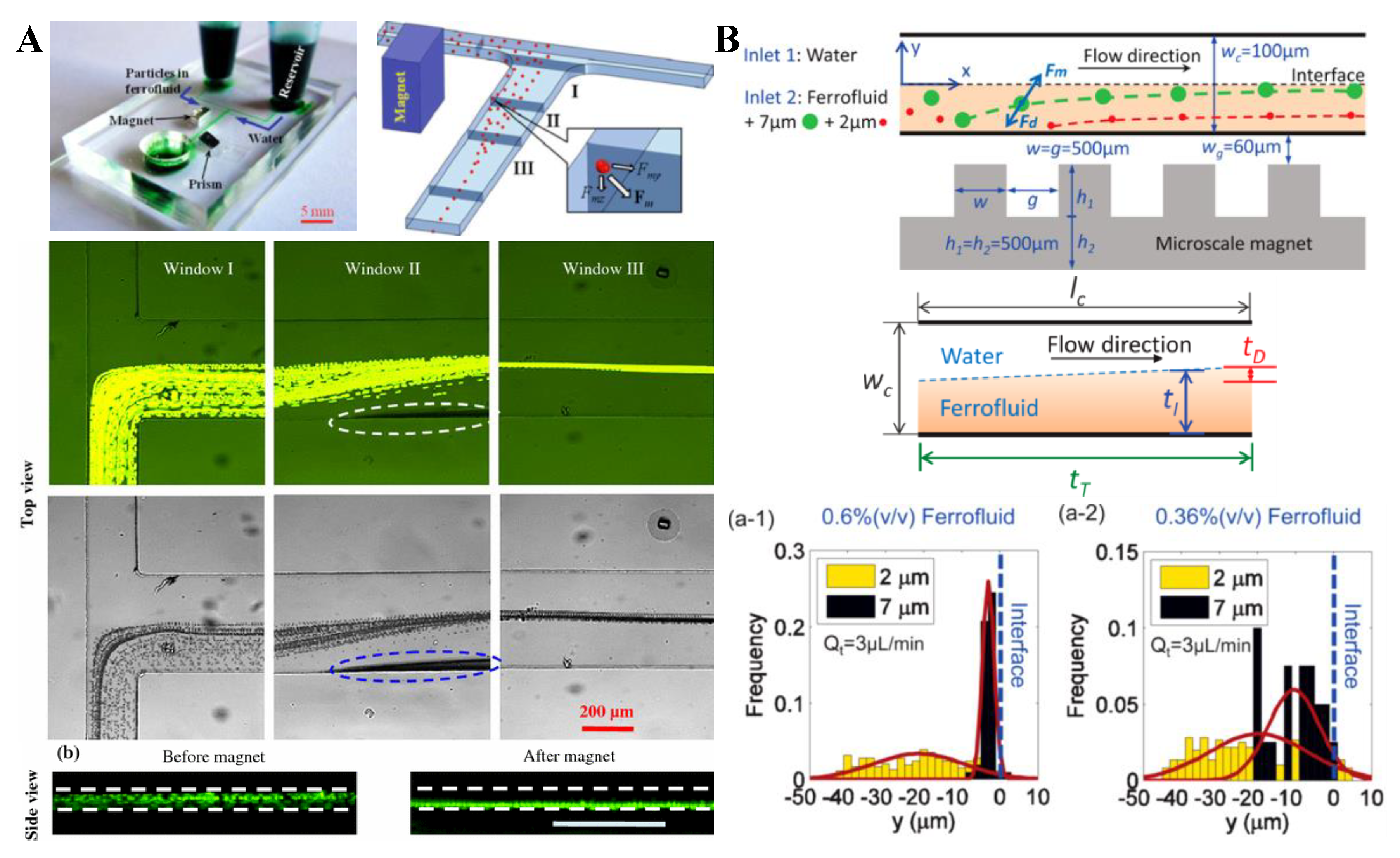
4.2. Single Magnet with a Sheath Flow
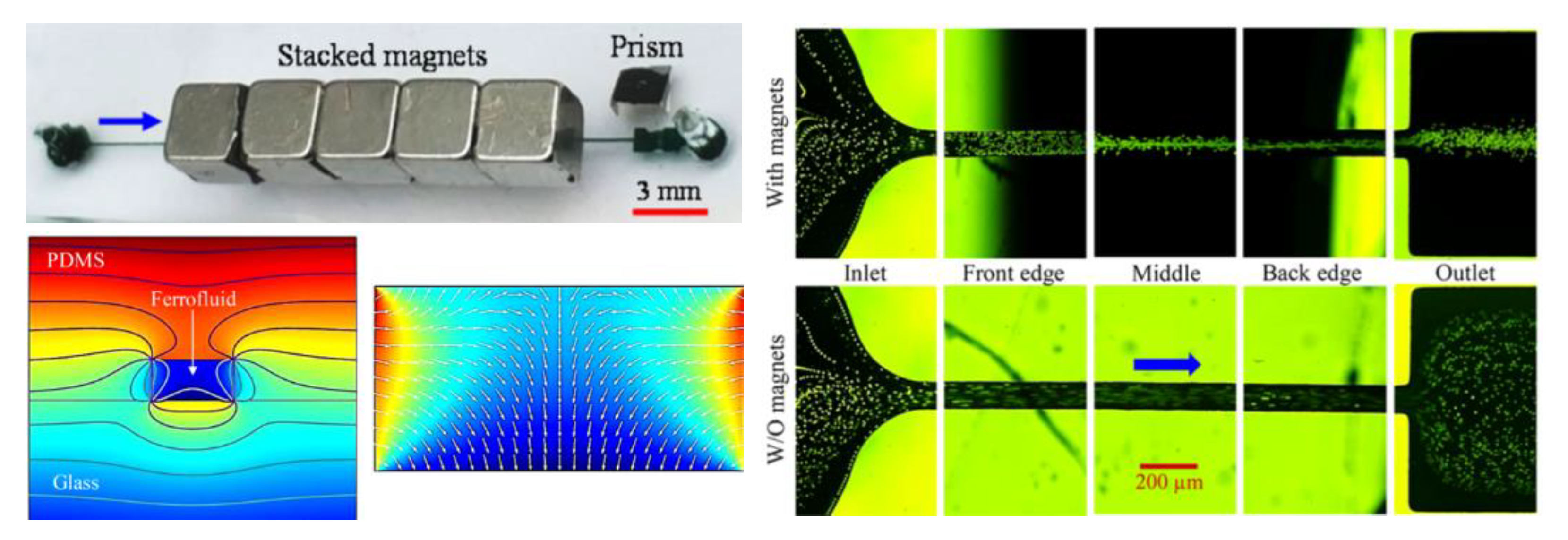
4.3. Single Magnet Only
4.4. Summary
| Sheath | Particles | Fluid | Magnet | Particle Flow Rate | References | |
|---|---|---|---|---|---|---|
| Configuration | Type | |||||
| - | 10 µm PS | 0.79 M MnCl2 | repulsing pair | permanent | 43 µL/h | [90] |
| - | 10/20 µm PS HaCaT cells | 0.79 M MnCl2/GdCl3 | repulsing pair | permanent | 30 µL/h | [44] |
| - | 10 µm PS | 50 mM Gadavist | repulsing pair | permanent | ~500 µL/h | [91] |
| - | 4.8/5.8/7.3 µm PS | 1.2% ferrofluid | repulsing pair | permanent | 60–480 µL/h | [92] |
| - | 5 µm PS yeast cells | 0.3% ferrofluid | repulsing pair | permanent | 50 µL/h | [93] |
| water sheath | 5/10 µm PS | 0.012% ferrofluid | single | permanent | ~50 µL/h | [94] |
| water sheath | 2/7 µm PS | 0.36/0.6% ferrofluid | single | permanent + micromagnet | 90 µL/h | [95] |
| - | 5–13 µm PS | 0.024–0.12% ferrofluid | single | permanent | 0.6–4.8 mL/h | [96] |
| - | 5/10/20 µm PS | 0.6–1.2% ferrofluid | stacked | permanent | 0.1–2 mL/h | [97] |
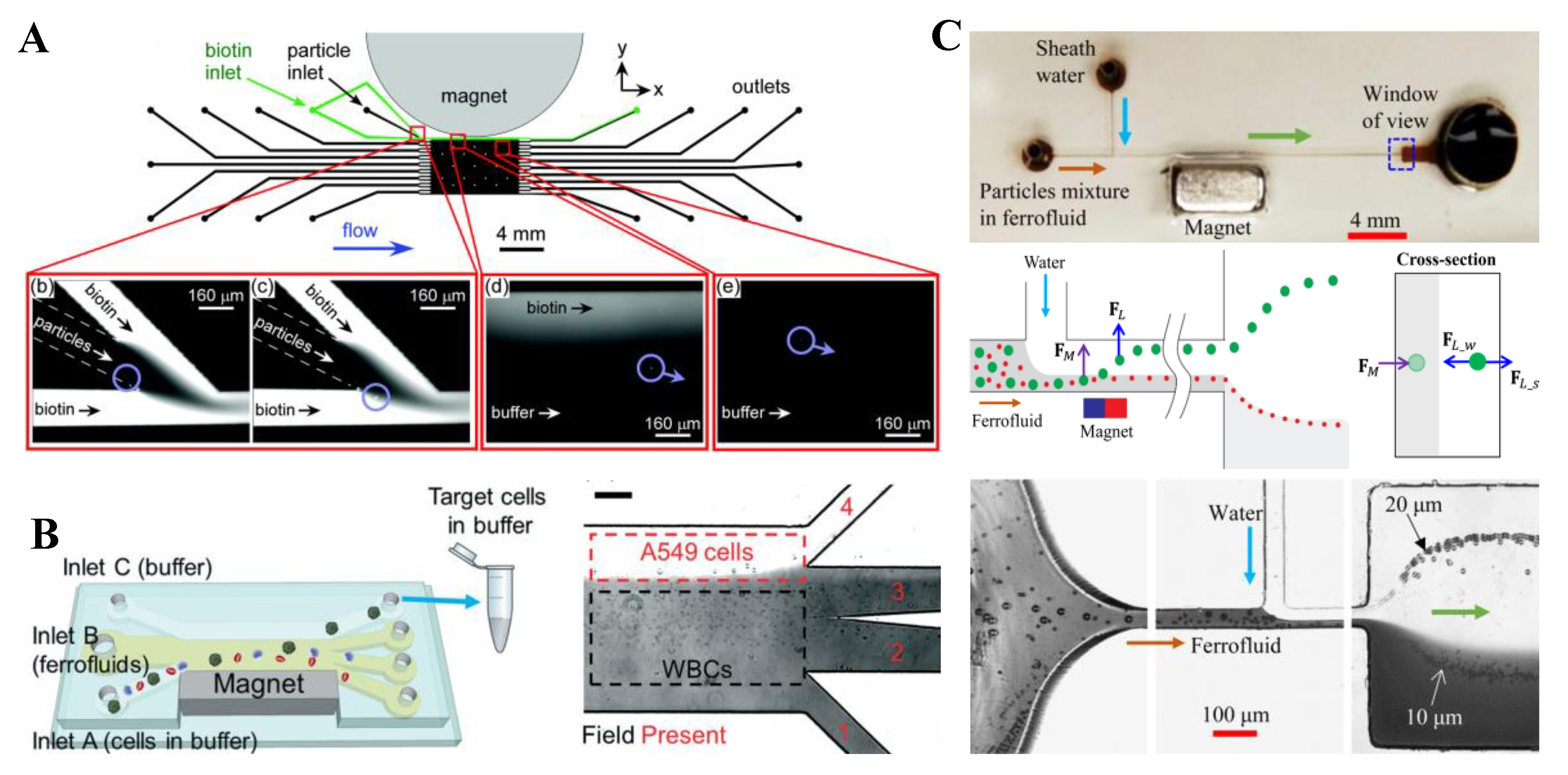
5. Particle Enrichment
5.1. Magnet Pair
5.2. Single Magnet
5.3. Summary
| Particles | Fluid | Magnet | Particle Flow Rate | References | |
|---|---|---|---|---|---|
| Configuration | Type | ||||
| 5/10/21 µm PS | 0.005% ferrofluid | repulsing pair | permanent | 0.24–1.2 mL/h | [104] |
| 10 µm PS | 0.79 M MnCl2 | attracting pair | permanent | 43 µL/h | [90] |
| 10 µm PS 8 µm mag | 0.79 M MnCl2 | attracting pair | permanent | 10 µL/h | [105] |
| 5 µm PS | 0.24% ferrofluid | attracting pair | permanent | 100–200 µL/h | [108] |
| 5 µm PS yeasts | 0.06% ferrofluid | attracting pair | permanent | 240 µL/h | [106] |
| 3.1/4.8 µm PS | 0.005–1% ferrofluid | attracting array | permanent | 0.6–6 mL/h | [107] |
| 9.9 µm PS 2.85 µm mag | 0.06% ferrofluid | single | permanent | ~50 µL/h | [109] |
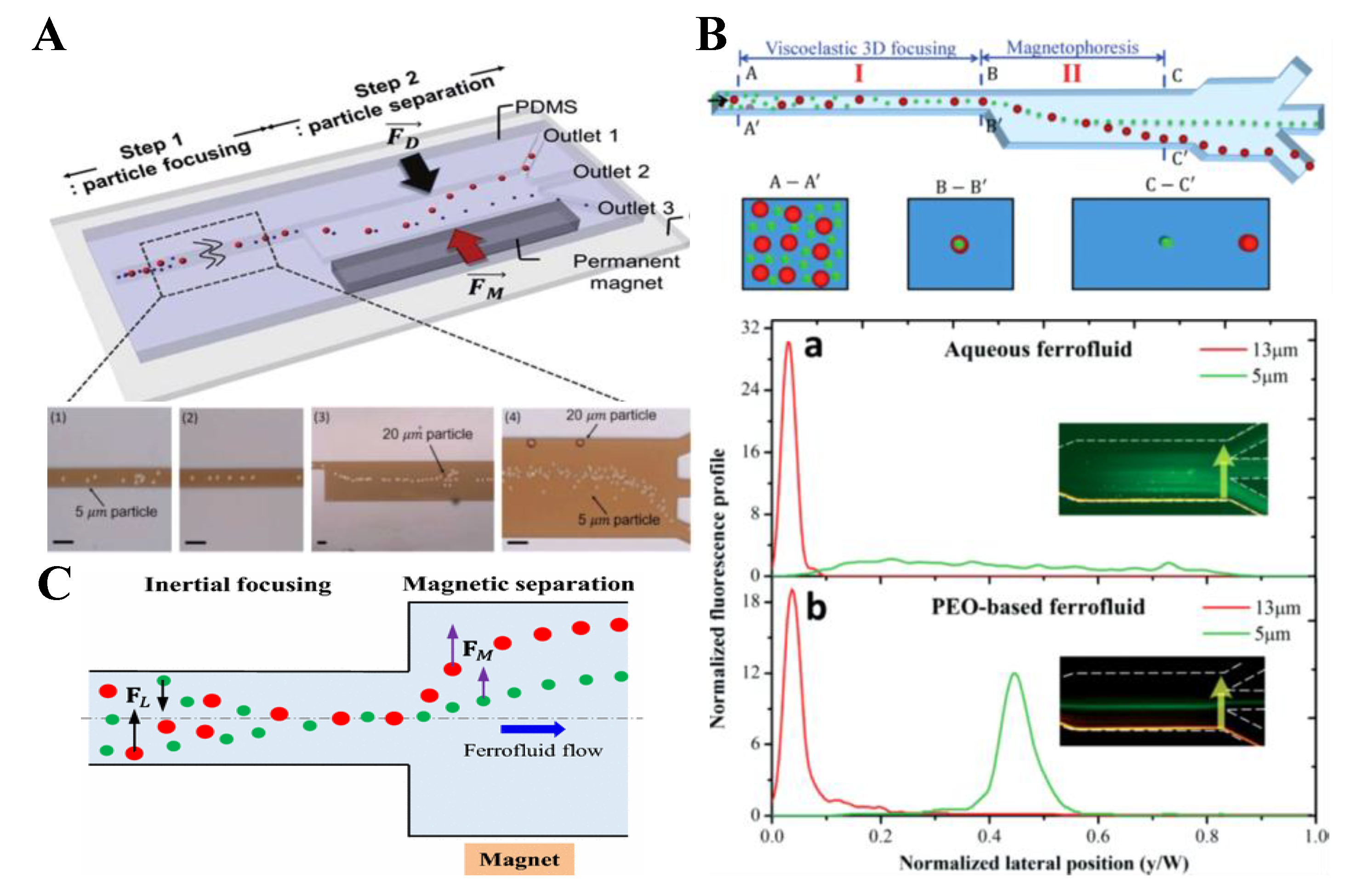
6. Particle Separation
6.1. One-Sheath-Flow Focusing
6.2. Two-Sheath-Flow Focusing
6.3. Sheath Free
6.4. Hybrid
6.5. Summary
| Pre-Focused | Particles | Fluid | Magnet | Particle Flow Rate | Reference | |
|---|---|---|---|---|---|---|
| Configuration | Type | |||||
| 1 sheath | 5/10 µm PS | 0.79 M MnCl2 | single | permanent | 20–60 µL/h | [90] |
| 1 sheath | 5/10 µm PS | 0.24–0.48 M MnCl2 | single | superconducting | 70 µL/h | [125] |
| 1 sheath | 1/3/6 µm PS | 1 M MnCl2 | single | superconducting | 58 µL/h | [126] |
| 1 sheath | 8/10 µm PS RBC/U937 | 0–80 mM Gd-DTPA | single | permanent + micromagnet | 19.2 µL/h | [127] |
| 1 sheath | 1/1.9/3.1/9.9 µm PS | 1.2% ferrofluid | single | permanent | 180 µL/h | [131] |
| 1 sheath | 1/7.3 µm PS yeast/E.coli | 1.2% ferrofluid | stacked | permanent | 90 µL/h | [132] |
| 1 sheath | 5.8/15. µm PS HeLa RBC | 0.3% ferrofluid | single | permanent | 480 µL/h | [128] |
| 1 sheath | cancer cells WBC | 0.26% ferrofluid | single | permanent | 1.2–6 mL/h | [133] |
| 1 sheath | cell containing droplets | 0.08% ferrofluid | single | permanent | - | [129] |
| 1 sheath | 6 µm spheres/peanuts | 0.36% ferrofluid | single | permanent | 6 µL/h | [135] |
| 1 sheath | drug treated yeasts | 0.12% ferrofluid | single | permanent | 9 µL/h | [130] |
| 2 sheathes | 15 µm PS/PMMA/BS | 125 mM Gd-DTPA | single | permanent + micromagnet | - | [137] |
| 2 sheathes | 6/10 µm PS+biomarkers | 10/25 mM Gd-DTPA | single | permanent + micromagnet | 1.2 µL/h | [47] |
| 2 sheathes | 2.2/4.8/9.9 µm PS | 5.8% ferrofluid | electrodes in quadrature | electromagnet | 24 µL/h | [138] |
| 2 sheathes | 2/7 µm PS | 0.36/0.6% ferrofluid | single | permanent + micromagnet | 50–120 µL/h | [95] |
| 2 sheathes | 3.2/4.8 µm PS | 0.25–1% ferrofluid | array | permanent | 60 µL/h | [139] |
| - | 2.2/9.9 µm PS RBC sickle cells bacteria | customized ferrofluid | electrodes in quadrature | electromagnet | - | [140] |
| - | 5/15 µm PS | 0.012% ferrofluid | single | permanent | ~20 µL/h | [141] |
| - | 5/15 µm PS | 0.6% ferrofluid | single | permanent | 450 µL/h | [142] |
| - | 3/10 µm PS yeast cells | 0.06% ferrofluid | two offset | permanent | 10–20 µL/h | [143] |
| - | 10 µm PS 2.85 µm mag | 0.12% ferrofluid | single | permanent | 240 µL/h | [144] |
| - | 4.2/7.3 µm PS 2.6/7.9 µm mag | 1.2% ferrofluid | single | permanent | ~200 µL/h | [145] |
| - | 10 µm PS blood | 50 mM Gadavist | repulsing pair | permanent | ~100 µL/h | [91] |
| - | 75–100 µm Merrifield resins | 250 mM GdCl3 | repulsing pair | permanent | 6–15 mL/h | [146] |
| elastic | 5/20 µm PS | 0.12% ferrofluid | single | permanent | 5–200 µL/h | [148] |
| elastic | 5/13 µm PS | 0.12% ferrofluid | single | permanent | 900 µL/h | [149] |
| inertial | 10/20 µm PS | 0.36–0.84% ferrofluid | single | permanent | 0.5–1.5 mL/h | [150] |
| Hydrophoretic | 13 µm PS 6 µm mag | 0.06% ferrofluid | single | permanent | 0.3–4.8 mL/h | [151] |
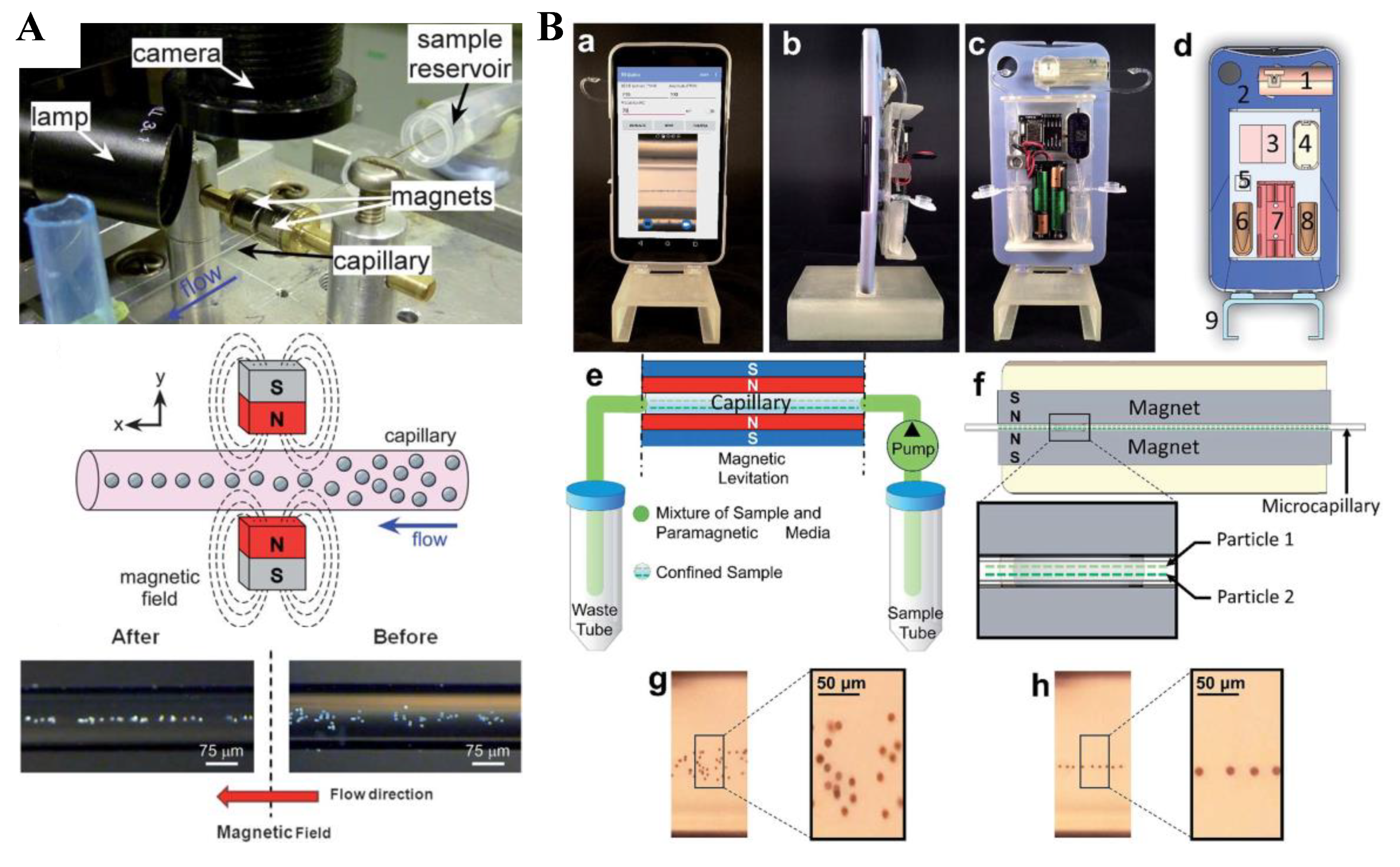
7. Particle Medium Exchange
7.1. Biocompatibility of Magnetic Fluids
7.2. Single Magnet
7.3. Summary
| Exchange Medium | Particles | Fluid | Magnet | Particle Flow Rate | References | |
|---|---|---|---|---|---|---|
| Configuration | Type | |||||
| buffer sheath | 4.3 µm PS | 0.79 M MnCl2 | single | permanent | 0.52 µL/h | [164] |
| buffer sheath | 5.8/15.7 µm PS cancer cells WBC | 0.26% ferrofluid | single | permanent | 1.2 mL/h | [165] |
| water sheath | 10/20 µm PS | 0.9% ferrofluid | single | permanent | 1 mL/h | [166] |
8. Conclusions and Perspectives
Funding
Acknowledgments
Conflicts of Interest
References
- Yousuff, C.M.; Ho, E.T.W.; Hussain, K.I.; Hamid, N.H.B. Microfluidic platform for cell isolation and manipulation based on cell properties. Micromachines 2017, 8, 15. [Google Scholar] [CrossRef]
- Nguyen, N.T.; Hejazian, M.; Ooi, C.H.; Kashaninejad, N. Recent advances and future perspectives on microfluidic liquid handling. Micromachines 2017, 8, 186. [Google Scholar] [CrossRef]
- Martinez-Rivas, A.; Gonzalez-Quijano, G.K.; Proa-Coronado, S.; Severac, C.; Dague, E. Methods of micropatterning and manipulation of cells for biomedical applications. Micromachines 2017, 8, 347. [Google Scholar] [CrossRef] [PubMed]
- Cai, G.Z.; Xue, L.; Zhang, H.L.; Lin, J.H. A review on micromixers. Micromachines 2017, 8, 274. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.Q.; Chang, H.L.; Neuzil, P. DEP-on-a-chip: Dielectrophoresis applied to microfluidic platforms. Micromachines 2019, 10, 423. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; He, Y.Q.; Jiao, F. Advances of particles/cells magnetic manipulation in microfluidic chips. Chin. J. Anal. Chem. 2017, 45, 1238–1246. [Google Scholar] [CrossRef]
- Xie, Y.; Bachman, H.; Huang, T.J. Acoustofluidic methods in cell analysis. TrAC Trend. Anal. Chem. 2019, 117, 280–290. [Google Scholar] [CrossRef]
- Kayani, A.A.; Khoshmanesh, K.; Ward, S.A.; Mitchell, A.; Kalantar-Zadeh, K. Optofluidics incorporating actively controlled micro and nano-particles. Biomicrofluid. 2012, 6, 031501. [Google Scholar] [CrossRef]
- Pamme, N. Magnetism and microfluidics. Lab Chip 2006, 6, 24–38. [Google Scholar] [CrossRef]
- Nguyen, N.T. Micro-magnetofluidics: Interactions between magnetism and fluid flow on the microscale. Microfluid. Nanofluid. 2012, 12, 1–16. [Google Scholar] [CrossRef]
- Alnaimat, F.; Dagher, S.; Mathew, B.; Hilal-Alnqbi, A.; Khashan, S. Microfluidics based magnetophoresis: A review. Chem. Rec. 2018, 18, 1596–1612. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Huang, M.; Wang, D.; Zhang, Z.; Li, C. Magnetic separation techniques in sample preparation for biological analysis: A review. J. Pharm. Biomed. Anal. 2014, 101, 84–101. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.; Huang, Y.; Hoshino, K.; Zhang, X. Multiscale immunomagnetic enrichment of circulating tumor cells: From tubes to microchips. Lab Chip 2014, 14, 446–458. [Google Scholar] [CrossRef] [PubMed]
- Hejazian, M.; Li, W.; Nguyen, N.T. Lab on a chip for continuous flow magnetic cell separation. Lab Chip 2015, 15, 959–970. [Google Scholar] [CrossRef] [PubMed]
- Borlido, L.; Azevedo, A.M.; Roque, A.C.A.; Aires-Barros, M.R. Magnetic separations in biotechnology. Biotechnol. Adv. 2013, 31, 1374–1385. [Google Scholar] [CrossRef] [PubMed]
- Cao, Q.; Han, X.; Li, L. Configurations and control of magnetic fields for manipulating magnetic particles in microfluidic applications: Magnet systems and manipulation mechanisms. Lab Chip 2014, 14, 2762–2777. [Google Scholar] [CrossRef]
- Munaz, A.; Shiddiky, M.J.A.; Nguyen, N.T. Recent advances and current challenges in magnetophoresis based micro magnetofluidics. Biomicrofluidics 2018, 12, 031501. [Google Scholar] [CrossRef]
- Zborowski, M.; Ostera, G.R.; Moore, L.R.; Milliron, S.; Chalmers, J.J.; Schechter, A.N. Red blood cell magnetophoresis. Biophys. J. 2003, 84, 2638–2645. [Google Scholar] [CrossRef]
- Lee, H.; Purdon, A.M.; Chu, V.; Westervelt, R.M. Controlled assembly of magnetic nanoparticles from magnetotactic bacteria using microelectromagnets arrays. Nano. Lett. 2004, 4, 995–998. [Google Scholar] [CrossRef]
- Watarai, H.; Suwa, M.; Iiguni, Y. Magnetophoresis and electromagnetophoresis of microparticles in liquids. Anal. Bioanal. Chem. 2004, 378, 1693–1699. [Google Scholar] [CrossRef]
- Suwa, M.; Watarai, H. Magnetoanalysis of micro/nanoparticles: A review. Anal. Chimica Acta 2011, 690, 137–147. [Google Scholar] [CrossRef]
- Yang, R.; Hou, H.; Wang, Y.; Fu, L. Micro-magnetofluidics in microfluidic systems: A review. Sens. Act. B 2016, 224, 1–15. [Google Scholar] [CrossRef]
- Zhao, W.; Cheng, R.; Miller, J.R.; Mao, L. Label-free microfluidic manipulation of particles and cells in magnetic liquids. Adv. Fun. Mat. 2016, 26, 3916–3932. [Google Scholar] [CrossRef] [PubMed]
- Gao, Q.H.; Zhang, W.M.; Zou, H.X.; Li, W.B.; Yan, H.; Peng, Z.K.; Meng, G. Label-free manipulation via the magneto-archimedes effect: Fundamentals, methodology and applications. Mater. Horiz. 2019, 6, 1359–1379. [Google Scholar] [CrossRef]
- Jones, T.B. Electromechanics of Particles; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Pankhurst, Q.A.; Connolly, J.; Jones, S.K.; Dobson, J. Applications of magnetic nanoparticles in biomedicine. J. Phys. D 2003, 36, R167–R181. [Google Scholar] [CrossRef] [Green Version]
- Ramadan, Q.; Gijs, M.A.M. Microfluidic applications of functionalized magnetic particles for environmental analysis: Focus on waterborne pathogen detection. Microfluid. Nanofluid. 2012, 13, 529–542. [Google Scholar] [CrossRef]
- Plouffe, B.D.; Murthy, S.K.; Lewis, L.H. Fundamentals and application of magnetic particles in cell isolation and enrichment: A review. Rep. Prog. Phys. 2015, 78, 016601. [Google Scholar] [CrossRef]
- Voltairas, P.A.; Fotiadis, D.I.; Michalis, L.K. Hydrodynamics of magnetic drug targeting. J. Biomech. 2002, 35, 813–821. [Google Scholar] [CrossRef]
- Gijs, M.A.M. Magnetic bead handling on-chip: New opportunities for analytical applications. Microfluid. Nanofluid. 2004, 1, 22–40. [Google Scholar] [CrossRef]
- Pamme, N. On-chip bioanalysis with magnetic particles. Curr. Opin. Chem. Biol. 2012, 16, 436–443. [Google Scholar] [CrossRef]
- Pamme, N.; Wilhelm, C. Continuous sorting of magnetic cells via on-chip free-flow magnetophoresis. Lab Chip 2006, 6, 974–980. [Google Scholar] [CrossRef] [PubMed]
- Adams, J.D.; Thévoz, P.; Shea, H.; Bruus, H.; Soh, H.T. Integrated acoustic and magnetic separation in microfluidic channels. Appl. Phys. Lett. 2009, 95, 254103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roberta, D.; Pamme, N.; Conjeauda, H.; Gazeaua, F.; Ilesb, A.; Wilhelm, C. Cell sorting by endocytotic capacity in a microfluidic magnetophoresis device. Lab Chip 2011, 11, 1902–1910. [Google Scholar] [CrossRef]
- Han, K.H.; Frazier, A.B. Paramagnetic capture mode magnetophoretic microseparator for high efficiency blood cell separations. Lab Chip 2006, 6, 265–273. [Google Scholar] [CrossRef] [PubMed]
- Adams, J.D.; Kim, U.; Soh, H.T. Multi-target magnetic activated cell sorter (MT-MACS). Proc. Natl. Acad. Sci. USA 2008, 105, 18165–18170. [Google Scholar] [CrossRef] [PubMed]
- Williams, P.S.; Carpino, F.; Zborowski, M. Magnetic nanoparticle drug carriers and their study by quadrupole magnetic field-flow fractionation. Mol. Pharm. 2009, 6, 1290–1306. [Google Scholar] [CrossRef]
- Lacharme, F.; Vandevyver, C.; Gijs, M.A.M. Full on-chip nanoliter immunoassay by geometrical magnetic trapping of nanoparticle chains. Anal. Chem. 2008, 80, 2905–2910. [Google Scholar] [CrossRef]
- Liu, C.X.; Stakenborg, T.; Peeters, S.; Lagae, L. Cell manipulation with magnetic particles toward microfluidic cytometry. J. Appl. Phys. 2009, 105, 102011–102014. [Google Scholar] [CrossRef]
- Gijs, M.A.M.; Lacharme, F.; Lehmann, U. Microfluidic applications of magnetic particles for biological analysis and catalysis. Chem. Rev. 2010, 110, 1518–1563. [Google Scholar] [CrossRef]
- Tekin, H.C.; Gijs, M.A.M. Ultrasensitive protein detection: A case for microfluidic magnetic bead-based assays. Lab Chip 2013, 13, 4711–4739. [Google Scholar] [CrossRef]
- Rikken, R.S.M.; Nolte, R.J.M.; Maan, J.C.; van Hest, J.C.M.; Wilson, D.A.; Christianen, P.C.M. Manipulation of micro- and nanostructure motion with magnetic fields. Soft Matter 2014, 10, 1295–1308. [Google Scholar] [CrossRef] [PubMed]
- Mirica, K.A.; Phillips, S.T.; Shevkoplyas, S.S.; Whitesides, G.M. Measuring densities of solids and liquids using magnetic levitation: Fundamentals. J. Am. Chem. Soc. 2009, 131, 10049–10058. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Villarreal, A.I.; Tarn, M.D.; Madden, L.A.; Lutz, J.B.; Greenman, J.; Samitier, J.; Pamme, N. Flow focusing of particles and cells based on their intrinsic properties using a simple diamagnetic repulsion setup. Lab Chip 2011, 11, 1240–1248. [Google Scholar] [CrossRef] [PubMed]
- Tarn, M.D.; Hirota, N.; Hes, A.; Pamme, N. On-chip diamagnetic repulsion in continuous flow. Sci. Technol. Adv. Mater. 2009, 10, 014611. [Google Scholar] [CrossRef]
- Winkleman, A.; Gudiksen, K.L.; Ryan, D.; Whitesides, G.M. A magnetic trap for living cells suspended in a paramagnetic buffer. Appl. Phys. Lett. 2004, 85, 2411–2413. [Google Scholar] [CrossRef] [Green Version]
- Hahn, Y.K.; Park, J.K. Versatile immunoassays based on isomagnetophoresis. Lab Chip 2011, 11, 2045–2048. [Google Scholar] [CrossRef]
- Rosensweig, R.E. Magnetic fluids. Annu. Rev. Fluid. Mech. 1987, 19, 437–463. [Google Scholar] [CrossRef]
- Rosensweig, R.E. Ferrohydrodynamics; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Hatch, A.; Kamholz, A.E.; Holman, G.; Yager, P.; Bohringer, K.F. A ferrofluidic magnetic micropump. J. MEMS 2001, 10, 215–221. [Google Scholar] [CrossRef]
- Yellen, B.B.; Friedman, G.; Feinerman, A. Printing superparamagnetic colloidal particle arrays on patterned magnetic film. J. Appl. Phys. 2003, 93, 7331–7333. [Google Scholar] [CrossRef]
- Yellen, B.B.; Friedman, G. Programmable assembly of colloidal particles using magnetic microwell templates. Langmuir 2004, 20, 2553–2559. [Google Scholar] [CrossRef]
- Yellen, B.B.; Hovorka, O.; Friedman, G. Arranging matter by magnetic nanoparticle assemblers. Proc. Natl. Acad. Sci. USA 2005, 102, 8860–8864. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Halverson, D.; Kalghatgi, S.; Yellen, B.; Friedman, G. Manipulation of nonmagnetic nanobeads in dilute ferrofluid. J. Appl. Phys. 2006, 99, 08P504. [Google Scholar] [CrossRef]
- Erb, R.M.; Yellen, B.B. Concentration gradients in mixed magnetic and nonmagnetic colloidal suspensions. J. Appl. Phys. 2008, 103, 07A312. [Google Scholar] [CrossRef]
- Erb, R.M.; Son, H.S.; Samanta, B.; Rotello, V.M.; Yellen, B.B. Magnetic assembly of colloidal superstructures with multipole symmetry. Nature 2009, 457, 999–1002. [Google Scholar] [CrossRef]
- Li, K.H.; Yellen, B.B. Magnetically tunable self-assembly of colloidal rings. Appl. Phys. Lett. 2010, 97, 083105. [Google Scholar] [CrossRef] [Green Version]
- Erb, R.M.; Yellen, B.B. Nanoscale magnetic materials and applications. In Magnetic Manipulation of Colloidal Particles; Liu, J.P., Ed.; Springer: Berlin, Germany, 2009; pp. 563–590. [Google Scholar]
- Friedman, G.; Yellen, B.B. Magnetic separation, manipulation, and assembly of solid phase in fluids. Curr. Opin. Colloid Interface Sci. 2005, 10, 158–166. [Google Scholar] [CrossRef]
- Pohl, H.A. Dielectrophoresis; Cambridge University Press: Cambridge, UK, 1978. [Google Scholar]
- Lapizco-Encinas, B.H. On the recent developments of insulator-based dielectrophoresis: A review. Electrophoresis 2019, 40, 358–375. [Google Scholar] [CrossRef]
- Furlani, E.P. Permanent Magnet and Electromechanical Devices: Materials, Analysis, and Applications; Academic Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Wen, C.Y.; Liang, K.P.; Chen, H.; Fu, L.M. Numerical analysis of a rapid magnetic microfluidic mixer. Electrophoresis 2011, 32, 3268–3276. [Google Scholar] [CrossRef]
- Zhu, G.; Nguyen, N.T. Magnetofluidic spreading in microchannels. Microfluid. Nanofluid. 2012, 13, 655–663. [Google Scholar] [CrossRef] [Green Version]
- Zhu, G.; Nguyen, N.T. Rapid magnetofluidic mixing in a uniform magnetic field. Lab Chip 2012, 12, 4772–4780. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Varma, V.B.; Wang, Z.P.; Ramanujan, R.V. Tuning magnetofluidic spreading in microchannels. J. Micromech. Microeng. 2015, 25, 124001. [Google Scholar] [CrossRef]
- Wang, Z.; Varma, V.B.; Xia, H.M.; Wang, Z.P.; Ramanujan, R.V. Spreading of a ferrofluid core in three-stream micromixer channels. Phys. Fluids 2015, 27, 052004. [Google Scholar] [CrossRef]
- Puri, I.K.; Ganguly, R. Particle transport in therapeutic magnetic fields. Annu. Rev. Fluid Mech. 2014, 46, 407–440. [Google Scholar] [CrossRef]
- Happel, J.; Brenner, H. Low Reynolds Number Hydrodynamics; Springer: Berlin, Germany, 1973. [Google Scholar]
- Turker, E.; Arslan-Yildiz, A. Recent advances in magnetic levitation: A biological approach from diagnostics to tissue engineering. ACS Biomater. Sci. Eng. 2018, 4, 787–799. [Google Scholar] [CrossRef]
- Ge, S.; Nemiroski, A.; Mirica, K.A.; Mace, C.R.; Hennek, J.W.; Kumar, A.A.; Whitesides, G.M. Magnetic levitation in chemistry, materials science, and biochemistry. Angew. Chem. Int. Ed. Eng. 2019. in Press. [Google Scholar] [CrossRef] [PubMed]
- Rinaldi, C. An invariant general solution for the magnetic fields within and surrounding a small spherical particle in an imposed arbitrary magnetic field and the resulting magnetic force and couple. Chem. Eng. Commun. 2009, 197, 92–111. [Google Scholar] [CrossRef]
- Torres-Díaz, I.; Rinaldi, C. Brownian dynamics simulations of ellipsoidal magnetizable particle suspensions. J. Phys. D 2014, 47, 235003. [Google Scholar] [CrossRef]
- Zhou, R.; Sobecki, C.A.; Zhang, J.; Zhang, Y.; Wang, C. Magnetic control of lateral migration of ellipsoidal microparticles in microscale flows. Phys. Rev. Appl. 2017, 8, 024019. [Google Scholar] [CrossRef]
- Okagawa, A.; Cox, R.G.; Mason, S.G. Particle behavior in shear and electric fields. VI. The microrheology of rigid spheroids. J. Colloid Interface Sci. 1974, 47, 536. [Google Scholar] [CrossRef]
- Shine, A.D.; Armstrong, R.C. The rotation of a suspended axisymmetric ellipsoid in a magnetic field. Rheol. Acta 1987, 26, 152. [Google Scholar]
- Pamme, N.; Eijkel, J.C.T.; Manz, A. On-chip free-flow magnetophoresis: Separation and detection of mixtures of magnetic particles in continuous flow. J. Magn. Magn. Mater. 2006, 307, 237–244. [Google Scholar] [CrossRef]
- Pamme, N.; Manz, A. On-chip free-flow magnetophoresis: Continuous flow separation of magnetic particles and agglomerates. Anal. Chem. 2004, 76, 7250–7256. [Google Scholar] [CrossRef] [PubMed]
- Liang, L.; Zhu, J.; Xuan, X. Three-dimensional diamagnetic particle deflection in ferrofluid microchannel flows. Biomicrofluid 2011, 5, 034110. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Liang, L.; Xuan, X. On-chip manipulation of nonmagnetic particles in paramagnetic solutions using embedded permanent magnets. Microfluid. Nanofluid. 2012, 12, 65–73. [Google Scholar] [CrossRef]
- Zhu, T.; Lichlyter, D.J.; Haidekker, M.A.; Mao, L. Analytical model of microfluidic transport of non-magnetic particles in ferrofluids under the influence of a permanent magnet. Microfluid. Nanofluid. 2011, 10, 1233–1245. [Google Scholar] [CrossRef]
- Cheng, R.; Zhu, T.; Mao, L. Three-dimensional and analytical modeling of microfluidic particle transport in magnetic fluids. Microfluid. Nanofluid. 2014, 16, 1143–1154. [Google Scholar] [CrossRef]
- Hejazian, M.; Nguyen, N.T. Negative magnetophoresis in diluted ferrofluid flow. Lab Chip 2015, 15, 2998–3005. [Google Scholar] [CrossRef] [Green Version]
- Zhu, G.P.; Hejiazan, M.; Huang, X.; Nguyen, N.T. Magnetophoresis of diamagnetic microparticles in a weak magnetic field. Lab Chip 2014, 14, 4609–4615. [Google Scholar] [CrossRef] [Green Version]
- Chung, T.D.; Kim, H.C. Recent advances in miniaturized microfluidic flow cytometry for clinical use. Electrophoresis 2007, 28, 4511–4520. [Google Scholar] [CrossRef]
- Zhou, T.; Song, Y.; Yuan, Y.; Li, D. A novel microfluidic resistive pulse sensor with multiple voltage input channels and a side sensing gate for particle and cell detection. Anal. chimica Acta 2019, 1052, 113–123. [Google Scholar] [CrossRef]
- Xuan, X.; Zhu, J.; Church, C. Particle focusing in microfluidic devices. Microfluid. Nanofluid. 2010, 9, 1–16. [Google Scholar] [CrossRef]
- Martel, J.M.; Toner, M. Inertial focusing in microfluidics. Annu. Rev. Biomed. Eng. 2014, 16, 371–396. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Yan, S.; Yuan, D.; Alici, G.; Nguyen, N.T.; Warkiani, M.E.; Li, W. Fundamentals and applications of inertial microfluidics: A review. Lab Chip 2016, 16, 10–34. [Google Scholar] [CrossRef] [PubMed]
- Peyman, S.A.; Kwan, E.Y.; Margarson, O.; Iles, A.; Pamme, N. Diamagnetic repulsion—A versatile tool for label-free particle handling in microfluidic devices. J. Chromatogr. A 2009, 1216, 9055–9062. [Google Scholar] [CrossRef] [PubMed]
- Amin, R.; Knowlton, S.; Yenilmez, B.; Hart, A.; Joshi, A.; Tasoglu, S. Smart-phone attachable, flow-assisted magnetic focusing device. RSC Adv. 2016, 6, 93922–93931. [Google Scholar] [CrossRef]
- Zhu, T.; Cheng, R.; Mao, L. Focusing microparticles in a microchannel with ferrofluids. Microfluid. Nanofluid. 2011, 11, 695–701. [Google Scholar] [CrossRef]
- Zeng, J.; Chen, C.; Vedantam, P.; Brown, V.; Tzeng, T.; Xuan, X. Three-dimensional magnetic focusing of particles and cells in ferrofluid flow through a straight microchannel. J. Micromech. Microeng. 2012, 22, 105018. [Google Scholar] [CrossRef]
- Liang, L.; Xuan, X. Diamagnetic particle focusing in ferromicrofluidics using a single magnet. Microfluid. Nanofluid. 2012, 13, 637–643. [Google Scholar] [CrossRef]
- Zhou, R.; Wang, C. Multiphase ferrofluid flows for micro-particle focusing and separation. Biomicrofluid 2016, 10, 034101. [Google Scholar] [CrossRef] [Green Version]
- Yan, S.; Zhang, J.; Chen, H.; Yuan, D.; Alici1, G.; Du, H.; Zhu, Y.; Li, W. Development of a novel magnetophoresis-assisted hydrophoresis microdevice for rapid particle ordering. Biomed. Microdevices 2016, 18, 54. [Google Scholar] [CrossRef]
- Chen, Q.; Li, D.; Malekanfard, A.; Cao, Q.; Lin, J.; Wang, M.H.; Han, X.; Xuan, X. Tunable, sheathless focusing of diamagnetic particles in ferrofluid microflows with a single set of overhead permanent magnets. Anal. Chem. 2018, 90, 8600–8606. [Google Scholar] [CrossRef] [PubMed]
- Johann, R.M. Cell trapping in microfluidic chips. Anal. Bioanal. Chem. 2006, 385, 408–412. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pratt, E.D.; Huang, C.; Hawkins, B.G.; Gleghorn, J.P.; Kirby, B.J. Rare cell capture in microfluidic devices. Chem. Eng. Sci. 2011, 66, 1508–1522. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Choudhury, D.; Mo, X.; Iliescu, C.; Tan, L.L.; Tong, W.H.; Yu, H. Exploitation of physical and chemical constraints for three-dimensional microtissue construction in microfluidics. Biomicrofluidics 2011, 5, 022203. [Google Scholar] [CrossRef] [Green Version]
- Nilsson, J.; Evander, M.; Hammarstrom, B.; Laurell, T. Review of cell and particle trapping in microfluidic systems. Anal. Chimica Acta 2009, 649, 141–157. [Google Scholar] [CrossRef]
- Huang, L.; Bian, S.; Cheng, Y.; Shi, G.; Liu, P.; Ye, X.; Wang, W. Microfluidics cell sample preparation for analysis: Advances in efficient cell enrichment and precise single cell capture. Biomicrofluidics 2017, 11, 011501. [Google Scholar] [CrossRef] [Green Version]
- Salari, A.; Thompson, M. Recent advances in AC electrokinetic sample enrichment techniquesfor biosensor development. Sens. and Actuat. B 2018, 255, 3601–3615. [Google Scholar] [CrossRef]
- Feinstein, E.; Prentiss, M. Three-dimensional self-assembly of structures using the pressure due to a ferrofluid in a magnetic field gradient. J. Appl. Phys. 2006, 99, 064901. [Google Scholar] [CrossRef]
- Tarn, M.D.; Peyman, S.A.; Pamme, N. Simultaneous trapping of magnetic and diamagnetic particle plugs for separations and bioassays. RSC Adv. 2013, 3, 7209–7214. [Google Scholar] [CrossRef]
- Hejazian, M.; Nguyen, N.T. Magnetofluidic concentration and separation of non-magnetic particles using two magnet arrays. Biomicrofluidics 2016, 10, 044103. [Google Scholar] [CrossRef] [Green Version]
- Zeng, J.; Chen, C.; Vedantam, P.; Tzeng, T.; Xuan, X. Magnetic concentration of particles and cells in ferrofluid flow through a straight microchannel using attracting magnets. Microfluid. Nanofluid. 2013, 15, 49–55. [Google Scholar] [CrossRef]
- Wilbanks, J.J.; Kiessling, G.; Zeng, J.; Zhang, C.; Xuan, X. Exploiting magnetic asymmetry to concentrate diamagnetic particles in ferrofluid microflows. J. Appl. Phys. 2014, 115, 044907. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Thanjavur Kumar, D.; Lu, X.; Kale, A.; DuBose, J.; Song, Y.; Wang, J.; Li, D.; Xuan, X. Simultaneous diamagnetic and magnetic particle trapping in ferrofluid microflows via a single permanent magnet. Biomicrofluidics 2015, 9, 044102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lenshof, A.; Laurell, T. Continuous separation of cells and particles in microfluidic systems. Chem. Soc. Rev. 2010, 39, 1203–1217. [Google Scholar] [CrossRef] [PubMed]
- Karimi, A.; Yazdi, S.; Ardekani, A.M. Hydrodynamic mechanisms of cell and particle trapping in microfluidics. Biomicrofluid 2013, 7, 021501. [Google Scholar] [CrossRef] [Green Version]
- Sajeesh, P.; Sen, A.K. Particle separation and sorting in microfluidic devices: A review. Microfluid. Nanofluid. 2014, 17, 1–52. [Google Scholar] [CrossRef]
- Shields IV, C.W.; Reyes, C.D.; Lopez, G.P. Microfluidic cell sorting: A review of the advances in the separation of cells from debulking to rare cell isolation. Lab Chip 2015, 15, 1230–1249. [Google Scholar] [CrossRef]
- Xuan, X. Recent advances in direct current electrokinetic manipulation of particles for microfluidic applications. Electrophoresis 2019, 40, 2484–2513. [Google Scholar] [CrossRef]
- Wu, M.; Ozcelik, A.; Rufo, J.; Wang, Z.; Fang, R.; Huang, T.J. Acoustofluidic separation of cells and particles. Microsys. Nanoeng. 2019, 5, 32. [Google Scholar] [CrossRef]
- Kim, S.B.; Yoon, S.Y.; Sung, H.J.; Kim, S.S. Cross-type optical particle separation in a microchannel. Anal. Chem. 2008, 80, 2628–2630. [Google Scholar] [CrossRef]
- Lu, X.; Liu, C.; Hu, G.; Xuan, X. Particle manipulations in non-Newtonian microfluidics: A review. J. Colloid Interf. Sci. 2017, 500, 182–201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, C.; Hu, G. High-throughput particle manipulation based on hydrodynamic effects in microchannels. Micromachines 2017, 8, 73. [Google Scholar] [CrossRef]
- Yuan, D.; Zhao, Q.; Yan, S.; Tang, S.Y.; Alici, G.; Zhang, J.; Li, W. Recent progress of particle migration in viscoelastic fluids. Lab Chip 2018, 18, 551–567. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Antfolk, M.; Laurell, T. Continuous flow microfluidic separation and processing of rare cells and bioparticles found in blood—A review. Anal. Chimica Acta 2017, 965, 9–35. [Google Scholar] [CrossRef] [PubMed]
- Sibbitts, J.; Sellens, K.A.; Jia, S.; Klasner, S.A.; Culbertson, C.T. Cellular analysis using microfluidics. Anal Chem. 2018, 90, 65–85. [Google Scholar] [CrossRef]
- Tang, W.; Jiang, D.; Li, Z.; Zhu, L.; Shi, J.; Yang, J.; Xiang, N. Recent advances in microfluidic cell sorting techniques based on both physical and biochemical principles. Electrophoresis 2019, 40, 930–954. [Google Scholar] [CrossRef]
- Zhang, C.X.; Manz, A. High-speed free-flow electrophoresis on chip. Anal. Chem. 2003, 75, 5759–5766. [Google Scholar] [CrossRef]
- Tarn, M.D.; Peyman, S.A.; Robert, D.; Iles, A.; Wilhelm, C.; Pamme, N. The importance of particle type selection and temperature control for on-chip free-flow magnetophoresis. J. Magn. Magn. Mater. 2009, 321, 4115–4122. [Google Scholar] [CrossRef]
- Vojtíšek, M.; Tarn, M.D.; Hirota, N.; Pamme, N. Microfluidic devices in superconducting magnets: On-chip free-flow diamagnetophoresis of polymer particles and bubbles. Microfluid. Nanofluid. 2012, 13, 625–635. [Google Scholar] [CrossRef]
- Kawano, M.; Watarai, H. Two-dimensional flow magnetophoresis of microparticle. Anal. Bioanal. Chem. 2012, 403, 2645–2653. [Google Scholar] [CrossRef]
- Shen, F.; Hwang, H.; Hahn, Y.K.; Park, J.K. Label-free cell separation using a tunable magnetophoretic repulsion force. Anal. Chem. 2012, 84, 3075–3081. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Zhu, T.; Cheng, R.; Liu, Y.; He, J.; Qiu, H.; Wang, L.; Nagy, T.; Querec, T.D.; Unger, E.R.; et al. Label-free and continuous-flow ferrohydrodynamic separation of HeLa cells and blood cells in biocompatible ferrofluids. Adv. Funct. Mater. 2016, 26, 3990–3998. [Google Scholar] [CrossRef] [PubMed]
- Navi, M.; Abbasi, N.; Jeyhani, M.; Gnyawalibcd, W.; Tsai, S.S.H. Microfluidic diamagnetic water-in-water droplets: A biocompatible cell encapsulation and manipulation platform. Lab Chip 2018, 18, 3361–3370. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Li, D.; Zielinski, J.; Kozubowski, L.; Lin, J.; Wang, M.H.; Xuan, X. Yeast cell fractionation by morphology in dilute ferrofluids. Biomicrofluidics 2017, 11, 064102. [Google Scholar] [CrossRef] [PubMed]
- Zhu, T.; Marrero, F.; Mao, L. Continuous separation of non-magnetic particles inside ferrofluids. Microfluid. Nanofluid. 2010, 9, 1003–1009. [Google Scholar] [CrossRef]
- Zhu, T.; Cheng, R.; Lee, S.A.; Rajaraman, E.; Eiteman, M.A.; Querec, T.D.; Unger, E.R.; Mao, L. Continuous-flow ferrohydrodynamic sorting of particles and cells in microfluidic devices. Microfluid. Nanofluid. 2012, 13, 645–654. [Google Scholar] [CrossRef] [Green Version]
- Zhao, W.; Cheng, R.; Jenkins, B.D.; Zhu, T.; Okonkwo, N.E.; Jones, C.E.; Davis, M.B.; Kavuri, S.K.; Hao, Z.; Schroeder, C.; et al. Label-free ferrohydrodynamic cell separation of circulating tumor cells. Lab Chip 2017, 17, 3097–3111. [Google Scholar] [CrossRef]
- Han, X.; Feng, Y.; Cao, Q.; Li, L. Three‑dimensional analysis and enhancement of continuous magnetic separation of particles in microfluidics. Microfluid. Nanofluid. 2015, 18, 1209–1220. [Google Scholar] [CrossRef]
- Zhou, Y.; Xuan, X. Diamagnetic particle separation by shape in ferrofluids. Appl. Phys. Lett. 2016, 109, 102405. [Google Scholar] [CrossRef]
- Zhou, R.; Bai, F.; Wang, C. Magnetic separation of microparticles by shape. Lab Chip 2017, 17, 401–406. [Google Scholar] [CrossRef]
- Kang, J.H.; Choi, S.; Lee, W.; Park, J.K. Isomagnetophoresis to discriminate subtle difference in magnetic susceptibility. J. Am. Chem. Soc. 2008, 130, 396–397. [Google Scholar] [CrossRef] [PubMed]
- Kose, A.R.; Koser, H. Ferrofluid mediated nanocytometry. Lab Chip 2012, 12, 190–196. [Google Scholar] [CrossRef] [PubMed]
- Munaz, A.; Shiddiky, M.J.A.; Nguyen, N.T. Magnetophoretic separation of diamagnetic particles through parallel ferrofluid streams. Sens. Actuat. B Chem. 2018, 275, 459–469. [Google Scholar] [CrossRef]
- Kose, A.R.; Fischer, B.; Mao, L.; Koser, H. Label-free cellular manipulation and sorting via biocompatible ferrofluids. Proc. Natl. Acad. Sci. USA 2009, 106, 21478–21483. [Google Scholar] [CrossRef] [Green Version]
- Liang, L.; Xuan, X. Continuous sheath-free magnetic separation of particles in a U-shaped microchannel. Biomicrofluidics 2012, 6, 044106. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Song, L.; Yu, L.; Xuan, X. Continuous-flow sheathless diamagnetic particle separation in ferrofluids. J. Magn. Magn. Mater. 2016, 412, 114–122. [Google Scholar] [CrossRef] [Green Version]
- Zeng, J.; Deng, Y.; Vedantam, P.; Tzeng, T.R.; Xuan, X. Magnetic separation of particles and cells in ferrofluid flow through a straight microchannel using two offset magnets. J. Magn. Magn. Mater. 2013, 346, 118–123. [Google Scholar] [CrossRef]
- Liang, L.; Zhang, C.; Xuan, X. Enhanced separation of magnetic and diamagnetic particles in a dilute ferrofluid. Appl. Phys. Lett. 2013, 102, 234101. [Google Scholar] [CrossRef]
- Zhu, T.; Cheng, R.; Liu, Y.; He, J.; Mao, L. Combining positive and negative magnetophoreses to separate particles of different magnetic properties. Microfluid. Nanofluid. 2014, 17, 973–982. [Google Scholar] [CrossRef]
- Winkleman, A.; Perez-Castillejos, R.; Gudiksen, K.L.; Phillips, S.T.; Prentiss, M.; Whitesides, G.M. Density-based diamagnetic separation: Devices for detecting binding events and for collecting unlabeled diamagnetic particles in paramagnetic solutions. Anal. Chem. 2007, 79, 6542–6550. [Google Scholar] [CrossRef]
- Yan, S.; Zhang, J.; Yuan, D.; Li, W. Hybrid microfluidics combined with active and passive approaches for continuous cell separation. Electrophoresis 2017, 37, 238–249. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.J.; Lee, D.J.; Youn, J.R.; Song, Y.S. Two step label free particle separation in a microfluidic system using elasto-inertial focusing and magnetophoresis. RSC Adv. 2016, 6, 32090–32097. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, S.; Yuan, D.; Zhao, Q.; Tan, S.; Nguyen, N.T.; Li, W. A novel viscoelastic-based ferrofluid for continuous sheathless microfluidic separation of nonmagnetic microparticles. Lab Chip 2016, 16, 3947–3956. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, Y.; Song, L.; Yu, L.; Xuan, X. Inertially focused diamagnetic particle separation in ferrofluids. Microfluid. Nanofluid. 2017, 21, 14. [Google Scholar] [CrossRef]
- Yan, S.; Zhang, J.; Yuan, D.; Zhao, Q.; Ma, J.; Li, W. High-throughput, sheathless, magnetophoretic separation of magnetic and nonmagnetic particles with a groove-based channel. Appl. Phys. Lett. 2016, 109, 214101. [Google Scholar] [CrossRef]
- Tarn, M.D.; Lopez-Martinez, M.J.; Pamme, N. On-chip processing of particles and cells via multilaminar flow streams. Anal. Bioanal. Chem. 2014, 406, 139–161. [Google Scholar] [CrossRef] [PubMed]
- Tornay, R.; Braschler, T.; Demierre, N.; Steitz, B.; Finka, A.; Hofmann, H.; Hubbell, J.A.; Renaud, P. Continuous-flow cell dipping and medium exchange in a microdevice using dielectrophoresis. Lab Chip 2008, 8, 267–273. [Google Scholar] [CrossRef]
- Chen, Y.; D’Silva, J.; Austin, R.H.; Sturm, J.C. Microfluidic chemical processing with on-chip washing by deterministic lateral displacement arrays with separator walls. Biomicrofluidics 2015, 9, 054105. [Google Scholar] [CrossRef] [Green Version]
- Dudani, J.S.; Go, D.E.; Gossett, D.R.; Tan, A.P.; Di Carlo, D. Mediating millisecond reaction time around particles and cells. Anal. Chem. 2014, 86, 1502–1510. [Google Scholar] [CrossRef]
- Yuan, D.; Tan, S.H.; Sluyter, R.; Zhao, Q.; Yan, S.; Nguyen, N.T.; Guo, J.; Zhang, J.; Li, W. On-chip microparticle and cell washing using coflow of viscoelastic fluid and newtonian fluid. Anal. Chem. 2017, 89, 9574–9582. [Google Scholar] [CrossRef]
- Caravan, P.; Ellison, J.J.; McMurry, T.J.; Lauffer, R.B. Gadolinium(III) Chelates as MRI contrast agents: Structure, dynamics, and applications. Chem. Rev. 1999, 99, 2293–2352. [Google Scholar] [CrossRef]
- Durmus, N.G.; Tekin, H.C.; Guven, S.; Sridhar, K.; Yildiz, A.A.; Calibasi, G.; Ghiran, I.; Davis, R.W.; Steinmetz, L.M.; Demirci, U. Magnetic levitation of single cells. Proc. Natl. Acad. Sci. USA 2015, 112, E3661–E3668. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kauffmann, P.; Ith, A.; OBrien, D.; Gaude, V.; Boue, F.; Combe, S.; Bruckert, F.; Schaack, B.; Dempsey, N.M.; Haguet, V.; et al. Diamagnetically trapped arrays of living cells above micromagnets. Lab Chip 2011, 11, 3153–3161. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Z.; Lu, Z.R. Gadolinium-based contrast agents for magnetic resonance cancer imaging. Wiley Interdiscip. Rev. Nanomed. Nanobiotechnol. 2013, 5, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Krebs, M.D.; Erb, R.M.; Yellen, B.B.; Samanta, B.; Bajaj, A.; Rotello, V.M.; Alsberg, E. Formation of ordered cellular structures in suspension via label-free negative magnetophoresis. Nano Lett. 2009, 9, 1812–1817. [Google Scholar] [CrossRef]
- Zhao, W.; Liu, Y.; Jenkins, B.D.; Cheng, R.; Harris, B.N.; Zhang, W.; Xie, J.; Murrow, J.R.; Hodgson, J.; Egan, M.; et al. Tumor antigen-independent and cell size variation-inclusive enrichment of viable circulating tumor cells. Lab Chip 2019, 19, 1860–1876. [Google Scholar] [CrossRef] [PubMed]
- Shaterabadi, Z.; Nabiyouni, G.; Soleymani, M. High impact of in situ dextran coating on biocompatibility, stability and magnetic properties of iron oxide nanoparticles. Mater. Sci. Eng. C 2017, 75, 947–956. [Google Scholar] [CrossRef] [Green Version]
- Tarn, M.D.; Elders, L.T.; Peyman, S.A.; Pamme, N. Diamagnetic repulsion of particles for multilaminar flow assays. RSC Adv. 2015, 5, 103776–103781. [Google Scholar] [CrossRef]
- Zhao, W.; Cheng, R.; Lim, S.H.; Miller, J.R.; Zhang, W.; Tang, W.; Xie, J.; Mao, L. Biocompatible and label-free separation of cancercells from cell culture lines from white blood cellsin ferrofluids. Lab Chip 2017, 17, 2243–2255. [Google Scholar] [CrossRef]
- Chen, Q.; Li, D.; Lin, J.; Wang, M.; Xuan, X. Simultaneous washing and separation of nonmagnetic particles in an inertial ferrofluid/water co-flow. Anal. Chem. 2017, 89, 6915–6920. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, R.; Wang, Z.; Ramanujan, R.V. Magnetic trapping of bacteria at low magnetic fields. Sci. Rep. 2016, 6, 26945. [Google Scholar] [CrossRef] [PubMed]

| Pre-Focused | Particles | Fluid | Magnet | Particle Flow Rate | References | |
|---|---|---|---|---|---|---|
| Configuration | Type | |||||
| - | 5/10 µm PS | 6/10% MnCl2 | single | superconducting | 400 µL/h | [45] |
| - | 2.2/5/10 µm PS | 0.3–1.2% ferrofluid | single | permanent | 45–960 µL/h | [79] |
| - | 5/10/15 µm PS | 0.04–1 M MnCl2 | stacked | permanent | 3.6–14.4 µL/h | [80] |
| ferrofluid sheath | 4.8/7.3 µm PS | 1.2% ferrofluid | single | permanent | 300 µL/h | [81] |
| ferrofluid sheath | 3.1/4.8 µm PS | 0.1% ferrofluid | single | permanent | 60 µL/h | [83] |
| water sheath | 1 µm PS | 1.0% ferrofluid | uniform field | electromagnet | 500 µL/h | [84] |
| ferrofluid sheath | 7 µm PS ellipsoid | 0.6% ferrofluid | Halbach array uniform field | permanent | 12 µL/h | [74] |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xuan, X. Recent Advances in Continuous-Flow Particle Manipulations Using Magnetic Fluids. Micromachines 2019, 10, 744. https://doi.org/10.3390/mi10110744
Xuan X. Recent Advances in Continuous-Flow Particle Manipulations Using Magnetic Fluids. Micromachines. 2019; 10(11):744. https://doi.org/10.3390/mi10110744
Chicago/Turabian StyleXuan, Xiangchun. 2019. "Recent Advances in Continuous-Flow Particle Manipulations Using Magnetic Fluids" Micromachines 10, no. 11: 744. https://doi.org/10.3390/mi10110744
APA StyleXuan, X. (2019). Recent Advances in Continuous-Flow Particle Manipulations Using Magnetic Fluids. Micromachines, 10(11), 744. https://doi.org/10.3390/mi10110744





