Nonlinear Coupled Vibration of Electrically Actuated Arch with Flexible Supports
Abstract
1. Introduction
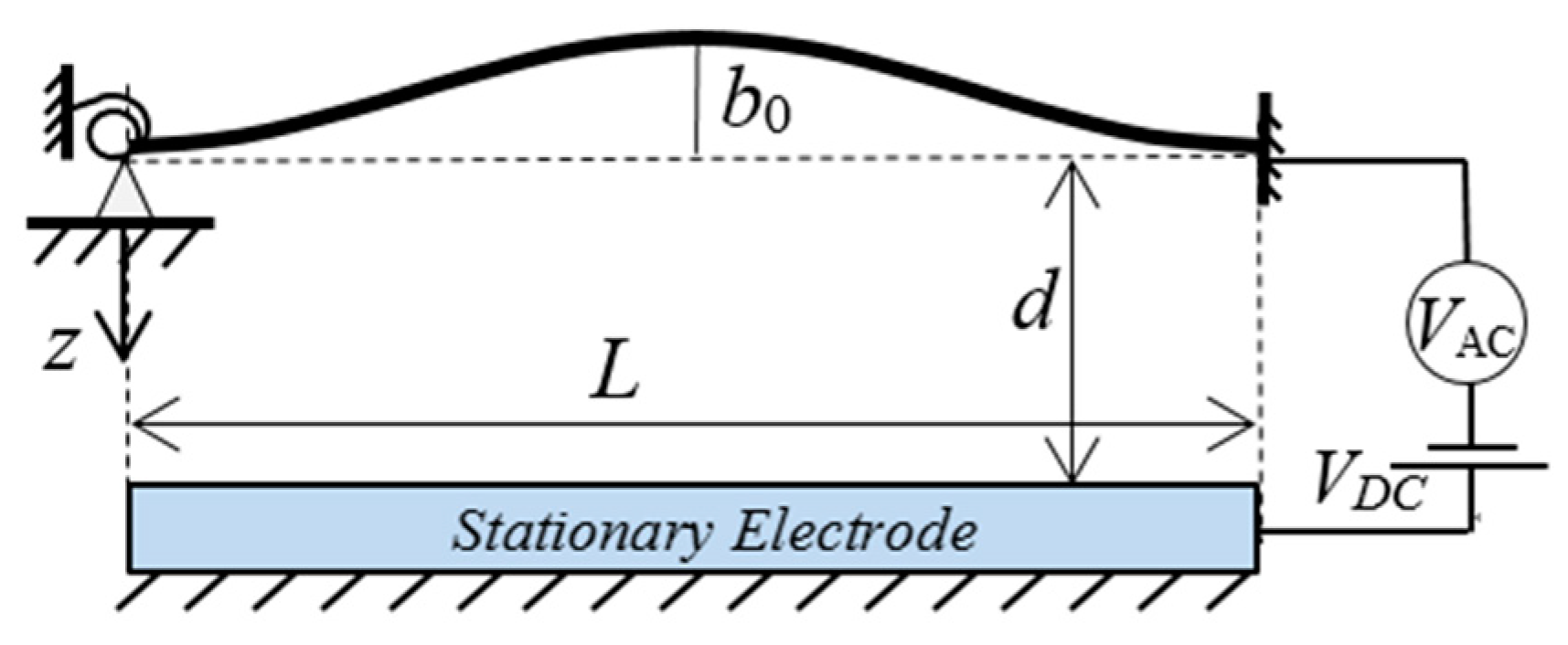
2. Problem Formulation
- The arch is shallow, i.e., ; hence, the parallel-plate assumption is valid;
- As the microbeam is slender, the Euler-Bernoulli beam theory is used, neglecting the effect of shear and rotary inertia;
- The simplest viscous damping model is adopted to model the dissipative mechanisms of the resonator;
- As the size of the structure is small, the size effects are considered.
3. The Method of Multiple Scales
3.1. Primary Resonance of the First Mode
3.2. Primary Resonance of the Second Mode
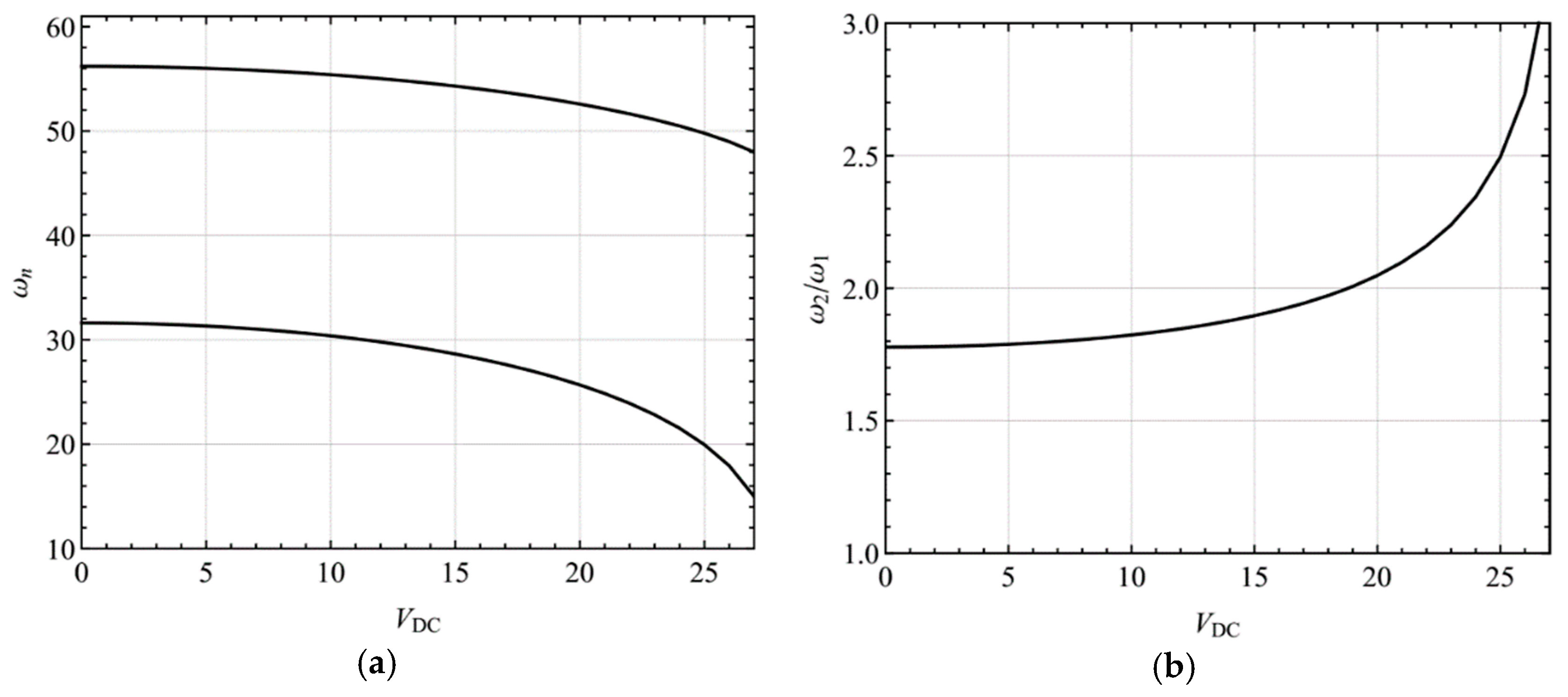
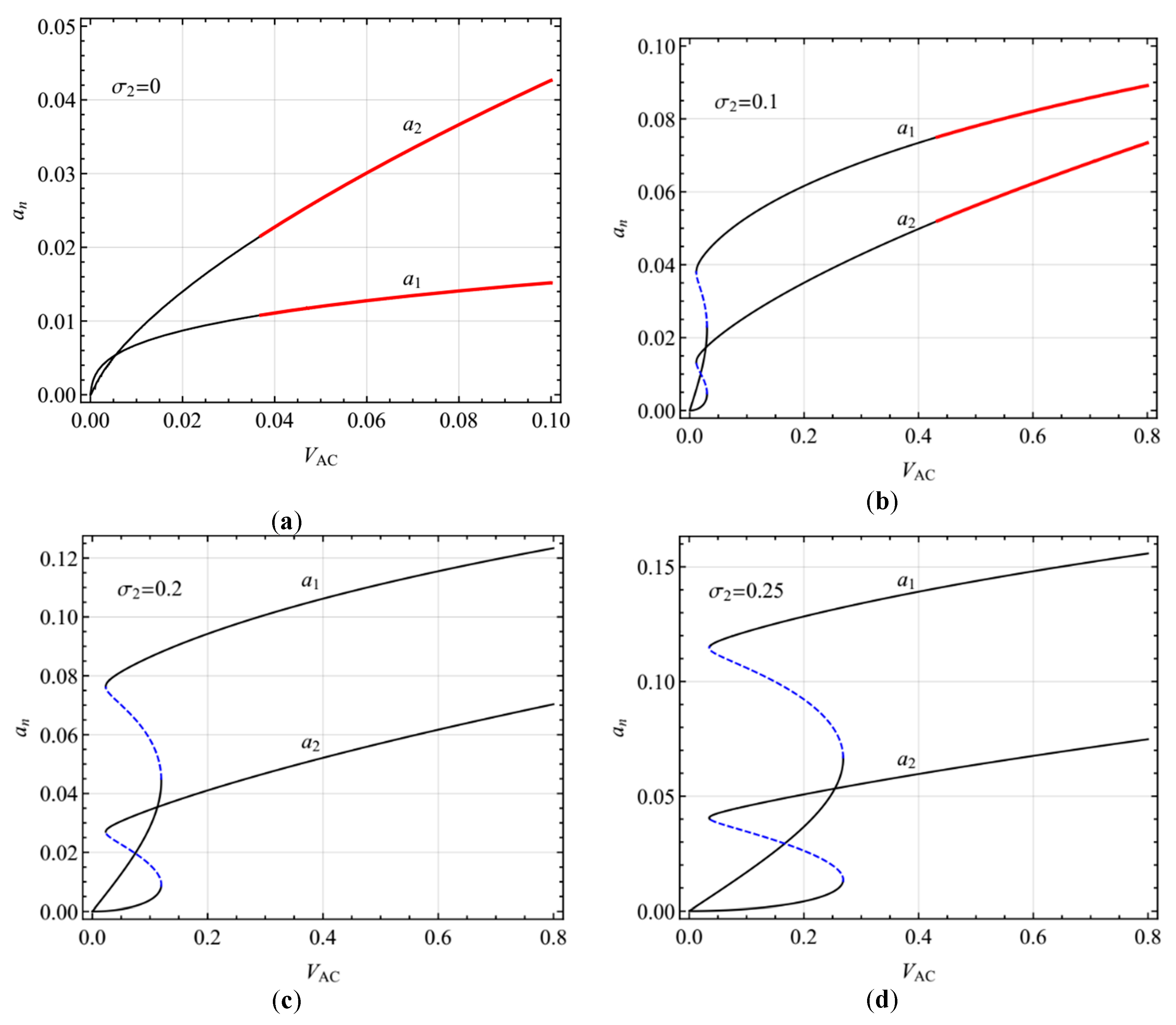
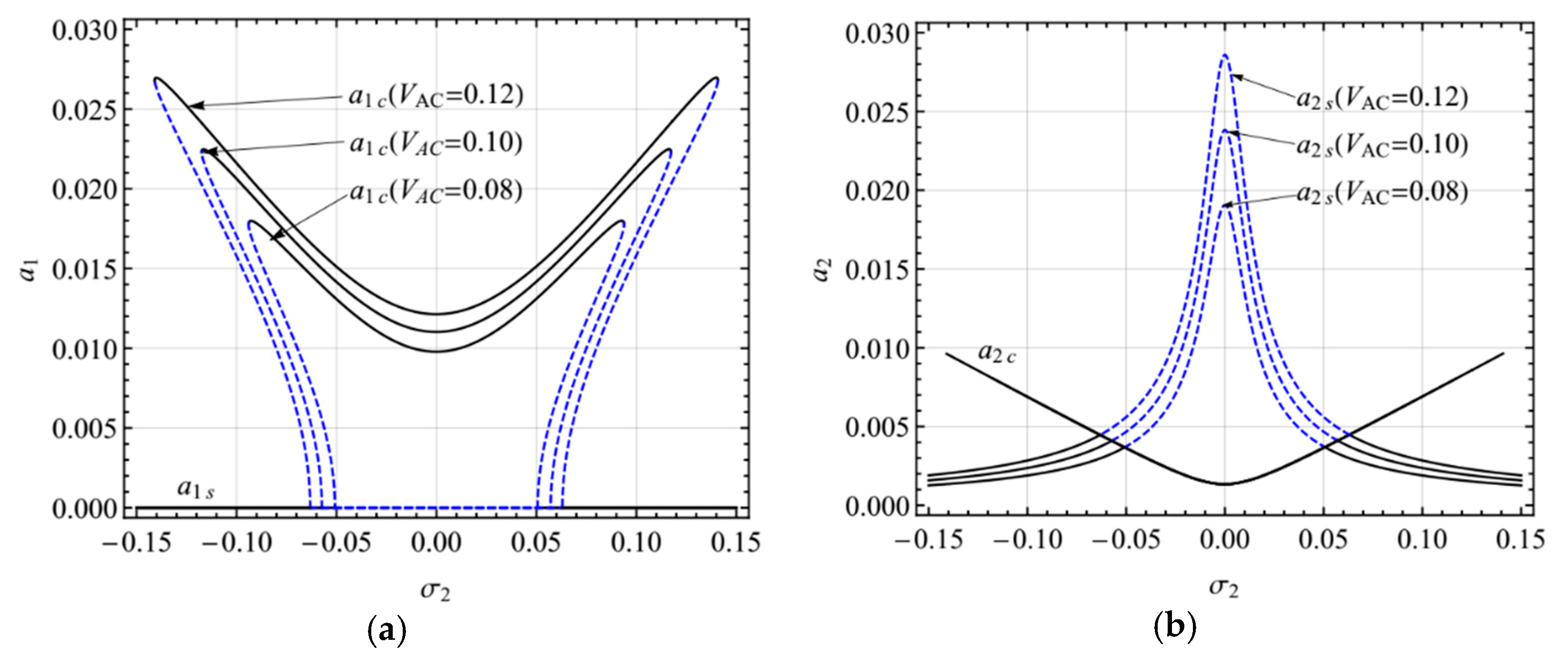
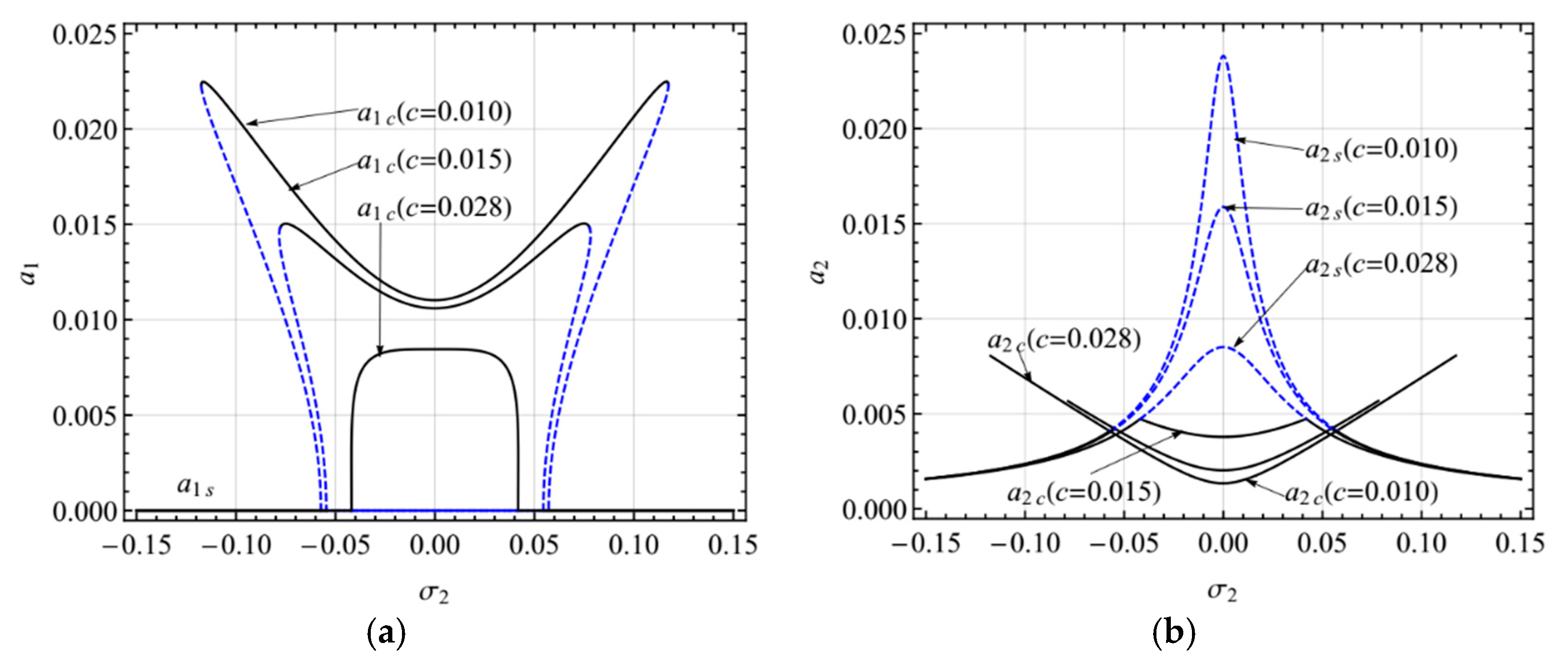
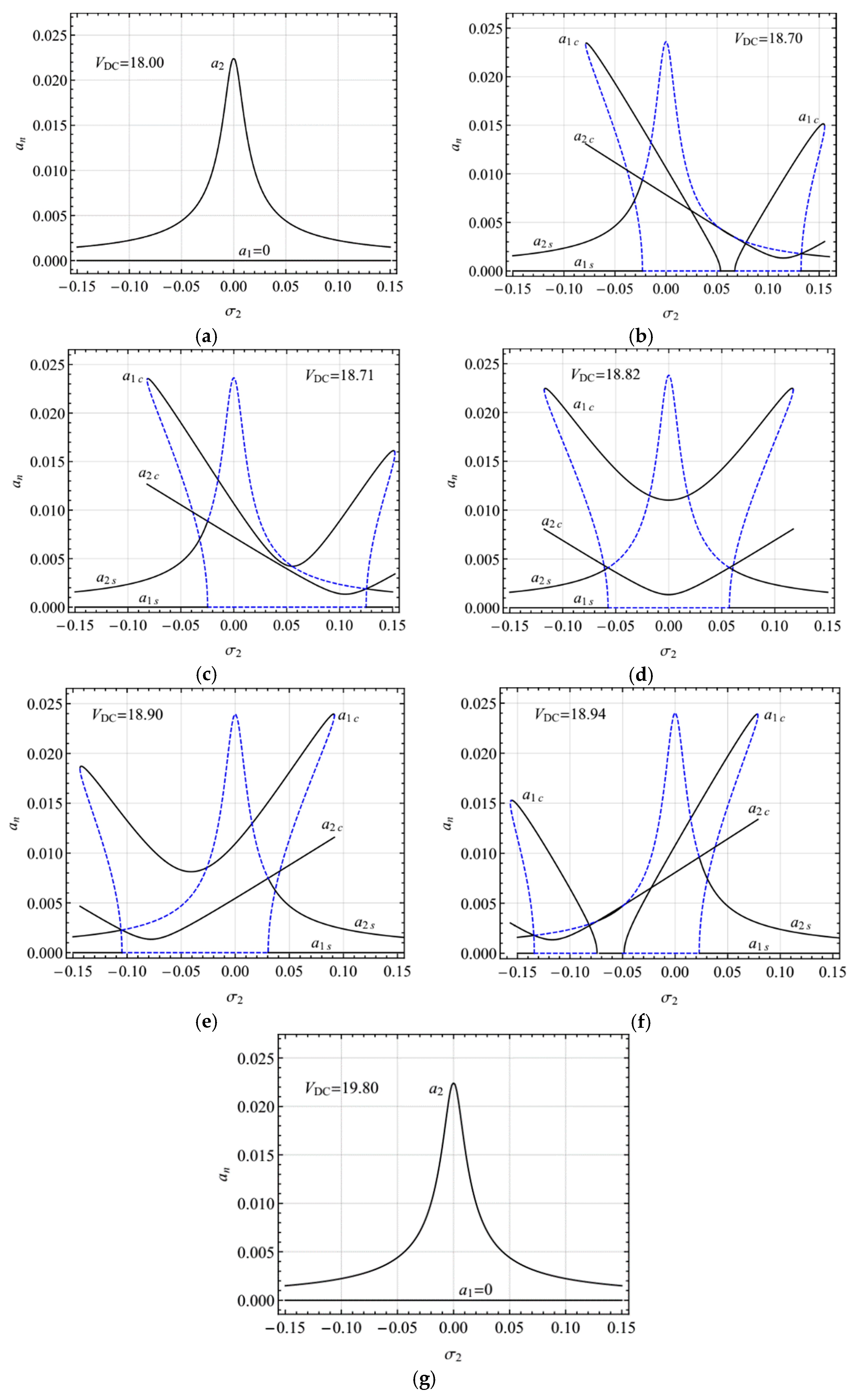
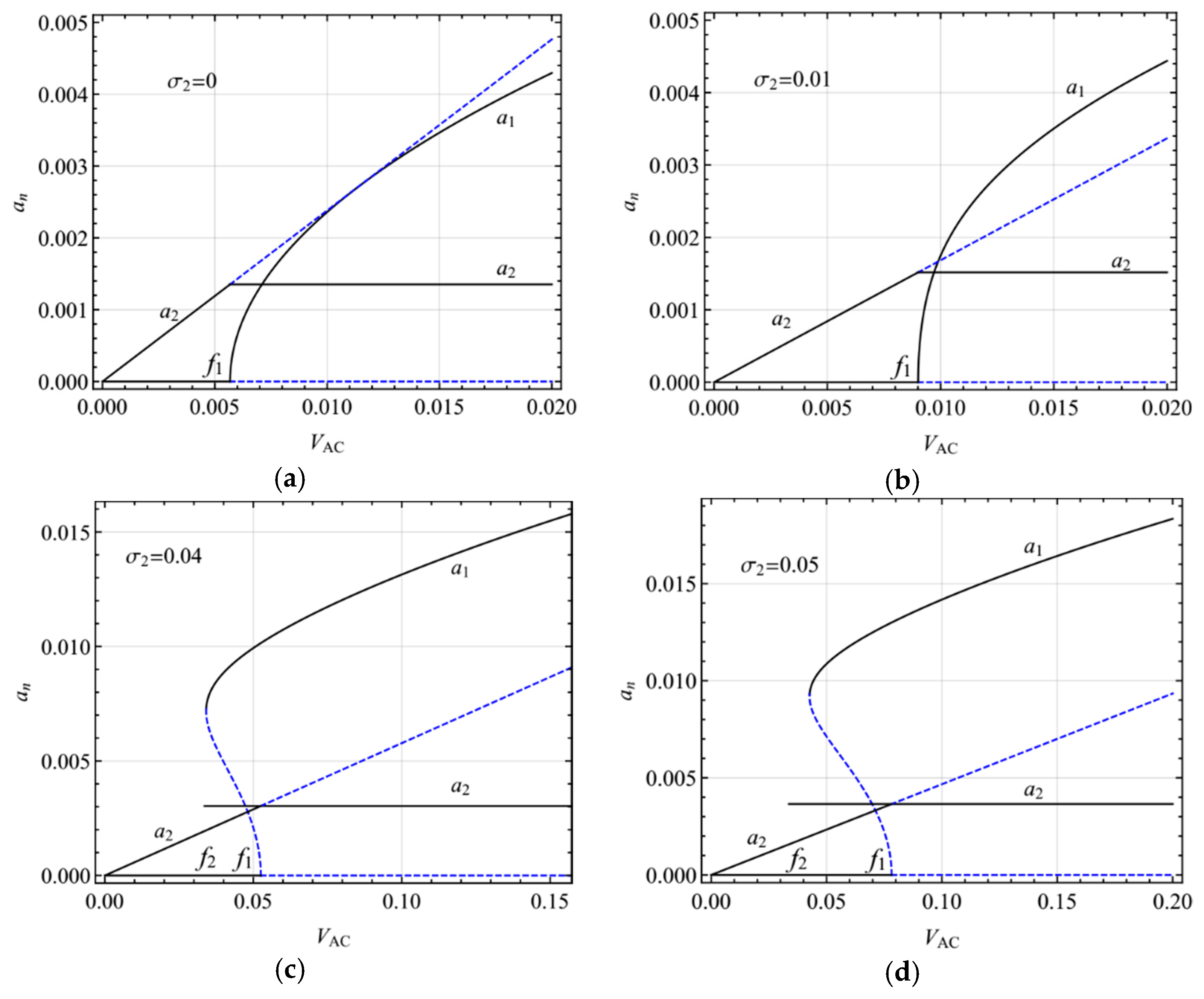
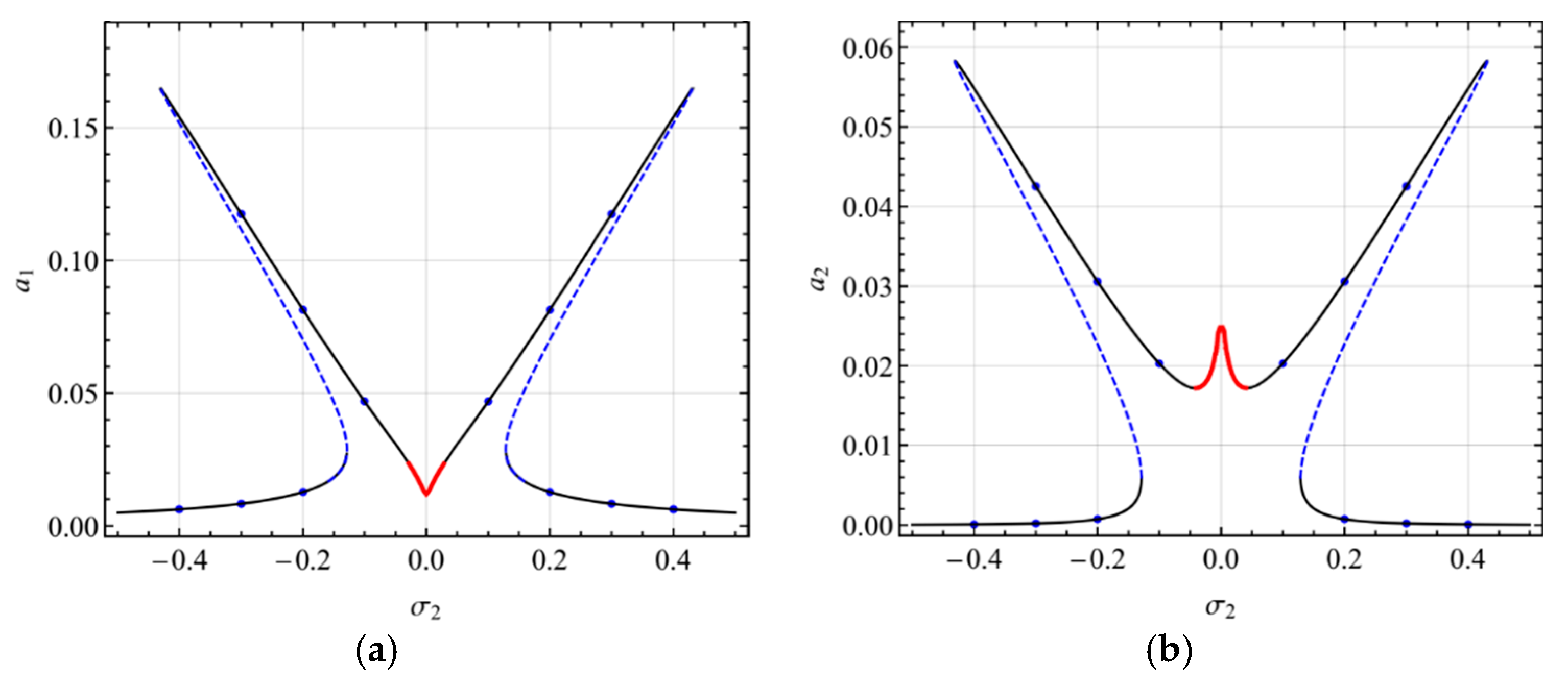
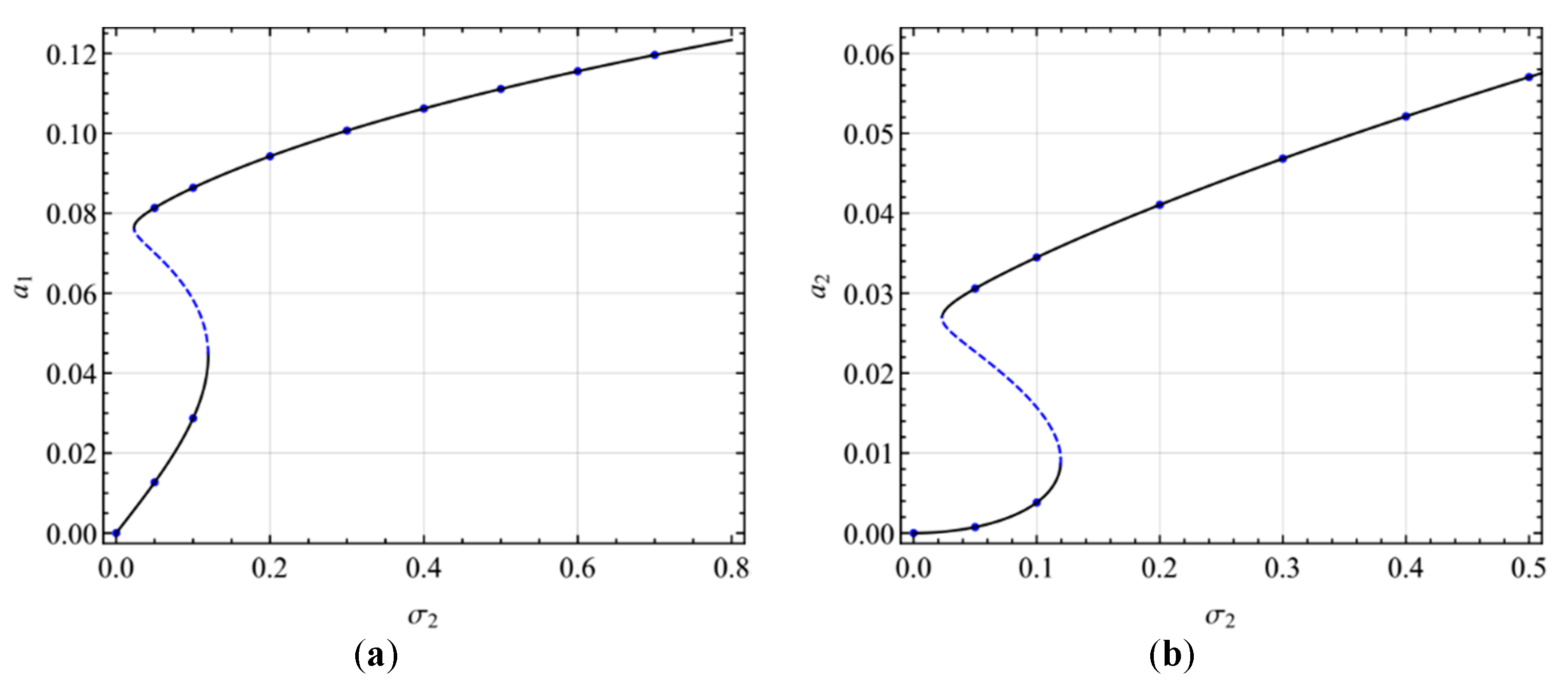
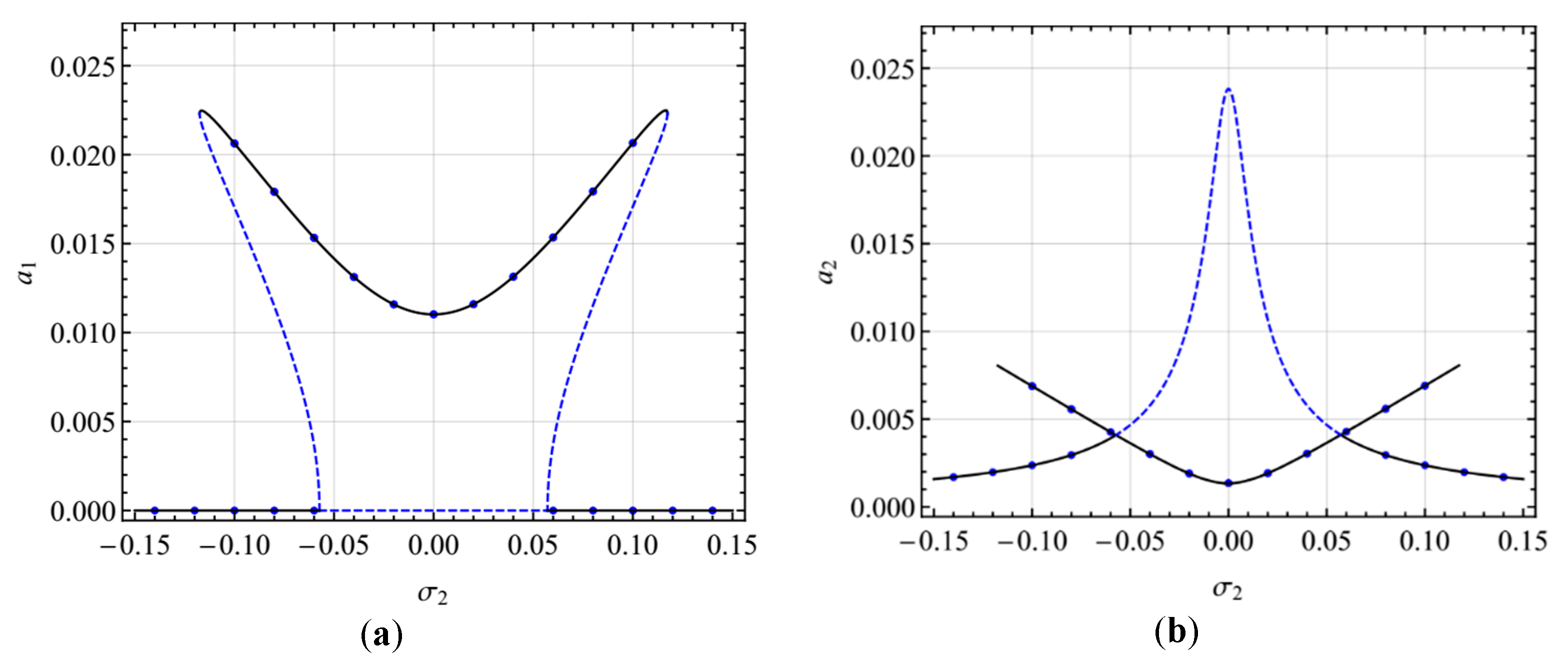
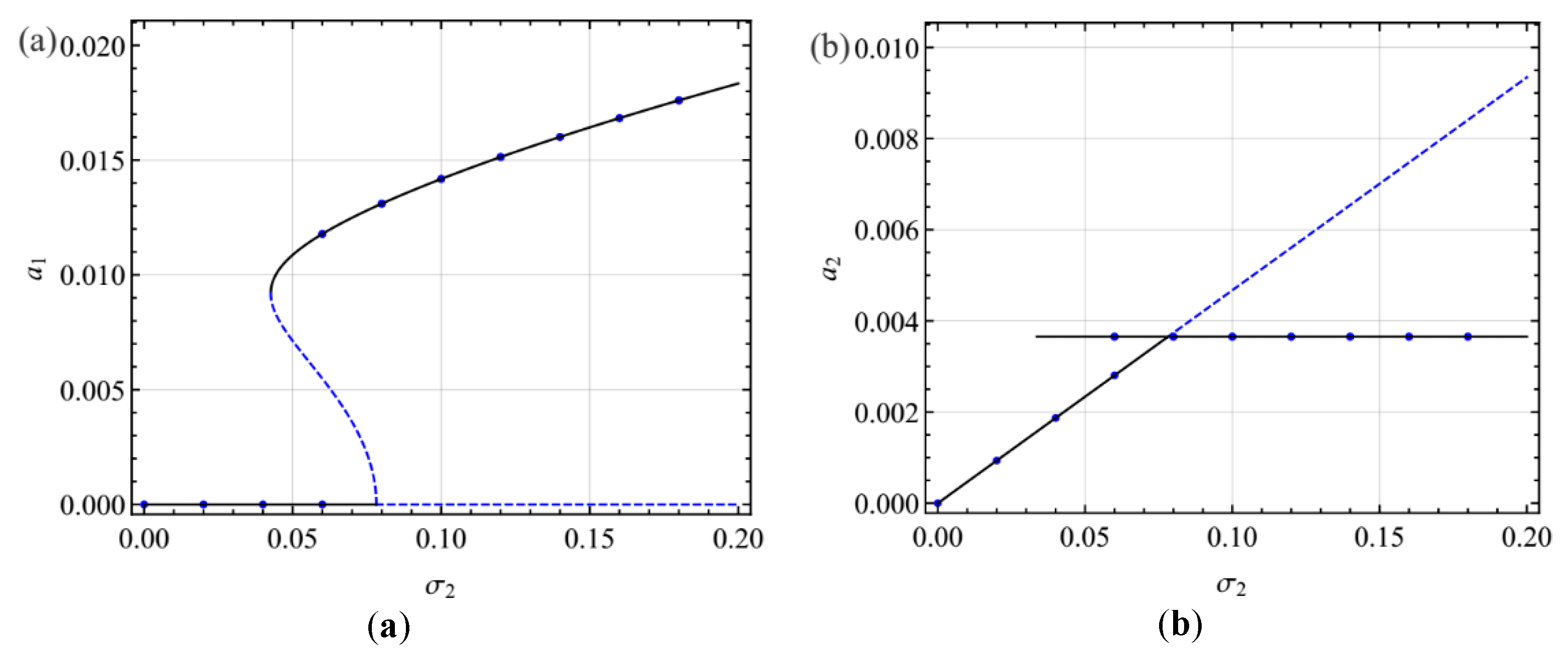
4. Numerical Results
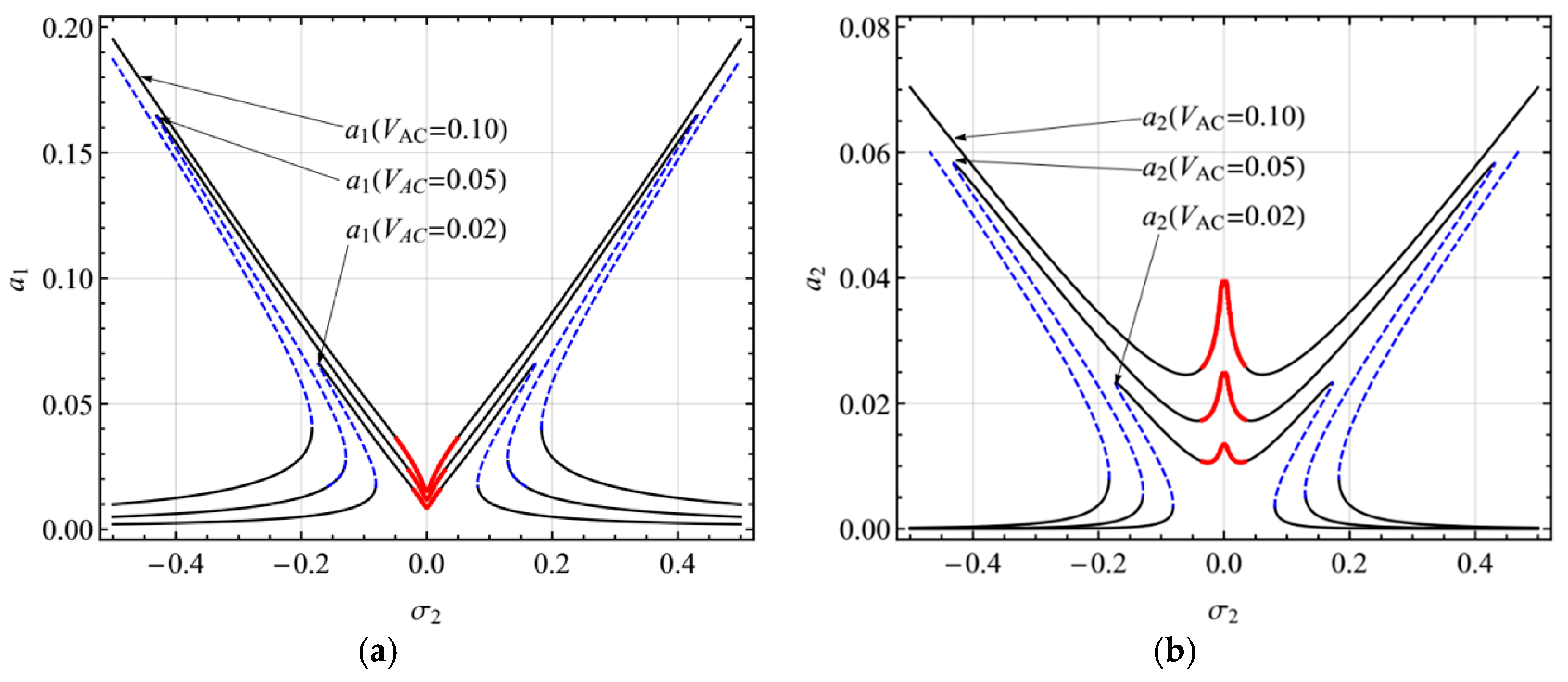
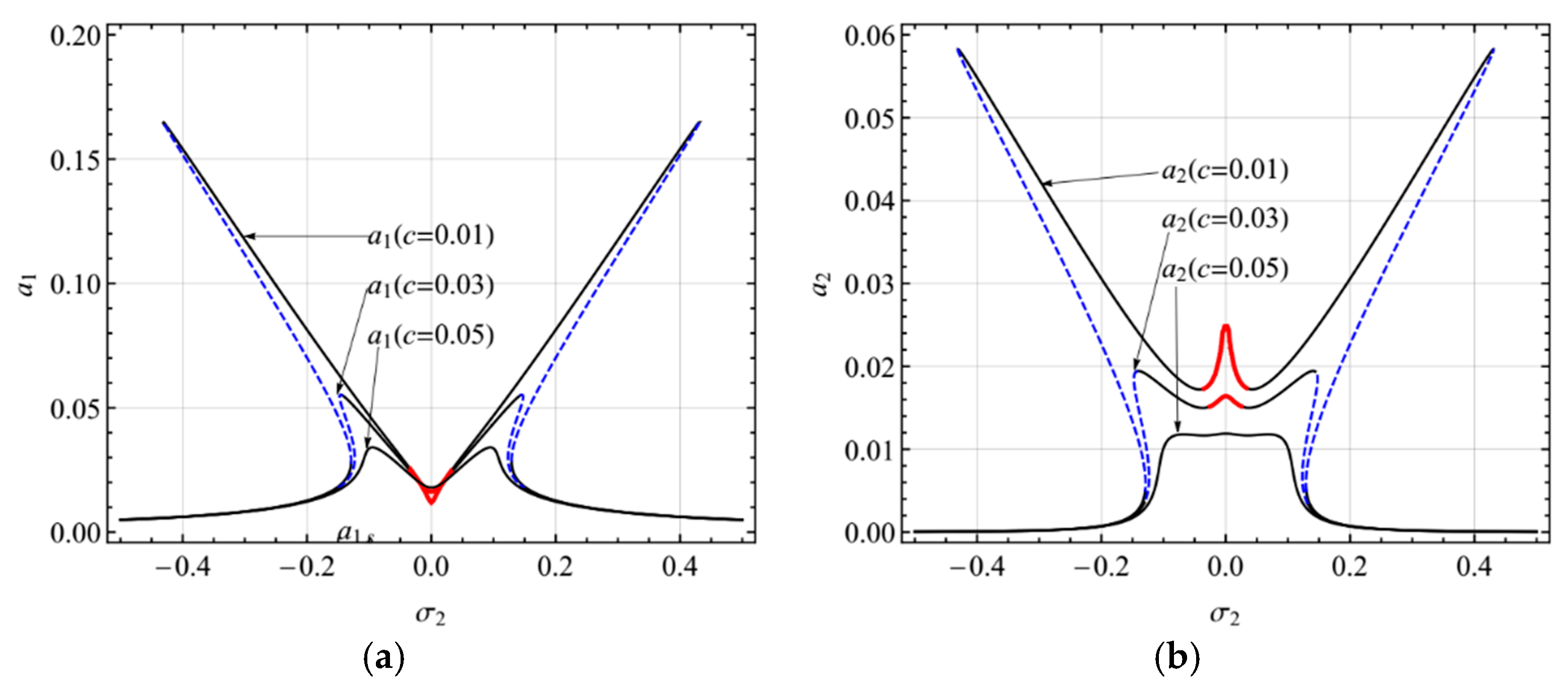
4.1. Primary Resonance of the First Mode
4.2. Primary Resonance of the Second Mode
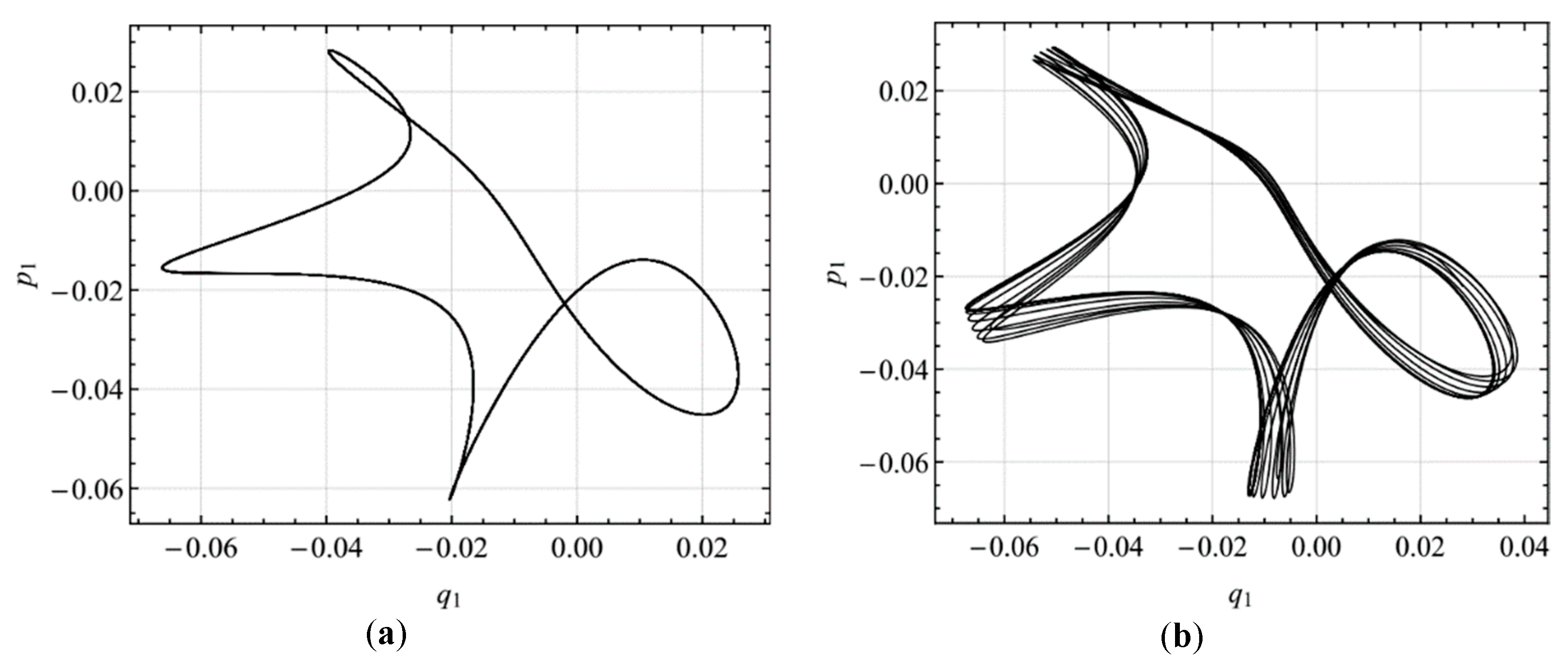
4.3. Numerical Verification
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hafiz, M.A.A.; Kosuru, L.; Ramini, A.; Chappanda, K.N.; Younis, M.I. In-plane MEMS shallow arch beam for mechanical memory. Micromachines 2016, 7, 191. [Google Scholar] [CrossRef] [PubMed]
- Younis, M.I.; Ouakad, H.M.; Alsaleem, F.M.; Miles, R.; Cui, W. Nonlinear dynamics of MEMS arches under harmonic electrostatic actuation. J. Microelectromech. Syst. 2010, 19, 647–656. [Google Scholar] [CrossRef]
- Zhang, H.; Zhong, J.; Yuan, W.; Yang, J.; Chang, H. Ambient pressure drift rejection of mode-localized resonant sensors. In Proceedings of the 2017 IEEE 30th International Conference on Micro Electro Mechanical Systems (MEMS), Las Vegas, NV, USA, 22–26 January 2017; Volume 2, pp. 1095–1098. [Google Scholar]
- Zhang, H.; Kang, H.; Chang, H. Suppression on Nonlinearity of Mode-Localized Sensors Using Algebraic Summation of Amplitude Ratios as the Output Metric. IEEE Sens. J. 2018, 18, 7802–7809. [Google Scholar] [CrossRef]
- Tran, N.; Ghayesh, M.H.; Arjomandi, M. Ambient vibration energy harvesters: A review on nonlinear techniques for performance enhancement. Int. J. Eng. Sci. 2018, 127, 162–185. [Google Scholar] [CrossRef]
- Hajjaj, A.Z.; Hafiz, M.A.; Younis, M.I. Mode Coupling and Nonlinear Resonances of MEMS Arch Resonators for Bandpass Filters. Sci. Rep. 2017, 7, 41820–41826. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Li, F.M. Nonlinear primary resonance of nano beam with axial initial load by nonlocal continuum theory. Int. J. Non-Linear. Mech. 2014, 61, 74–79. [Google Scholar] [CrossRef]
- Han, J.; Jin, G.; Zhang, Q.; Wang, W.; Li, B.; Qi, H. Dynamic evolution of a primary resonance MEMS resonator under prebuckling pattern. Nonlinear Dyn. 2018, 93, 2357–2378. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. Nonlinear thermo-mechanical behaviour of MEMS resonators. Microsyst. Technol. 2017, 23, 5303–5315. [Google Scholar] [CrossRef]
- Ruzziconi, L.; Lenci, S.; Younis, M.I. An Imperfect Microbeam Under an Axial Load and Electric Excitation: Nonlinear Phenomena and Dynamical Integrity. Int. J. Bifurc. Chaos. 2013, 23, 1350026. [Google Scholar] [CrossRef]
- Ramini, A.; Bellaredj, M.L.F.; Hafiz, M.A.A.; Younis, M.I. Experimental investigation of snap-through motion of in-plane MEMS shallow arches under electrostatic excitation. J. Micromech. Microeng. 2015, 26, 075012. [Google Scholar] [CrossRef]
- Ruzziconi, L.; Younis, M.I.; Lenci, S. Nonlinear dynamics of an electrically actuated imperfect microbeam resonator: experimental investigation and reduced-order modeling. J. Comput. Nonlinear Dyn. 2013, 8, 011014. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. Nonlinear resonant response of imperfect extensible Timoshenko microbeams. Int. J. Mech. Mater. Des. 2017, 13, 43–55. [Google Scholar] [CrossRef]
- Kazemirad, S.; Ghayesh, M.H.; Amabili, M. Thermo-mechanical nonlinear dynamics of a buckled axially moving beam. Arch. Appl. Mech. 2013, 83, 25–42. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H.; Hussain, S. Large-amplitude dynamical behaviour of microcantilevers. Int. J. Eng. Sci. 2016, 106, 29–41. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Kazemirad, S.; Darabi, M.A. A general solution procedure for vibrations of systems with cubic nonlinearities and nonlinear/time-dependent internal boundary conditions. J. Sound Vib. 2011, 330, 5382–5400. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Kazemirad, S.; Reid, T. Nonlinear vibrations and stability of parametrically exited systems with cubic nonlinearities and internal boundary conditions: A general solution procedure. Appl. Math. Model. 2012, 36, 3299–3311. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Nonlinear vibration analysis of axially functionally graded shear-deformable tapered beams. Appl. Math. Model. 2018, 59, 583–596. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Functionally graded microbeams: Simultaneous presence of imperfection and viscoelasticity. Int. J. Mech. Sci. 2018, 140, 339–350. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. Supercritical nonlinear parametric dynamics of Timoshenko microbeams. Commun. Nonlinear Sci. Numer. Simul. 2017, 59, 592–605. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H.; Amabili, M. Nonlinear resonant behavior of microbeams over the buckled state. Appl. Phys. A. 2013, 113, 297–307. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Amabili, M.; Farokhi, H. Coupled global dynamics of an axially moving viscoelastic beam. Int. J. Non. Linear. Mech. 2013, 51, 54–74. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Moradian, N. Nonlinear dynamic response of axially moving, stretched viscoelastic strings. Arch. Appl. Mech. 2011, 81, 781–799. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Subharmonic dynamics of an axially accelerating beam. Arch. Appl. Mech. 2012, 82, 1169–1181. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Yourdkhani, M.; Balar, S.; Reid, T. Vibrations and stability of axially traveling laminated beams. Appl. Math. Comput. 2010, 217, 545–556. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Dynamics of functionally graded viscoelastic microbeams. Int. J. Eng. Sci. 2018, 124, 115–131. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. Nonlinear mechanics of electrically actuated microplates. Int. J. Eng. Sci. 2018, 123, 1339–1351. [Google Scholar] [CrossRef]
- Younis, M.I.; Nayfeh, A.H. A study of the nonlinear response of a resonant microbeam to an electric actuation. Nonlinear Dyn. 2003, 31, 91–117. [Google Scholar] [CrossRef]
- Antonio, D.; Zanette, D.H.; López, D. Frequency stabilization in nonlinear micromechanical oscillators. Nat. Commun. 2012, 3, 806–812. [Google Scholar] [CrossRef]
- Zanette, D.H. Stability of two-mode internal resonance in a nonlinear oscillator. Eur. Phys. J. B Condens. Matter Complex Syst. 2018, 91, 89–95. [Google Scholar] [CrossRef]
- Zanette, D.H.; Czaplewski, D.A.; Shaw, S.; Lo, D.; Chen, C. Direct observation of coherent energy transfer in nonlinear micromechanical oscillators. Nat. Commun. 2017, 8, 15523–15530. [Google Scholar]
- Kambali, P.N.; Swain, G.; Pandey, A.K.; Buks, E.; Gottlieb, O. Coupling and tuning of modal frequencies in direct current biased microelectromechanical systems arrays. Appl. Phys. Lett. 2015, 107, 063104. [Google Scholar] [CrossRef]
- Wang, Z.; Ren, J. Three-to-One Internal Resonance in MEMS Arch Resonators. Sensors 2019, 19, 1888. [Google Scholar] [CrossRef] [PubMed]
- Alfosail, F.K.; Hajjaj, A.Z.; Younis, M.I. Theoretical and Experimental Investigation of Two-to-One Internal Resonance in MEMS Arch Resonators. J. Comput. Nonlinear Dyn. 2019, 14, 011001. [Google Scholar] [CrossRef]
- Hajjaj, A.Z.; Alfosail, F.K.; Younis, M.I. Two-to-one internal resonance of MEMS arch resonators. Int. J. Non. Linear. Mech. 2018, 107, 64–72. [Google Scholar] [CrossRef]
- Hajjaj, A.Z.; Alcheikh, N.; Younis, M.I. The static and dynamic behavior of MEMS arch resonators near veering and the impact of initial shapes. Int. J. Non. Linear. Mech. 2017, 95, 277–286. [Google Scholar] [CrossRef]
- Ouakad, H.M.; Sedighi, H.M.; Younis, M.I. One-to-One and Three-to-One Internal Resonances in MEMS Shallow Arches. J. Comput. Nonlinear Dyn. 2017, 12, 1–11. [Google Scholar] [CrossRef]
- Mullen, R.L.; Mehregany, M.; Omar, M.P.; Ko, W.H. Theoretical modeling of boundary conditions in microfabricated beams. In Proceedings of the IEEE Micro Electro Mechanical Systems, Nara, Japan, 30 December 1990–2 January 1991; pp. 154–159. [Google Scholar]
- Ekici, H.O.; Boyaci, H. Effects of non-ideal boundary conditions on vibrations of microbeams. J. Vib. Control. 2007, 13, 1369–1378. [Google Scholar] [CrossRef]
- Alkharabsheh, S.A.; Younis, M.I. The Dynamics of MEMS Arches of Non-Ideal Boundary Conditions. In Proceedings of the ASME 2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Washington, DC, USA, 28–31 August 2011; pp. 197–207. [Google Scholar]
- Alkharabsheh, S.A.; Younis, M.I. Dynamics of MEMS arches of flexible supports. J. Microelectromech. Syst. 2013, 22, 216–224. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H.; Hussain, S. Pull-in characteristics of electrically actuated MEMS arches. Mech. Mach. Theory. 2016, 98, 133–150. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Amabili, M.; Farokhi, H. Three-dimensional nonlinear size-dependent behaviour of Timoshenko microbeams. Int. J. Eng. Sci. 2013, 71, 1–14. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Viscoelastic mechanics of Timoshenko functionally graded imperfect microbeams. Compos. Struct. 2019, 225, 110974. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Mechanics of viscoelastic functionally graded microcantilevers. Eur. J. Mech. A/Solids. 2019, 73, 492–499. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Asymmetric viscoelastic nonlinear vibrations of imperfect AFG beams. Appl. Acoust. 2019, 154, 121–128. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Dynamical analysis of multilayered cantilevers. Commun. Nonlinear Sci. Numer. Simul. 2019, 71, 244–253. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Nonlinear oscillations of FG cantilevers. Appl. Acoust. 2019, 145, 393–398. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Resonant vibrations of FG viscoelastic imperfect Timoshenko beams. J. Vib. Control. 2019, 25, 1823–1832. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Viscoelastic nonlinear dynamic behaviour of Timoshenko FG beams. Eur. Phys. J. Plus. 2019, 134, 401–412. [Google Scholar] [CrossRef]
- Gholipour, A.; Farokhi, H.; Ghayesh, M.H. In-plane and out-of-plane nonlinear size-dependent dynamics of microplates. Nonlinear Dyn. 2015, 79, 1771–1785. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Amabili, M. Nonlinear dynamics of a microscale beam based on the modified couple stress theory. Compos. Part B Eng. 2013, 50, 318–324. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Viscoelastic dynamics of axially FG microbeams. Int. J. Eng. Sci. 2019, 135, 75–85. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Amabili, M. In-plane and out-of-plane motion characteristics of microbeams with modal interactions. Compos. Part B Eng. 2014, 60, 423–439. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H. Chaotic motion of a parametrically excited microbeam. Int. J. Eng. Sci. 2015, 96, 34–45. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Alici, G. Size-dependent performance of microgyroscopes. Int. J. Eng. Sci. 2016, 100, 99–111. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H.; Amabili, M. Nonlinear dynamics of a geometrically imperfect microbeam based on the modified couple stress theory. Int. J. Eng. Sci. 2013, 68, 11–23. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H. Nonlinear dynamics of microplates. Int. J. Eng. Sci. 2015, 86, 60–73. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. Thermo-mechanical dynamics of perfect and imperfect Timoshenko microbeams. Int. J. Eng. Sci. 2015, 91, 12–33. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Amabili, M. Nonlinear behaviour of electrically actuated MEMS resonators. Int. J. Eng. Sci. 2013, 71, 137–155. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Amabili, M.; Farokhi, H. Nonlinear forced vibrations of a microbeam based on the strain gradient elasticity theory. Int. J. Eng. Sci. 2013, 63, 52–60. [Google Scholar] [CrossRef]
- Ouakad, H.M.; Younis, M.I. The dynamic behavior of MEMS arch resonators actuated electrically. Int. J. Non. Linear. Mech. 2010, 45, 704–713. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Ren, J. Nonlinear Coupled Vibration of Electrically Actuated Arch with Flexible Supports. Micromachines 2019, 10, 729. https://doi.org/10.3390/mi10110729
Wang Z, Ren J. Nonlinear Coupled Vibration of Electrically Actuated Arch with Flexible Supports. Micromachines. 2019; 10(11):729. https://doi.org/10.3390/mi10110729
Chicago/Turabian StyleWang, Ze, and Jianting Ren. 2019. "Nonlinear Coupled Vibration of Electrically Actuated Arch with Flexible Supports" Micromachines 10, no. 11: 729. https://doi.org/10.3390/mi10110729
APA StyleWang, Z., & Ren, J. (2019). Nonlinear Coupled Vibration of Electrically Actuated Arch with Flexible Supports. Micromachines, 10(11), 729. https://doi.org/10.3390/mi10110729



