Multi-Response Optimization of Electrical Discharge Machining Using the Desirability Function †
Abstract
1. Introduction
2. Materials and Methods
2.1. Uncertainty Evaluation Procedure
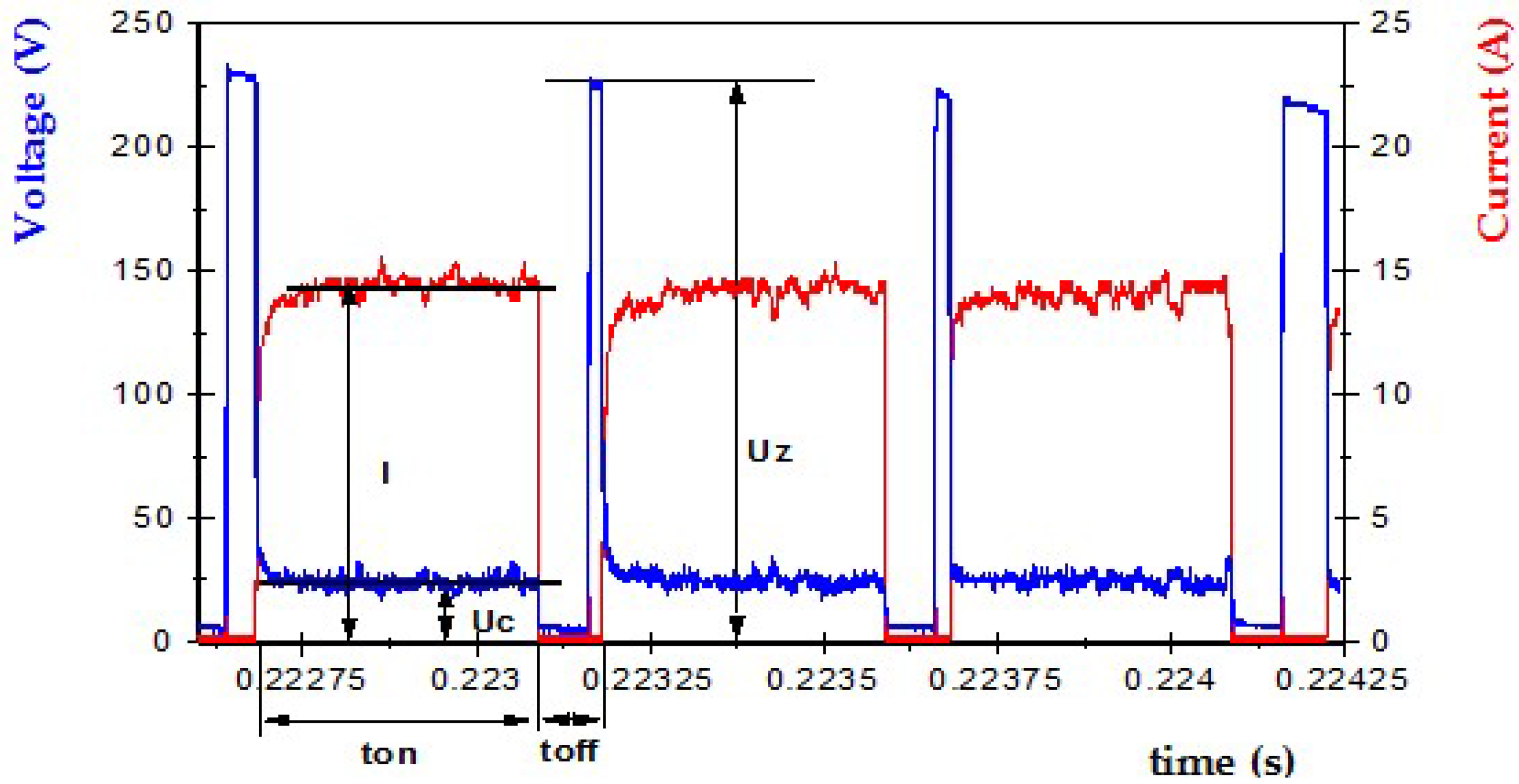
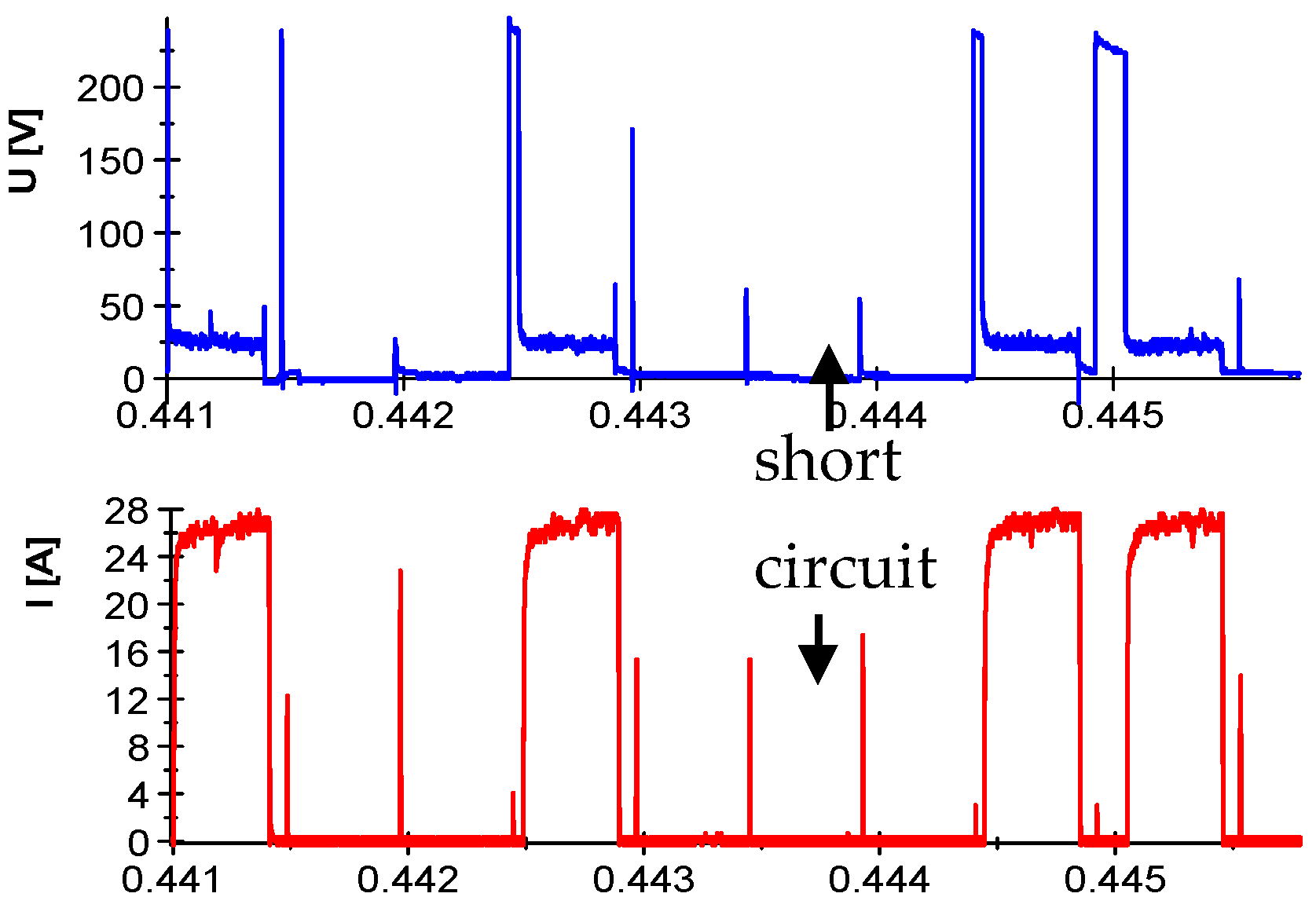
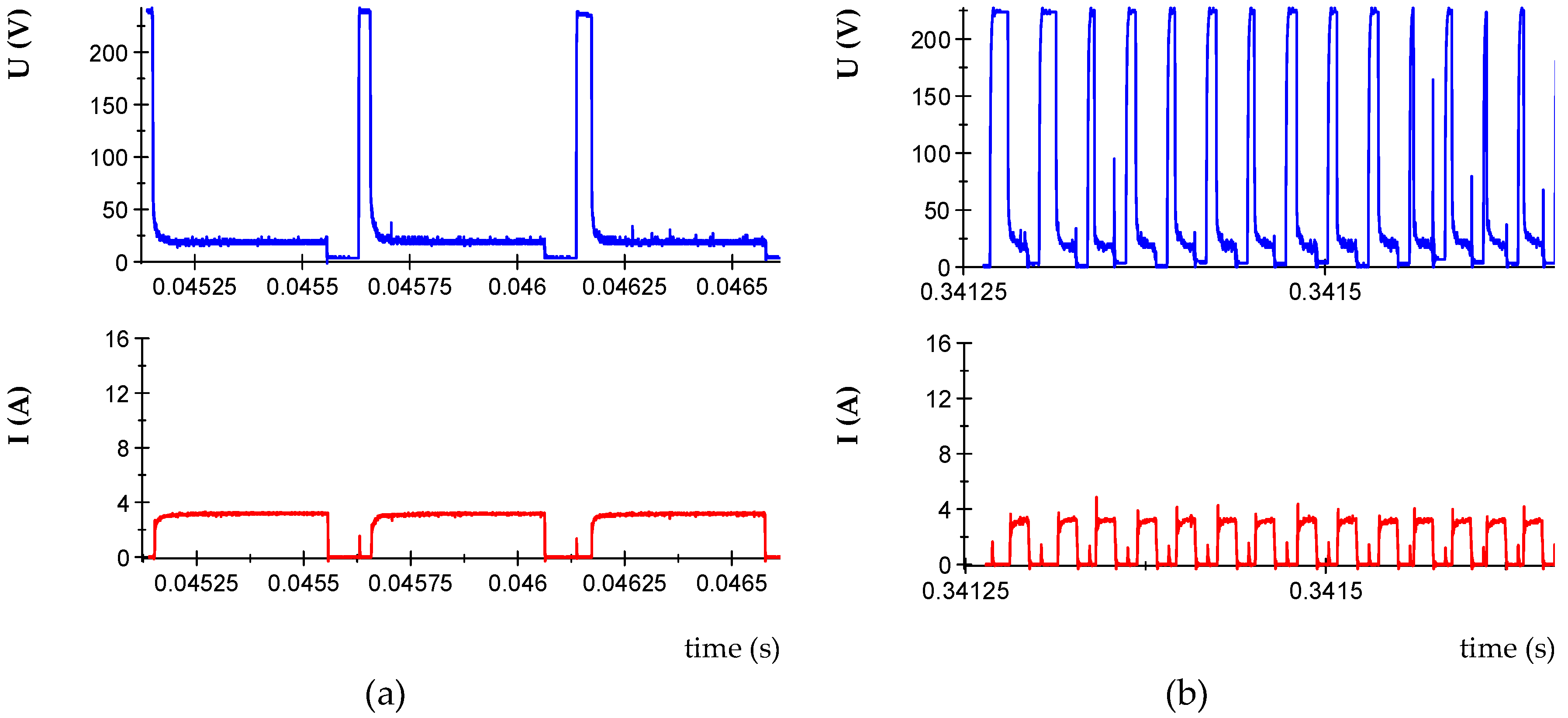
2.2. Analyses of Current and Voltage Waveforms.
- I = the height of the peak current during discharging,
- Uz = open circuit voltage, this is the system voltage when the EDM circuit is in the open state, and the energy has been built up for discharge,
- Uc = discharge voltage,
- ton = pulse time, the time required for the current to rise and fall during discharging,
- toff = time interval, this is the time from the end of one pulse to the beginning of the next pulse with the current.
3. Results and Discussion
3.1. Analysis of Surface Integrity
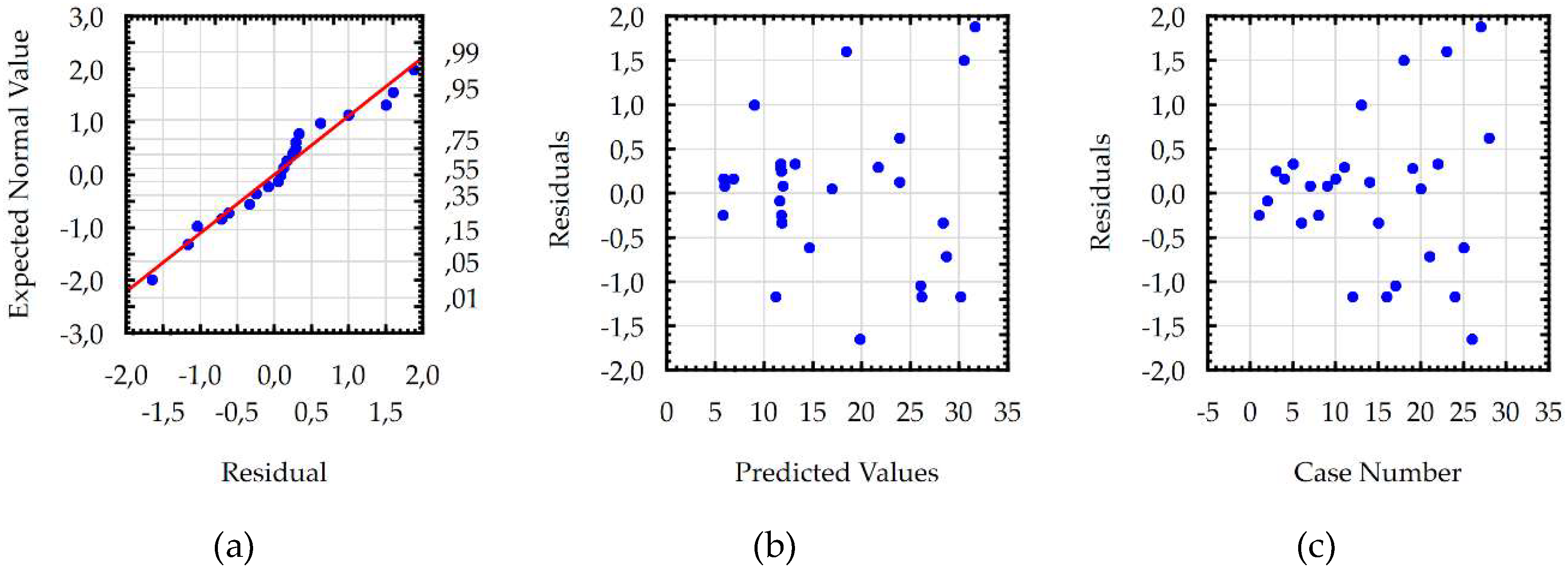
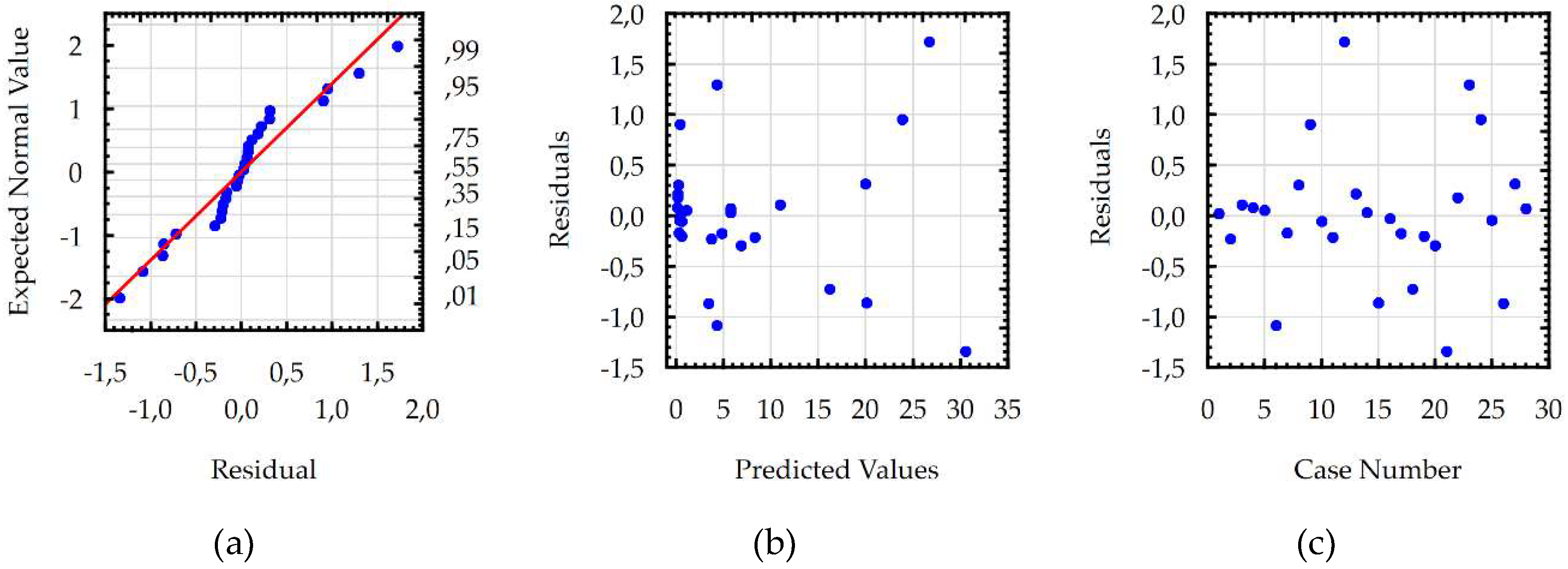
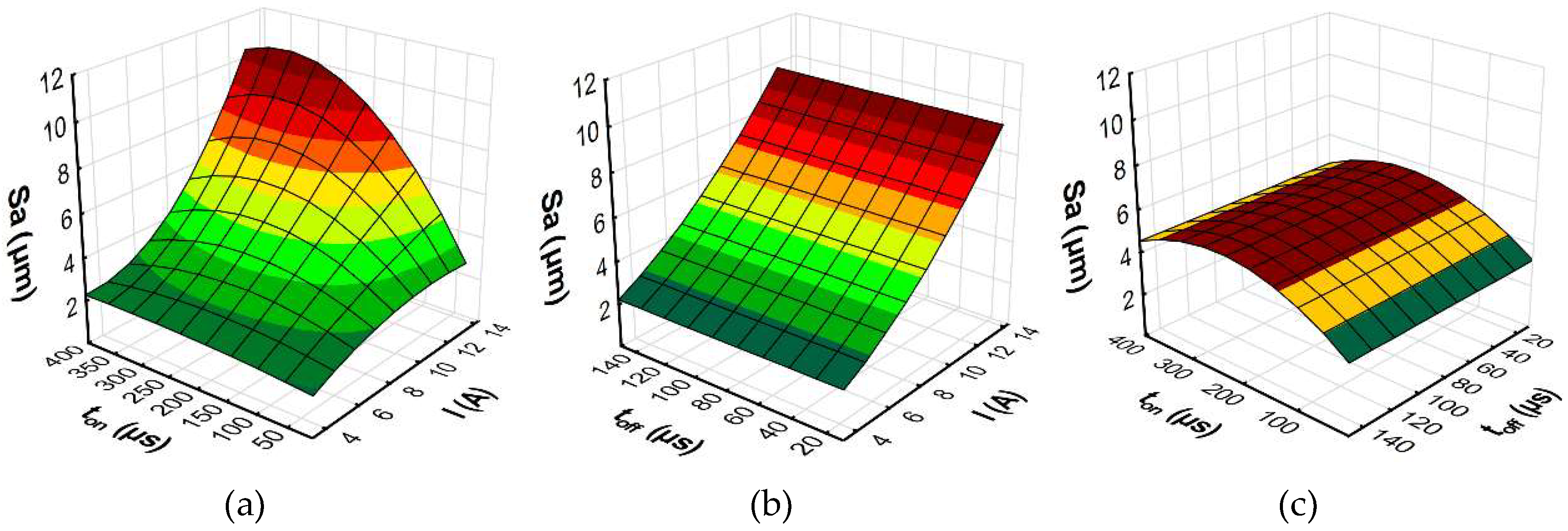
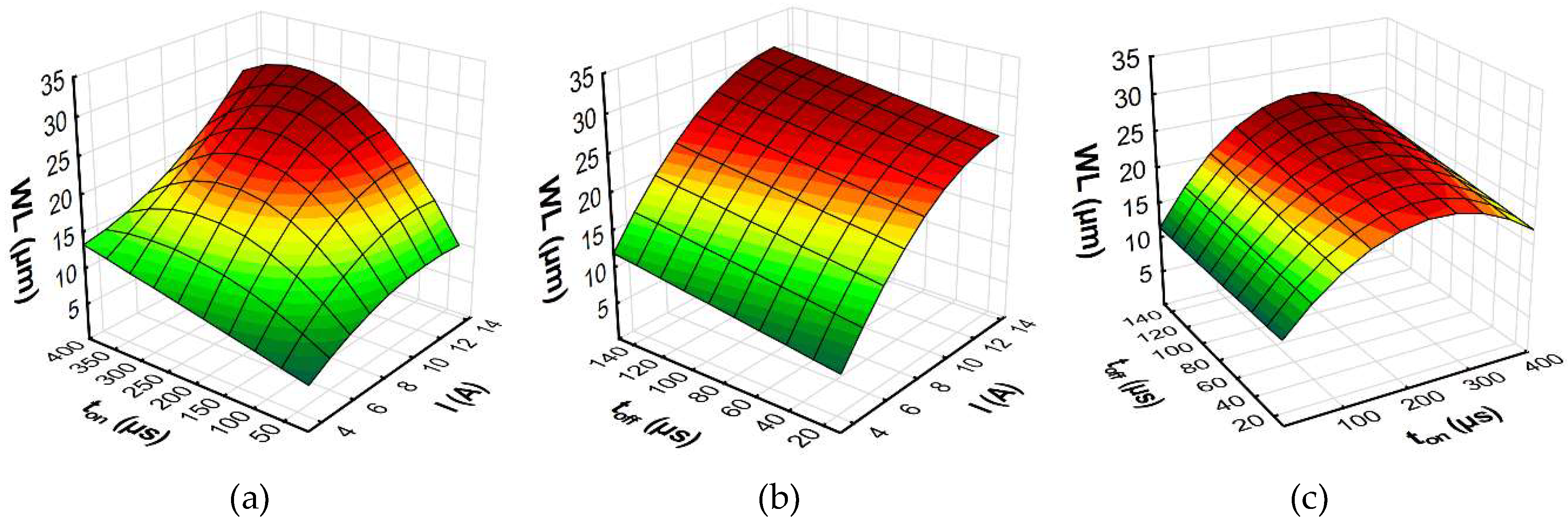
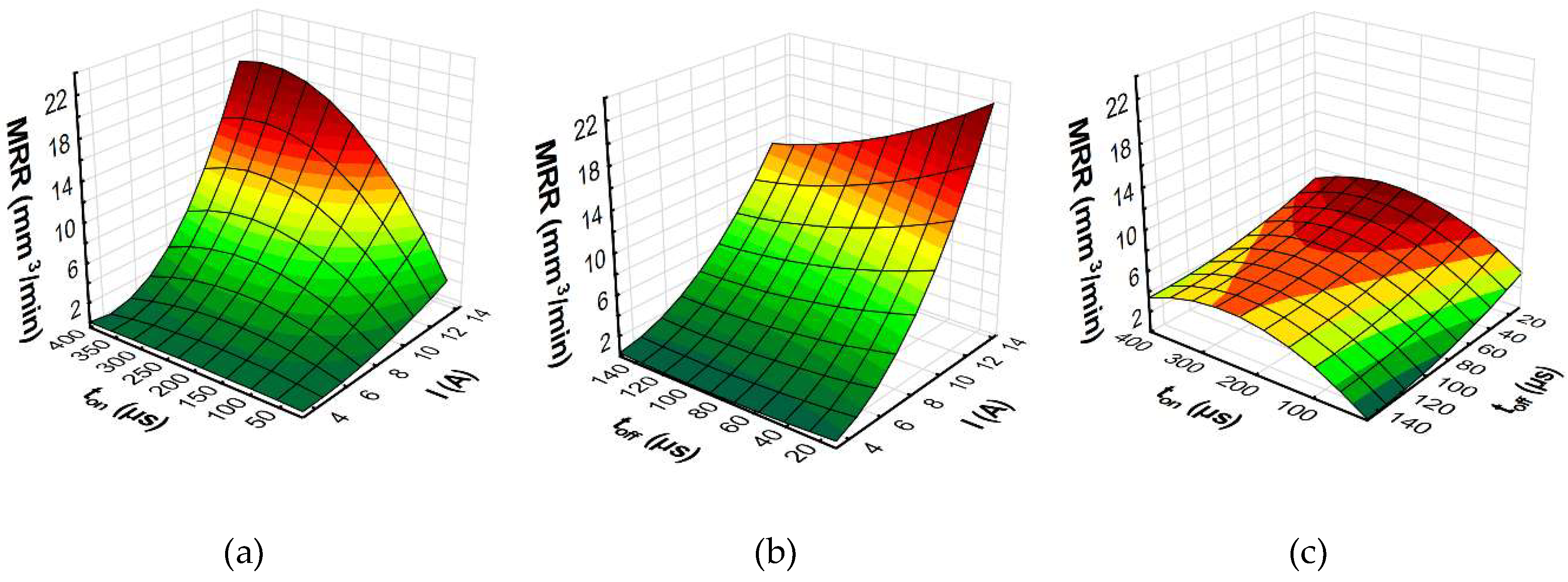
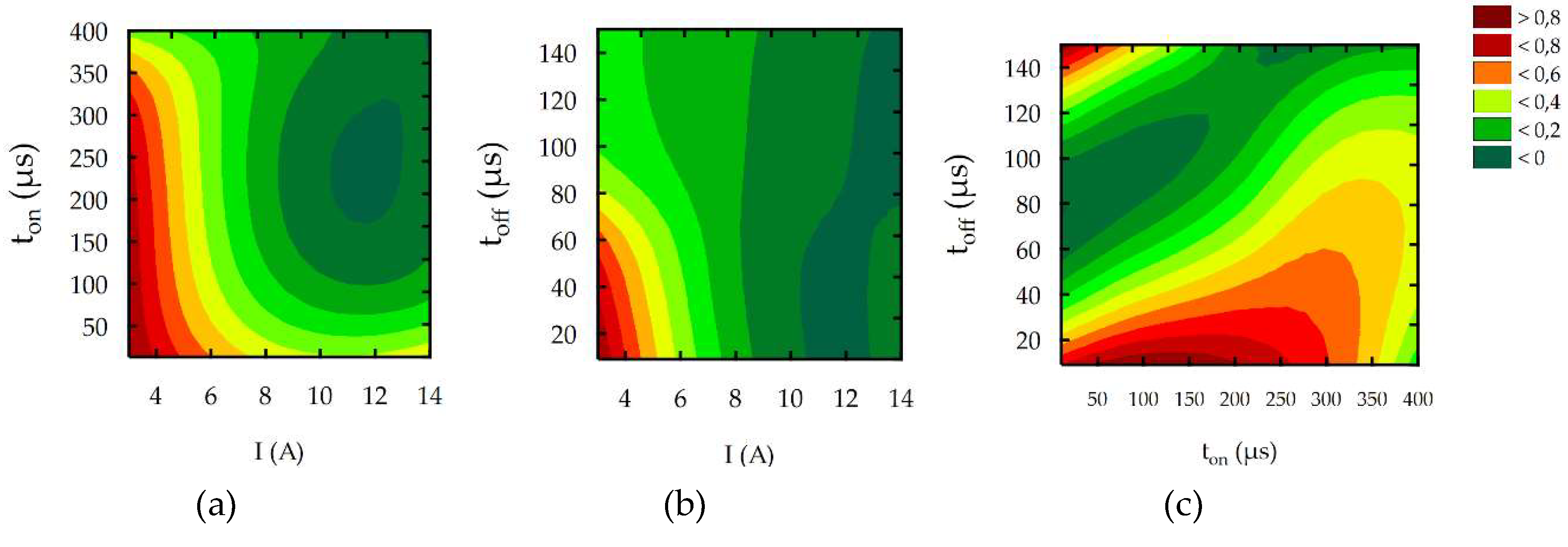
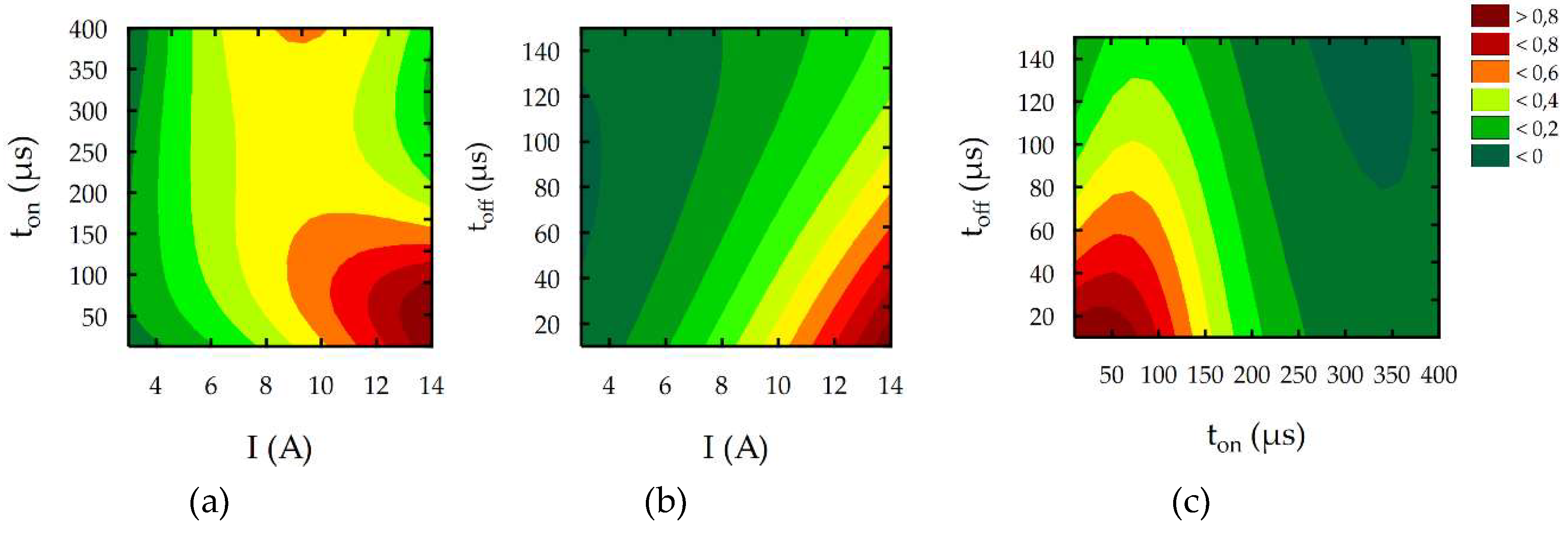
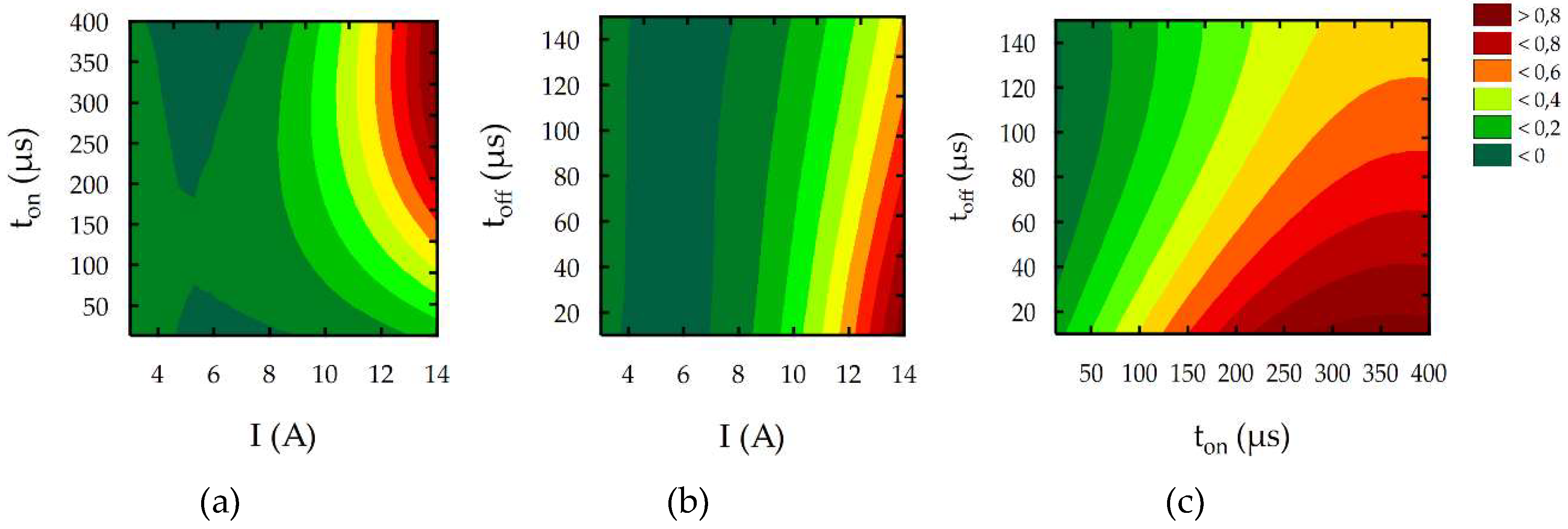
3.2. Response Surface Methodology
− 0.000007 I ton2 + 0.0003 I2 ton
− 0.0014 I2 ton + 0.000005 I2 ton2 + 0.00027 ton toff − 0.000001 ton2 toff
+ 0.00096 I ton − 0.00001 I ton2 + 0.00057 I2 ton − 0.00668 I toff
4. Conclusions
- Experimental research on the influence of discharge current, pulse time, and pulse interval on the surface roughness (Sa), white layer thickness, and the MRR showed that the discharge current had the main effect on Sa, WL, and the MRR. With an increase in the discharge current and pulse time, the amount of energy delivered to the workpiece caused the melting and evaporation of a higher volume of material, which generated craters with a larger depth and diameter. However, more material which melted in the single crater was not removed from the surface of the workpiece and it re-solidified on the core. The time interval between pulses did not significantly affect the change in surface integrity and the MRR, but it played an important role in the stability of the process.
- The desirability function was used in the multi-response optimization of three functions: Sa, WL, and MRR. For the three cases of EDM—finishing, semi-finishing, and roughing operations—the optimal parameters were established. The confirmation tests for the established optimal parameters showed that the maximal errors between the predicted and the obtained values did not exceed 6%, which could be considered as a very good result.
- The developed regression equations could be used in electrical discharge machining as a guideline for the selection of EDM parameters.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hsu, W.-H.; Chien, W.-T. Effect of electrical discharge machining on stress concentration in titanium alloy holes. Materials 2016, 9, 957. [Google Scholar] [CrossRef] [PubMed]
- Ramulu, M.; Spaulding, M. Drilling of hybrid titanium composite laminate (HTCL) with electrical discharge machining. Materials 2016, 9, 746. [Google Scholar] [CrossRef] [PubMed]
- Górka, J. Assessment of steel subjected to the thermomechanical control process with respect to weldability. Metals 2018, 8, 169. [Google Scholar] [CrossRef]
- Świercz, R.; Oniszczuk-Świercz, D.; Dąbrowski, L.; Zawora, J. Optimization of machining parameters of electrical discharge machining tool steel 1.2713. AIP Conf. Proc. 2018, 2017, 020032. [Google Scholar] [CrossRef]
- Liang, J.F.; Liao, Y.S.; Kao, J.Y.; Huang, C.H.; Hsu, C.Y. Study of the EDM performance to produce a stable process and surface modification. Int. J. Adv. Manuf. Technol. 2018, 95, 1743–1750. [Google Scholar] [CrossRef]
- Valíček, J.; Držík, M.; Hryniewicz, T.; Harničárová, M.; Rokosz, K.; Kušnerová, M.; Barčová, K.; Bražina, D. Non-contact method for surface roughness measurement after machining. Meas. Sci. Rev. 2012, 12, 184–188. [Google Scholar] [CrossRef]
- Klocke, F.; Zeis, M.; Klink, A. Interdisciplinary modelling of the electrochemical machining process for engine blades. CIRP Ann. 2015, 64, 217–220. [Google Scholar] [CrossRef]
- Kozak, J.; Zybura-Skrabalak, M. Some problems of surface roughness in electrochemical machining (ECM). Procedia CIRP 2016, 42, 101–106. [Google Scholar] [CrossRef]
- Gusarov, A.V.; Grigoriev, S.N.; Volosova, M.A.; Melnik, Y.A.; Laskin, A.; Kotoban, D.V.; Okunkova, A.A. On productivity of laser additive manufacturing. J. Mater. Process. Technol. 2018, 261, 213–232. [Google Scholar] [CrossRef]
- Wyszyński, D.; Ostrowski, R.; Zwolak, M.; Bryk, W. Laser beam machining of polycrystalline diamond for cutting tool manufacturing. AIP Conf. Proc. 2017, 1896, 180007. [Google Scholar] [CrossRef]
- Chmielewski, T.; Golański, D.; Włosiński, W.; Zimmerman, J. Utilizing the energy of kinetic friction for the metallization of ceramics. Bull. Pol. Acad. Sci. Tech. Sci. 2015, 63, 201–207. [Google Scholar] [CrossRef]
- Rokosz, K.; Hryniewicz, T.; Matýsek, D.; Raaen, S.; Valíček, J.; Dudek, Ł.; Harničárová, M. SEM, EDS and XPS analysis of the coatings obtained on titanium after plasma electrolytic oxidation in electrolytes containing copper nitrate. Materials 2016, 9, 318. [Google Scholar] [CrossRef] [PubMed]
- Skoczypiec, S.; Ruszaj, A. A sequential electrochemical–electrodischarge process for micropart manufacturing. Precis. Eng. 2014, 38, 680–690. [Google Scholar] [CrossRef]
- Gołąbczak, M.; Święcik, R.; Gołąbczak, A.; Nouveau, C.; Jacquet, P.; Blanc, C. Investigations of surface layer temperature and morphology of hard machinable materials used in aircraft industry during abrasive electrodischarge grinding process. Materialwissenschaft und Werkstofftechnik 2018, 49, 568–576. [Google Scholar] [CrossRef]
- Kelemesh, A.; Gorbenko, O.; Dudnikov, A.; Dudnikov, I. Research of wear resistance of bronze bushings during plastic vibration deformation. East.-Eur. J. Enterp. Technol. 2017, 2, 16–21. [Google Scholar] [CrossRef]
- Golański, D.; Dymny, G.; Kujawińska, M.; Chmielewski, T. Experimental investigation of displacement/strain fields in metal coatings deposited on ceramic substrates by thermal spraying. Solid State Phenom. 2016, 240, 174–182. [Google Scholar] [CrossRef]
- Salacinski, T.; Winiarski, M.; Chmielewski, T.; Świercz, R. Surface finishing using ceramic fibre brush tools. In Proceedings of the 26th International Conference on Metallurgy and Materials, Brno, Czech Republi, 24–26 May 2017; pp. 1220–1226. [Google Scholar]
- Guo, J.; Wang, H.; Goh, M.H.; Liu, K. Investigation on surface integrity of rapidly solidified aluminum RSA 905 by magnetic field-assisted finishing. Micromachines 2018, 9, 146. [Google Scholar] [CrossRef]
- Kunieda, M.; Lauwers, B.; Rajurkar, K.P.; Schumacher, B.M. Advancing EDM through fundamental insight into the process. CIRP Ann. Manuf. Technol. 2005, 54, 64–87. [Google Scholar] [CrossRef]
- Izquierdo, B.; Sánchez, J.A.; Plaza, S.; Pombo, I.; Ortega, N. A numerical model of the EDM process considering the effect of multiple discharges. Int. J. Mach. Tools Manuf. 2009, 49, 220–229. [Google Scholar] [CrossRef]
- Izquierdo, B.; Sánchez, J.A.; Ortega, N.; Plaza, S.; Pombo, I. Insight into fundamental aspects of the EDM process using multidischarge numerical simulation. Int. J. Adv. Manuf. Technol. 2011, 52, 195–206. [Google Scholar] [CrossRef]
- Ming, W.; Zhang, Z.; Wang, S.; Huang, H.; Zhang, Y.; Zhang, Y.; Shen, D. Investigating the energy distribution of workpiece and optimizing process parameters during the EDM of Al6061, Inconel718, and SKD11. Int. J. Adv. Manuf. Technol. 2017, 92, 4039–4056. [Google Scholar] [CrossRef]
- Gulbinowicz, Z.; Świercz, R.; Oniszczuk-Świercz, D. Influence of electrical parameters in electro discharge machining of tungsten heavy alloys on surface texture properties. AIP Conf. Proc. 2018, 2017, 020007. [Google Scholar] [CrossRef]
- Salcedo, A.T.; Arbizu, I.P.; Pérez, C.J.L. Analytical modelling of energy density and optimization of the EDM machining parameters of Inconel 600. Metals 2017, 7, 166. [Google Scholar] [CrossRef]
- Rahang, M.; Patowari, P.K. Parametric optimization for selective surface modification in EDM using taguchi analysis. Mater. Manuf. Process. 2016, 31, 422–431. [Google Scholar] [CrossRef]
- Vagaská, A.; Gombár, M. Comparison of usage of different neural structures to predict AAO layer thickness. Tehnički Vjesnik 2017, 24, 333–339. [Google Scholar] [CrossRef]
- Wojciechowski, S.; Maruda, R.W.; Królczyk, G.M. The application of response surface method to optimization of precision ball end milling. MATEC Web Conf. 2017, 112, 01004. [Google Scholar] [CrossRef]
- Adalarasan, R.; Santhanakumar, M.; Rajmohan, M. Optimization of laser cutting parameters for Al6061/SiCp/Al2O3 composite using grey based response surface methodology (GRSM). Measurement 2015, 73, 596–606. [Google Scholar] [CrossRef]
- Vera Candioti, L.; De Zan, M.M.; Cámara, M.S.; Goicoechea, H.C. Experimental design and multiple response optimization. Using the desirability function in analytical methods development. Talanta 2014, 124, 123–138. [Google Scholar] [CrossRef]
- Ayesta, I.; Izquierdo, B.; Sanchez, J.A.; Ramos, J.M.; Plaza, S.; Pombo, I.; Ortega, N. Optimum electrode path generation for EDM manufacturing of aerospace components. Robot. Comput.-Integr. Manuf. 2016, 37, 273–281. [Google Scholar] [CrossRef]
- Abidi, M.H.; Al-Ahmari, A.M.; Siddiquee, A.N.; Mian, S.H.; Mohammed, M.K.; Rasheed, M.S. An investigation of the micro-electrical discharge machining of nickel-titanium shape memory alloy using grey relations coupled with principal component analysis. Metals 2017, 7, 486. [Google Scholar] [CrossRef]
- Rubio, E.M.; Villeta, M.; Valencia, J.L.; Sáenz de Pipaón, J.M. Experimental study for improving the repair of magnesium–aluminium hybrid parts by turning processes. Metals 2018, 8, 59. [Google Scholar] [CrossRef]
- Chabbi, A.; Yallese, M.A.; Meddour, I.; Nouioua, M.; Mabrouki, T.; Girardin, F. Predictive modeling and multi-response optimization of technological parameters in turning of Polyoxymethylene polymer (POM C) using RSM and desirability function. Measurement 2017, 95, 99–115. [Google Scholar] [CrossRef]
- Kilickap, E.; Yardimeden, A.; Çelik, Y.H. Mathematical modelling and optimization of cutting force, tool wear and surface roughness by using artificial neural network and response surface methodology in milling of Ti-6242S. Appl. Sci. 2017, 7, 1064. [Google Scholar] [CrossRef]
- Rogalski, G.; Fydrych, D.; Łabanowski, J. Underwater wet repair welding of API 5L X65M pipeline steel. Pol. Marit. Res. 2017, 24, 188–194. [Google Scholar] [CrossRef]
- Unune, D.R.; Mali, H.S. Parametric modeling and optimization for abrasive mixed surface electro discharge diamond grinding of Inconel 718 using response surface methodology. Int. J. Adv. Manuf. Technol. 2017, 93, 3859–3872. [Google Scholar] [CrossRef]
- Hlaváč, L.M.; Krajcarz, D.; Hlaváčová, I.M.; Spadło, S. Precision comparison of analytical and statistical-regression models for AWJ cutting. Precis. Eng. 2017, 50, 148–159. [Google Scholar] [CrossRef]
- Ghodsiyeh, D.; Golshan, A.; Izman, S. Multi-objective process optimization of wire electrical discharge machining based on response surface methodology. J. Braz. Soc. Mech. Sci. Eng. 2014, 36, 301–313. [Google Scholar] [CrossRef]
- Alavi, F.; Jahan, M.P. Optimization of process parameters in micro-EDM of Ti-6Al-4V based on full factorial design. Int. J. Adv. Manuf. Technol. 2017, 92, 167–187. [Google Scholar] [CrossRef]
- Selvarajan, L.; Manohar, M.; Kumar, A.U.; Dhinakaran, P. Modelling and experimental investigation of process parameters in EDM of Si3N4-TiN composites using GRA-RSM. J. Mech. Sci. Technol. 2017, 31, 111–122. [Google Scholar] [CrossRef]
- Świercz, R.; Oniszczuk-Świercz, D. Influence of electrical discharge pulse energy on the surface integrity of tool steel 1.2713. Proceedings of 26th International Conference on Metallurgy and Materials, Brno, Czech Republic, 24–26 May 2017; pp. 1452–1457. [Google Scholar]
- Kumaran, S.T.; Ko, T.J.; Kurniawan, R. Grey fuzzy optimization of ultrasonic-assisted EDM process parameters for deburring CFRP composites. Measurement 2018, 123, 203–212. [Google Scholar] [CrossRef]
- Gu, L.; Zhu, Y.; Zhang, F.; Farhadi, A.; Zhao, W. Mechanism analysation and parameter optimisation of electro discharge machining of titanium-zirconium-molybdenum alloy. J. Manuf. Process. 2018, 32, 773–781. [Google Scholar] [CrossRef]
- Dang, X.-P. Constrained multi-objective optimization of EDM process parameters using kriging model and particle swarm algorithm. Mater. Manuf. Process. 2018, 33, 397–404. [Google Scholar] [CrossRef]
- Mohanty, C.P.; Mahapatra, S.S.; Singh, M.R. An intelligent approach to optimize the EDM process parameters using utility concept and QPSO algorithm. Eng. Sci. Technol. Int. J. 2017, 20, 552–562. [Google Scholar] [CrossRef]
- Maity, K.; Mishra, H. ANN modelling and Elitist teaching learning approach for multi-objective optimization of μ-EDM. J. Intell. Manuf. 2018, 29, 1599–1616. [Google Scholar] [CrossRef]
- Tripathy, S.; Tripathy, D.K. Multi-response optimization of machining process parameters for powder mixed electro-discharge machining of H-11 die steel using grey relational analysis and topsis. Mach. Sci. Technol. 2017, 21, 362–384. [Google Scholar] [CrossRef]
- Nguyen, H.-P.; Pham, V.-D.; Ngo, N.-V. Application of TOPSIS to Taguchi method for multi-characteristic optimization of electrical discharge machining with titanium powder mixed into dielectric fluid. Int. J. Adv. Manuf. Technol. 2018, 98, 1179–1198. [Google Scholar] [CrossRef]
- Roy, T.; Dutta, R.K. Integrated fuzzy AHP and fuzzy TOPSIS methods for multi-objective optimization of electro discharge machining process. Soft Comput. 2018. [Google Scholar] [CrossRef]
- Kandpal, B.C.; Kumar, J.; Singh, H. Optimization and characterization of EDM of AA 6061/10%Al2O3 AMMC using Taguchi’s approach and utility concept. Prod. Manuf. Res. 2017, 5, 351–370. [Google Scholar] [CrossRef]
- D’Urso, G.; Giardini, C.; Quarto, M.; Maccarini, G. Cost index model for the process performance optimization of micro-EDM drilling on tungsten carbide. Micromachines 2017, 8, 251. [Google Scholar] [CrossRef]
- Parsana, S.; Radadia, N.; Sheth, M.; Sheth, N.; Savsani, V.; Prasad, N.E.; Ramprabhu, T. Machining parameter optimization for EDM machining of Mg–RE–Zn–Zr alloy using multi-objective Passing Vehicle Search algorithm. Arch. Civil Mech. Eng. 2018, 18, 799–817. [Google Scholar] [CrossRef]
- Hadad, M.; Bui, L.Q.; Nguyen, C.T. Experimental investigation of the effects of tool initial surface roughness on the electrical discharge machining (EDM) performance. Int. J. Adv. Manuf. Technol. 2018, 95, 2093–2104. [Google Scholar] [CrossRef]
- Baruffi, F.; Parenti, P.; Cacciatore, F.; Annoni, M.; Tosello, G. On the application of replica molding technology for the indirect measurement of surface and geometry of micromilled components. Micromachines 2017, 8, 195. [Google Scholar] [CrossRef]
- ISO. IOS 15530-3: Geometrical Product Specifications (GPS)—Coordinate Measuring Machines (CMM): Technique for Determining the Uncertainty of Measurement; IOS: Geneva, Switzerland, 2011. [Google Scholar]
- Xin, B.; Li, S.; Yin, X.; Lu, X. Dynamic observer modeling and minimum-variance self-tuning control of EDM interelectrode gap. Appl. Sci. 2018, 8, 1443. [Google Scholar] [CrossRef]
- Gopalakannan, S.; Senthilvelan, T. Optimization of machining parameters for EDM operations based on central composite design and desirability approach. J. Mech. Sci. Technol. 2014, 28, 1045–1053. [Google Scholar] [CrossRef]
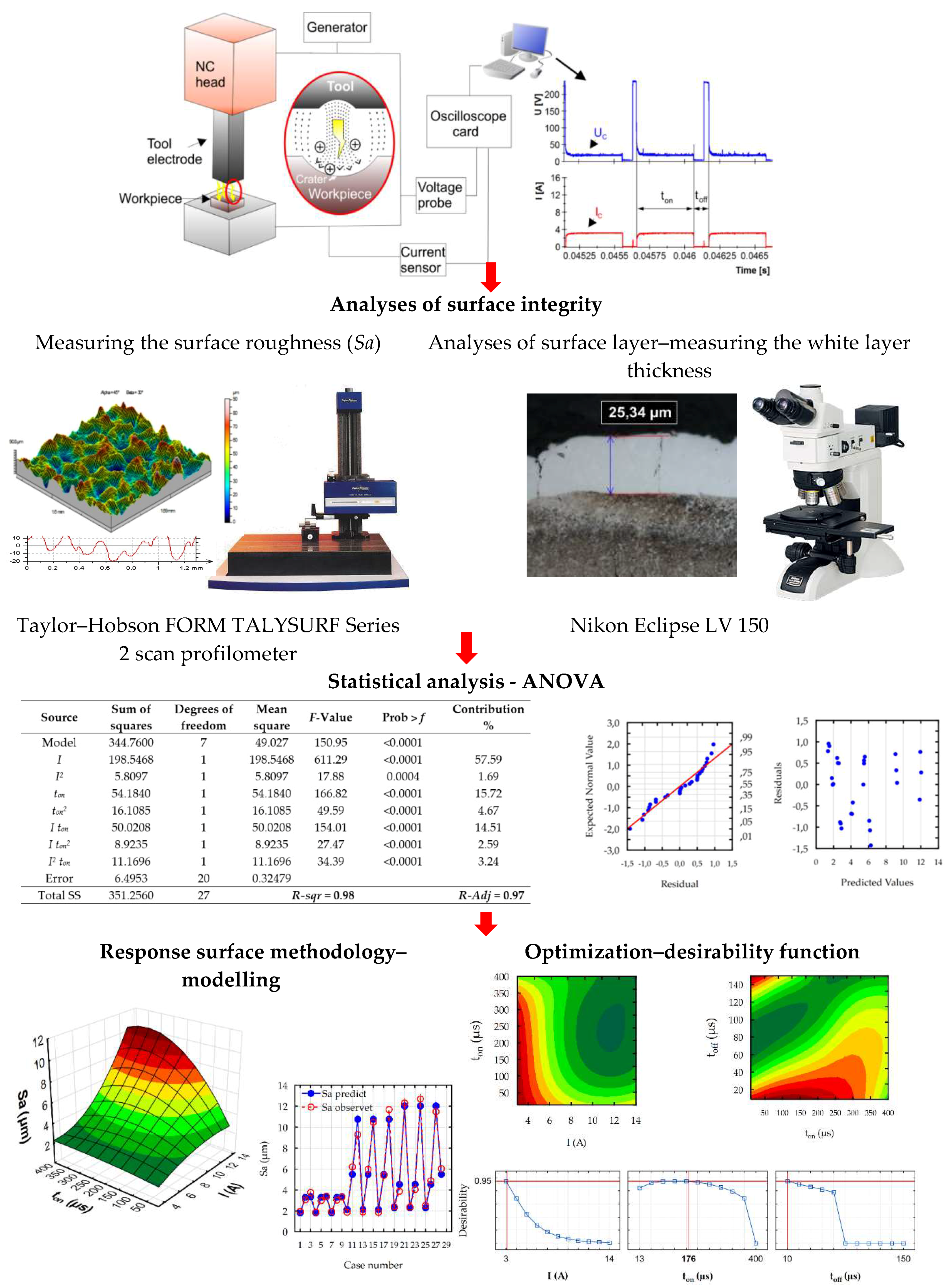
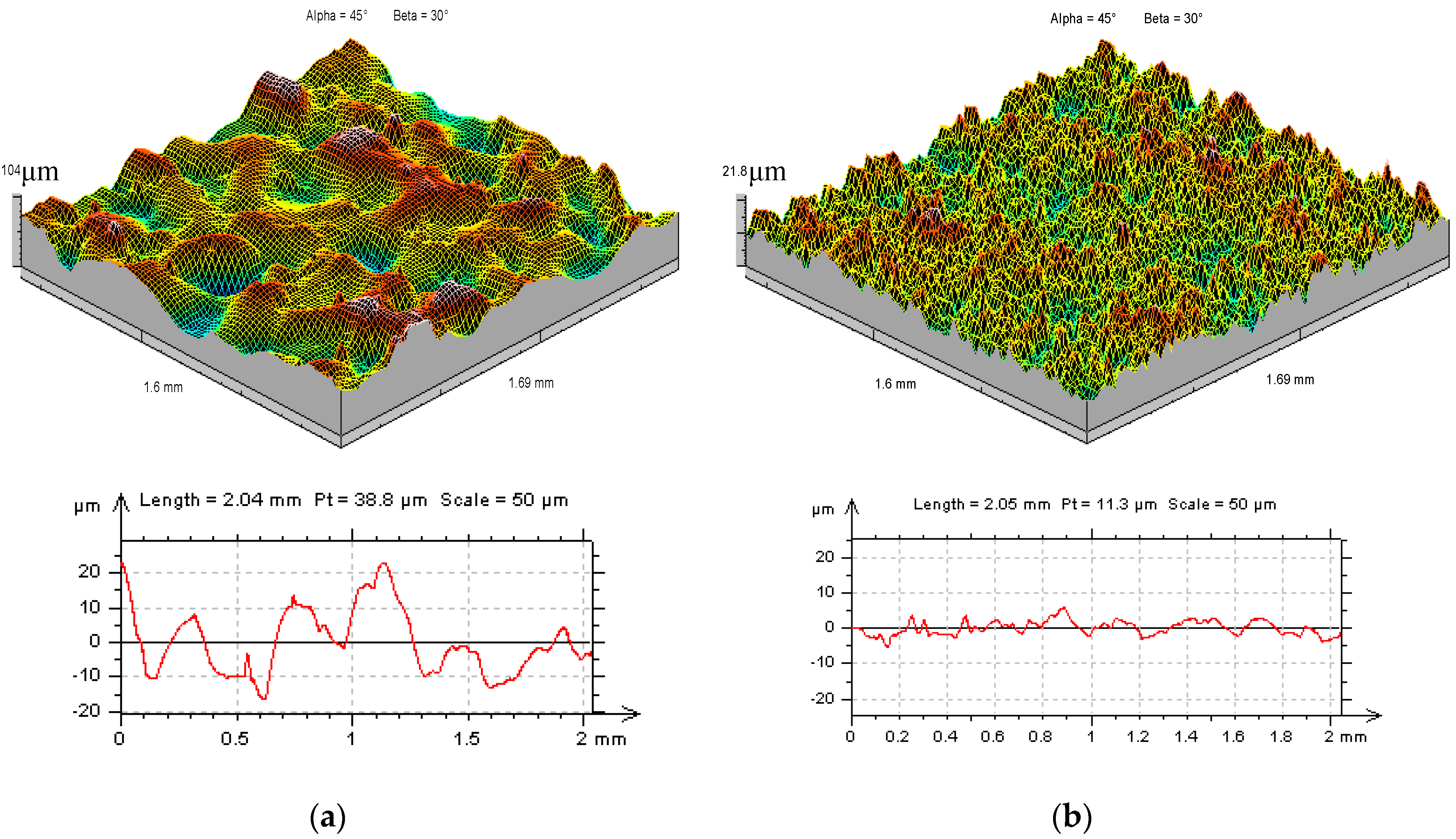



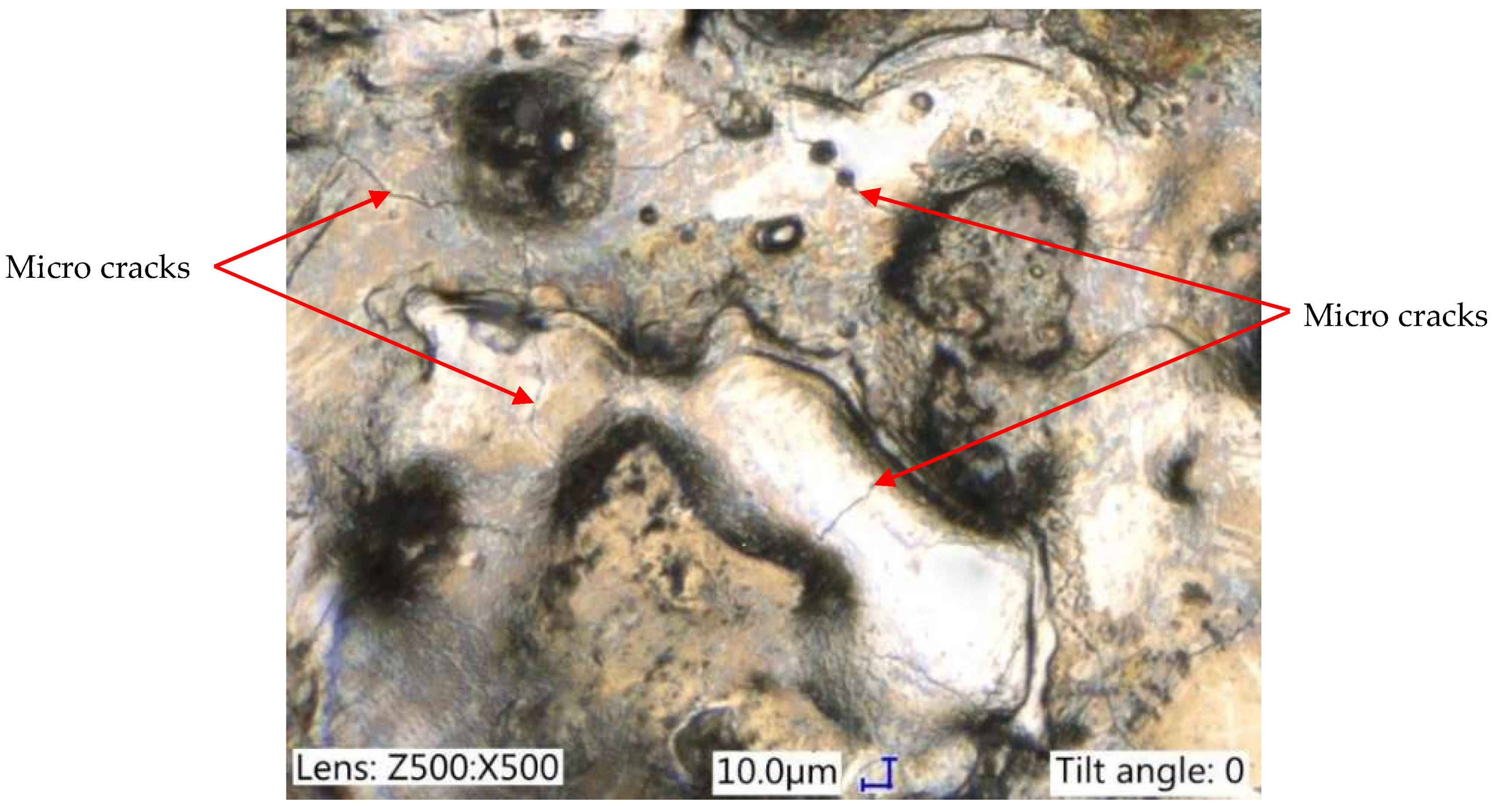
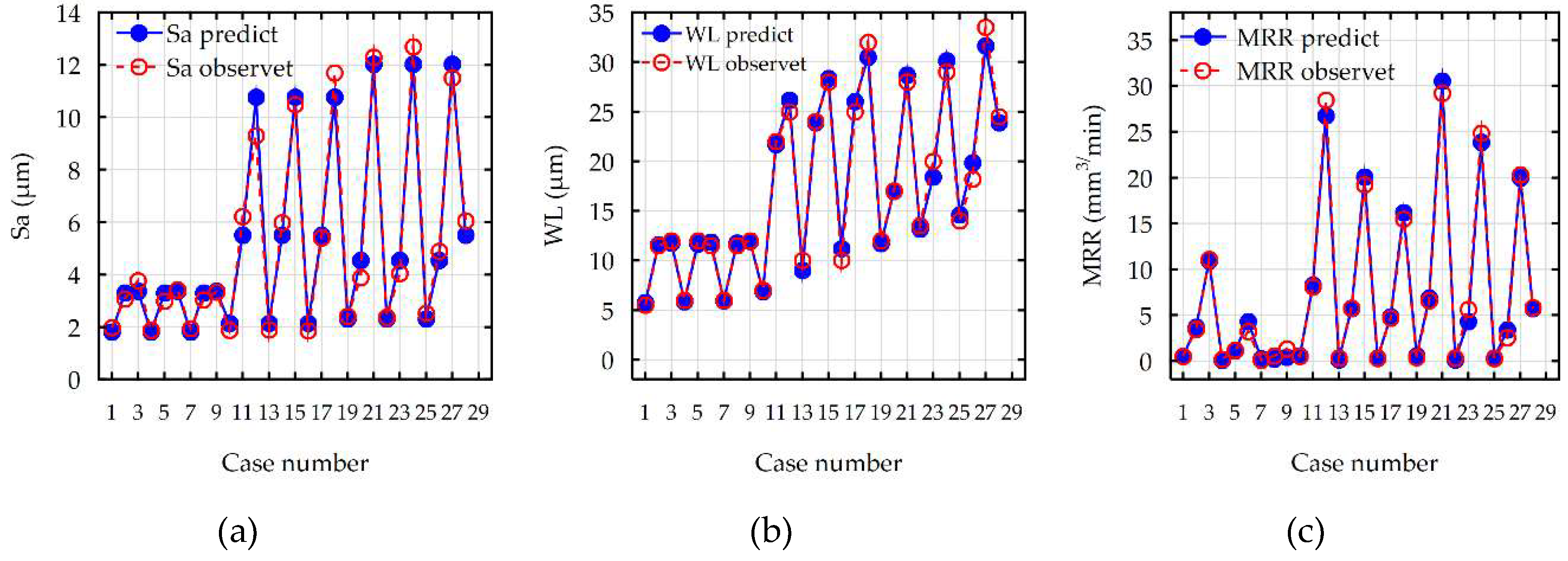
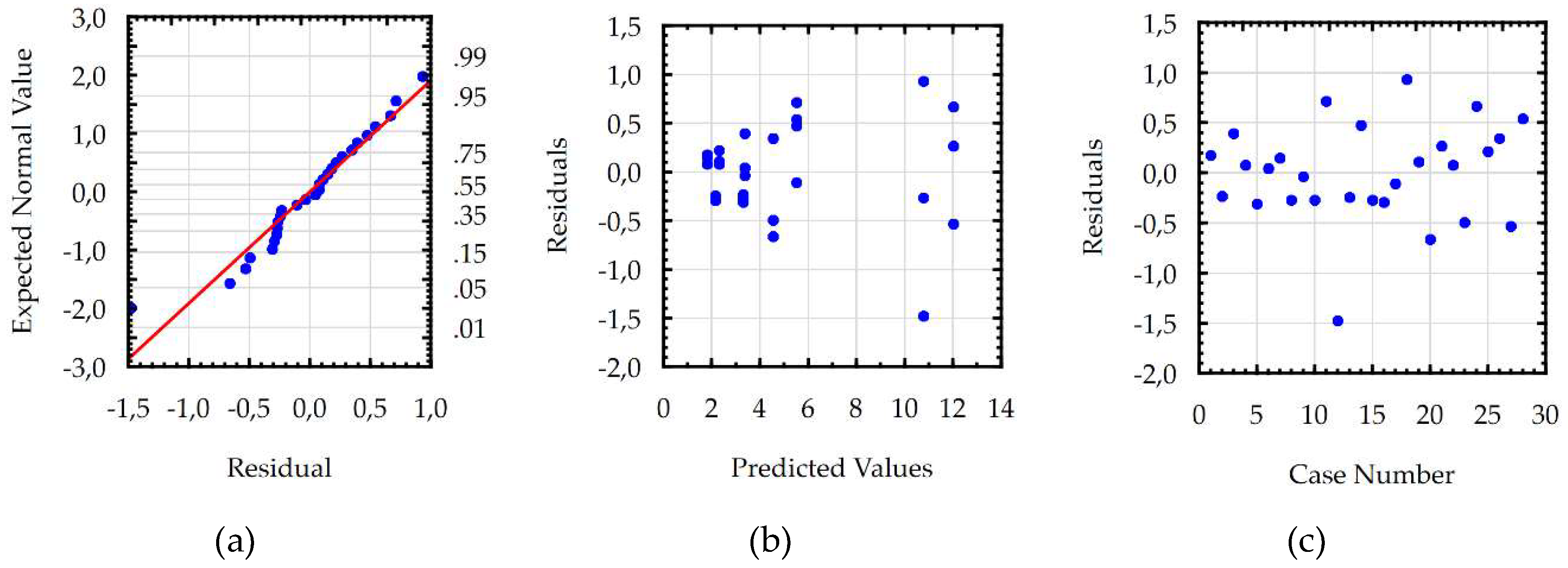
| Uncertainty Contributions (nm) | |||||
|---|---|---|---|---|---|
| ucal | up | ures,PROF | UPROF | USa, EDM | U95,Sa |
| 20 | 2 | 3 | 20.5 | 5 | 42 |
| Uncertainty Contributions (μm) | ||||
|---|---|---|---|---|
| ucal | up | ures,OM | UOM | U95,WL |
| 0.060 | 0.048 | 0.312 | 0.321 | 0.6 |
| Uncertainty Contributions (mg) | |||||
|---|---|---|---|---|---|
| um1 | ures | ui | uie | UB | U95,W |
| 0.02 | 0.0029 | 0.0058 | 0.01 | 0.023 | 0.046 |
| EDM Parameters | Level 1 | Level 2 | Level 3 |
|---|---|---|---|
| discharge current I (A) | 3 | 8.5 | 14 |
| pulse time ton (μs) | 13 | 206 | 400 |
| time interval toff (μs) | 9 | 80 | 150 |
| Exp. no. | EDM Parameters | Observed Values | ||||
|---|---|---|---|---|---|---|
| Discharge Current I (A) | Pulse Time ton (μs) | Time Interval toff (μs) | Surface Roughness Sa (μm) | Maximal Thickness of the White Layer (μm) | MRR (mm3/min) | |
| 1 | 3 | 13 | 10 | 2.0 | 5.5 | 0.54 |
| 2 | 8.5 | 13 | 10 | 3.1 | 11.5 | 3.47 |
| 3 | 14 | 13 | 10 | 3.8 | 12 | 11.06 |
| 4 | 3 | 13 | 80 | 1.9 | 6 | 0.17 |
| 5 | 8.5 | 13 | 80 | 3.0 | 12 | 1.18 |
| 6 | 14 | 13 | 80 | 3.4 | 11.5 | 3.21 |
| 7 | 3 | 13 | 150 | 1.9 | 6 | 0.10 |
| 8 | 8.5 | 13 | 150 | 3.0 | 11.5 | 0.55 |
| 9 | 14 | 13 | 150 | 3.3 | 12 | 1.31 |
| 10 | 3 | 206 | 10 | 1.9 | 7 | 0.51 |
| 11 | 8.5 | 206 | 10 | 6.2 | 22 | 8.09 |
| 12 | 14 | 206 | 10 | 9.3 | 25.4 | 28.46 |
| 13 | 3 | 206 | 80 | 1.9 | 10 | 0.36 |
| 14 | 8.5 | 206 | 80 | 6.0 | 24 | 5.77 |
| 15 | 14 | 206 | 80 | 10.5 | 28 | 19.23 |
| 16 | 3 | 206 | 150 | 1.8 | 10 | 0.29 |
| 17 | 8.5 | 206 | 150 | 5.4 | 25 | 4.68 |
| 18 | 14 | 206 | 150 | 11.7 | 32 | 15.48 |
| 19 | 3 | 400 | 10 | 2.4 | 12 | 0.37 |
| 20 | 8.5 | 400 | 10 | 3.9 | 17 | 6.58 |
| 21 | 14 | 400 | 10 | 12.3 | 28 | 29.19 |
| 22 | 3 | 400 | 80 | 2.4 | 13.5 | 0.34 |
| 23 | 8.5 | 400 | 80 | 4.0 | 20 | 5.61 |
| 24 | 14 | 400 | 80 | 12.7 | 29 | 24.84 |
| 25 | 3 | 400 | 150 | 2.5 | 14 | 0.28 |
| 26 | 8.5 | 400 | 150 | 4.9 | 18.4 | 2.56 |
| 27 | 14 | 400 | 150 | 11.5 | 33.5 | 20.31 |
| 28 | 8.5 | 206 | 80 | 6.1 | 24.5 | 5.88 |
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F-Value | Prob > f | Contribution % |
|---|---|---|---|---|---|---|
| Model | 344.7600 | 7 | 49.027 | 150.95 | <0.0001 | - |
| I | 198.5468 | 1 | 198.5468 | 611.29 | <0.0001 | 57.6 |
| I2 | 5.8097 | 1 | 5.8097 | 17.88 | 0.0004 | 1.7 |
| ton | 54.1840 | 1 | 54.1840 | 166.82 | <0.0001 | 15.7 |
| ton2 | 16.1085 | 1 | 16.1085 | 49.59 | <0.0001 | 4.7 |
| I ton | 50.0208 | 1 | 50.0208 | 154.01 | <0.0001 | 14.5 |
| I ton2 | 8.9235 | 1 | 8.9235 | 27.47 | <0.0001 | 2.6 |
| I2 ton | 11.1696 | 1 | 11.1696 | 34.39 | <0.0001 | 3.2 |
| Error | 6.4953 | 20 | 0.32479 | - | - | - |
| Total SS | 351.2560 | 27 | R-sqr = 0.98 | R-Adj = 0.97 | ||
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F-Value | Prob > f | Contribution % |
|---|---|---|---|---|---|---|
| Model | 1886.366 | 11 | 171.48 | 141.26 | <0.0001 | - |
| I | 896.656 | 1 | 896.656 | 738.59 | 0.0022 | 47.5 |
| I2 | 16.041 | 1 | 16.041 | 13.21 | <0.0001 | 0.8 |
| ton | 524.880 | 1 | 524.880 | 432.35 | <0.0001 | 27.8 |
| ton2 | 174.366 | 1 | 174.366 | 143.62 | 0.0002 | 9.2 |
| toff | 27.406 | 1 | 27.406 | 22.57 | <0.0001 | 1.4 |
| I ton | 90.750 | 1 | 90.750 | 74.75 | 0.0004 | 4.8 |
| I ton2 | 61.584 | 1 | 61.583 | 50.72 | 0.0031 | 3.3 |
| I2ton | 37.210 | 1 | 37.210 | 30.65 | 0.0071 | 2.0 |
| I2ton2 | 44.018 | 1 | 44.017 | 36.25 | <0.0001 | 2.3 |
| tontoff | 5.603 | 1 | 5.603 | 4.61 | <0.0001 | 0.3 |
| ton2toff | 7.860 | 1 | 7.859 | 6.47 | 0.0473 | 0.4 |
| Error | 19.424 | 16 | 1.2140 | 738.59 | 0.0216 | - |
| Total SS | 1905.799 | 27 | R-sqr = 0.99 | R-Adj = 0.98 | ||
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F-Value | Prob > f | Contribution % |
|---|---|---|---|---|---|---|
| Model | 2243.49 | 9 | 247.881 | 208.65 | <0.0001 | - |
| I | 1253.287 | 1 | 1253.287 | 1055.08 | <0.0001 | 55.9 |
| I2 | 126.243 | 1 | 126.243 | 106.27 | <0.0001 | 5.6 |
| ton | 260.655 | 1 | 260.655 | 219.43 | <0.0001 | 11.6 |
| ton2 | 56.489 | 1 | 56.489 | 47.55 | <0.0001 | 2.5 |
| toff | 101.381 | 1 | 101.381 | 85.34 | <0.0001 | 4.5 |
| I ton | 285.948 | 1 | 285.948 | 240.72 | <0.0001 | 12.7 |
| I ton2 | 36.030 | 1 | 36.030 | 30.33 | <0.0001 | 1.6 |
| I2ton | 44.106 | 1 | 44.106 | 37.13 | <0.0001 | 2.0 |
| I toff | 79.350 | 1 | 79.350 | 66.80 | <0.0001 | 3.5 |
| Error | 21.381 | 18 | 1.188 | - | - | - |
| Total SS | 2264.87 | 27 | R-sqr = 0.99 | R-Adj = 0.99 | ||
| Factors | Goal | Lower Limit | Upper Limit | Weight | Importance | ||
|---|---|---|---|---|---|---|---|
| Finishing EDM | Semi-Finishing | Roughing | |||||
| I (A) | In range | 3 | 14 | 1 | - | - | - |
| ton (µs) | In range | 13 | 400 | 1 | - | - | - |
| toff (µs) | In range | 10 | 150 | 1 | - | - | - |
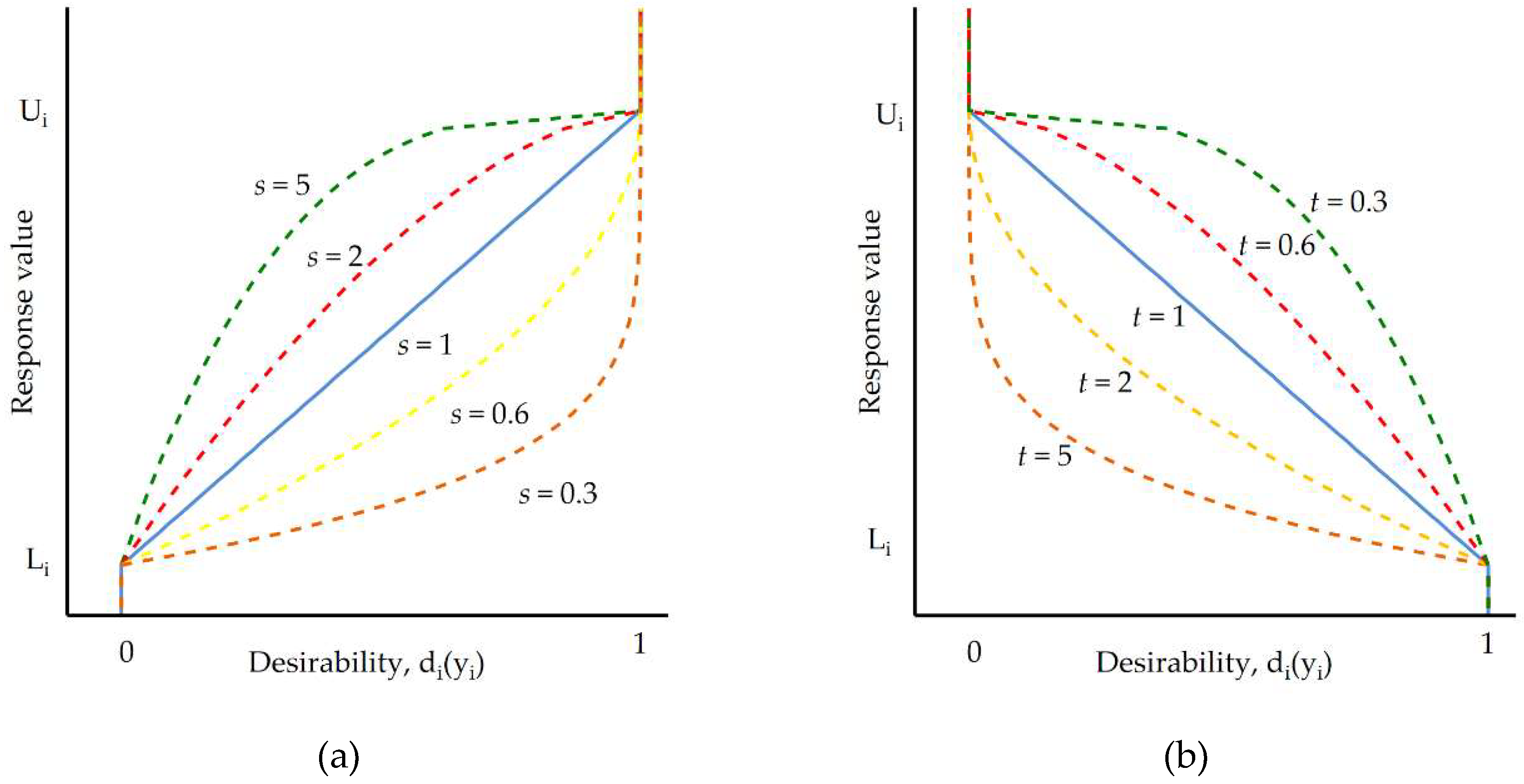
| Sa (µm) | Minimize | 1.85 | 12.7 | 1 | t = 5 | t = 3 | t = 0.3 |
| WL (µm) | Minimize | 5.5 | 33.5 | 1 | t = 5 | t = 3 | t = 0.3 |
| MRR (mm3/min) | Maximize | 0.01 | 29.19 | 1 | s = 0.3 | s = 3 | s = 5 |
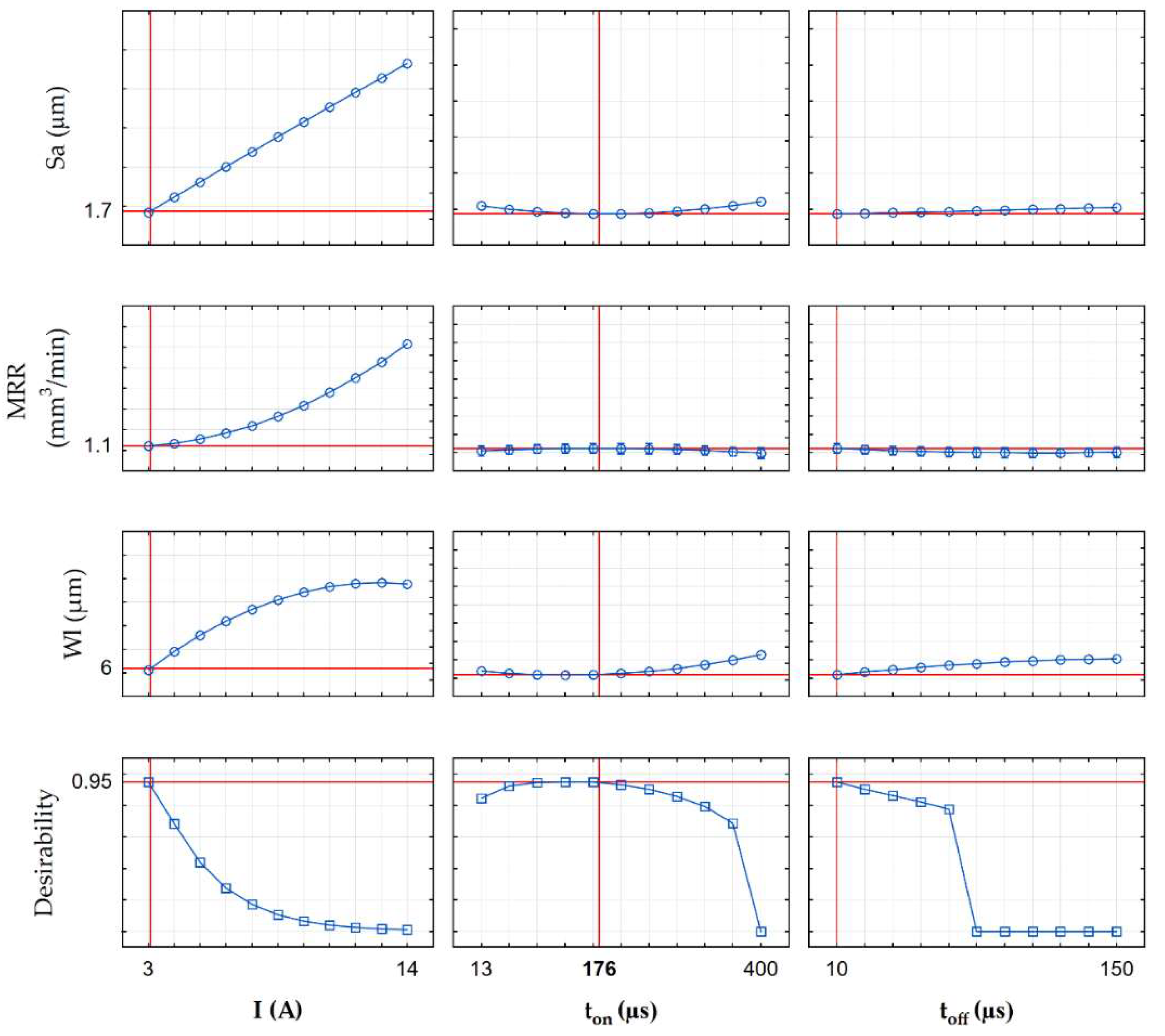
| Optimal EDM Parameters | Summary of Values Obtained in Optimization | ||||
|---|---|---|---|---|---|
| Response | Predicted | Experimental Verification | Error% | ||
| Finishing | I = 3 A ton = 176 µs toff = 10 µs | Sa (µm) | 1.7 | 1.8 | 6 |
| WL (µm) | 6 | 6.3 | 5 | ||
| MRR (mm3/min) | 1.13 | 1.06 | 6 | ||
| Semi- finishing | I = 14 A ton = 52 µs toff = 24 µs | Sa (µm) | 5.2 | 5.4 | 4 |
| WL (µm) | 15 | 15.8 | 5 | ||
| MRR (mm3/min) | 14.5 | 15 | 3 | ||
| Roughing | I = 14 A ton = 361 µs toff = 24 µs | Sa (µm) | 12.1 | 12.7 | 5 |
| WL (µm) | 28.8 | 30.5 | 6 | ||
| MRR (mm3/min) | 29.2 | 28.1 | 4 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Świercz, R.; Oniszczuk-Świercz, D.; Chmielewski, T. Multi-Response Optimization of Electrical Discharge Machining Using the Desirability Function. Micromachines 2019, 10, 72. https://doi.org/10.3390/mi10010072
Świercz R, Oniszczuk-Świercz D, Chmielewski T. Multi-Response Optimization of Electrical Discharge Machining Using the Desirability Function. Micromachines. 2019; 10(1):72. https://doi.org/10.3390/mi10010072
Chicago/Turabian StyleŚwiercz, Rafał, Dorota Oniszczuk-Świercz, and Tomasz Chmielewski. 2019. "Multi-Response Optimization of Electrical Discharge Machining Using the Desirability Function" Micromachines 10, no. 1: 72. https://doi.org/10.3390/mi10010072
APA StyleŚwiercz, R., Oniszczuk-Świercz, D., & Chmielewski, T. (2019). Multi-Response Optimization of Electrical Discharge Machining Using the Desirability Function. Micromachines, 10(1), 72. https://doi.org/10.3390/mi10010072







