Microswimmer Propulsion by Two Steadily Rotating Helical Flagella
Abstract
1. Introduction
2. Modelling and Methods
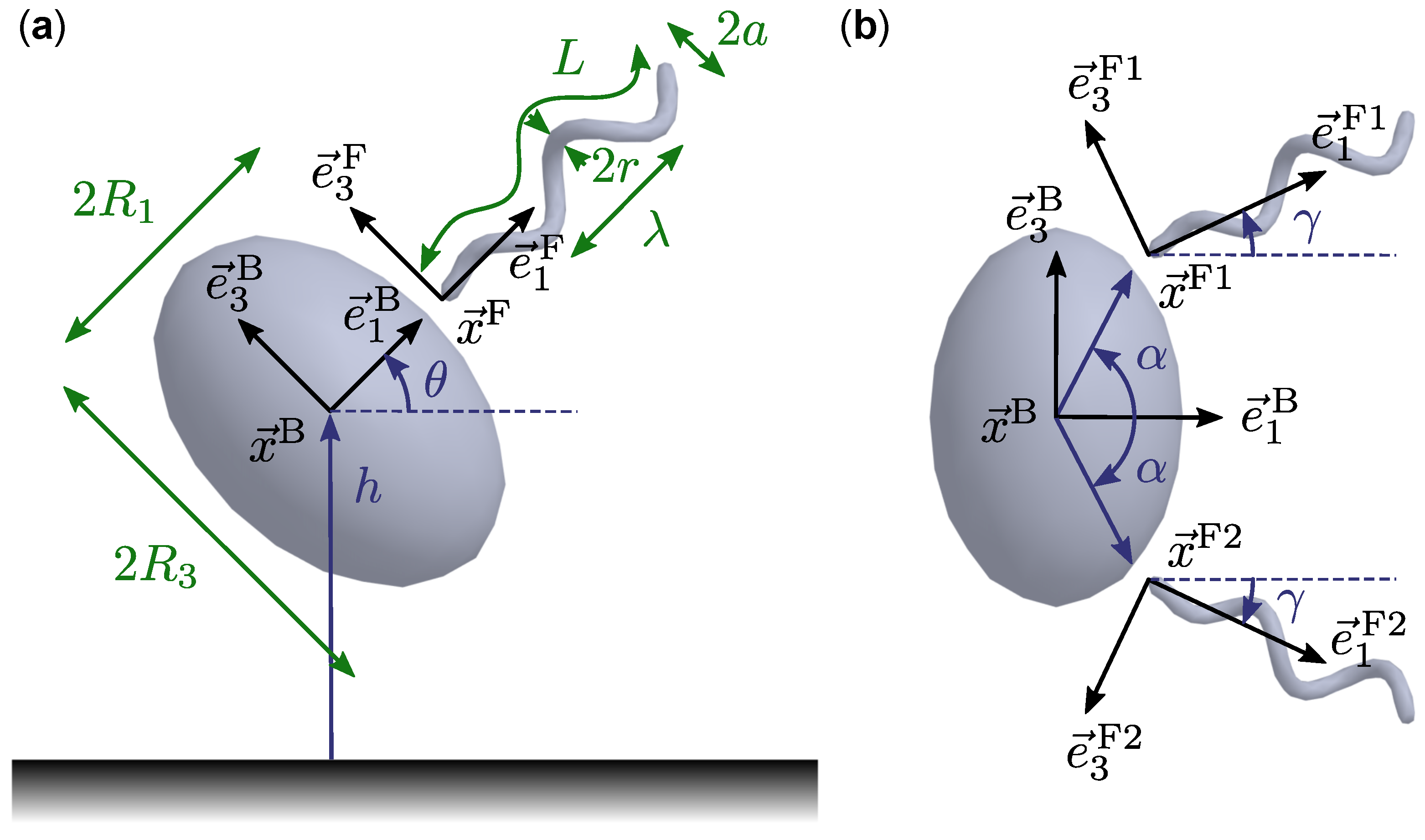
2.1. Geometric and Kinematic Model
2.2. Dynamics
2.3. Numerical Methods
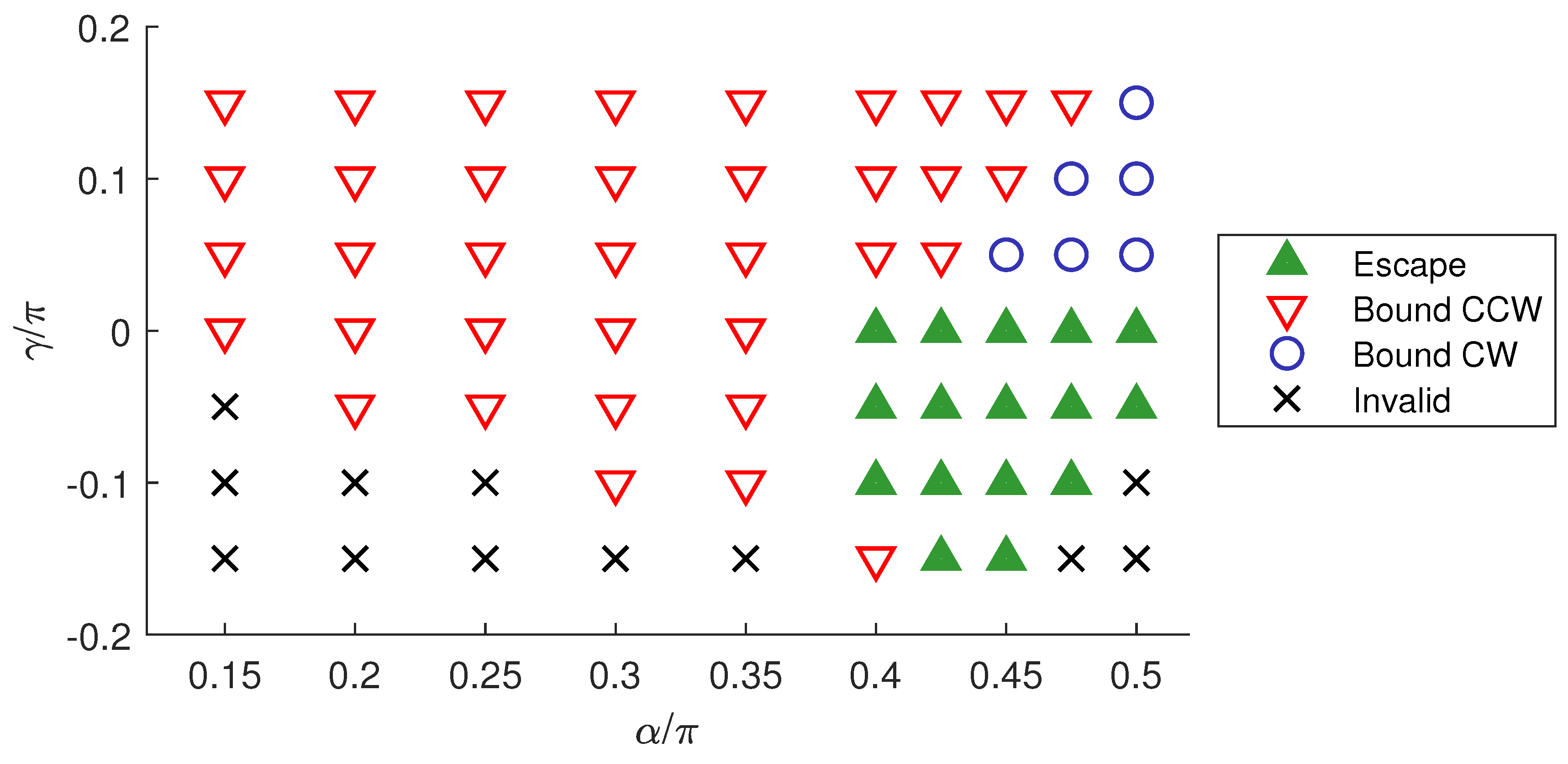
3. Results
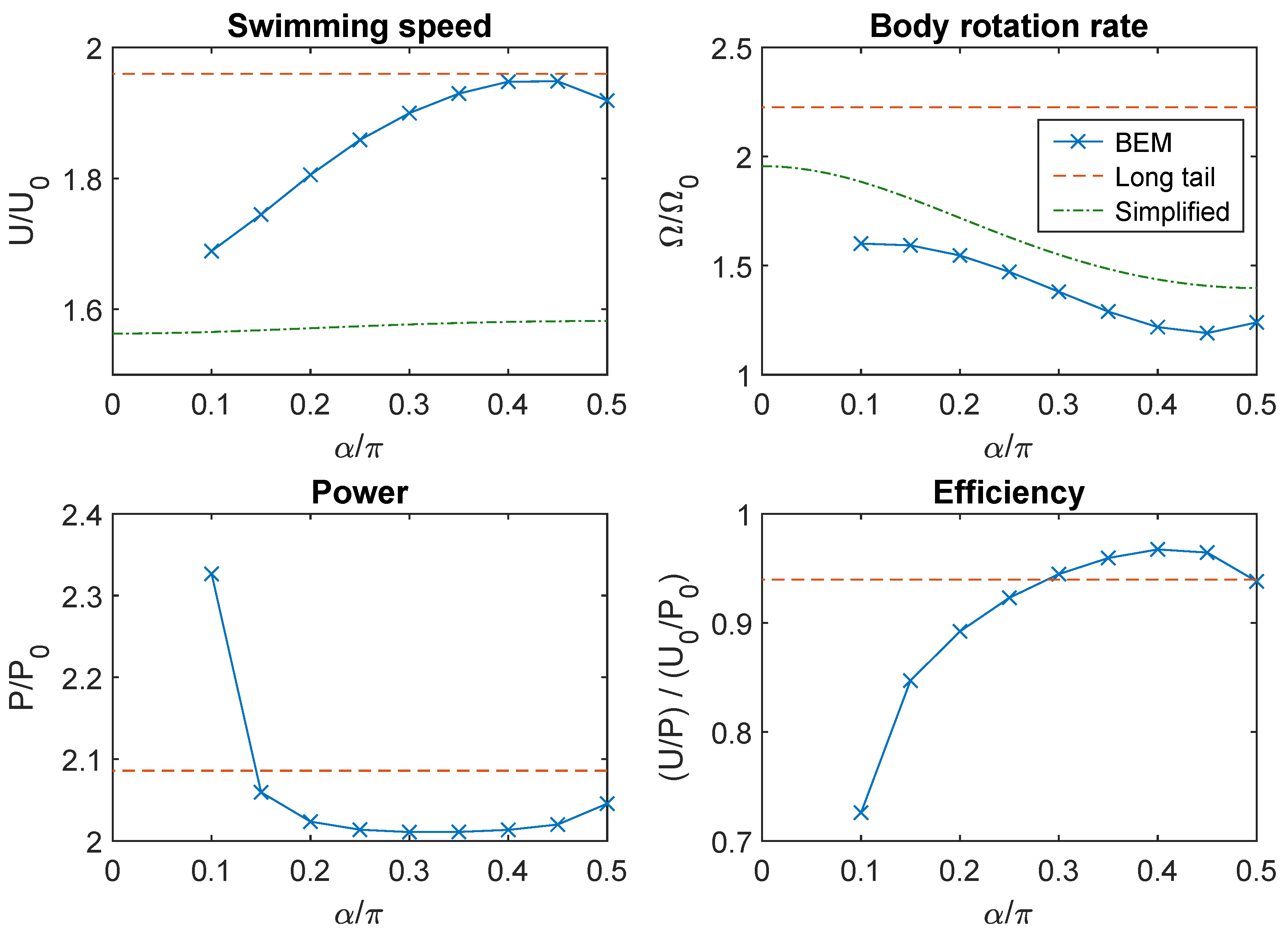
3.1. Swimming in Bulk Fluid
3.2. Analytical Results from a Simplified Hydrodynamic Model
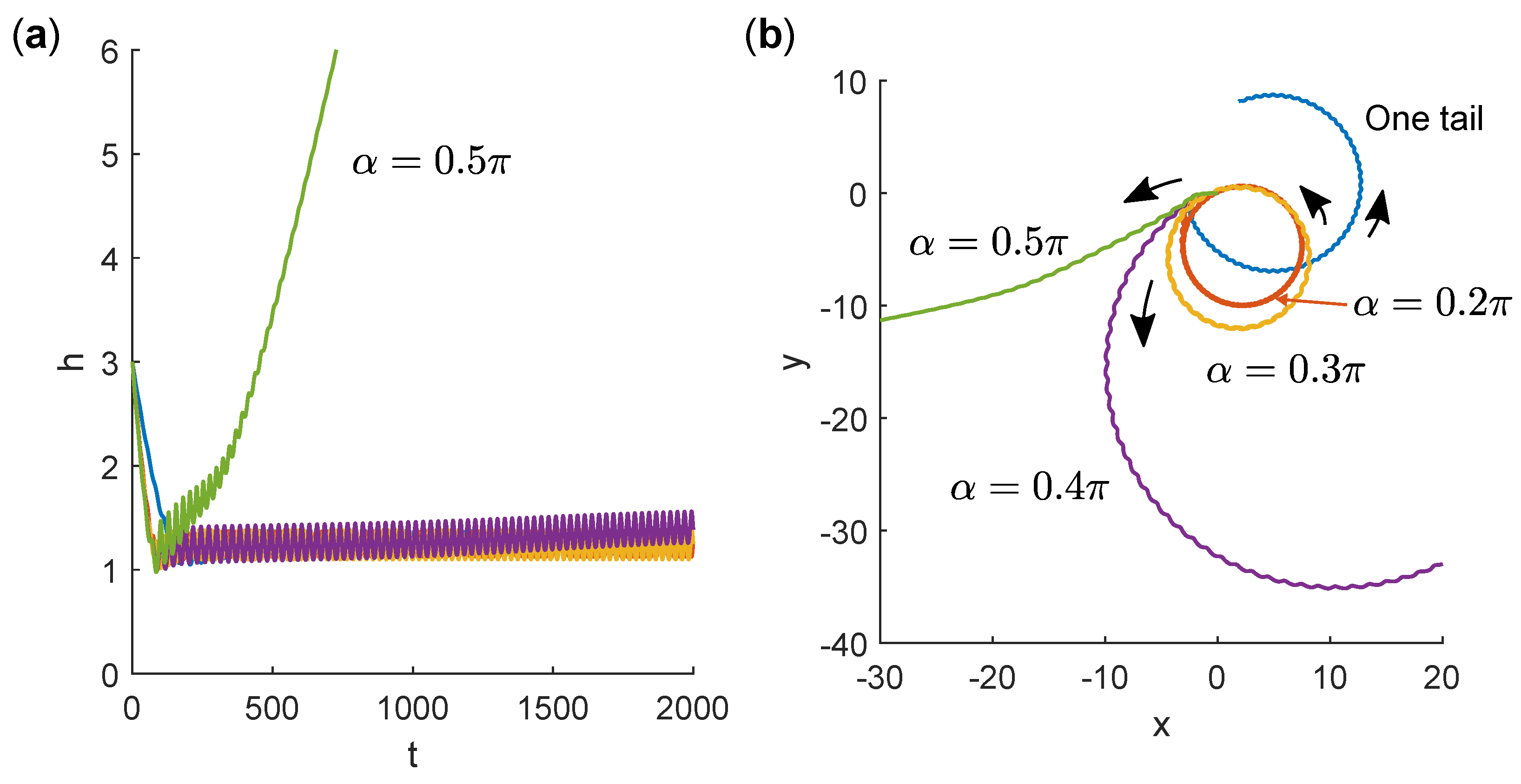
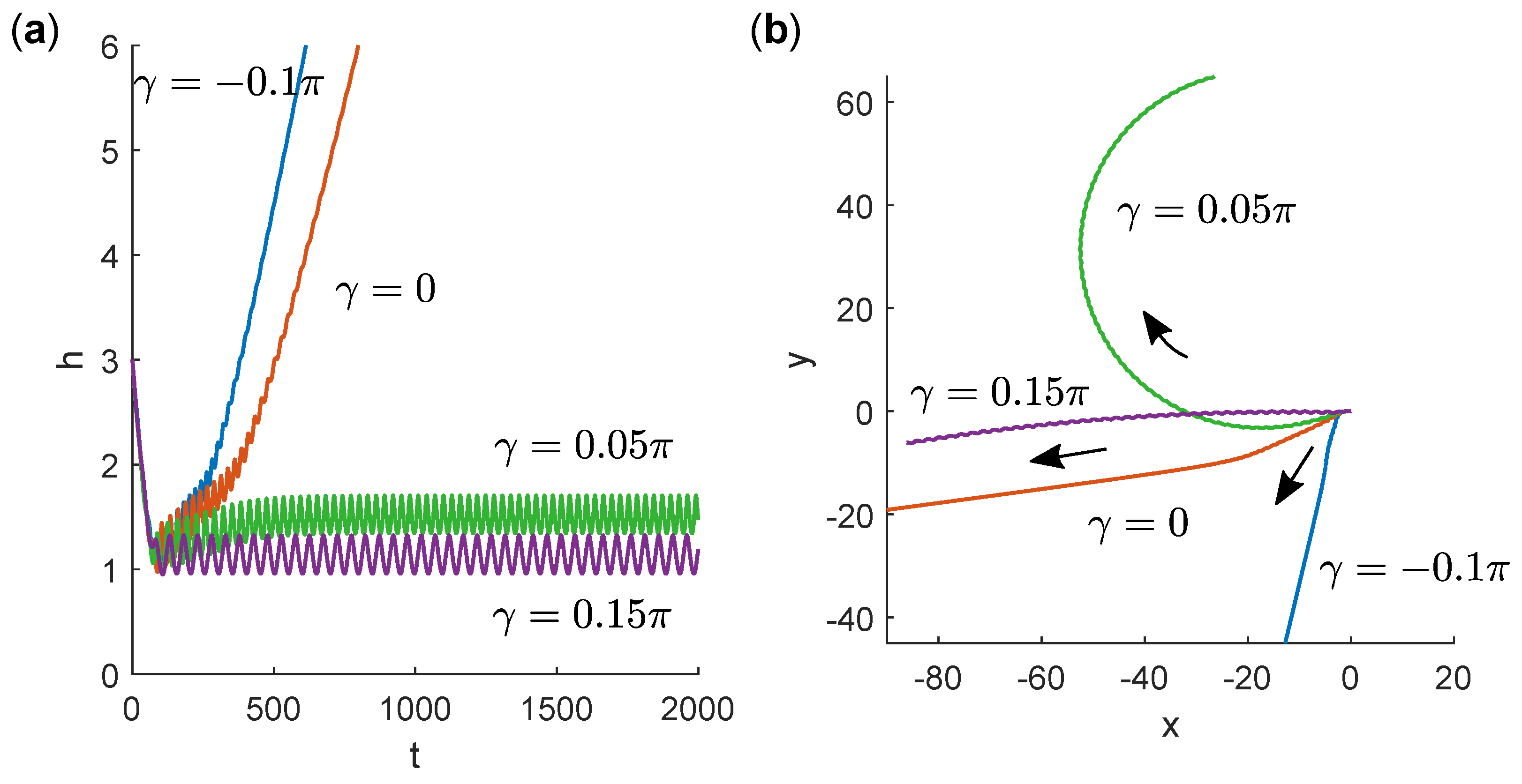
3.3. Swimming Near a No-Slip Wall
4. Discussion
Supplementary Materials
Acknowledgments
Conflicts of Interest
References
- Taylor, G. Analysis of the Swimming of Microscopic Organisms. Proc. R. Soc. Lond. Ser. A 1951, 209, 447–461. [Google Scholar] [CrossRef]
- Peyer, K.E.; Zhang, L.; Nelson, B.J. Bio-inspired magnetic swimming microrobots for biomedical applications. Nanoscale 2013, 5, 1259–1272. [Google Scholar] [CrossRef] [PubMed]
- Martel, S. Swimming microorganisms acting as nanorobots versus artificial nanorobotic agents: A perspective view from an historical retrospective on the future of medical nanorobotics in the largest known three-dimensional biomicrofluidic networks. Biomicrofluidics 2016, 10, 021301. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.V.; Hosseinidoust, Z.; Park, B.W.; Yasa, O.; Sitti, M. Microemulsion-Based Soft Bacteria-Driven Microswimmers for Active Cargo Delivery. ACS Nano 2017, 11, 9759–9769. [Google Scholar] [CrossRef] [PubMed]
- Klumpp, S.; Lefèvre, C.T.; Bennet, M.; Faivre, D. Swimming with magnets: From biological organisms to synthetic devices. Phys. Rep. 2018. [Google Scholar] [CrossRef]
- Alapan, Y.; Yasa, O.; Yigit, B.; Yasa, I.C.; Erkoc, P.; Sitti, M. Microrobotics and Microorganisms: Biohybrid Autonomous Cellular Robots. Annu. Rev. Control Robot. Auton. Syst. 2019, 2. [Google Scholar] [CrossRef]
- Pan, Y.; Lin, W.; Li, J.; Wu, W.; Tian, L.; Deng, C.; Liu, Q.; Zhu, R.; Winklhofer, M.; Petersen, N. Reduced Efficiency of Magnetotaxis in Magnetotactic Coccoid Bacteria in Higher than Geomagnetic Fields. Biophys. J. 2009, 97, 986–991. [Google Scholar] [CrossRef]
- Yazdi, S.R.; Nosrati, R.; Stevens, C.A.; Vogel, D.; Davies, P.L.; Escobedo, C. Magnetotaxis Enables Magnetotactic Bacteria to Navigate in Flow. Small 2018, 14, 1702982. [Google Scholar] [CrossRef]
- Santomauro, G.; Singh, A.V.; Park, B.W.; Mohammadrahimi, M.; Erkoc, P.; Goering, E.; Schütz, G.; Sitti, M.; Bill, J. Incorporation of Terbium into a Microalga Leads to Magnetotactic Swimmers. Adv. Biosys. 2018, 2, 1800039. [Google Scholar] [CrossRef]
- Lefèvre, C.T.; Bernadac, A.; Yu-Zhang, K.; Pradel, N.; Wu, L.F. Isolation and characterization of a magnetotactic bacterial culture from the Mediterranean Sea. Environ. Microbiol. 2009, 11, 1646–1657. [Google Scholar] [CrossRef]
- Zhang, S.D.; Petersen, N.; Zhang, W.J.; Cargou, S.; Ruan, J.; Murat, D.; Santini, C.L.; Song, T.; Kato, T.; Notareschi, P.; Li, Y.; Namba, K.; Gué, A.M.; Wu, L.F. Swimming behaviour and magnetotaxis function of the marine bacterium strain MO-1: Magnetotaxis of MO-1. Environ. Microbiol. Rep. 2014, 6, 14–20. [Google Scholar] [CrossRef] [PubMed]
- Ruan, J.; Kato, T.; Santini, C.L.; Miyata, T.; Kawamoto, A.; Zhang, W.J.; Bernadac, A.; Wu, L.F.; Namba, K. Architecture of a flagellar apparatus in the fast-swimming magnetotactic bacterium MO-1. Proc. Natl. Acad. Sci. USA 2012, 109, 20643–20648. [Google Scholar] [CrossRef] [PubMed]
- Higdon, J.J.L. The hydrodynamics of flagellar propulsion: helical waves. J. Fluid Mech. 1979, 94, 331–351. [Google Scholar] [CrossRef]
- Phan-Thien, N.; Tran-Cong, T.; Ramia, M. A boundary-element analysis of flagellar propulsion. J. Fluid Mech. 1987, 184, 533–549. [Google Scholar] [CrossRef]
- Shum, H.; Gaffney, E.A.; Smith, D.J. Modelling bacterial behaviour close to a no-slip plane boundary: The influence of bacterial geometry. Proc. R. Soc. A 2010, 466, 1725–1748. [Google Scholar] [CrossRef]
- Giacché, D.; Ishikawa, T.; Yamaguchi, T. Hydrodynamic entrapment of bacteria swimming near a solid surface. Phys. Rev. E 2010, 82, 056309. [Google Scholar] [CrossRef]
- Berke, A.P.; Turner, L.; Berg, H.C.; Lauga, E. Hydrodynamic Attraction of Swimming Microorganisms by Surfaces. Phys. Rev. Lett. 2008, 101, 038102. [Google Scholar] [CrossRef] [PubMed]
- Lauga, E.; DiLuzio, W.R.; Whitesides, G.M.; Stone, H.A. Swimming in Circles: Motion of Bacteria near Solid Boundaries. Biophys. J. 2006, 90, 400–412. [Google Scholar] [CrossRef]
- Lin, H.Y. Motility and Intelligence of Microorganisms in Microconfined Networks. Master’s Thesis, McGill University, Montreal, QC, Canada, 2017. [Google Scholar]
- Hyon, Y.; Powers, T.R.; Stocker, R.; Fu, H.C. The wiggling trajectories of bacteria. J. Fluid Mech. 2012, 705, 58–76. [Google Scholar] [CrossRef]
- Yang, C.; Chen, C.; Ma, Q.; Wu, L.; Song, T. Dynamic Model and Motion Mechanism of Magnetotactic Bacteria with Two Lateral Flagellar Bundles. J. Bionic Eng. 2012, 9, 200–210. [Google Scholar] [CrossRef]
- Kanehl, P.; Ishikawa, T. Fluid mechanics of swimming bacteria with multiple flagella. Phys. Rev. E 2014, 89, 042704. [Google Scholar] [CrossRef] [PubMed]
- Riley, E.E.; Das, D.; Lauga, E. Swimming of peritrichous bacteria is enabled by an elastohydrodynamic instability. arXiv, 2018; arXiv:1806.01902. [Google Scholar] [CrossRef] [PubMed]
- Ramia, M.; Tullock, D.; Phan-Thien, N. The role of hydrodynamic interaction in the locomotion of microorganisms. Biophys. J. 1993, 65, 755–778. [Google Scholar] [CrossRef]
- Lefèvre, C.T.; Santini, C.L.; Bernadac, A.; Zhang, W.J.; Li, Y.; Wu, L.F. Calcium ion-mediated assembly and function of glycosylated flagellar sheath of marine magnetotactic bacterium. Mol. Microbiol. 2010, 78, 1304–1312. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, T.; Hota, M. Interaction of two swimming Paramecia. J. Exp. Biol. 2006, 209, 4452–4463. [Google Scholar] [CrossRef] [PubMed]
- Shum, H.; Yeomans, J.M. Entrainment and scattering in microswimmer-colloid interactions. Phys. Rev. Fluids 2017, 2, 113101. [Google Scholar] [CrossRef]
- Kim, S.; Karrila, S.J. Microhydrodynamics: Principles and Selected Applications; Dover Publications: Mineola, NY, USA, 2005. [Google Scholar]
- Blake, J.R. A note on the image system for a stokeslet in a no-slip boundary. Math. Proc. Camb. Philos. Soc. 1971, 70, 303–310. [Google Scholar] [CrossRef]
- Shum, H.; Gaffney, E.A. The effects of flagellar hook compliance on motility of monotrichous bacteria: A modeling study. Phys. Fluids 2012, 24, 061901. [Google Scholar] [CrossRef]
- Purcell, E.M. The efficiency of propulsion by a rotating flagellum. Proc. Natl. Acad. Sci. USA 1997, 94, 11307–11311. [Google Scholar] [CrossRef]
- Happel, J.; Brenner, H. Low Reynolds Number Hydrodynamics: With Special Applications to Particulate Media; Prentice-Hall: Upper Saddle River, NJ, USA, 1965. [Google Scholar]
- Chwang, A.T.; Wu, T.Y.T. Hydromechanics of Low-Reynolds-Number Flow. Part 2. Singularity Method for Stokes Flows. J. Fluid Mech. 1975, 67, 787–815. [Google Scholar] [CrossRef]
- Gray, J.; Hancock, G.J. The Propulsion of Sea-Urchin Spermatozoa. J. Exp. Biol. 1955, 32, 802–814. [Google Scholar]
- Shum, H.; Gaffney, E.A. Hydrodynamic analysis of flagellated bacteria swimming near one and between two no-slip plane boundaries. Phys. Rev. E 2015, 91, 033012. [Google Scholar] [CrossRef] [PubMed]
- Powers, T.R. Role of body rotation in bacterial flagellar bundling. Phys. Rev. E 2002, 65, 040903. [Google Scholar] [CrossRef] [PubMed]
- Vogel, R.; Stark, H. Motor-driven bacterial flagella and buckling instabilities. Eur. Phys. J. E 2012, 35, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Jawed, M.; Khouri, N.; Da, F.; Grinspun, E.; Reis, P. Propulsion and Instability of a Flexible Helical Rod Rotating in a Viscous Fluid. Phys. Rev. Lett. 2015, 115, 168101. [Google Scholar] [CrossRef] [PubMed]
- Steinberger, B.; Petersen, N.; Petermann, H.; Weiss, D.G. Movement of magnetic bacteria in time-varying magnetic fields. J. Fluid Mech. 1994, 273, 189. [Google Scholar] [CrossRef]
| Description | Symbol | Value (Dimensionless) | Value (Dimensional) |
|---|---|---|---|
| Body short semi-axis | 0.874 | 0.65 m | |
| Body aspect ratio | 1.50 | 1.50 | |
| Flagellum length | L | 3.00 | 2.2 m |
| Filament radius | r | 0.067 | 50 nm |
| Helical amplitude | a | 0.200 | 0.15 m |
| Helical pitch | 1.00 | 0.74 m | |
| Amplitude growth factor | 2.8 m | ||
| Body–flagellum gap | 100 nm |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shum, H. Microswimmer Propulsion by Two Steadily Rotating Helical Flagella. Micromachines 2019, 10, 65. https://doi.org/10.3390/mi10010065
Shum H. Microswimmer Propulsion by Two Steadily Rotating Helical Flagella. Micromachines. 2019; 10(1):65. https://doi.org/10.3390/mi10010065
Chicago/Turabian StyleShum, Henry. 2019. "Microswimmer Propulsion by Two Steadily Rotating Helical Flagella" Micromachines 10, no. 1: 65. https://doi.org/10.3390/mi10010065
APA StyleShum, H. (2019). Microswimmer Propulsion by Two Steadily Rotating Helical Flagella. Micromachines, 10(1), 65. https://doi.org/10.3390/mi10010065





