Multiple Laser Stripe Scanning Profilometry Based on Microelectromechanical Systems Scanning Mirror Projection
Abstract
1. Introduction
2. Methods and Principles
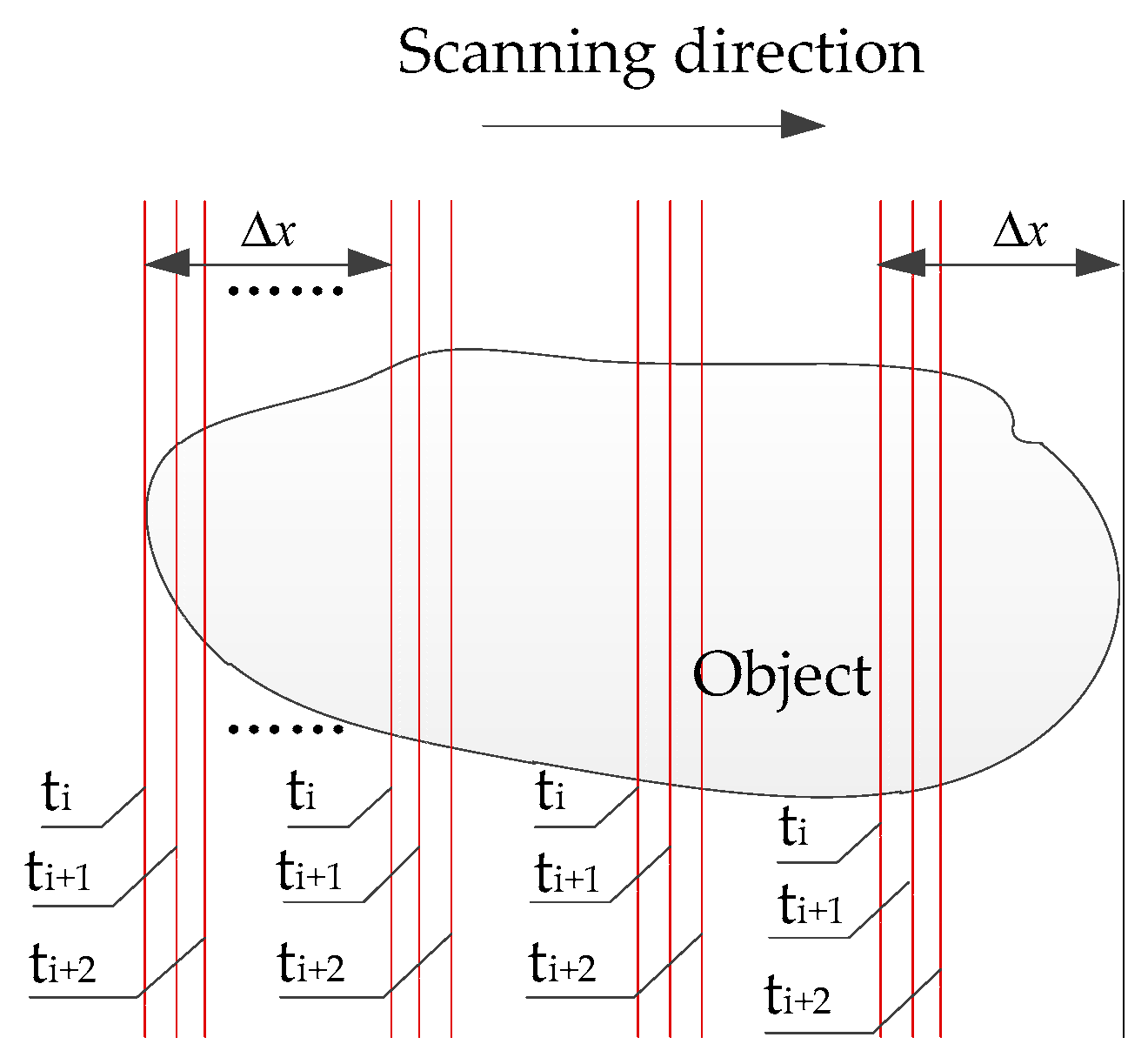
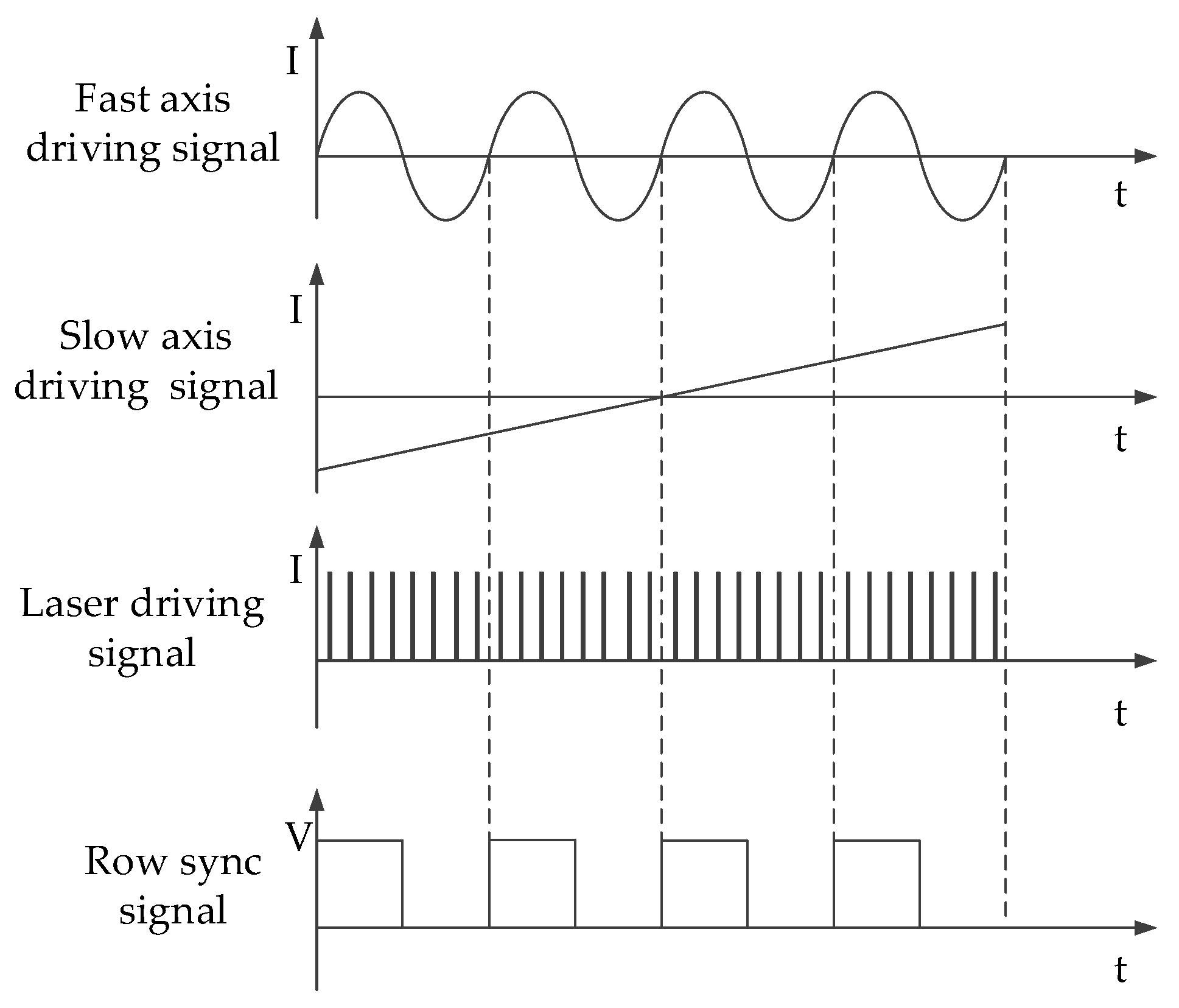
2.1. Multiple Laser Stripe Coding Method
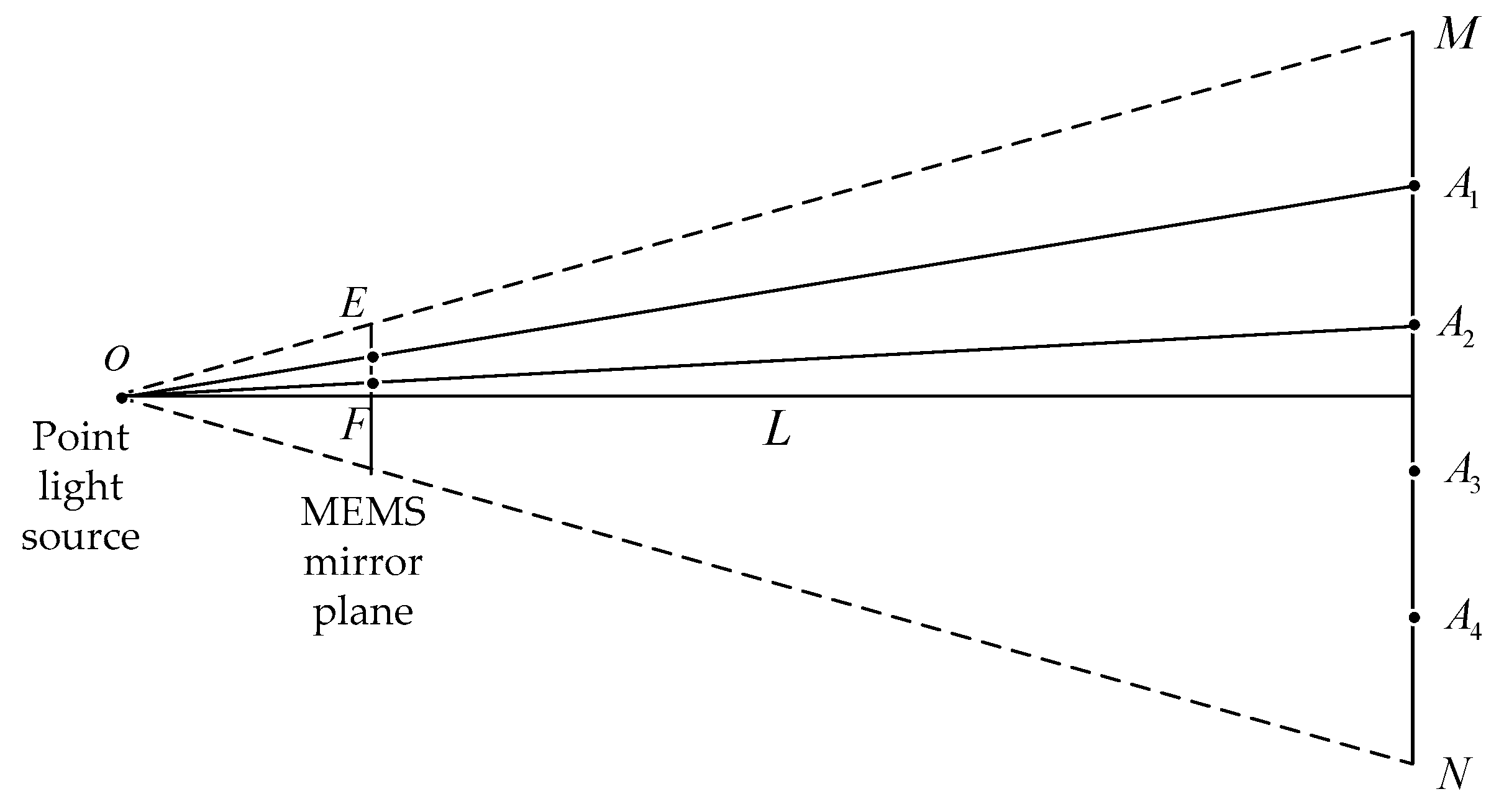
2.2. 3D Reconstruction Mechanism
3. Experiment and Analysis
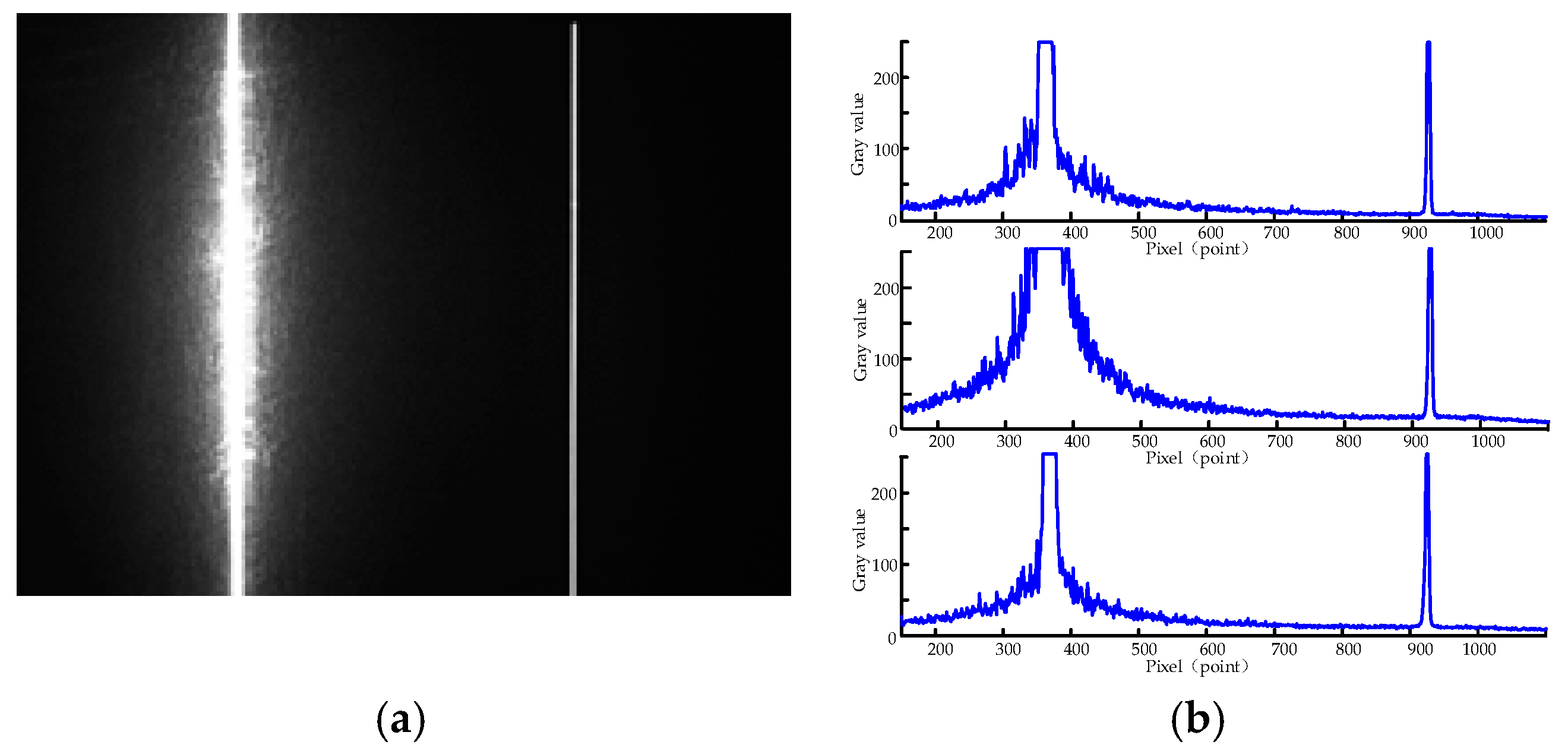
3.1. Robust Test
3.2. Reconstruction of A Face Plaster Model
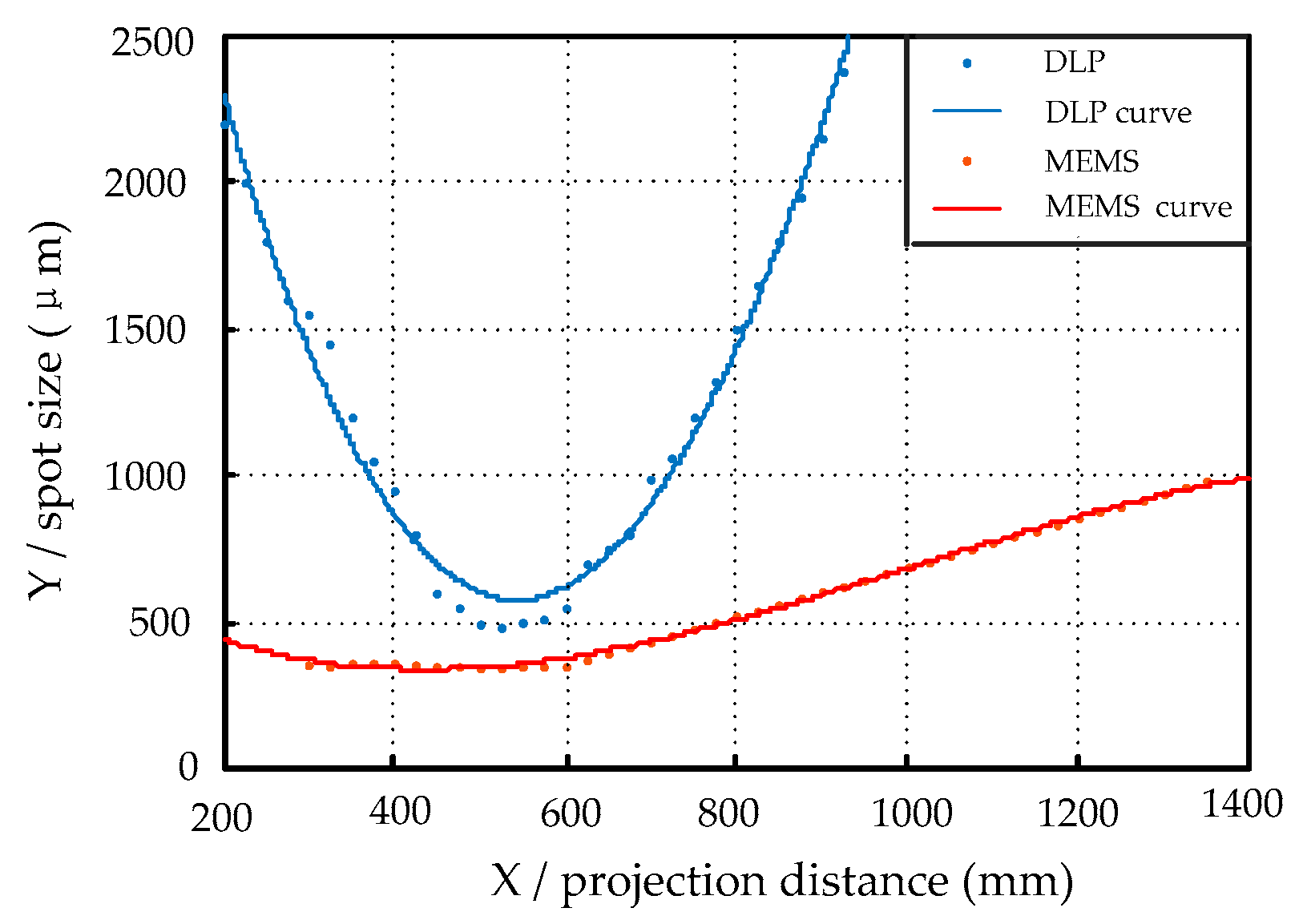
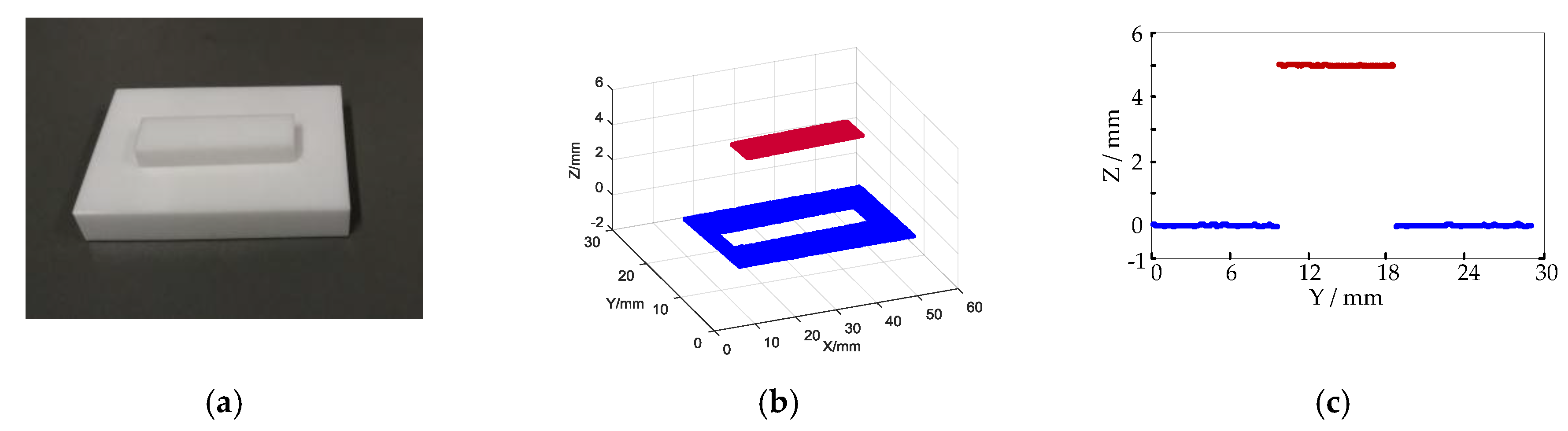
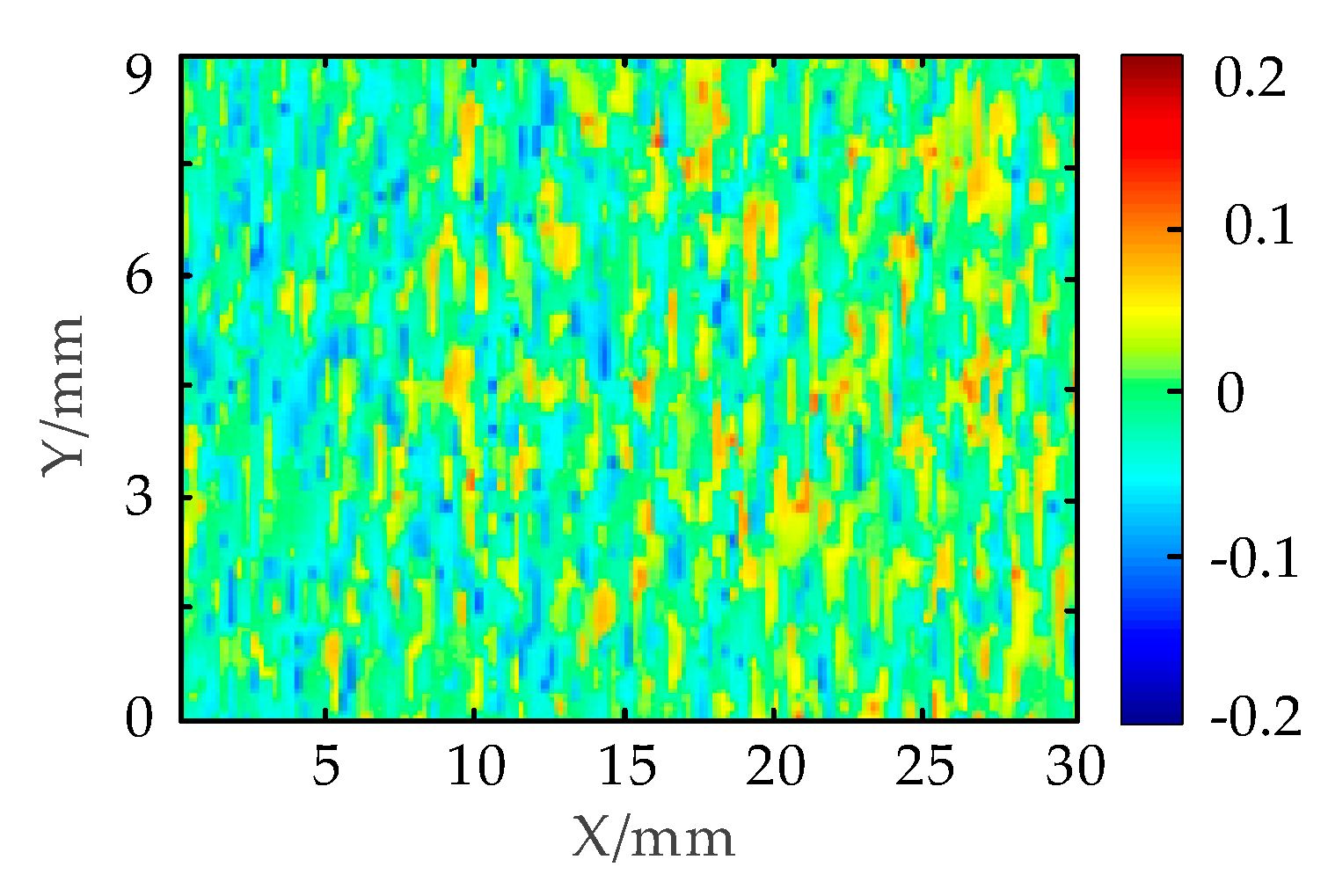
3.3. Accuracy Test
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gong, Z.; Sun, J.; Zhang, G. Dynamic structured-light measurement for wheel diameter based on the cycloid constraint. Appl. Opt. 2016, 55, 198–207. [Google Scholar] [CrossRef]
- Usamentiaga, R.; Molleda, J.; Garcia, D.F. Structured-Light Sensor Using Two Laser Stripes for 3D Reconstruction without Vibrations. Sensors 2014, 14, 20041–20063. [Google Scholar] [CrossRef]
- Nguyen, H.; Nguyen, D.; Wang, Z.; Kieu, H.; Le, M. Real-time, high-accuracy 3D imaging and shape measurement. Appl. Opt. 2015, 54, 9–17. [Google Scholar] [CrossRef]
- Lochner, S.J.; Huissoon, J.P.; Bedi, S.S. Development of a patient-specific anatomical foot model from structured light scan data. Comput. Methods Biomech. Biomed. Eng. 2012, 17, 1198–1205. [Google Scholar] [CrossRef]
- Feng, S.; Zhang, Y.; Chen, Q.; Zuo, C.; Li, R.; Shen, G. General solution for high dynamic range three-dimensional shape measurement using the fringe projection technique. Opt. Lasers Eng. 2014, 59, 56–71. [Google Scholar] [CrossRef]
- Trinderup, C.H.; Kim, Y.H.B. Fresh meat color evaluation using a structured light imaging system. Food Res. Int. 2015, 71, 100–107. [Google Scholar] [CrossRef]
- Verdú, S.; Ivorra, E.; Sánchez, A.J.; Barat, J.M.; Grau, R. Relationship between fermentation behavior, measured with a 3D vision structured light technique and the internal structure of bread. Food Eng. 2015, 146, 227–233. [Google Scholar] [CrossRef]
- He, L.; Wu, S.; Wu, C. Robust laser stripe extraction for three-dimensional reconstruction based on a cross-structured light sensor. Appl. Opt. 2017, 56, 823–832. [Google Scholar] [CrossRef]
- Li, B.; Gibson, J.; Middendorf, J.; Wang, Y.; Zhang, S. Comparison between LCOS projector and DLP projector in generating digital sinusoidal fringe patterns. In Proceedings of the 2013 Conference on Dimensional Optical Metrology and Inspection for Practical Applications, San Diego, CA, USA, 25–26 August 2013. [Google Scholar]
- Kannegulla, A.; Shams, M.I.B.; Liu, L.; Cheng, L. Photo-induced spatial modulation of THz waves: Opportunities and limitations. Opt. Express 2015, 23, 32098–32112. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Pan, J. High contrast ratio and compact-sized prism for DLP projection system. Opt. Express 2014, 22, 17016–17029. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; van der Weide, D.; Oliver, J. Superfast phase-shifting method for 3-D shape measurement. Opt. Express 2010, 18, 9684–9689. [Google Scholar] [CrossRef]
- Zuo, C.; Chen, Q.; Gu, G.; Feng, S.; Feng, F. High-speed three-dimensional profilometry for multiple objects with complex shapes. Opt. Express 2012, 20, 19493–19510. [Google Scholar] [CrossRef]
- Zhou, X.; Yang, T.; Zou, H.; Zhao, H. Multivariate empirical mode decomposition approach for adaptive denoising of fringe patterns. Opt. Lett. 2012, 37, 1904–1906. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhang, J.; Luo, B. High dynamic range 3D measurement based on spectral modulation and hyperspectral imaging. Opt. Express 2018, 26, 34442–34450. [Google Scholar] [CrossRef]
- Sun, Q.; Chen, J.; Li, C. A robust method to extract a laser stripe centre based on grey level moment. Opt. Lasers Eng. 2014, 59, 56–71. [Google Scholar] [CrossRef]
- Yin, X.Q.; Tao, W.; Feng, Y.Y.; Gao, Q.; He, Q.Z.; Zhao, H. Laser stripe extraction method in industrial environments utilizing self-adaptive convolution technique. Appl. Opt. 2017, 56, 2653–2660. [Google Scholar] [CrossRef]
- Usamentiaga, R.; Garcia, D.; Molleda, J.; Bulnes, F.; Bonet, G. Vibrations in steel strips: Effects on flatness measurement and filtering. IEEE Trans. Ind. Appl. 2014, 50, 3103–3112. [Google Scholar] [CrossRef]
- Petersen, K.E. Silicon torsional scanning mirror. IBM J. Res. Dev. 1980, 24, 631–637. [Google Scholar] [CrossRef]
- Takashima, Y.; Hellman, B.; Rodriguez, J.; Chen, G.; Smith, B.; Gin, A.; Espinoza, A.; Winkler, P.; Perl, C.; Luo, C. MEMS-based Imaging LIDAR. In Proceedings of the Light, Energy and the Environment Congress 2018 in Sentosa Island, Singapore, 5–8 November 2018. [Google Scholar]
- Tan, Y.; Dong, R. Nonlinear Model Based Control of MEMS Micro-Mirror. In Proceedings of the 2018 14th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications (MESA), Oulu, Finland, 2–4 July 2018. [Google Scholar]
- Sun, H.B.; Kawata, S. Two-Photon Laser Precision Microfabrication and Its Applications to Micro–Nano Devices and Systems. J. Lightw. Technol. 2003, 21, 624–633. [Google Scholar]
- Liu, J.; Wang, J.; Wang, Y.; Tian, D.; Zheng, Q.; Lin, X.; Wang, L.; Yang, Q. Research on the compensation of laser launch optics to improve the performance of the LGS spot. Appl. Opt. 2018, 57, 648–651. [Google Scholar] [CrossRef]
- Qi, W.; Chen, Q.; Guo, H.; XieD, H.; Xi, L. Miniaturized Optical Resolution Photoacoustic Microscope Based on a Microelectromechanical Systems Scanning Mirror. Micromachines 2018, 9, 288. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Zhou, P.; Wang, T.; He, J.; Yu, H.; Shen, W. A Large-Size MEMS Scanning Mirror for Speckle Reduction Application. Micromachines 2017, 8, 140. [Google Scholar] [CrossRef]
- Isamoto, K.; Totsuka, K.; Suzuki, T.; Sakai, T.; Morosawa, A.; Chong, C.; Fujita, H.; Toshiyoshi, H. A high speed MEMS scanner for 140-kHz SS-OCT. In Proceedings of the 2018 International Conference on Optical MEMS and Nanophotonics(OMN), Lausanne, Switzerland, 29 July–2 August 2018. [Google Scholar]
- Isamoto, K.; Totsuka, K.; Sakai, T.; Suzuki, T.; Morosawa, A.; Chong, C.; Fujita, H.; Toshiyoshi, H. High speed MEMS scanner based swept source laser for SS-OCT. IEEE J. Trans. Sens. Micromach. MEMS Packag. Microfabr. Technol. 2012, 132, 254–260. [Google Scholar] [CrossRef]
- Niclass, C.; Ito, K.; Soga, M.; Matsubara, H.; Aoyagi, I.; Kato, S.; Kagami, M. Design and characterization of a 256 × 64-pixel single-photon imager in CMOS for a MEMS-based laser scanning time-of-flight sensor. Opt. Express 2012, 20, 11863–11881. [Google Scholar] [CrossRef]
- Liu, L.; Xie, H. 3-D Confocal Laser Scanning Microscopy Based on a Full-MEMS Scanning System. IEEE Photonics Technol. Lett. 2013, 25, 1478–1480. [Google Scholar] [CrossRef]
- Pan, Y.; Xie, H.; Fedder, G.K. Endoscopic optical coherence tomography based on a microelectromechanical mirror. Opt. Lett. 2001, 26, 1966–1968. [Google Scholar] [CrossRef]
- Miyajima, H.; Asaoka, N.; Isokawa, T.; Ogata, M.; Aoki, Y.; Imai, M.; Fujimori, O.; Katashiro, M.; Matsumoto, K. A MEMS electromagnetic optical scanner for a commercial confocal laser scanning microscope. J. Microelectromech. 2003, 12, 243–251. [Google Scholar] [CrossRef]
- Raboud, D.; Barras, T.; Conte, F.L.; Fabre, L.; Kilcher, L.; Kechana, F.; Abelé, N.; Kayal, M. MEMS based color-VGA micro-projector system. Procedia Eng. 2010, 5, 260–263. [Google Scholar] [CrossRef]
- Khayatzadeh, R.; Civitci, F.; Ferhanoglu, O.; Urey, H. Scanning fiber microdisplay: design, implementation, and comparison to MEMS mirror-based scanning displays. Opt. Express 2018, 26, 5576–5590. [Google Scholar] [CrossRef]
- Tanguy, Q.A.; Bargiel, S.; Xie, H.; Passilly, N.; Barthès, M.; Gaiffe, O.; Rutkowski, J.; Lutz, P.; Gorecki, C. Design and fabrication of a 2-Axis Electrothermal MEMS Micro-scanner for optical Coherence Tomography. Micromachines 2017, 8, 146. [Google Scholar] [CrossRef]
- Zhao, B.H.; Wang, B.X.; Zhang, J.; Luo, X.Z. Extraction of laser stripe center on rough metal surface. Opt. Precis. Eng. 2011, 19, 2138–2145. [Google Scholar] [CrossRef]




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, G.; Zhou, X.; Zhang, G.; Zhang, C.; Li, D.; Wang, G. Multiple Laser Stripe Scanning Profilometry Based on Microelectromechanical Systems Scanning Mirror Projection. Micromachines 2019, 10, 57. https://doi.org/10.3390/mi10010057
Hu G, Zhou X, Zhang G, Zhang C, Li D, Wang G. Multiple Laser Stripe Scanning Profilometry Based on Microelectromechanical Systems Scanning Mirror Projection. Micromachines. 2019; 10(1):57. https://doi.org/10.3390/mi10010057
Chicago/Turabian StyleHu, Gailing, Xiang Zhou, Guanliang Zhang, Chunwei Zhang, Dong Li, and Gangfeng Wang. 2019. "Multiple Laser Stripe Scanning Profilometry Based on Microelectromechanical Systems Scanning Mirror Projection" Micromachines 10, no. 1: 57. https://doi.org/10.3390/mi10010057
APA StyleHu, G., Zhou, X., Zhang, G., Zhang, C., Li, D., & Wang, G. (2019). Multiple Laser Stripe Scanning Profilometry Based on Microelectromechanical Systems Scanning Mirror Projection. Micromachines, 10(1), 57. https://doi.org/10.3390/mi10010057




