Magnetically Induced Flow Focusing of Non-Magnetic Microparticles in Ferrofluids under Inclined Magnetic Fields
Abstract
:1. Introduction
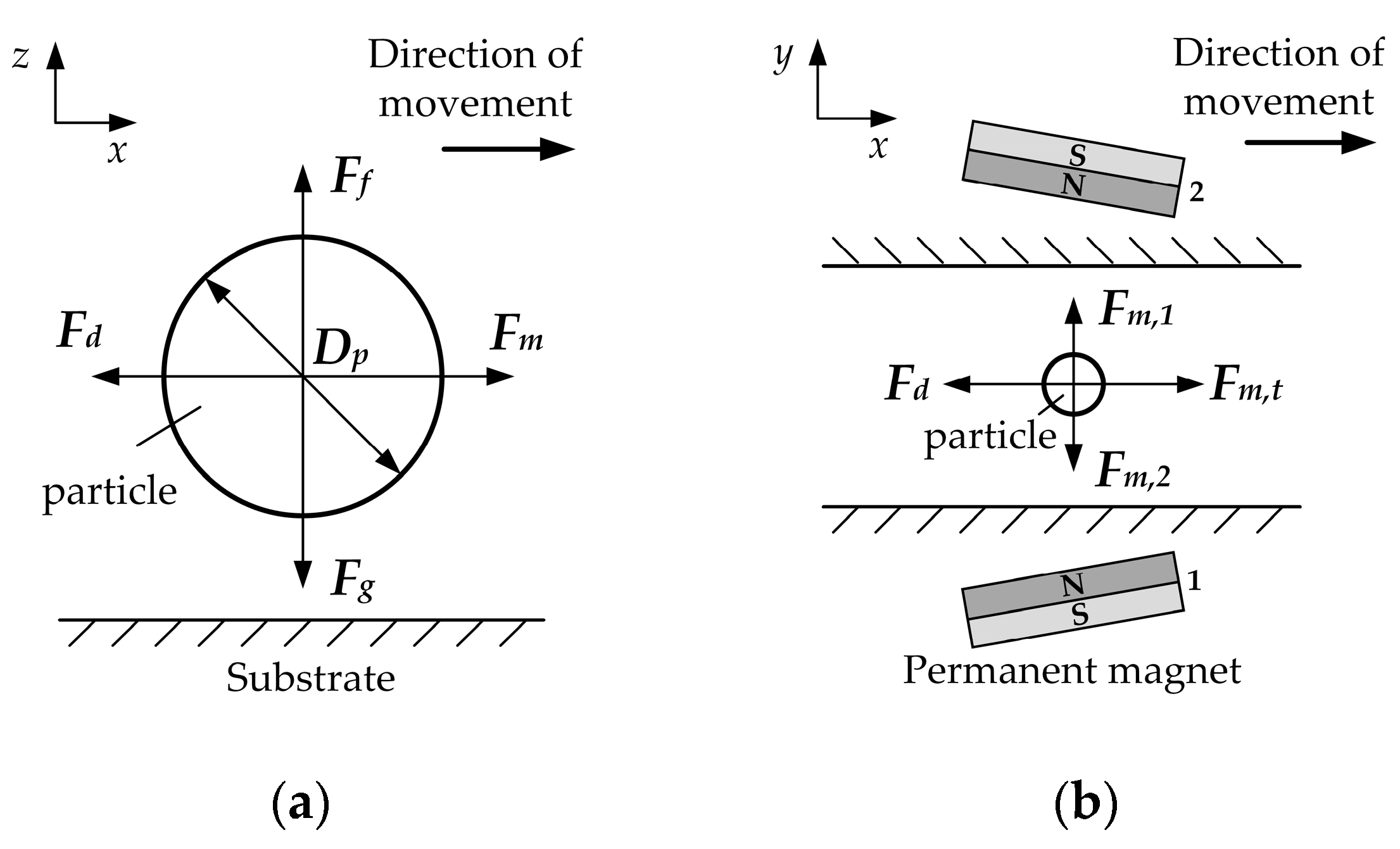
2. Theoretical Analysis
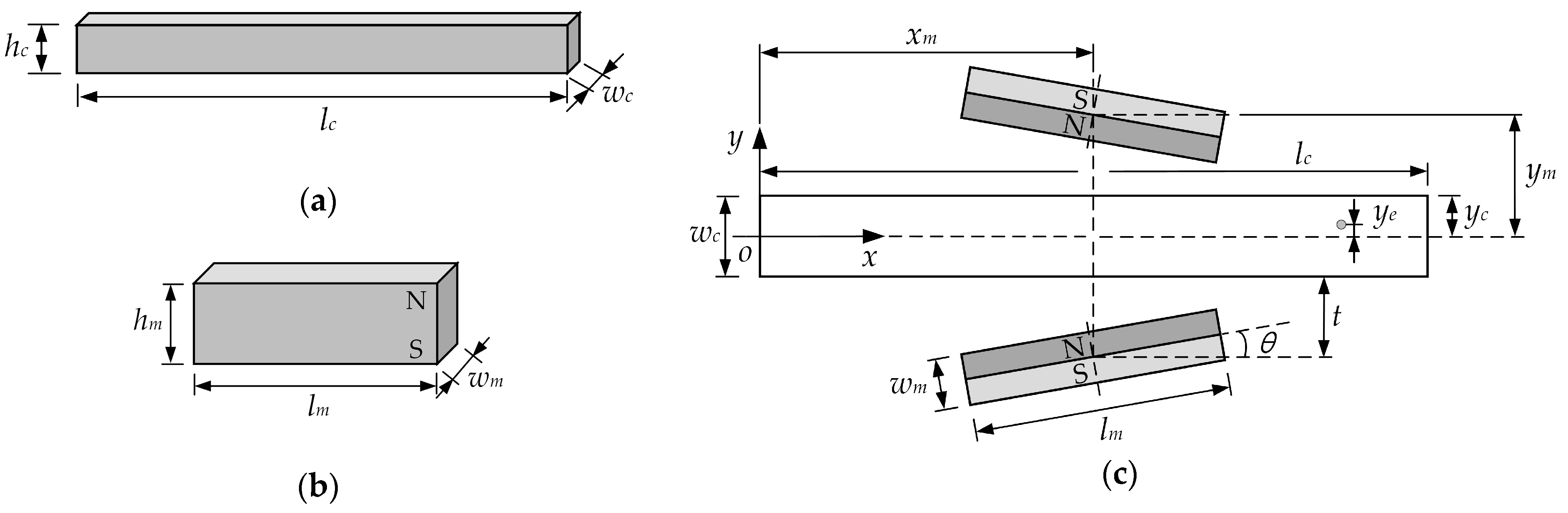
2.1. Magnetic Force
2.2. Viscous Drag Force
2.3. Gravity and Buoyancy
2.4. Brown Force
2.5. The Motion Equation of Particles
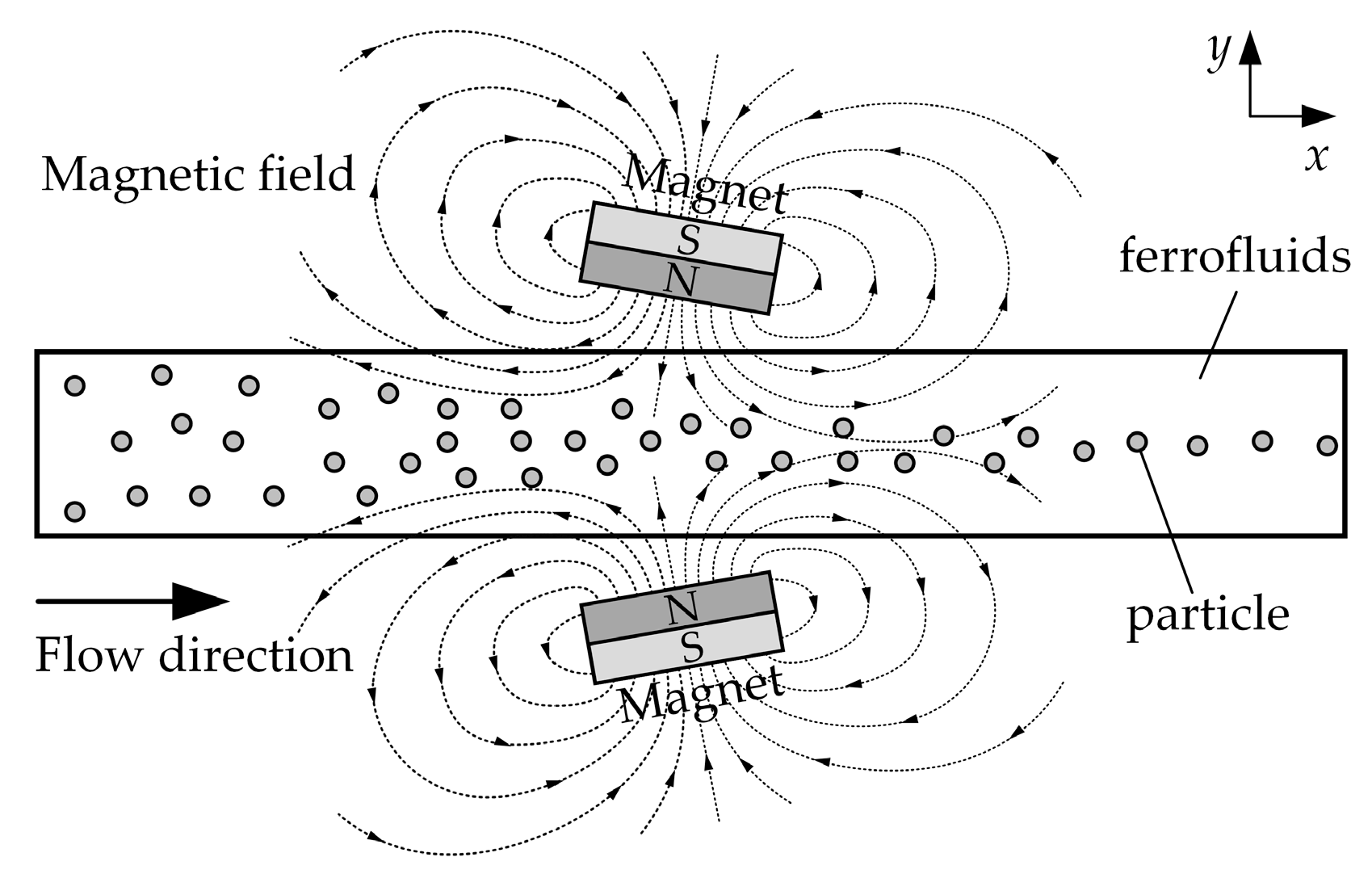
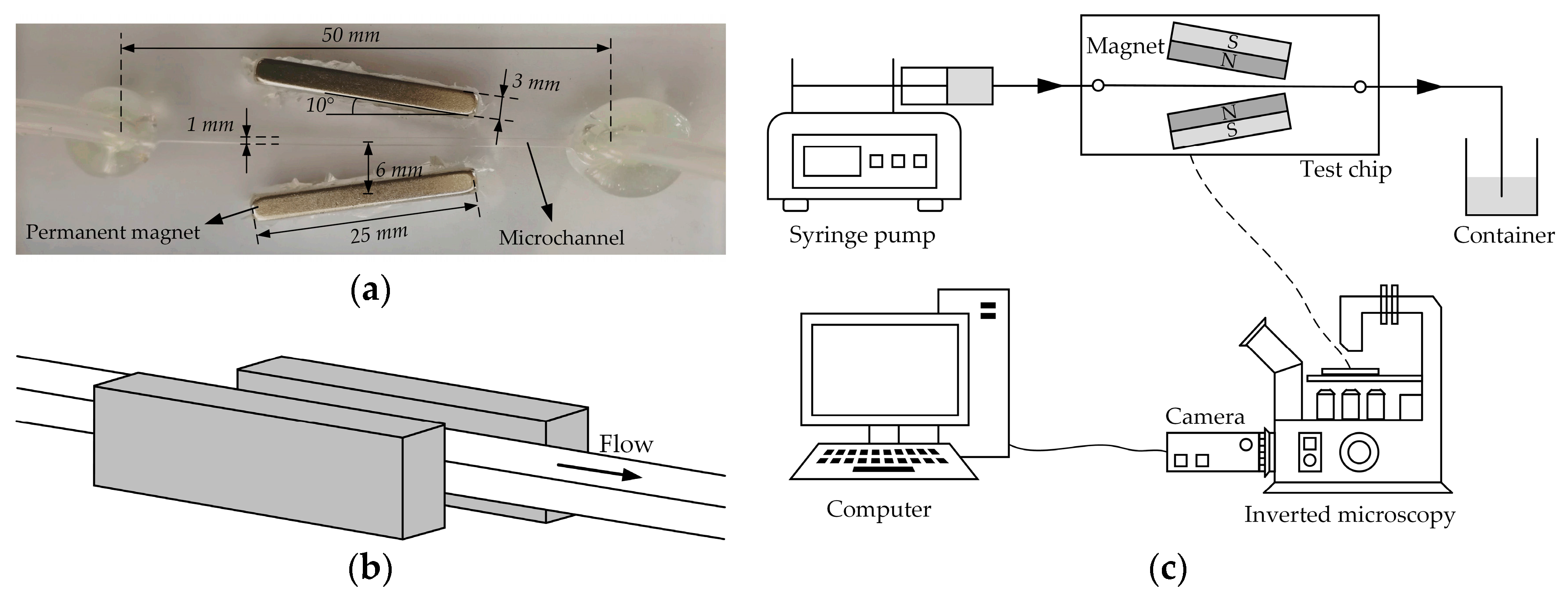
3. Materials and Methods
4. Results and Discussion
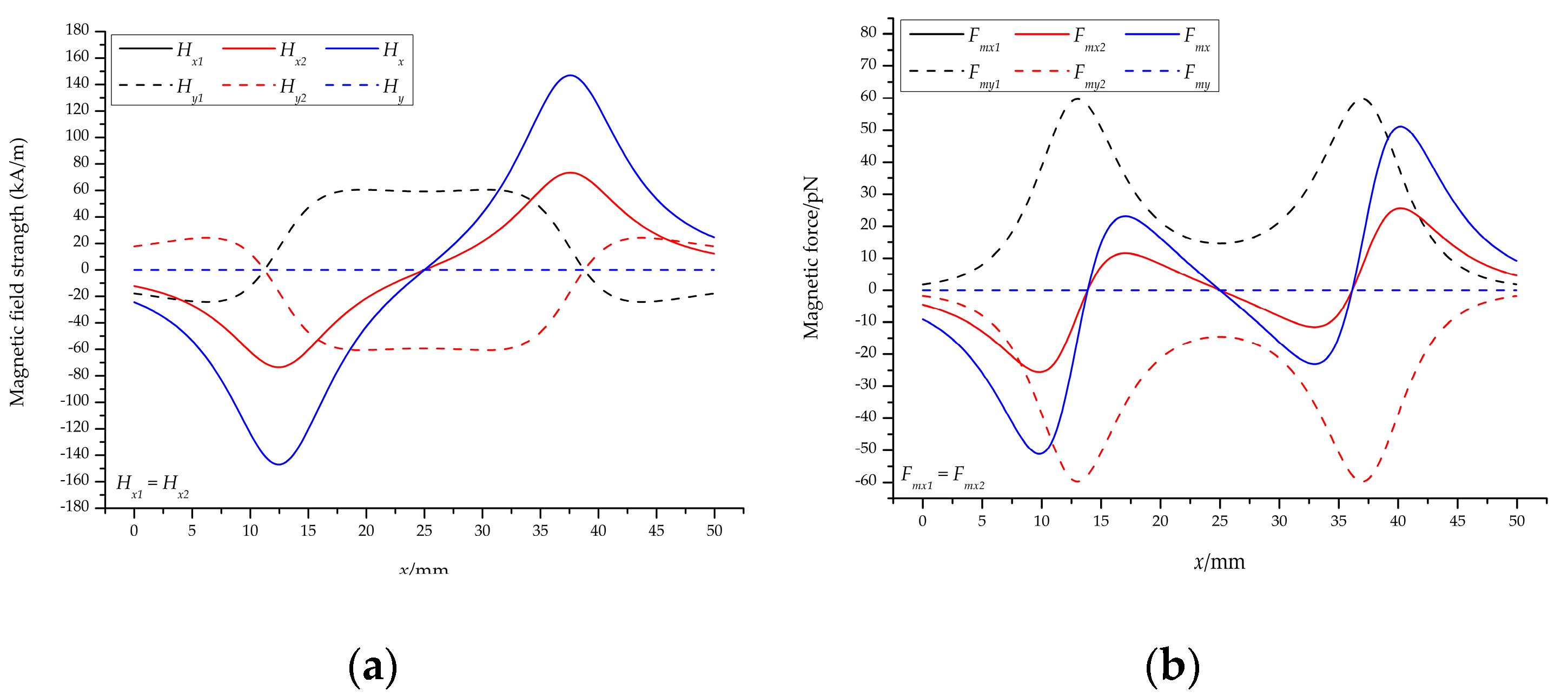
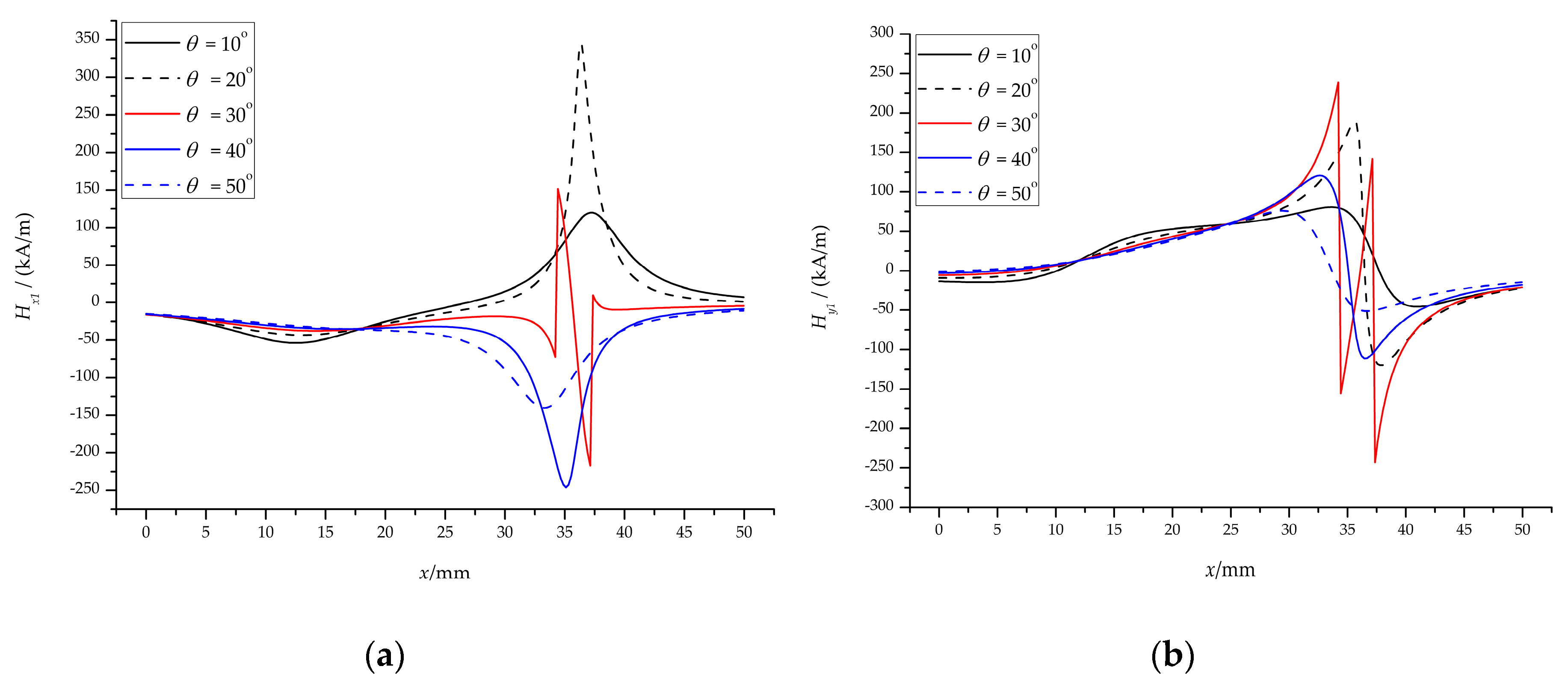
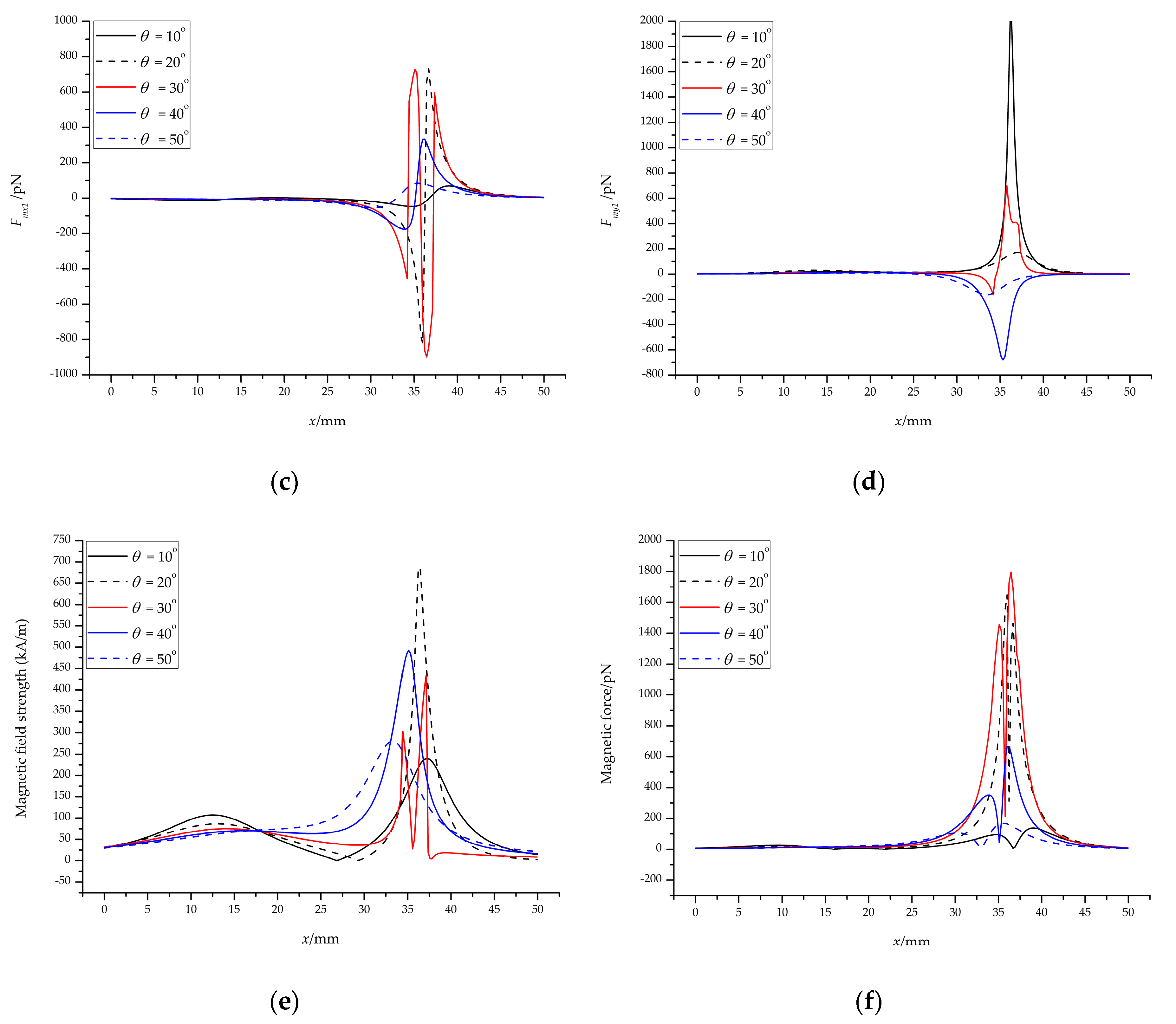
4.1. Magnetic Field
4.1.1. The Vertical Magnet Filed
4.1.2. The Inclined Magnet Field
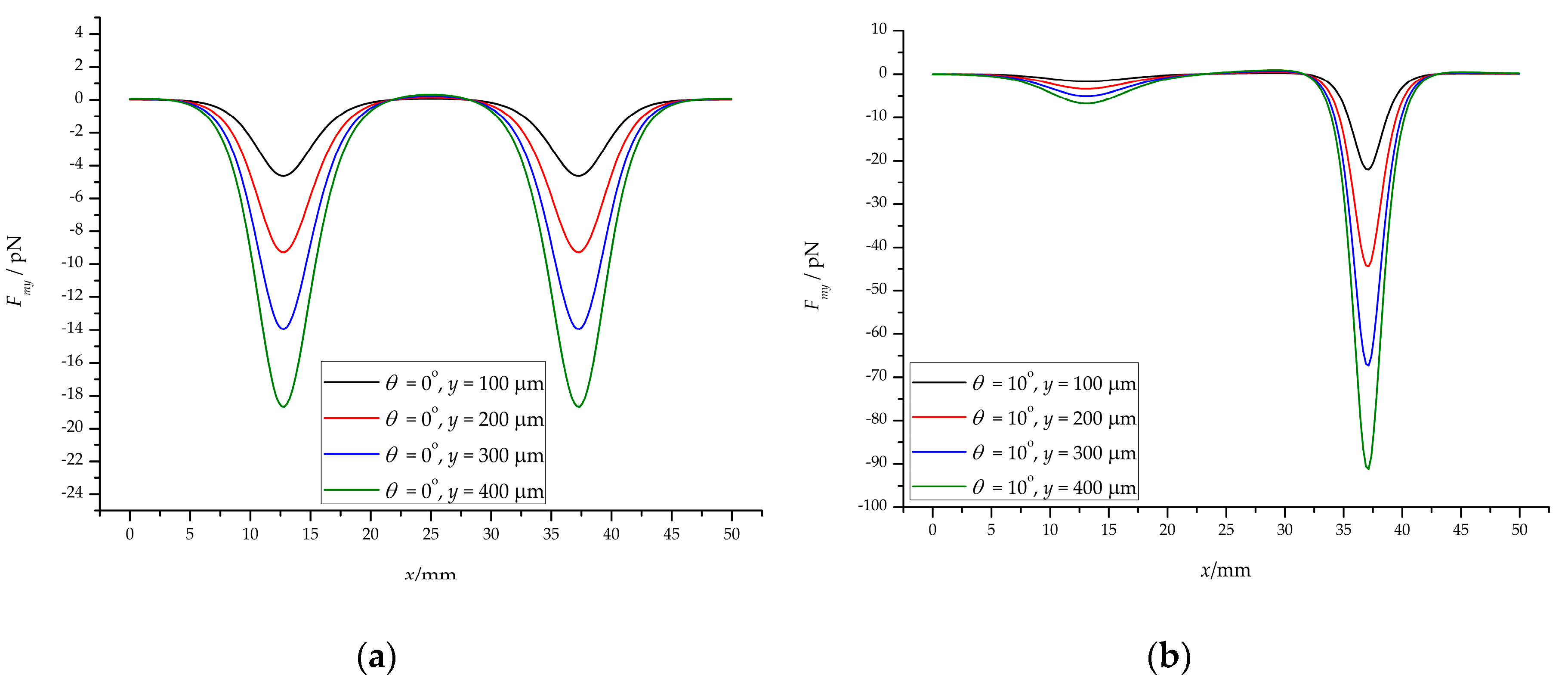
4.2. Flow Field
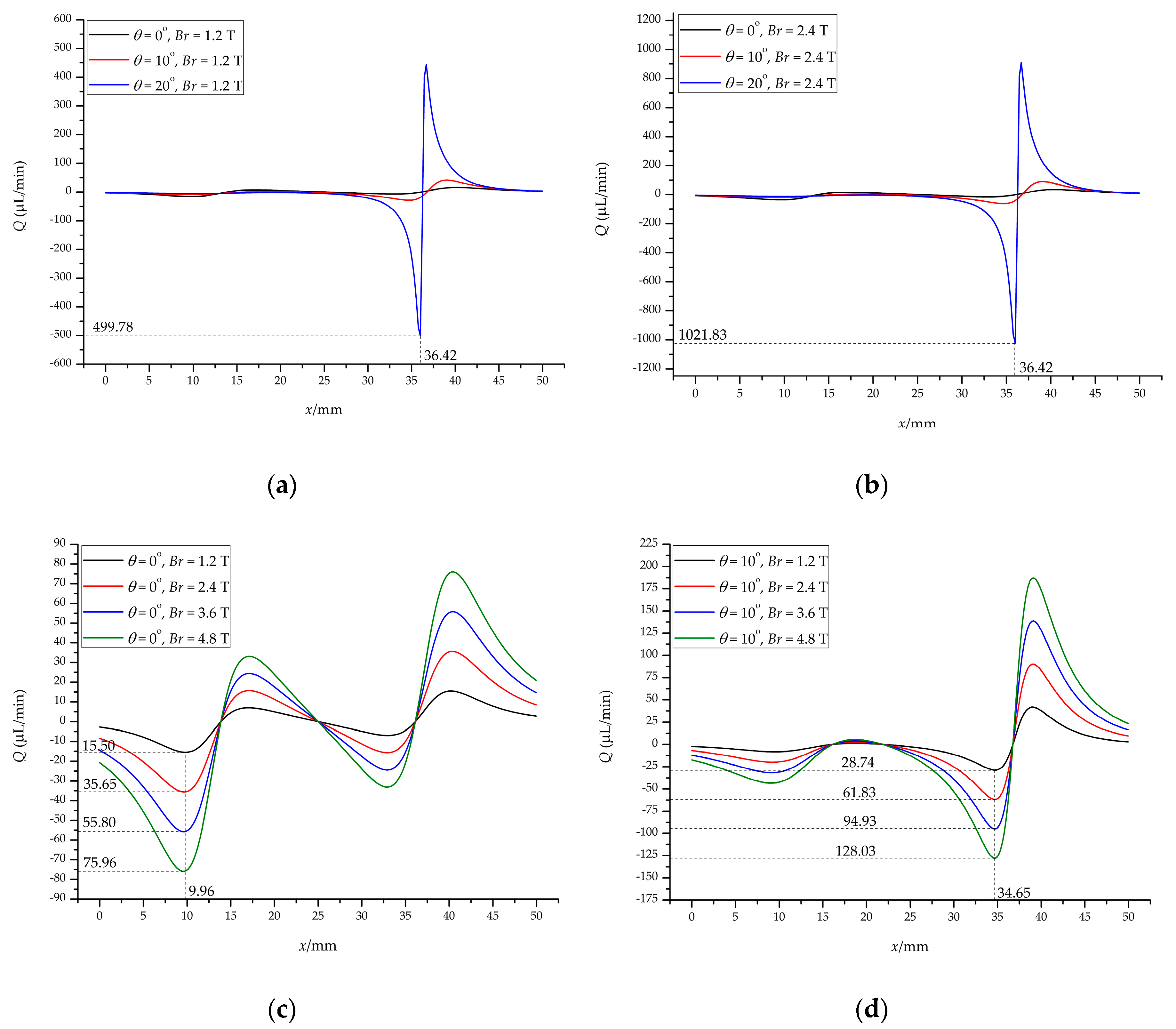
4.3. Magnetic Field and Flow Field Threshold
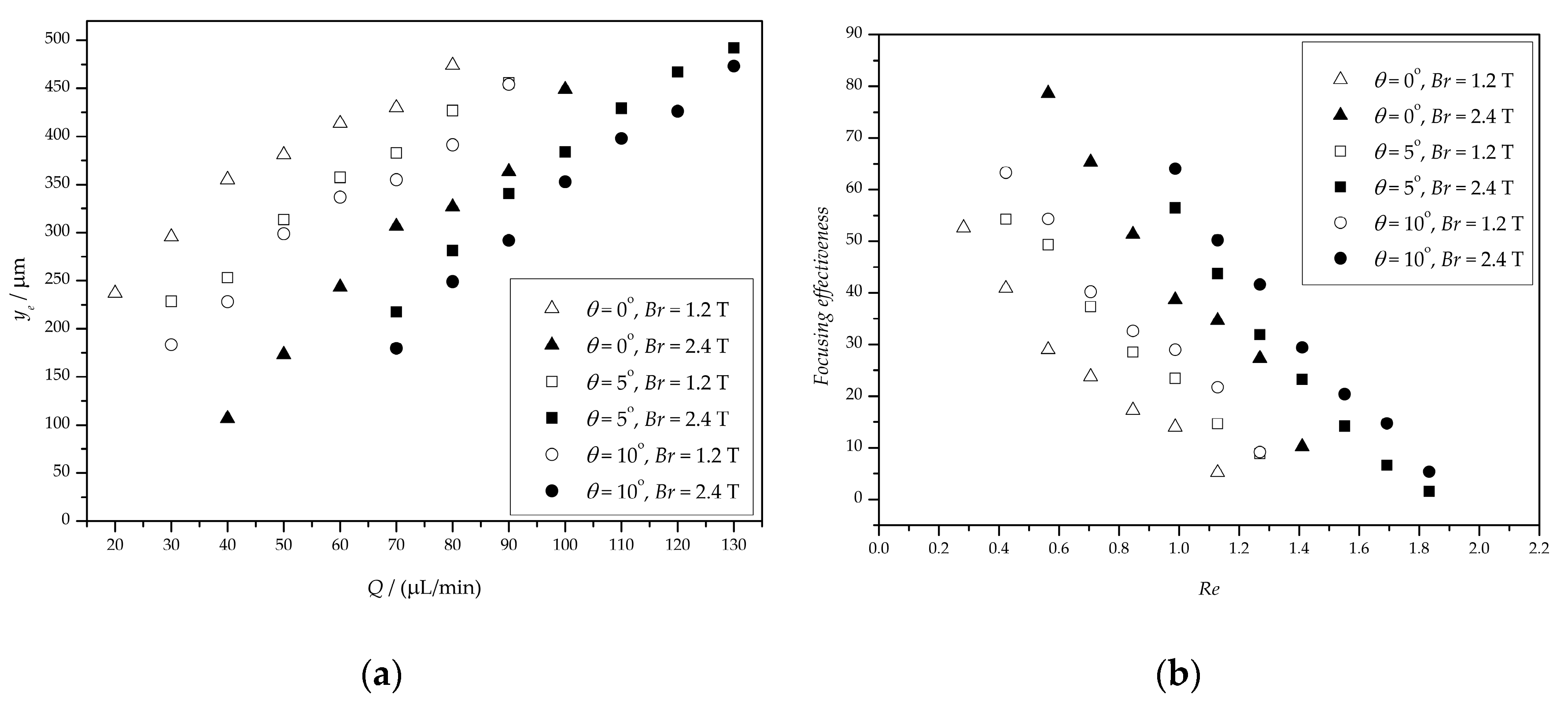
4.4. Focusing Effectiveness
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tang, W.; Tang, D.; Ni, Z.; Xiang, N.; Yi, H. A microfluidic impedance cytometer with inertial focusing and liquid electrodes for high-throughput cell counting and discrimination. Anal. Chem. 2017, 89, 3154–3161. [Google Scholar] [CrossRef] [PubMed]
- Xiao, W.; Matthew, Z.; Chia-Chi, H.; Necati, K.; Ian, P. Single stream inertial focusing in a straight microchannel. Lab Chip 2015, 15, 1812–1821. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.; He, Y.Q.; Jiao, F. Advances of particles/cells magnetic manipulation in microfluidic chips. Chin. J. Anal. Chem. 2017, 45, 1238–1246. [Google Scholar] [CrossRef]
- Shields, C.W., IV; Reyes, C.D.; López, G.P. Microfluidic cell sorting: A review of the advances in the separation of cells from debulking to rare cell isolation. Lab Chip 2015, 15, 1230–1249. [Google Scholar] [CrossRef] [PubMed]
- Xavier, M.; Oreffo, R.O.C.; Morgan, H. Skeletal stem cell isolation: A review on the state-of-the-art microfluidic label-free sorting techniques. Biotechnol. Adv. 2016, 34, 908–923. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shi, J.; Yazdi, S.; Lin, S.C.; Ding, X.; Chiang, I.K.; Sharp, K.; Huang, T.J. Three-dimensional continuous particle focusing in a microfluidic channel via standing surface acoustic waves (SSAW). Lab Chip 2011, 11, 2319–2324. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chang, C.C.; Huang, Z.X.; Yang, R.J. Three-dimensional hydrodynamic focusing in two-layer polydimethylsiloxane (PDMS) microchannels. J. Micromech. Microeng. 2007, 17, 1479–1486. [Google Scholar] [CrossRef]
- Erb, R.M.; Martin, J.J.; Soheilian, R.; Pan, C.; Barber, J.R. Actuating soft matter with magnetic torque. Adv. Funct. Mater. 2016, 26, 3859–3880. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, S.; Yuan, D.; Zhao, Q.; Tan, S.H.; Nguyen, N.T.; Li, W. A novel viscoelastic-based ferrofluid for continuous sheathless microfluidic separation of nonmagnetic microparticles. Lab Chip 2016, 16, 3947–3956. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.; Zhang, F.; Zhou, T.; Mawatari, Y. A model for estimating agglomerate sizes of non-magnetic nanoparticles in magnetic fluidized beds. Korean J. Chem. Eng. 2013, 30, 501–507. [Google Scholar] [CrossRef]
- Pamme, N.; Manz, A. On-chip free-flow magnetophoresis: Continuous flow separation of magnetic particles and agglomerates. Anal. Chem. 2004, 76, 7250–7256. [Google Scholar] [CrossRef] [PubMed]
- Friedman, G.; Yellen, B. Magnetic separation, manipulation and assembly of solid phase in fluids. Curr. Opin. Colloid Interface Sci. 2005, 10, 158–166. [Google Scholar] [CrossRef]
- Nezihi Murat, K.; Spuhler, P.S.; Fabio, F.; Lim, E.J.; Vincent, P.; Emre, O.; Martel, J.M.; Nikola, K.; Kyle, S.; Pin-I, C. Microfluidic, marker-free isolation of circulating tumor cells from blood samples. Nat. Protoc. 2014, 9, 694–710. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Song, L.; Yu, L.; Xuan, X. Inertially focused diamagnetic particle separation in ferrofluids. Microfluid. Nanofluid. 2017, 21, 14. [Google Scholar] [CrossRef]
- Zeng, J.; Chen, C.; Vedantam, P.; Brown, V.; Tzeng, T.R.J.; Xuan, X. Three-dimensional magnetic focusing of particles and cells in ferrofluid flow through a straight microchannel. J. Micromech. Microeng. 2012, 22, 105018. [Google Scholar] [CrossRef]
- Zhu, J.; Liang, L.; Xuan, X. On-chip manipulation of nonmagnetic particles in paramagnetic solutions using embedded permanent magnets. Microfluid. Nanofluid. 2012, 12, 65–73. [Google Scholar] [CrossRef]
- Sharifi, A.; Motlagh, S.Y.; Badfar, H. Ferro hydro dynamic analysis of heat transfer and biomagnetic fluid flow in channel under the effect of two inclined permanent magnets. J. Magn. Magn. Mater. 2019, 472, 115–122. [Google Scholar] [CrossRef]
- Hennenberg, M.; Weyssow, B.; Slavtchev, S.; Desaive, T.; Scheid, B. Steady flows of a laterally heated ferrofluid layer: Influence of inclined strong magnetic field and gravity level. Phys. Fluids 2006, 18, 093602. [Google Scholar] [CrossRef] [Green Version]
- Bég, O.A.; Sim, L.; Zueco, J.; Bhargava, R. Numerical study of magnetohydrodynamic viscous plasma flow in rotating porous media with Hall currents and inclined magnetic field influence. Commun. Nonlinear Sci. 2010, 15, 345–359. [Google Scholar] [CrossRef]
- Nguyen, N.T. Micro-magnetofluidics: Interactions between magnetism and fluid flow on the microscale. Microfluid. Nanofluid. 2012, 12, 1–16. [Google Scholar] [CrossRef]
- Rosensweig, R.E. Ferrohydrodynamics; Dover Publications: New York, NY, USA, 2014; pp. 54–61, 74–84. ISBN 978-0-486-67834-4. [Google Scholar]
- Wirix-Speetjens, R.; Fyen, W.; Xu, K.; Boeck, J.D.; Borghs, G. A force study of on-chip magnetic particle transport based on tapered conductors. IEEE Trans. Magn. 2005, 41, 4128–4133. [Google Scholar] [CrossRef]
- Kim, M.M.; Zydney, A.L. Effect of electrostatic, hydrodynamic, and Brownian forces on particle trajectories and sieving in normal flow filtration. J. Colloid Interface Sci. 2004, 269, 425–431. [Google Scholar] [CrossRef] [PubMed]
- Gerber, R.; Takayasu, M.; Friedlaender, F.J. Generalization of HGMS theory: The capture of ultra-fine particles. IEEE Trans. Magn. 1983, 19, 2115–2117. [Google Scholar] [CrossRef]
- Duffy, C.D.; McDonald, J.C.; Schueller, O.J.; Whitesides, G.M. Rapid prototyping of microfluidic systems in poly (dimethylsiloxane). Anal. Chem. 1998, 70, 4974–4984. [Google Scholar] [CrossRef] [PubMed]
- Furlani, E.P.; Sahoo, Y. Analytical model for the field and force in a magnetophoretic microsystem. J. Phys. D Appl. Phys. 2006, 39, 1724–1732. [Google Scholar] [CrossRef]
- Brody, J.P.; Yager, P.; Goldstein, R.E.; Austin, R.H. Biotechnology at low Reynolds numbers. Biophys. J. 1996, 71, 3430–3441. [Google Scholar] [CrossRef] [Green Version]
- Naoki, I.; Kazuo, H.; Ryutaro, M. Interface motion of capillary-driven flow in rectangular microchannel. J. Colloid Interface Sci. 2004, 280, 155–164. [Google Scholar] [CrossRef]
- Zhu, T.; Lichlyter, D.J.; Haidekker, M.A.; Mao, L. Analytical model of microfluidic transport of non-magnetic particles in ferrofluids under the influence of a permanent magnet. Microfluid. Nanofluid. 2011, 10, 1233–1245. [Google Scholar] [CrossRef]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, L.; He, Y. Magnetically Induced Flow Focusing of Non-Magnetic Microparticles in Ferrofluids under Inclined Magnetic Fields. Micromachines 2019, 10, 56. https://doi.org/10.3390/mi10010056
Luo L, He Y. Magnetically Induced Flow Focusing of Non-Magnetic Microparticles in Ferrofluids under Inclined Magnetic Fields. Micromachines. 2019; 10(1):56. https://doi.org/10.3390/mi10010056
Chicago/Turabian StyleLuo, Laan, and Yongqing He. 2019. "Magnetically Induced Flow Focusing of Non-Magnetic Microparticles in Ferrofluids under Inclined Magnetic Fields" Micromachines 10, no. 1: 56. https://doi.org/10.3390/mi10010056
APA StyleLuo, L., & He, Y. (2019). Magnetically Induced Flow Focusing of Non-Magnetic Microparticles in Ferrofluids under Inclined Magnetic Fields. Micromachines, 10(1), 56. https://doi.org/10.3390/mi10010056




