A Study on Parametric Amplification in a Piezoelectric MEMS Device
Abstract
1. Introduction
2. Materials and Methods
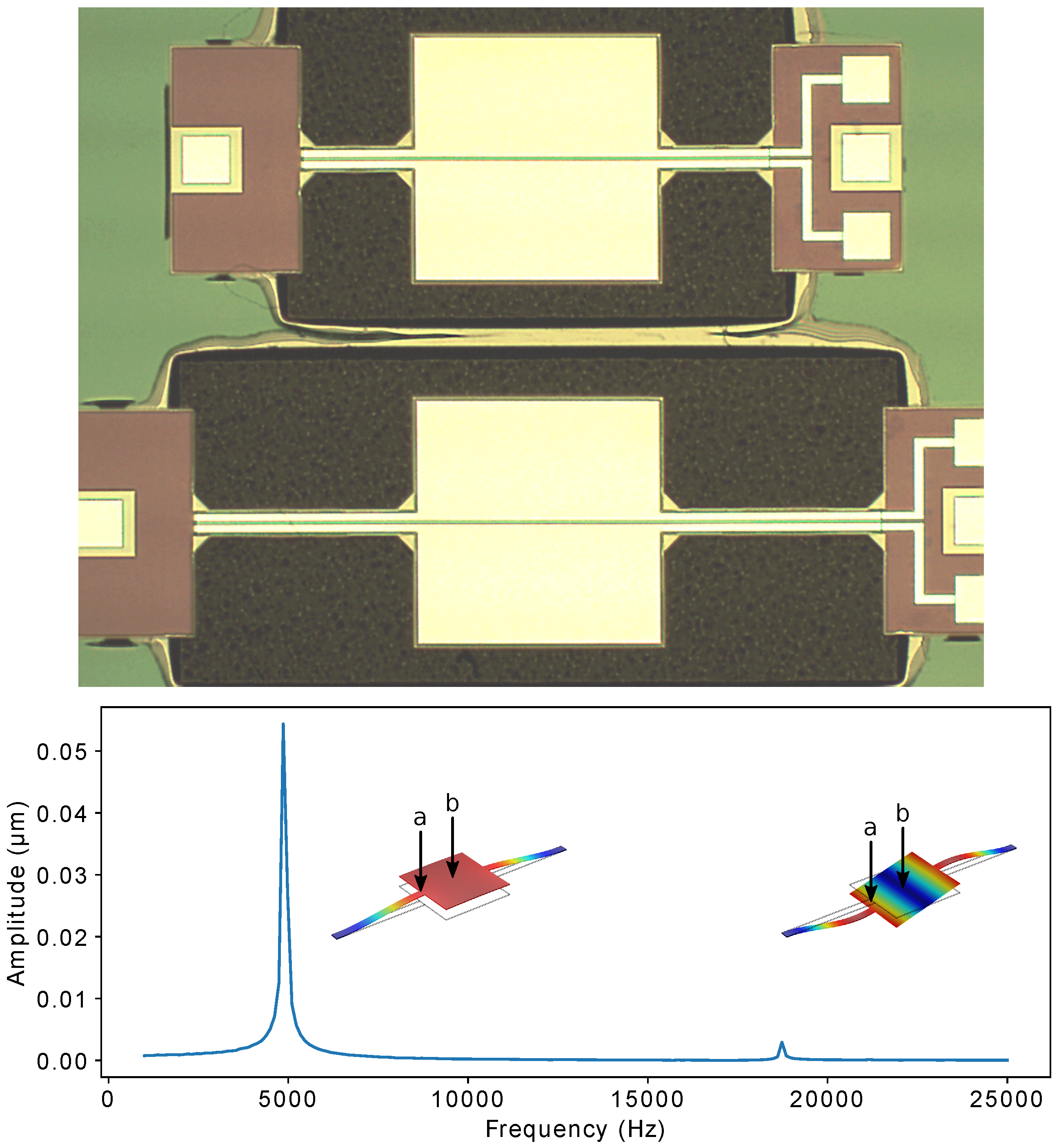
2.1. MEMS Device
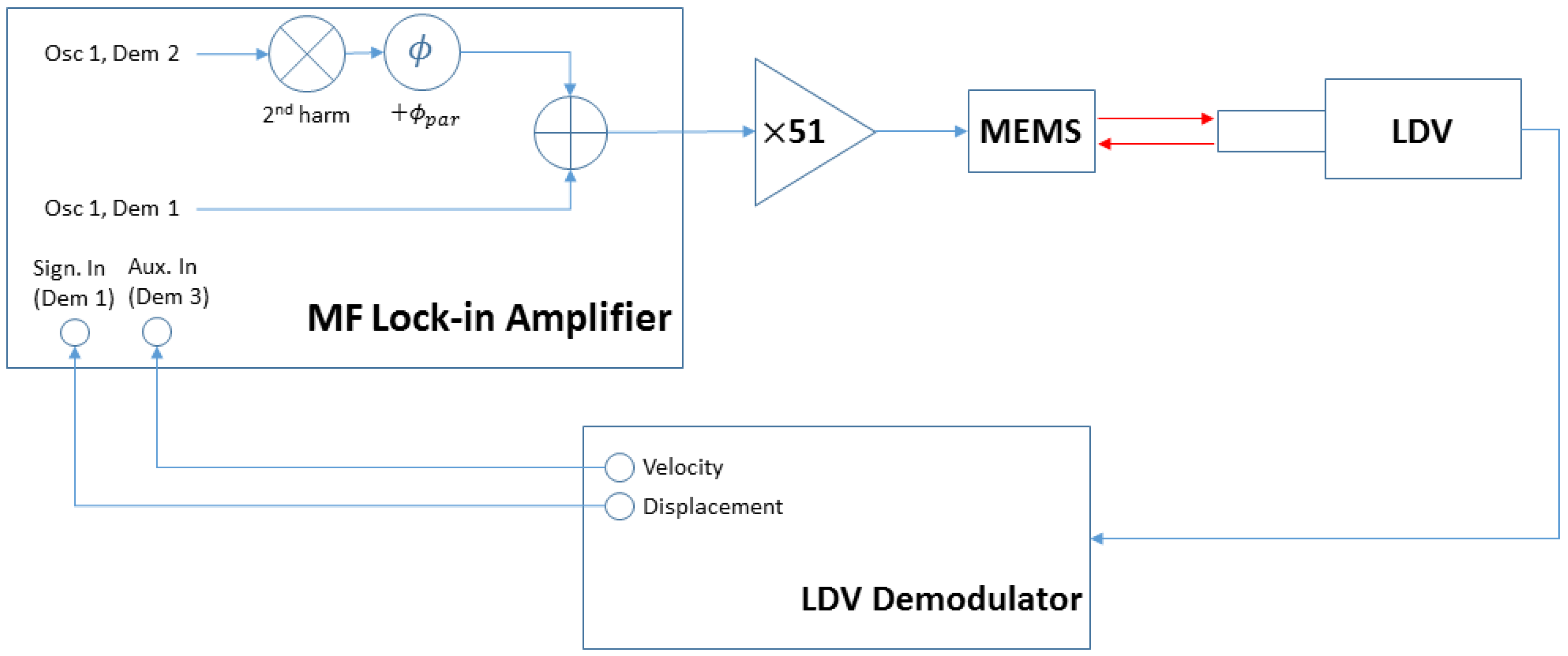
2.2. Measurement Scheme
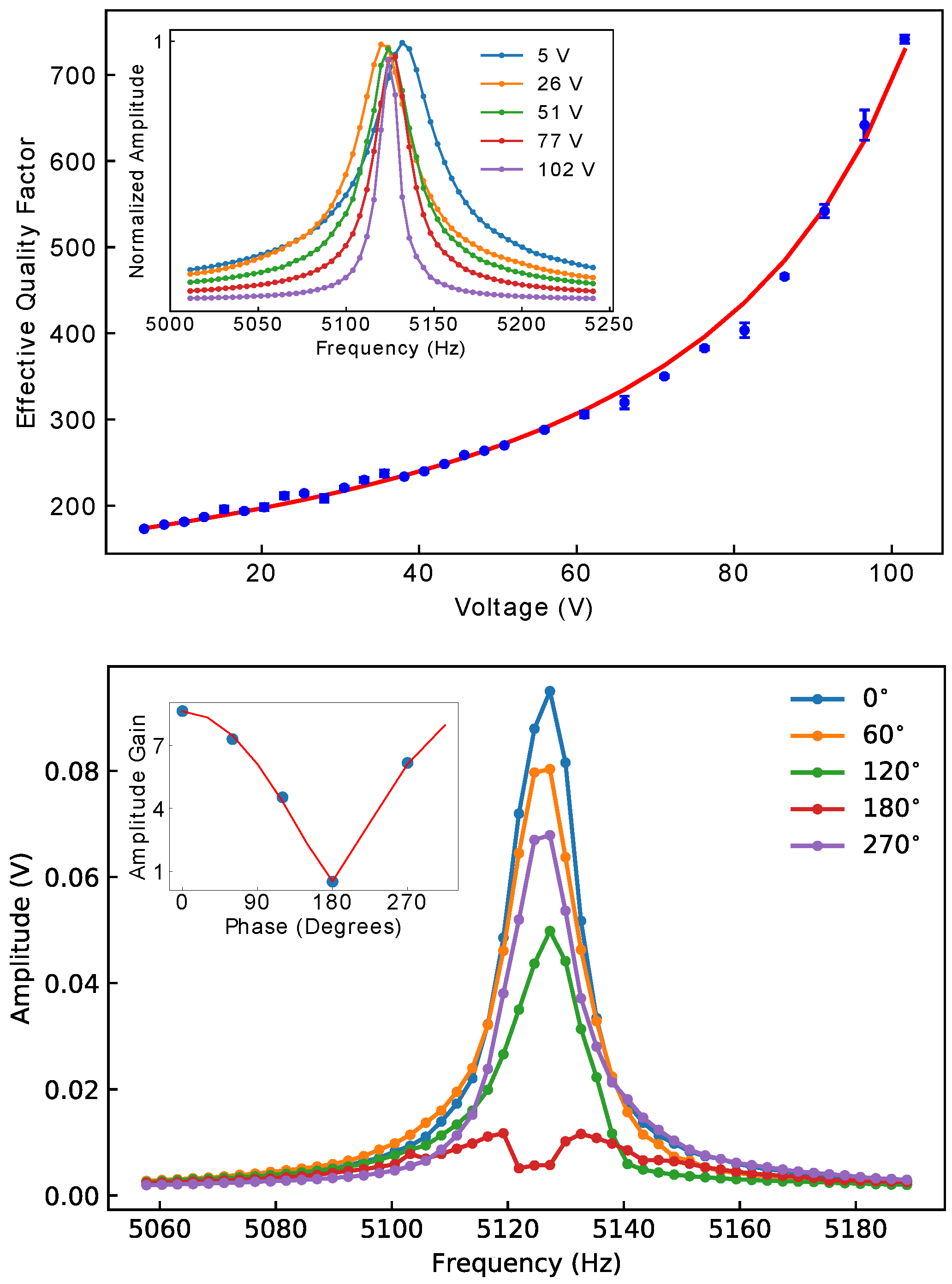
3. Results
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Manzaneque, T.; Ruiz-Díez, V.; Hernando-García, J.; Wistrela, E.; Kucera, M.; Schmid, U.; Sánchez-Rojas, J.L. Piezoelectric MEMS resonator-based oscillator for density and viscosity sensing. Sens. Actuators A Phys. 2014, 220, 305–315. [Google Scholar] [CrossRef]
- Calleja, M.; Kosaka, P.M.; San Paulo, Á.; Tamayo, J. Challenges for nanomechanical sensors in biological detection. Nanoscale 2012, 4, 4925. [Google Scholar] [CrossRef] [PubMed]
- Patimisco, P.; Sampaolo, A.; Dong, L.; Tittel, F.K.; Spagnolo, V. Recent advances in quartz enhanced photoacoustic sensing. Appl. Phys. Rev. 2018, 5, 011106. [Google Scholar] [CrossRef]
- Patimisco, P.; Sampaolo, A.; Mackowiak, V.; Rossmadl, H.; Cable, A.; Tittel, F.K.; Spagnolo, V. Loss Mechanisms Determining the Quality Factors in Quartz Tuning Forks Vibrating at the Fundamental and First Overtone Mode. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2018, 65, 1951–1957. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, M.; Seren, H.R.; Ham, G.; Buzi, E.; Bernero, G.; Deffenbaugh, M. Viscosity and Density Measurements Using Mechanical Oscillators in Oil and Gas Applications. IEEE Trans. Instrum. Meas. 2018, 67, 804–810. [Google Scholar] [CrossRef]
- Karabacak, D.M.; Yakhot, V.; Ekinci, K.L. High-Frequency Nanofluidics: An Experimental Study Using Nanomechanical Resonators. Phys. Rev. Lett. 2007, 98, 254505. [Google Scholar] [CrossRef] [PubMed]
- Franosch, T.; Grimm, M.; Belushkin, M.; Mor, F.M.; Foffi, G.; Forró, L.; Jeney, S. Resonances arising from hydrodynamic memory in Brownian motion. Nature 2011, 478, 85–88. [Google Scholar] [CrossRef] [PubMed]
- Paul, M.R.; Cross, M.C. Stochastic Dynamics of Nanoscale Mechanical Oscillators Immersed in a Viscous Fluid. Phys. Rev. Lett. 2004, 92, 235501. [Google Scholar] [CrossRef]
- González, M.; Zheng, P.; Garcell, E.; Lee, Y.; Chan, H.B. Comb-drive micro-electro-mechanical systems oscillators for low temperature experiments. Rev. Sci. Instrum. 2013, 84, 025003. [Google Scholar] [CrossRef]
- González, M.; Jiang, W.G.; Zheng, P.; Barquist, C.S.; Chan, H.B.; Lee, Y. Temperature dependence of viscosity in normal fluid He3 below 800 mK determined by a microelectromechanical oscillator. Phys. Rev. B 2016, 94, 014505. [Google Scholar] [CrossRef]
- Zheng, P.; Jiang, W.; Barquist, C.; Lee, Y.; Chan, H. Critical Velocity in the Presence of Surface Bound States in Superfluid He 3—B. Phys. Rev. Lett. 2017, 118, 065301. [Google Scholar] [CrossRef]
- Kokavecz, J.; Horváth, Z.L.; Mechler, A. Dynamical properties of the Q-controlled atomic force microscope. Appl. Phys. Lett. 2004, 85, 3232–3234. [Google Scholar] [CrossRef]
- Moran, K.; Burgner, C.; Shaw, S.; Turner, K. A review of parametric resonance in microelectromechanical systems. Nonlinear Theory Appl. IEICE 2013, 4, 198–224. [Google Scholar] [CrossRef]
- Shaw, S.W. Nonlinearity and parametric pumping in sensors: Opportunities and limitations. In Proceedings of the 2017 IEEE SENSORS, Glasgow, UK, 29 October–1 November 2017; pp. 1–3. [Google Scholar] [CrossRef]
- José, J.; Saletan, E. Classical Dynamics: A Contemporary Approach; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Rugar, D.; Grütter, P. Mechanical parametric amplification and thermomechanical noise squeezing. Phys. Rev. Lett. 1991, 67, 699–702. [Google Scholar] [CrossRef]
- Karabalin, R.B.; Masmanidis, S.C.; Roukes, M.L. Efficient parametric amplification in high and very high frequency piezoelectric nanoelectromechanical systems. Appl. Phys. Lett. 2010, 97, 183101. [Google Scholar] [CrossRef]
- Moreno-Moreno, M.; Raman, A.; Gomez-Herrero, J.; Reifenberger, R. Parametric resonance based scanning probe microscopy. Appl. Phys. Lett. 2006, 88, 193108. [Google Scholar] [CrossRef]
- Prakash, G.; Raman, A.; Rhoads, J.; Reifenberger, R.G. Parametric noise squeezing and parametric resonance of microcantilevers in air and liquid environments. Rev. Sci. Instrum. 2012, 83, 065109. [Google Scholar] [CrossRef]
- Papariello, L.; Zilberberg, O.; Eichler, A.; Chitra, R. Ultrasensitive hysteretic force sensing with parametric nonlinear oscillators. Phys. Rev. E 2016, 94, 022201. [Google Scholar] [CrossRef]
- Zhang, W.; Baskaran, R.; Turner, K.L. Effect of cubic nonlinearity on auto-parametrically amplified resonant MEMS mass sensor. Sens. Actuators A Phys. 2002, 102, 139–150. [Google Scholar] [CrossRef]
- Carr, D.W.; Evoy, S.; Sekaric, L.; Craighead, H.G.; Parpia, J.M. Parametric amplification in a torsional microresonator. Appl. Phys. Lett. 2000, 77, 1545–1547. [Google Scholar] [CrossRef]
- Collin, E.; Moutonet, T.; Heron, J.S.; Bourgeois, O.; Bunkov, Y.M.; Godfrin, H. Nonlinear parametric amplification in a triport nanoelectromechanical device. Phys. Rev. B 2011, 84, 054108. [Google Scholar] [CrossRef]
- Thomas, O.; Mathieu, F.; Mansfield, W.; Huang, C.; Trolier-Mckinstry, S.; Nicu, L. Piezoelectric parametric amplifiers with integrated actuation and sensing capabilities. In Proceedings of the 2013 IEEE 26th International Conference on Micro Electro Mechanical Systems (MEMS), Taipei, Taiwan, 20–24 January 2013; pp. 588–591. [Google Scholar]
- Thomas, O.; Mathieu, F.; Mansfield, W.; Huang, C.; Trolier-McKinstry, S.; Nicu, L. Efficient parametric amplification in micro-resonators with integrated piezoelectric actuation and sensing capabilities. Appl. Phys. Lett. 2013, 102, 163504. [Google Scholar] [CrossRef]
- Jia, Y.; Du, S.; Seshia, A.A. Twenty-Eight Orders of Parametric Resonance in a Microelectromechanical Device for Multi-band Vibration Energy Harvesting. Sci. Rep. 2016, 6, 30167. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Sheng, J.; Zhang, X.; Wu, Y.; Wu, H. Parametric excitation of a SiN membrane via piezoelectricity. AIP Adv. 2018, 8, 015209. [Google Scholar] [CrossRef]
- Cowen, A.; Hames, G.; Glukh, K.; Hardy, B. PiezoMUMPs Design Handbook; MEMSCAP Inc.: Durham, NC, USA, 2014. [Google Scholar]
- Lifshitz, R.; Cross, M.C. Nonlinear Dynamics of Nanomechanical and Micromechanical Resonators. In Reviews of Nonlinear Dynamics and Complexity; Schuster, H.G., Ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2008; pp. 1–52. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonzalez, M.; Lee, Y. A Study on Parametric Amplification in a Piezoelectric MEMS Device. Micromachines 2019, 10, 19. https://doi.org/10.3390/mi10010019
Gonzalez M, Lee Y. A Study on Parametric Amplification in a Piezoelectric MEMS Device. Micromachines. 2019; 10(1):19. https://doi.org/10.3390/mi10010019
Chicago/Turabian StyleGonzalez, Miguel, and Yoonseok Lee. 2019. "A Study on Parametric Amplification in a Piezoelectric MEMS Device" Micromachines 10, no. 1: 19. https://doi.org/10.3390/mi10010019
APA StyleGonzalez, M., & Lee, Y. (2019). A Study on Parametric Amplification in a Piezoelectric MEMS Device. Micromachines, 10(1), 19. https://doi.org/10.3390/mi10010019



