A Population Model of Folate-Mediated One-Carbon Metabolism
Abstract
:1. Introduction
2. Experimental Section
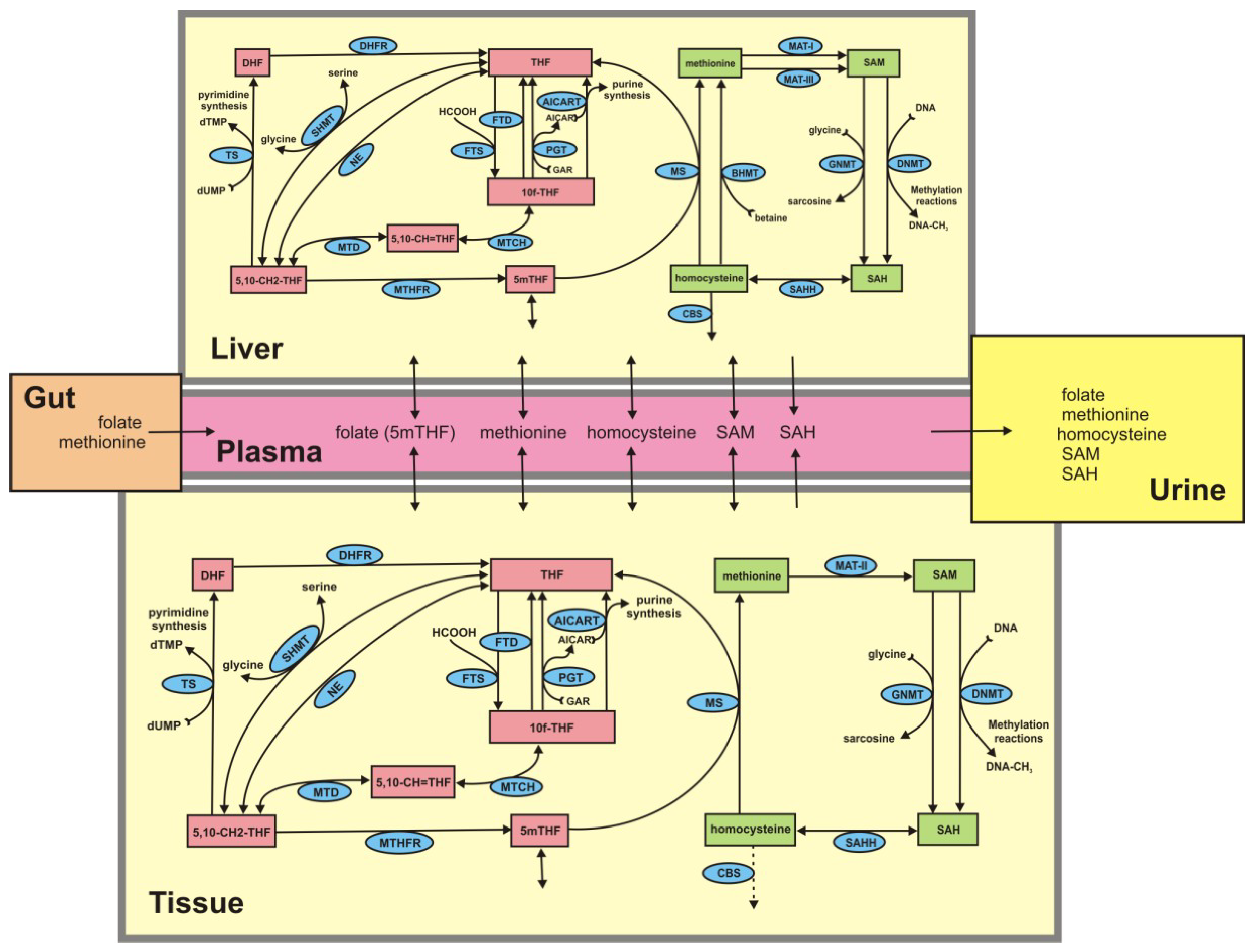
3. Results
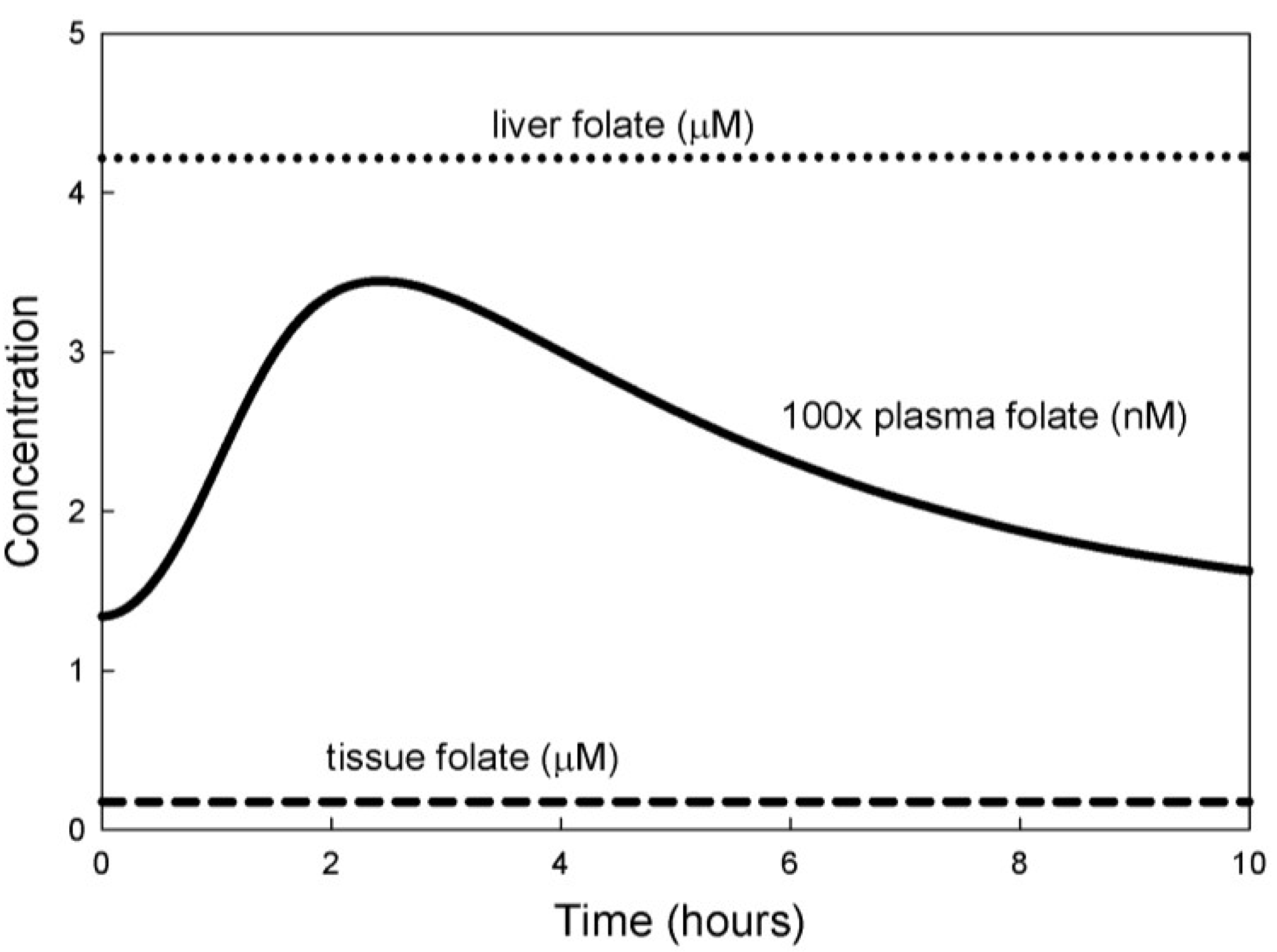
3.1. Experiments on Model Individuals
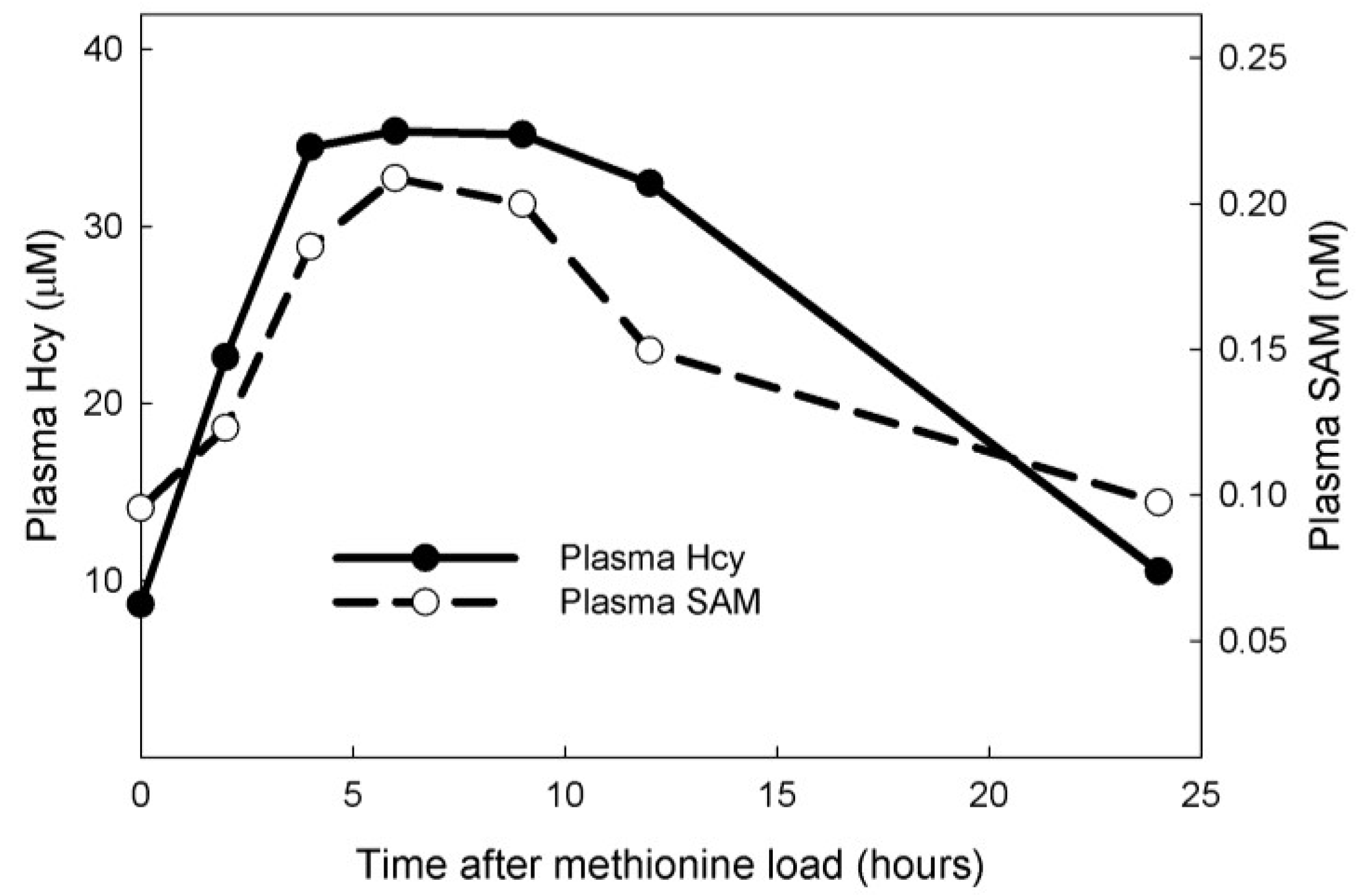
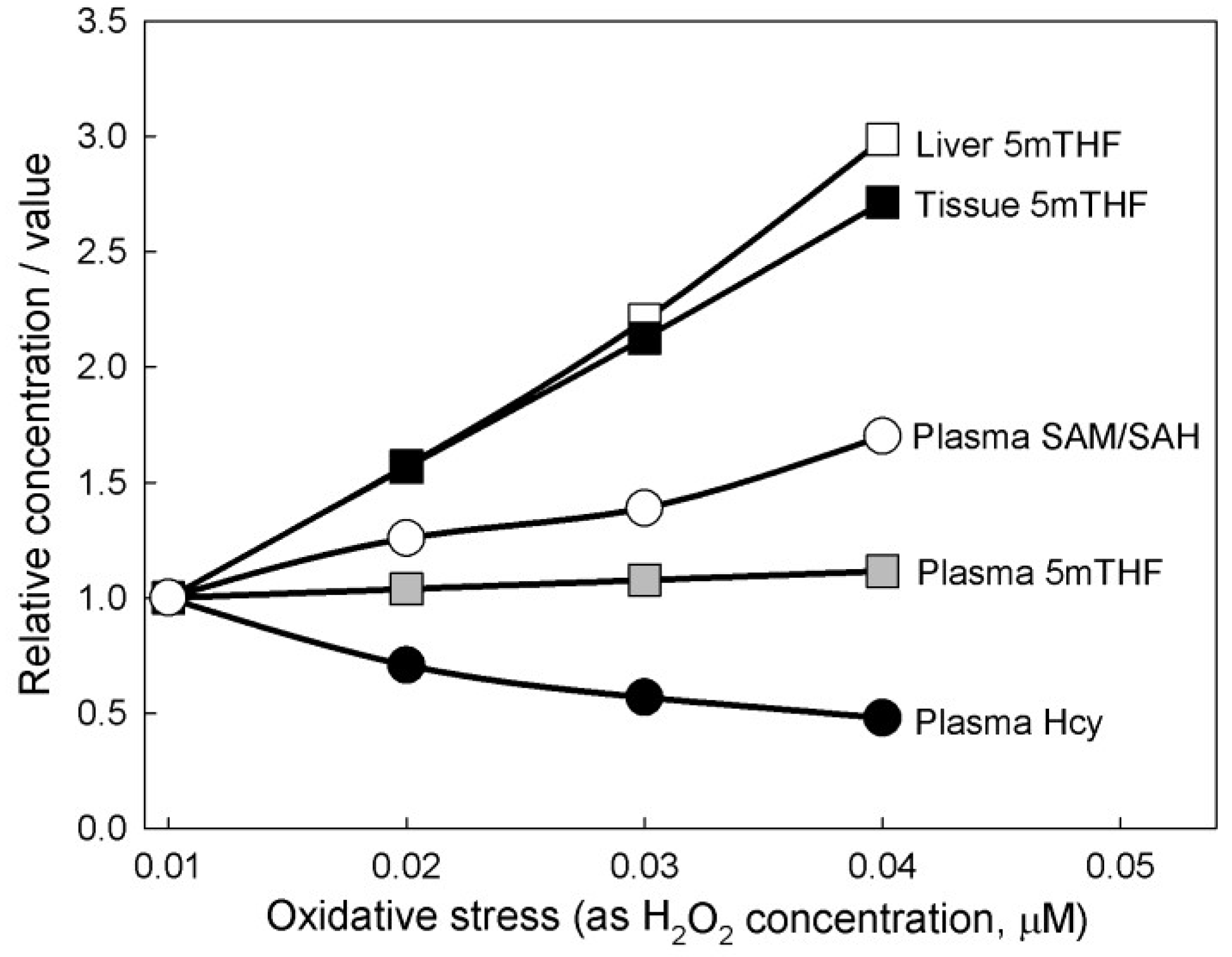
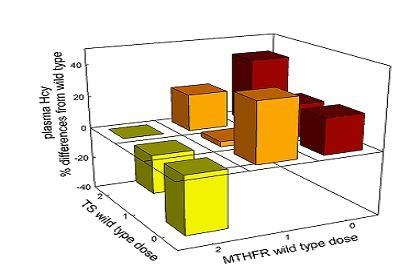
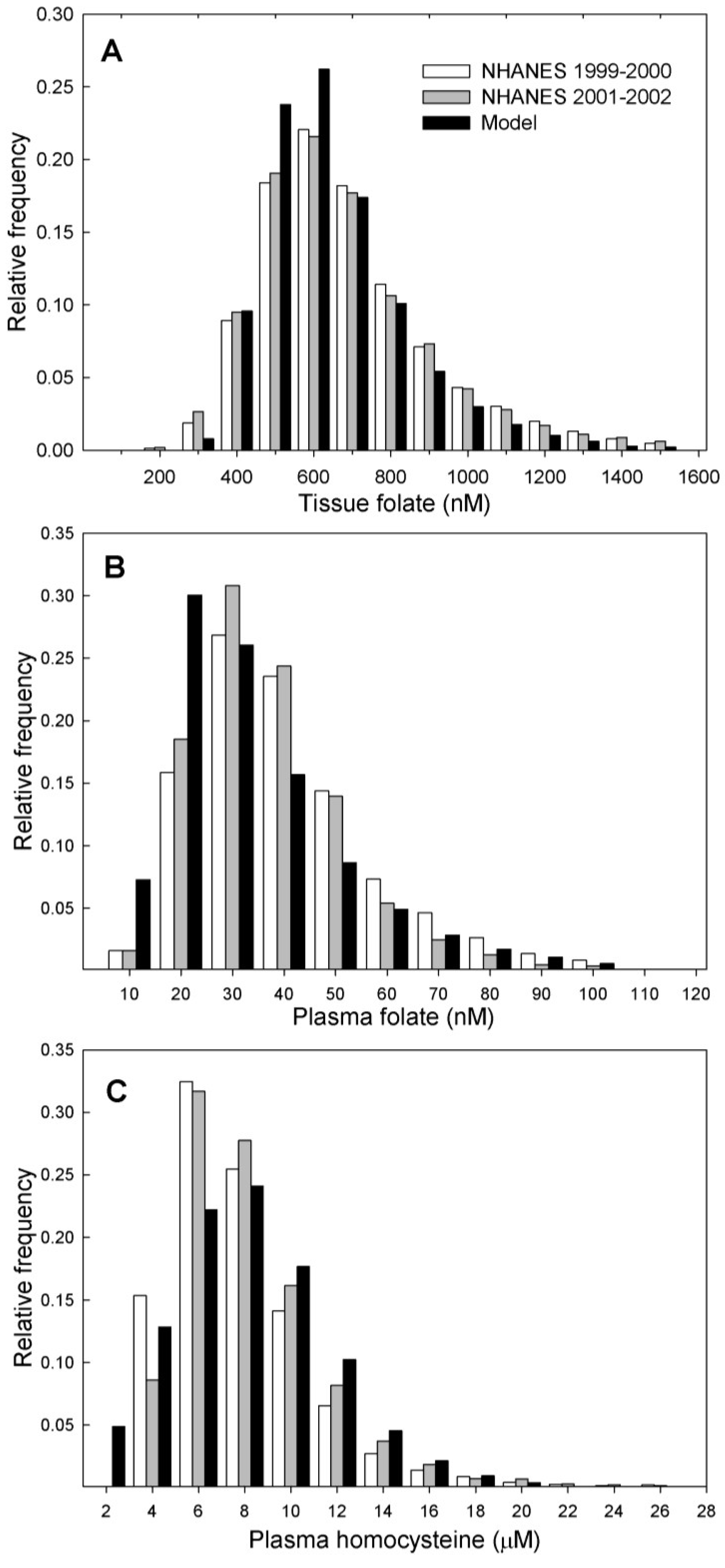
3.2. Population Studies
3.2.1. Comparison with NHANES Data
| Metabolite | N | Mean | |
|---|---|---|---|
| Plasma folate * | |||
| Model 1 (post-fortification) | 10,000 | 29.7 ± 0.2 | |
| NHANES 2,3 (1999–2000) | 3223 | 30.2 ± 0.7 | |
| NHANES 2,3 (2001–2002) | 3931 | 27.8 ± 0.5 | |
| Tissue folate * | |||
| Model 1 (post-fortification) | 10,000 | 602 ± 2.15 | |
| NHANES 2,3 (1999–2000) | 3249 | 618 ± 0.11 | |
| NHANES 2,3 (2001–2002) | 3977 | 611 ± 0.9 | |
| Plasma Hcy ** | |||
| Model 1 (post-fortification) | 10,000 | 7.1 ± 0.03 | |
| NHANES 2,3 (1999–2000) | 3246 | 7.0 ± 0.01 | |
| NHANES 2,3 (2001–2002) | 3976 | 7.3 ± 0.01 | |
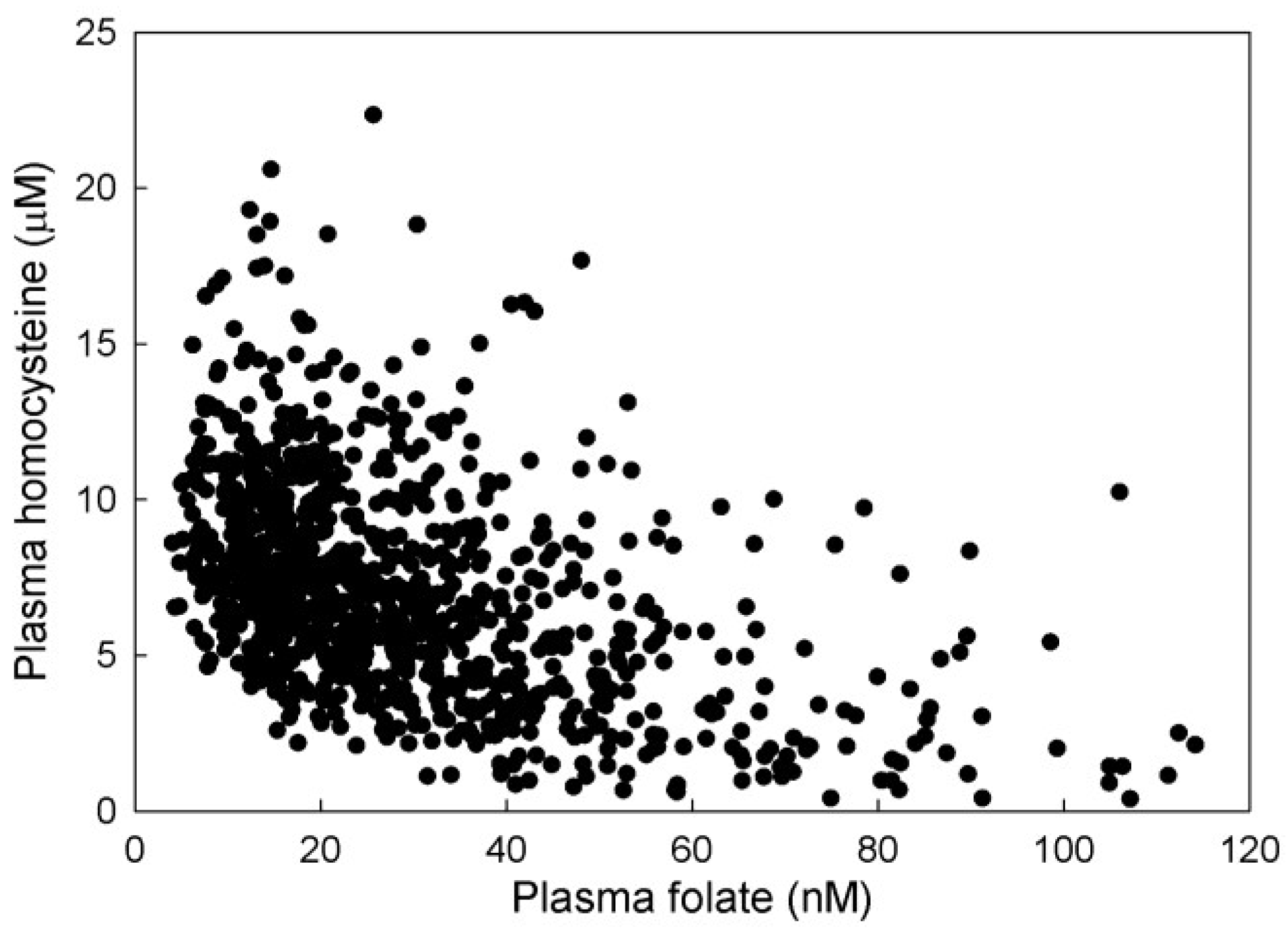
3.2.2. Plasma Hcy and 5mTHF
3.2.3. Methylation Capacity
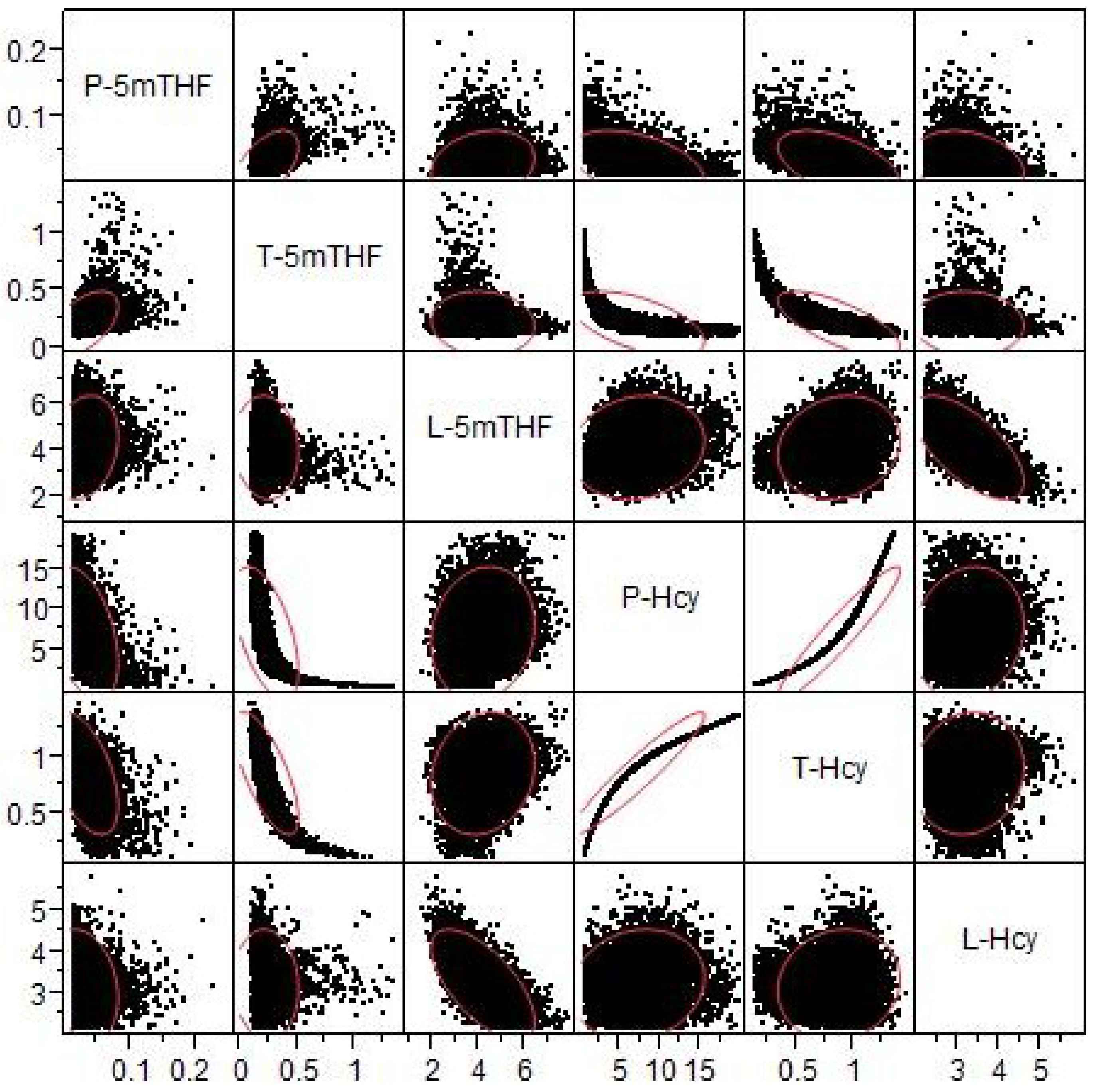
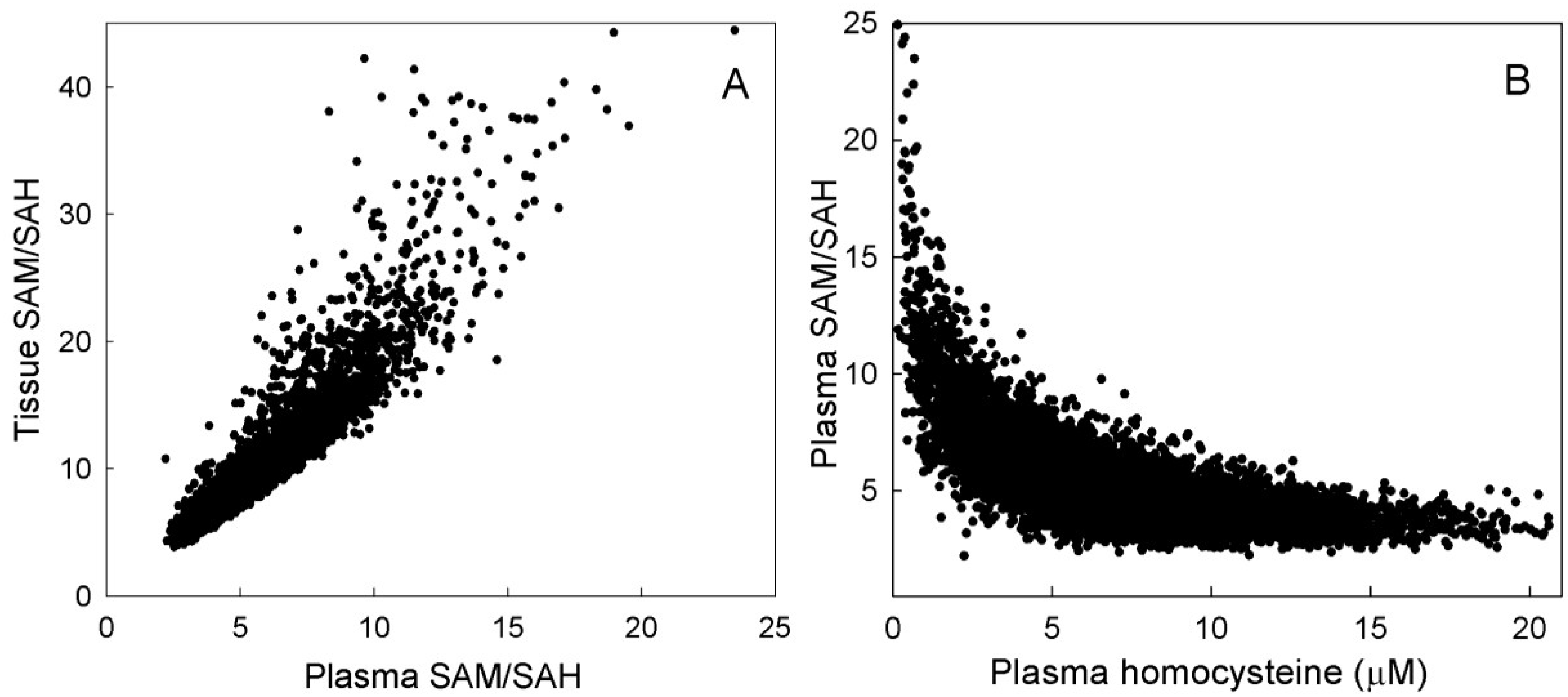
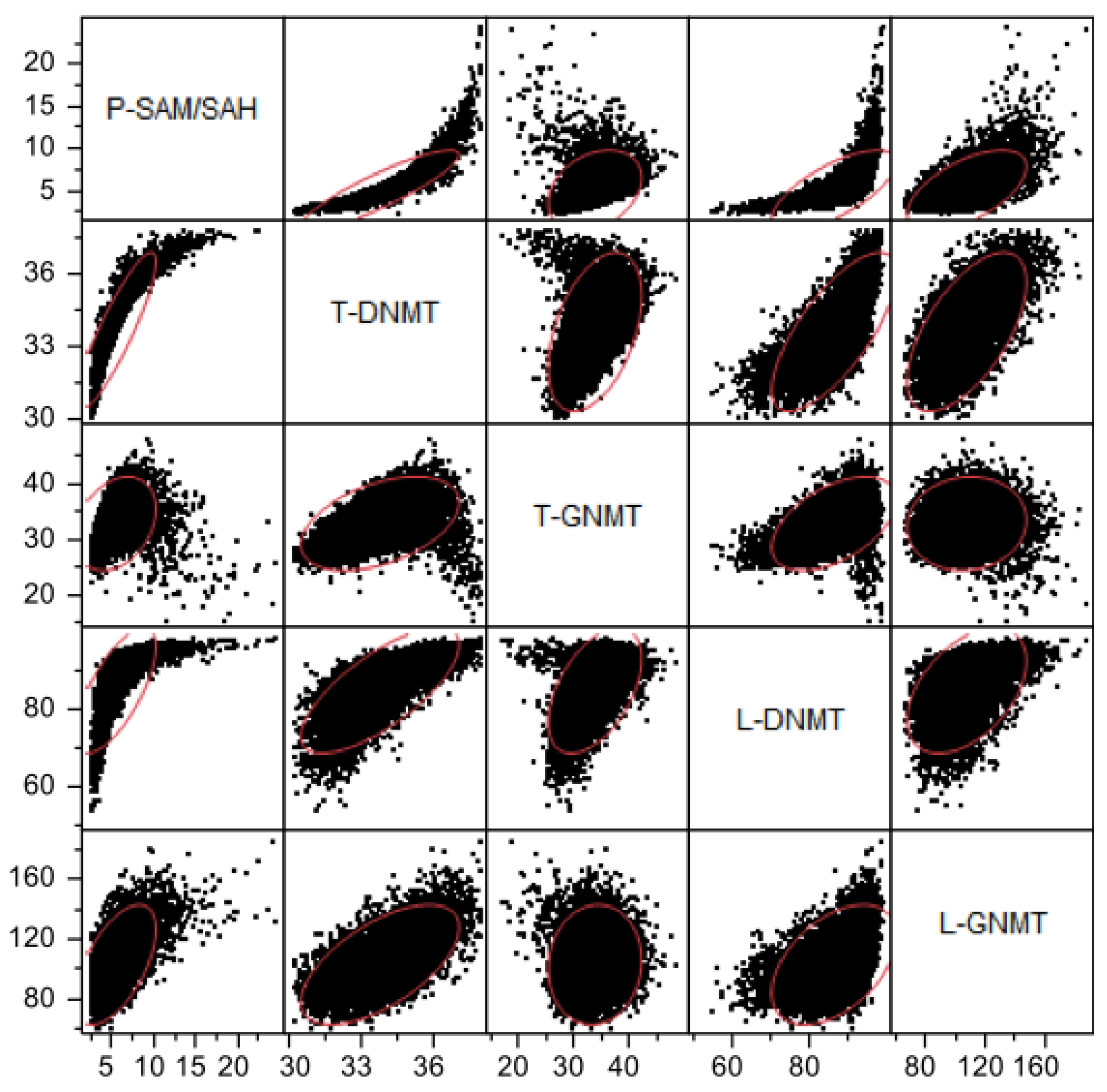
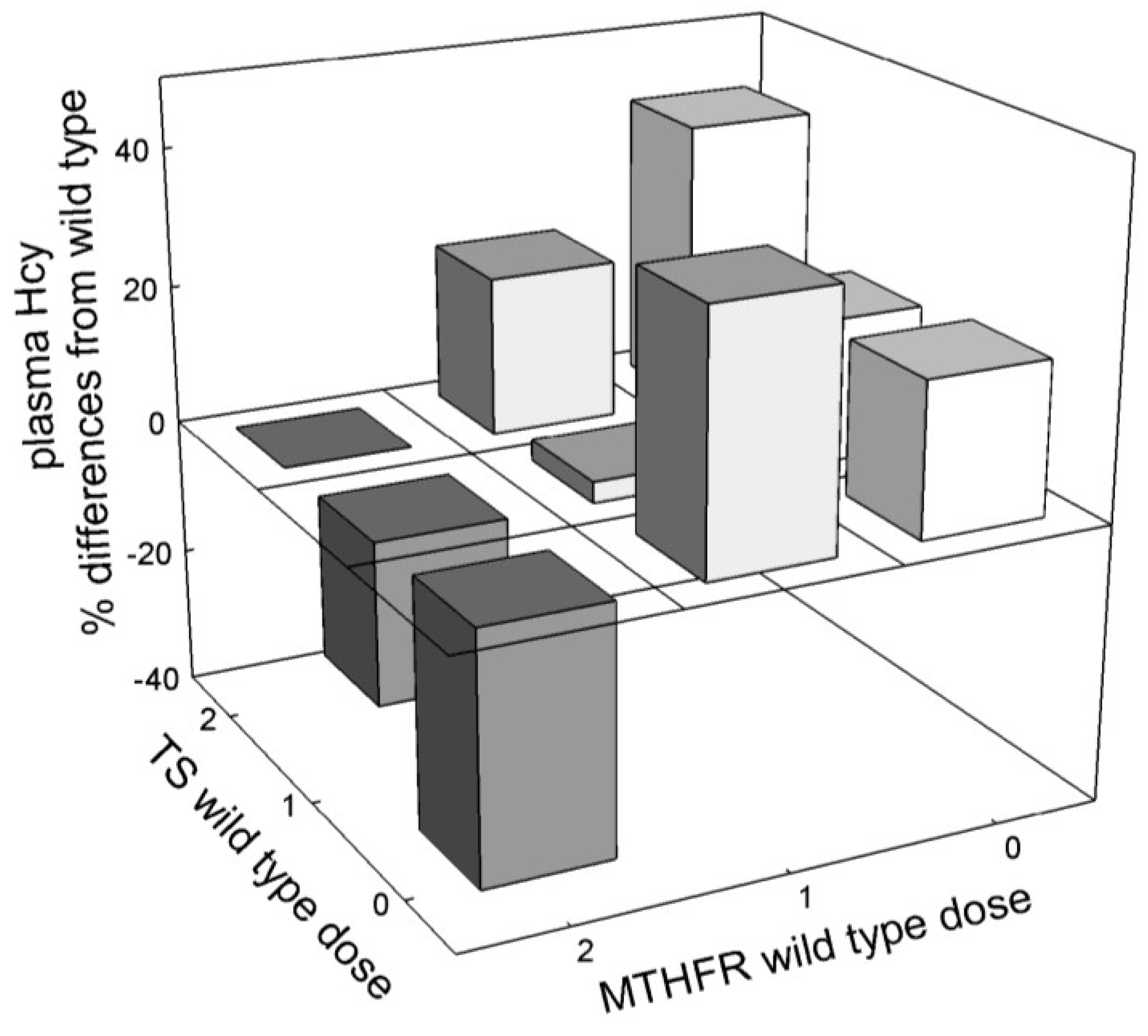
3.2.4. Interaction among Mutations
3.2.5. Correlations with Extreme Plasma Hcy Values

3.2.6. Nonlinear Relationships
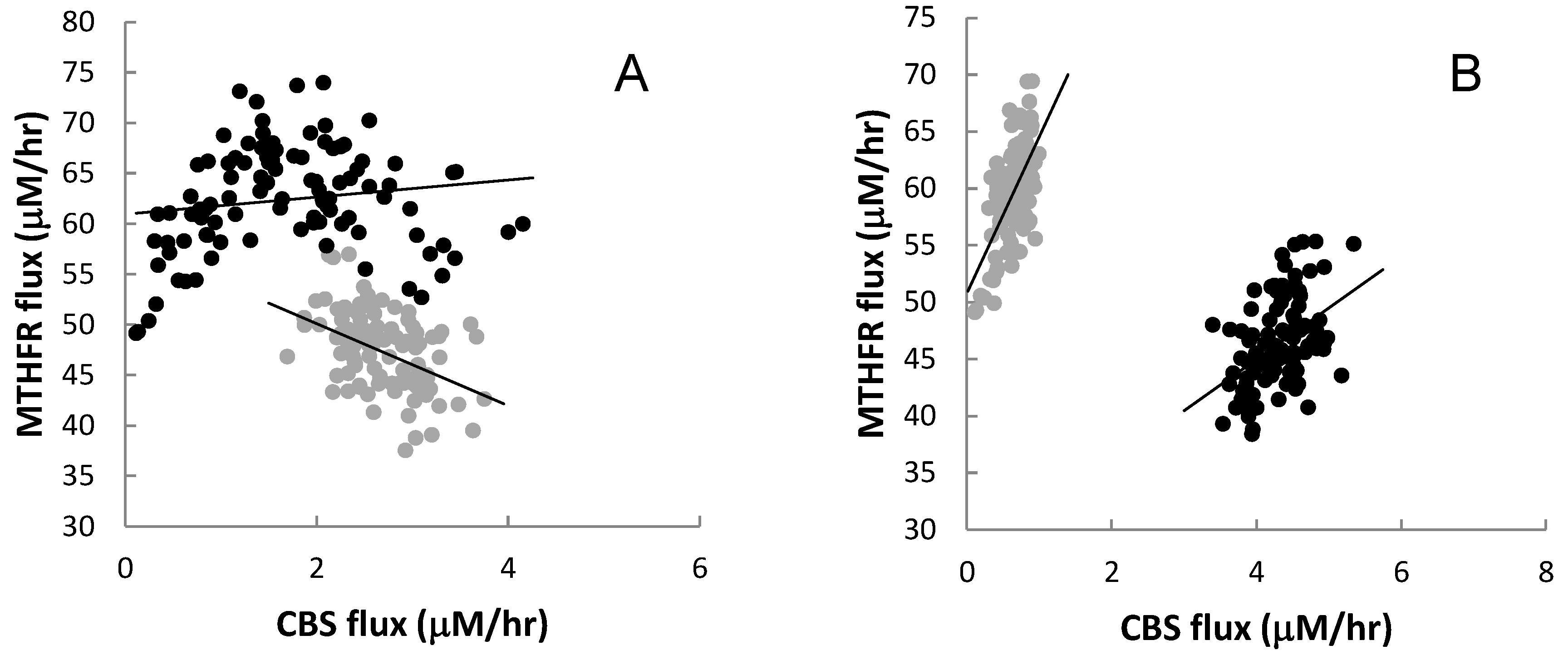
4. Discussion
5. Conclusions
Acknowledgments
Conflict of Interest
References
- Bailey, L.B. Folate in Health and Disease; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Carmel, R.; Jacobsen, D. Homocysteine in Health and Disease; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Duthie, S.J. Folic acid deficiency and cancer: Mechanisms of DNA instability. Br. Med. Bull. 1999, 55, 578–592. [Google Scholar] [CrossRef]
- Potter, J.D. Colorectal cancer: Molecules and populations. J. Natl. Cancer Inst. 1999, 91, 916–932. [Google Scholar]
- Eskes, T.K.A.B. Homocysteine in Human Reproduction. In Homocysteine in Health and Disease; Carmel, R., Jacobsen, D.W., Eds.; Cambridge University Press: Cambridge, UK, 2001; pp. 451–465. [Google Scholar]
- Refsum, H.; Ueland, P.M.; Nygard, O.; Vollset, S.E. Homocysteine and cardiovascular disease. Annu. Rev. Med. 1998, 49, 31–62. [Google Scholar] [CrossRef]
- Liu, Y.; Xia, Q.; Jia, Y.; Guo, H.; Wei, B.; Hua, Y.; Yang, S. Significance of differential expression of thymidylate synthase in normal and primary tumor tissues from patients with colorectal cancer. J. Hematol. Oncol. 2011, 4, 33. [Google Scholar] [CrossRef]
- Lennard, L. Methyltransferases; Elsevier: Kidlington, UK, 2010. [Google Scholar]
- James, S.J.; Cutler, P.; Melnyk, S.; Jernigan, S.; Janak, L.; Gaylor, D.W.; Neubrander, J.A. Metabolic biomarkers of increased oxidative stress and impaired methylation capacity in children with autism. Am. J. Clin. Nutr. 2004, 80, 1611–1617. [Google Scholar]
- Wu, G.; Fang, Y.-Z.; Yang, S.; Lupton, J.R.; Turner, N.D. Glutathione metabolism and its implications for health. J. Nutr. 2004, 134, 489–492. [Google Scholar]
- Ishibashi, M.; Akazawa, S.; Sakamaki, H.; Matsumoto, K.; Yamasaki, H.; Yamaguchi, Y.; Goto, S.; Urata, Y.; Kondo, T.; Nagataki, S. Oxygen-induced embryopathy and the significance of glutathione-dependent antioxidant system in the rat embryo during early organogenesis. Free Radic. Biol. Med. 1997, 22, 447–454. [Google Scholar] [CrossRef]
- Melnyk, S.; Pogribna, M.; Pogribny, I.; Yi, P.; James, S. Measurement of plasma and intracellular S-adenosylmethionine and S-adenosylhomocysteine utilizing coulometric electrochemical detection: Alterations with plasma homocysteine and pyridoxal 5′-phosphate concentrations. Clin. Chem. 2001, 47, 612. [Google Scholar]
- Duncan, T.; Reed, M.; Nijhout, H. The relationship between intracellular and plasma levels of folate and metabolites in the methionine cycle: A model. Mol. Nutr. Food Res. 2013, 57, 626–638. [Google Scholar]
- Nijhout, H.; Reed, M.; Anderson, D.; Mattingly, J.; James, J.; Ulrich, C. Long-range allosteric interactions between the folate and methionine cycles stabilize DNA methylation reaction rate. Epigenetics 2006, 1, 81–87. [Google Scholar]
- Nijhout, H.F.; Reed, M.C.; Budu, P.; Ulrich, C.M. A mathematical model of the folate cycle––New insights into folate homeostasis. J. Biol. Chem. 2004, 279, 55008–55016. [Google Scholar] [CrossRef]
- Reed, M.C.; Nijhout, H.F.; Neuhouser, M.L.; Gregory, J.F.; Shane, B.; James, S.J.; Boynton, A.; Ulrich, C.M. A mathematical model gives insights into nutritional and genetic aspects of folate-mediated one-carbon metabolism. J. Nutr. 2006, 136, 2653–2661. [Google Scholar]
- Reed, M.; Nijhout, H.; Sparks, R.; Ulrich, M. A mathematical model of the methionine cycle. J. Theor. Biol. 2004, 226, 33–43. [Google Scholar] [CrossRef]
- Limpert, E.; Stahel, W.; Abbt, M. Log-normal distributions across the sciences: Keys and clues. BioScience 2001, 51, 341–352. [Google Scholar] [CrossRef]
- Ulrich, C.M.; Neuhouser, M.; Liu, A.Y.; Boynton, A.; Gregory, J.F., III; Shane, B.; James, S.J.; Reed, M.C.; Nijhout, H.F. Mathematical modeling of folate metabolism: Predicted effects of genetic polymorphisms on mechanisms and biomarkers relevant to carcinogenesis. Cancer Epidemiol. Biomark. Prev. 2008, 17, 1822–1831. [Google Scholar] [CrossRef]
- Ueland, P.M.; Refsum, H. Plasma homocysteine, a risk factor for vascular disease: Plasma levels in health, disease, and drug therapy. J. Lab. Clin. Med. 1989, 114, 473–501. [Google Scholar]
- James, S.J.; Melnyk, S.; Jernigan, S.; Cleves, M.A.; Halsted, C.H.; Wong, D.H.; Cutler, P.; Bock, K.; Boris, M.; Bradstreet, J.J.; et al. Metabolic endophenotype and related genotypes are associated with oxidative stress in children with autism. Am. J. Med. Genet. B 2006, 141B, 947–956. [Google Scholar] [CrossRef]
- Reed, M.; Thomas, R.; Pavisic, J.; James, S.; Ulrich, C.; Nijhout, H. A mathematical model of glutathione metabolism. Theor. Biol. Med. Model. 2008, 5. [Google Scholar] [CrossRef]
- Pajares, M.; Duran, C.; Corrales, F.; Pliego, M.; Mato, J. Modulation of rat liver S-adenosylmethionine synthetase activity by glutathione. J. Biol. Chem. 1992, 267, 17598–17605. [Google Scholar]
- Gregory, J.F. Case study: Folate bioavailability. J. Nutr. 2001, 131, 1376S–1382S. [Google Scholar]
- Wright, A.J.A.; Finglas, P.M.; Dainty, J.R.; Hart, D.J.; Wolfe, C.A.; Southon, S.; Gregory, J.F. Single oral doses of 13c forms of pteroylmonoglutamic acid and 5-formyltetrahydrofolic acid elicit differences in short-term kinetics of labelled and unlabelled folates in plasma: Potential problems in interpretation of folate bioavailability studies. Br. J. Nutr. 2003, 90, 363–371. [Google Scholar]
- Gregory, J.F.; Quinlivan, E.P.; Davis, S.R. Integrating the issues of bioavailability, intake and metabolism in the era of fortification. Trends Food Sci. Technol. 2005, 16, 229–240. [Google Scholar] [CrossRef]
- McKillop, D.J.; McNulty, H.; Scott, J.M.; McPartlin, J.M.; Strain, J.; Bradbury, I.; Girvan, J.; Hoey, L.; McCreedy, R.; Alexander, J.; et al. The rate of intestinal absorption of natural food folates is not related to the extent of folate conjugation. Am. J. Clin. Nutr. 2006, 84, 167–173. [Google Scholar]
- Ganji, V.; Kafai, M. Trends in serum folate, rbc folate, and circulating total homocysteine concentrations in the united states: Analysis of data from national health and nutrition examination surveys, 1988–1994, 1999–2000, and 2001–2002. J. Nutr. 2006, 136, 153–158. [Google Scholar]
- Lindenbaum, J.; Allen, R. Clincal Spectrum and Diagnosis of Folate Deficiency. In Folate in Health and Disease; Bailey, L.B., Ed.; Marcel Dekker, Inc.: New York, NY, USA, 1995; pp. 43–74. [Google Scholar]
- Yetley, E.A.; Johnson, C.L. Folate and vitamin B-12 biomarkers in nhanes: History of their measurement and use. Am. J. Clin. Nutr. 2011, 94. [Google Scholar] [CrossRef]
- Selhub, J.; Jacques, P.F.; Wilson, P.W.F.; Rush, D.; Rosenberg, I.H. Vitamin status and intake as primary determinants of homocysteinemia in an elderly population. J. Am. Med. Assoc. 1993, 270, 2693–2698. [Google Scholar] [CrossRef]
- Williams, K.T.; Schalinske, K.L. New insights into the regulation of methyl group and homocysteine metabolism. J. Nutr. 2007, 137, 311–314. [Google Scholar]
- Caudill, M.A.; Wang, J.C.; Melnyk, S.; Pogribny, I.P.; Jernigan, S.; Collins, M.D.; Santos-Guzman, J.; Swendseid, M.E.; Cogger, E.A.; James, S.J. Intracellular S-adenosylhomocysteine concentrations predict global DNA hypomethylation in tissues of methyl-deficient cystathionine beta-synthase heterozygous mice. J. Nutr. 2001, 131, 2811–2818. [Google Scholar]
- Stam, F.; van Guldener, C.; ter Wee, P.M.; Kulik, W.; Smith, D.E.C.; Jakobs, C.; Stehouwer, C.D.A.; de Meer, K. Homocysteine clearance and methylation flux rates in health and end-stage renal disease: Association with S-adenosylhomocysteine. Am. J. Physiol. Ren. Physiol. 2004, 287, F215–F223. [Google Scholar] [CrossRef]
- Kealey, C.; Brown, K.; Woodside, J.; Young, I.; Murray, L.; Boreham, C.; McNulty, H.; Strain, J.J.; McPartlin, J.; Scott, J.; et al. A common insertion/deletion polymorphism of the thymidylate synthase (TYMS) gene is a determinant of red blood cell folate and homocysteine concentrations. Hum. Genet. 2005, 116, 347–353. [Google Scholar] [CrossRef]
- De Bree, A.; Verschuren, W.; Bjørke-Monsen, A.; van der Put, N.; Heil, S.; Trijbels, F.; Blom, H. Effect of the methylenetetrahydrofolate reductase 677c→T mutation on the relations among folate intake and plasma folate and homocysteine concentrations in a general population sample. Am. J. Clin. Nutr. 2003, 77, 687–693. [Google Scholar]
Supplementary Files
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Duncan, T.M.; Reed, M.C.; Nijhout, H.F. A Population Model of Folate-Mediated One-Carbon Metabolism. Nutrients 2013, 5, 2457-2474. https://doi.org/10.3390/nu5072457
Duncan TM, Reed MC, Nijhout HF. A Population Model of Folate-Mediated One-Carbon Metabolism. Nutrients. 2013; 5(7):2457-2474. https://doi.org/10.3390/nu5072457
Chicago/Turabian StyleDuncan, Tanya M., Michael C. Reed, and H. Frederik Nijhout. 2013. "A Population Model of Folate-Mediated One-Carbon Metabolism" Nutrients 5, no. 7: 2457-2474. https://doi.org/10.3390/nu5072457
APA StyleDuncan, T. M., Reed, M. C., & Nijhout, H. F. (2013). A Population Model of Folate-Mediated One-Carbon Metabolism. Nutrients, 5(7), 2457-2474. https://doi.org/10.3390/nu5072457