Plate Waste Forecasting Using the Monte Carlo Method for Effective Decision Making in Latvian Schools
Abstract
:1. Introduction
2. Related Work
3. Materials and Methods
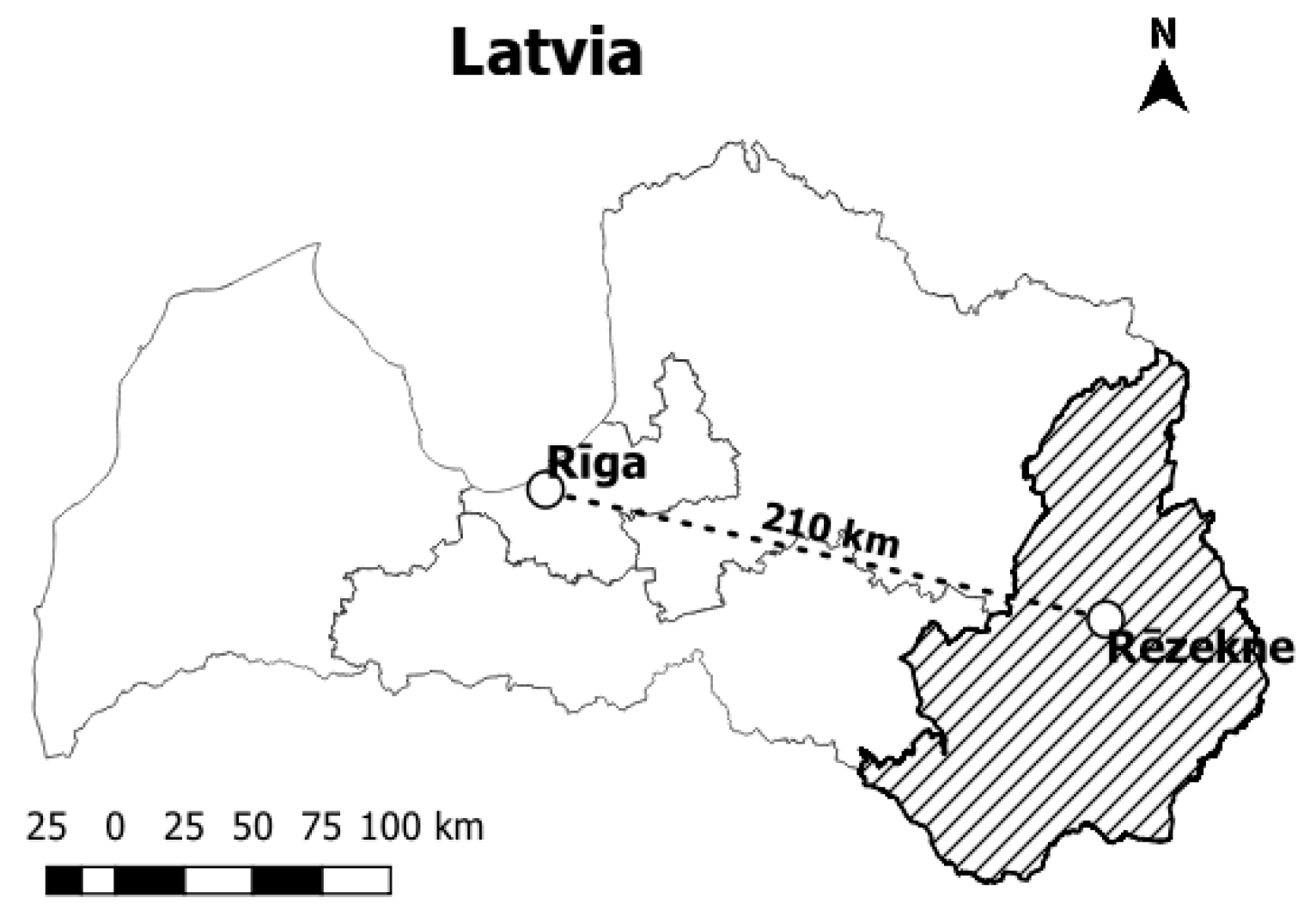
3.1. Methodology and Research Ethic
3.2. Important Parameters
3.2.1. A portion Size
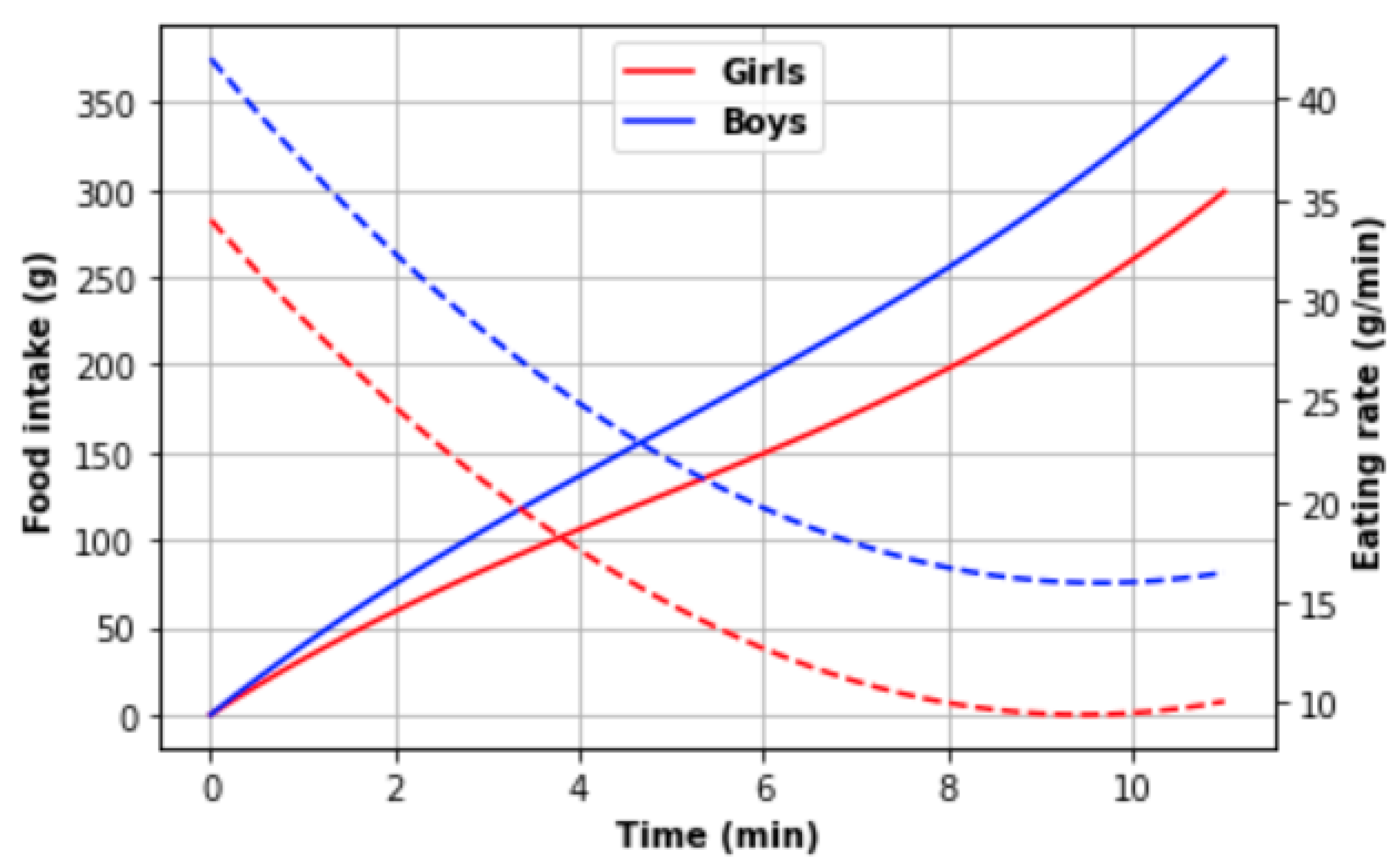
3.2.2. An Eating Rate
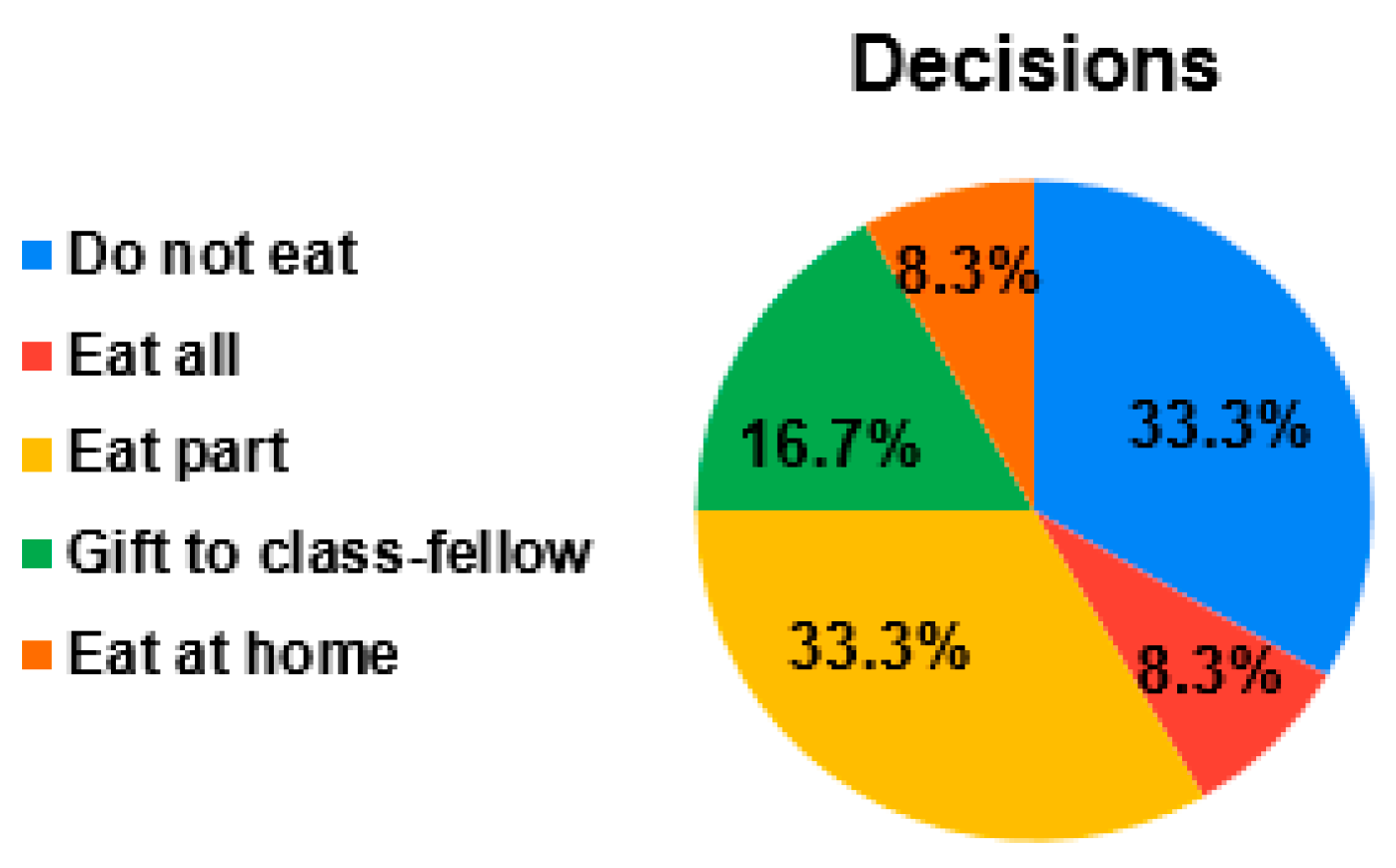
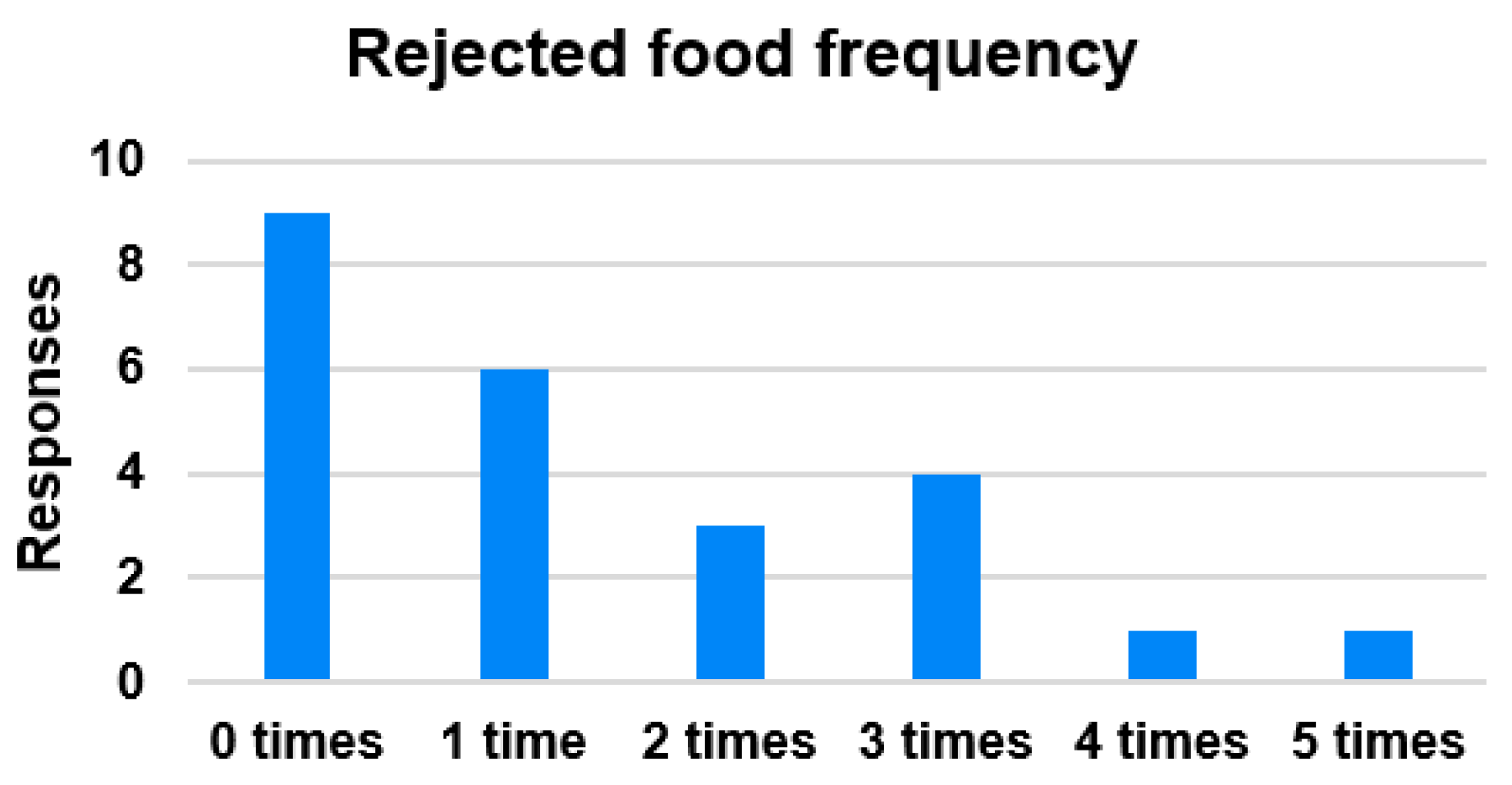
3.2.3. Children’s Eating Habits
3.2.4. Children’s Food Preferences
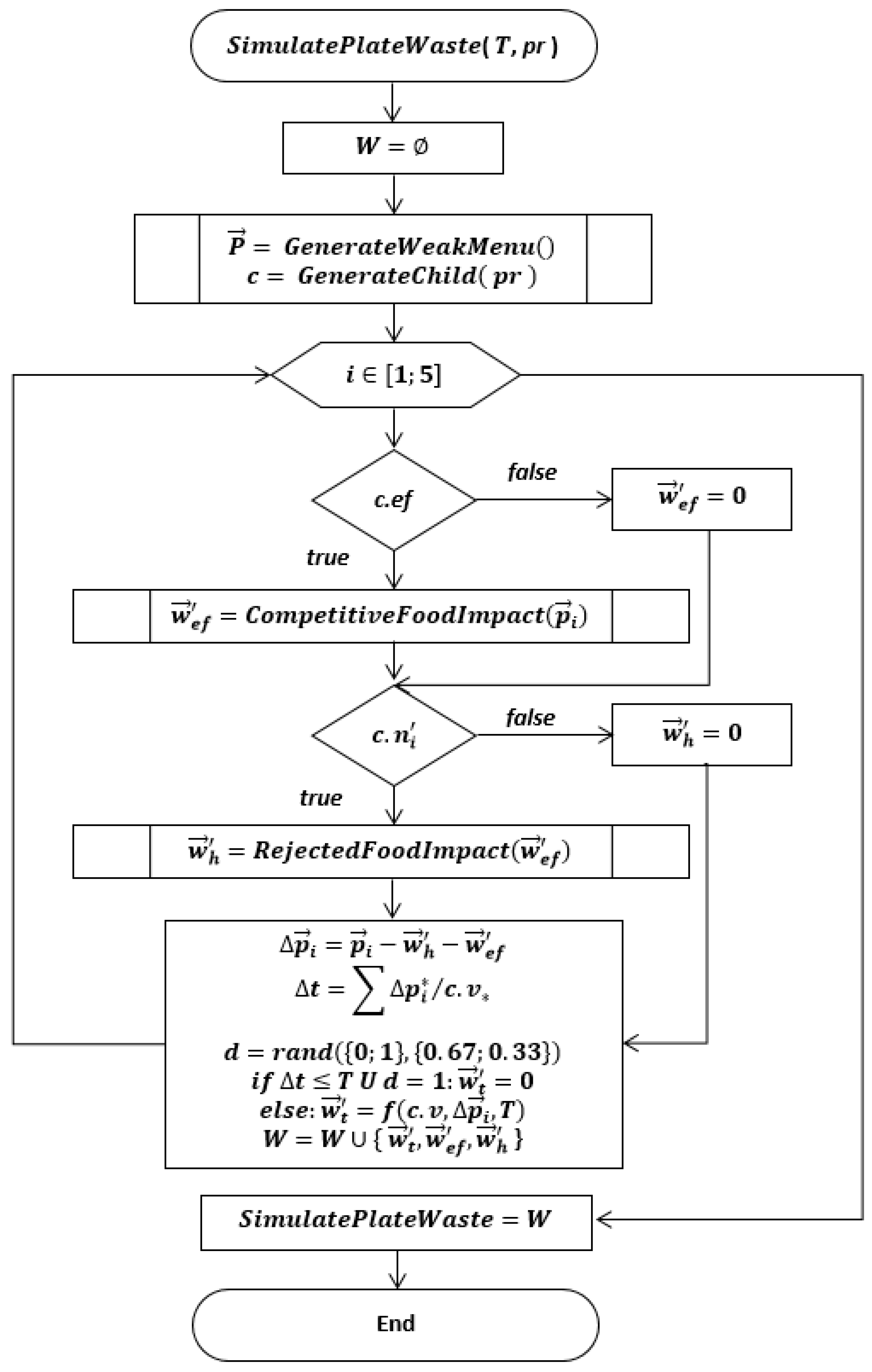
3.3. The Monte Carlo Model
3.4. Quality Control
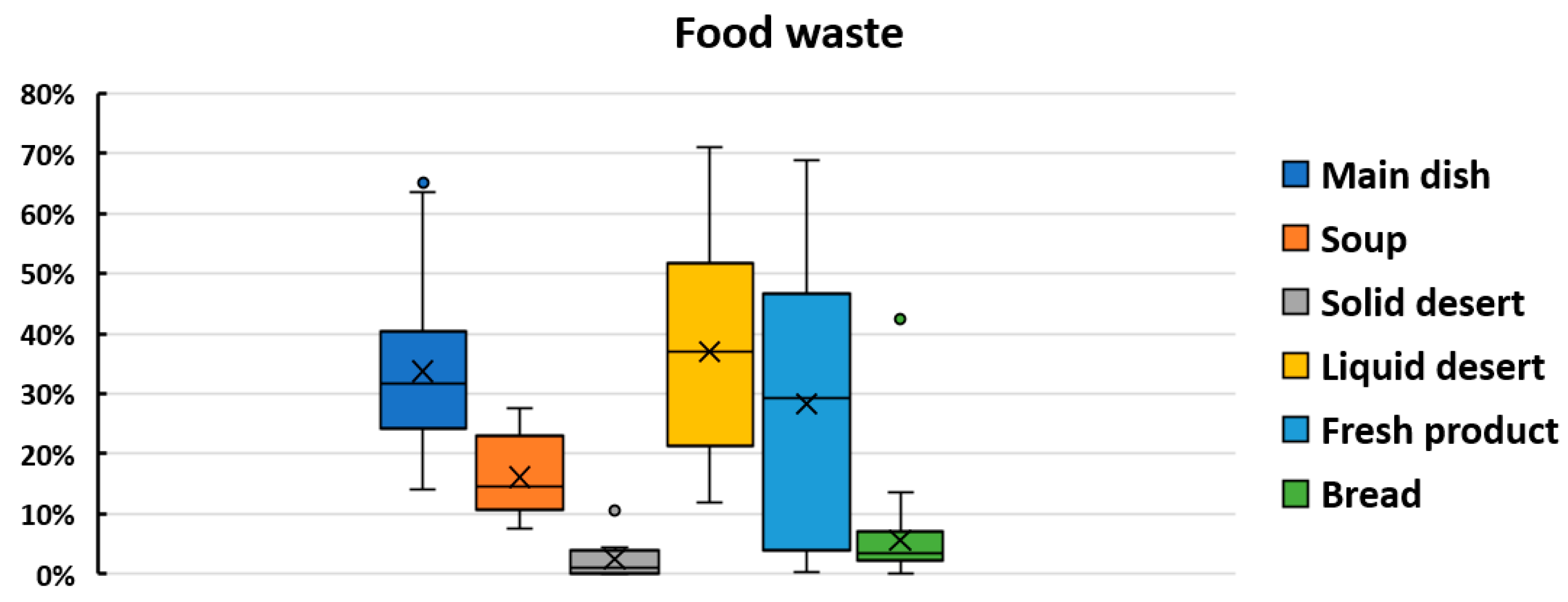
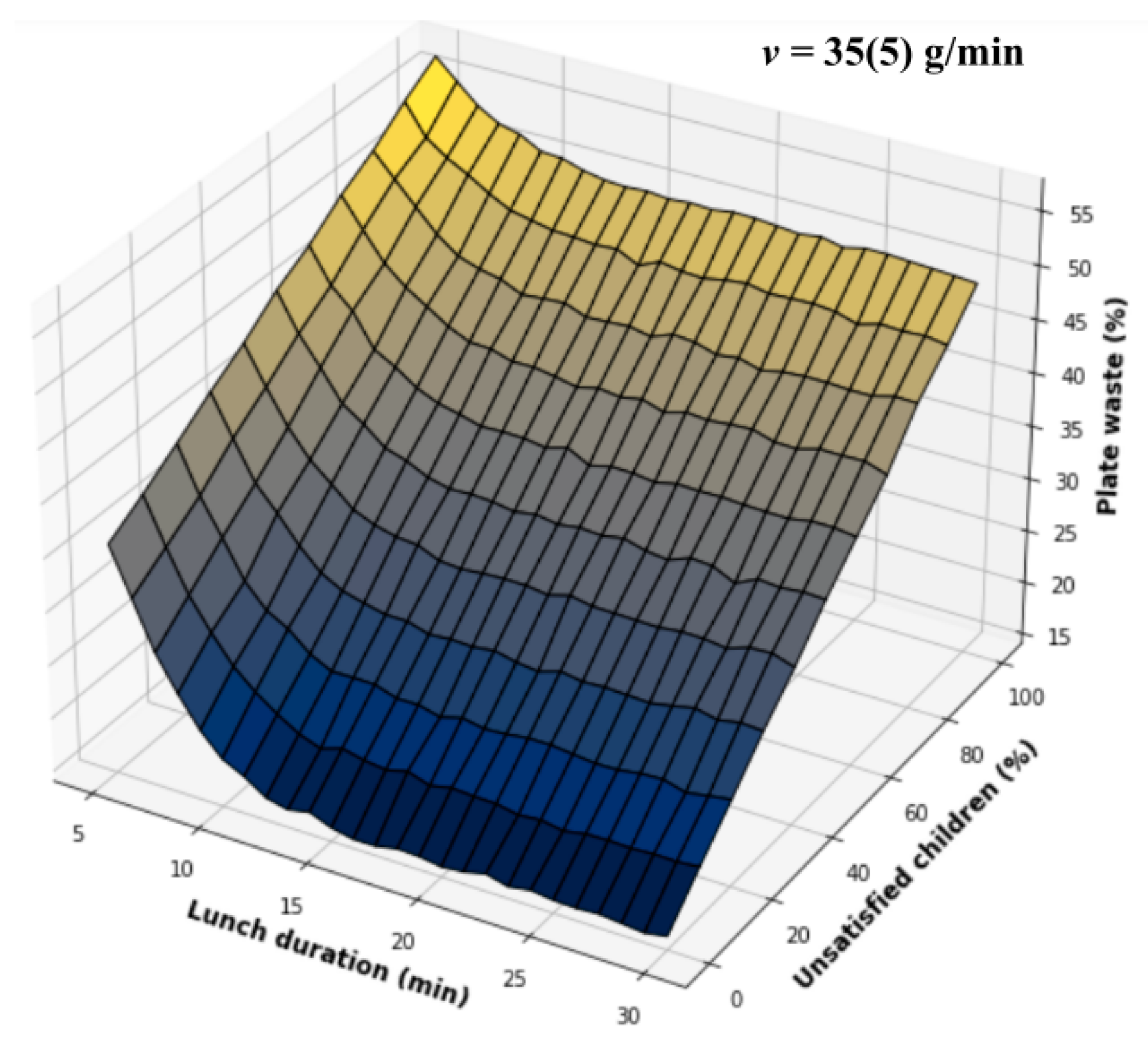
4. Experiment Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Food and Agriculture Organization of the United Nations. The State of Food Agriculture. Moving Forward on Food Loss and Waste Reduction. 2019. Available online: https://www.fao.org/3/ca6030en/ca6030en.pdf (accessed on 3 December 2021).
- Schanes, K.; Dobernig, K.; Goezet, B. Food waste matters—A systematic review of household food waste practices and their policy implications. J. Clean. Prod. 2018, 182, 978–991. [Google Scholar] [CrossRef]
- Cattaneo, A.; Sánchez, M.V.; Torero, M.; Vos, R. Reducing food loss and waste: Five challenges for policy and research. Food Policy 2021, 98, 101974. [Google Scholar] [CrossRef] [PubMed]
- Thyberg, K.L.; Tonjes, D.J. A Management Framework for Municipal Solid Waste Systems and Its Application to Food Waste Prevention. Systems 2015, 3, 133–151. [Google Scholar] [CrossRef] [Green Version]
- Thyberg, K.L.; Tonjes, D.J. Drivers of food waste and their implications for sustainable policy development. Resour. Conserv. Recycl. 2016, 106, 110–123. [Google Scholar] [CrossRef]
- Martin-Rios, C.; Demen-Meier, C.; Gössling, S.; Cornuz, C. Food waste management innovations in the foodservice industry. Waste Manag. 2018, 79, 196–206. [Google Scholar] [CrossRef] [Green Version]
- Betz, A.; Buchli, J.; Göbel, C.; Müller, C. Food waste in the Swiss food service industry—Magnitude and potential for reduction. Waste Manag. 2015, 35, 218–226. [Google Scholar] [CrossRef]
- Yui, S.; Biltekoff, C. How Food Becomes Waste: Students as “Carriers of Practice” in the UC Davis Dining Commons. J. Hunger Environ. Nutr. 2020, 16, 684–705. [Google Scholar] [CrossRef]
- Wilkie, A.C.; Graunke, R.E.; Cornejo, C. Food Waste Auditing at Three Florida Schools. Sustainability 2015, 7, 1370–1387. [Google Scholar] [CrossRef] [Green Version]
- Benvenuti, L.; De Santis, A.; Santesarti, F.; Tocca, L. An optimal plan for food consumption with minimal environmental impact: The case of school lunch menus. J. Clean. Prod. 2016, 129, 704–713. [Google Scholar] [CrossRef]
- Martin, C.K.; Newton, R.L., Jr.; Anton, S.D.; Allen, H.R.; Alfonso, A.; Han, H.; Stewart, T.; Sothern, M.; Williamson, D.A. Measurement of children’s food intake with digital photography and the effects of second servings upon food intake. Eat. Behav. 2007, 8, 148–156. [Google Scholar] [CrossRef]
- Grainger, M.; Stewart, G.; Piras, S.; Righi, S.; Setti, M.; Vittuari, M. D4.2-Model Development and Data Proto-Col. Technical Report. Available online: http://edepot.wur.nl/399920 (accessed on 3 December 2021).
- Craven, T.J.; Krejci, C.C. An agent-based model of regional food supply chain disintermediation. In Proceedings of the Agent-Directed Simulation Symposium (ADS ’17). Society for Computer Simulation International, San Diego, CA, USA, 23–26 April 2017; Article 8. pp. 1–10. [Google Scholar]
- Van Voorn, G.; Hengeveld, G.; Verhagen, J. An agent based model representation to assess resilience and efficiency of food supply chains. PLoS ONE 2020, 15, e0242323. [Google Scholar] [CrossRef] [PubMed]
- Scalco, A.; MacDiarmid, J.I.; Craig, T.; Whybrow, S.; Horgan, G.W. An Agent-Based Model to Simulate Meat Consumption Behaviour of Consumers in Britain. J. Artif. Soc. Soc. Simul. 2019, 22, 8. [Google Scholar] [CrossRef]
- Achmad, A.L.H.; Chaerani, D.; Perdana, T. Designing a food supply chain strategy during COVID-19 pandemic using an integrated Agent-Based Modelling and Robust Optimization. Heliyon 2021, 7, e08448. [Google Scholar] [CrossRef] [PubMed]
- Ravandi, B.; Jovanovic, N. Impact of plate size on food waste: Agent-based simulation of food consumption. Resour. Conserv. Recycl. 2019, 149, 550–565. [Google Scholar] [CrossRef]
- Dolnicar, S.; Juvan, E. Drivers of plate waste: A mini theory of action based on staff observations. Ann. Tour. Res. 2019, 78, 102731. [Google Scholar] [CrossRef]
- Juvan, E.; Grün, B.; Baruca, P.Z.; Dolnicar, S. Drivers of plate waste at buffets: A comprehensive conceptual model based on observational data and staff insights. Ann. Tour. Res. Empir. Insights 2021, 2, 100010. [Google Scholar] [CrossRef]
- Anderson, S.M.; Olds, D.A.; Wolfe, K.L. The Impact of a Portion Plate on Plate Waste in a University Dining Hall. J. Foodserv. Manag. Educ. 2021, 15, 1–7. Available online: https://fsmec.org/wp-content/uploads/2021/11/15-2.pdf (accessed on 3 December 2021).
- Malefors, C.; Strid, I.; Hansson, P.-A.; Eriksson, M. Potential for using guest attendance forecasting in Swedish public catering to reduce overcatering. Sustain. Prod. Consum. 2021, 25, 162–172. [Google Scholar] [CrossRef]
- Malefors, C.; Secondi, L.; Marchetti, S.; Eriksson, M. Food waste reduction and economic savings in times of crisis: The potential of machine learning methods to plan guest attendance in Swedish public catering during the COVID-19 pandemic. Socio-Econ. Plan. Sci. 2021, 101041. [Google Scholar] [CrossRef]
- Fagerberg, P.; Charmandari, E.; Diou, C.; Heimeier, R.; Karavidopoulou, Y.; Kassari, P.; Koukoula, E.; Lekka, I.; Maglaveras, N.; Maramis, C.; et al. Fast Eating Is Associated with Increased BMI among High-School Students. Nutrients 2021, 13, 880. [Google Scholar] [CrossRef]
- Liz Martins, M.; Rodrigues, S.S.; Cunha, L.M.; Rocha, A. Factors influencing food waste during lunch of fourth-grade school children. Waste Manag. 2020, 113, 439–446. [Google Scholar] [CrossRef] [PubMed]
- Zandian, M.; Ioakimidis, I.; Bergström, J.; Brodin, U.; Bergh, C.; Leon, M.; Shield, J.; Södersten, P. Children eat their school lunch too quickly: An exploratory study of the effect on food intake. BMC Public Health 2012, 12, 351. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kodors, S.; Zhukov, V.; Zarembo, I.; Litavniece, L.; Lonska, J.; Zvaigzne, A. Simulation of a school canteen to understand meal duration impact on food waste. In Proceedings of the 13th International Scientific and Practical Conference Environment, Technology, Resources, Rezekne, Latvia, 17–18 June 2021; Volume 2, pp. 84–87. [Google Scholar] [CrossRef]
- Ferriday, D.; Bosworth, M.; Lai, S.; Godinot, N.; Martin, N.; Martin, A.A.; Rogers, P.J.; Brunstrom, J. Effects of eating rate on satiety: A role for episodic memory? Physiol. Behav. 2015, 152 Pt B, 389–396. [Google Scholar] [CrossRef] [Green Version]
- Scaglioni, S.; Arrizza, C.; Vecchi, F.; Tedeschi, S. Determinants of children’s eating behavior. Am. J. Clin. Nutr. 2011, 94, 2006S–2011S. [Google Scholar] [CrossRef] [PubMed]
- De Cosmi, V.; Scaglioni, S.; Agostoni, C. Early Taste Experiences and Later Food Choices. Nutrients 2017, 9, 107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scaglioni, S.; De Cosmi, V.; Ciappolino, V.; Parazzini, F.; Brambilla, P.; Agostoni, C. Factors Influencing Children’s Eating Behaviours. Nutrients 2018, 10, 706. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ragelienė, T. Do children favor snacks and dislike vegetables? Exploring children’s food preferences using drawing as a projective technique. A cross-cultural study. Appetite 2021, 165, 105276. [Google Scholar] [CrossRef] [PubMed]
- Cohen, J.F.; Jahn, J.L.; Richardson, S.; Cluggish, S.A.; Parker, E.; Rimm, E.B. Amount of Time to Eat Lunch Is Associated with Children’s Selection and Consumption of School Meal Entrée, Fruits, Vegetables, and Milk. J. Acad. Nutr. Diet. 2016, 116, 123–128. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hamdi, N.; Ellison, B.; McCaffrey, J.; Metcalfe, J.J.; Hoffman, A.; Haywood, P.; Prescott, M.P. Implementation of a Multi-Component School Lunch Environmental Change Intervention to Improve Child Fruit and Vegetable Intake: A Mixed-Methods Study. Int. J. Environ. Res. Public Health 2020, 17, 3971. [Google Scholar] [CrossRef] [PubMed]
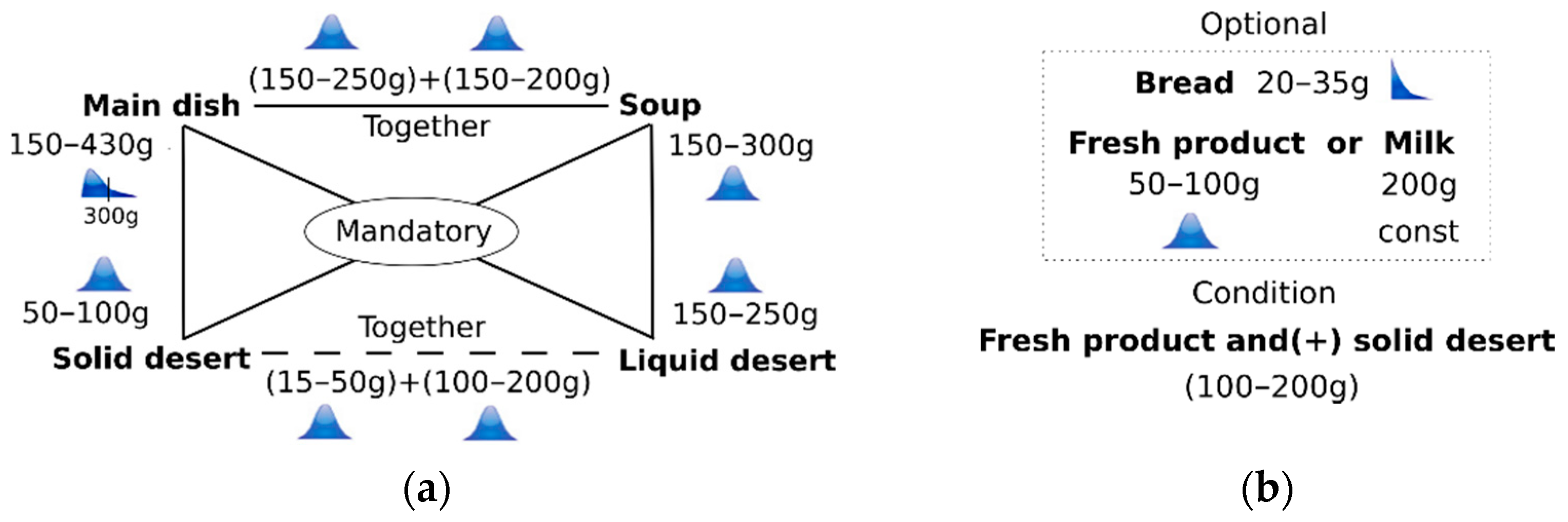
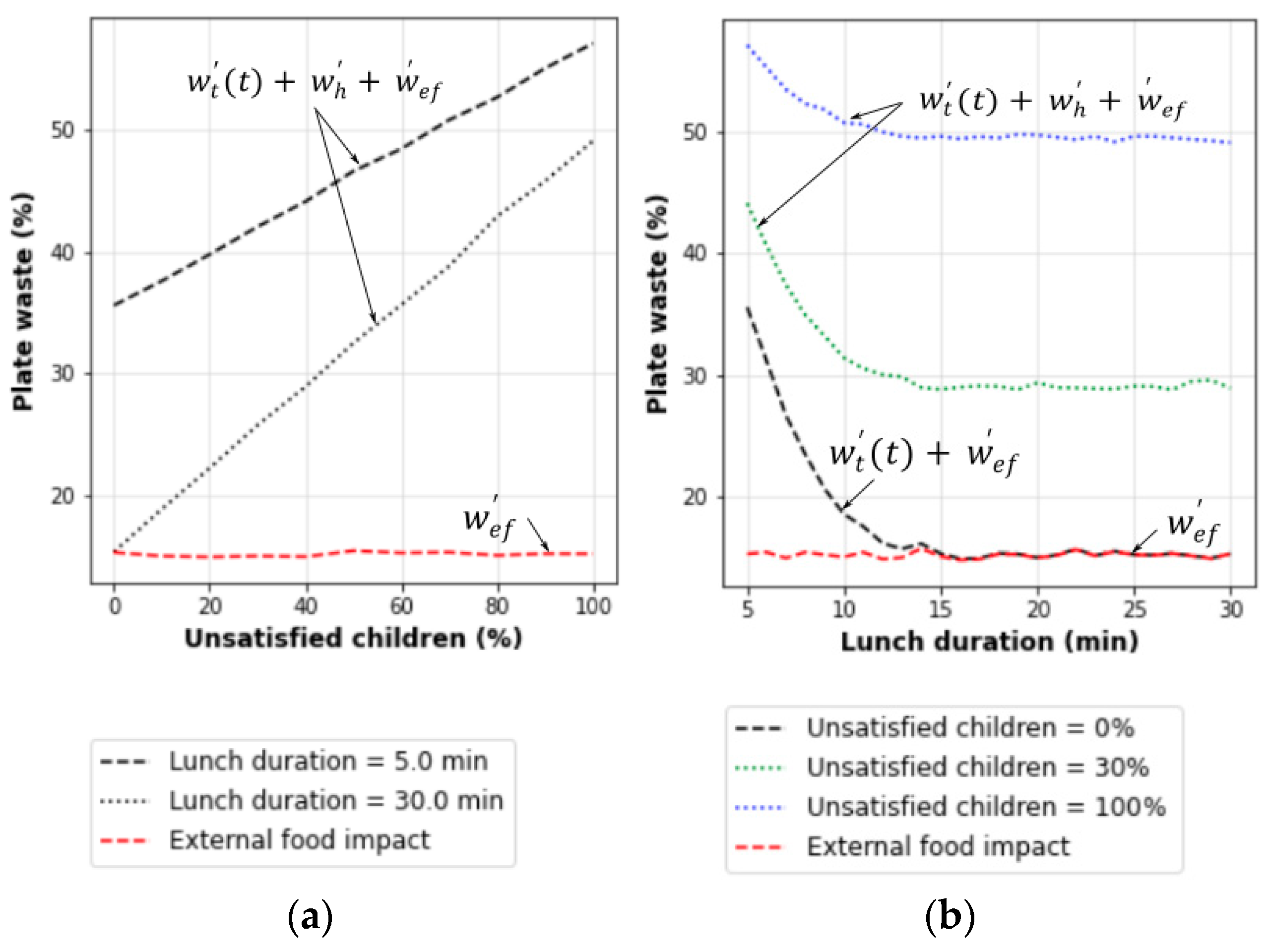
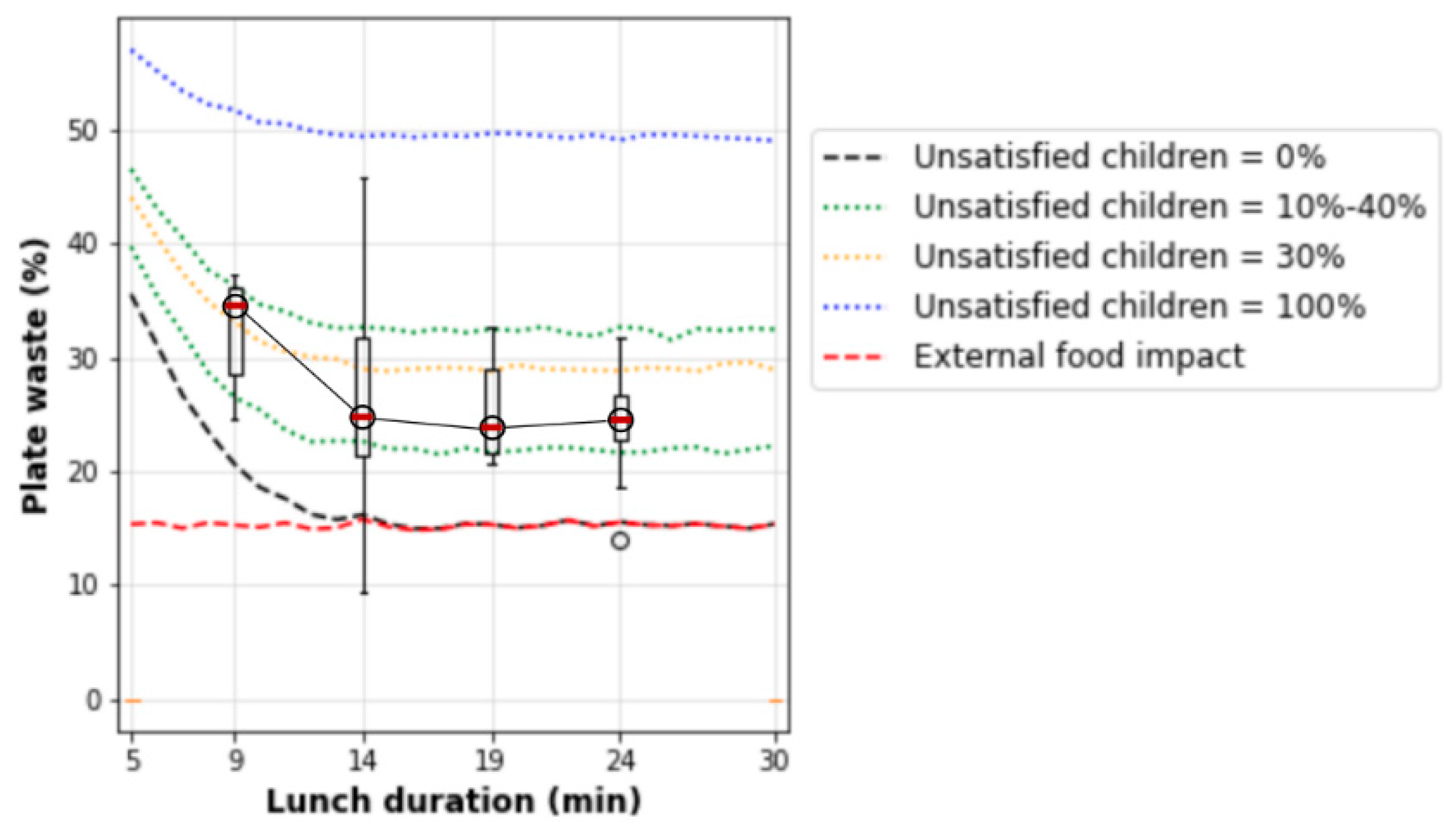
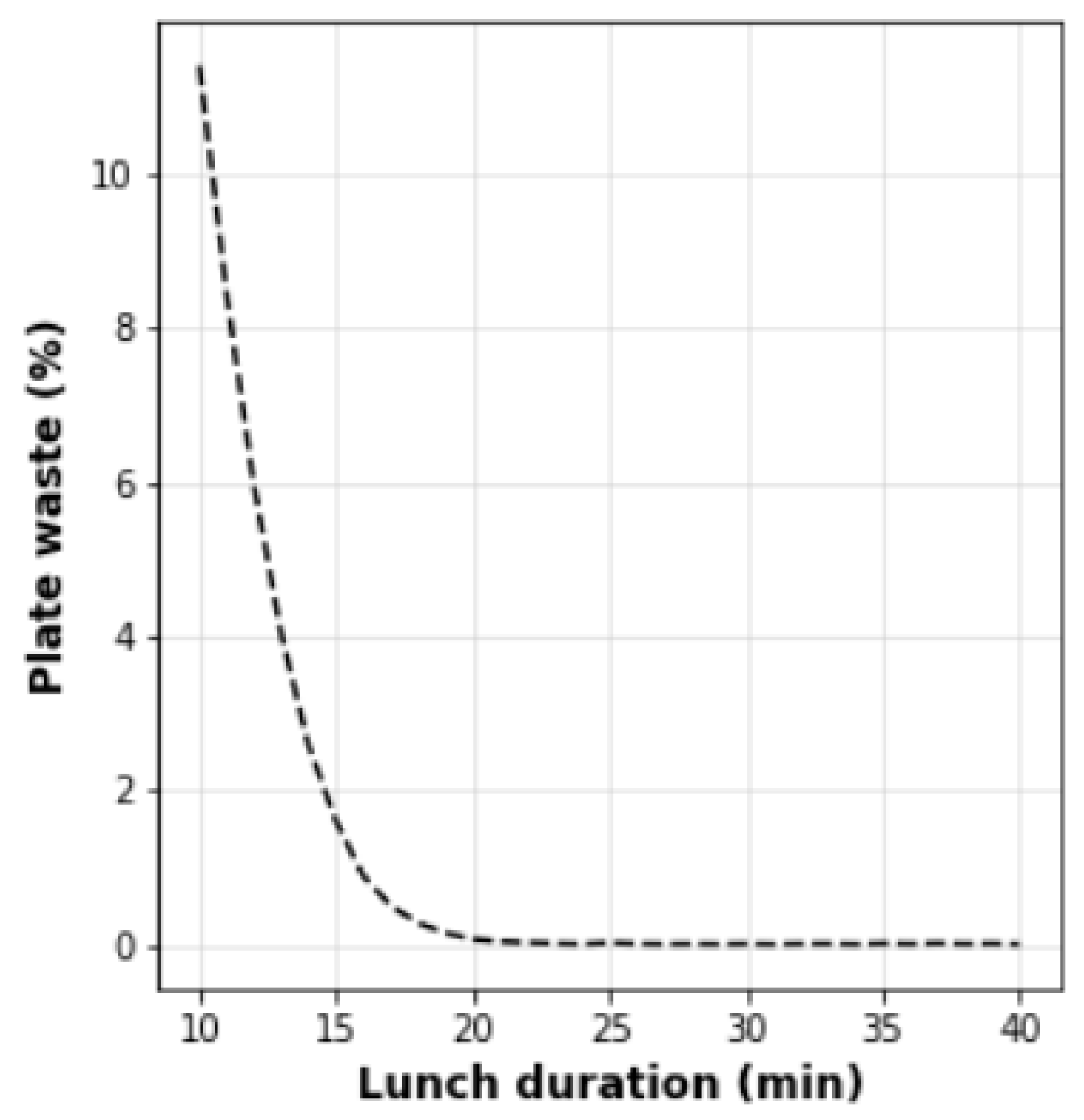

| Meal Component | Weight (g) | Distribution | Python |
|---|---|---|---|
| Main dish (M) | [150; 430] | gumbel | np.random.gumbel (225, 37.5) |
| Soup (S) | [150; 300] | normal | np.random.normal (225, 37.5) |
| Solid dessert (Sd) | [50; 100] | normal | np.random.normal (75, 12.5) |
| Liquid dessert (Ld) | [150; 250] | normal | np.random.normal (200, 25) |
| Bread (B) | [20; 35] | exponential | np.random.exponential (1.2) + 20 |
| Fresh product (Fp) | [50; 100] | normal | np.random.normal (75, 12.5) |
| Milk (Mk) | 200 | const | 200 |
| Main dish & soup (MS) | [150; 250] + [150; 200] | normal × 2 | np.random.normal (200, 25) np.random.normal (175, 12.5) |
| Solid & liquid dessert (D) | [15; 50] + [100; 200] | normal × 2 | np.random.normal (32.5, 8.75) np.random.normal (150, 25) |
| Day | m (g) | s (g) | sd (g) | ld (g) | b (g) | fp (g) | mk (g) | p (g) |
|---|---|---|---|---|---|---|---|---|
| Mon | 300 | 0 | 40 | 210 | 25 | 0 | 0 | 575 |
| Tue | 205 | 0 | 180 | 200 | 25 | 25 | 0 | 635 |
| Wed | 230 | 255 | 0 | 200 | 25 | 30 | 0 | 740 |
| Thu | 230 | 0 | 180 | 200 | 25 | 30 | 0 | 665 |
| Fri | 240 | 125 | 0 | 200 | 25 | 0 | 0 | 590 |
| Answers | Impact of the School Optional Menu | Impact of Competitive Food from Outside the School |
|---|---|---|
| Eat 0–24% | 22.2% | 25.0% |
| Eat 25–49% | 11.1% | 25.0% |
| Eat 50–74% | 33.3% | 25.0% |
| Eat 75–100% | 33.3% | 25.0% |
| Answers | Home Food | School Optional Menu | Outside the School | Probability of Competitive Food |
|---|---|---|---|---|
| Yes | 12.5% | 33.3% | 16.7% | 21.0% |
| No | 75.0% | 45.8% | 54.2% | 58.0% |
| Sometimes | 12.5% | 20.8% | 29.2% | 21.0% |
| Answers | Do Not Eat Soup | Do Not Eat the Main Dish | Do Not Drink Sweet Drinks |
|---|---|---|---|
| Yes | 50% | 8% | 0% |
| No | 50% | 92% | 100% |
| Attributes | Pseudocode |
|---|---|
| —type of menu; MS—distribution “main dish & soup”; —distribution “main dish & dessert”; —distribution “soup & dessert”; —main dish (g); —soup (g). | |
ld—liquid dessert (g). | |
mk—milk (g). | |
| —meal portion. |
| Attributes | Pseudocode |
|---|---|
u—child unsatisfied with school food. | |
| —days of rejected food. | |
| —child. |
| Attributes | Pseudocode |
|---|---|
—plate waste due to competitive food. | |
| Attributes | Pseudocode |
|---|---|
| —plate waste due to rejected food; waste distributions by food categories; child does not eat soup; —child does not eat the main dish. | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kodors, S.; Zvaigzne, A.; Litavniece, L.; Lonska, J.; Silicka, I.; Kotane, I.; Deksne, J. Plate Waste Forecasting Using the Monte Carlo Method for Effective Decision Making in Latvian Schools. Nutrients 2022, 14, 587. https://doi.org/10.3390/nu14030587
Kodors S, Zvaigzne A, Litavniece L, Lonska J, Silicka I, Kotane I, Deksne J. Plate Waste Forecasting Using the Monte Carlo Method for Effective Decision Making in Latvian Schools. Nutrients. 2022; 14(3):587. https://doi.org/10.3390/nu14030587
Chicago/Turabian StyleKodors, Sergejs, Anda Zvaigzne, Lienite Litavniece, Jelena Lonska, Inese Silicka, Inta Kotane, and Juta Deksne. 2022. "Plate Waste Forecasting Using the Monte Carlo Method for Effective Decision Making in Latvian Schools" Nutrients 14, no. 3: 587. https://doi.org/10.3390/nu14030587
APA StyleKodors, S., Zvaigzne, A., Litavniece, L., Lonska, J., Silicka, I., Kotane, I., & Deksne, J. (2022). Plate Waste Forecasting Using the Monte Carlo Method for Effective Decision Making in Latvian Schools. Nutrients, 14(3), 587. https://doi.org/10.3390/nu14030587








