Evaluation of Latent Models Assessing Physical Fitness and the Healthy Eating Index in Community Studies: Time-, Sex-, and Diabetes-Status Invariance
Abstract
1. Introduction
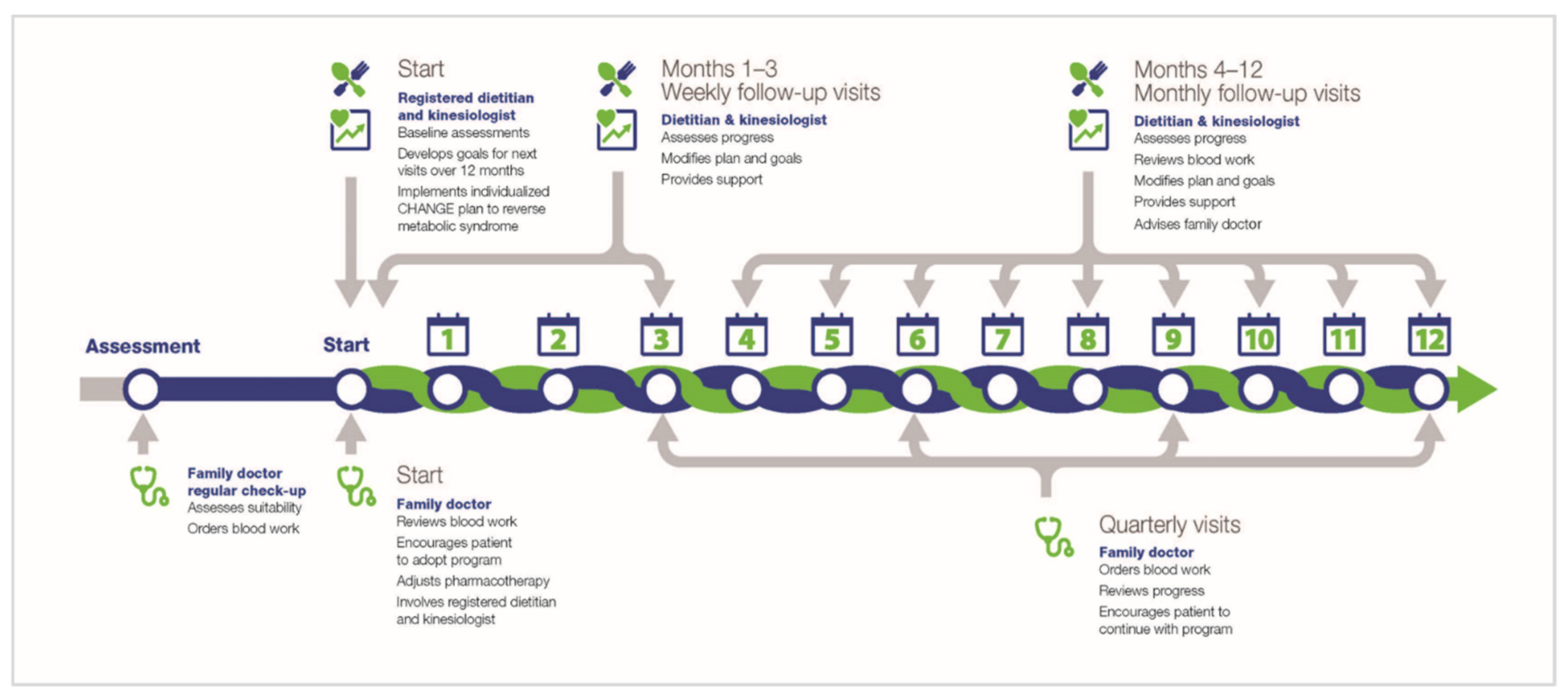
1.1. Lifestyle Treatment of Cardio-Metabolic Conditions
1.2. Measurement Issues
1.3. Fitness Assessment
1.4. Diet Quality Assessment
1.5. Structural Equation Modeling and Measurement Equivalence/Invariance (ME/I)
2. Methods
2.1. Data from Original Study
2.2. Available Measures
2.2.1. Physical Activity/Fitness
2.2.2. Diet Quality—HEI-C
2.2.3. Other Variables
2.3. Analytics Plan
3. Results
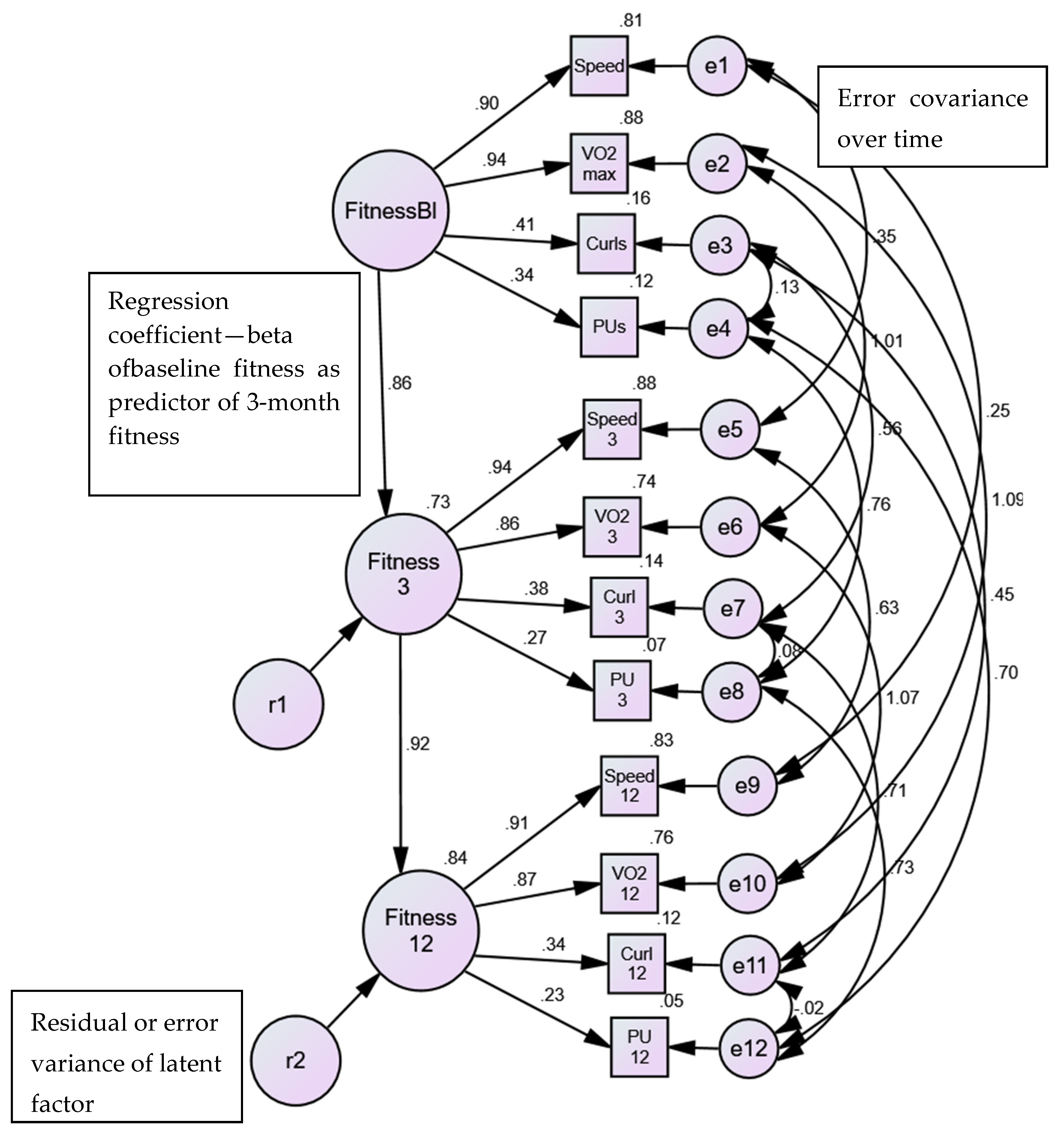
3.1. Physical Activity/Fitness
3.1.1. Exploratory Factor Analysis Model
| Model # | Model | X2 (df) | X2 p-Value | CFI | NNFI | RMSEA [95% CI] | ΔX2 ΔCFI ΔRMSEA |
|---|---|---|---|---|---|---|---|
| Desirable Criterion or Range | NS desirable | >0.9 | >0.9 | 0.05–0.08 acceptable; lower better | ΔX2 = NS ΔCFI ≤ 0.005 ΔRMSEA ≤ 0.01 | ||
| Longitudinal Invariance | |||||||
| 1 | 1-Factor Model | 0.939 (1) | 0.333 | 1.00 | 1.00 | 0.000 0.000–0.153 | |
| 2 | Longitudinal Configural | 139.29 (37) | 0.001 | 0.97 | 0.94 | 0.097 0.080–0.115 | |
| 3 | Longitudinal Metric | 159.36 (43) | 0.001 | 0.96 | 0.93 | 0.096 0.081–0.112 | Reject. Accept Accept |
| 4 | Longitudinal Intercepts Only | 394.09 (45) | 0.001 | 0.89 | 0.80 | 0.157 0.148–0.178 | Reject Reject Reject |
| 5 | Longitudinal Loadings and Intercepts | 415.82 (51) | 0.001 | 0.88 | 0.82 | 0.157 0.143–0.171 | Reject Reject Reject |
| 6 | Longitudinal Model Residuals | Not tested as invariant intercepts not found | |||||
| Sex Models—Female | |||||||
| 7 | Female Baseline | 0.100 (1) | 0.752 | 1.00 | 1.00 | 0.000 0.000–0.148 | |
| 8 | Female Longitudinal Configural | 56.99 (37) | 0.019 | 0.98 | 0.96 | 0.060 0.025–0.089 | |
| 9 | Female Longitudinal Metric | 66.57 (43) | 0.012 | 0.98 | 0.96 | 0.060 0.029–0.088 | Accept Accept Accept |
| 10 | Female Intercepts Only | 171.13 (45) | 0.001 | 0.88 | 0.80 | 0.136 0.115–0.158 | Reject Reject Reject |
| 11 | Female Loadings and Intercepts | 180.89 (51) | 0.001 | 0.88 | 0.82 | 0.130 0.110–0.151 | Accept Accept Accept |
| 12 | Female Residuals | Not tested as invariant intercepts not found | |||||
| Sex Models—Male | |||||||
| 13 | Male Baseline | 3.94 (1) | 0.047 | 0.99 | 0.90 | 0.145 0.014–0.307 | |
| 14 | Males Longitudinal Configural | 117.59 (37) | 0.001 | 0.95 | 0.90 | 0.125 0.100–0.150 | |
| 15 | Males Longitudinal Metric | 136.59 (43) | 0.001 | 0.95 | 0.90 | 0.125 0.102–0.149 | Reject Accept Accept |
| 16 | Male Intercepts Only | 250.41 (45) | 0.001 | 0.88 | 0.80 | 0.181 0.159–0.203 | Reject Reject Reject |
| 17 | Male Loadings and Intercepts | 275.94 (51) | 0.001 | 0.87 | 0.80 | 0.177 0.157–0.198 | Reject Reject Reject |
| 18 | Male Residuals | Not tested as invariant intercepts not found | |||||
| Gender Invariance of Longitudinal Fitness Model | |||||||
| 19 | Sex Invar. Configural | 174.60 (74) | 0.001 | 0.96 | 0.93 | 0.068 0.055–0.082 | |
| 20 | Sex Model Sex Invariant | 180.76 (83) | 0.001 | 0.97 | 0.94 | 0.064 0.051–0.076 | Accept Accept Accept |
| 21 | Sex Model Time Invariant | 206.58 (89) | 0.001 | 0.96 | 0.93 | 0.067 0.055–0.079 | Reject Accept Accept |
| 22 | Sex Model Intercepts | Not run based on previous intercept models | |||||
| 23 | Sex Model Residuals | Not run as intercept models were not accepted | |||||
| Disease-State Models—No Diabetes | |||||||
| 24 | NoDM Baseline | 1.12 (1) | 0.290 | 1.00 | 0.96 | 0.029 0.000–0.228 | |
| 25 | NoDM Longitudinal Configural | 97.42 (37) | 0.001 | 0.96 | 0.91 | 0.108 0.082–0.134 | |
| 26 | NoDM Longitudinal Metric | 106.96 (43) | 0.001 | 0.95 | 0.91 | 0.103 0.079–0.128 | Accept Accept Accept |
| 27 | NoDM Longitudinal Intercepts Only | 218.98 (45) | 0.001 | 0.87 | 0.78 | 0.166 0.145–0.189 | Reject Reject Reject |
| 28 | NoDM Residuals | Not tested as invariant intercepts not found | |||||
| Disease-State Models—Diabetes | |||||||
| 29 | DM Baseline | 0.002 (1) | 0.968 | 1.00 | 1.00 | 0.000 0.000–0.000 | |
| 30 | DM Longitudinal Configural | 72.57 (37) | 0.001 | 0.98 | 0.96 | 0.080 0.052–0.107 | |
| 31 | DM Longitudinal Metric | 89.75 (43) | 0.001 | 0.97 | 0.95 | 0.085 0.060–0.110 | Reject Accept Accept |
| 32 | DM Longitudinal Intercepts Only | 215.14 (45) | 0.001 | 0.91 | 0.84 | 0.158 0.137–0.180 | Reject Reject Reject |
| 33 | DM Residuals | Not tested as invariant intercepts not found | |||||
| Disease Invariance of Longitudinal Fitness Model | |||||||
| 34 | Disease Model Configural | 170.00 (74) | 0.001 | 0.97 | 0.94 | 0.067 0.054–0.080 | |
| 35 | Disease Model Disease Invariant | 184.87 (83) | 0.001 | 0.97 | 0.94 | 0.065 0.052–0.078 | Accept Accept Accept |
| 36 | Disease Model Time Invariant | 201.93 (89) | 0.001 | 0.96 | 0.94 | 0.066 0.054–0.078 | Reject Accept Accept |
| 37 | Disease Model Intercepts | Not run based on previous intercept models | |||||
| 38 | Disease Model Residuals | Not run as intercept models were not accepted | |||||
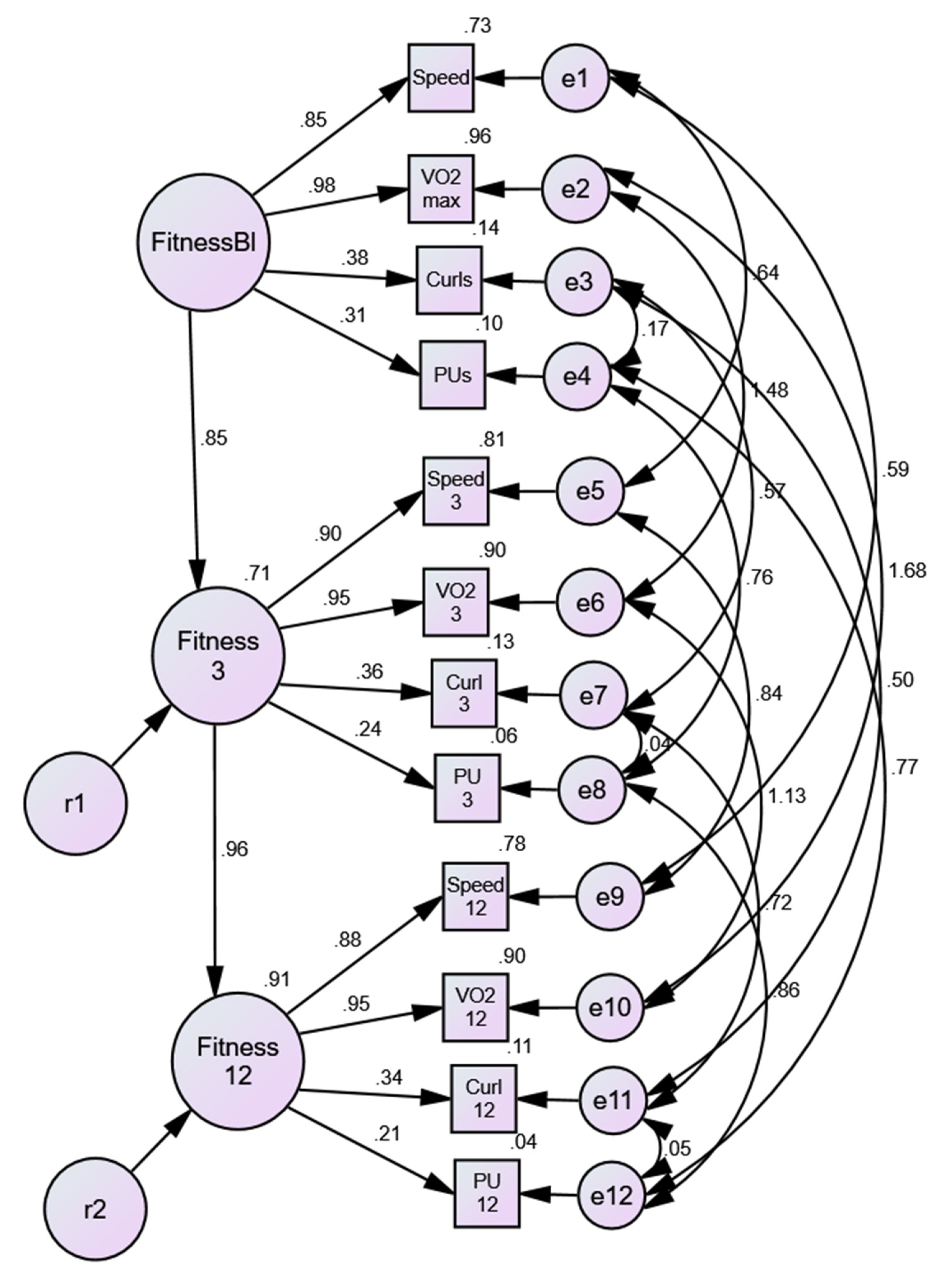
3.1.2. Longitudinal Extension of Physical Activity/Fitness Model
3.1.3. Sex Invariance of Physical Activity/Fitness Model
3.1.4. Disease-State Invariance of Physical Activity/Fitness Model
3.2. Healthy Eating Index (HEI-C)
3.2.1. Exploratory Factor Analysis Model
3.2.2. Testing the Reduced HEI-C in CFA/SEM
| Model # | Model | X2 (df) | X2 p-value | CFI | NNFI | RMSEA [95% CI] | ΔX2 ΔCFI ΔRMSEA |
|---|---|---|---|---|---|---|---|
| Desirable Criterion or Range | NS desirable | >0.9 | >0.9 | 0.05–0.08 acceptable; lower better | ΔX2 = NS ΔCFI ≤ 0.005 ΔRMSEA ≤ 0.01 | ||
| Longitudinal Invariance | |||||||
| 1 | 1-Factor Model | 11.10 (12) | 0.521 | 1.00 | 1.00 | 0.000 0.000 -0.056 | |
| 2 | Longitudinal Configural | 205.15 (160) | 0.009 | 0.95 | 0.93 | 0.031 0.046–0.063 | |
| 3 | Longitudinal Metric | 219.33 (172) | 0.009 | 0.95 | 0.94 | 0.031 0.016–0.042 | Accept Accept Accept |
| 4 | Longitudinal Intercepts Only | 371.10 (174) | 0.001 | 0.80 | 0.74 | 0.062 0.054–0.071 | Reject Reject Reject |
| 5 | Longitudinal Loadings and Intercepts | 388.17 (186) | 0.001 | 0.80 | 0.75 | 0.061 0.052–0.070 | Accept Accept Accept |
| 6 | Longitudinal Model Residuals | Not tested as invariant intercepts not found | |||||
| Sex Models—Female | |||||||
| 7 | Female Baseline | 25.39 (12) | 0.019 | 0.90 | 0.77 | 0.086 0.038–0.133 | |
| 8 | Female Longitudinal Configural | 200.85 (160) | 0.016 | 0.93 | 0.89 | 0.041 0.019–0.058 | |
| 9 | Female Longitudinal Metric | 219.28 (172) | 0.009 | 0.92 | 0.89 | 0.043 0.028–0.059 | Accept Accept Accept |
| 10 | Female Intercepts Only | 290.84 (174) | 0.001 | 0.79 | 0.72 | 0.067 0.053–0.080 | Reject Reject Reject |
| 11 | Female Loadings and Intercepts | 309.48 (186) | 0.001 | 0.78 | 0.72 | 0.066 0.053–0.079 | Accept Accept Accept |
| 12 | Female Residuals | Not tested as invariant intercepts not found | |||||
| Sex Models—Male | |||||||
| 13 | Male Baseline | 8.11 (12) | 0.777 | 10.00 | 10.00 | 0.000 0.000–0.059 | |
| 14 | Males Longitudinal Configural | 210.31 (160) | 0.005 | 0.90 | 0.85 | 0.047 0.027–0.064 | |
| 15 | Males Longitudinal Metric | 219.33 (172) | 0.009 | 0.95 | 0.94 | 0.031 0.016–0.042 | Accept Accept Accept |
| 16 | Male Intercept Only | 310.29 (174) | 0.001 | 0.72 | 0.63 | 0.072 0.061–0.088 | Reject Reject Reject |
| 17 | Male Loadings and Intercepts | 324.04 (186) | 0.001 | 0.72 | 0.65 | 0.073 0.059–0.086 | Reject Reject Reject |
| 18 | Male Residuals | Not tested as invariant intercepts not found | |||||
| Sex Invariance of Longitudinal HEI-C Model | |||||||
| 19 | Sex Invar. Configural | 415.75 (320) | 0.001 | 0.94 | 0.91 | 0.026 0.018–0.033 | |
| 20 | Sex Model Sex Invariant | 420.65 (338) | 0.001 | 0.92 | 0.88 | 0.030 0.019–0.038 | Accept Accept Accept |
| 21 | Sex Model Time Invariant | 454.23 (350) | 0.001 | 0.90 | 0.87 | 0.032 0.023–0.040 | Reject Accept Accept |
| 22 | Sex Model Intercepts | Not run based on previous intercept models | |||||
| 23 | Sex Model Residuals | Not run as intercept models were not accepted | |||||
| Disease-State Models—No Diabetes | |||||||
| 24 | NoDM Baseline | 16.12 (12) | 0.186 | 0.96 | 0.91 | 0.059 0.000–0.106 | |
| 25 | NoDM Longitudinal Configural | 205.10 (160) | 0.009 | 0.91 | 0.87 | 0.045 0.023–0.062 | |
| 26 | NoDM Longitudinal Metric | 224.15 (172) | 0.005 | 0.89 | 0.86 | 0.047 0.027–0.063 | Accept Accept Accept |
| 27 | NoDM Longitudinal Intercepts Only | 283.75 (174) | 0.001 | 0.77 | 0.70 | 0.067 0.053–0.081 | Reject Reject Reject |
| 28 | NoDM Residuals | Not tested as invariant intercepts not found | |||||
| Disease-State Models—Diabetes | |||||||
| 29 | DM Baseline | 9.50 (12) | 0.660 | 1.00 | 1.00 | 0.000 0.000–0.068 | |
| 30 | DM Longitudinal Configural | 172.59 (160) | 0.235 | 0.98 | 0.96 | 0.023 0.000–0.045 | |
| 31 | DM Longitudinal Metric | 183.88 (172) | 0.254 | 0.98 | 0.97 | 0.021 0.000–0.043 | Accept Accept Accept |
| 32 | DM Longitudinal Intercepts Only | 276.63 (174) | 0.001 | 0.80 | 0.73 | 0.063 0.048–0.076 | Reject Reject Reject |
| 33 | DM Residuals | Not tested as invariant intercepts not found | |||||
| Disease Invariance of Longitudinal HEI-C Model | |||||||
| 34 | Disease Model Configural | 377.70 (320) | 0.015 | 0.95 | 0.92 | 0.025 0.012–0.034 | |
| 35 | Disease Model Disease Invariant | 397.95 (338) | 0.014 | 0.94 | 0.92 | 0.025 0.012–0.034 | Accept Accept Accept |
| 36 | Disease Model Time Invariant | 410.90 (350) | 0.014 | 0.94 | 0.92 | 0.024 0.012–0.034 | Accept Accept Accept |
| 37 | Disease Model Intercepts | Not run based on previous intercept models | |||||
| 38 | Disease Model Residuals | Not run as intercept models were not accepted | |||||
3.2.3. Longitudinal Extension of Reduced HEI-C Model
3.2.4. Sex Invariance of Reduced HEI-C Model
3.2.5. Disease State Invariance of Reduced HEI-C Model
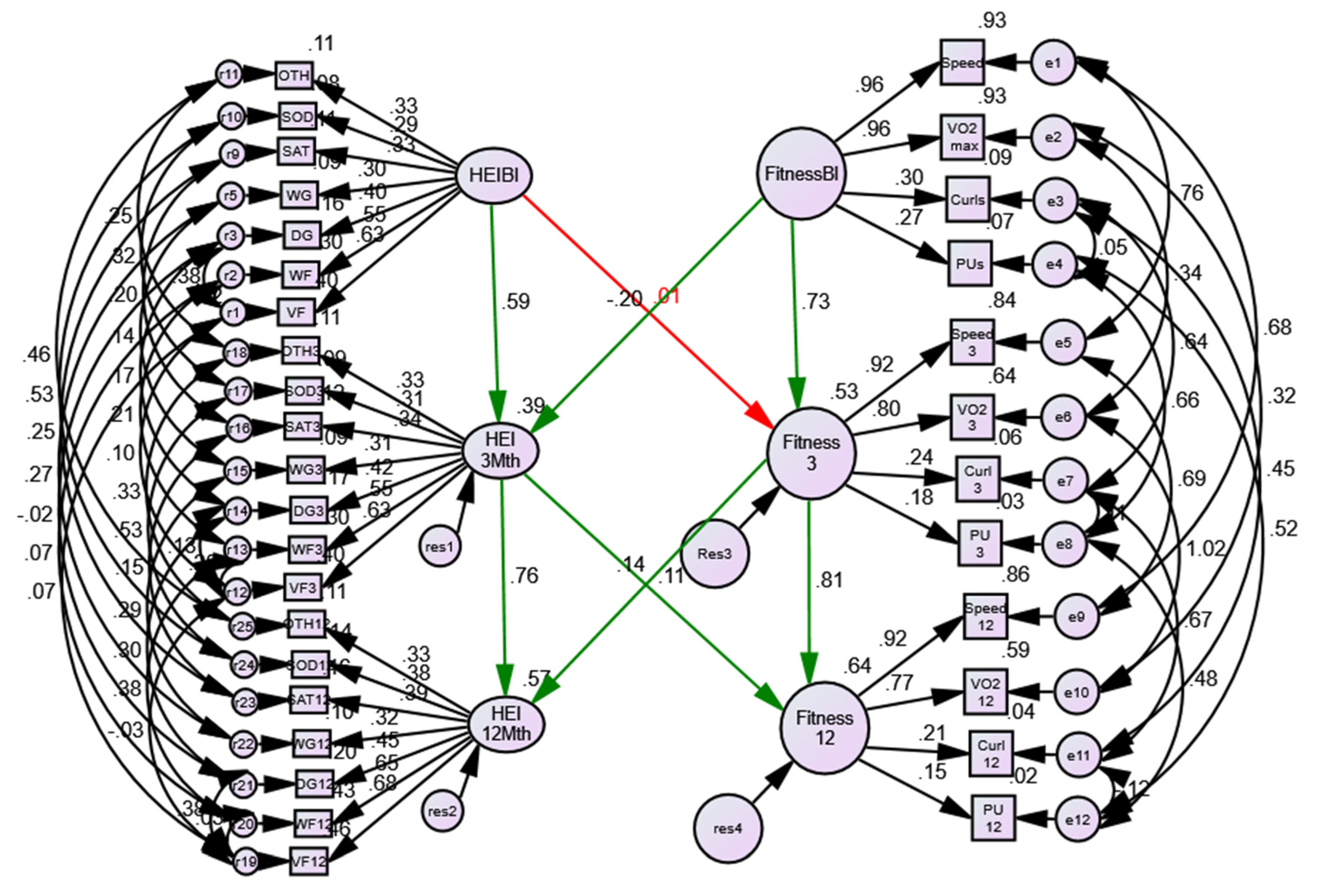
3.3. Assessment of Associations between Physical Activity/Fitness and Reduced HEI-C
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Babio, N.; Toledo, E.; Estruch, R.; Ros, E.; Martínez-González, M.A.; Castañer, O.; Bulló, M.; Corella, D.; Arós, F.; Gómez-Gracia, E.; et al. Mediterranean diets and metabolic syndrome status in the PREDIMED randomized trial. CMAJ 2014, 186, E649–E657. [Google Scholar] [CrossRef]
- Estruch, R.; Ros, E.; Salas-Salvado, J.; Covas, M.I.; Corella, D.; Aros, F.; Gomez-Gracia, E.; Ruiz-Gutierrez, V.; Fiol, M.; Lapetra, J.; et al. Primary Prevention of Cardiovascular Disease with a Mediterranean Diet Supplemented with Extra-Virgin Olive Oil or Nuts. N. Engl. J. Med. 2018, 378, e34. [Google Scholar] [CrossRef]
- Knowler, W.C.; Barrett-Connor, E.; Fowler, S.E.; Hamman, R.F.; Lachin, J.M.; Walker, E.A.; Nathan, D.M. Reduction in the incidence of type 2 diabetes with lifestyle intervention or metformin. N. Engl. J. Med. 2002, 346, 393–403. [Google Scholar] [CrossRef] [PubMed]
- Look Ahead Research Group; Wing, R.R.; Bolin, P.; Brancati, F.L.; Bray, G.A.; Clark, J.M.; Coday, M.; Crow, R.S.; Curtis, J.M.; Egan, C.M.; et al. Cardiovascular effects of intensive lifestyle intervention in type 2 diabetes. N. Engl. J. Med. 2013, 369, 145–154. [Google Scholar] [CrossRef]
- Goldberg, R.B.; Mather, K. Targeting the consequences of the metabolic syndrome in the Diabetes Prevention Program. Arterioscler. Thromb. Vasc. Biol. 2012, 32, 2077–2090. [Google Scholar] [CrossRef]
- Galaviz, K.I.; Weber, M.B.; Straus, A.; Haw, J.S.; Narayan, K.M.V.; Ali, M.K. Global Diabetes Prevention Interventions: A Systematic Review and Network Meta-analysis of the Real-World Impact on Incidence, Weight, and Glucose. Diabetes Care 2018, 41, 1526–1534. [Google Scholar] [CrossRef]
- Mudaliar, U.; Zabetian, A.; Goodman, M.; Echouffo-Tcheugui, J.B.; Albright, A.L.; Gregg, E.W.; Ali, M.K. Cardiometabolic Risk Factor Changes Observed in Diabetes Prevention Programs in US Settings: A Systematic Review and Meta-analysis. PLoS Med. 2016, 13, e1002095. [Google Scholar] [CrossRef]
- GBD 2017 Risk Factor Collaborators. Global, regional, and national comparative risk assessment of 84 behavioural, environmental and occupational, and metabolic risks or clusters of risks for 195 countries and territories, 1990–2017: A systematic analysis for the Global Burden of Disease Study 2017. Lancet 2018, 392, 1923–1994. [Google Scholar] [CrossRef]
- Alberti, K.G.; Eckel, R.H.; Grundy, S.M.; Zimmet, P.Z.; Cleeman, J.I.; Donato, K.A.; Fruchart, J.C.; James, W.P.; Loria, C.M.; Smith, S.C., Jr.; et al. Harmonizing the metabolic syndrome: A joint interim statement of the International Diabetes Federation Task Force on Epidemiology and Prevention; National Heart, Lung, and Blood Institute; American Heart Association; World Heart Federation; International Atherosclerosis Society; and International Association for the Study of Obesity. Circulation 2009, 120, 1640–1645. [Google Scholar] [CrossRef]
- Diamantopoulos, E.J.; Andreadis, E.A.; Tsourous, G.I.; Ifanti, G.K.; Katsanou, P.M.; Georgiopoulos, D.X.; Vassilopoulos, C.V.; Dimitriadis, G.; Raptis, S.A. Metabolic syndrome and prediabetes identify overlapping but not identical populations. Exp. Clin. Endocrinol. Diabetes Off. J. Ger. Soc. Endocrinol. Ger. Diabetes Assoc. 2006, 114, 377–383. [Google Scholar] [CrossRef]
- Liu, J.; Grundy, S.M.; Wang, W.; Smith, S.C.; Lena Vega, G.; Wu, Z.; Zeng, Z.; Wang, W.; Zhao, D. Ten-year risk of cardiovascular incidence related to diabetes, prediabetes, and the metabolic syndrome. Am. Heart J. 2007, 153, 552–558. [Google Scholar] [CrossRef]
- Leiter, L.A.; Fitchett, D.H.; Gilbert, R.E.; Gupta, M.; Mancini, G.B.; McFarlane, P.A.; Ross, R.; Teoh, H.; Verma, S.; Anand, S.; et al. Identification and management of cardiometabolic risk in Canada: A position paper by the cardiometabolic risk working group (executive summary). Can. J. Cardiol. 2011, 27, 124–131. [Google Scholar] [CrossRef]
- Roth, G.A.; Mensah, G.A.; Johnson, C.O.; Addolorato, G.; Ammirati, E.; Baddour, L.M.; Barengo, N.C.; Beaton, A.Z.; Benjamin, E.J.; Benziger, C.P.; et al. Global Burden of Cardiovascular Diseases and Risk Factors, 1990–2019: Update From the GBD 2019 Study. J. Am. Coll. Cardiol. 2020, 76, 2982–3021. [Google Scholar] [CrossRef] [PubMed]
- Hostalek, U. Global epidemiology of prediabetes—Present and future perspectives. Clin. Diabetes Endocrinol. 2019, 5, 5. [Google Scholar] [CrossRef]
- Saklayen, M.G. The Global Epidemic of the Metabolic Syndrome. Curr. Hypertens. Rep. 2018, 20, 12. [Google Scholar] [CrossRef] [PubMed]
- Statistics Canada. Metabolic Syndrome in Adults, 2012 to 2013. Available online: https://www150.statcan.gc.ca/n1/pub/82-625-x/2014001/article/14123-eng.htm (accessed on 13 June 2018).
- Aguilar, M.; Bhuket, T.; Torres, S.; Liu, B.; Wong, R.J. Prevalence of the Metabolic Syndrome in the United States, 2003–2012. JAMA 2015, 313, 1973. [Google Scholar] [CrossRef]
- McQueen, R.; Ghushchyan, V.; Olufade, T.; Sheehan, J.; Nair, K.; Saseen, J. Incremental increases in economic burden parallels cardiometabolic risk factors in the US. Diabetes Metab. Syndr. Obes. Targets Ther. 2016, 9, 233–241. [Google Scholar] [CrossRef] [PubMed]
- Clark, A.; Jit, M.; Warren-Gash, C.; Guthrie, B.; Wang, H.H.X.; Mercer, S.W.; Sanderson, C.; McKee, M.; Troeger, C.; Ong, K.L.; et al. Global, regional, and national estimates of the population at increased risk of severe COVID-19 due to underlying health conditions in 2020: A modelling study. Lancet Glob. Health 2020, 8, e1003–e1017. [Google Scholar] [CrossRef]
- Ghoneim, S.; Butt, M.U.; Hamid, O.; Shah, A.; Asaad, I. The incidence of COVID-19 in patients with metabolic syndrome and non-alcoholic steatohepatitis: A population-based study. Metab. Open 2020, 8, 100057. [Google Scholar] [CrossRef]
- Arnett, D.K.; Blumenthal, R.S.; Albert, M.A.; Buroker, A.B.; Goldberger, Z.D.; Hahn, E.J.; Himmelfarb, C.D.; Khera, A.; Lloyd-Jones, D.; McEvoy, J.W.; et al. 2019 ACC/AHA Guideline on the Primary Prevention of Cardiovascular Disease: Executive Summary: A Report of the American College of Cardiology/American Heart Association Task Force on Clinical Practice Guidelines. Circulation 2019, 140, e563–e595. [Google Scholar] [CrossRef]
- Tobe, S.W.; Stone, J.A.; Anderson, T.; Bacon, S.; Cheng, A.Y.Y.; Daskalopoulou, S.S.; Ezekowitz, J.A.; Gregoire, J.C.; Gubitz, G.; Jain, R.; et al. Canadian Cardiovascular Harmonized National Guidelines Endeavour (C-CHANGE) guideline for the prevention and management of cardiovascular disease in primary care: 2018 update. CMAJ 2018, 190, E1192–E1206. [Google Scholar] [CrossRef]
- National Institute for Health and Care Excellence. NICE Pathway: Cardiovascular Disease Prevention Overview. Available online: https://pathways.nice.org.uk/pathways/cardiovascular-disease-prevention/cardiovascular-disease-prevention-overview (accessed on 19 June 2020).
- Royal Australian College of General Practitioners. Chap. 8. Prevention of vascular and metabolic disease. In Guidelines for Preventive Actitivies in General Practice, 9th ed.; Royal Australian College of General Practitioners Ltd.: East Melbourne, MEL, Australia, 2018. [Google Scholar]
- Teoh, H.; Despres, J.P.; Dufour, R.; Fitchett, D.H.; Goldin, L.; Goodman, S.G.; Harris, S.B.; Langer, A.; Lau, D.C.; Lonn, E.M.; et al. Identification and management of patients at elevated cardiometabolic risk in canadian primary care: How well are we doing? Can. J. Cardiol. 2013, 29, 960–968. [Google Scholar] [CrossRef]
- Jeejeebhoy, K.; Dhaliwal, R.; Heyland, D.K.; Leung, R.; Day, A.G.; Brauer, P.; Royall, D.; Tremblay, A.; Mutch, D.M.; Pliamm, L.; et al. Family physician-led, team-based, lifestyle intervention in patients with metabolic syndrome: Results of a multicentre feasibility project. CMAJ Open 2017, 5, E229–E236. [Google Scholar] [CrossRef]
- Assmann, G.; Schulte, H.; Seedorf, U. Cardiovascular risk assessment in the metabolic syndrome: Results from the Prospective Cardiovascular Munster (PROCAM) Study. Int. J. Obes. (2005) 2008, 32 (Suppl. S2), S11–S16. [Google Scholar] [CrossRef]
- Geller, K.; Lippke, S.; Nigg, C.R. Future directions of multiple behavior change research. J. Behav. Med. 2017, 40, 194–202. [Google Scholar] [CrossRef]
- Meader, N.; King, K.; Wright, K.; Graham, H.M.; Petticrew, M.; Power, C.; White, M.; Sowden, A.J. Multiple Risk Behavior Interventions: Meta-analyses of RCTs. Am. J. Prev. Med. 2017, 53, e19–e30. [Google Scholar] [CrossRef]
- Kaplan, D. Structural Equation Modeling (2nd ed.): Foundations and Extensions, 2nd ed.; SAGE Publications, Inc.: Thousand Oaks, CA, USA, 2009. [Google Scholar] [CrossRef]
- Raghuveer, G.; Hartz, J.; Lubans, D.R.; Takken, T.; Wiltz, J.L.; Mietus-Snyder, M.; Perak, A.M.; Baker-Smith, C.; Pietris, N.; Edwards, N.M. Cardiorespiratory Fitness in Youth: An Important Marker of Health: A Scientific Statement From the American Heart Association. Circulation 2020, 142, e101–e118. [Google Scholar] [CrossRef] [PubMed]
- Ross, R.; Blair, S.N.; Arena, R.; Church, T.S.; Després, J.-P.; Franklin, B.A.; Haskell, W.L.; Kaminsky, L.A.; Levine, B.D.; Lavie, C.J.; et al. Importance of Assessing Cardiorespiratory Fitness in Clinical Practice: A Case for Fitness as a Clinical Vital Sign: A Scientific Statement From the American Heart Association. Circulation 2016, 134, e653–e699. [Google Scholar] [CrossRef]
- Peterman, J.E.; Harber, M.P.; Imboden, M.T.; Whaley, M.H.; Fleenor, B.S.; Myers, J.; Arena, R.; Kaminsky, L.A. Accuracy of Exercise-based Equations for Estimating Cardiorespiratory Fitness. Med. Sci. Sports Exerc. 2021, 53, 74–82. [Google Scholar] [CrossRef] [PubMed]
- Castro-Barquero, S.; Ruiz-León, A.M.; Sierra-Pérez, M.; Estruch, R.; Casas, R. Dietary Strategies for Metabolic Syndrome: A Comprehensive Review. Nutrients 2020, 12, 2983. [Google Scholar] [CrossRef] [PubMed]
- Kirkpatrick, S.I.; Reedy, J.; Krebs-Smith, S.M.; Pannucci, T.E.; Subar, A.F.; Wilson, M.M.; Lerman, J.L.; Tooze, J.A. Applications of the Healthy Eating Index for Surveillance, Epidemiology, and Intervention Research: Considerations and Caveats. J. Acad. Nutr. Diet. 2018, 118, 1603–1621. [Google Scholar] [CrossRef] [PubMed]
- Brauer, P.; Royall, D.; Rodrigues, A. Use of the Healthy Eating Index in Intervention Studies for Cardiometabolic Risk Conditions: A Systematic Review. Adv. Nutr. 2021, 12, 1317–1331. [Google Scholar] [CrossRef]
- Zaragoza-Martí, A.; Cabañero-Martínez, M.; Hurtado-Sánchez, J.; Laguna-Pérez, A.; Ferrer-Cascales, R. Evaluation of Mediterranean diet adherence scores: A systematic review. BMJ Open 2018, 8, e019033. [Google Scholar] [CrossRef] [PubMed]
- Miller, V.; Webb, P.; Micha, R.; Mozaffarian, D. Defining diet quality: A synthesis of dietary quality metrics and their validity for the double burden of malnutrition. Lancet Planet. Health 2020, 4, e352–e370. [Google Scholar] [CrossRef]
- Hayduk, L.A. Improving measurement-invariance assessments: Correcting entrenched testing deficiencies. BMC Med. Res. Methodol. 2016, 16, 130. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Reimer, H.D.; Keller, H.H.; Maitland, S.B.; Jackson, J. Nutrition Screening Index for Older Adults (SCREEN II©) Demonstrates Sex and Age Invariance. J. Nutr. Elder. 2010, 29, 192–210. [Google Scholar] [CrossRef]
- Vandenberg, R.J.; Lance, C.E. A Review and Synthesis of the Measurement Invariance Literature: Suggestions, Practices, and Recommendations for Organizational Research. Organ. Res. Methods 2000, 3, 4–70. [Google Scholar] [CrossRef]
- Van De Schoot, R.; Lugtig, P.; Hox, J. A checklist for testing measurement invariance. Eur. J. Dev. Psychol. 2012, 9, 486–492. [Google Scholar] [CrossRef]
- Maitland, S.B.; Nyberg, L.; Bäckman, L.; Nilsson, L.-G.; Adolfsson, R. On the structure of personality: Are there separate temperament and character factors? Personal. Individ. Differ. 2009, 47, 180–184. [Google Scholar] [CrossRef]
- Royall, D.; Brauer, P.; Bjorklund, L.; O'Young, O.; Tremblay, A.; Jeejeebhoy, K.; Heyland, D.; Dhaliwal, R.; Klein, D.; Mutch, D.M. Development of a Dietary Management Care Map for Metabolic Syndrome. Can. J. Diet. Pract. Res. 2014, 75, 132–139. [Google Scholar] [CrossRef]
- Klein, D.; Jeejeebhoy, K.; Tremblay, A.; Kallio, M.; Rheaume, C.; Humphries, S.; Royall, D.; Brauer, P.; Heyland, D.; Dhaliwal, R.; et al. The CHANGE program: Exercise intervention in primary care. Can. Fam. Physician 2017, 63, 546–552. [Google Scholar] [PubMed]
- Klein, J.; Brauer, P.; Royall, D.; Israeloff-Smith, M.; Klein, D.; Tremblay, A.; Dhaliwal, R.; Rheaume, C.; Mutch, D.M.; Jeejeebhoy, K. Patient experiences of a lifestyle program for metabolic syndrome offered in family medicine clinics: A mixed methods study. BMC Fam. Pr. 2018, 19, 148. [Google Scholar] [CrossRef] [PubMed]
- Ebbeling, C.B.; Ward, A.; Puleo, E.M.; Widrick, J.; Rippe, J.M. Development of a single-stage submaximal treadmill walking test. Med. Sci. Sports Exerc. 1991, 23, 966–973. [Google Scholar] [CrossRef]
- Tremblay, A.; Bélanger, M.P.; Dhaliwal, R.; Brauer, P.; Royall, D.; Mutch, D.M.; Rhéaume, C. Impact of a multidisciplinary intervention on physical fitness, physical activity habits and the association between aerobic fitness and components of metabolic syndrome in adults diagnosed with metabolic syndrome. Arch. Public Health 2020, 78, 22. [Google Scholar] [CrossRef]
- Hayduk, L.A.; Littvay, L. Should researchers use single indicators, best indicators, or multiple indicators in structural equation models? BMC Med. Res. Methodol. 2012, 12, 159. [Google Scholar] [CrossRef]
- Brauer, P.; Royall, D.; Li, A.; Rodrigues, A.; Green, J.; Macklin, S.; Craig, A.; Pasanen, J.; Brunelle, L.; Maitland, S.; et al. Nutrient intake and dietary quality changes within a personalized lifestyle intervention program for metabolic syndrome in primary care. Appl. Physiol. Nutr. Metab. 2019, 44, 1297–1304. [Google Scholar] [CrossRef]
- Garriguet, D. Diet quality in Canada. Health Rep. 2009, 20, 41–52. [Google Scholar]
- Health Canada. Eating Well with Canada’s Food Guide. Available online: https://www.canada.ca/en/health-canada/services/canada-food-guides.html (accessed on 19 January 2018).
- van Vliet-Ostaptchouk, J.V.; Nuotio, M.-L.; Slagter, S.N.; Doiron, D.; Fischer, K.; Foco, L.; Gaye, A.; Gögele, M.; Heier, M.; Hiekkalinna, T.; et al. The prevalence of metabolic syndrome and metabolically healthy obesity in Europe: A collaborative analysis of ten large cohort studies. BMC Endocr. Disord. 2014, 14, 9. [Google Scholar] [CrossRef]
- Bentler, P.M. On tests and indices for evaluating structural models. Personal. Individ. Differ. 2007, 42, 825–829. [Google Scholar] [CrossRef]
- Cheung, G.W.; Rensvold, R.B. Evaluating goodness-of-fit indexes for testing measurement invariance. Struct. Equ. Modeling 2002, 9, 233–255. [Google Scholar] [CrossRef]
- Kline, R.B. Principles and Practice of Structural Equation Modeling; Guilford Publications: New York, NY, USA, 2015. [Google Scholar]
- Lai, K.; Green, S.B. The Problem with Having Two Watches: Assessment of Fit When RMSEA and CFI Disagree. Multivar. Behav. Res. 2016, 51, 220–239. [Google Scholar] [CrossRef]
- McNeish, D.; An, J.; Hancock, G.R. The Thorny Relation Between Measurement Quality and Fit Index Cutoffs in Latent Variable Models. J. Pers. Assess 2018, 100, 43–52. [Google Scholar] [CrossRef]
- Little, T.D. Longitudinal Structural Equation Modeling; Guilford Press: New York, NY, USA, 2013; pp. xxii, 386–xxii, 386. [Google Scholar]
- Meredith, W. Measurement invariance, factor analysis and factorial invariance. Psychometrika 1993, 58, 525–543. [Google Scholar] [CrossRef]
- Millsap, R.E. Structural equation modeling made difficult. Personal. Individ. Differ. 2007, 42, 875–881. [Google Scholar] [CrossRef]
- Horn, J.L.; McArdle, J.J.; Mason, R. When is invariance not invarient: A practical scientist's look at the ethereal concept of factor invariance. South. Psychol. 1983, 1, 179–188. [Google Scholar]
- Chen, F.F. Sensitivity of goodness of fit indexes to lack of measurement invariance. Struct. Equ. Modeling A Multidiscip. J. 2007, 14, 464–504. [Google Scholar] [CrossRef]
- Kennedy, E.T.; Ohls, J.; Carlson, S.; Fleming, K. The Healthy Eating Index: Design and applications. J. Am. Diet. Assoc. 1995, 95, 1103–1108. [Google Scholar] [CrossRef]
- Lafrenière, J.; Carbonneau, É.; Laramée, C.; Corneau, L.; Robitaille, J.; Labonté, M.-È.; Lamarche, B.; Lemieux, S. Is the Canadian Healthy Eating Index 2007 an Appropriate Diet Indicator of Metabolic Health? Insights from Dietary Pattern Analysis in the PREDISE Study. Nutrients 2019, 11, 1597. [Google Scholar] [CrossRef]
- Spring, B.; Schneider, K.; McFadden, H.G.; Vaughn, J.; Kozak, A.T.; Smith, M.; Moller, A.C.; Epstein, L.H.; Demott, A.; Hedeker, D.; et al. Multiple behavior changes in diet and activity: A randomized controlled trial using mobile technology. Arch. Intern. Med. 2012, 172, 789–796. [Google Scholar] [CrossRef]
- Chevance, G.; Golaszewski, N.M.; Baretta, D.; Hekler, E.B.; Larsen, B.A.; Patrick, K.; Godino, J. Modelling multiple health behavior change with network analyses: Results from a one-year study conducted among overweight and obese adults. J. Behav. Med. 2020, 43, 254–261. [Google Scholar] [CrossRef]
- Heredia, N.I.; Fernandez, M.E.; van den Berg, A.E.; Durand, C.P.; Kohl, H.W.; Reininger, B.M.; Hwang, K.O.; McNeill, L.H. Coaction Between Physical Activity and Fruit and Vegetable Intake in Racially Diverse, Obese Adults. Am. J. Health Promot. 2020, 34, 238–246. [Google Scholar] [CrossRef]
- Tarka, P. An overview of structural equation modeling: Its beginnings, historical development, usefulness and controversies in the social sciences. Qual. Quant. 2018, 52, 313–354. [Google Scholar] [CrossRef] [PubMed]
- Tomarken, A.J.; Waller, N.G. Structural equation modeling: Strengths, limitations, and misconceptions. Annu. Rev. Clin. Psychol 2005, 1, 31–65. [Google Scholar] [CrossRef] [PubMed]
- Schaie, K.W.; Maitland, S.B.; Willis, S.L.; Intrieri, R.C. Longitudinal invariance of adult psychometric ability factor structures across 7 years. Psychol Aging 1998, 13, 8–20. [Google Scholar] [CrossRef] [PubMed]
- Maitland, S.B.; Intrieri, R.C.; Schaie, W.K.; Willis, S.L. Gender differences and changes in cognitive abilities across the adult life span. Aging Neuropsychol. Cogn. 2000, 7, 32–53. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maitland, S.B.; Brauer, P.; Mutch, D.M.; Royall, D.; Klein, D.; Tremblay, A.; Rheaume, C.; Dhaliwal, R.; Jeejeebhoy, K. Evaluation of Latent Models Assessing Physical Fitness and the Healthy Eating Index in Community Studies: Time-, Sex-, and Diabetes-Status Invariance. Nutrients 2021, 13, 4258. https://doi.org/10.3390/nu13124258
Maitland SB, Brauer P, Mutch DM, Royall D, Klein D, Tremblay A, Rheaume C, Dhaliwal R, Jeejeebhoy K. Evaluation of Latent Models Assessing Physical Fitness and the Healthy Eating Index in Community Studies: Time-, Sex-, and Diabetes-Status Invariance. Nutrients. 2021; 13(12):4258. https://doi.org/10.3390/nu13124258
Chicago/Turabian StyleMaitland, Scott B., Paula Brauer, David M. Mutch, Dawna Royall, Doug Klein, Angelo Tremblay, Caroline Rheaume, Rupinder Dhaliwal, and Khursheed Jeejeebhoy. 2021. "Evaluation of Latent Models Assessing Physical Fitness and the Healthy Eating Index in Community Studies: Time-, Sex-, and Diabetes-Status Invariance" Nutrients 13, no. 12: 4258. https://doi.org/10.3390/nu13124258
APA StyleMaitland, S. B., Brauer, P., Mutch, D. M., Royall, D., Klein, D., Tremblay, A., Rheaume, C., Dhaliwal, R., & Jeejeebhoy, K. (2021). Evaluation of Latent Models Assessing Physical Fitness and the Healthy Eating Index in Community Studies: Time-, Sex-, and Diabetes-Status Invariance. Nutrients, 13(12), 4258. https://doi.org/10.3390/nu13124258







