Artificial Neural Network Algorithms to Predict Resting Energy Expenditure in Critically Ill Children
Abstract
1. Introduction
2. Methods
2.1. Study Design and Study Population
2.2. Nutritional Status and Clinical Characteristics
2.3. Modelling of REE with Artificial Neural Networks
2.3.1. Data Pre-Processing
2.3.2. Data Set Analysis
2.3.3. TWIST (Training with Input Selection and Testing) System
2.4. Statistical Analysis
3. Results
3.1. Data Set 1
3.1.1. Population Characteristics
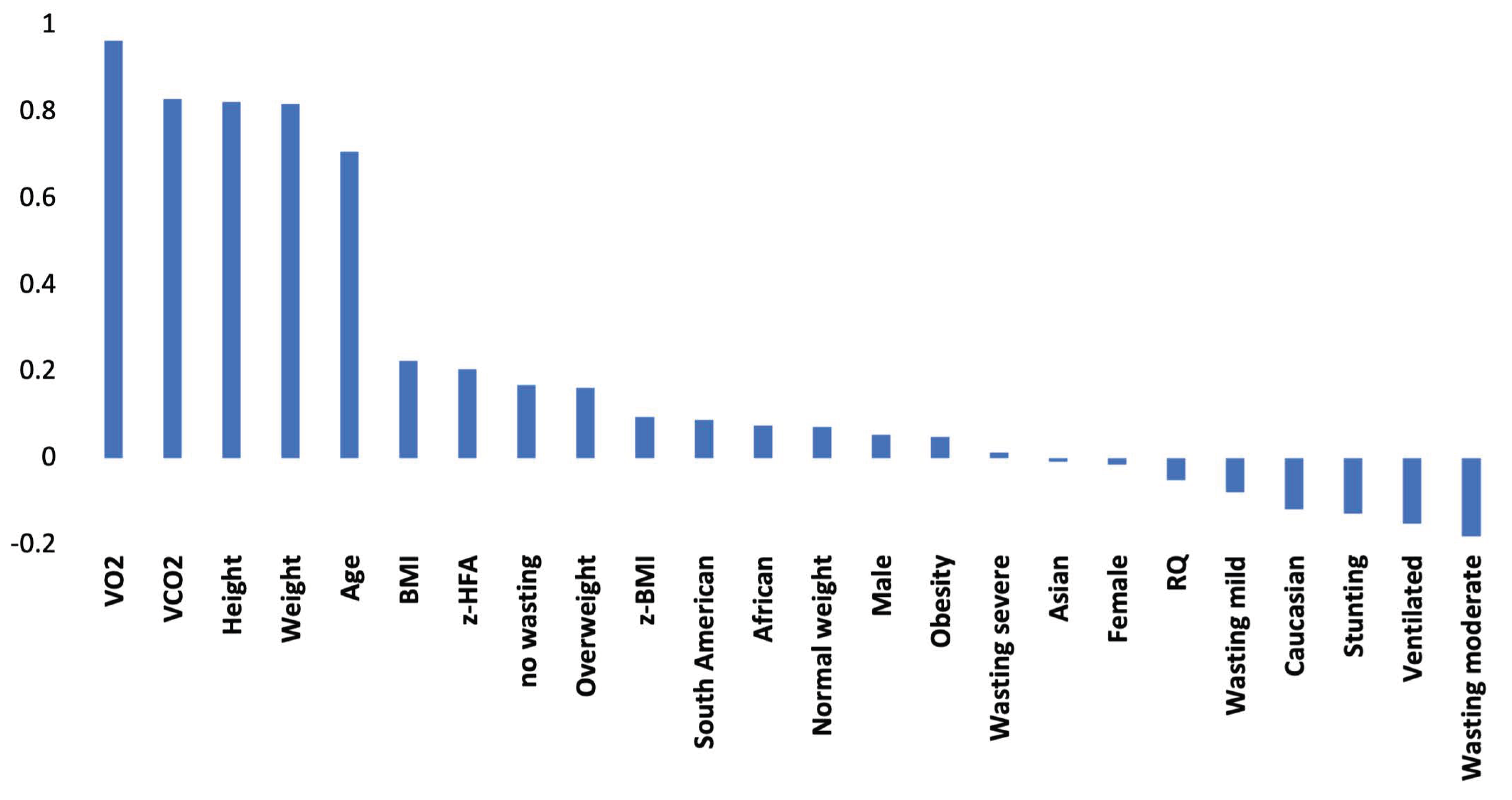
3.1.2. Linear Correlations
3.1.3. Fitting of REE with the Equations
3.1.4. Fitting of REE with Artificial Neural Networks: Baseline Analysis (24 variables)
3.1.5. Comparative Statistics between Tests on Study
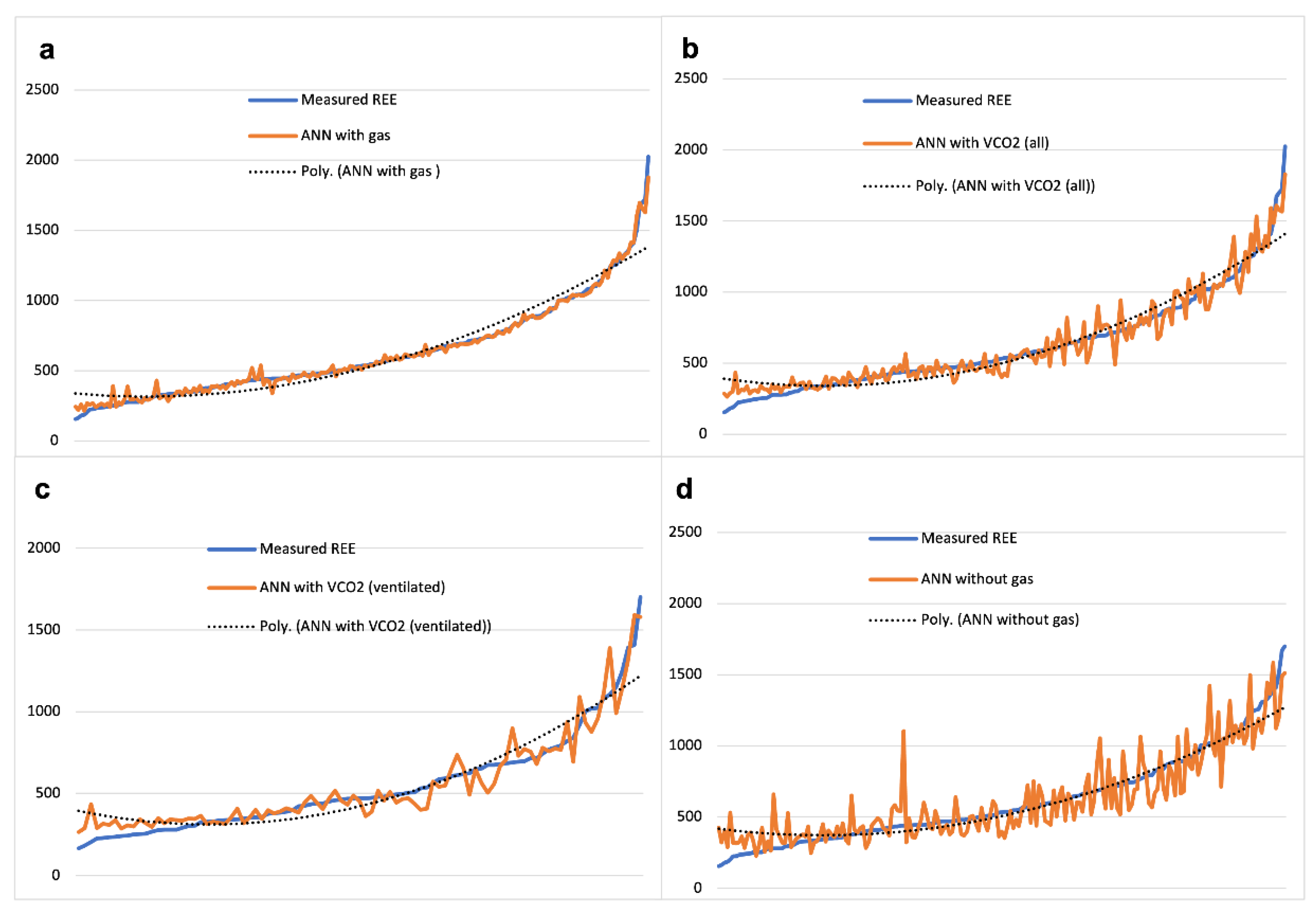
3.1.6. ANN Analysis to Evaluate the Contribution Given by Gas Values to REE Fitting
3.2. Data Set 2
3.2.1. Population Characteristics
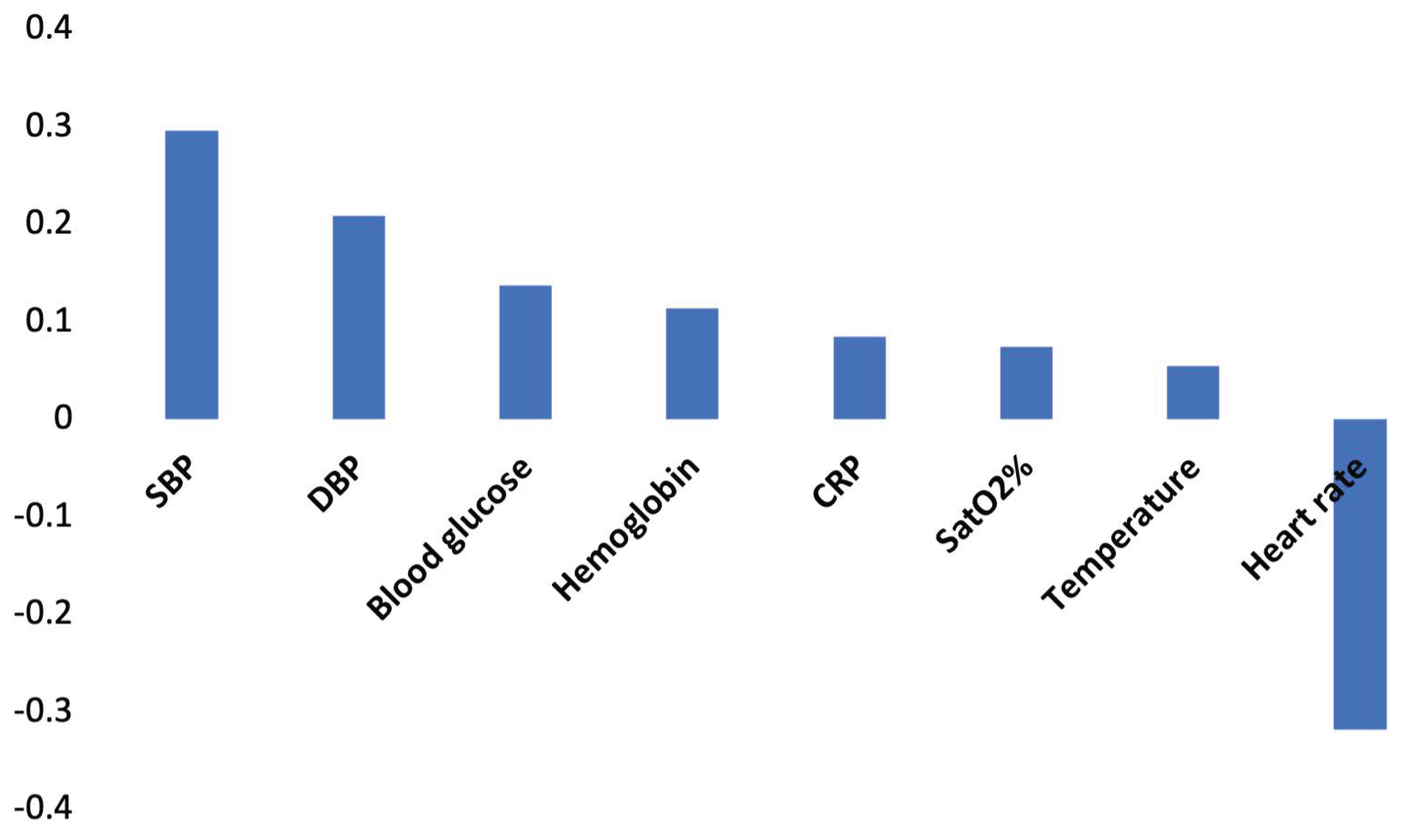
3.2.2. Linear Correlations
3.2.3. Real REE Approximation with Artificial Neural Networks
3.2.4. Comparative Statistics between All Methods on Study
3.2.5. ANN Analysis to Evaluate the Contribution Given by Gas Values to REE Fitting
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
References
- De Cosmi, V.; Milani, G.P.; Mazzocchi, A.; D’Oria, V.; Silano, M.; Calderini, E.; Agostoni, C. The Metabolic Response to Stress and Infection in Critically Ill Children: The Opportunity of an Individualized Approach. Nutrients 2017, 9, 1032. [Google Scholar] [CrossRef] [PubMed]
- EFSA Panel on Dietetic Products. Nutrition and Allergies. Scientific Opinion on nutrient requirements and dietary intakes of infants and young children in the European Union. EFSA J. 2013, 11, 3408. [Google Scholar]
- Mehta, N.M.; Smallwood, C.D.; Graham, R.J. Current applications of metabolic monitoring in the pediatric intensive care unit. Nutr. Clin. Pract. 2014, 29, 338–347. [Google Scholar] [CrossRef] [PubMed]
- Kerklaan, D.; Fivez, T.; Mehta, N.M.; Mesotten, D.; van Rosmalen, J.; Hulst, J.M.; Van den Berghe, G.; Joosten, K.F.; Verbruggen, S.C. Worldwide Survey of Nutritional Practices in PICUs. Pediatric Crit. Care Med. 2016, 17, 10–18. [Google Scholar] [CrossRef]
- Agostoni, C.; Edefonti, A.; Calderini, E.; Fossali, E.; Colombo, C.; Battezzati, A.; Bertoli, S.; Milani, G.; Bisogno, A.; Perrone, M.; et al. Accuracy of Prediction Formulae for the Assessment of Resting Energy Expenditure in Hospitalized Children. J. Pediatric Gastroenterol. Nutr. 2016, 63, 708–712. [Google Scholar] [CrossRef] [PubMed]
- Van den Berghe, G. Intensive insulin therapy in the ICU—Reconciling the evidence. Nat. Rev. Endocrinol. 2012, 8, 374–378. [Google Scholar] [CrossRef] [PubMed]
- De Cosmi, V.; Mazzocchi, A.; Milani, G.P.; Calderini, E.; Scaglioni, S.; Bettocchi, S.; D’Oria, V.; Langer, T.; Spolidoro, G.C.; Leone, L.; et al. Prediction of Resting Energy Expenditure in Children: May Artificial Neural Networks Improve Our Accuracy? J. Clin. Med. 2020, 9, 1026. [Google Scholar] [CrossRef]
- Grossi, E.; Buscema, M. Introduction to artificial neural networks. Eur. J. Gastroenterol. Hepatol. 2007, 19, 1046–1054. [Google Scholar] [CrossRef] [PubMed]
- De Cosmi, V.; Mehta, N.M.; Boccazzi, A.; Milani, G.P.; Esposito, S.; Bedogni, G.; Agostoni, C. Nutritional status, metabolic state and nutrient intake in children with bronchiolitis. Int. J. Food Sci. Nutr. 2017, 68, 378–383. [Google Scholar] [CrossRef] [PubMed]
- de Onís, M.; Monteiro, C.; Akré, J.; Glugston, G. The worldwide magnitude of protein-energy malnutrition: An overview from the WHO Global Database on Child Growth. Bull. World Health Organ. 1993, 71, 703–712. [Google Scholar]
- Weir, J.B. New methods for calculating metabolic rate with special reference to protein metabolism. Nutrition 1990, 6, 213–221. [Google Scholar] [CrossRef]
- Harris, J.A.; Benedict, F.G. A Biometric Study of Human Basal Metabolism. Proc. Natl. Acad. Sci. USA 1918, 4, 370–373. [Google Scholar] [CrossRef]
- Schofield, W.N. Predicting basal metabolic rate, new standards and review of previous work. Hum. Nutr. Clin. Nutr. 1985, 39 (Suppl. 1), 5–41. [Google Scholar] [PubMed]
- Henry, C.J. Basal metabolic rate studies in humans: Measurement and development of new equations. Public Health Nutr. 2005, 8, 1133–1152. [Google Scholar] [CrossRef] [PubMed]
- FAO/WHO/UNU. Human Energy Requirements. Report of a Joint FAO/WHO/UNU Expert Consultation; FAO: Rome, Italy, 2004. [Google Scholar]
- Talbot, F.B. Basal metabolism standards for children. Am. J. Dis. Child. 1938, 55, 455–459. [Google Scholar] [CrossRef]
- Mehta, N.M.; Smallwood, C.D.; Joosten, K.F.; Hulst, J.M.; Tasker, R.C.; Duggan, C.P. Accuracy of a simplified equation for energy expenditure based on bedside volumetric carbon dioxide elimination measurement—A two-center study. Clin. Nutr. 2015, 34, 151–155. [Google Scholar] [CrossRef] [PubMed]
- Kerklaan, D.; Augustus, M.E.; Hulst, J.M.; van Rosmalen, J.; Verbruggen, S.; Joosten, K.F.M. Validation of ventilator-derived VCO2 measurements to determine energy expenditure in ventilated critically ill children. Clin. Nutr. 2017, 36, 452–457. [Google Scholar] [CrossRef] [PubMed]
- Penco, S.; Buscema, M.; Patrosso, M.C.; Marocchi, A.; Grossi, E. New application of intelligent agents in sporadic amyotrophic lateral sclerosis identifies unexpected specific genetic background. BMC Bioinform. 2008, 9, 254. [Google Scholar] [CrossRef] [PubMed]
- Buscema, M.; Breda, M.; Lodwick, W. Training with Input Selection and Testing (TWIST) Algorithm: A Significant Advance in Pattern Recognition Performance of Machine Learning. J. Intell. Learn. Syst. Appl. 2013, 5, 29–38. [Google Scholar] [CrossRef]
- Buscema, M. Genetic doping algorithm (GenD): Theory and applications. Expert Syst. 2004, 21, 63–79. [Google Scholar] [CrossRef]
- Smallwood, C.D.; Mehta, N.M. Estimating Energy Expenditure in Critically Ill Children: Still Shooting in the Dark? J. Pediatr. 2017, 184, 10–12. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Disse, E.; Ledoux, S.; Bétry, C.; Caussy, C.; Maitrepierre, C.; Coupaye, M.; Laville, M.; Simon, C. An artificial neural network to predict resting energy expenditure in obesity. Clin. Nutr. 2018, 37, 1661–1669. [Google Scholar] [CrossRef]
- Veldscholte, K.; Joosten, K.; Jotterand Chaparro, C. Energy expenditure in critically ill children. Pediatr. Med. 2020, 3, 18. [Google Scholar] [CrossRef]
- Ingels, C.; Vanhorebeek, I.; Van den Berghe, G. Glucose homeostasis, nutrition and infections during critical illness. Clin. Microbiol. Infect. 2018, 24, 10–15. [Google Scholar] [CrossRef] [PubMed]


| N = 257 | |||
|---|---|---|---|
| Demographic | Metabolic (Indirect calorimetry) | ||
| Age, years | 2.4 (6.0) # | VO2, L/min | 0.09 (0.05) |
| Male | 145 (56.4) | VCO2, L/min | 0.07 (0.04) |
| Anthropometric | RQ | 0.77 (0.12) | |
| Weight, kg | 15.6 (12.2) | Resting Energy Expenditure, kcal/die | 623.3 (325.7) |
| Height, cm | 93.4 (30.5) | Metabolic (equations/formulae) | |
| BMI, kg/m2 | 15.9 (3.2) | REE Harris–Benedict equation | 824.3 (260.2) |
| z-score BMI | −0.7 (2.0) | REE Harris–Benedict equation for infants | 964.3 (134.6) |
| z-score weight for age | −0.9 (1.7) | Schofield (weight) equation | 700.9 (347.6) |
| z-score height for age | −1.2 (1.9) | Schofield (weight and height) equation | 703.0 (344.3) |
| z-score weight for height | −0.6 (2.0) | FAO/WHO/UNU equation | 701.4 (353.1) |
| Outcomes | Oxford (weight) equation | 703.1 (335.9) | |
| Mechanically ventilated | 102 (39.5) | Oxford (weight and height) equation | 705.0 (332.8) |
| Length of PICU stay, days | 6.0 (12.0) # | Talbot (weight) equation | 650.1 (332.4) |
| Talbot (height) equation | 675.6 (325.5) | ||
| Mehta equation * | 475.6 (257.0) | ||
| Overall Group (N = 257), Measured REE = 623.3 (325.7) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| FITTING METHOD | Predicted REE | Absolute Error | Accuracy | Relative Error | Accuracy | F-Test Two-Sample | |||
| Mean | SD | Mean | % | Mean | % | F-Statistic | p-Value (Two Tails) | Pearson (R2) | |
| ANN with gas (baseline) | 651.4 | 329.0 | 38.1 | 93.9 | 0.058 | 94.2 | 0.982 | 0.881 | 0.928 |
| Harris–Benedict | 824.3 | 260.2 | 244.2 | 60.8 | 0.610 | 38.9 | 1.567 | <0.001 | 0.497 |
| Harris–Benedict for infants | 299.5 | 64.5 | 103.3 | 72.8 | 0.254 | 74.6 | 3.739 | <0.0001 | 0.288 |
| Schofield (weight) | 700.9 | 347.6 | 164.7 | 73.6 | 0.351 | 64.9 | 0.878 | 0.298 | 0.664 |
| Schofield (weight and height) | 703.0 | 344.3 | 160.8 | 74.2 | 0.348 | 65.2 | 0.895 | 0.374 | 0.671 |
| FAO/WHO/ UNU | 701.4 | 353.1 | 168.7 | 72.9 | 0.358 | 64.2 | 0.851 | 0.196 | 0.653 |
| Oxford (weight) | 703.1 | 335.9 | 163.7 | 73.7 | 0.352 | 64.8 | 0.941 | 0.624 | 0.655 |
| Oxford (weight and height) | 705.0 | 332.8 | 158.7 | 74.5 | 0.344 | 65.6 | 0.958 | 0.733 | 0.671 |
| Talbot (weight) | 650.1 | 332.4 | 142.3 | 77.2 | 0.300 | 70.0 | 0.960 | 0.746 | 0.691 |
| Talbot (height) | 675.6 | 325.5 | 147.6 | 76.3 | 0.320 | 68.0 | 1.002 | 0.989 | 0.684 |
| Mehta * | 475.6 | 257.0 | 89.7 | 84.0 | 0.160 | 84.0 | 1.380 | 0.107 | 0.906 |
| Data Set 1 | Baseline | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Variables number of the data set | 24 | 21 | 22 | 22 | 22 |
| Gas variables | VO2; VCO2; RQ | none | VO2 | VCO2 | RQ |
| Variables selected by TWIST system | male | female | Weight | African | mechanically ventilated |
| female | age | BMI | weight | male | |
| weight | weight | Obese | height | female | |
| BMI | height | VO2 | z-HFA | Asiatic | |
| VO2 | z-BMI | overweight | weight | ||
| VCO2 | z-HFA | Wasting (severe) | height | ||
| RQ | No wasting | VCO2 | BMI | ||
| wasting (mild) | z-HFA | ||||
| wasting (moderate) | normal weight | ||||
| wasting (severe) | Wasting (severe) | ||||
| stunting | RQ | ||||
| predictive accuracy | 93.9% | 75.6% | 92.9% | 84.4% | 78.0% |
| mean absolute error | 38.1 | 149.1 | 44.0 | 96.9 | 136.8 |
| Person R2 | 0.928 | 0.713 | 0.914 | 0.829 | 0.701 |
| N = 199 | |||
|---|---|---|---|
| Demographic | Metabolic (Indirect calorimetry) | ||
| Age, years | 2.3 (6.4) # | VO2, L/min | 0.09 (0.05) |
| Male | 112 (56.3) | VCO2, L/min | 0.07 (0.04) |
| Anthropometric | RQ | 0.75 (0.11) | |
| Weight, kg | 16.1 (12.7) | Resting Energy Expenditure, kcal/die | 632.3 (339.9) |
| Height, cm | 94.0 (31.1) | Metabolic (equations/formulae) | |
| BMI, kg/m2 | 16.1 (3.4) | REE Harris–Benedict equation | 833.5 (262.3) |
| z-score BMI | −0.6 (2.1) | REE Harris–Benedict equation for infants | 718.9 (357.7) |
| z-score weight for age | −0.9 (1.7) | Schofield (weight) equation | 711.5 (353.4) |
| z-score height for age | −1.1 (1.9) | Schofield (weight and height) equation | 712.6 (351.0) |
| z-score weight for height | −0.6 (2.0) | FAO/WHO/UNU equation | 712.4 (358.9) |
| Outcomes | Oxford (weight) equation | 713.1 (340.6) | |
| Mechanically ventilated | 93 (46.7) | Oxford (weight and height) equation | 714.3 (338.3) |
| Length of PICU stay, days | 7.0 (13.0) # | Talbot (weight) equation | 661.5 (342.0) |
| Vital signs | Talbot (height) equation | 684.7 (332.8) | |
| Heart rate, bpm | 117.6 (30.3) | Mehta equation * | 463.4 (257.2) |
| Systolic Blood Pressure, mmHg | 103.5 (18.3) | ||
| Diastolic Blood Pressure, mmHg | 61.0 (14.9) | ||
| Body Temperature, °C | 36.6 (0.7) | ||
| Oxygen Saturation, % | 97.7 (2.7) | ||
| Blood values | |||
| Hemoglobin, mg/dl | 9.9 (1.8) | ||
| Blood glucose, mg/dl | 106.4 (37.3) | ||
| C-Reactive Protein, mg/dl | 2.3 (6.7) # | ||
| Overall Group (N = 199), Measured REE = 632.3 (339.1) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| FITTING METHOD | Predicted REE | Absolute Error | Accuracy | Relative Error | Accuracy | F-Test Two-Sample | |||
| Mean | SD | Mean | % | Mean | % | F-Statistic | p-Value (Two Tails) | Pearson (R2) | |
| ANN with gas | 631.0 | 331.3 | 23.3 | 96.3 | 0.050 | 95.0 | 1.053 | 0.718 | 0.968 |
| ANN with VCO2 | 637.3 | 332.5 | 65.6 | 89.6 | 0.126 | 87.4 | 1.046 | 0.754 | 0.921 |
| ANN with VCO2 (ventilated) | 553.1 | 288.6 | 66.4 | 88.0 | 0.144 | 85.6 | 1.101 | 0.647 | 0.866 |
| ANN without gas | 628.4 | 312.5 | 111.7 | 82.3 | 0.212 | 78.8 | 1.183 | 0.237 | 0.808 |
| Harris–Benedict | 833.5 | 261.6 | 245.4 | 61.2 | 0.603 | 39.7 | 1.680 | <0.0001 | 0.529 |
| Harris–Benedict for infants | 718.9 | 356.8 | 182.4 | 71.2 | 0.370 | 63.0 | 0.903 | 0.474 | 0.623 |
| Schofield (weight) | 711.5 | 352.5 | 155.4 | 75.4 | 0.310 | 69.0 | 0.853 | 0.265 | 0.725 |
| Schofield (weight and height) | 712.6 | 350.9 | 151.9 | 76.0 | 0.307 | 69.3 | 0.938 | 0.654 | 0.735 |
| FAO/WHO /UNU | 712.4 | 357.9 | 160.1 | 74.7 | 0.317 | 68.3 | 0.897 | 0.446 | 0.715 |
| Oxford (weight) | 713.1 | 339.7 | 155.0 | 75.5 | 0.312 | 68.8 | 0.996 | 0.979 | 0.722 |
| Oxford (weight and height) | 714.3 | 337.5 | 150.5 | 76.2 | 0.306 | 69.4 | 1.010 | 0.946 | 0.737 |
| Talbot (weight) | 661.5 | 341.1 | 132.7 | 79.0 | 0.264 | 73.6 | 0.988 | 0.933 | 0.751 |
| Talbot (height) | 681.2 | 333.4 | 136.0 | 78.4 | 0.274 | 72.6 | 0.985 | 0.913 | 0.758 |
| Mehta * | 463.4 | 257.2 | 90.8 | 83.5 | 0.164 | 83.6 | 1.386 | 0.647 | 0.901 |
| Data Set 2 | Baseline | 1 | 2 |
|---|---|---|---|
| Variables number of the data set | 32 | 29 | 30 |
| Gas variables | VO2; VCO2; RQ | none | VCO2 |
| Variables selected by TWIST system | African | mechanically ventilated | South American |
| height | male | African | |
| wasting mild | Asian | weight | |
| VO2 | African | height | |
| VCO2 | weight | BMI | |
| RQ | height | obesity | |
| SatO2% | BMI z-HFA wasting mild body temperature SatO2% CRP | VCO2 Blood glucose CRP | |
| predictive accuracy | 96.3% | 82.3% | 89.5% |
| mean absolute error | 23.3 | 111.7 | 65.6 |
| Person R2 | 0.968 | 0.808 | 0.921 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spolidoro, G.C.I.; D’Oria, V.; De Cosmi, V.; Milani, G.P.; Mazzocchi, A.; Akhondi-Asl, A.; Mehta, N.M.; Agostoni, C.; Calderini, E.; Grossi, E. Artificial Neural Network Algorithms to Predict Resting Energy Expenditure in Critically Ill Children. Nutrients 2021, 13, 3797. https://doi.org/10.3390/nu13113797
Spolidoro GCI, D’Oria V, De Cosmi V, Milani GP, Mazzocchi A, Akhondi-Asl A, Mehta NM, Agostoni C, Calderini E, Grossi E. Artificial Neural Network Algorithms to Predict Resting Energy Expenditure in Critically Ill Children. Nutrients. 2021; 13(11):3797. https://doi.org/10.3390/nu13113797
Chicago/Turabian StyleSpolidoro, Giulia C. I., Veronica D’Oria, Valentina De Cosmi, Gregorio Paolo Milani, Alessandra Mazzocchi, Alireza Akhondi-Asl, Nilesh M. Mehta, Carlo Agostoni, Edoardo Calderini, and Enzo Grossi. 2021. "Artificial Neural Network Algorithms to Predict Resting Energy Expenditure in Critically Ill Children" Nutrients 13, no. 11: 3797. https://doi.org/10.3390/nu13113797
APA StyleSpolidoro, G. C. I., D’Oria, V., De Cosmi, V., Milani, G. P., Mazzocchi, A., Akhondi-Asl, A., Mehta, N. M., Agostoni, C., Calderini, E., & Grossi, E. (2021). Artificial Neural Network Algorithms to Predict Resting Energy Expenditure in Critically Ill Children. Nutrients, 13(11), 3797. https://doi.org/10.3390/nu13113797








