Repeatability of Taste Recognition Threshold Measurements with QUEST and Quick Yes–No
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Procedure
2.2.1. Experimental Sessions
2.2.2. Eating Behavior, Taste Liking, and Food Consumption
2.2.3. Taste Recognition Thresholds
Procedure
Taste Stimuli
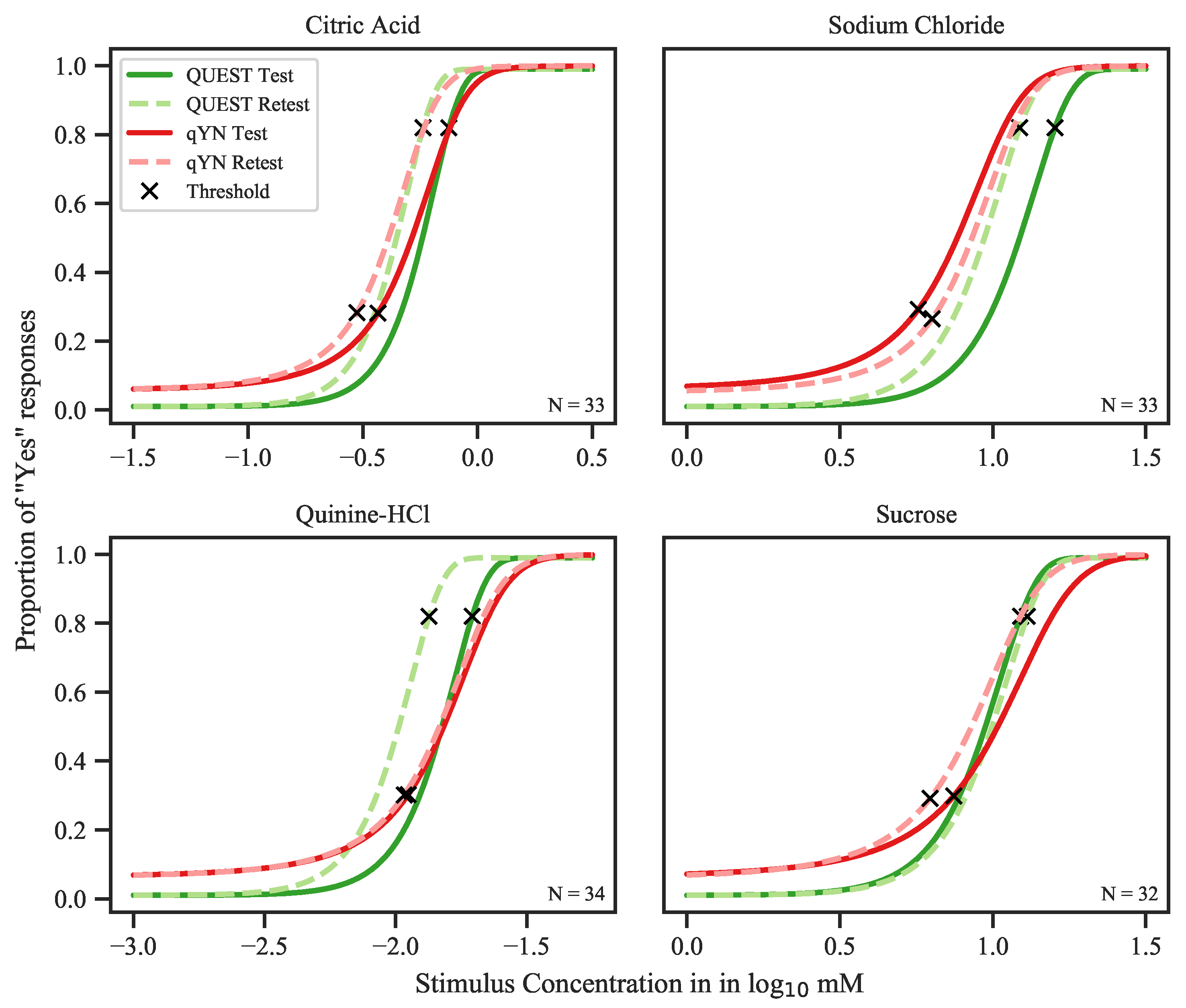
Psychometric Functions
Stimulus Selection
Taste Recognition Termination
Parameter Estimates
2.3. Analysis
2.3.1. Ratings
2.3.2. Taste Recognition Data Cleaning
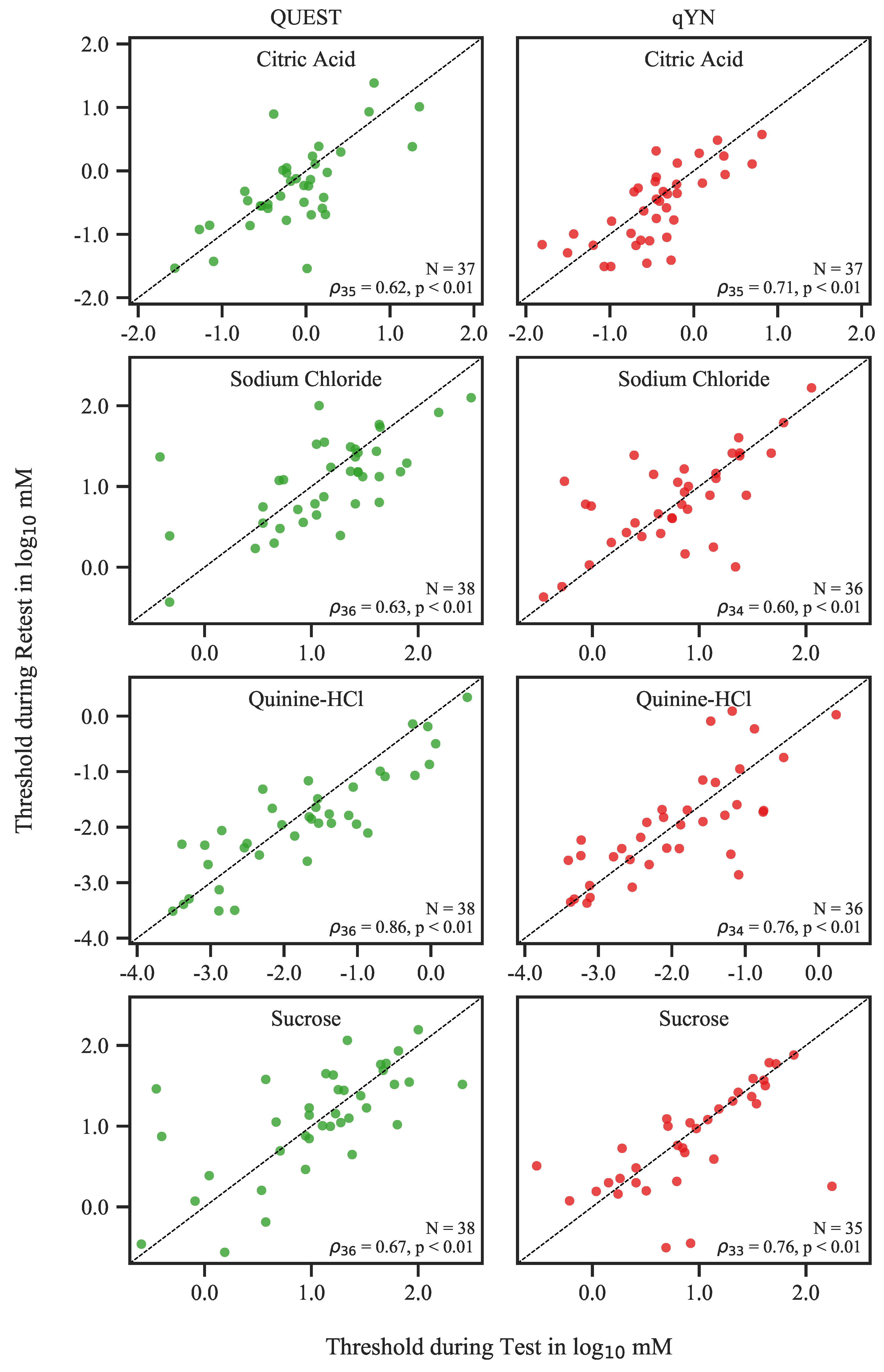
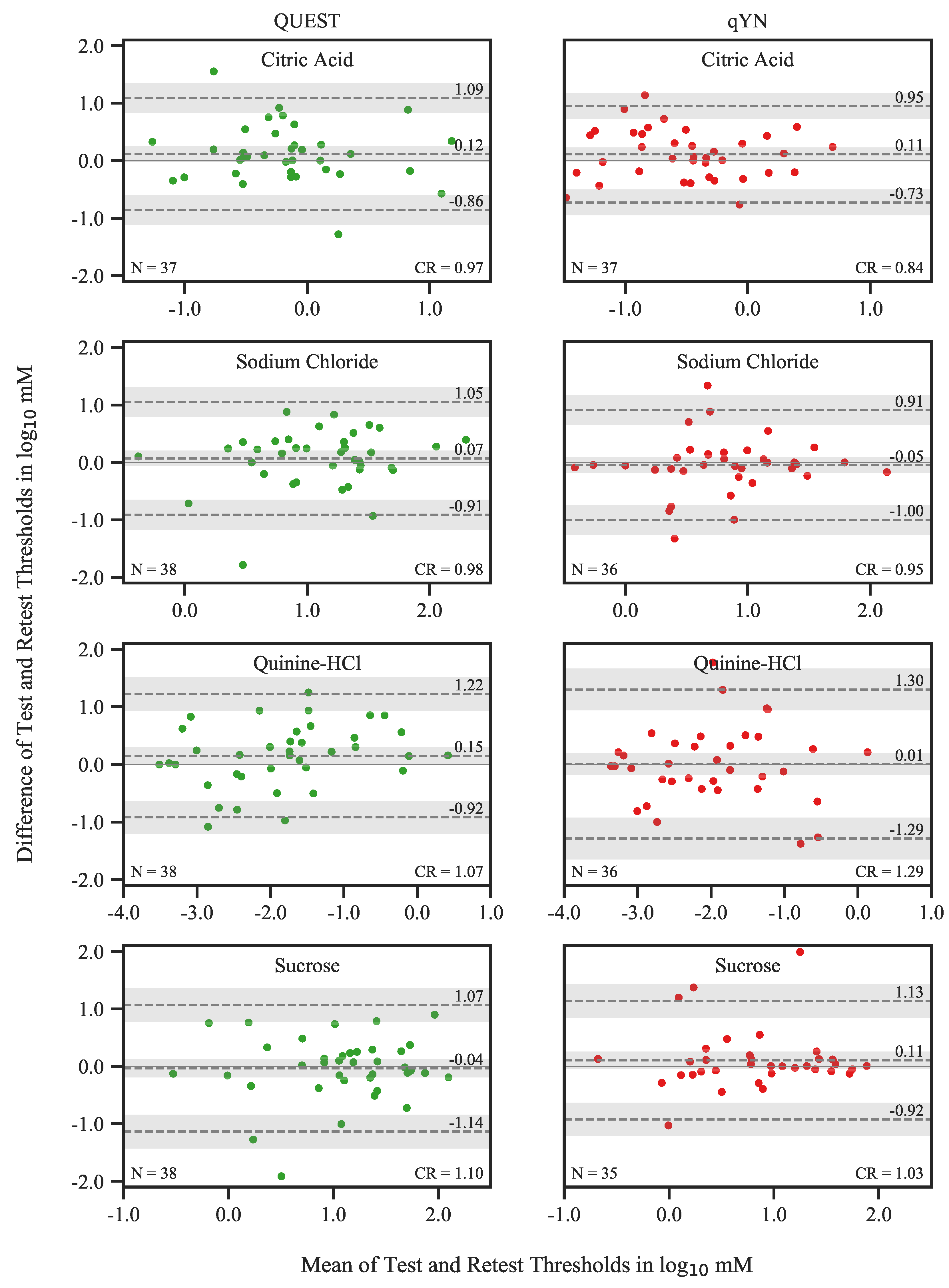
2.3.3. Test–Retest Reliability
Threshold
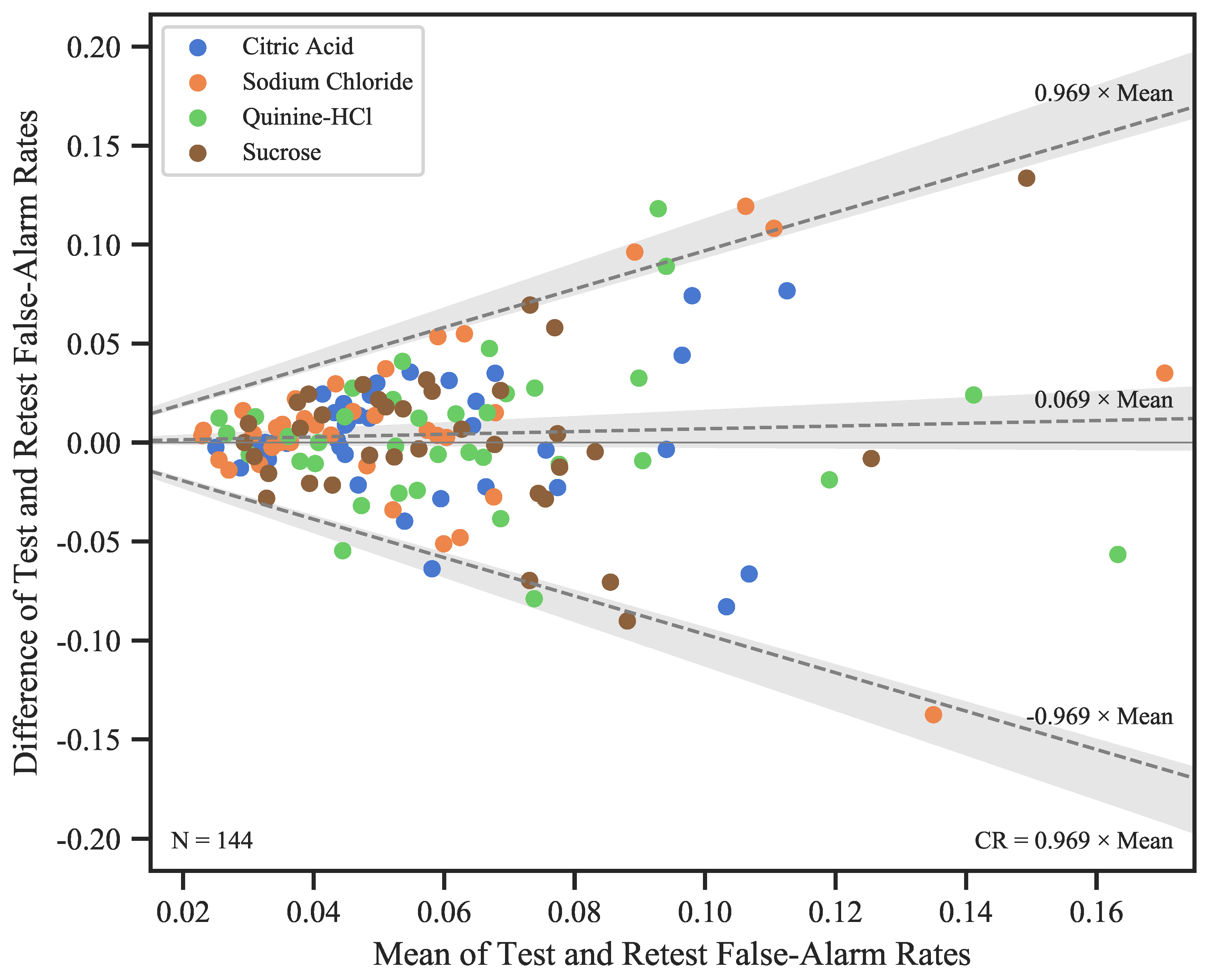
False-Alarm Rate (FAR)
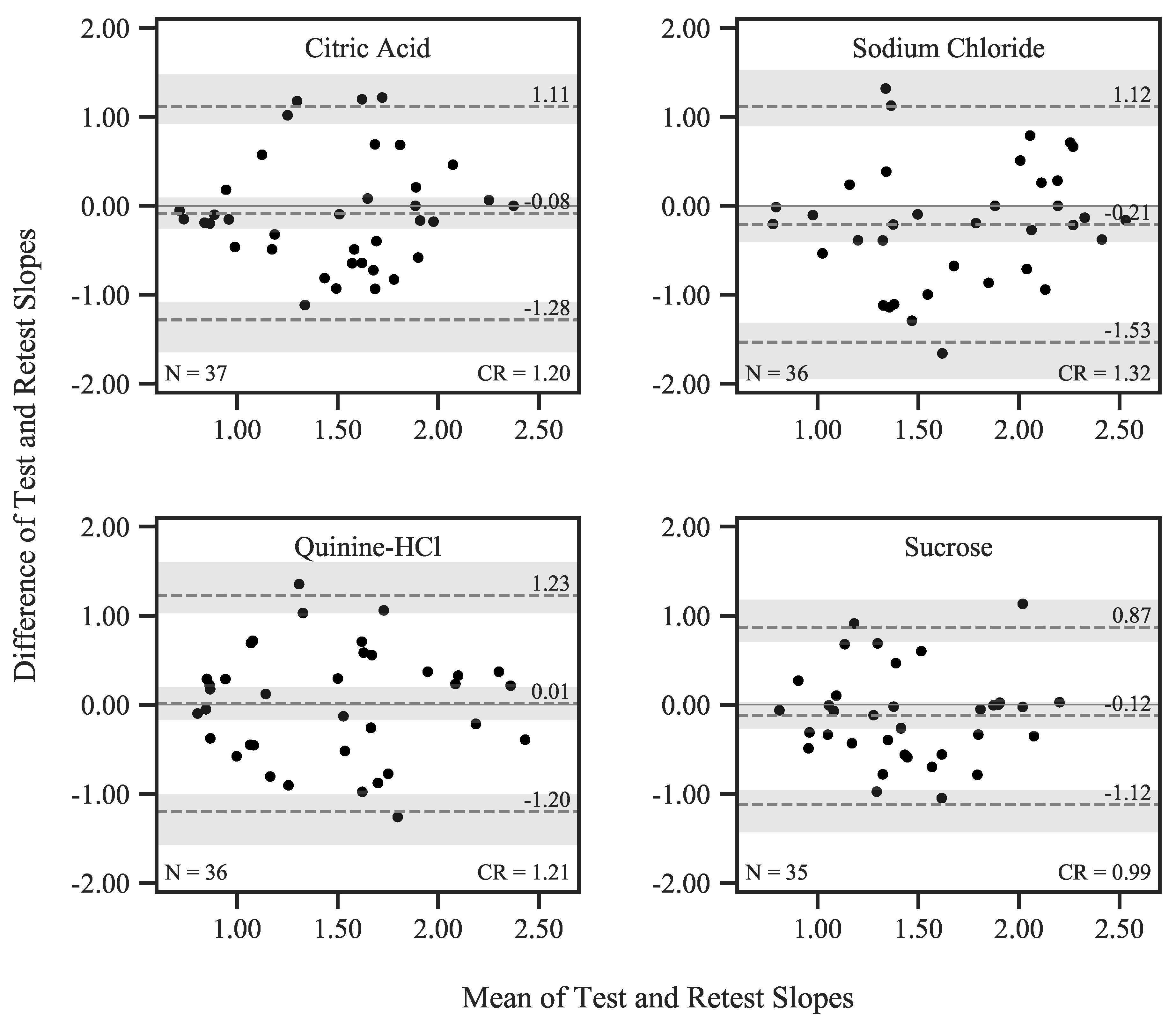
Slope
Relationship between FAR and Slope
2.3.4. Software
3. Results
3.1. Eating Behavior, Taste Liking, and Food Consumption
3.2. Taste Recognition
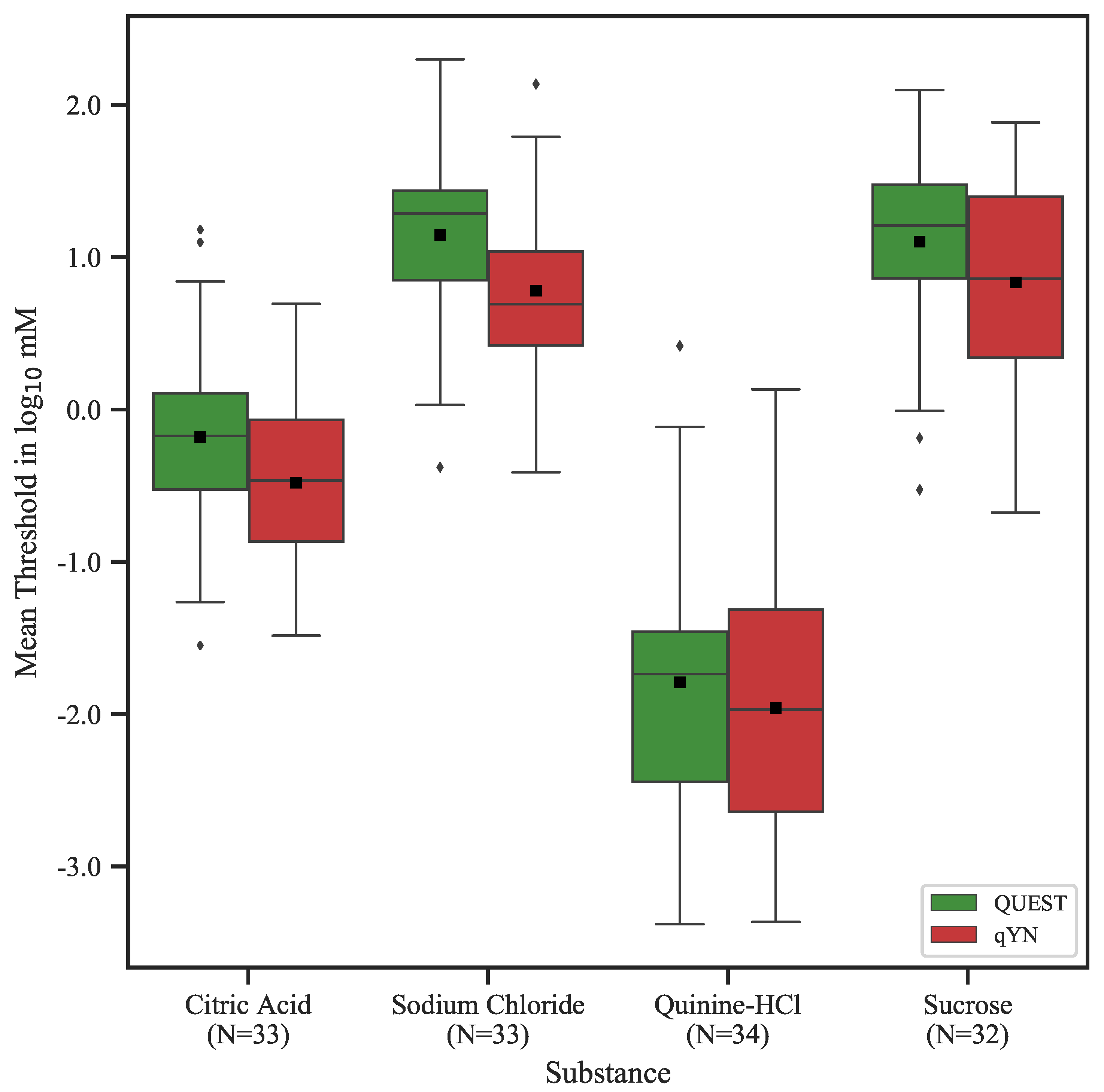
3.2.1. Threshold Repeatability
3.2.2. False-Alarm Rates and Psychometric Function Slopes
4. Discussion
4.1. Taste Recognition Thresholds
4.2. Threshold Repeatability
4.3. False-Alarm Rates and Slopes
4.4. Measurement Duration
4.5. Taste Sensitivity, Taste Liking, and Food Preference
5. Conclusions
6. Data and Software Availability
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Watson, A.B.; Pelli, D.G. Quest: A Bayesian adaptive psychometric method. Percept. Psychophys. 1983, 33, 113–120. [Google Scholar] [CrossRef]
- Höchenberger, R.; Ohla, K. Rapid Estimation of Gustatory Sensitivity Thresholds with SIAM and QUEST. Front. Psychol. 2017, 8, 981. [Google Scholar] [CrossRef]
- Hardikar, S.; Höchenberger, R.; Villringer, A.; Ohla, K. Higher sensitivity to sweet and salty taste in obese compared to lean individuals. Appetite 2017, 111, 158–165. [Google Scholar] [CrossRef]
- Green, D.M.; Swets, J.A. Signal Detection Theory and Psychophysics; Wiley: New York, NY, USA, 1966. [Google Scholar]
- Macmillan, N.A.; Creelman, C.D. Detection Theory: A User’s Guide, 2nd ed.; Lawrence Erdbaum Associates, Inc.: Mahwah, NJ, USA, 2010. [Google Scholar]
- Klein, S.A. Measuring, estimating, and understanding the psychometric function: A commentary. Percept. Psychophys. 2001, 63, 1421–1455. [Google Scholar] [CrossRef]
- Höchenberger, R.; Ohla, K. Estimation of Olfactory Sensitivity Using a Bayesian Adaptive Method. Nutrients 2019, 11, 1278. [Google Scholar] [CrossRef]
- Lesmes, L.A.; Lu, Z.L.; Baek, J.; Tran, N.; Dosher, B.A.; Albright, T.D. Developing Bayesian adaptive methods for estimating sensitivity thresholds (d′) in Yes-No and forced-choice tasks. Front. Psychol. 2015, 6, 1070. [Google Scholar] [CrossRef]
- van Strien, T.; Frijters, J.E.R.; Bergers, G.P.A.; Defares, P.B. The Dutch Eating Behavior Questionnaire (DEBQ) for assessment of restrained, emotional, and external eating behavior. Int. J. Eat. Disord. 1986, 5, 295–315. [Google Scholar] [CrossRef]
- King-Smith, P.E.; Grigsby, S.S.; Vingrys, A.J.; Benes, S.C.; Supowit, A. Efficient and unbiased modifications of the QUEST threshold method: Theory, simulations, experimental evaluation and practical implementation. Vis. Res. 1994, 34, 885–912. [Google Scholar] [CrossRef]
- Vaz, S.; Falkmer, T.; Passmore, A.E.; Parsons, R.; Andreou, P. The Case for Using the Repeatability Coefficient When Calculating Test–Retest Reliability. PLoS ONE 2013, 8, e73990. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. Measuring agreement in method comparison studies. Stat. Methods Med. Res. 1999, 8, 135–160. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. Applying the right statistics: analyses of measurement studies. Ultrasound Obstet. Gynecol. 2003, 22, 85–93. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 327, 307–310. [Google Scholar] [CrossRef]
- Carkeet, A. Exact Parametric Confidence Intervals for Bland-Altman Limits of Agreement. Optom. Vis. Sci. 2015, 92, e71–e80. [Google Scholar] [CrossRef]
- Euser, A.M.; Dekker, F.W.; le Cessie, S. A practical approach to Bland-Altman plots and variation coefficients for log transformed variables. J. Clin. Epidemiol. 2008, 61, 978–982. [Google Scholar] [CrossRef]
- Peirce, J.; Gray, J.R.; Simpson, S.; MacAskill, M.; Höchenberger, R.; Sogo, H.; Kastman, E.; Lindeløv, J.K. PsychoPy2: Experiments in behavior made easy. Behav. Res. Methods 2019, 51, 195–203. [Google Scholar] [CrossRef]
- Vallat, R. Pingouin: statistics in Python. J. Open Source Softw. 2018, 3, 1026. [Google Scholar] [CrossRef]
- Nagl, M.; Hilbert, A.; de Zwaan, M.; Braehler, E.; Kersting, A. The German Version of the Dutch Eating Behavior Questionnaire: Psychometric Properties, Measurement Invariance, and Population-Based Norms. PLoS ONE 2016, 11, e0162510. [Google Scholar] [CrossRef]
- Wise, P.M.; Breslin, P.A.S. Individual Differences in Sour and Salt Sensitivity: Detection and Quality Recognition Thresholds for Citric Acid and Sodium Chloride. Chem. Sens. 2013, 38, 333–342. [Google Scholar] [CrossRef]
- Mattes, R.D. Reliability of psychophysical measures of gustatory function. Percept. Psychophys. 1988, 43, 107–114. [Google Scholar] [CrossRef]
- Mueller, C.; Kallert, S.; Renner, B.; Stiassny, K.; Temmel, A.F.; Hummel, T.; Kobal, G. Quantitative assessment of gustatory function in a clinical context using impregnated “taste strips”. Rhinology 2003, 41, 2–6. [Google Scholar]
- Altman, D.G.; Bland, J.M. Measurement in Medicine: The Analysis of Method Comparison Studies. Statistician 1983, 32, 307. [Google Scholar] [CrossRef]
- Cattaneo, C.; Riso, P.; Laureati, M.; Gargari, G.; Pagliarini, E. Exploring Associations between Interindividual Differences in Taste Perception, Oral Microbiota Composition, and Reported Food Intake. Nutrients 2019, 11, 1167. [Google Scholar] [CrossRef]
- Sauer, H.; Ohla, K.; Dammann, D.; Teufel, M.; Zipfel, S.; Enck, P.; Mack, I. Changes in Gustatory Function and Taste Preference Following Weight Loss. J. Pediatr. 2017, 182, 120–126. [Google Scholar] [CrossRef]
- Rasmussen, M.; Krølner, R.; Klepp, K.I.; Lytle, L.; Brug, J.; Bere, E.; Due, P. Determinants of fruit and vegetable consumption among children and adolescents: A review of the literature. Part I: Quantitative studies. Int. J. Behav. Nutr. Phys. Act. 2006, 3, 22. [Google Scholar] [CrossRef]
| Measure | Mean | SD | N |
|---|---|---|---|
| DEBQ emotional eating | 2.22 | 0.64 | 40 |
| DEBQ restrained eating | 2.55 | 0.67 | 40 |
| DEBQ external eating | 3.02 | 0.65 | 40 |
| Liking of salty | 3.41 | 1.05 | 37 |
| Liking of sour | 3.05 | 1.09 | 37 |
| Liking of sweet | 4.11 | 0.83 | 37 |
| Liking of bitter | 1.89 | 0.98 | 37 |
| Consumption of salty | 3.64 | 1.33 | 37 |
| Consumption of sour | 4.19 | 1.10 | 37 |
| Consumption of sweet | 4.70 | 1.03 | 37 |
| Consumption of bitter | 4.00 | 1.24 | 37 |
| Procedure | Tastant | N | Session | Threshold in mM | |||
|---|---|---|---|---|---|---|---|
| mean | min | max | SD | ||||
| QUEST | Citric Acid | 37 | Test | −0.141 | −1.564 | 1.350 | 0.621 |
| Retest | −0.256 | −1.540 | 1.385 | 0.666 | |||
| Sodium Chloride | 38 | Test | 1.140 | −0.417 | 2.495 | 0.631 | |
| Retest | 1.069 | −0.432 | 2.100 | 0.544 | |||
| Quinine−HCl | 38 | Test | −1.737 | −3.514 | 0.496 | 1.101 | |
| Retest | −1.889 | −3.514 | 0.339 | 0.953 | |||
| Sucrose | 38 | Test | 1.054 | −0.592 | 2.414 | 0.705 | |
| Retest | 1.089 | −0.563 | 2.194 | 0.660 | |||
| qYN | Citric Acid | 37 | Test | −0.446 | −1.807 | 0.812 | 0.563 |
| Retest | −0.558 | −1.508 | 0.574 | 0.598 | |||
| Sodium Chloride | 36 | Test | 0.785 | −0.457 | 2.052 | 0.607 | |
| Retest | 0.831 | −0.369 | 2.222 | 0.571 | |||
| Quinine−HCl | 35 | Test | −1.974 | −3.409 | 0.239 | 0.952 | |
| Retest | −1.980 | −3.369 | 0.091 | 0.962 | |||
| Sucrose | 36 | Test | 0.871 | −0.613 | 2.243 | 0.677 | |
| Retest | 0.765 | −0.742 | 1.881 | 0.669 | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Höchenberger, R.; Ohla, K. Repeatability of Taste Recognition Threshold Measurements with QUEST and Quick Yes–No. Nutrients 2020, 12, 24. https://doi.org/10.3390/nu12010024
Höchenberger R, Ohla K. Repeatability of Taste Recognition Threshold Measurements with QUEST and Quick Yes–No. Nutrients. 2020; 12(1):24. https://doi.org/10.3390/nu12010024
Chicago/Turabian StyleHöchenberger, Richard, and Kathrin Ohla. 2020. "Repeatability of Taste Recognition Threshold Measurements with QUEST and Quick Yes–No" Nutrients 12, no. 1: 24. https://doi.org/10.3390/nu12010024
APA StyleHöchenberger, R., & Ohla, K. (2020). Repeatability of Taste Recognition Threshold Measurements with QUEST and Quick Yes–No. Nutrients, 12(1), 24. https://doi.org/10.3390/nu12010024





