Spatio-Temporal Variability and Model Parameter Sensitivity Analysis of Ice Production in Ross Ice Shelf Polynya from 2003 to 2015
Abstract
1. Introduction
2. Method and Materials
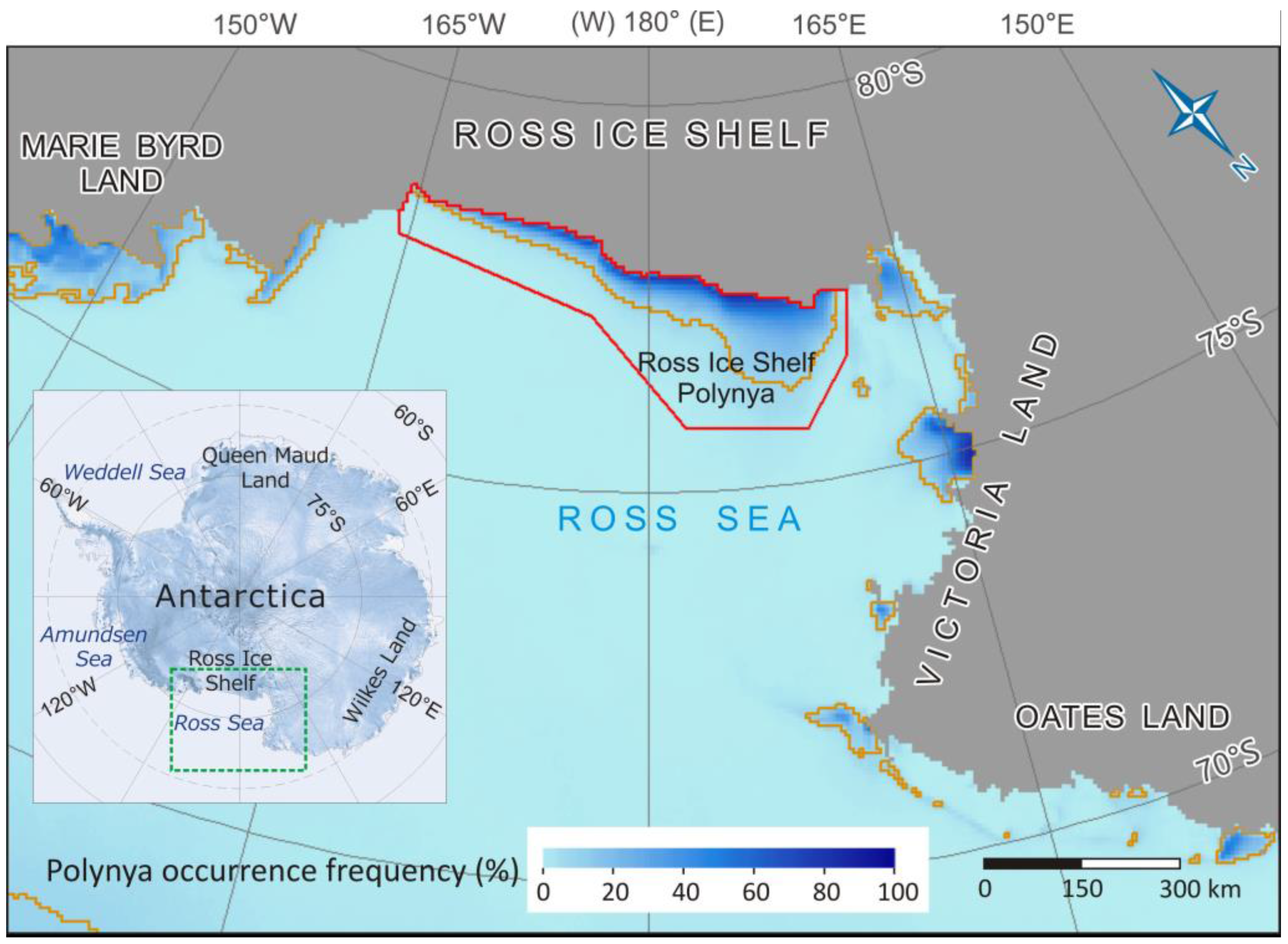
2.1. Study Area and Period
2.2. Data
2.2.1. ECMWF Re-Analysis Data
2.2.2. Sea Ice Concentration (SIC) Maps
2.2.3. Landmask
2.3. Sea Ice Production Model
2.4. Trend Analysis
2.5. Sensitivity Test
3. Results
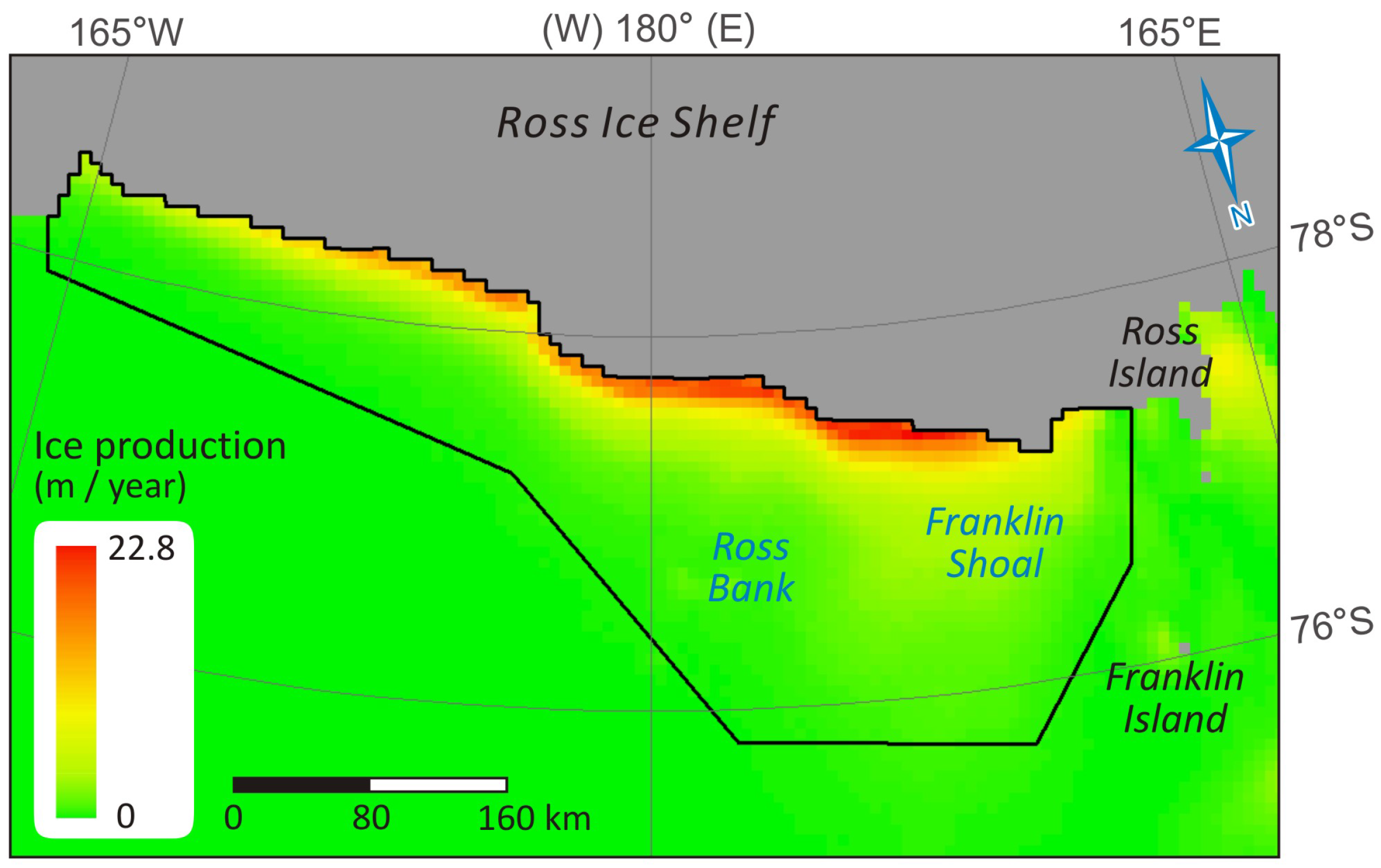
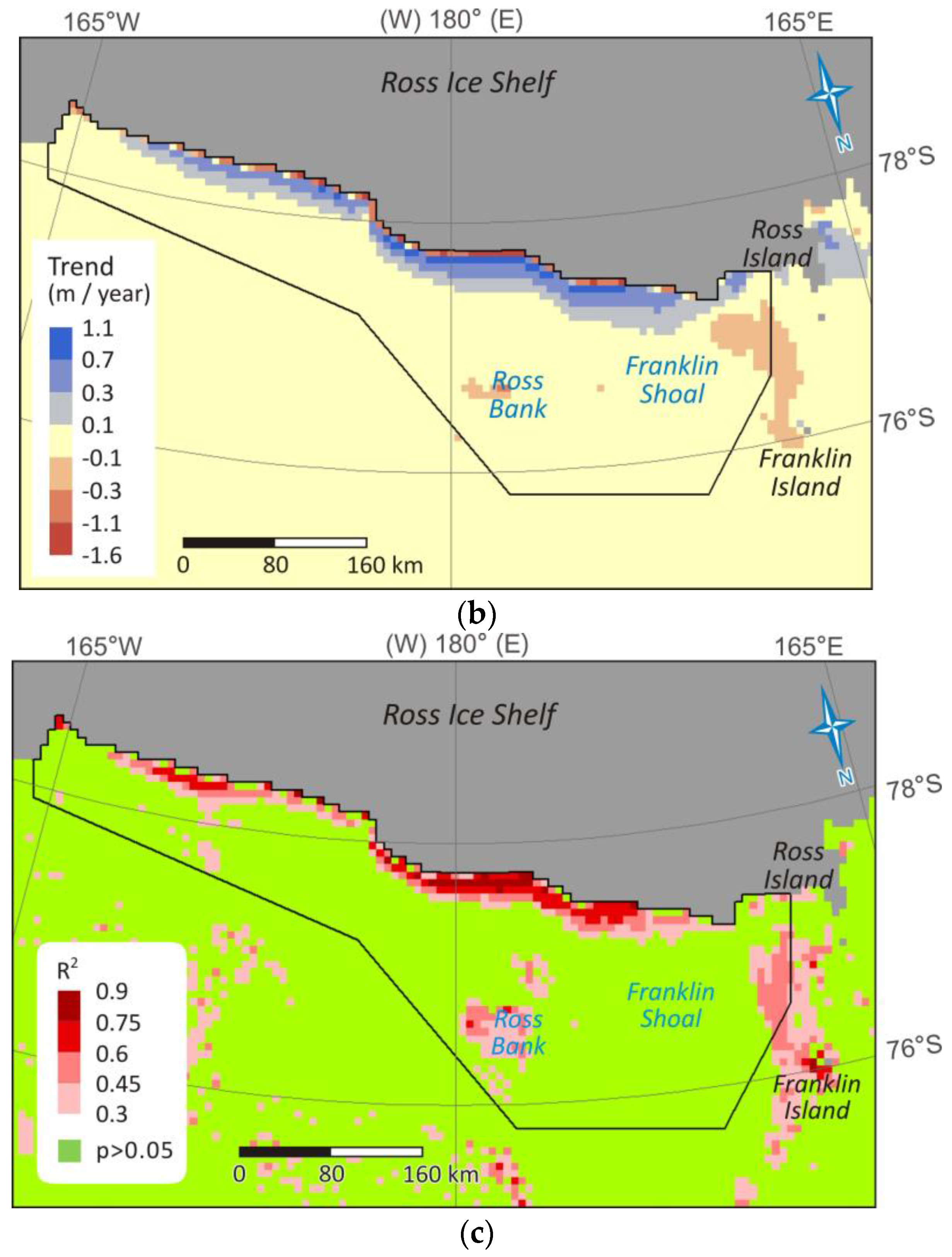
3.1. Spatial Trend
3.2. Monthly Trend
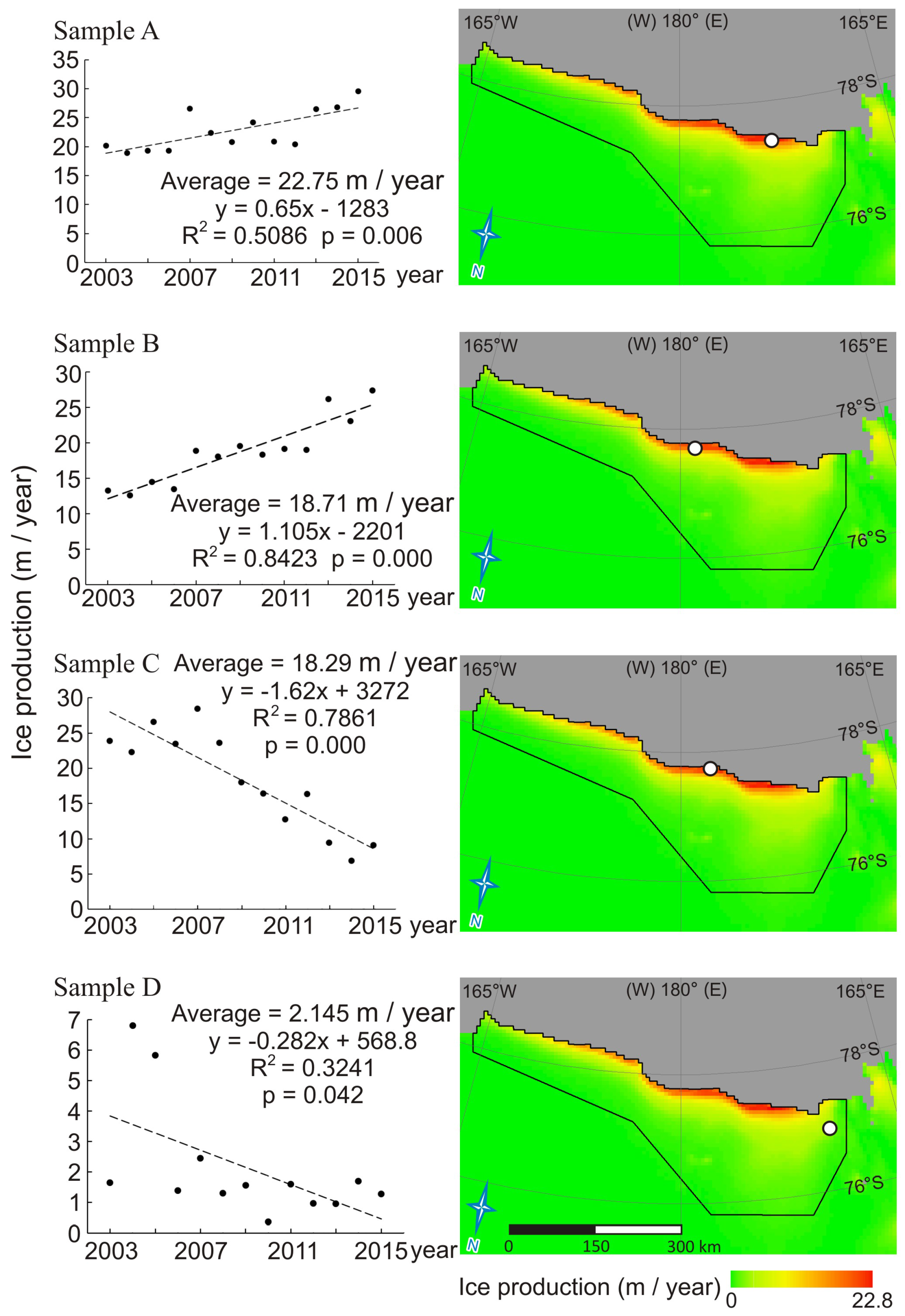
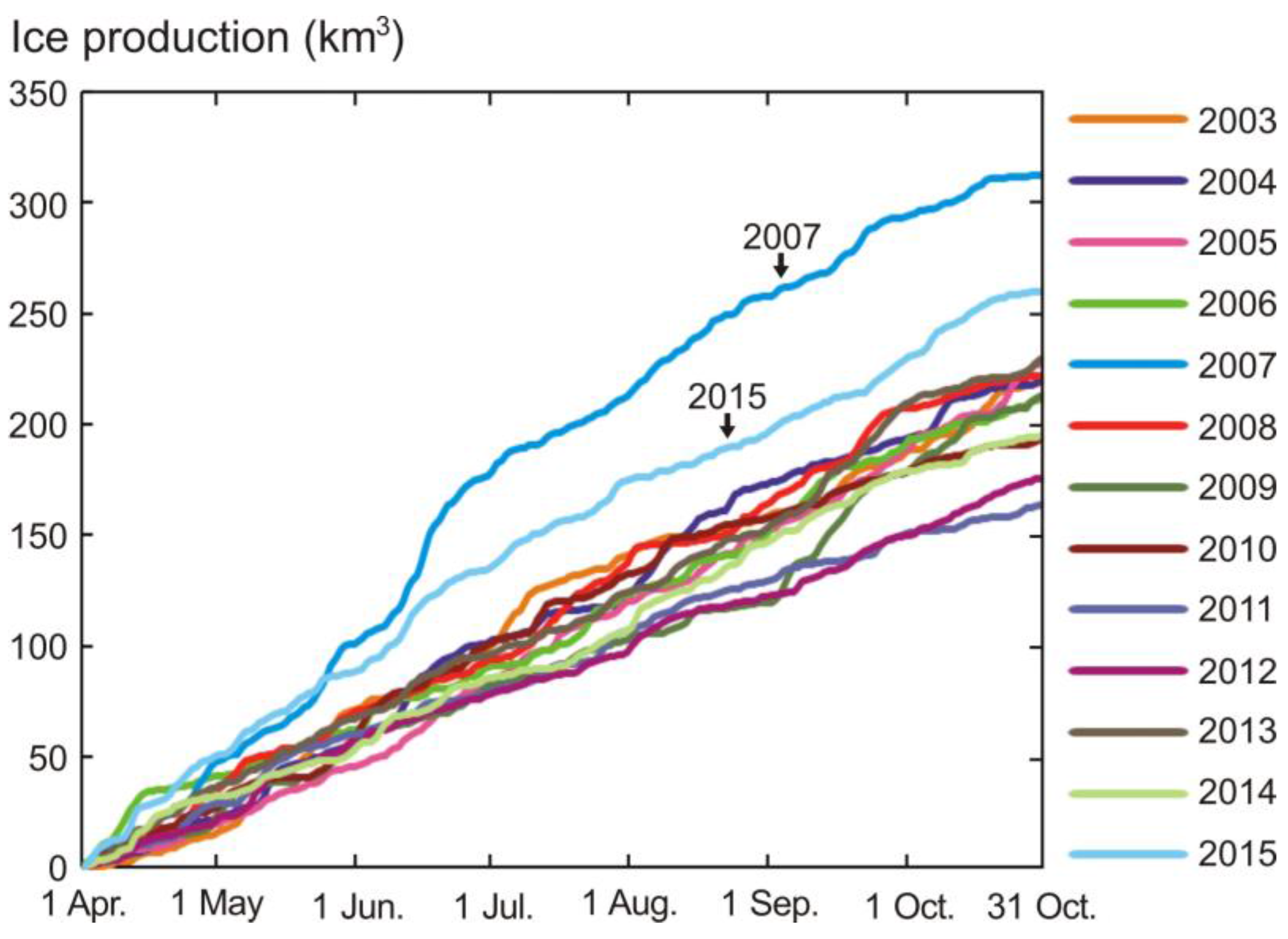
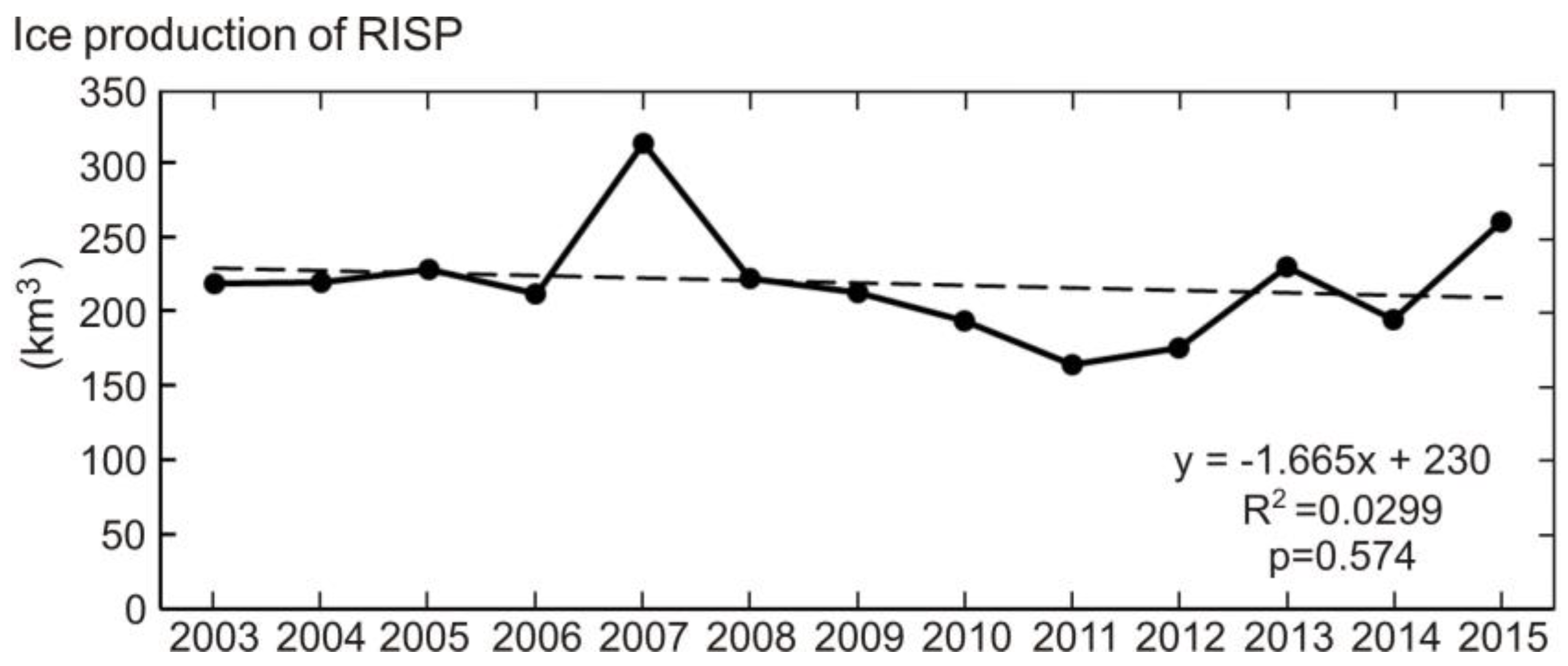
3.3. Interannual Trend
3.4. Sensitivity Test
4. Discussion
5. Conclusions
Acknowledgements
Author Contributions
Conflicts of Interest
References
- Smith, S.D.; Muench, R.D.; Pease, C.H. Polynyas and leads: An overview of physical processes and environment. J. Geophys. Res. 1990, 95, 9461–9479. [Google Scholar] [CrossRef]
- Morales-Maqueda, M.; Willmott, A.; Biggs, N. Polynya dynamics: A review of observations and modeling. Rev. Geophys. 2004, 42. [Google Scholar] [CrossRef]
- Kern, S. Wintertime Antarctic coastal polynya area: 1992–2008. Geophys. Res. Lett. 2009, 36, L14501. [Google Scholar] [CrossRef]
- Cavalieri, D.J.; Martin, S. A passive microwave study of polynyas along the Antarctic Wilkes Land coast. In Oceanology of the Antarctic Continental Shelf; American Geophysical Union: Washington, DC, USA, 1985; Volume 43, pp. 227–252. [Google Scholar]
- Lemke, P. Open windows to the polar oceans. Science 2001, 292, 1670–1671. [Google Scholar] [CrossRef] [PubMed]
- Comiso, J.C.; Gordon, A.L. Interannual variability in summer sea ice minimum, coastal polynyas and bottom water formation in the Weddell Sea. In Antarctic Sea Ice: Physical Processes, Interactions and Variability; American Geophysical Union: Washington, DC, USA, 1998; Volume 74, pp. 293–315. [Google Scholar]
- Tamura, T.; Ohshima, K.I.; Nihashi, S. Mapping of sea ice production for Antarctic coastal polynyas. Geophys. Res. Lett. 2008, 35, L07606. [Google Scholar] [CrossRef]
- Tamura, T.; Ohshima, K.I.; Fraser, A.D.; Williams, G.D. Sea ice production variability in Antarctic coastal polynyas. J. Geophys. Res. 2016, 121, 2967–2979. [Google Scholar] [CrossRef]
- Nihashi, S.; Ohshima, K.I. Circumpolar mapping of Antarctic coastal polynyas and landfast sea ice: Relationship and variability. J. Clim. 2015, 28, 3650–3670. [Google Scholar] [CrossRef]
- Comiso, J.C.; Kwok, R.; Martin, S.; Gordon, A.L. Variability and trends in sea ice extent and ice production in the Ross Sea. J. Geophys. Res. 2011, 116, C04021. [Google Scholar] [CrossRef]
- Whitworth, T.; Orsi, A.H. Antarctic Bottom Water production and export by tides in the Ross Sea. Geophys. Res. Lett. 2006, 33, L12609. [Google Scholar] [CrossRef]
- Ohshima, K.I.; Fukamachi, Y.; Williams, G.D.; Nihashi, S.; Roquet, F.; Kitade, Y.; Tamura, T.; Hirano, D.; Herraiz-Borreguero, L.; Field, I.; et al. Antarctic Bottom Water production by intense sea-ice formation in the Cape Darnley polynya. Nat. Geosci. 2013, 6, 235–240. [Google Scholar] [CrossRef]
- Ciappa, A.; Pietranera, L.; Budillon, G. Observations of the Terra Nova Bay (Antarctica) polynya by MODIS ice surface temperature imagery from 2005 to 2010. Remote Sens. Environ. 2012, 119, 158–172. [Google Scholar] [CrossRef]
- Paul, S.; Willmes, S.; Heinemann, G. Long-term coastal-polynya dynamics in the southern Weddell Sea from MODIS thermal-infrared imagery. Cryosphere 2015, 9, 2027–2041. [Google Scholar] [CrossRef]
- Martin, S. Estimation of the thin ice thickness and heat flux for the Chukchi Sea Alaskan coast polynya from Special Sensor Microwave/Imager data, 1990–2001. J. Geophys. Res. 2004, 109, C10. [Google Scholar] [CrossRef]
- Iwamoto, K.; Ohshima, K.I.; Tamura, T.; Nihashi, S. Estimation of thin ice thickness from AMSR-E data in the Chukchi Sea. Int. J. Remote Sens. 2013, 34, 468–489. [Google Scholar] [CrossRef]
- Yu, Y.; Lindsay, R. Comparison of thin ice thickness distributions derived from RADARSAT Geophysical Processor System and advanced very high resolution radiometer data sets. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Parmiggiani, F. Fluctuations of Terra Nova Bay polynya as observed by active (ASAR) and passive (AMSR-E) microwave radiometers. Int. J. Remote Sens. 2006, 27, 2459–2467. [Google Scholar] [CrossRef]
- Markus, T.; Burns, B.A. A method to estimate subpixel-scale coastal polynyas with satellite passive microwave data. J. Geophys. Res. 1995, 100, 4473–4487. [Google Scholar] [CrossRef]
- Massom, R.A.; Harris, P.T.; Michael, K.J.; Potter, M.J. The distribution and formative processes of latent-heat polynyas in East Antarctica. Ann. Glaciol. 1998, 27, 420–426. [Google Scholar]
- Martin, S. Improvements in the estimates of ice thickness and production in the Chukchi Sea polynyas derived from AMSR-E. Geophys. Res. Lett. 2005, 32, 5. [Google Scholar] [CrossRef]
- Martin, S.; Drucker, R.S.; Kwok, R. The areas and ice production of the western and central Ross Sea polynyas, 1992–2002, and their relation to the B-15 and C-19 iceberg events of 2000 and 2002. J. Mar. Syst. 2007, 68, 201–214. [Google Scholar] [CrossRef]
- Kern, S.; Spreen, G.; Kaleschke, L.; de La Rosa, S.; Heygster, G. Polynya Signature Simulation Method polynya area in comparison to AMSR-E 89 GHz sea-ice concentrations in the Ross Sea and off the Adélie Coast, Antarctica, for 2002–05: First results. Ann. Glaciol. 2007, 46, 409–418. [Google Scholar] [CrossRef]
- Maykut, G.A. Large-scale heat exchange and ice production in the central Arctic. J. Geophys. Res. 1982, 87, 7971–7984. [Google Scholar] [CrossRef]
- Markus, T.; Kottmeier, C.; Fahrbach, E. Ice formation in coastal polynyas in the Weddell Sea and their impact on oceanic salinity. In Antarctic Sea Ice: Physical Processes, Interactions and Variability; American Geophysical Union: Washington, DC, USA, 1998. [Google Scholar]
- Haid, V.; Timmermann, R. Simulated heat flux and sea ice production at coastal polynyas in the southwestern Weddell Sea. J. Geophys. Res. 2013, 118, 2640–2652. [Google Scholar] [CrossRef]
- Drucker, R.; Martin, S.; Kwok, R. Sea ice production and export from coastal polynyas in the Weddell and Ross Seas. Geophys. Res. Lett. 2011, 38, L17502. [Google Scholar] [CrossRef]
- Nakata, K.; Ohshima, K.I.; Nihashi, S.; Kimura, N.; Tamura, T. Variability and ice production budget in the Ross Ice Shelf Polynya based on a simplified polynya model and satellite observations. J. Geophys. Res. 2015, 120, 6234–6252. [Google Scholar] [CrossRef]
- Petrelli, P.; Bindoff, N.L.; Bergamasco, A. The sea ice dynamics of Terra Nova Bay and Ross Ice Shelf Polynyas during a spring and winter simulation. J. Geophys. Res. 2008, 113, C9. [Google Scholar] [CrossRef]
- Dale, E.R.; McDonald, A.J.; Coggins, J.H.J.; Rack, W. Atmospheric forcing of sea ice anomalies in the Ross Sea polynya region. Cryosphere 2017, 11, 267–280. [Google Scholar] [CrossRef]
- Adams, S.; Willmes, S.; Heinemann, G.; Rozman, P.; Timmermann, R.; Schroeder, D. Evaluation of simulated sea-ice concentrations from sea-ice/ocean models using satellite data and polynya classification methods. Polar Res. 2011, 30. [Google Scholar] [CrossRef]
- Martin, S.; Polyakov, I.; Markus, T.; Drucker, R. Okhotsk Sea Kashevarov Bank polynya: Its dependence on diurnal and fortnightly tides and its initial formation. J. Geophys. Res. Oceans 2004, 109. [Google Scholar] [CrossRef]
- Andreas, E.L.; Murphy, B. Bulk transfer coefficients for heat and momentum over leads and polynyas. J. Phys. Oceanogr. 1986, 16, 1875–1883. [Google Scholar] [CrossRef]
- Andreas, E.L.; Cash, B.A. Convective heat transfer over wintertime leads and polynyas. J. Geophys. Res. Oceans 1999, 104, 25721–25734. [Google Scholar] [CrossRef]
- Adams, S.; Willmes, S.; Schroeder, D.; Heinemann, G.; Bauer, M.; Krumpen, T. Improvement and sensitivity analysis of thermal thin-ice retrievals. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3306–3318. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- ERA Interim, Daily, ECMWF. Available online: http://apps.ecmwf.int/datasets/data/interim-full-daily/levtype=sfc/ (accessed on 29 June 2017).
- Spreen, G.; Melsheimer, C.; Heygster, G. Sea Ice Remote Sensing at the University of Bremen, Sea Ice Concentration. Available online: https://seaice.uni-bremen.de/sea-ice-concentration/ (accessed on 29 June 2017).
- Spreen, G.; Kaleschke, L.; Heygster, G. Sea ice remote sensing using AMSR-E 89 GHz channels. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Beitsch, A.; Kaleschke, L.; Kern, S. Investigating high-resolution AMSR2 sea ice concentrations during the February 2013 fracture event in the Beaufort Sea. Remote Sens. 2014, 6, 3841–3856. [Google Scholar] [CrossRef]
- Kern, S. Antarctic Daily Winter-Time Polynya Distribution from SSM/I Brightness Temperature Data, 2003–2008. Available online: http://icdc.cen.uni-hamburg.de/1/daten/cryosphere/polynya-ant.html (accessed on 29 June 2017).
- AMSR-E/Aqua Daily L3 6.25 km 89 GHz Brightness Temperature Polar Grids, Version 3. Available online: http://nsidc.org/data/ae_si6/ (accessed on 29 June 2017).
- Zwally, H.J.; Comiso, J.C.; Gordon, A.L. Antarctic offshore leads and polynyas and oceanographic effects. In Oceanology of the Antarctic Continental Shelf; American Geophysical Union: Washington, DC, USA, 1985; Volume 43, pp. 203–226. [Google Scholar]
- Motoi, T.; Ono, N.B.; Wakatsuchi, M. A mechanism for the formation of the Weddell Polynya in 1974. J. Phys. Oceanogr. 1987, 17, 2241–2247. [Google Scholar] [CrossRef]
- World Ocean Atlas 2013 Version 2. Available online: https://www.nodc.noaa.gov/OC5/woa13/ (accessed on 29 June 2017).
- Yu, L.; Jin, X.; Weller, R.A. Multidecade Global Flux Datasets from the Objectively Analyzed Air-Sea Fluxes (OAFlux) Project: Latent and Sensible Heat Fluxes, Ocean Evaporation, and Related Surface Meteorological Variables; OAFlux Project Technical Report. OA-2008-01; Woods Hole Oceanographic Institution: Woods Hole, MA, USA, 2008; 64p. [Google Scholar]
- Alduchov, O.A.; Eskridge, R.E. Improved Magnus form approximation of saturation vapor pressure. J. Appl. Meteorol. 1996, 35, 601–609. [Google Scholar] [CrossRef]
- Mohammed, S.; Nirmal, S. Sea Ice Physics and Remote Sensing; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015; Chapter 3; p. 124. [Google Scholar]
- Mohammed, S.; Nirmal, S. Sea Ice Physics and Remote Sensing; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015; Chapter 3; p. 109. [Google Scholar]
- Yu, Y.; Rothrock, D.A. Thin ice thickness from satellite thermal imagery. J. Geophys. Res. 1996, 101, 25753–25766. [Google Scholar] [CrossRef]
- Fu, H.; Zhao, J.; Frey, K.E. Investigation of polynya dynamics in the northern Bering Sea using greyscale morphology image-processing techniques. Int. J. Remote Sens. 2012, 33, 2214–2232. [Google Scholar] [CrossRef]
- Nihashi, S.; Ohshima, K.I. Relationship between ice decay and solar heating through open water in the Antarctic sea ice zone. J. Geophys. Res. 2001, 106, 16767–16782. [Google Scholar] [CrossRef]
- Ohshima, K.I.; Watanabe, T.; Nihashi, S. Surface heat budget of the Sea of Okhotsk during 1987–2001 and the role of sea ice on it. J. Meteorol. Soc. Jpn. 2003, 81, 653–677. [Google Scholar] [CrossRef]
- Pease, C.H. The size of wind-driven coastal polynyas. J. Geophys. Res. 1987, 92, 7049–7059. [Google Scholar] [CrossRef]
- Martin, S.; Cavalieri, D.J. Contributions of the Siberian shelf polynyas to the Arctic Ocean intermediate and deep water. J. Geophys. Res. 1989, 94, 12725–12738. [Google Scholar] [CrossRef]
- Omstedt, A. Modelling frazil ice and grease ice formation in the upper layers of the ocean. Cold Reg. Sci. Technol. 1985, 11, 87–98. [Google Scholar] [CrossRef]
- Jardon, F.P.; Vivier, F.; Bouruet-Aubertot, P.; Lourenço, A.; Cuypers, Y.; Willmes, S. Ice production in Storfjorden (Svalbard) estimated from a model based on AMSR-E observations: Impact on water mass properties. J. Geophys. Res. Oceans 2014, 119, 377–393. [Google Scholar] [CrossRef]
- Parmiggiani, F. Multi-year measurement of Terra Nova Bay winter polynya extents. Eur. Phys. J. Plus 2011, 126, 39. [Google Scholar] [CrossRef]
- Comiso, J.C.; Gordon, A.L. Cosmonaut polynya in the Southern Ocean: Structure and variability. J. Geophys. Res. Oceans 1996, 101, 18297–18313. [Google Scholar] [CrossRef]
- Arbetter, T.E. Relationship between synoptic forcing and polynya formation in the Cosmonaut Sea: 1. Polynya climatology. J. Geophys. Res. 2004, 109, C4. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, C.-X.; E, D.-C.; An, J.-C. Monitoring the change of Antarctic ice shelves and coastline based on multiple-source remote sensing data. Chin. J. Geophys. 2013, 56, 3302–3312. (In Chinese) [Google Scholar]
- Remy, J.P.; Becquevort, S.; Haskell, T.G.; Tison, J.L. Impact of the B-15 iceberg “stranding event” on the physical and biological properties of sea ice in McMurdo Sound, Ross Sea, Antarctica. Antarct. Sci. 2008, 20, 593–604. [Google Scholar] [CrossRef]
- Robinson, N.J.; Williams, M.J.M. Iceberg-induced changes to polynya operation and regional oceanography in the southern Ross Sea, Antarctica, from in situ observations. Antarct. Sci. 2012, 24, 514–526. [Google Scholar] [CrossRef]
- Kovacs, A. Sea Ice. Part 1. Bulk Salinity versus Ice Floe Thickness; Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 1996. [Google Scholar]
- Smedsrud, L.H.; Skogseth, R. Field measurements of Arctic grease ice properties and processes. Cold Reg. Sci. Technol. 2006, 44, 171–183. [Google Scholar] [CrossRef]
- Notz, D.; Worster, M.G. In situ measurements of the evolution of young sea ice. J. Geophys. Res. Oceans 2008, 113. [Google Scholar] [CrossRef]
- Ehn, J.K.; Hwang, B.J.; Galley, R.; David, G.B. Investigations of newly formed sea ice in the Cape Bathurst polynya: 1. Structural, physical, and optical properties. J. Geophys. Res. Oceans 2007, 112. [Google Scholar] [CrossRef]
- Timco, G.W.; Frederking, R.M.W. A review of sea ice density. Cold Reg. Sci. Technol. 1996, 24, 1–6. [Google Scholar] [CrossRef]
- Alexandrov, V.; Sandven, S.; Wahlin, J.; Johannessen, O.M. The relation between sea ice thickness and freeboard in the Arctic. Cryosphere 2010, 4, 373–380. [Google Scholar] [CrossRef]


| Original Parameter Values | Tested Parameter Values | ||
|---|---|---|---|
| Test 1 | 0.99 [51] | 0.97 [50,53] | |
| Test 2 | (J·kg−1) | 2.51 × 106 | 2.52 × 106 [50,53] |
| Test 3 | = | 1.44 × 10−3 [50] | 2 × 10−3 [54,55] |
| Test 4 | = | 1.44 × 10−3 | 3 × 10−3 [50,51] |
| Test 5 | (J·kg−1) | 2.79 × 105 | 2.76 × 105 [50] |
| Test 6 | (J·kg−1) | 2.79 × 105 | 3.34 × 105 [9,19,51,54,55] |
| Test 7 | (kg·m−3) | 0.92 × 103 [9,51,55,56] | 0.90 × 103 [7,50,53] |
| Test 8 | (kg·m−3) | 0.92 × 103 | 0.95 × 103 [19,54,57] |
| Test 9 | Threshold of SIC | 75% [20] | 70% [18,58] |
| Test 10 | Threshold of SIC | 75% | 80% [59,60] |
| Tests and Replaced Parameters | Original Parameter Values | Tested Parameter Values | Ice Productions of Tests (km3) | Variation of Ice Productions (%) |
|---|---|---|---|---|
| Test 1 () | 0.99 | 0.97 | 216 | −1.2 |
| Test 2 () | 2.51 × 106 (J·kg−1) | 2.52 × 106 (J·kg−1) | 219 | 0.08 |
| Test 3 ( = ) | 1.44 × 10−3 | 2 × 10−3 | 287 | 31.3 |
| Test 4 ( = ) | 1.44 × 10−3 | 3 × 10−3 | 409 | 87.1 |
| Test 5 () | 2.79 × 105 (J·kg−1) | 2.76 × 105 (J·kg−1) | 221 | 1.1 |
| Test 6 () | 2.79 × 105 (J·kg−1) | 3.34 × 105 (J·kg−1) | 183 | −16.5 |
| Test 7 () | 0.92 × 103 (kg·m−3) | 0.90 × 103 (kg·m−3) | 224 | 2.2 |
| Test 8 () | 0.92 × 103 (kg·m−3) | 0.95 × 103 (kg·m−3) | 212 | −3.2 |
| Test 9 (Threshold of SIC) | 75% | 70% | 200 | −8.6 |
| Test 10 (Threshold of SIC) | 75% | 80% | 238 | 8.7 |
| Ice Production of RISP (km3) | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | Average | Trend (km3/year) | Period of Trend and Average | Calculation Period |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| This study | 219 | 220 | 228 | 211 | 313 | 222 | 213 | 194 | 164 | 176 | 230 | 219 | - | 2003–2015 | April–October |
| Sensitivity tests of this study | 183~415 | 183~408 | 190~438 | 177~393 | 261~577 | 185~410 | 178~398 | 162~360 | 137~306 | 147~333 | 192~430 | 183~409 | - | - | - |
| Tamura et al. [8] | 320 | 340 | 380 | 360 | 430 | 350 | 340 | 330 | 340 | 370 | 360 | 382 | −4.2 | 1992–2013 | March–October |
| Nakata et al. [28] | 170 | 180 | 170 | 150 | 220 | 190 | 180 | 160 | - | - | - | 190 | - | 2003–2010 | April–October |
| Drucker et al. [27] | 589 | 602 | 649 | 510 | 730 | 529 | - | - | - | - | - | 602 | - | 2003–2008 | April–October |
| Comiso et al. [10] | 620 | 610 | 680 | 530 | 800 | 540 | - | - | - | - | - | 500 | 20 | 1992–2008 | Varying |
| Tamura et al. [7] | 310 | 295 | 330 | - | - | - | - | - | - | - | - | 390 | −8.5 | 1992–2001 | March–October |
| Martin et al. [22] | - | - | - | - | - | - | - | - | - | - | - | 400 | 10 | 1992–2002 | Varying |
| Nihashi and Ohshima [9] | - | - | - | - | - | - | - | - | - | - | - | 300 | - | 2003–2010 | March–October |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Z.; Pang, X.; Zhao, X.; Tan, C. Spatio-Temporal Variability and Model Parameter Sensitivity Analysis of Ice Production in Ross Ice Shelf Polynya from 2003 to 2015. Remote Sens. 2017, 9, 934. https://doi.org/10.3390/rs9090934
Cheng Z, Pang X, Zhao X, Tan C. Spatio-Temporal Variability and Model Parameter Sensitivity Analysis of Ice Production in Ross Ice Shelf Polynya from 2003 to 2015. Remote Sensing. 2017; 9(9):934. https://doi.org/10.3390/rs9090934
Chicago/Turabian StyleCheng, Zian, Xiaoping Pang, Xi Zhao, and Cheng Tan. 2017. "Spatio-Temporal Variability and Model Parameter Sensitivity Analysis of Ice Production in Ross Ice Shelf Polynya from 2003 to 2015" Remote Sensing 9, no. 9: 934. https://doi.org/10.3390/rs9090934
APA StyleCheng, Z., Pang, X., Zhao, X., & Tan, C. (2017). Spatio-Temporal Variability and Model Parameter Sensitivity Analysis of Ice Production in Ross Ice Shelf Polynya from 2003 to 2015. Remote Sensing, 9(9), 934. https://doi.org/10.3390/rs9090934






