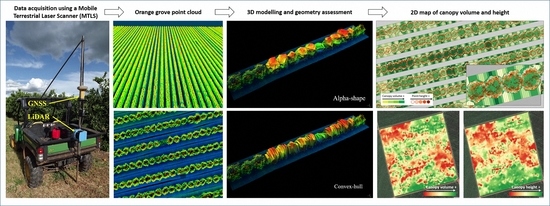
A Method to Obtain Orange Crop Geometry Information Using a Mobile Terrestrial Laser Scanner and 3D Modeling
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of Data Acquisition and Processing
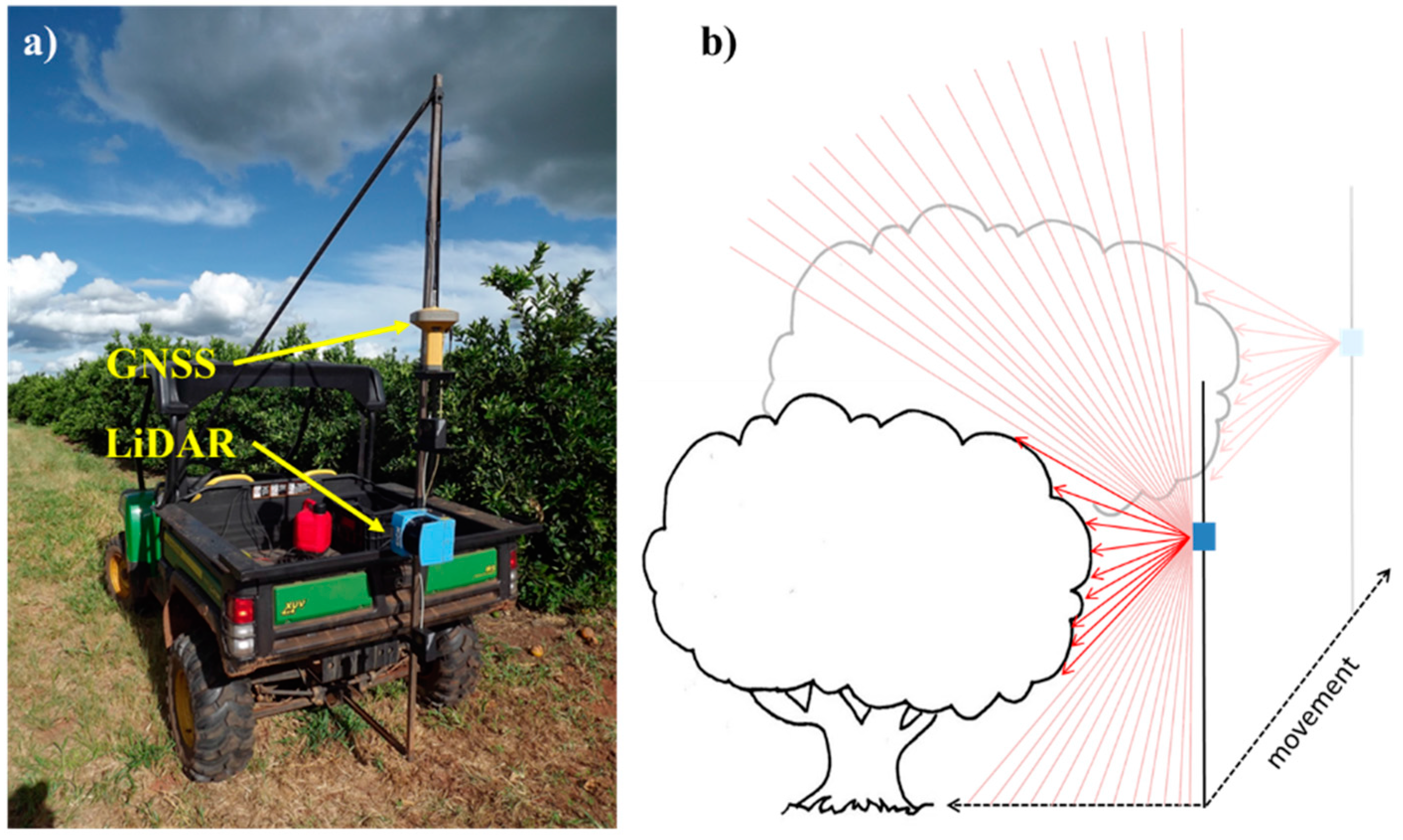
2.1.1. The Equipment and Data Acquisition
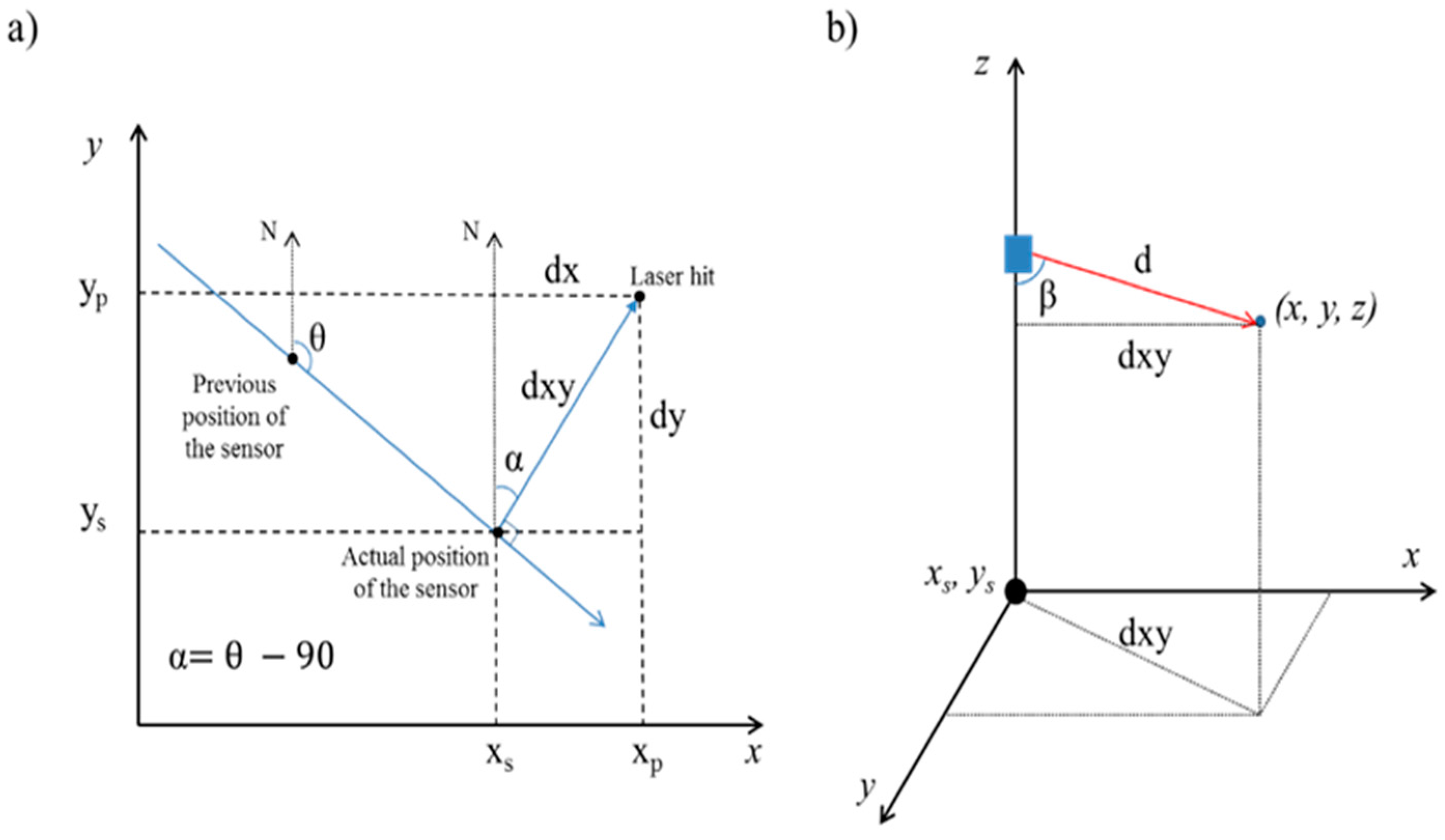
2.1.2. Data Processing
2.2. Demonstrating and Evaluating the Proposed Method
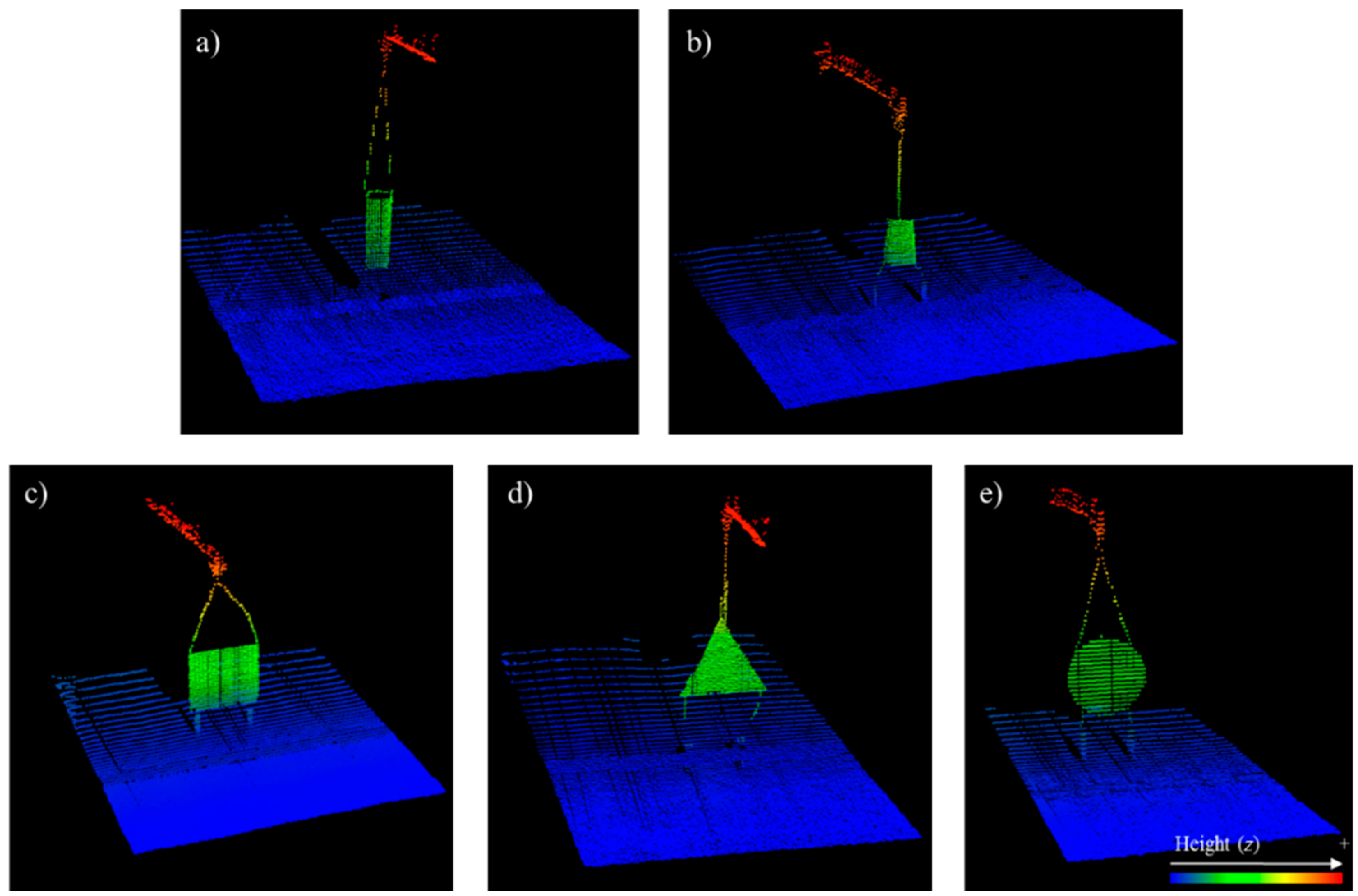
2.2.1. Validation of the Point Cloud Accuracy—Laboratory Testing
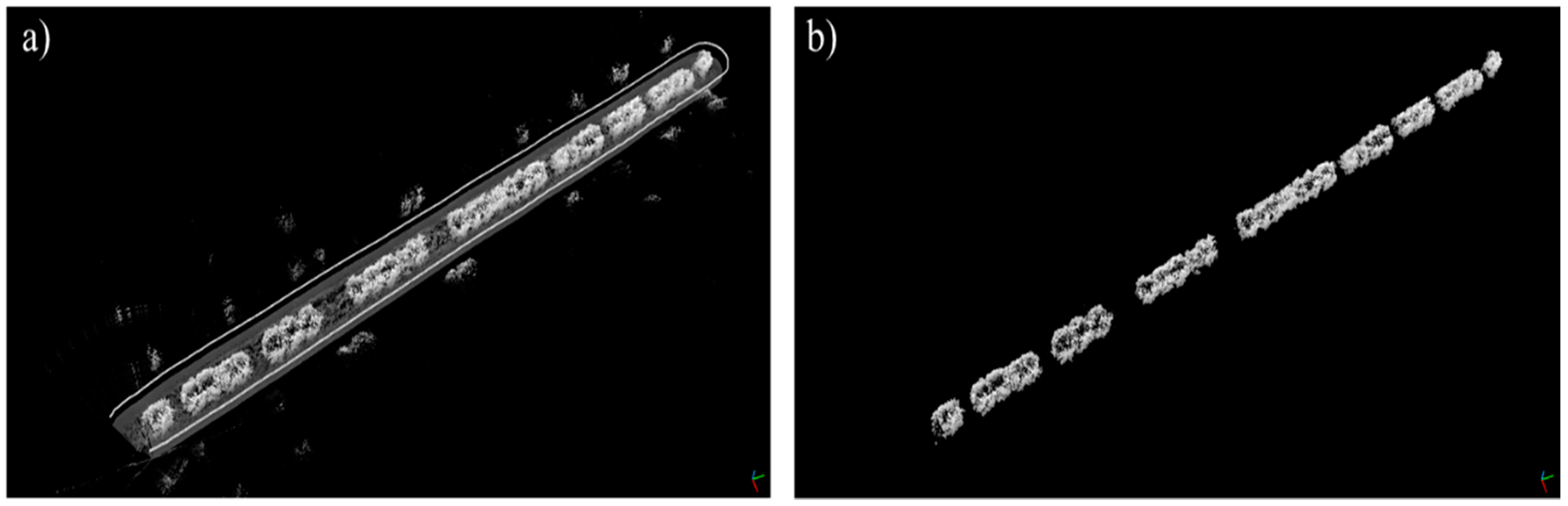
2.2.2. Data Acquisition in a Commercial Orange Grove
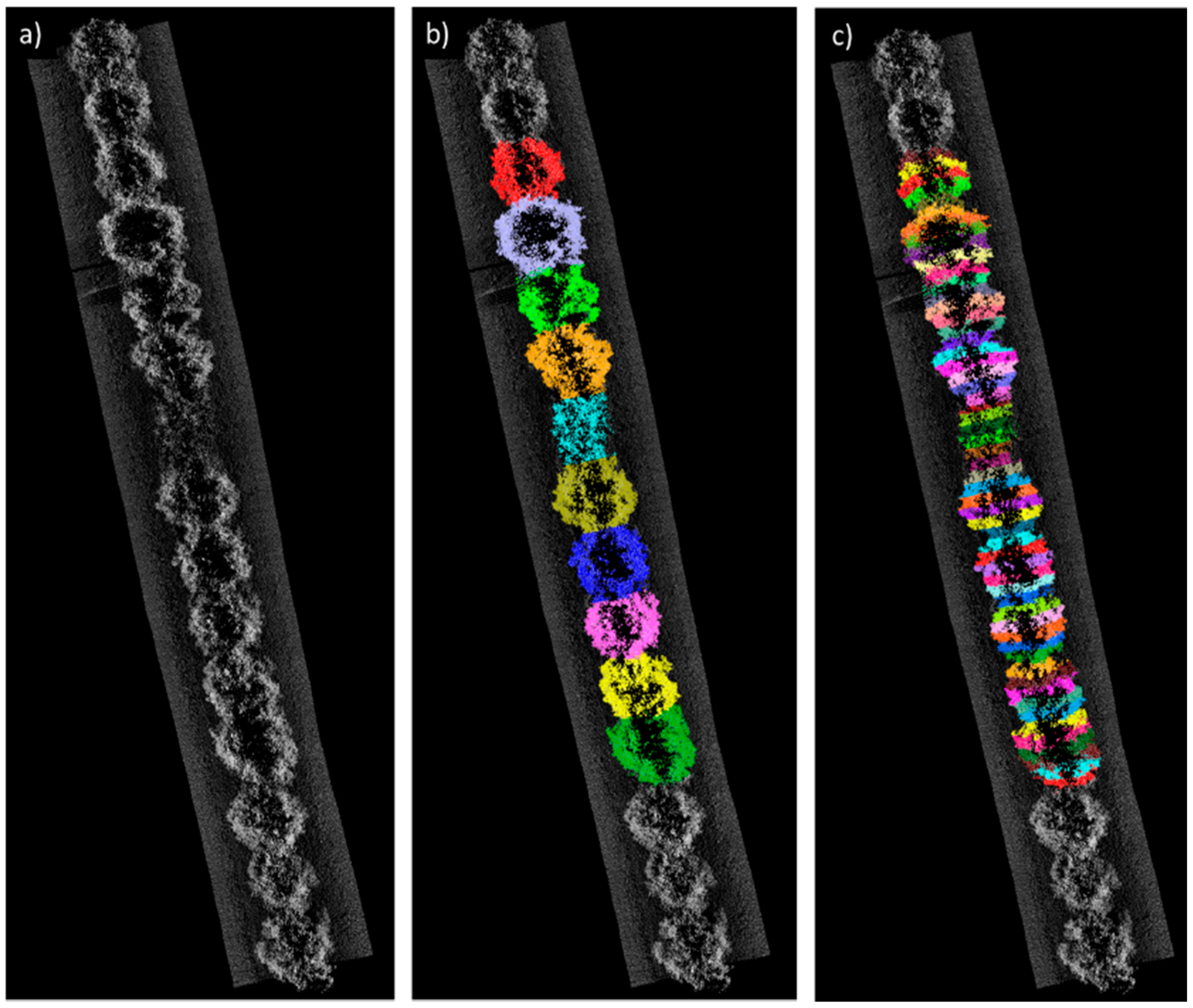
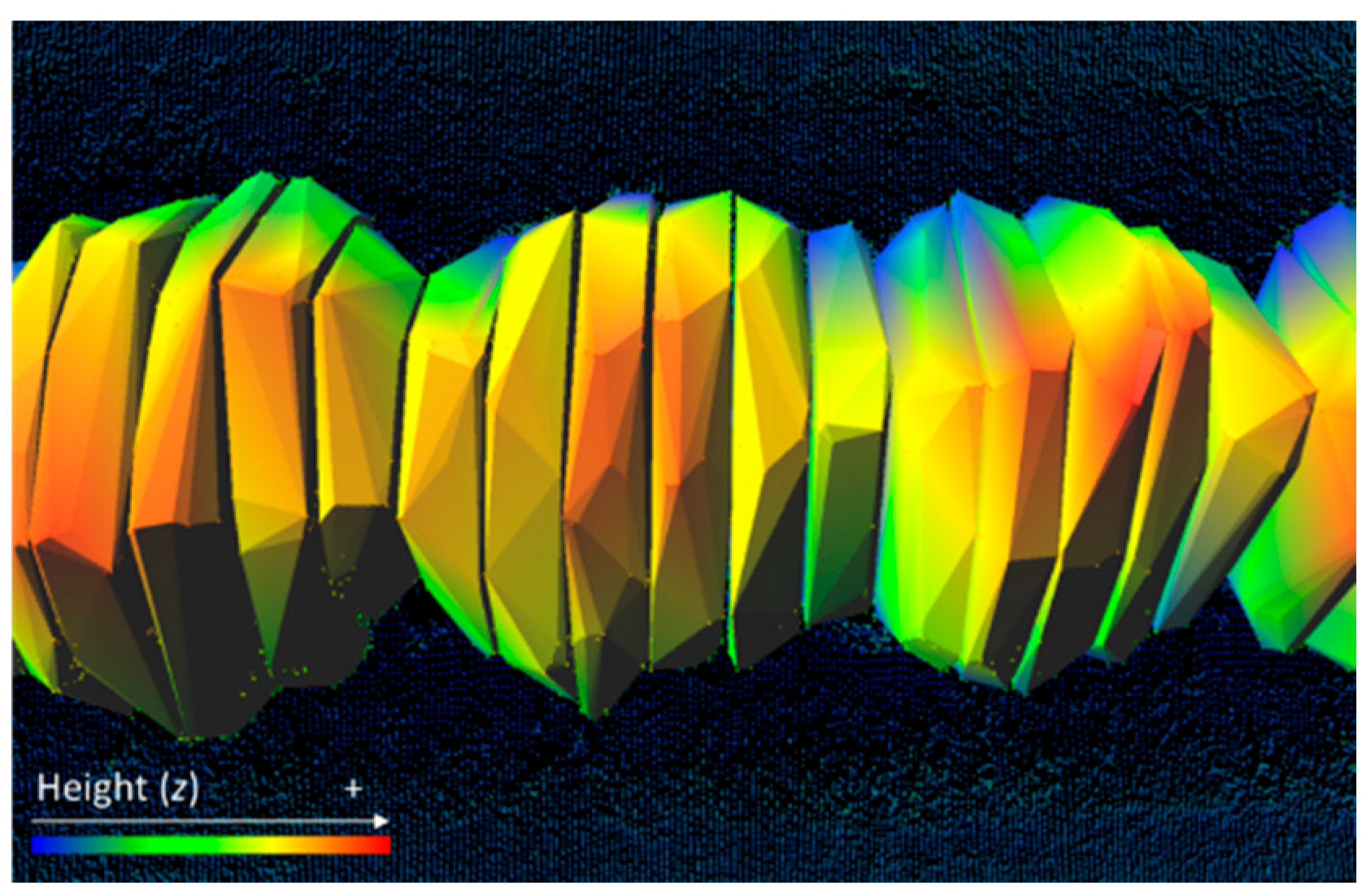
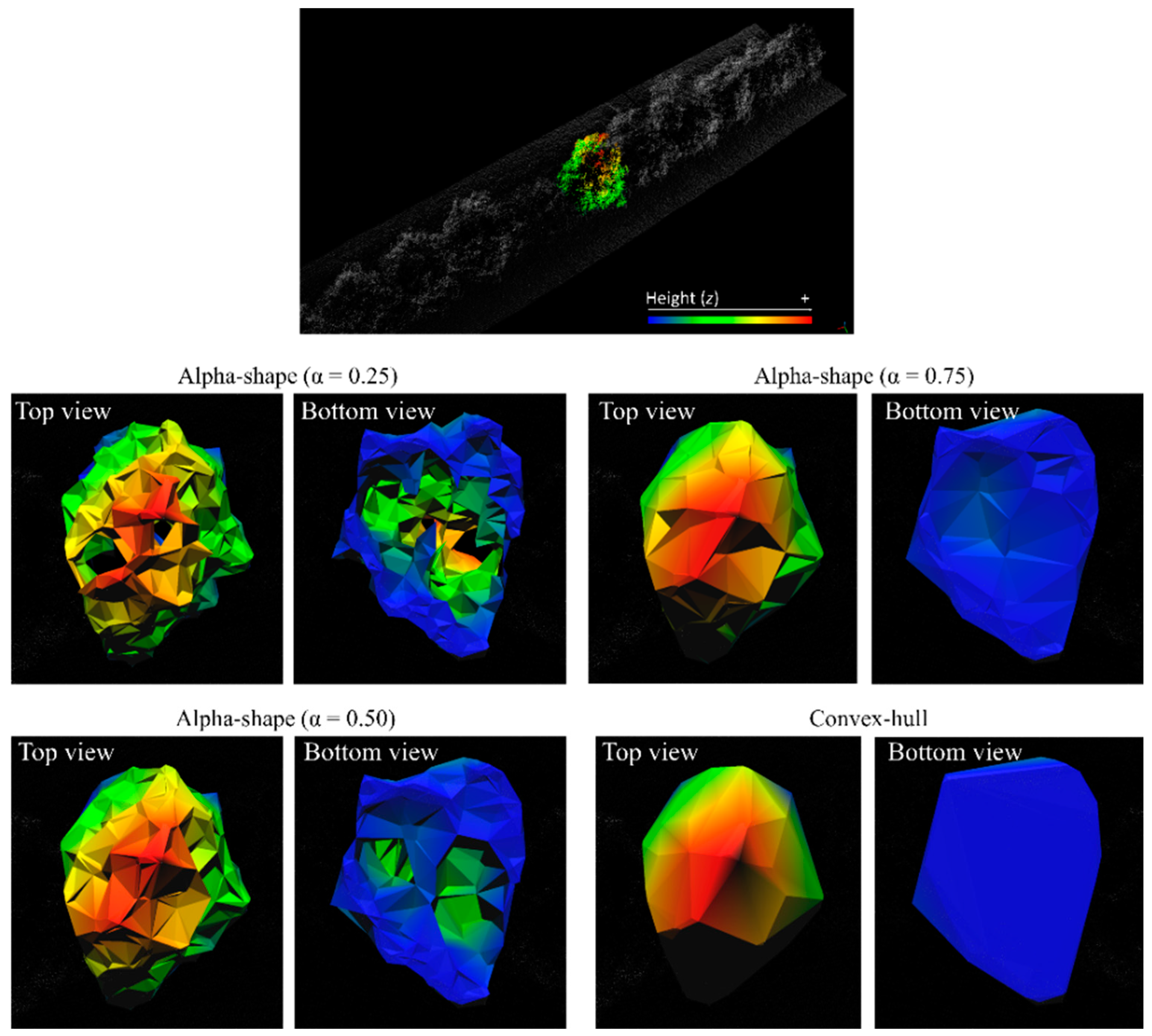
2.2.3. Evaluating Point Cloud Classification and 3D Modeling Options
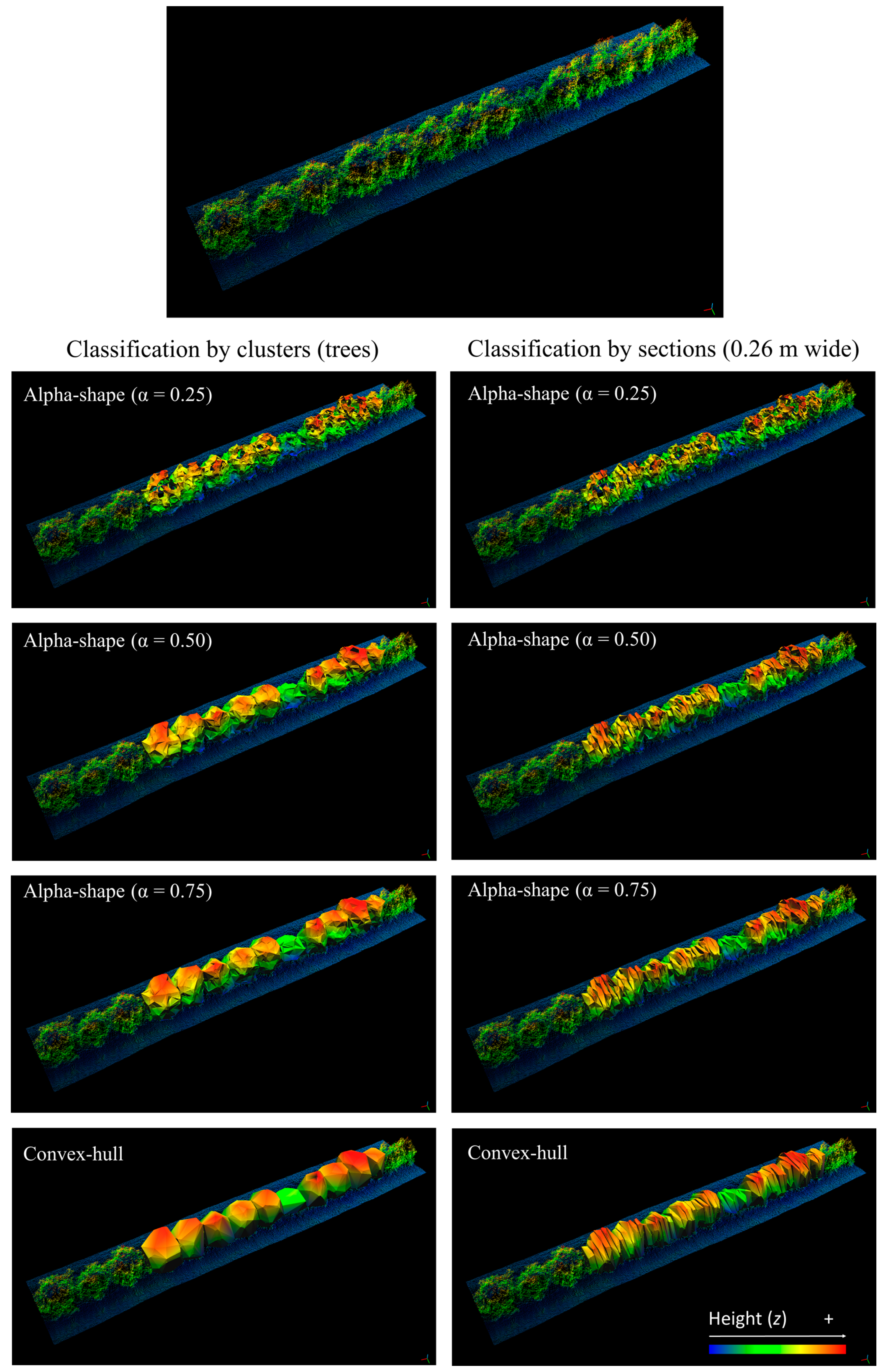
2.2.4. Mapping of Canopy Volume and Height of a Commercial Orange Grove
3. Results and Discussion
3.1. Validation of the Point Cloud Accuracy—Laboratory Testing
3.2. Data Acquisition in a Commercial Grove
3.3. Modeling of 3D Objects from the Point Cloud
3.4. Mapping of Canopy Volume and Height in a Commercial Orange Grove
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dworak, V.; Selbeck, J.; Ehlert, D. Ranging sensors for vehicle-based measurement of crop stand and orchard parameters: A review. Trans. ASABE 2011, 54, 1497–1510. [Google Scholar] [CrossRef]
- Rosell-Polo, J.R.; Sanz, R. A review of methods and applications of the geometric characterization of tree crops in agricultural activities. Comput. Electron. Agric. 2012, 81, 124–141. [Google Scholar] [CrossRef]
- Berk, P.; Hocevar, M.; belsak, A. Development of alternative plant protection product application techniques in orchards, based on measurement sensing systems: A review. Comput. Electron. Agric. 2016, 124, 273–288. [Google Scholar] [CrossRef]
- Gil, E.; Arnó, J.; Llorens, J.; Sanz, R.; Llop, J.; Rosell-Polo, J.R.; Gallart, M.; Escolà, A. Advanced technologies for the improvement of spray application techniques in Spanish viticulture: An overview. Sensors 2014, 14, 691–708. [Google Scholar] [CrossRef] [PubMed]
- Underwood, J.P.; Hung, C.; Whelan, B.; Sukkarieh, S. Mapping almond orchard canopy volume, flowers, fruit and yield using lidar and vision sensors. Comput. Electron. Agric. 2016, 130, 83–96. [Google Scholar] [CrossRef]
- Underwood, J.P.; Jagbrant, G.; Nieto, J.I.; Sukkarieh, S. Lidar-Based Tree Recognition and Platform Localization in Orchards. J. Field Robot. 2015, 32, 1056–1074. [Google Scholar] [CrossRef]
- Escolà, A.; Martínez-Casasnovas, J.A.; Rufat, J.; Arnó, J.; Arbonés, A.; Sebé, F.; Pascual, M.; Gregorio, E.; Rosell-Polo, J.R. Mobile terrestrial laser scanner applications in precision fruticulture/horticulture and tools to extract information from canopy point clouds. Precis. Agric. 2017, 18, 111–132. [Google Scholar] [CrossRef]
- Escolà, A.; Rosell-Polo, J.R.; Planas, S.; Gil, E.; Pomar, J.; Camp, F.; Llorens, J.; Solanelles, F. Variable rate sprayer. Part 1—Orchard prototype: Design, implementation and validation. Comput. Electron. Agric. 2013, 95, 122–135. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, H.; Ozkan, H.E. Development of a variable-rate sprayer with laser scanning sensor to synchronize spray outputs to tree structures. Trans. ASABE 2012, 55, 773–781. [Google Scholar] [CrossRef]
- Rosell-Polo, J.R.; Gregorio, E.; Gené, J.; Llorens, J.; Torrent, X.; Arnó, J.; Escolà, A. Kinect v2 sensor-based mobile terrestrial laser scanner for agricultural outdoor applications. IEEE/ASME Trans. Mech. 2017. [Google Scholar] [CrossRef]
- Méndez, V.; Rosell-Polo, J.R.; Sanz, R.; Escolà, A.; Catalán, H. Deciduous tree reconstruction algorithm based on cylinder fitting from mobile terrestrial laser scanned point clouds. Biosyst. Eng. 2014, 124, 78–88. [Google Scholar] [CrossRef]
- Del-Moral-Martínez, I.; Rosell-Polo, J.R.; Company, J.; Sanz, R.; Escolà, A.; Masip, J.; Martínez-Casasnovas, J.A.; Arnó, J. Mapping vineyard leaf area using mobile terrestrial laser scanners: should rows be scanned on-the-go or discontinuously sampled? Sensors 2016, 16, 119. [Google Scholar] [CrossRef] [PubMed]
- Arnó, J.; Escolà, A.; Rosell-Polo, J.R. Setting the optimal length to be scanned in rows of vines by using mobile terrestrial laser scanners. Precis. Agric. 2017, 18, 145–151. [Google Scholar] [CrossRef]
- Lee, K.H.; Ehsani, R. A laser scanner based measurement system for quantification of citrus tree geometric. Appl. Eng. Agric. 2009, 25, 777–788. [Google Scholar] [CrossRef]
- Rosell-Polo, J.R.; Llorens, J.; Sanz, R.; Arnó, J.; Ribes-Dasi, M.; Masip, J.; Escolà, A.; Camp, F.; Solanelles, F.; Gràcia, F.; et al. Obtaining the three-dimensional structure of tree orchards from remote 2D terrestrial LIDAR scanning. Agric. For. Meteorol. 2009, 149, 1505–1515. [Google Scholar] [CrossRef]
- Tumbo, S.D.; Salyani, M.; Whitney, J.D.; Wheaton, T.A.; Miller, W.M. Investigation of laser and ultrasonic ranging sensors for measurements of citrus canopy volume. Appl. Eng. Agric. 2002, 18, 367–372. [Google Scholar] [CrossRef]
- Wei, J.; Salyani, M. Development of a laser scanner for measuring tree canopy characteristics: Phase 1. Prototype development. Trans. ASABE 2004, 47, 2101–2108. [Google Scholar] [CrossRef]
- Del-Moral-Martínez, I.; Arnó, J.; Escolà, A.; Sanz, R.; Masip-Vilalta, J.; Company-Messa, J.; Rosell-Polo, J.R. Georeferenced Scanning System to Estimate the LeafWall Area in Tree Crops. Sensors 2015, 15, 8382–8405. [Google Scholar] [CrossRef] [PubMed]
- Auat Cheein, F.A.; Guivant, J.; Sanz, R.; Escolà, A.; Yandún, F.; Torres-Torriti, M.; Rosell-Polo, J.R. Real-time approaches for characterization of fully and partially scanned canopies in groves. Comput. Electron. Agric. 2015, 118, 361–371. [Google Scholar] [CrossRef]
- Food and Agriculture Organization (FAO). Faostat. 2014. Available online: http://faostat.fao.org (accessed on 2 April 2017).
- Colaço, A.F.; Molin, J.P. Variable rate fertilization in citrus: A long term study. Precis. Agric. 2017, 18, 169–191. [Google Scholar] [CrossRef]
- Processing v2, 2014. Available online: https://processing.org (accessed on 28 October 2014).
- SICK AG. Telegrams for Operating/Configuring the LMS2XX Laser Measurement Systems; Firmware Version V.2.10/X1.14; 2003. Available online: http://sicktoolbox.sourceforge.net/docs/sick-lms-telegram-listing.pdf (accessed on 28 October 2014).
- R v3.2.2—R Core Team. R: A Language and Environment for Statistical Computing; Software; R Foundation for Statistical Computing: Vienna, Austria, 2015; Available online: http://www.R-project.org (accessed on 13 May 2015).
- CloudCompare [GPL Software] v2.6.1. 2015. Available online: http://www.cloudcompare.org (accessed on 15 March 2015).
- Pateiro-López, B.; Rodríguez-Casal, A. Generalizing the convex-hull of a sample: The R package alphahull. J. Stat. Softw. 2010, 34. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Mucke, E.P. Three-Dimensional alpha shapes. ACM Trans. Graph. 1994, 13, 43–72. [Google Scholar] [CrossRef]
- Van der Zande, D.; Hoet, W.; Jonckheere, I.; van Aardt, J.; Coppin, P. Influence of measurement set-up of ground-based LiDAR for derivation of tree structure. Agric. For. Meteorol. 2006, 141, 147–160. [Google Scholar] [CrossRef]
- Velázquez-Martí, B.; Estornell, J.; López-Cortéz, I.; Martí-Gavilá, J. Calculation of biomass volume of citrus trees from an adapted dendrometry. Biosyst. Eng. 2012, 112, 285–292. [Google Scholar] [CrossRef]
- Mendel, K. Rootstock-scion relationships in Shamouti trees on light soil. Katavim 1956, 6, 35–60. [Google Scholar]
- Schinor, E.H.; Cristofani-Yaly, M.; Bastianel, M.; Machado, M.A. Sunki Mandarin vs Poncirus trifoliate hybrids as rootstocks for Pera sweet orange. J. Agric. Sci. 2013, 5, 190–200. [Google Scholar] [CrossRef]
- Scapin, M.S.; Behlau, F.; Scandelai, L.J.M.; Fernandes, R.S.; Silva, G.J., Jr.; Ramos, H.H. Tree-row-volume-based sprays of copper bactericide for control of citrus canker. Crop Prot. 2015, 77, 119–126. [Google Scholar] [CrossRef]
- Silva, G.J., Jr.; Scapin, M.S.; Silva, F.P.; Silva, A.R.P.; Behlau, F.; Ramos, H.H. Spray volume and fungicide rates for citrus black spot control based on tree canopy volume. Crop Prot. 2016, 85, 38–45. [Google Scholar] [CrossRef]
- QGIS v2.10—QGIS Development Team. QGIS Geographic Information System. Open Source Geospatial Foundation Project. 2015. Available online: http://www.qgis.org (accessed on 15 March 2015).
- Minasny, B.; McBratney, A.B.; Whelan, B.M. VESPER Version 1.62; Precision Agriculture Laboratory, Faculty of Agriculture and Environment, University of Sydney: Sydney, Australia, 2006. [Google Scholar]
- Map Comparison Kit v3.2. 2016. Available online: http://mck.riks.nl (accessed on 17 December 2016).
- Hagen, A. Fuzzy set approach to assessing similarity of categorical maps. Int. J. Geogr. Inf. Sci. 2003, 17, 235–249. [Google Scholar] [CrossRef]
- Lee, W.S.; Ehsani, R. Comparison of two 2D laser scanners for sensing object distances, shapes, and surfaces patterns. Comput. Electron. Agric. 2008, 60, 250–262. [Google Scholar] [CrossRef]



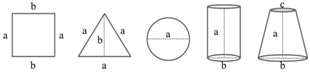
| Objects | a | b | c | ||||||
|---|---|---|---|---|---|---|---|---|---|
| (i) | (ii) | (iii) | (i) | (ii) | (iii) | (i) | (ii) | (iii) | |
| (cm) | |||||||||
| Square | 98.60 | 98.29 | 100.00 | 94.23 | 100.25 | 100.00 | - | - | - |
| Triangle | 98.22 | 98.33 | 100.00 | 84.64 | 88.48 | 87.00 | - | - | - |
| Circle | 101.17 | 99.96 | 100.00 | - | - | - | - | - | - |
| Cylinder I | 79.58 | 79.78 | 80.00 | 29.58 | 30.13 | 30.00 | - | - | - |
| Cylinder II | 80.92 | 83.21 | 83.00 | 19.74 | 20.28 | 20.00 | - | - | - |
| Body of cone | 62.65 | 63.31 | 64.00 | 44.95 | 45.05 | 45.00 | 31.15 | 30.90 | 31.00 |
| Algorithm | Number of Sections Per Tree | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 5 | 7 | 10 | ||||||
| Mean Canopy Volume of 25 Individual Trees (m3) | ||||||||||
| Cube-fit | 22.65 | a | - | - | - | - | ||||
| Cylinder-fit | 11.90 | c | - | - | - | - | ||||
| Convex-hull | 16.07 | b,a | 14.71 | a,ab | 13.97 | a,ab | 13.46 | a,ab | 12.86 | a,b |
| α-shape (α = 0.75) | 14.31 | c,a | 11.57 | b,b | 10.02 | b,bc | 8.66 | b,cd | 7.34 | b,d |
| α-shape (α = 0.50) | 12.16 | c,a | 9.77 | b,b | 8.19 | b,bc | 6.98 | c,cd | 5.72 | c,d |
| α-shape (α = 0.25) | 6.19 | d,a | 5.32 | c,b | 4.47 | c,bc | 4.15 | d,c | 3.34 | d,d |
| Canopy Variable | Method * | Mean | Minimum | Maximum | Coef. of Variation |
|---|---|---|---|---|---|
| m3 | |||||
| Volume | 1 | 11.94 | 7.64 | 18.57 | 0.09 |
| 2 | 12.13 | 8.05 | 17.30 | 0.09 | |
| m | |||||
| Height | 1 | 2.85 | 2.47 | 3.39 | 0.03 |
| 2 | 2.87 | 2.44 | 3.43 | 0.04 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Colaço, A.F.; Trevisan, R.G.; Molin, J.P.; Rosell-Polo, J.R.; Escolà, A. A Method to Obtain Orange Crop Geometry Information Using a Mobile Terrestrial Laser Scanner and 3D Modeling. Remote Sens. 2017, 9, 763. https://doi.org/10.3390/rs9080763
Colaço AF, Trevisan RG, Molin JP, Rosell-Polo JR, Escolà A. A Method to Obtain Orange Crop Geometry Information Using a Mobile Terrestrial Laser Scanner and 3D Modeling. Remote Sensing. 2017; 9(8):763. https://doi.org/10.3390/rs9080763
Chicago/Turabian StyleColaço, André F., Rodrigo G. Trevisan, José P. Molin, Joan R. Rosell-Polo, and Alexandre Escolà. 2017. "A Method to Obtain Orange Crop Geometry Information Using a Mobile Terrestrial Laser Scanner and 3D Modeling" Remote Sensing 9, no. 8: 763. https://doi.org/10.3390/rs9080763
APA StyleColaço, A. F., Trevisan, R. G., Molin, J. P., Rosell-Polo, J. R., & Escolà, A. (2017). A Method to Obtain Orange Crop Geometry Information Using a Mobile Terrestrial Laser Scanner and 3D Modeling. Remote Sensing, 9(8), 763. https://doi.org/10.3390/rs9080763