Envisat RA-2 Individual Echoes: A Unique Dataset for a Better Understanding of Inland Water Altimetry Potentialities
Abstract
:1. Introduction
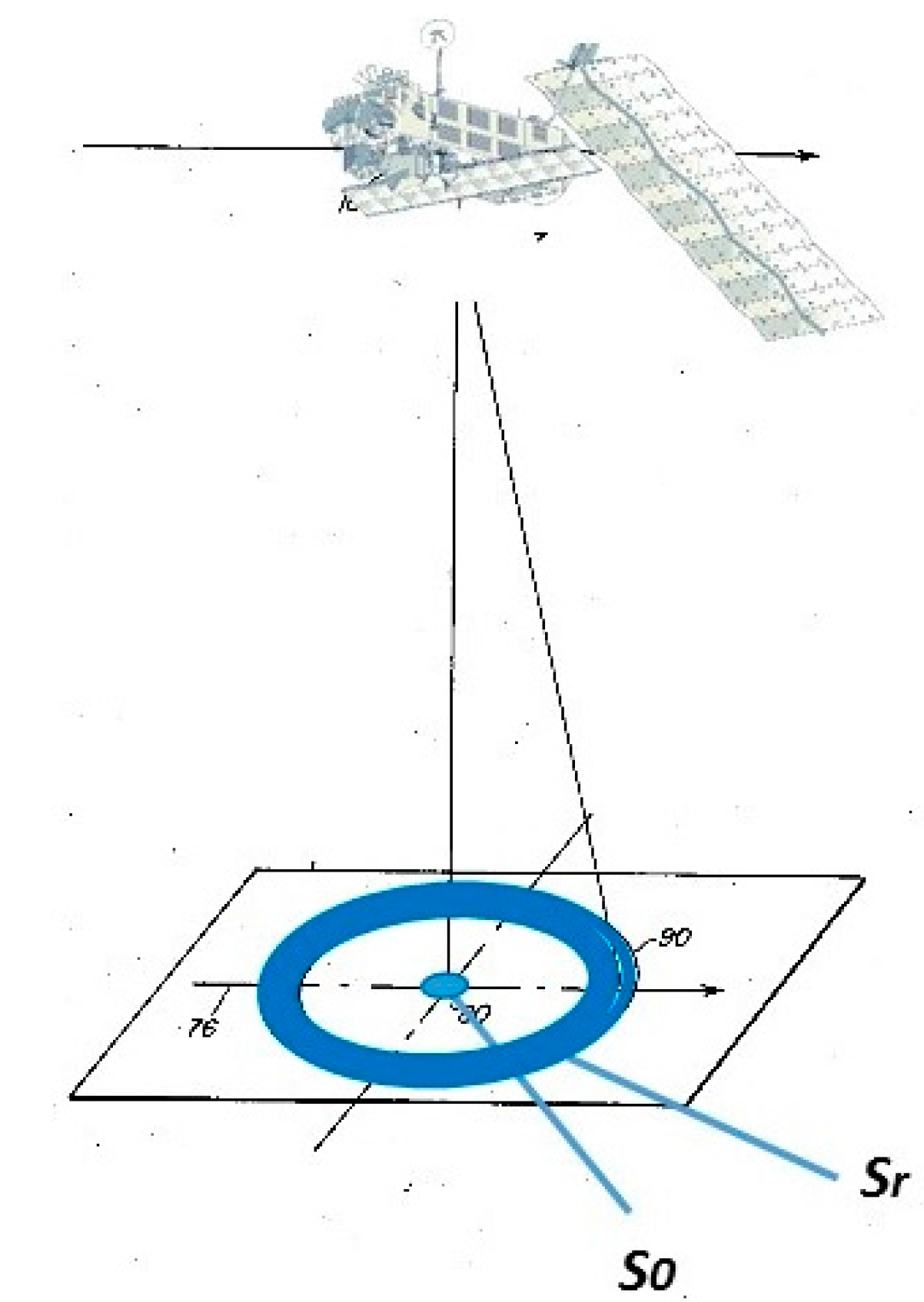
2. Theoretical Model of Specular Returns from Inland Waters
2.1. The Theoretical Complex Radar Altimeter Echo, (n,r)
- -
- There is zero reflectivity from land: all reflectivity is from water surfaces.
- -
- Water surfaces are flat: there is no wind roughening.
- -
- The water surface area is known exactly: location and extent.
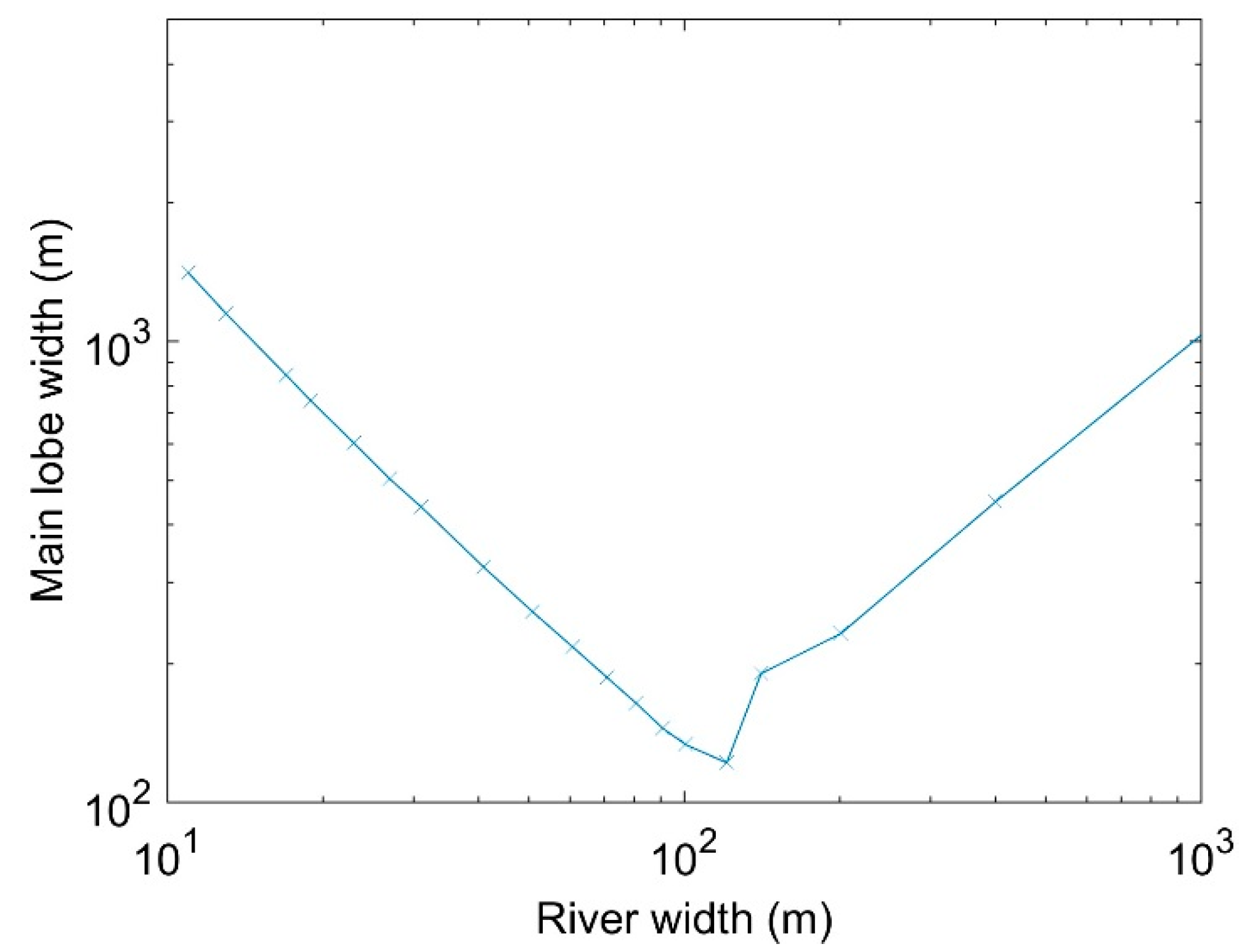
2.2. The Spatial Extent of Specular Echoes and Its Implications
2.3. Very Small Water Bodies
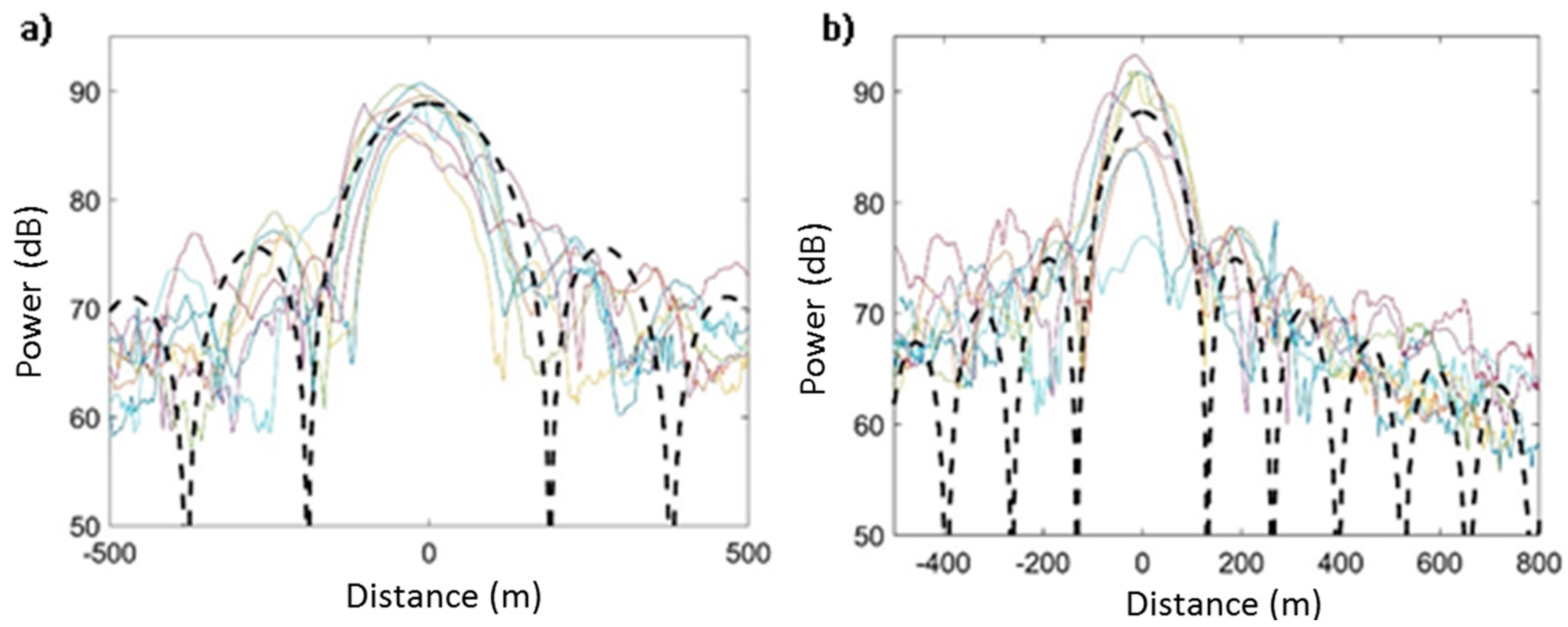
2.4. Model Examples for Larger Water Bodies
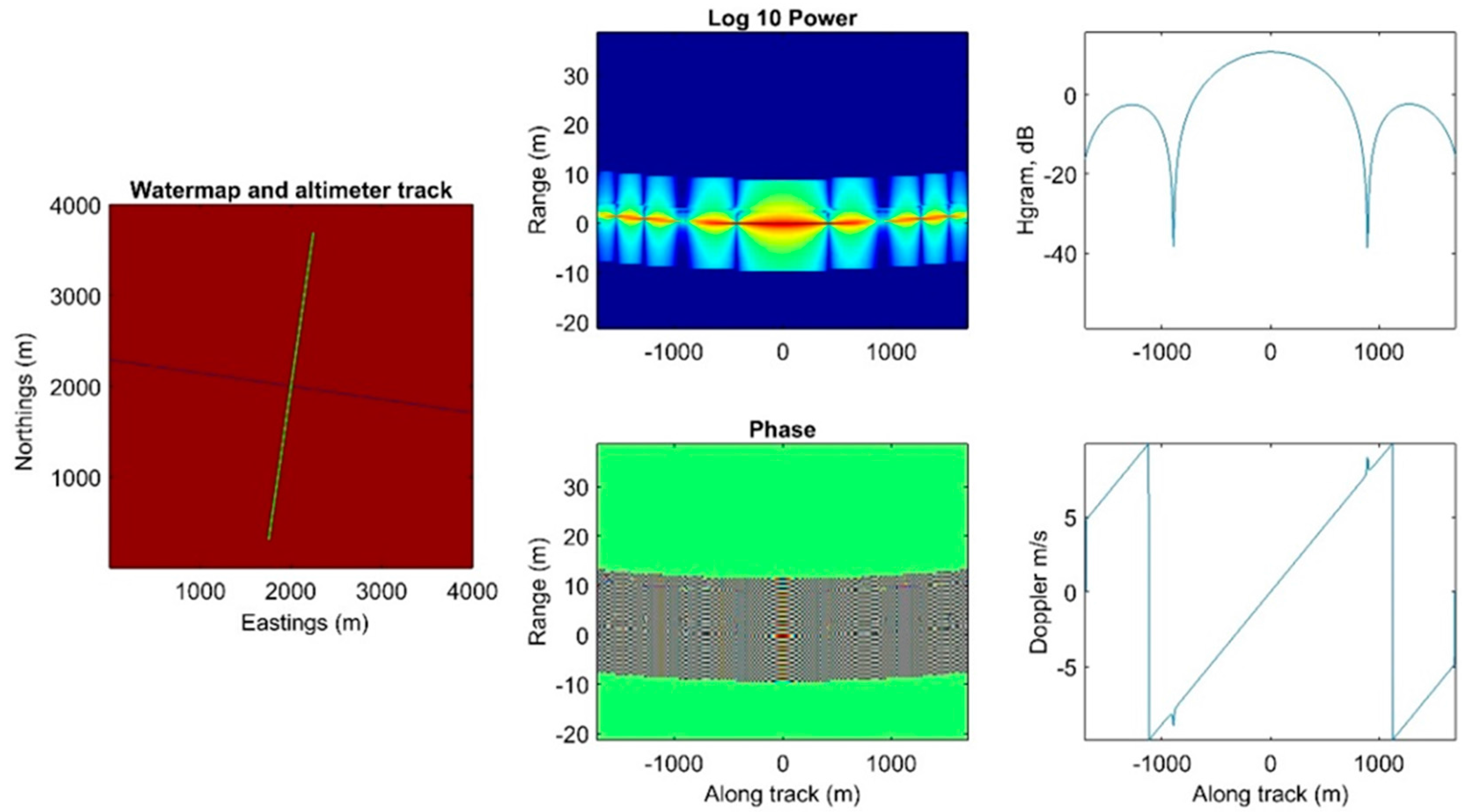
3. Range Determination for a Specular Target
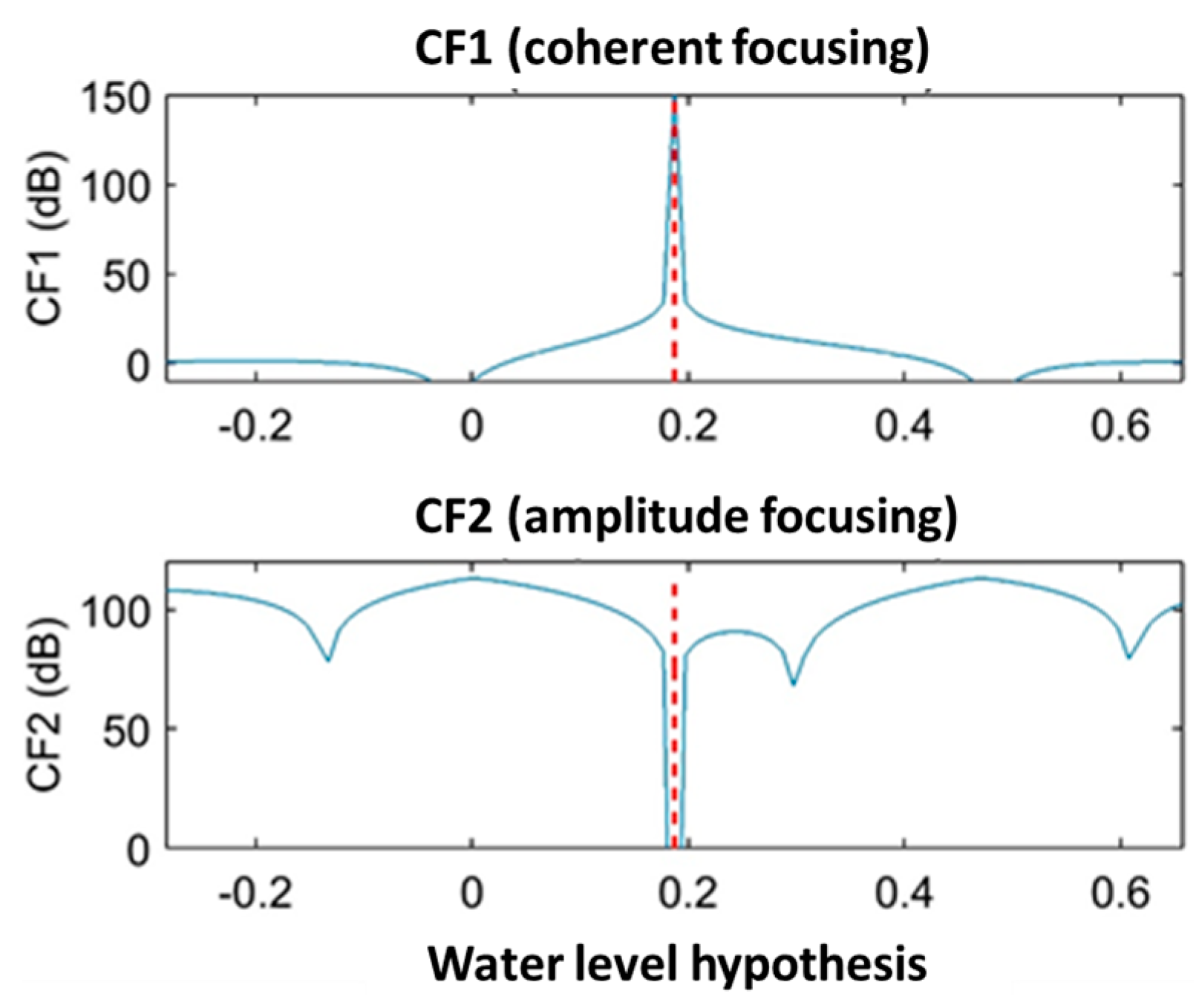
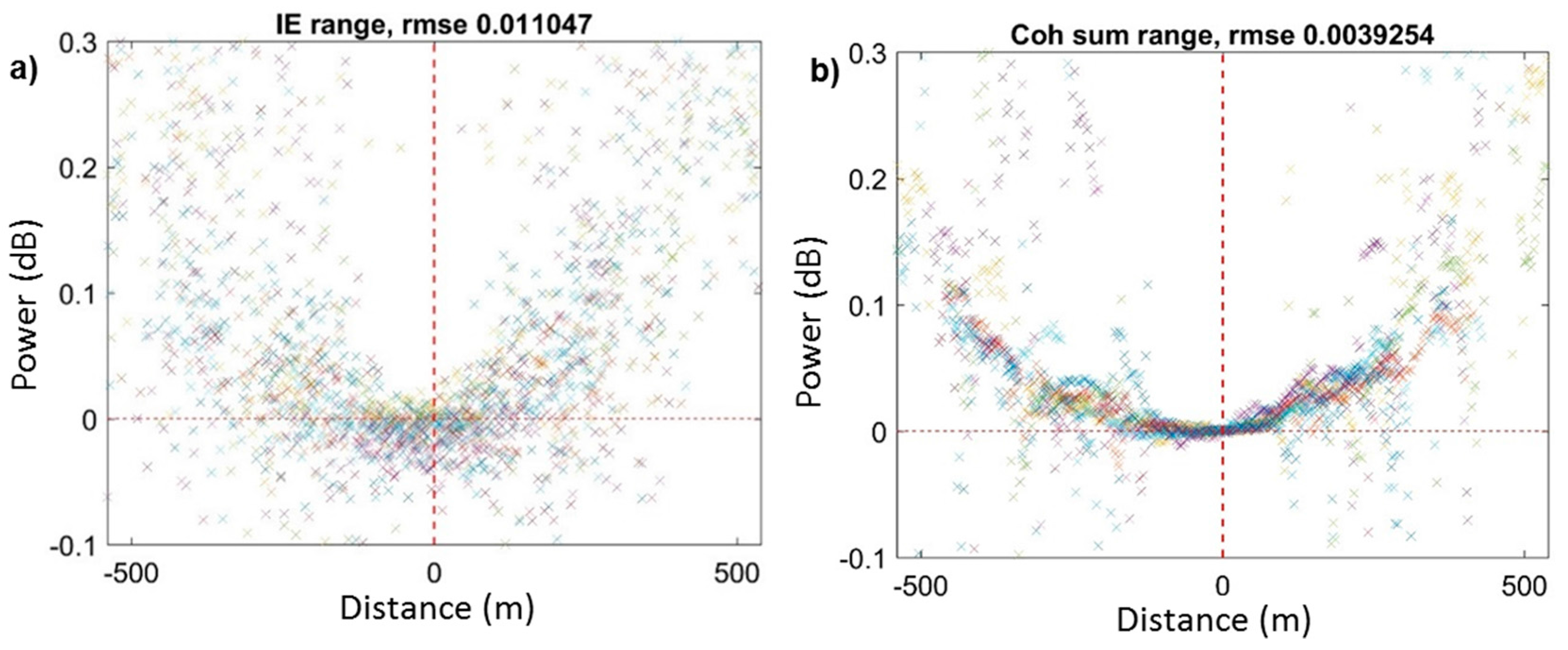
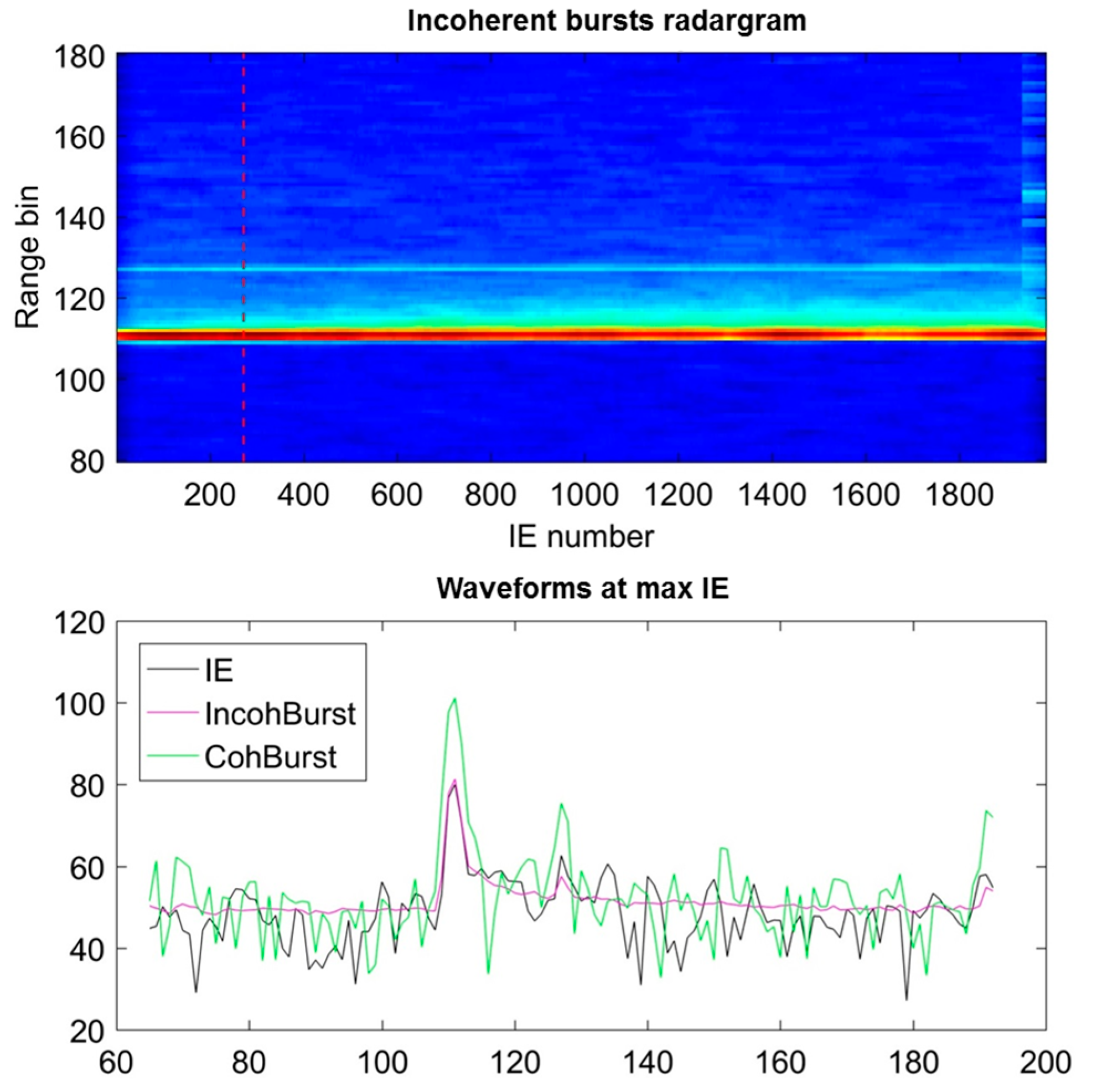
3.1. Phase-Focused Method
3.2. Simplified Algorithm
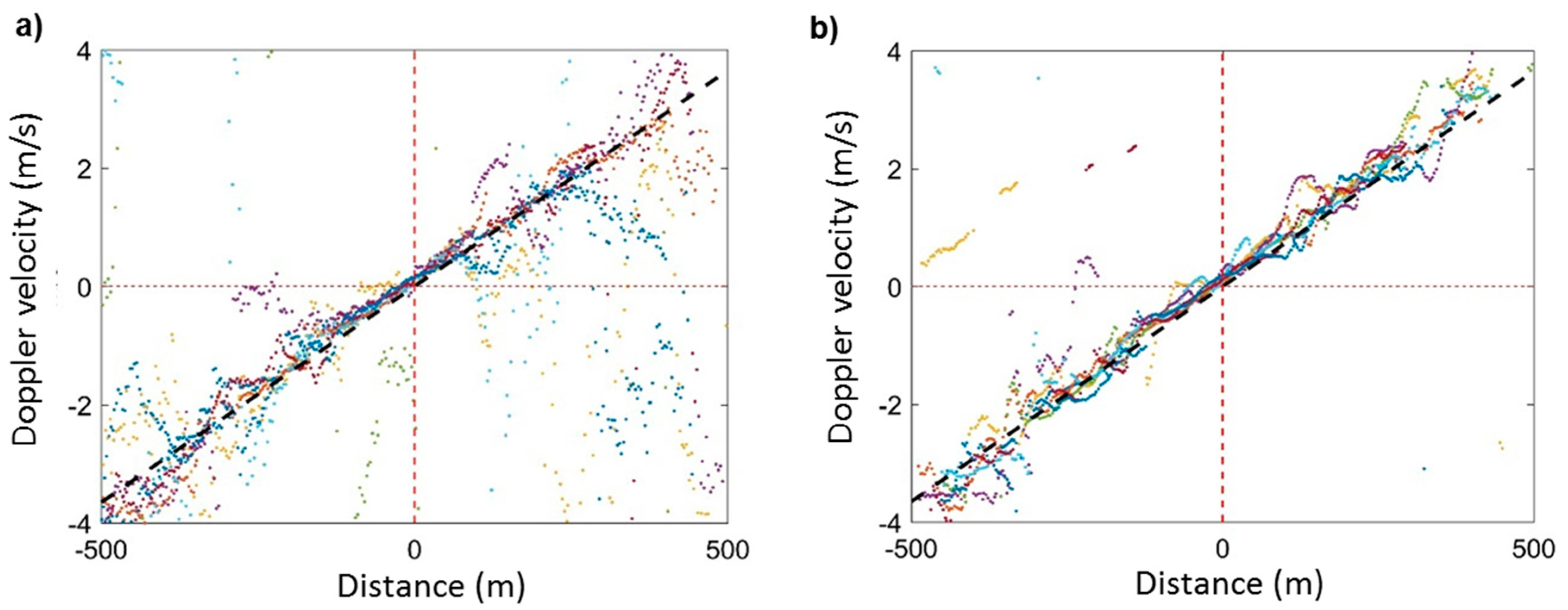
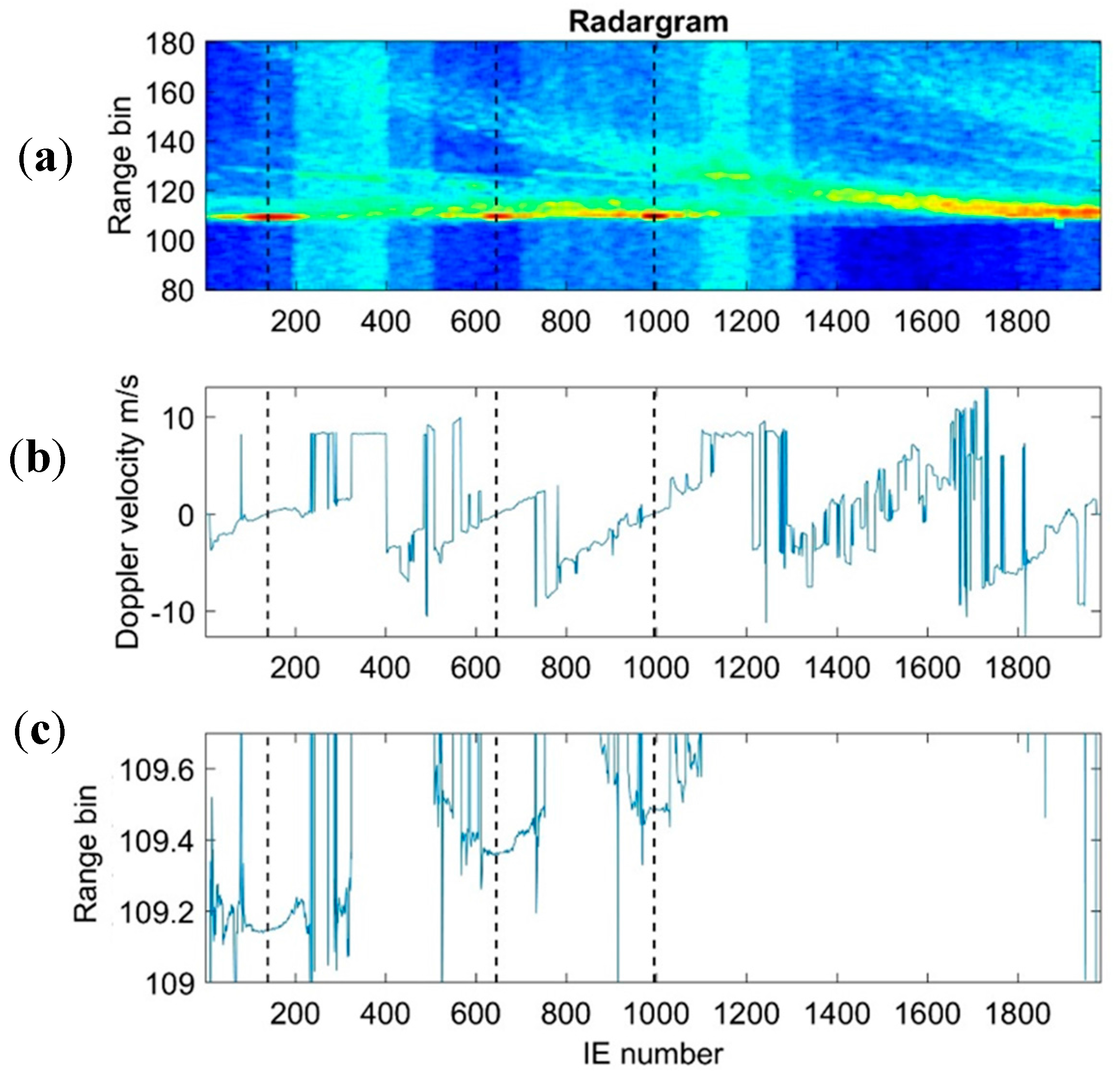
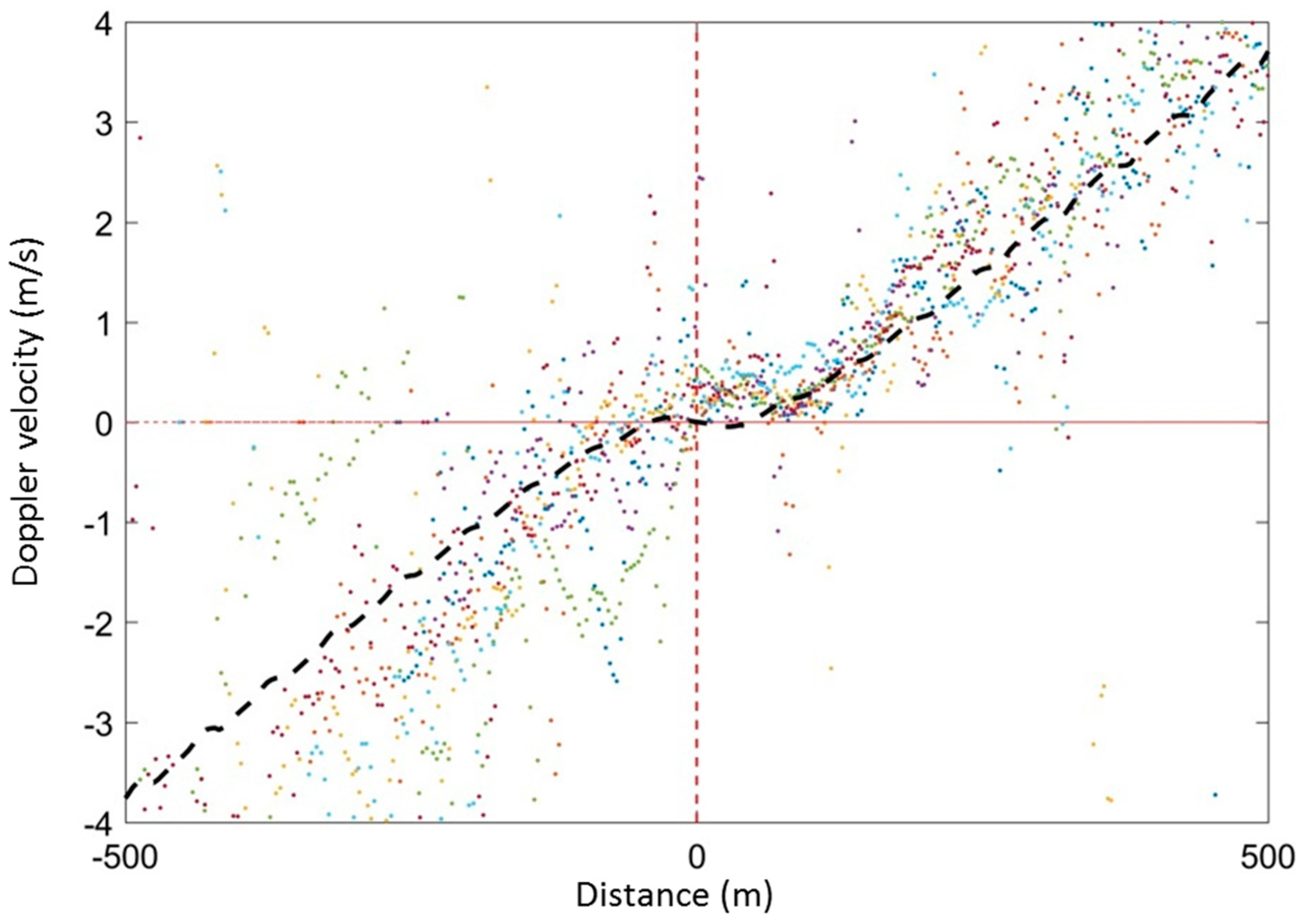
3.2.1. Doppler Velocity Estimation
3.2.2. Coherence Estimation
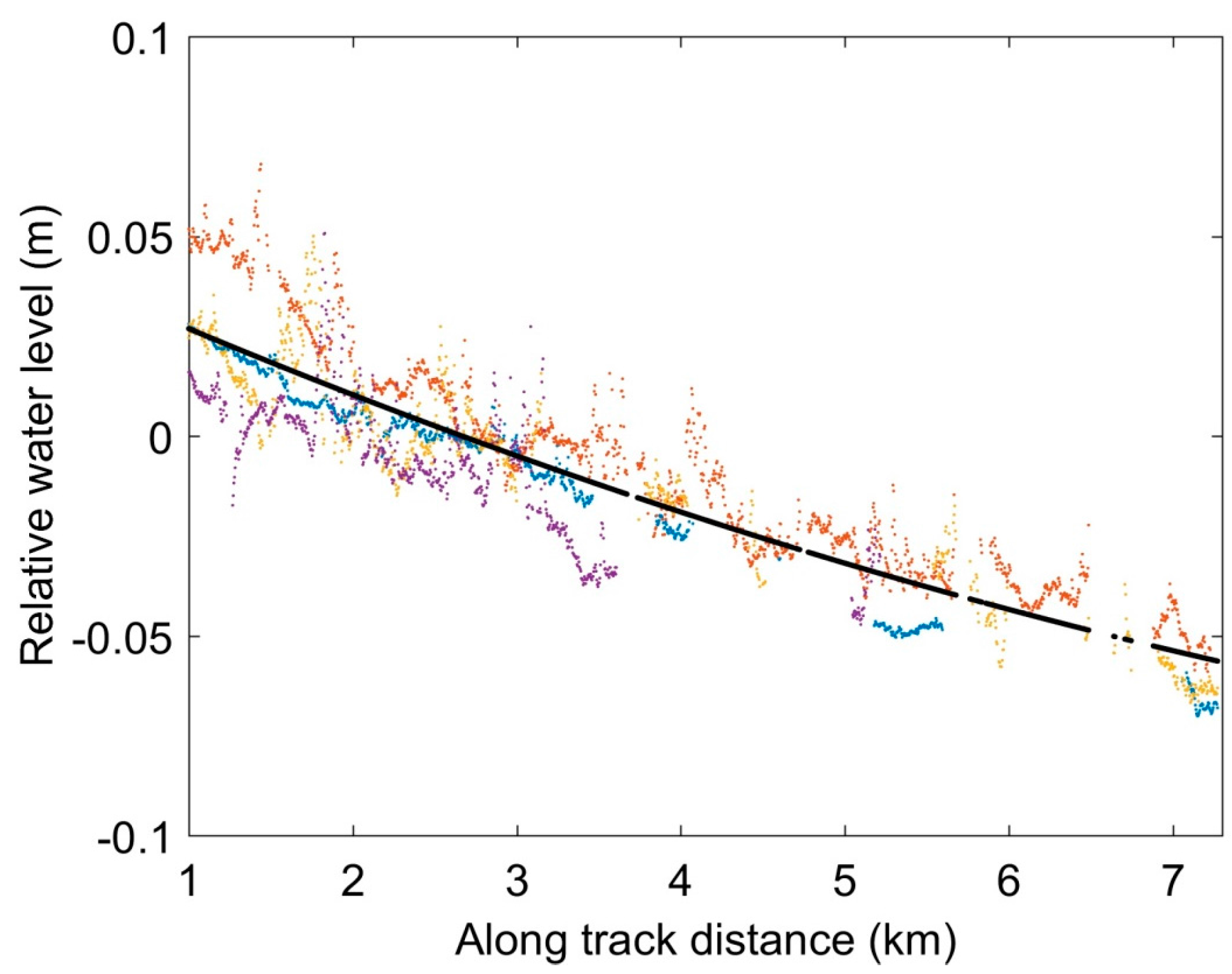
3.2.3. Water Level
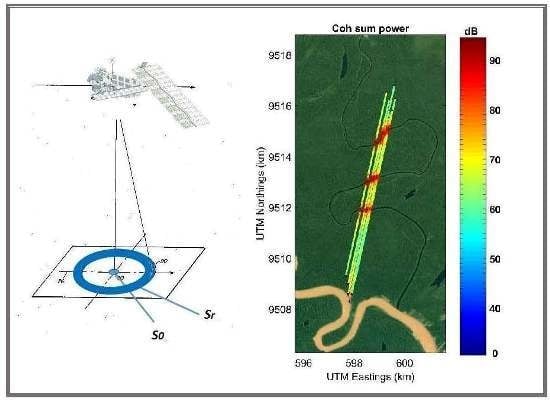
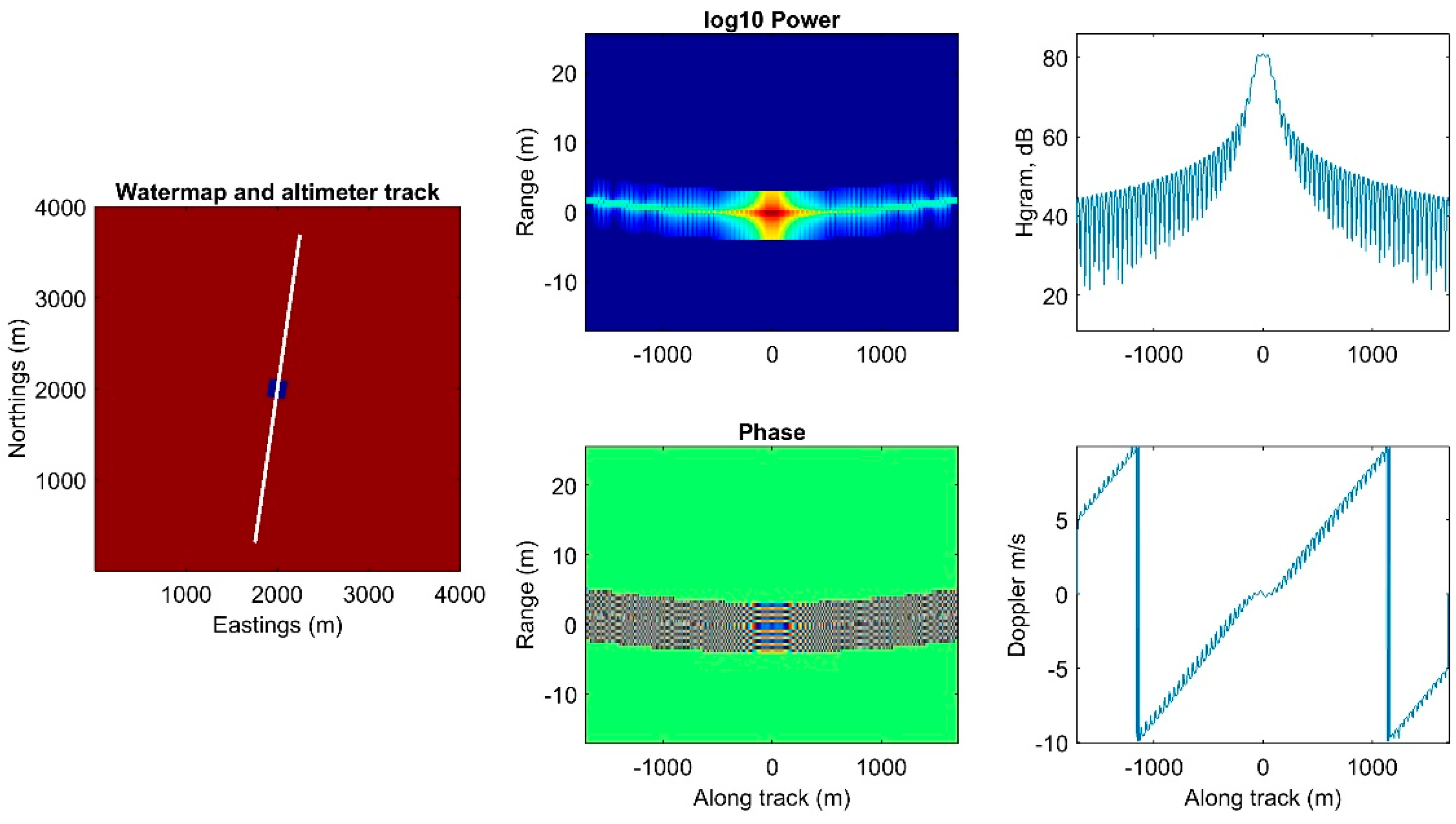
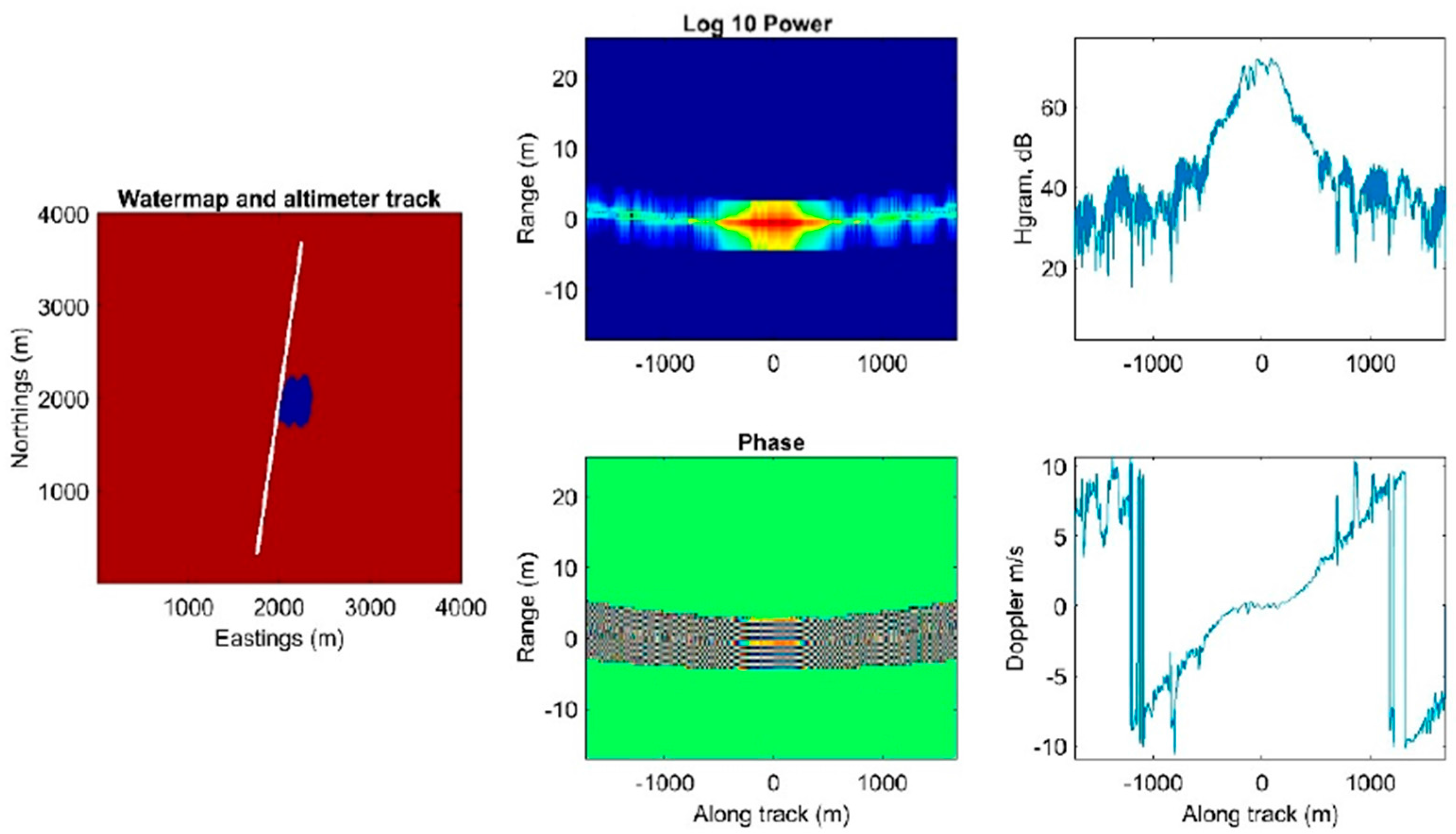
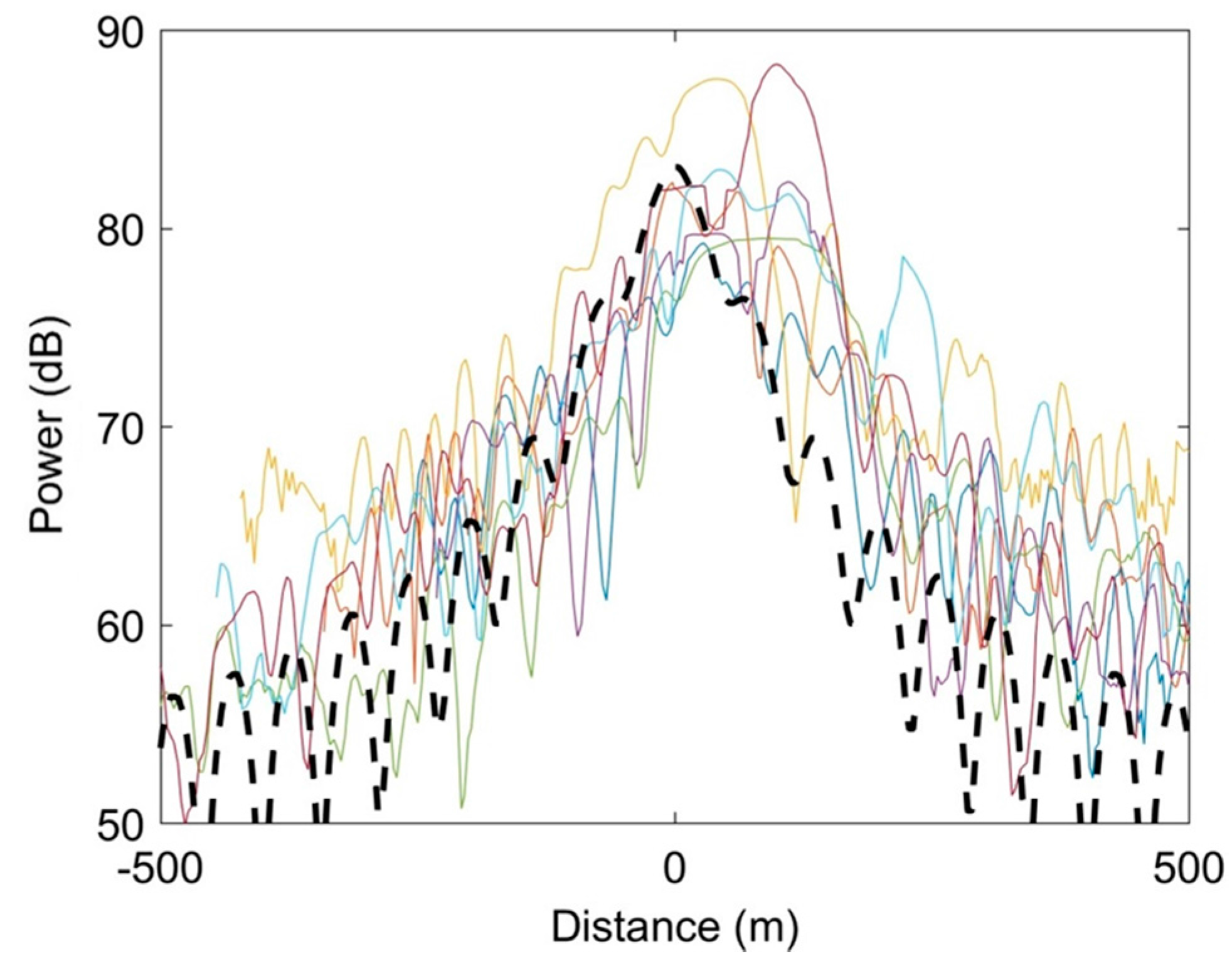
4. Selected Case Studies
4.1. Description of the Dataset
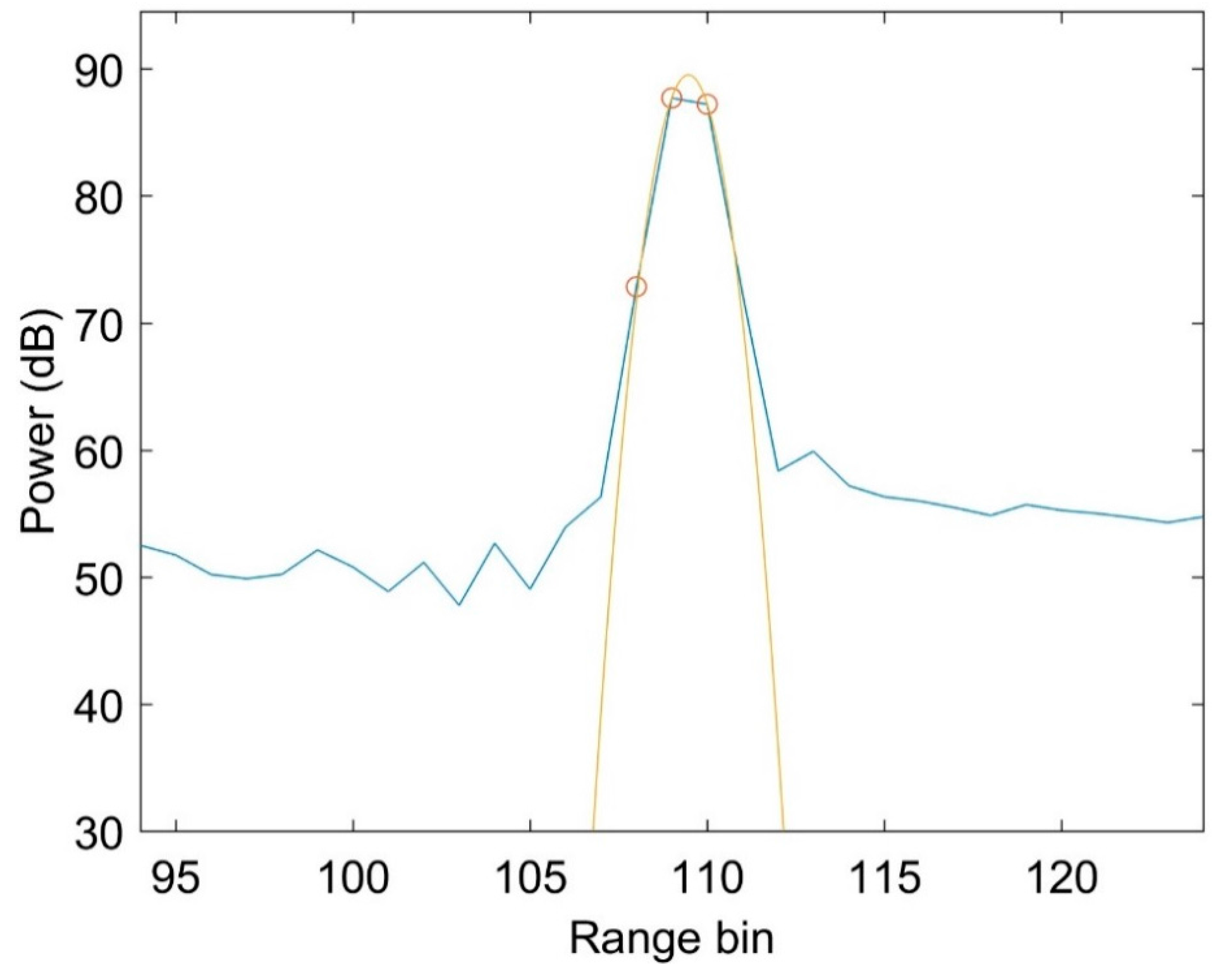
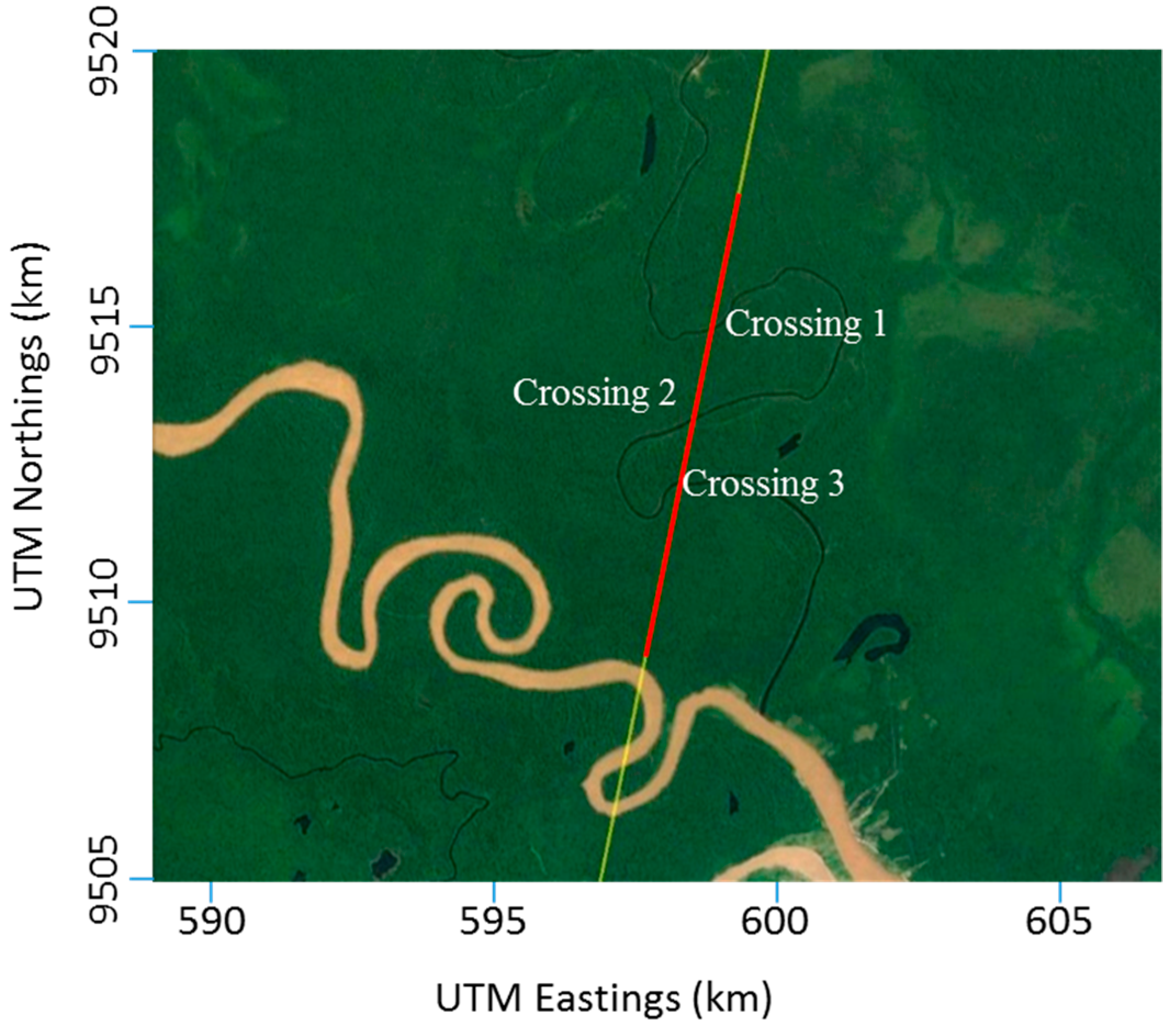
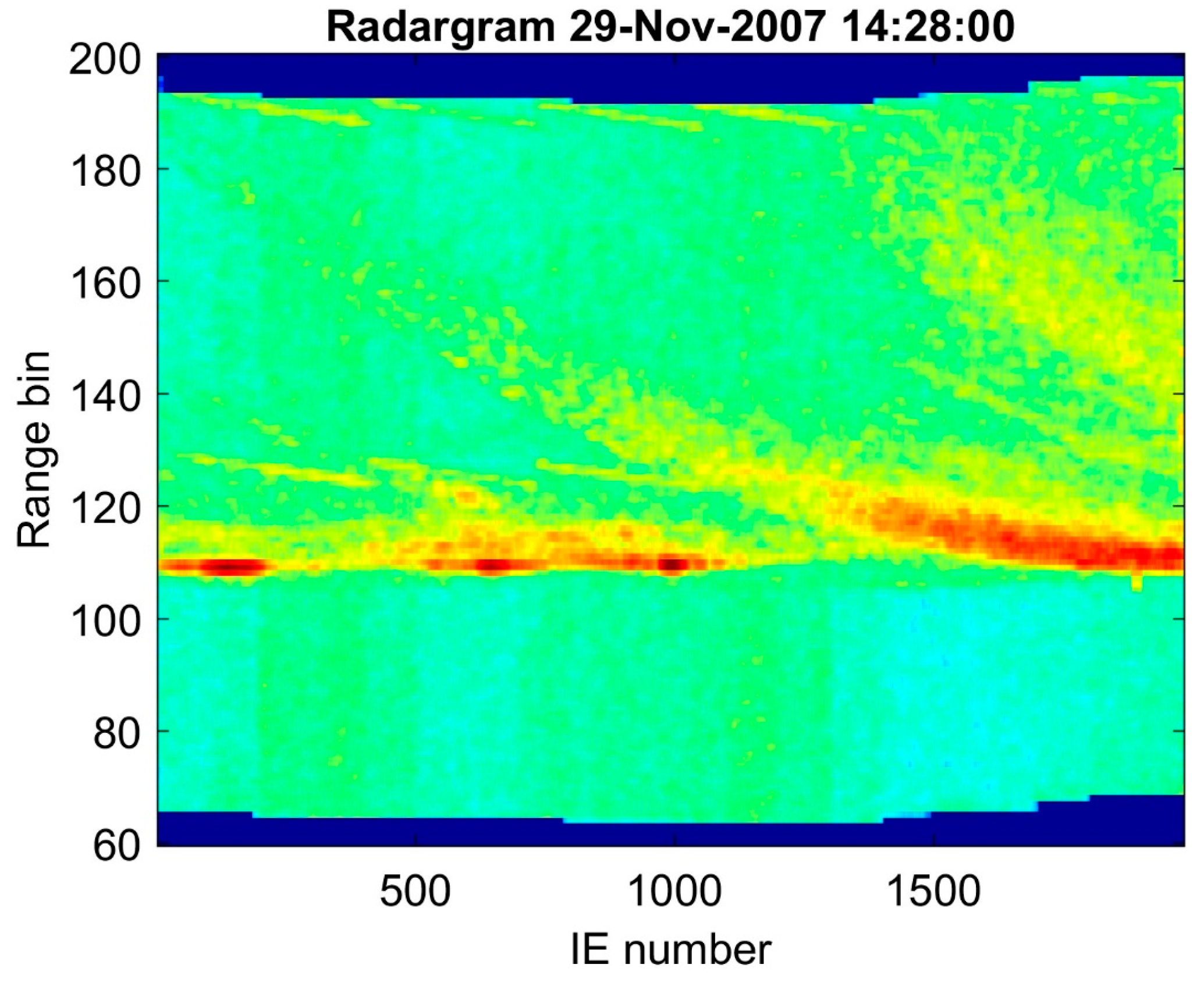
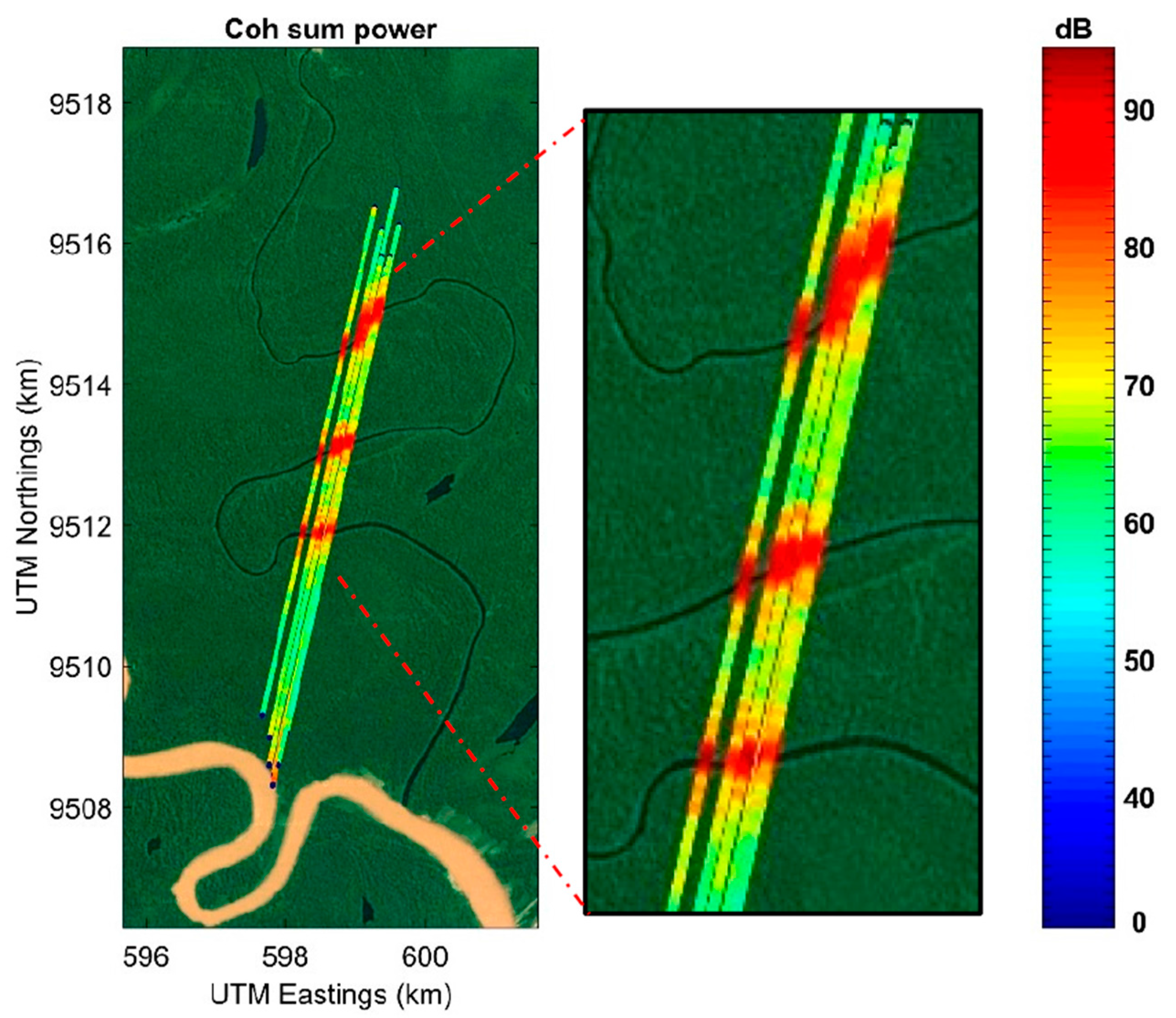
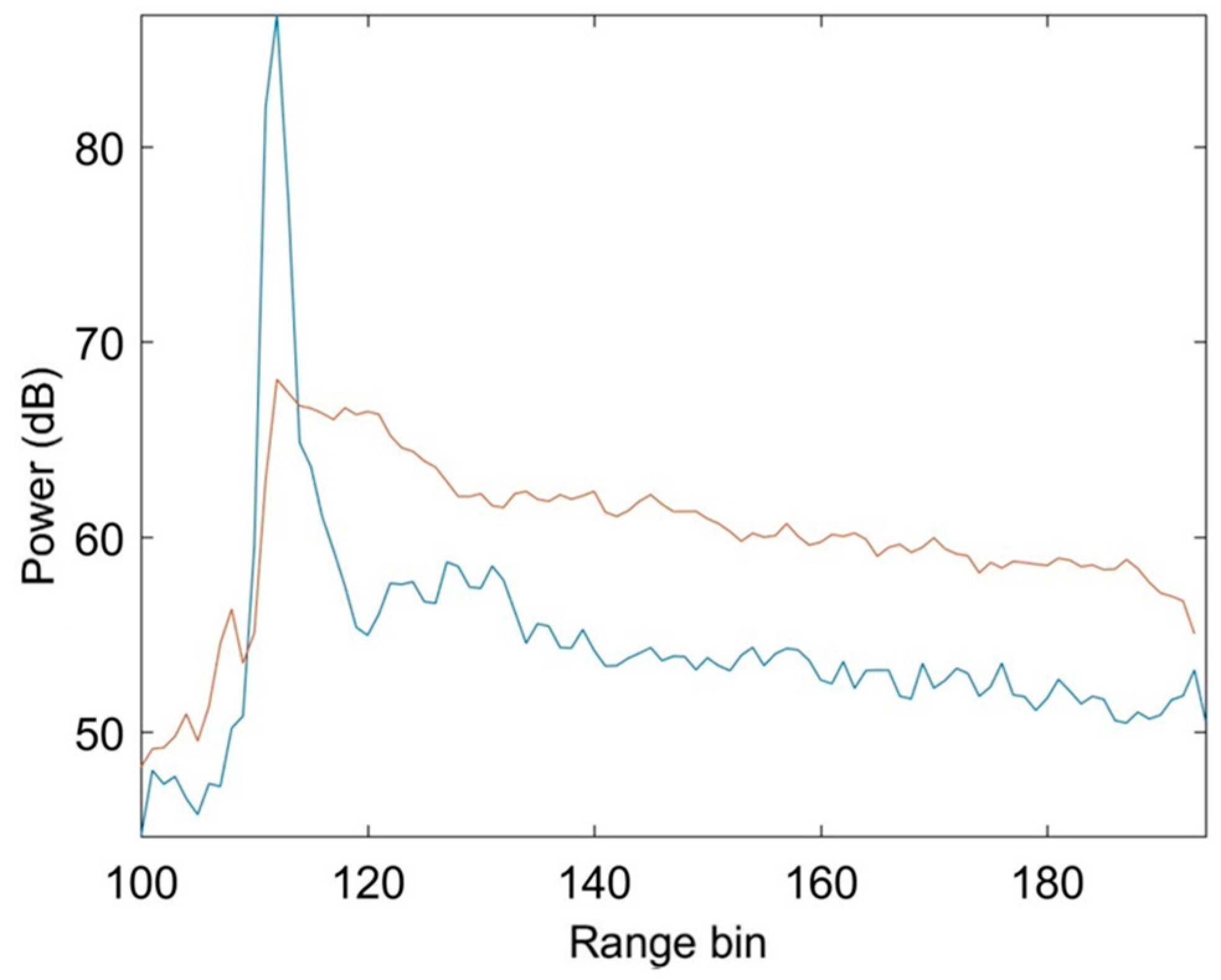
4.2. Rio Nahuapa
4.3. Semliki River
4.4. Prek Toal Flood Area
5. Discussion and Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| AGC | Automatic Gain Control |
| CPA | Closest Point of Approach |
| ESA | European Space Agency |
| GPU | Graphics Processing Unit |
| IE | Individual Echo |
| Jason-CS | Jason Continuity of Service (now Sentinel-6) |
| LRM | Low Resolution Mode |
| MSC | Magnitude Squared Coherence |
| OSTST | Ocean Surface Topography Science Team |
| PRF | Pulse Repetition Frequency |
| RA-2 | Radar Altimeter 2 |
| RAIES | RA-2 Individual Echoes and S-band data for new scientific applications for ocean, coastal, land and ice remote sensing |
| RCS | Radar Cross Section |
| RGW | Range Gate Width |
| SAR | Synthetic Aperture Radar |
| SARAL | Satellite with ARgos and ALtiKa |
| SNR | Signal-to-Noise ratio |
| SWOT | Surface Water and Ocean Topography |
Appendix A. Fitz Doppler Algorithm
References
- Resti, A.; Benveniste, J.; Roca, M.; Levrini, G. The Envisat Radar Altimeter System (RA-2). ESA Bull. 1999, 98, 8. [Google Scholar]
- Roca, M.; Martínez, D.; Reche, M. Preliminary results obtained using the EnviSat RA-2 individual echoes (full-rate waveforms with phase information). In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Seoul, Korea, 25–29 July 2005. [Google Scholar] [CrossRef]
- Roca, M.; Martinez, D.; Reche, M. The RA-2 individual echoes processing description and some scientific results. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–27 July 2007; pp. 3541–3546. [Google Scholar] [CrossRef]
- Bramer, S.M.S.; Berry, P.A.M.; Freeman, J.A.; Rommen, B. Global Analysis of Envisat Ku and S Band Sigma0 Over All Surfaces. In Proceedings of the Envisat Symposium, Montreux, Switzerland, 23–27 April 2007. [Google Scholar]
- Quartly, G.D.; Passaro, M. Initial Examination of AltiKa’s Individual Echoes. Mar. Geod. 2015, 38 (Suppl. S1), 73–85. [Google Scholar] [CrossRef]
- Biancamaria, S.; Frappart, F.; Leleu, A.S.; Marieu, V.; Blumstein, D.; Desjonquères, J.-D.; Boyd, F.; Sottolichioc, A.; Valle-Levinson, A. Satellite radar altimetry water elevations performance over a 200 m wide river: Evaluation over the Garonne River. Adv. Space Res. 2016, in press. [Google Scholar] [CrossRef]
- Fu, L.L.; Alsdorf, D.; Morrow, R.; Rodriguez, E.; Mognard, N. SWOT: The Surface Water and Ocean Topography Mission. Wide-Swath Altimetric Measurement of Water Elevation on Earth; NASA JPL Publication: Pasadena, CA, USA, 2012; Volume 5, p. 228. [Google Scholar]
- Abileah, R.; Gómez-Enri, J.; Scozzari, A.; Vignudelli, S. Coherent ranging with Envisat radar altimeter: A new perspective in analyzing altimeter data using Doppler processing. Remote Sens. Environ. 2013, 139, 271–276. [Google Scholar] [CrossRef]
- Li, X.; Zhang, B.; Mouche, A.; He, Y.; Perrie, W. Ku-Band Sea Surface Radar Backscatter at Low Incidence Angles under Extreme Wind Conditions. Remote Sens. 2017, 9, 474. [Google Scholar] [CrossRef]
- Brown, G. The average impulse response of a rough surface and its applications. IEEE Trans. Antennas Propag. 1977, 25, 67–74. [Google Scholar] [CrossRef]
- Walsh, E.J. Pulse-to-pulse correlation in satellite radar altimeters. Radio Sci. 1982, 17, 786–800. [Google Scholar] [CrossRef]
- Harish, A.R.; Sachidananda, M. Antennas and Wave Propagation; Oxford University Press: Oxford, UK, 2007; p. 411. ISBN 978-0-19-568666-1. [Google Scholar]
- Scozzari, A.; Gómez-Enri, J.; Vignudelli, S.; Soldovieri, F. Understanding target-like signals in coastal altimetry: Experimentation of a tomographic imaging technique. Geophys. Res. Lett. 2012, 39, L02602. [Google Scholar] [CrossRef]
- Gómez-Enri, J.; Vignudelli, S.; Quartly, G.D.; Gommenginger, C.P.; Cipollini, P.; Challenor, P.G.; Benveniste, J. Modeling Envisat RA-2 waveforms in the coastal zone: Case-study of calm water contamination. IEEE Geosci. Remote Sens. Lett. 2010, 7, 474–478. [Google Scholar] [CrossRef]
- Tournadre, J. Signature of lighthouses, ships, and small islands in altimeter waveforms. J. Atmos. Ocean. Technol. 2007, 24, 1143–1149. [Google Scholar] [CrossRef]
- Egido, A.; Smith, W.H. Fully Focused SAR Altimetry: Theory and Applications. IEEE Trans. Geosci. Remote Sens. 2017, 55, 392–406. [Google Scholar] [CrossRef]
- Fitz, M.P. Further results in the fast estimation of a single frequency. IEEE Trans. Commun. 1994, 42, 862–864. [Google Scholar] [CrossRef]
- Rummler, W.D. Introduction of a new estimator for velocity spectral parameters. In Technical Memo; MM-684121-5; Bell Telephone Labs: Whippany, NJ, USA, 1968. [Google Scholar]
- Miller, K.; Rochwarger, M. A covariance approach to spectral moment estimation. IEEE Trans. Inf. Theory 1972, 18, 588–596. [Google Scholar] [CrossRef]
- Garcia, E.S.; Sandwell, D.T.; Smith, W.H. Retracking CryoSat-2, Envisat and Jason-1 radar altimetry waveforms for improved gravity field recovery. Geophys. J. Int. 2014, 196, 1402–1422. [Google Scholar] [CrossRef]
- Haynes, S.; Rogers, C.; le Duc, I. RAIES Individual Echoes Processor. In Technical Specification Report; Ref S & D/SPE/002, 31/07/2007; European Space Agency, ESRIN: Rome, Italy, 2007; p. 105. [Google Scholar]
- Choi, J.H.; Lee, C.W.; Won, J.S. Flood Monitoring in Tonle Sap floodplain using SAR Interferometry. In Proceedings of the 30th Asian Conference on Remote Sensing, Beijing, China, 18–23 October 2009; Asian Association on Remote Sensing: Pathumthani, Thailand, 2009. ISBN 9781615679843. [Google Scholar]
- Choi, J.H.; Van Trung, N.; Won, J.S. Inundation mapping using time series satellite images. In Proceedings of the 3rd International Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Seoul, Korea, 26–30 September 2011; p. 3. [Google Scholar]
- Van Trung, N.; Choi, J.H.; Won, J.S. A Land Cover Variation Model of Water Level for the Floodplain of Tonle Sap, Cambodia, Derived from ALOS PALSAR and MODIS Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 2238–2253. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| Orbital height | 773 km |
| Orbital inclination | 98.276° |
| Radar frequency | 13.5753 GHz |
| Doppler velocity Nyquist | 9.91 m/s |
| Range gate | 0.4688 m |
| PRF | 1795 |
| Number of echoes in a record | 1984 (1.1 s) |
| Ground distance between echoes | 3.8 m |
| Date | Tonle Sap Level (m) (Ref. ESA) |
|---|---|
| 30 May 2007 | 3.8 |
| 4 July 2007 | 5.1 |
| 8 August 2007 | 6.7 |
| 12 September 2007 | 9.1 |
| 17 October 2007 | 10.4 |
| 21 November 2007 | 10.3 |
| 26 December 2007 | 7.5 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abileah, R.; Scozzari, A.; Vignudelli, S. Envisat RA-2 Individual Echoes: A Unique Dataset for a Better Understanding of Inland Water Altimetry Potentialities. Remote Sens. 2017, 9, 605. https://doi.org/10.3390/rs9060605
Abileah R, Scozzari A, Vignudelli S. Envisat RA-2 Individual Echoes: A Unique Dataset for a Better Understanding of Inland Water Altimetry Potentialities. Remote Sensing. 2017; 9(6):605. https://doi.org/10.3390/rs9060605
Chicago/Turabian StyleAbileah, Ron, Andrea Scozzari, and Stefano Vignudelli. 2017. "Envisat RA-2 Individual Echoes: A Unique Dataset for a Better Understanding of Inland Water Altimetry Potentialities" Remote Sensing 9, no. 6: 605. https://doi.org/10.3390/rs9060605
APA StyleAbileah, R., Scozzari, A., & Vignudelli, S. (2017). Envisat RA-2 Individual Echoes: A Unique Dataset for a Better Understanding of Inland Water Altimetry Potentialities. Remote Sensing, 9(6), 605. https://doi.org/10.3390/rs9060605