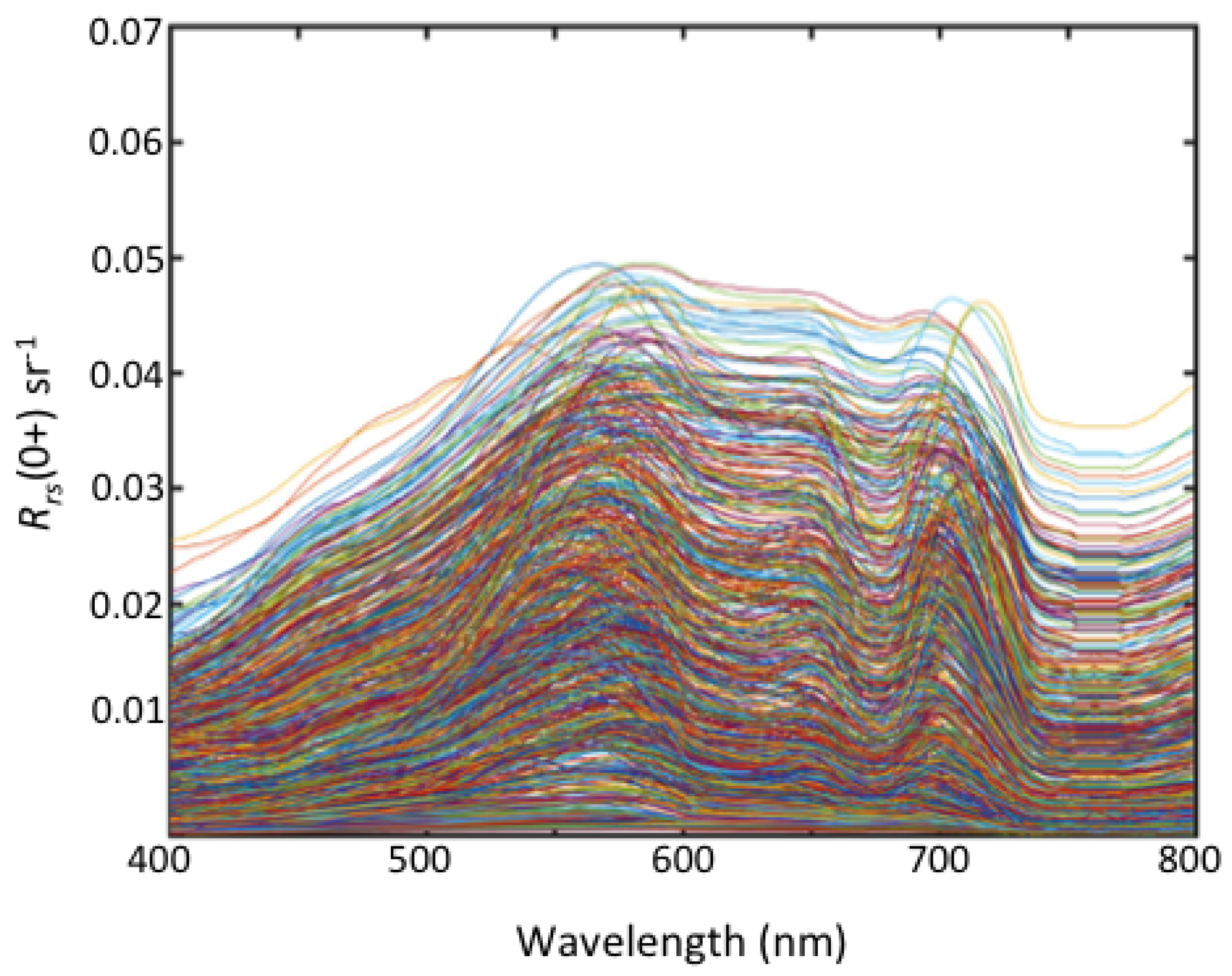
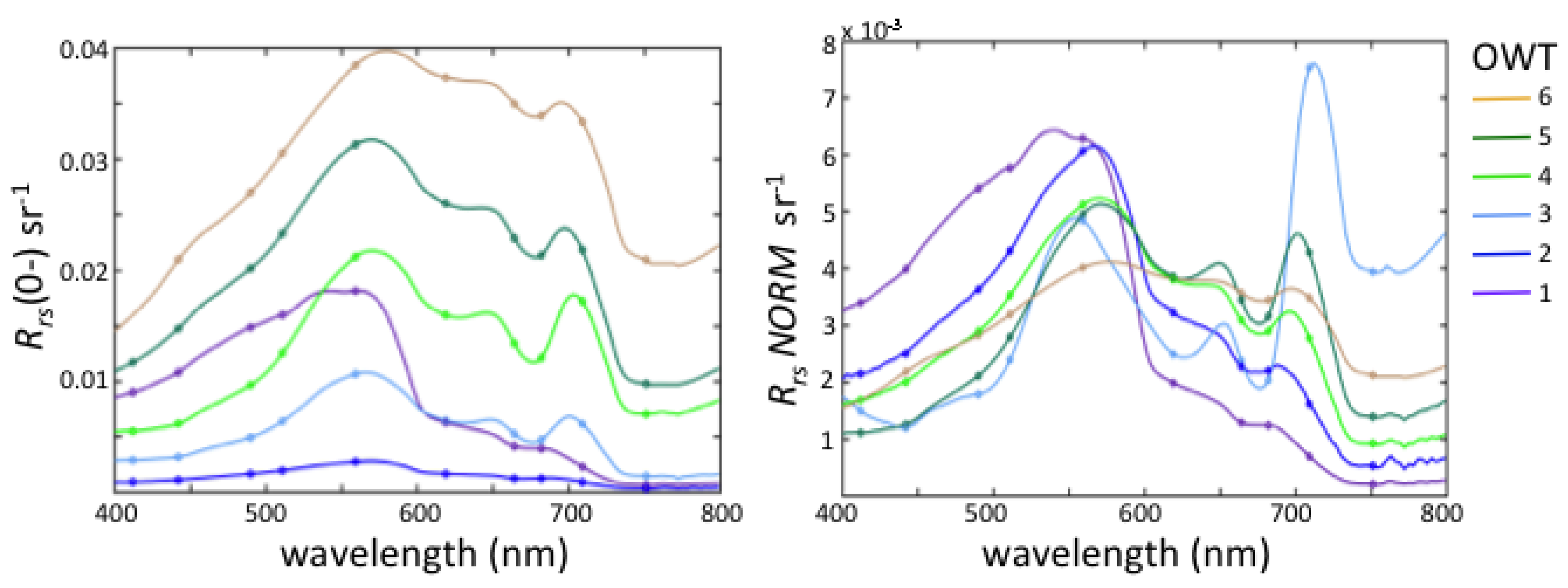
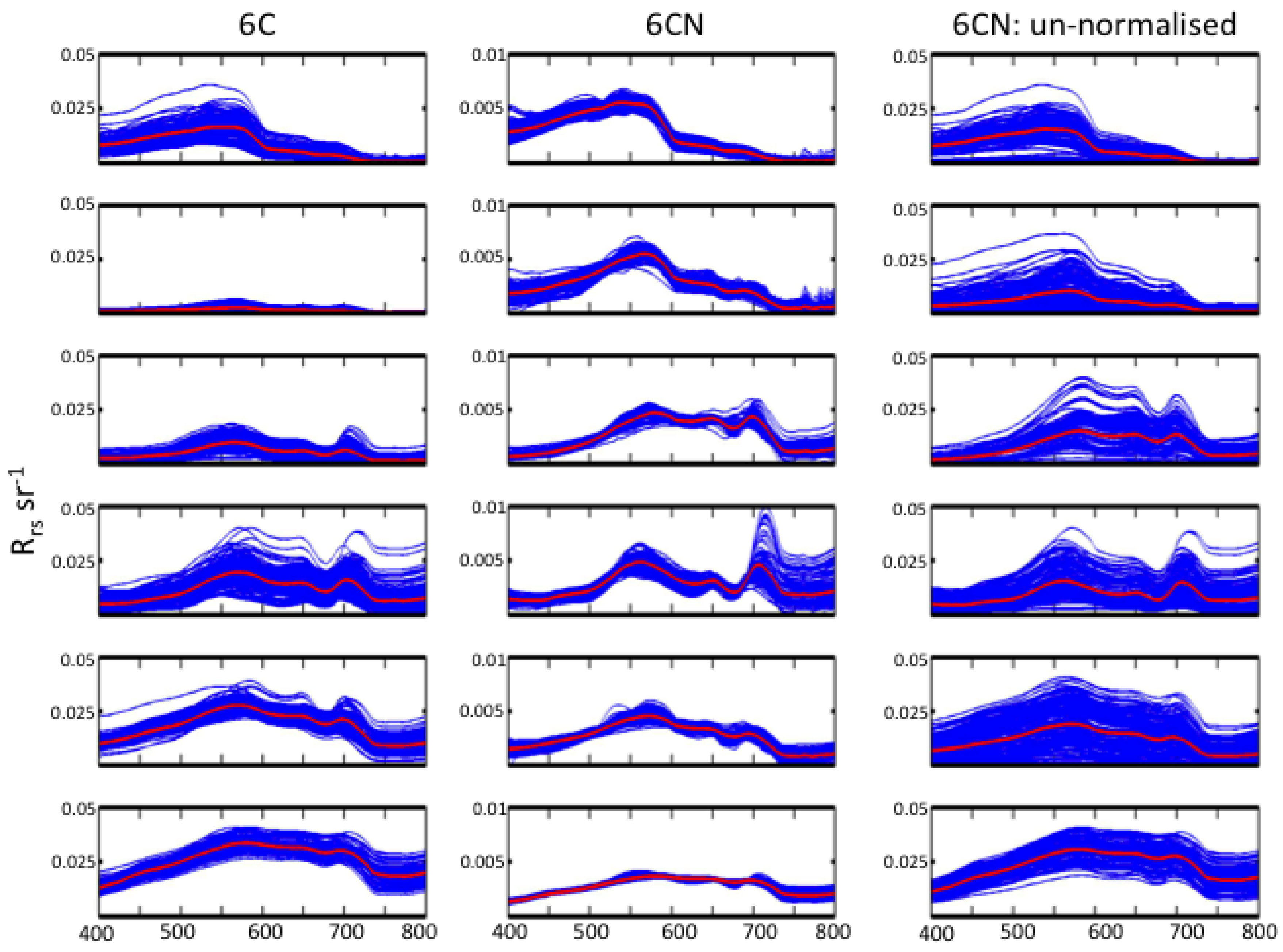
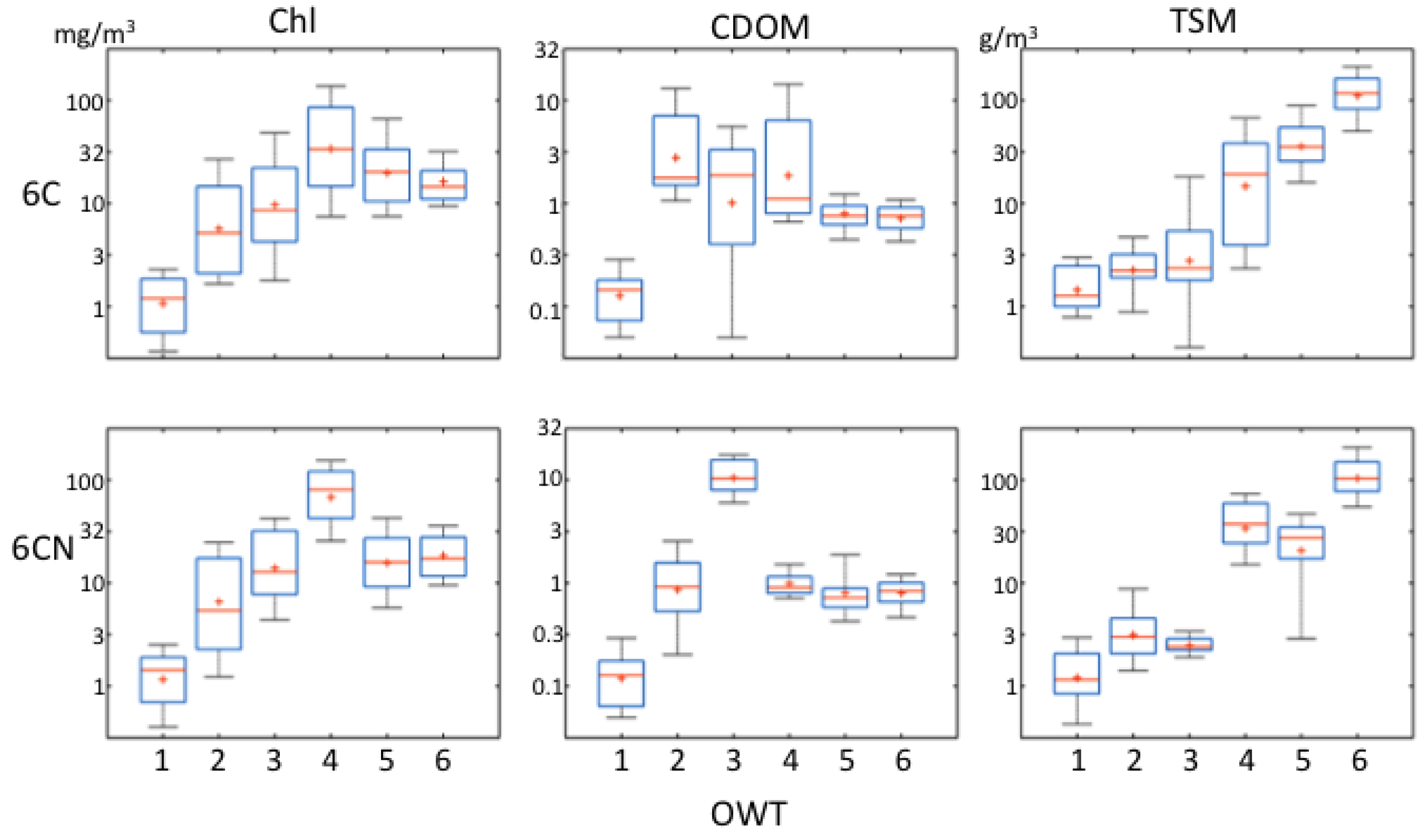
1. Introduction
Freshwater lakes, reservoirs and rivers are an essential resource for human and animal survival. Population increase coupled with change in land use, hydrologic regimes and climate are stressing these systems worldwide, threatening their function as sources for drinking water, socio-economic activities and ecological environments. Over the last decade, there has been an increase in the capacity and availability of remote sensing imagery from satellites for lake systems worldwide, promoting the usage and creating new demands for reliable remotely-sensed datasets. These new capabilities stem in part from newly-launched satellites, such as the MultiSpectral Imager (MSI) on board the European Space Agency’s (ESA) Sentinel-2 satellite and the Ocean Land Colour Imager (OLCI) on board ESA’s Sentinel-3 satellite. The OLCI sensor is similar in spectral capabilities as the Medium Resolution Imaging Spectrometer (MERIS) sensor (2002–2012), containing spectral channels well suited to derive bio-optical parameters over the large range of optical conditions exhibited in lakes [
1,
2]. Sentinel-3A was launched in February 2016, and its twin Sentinel-3B is expected to be launched in 2017. The tandem missions of Sentinel-3A/B and follow ups will provide unprecedented monitoring capabilities for lake water quality because of the favorable band settings, high signal/noise ratios, full spatial resolution (300 m) and high overpass frequency.
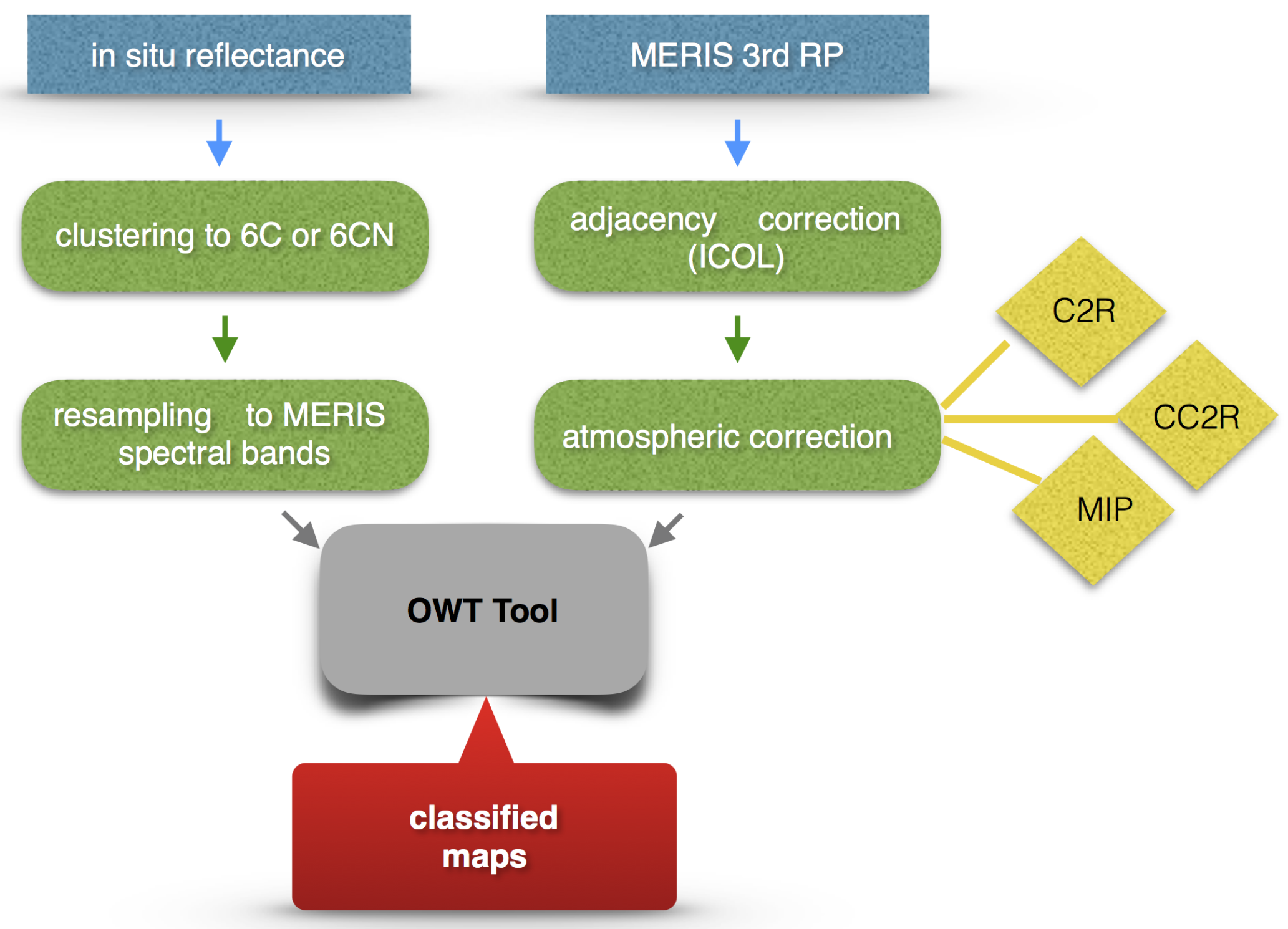
A prototype infrastructure for handling of bio-optical algorithms and data products specific to freshwater lakes was prepared within the EU Global Lakes Sentinel Services (GLaSS) project (
www.glass-project.eu). GLaSS aimed to develop generic methods and tools for Sentinel-2 and Sentinel-3 data, using legacy datasets, and in support of water quality management for any lake worldwide. One of the GLaSS products developed for lake image analysis is a classification tool based on the spectral matching method of Moore et al. [
3] as an expression of optical water types (OWTs). The OWT tool operates on atmospherically-corrected and quality-checked images prior to the application of bio-optical algorithms and provides users with a powerful data analysis technique to visualize and discover the (variability of) optical conditions across image scenes.
Classification schemes are more common to terrestrial imagery, but are gaining traction in aquatic applications and share basic similarities [
4,
5]. In both cases, the classification systems are based on features (i.e., spectral channels) in a spectral signal related to underlying types with ecological meaning. The features stem from the spectral reflectance shape and magnitude and are ultimately limited by the spectral resolution of the sensors when utilized for image classification. For aquatic uses, water types are analogous to land cover types, representing an optical condition, and hence, are referred to as optical water types or OWTs. This notion of optical type has origins in [
6,
7], where water types were defined by the diffuse attenuation coefficient of downwelling light. These Jerlov types are still used in marine applications [
8], and were used in a recent modeling study to generate Inherent Optical Properties (IOPs) for each type [
9], directly utilizing type-specific parameters.
More recent water type schemes have been introduced over the last 20 years using a variety of methods based on in situ and/or satellite reflectance data. Regardless of the method, OWTs provide information on the spatial distribution of optical states across image scenes when applied to satellite data. These mapped products function as weighting factors for optimizing bio-optical algorithms and product uncertainties for image scenes [
3,
10,
11,
12]. In these cases, they are intermediary products that are not needed themselves for analysis and are invisible to users. However, OWTs are depictions of optical states, providing information on underlying water conditions that in and of themselves have intrinsic ecological value. They have been used directly for interpretive analysis for ecological diversity [
13] and ecological patterns [
14] that may not be obvious from other bio-optical products, such as chlorophyll concentration, which may be hard to retrieve in complex lake waters, because of the complex atmospheric and in-water optical properties. In some cases, OWTs have been linked to distinct optical phenomena that relate to specific phytoplankton [
15]. These studies collectively illustrate the varying roles and uses for water types, whether freshwater or marine, when applied to remote sensing data.
The GLaSS optical water types are a follow up of [
3] that presented OWTs derived from lake and coastal waters. The GLaSS dataset comprises lake data only, encompassing a larger dataset that includes more diverse lakes from across the globe. Within this paper, we introduce this classification method (called GLaSS-OWT or GLaSS optical water type method). The water types were derived from a cluster analysis. The classification system that we present has two main implementation options: a set of optical water types for un-modified reflectance data and a set of water types for normalized reflectance data, an aspect not presented in [
3]. The method is designed to be applicable to any lake system, covering a large range of biophysical types from shallow turbid to clear and deep, as well as eutrophic and dark absorbing colored dissolved organic matter (CDOM)-rich waters.
We describe the development of the classification method and demonstrate its application to a variety of lake systems processed with different atmospheric correction schemes. The variations in OWT image products are discussed in the context of atmospheric correction. We also examine the strengths and differences of the different OWT schemes and how they may be appropriate for different global lakes with unknown optical properties.
4. Discussion
The GLaSS lake OWTs were developed by extending the OWTs derived in [
3]. In that earlier study, seven OWTs were identified, but represented coastal marine waters, as well as inland freshwater. The number of OWTs we found in a larger dataset but exclusive to freshwater was six. The impact of adding more data did not significantly alter the partitioning of reflectance space into clusters. We purposefully omitted spectra associated with floating algae because of too few instances to derive stable statistics, but we believe this is a water type that exists and should be incorporated in future renditions.
In addition to the development of the six OWTs on un-modified spectra (6C), we developed a parallel set using normalized spectra (6CN), accentuating absorption features by removing scaled magnitude effects solely attributable to concentration levels [
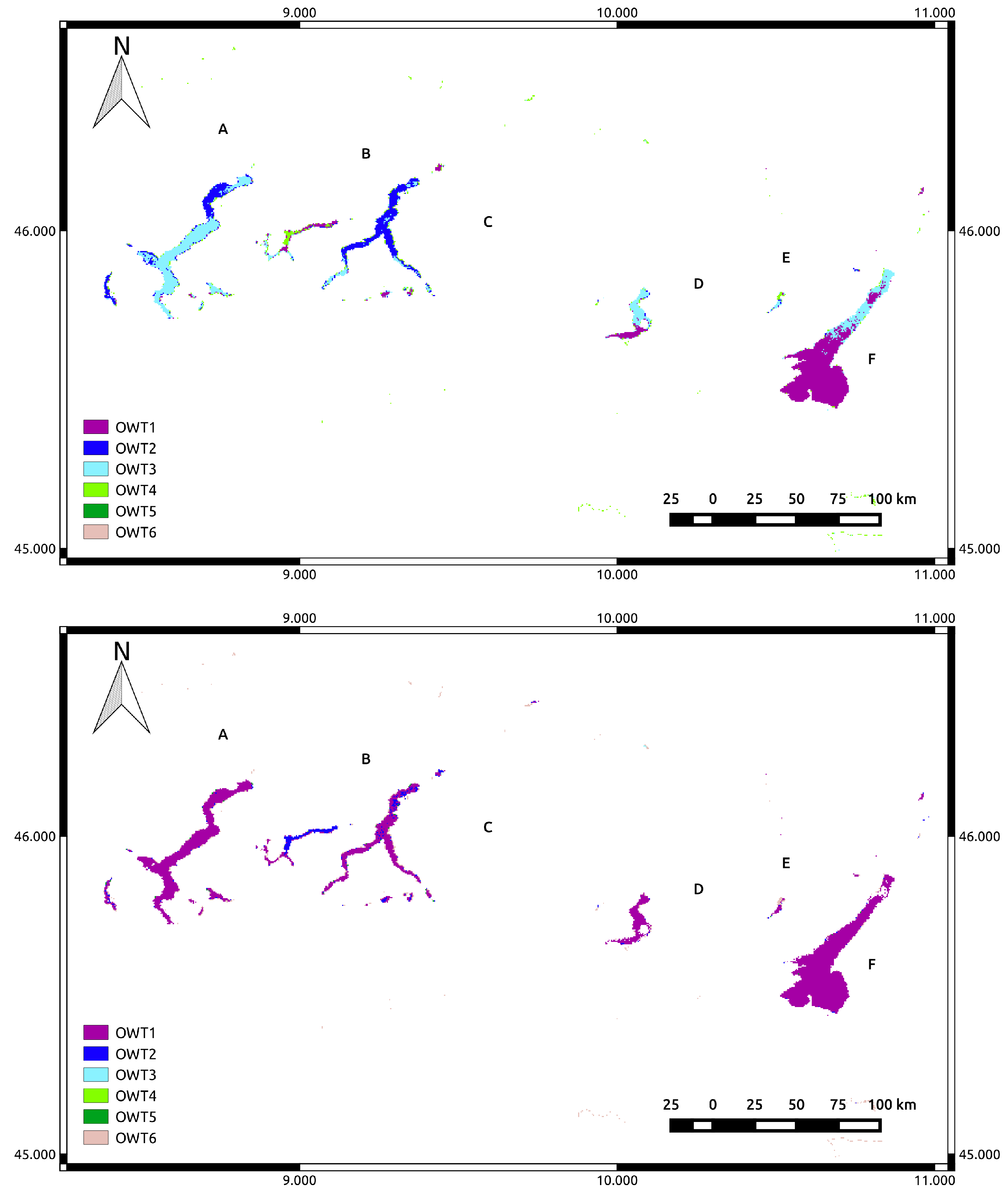
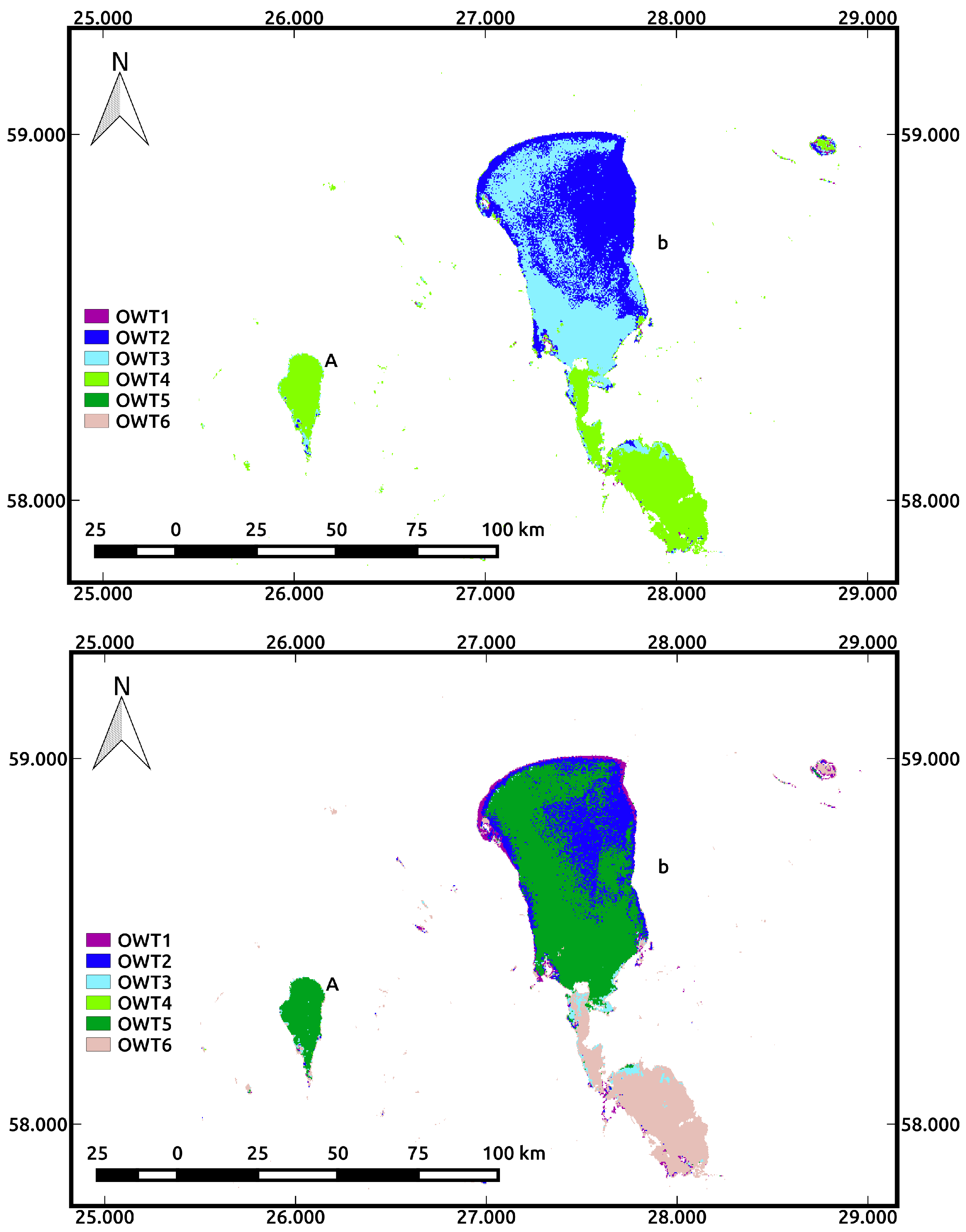
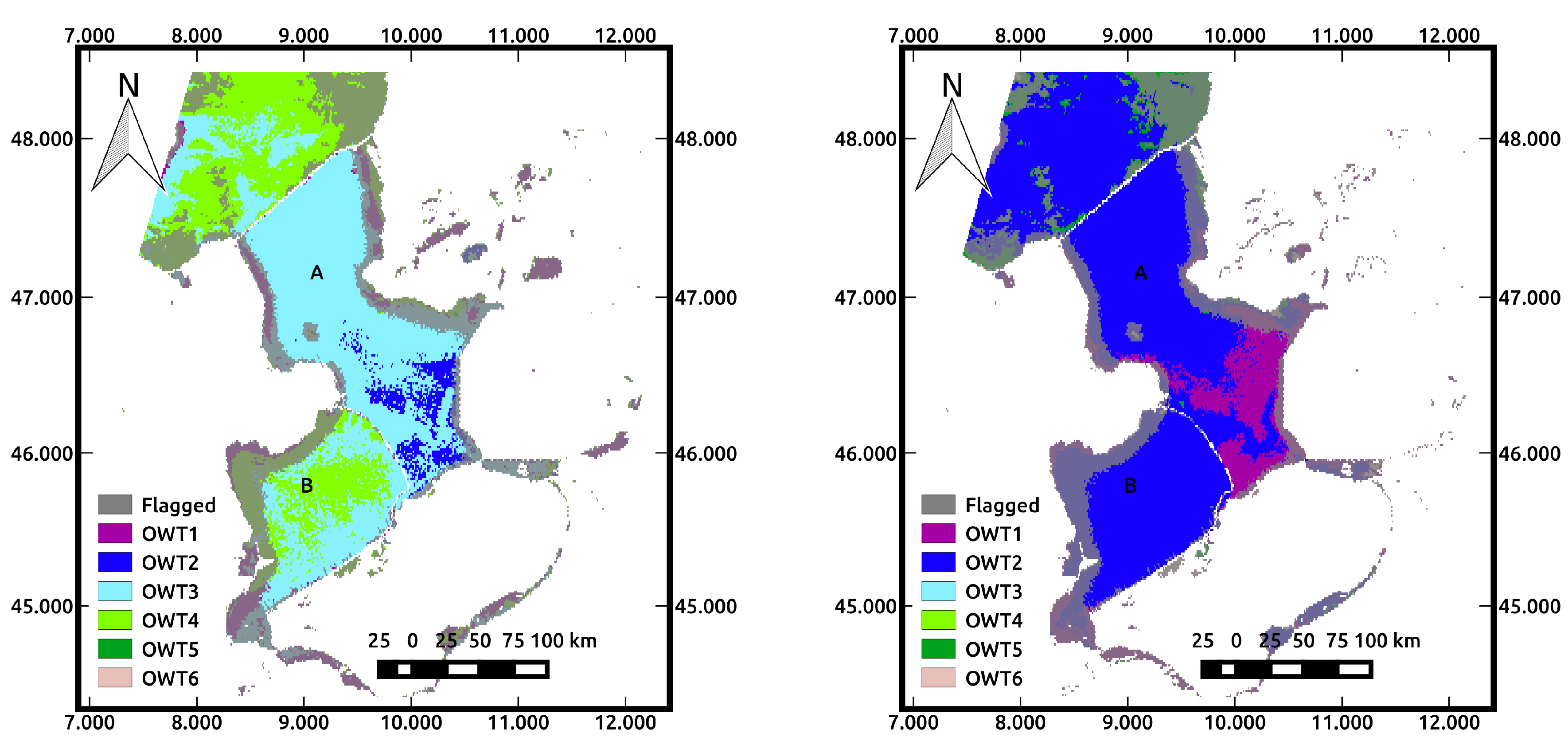
45]. The GLaSS tool contains both options for OWT processing. It is yet to be determined which choice of the classification scheme is best for a given lake (i.e., 6C or 6CN). This will depend on how the classification maps might be used and the nature of the lake system. In the Dutch and Estonian lakes (the lakes with a higher sediment load), the 6C classification performs better, while for the Italian and Swedish lakes (mainly for the clear Lake Vättern), the 6CN classification provided the best results based on the current analysis. This is consistent with our expectations: the normalized method discriminates ‘low reflecting’ lakes (either clear blue lakes or brown/yellow CDOM lakes) that would otherwise end up in the same ‘low’ reflectance OWT using non-normalized classification. For the Finnish lakes, however, the results from both classification schemes seem not very convincing: there are large contrasts between the classified in situ reflectance values (Tables 4 and 5) and the image results. We believe this is caused by atmospheric correction problems over dark waters. For these dark absorbing lakes, such as the ones in Finland and Sweden, it is known that the FUB processor performs best. However, due to missing spectral bands, the output of this processor cannot be fed into the OWT tool.
These AC test results highlight a new role for the OWT classification in identifying atmospheric correction problems, as an overall aim of the GLaSS OWT tool is to improve water quality products generated from satellite image processing for any lake system. A general problem with image processing over lakes is that certain AC and bio-optical algorithm retrieval schemes are more suitable for some optical conditions, while other schemes work better for other conditions (e.g., clear versus turbid waters). Selecting the most suitable AC and retrieval algorithm schemes is the most critical decision for producing accurate and meaningful water quality products. The OWT classification provides a mechanism to assist, for example by indicating whether a dark-pixel correction is possible (non-turbid) or not.
Using OWTs for improving the results of atmospheric correction for imagery over lakes would be a new application for these products. Currently, one iteration of atmospheric correction combined with the application of the OWT tool shows the distribution of OWTs over the whole lake. In cases that lakes contain water types that have a better performance with different AC schemes, one could imagine an iterative system where standard AC processing is executed and OWTs are computed, and then, if certain water types are found (assuming error in the turbid areas), a re-application of AC over the scene could be applied with a scheme more suitable to turbid conditions for those pixels assigned to the OWT that is connected to a different AC scheme. This approach is conceptually similar to the switching scheme between the NIR and SWIR AC models originally suggested by [
46] and further tested by [
47,
48] for MODIS imagery over various coastal locations, as well as for MERIS Case 1 and Case 2 atmospheric correction [
49,
50,
51,
52]. In the present case, multiple AC schemes could be available for selection, with images re-combined similar to the algorithm blending method for in-water retrievals, e.g., [
3]. This approach would require further testing of different AC schemes with different image scenes containing a variety of OWTs, but offers an avenue for blending AC schemes within a single image.
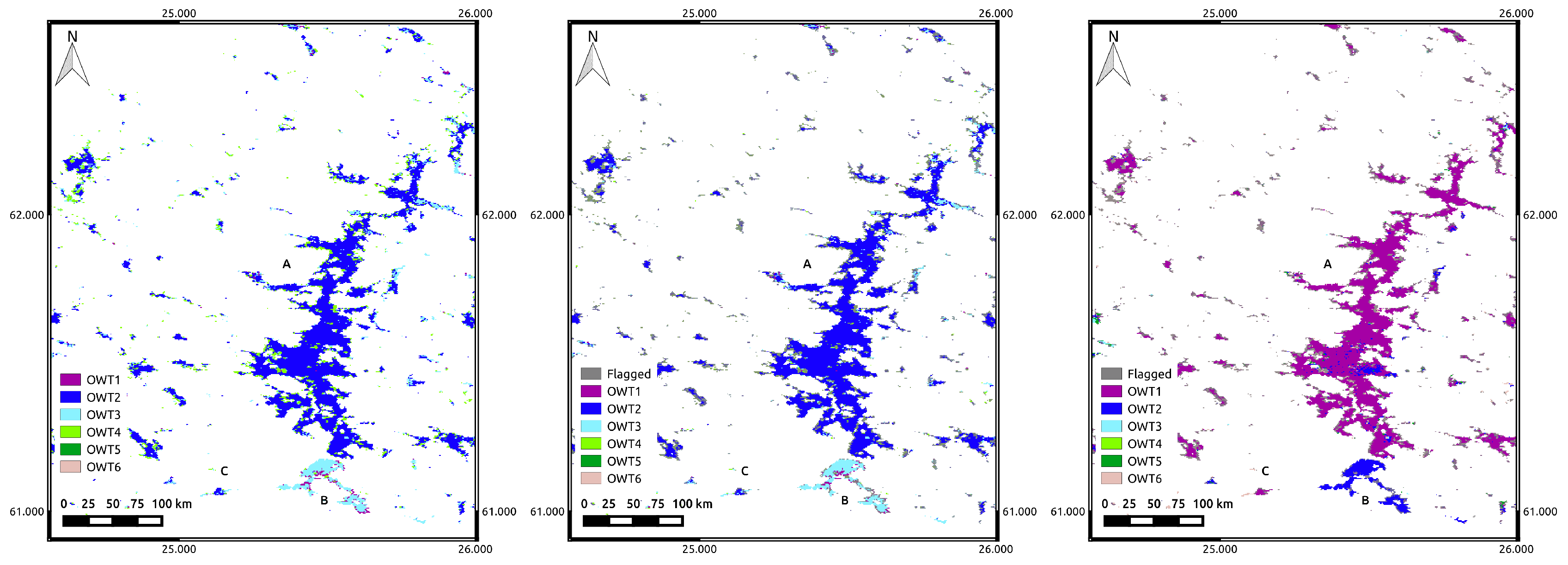
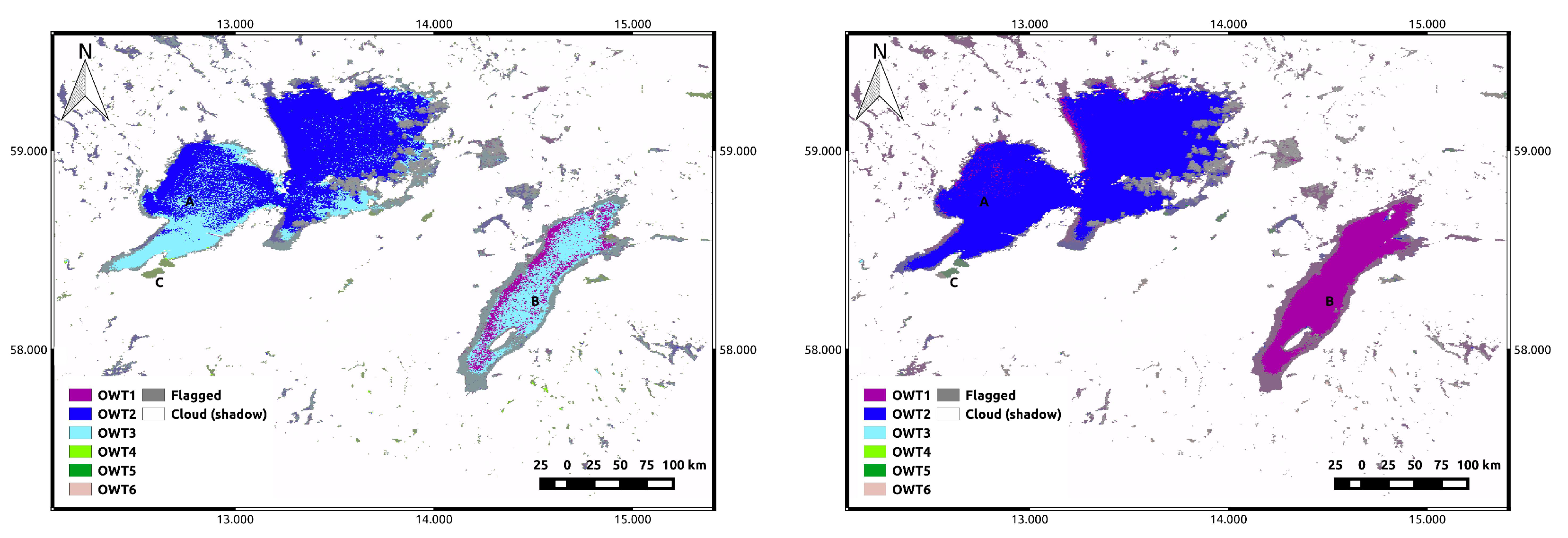
One important issue to mention concerns the use of the flags derived from the pre-processing of the scenes and the atmospheric correction method used. In the scenes analyzed, the ‘L2R suspect’ and the ‘L2R invalid’ flags removed some misclassified pixels along the lake shores, which could be caused by the remaining adjacency effect or by mixed land-water pixels. Those flags can be used to mask out these problematic pixels, but they can also mask large areas of valid pixels. Therefore, to determine to which class the main part of the lake belongs, it is advised not to use additional flagging besides the land- and cloud-related flags. It is also wise to ignore the much higher classes that are found in the 1–2 pixels along the shores of the lakes when they appear.
The classification maps produced from the GLaSS tool also serve as stand-alone products that provide spatial information for understanding the distributions and long-term trends of optical states that have environmental and ecological linkages. ESA’s Diversity II Project (
http://www.diversity2.info/) used the dominant OWT class as a monthly inland waters product from MERIS imagery for a variety of globally-distributed lakes. Time series of these classification maps provide indications of how a given system may be trending or changing as expressed OWT changes. Frequency maps of OWTs can be generated and are useful for understanding the distributions of the dominant water types for a given lake, leading to a first order indication of the types of AC schemes and retrieval algorithms that may be needed for processing, e.g., [
3]. There is much interest in using remote sensing to support reporting for the European Water Framework Directive and U.S. Clean Water Act [
53,
54]. Frequent OWT maps can provide an insight into the state and seasonal patterns that occur in lakes. Longer term or unexpected changes can be a reason to perform a full processing and taking additional samples for detailed analysis.
The 6C and 6CN classification methods analyzed here are similar in their implementation, but represent different approaches in classification and interpretation. The non-normalized approach (6C) is based on absolute values and thus can differentiate ‘dark’ from ‘bright’ waters more effectively than the normalized scheme (6CN), which essentially removes magnitude effects attributable to particle scattering. The normalized class partitioning is driven by spectral shape effects, largely from spectral-varying absorption properties. These considerations may be relevant to how the classification tool is ultimately used for a lake, such as to determine the most suitable tuning of a bio-optical algorithm or for general optical assessment.
Water classification is a somewhat recent and evolving discipline. Classification schemes exist that use normalized and non-normalized
spectra, but there has been no attempt anywhere to connect the two approaches. Currently, each approach has been treated separately without the other, and each has advantages and disadvantages. However, it is possible to unify the two schemes.
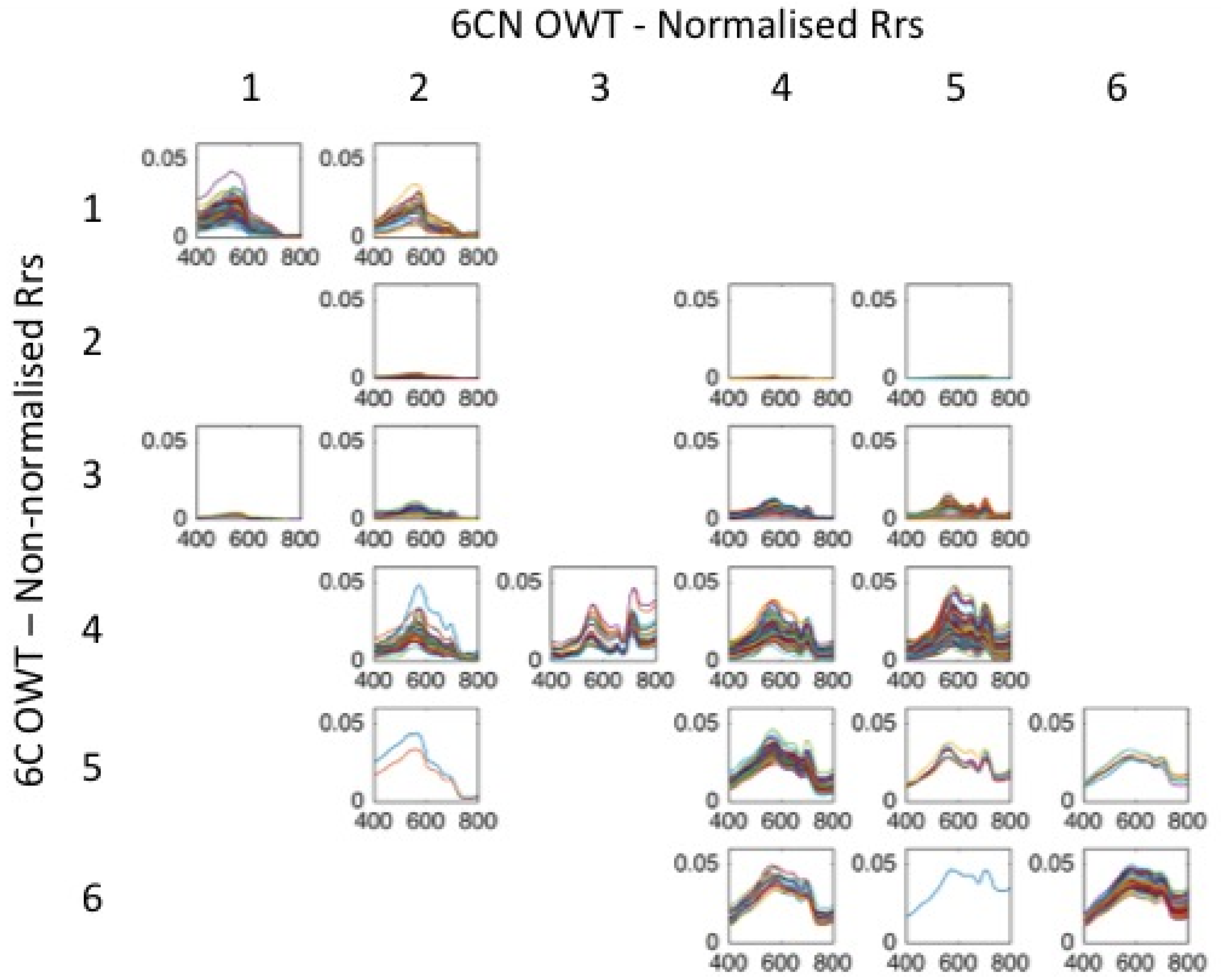
Figure 11 shows a view of the combined system as a matrix with the normalized and non-normalized normalized input remote sensing reflectance (Rrs) spectra separated into their respective clusters using the six-class scheme for both, resulting in 36 potential variations. Based on our results, 20 of the 36 possibilities are encountered. One approach for integrating the different schemes would be to use one classification system subsidiary to the other. Under this approach, fuzzy memberships would be derived for one scheme as the master factor, and a second sorting could take place according to the dominant OWT of the subsidiary scheme. This approach avoids intermingling fuzzy memberships, which is not yet feasible, but does add a new layer of classification by further discriminating shapes within a class. As an example, the new integrated scheme would use the fuzzy memberships for non-normalized classes as the main fuzzy value for pixel weighting if serving that function, and the dominant class of the normalized data as a subset variation of the non-normalized class. Theoretically, each non-normalized class has six normalized potential assignments when combining 6C and 6CN. This approach has not been tested, but could be a way to take full advantage of the classification tool. It is beyond the scope of this study to develop these concepts further and remains a gap that future work should address.
The selection of algorithms optimized for local conditions can also be facilitated by using the OWT approach to direct the algorithm selection and output blending. As has been demonstrated by [
3], the best performing algorithm to a particular water type can be determined through algorithm analysis a priori. During operational classification, the class memberships can then be used to weigh retrievals from multiple algorithms into a blended product. This assumes that algorithm performance for specific OWTs are globally representative. This assumption should be checked for a given lake system though. Variations in local optical drivers or specific Inherent Optical Properties (sIOPs) may deviate from global behavior or conditions.
5. Conclusions
Optical water type classification is a developing research topic in aquatic remote sensing. It has evolved from Jerlov water types as descriptors of marine waters, to a variety of marine and freshwater schemes designed for use with remote sensing image applications. We have developed a new tool specific for classifying lake remote sensing images, now available in the BEAM software. The development of the tool is an outgrowth of the method presented by [
3], differentiated by new data and new scheme configurations. Optical data from different lakes across Europe, the U.S. and China were merged, covering a wide range of environmental conditions, including dark lake waters, turbid waters and highly eutrophic waters comprising cyanobacteria blooms. We have re-developed lake optical water types with both a spectral-normalized and non-normalized treatment, resulting in two separate, but linked schemes. The resulting water types in each scheme were described by in-water concentrations of chlorophyll-a, CDOM and total suspended matter. While each scheme differs at a fundamental level, they serve the same roles for downstream applications, which in the past have included using them as intermediary products for optimizing bio-optical algorithm selection and as stand-alone products for supporting biogeochemical and biodiversity system analysis. We have focused our research on the development of the schemes within the tool and its use with remote sensing imagery from the MERIS sensor for a variety of European lakes as case studies with different optical conditions. We found that each scheme had merits for generating mapped water type products, depending on the lake. While the images used are a small subset of conditions likely to be found globally, the analysis is useful as a means for contrasting the different approaches for different lake conditions. The best scheme for any system requires a fundamental a priori knowledge of optical drivers, necessary for interpreting the images. For example, Lake Vättern in Sweden showed better results for the normalized scheme, while other lakes such as Lake Võrtsjärv and Lake Markermeer and IJseelmeer in the Netherlands showed better performance with the non-normalized approach. These approaches were assessed by how accurately we believed the classification maps depicted the underlying optics.
Although a prime use of classification maps is for bio-optical algorithm application, we did not set out to test or develop the tool with algorithms, as was done in [
3]. There is a wide variety in algorithms and intended purposes of algorithms, and this type of evaluation with the two-scheme approach was beyond the scope of this work. However, we presented a new use for classification maps as related to guiding atmospheric corrections schemes. As the tool operates directly on the spectral
, the atmospheric correction scheme will impact the effectiveness of the classification tool. We tested several different atmospheric correction schemes with each image, producing different classification maps for each test image. The classification results provided feedback on the performance of the atmospheric correction scheme, and we believe that the classification map interpretations are useful in assessing the performance of atmospheric correction when in situ match-up data are not available, which is generally the case. Thus, another use of classification maps is for atmospheric correction assessment and possibly selecting and blending, as well, although we speculate on how this may be done.
These two scheme variations presented here—spectral-normalized and non-normalized—represent the current options available to developers and users of images produced from optical water type classification, regardless of origin. We have shown how these schemes differ spectrally and in use, as well as in in-water characterizations. We have also shown how they are linked through a classification matrix and speculate on the potential to unify the two schemes, which could provide a way to maximize the advantages of each scheme together. This is an evolving area of research, and the guidelines and uses of optical water type schemes are still being explored and discovered.