Abstract
The parameterization of crop coefficients (kc) is critical for determining a water balance. We used satellite-based and literature-based methods to derive kc values for a distributed hydrologic model. We evaluated the impact of different kc parametrization methods on the water balance and simulated hydrologic response at the basin and sub-basin scale. The hydrological model SPHY was calibrated and validated for a period of 15 years for the upper Segura basin (~2500 km2) in Spain, which is characterized by a wide range of terrain, soil, and ecosystem conditions. The model was then applied, using six kc parameterization methods, to determine their spatial and temporal impacts on actual evapotranspiration, streamflow, and soil moisture. The parameterization methods used include: (i) Normalized Difference Vegetation Index (NDVI) observations from MODIS; (ii) seasonally-averaged NDVI patterns, cell-based and landuse-based; and (iii) literature-based tabular values per land use type. The analysis shows that the influence of different kc parametrization methods on basin-level streamflow is relatively small and constant throughout the year, but it has a bigger effect on seasonal evapotranspiration and soil moisture. In the autumn especially, deviations can go up to about 15% of monthly streamflow. At smaller, sub-basin scale, deviations from the NDVI-based reference run can be more than 30%. Overall, the study shows that modeling of future hydrological changes can be improved by using remote sensing information for the parameterization of crop coefficients.
1. Introduction
In semi-arid areas, evapotranspiration is generally the largest outgoing flux of the annual water balance. Accurate parameterization of the crop response to soil water availability is thus crucial when hydrological models are used for water balance studies [1]. Many hydrological models use a coefficient-based approach depending on land cover and season, while others use a physical based approach to simulate actual vegetation growth, allowing for more feedbacks between vegetation and the soil water component.
Models that focus on simulation of streamflow only, often use only a few parameters and a very simple representation of the vegetation component [2,3]. Accurate simulation of evapotranspiration, soil moisture, or spatial variability of catchment climatic conditions require a more realistic modelling of vegetation conditions on a spatial level [4,5,6]. This especially applies to scenario analysis of land use and climate change [7,8,9].
Spatially distributed hydrological models generally parameterize the vegetation status depending on land cover or land use maps [10,11,12,13,14]. Different coefficients are used for different land cover classes depending on its evapotranspiration demand under unlimited water availability. Actual evapotranspiration is then calculated based on actual soil moisture status. This approach is also typical for agro-hydrological models that use the guidelines developed by FAO for estimation of crop evapotranspiration [15].
Other spatially distributed hydrological models simulate vegetation status by means of a dynamic vegetation growth module, as for example the popular Soil Water and Assessment Tool (SWAT) [16]. However, this physically-based approach has its limitations because of high data requirements [17,18] and its complexity, which has a relatively high risk of modelling errors [19].
Remote sensing information is increasingly used in hydrological modelling to characterise and quantify vegetation and evapotranspiration dynamics at regional and global scales [20,21]. For regional studies on irrigation and water use, a combination of the FAO-based method and remote sensing information has been found useful by several authors [22,23,24,25,26,27]. At the plot-scale, remote sensing information is also increasingly used to derive crop coefficients in agro-hydrological modelling [28,29,30,31].
On the basin scale, satellite information is increasingly used to characterize vegetation cover and response to water availability in spatially distributed models [32]. Already rather common is the use of satellite-based precipitation dataset to force hydrological models [33]. But increasingly, satellite-based information is used to force the evapotranspiration process at this scale [34,35]. Also, satellite-based estimates of vegetation indices or evapotranspiration can be used to calibrate hydrological models [36,37,38,39].
The Leaf Area Index (LAI) is a variable that is sometimes parameterized using remote sensing data in a distributed hydrological models [40,41]. It has been shown that this can have substantial impacts on the spatial patterns of the evapotranspiration predictions compared to a more standard approach [42]. Also, many distributed hydrological models use a crop coefficient-based approach as for example the one based on the Penman-Monteith adapted by FAO [15]. Vegetation indices as the Normalized Difference Vegetation Index (NDVI) [22,43] and the Enhanced Vegetation Index (EVI) [44,45] have been used to derive crop coefficients for these models.
The reliability of the predictions by distributed hydrological models depends on high-resolution and accurate information to derive crop coefficients both in time and space. Remote sensing offers the unique opportunity to provide this information [46]. However, hydrological modelers are often confronted with the reality that this information is not available due to various reasons. Land use maps from which literature-based crop coefficients can be derived use often very generic classes, especially for agricultural areas. Also, land use changes may cause the land use map to be out of date, potentially leading to modeling errors. Generally, the hydrological modeler does not have the possibility to carry out remote sensing-based land use change mapping due to time, budget, or capacity constraints.
Even more important is that hydrological models are often used to make future projections for which, obviously, no remote sensing is available. Hydrologists therefore use all kinds of proxies to derive crop coefficients with little knowledge of the impact it has on model predictions.
The aim of this study is to evaluate the sensitivity of the hydrologic response derived from a basin-scale hydrological model to various NDVI-based and literature-based crop coefficient parameterizations. We used a time series of NDVI data as the best available proxy to assess the crop coefficient and calibrate a hydrological model (Spatial Processes in Hydrology—SPHY) with monthly reservoir inflows. We then looked at different hydrological outputs at basin and sub-basin scale to evaluate the sensitivity of the model to changes in the parameterization methods based on NDVI, land use, and tabular (not remotely-sensed) crop coefficients (the traditional approach in which kc values are derived from crop-specific literature values).
2. Methods
2.1. Study Area
The study was performed in the Upper Segura basin in south-eastern Spain. The basin area is 2592 km2 and it has an elevation that ranges between 488 and 1749 m.a.s.l. The basin has a sub-humid to semi-arid Mediterranean climate with mean annual rainfall of 470 mm (ranges between 330 and 780 mm during the study period). During winter, temperatures can drop below 0 in the higher parts of the basin, which means that there is some influence of snow on the hydrological response.
The dominant lithology consists of marls and limestones. Land use is rainfed farming (20%), forest (35%), shrubland and woodland (40%), and the remainder grasslands and sparsely vegetated areas (Figure 1).
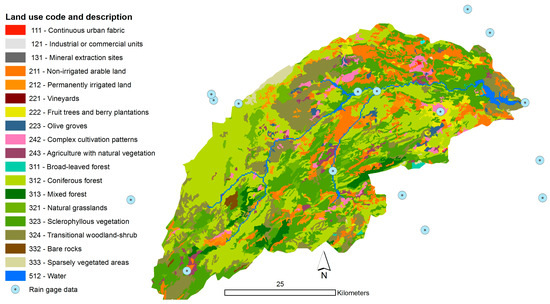
Figure 1.
Land use of the Upper Segura basin (source: CLC2006).
The basin is the main source of water for downstream urban and industrial water use and large intensively irrigated areas. It has five water storage reservoirs with a total storage capacity of 704 million m3; their main purpose being irrigation water storage, but they serve also for flood protection and limited hydropower generation.
2.2. Hydrological Model and Input Data
SPHY (Spatial Processes in Hydrology) is a spatially distributed hydrological model that is applied on a cell-by-cell basis [47]. SPHY simulates soil water dynamics using a two-layer stack of leaky buckets and two groundwater storage components. It includes a simple routing module based on the flow recession concept. As many basin-scale hydrological models, it adopts the FAO crop coefficient approach [15] by calculating reference evapotranspiration ETr using the Hargreaves method, and multiplying this with a crop-specific coefficient (kc) to calculate the potential evapotranspiration ETp for the crop. The equation is
for a moment t in time. The kc values can be fixed values depending on land use and cropping season, or temporally dynamic inputs, depending on NDVI (further detailed hereafter). Actual evapotranspiration is then calculated from the potential evapotranspiration considering water availability in the root-zone layer:
in which ETredwet,t is a stress coefficient for water excess, and ETreddry,t a reduction coefficient for lack of water. This water stress coefficient assumes a linear decline in water uptake when soil water availability falls below a certain threshold [47].
The SPHY model has been applied successfully in various studies ranging from real-time soil moisture predictions in flat lands to operational reservoir inflow forecasting in mountainous catchments, irrigation studies in the Nile Basin, and climate change impact studies of glacier-fed rivers in the Himalayan region [48].
The SPHY model has 23 model parameters if the glacier module is not used (as in this study) [48]. In total, nine parameters are related to soil physical parameters of the first soil layer (rootzone) and the second soil layer. There are four parameters related to the NDVI-based estimation of the crop coefficient (see the next section). The routing module requires three parameters related to baseflow and one flow recession parameter that generally is obtained through calibration with observed streamflow. Most of the input parameters can be given as single value for the entire area or as map. More details on the model conceptualization, processes, equations, and its applications are given by [48].
All input data for the SPHY model application to the Upper Segura basin were prepared at 250 m resolution. The digital elevation model extracted from the global SRTM (Shuttle Radar Topography Mission) elevation dataset at 90 m resolution was used. The Corine Land Cover (CLC) 2006 database [49] was used for land cover (Figure 1). For physical soil properties, data on texture and organic matter content of the LUCDEME dataset [50] were averaged per lithology class of the MAGNA geological maps [51]. Then, pedo-transfer functions were used [52] to derive field capacity, saturated water content, saturated hydraulic conductivity, and wilting point.
For this study, the model runs at a daily time-step. Daily rainfall data for the simulation period (2000–2015) were obtained for 24 stations (Figure 1) from the Segura River Basin Agency (Confederación Hidrográfica del Segura) and the Guadalquivir River Basin Agency (Confederación Hidrográfica del Guadalquivir). These rainfall inputs were spatially interpolated using ordinary kriging and resampled to the model resolution. It must be noted that more advanced interpolation techniques including geographical variables as elevation and satellite-based rainfall data could lead to more accurate rainfall forcings but for this modelling study this approach was considered suitable. Daily temperature data were available for a central location in the basin (Fuensanta reservoir) together with monthly-averaged high-resolution temperature maps based on multiple regressions with elevation and other variables [53]. The absolute temperature difference between the daily data and each pixel of the monthly maps was added to the daily temperature data to obtain daily temperature maps.
2.3. Crop Coefficient Parameterization Methods
Many authors have established relationships between NDVI and crop coefficients [54,55,56,57]. The SPHY model uses a linear relationship between NDVI-kc that depends on the minimum and maximum NDVI values in the observed period, and the minimum and maximum crop coefficient values for a given land use [47]. The equation to calculate the crop coefficient from NDVI is as follows:
where kct is the crop coefficient for a given moment in time, NDVIt is the NDVI observed, NDVImin is the NDVI value of bare soil (generally between −0.1 and 0.1; here assumed NDVI = 0), NDVImax is the maximum NDVI value in the area (0.8). The coefficients kcmin and kcmax are respectively the minimum and maximum values for the crop coefficient for the specific land use in the area (here kcmin = 0.4 and kcmax = 1.2).
The impact on hydrologic response of different kc parameterizations was studied based on NDVI, crop-specific FAO literature values for kc, and land cover (Table 1). More specific, three methods are based on NDVI, two on FAO literature values, and one method assumes kc equal to unity, i.e., Crop water requirements equal to reference evapotranspiration for all time-steps. This last parameterization method was added to assess the impact on the hydrological response when the influence of vegetation status on evapotranspiration was excluded [58].

Table 1.
Description and inputs for the crop coefficient parameterization methods used.
Figure 2 shows the maps of the mean annual crop coefficient for each of the parameterization methods. Methods 0 and 1 are based on pixel-level Normalized Difference Vegetation Index (NDVI). Methods 2–4 are based on the spatial distribution of the land use. Method 5 corresponds to a single value (1) for the entire basin.
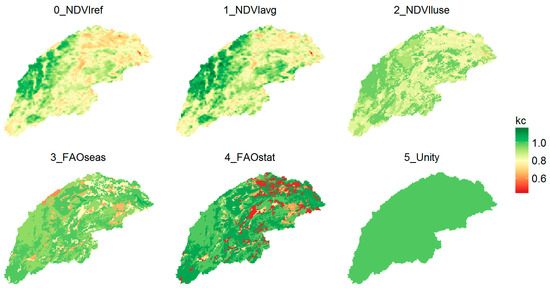
Figure 2.
Maps of the mean annual crop coefficient for the different parameterization methods.
2.4. Reference Model Calibration and Validation
The SPHY model forced with a continuous time series of NDVI observations each 16 days to derive crop coefficients (0_NDVIref) can be considered as the most accurate model because it includes all available information on temporal variation in vegetation status. It is termed the “reference model” for our comparison of parameterization methods. This reference model was calibrated using monthly reservoir inflow data (Fuensanta reservoir) for a period of 10 years (2001–2010). The validation period of the model is 2011–2015. A model initialisation period of one year was taken (year 2000).
The calibration was carried out using the optimization package PEST, with the local gradient-based Marquard–Levenberg algorithm, for parameter optimization [59]. This optimization package allows for a straightforward sensitivity analysis. The most sensitive parameters for monthly streamflow were selected from a total of nine soil physical parameters and three baseflow parameters. This resulted in a total of five SPHY model parameters used for calibration: the recession routing coefficient (kx), field capacity of root zone (RootField), saturated hydraulic conductivity of the rootzone (RootKsat), rooting depth (RootDepth), and days for water leaving soil to aquifer (DeltaGW).
Streamflow simulation outputs were firstly compared visually with observations. Next, three performance indicators were used for calibration and validation purposes. Threshold values for the three performance indicators were as follows [53]:
- -
- NSE: Nash-Sutcliffe efficiency (>0.50).
- -
- PBIAS: the percent bias (<25% or >−25%),
- -
- RSR: ratio of the root mean square error to the standard deviation of measured data (<0.70)

Table 2.
Performance indicators PBIAS (percent bias), RSR (ratio of the root mean square error to the standard deviation), and NSE (Nash-Sutcliffe efficiency) for the calibration and validation period.
2.5. Evaluation of Methods and Scale
The impact of the different kc parametrization methods was assessed based on model simulations for the entire period (2001–2015). Simulated streamflow, evapotranspiration, and soil moisture were compared to simulations by the reference model (0_NDVIref). The absolute deviations in mm and the relative deviations on a monthly basis were used to evaluate the parameterization methods.
The hydrologic response of the different methods was evaluated at basin level, but also at smaller sub-basin level. Distributed models are often used for land use scenario analyses, for which outputs at a smaller scale become relevant. Sensitivity analyses of the hydrologic response were thus also done at smaller sub-basin level. In total, 250 sub-basins with areas of 0.1, 1.0, and 10 km2 were randomly selected to have a representative sample.
3. Results
The calibrated and validated reference model (0_NDVIref) simulations of mean annual evapotranspiration and streamflow are presented as maps in Figure 3. Streamflow in this figure could also be termed “routed runoff”: all flow that is concentrated in the drainage network, expressed in mm, i.e., normalized by catchment area. Model simulations with different kc parameterization methods (Table 1) were subsequently done and compared with the reference model simulations at basin and sub-basin scale.
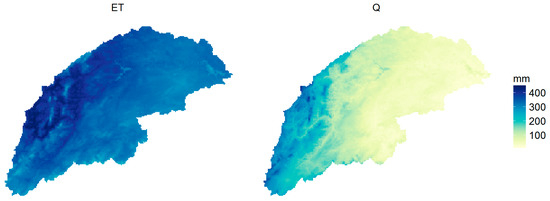
Figure 3.
Maps of mean annual evapotranspiration and streamflow based on simulated outputs of the NDVI-based reference model (mm).
Rainfall is highly variable in this basin, which causes high variability in the storage compartments (soil and groundwater) of the hydrological system. Figure 4 shows the monthly water balance for the entire basin, including precipitation (P), evapotranspiration (ET), streamflow (Q), and soil and groundwater storage (dS) based on the simulations using the NDVI-based reference model (0_NDVIref).
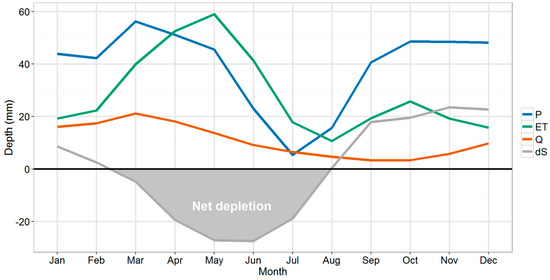
Figure 4.
Average monthly water balance of the basin including precipitation (P), evapotranspiration (ET), streamflow (Q) and change in soil and groundwater storage (dS) (all in mm).
On average, 27% of rainfall leaves the basin as streamflow, while the remainder is evapotranspiration. The storage component dS of the water balance is positive from September to January, when soil and groundwater storage components refill, while it is negative from March to July, when there is net depletion of soil water and groundwater. From May to July, actual evapotranspiration exceeds rainfall amounts.
In many hydrological models, crop coefficients are based on the FAO-56 tabular values [15], taking into account the crop seasonal cycle and land use patterns. To understand how such a parameterization approach compares to the NDVI-based method, the outputs of the 3_FAOseas model were compared to the reference model. This was done for the principal output variables of the water balance (soil moisture, evapotranspiration, and streamflow).
Figure 5 shows a boxplot of the deviations between the 3_FAOseas model and the reference model outputs for monthly values of each of these variables. The variability shown by the whisker boxes of the boxplot corresponds to the inter-annual variability based on the 15-year simulation period.
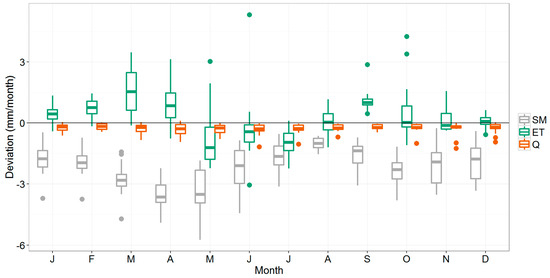
Figure 5.
Boxplots showing the deviation (mm/month) of the 3_FAOseas method compared to the reference model for soil moisture (SM), actual evapotranspiration (ET), and streamflow (Q) at basin-scale. The boxes demonstrate the interquartile range in which the median is indicated as a line; the fences indicate the values that are within 1.5 times de interquartile range, and the dots the values outside of this range (“outliers”).
4. Discussions
4.1. Basin Response
As can be seen, the 3_FAOseas modeled streamflow is slightly lower than the reference model outputs. Actual evapotranspiration is generally significantly higher for January–April, and September (tested with the Wilcoxon Signed-Rank Test at 0.05 significance level). June and July values are significantly lower. Soil moisture deviates negatively from the NDVI-based reference model—the highest deviations happening in spring. During summer, model outputs are closest to each other, with small negative deviations for the three variables; water available for streamflow generation and for evapotranspiration is lower as it has been consumed already in spring. Low rainfall amounts in summer cause soil moisture and evapotranspiration to reach their lowest levels (Figure 4), thus making the absolute difference between the methods smaller.
Most interestingly, despite a notable seasonal impact on evapotranspiration and soil moisture predictions, deviations in streamflow do not follow a seasonal pattern. The deviation from the NDVI-based reference model is more or less constant throughout the year: approximately −0.3 mm/month, which represents an average of 4% on an annual basis. However, because of the high variability in monthly streamflow, relative deviations of monthly streamflow range between 1% and −15% and is highest in summer and autumn.
The deviations of the other methods from the NDVI-based reference model show similar trends as 3_FAOseas (Figure 6). The largest deviations are seen for 5_Unity, which assumes a crop coefficient = 1. For this parameterization method, the average monthly deviation of streamflow is −0.7 mm/month, which corresponds to a relative deviation of −10%. For the other NDVI-based methods, deviations are around −0.2 mm/month (−3%) and for the FAO-based methods around −0.3 mm/month (−4%).
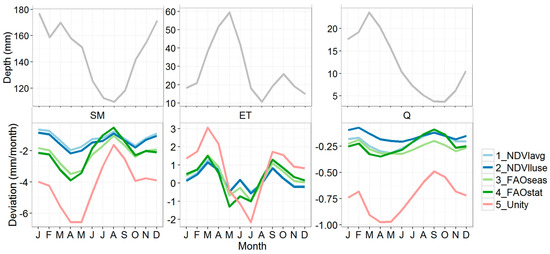
Figure 6.
Average monthly deviation of the five different kc parameterization methods (see Table 1 for explanation), compared to the reference model 0_NDVIref. The upper panels show the absolute mean monthly values for 0_NDVIref for soil moisture (SM), actual evapotranspiration (ET), and streamflow (Q). For SM, this refers to basin-averaged soil moisture content (mm). Negative deviations mean lower values compared to the reference model.
For ET, the mean monthly deviation is close to 0 for all methods, but as can be seen in Figure 6, there is a clear monthly pattern in the deviation: spring and summer deviations are positive, while in summer the deviations are generally negative. The highest values are reached in March (1.3 mm/month, corresponding to a relative deviation of about 3%). For 5_Unity, this goes up to 3.1 mm/month (7%) deviation.
For soil moisture, the highest deviations occur in spring (Figure 6), when ET deviations are also highest. As could also be seen in Figure 5, negative deviations in soil moisture correspond with positive deviations in ET. This has interesting implications for streamflow and can explain why for all parameterization methods the deviation in streamflow is less variable over the year than ET and soil moisture. The kc parameterization method influences the crop water demand and thus soil water extraction by vegetation and evapotranspiration. The effects of ET and soils moisture extractions on streamflow are buffered by soil moisture and groundwater storage components, causing the impact of kc parameterization on streamflow to be less variable throughout the year.
The relatively small and constant deviation in streamflow can be irrelevant for many applications focusing on basin-scale streamflow prediction, as it can be corrected by model calibration. In fact, it may remain unnoted by the modeller: rainfall forcing is often the main source of input uncertainty in hydrological modelling, most likely leading to comparable or higher deviations than those caused by kc parameterization [60]. This may explain why often little attention is paid to the crop response to soil water availability in hydrological models used solely for streamflow prediction.
Still, relative deviations in streamflow prediction can be considerable, especially for the autumn period at the start of the rainy season (on average −6% in October for 3_FAOseas and −15% for 5_Unity). In a few days, the basin can change from a dry status to a wet status, so it is likely that small changes in the parameterization will have notable effects on that time scale. The focus of this study has been on the monthly response, since no daily discharge data were available and the model error on such high temporal resolution is generally much higher as well. Nevertheless, more study is required to understand how our findings on the impact of crop coefficient parametrization extrapolate to daily hydrological response and its implications for hydrometeorological extremes and flood risk prediction.
4.2. Sub-Basin Response
Figure 7 shows the same boxplot of monthly deviations for the sub-basins (0.1 to 10 km2), as for the basin-scale outputs (Figure 5). Overall, the same seasonal trend can be observed in the deviations of the three variables shown. However, Figure 7 shows that the deviations can be considerably higher at this smaller scale. For a certain portion of the sub-basins, deviations can be several factors higher than what was seen at the basin scale.
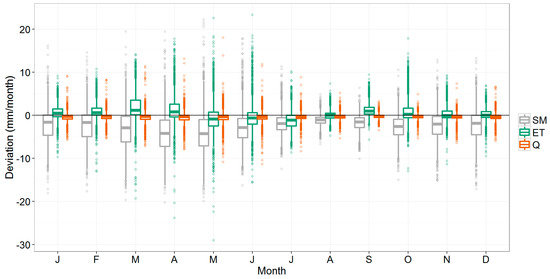
Figure 7.
Boxplot showing the deviation (mm/month) of the 3_FAOseas method compared to the reference model for soil moisture (SM), actual evapotranspiration (ET), and streamflow (Q) at the sub-basin-scale. The variability shown corresponds to the interannual variability of all sub-basins.
More specifically, Table 3 shows how the deviations of the sub-basin outputs differ from those at the basin-level. The table shows the 10th, 50th, and 90th percentiles, and both the absolute (mm) as well as the relative deviations (%). As expected, the median (50th percentile) is very similar between the basin and sub-basin levels: outputs were based on the same simulations, so the overall trend should be the same. However, there are considerable differences in the tail ends of the distribution, i.e. the 10th and the 90th percentile. Absolute deviations (mm) can be more than two times higher at the sub-basin scale than at the basin scale. As an example, 10% of the monthly evapotranspiration predictions deviate −2.3 mm/month or more from the 0_NDVIref run, while at the basin scale this value was −1.1 mm/month. This corresponds to a relative deviation of 5% at the basin scale, and 10% at the sub-basin scale. For soil moisture, similar differences were found between the scale levels.

Table 3.
Absolute and relative deviations for the 3_FAOseas run compared to the 0_NDVIref run, indicating the 10th, 50th (median) and 90th percentiles, for the basin and the sub-basin scale.
For streamflow, deviations (mm) can increase by a factor 3 or more from the basin to the sub-basin level. Table 3 shows that 10% of the predictions show a deviation of −8% or more with the reference run at the basin scale, while deviations can be −28% or more at the sub-basin scale.
The larger the basin, the more diverse in terms of land use, climate, and other biophysical conditions. Therefore, the relevance of bringing in more detail in the kc parameterization will depend on the size of the basin [61,62]. Often, hydrological impacts of land-use and management change are studied using distributed models like the one used in this analysis. What the above results show is that parameterizing crop coefficients from high-resolution observations of vegetative status (0_NDVIref) can deviate substantially from a more classical approach using literature-based values for the kc values, especially at the sub-basin scale.
For future scenario analysis, remote sensing data to characterize the crop status are not available. Therefore, hydrologists often use the tabulated FAO-56 values for the crop coefficients. However, as was shown previously, there can be considerable deviations with an approach using high-resolution information on crop status, as is provided by remote sensing, especially at the sub-basin scale. When outputs at smaller scale become the focal point of study, for example for prioritizing measures across the landscape [63], literature-based values will result in a loss of information and consequent inaccurate results.
Figure 8 shows a comparison of all methods at the sub-basin scale. It shows the area between the 10th–90th percentiles (green band) as in Table 3 but for all parameterizations instead of only 3_FAOseas. In addition, it includes the 5th–95th percentiles (reddish colour).
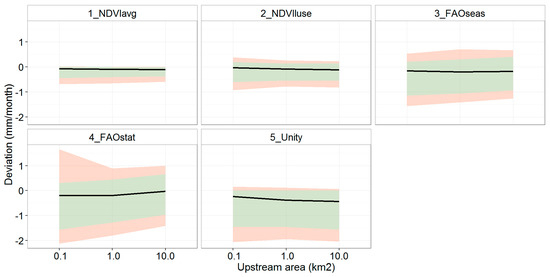
Figure 8.
Streamflow deviations for all methods, with 50th percentile (black line), the interval between the 10th and 90th percentiles (green), and the 5th and 95th percentiles (red).
The two NDVI-based methods have the smallest deviation compared to the reference model: the 50th percentile is closest to zero (Figure 8). Also, the percentile intervals (green and red) are narrower compared to the other methods, so overall less variability in the deviation with the reference model can be expected when choosing one of these two methods. This result is not fully surprising because the same NDVI information was used for these two models and the reference model, but in an aggregated and simplified way. The advantage of these methods is that they can be used for kc parameterization of hydrological models in future scenario analysis.
The FAO-based methods 3_FAOseas and 4_FAOstat show a similar deviation (50th percentile) for the sub-basins, but using a static (non-seasonal) crop coefficient (4_FAOstat) clearly increases the spread in the deviation of the streamflow predictions. For 5_Unity, the median indicates that the deviation is largest of all methods. On the other hand, positive deviations are less likely to occur compared to the FAO-based methods, causing the bands to be narrower. This is because this method assumes a kc = 1, while in the other methods the mean kc is lower (see also Figure 2), thus causing higher crop water demand and less water available for runoff and streamflow.
The results shown are based on a Mediterranean basin, with a wide range of biophysical conditions, but with a typical hydrological regime (potential evapotranspiration higher than rainfall, and streamflow highly variable and overall much lower than evapotranspiration). Therefore, these findings are limited to this type of hydro-climatic conditions as they are very much influenced by the fact that during most of the year the actual evapotranspiration is limited by soil water availability in semi-arid systems. It can be expected that in more humid or even more arid basins the sensitivity to the evapotranspiration component and the impact on streamflow will be different [64,65]. To generalize the findings in this paper, it could be interesting to apply a similar approach in basins with different climate and other biophysical conditions. A statistical analysis could be carried out to identify the dominant factors (rainfall, landuse, slope, catchment area, etc.) that explain the deviations. This could potentially lead to practical guidelines for hydrological modeling and crop coefficients. This should also consider that, for more humid conditions, the use of NDVI to derive crop coefficients has its limitations due to saturation issues that make NDVI a less adequate proxy for the crop coefficient [55].
The hydrological model SPHY is a typical bucket-type grid-based model, using process descriptions used in many other hydrological models. So we expect the results of the sensitivity analysis here to be valuable also to many other similar models. The sensitivity of course also depends on the model conceptualization. Hydrological models that use for example the “hydrological response unit” (SWAT, TOPMODEL, etc), instead of cell-based calculation units, or that use conceptualizations and descriptions of soil water dynamics that are different to the typical bucket-approach, may respond differently to different kc parameterizations as is shown here.
This study compared the different kc approaches with a reference model calibrated using streamflow data. Several studies have evaluated the usefulness of actual evapotranspiration estimates derived from remote sensing data and energy-balance methods for the calibration of hydrological models [37,38,39]. This can lead to a more accurate spatial distribution of the model parameters, especially in semi-arid areas like in this study [36]. A recommendation therefore for follow-up work is to evaluate different kc parameterization approaches by calibrating these independently using remote sensing-based observations of evapotranspiration rates. Calibration performance coefficients—for example those used in this work—could be used to assess which method performs better than others. A more in-depth analysis could be performed for this evaluation as well, by using spatial metrics that assess the degree of similarity between of the spatial patterns in the model simulations [66,67].
5. Conclusions
This study evaluated the effect of various NDVI and literature based crop coefficient parameterization methods, on the hydrological response of a basin-scale hydrological model. Compared to the reference model that was based on actual 16-day interval NDVI observations, the other, more simplified and aggregated methods overestimated actual evapotranspiration in spring and underestimated actual evapotranspiration in summer and autumn. For soil moisture, the highest deviations from the reference model were found in spring, when soil moisture levels are high. The effect on basin-level streamflow is buffered by the interaction between soil moisture and evapotranspiration, leading to an annual deviation of about 3%–4% with the reference model. In autumn, these deviations can be higher, potentially leading to a bias of up to 15% in monthly predicted streamflow. Overall, we conclude that the choice of the kc parameterization method can lead to deviations of around 5%–10% in basin streamflow predictions in the summer and autumn.
Results further indicated that the deviations in model output can be substantially higher for smaller sub-basins. For about 5% of the sub-basins, deviations from simulated streamflow went up to 30%, using the FAO-based parameterization. This has implications for land use and management change analyses and other hydrological assessments in which the outputs at a finer scale become relevant, such as for assessing impacts of management interventions, for example. The results suggest that for this type of distributed model applications, preference should be given to high-resolution remote sensing-based information to parameterize crop coefficients. Aggregated approaches like the typical FAO-based approach can lead to wrong (generally under-estimated) streamflow simulations. NDVI-based crop coefficients have the advantage over literature based values in that local conditions that influence crops are considered.
We conclude that for hydrological model applications at basin and sub-basin scale crop coefficient parameterization using satellite-based NDVI data is preferable, given the fact that sufficient long term series of NDVI data are now available for seasonal analyses at high resolution. Also for future scenario studies, combining historic observations of a vegetation index like NDVI and land use maps is preferred, rather than using literature-based crop coefficients.
Supplementary Materials
All modeling inputs and outputs are available in a public data repository: https://dx.doi.org/10.6084/m9.figshare.4578526.
Acknowledgments
We acknowledge financial support from the European Union’s Horizon 2020 project IMPREX (Grant agreement number 641811), from the Spanish Ministry of Science and Innovation (CGL2013-42009-R), and the Séneca foundation of the regional government of Murcia (118933/JLI/13).
Author Contributions
Peter Droogers and Johannes Hunink initiated the research; Johannes Hunink, Joris de Vente, and Joris Eekhout designed the research; Joris Eekhout performed the model analysis; Johannes Hunink and Joris Eekhout analyzed the data; Johannes Hunink wrote the paper with contributions from all authors.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; and in the decision to publish the results.
References
- Li, S.; Kang, S.; Zhang, L.; Zhang, J.; Du, T.; Tong, L.; Ding, R. Evaluation of six potential evapotranspiration models for estimating crop potential and actual evapotranspiration in arid regions. J. Hydrol. 2016. [Google Scholar] [CrossRef]
- Ye, W.; Bates, B.C.; Viney, N.R.; Sivapalan, M.; Jakeman, A.J. Performance of conceptual rainfall-runoff models in low-yielding ephemeral catchments. Water Resour. Res. 1997, 33, 153–166. [Google Scholar] [CrossRef]
- Skaugen, T.; Peerebom, I.O.; Nilsson, A. Use of a parsimonious rainfall-run-off model for predicting hydrological response in ungauged basins. Hydrol. Process. 2015, 29, 1999–2013. [Google Scholar] [CrossRef]
- Öztürk, M.; Copty, N.K.; Saysel, A.K. Modeling the impact of land use change on the hydrology of a rural watershed. J. Hydrol. 2013, 497, 97–109. [Google Scholar] [CrossRef]
- Hughes, D.A. Monthly rainfall-runoff models applied to arid and semiarid catchments for water resource estimation purposes. Hydrol. Sci. J. 1995, 40, 751–769. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, X.; Zhang, Q.; Liang, K.; Liu, C. Investigation of factors affecting intra-annual variability of evapotranspiration and streamflow under different climate conditions. J. Hydrol. 2016. [Google Scholar] [CrossRef]
- Wegehenkel, M. Modeling of vegetation dynamics in hydrological models for the assessment of the effects of climate change on evapotranspiration and groundwater recharge. Adv. Geosci. 2009, 21, 109–115. [Google Scholar] [CrossRef]
- Parr, D.; Wang, G.; Bjerklie, D.; Parr, D.; Wang, G.; Bjerklie, D. Integrating Remote Sensing Data on Evapotranspiration and Leaf Area Index with Hydrological Modeling: Impacts on Model Performance and Future Predictions. J. Hydrometeorol. 2015, 16, 2086–2100. [Google Scholar] [CrossRef]
- Wi, S.; Yang, Y.C.E.; Steinschneider, S.; Khalil, A.; Brown, C.M. Calibration approaches for distributed hydrologic models in poorly gaged basins: Implication for streamflow projections under climate change. Hydrol. Earth Syst. Sci. 2015, 19, 857–876. [Google Scholar] [CrossRef]
- Vázquez, R.F. Effect of potential evapotranspiration estimates on effective parameters and performance of the MIKE SHE-code applied to a medium-size catchment. J. Hydrol. 2003, 270, 309–327. [Google Scholar] [CrossRef]
- Alcamo, J.; Döll, P.; Henrichs, T.; Kaspar, F.; Lehner, B.; Rösch, T. Development and testing of the WaterGAP 2 global model of water use and availability. Hydrol. Sci. J. 2003, 48, 317–337. [Google Scholar] [CrossRef]
- Van Der Knijff, J.M.; Younis, J.; De Roo, A.P.J. LISFLOOD: A GIS-based distributed model for river basin scale water balance and flood simulation. Int. J. Geogr. Inf. Sci. 2010, 24, 189–212. [Google Scholar] [CrossRef]
- Yates, D.; Purkey, D.; Sieber, J.; Huber-Lee, A.; Galbraith, H.; West, J.; Herrod-Julius, S.; Young, C.; Joyce, B.; Rayej, M. Climate Driven Water Resources Model of the Sacramento Basin, California. J. Water Resour. Plan. Manag. 2009, 135, 303–313. [Google Scholar] [CrossRef]
- Meenu, R.; Rehana, S.; Mujumdar, P.P. Assessment of hydrologic impacts of climate change in Tunga-Bhadra river basin, India with HEC-HMS and SDSM. Hydrol. Process. 2013, 27, 1572–1589. [Google Scholar] [CrossRef]
- Allen, R.; Pereira, L.; Raes, D.; Smith, M. Crop Evapotranspiration - Guidelines for Computing Crop Water Requirements; FAO: Rome, Italy, 1998. [Google Scholar]
- Kiniry, J.R.; Macdonald, J.D.; Kemanian, A.R.; Watson, B.; Putz, G.; Prepas, E.E. Plant growth simulation for landscape-scale hydrological modelling. Hydrol. Sci. J. 2008, 53, 1030–1042. [Google Scholar] [CrossRef]
- Strauch, M.; Volk, M. SWAT plant growth modification for improved modeling of perennial vegetation in the tropics. Ecol. Modell. 2013, 269, 98–112. [Google Scholar] [CrossRef]
- Luo, Y.; He, C.; Sophocleous, M.; Yin, Z.; Hongrui, R.; Ouyang, Z. Assessment of crop growth and soil water modules in SWAT2000 using extensive field experiment data in an irrigation district of the Yellow River Basin. J. Hydrol. 2008, 352, 139–156. [Google Scholar] [CrossRef]
- Van Griensven, A.; Ndomba, P.; Yalew, S.; Kilonzo, F. Critical review of SWAT applications in the upper Nile basin countries. Hydrol. Earth Syst. Sci. 2012, 16, 3371–3381. [Google Scholar] [CrossRef]
- Simons, G.; Bastiaanssen, W.; Ngô, L.; Hain, C.; Anderson, M.; Senay, G. Integrating Global Satellite-Derived Data Products as a Pre-Analysis for Hydrological Modelling Studies: A Case Study for the Red River Basin. Remote Sens. 2016, 8, 279. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Saadi, S.; Simonneaux, V.; Boulet, G.; Raimbault, B.; Mougenot, B.; Fanise, P.; Ayari, H.; Lili-Chabaane, Z. Monitoring Irrigation Consumption Using High Resolution NDVI Image Time Series: Calibration and Validation in the Kairouan Plain (Tunisia). Remote Sens. 2015, 7, 13005–13028. [Google Scholar] [CrossRef]
- Amri, R.; Zribi, M.; Lili-Chabaane, Z.; Szczypta, C.; Calvet, J.; Boulet, G. FAO-56 Dual Model Combined with Multi-Sensor Remote Sensing for Regional Evapotranspiration Estimations. Remote Sens. 2014, 6, 5387–5406. [Google Scholar] [CrossRef]
- Er-Raki, S.; Chehbouni, A.; Duchemin, B. Combining Satellite Remote Sensing Data with the FAO-56 Dual Approach for Water Use Mapping in Irrigated Wheat Fields of a Semi-Arid Region. Remote Sens. 2010, 2, 375–387. [Google Scholar] [CrossRef]
- Johnson, L.F.; Trout, T.J. Satellite NDVI Assisted Monitoring of Vegetable Crop Evapotranspiration in California’s San Joaquin Valley. Remote Sens. 2012, 4, 439–455. [Google Scholar] [CrossRef]
- Teixeira, A.H.C. Determining Regional Actual Evapotranspiration of Irrigated Crops and Natural Vegetation in the São Francisco River Basin (Brazil) Using Remote Sensing and Penman-Monteith Equation. Remote Sens. 2010, 2, 1287–1319. [Google Scholar] [CrossRef]
- Hunink, J.E.; Contreras, S.; Soto-García, M.; Martin-Gorriz, B.; Martinez-Álvarez, V.; Baille, A. Estimating groundwater use patterns of perennial and seasonal crops in a Mediterranean irrigation scheme, using remote sensing. Agric. Water Manag. 2015, 162, 47–56. [Google Scholar] [CrossRef]
- Pôças, I.; Paço, T.; Paredes, P.; Cunha, M.; Pereira, L. Estimation of Actual Crop Coefficients Using Remotely Sensed Vegetation Indices and Soil Water Balance Modelled Data. Remote Sens. 2015, 7, 2373–2400. [Google Scholar] [CrossRef]
- Maselli, F.; Papale, D.; Chiesi, M.; Matteucci, G.; Angeli, L.; Raschi, A.; Seufert, G. Operational monitoring of daily evapotranspiration by the combination of MODIS NDVI and ground meteorological data: Application and evaluation in Central Italy. Remote Sens. Environ. 2014, 152, 279–290. [Google Scholar] [CrossRef]
- Le Page, M.; Berjamy, B.; Fakir, Y.; Bourgin, F.; Jarlan, L.; Abourida, A.; Benrhanem, M.; Jacob, G.; Huber, M.; Sghrer, F.; Simonneaux, V.; Chehbouni, G. An Integrated DSS for Groundwater Management Based on Remote Sensing. The Case of a Semi-arid Aquifer in Morocco. Water Resour. Manag. 2012, 26, 3209–3230. [Google Scholar] [CrossRef]
- Milella, P.; Bisantino, T.; Gentile, F.; Iacobellis, V.; Trisorio Liuzzi, G. Diagnostic analysis of distributed input and parameter datasets in Mediterranean basin streamflow modeling. J. Hydrol. 2012, 472, 262–276. [Google Scholar] [CrossRef]
- Fatichi, S.; Vivoni, E.R.; Ogden, F.L.; Ivanov, V.Y.; Mirus, B.; Gochis, D.; Downer, C.W.; Camporese, M.; Davison, J.H.; Ebel, B.; et al. An overview of current applications, challenges, and future trends in distributed process-based models in hydrology. J. Hydrol. 2016, 537, 45–60. [Google Scholar] [CrossRef]
- Knoche, M.; Fischer, C.; Pohl, E.; Krause, P.; Merz, R. Combined uncertainty of hydrological model complexity and satellite-based forcing data evaluated in two data-scarce semi-arid catchments in Ethiopia. J. Hydrol. 2014, 519, 2049–2066. [Google Scholar] [CrossRef]
- Spies, R.R.; Franz, K.J.; Hogue, T.S.; Bowman, A.L. Distributed Hydrologic Modeling Using Satellite-Derived Potential Evapotranspiration. J. Hydrometeorol. 2015, 16, 129–146. [Google Scholar] [CrossRef]
- Blöschl, G.; Sivapalan, M.; Wagener, T.; Viglione, A.; Savenije, H. Runoff Prediction in Ungauged Basins: Synthesis Across Processes, Places and Scales; Cambridge University Press: Cambridge University, Cambridge, UK, 2013; Volume 95. [Google Scholar]
- Kunnath-Poovakka, A.; Ryu, D.; Renzullo, L.J.; George, B. The efficacy of calibrating hydrologic model using remotely sensed evapotranspiration and soil moisture for streamflow prediction. J. Hydrol. 2016, 535, 509–524. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Droogers, P. Calibration of a distributed hydrological model based on satellite evapotranspiration. J. Hydrol. 2008, 349, 411–424. [Google Scholar] [CrossRef]
- Demirel, M.C.; González, G.M.; Mai, J.; Stisen, S. Calibration of a distributed hydrologic model using observed spatial patterns from MODIS data. In Proceedings of EGU General Assembly Conference, Vienna, Austria, 17–22 April 2016.
- Rientjes, T.H.M.; Muthuwatta, L.P.; Bos, M.G.; Booij, M.J.; Bhatti, H.A. Multi-variable calibration of a semi-distributed hydrological model using streamflow data and satellite-based evapotranspiration. J. Hydrol. 2013, 505, 276–290. [Google Scholar] [CrossRef]
- Boegh, E.; Thorsen, M.; Butts, M.; Hansen, S.; Christiansen, J.; Abrahamsen, P.; Hasager, C.; Jensen, N.; van der Keur, P.; Refsgaard, J.; et al. Incorporating remote sensing data in physically based distributed agro-hydrological modelling. J. Hydrol. 2004, 287, 279–299. [Google Scholar] [CrossRef]
- Chen, J.M.; Chen, X.; Ju, W.; Geng, X. Distributed hydrological model for mapping evapotranspiration using remote sensing inputs. J. Hydrol. 2005, 305, 15–39. [Google Scholar] [CrossRef]
- Stisen, S.; Jensen, K.H.; Sandholt, I.; Grimes, D.I.F. A remote sensing driven distributed hydrological model of the Senegal River basin. J. Hydrol. 2008, 354, 131–148. [Google Scholar] [CrossRef]
- González-Dugo, M.P.; Escuin, S.; Cano, F.; Cifuentes, V.; Padilla, F.L.M.; Tirado, J.L.; Oyonarte, N.; Fernández, P.; Mateos, L. Monitoring evapotranspiration of irrigated crops using crop coefficients derived from time series of satellite images. II. Application on basin scale. Agric. Water Manag. 2013, 125, 92–104. [Google Scholar] [CrossRef]
- Contreras, S.; Alcaraz-Segura, D.; Scanlon, B.; Jobbágy, E.G. Detecting ecosytem reliance on groundwater based on satellite-derived greenness anomalies and temporal dynamics. In Earth Observation of Ecosystem Services; Alcaraz-Segura, D., di Bella, C.M., Straschnoy, J.V., Eds.; CRC Press: Boca Raton, FL, USA, 2013; pp. 283–302. [Google Scholar]
- Contreras, S.; Jobbágy, E.G.; Villagra, P.E.; Nosetto, M.D.; Puigdefábregas, J. Remote sensing estimates of supplementary water consumption by arid ecosystems of central Argentina. J. Hydrol. 2011, 397, 10–22. [Google Scholar] [CrossRef]
- Pereira, L.S.; Allen, R.G.; Smith, M.; Raes, D. Crop evapotranspiration estimation with FAO56: Past and future. Agric. Water Manag. 2015, 147, 4–20. [Google Scholar] [CrossRef]
- Terink, W.; Lutz, A.F.; Simons, G.W.H.; Immerzeel, W.W.; Droogers, P. SPHY v2.0: Spatial Processes in HYdrology. Geosci. Model Dev. 2015, 8, 2009–2034. [Google Scholar] [CrossRef]
- Lutz, A.F.; Immerzeel, W.W.; Shrestha, A.B.; Bierkens, M.F.P. Consistent increase in High Asia’s runoff due to increasing glacier melt and precipitation. Nat. Clim. Chang. 2014, 4, 587–592. [Google Scholar] [CrossRef]
- Corine Land Cover (CLC). Database. Available online: http://www.eea.europa.eu/data-and-maps/data/clc-2006-vector-data-version-3 (accessed on 4 November 2016).
- LUCDEME Soil Dataset, Spain. Available online: http://www.mapama.gob.es/es/desarrollo-rural/temas/politica-forestal/desertificacion-restauracion-forestal/lucha-contra-la-desertificacion/lch_lucdeme.aspx (accessed on 4 November 2016).
- MAGNA-IGME Geological Maps, Spain. Available online: http://info.igme.es/cartografia/magna50.asp (accessed on 4 November 2016).
- Saxton, K.E.; Rawls, W.J. Soil water characteristic estimates by texture and organic matter for hydrologic solutions. Soil Sci. Soc. Am. J. 2006, 70, 1569–1578. [Google Scholar] [CrossRef]
- Ninyerola, M.; Pons, X.; Roure, J.M. Atlas Climático Digital de la Península Ibérica. Metodología y Aplicaciones en Bioclimatología y Geobotánica; Bellaterra: Barcelona, Spain, 2005. [Google Scholar]
- Senay, G.B.; Leake, S.; Nagler, P.L.; Artan, G.; Dickinson, J.; Cordova, J.T.; Glenn, E.P. Estimating basin scale evapotranspiration (ET) by water balance and remote sensing methods. Hydrol. Process. 2011, 25, 4037–4049. [Google Scholar] [CrossRef]
- Glenn, E.P.; Neale, C.M.U.; Hunsaker, D.J.; Nagler, P.L. Vegetation index-based crop coefficients to estimate evapotranspiration by remote sensing in agricultural and natural ecosystems. Hydrol. Process. 2011, 25, 4050–4062. [Google Scholar] [CrossRef]
- Mutiibwa, D.; Irmak, S. AVHRR-NDVI-based crop coefficients for analyzing long-term trends in evapotranspiration in relation to changing climate in the U.S. High Plains. Water Resour. Res. 2013, 49, 231–244. [Google Scholar] [CrossRef]
- Kamble, B.; Irmak, A.; Hubbard, K. Estimating Crop Coefficients Using Remote Sensing-Based Vegetation Index. Remote Sens. 2013, 5, 1588–1602. [Google Scholar] [CrossRef]
- Arnell, N. A simple water balance model for the simulation of streamflow over a large geographic domain. J. Hydrol. 1999, 217, 314–335. [Google Scholar] [CrossRef]
- Doherty, J.; Brebber, L.; Whyte, P. PEST: Model-independent parameter estimation. Watermark Comput. Corinda Aust. 1994, 122. [Google Scholar]
- Conradt, T.; Koch, H.; Hattermann, F.F.; Wechsung, F. Precipitation or evapotranspiration? Bayesian analysis of potential error sources in the simulation of sub-basin discharges in the Czech Elbe River basin. Reg. Environ. Chang. 2012, 12, 649–661. [Google Scholar] [CrossRef]
- Mascaro, G.; Vivoni, E.R.; Méndez-Barroso, L.A. Hyperresolution hydrologic modeling in a regional watershed and its interpretation using empirical orthogonal functions. Adv. Water Resour. 2015, 83, 190–206. [Google Scholar] [CrossRef]
- Donohue, R.J.; Roderick, M.L.; McVicar, T.R. On the importance of including vegetation dynamics in Budyko’s hydrological model. Hydrol. Earth Syst. Sci. 2007, 11, 983–995. [Google Scholar] [CrossRef]
- Hunink, J.E.; Niadas, I.A.; Antonaropoulos, P.; Droogers, P.; de Vente, J. Targeting of intervention areas to reduce reservoir sedimentation in the Tana catchment (Kenya) using SWAT. Hydrol. Sci. J. 2013, 58, 600–614. [Google Scholar] [CrossRef]
- Robles-Morua, A.; Vivoni, E.R.; Mayer, A.S. Distributed Hydrologic Modeling in Northwest Mexico Reveals the Links between Runoff Mechanisms and Evapotranspiration. J. Hydrometeorol. 2012, 13, 785–807. [Google Scholar] [CrossRef]
- Guse, B.; Pfannerstill, M.; Strauch, M.; Reusser, D.E.; Lüdtke, S.; Volk, M.; Gupta, H.; Fohrer, N. On characterizing the temporal dominance patterns of model parameters and processes. Hydrol. Process. 2016, 30, 2255–2270. [Google Scholar] [CrossRef]
- Rees, W.G. Comparing the spatial content of thematic maps. Int. J. Remote Sens. 2008, 29, 3833–3844. [Google Scholar] [CrossRef]
- Koch, J.; Jensen, K.H.; Stisen, S. Toward a true spatial model evaluation in distributed hydrological modeling: Kappa statistics, Fuzzy theory, and EOF-analysis benchmarked by the human perception and evaluated against a modeling case study. Water Resour. Res. 2015, 51, 1225–1246. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).