Next Article in Journal
Topology Adaptive Water Boundary Extraction Based on a Modified Balloon Snake: Using GF-1 Satellite Images as an Example
Previous Article in Journal
The Highest Gradient Model: A New Method for Analytical Assessment of the Efficiency of LiDAR-Derived Visualization Techniques for Landform Detection and Mapping
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 9
Issue 2
10.3390/rs9020144
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

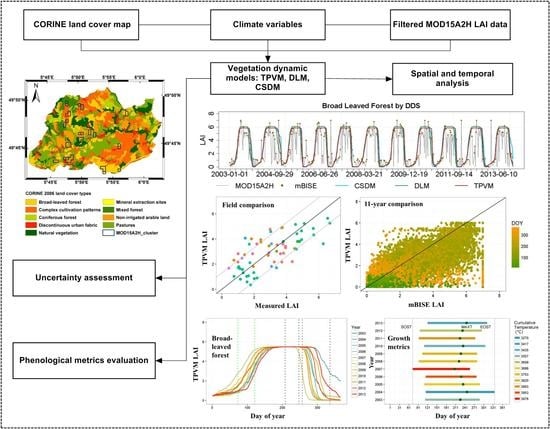
Spatio-Temporal LAI Modelling by Integrating Climate and MODIS LAI Data in a Mesoscale Catchment

by
Liya Sun
1,2,* and
Karsten Schulz
2
1
Department of Geography, LMU München, 80333 München, Germany
2
Institute for Water Management, Hydrology and Hydraulic Engineering (IWHW), University of Natural Resources and Life Sciences (BOKU) Vienna, 1190 Vienna, Austria
*
Author to whom correspondence should be addressed.
Remote Sens. 2017, 9(2), 144; https://doi.org/10.3390/rs9020144
Submission received: 27 June 2016 / Revised: 23 January 2017 / Accepted: 25 January 2017 / Published: 10 February 2017
Browse Figures
Versions Notes

Abstract

:
Vegetation is often represented by the leaf area index (LAI) in many ecological, hydrological and meteorological land surface models. However, the spatio-temporal dynamics of the vegetation are important to represent in these models. While the widely applied methods, such as the Canopy Structure Dynamic Model (CSDM) and the Double Logistic Model (DLM) are solely based on cumulative daily mean temperature data as input, a new spatio-temporal LAI prediction model referred to as the Temperature Precipitation Vegetation Model (TPVM) is developed that also considers cumulative precipitation data as input into the modelling process. TPVM as well as CDSM and DLM model performances are compared and evaluated against filtered LAI data from the Moderate Resolution Imaging Spectroradiometer (MODIS). The calibration/validation results of a cross-validation performed in the meso-scale Attert catchment in Luxembourg indicated that the DLM and TPVM generally provided more realistic and accurate LAI data. The TPVM performed superiorly for the agricultural land cover types compared to the other two models, which only used the temperature data. The Pearson’s correlation coefficient (CC) between TPVM and the field measurement is 0.78, compared to 0.73 and 0.69 for the DLM and CSDM, respectively. The phenological metrics were derived from the TPVM model to investigate the interaction between the climate variables and the LAI variations. These interactions illustrated the dominant control of temperature on the LAI dynamics for deciduous forest cover, and a combined influence of temperature with precipitation for the agricultural land use areas.

Graphical Abstract

1. Introduction

Vegetation dynamics have been studied for a long time to understand their functioning in the terrestrial ecosystems, including land cover and land use change assessment, land surface process research, hydrological or climate change modelling and prediction [1,2,3]. Vegetation dynamics can reflect many climatic factors, including the temperature, precipitation, length of sun time, humidity and water use [4,5,6]. Leaf Area Index (LAI) is a dimensionless canopy indicator, which was defined by Watson [7] as the total one-sided area of leaf tissue per unit ground surface area. It is a key measure for evapotranspiration and photosynthesis models by reflecting the radiation absorption and turbulent transfers between vegetation and the atmosphere [8]. Moreover, the LAI of vegetation serves as an important state parameter in the eco-hydrological models, such as the Soil-Vegetation-Atmosphere Transfer (SVAT), Surface Energy Balance (SEB), and Global Climate Models (GCM) [9]. The water interception amount and vegetation storage capacity were found to be directly related with the LAI depending on the vegetation type and the phenological stage [10]. The changing LAI modifies the surface water and energy budget which in turn affects the biochemical and hydrological cycles [11]. Therefore, accurate estimation of continuous LAI for the various land cover types has pronounced significance in the land surface modelling.
The seasonal dynamics of LAI respond differently to climate changes depending on the land cover types. The seasonality can also be referred to the vegetation phenology, which can provide valuable information about the interaction between climate change, the ecosystem and temporal scales (e.g., intra- and interannual) [12,13,14], which again are closely linked to climate variability and hydrological processes at different spatial scales [15,16,17]. The key factors controlling the vegetation phenology are similar to those influencing vegetation dynamics and include air temperature, soil temperature, and water availability [18,19,20,21].
Traditional in situ observations of phenological events include the national phenological networks, global student observations [22] and phenological gardens, which can provide detailed and realistic timing data. However, ground-based observations are time consuming and cost expensive. With the advances of computer science and the concern for global warming, more efforts have been made in phenological model development. For the past decades, these efforts range from examining the controls of environmental factors, biological processes, and intrinsic traits [23,24] on phenology, modelling techniques [25,26,27], to ecosystem-level and evolutionary consequences of phenological changes [28,29].
In 1735, Reaumur proposed the most important assumption in the plant phenology modelling [20]: differences between years and locations in the date of phenological events could be explained by differences in daily temperatures from an arbitrary date to the date of the phenological event considered. Schwartz et al. [2] employed a regression model to test the significance and estimate the magnitude of changes in the relationship between thickness-maximum temperatures relative to first leaf date. Chuine et al. [30] proposed several phenological models in the ecosystem research such as the Spring Warming Model, SeqSpar Model, or SparSar Model. The onset models assume that budburst occurs when a critical state of forcing temperature is reached, the state of forcing being the sum of the daily rate of forcing, which is solely a function of temperature. Chuine [31] also pointed out that the empirical and bioclimatic models should be species specific and calibrated at local scales.
Since the 1980s, remote sensing techniques with low-cost and good temporal availability have been frequently used for the repetitive monitoring of vegetation dynamics and plant phenology modelling [32,33,34]. Measured by the remote sensors, the characteristics of vegetation dynamics are usually represented by vegetative indicators (VIs). The most frequently used indices include the normalized difference vegetation index (NDVI), enhanced vegetation index (EVI), and the fraction of absorbed photosynthetically active radiation (FPAR). These VI variables normally serve as proxies for the estimation of canopy state variables to characterize the status of plant growth [35].
Time series of VIs as derived from satellite images support researchers in studying the phenological events across different scales [1,36,37,38]. The contamination of satellite images by cloud or snow cover as well as the instability of data processing algorithms are main reasons for the significant discontinuities contained in remotely sensed VI products [39,40] which need to be smoothed before application in the modelling process. White et al. [1] utilized the Best Index Slope Extraction (BISE) to smooth the daily Advanced Very High-Resolution Radiometer (AVHRR) NDVI data and to detect the phenological events with predictive phenology models. They concluded that these predictive phenology models could potentially be applied in large-scale biogeochemical models and for monitoring vegetation response to inter-annual climatic variability. Schwartz et al. [2] compared the start-of-season dates from the AVHRR data using different models and affirmed that the integrated satellite start-of-season with other regional phenology models offer considerable capabilities at the continental-scale monitoring of the spring onset. Zhang et al. [41] proposed a series of piecewise logistic functions to fit the satellite-derived VI data and demonstrated the successful model application with Moderate Resolution Imaging Spectroradiometer (MODIS) data in vegetation phenology monitoring over the United States. Moreover, other well-known functions applied in this context include the Savitzky–Golay filter, the asymmetric Gaussian, double logistic functions (DL) [42], and the curve-fit methodology [36].
Previous LAI prediction models using the remote sensing data range from the reflectance model to the relationship between NDVI and LAI. Fang et al. [43] estimated the LAI data using a radiative transfer model by applying generic algorithms and got the best R2 as 0.776. Houborg and Boegh [44] retrieved the LAI data using the reflectance data with inverse and forward canopy reflectance models and obtained the reliable quantitative estimates of LAI with an overall root mean square deviation of 0.74. Koetz et al. [34] integrated the canopy structure dynamics and radiative transfer models to simulate the LAI data using the air temperature and reflectance data with an average R2 of 0.663. As the integration between climate variables and remote sensing data, temperature as a climate control for phenology has been studied for a long time [19,45]. However, less emphasis has been given to study the effect of precipitation when modelling vegetation dynamics. Riha et al. [45] reported that the air temperature and precipitation are the major driving variables for crop simulation models, and these models implicitly respond to the changes in both, average temperature and precipitation. Kramer et al. [19] recommended that the seasonality of climatic drivers affecting the phenological aspects of trees should be developed and carefully tested within phenological models.
Embedded in the German Research Foundation project CAOS (“Catchments as Organised Systems”) [46,47], the main objective of this study is to develop a simple spatio-temporal LAI model, which could provide the spatially distributed and temporally continuous LAI data for the Attert Catchment. Here, a new model “temperature-precipitation vegetation dynamic model” (TPVM) was developed. Besides, the double logistic model (DLM) and the canopy structure dynamic model (CSDM) based on the cumulative temperature, data were also implemented for comparison. Furthermore, the phenological metrics were derived from the time series of modelled LAI data and were analysed for the seasonal patterns. The detailed abbreviations and definitions used in the paper are listed in Table 1.

2. Study Area and Data Sources

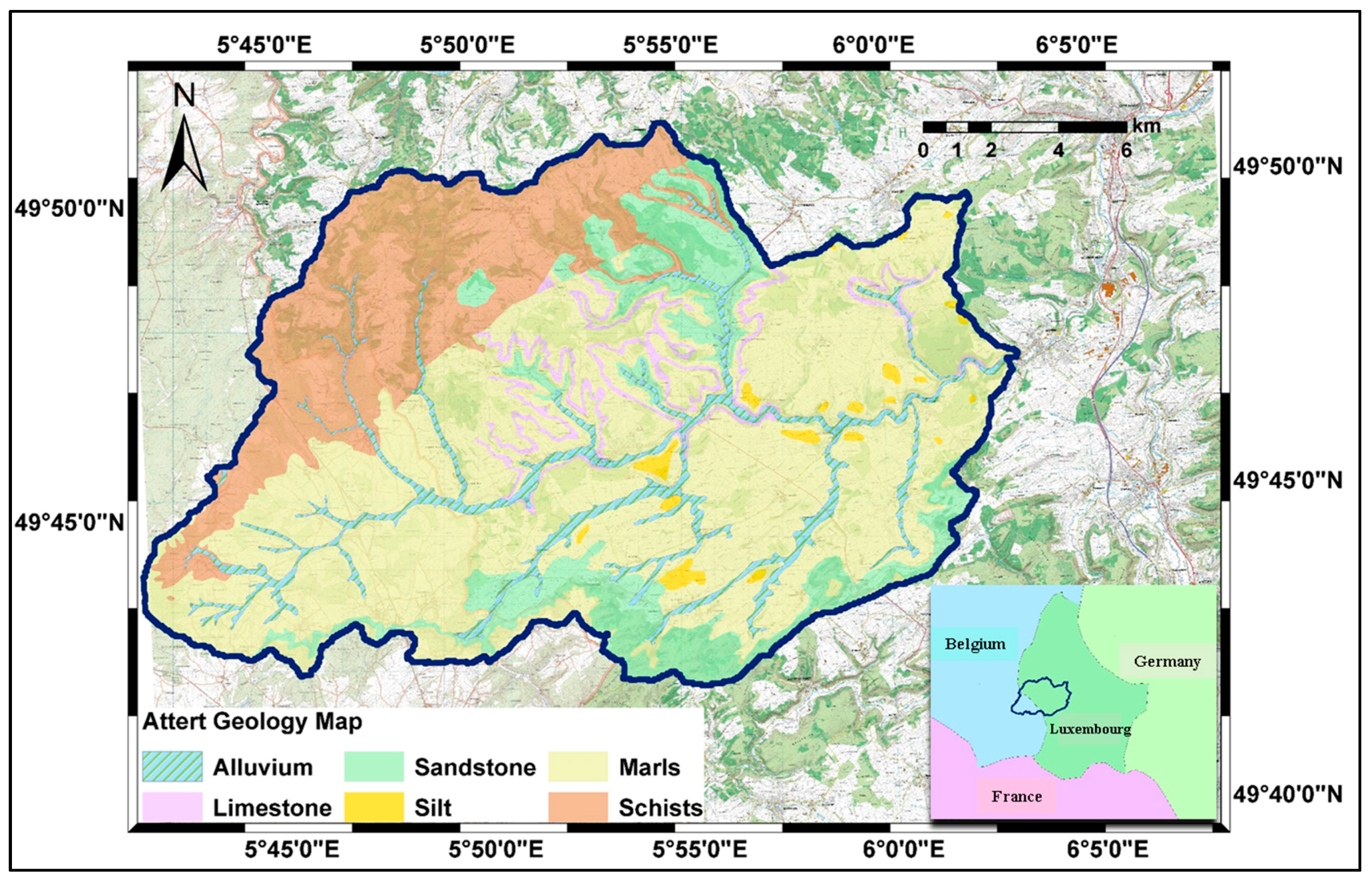
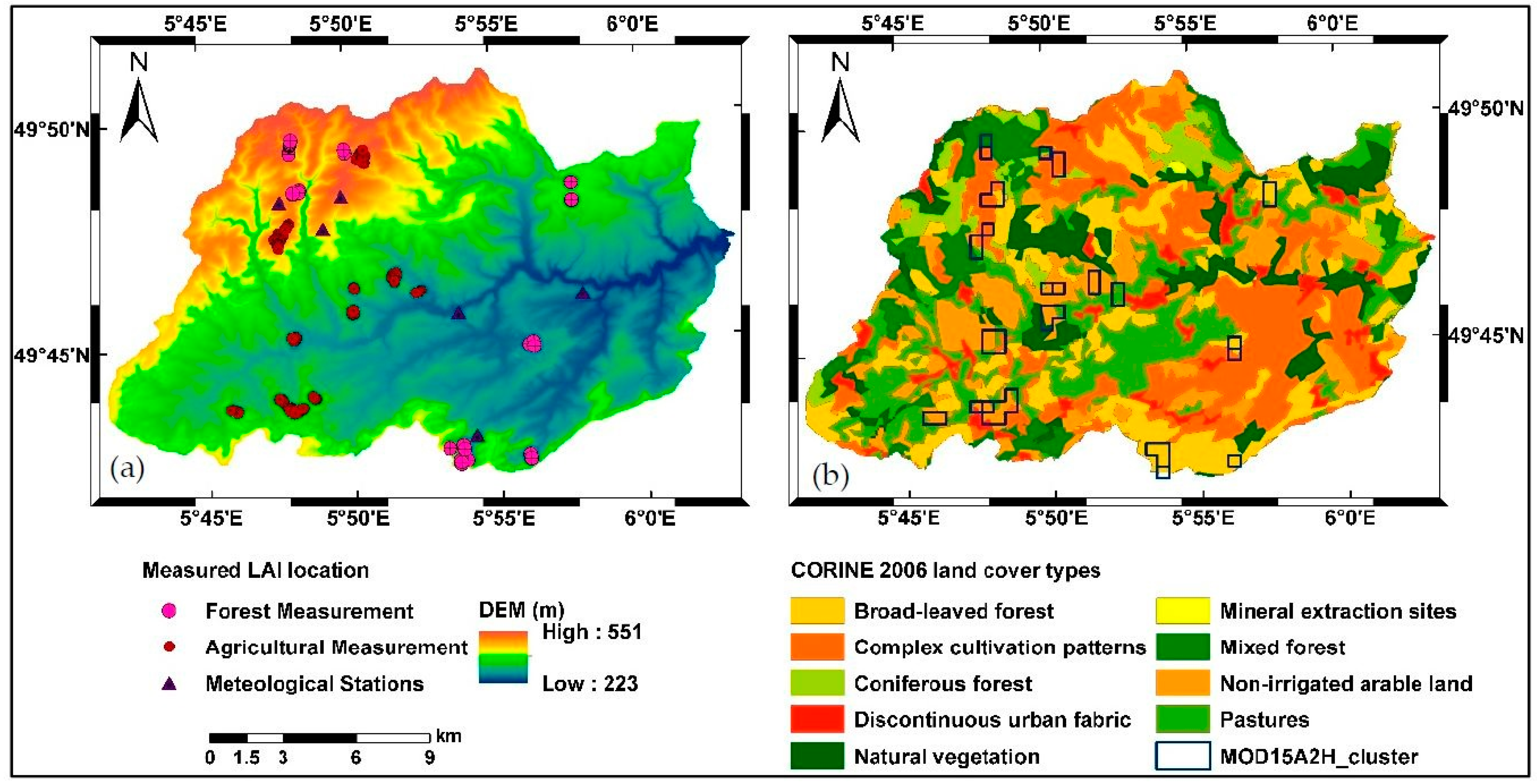
2.1. Study Area

The Attert catchment as the main test site is located in the midwestern part of the Grand Duchy of Luxembourg and partially in Belgium (Figure 1). The catchment covers a total area of 288 km2. As shown in Figure 1, the catchment has very distinct geologies with a large area of marls, schists and small proportions of sandstones. Correspondingly, most of the dense deciduous and coniferous forests distribute at the northwest part of the schist area and the southeast sandstone areas. The spacious pasture and croplands locate at the middle of the marls area and sparse residential areas spread along the alluvium. With a temperate climate, the mean monthly temperatures reach a maximum of about 18 °C in July and a minimum of 0 °C in January. The mean annual precipitation is about 850 mm (1971–2000) [48] characterized by the high summer evapotranspiration from July to September (Figure 2). According to the CORINE (CoORdination of INformation on the Environment) land cover map in 2006 (Figure 3), the agricultural area takes up 65% and forest accounts for about 30% of the catchment. The elevation of the Attert basin ranges from 238 m to 539 m and the digital elevation map (DEM) is shown in Figure 3.

2.2. Data Sources

2.2.1. MODIS LAI Product

In the MOD15A2H product, the LAI of broadleaf canopy is defined as the one-sided green leaf area per unit ground area in broadleaf canopies and as one-half the total needle surface area per unit ground area in coniferous canopy. The MOD15A2H version 6 Level 4 LAI product is provided by the Land Processes Distributed Active Archive Center (LP DAAC) managed by the NASA Earth Science Data and Information System (ESDIS) project [49]. The 8-day composite dataset together with the quality criteria (QC) layer are retrieved from the Terra MODIS platform with a 500 m pixel size.
The processing algorithm of the MOD15A2H LAI product includes a main Look-up-Table (LUT) and a back-up algorithm. The LUT is generated from the spectral information content of MODIS red and near-infrared surface reflectance by utilizing the 3D radiative transfer equation [50]. The back-up algorithm uses empirical relationships between NDVI and canopy LAI, and FPAR. When the LUT method fails, the back-up method is utilized. Then, according to the data quality, the algorithm chooses the “best” pixel available from all the acquisitions of the Terra sensor from within the 8-day period [51].
Horn and Schulz [52] analysed and compared the MODIS LAI products with different quality criteria from both the Terra and Aqua platform. They suggest that QC filtering should not be applied for the times series of MODIS LAI products and it would be advantageous to make use of all pixels from the subset [52]. Following these recommendations, all product pixel values were kept to maximize the number of retrievals. However, due to noise in the data, data filtering had to be performed before further processing. The modified best index slope extraction (mBISE) method [53] was utilized in this study for the noise filtering. The mBISE method filters the noise by using a 24-day (3 image) sliding window and sets the threshold of local gradient of the spurious spikes as 0.1. From the first point of the time series, the algorithm searches forward accepting the points when their value is greater than the preceding one but the increase should be less than a pre-defined threshold. If the point decreases over the 24-day sliding window, the search continues and it will only be accepted if it is followed by a consistent increase similar to the regrowth. The filtered data were linearly interpolated to derive continuous LAI datasets, which are considered as spatially and temporally distributed LAI observation/reference data in the following.

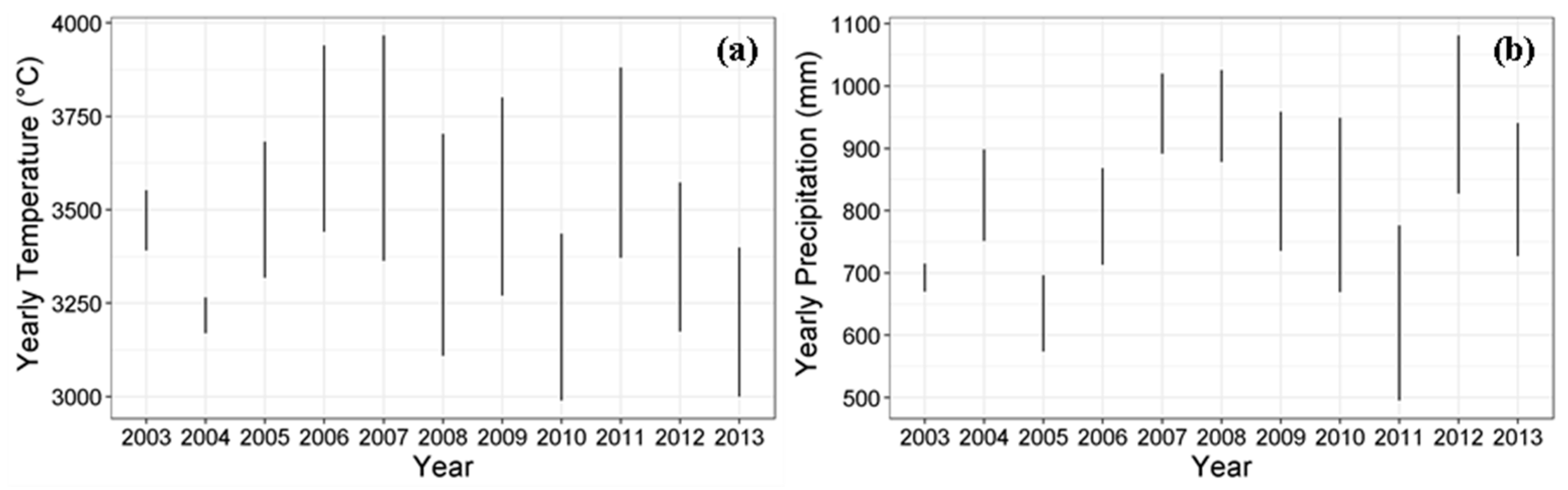
2.2.2. Climate Data

Within our LAI modelling framework, we aim at predicting the daily gridded LAI data with a 500-m spatial resolution. The input variables of the model system include cumulated daily mean temperatures and daily sums of precipitation that are required at the same spatial extent as the LAI data are provided. The temperature and precipitation datasets were obtained from the metrological stations located in the Attert Catchment. The 2-m air temperature data were interpolated from four meteorological stations and the precipitation data were interpolated from six meteorological stations. Due to the few number of the available meteorological stations, simple Thiessen Polygons are used to interpolate the climate data into the 500-m grid. Table 2 and Figure 2 give the range of yearly cumulative temperature and precipitation data from 2003 to 2013. The locations of the meteorological stations are indicated in Figure 3.

2.2.3. Land Cover Maps

The reference land cover map in 2006 was accessed from the CORINE program. CORINE 2006 was created with the joint efforts of about 38 countries in Europe and was published by the European Environment Agency. In this study, Level-3 of the CORINE map was used, identifying nine types of land cover in the Attert catchment, including broad-leaved forest, complex cultivation patterns, coniferous forest, discontinuous urban fabric, land principally occupied by agriculture with significant areas of natural vegetation (hereafter named as natural vegetation), very small area of mineral extraction sites, mixed forest, non-irrigated arable land, and pasture. The artificial areas including the discontinuous urban fabric and mineral extraction sites were ignored. Figure 3 presents the distribution map of land cover types in the Attert Catchment.

2.2.4. Field LAI Measurement

The ground truth LAI measurements were conducted for two main land cover types, forest and agricultural areas. All the field measurements used the LI-COR LAI-2200 Plant Canopy Analyzer and analysed using the FV-2200 software [54]. The LAI-2200 and software calculate the LAI values as well as the apparent clumping factor, mean tilt angle, and other LAI statistics directly from light measurements made with a “fish-eye” optical sensor. Above and below measurements are taken to calculate canopy light interception. The measurement can be further processed with the FV-2200 software for row crops. The forest plots were mainly measured with the 90° view cap at sunset during two periods including the summer (foliated in August 2012, May 2014 and September 2014) and the winter (defoliated in March 2014). Two LAI-2200 devices were used for measuring the above and below readings of the forest separately. The above readings were automatically measured outside the forest with clear view, and the below readings were measured inside the forest with the 90° view cap. The measurement plots were 20 m × 20 m in size and one below reading was taken every 4 m resulting in a total of 36 measurements for each plot from where the mean LAI was calculated. For the agricultural areas, the measurements were mainly conducted with a 180° view cap in cloudy conditions or with an umbrella under sunny conditions to avoid the direct sunlight. In the row crop area, one above and four below readings were taken for one row and at least four to six rows were measured in one plot. The distribution of measurement clusters and the corresponding MOD15A2H pixels can found in Figure 3. The agricultural lands were measured during 22–26 July 2013 and mainly consist of corn, wheat, barley, grassland, rapeseeds, triticale, and small areas of oat. Besides, grassland and corn were measured for three times on 23 July, 11 August and 9 September, 2013 respectively.
In this study, in situ LAI measurements are used for comparison with the LAI model predictions. Due to the spatial resolution mismatch between the plot measurement and the 500-m grid of the MODIS data, the measured LAI values were averaged for each corresponding pixel of the MOD15A2H map. Therefore, 46 plots of forest were aggregated to 22 pixels and 195 plots of agricultural areas were averaged to 42 pixels. In the following, all the LAI measurements were compared with modelled LAI data at the same date. Due to the lack of climate observation data in 2014 and the relatively stable state of deciduous trees during fully leaf-off or leaf-on stages, we took the modelled data in 2013 to compare with the field LAI measurement in 2014.

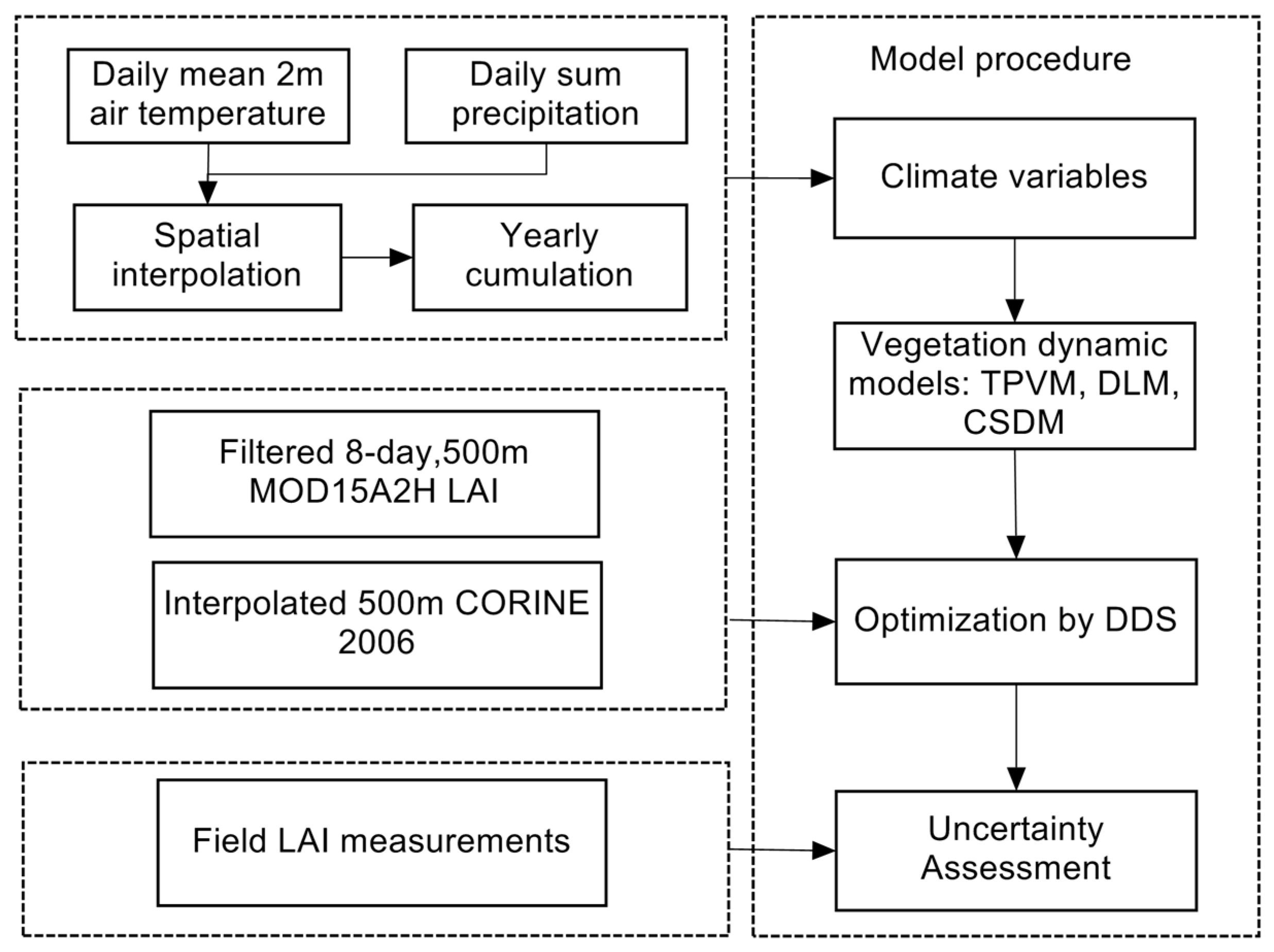
3. Methodology

The main processing steps in this work include the above-mentioned data source preprocessing, model development, model optimization and uncertainty assessment with field measurements. Figure 4 displays the generalized workflow of this paper.

3.1. Model Development

The phenological phases of the plants, such as the budburst, leaf development, flowering and leaf senescence, differ according to vegetation type and the prevailing climate conditions. The general sigmoid structure of the phenological models suppose that the probability of the emergence of a single leaf in a day-of- year (DOY) is normally distributed, therefore the total amount of green cover through time is an accumulation, which is similar to the logistic growth curve [41]. In this sense, the annual leaf area of deciduous vegetation normally shows an exponential rise when the climate factors are satisfied and then reaches a maximum during summer time. After the maturity period, the growth rate is modulated and dominated by the leaf senescence. Then the leaf area declines until all the leaves finally fall down. In contrast, the LAI of coniferous vegetation changes far less over the year.
A new TPVM model is proposed in this study by integrating the observed daily mean air temperature and daily sum precipitation data (Equation (1)). In TPVM, we assume that the annual course of the LAI is not solely controlled by temperature, but rather effected by both temperature and precipitation. When the temperature and precipitation data cumulate to a certain level, the plant leaves start to emerge or disappear. In this study, for each year, the daily cumulative value of the temperature and precipitation were calculated starting from the first DOY (Day 1) to the end DOY (Day 365 or 366). Two other models, the CSDM and DLM, were also considered for comparison. Instead of using DOY as input variables as most of the studies [36], the cumulative temperature data were implemented in the DLM (Equation (2)). In addition, the CSDM model defines the canopy growth and senescence using the cumulative air temperature data shown as Equation (3). The slight difference of the CSDM in this study with the original model is that we add an initial background parameter c to be consistent with the proposed TPVM.
The newly proposed TPVM can be derived by Equation (1):
A I ( T , P ) = L A I A m p ( 1 1 + e α ( T i − T r i ) + ( 1 − α ) ( P i − P r i ) − 1 1 + e α ( T s − T r s ) + ( 1 − α ) ( P s − P r s ) ) + c
The DLM model follows the structure in TIMESAT [55] by Equation (2):
L A I ( T ) = L A I A m p ( 1 1 + e ( T i − T r i ) − 1 1 + e ( T s − T r s ) ) + c
The CSDM model can be calculated by Equation (3):
A I ( T ) = L A I A m p [ 1 1 + e − b ( T − T i ) − e − a ( T − T s ) ] + c
where T is defined as the accumulated daily mean air temperature above 0 °C; P represents the cumulative daily sum precipitation; b is the relative growth rate at the inflexion point expressed as the cumulative temperature Ti; a is the relative growth rate at the senescence point Ts; ri and rs are the rate of change at the flexion points during leaf-on and leaf-off period respectively; LAIAmp indicates the amplitude of maximal leaf area; and c is the background LAI value at the initial background LAI value.

3.2. Optimization

Dynamically dimensioned search (DDS) as proposed by Bryan A. Tolson [56] was adopted as the global optimization method in this study. The simple stochastic DDS algorithm is designed for finding the good global solutions based on heuristic global search algorithm. The only stopping criterion is the user-specified maximum evaluation limit. DDS searches globally from the beginning and becomes a more local search when iteration number approaches the defined maximum number of evaluations. In the DDS algorithm, the calibrating model parameters serve as the decision variables and the varying dimension is the changing number of the model parameter values. The number of dimensions in the neighbourhood is dynamically and probabilistically reduced to a new search neighbourhood and then the global search is adjusted to the local. The algorithm randomly selects the dimensions for perturbations and generates the candidate solutions by perturbing the current solutions within the magnitudes randomly sampled from the standard normal distribution. The scalar neighbourhood size perturbation parameter (r) in DDS is set to 0.2 in this study as recommended by the author [56]. The DDS algorithm converges to the region of the global optimum instead of the precise global optimum.
In this study, we firstly tested the maximum evaluation number of DDS evaluations for the TPVM model and then chose the parameter set with the minimum objective value from all the evaluation results as the optimal solution. While the DDS algorithm is a very effective and easy to implement algorithm, any other local or global optimization algorithm can be applied instead.

3.3. Objective Function and Error Measures

Root mean squared error (RMSE) and mean absolute error (MAE) as given in Equations (4) and (5) were calculated as evaluation criteria in the model assessment. Followed the generalized weighting process [42], the objective function in Equation (6) combines the RMSE with a weighted parameter wi to better fit model results to the upper envelope of the LAI times series of satellite data, thus reducing the effect of discontinues and sudden drops in LAI values caused by cloud impact or retrieval errors. The optimization of the objective function with weight factors is a two-step procedure. Firstly, the weight parameters wi are set equally to 1 for each data point and an optimal model parameterization is calculated. Secondly, the predicted LAI time series with optimal parameters from the first step is compared with the remotely observed LAI. If the remotely observed LAI is below the predicted LAI, the weight parameter value will be adjusted to higher value. In this study, the value is tested starting with 2, and was finally set as 10. The model is optimized again with the new weights and the optimal parameter set is returned as the best solution.
R M S E = ∑ i = 1 n ( f i − y i ) 2 n 2
M A E = 1 n ∑ i = 1 n | f i − y i |
O b j l a i = ∑ i = 1 n ( f i − y i w i ) 2 n 2
where n is the size of the dataset; fi and yi are the predicted and the observed LAI at the point i of the dataset, respectively; wi is the weighted parameter; and Objlai is the objective function for the DDS optimization.

4. Model Results and Evaluation

The three models were tested in a pixel-wise way for the whole catchment. In the following sections, the discussion is based on an evaluation and comparison of the temporal and spatial pattern of modelled LAI and the original MODIS data, as well as the field measurements. Before, we tested different maximum evaluation numbers for the optimal search of DDS.

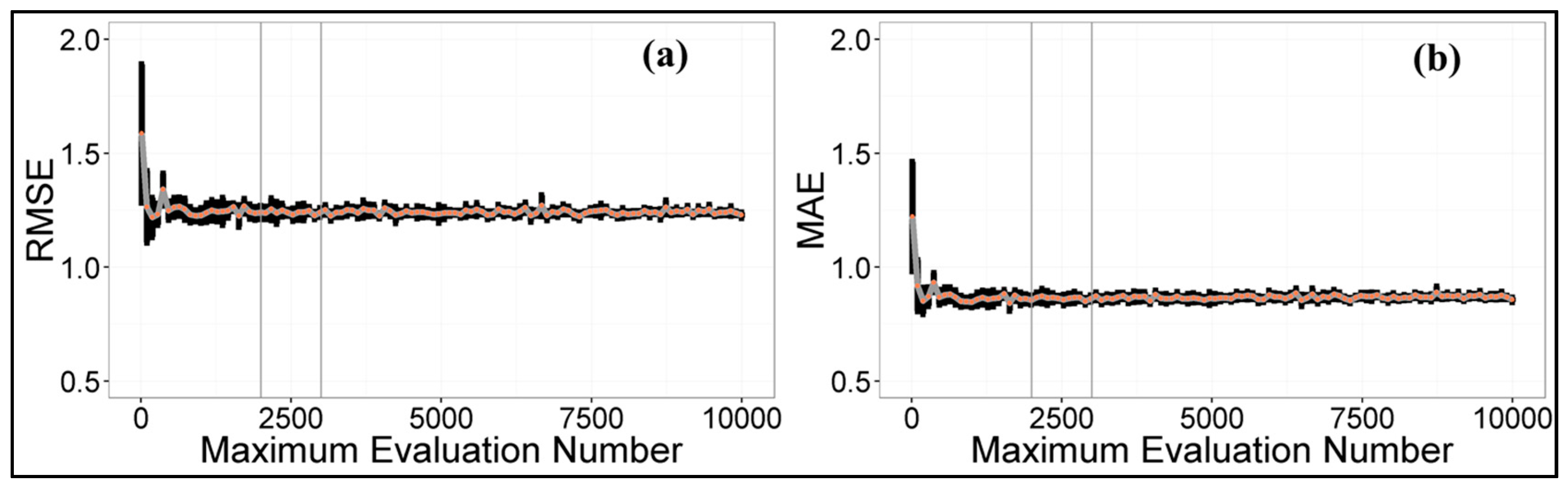
4.1. Maximum Evaluation Number Determination of DDS

As introduced in Section 3, we firstly filter the MODIS LAI products with the mBISE method. Using the cumulative temperature and precipitation data as input, the CSDM, DLM and TPVM models are calibrated/optimized by applying the DDS method. In order to find an appropriate optimal “evaluation number” (the only hyper-parameter in the DDS-method), we tested the performance of the calibration by varying the evaluation number between values of 10 and 10,000 with increments of 90. As the DDS procedure involves random processes, each “evaluation number” test was repeated 10 times. Figure 5 displays the RMSE and MAE variations for each “evaluation number”. The orange points and black error bars represent the mean values and variations, respectively. In Figure 5a,b, we can see that the RMSE and MAE decrease dramatically with the increase of the maximum evaluation number and show stable variance ranges starting with a maximum evaluation number around 2000. Therefore, in this study, we set our evaluation number as 2500 for all the DDS runs.

4.2. Model Results

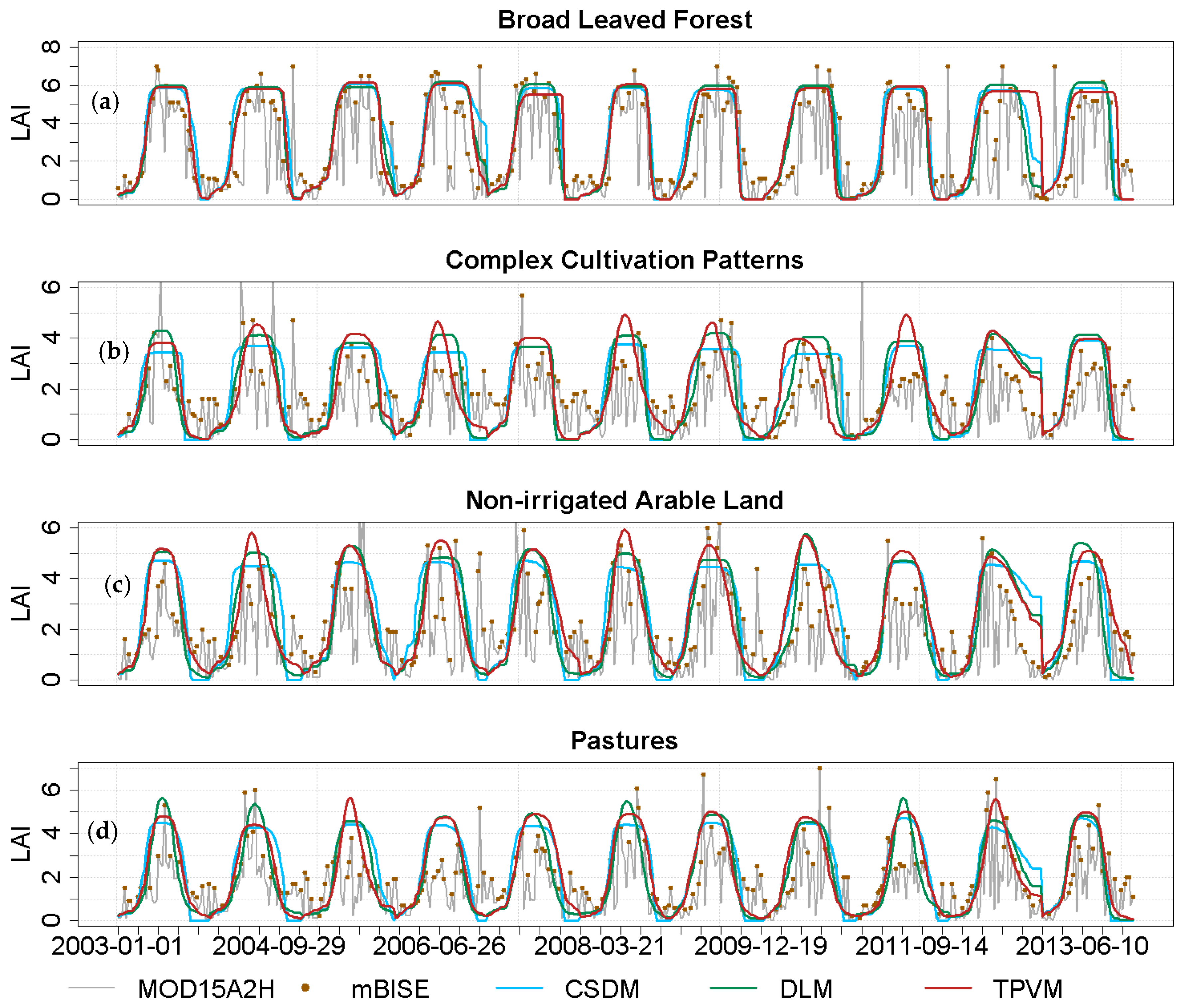
4.2.1. Analysis of Temporal LAI Pattern

Based on their dominance in the catchment, we selected four main land cover types for the following evaluation, including broad-leaved forest, complex cultivation patterns, non-irrigated arable land and pastures. Figure 6 shows the LAI prediction results of selected pixels for each land cover type from 2003 to 2013. The LAI time series of each year were calculated based on the optimal parameter set using the other 10-year’s data for calibration, which is similar to the “Leave-One-Out” cross validation strategy. The red points indicate the mBISE filtered data while the grey lines represent the original MOD15A2H data. The cyan, green and red lines illustrate the modelling results of CSDM, DLM and TPVM, respectively.
As shown in the Figure 6, MODIS data fluctuates frequently with several sudden falls in the time slices, resulting in confusion for the vegetation dynamics interpretation. It is clear to see that the mBISE method effectively accepts the LAI points in the time series using the 0.1 spike threshold within the 24-day sliding window. The sudden decrease of data due to the atmospheric conditions or bidirectional reflectance distribution function effects [57] were avoided in most of the cases and the high value data with more significance over the growth season were well kept. This pre-processing step provided more continuous datasets compared to the original MODIS data and helped significantly in the following modelling process. The modelled LAI datasets generally produce reasonable trajectories and effectively omit the anomalous extreme values.
Especially for the broad-leaved forest, accompanied with the increase of cumulative temperature, the deciduous trees grow up with no leaf-on to the fast emergence of leaves during the green-up season. The three models retrieve very similar patterns at the start of the green-up season and then come to slight differences in the maximum amplitude of LAI among the three models during the maturity period. Besides, the model results also outline the slight inter-annual differences for the broad-leaved forest, for example in the year of 2003, 2005 and 2012. Compared to other land cover types, the broad-leaved forest shows relatively stable growth status. The similar predictions also indicate the dominance role of temperature on the broad-leaved forest.
Dynamic patterns of the agricultural land cover types are more difficult to describe compared to broad-leaved forest. Complex cultivation patterns and non-irrigated arable land in the Attert Catchment are generally cultivated with wheat, barley or corn for one or two seasons. Pastures include the dense, predominantly graminoid grass cover for grazing. Some pasture fodder areas are possibly mechanically harvested several times during the growing season causing pasture LAI values to be more fluctuating than the arable lands. The identified points of complex cultivation patterns, non-irrigated arable land and pasture may contain several spurious spikes, even after mBISE filtering. For the non-irrigated arable land and the complex cultivation patterns, the prediction results for different years vary largely (Figure 6). Previous studies [58] also showed that the accuracy of different LAI interpolation methods highly depends on the underlying land cover types. Considering the selected pixels in the present study, it seems that the three models retrieved the temporal LAI data with large discrepancies for the agricultural land cover types, shown with clearly distinct patterns in Figure 6. Besides, the LAI values of complex cultivation patterns were retrieved with higher variabilities among the three models. The phenomenon may result from the data limitation of in situ cultivation seasons, as well as from the mixture of small parcels of diverse annual crops, pasture or permanent crops. When including the precipitation data in TPVM, the modelled LAI values of non-irrigated arable land and pasture fitted well to the filtered MODIS data than the results of CSDM and DLM only making use of the temperature data (Figure 6 the example of non-irrigated arable land and pasture). Specification of season numbers for complex cultivation patterns or finer classified remotely sensed images with higher spatial resolution will certainly help to improve the modelling results.

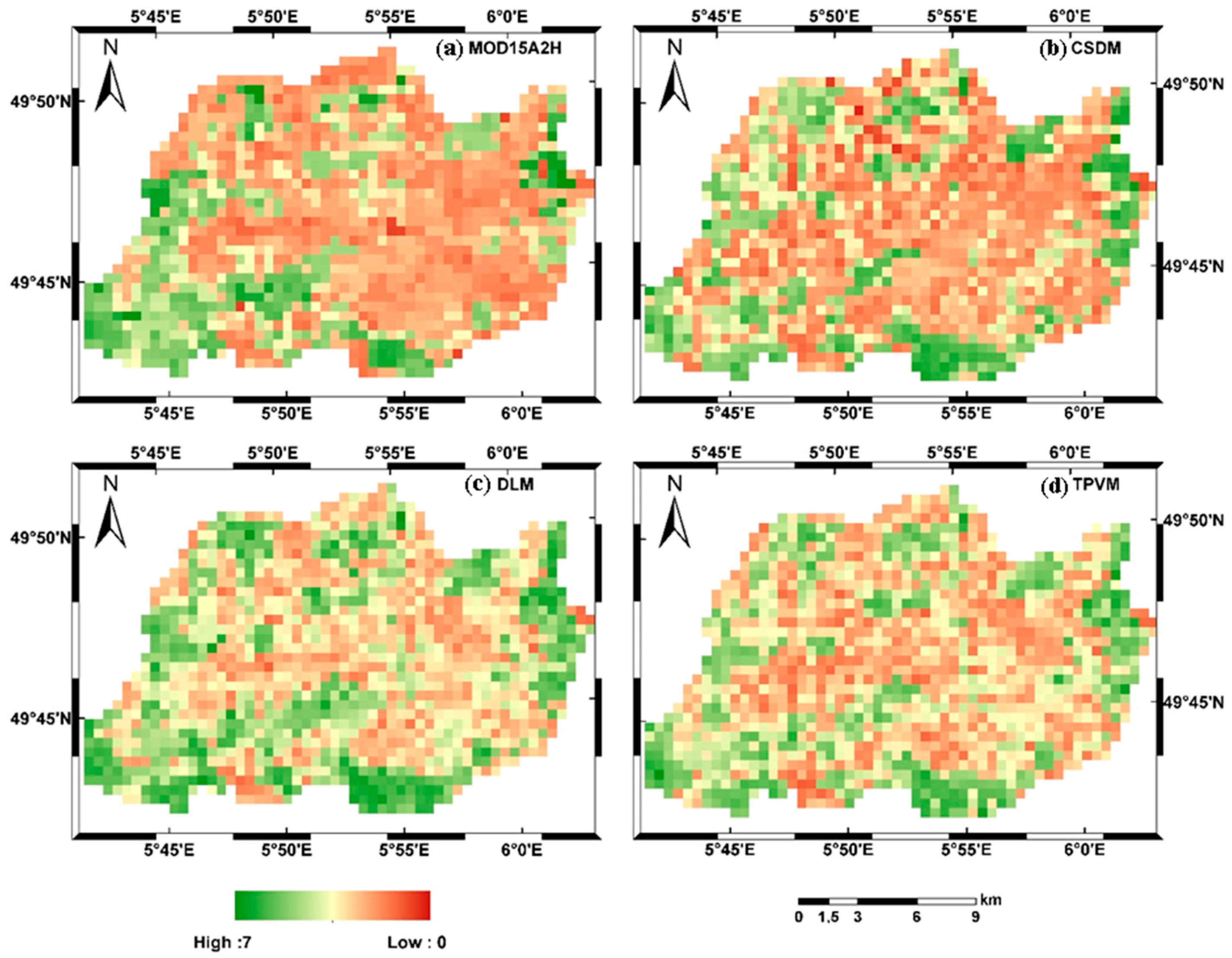
4.2.2. Analysis of Spatial LAI Pattern

As mentioned in Section 3, the three LAI-models were applied for each pixel for the period 2003 to 2013. Here, the predictions were based on a calibration over the full 11-year period. Figure 7 presents the spatial distributed LAI data from MODIS (MOD15A2H) as well as the three model predictions (CSDM, DLM, and TPVM) for the Attert Catchment on 23 July 2013. The MODIS LAI data indicate large amounts of low values in the agricultural areas and small proportions of the forest area in the south of Attert Catchment. Based on our field observation, such large amounts of low values in the forest and agricultural areas from MODIS data were unreasonable. Consistent with the pixel examples in the above analysis, the three models provided comparable results for broad-leaved forest but produced large variabilities in the agricultural areas (Figure 7). CSDM retrieved similar overall LAI patterns compared to the MODIS data, with large parts of lower LAI values in the agricultural areas. Besides, for a few pixels in the agricultural and forest area TPVM predicted lower values when compared to the DLM predictions. In general, DLM and TPVM obtained comparable results for the whole catchment.

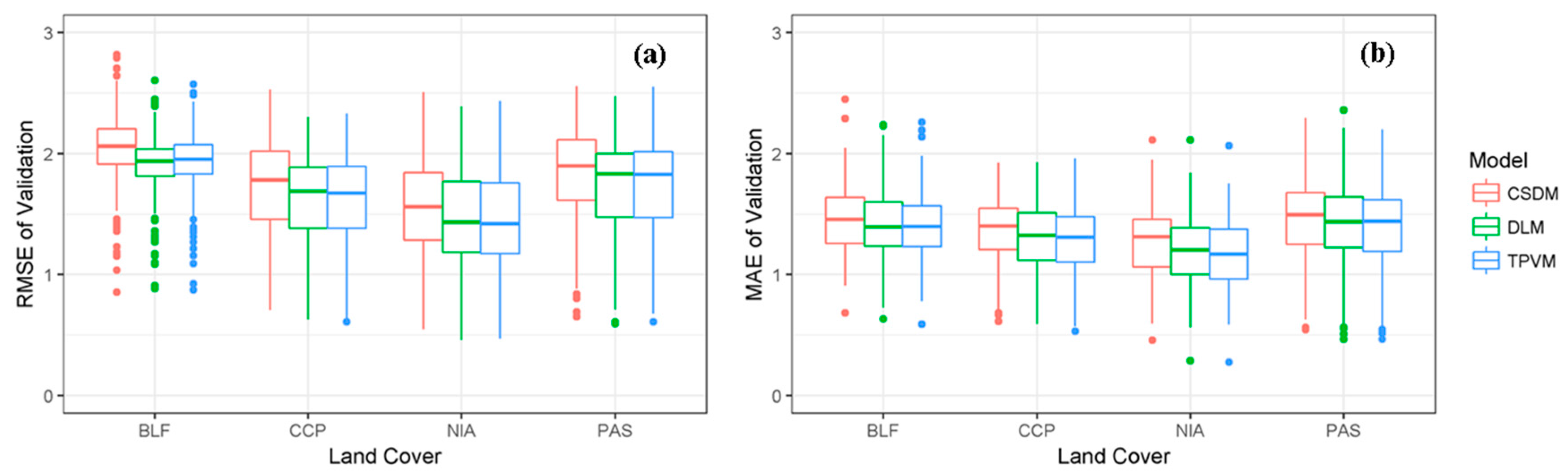
4.3. Uncertainty Assessment

4.3.1. Accuracy of Model Fit Evaluation

In this section, the different model performances when predicting LAI data for each year are evaluated based on a 10-year calibration and one-year validation cross validation method. Figure 8 provides the RMSE and MAE variations for the dominated four land cover types in the Attert Catchment. Considering all land cover types, DLM and TPVM provide slightly lower RMSE and MAE values compared to the results of CSDM. The average RMSE and MAE of DLM and TPVM are about 0.1 lower than for the CSDM model. This is more obvious for the complex cultivation patterns and non-irrigated arable land with overall lower RMSE and MAE than other land cover types. Moreover, for most of the land cover types, only comparing the derivation of RMSE and MAE, TPVM incorporating the temperature and precipitation data reconstructed the continuous LAI values with at least similar or even lower variances compared to the other two models using only the temperature data.

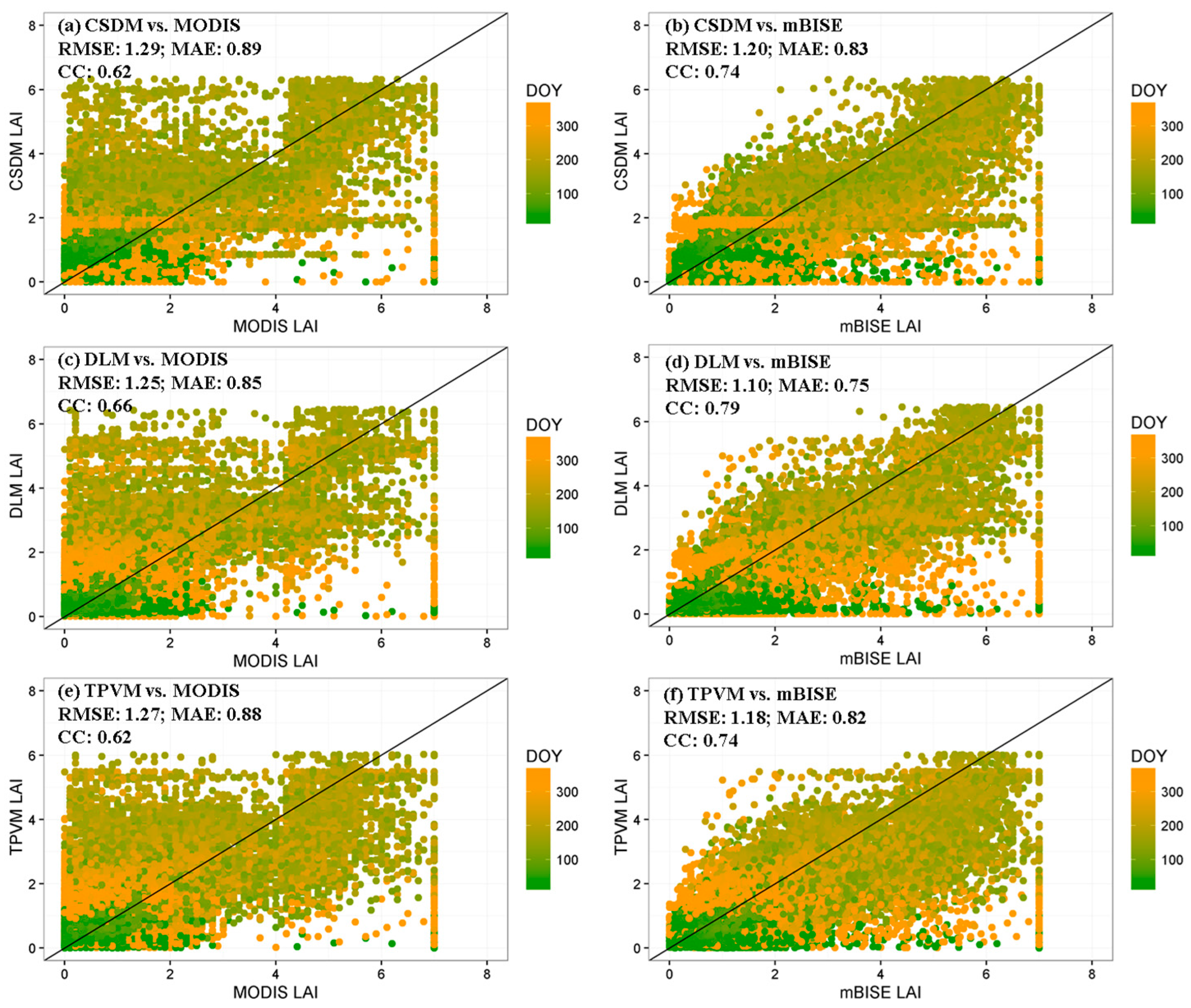
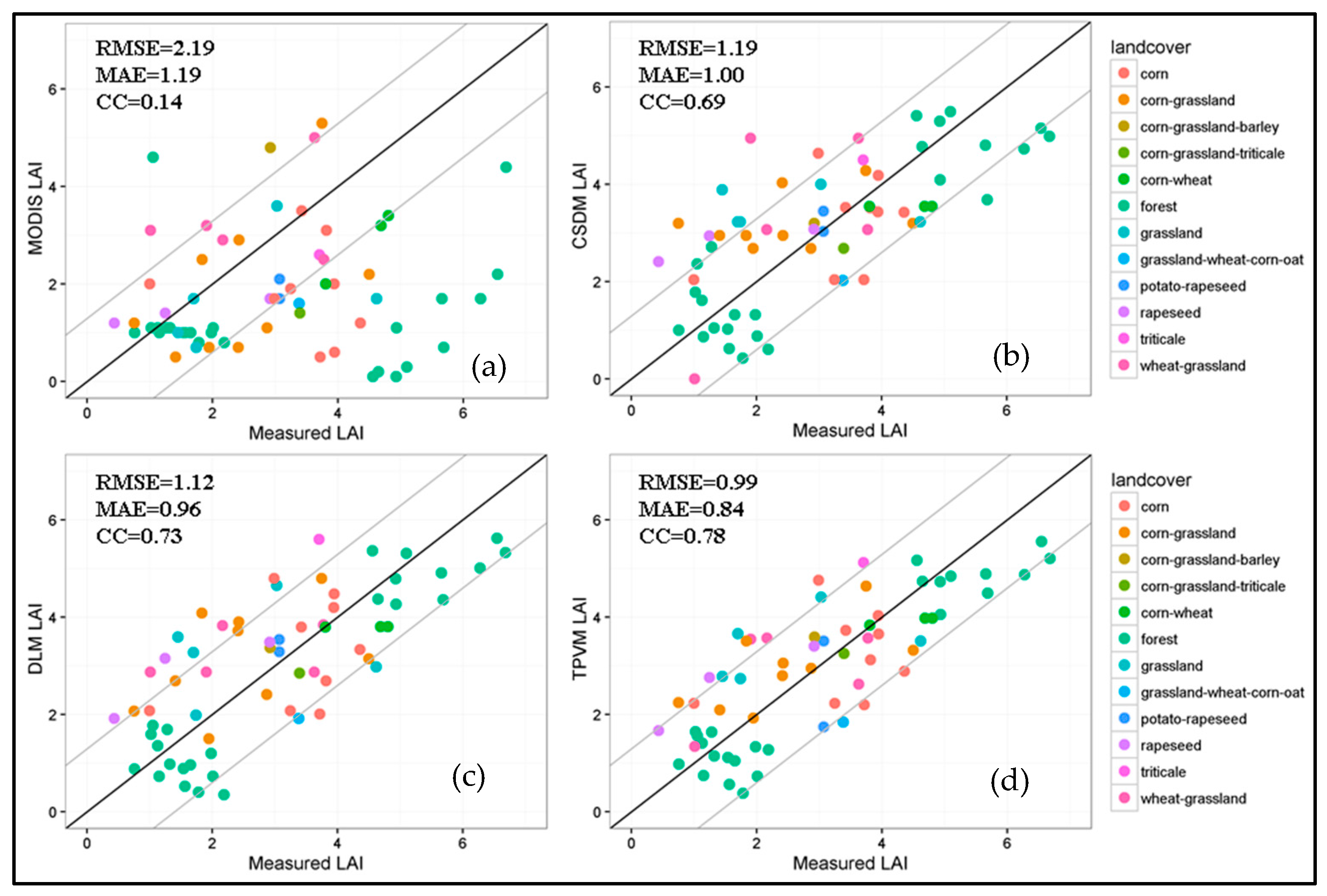
4.3.2. Comparison with MODIS Data and Field Measurement

As mentioned in Section 2.2.4, the plot LAI measurements (20 m × 20 m) were aggregated to the pixel size of the MOD15A2H product (500 m × 500 m). The LAI values of all the plots located in the pixel were averaged as the reference data for each corresponding pixel. Besides, 15 plots of forest and agricultural area were measured in the same year or different years for three or four time steps. In total, 42 pixels of the agricultural area and 22 pixels of the forest were available for comparison with the model results.
For all pixels containing field measurements, the temporal coherence between the modelled data and the original MODIS as well as the mBISE filtered data is plotted in Figure 9a–f over the 11-year period. The colour displays the differences in the DOY. In general, because the mBISE data are used as the optimization target for the three models, the modelled results correlate better to the mBISE data than to the original MODIS data. Moreover, the modelled results from CSDM and TPVM obtain the same Person’s correlation coefficient (CC) data, which is lower than the DLM derived CC of 0.66 and 0.79 corresponding to the MODIS and mBISE data, respectively. DLM also derives the best RMSE and MAE values when compared to CSDM and TPVM. Although the CSDM and TPVM predictions produce similar error metrics values, the patterns of the two methods differ greatly. Comparing to the random points in the middle part (around LAI values of 2) for CSDM, TPVM provides more compact dataset than DLM.
Figure 10 illustrates the coherence between the field measured LAI data, the original MOD15A2H LAI product, and the predicted LAI values of the three models. The coloured points represent the field-measured values that are labelled according to the land cover types on one specific date. The original MOD15A2H product shows large differences to the measured LAI with a CC of only 0.14, a RMSE of 2.19 and a MAE of 1.69. The correlation between measured data and models however improved significantly. The CC varies from 0.69 to 0.73 for the CSDM and DLM model. In addition, TPVM derives the best CC of 0.78 with the lowest RMSE of 0.99 and a MAE of 0.84. Some important uncertainties related to the field measurements have to be considered in the interpretation of these results. The heterogeneous features of the mixed crops also including areas of bare soil may increase the discrepancy between the measured LAI and the remotely sensed LAI or the modelled LAI. Therefore, when the measurement plots is not fully covering the MODIS pixel, their averaged LAI value may still have difficulties in representing all the features of the corresponding pixel. In July 2013, the corn fields were cultivated for about one month, whereas most of the wheat, barley and rapeseeds maturated readily for harvest. The forage grasslands were cultivated and harvested in turn during the time of the LAI measurements. Aside from those uncertainties and based on the scatterplots in Figure 10, the modelled LAI of forest pixels in summer fit very well with the measured LAI. DLM and TPVM achieved almost identical forest LAI in summer. Nevertheless, for most of the croplands, TPVM performed superior to the DLM and CSDM models with more compatible results compared to the measured data. This is easily explained by the fact that temperature predominantly affected the broad-leaved forest but combined with precipitation exert significantly influence on the agricultural land covers.

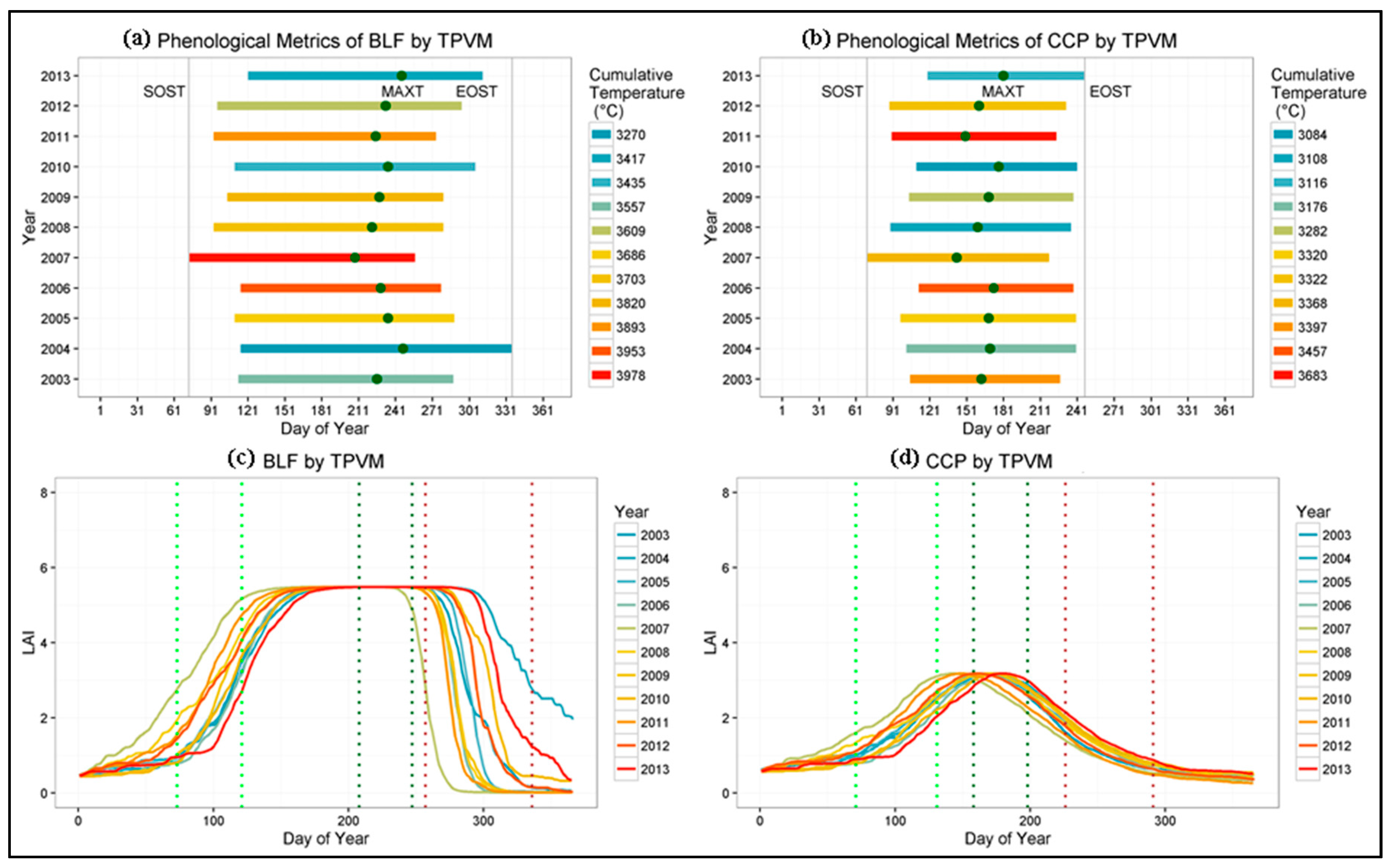
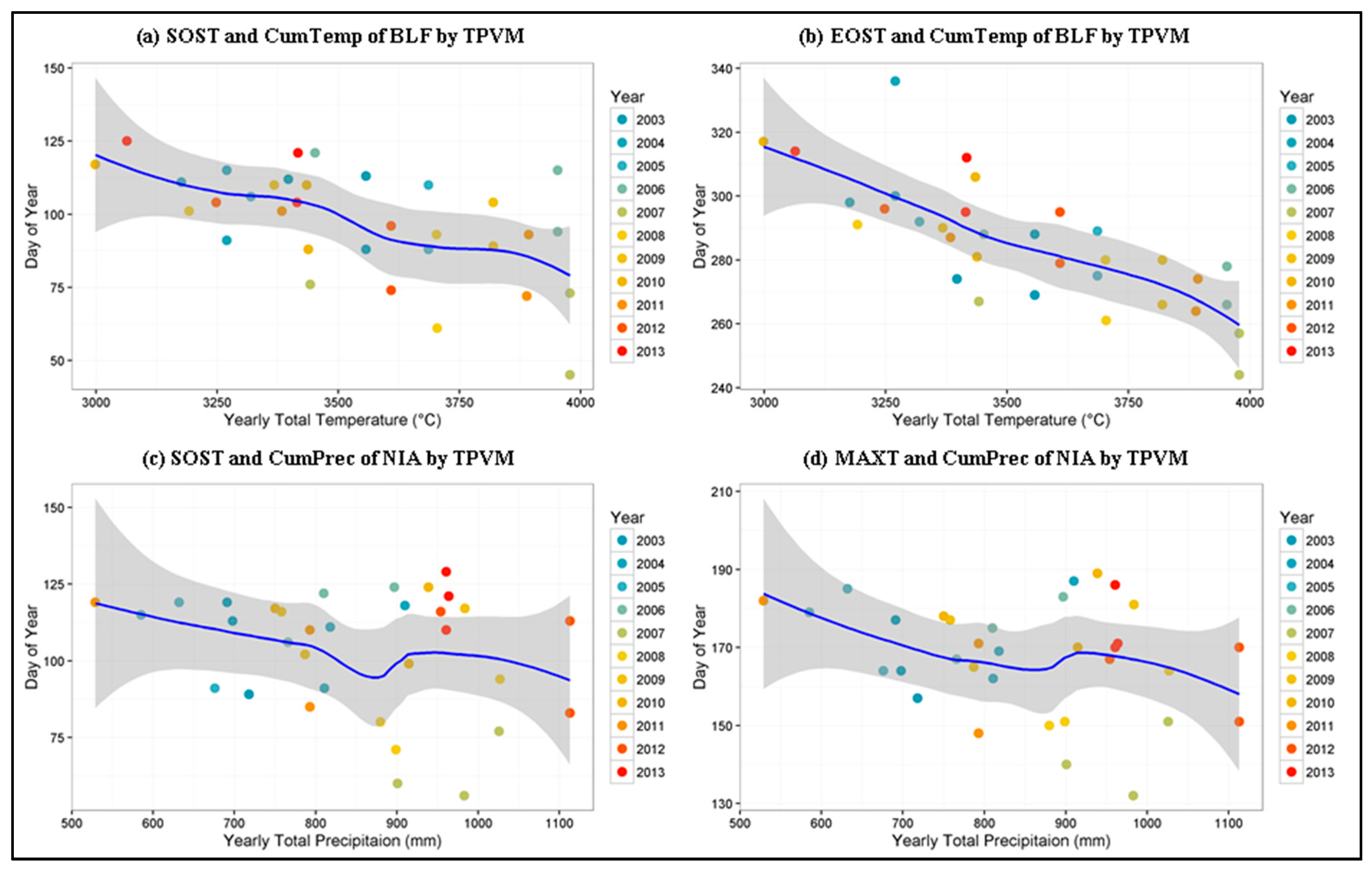
4.4. Phenological Metrics and Climate Controls Evaluation

With an increasing awareness for the importance of phenology in climate change studies, plant phenology combined with remotely sensed data have been frequently studied in land surface modelling. Plant phenology interacts with the climate and varies with the climate zone, vegetation type and inter-annual variability of the start and end of the growing season [59]. The phenology metrics derived from the satellite data could serve as an indicator of climate change on the terrestrial ecosystems [60]. According to the report of Reed [33] and the USGS description of remote sensing phenology metrics [61], in the present study, the start-of-season time (SOST), the end of season time (EOST), the time of maximum LAI value (MAXT), and the length of the growing season (LOGS) were derived for the climate impact evaluation. SOST and EOST indicate the start and end of measurable photosynthesis in the vegetation canopy, which normally are described as DOY having a consistent upward or downward trend in LAI time series. We calculated the SOST and EOST as the half-maximum-mid-point between minimum and maximum LAI. Therefore, based on the SOST and EOST, LOGS can be calculated as the number of days during the growing season. MAXT represents the time of maximum photosynthesis in the canopy.
Representative pixels of broad-leaved forest, complex cultivation patterns and non-irrigated arable land from Attert Catchment were chosen for the phenology analysis. Figure 11 delineates the phenological metrics in DOY of broad-leaved forest and complex cultivation patterns from 2003 to 2013. Figure 11a,b displays the growing seasons of broad-leaved forest and complex cultivation patterns in different colours ranked by the yearly total temperature from 2003 to 2013. The green points on each line represent the time when the leaves reach the maximum value during the maturity period. The red line of broad-leaved forest in Figure 11a demonstrates that the highest cumulative temperature of 3978 °C in 2007 was accompanied with the early beginning of the growing season at DOY 73. The differences of LOGS between broad-leaved forest and complex cultivation patterns can also be clearly seen, with mean DOY between 175 and 186. This phenomenon further proves that the warming weather can advance the start-of-season in the spring especially for temperate deciduous forest. Moreover, the unusual warming weather can also speed up the maturity and shorten the growing season. For example, in 2003, known as the European heat wave year, LOGS was the shortest compared to other years. The accelerating effect became more obvious for the complex cultivation patterns with the LOGS of 122 compared to the 11-year mean LOGS of 135. Figure 11c,d demonstrate the influences of inter-annual temperature variabilities on the LAI values of broad-leaved forest and complex cultivation patterns. The green, dark-green and red dash lines respectively were subdivided as the range of SOST, MAXT and EOST within the 11 years. Uniformly, the forest area exhibited more stable manners than the agricultural sites.
Regarding the relationship of temperature and precipitation changes on the SOST, MAXT and EOST, three exemplary pixels from broad-leaved forest and non-irrigated arable land were plotted in Figure 12. SOST and EOST of broad-leaved forest correlate tightly with the yearly cumulative temperature data, confirming that the higher temperature result in earlier SOST and EOST data for broad-leaved forest. Although temperature greatly influences the non-irrigated arable land, complex cultivation patterns and pastures, there is no such clear relationship shown for the broad-leaved forest. On the other hand, the precipitation data accelerates the SOST and MAXT of the non-irrigated arable land shown in Figure 12c,d. The MAXT and SOST data calculated from TPVM verified that the crop growing would be delayed in case of insufficient precipitation in the non-irrigated agricultural areas. Conversely, crop growth might be enhanced by an increase of the total precipitation and available water.

5. Conclusions

By integrating the climate data from meteorological stations and remotely sensed data, a new spatio-temporal LAI model (TPVM) was proposed in this study. TPVM takes the observed cumulative daily mean temperature and cumulative daily precipitation data as input variables, and optimizes the results by a global optimization method (DDS) to the filtered MODIS LAI dataset. Besides TPVM, CSDM and DLM models with the single input of cumulative temperature data were also implemented for comparison. TPVM derives comparable continuous LAI predictions for the deciduous forest area and superior data for the agricultural areas when compared to the models solely depending on the temperature data. This indicates a dominant control of LAI by temperature only and a sufficient availability of soil moisture for the forested areas within the catchment. However, agricultural crops with lower root depth and therefore access to soil moisture resources are also controlled by precipitation dynamics in their development.
The pre-processing of MODIS data by the mBISE method produced more continuous datasets by reducing the large amount of noises. Besides that, the weighted scheme also provided great assistance in the LAI prediction through the optimization procedure. Comparing the three models on a pixel-base, both, the temporal and spatial pattern evaluations demonstrate that the three models work quite well for the broad-leaved forest, but have large discrepancies over the agricultural areas. The variances of RMSE and MAE for the four land covers indicate that most of the TPVM predictions retrieve the continuous LAI data with lower uncertainties than those of DLM and CSDM. In respect to the different land cover types, the overall patterns of DLM and TPVM are more realistic and continuous compared to the CSDM. Compared to the field measurements, all the three models retrieved more realistic LAI data than the original MODIS data indicated by the raise of the lowest CC of 0.14 to a higher level (ranging from 0.69 to 0.78). Nevertheless, TPVM manifested the superiority over the prediction of the agricultural fields with the overall CC of 0.78.
The phenological metrics including the SOST, EOST, MAXT and LOGS were derived from the time series of LAI values predicted by TPVM from 2003 to 2013. Consistent with the previous research [60], the SOST and EOST of broad-leaved forest advance with the warming temperature. The LOGS of complex cultivation patterns shortens due to the higher temperature and less precipitation, as illustrated for the European heat wave in 2003. Besides that, the precipitation data exert more influences on the non-irrigated arable land, indicating with relatively early SOST and MAXT when more precipitation were available.
In the study, we only applied the models in the meso-scale Attert Catchment, which has modest climate variabilities over the whole catchment. For future studies, we would recommend the implementation of the TPVM model in larger and more heterogeneous catchment to test its applicability. Furthermore, in the larger-scale terrestrial ecosystem, the vegetation dynamic and the climate changes interact far more complicatedly. Other climate factors such as the photoperiod, soil moisture, soil temperature or topographic factors could also significantly affect the vegetation dynamics in different ways. Therefore, the integration with effective climate controls, more meteorological observations, and finer spatial-resolution remotely sensed data could further mitigate the uncertain predictions in the vegetation dynamics modelling.

Acknowledgments

The authors would like to sincerely thank the German Research Foundation (DFG) and the Austrian Science Fund (FWF) for funding this research through the CAOS (Catchments as Organized Systems) Research Unit (FOR 1598, SCHU1271/5-1, and FWF-I2142-N29), and the China Scholarship Committee for the support of the research. The authors are grateful for the free access to the MODIS products provided by the USGS and all the kind help from Sibylle Hassler during the field LAI measurement campaigns in the CAOS project. The authors also wish to thank all the reviewers for their valuable comments and suggestions.

Author Contributions

The authors contributed equally to the paper.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. White, M.A.; Thornton, P.E.; Running, S.W. A continental phenology model for monitoring vegetation responses to interannual climatic variability. Glob. Biogeochem. Cycles 1997, 11, 217–234. [Google Scholar] [CrossRef]
  2. Schwartz, M.D.; Reed, B.C.; White, M.A. Assessing satellite-derived start-of-season measures in the conterminous USA. Int. J. Climatol. 2002, 22, 1793–1805. [Google Scholar] [CrossRef]
  3. Sitch, S.; Smith, B.; Prentice, I.C.; Arneth, A.; Bondeau, A.; Cramer, W.; Kaplan, J.O.; Levis, S.; Lucht, W.; Sykes, M.T.; et al. Evaluation of ecosystem dynamics, plant geography and terrestrial carbon cycling in the LPJ dynamic global vegetation model. Glob. Chang. Biol. 2003, 9, 161–185. [Google Scholar] [CrossRef]
  4. De Beurs, K.M.; Henebry, G.M. Land surface phenology, climatic variation, and institutional change: Analyzing agricultural land cover change in Kazakhstan. Remote Sens. Environ. 2004, 89, 497–509. [Google Scholar] [CrossRef]
  5. Peñuelas, J.; Filella, I.; Zhang, X.; Llorens, L.; Ogaya, R.; Lloret, F.; Comas, P.; Estiarte, M.; Terradas, J. Complex spatiotemporal phenological shifts as a response to rainfall changes. New Phytol. 2004, 161, 837–846. [Google Scholar] [CrossRef]
  6. Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Liu, Z. Monitoring the response of vegetation phenology to precipitation in Africa by coupling MODIS and TRMM instruments. J. Geophys. Res. Atmos. 2005. [Google Scholar] [CrossRef]
  7. Watson, D.J. Comparative physiological studies on the growth of field crops: I. Variation in net assimilation rate and leaf area between species and varieties, and within and between years. Ann. Bot. 1947, 11, 41–76. [Google Scholar] [CrossRef]
  8. Tesemma, Z.K.; Wei, Y.; Western, A.W.; Peel, M.C. Leaf Area Index variation for crop, pasture, and tree in response to climatic variation in the goulburn–broken catchment, Australia. J. Hydrometeorol. 2014, 15, 1592–1606. [Google Scholar] [CrossRef]
  9. Glenn, E.; Huete, A.; Nagler, P.; Nelson, S. Relationship between remotely-sensed vegetation indices, canopy attributes and plant physiological processes: What vegetation indices can and cannot tell us about the landscape. Sensors 2008, 8, 2136. [Google Scholar] [CrossRef] [PubMed]
  10. Xiao, Q.; McPherson, E.G.; Simpson, J.R.; Ustin, S.L. Rainfall interception by sacramento’s urban forest. J. Arboric. 1998, 24, 235–244. [Google Scholar]
  11. Running, S.W.; Coughlan, J.C. A general model of forest ecosystem processes for regional applications I. Hydrologic balance, canopy gas exchange and primary production processes. Ecol. Model. 1988, 42, 125–154. [Google Scholar] [CrossRef]
  12. Liang, L.; Schwartz, M. Landscape phenology: An integrative approach to seasonal vegetation dynamics. Landsc. Ecol. 2009, 24, 465–472. [Google Scholar] [CrossRef]
  13. Schwartz, M.D.; Karl, T.R. Spring phenology: Nature’s experiment to detect the effect of “green-up” on surface maximum temperatures. Mon. Weather Rev. 1990, 118, 883–890. [Google Scholar] [CrossRef]
  14. González-Sanpedro, M.C.; Le Toan, T.; Moreno, J.; Kergoat, L.; Rubio, E. Seasonal variations of Leaf Area Index of agricultural fields retrieved from Landsat data. Remote Sens. Environ. 2008, 112, 810–824. [Google Scholar] [CrossRef]
  15. Atzberger, C.; Klisch, A.; Mattiuzzi, M.; Vuolo, F. Phenological metrics derived over the European continent from NDVI3g data and MODIS time series. Remote Sens. 2013, 6, 257. [Google Scholar] [CrossRef]
  16. Hwang, T.; Song, C.; Bolstad, P.V.; Band, L.E. Downscaling real-time vegetation dynamics by fusing multi-temporal MODIS and Landsat NDVI in topographically complex terrain. Remote Sens. Environ. 2011, 115, 2499–2512. [Google Scholar] [CrossRef]
  17. AghaKouchak, A.; Farahmand, A.; Melton, F.S.; Teixeira, J.; Anderson, M.C.; Wardlow, B.D.; Hain, C.R. Remote sensing of drought: Progress, challenges and opportunities. Rev. Geophys. 2015, 53, 452–480. [Google Scholar] [CrossRef]
  18. Thuiller, W. Biodiversity: Climate change and the ecologist. Nature 2007, 448, 550–552. [Google Scholar] [CrossRef] [PubMed]
  19. Kramer, K.; Leinonen, I.; Loustau, D. The importance of phenology for the evaluation of impact of climate change on growth of boreal, temperate and Mediterranean Forests Ecosystems: An overview. Int. J. Biometeorol. 1999, 44, 67–75. [Google Scholar] [CrossRef]
  20. Chuine, I.; Kramer, K.; Hänninen, H. Plant development models. In Phenology: An Integrative Environmental Science; Schwartz, M.D., Ed.; Springer: Dordrecht, The Netherlands, 2003; pp. 217–235. [Google Scholar]
  21. Forrest, J.; Miller-Rushing, A.J. Toward a synthetic understanding of the role of phenology in ecology and evolution. Philos. Trans. R. Soc. London B Biol. Sci. 2010, 365, 3101–3112. [Google Scholar] [CrossRef] [PubMed]
  22. The Globe Program. A Worldwide Science and Education Program. Available online: https://www.globe.gov/globe-data (accessed on 1 May 2013).
  23. Schwartz, M.D.; Ahas, R.; Aasa, A. Onset of spring starting earlier across the Northern Hemisphere. Glob. Chang. Biol. 2006, 12, 343–351. [Google Scholar] [CrossRef]
  24. Migliavacca, M.; Cremonese, E.; Colombo, R.; Busetto, L.; Galvagno, M.; Ganis, L.; Meroni, M.; Pari, E.; Rossini, M.; Siniscalco, C.; et al. European larch phenology in the Alps: Can we grasp the role of ecological factors by combining field observations and inverse modelling? Int. J. Biometeorol. 2008, 52, 587–605. [Google Scholar] [CrossRef] [PubMed]
  25. Palacios-Orueta, A.; Huesca, M.; Whiting, M.L.; Litago, J.; Khanna, S.; Garcia, M.; Ustin, S.L. Derivation of phenological metrics by function fitting to time-series of spectral shape indexes AS1 and AS2: Mapping cotton phenological stages using MODIS time series. Remote Sens. Environ. 2012, 126, 148–159. [Google Scholar] [CrossRef]
  26. Kathuroju, N.; White, M.A.; Symanzik, J.; Schwartz, M.D.; Powell, J.A.; Nemani, R.R. On the use of the advanced very high resolution radiometer for development of prognostic land surface phenology models. Ecol. Model. 2007, 201, 144–156. [Google Scholar] [CrossRef]
  27. Chuine, I.; Belmonte, J.; Mignot, A. A modelling analysis of the genetic variation of phenology between tree populations. J. Ecol. 2000, 88, 561–570. [Google Scholar] [CrossRef]
  28. Chuine, I.; Yiou, P.; Viovy, N.; Seguin, B.; Daux, V.; Ladurie, E.L.R. Historical phenology: Grape ripening as a past climate indicator. Nature 2004, 432, 289–290. [Google Scholar] [CrossRef] [PubMed]
  29. Cleland, E.E.; Chuine, I.; Menzel, A.; Mooney, H.A.; Schwartz, M.D. Shifting plant phenology in response to global change. Trends Ecol. Evol. 2007, 22, 357–365. [Google Scholar] [CrossRef] [PubMed]
  30. Chuine, I.; Cour, P.; Rousseau, D.D. Selecting models to predict the timing of flowering of temperate trees: Implications for tree phenology modelling. Plant Cell Environ. 1999, 22, 1–13. [Google Scholar] [CrossRef]
  31. Chuine, I.; Cambon, G.; Comtois, P. Scaling phenology from the local to the regional level: Advances from species-specific phenological models. Glob. Chang. Biol. 2000, 6, 943–952. [Google Scholar] [CrossRef]
  32. Justice, C.O.; Townshend, J.R.G.; Holben, B.N.; Tucker, C.J. Analysis of the phenology of global vegetation using meteorological satellite data. Int. J. Remote Sens. 1985, 6, 1271–1318. [Google Scholar] [CrossRef]
  33. Reed, B.C.; Brown, J.F.; VanderZee, D.; Loveland, T.R.; Merchant, J.W.; Ohlen, D.O. Measuring phenological variability from satellite imagery. J. Veg. Sci. 1994, 5, 703–714. [Google Scholar] [CrossRef]
  34. Koetz, B.; Baret, F.; Poilvé, H.; Hill, J. Use of coupled canopy structure dynamic and radiative transfer models to estimate biophysical canopy characteristics. Remote Sens. Environ. 2005, 95, 115–124. [Google Scholar] [CrossRef]
  35. Sakamoto, T.; Yokozawa, M.; Toritani, H.; Shibayama, M.; Ishitsuka, N.; Ohno, H. A crop phenology detection method using time-series MODIS data. Remote Sens. Environ. 2005, 96, 366–374. [Google Scholar] [CrossRef]
  36. Fisher, J.I.; Mustard, J.F.; Vadeboncoeur, M.A. Green leaf phenology at landsat resolution: Scaling from the field to the satellite. Remote Sens. Environ. 2006, 100, 265–279. [Google Scholar] [CrossRef]
  37. Zhang, X.; Friedl, M.A.; Schaaf, C.B. Global vegetation phenology from Moderate Resolution Imaging Spectroradiometer (MODIS): Evaluation of global patterns and comparison with in situ measurements. J. Geophys. Res. Biogeosci. 2006. [Google Scholar] [CrossRef]
  38. Beck, P.S.A.; Atzberger, C.; Høgda, K.A.; Johansen, B.; Skidmore, A.K. Improved monitoring of vegetation dynamics at very high latitudes: A new method using MODIS NDVI. Remote Sens. Environ 2006, 100, 321–334. [Google Scholar] [CrossRef]
  39. Weiss, M.; Baret, F.; Garrigues, S.; Lacaze, R. LAI and FAPAR cyclopes global products derived from vegetation. Part 2: Validation and comparison with MODIS collection 4 products. Remote Sens. Environ. 2007, 110, 317–331. [Google Scholar] [CrossRef]
  40. Kandasamy, S.; Baret, F.; Verger, A.; Neveux, P.; Weiss, M. A comparison of methods for smoothing and gap filling time series of remote sensing observations – application to MODIS LAI products. Biogeosciences 2013, 10, 4055–4071. [Google Scholar]
  41. Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.F.; Gao, F.; Reed, B.C.; Huete, A. Monitoring vegetation phenology using MODIS. Remote Sens. Environ. 2003, 84, 471–475. [Google Scholar] [CrossRef]
  42. Jonsson, P.; Eklundh, L. Seasonality extraction by function fitting to time-series of satellite sensor data. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1824–1832. [Google Scholar] [CrossRef]
  43. Fang, H.; Liang, S.; Kuusk, A. Retrieving leaf area index using a genetic algorithm with a canopy radiative transfer model. Remote Sens. Environ. 2003, 85, 257–270. [Google Scholar] [CrossRef]
  44. Houborg, R.; Boegh, E. Mapping leaf chlorophyll and Leaf Area Index using inverse and forward canopy reflectance modeling and spot reflectance data. Remote Sens. Environ. 2008, 112, 186–202. [Google Scholar] [CrossRef]
  45. Riha, S.; Wilks, D.; Simoens, P. Impact of temperature and precipitation variability on crop model predictions. Clim. Chang. 1996, 32, 293–311. [Google Scholar] [CrossRef]
  46. Zehe, E.; Ehret, U.; Pfister, L.; Blume, T.; Schröder, B.; Westhoff, M.; Jackisch, C.; Schymanski, S.J.; Weiler, M.; Schulz, K.; et al. Hess opinions: From response units to functional units: A thermodynamic reinterpretation of the HRU concept to link spatial organization and functioning of intermediate scale catchments. Hydrol. Earth Syst. Sci. 2014, 18, 4635–4655. [Google Scholar] [CrossRef]
  47. Caos: From Catchments as Organised Systems to Models Based on Functional Units. Available online: http://www.caos-project.de/ (accessed on 6 May 2016).
  48. Sun, L.; Schulz, K. The improvement of land cover classification by thermal remote sensing. Remote Sens. 2015, 7. [Google Scholar] [CrossRef]
  49. Myneni, R.; Park, Y.K.T. MOD15A2H MODIS/TERRA Leaf Area Index/FPAR 8-Day l4 Global 500 m Sin Grid v006. Available online: https://lpdaac.usgs.gov/node/863 (accessed on 1 January 2016).
  50. Knyazikhin, Y.; Martonchik, J.V.; Myneni, R.B.; Diner, D.J.; Running, S.W. Synergistic algorithm for estimating vegetation canopy leaf area index and fraction of absorbed photosynthetically active radiation from MODIS and MISR data. J. Geophys. Res. Atmos. 1998, 103, 32257–32275. [Google Scholar] [CrossRef]
  51. Myneni, R.; Park, Y.K.T. MODIS Collection 6 (C6) LAI/FPAR Product User’s Guide. Available online: https://lpdaac.usgs.gov/sites/default/files/public/product_documentation/mod15_user_guide.pdf (accessed on 1 January 2016).
  52. Horn, J.; Schulz, K. Post-processing analysis of MODIS Leaf Area Index subsets. J. Appl. Remote Sens. 2010. [Google Scholar] [CrossRef]
  53. Lovell, J.L.; Graetz, R.D. Filtering pathfinder AVHRR land NDVI data for Australia. Int. J. Remote Sens. 2001, 22, 2649–2654. [Google Scholar] [CrossRef]
  54. LI-COR Inc. LAI-2200 Plant Canopy Analyzer: Instruction Manual; LI-COR Inc.: Lincoln, NE, USA, 2010. [Google Scholar]
  55. Jönsson, P.; Eklundh, L. Timesat—A program for analyzing time-series of satellite sensor data. Comput. Geosci. 2004, 30, 833–845. [Google Scholar] [CrossRef]
  56. Tolson, B.A.; Shoemaker, C.A. Dynamically dimensioned search algorithm for computationally efficient watershed model calibration. Water Resour. Res. 2007, 43, W01413. [Google Scholar] [CrossRef]
  57. Atkinson, P.M.; Jeganathan, C.; Dash, J.; Atzberger, C. Inter-comparison of four models for smoothing satellite sensor time-series data to estimate vegetation phenology. Remote Sens. Environ. 2012, 123, 400–417. [Google Scholar] [CrossRef]
  58. Borak, J.S.; Jasinski, M.F. Effective interpolation of incomplete satellite-derived leaf-area index time series for the continental united states. Agric. For. Meteorol. 2009, 149, 320–332. [Google Scholar] [CrossRef]
  59. Richardson, A.D.; Keenan, T.F.; Migliavacca, M.; Ryu, Y.; Sonnentag, O.; Toomey, M. Climate change, phenology, and phenological control of vegetation feedbacks to the climate system. Agric. For. Meteorol. 2013, 169, 156–173. [Google Scholar] [CrossRef]
  60. Menzel, A.; Fabian, P. Growing season extended in Europe. Nature 1999, 397, 659. [Google Scholar] [CrossRef]
  61. USGS Remote Sensing Phenology. Available online: http://phenology.cr.usgs.gov/methods_metrics.php (accessed on 7 June 2016).
Remotesensing 09 00144 g001 550
Figure 1. The geology and topography map of the Attert Catchment; the right-bottom overview map indicates the location of the Attert Catchment across Belgium and Luxembourg.
Figure 1. The geology and topography map of the Attert Catchment; the right-bottom overview map indicates the location of the Attert Catchment across Belgium and Luxembourg.
Remotesensing 09 00144 g001
Remotesensing 09 00144 g002 550
Figure 2. Range of interpolated data for Attert Catchment from 2003 to 2013: (a) yearly cumulative temperature; and (b) yearly cumulative precipitation.
Figure 2. Range of interpolated data for Attert Catchment from 2003 to 2013: (a) yearly cumulative temperature; and (b) yearly cumulative precipitation.
Remotesensing 09 00144 g002
Remotesensing 09 00144 g003 550
Figure 3. (a) DEM data with the measured LAI points in Attert Catchment; and (b) CORINE Land cover map overlaid by the blue boxes of MODIS pixels corresponding to the field measurements.
Figure 3. (a) DEM data with the measured LAI points in Attert Catchment; and (b) CORINE Land cover map overlaid by the blue boxes of MODIS pixels corresponding to the field measurements.
Remotesensing 09 00144 g003
Remotesensing 09 00144 g004 550
Figure 4. The model procedure lists the data preprocessing of climate variable, then implementation of the three vegetation dynamic models, and the uncertainty assessment comparing with the field measured LAI.
Figure 4. The model procedure lists the data preprocessing of climate variable, then implementation of the three vegetation dynamic models, and the uncertainty assessment comparing with the field measured LAI.
Remotesensing 09 00144 g004
Remotesensing 09 00144 g005 550
Figure 5. RMSE (a); and MAE (b) variances calculated from the modelled LAI of TPVM and MODIS LAI data for different evaluation numbers ranging from 10 to 10,000.
Figure 5. RMSE (a); and MAE (b) variances calculated from the modelled LAI of TPVM and MODIS LAI data for different evaluation numbers ranging from 10 to 10,000.
Remotesensing 09 00144 g005
Remotesensing 09 00144 g006 550
Figure 6. (a–d) LAI prediction data of each year from 2003 to 2013 based on the remaining 10-year’s calibration data for four land covers (broad-leaved forest, complex cultivation patterns, non-irrigated arable land, and pasture) were from the original MOD15A2H (grey lines), mBISE (red points), CSDM (cyan lines), DLM (green lines) and TPVM (red lines), respectively.
Figure 6. (a–d) LAI prediction data of each year from 2003 to 2013 based on the remaining 10-year’s calibration data for four land covers (broad-leaved forest, complex cultivation patterns, non-irrigated arable land, and pasture) were from the original MOD15A2H (grey lines), mBISE (red points), CSDM (cyan lines), DLM (green lines) and TPVM (red lines), respectively.
Remotesensing 09 00144 g006
Remotesensing 09 00144 g007 550
Figure 7. The LAI images of Attert Catchment on 28 July 2013 were, respectively, derived from: (a) MOD15A2H; (b) CSDM; (c) DLM; and (d) TPVM.
Figure 7. The LAI images of Attert Catchment on 28 July 2013 were, respectively, derived from: (a) MOD15A2H; (b) CSDM; (c) DLM; and (d) TPVM.
Remotesensing 09 00144 g007
Remotesensing 09 00144 g008 550
Figure 8. The goodness of fit measures between the MODIS LAI and the predicted LAI data using the three models (CSDM, DLM, and TPVM) for Attert Catchment: (a) RMSE for the four land cover types; and (b) MAE for the four land cover types. Considered land cover types are broad-leaved forest (BLF), complex cultivation patterns (CCP), coniferous forest (CF), mixed forest (MF), non-irrigated arable land (NIA), natural vegetation (NV), pastures (PAS).
Figure 8. The goodness of fit measures between the MODIS LAI and the predicted LAI data using the three models (CSDM, DLM, and TPVM) for Attert Catchment: (a) RMSE for the four land cover types; and (b) MAE for the four land cover types. Considered land cover types are broad-leaved forest (BLF), complex cultivation patterns (CCP), coniferous forest (CF), mixed forest (MF), non-irrigated arable land (NIA), natural vegetation (NV), pastures (PAS).
Remotesensing 09 00144 g008
Remotesensing 09 00144 g009 550
Figure 9. (a–f) Plots comparing the original MODIS, mBISE LAI data with the modelled LAI data for the corresponding field measured pixels from 2003 to 2013. The colour bar indicates the day of year (DOY).
Figure 9. (a–f) Plots comparing the original MODIS, mBISE LAI data with the modelled LAI data for the corresponding field measured pixels from 2003 to 2013. The colour bar indicates the day of year (DOY).
Remotesensing 09 00144 g009
Remotesensing 09 00144 g010 550
Figure 10. (a–d) Scatterplots comparing measured LAI values and the LAI data from MOD15A2H, CSDM, DLM and TPVM, respectively. The dark line indicates the 1:1 line and the two grey lines represent the lines with intercept of 1 and −1. The coloured points represent the different land covers according to the legend.
Figure 10. (a–d) Scatterplots comparing measured LAI values and the LAI data from MOD15A2H, CSDM, DLM and TPVM, respectively. The dark line indicates the 1:1 line and the two grey lines represent the lines with intercept of 1 and −1. The coloured points represent the different land covers according to the legend.
Remotesensing 09 00144 g010
Remotesensing 09 00144 g011 550
Figure 11. The growing season plots including the phenological metrics (SOST, MAXT, EOST) were derived from TPVM for two land covers: (a) broad-leaved forest (BLF); (b) complex cultivation patterns (CCP); and (c,d) the LAI dynamics in terms of day of year from 2003 to 2013 for BLF and CCP, respectively.
Figure 11. The growing season plots including the phenological metrics (SOST, MAXT, EOST) were derived from TPVM for two land covers: (a) broad-leaved forest (BLF); (b) complex cultivation patterns (CCP); and (c,d) the LAI dynamics in terms of day of year from 2003 to 2013 for BLF and CCP, respectively.
Remotesensing 09 00144 g011
Remotesensing 09 00144 g012 550
Figure 12. Climate variables relationship with the phenological metrics from 2003 to 2013 were plotted: (a) the relationship of SOST from broad-leaved forest (BLF) by TPVM and yearly cumulative temperature; (b) the relationship of EOST from BLF by TPVM and yearly cumulative temperature; (c) the relationship of SOST from non-irrigated arable land (NIA) by TPVM and yearly cumulative precipitation; and (d) the relationship of MAXT from NIA by TPVM and yearly cumulative precipitation.
Figure 12. Climate variables relationship with the phenological metrics from 2003 to 2013 were plotted: (a) the relationship of SOST from broad-leaved forest (BLF) by TPVM and yearly cumulative temperature; (b) the relationship of EOST from BLF by TPVM and yearly cumulative temperature; (c) the relationship of SOST from non-irrigated arable land (NIA) by TPVM and yearly cumulative precipitation; and (d) the relationship of MAXT from NIA by TPVM and yearly cumulative precipitation.
Remotesensing 09 00144 g012
Table
Table 1. List of abbreviation and acronyms used in the paper.
Table 1. List of abbreviation and acronyms used in the paper.
Abbreviation DefinitionAbbreviation Definition
AVHRR Advanced Very High-Resolution RadiometerLOGSLength of Growing Season
BISEBest Index Slope ExtractionLP DAACLand Processes Distributed Active Archive Center
CAOSCatchments as Organised SystemsLUTLook-Up Table
CCPerson’s Correlation CoefficientMAEMean Absolute Error
CORINECoORdination of INformation on the EnvironmentMAXTTime of Maximum LAI value
CSDMCanopy Structure Dynamic ModelmBISEModified Best Index Slope Extraction
DDSDynamically Dimensioned SearchMODISModerate Resolution Imaging Spectroradiometer
DEMDigital Elevation MapNDVINormalized Difference Vegetation Index
DLMDouble Logistic ModelQCQuality Criteria
DOYDay of YearRMSERoot Mean Squared Error
EOSTEnd of Season Time SEBSurface Energy Balance
ESDISEarth Science Data and Information SystemSOSTStart of Season Time
EVIEnhanced Vegetation IndexSVATSoil-Vegetation-Atmosphere Transfer
FPARFraction of absorbed Photosynthetically Active RadiationTPVMTemperature Precipitation Vegetation Model
GCMGlobal Climate ModelsVIVegetative Indicator
LAILeaf Area Index
Table
Table 2. Minimum and maximum temperature and precipitation data for each year from 2003 to 2013 for Attert Catchment.
Table 2. Minimum and maximum temperature and precipitation data for each year from 2003 to 2013 for Attert Catchment.
YearYearly Cumulative Temperature (°C)Yearly Cumulative Precipitation (mm)
MinimumMaximumMinimumMaximum
200333913552670715
200431703265751899
200533183683574697
200634413940713868
2007336339678921020
2008310837048781025
200932703801736959
201029893436669949
201133713881495777
2012317435738271082
201330003399727941

Share and Cite

MDPI and ACS Style

Sun, L.; Schulz, K. Spatio-Temporal LAI Modelling by Integrating Climate and MODIS LAI Data in a Mesoscale Catchment. Remote Sens. 2017, 9, 144. https://doi.org/10.3390/rs9020144

AMA Style

Sun L, Schulz K. Spatio-Temporal LAI Modelling by Integrating Climate and MODIS LAI Data in a Mesoscale Catchment. Remote Sensing. 2017; 9(2):144. https://doi.org/10.3390/rs9020144

Chicago/Turabian Style

Sun, Liya, and Karsten Schulz. 2017. "Spatio-Temporal LAI Modelling by Integrating Climate and MODIS LAI Data in a Mesoscale Catchment" Remote Sensing 9, no. 2: 144. https://doi.org/10.3390/rs9020144

APA Style

Sun, L., & Schulz, K. (2017). Spatio-Temporal LAI Modelling by Integrating Climate and MODIS LAI Data in a Mesoscale Catchment. Remote Sensing, 9(2), 144. https://doi.org/10.3390/rs9020144

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop