Modeling the Observed Microwave Emission from Shallow Multi-Layer Tundra Snow Using DMRT-ML
Abstract
1. Introduction
2. Methodology
2.1. Description of the DMRT-ML Snow Emission Model
2.2. Data Analysis Workflow
3. Data and Data Processing
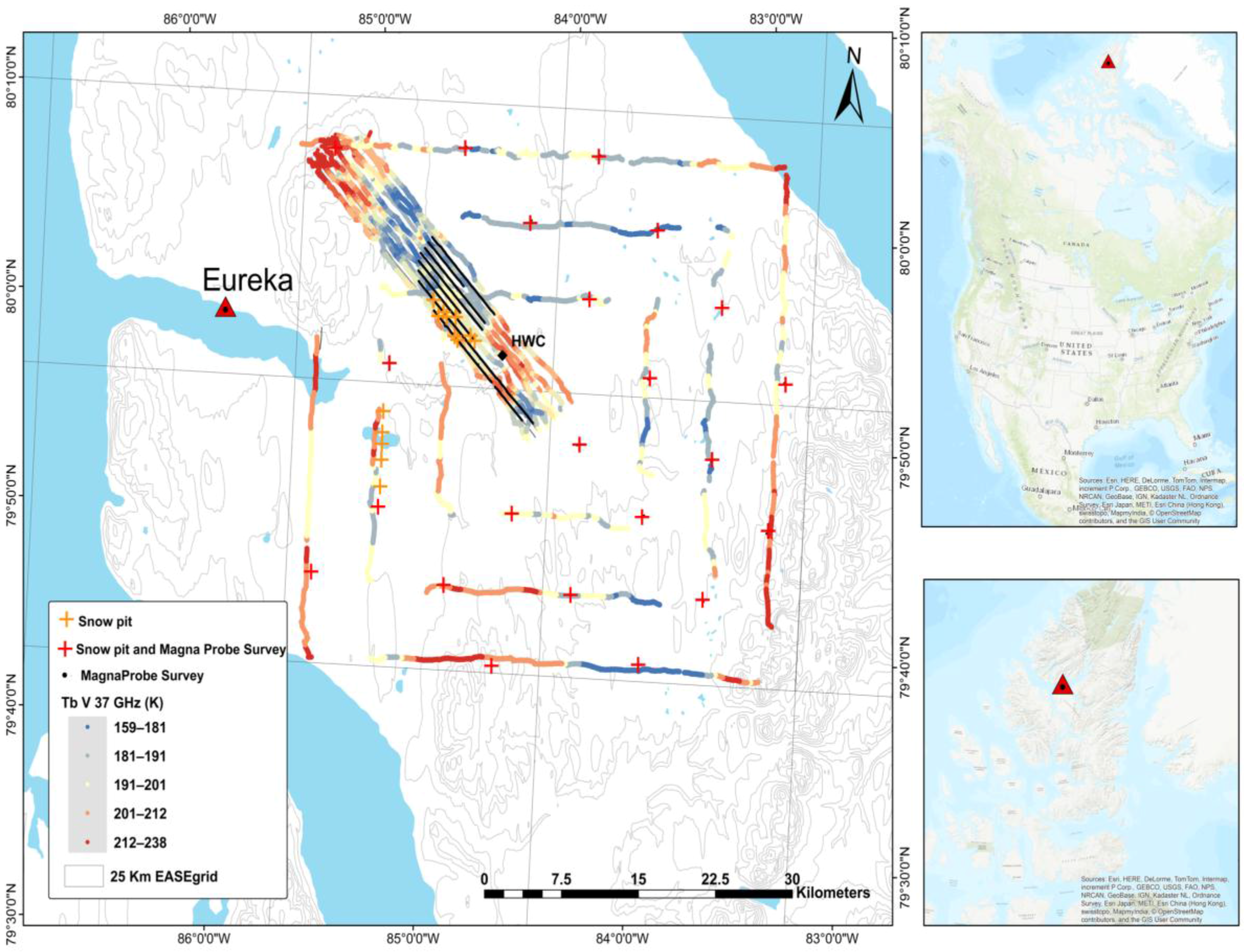
3.1. Study Area
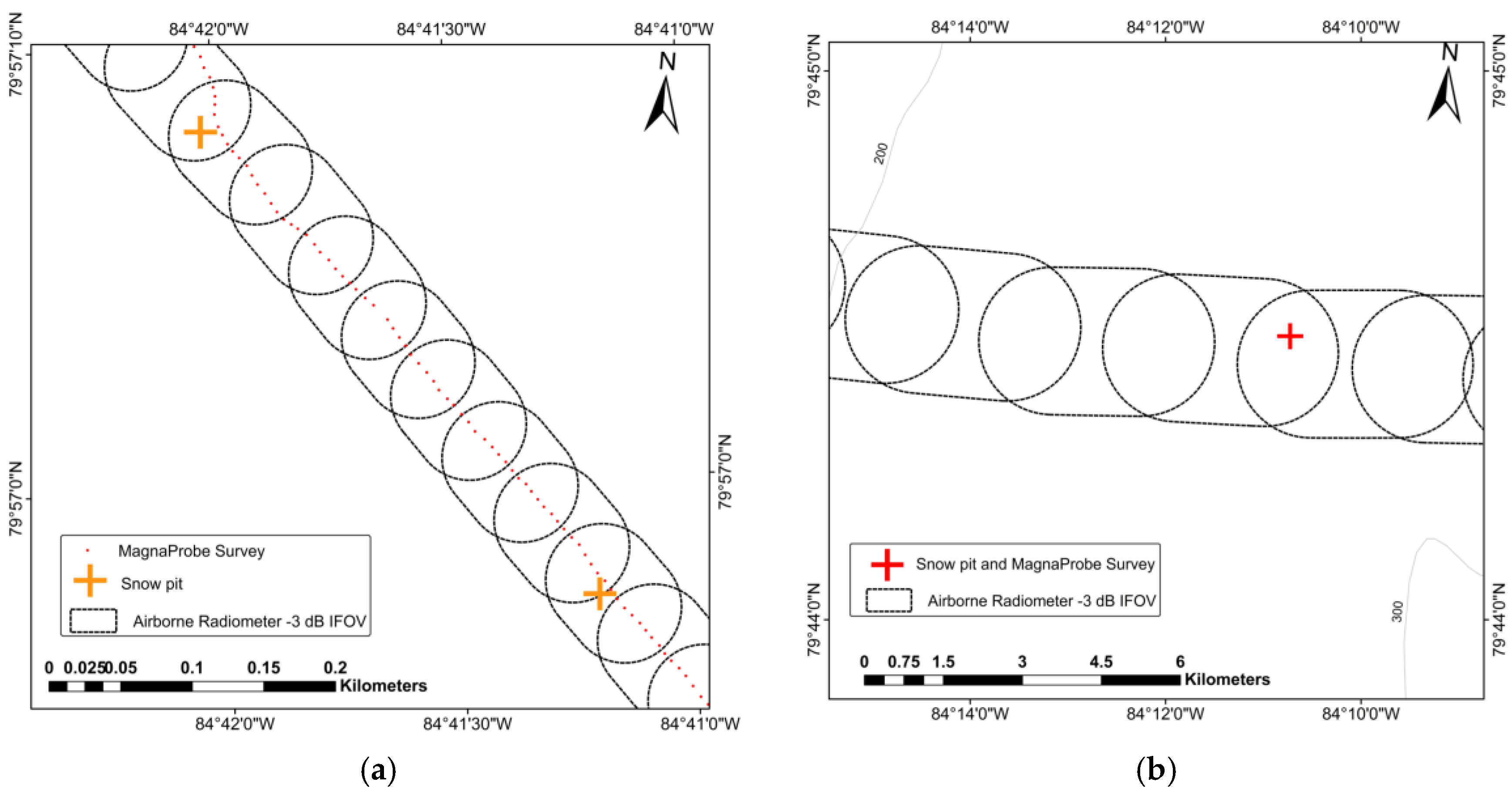
3.2. Airborne Data
- Local-scale grid (33 km × 6 km) low altitude flight (~350 m above ground level [a.g.l]), flown on 20 April.
- Local-scale grid (33 km × 6 km) high altitude flight (~2900 m a.g.l.), flown on 21 April.
- Regional-scale grid 48 km × 48 km high altitude flight (~2700 m a.g.l), flown on 21 April.
3.3. Satellite Data
3.4. Ground Based In Situ Data
4. Results
4.1. Airborne Microwave Tb Observations of Snow
4.2. Parameterization of the DMRT-ML
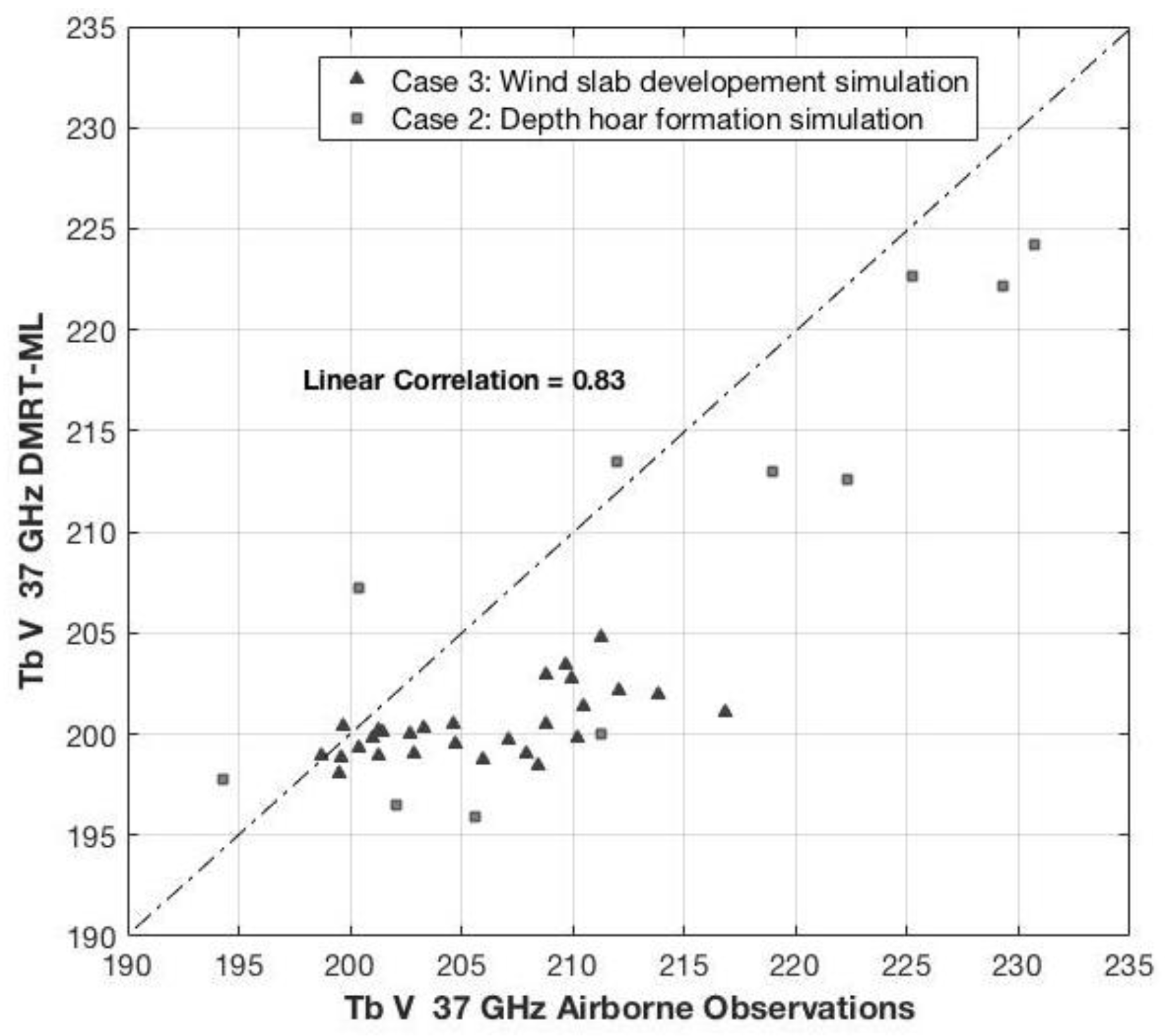
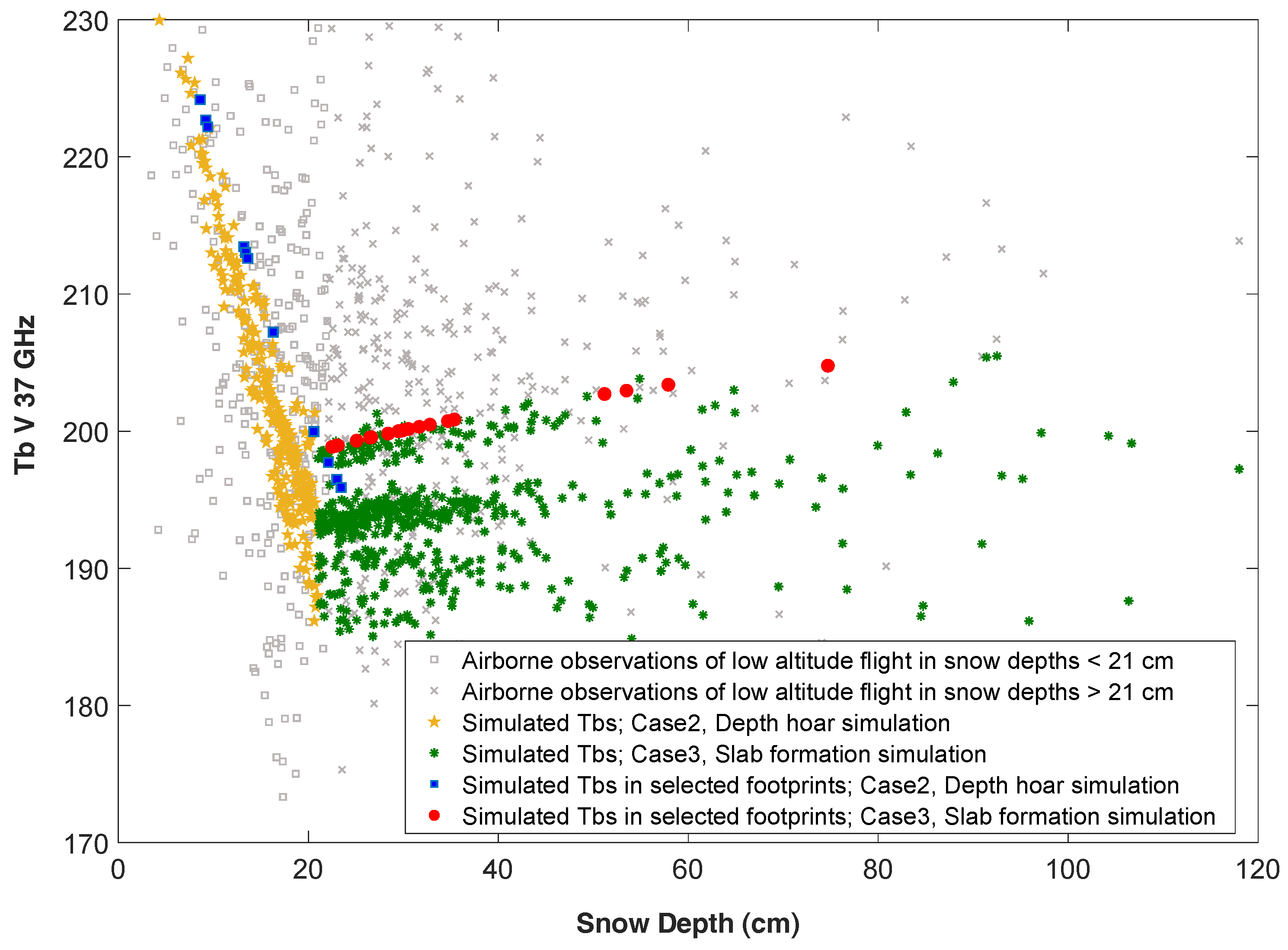
4.3. Comparison of DMRT-ML Modeled Tb with Observations
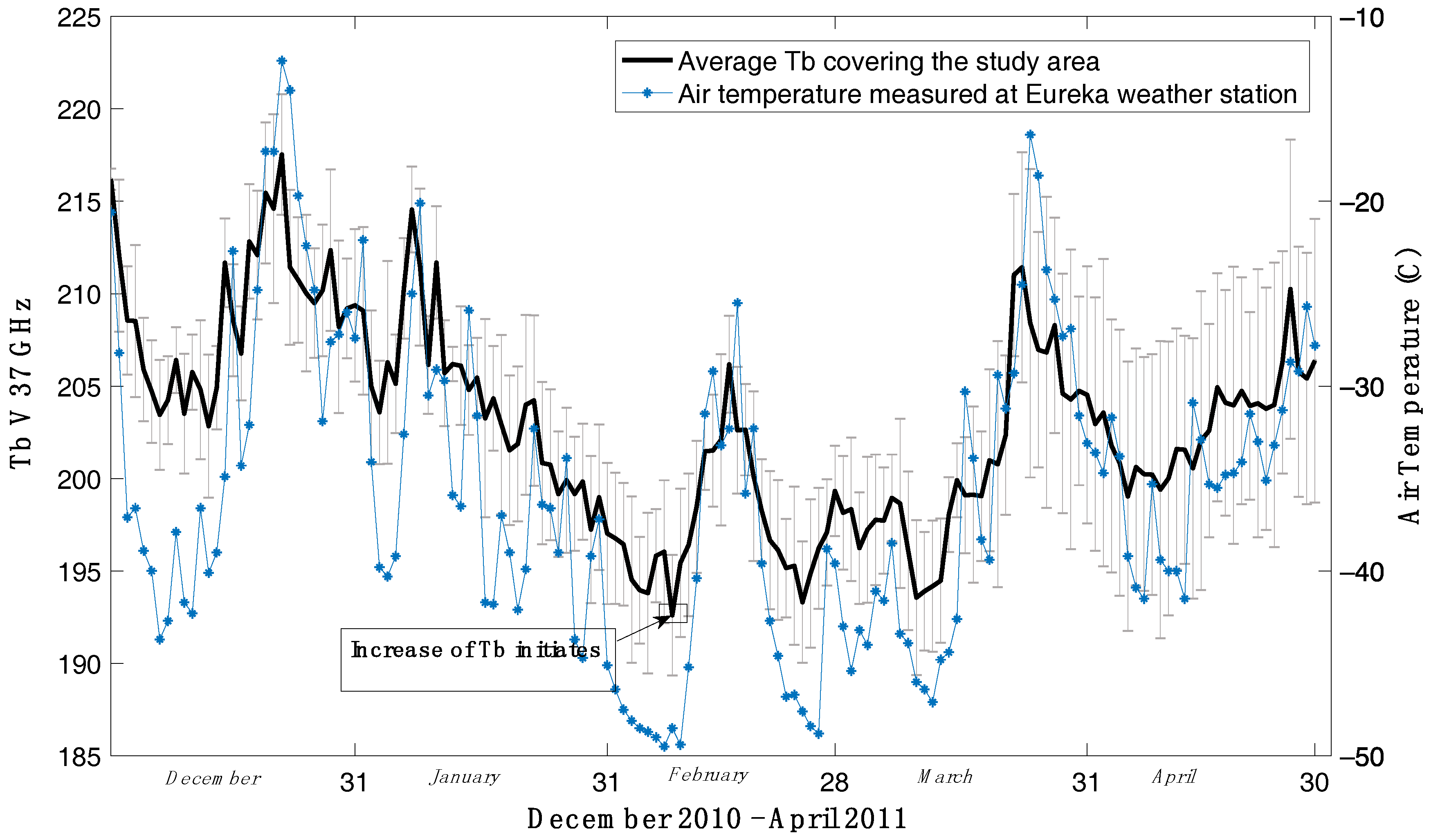
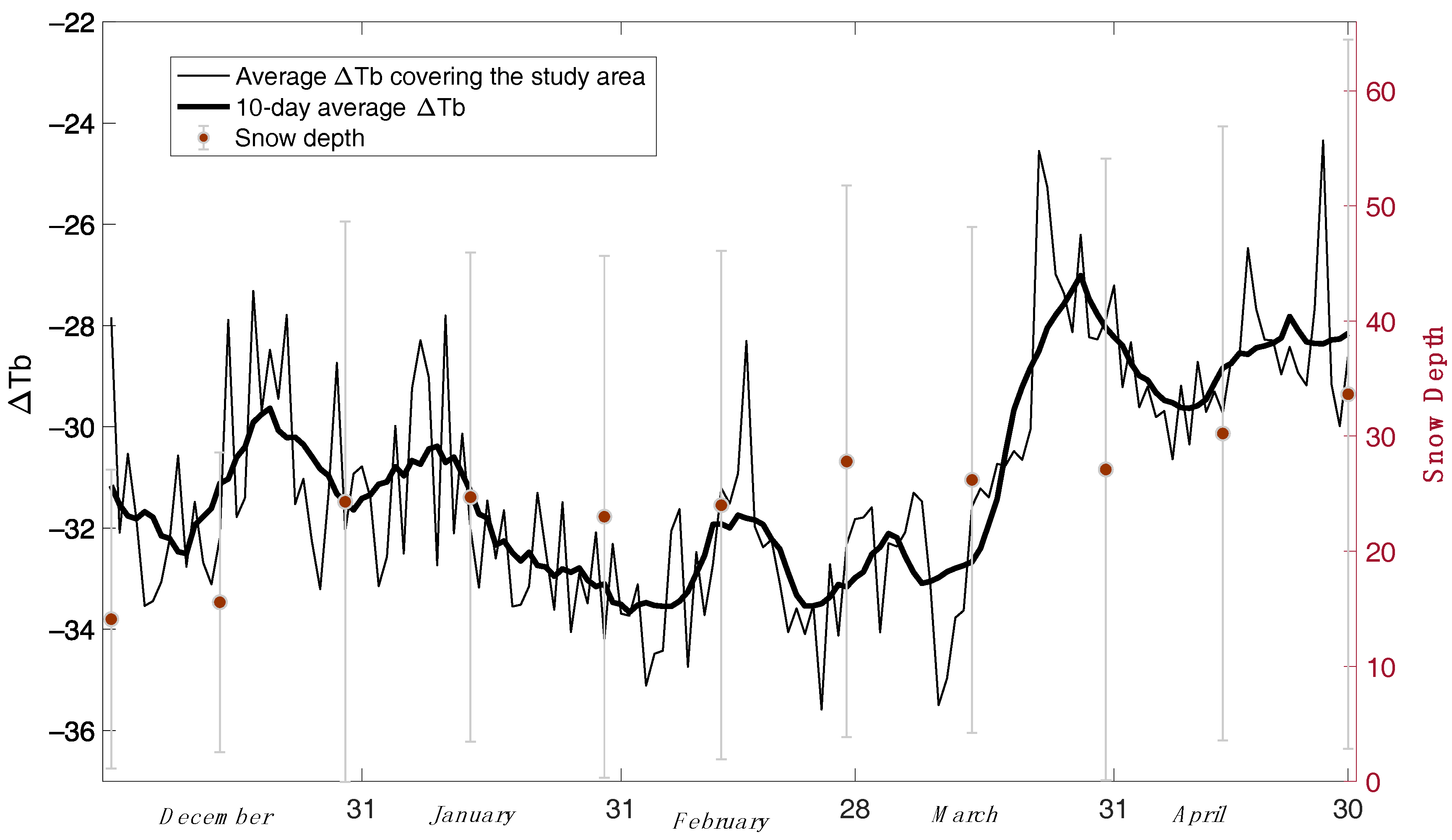
4.4. Application to AMSR-E Time Series Data
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rees, A.; English, M.; Derksen, C.; Toose, P.; Silis, A. Observations of late winter Canadian tundra snow cover properties. Hydrol. Process. 2014, 28, 3962–3977. [Google Scholar] [CrossRef]
- Cohen, J.; Rind, D. The effect of snow cover on the climate. J. Clim. 1991, 4, 689–706. [Google Scholar] [CrossRef]
- Fletcher, C.G.; Kushner, P.J.; Hall, A.; Qu, X. Circulation responses to snow albedo feedback in climate change. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Takala, M.; Luojus, K.; Pulliainen, J.; Derksen, C.; Lemmetyinen, J.; Kärnä, J.-P.; Koskinen, J.; Bojkov, B. Estimating northern hemisphere snow water equivalent for climate research through assimilation of space-borne radiometer data and ground-based measurements. Remote Sens. Environ. 2011, 115, 3517–3529. [Google Scholar] [CrossRef]
- Luojus, K.; Pulliainen, J.; Takala, M.; Lemmetyinen, J.; Derksen, C.; Wang, L. Snow Water Equivalent (SWE) Product Guide; European Space Agency Study Contract Report; Finnish Meteorological Institute: Helsinki, Finland.
- Kelly, R. The AMSR-E Snow Depth Algorithm: Description and Initial Results. J. Remote Sens. Soc. Jpn. 2009, 29, 307–317. [Google Scholar]
- Tedesco, M.; Pulliainen, J.; Takala, M.; Hallikainen, M.; Pampaloni, P. Artificial neural network-based techniques for the retrieval of SWE and snow depth from SSM/I data. Remote Sens. Environ. 2004, 90, 76–85. [Google Scholar] [CrossRef]
- Pulliainen, J. Mapping of snow water equivalent and snow depth in boreal and sub-arctic zones by assimilating space-borne microwave radiometer data and ground-based observations. Remote Sens. Environ. 2006, 101, 257–269. [Google Scholar] [CrossRef]
- Sturm, M.; Holmgren, J.; Liston, G.E. A Seasonal Snow Cover Classification System for Local to Global Applications. J. Clim. 1995, 8, 1261–1283. [Google Scholar] [CrossRef]
- Sturm, M.; Taras, B.; Liston, G.E.; Derksen, C.; Jonas, T.; Lea, J. Estimating Snow Water Equivalent Using Snow Depth Data and Climate Classes. J. Hydrometeorol. 2010, 11, 1380–1394. [Google Scholar] [CrossRef]
- Derksen, C.; Toose, P.; Rees, A.; Wang, L.; English, M.; Walker, A.; Sturm, M. Development of a tundra-specific snow water equivalent retrieval algorithm for satellite passive microwave data. Remote Sens. Environ. 2010, 114, 1699–1709. [Google Scholar] [CrossRef]
- Derksen, C.; Lemmetyinen, J.; Toose, P.; Silis, A.; Pulliainen, J.; Sturm, M. Physical properties of Arctic versus subarctic snow: Implications for high latitude passive microwave snow water equivalent retrievals. J. Geophys. Res. Atmos. 2014, 119, 7254–7270. [Google Scholar] [CrossRef]
- Derksen, C.; Toose, P.; Lemmetyinen, J.; Pulliainen, J.; Langlois, A.; Rutter, N.; Fuller, M.C. Evaluation of passive microwave brightness temperature simulations and snow water equivalent retrievals through a winter season. Remote Sens. Environ. 2012, 117, 236–248. [Google Scholar] [CrossRef]
- Rosenfeld, S.; Grody, N. Anomalous microwave spectra of snow cover observed from Special Sensor Microwave/Imager measurements. J. Geophys. Res. 2000, 105, 14913. [Google Scholar] [CrossRef]
- Liang, D.; Xu, X.; Tsang, L.; Andreadis, K.M.; Josberger, E.G. The effects of layers in dry snow on its passive microwave emissions using dense media radiative transfer theory based on the quasicrystalline approximation (QCA/DMRT). IEEE Trans. Geosci. Remote Sens. 2008, 46, 3663–3671. [Google Scholar] [CrossRef]
- Picard, G.; Brucker, L.; Roy, A.; Dupont, F.; Fily, M.; Royer, A. Simulation of the microwave emission of multi-layered snowpacks using the dense media radiative transfer theory: The DMRT-ML model. Geosci. Model Dev. Discuss. 2012, 5, 3647–3694. [Google Scholar] [CrossRef]
- Roy, A.; Picard, G.; Royer, A.; Montpetit, B. Brightness temperature simulations of the Canadian seasonal snowpack driven by measurements of the snow specific surface area. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4692–4704. [Google Scholar] [CrossRef]
- Tsang, L.; Chen, C.-T.; Chang, A.T.C.; Guo, J.; Ding, K.-H. Dense media radiative transfer theory based on quasicrystalline approximation with applications to passive microwave remote sensing of snow. Radio Sci. 2000, 35, 731–749. [Google Scholar] [CrossRef]
- Brucker, L.; Picard, G.; Fily, M. Snow grain-size profiles deduced from microwave snow emissivities in Antarctica. J. Glaciol. 2010, 56, 514–526. [Google Scholar] [CrossRef]
- Kelly, R.; Chang, A.T.; Tsang, L.; Foster, J.L. A prototype AMSR-E global snow area and snow depth algorithm. IEEE Trans. Geosci. Remote Sens. 2003, 41, 230–242. [Google Scholar] [CrossRef]
- Wen, B.; Tsang, L.; Winebrenner, D.P.; Ishimaru, A. Dense medium radiative transfer theory: Comparison with experiment and application to microwave remote sensing and polarimetry. IEEE Trans. Geosci. Remote Sens. 1990, 28, 46–59. [Google Scholar] [CrossRef]
- Jin, Y.Q. Electromagnetic Scattering Modelling for Quantitative Remote Sensing; World Scientific: Singapore, 1993; ISBN 9810216483. [Google Scholar]
- Chandrasekhar, S. Radiative Transfer; McGraw-Hill: New York, NY, USA, 1960. [Google Scholar]
- Grody, N. Relationship between snow parameters and microwave satellite measurements: Theory compared with Advanced Microwave Sounding Unit observations from 23 to 150 GHz. J. Geophys. Res. 2008, 113, D22108. [Google Scholar] [CrossRef]
- Royer, A.; Roy, A.; Montpetit, B.; Saint-Jean-Rondeau, O.; Picard, G.; Brucker, L.; Langlois, A. Remote Sensing of Environment Comparison of commonly-used microwave radiative transfer models for snow remote sensing. Remote Sens. Environ. 2017, 190, 247–259. [Google Scholar] [CrossRef]
- Foster, J.L.; Sun, C.; Walker, J.P.; Kelly, R.; Chang, A.; Dong, J.; Powell, H. Quantifying the uncertainty in passive microwave snow water equivalent observations. Remote Sens. Environ. 2005, 94, 187–203. [Google Scholar] [CrossRef]
- Durand, M.; Kim, E.; Margulis, S. Quantifying Uncertainty in Modeling Snow Microwave Radiance for a Mountain Snowpack at the Point-Scale, Including Stratigraphic Effects. Geosci. Remote. 2008, 46, 1753–1767. [Google Scholar] [CrossRef]
- Roy, A.; Royer, A.; Montpetit, B.; Bartlett, P.A.; Langlois, A. Snow specific surface area simulation using the one-layer snow model in the Canadian LAnd Surface Scheme (CLASS). Cryosphere 2013, 7, 961–975. [Google Scholar] [CrossRef]
- Gallet, J.C.; Domine, F.; Zender, C.S.; Picard, G. Measurement of the specific surface area of snow using infrared reflectance in an integrating sphere at 1310 and 1550 nm. Cryosphere 2009, 3, 167–182. [Google Scholar] [CrossRef]
- Environment and Climate Change Canada (ECCC). Eureka Weather Station, Canadian Climate Normal. 1981. Available online: http://climate.weather.gc.ca/climate_normals/index_e.html (accessed on 4 December 2017).
- Woo, M.; Heron, R.; Marsh, P.; Steer, P. Comparison of weather station snowfall with winter snow accumulation in high arctic basins. Atmos. Ocean 1983, 21, 312–325. [Google Scholar] [CrossRef]
- Edlund, S.A.; Woo, M.-K.; Young, K.L. Climate, hydrology and vegetation patterns Hot Weather Creek, Ellesmere Island, Arctic Canada. Nord. Hydrol. 1990, 21, 273–286. [Google Scholar]
- Woo, M.; Young, K.L. Hydrology of a Small Drainage Basin with Polar Oasis Environment, Fosheim Peninsula, Ellesmere Island, Canada. Permafr. Periglac. Process. 1997, 8, 257–277. [Google Scholar] [CrossRef]
- Woo, M.; Walker, A.; Yang, D.; Goodison, B. Pixel-scale ground snow survey for passive microwave study of the Arctic snow cover. In Proceedings of the 52nd Eastern Snow Conference, Toronto, ON, Canada, 6–8 June 1995; pp. 51–57. [Google Scholar]
- Brodzik, M.J.; Billingsley, B.; Haran, T.; Raup, B.; Savoie, M.H. EASE-Grid 2.0: Incremental but Significant Improvements for Earth-Gridded Data Sets. ISPRS Int. J. Geo Inf. 2012, 1, 32–45. [Google Scholar] [CrossRef]
- Knowles, K.; Savoie, M.; Armstrong, R.; Brodzik, M. AMSR-E/Aqua Daily EASE-Grid Brightness Temperatures; National Snow and Ice Data Center (NSIDC): Boulder, CO, USA, 2006; Available online: http://dx.doi.org/10.5067/XIMNXRTQVMOX (accessed on 1 March 2016).
- Strum, M.; Liston, G.E. The snow cover on lakes of the Arctic Coastal Plain of Alaska, USA. J. Glaciol. 2003, 49, 370–380. [Google Scholar] [CrossRef]
- Farnes, P.E.; Peterson, N.R.; Goodison, B.E.; Richards, R.P. Metrication of manual snow sampling equipment by western snow conference metrication committee. In Proceedings of the 50th Annual Meeting of the Western Snow Conference, Reno, NV, USA, 19–23 April 1982; pp. 120–132. [Google Scholar]
- Macqueen, J. Some methods for classification and analysis of multivariate observations. Proc. Fifth Berkeley Symp. Math. Stat. Probab. 1967, 1, 281–297. [Google Scholar]
- Li, D.; Durand, M.; Margulis, S.A. Potential for hydrologic characterization of deep mountain snowpack via passive microwave remote sensing in the Kern River basin, Sierra Nevada, USA. Remote Sens. Environ. 2012, 125, 34–48. [Google Scholar] [CrossRef]
- Rees, A.; Lemmetyinen, J.; Derksen, C.; Pulliainen, J.; English, M. Observed and modelled effects of ice lens formation on passive microwave brightness temperatures over snow covered tundra. Remote Sens. Environ. 2010, 114, 116–126. [Google Scholar] [CrossRef]
- Saberi, N.; Kelly, R. An evaluation of DMRT-ML for AMSR2 estimates of snow depth. In Proceedings of the Geoscience and Remote Sensing Symposium (IGARSS), IEEE International, Quebec City, QC, Canada, 13–18 July 2014; pp. 1943–1946. [Google Scholar]
- Lemmetyinen, J.; Schwank, M.; Rautiainen, K.; Kontu, A.; Parkkinen, T.; Mätzler, C.; Wiesmann, A.; Wegmüller, U.; Derksen, C.; Toose, P.; et al. Snow density and ground permittivity retrieved from L-band radiometry: Application to experimental data. Remote Sens. Environ. 2016, 180, 377–391. [Google Scholar] [CrossRef]
- Sturm, M.; Grenfell, T.C.; Perovich, D.K. Passive microwave measurements of tundra and taiga snow covers in Alaska, USA. Ann. Glaciol. 1993, 17, 125–130. [Google Scholar] [CrossRef]
- Sturm, M.; Benson, C. Vapor transport, grain growth and depth-hoar development in the subarctic snow. J. Glaciol. 1997, 43, 42–59. [Google Scholar] [CrossRef]
- Roy, A.; Royer, A.; Montpetit, B.; Langlois, A. Microwave snow emission modeling of boreal forest environments. In Proceedings of the Geoscience and Remote Sensing Symposium (IGARSS), IEEE International, Milan, Italy, 26–31 July 2015; pp. 754–757. [Google Scholar]
- Langlois, A.; Royer, A.; Derksen, C.; Montpetit, B.; Dupont, F.; Goïta, K. Coupling the snow thermodynamic model SNOWPACK with the microwave emission model of layered snowpacks for subarctic and arctic snow water equivalent retrievals. Water Resour. Res. 2012, 48, W12524. [Google Scholar] [CrossRef]
- Kontu, A.; Lemmetyinen, J.; Vehviläinen, J.; Leppänen, L.; Pulliainen, J. Remote Sensing of Environment Coupling SNOWPACK-modeled grain size parameters with the HUT snow emission model. Remote Sens. Environ. 2017, 194, 33–47. [Google Scholar] [CrossRef]
- Josberger, E.; Mognard, N. A passive microwave snow depth algorithm with a proxy for snow metamorphism. Hydrol. Process. 2002, 16, 1557–1568. [Google Scholar] [CrossRef]



| Statistics | Depth (cm) | Density (kg m−3) | SWE (mm) |
|---|---|---|---|
| Number of Samples | 15,251 | 576 | 576 |
| Mean | 26.9 | 246 | 67.0 |
| Standard deviation | 23.9 | 82 | 63.1 |
| Coefficient of variation | 89% | 33% | 94% |
| Layers 2 and 3 | Layers 4 and 5 (Base) | ||||||
|---|---|---|---|---|---|---|---|
| Layer Type | Soft Slab, Slab to Hoar, Medium Grained, Hard Slab, Moderate Slab | Chains of Hoar Indurated Depth Hoar, Chains of Hoar | Bulk Total | ||||
| Statistic (M,S,C) | M | S | C% | M | S | C% | |
| layer thickness (cm) | 4.2 | 3.5 | 84 | 6.2 | 2.7 | 43 | 2.4 |
| layer temperature (C) | −27.2 | 1.7 | 0.69 | −26.7 | 1.6 | 0.6 | −27.0 |
| grain size—long (mm) | 0.9 | 0.6 | 62 | 5.6 | 2.4 | 43 | 2.4 |
| grain size—short (mm) | 0.4 | 0.3 | 72 | 2 | 1.1 | 56 | 0.9 |
| Density (kg m−3) | 324 | 88 | 27 | 215.6 | 41 | 19 | 300.1 |
| Input Parameters | Case 1: One Layer: Depth Hoar Development | Case 2: Two Layers: Static Wind Slab to Depth Hoar Ratio 2:1 | Case 3: Two Layers-Static 7 cm Depth Hoar Layer with a Thickening Wind Slab Layer above |
|---|---|---|---|
| Effective Grain size | 400 µm–1000 µm | Wind slab: 400 µm–700 µm; Depth hoar: 900 µm–1200 µm | Wind slab: 400 µm–700 µm; Depth hoar: 900 µm–1200 µm |
| Density | 300 kg m−3 | Wind slab: 324 kg m−3; Depth hoar: 215 kg m−3 | Wind slab: 324 kg m−3; Depth hoar: 215 kg m−3 |
| Snow Depth | 10 cm–50 cm | Wind slab: 3.3 cm–16.6 cm; Depth hoar: 6.6 cm–33.3 cm | Wind slab: 3 cm–43 cm; Depth hoar: 7 cm |
| Substratum | Constant at 247.0 K | ||
| Temperature | Soil model = None; Semi-infinite snowpack | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saberi, N.; Kelly, R.; Toose, P.; Roy, A.; Derksen, C. Modeling the Observed Microwave Emission from Shallow Multi-Layer Tundra Snow Using DMRT-ML. Remote Sens. 2017, 9, 1327. https://doi.org/10.3390/rs9121327
Saberi N, Kelly R, Toose P, Roy A, Derksen C. Modeling the Observed Microwave Emission from Shallow Multi-Layer Tundra Snow Using DMRT-ML. Remote Sensing. 2017; 9(12):1327. https://doi.org/10.3390/rs9121327
Chicago/Turabian StyleSaberi, Nastaran, Richard Kelly, Peter Toose, Alexandre Roy, and Chris Derksen. 2017. "Modeling the Observed Microwave Emission from Shallow Multi-Layer Tundra Snow Using DMRT-ML" Remote Sensing 9, no. 12: 1327. https://doi.org/10.3390/rs9121327
APA StyleSaberi, N., Kelly, R., Toose, P., Roy, A., & Derksen, C. (2017). Modeling the Observed Microwave Emission from Shallow Multi-Layer Tundra Snow Using DMRT-ML. Remote Sensing, 9(12), 1327. https://doi.org/10.3390/rs9121327





