Abstract
The observed brightness temperatures (Tb) at 37 GHz from typical moderate density dry snow in mid-latitudes decreases with increasing snow water equivalent (SWE) due to volume scattering of the ground emissions by the overlying snow. At a certain point, however, as SWE increases, the emission from the snowpack offsets the scattering of the sub-nivean emission. In tundra snow, the Tb slope reversal occurs at shallower snow thicknesses. While it has been postulated that the inflection point in the seasonal time series of observed Tb V 37 GHz of tundra snow is controlled by the formation of a thick wind slab layer, the simulation of this effect has yet to be confirmed. Therefore, the Dense Media Radiative Transfer Theory for Multi Layered (DMRT-ML) snowpack is used to predict the passive microwave response from airborne observations over shallow, dense, slab-layered tundra snow. Airborne radiometer observations coordinated with ground-based in situ snow measurements were acquired in the Canadian high Arctic near Eureka, NT, in April 2011. The DMRT-ML was parameterized with the in situ snow measurements using a two-layer snowpack and run in two configurations: a depth hoar and a wind slab dominated pack. With these two configurations, the calibrated DMRT-ML successfully predicted the Tb V 37 GHz response (R correlation of 0.83) when compared with the observed airborne Tb footprints containing snow pits measurements. Using this calibrated model, the DMRT-ML was applied to the whole study region. At the satellite observation scale, observations from the Advanced Microwave Scanning Radiometer-Earth Observing System (AMSR-E) over the study area reflected seasonal differences between Tb V 37 GHz and Tb V 19 GHz that supports the hypothesis of the development of an early season volume scattering depth hoar layer, followed by the growth of the late season emission-dominated wind slab layer. This research highlights the necessity to consider the two-part emission characteristics of a slab-dominated tundra snowpack at 37 GHz Tb.
1. Introduction
Tundra snow cover is a key variable in the cryosphere that can significantly control local to regional scale surface water balances, energy fluxes, as well as ecosystem functioning and permafrost dynamics [1]. At regional and global scales, snow cover affects atmospheric circulation through variations in radiative forcing and the snow-albedo feedback effect [2,3]. While satellite-based mapping of snow cover extent is routine, satellite based mapping of snow water equivalent (SWE) is less mature and it is still challenging to estimate snow accumulation regionally and globally to the desired accuracy that can inform climate change or catchment-based hydrology applications. Significant progress has been made in this area [4,5,6,7,8], yet there is still uncertainty in the retrievals, primarily because the spatial resolution of the observation, most notably from passive microwave (PM) instruments (regional-scale), does not match the spatial resolution of SWE variability (local-scale). Furthermore, there are uncertainties in the retrieval process likely linked to the unique snow properties found in certain environments, such as the tundra snow, which accounts for 16% of the total northern hemisphere land surface [9,10].
Snow microphysical structure (depth, grain size, density and temperature profile) evolves during the winter season. In situ measurements of tundra snow properties reported in previous studies [1,11,12] provide a reference for tundra specific emission modeling with studies showing that one layer of early season snowpack develops to two predominant layer types of slab and hoar, as a result of kinetic grain metamorphism due strong vertical temperature gradients [9]. A fresh or recent snow at the surface of the pack is subject to wind redistribution [13]. The slab fraction increases even with increased overall pack depth, and as a multi-layer medium, the discrete layers in the snow add complexity to the bulk microwave emission from the pack since each snow layer evolves differently as the season progresses and from year to year.
In terms of the general microwave emission from a typical low to moderate density dry snowpack, an increased snowpack thickness from progressive snow accumulation manifests itself as a decrease in microwave emission at shorter wavelengths (>25 GHz), as measured by the brightness temperature (Tb). This is because the microwave scattering coefficient dominates the emission process. However, beyond a threshold of SWE, the Tb increase as emission from the snowpack increases the Tb and overrides the scattering signature. In shallow tundra snow, unique layering characteristics coupled with high density, slab-dominated snowpacks produce an increase in the Tb response, as the winter season progresses, at shallower snow depths relative to other environments such as the boreal forest or alpine regions.
The slope reversal from decreasing to increasing Tb at 37 GHz with increasing snow accumulation has been observed in a limited number of studies. Rosenfeld and Grody [14] discussed the inflection behavior observed by the Special Sensor Microwave/Image (SSMI) as an anomaly in microwave spectra and simulated the inverted Tb applying Dense Media Theory (DMT) radiative transfer approach successfully for a two-layer snowpack of crust and aged snow. This work provided limited details on the in situ measurements. Derksen et al. [11] explored the seasonal 37 GHz Tb slope reversal in an empirical fashion for spaceborne SWE retrievals based on cumulative absolute difference of Tbs. Using a physically-based approach, Liang et al. [15] applied the Dense Media Radiative Transfer approach based on the quasi-crystalline approximation (QCA) with stickiness to simulate Tbs from multilayered stratified medium depth to deep snow (~40–80 cm). They demonstrated the Tb inflection behavior, which was driven by ground based snow microstructure measurements of a multi-layer pack with larger grains at depth and smaller ones above with lower densities. However, Liang et al. [15] used a multilayer simulation (>6 layers) with exact input variables for each layer from in situ measurements. While the approach yielded good results, physical stratification of the snow adds significant complexity to the model implementation and may lead to overfitting in the process of finding the best correlation between simulations and observations. Therefore, model applicability to airborne or spaceborne observations for snow depth retrieval is not straightforward. Moreover, the representation of slab on depth-hoar that is frequently seen in tundra environments, is less well tested by these models.
Determining the stratigraphic and microstructure layering of snow, at least in general form, is an operational prerequisite if physical modeling approaches are to be used in SWE retrievals. While the study by Derksen et al. [11] explores the empirical evidence of the Tb reversal at 37 GHz, it does not attempt to explain the Tb response from a physical perspective while the Rosenfeld and Grody [14] study does not provide any direct experimental evidence of the existence of a dense layer, except through inference from Tb variations observed from satellite Tb measurements. Therefore, this study develops the ideas of Derksen et al. and Rosenfeld and Grody [11,14] by parameterizing and testing a physically-based model that predicts the Tb response, including the Tb slope reversal from an Arctic tundra snowpack using DMRT-ML and in situ snow pit observations. The model results are compared and validated against coincident multi-resolution airborne microwave Tb observations. The goal of this research is to be able to apply this model in a manner requiring only a minimal parameterization scheme that is independent of ground-based data for satellite SWE retrievals.
2. Methodology
2.1. Description of the DMRT-ML Snow Emission Model
Electromagnetic radiation passing through a multi-layered dry snowpack medium can be modeled by scattering, absorption, reflection, refraction and transmission considering dielectric properties of the medium. Three different groups of empirical, semi-empirical and physical emission models have been developed to derive estimates of a snowpack’s physical parameters using radiometry. Empirical models typically do not account for snowpack microstructure metamorphism, which significantly impacts the microwave signature of a snowpack. Semi-empirical and physical models of the microwave emission from snow have evolved as our understanding from experiments of snow microwave emission has improved and has been fed back to model design. The Dense Media Radiative Transfer Model-Multi-Layer (DMRT-ML) is a physically-based model that couples the microstructural properties of a snowpack to its emission signature. DMRT-ML has been employed in several studies using ground-based radiometers and in situ snow measurements [16,17]. The Dense Media Radiative Transfer (DMRT) model [18] and DMRT-ML have also been employed and evaluated for SWE retrievals using spaceborne radiometry (e.g., [19,20]). However, using DMRT-ML to retrieve snow depth globally needs parameterization of the dynamic state of the snowpack. Observations from airborne radiometry together with in situ measurements on the ground makes it possible to constrain the DMRT-ML for inversion and snow depth retrieval.
DMRT theory was developed by Tsang et al. [18] for a layered snowpack, and was originally based on the Quasi Crystalline Approximation (QCA) of scattering behavior of particles in a dense medium, where the particles occupy more than 20% of the fractional volume [21,22]. Picard et al. [16] employed Quasi Crystalline Approximation-Coherent Potential (QCA-CP) to model emission for a multi-layered snowpack in a range of 1–200 GHz. QCA and QCA-CP approximations let us model particle positions pair distribution functions while coherent wave interactions are assumed. In so doing, these approximations allow wave interactions to be modeled in a dense medium [18]. For DMRT-ML, snow scattering and extinction coefficients and the form of the phase function are computed based on DMRT theory, whereby the radiative transfer equation, based on the work of Jin [22], is solved using the Discrete Ordinate method (DISORT) [23]. Our implementation follows the approach of a mono-disperse assumption in a grain size distribution within a layer with the empirical method for large particles [24].
The DMRT-ML model is implemented by providing snowpack inputs including grain size, density, physical temperature, and thickness of each layer. For ground-based radiometer studies this is straightforward because the radiometer typically senses an instantaneous field of view (IFOV) of the order of a few meters at most, depending on the target-sensor separation. However, at the spatial scale of airborne observations (with typical IFOVs at the 100 s of meters) the spatial and temporal variability of snowpack physical properties can make it challenging to constrain the DMRT-ML model parameter set. This might also be exacerbated by spatial miss-match between flight lines and ground measurements. By characterizing the spatial variability of snowpack properties from field data using information given by a semivariogram, the spatial mismatch between observations on the ground and from air can be rendered acceptable by establishing geographical limits in the analysis beyond which ground and air observations should no longer be compared directly because they are too far apart and no longer spatially autocorrelated.
Accurate DMRT-ML model parameterization is of the utmost importance. Ground-based measurements of snowpack properties do not always match model input requirements. For example, one of the most commonly measured snow grain metrics observed by snow surveyors in the field is the maximum physical dimension(s) of the snow grain. Unfortunately, this metric cannot be directly input into the DMRT-ML model which represents the snow grains as spheres. Current research in this area is attempting to resolve differences between different snow grain size representations and how these differences influence model results [25]. Standard snow grain size measurements protocols need to be established because: (a) the models require a more sophisticated representation of snow grains (optical grain size, correlation length, specific surface area (SSA); and (b) the traditional observed measurement of the maximum dimension of the snow grain is inherently subjective depending on the surveyor and can vary between different surveyors using the same sampling equipment [26,27]. A simple scaling factor has been developed by Roy et al. [28] to convert measured SSA [29] to effective grain size into DMRT-ML. While it is recognized that this scaling factor is optimized to produce the best results with the given snow survey data and may not be applicable to other snow survey data collected in different regions, it provides a starting point for defining snow microstructure inputs to DMRT-ML.
2.2. Data Analysis Workflow
This study investigates the DMRT-ML model performance over a high Arctic tundra snowpack by comparing simulated Tb V 37 GHz results with airborne Tbs measured at moderate resolutions and spaceborne Tb observations at coarse resolutions. The objective is to characterize and predict the observed Tb slope reversal in emission behavior at 37 GHz for tundra snow using the DMRT-ML model. The methodology workflow includes: (1) the pre-processing of airborne observations to match with snow surveys; (2) the generalizing of snowpack characteristics for emission modeling; (3) DMRT-ML parametrization; (4) analyzing the emission behavior of tundra snow in the study area using airborne observations; (5) implementing the DMRT-ML model in selected sites and then in all footprints with significant number of snow depth measurements; and (6) analysis of the AMSR-E Tb V 37 GHz signature of the study area through the same snow accumulation season.
3. Data and Data Processing
3.1. Study Area
Snow survey and passive microwave airborne brightness temperature measurements were made across the Fosheim Peninsula, near the Eureka weather station on Ellesmere Island (~80° N; 84° W) between 13 and 22 April 2011 (Figure 1). The region is cold and dry with an average annual air temperature at the Eureka weather station of −18.8 °C and total yearly precipitation of 79 mm (1981–2010), with almost 60% falling as snow [30]. The snow survey study area centered on a previously studied inland drainage basin, Hot Weather Creek (HWC), approximately 30 km inland from the weather station [12,31,32,33]. The HWC study area has been described as a polar oasis within the High Arctic polar desert because of its unique geography of being protected by surrounding mountain ranges resulting in less cloud cover and warmer temperatures and subsequent abundance of vegetation compared to the surrounding High Arctic environments [32,33]. However, despite the greater presence and variety of tundra vegetation in this region relative to other regions of the High Arctic, the main controlling influence on the depth and distribution of snow across this region is local scale topography, as existing vegetation is extremely sparse (bare ground), or is very low-lying [31]. The terrain of the study area is generally flat land consisting of upper plateaus, gently rolling hills and long slopes of varying aspects, accounting for approximately 90% of the study area, with the remain 10% made up narrow incised river/stream drainage channels draining into flat wetlands, lakes and valley bottoms [33]. The Fosheim Peninsula is only approximately 75 km wide, but the extent of the generally flat terrain is large and far enough away from the coast to minimize the influence of the sea ice and surrounding mountain ranges on satellite-scale passive microwave swath data [34], and includes the coverage of multiple re-sampled 25 km Equal-Area Scalable Earth Grids (EASE-Grids) [35].
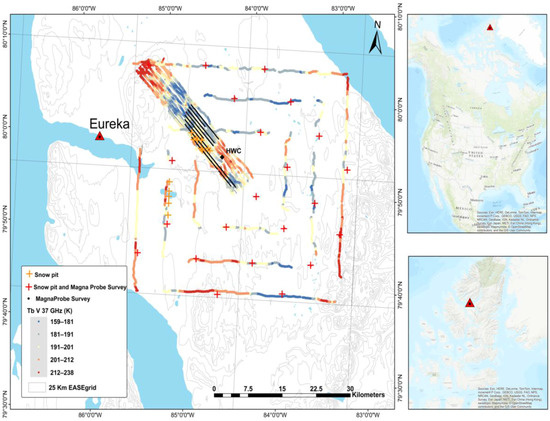
Figure 1.
(a) Snow survey locations, snow pits and MagnaProbe transects, and EASE-Grid pixel boundaries; and (b,c) the location of the study area in North America and Nunavut, respectively.
3.2. Airborne Data
Airborne Tb data were acquired from dual-polarized 19, 37 and 89 GHz microwave radiometers mounted on the Alfred Wegener Institute Polar-5 research aircraft. The radiometers were aft-viewing at a 53° incidence angle to simulate the earth-viewing characteristics of the satellite-based SSM/I and AMSR-E passive microwave sensors. The 19, 37 and 89 GHz radiometers all have the same 6° half-power beamwidth. After instrument calibration using warm and cold targets, the calibrated brightness accuracy was reported as <1 K for the 37 GHz and 89 GHz and <2 K for 19 GHz radiometers. The aircraft was based out of the Eureka weather station from 19 to 23 April 2011. Aircraft positional information was recorded using an AIMMS-20 system recording GPS data and platform attitude information which were used to precisely calculate the passive microwave radiometer footprint locations on the ground. All positional information was collected using the WGS 84 datum.
Three flight plans were devised to record multi-scale measurements of high Arctic tundra snow using passive microwave airborne radiometers. These multi-scale measurements include the following flights:
- Local-scale grid (33 km × 6 km) low altitude flight (~350 m above ground level [a.g.l]), flown on 20 April.
- Local-scale grid (33 km × 6 km) high altitude flight (~2900 m a.g.l.), flown on 21 April.
- Regional-scale grid 48 km × 48 km high altitude flight (~2700 m a.g.l), flown on 21 April.
Flights 1 and 2 constitute the local scale analysis data set while Flight 3 constitutes the regional scale analysis. Observations taken from a KT-19 infrared surface temperature sensor mounted on the aircraft with the same incidence angle and orientation as the high frequency radiometer were used in the regional scale modeling analysis to estimate the snow surface temperature. Figure 1 shows airborne flight lines, snow survey locations, HWC location as well as EASE grid pixel boundaries.
The approach used in this analysis to spatially link ground snow depth measurements to airborne passive microwave footprints is similar to that used by [11], where the IFOV of the airborne radiometer is calculated, and measured snow that falls within and around the bounds of this IFOV are linked to particular airborne measurement. The airborne radiometer’s IFOV dimension is dependent on the aircraft’s ground speed, altitude, roll, pitch and yaw, as well as the radiometer beamwidth, view angle, and integration time. The radiometer variables remain constant during data acquisition: beamwidth = 6°; view angle = 53°; and integration time = 1 s. The aircraft’s altitude above sea level remained stable along each flight line, however due to changes in terrain height, the height above ground varied, but on average was approximately 350 m above ground for the low altitude flights, and 2700 m (regional grid) to 2900 m (local grid) above ground for the high altitude flights. Variables such as aircraft heading and speed varied slightly during each flight, but overall was quite consistent at approximately 155 nautical miles per hour (~80 m/s). The aircraft’s roll, pitch and yaw varied substantially during turns, with the radiometer’s IFOV often pointed towards the horizon, rather than at the surface, and therefore these airborne measurements were removed from the analysis. If the airborne radiometer system was mounted on a stationary platform, the typical ground-projected IFOV for the low altitude flights would be approximately 100 m deep by 60 m wide. However, because the aircraft is moving, and the radiometer’s have a 1-s integration time, the IFOV between two observations is elongated in the along-track axis, producing a “smeared footprint” [13]. The (smeared) footprint dimensions at low altitude were calculated as 120 m × 102 m (along-track × across-track).
The size of the footprints produced during the high altitude flights at ~2900 m above ground was approximately 850 m × 510 m. Figure 2 shows footprints in the Eureka low altitude flight grid. The flight lines were designed in this pattern to assist in the scaling up of Tbs from the airborne to the satellite scale and ensure complete coverage at different spatial resolutions of Tb products.
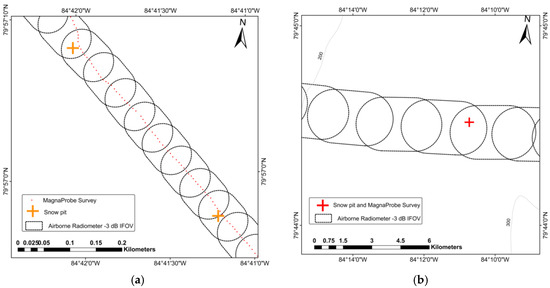
Figure 2.
(a) Example of projected IFOV of the airborne radiometer at low altitude ~350 m; an average flight altitude for each flight line is used to calculate footprint dimensions. (b) Footprints of the radiometer at high altitude ~2900 m after an average filter preprocess; an average flight altitude for the whole flight region is used to calculate footprints dimension.
The lengthening of the radiometer footprint in the along-track axis is an important consideration when analyzing the high resolution, local-scale airborne data because the total number of snow measurements that fall within the radiometer’s IFOV varies depending on the size of the IFOV. This effect becomes less important when working with coarser resolution airborne data because the extent of the IFOV becomes larger than the distance traveled during the one second integration time and therefore adjacent Tbs are heavily overlapped, leading to an over-sampled dataset. To reduce computational time when working with the oversampled high altitude airborne data, the data were thinned by taking the average of every 10 airborne observations. Consequently, the dimensions of footprints for these filtered observations were based on the average flight height for all 10 measurements (Figure 2b).
3.3. Satellite Data
AMSR-E/Aqua Daily EASE-Grid Tbs from 1 December to 30 April were downloaded from the National Snow and Ice Data Center (NSIDC; [36]) to produce seasonal time series of brightness temperatures. The AMSR-E/Aqua Daily EASE-Grid Tbs were produced from the interpolation method of Inverse Distance Square, using AMSR-E/Aqua L2A Global Swath Spatially-Resampled Brightness Temperatures (AE_L2A), projected into EASE-Grid (north and south Lambert azimuthal and global cylindrical) at 25 km resolution [36].
3.4. Ground Based In Situ Data
Between 12 and 22 April, two types of snow surveys were conducted along the airborne radiometer flight lines. A regional-scale snow survey covering much of the Fosheim Peninsula was conducted via helicopter, with the purpose of evaluating the variability in snow properties at the 25 km EASE-Grid scale. The regional snow surveys involved snow depth transects and snow pits measuring snow properties including layering, density, temperature and mean geometrical maximum (Dmax) grain size using a field microscope and a 2 mm comparator card, for 22 regional sites (these sites are presented by red crosses in the Figure 1). The regional snow conditions were relatively homogeneous; there was minimal terrain influence (generally flat), and no emergent vegetation above the snowpack was visible [12]. Snow depth was measured using a GPS enabled, self-recording snow depth probe [37], called a MagnaProbe. Depth measurements were made at 5 to 10 m intervals along a 100 m sided-square centered on a snow pit. Total number of snow depth measurements made at each site ranged from 133 to 176 (average of 150) for a total of 2656 snow depths at all 22 sites. These measurements were used to determine the statistical distribution of snow depth at each site. An ESC-30 snow corer with a cross-sectional area of 30 cm2 [38] was also used to record bulk SWE and density measurements at each site three times, for a total of 66 times.
The second type of in situ snow survey was conducted to characterize local-scale snow properties. The local-scale survey involved using a snowmobile to mark and set multi-kilometer snow depth/bulk SWE transects across the HWC study area, along the local grid airborne radiometer flight lines. A total of ten snow depth transects were surveyed, ranging in length from 2 to 15 km, with snow surveyors walking these lines and recording snow depths every 5–8 m and bulk ESC-30 SWE every 150–180 m. Eight of these lines were parallel, spaced approximately 900 m apart, creating a multi-kilometer snow survey grid. A total of 12,595 snow depths and 510 bulk SWE measurements were recorded within and around this grid. A total of 27 snow pits were measured along the local scale survey transects, following the same survey protocol used during the regional helicopter surveys [12]. A summary of snowpack physical properties from the snow surveys is provided in Table 1. The high coefficient of variation (CoV) of snow depth measurements confirms high spatial variability in the region that will contribute to higher uncertainties in evaluating the microwave emission modeling results in this region.

Table 1.
Summary statistics of the combined local and regional scale snow depth, density, and SWE measurements.
The data summarized in the Table 1 differ from the data presented by [12] which reported exclusively on the regional-scale transects and snow pits. Table 1 gives the total summary statistics for all snow depth, snow density and SWE measurements from the Eureka field campaign used in this analysis. The measurements from the local scale transects were recorded mostly within a 33 km × 6 km grid while the regional-scale measurements were recorded across a larger 48 km × 48 km grid. An additional five snow pits were used in the generalization of snowpack characteristics analysis (see below). Table 1 illustrates that bulk snow density has the lowest coefficient of variation while the SWE has the greatest, indicating that the bulk density changes less over the study area than the depth (SWE is the product of depth and density). The conclusion from this feature is that any radiative transfer modeling should be driven by snowpack properties that likely have a low spatial variability (e.g., snow density) and high spatial variability (e.g., snow depth). It is necessary, therefore, to consider how the data can be effectively generalized while retaining the underlying statistical structural characteristics.
The average number of layers identified in all 49 snow pits was five but there was a variety of different snow types that were observed; including: recent, fine-grained (F.G.), medium-grained (M.G.), crust, soft slab (S.S.), medium slab (M.S.), hard slab (H.S.), slab-to-hoar (Slab-Hoar), chains of hoar (indurated) (CoHI), chains of hoar, depth hoar and icy hoar. Typically, the upper snow layers (recent, fine and medium grained and crusts) are the thinnest while the mid-pack slab layers have largest densities and the middle and lower layers have the largest grain sizes.
To undertake the DMRT-ML modeling, the snowpack characterization had to be generalized. An unsupervised K-means clustering [39] of average grain size and snow density was conducted for 10 of the snow layer type classes (fine grained and icy hoar were excluded from the clustering because of the small sample size). The cluster analysis calculated five cluster means; this number of classes was set based on the average number of layers found in all pits. The hoar classes have cluster means that are low in density but have the largest grain sizes (and grain size range) while the recent and crust layers have the smallest grains and moderate density. The slab layers have the largest densities and the largest range of density values. Cluster 1 has very small layers with small grain sizes (top layer), while Clusters 2 and 3 have the largest densities (wind slabs) and Clusters 4 and 5 have the largest grain sizes (depth hoar).
For the DMRT-ML modeling, the upper cluster contained radiometrically insignificant layers since the layer thicknesses were small (~7% of total thickness) and the grains were also very small. Therefore, this class was removed from the analysis for further generalization. The effect of a layer with small scatterers on top of thick layers with medium-sized grains is simulated by [15] where the 37 GHz Tb slope reversal was seen. They show that, when a snowpack is thick (~70 cm), a thin layer of new snow decreases attenuation of the ground emission, thus 37 GHz Tb increases, and, when a snowpack is shallow and composed of new snow, the emission (and Tb) decreases. It is noteworthy that, in all investigated cases discussed by Liang et al. [15], a topmost layer of new snow, at least 10 cm in thickness, was present showing consistency with our study.
The remaining four classes are further combined into two layers: slab (Clusters 2 and 3) and hoar layers (Clusters 4 and 5). The combined statistics for the slab and hoar layers are shown in the layer temperatures and densities for both structures, were relatively consistent with low coefficient of variations while layer thickness and the grain sizes had high standard deviations. The summary of generalized statistics is presented in Table 2.

Table 2.
Summary statistics of pits classified to two major layers merged from K-Means clustering results.
For the model inputs, it is necessary to use in situ forcing data (snow depth and snow pit) that are spatially coincident with the Tb observations. Tb observations represent snow emission from distributed areas across the radiometer’s IFOV whilst in situ ground measurements are made at the point scale. To evaluate the spatial variability of the in situ data (and determine the spatial representativeness of each in situ measurement) semivariograms of the MagnaProbe snow depths were calculated. Semivariograms provide an unbiased description of the scale and pattern of spatial variation of snow depth, determining what the threshold distance (range) is beyond which snow depths are no longer spatially autocorrelated. Figure 3 shows the semivariogram fitted with a spherical model highlighting the range to be at ~58 m (range is identified where the variogram model line levels out). Snow depth (and snow structure from snow pits) separated by distances greater than the range value (58 m) are no longer spatially autocorrelated. To ensure a strong assumption of correlation between the in situ snow survey data and the airborne radiometer measurements the 58 m range value was used as an inclusion/exclusion threshold, where snow survey data within 58 m of the calculated radiometer IFOV were likely to be spatially autocorrelated to the snow found within the IFOV and therefore were used in this analysis. For snow depth data from MagnaProbe measurements, the CoV (%) of snow depth measured within each individual footprint varied from 22% to 100%, suggesting the presence of high spatial variability within a single footprint. Therefore, only snow depth within IFOVs were used. After screening, 38 out of the total 49 snow pits and 12,671 MagnaProbe measurements were used in the DMRT-ML model analysis.
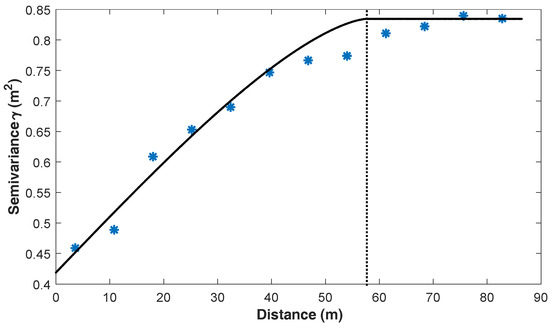
Figure 3.
Averaged semivariogram of snow depth values for pairs with a seven-meter lag size and a fitted spherical model (black line). The range (58 m) is indicated by the vertical dotted line.
4. Results
4.1. Airborne Microwave Tb Observations of Snow
Airborne observations were used first to analyze the emission behavior of tundra snow in the study area. Figure 4 presents Tbs matched with coincident snow depth measurements sampled along the intensive flight paths for low and high altitude flights. In this study, only the vertical polarization at Tb 37 GHz response were studied due to less sensitivity to layering and ice lens structures in the snowpack than horizontal polarization [40,41]. In Figure 4a, each data point shows an average value of minimum 10 MagnaProbe snow depth measurements inside the footprint for a total of 601 Tbs with 6628 coincident depth measurements. When snow depth increases to about 20 cm, the Tb V 37 GHz signal decreases rapidly as scattering dominates the emission signal. Above this depth Tbs increase. To define this inflection point, a simple iterative regression equation search was applied to locate the depth at which the Tb was minimal based on the highest correlation coefficient (R). The best R correlation was −0.4 with a snow depth of 21 cm observed which equals SWE of 65 mm with an average density of 310 kg m−3. At depths exceeding this threshold, Tbs increased, albeit with a relatively weak R coefficient (+0.1), in response to contributions of microwave emission from the snow itself. Both correlation coefficients are significant at the 95% confidence level.
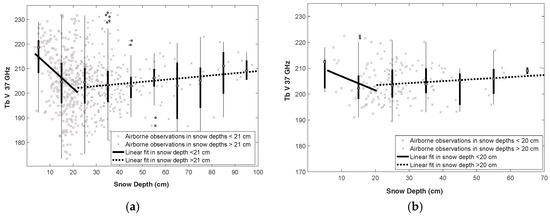
Figure 4.
Measured snow depth coordinated with footprint in Tb V 37 GHz from: (a) low altitude Tb data; and (b) high altitude Tb data, and boxplots of snow depths grouped by 10 cm.
This weak positive relationship between Tb and snow depth greater than 21 cm in this study area can be explained by wind slab formation, where emission is the main contributor rather than scattering. The high average value of measured slab fraction from the snow pit observations (50% from 26 sites) confirms this explanation. In a layer of wind-slab, mechanical processes of compaction dominate the upper layer metamorphism and snow is no longer an efficient insulating medium. The temperature gradient is very small and, therefore, thermal processes promoting snow crystal growth is minimized. While depth hoar is expected to continue to contribute to the signal, its effect is moderated by the overlying slab layer emission.
In Figure 4b, each point shows an average value containing MagnaProbe snow depth measurements inside the footprint in a total of 160 high altitude sample Tbs with 7829 coincident SWE measurements. Footprints are much larger for high altitude IFOVs than the low altitude observations (by 700 times). In situ snow depth measurements are less representative of the IFOV’s snow depth variability and, therefore, a higher level of uncertainty in characterizing the IFOV snow depth is likely. The R correlation between spatially correlated high and low altitude Tb V 37 GHz was 0.66. A 20 K standard deviation was calculated for low altitude Tbs found within the IFOV of high altitude footprints. The linear correlation coefficient of high altitude Tbs and snow depth is −0.25 over snow depth range of 0–20 cm and 0.12 for the depth of 20–90 cm (both significant at 95%).
4.2. Parameterization of the DMRT-ML
In the implementation of DMRT-ML, theoretical simulations of extinction and scattering coefficients are calculated based on the QCA-CP theory that can only solve small particle interactions with electromagnetic radiation with respect to Rayleigh scattering [16]. For larger grains (>1.6 mm) where QCA-CP is not applicable for Mie scattering, an empirical approach [24] is implemented in DMRT-ML imposing a limit for scattering efficiency. However, using simulated characteristics in this study, QCA-CP is valid for non-sticky grains assumption (see Figure 6 “Range of grain sizes for which the DMRT QCA-CP non-sticky is reasonably valid” in [16]). In our simulations, it is assumed that soil layer’s contribution in 37 GHz emission is minimal and snow extinction is dominant which occurs when there are numerous snow grains through emission (thick or very dense snowpack) and/or snow grains are quite large. In the tundra snowpack of the late snow season with depth hoar and slab layers, the aforementioned assumption is valid. In addition, this assumption was evaluated using sensitivity analysis of the model to soil configurations (interface model, prescribed or modeled dielectric constant, and soil material), and the minimal effect of soil layer was verified. Here, in the DMRT-ML implementation, the snowpack is represented as a semi-infinite layer of high density snow slab over a layer of depth hoar. The combined pack is equivalent to the weighted average of the measured variables from the field site with different proportions based on different in situ measurements.
Having explored the airborne Tb observations, the DMRT-ML was used to simulate the Tb V 37 GHz response to replicate airborne and AMSR-E tendencies. The model was set up to be run for three broad scenarios, hereafter termed cases. Setup parameters for each case are summarized in Table 3. Density values were acquired from snow pit measurements based on Table 2. A range of grain size was used in all cases based on previous modeling studies to represent grain size parameterization [17,42]. DMRT-ML requires the optical diameter (Dopt) of grain size as an input. However, human-observed in situ grain size measurements are typically recorded as a geometrical maximum (Dmax) and minimum (Dmin) dimension. There is currently no established methodology widely accepted to adjust Dmax or Dmin to values of Dopt [25]; and in situ data from this experiment were not extensive enough to optimize grain size using observations and simulations. Uncertainties in the representation of grain size, particularly when converting Dmax to Dopt, are likely to be compounded when upscaling to the airborne footprint observations. Therefore, in this research, effective grain size (Deff) that is a scaled value of Dopt justified for snowpack’s microwave emission models is used. The physical temperature range measured in all snow pits was a maximum of 2 K. Therefore, for the DMRT-ML model simulations the average temperature for all 49 snow pits over the nine days was calculated (247.0 K) and used for the parameterization experiments.

Table 3.
Three cases input parameters for DMRT-ML.
In Case 1, depth hoar development and subsequent 37 GHz volume scatter was simulated in a single homogenous layer model by running the model with increasing grain sizes, using a constant density of 300 kg m−3. Snow depth was increased from 10 to 50 cm and the grain size was increased from 400 to 1000 µm, resulting in a decrease in Tb V 37 GHz (Figure 6a). In Case 2, the same grain size and snow depth inputs as Case 1 were used, but this time a two-layer model that maintained a 2:1 ratio of wind-slab to depth hoar as depth increased was run to simulate early season snowpack evolution as a more realistic simulation (Figure 6b). For Case 2, the slope of Tb-snow depth relation using relatively large grain sizes of 800 µm–1000 µm [17], which should be employed for DMRT-ML modeling of a snowpack that contains depth hoar, is less than for Case 1 which better matches the observations in Figure 5. In Case 3, a simulation representing the mid-to-late season snowpack evolution where the wind slab layer grows, while the depth hoar layer thickness remains stable was modeled by running a two-layer snowpack with a fixed depth of the underlying depth hoar layer (7 cm) and a progressively increasing wind slab layer thickness (Figure 6c). To simulate the rise of Tb with depth increase in a two-layer snowpack, based on our simulation runs, the minimum depth for the depth hoar layer is calculated as 7 cm which is measured as 6.2 cm for the average depth of base layer (Table 2). The progressively growing wind slab increased the absorption coefficient and decreased the scattering coefficient with a net effect of decreasing the extinction coefficient. It should be noted that, while formal DMRT theory related to highly compacted snow with densities in the range of 300–500 kg m−3 is imprecise, the model formulation uses a technique to approximate the coefficients at this range following the methods of [16].
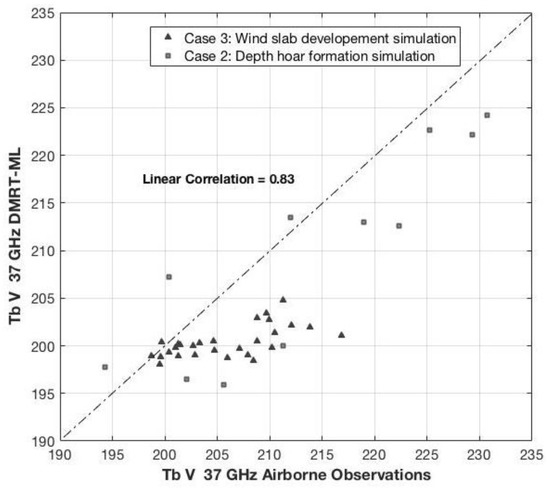
Figure 6.
Simulated vs. observed 37 GHz Tbs (vertical polarization) for individual airborne footprints with data from 38 snow pits and associated MagaProbe measurements. Squares show Case 2 simulations with a two-layer model with fractions of 2:1 ratio of wind slab layer to depth hoar. Triangles show Case 3 simulations from a two-layer wind slab and depth hoar pack with fixed depth hoar thickness. The 1:1 line of agreement is shown as the dashed line.
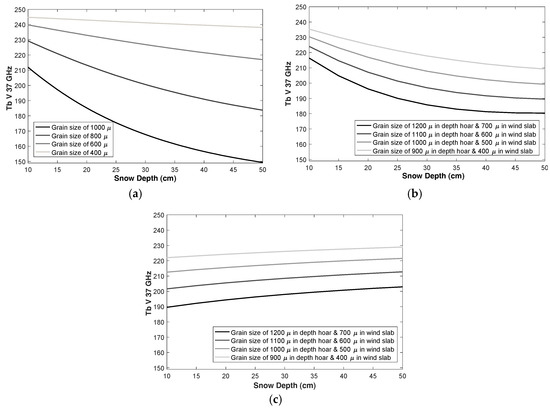
Figure 5.
DMRT-ML simulations of the three experiment cases: (a) depth hoar formation simulation using a single snow layer; (b) two-layer snowpack of wind slab and depth hoar with a wind slab to depth hoar ratio of 2:1; and (c) two-layer snowpack of wind slab and depth hoar with static depth hoar of 7 cm.
The simulation approach for Cases 2 and 3, when taken together, illustrate a tendency that agrees with field observations showing the drop and rise in Tb with increased snow accumulation, as demonstrated documented in previous studies such as [1,2,3,4,5,6,7,8,9,10,11,12], and as illustrated by the field measurements presented in Figure 6. Cases 2 and 3 form the basis for the comparison between simulated and observed Tbs at the regional and local scales in Section 4.3.
4.3. Comparison of DMRT-ML Modeled Tb with Observations
Snowpack data from 38 pits coincident with airborne Tbs (see Section 3.4) were used to simulate the Tb V 37 responses that coincided with the high and low altitude airborne radiometer observations. To reflect small variations in snowpack physical temperatures over the study domain, the average physical temperatures of 246.6 K and 247.4 K were used for the local and regional scale model simulations respectively. Depth hoar and wind slab layer influences on emission were simulated using two-layer snow packs as demonstrated in Section 4.2 via Case 2 (depth hoar formation) and Case 3 (wind slab development). Based on in situ measurements and a cluster analysis (Table 2), the average snow density of 215 kg m−3 and 324 kg m−3 were used for depth hoar and wind slab layers respectively. Effective grain size (Deff) values are used based on previous studies with similar snowpack characteristics. Representative grain size values were used for a wind slab layer and depth hoar layer characteristics defined by [17]; the optical grain size (Dopt) was set to 330 µm for a depth hoar and 170 µm for a wind slab layer. These values were scaled by a factor of 3.3 [17] to achieve the effective grain size (Deff) of 561 and 1089 respectively.
Figure 6 presents a scatterplot of simulated vs. observed Tb of depth hoar formation and wind slab development for both Cases 2 and 3. The correlation of 0.83 at a significance level of p-value = 4 × 10−11 was found, with a 0.88 correlation value for Case 2 and 0.61 for Case 3 simulations. Footprints with data from snow pits at local scale observations (high and low altitudes) were simulated in Case 3 since the snowpack was determined to be deeper and denser locally, while footprints with data from snow pits from the regional scale observations (high altitude) were simulated in Case 2, due to the presence of snow depths less than 21 cm (the previously calculated inflection depth). Data points in the scatterplot are shown in two groups of depth hoar (Case 2) and wind slab (Case 3) simulations. Lower correlation of Case 3 simulations is mainly due to the coarser spatial resolution of observations.
Figure 7 is a repeat of Figure 4a with the Tb V 37 GHz simulations in Figure 6 overlain to show how the depth hoar and wind slab dominated snowpacks control the Tb V 37 GHz emission behavior measured by the airborne radiometer. The plot also includes the model simulations for each airborne radiometer Tb IFOV with a minimum of 10 MagnaProbe snow depth measurements inside. Depth hoar development and wind slab formation were simulated using a two-layer snowpack as presented earlier. KT-19 infrared surface temperature measurements recorded coincidently with each airborne Tb were used as model inputs for snowpack temperatures. The simulation results using the airborne KT-19 snow temperatures inputs produced parallel patterns of simulated Tbs that can be seen in (specifically in the Case 3 wind slab growth simulations). These parallel patterns of Tbs are a result of small variations in KT-19 snow surface temperatures between areas along the flight lines, highlighting the model sensitivity to this input variable. Overall, the model simulations of Tb have a smaller variance compared to observed airborne Tbs due to a smaller range of snow density, and grain size used as model inputs which arises from the generalization process of the in situ snow survey data.
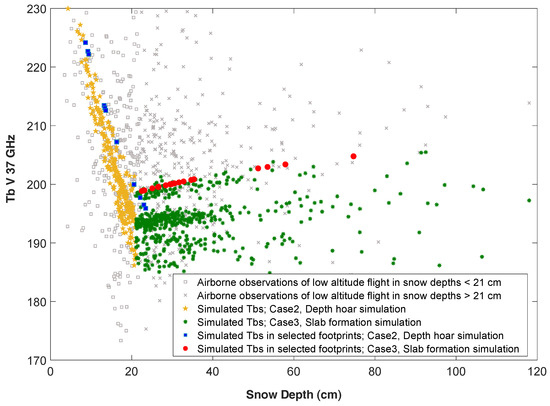
Figure 7.
Tbs from airborne observations and simulations of all footprints using generalized density, physical temperature and grain sizes along with MagnaProbe data.
The non-parametric test of Kolmogrov–Smirnov (KS test) was run to compare simulated and observed Tb V 37 GHz with the null hypothesis, H0, that observations and simulations come from populations with the same distribution, and an alternative hypothesis that the cumulative distribution function (CDF) of observations is larger than the CDF of the simulations. The test returned value of H0 = 1 which indicates KS test rejects the null hypothesis, in favor of the alternative hypothesis that the CDF of the observation is larger than the CDF of the simulations, at the default 5% significance level. The rejection of the null hypothesis can likely be explained by the presence of random errors as well as simplified snow properties/variability that are not represented by the generalized DMRT-ML model forcing data.
4.4. Application to AMSR-E Time Series Data
Satellite AMSR-E Tb V 37 GHz observations (AMSR-E 36.5 GHz frequency is rounded up and reported as 37 GHz for convenience) covering the study area were obtained to illustrate the Tb trend throughout the whole snow season (December-May) (Figure 8). Error bars represent the standard deviation of the four AMSR-E footprints covering the study area. Air temperatures measured by Eureka weather station are also added to the right hand axis. Figure 8 shows a gradual decrease in early to mid-season, and an increase afterwards. The high correlation of 0.84 between air temperature and Tb V 37 GHz indicates that Tbs are dominated by surface temperature and interpretations using these Tb values about snowpack’s metamorphism are spurious. The error bars increase in size from March through to the end of the season likely as a result of high variation in two of the four pixels; one has a moderate topographic heterogeneity (900 m variability) and the other has the greatest adjacency to waterbodies. The regional airborne Tb observations covering these pixels also had the highest standard deviation compared with the other regions in the study areas.
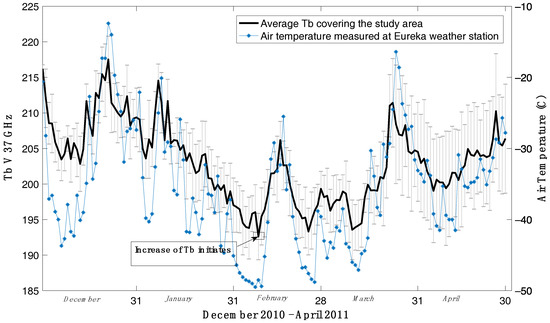
Figure 8.
Average of 2 × 2 footprint AMSR-E Tbs covering the study area with error bars showing the standard deviation.
To characterize the impact of background emission on Figure 8, differences between Tb V 37 GHz and Tb V 19 GHz (abbreviated to ΔTb) are used and shown in Figure 9. This difference is typically used to represent emissivity processes in the snow. In Figure 9, snow survey data recorded by the Eureka weather station on the 1st and 15th days of every month are added to the right-hand axis for comparison. Error bars show the standard deviation of the 10 snow depth measurements made on each day and indicate that heteroscedacity is present. After an increase in snow accumulation during December, the record is characterized as a period of gradual snow depth increase until the end of the record on 30 April. During the same period, ΔTb shows gradual decrease in ΔTb until middle to end of February. This decrease is interpreted as being the result of the combined effect of snow accumulation and snow grain metamorphism of the depth hoar layer which enhances the scattering of subnivean soil emissions. From mid to late February, the ΔTb signal likely increases, as the wind slab layer increases in depth, relative to the depth hoar layer. The increasing thickness of the wind slab reduces the penetration depth of the 37 GHz V signal, and the scattering effect of the depth hoar is suppressed by the emission component of the high density, small grained wind slab. The snow survey data at the Eureka weather station verifies that on 1 February the average snow depth exceeded 23 cm, which is very close to the defined threshold of 21 cm found in the airborne data (see Section 4.1). Although the ΔTb in Figure 9 has reduced physical temperature effects, residual variability can be explained by the variations in physical air/snow temperature, snowfall events, and local snow redistribution processes.
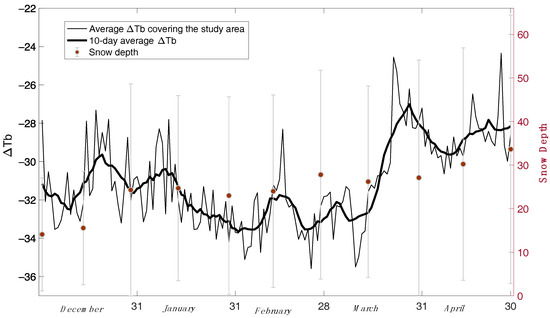
Figure 9.
Average of 2 × 2 footprint AMSR-E ΔTb covering the study area, a 10-day average ΔTb and an overlaid local snow depth measurements recorded by Eureka weather station.
An interesting interpretation of Figure 9 is that the increased emission of wind slab can be explained by spatial processes observed through a field experiment and a temporal process from consistent satellite observations. The temporal process of increasing Tb V 37 GHz and ΔTb during the late accumulation season was shown by Rosenfeld and Grody [14] from SSM/I observations. In their study, the accumulation of fresh snow was presumed to increase scattering, followed by metamorphic changes in crystalline structure that decrease the single-scattering albedo. They explained the Tb reversal, by presence of consolidated ice layers developed from subsurface melt-refreeze and overlaid on top of coarse-grained snow. While similar processes are present in Figure 7 and Figure 9, the analysis of airborne measurements in the late season strongly indicates that a sharp decrease and a mild increase in emissivity can be explained first by the thickening of a depth hoar layer in the earlier (December–mid-February) followed by the continued thickening of the wind slab layer after mid-February as the depth hoar layer remains relatively constant.
The ΔTbs in Figure 9 are likely affected by the snowpack and or soil physical temperature. The use of emissivities (vertical and horizontal polarizations at 37 GHz) would help clarify this issue. To calculate the emissivities, the effective temperature of the snowpack and the brightness temperature of the sky are required but are not available for the complete AMSR-E record. The polarization ratio (PR) H-pol/V-pol at 37 GHz (the emissivity ratio of horizontal to vertical polarization at 37 GHz) could be calculated in lieu of emissivities to characterize snowpack microstructure properties and conclusively investigate the snowpack’s self-emission. In a previous study [43], it was suggested that the PR can be used for density retrievals as its decrease and increase can verify the development of depth hoar and wind slab layers, respectively. However, due to the coarse resolution of AMSR-E observations and the high variability of snow properties in a footprint, PR values ranged from 0.90 to 0.95 with a low CoV (%) of 1 were not reliable enough for further analysis and interpretation.
5. Discussion
The DMRT-ML model was run using in situ measurements surveyed between 13 and 22 April 2011, and compared against airborne Tb observations measured on 20 and 21 April. Model and observation comparisons were made at 37 GHz frequency, which is the most sensitive frequency channel to characterize moderate snow depth. Only the vertical polarization response were investigated since the microwave response from snow at Tb 37 GHz in vertical polarization is known to be less sensitive to ice lens structures in the pack than horizontal polarization Tbs [40,41]. The DMRT-ML model successfully simulated the seasonal Tb V 37 GHz response from high Arctic tundra snow by separately modeling the depth hoar growth (Case 2 simulations) and the wind slab development (Case 3 simulations). The Case 2 simulations modeled a two-layer slab and depth hoar snowpack with a fixed depth ratio of 2:1. Comparisons with observed airborne Tbs indicate that DMRT-ML can be used to simulate the Tb V 37 GHz decrease with increasing snow depth up to 21 cm, whilst a two-layer slab and depth hoar with fixed depth hoar thickness (7 cm) and increasing wind slab thickness can successfully simulate Tb increases as the snowpack thickens beyond 21 cm which occurs more commonly later in the season. Finally, the AMSR-E time series response of ΔTbs in the region, shows a declining in the early season followed by an inflection on mid-February after which the emission begins to increase in magnitude, which may presumably be in response to the continued wind slab growth as the season progresses.
The high spatial variability of snow properties observed in our study area is averaged across the footprint scale in the airborne Tbs observations. Inevitably, this causes the sensitivity of observed Tbs to be lower than the model estimates, when the model is driven by point-scale in situ snow pit measurements that have a high degree of spatial variability. Furthermore, even different footprint sizes acquired from the same location from different altitudes with the same sensor produce different Tbs because the underlying natural emission signal is variable. The calibration of a physical emission model using in situ snow pits will likely lead to uncertainties for larger scale applications. Therefore, it is necessary to develop robust schemes such as the unsupervised K-means cluster analysis to generalize snowpack structural elements that can be adopted for snowpack emission modeling and snow retrievals.
6. Conclusions
The obtained 21 cm threshold in the Tb-snow depth inflection is lower but comparable to other findings elsewhere. For example, Sturm et al. [44] observed a 110 mm SWE (31 cm snow depth) threshold using ground-based observations. Rosenfeld and Grody [14] showed threshold minima of 20 cm and 45 cm using spaceborne observations in different case studies while explaining this phenomenon as an anomalous signature and modeling it using a two-stream Dense Media Theory. However, no comprehensive in situ snow pit data with snow structural information were available to conclusively support these findings. In the study by Derksen et al. [11], a threshold of 130 mm of SWE was observed but neither averaged density nor equivalent snow depth were reported at the airborne observation scale (70 m × 120 m). The range of differences is likely attributed to the differences between the sampling of high spatially variable snow properties at different scales: point ground measurements [10,15] and area airborne measurements [11]. The presence of dominant wind slab layers with high snow densities in our study area likely resulted in a lower threshold for the observed 37 GHz Tb V inflection point, explaining why the inflection point of 68 mm of SWE (21 cm snow depth) was lower than those values reported in previous studies. The measured airborne Tbs and the DMRT-ML simulated slope reversal of Tb at 37 GHz, documented in this study suggests that this threshold, and the modeling approach taken, is generalizable to other Arctic tundra snow environments.
In this research, airborne observations and field data measurements were made over a ten-day period through almost consistent air temperature with likely negligible snow structural changes. Therefore, it is assumed that no metamorphism occurred during the field campaign period. However, in the presence of seasonal snow evolution, emission models of snow should account for snowpack seasonal metamorphosis. Various methods can provide estimates of snowpack structure (grain size, density) to couple with microwave emission models: the empirical densification approach of Sturm et al. [10] and the grain growth model of Sturm et al. [45]; land surface models such as the Canadian land surface scheme [46] or snow microstructure models such as SNOWPACK snow microstructure model [47,48]; and seasonal/event densification and grain crystal development through using the snowpack’s recent thermal history [20,49]. Each of these approaches can improve estimates of the state of the snow whereas there are limitations in large scale applications. Knowledge about this inflection point can inform these approaches and help constrain the retrieval process if a physically-based emission model is used. Future work should continue to develop strategies that improve the current explicit inverse solutions using generalizable models/methods for parameterizing snowpack structure.
Acknowledgments
This research was supported by the Japan Aerospace Exploration Agency through the GCOM-W1/AMSR2 project and by the National Science and Engineering Research Council of Canada. The Eureka snow and airborne radiometer measurements were supported by Environment Canada as part of the PAMARCMIP 2011 campaign. Thanks to Arvids Silis, Stephen Howell and Dave Halpin for the work in collecting the snow survey data, and Mike Harwood, Walter Strapp and Ken Asmus for their help in conducting the airborne radiometer surveys.
Author Contributions
Chris Derksen and Peter Toose designed the experiments; Peter Toose performed the experiments; astaran Saberi analyzed the data and designed the framework of study; Richard Kelly co-developed the framework of this study and significantly revised the manuscript written by astaran Saberi; and all other authors contributed valuable edits and suggestions throughout the modeling and writing process.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rees, A.; English, M.; Derksen, C.; Toose, P.; Silis, A. Observations of late winter Canadian tundra snow cover properties. Hydrol. Process. 2014, 28, 3962–3977. [Google Scholar] [CrossRef]
- Cohen, J.; Rind, D. The effect of snow cover on the climate. J. Clim. 1991, 4, 689–706. [Google Scholar] [CrossRef]
- Fletcher, C.G.; Kushner, P.J.; Hall, A.; Qu, X. Circulation responses to snow albedo feedback in climate change. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Takala, M.; Luojus, K.; Pulliainen, J.; Derksen, C.; Lemmetyinen, J.; Kärnä, J.-P.; Koskinen, J.; Bojkov, B. Estimating northern hemisphere snow water equivalent for climate research through assimilation of space-borne radiometer data and ground-based measurements. Remote Sens. Environ. 2011, 115, 3517–3529. [Google Scholar] [CrossRef]
- Luojus, K.; Pulliainen, J.; Takala, M.; Lemmetyinen, J.; Derksen, C.; Wang, L. Snow Water Equivalent (SWE) Product Guide; European Space Agency Study Contract Report; Finnish Meteorological Institute: Helsinki, Finland.
- Kelly, R. The AMSR-E Snow Depth Algorithm: Description and Initial Results. J. Remote Sens. Soc. Jpn. 2009, 29, 307–317. [Google Scholar]
- Tedesco, M.; Pulliainen, J.; Takala, M.; Hallikainen, M.; Pampaloni, P. Artificial neural network-based techniques for the retrieval of SWE and snow depth from SSM/I data. Remote Sens. Environ. 2004, 90, 76–85. [Google Scholar] [CrossRef]
- Pulliainen, J. Mapping of snow water equivalent and snow depth in boreal and sub-arctic zones by assimilating space-borne microwave radiometer data and ground-based observations. Remote Sens. Environ. 2006, 101, 257–269. [Google Scholar] [CrossRef]
- Sturm, M.; Holmgren, J.; Liston, G.E. A Seasonal Snow Cover Classification System for Local to Global Applications. J. Clim. 1995, 8, 1261–1283. [Google Scholar] [CrossRef]
- Sturm, M.; Taras, B.; Liston, G.E.; Derksen, C.; Jonas, T.; Lea, J. Estimating Snow Water Equivalent Using Snow Depth Data and Climate Classes. J. Hydrometeorol. 2010, 11, 1380–1394. [Google Scholar] [CrossRef]
- Derksen, C.; Toose, P.; Rees, A.; Wang, L.; English, M.; Walker, A.; Sturm, M. Development of a tundra-specific snow water equivalent retrieval algorithm for satellite passive microwave data. Remote Sens. Environ. 2010, 114, 1699–1709. [Google Scholar] [CrossRef]
- Derksen, C.; Lemmetyinen, J.; Toose, P.; Silis, A.; Pulliainen, J.; Sturm, M. Physical properties of Arctic versus subarctic snow: Implications for high latitude passive microwave snow water equivalent retrievals. J. Geophys. Res. Atmos. 2014, 119, 7254–7270. [Google Scholar] [CrossRef]
- Derksen, C.; Toose, P.; Lemmetyinen, J.; Pulliainen, J.; Langlois, A.; Rutter, N.; Fuller, M.C. Evaluation of passive microwave brightness temperature simulations and snow water equivalent retrievals through a winter season. Remote Sens. Environ. 2012, 117, 236–248. [Google Scholar] [CrossRef]
- Rosenfeld, S.; Grody, N. Anomalous microwave spectra of snow cover observed from Special Sensor Microwave/Imager measurements. J. Geophys. Res. 2000, 105, 14913. [Google Scholar] [CrossRef]
- Liang, D.; Xu, X.; Tsang, L.; Andreadis, K.M.; Josberger, E.G. The effects of layers in dry snow on its passive microwave emissions using dense media radiative transfer theory based on the quasicrystalline approximation (QCA/DMRT). IEEE Trans. Geosci. Remote Sens. 2008, 46, 3663–3671. [Google Scholar] [CrossRef]
- Picard, G.; Brucker, L.; Roy, A.; Dupont, F.; Fily, M.; Royer, A. Simulation of the microwave emission of multi-layered snowpacks using the dense media radiative transfer theory: The DMRT-ML model. Geosci. Model Dev. Discuss. 2012, 5, 3647–3694. [Google Scholar] [CrossRef]
- Roy, A.; Picard, G.; Royer, A.; Montpetit, B. Brightness temperature simulations of the Canadian seasonal snowpack driven by measurements of the snow specific surface area. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4692–4704. [Google Scholar] [CrossRef]
- Tsang, L.; Chen, C.-T.; Chang, A.T.C.; Guo, J.; Ding, K.-H. Dense media radiative transfer theory based on quasicrystalline approximation with applications to passive microwave remote sensing of snow. Radio Sci. 2000, 35, 731–749. [Google Scholar] [CrossRef]
- Brucker, L.; Picard, G.; Fily, M. Snow grain-size profiles deduced from microwave snow emissivities in Antarctica. J. Glaciol. 2010, 56, 514–526. [Google Scholar] [CrossRef]
- Kelly, R.; Chang, A.T.; Tsang, L.; Foster, J.L. A prototype AMSR-E global snow area and snow depth algorithm. IEEE Trans. Geosci. Remote Sens. 2003, 41, 230–242. [Google Scholar] [CrossRef]
- Wen, B.; Tsang, L.; Winebrenner, D.P.; Ishimaru, A. Dense medium radiative transfer theory: Comparison with experiment and application to microwave remote sensing and polarimetry. IEEE Trans. Geosci. Remote Sens. 1990, 28, 46–59. [Google Scholar] [CrossRef]
- Jin, Y.Q. Electromagnetic Scattering Modelling for Quantitative Remote Sensing; World Scientific: Singapore, 1993; ISBN 9810216483. [Google Scholar]
- Chandrasekhar, S. Radiative Transfer; McGraw-Hill: New York, NY, USA, 1960. [Google Scholar]
- Grody, N. Relationship between snow parameters and microwave satellite measurements: Theory compared with Advanced Microwave Sounding Unit observations from 23 to 150 GHz. J. Geophys. Res. 2008, 113, D22108. [Google Scholar] [CrossRef]
- Royer, A.; Roy, A.; Montpetit, B.; Saint-Jean-Rondeau, O.; Picard, G.; Brucker, L.; Langlois, A. Remote Sensing of Environment Comparison of commonly-used microwave radiative transfer models for snow remote sensing. Remote Sens. Environ. 2017, 190, 247–259. [Google Scholar] [CrossRef]
- Foster, J.L.; Sun, C.; Walker, J.P.; Kelly, R.; Chang, A.; Dong, J.; Powell, H. Quantifying the uncertainty in passive microwave snow water equivalent observations. Remote Sens. Environ. 2005, 94, 187–203. [Google Scholar] [CrossRef]
- Durand, M.; Kim, E.; Margulis, S. Quantifying Uncertainty in Modeling Snow Microwave Radiance for a Mountain Snowpack at the Point-Scale, Including Stratigraphic Effects. Geosci. Remote. 2008, 46, 1753–1767. [Google Scholar] [CrossRef]
- Roy, A.; Royer, A.; Montpetit, B.; Bartlett, P.A.; Langlois, A. Snow specific surface area simulation using the one-layer snow model in the Canadian LAnd Surface Scheme (CLASS). Cryosphere 2013, 7, 961–975. [Google Scholar] [CrossRef]
- Gallet, J.C.; Domine, F.; Zender, C.S.; Picard, G. Measurement of the specific surface area of snow using infrared reflectance in an integrating sphere at 1310 and 1550 nm. Cryosphere 2009, 3, 167–182. [Google Scholar] [CrossRef]
- Environment and Climate Change Canada (ECCC). Eureka Weather Station, Canadian Climate Normal. 1981. Available online: http://climate.weather.gc.ca/climate_normals/index_e.html (accessed on 4 December 2017).
- Woo, M.; Heron, R.; Marsh, P.; Steer, P. Comparison of weather station snowfall with winter snow accumulation in high arctic basins. Atmos. Ocean 1983, 21, 312–325. [Google Scholar] [CrossRef]
- Edlund, S.A.; Woo, M.-K.; Young, K.L. Climate, hydrology and vegetation patterns Hot Weather Creek, Ellesmere Island, Arctic Canada. Nord. Hydrol. 1990, 21, 273–286. [Google Scholar]
- Woo, M.; Young, K.L. Hydrology of a Small Drainage Basin with Polar Oasis Environment, Fosheim Peninsula, Ellesmere Island, Canada. Permafr. Periglac. Process. 1997, 8, 257–277. [Google Scholar] [CrossRef]
- Woo, M.; Walker, A.; Yang, D.; Goodison, B. Pixel-scale ground snow survey for passive microwave study of the Arctic snow cover. In Proceedings of the 52nd Eastern Snow Conference, Toronto, ON, Canada, 6–8 June 1995; pp. 51–57. [Google Scholar]
- Brodzik, M.J.; Billingsley, B.; Haran, T.; Raup, B.; Savoie, M.H. EASE-Grid 2.0: Incremental but Significant Improvements for Earth-Gridded Data Sets. ISPRS Int. J. Geo Inf. 2012, 1, 32–45. [Google Scholar] [CrossRef]
- Knowles, K.; Savoie, M.; Armstrong, R.; Brodzik, M. AMSR-E/Aqua Daily EASE-Grid Brightness Temperatures; National Snow and Ice Data Center (NSIDC): Boulder, CO, USA, 2006; Available online: http://dx.doi.org/10.5067/XIMNXRTQVMOX (accessed on 1 March 2016).
- Strum, M.; Liston, G.E. The snow cover on lakes of the Arctic Coastal Plain of Alaska, USA. J. Glaciol. 2003, 49, 370–380. [Google Scholar] [CrossRef]
- Farnes, P.E.; Peterson, N.R.; Goodison, B.E.; Richards, R.P. Metrication of manual snow sampling equipment by western snow conference metrication committee. In Proceedings of the 50th Annual Meeting of the Western Snow Conference, Reno, NV, USA, 19–23 April 1982; pp. 120–132. [Google Scholar]
- Macqueen, J. Some methods for classification and analysis of multivariate observations. Proc. Fifth Berkeley Symp. Math. Stat. Probab. 1967, 1, 281–297. [Google Scholar]
- Li, D.; Durand, M.; Margulis, S.A. Potential for hydrologic characterization of deep mountain snowpack via passive microwave remote sensing in the Kern River basin, Sierra Nevada, USA. Remote Sens. Environ. 2012, 125, 34–48. [Google Scholar] [CrossRef]
- Rees, A.; Lemmetyinen, J.; Derksen, C.; Pulliainen, J.; English, M. Observed and modelled effects of ice lens formation on passive microwave brightness temperatures over snow covered tundra. Remote Sens. Environ. 2010, 114, 116–126. [Google Scholar] [CrossRef]
- Saberi, N.; Kelly, R. An evaluation of DMRT-ML for AMSR2 estimates of snow depth. In Proceedings of the Geoscience and Remote Sensing Symposium (IGARSS), IEEE International, Quebec City, QC, Canada, 13–18 July 2014; pp. 1943–1946. [Google Scholar]
- Lemmetyinen, J.; Schwank, M.; Rautiainen, K.; Kontu, A.; Parkkinen, T.; Mätzler, C.; Wiesmann, A.; Wegmüller, U.; Derksen, C.; Toose, P.; et al. Snow density and ground permittivity retrieved from L-band radiometry: Application to experimental data. Remote Sens. Environ. 2016, 180, 377–391. [Google Scholar] [CrossRef]
- Sturm, M.; Grenfell, T.C.; Perovich, D.K. Passive microwave measurements of tundra and taiga snow covers in Alaska, USA. Ann. Glaciol. 1993, 17, 125–130. [Google Scholar] [CrossRef]
- Sturm, M.; Benson, C. Vapor transport, grain growth and depth-hoar development in the subarctic snow. J. Glaciol. 1997, 43, 42–59. [Google Scholar] [CrossRef]
- Roy, A.; Royer, A.; Montpetit, B.; Langlois, A. Microwave snow emission modeling of boreal forest environments. In Proceedings of the Geoscience and Remote Sensing Symposium (IGARSS), IEEE International, Milan, Italy, 26–31 July 2015; pp. 754–757. [Google Scholar]
- Langlois, A.; Royer, A.; Derksen, C.; Montpetit, B.; Dupont, F.; Goïta, K. Coupling the snow thermodynamic model SNOWPACK with the microwave emission model of layered snowpacks for subarctic and arctic snow water equivalent retrievals. Water Resour. Res. 2012, 48, W12524. [Google Scholar] [CrossRef]
- Kontu, A.; Lemmetyinen, J.; Vehviläinen, J.; Leppänen, L.; Pulliainen, J. Remote Sensing of Environment Coupling SNOWPACK-modeled grain size parameters with the HUT snow emission model. Remote Sens. Environ. 2017, 194, 33–47. [Google Scholar] [CrossRef]
- Josberger, E.; Mognard, N. A passive microwave snow depth algorithm with a proxy for snow metamorphism. Hydrol. Process. 2002, 16, 1557–1568. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).