Annual Seasonality Extraction Using the Cubic Spline Function and Decadal Trend in Temporal Daytime MODIS LST Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
2.2.1. MODIS LST
2.2.2. Meteorological Data
2.3. Methods
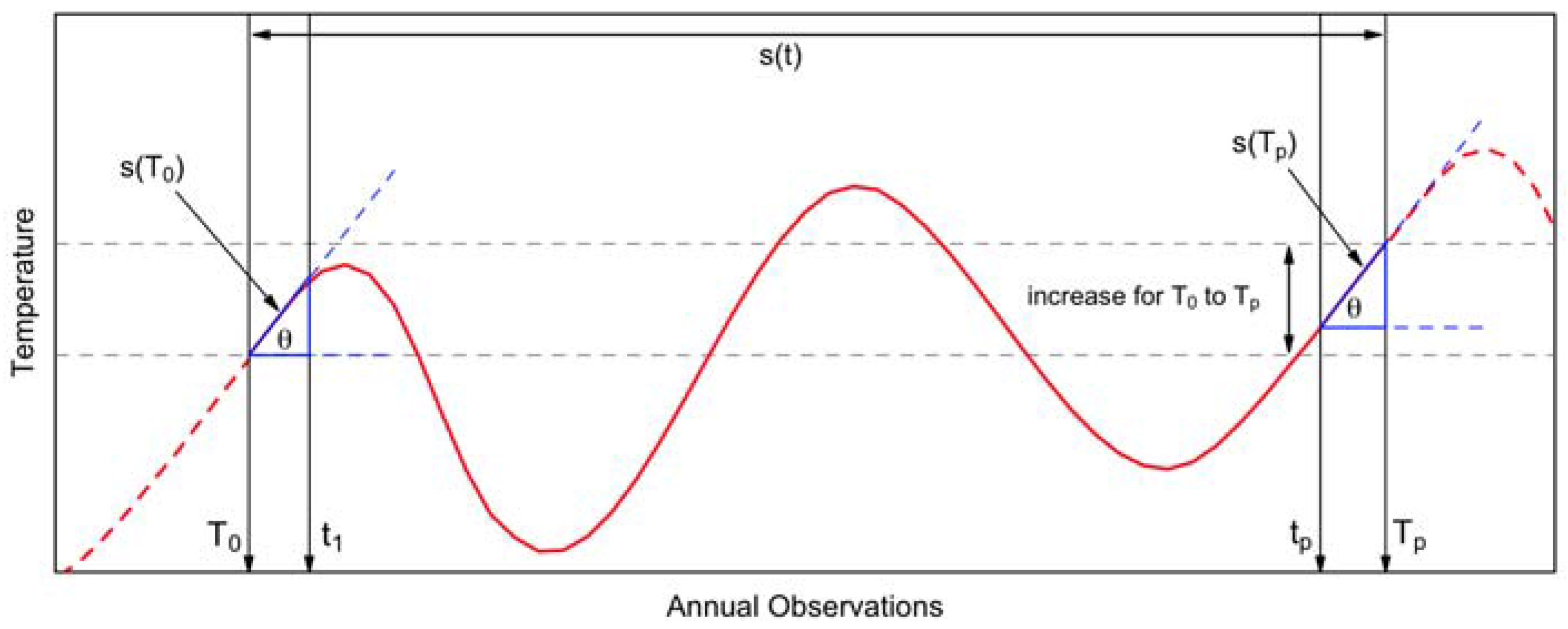
2.3.1. Cubic Spline Function
2.3.2. Knots Selection
2.3.3. LST Outlier Elimination
2.3.4. Weighted Least Squares Regression
3. Results
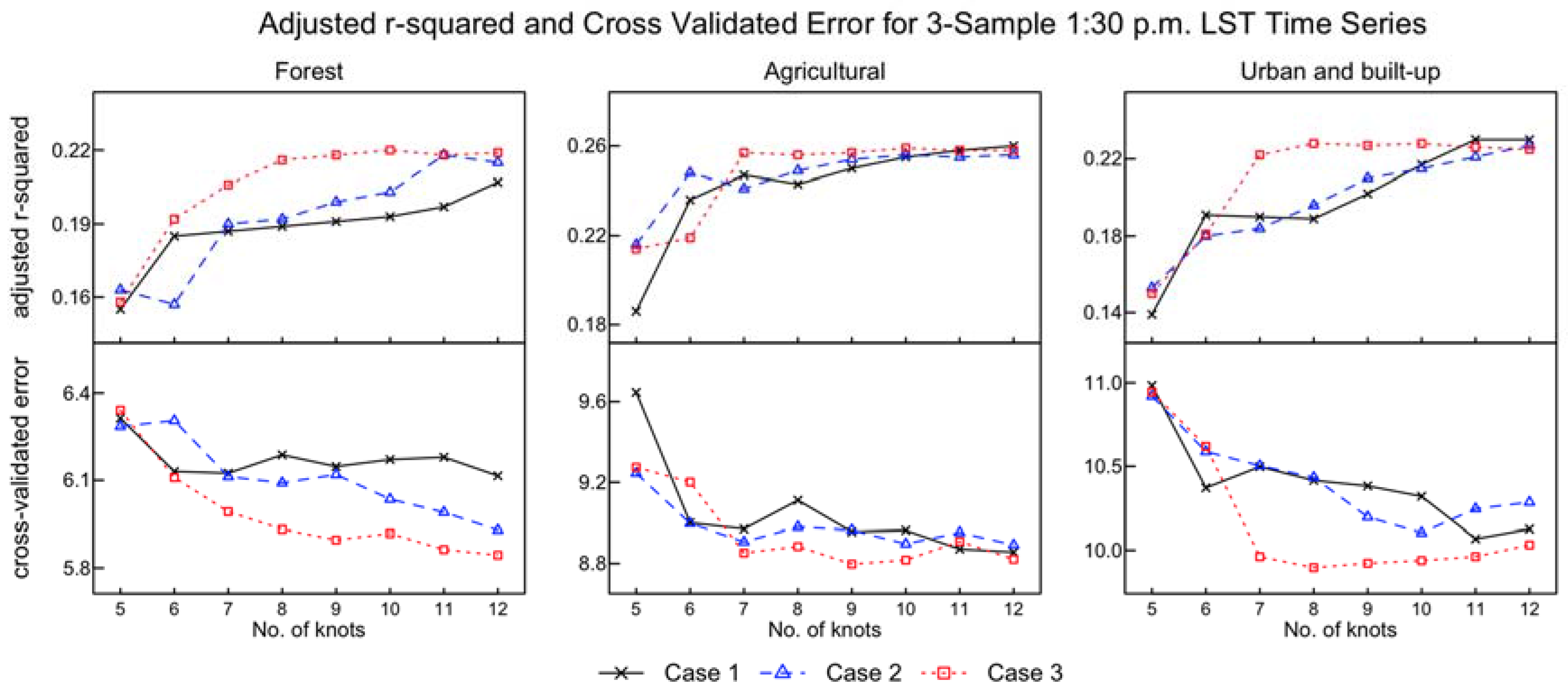
3.1. Placement and Number of Knots
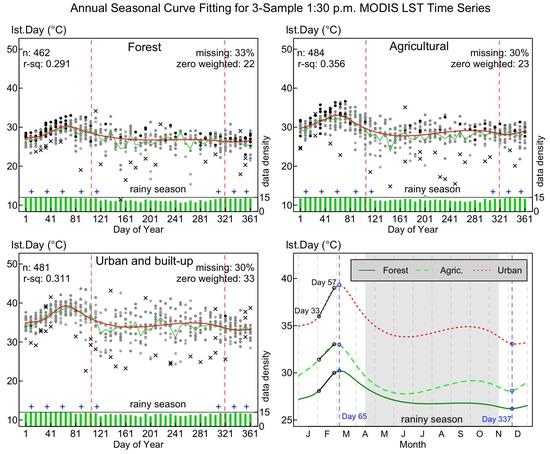
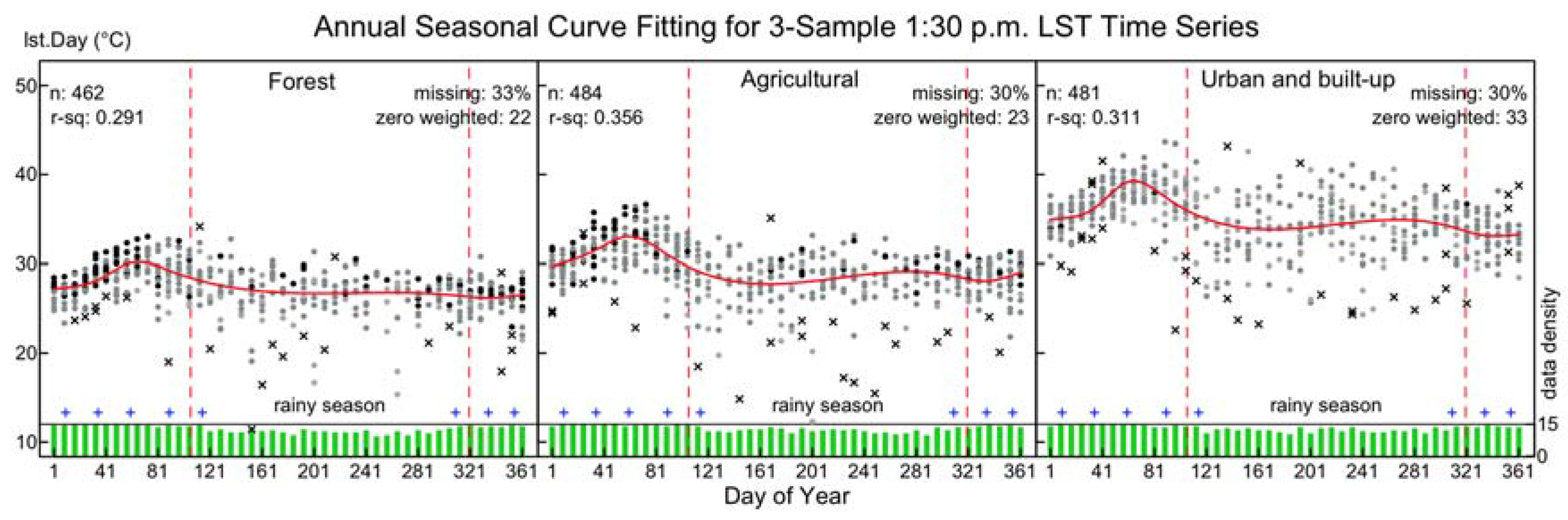
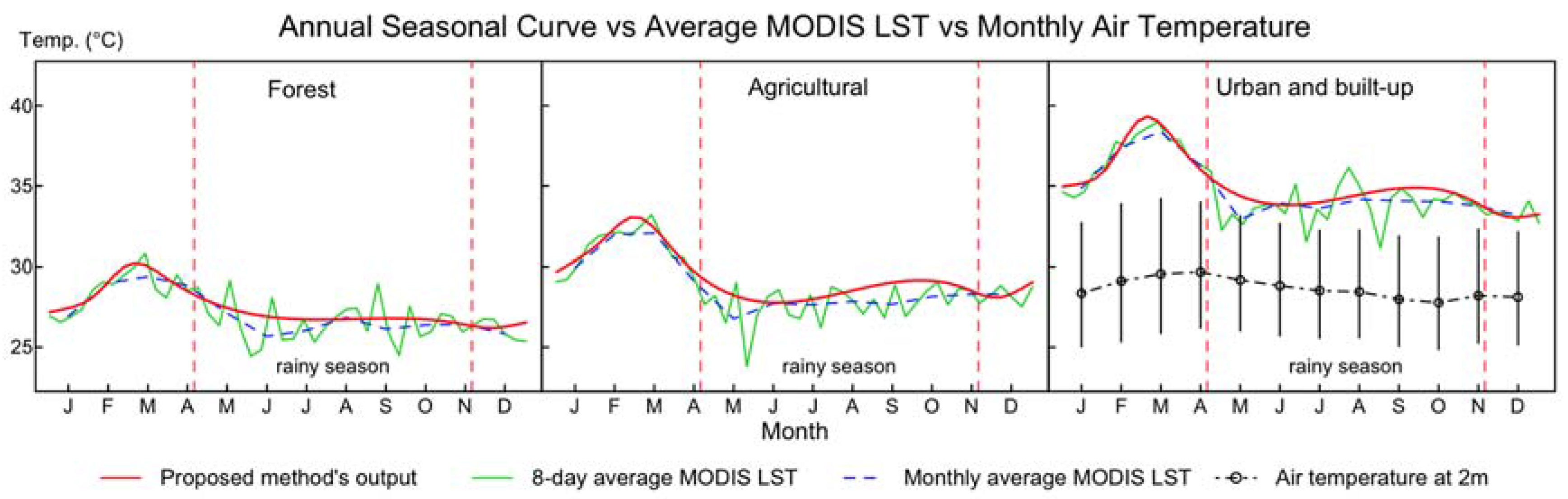
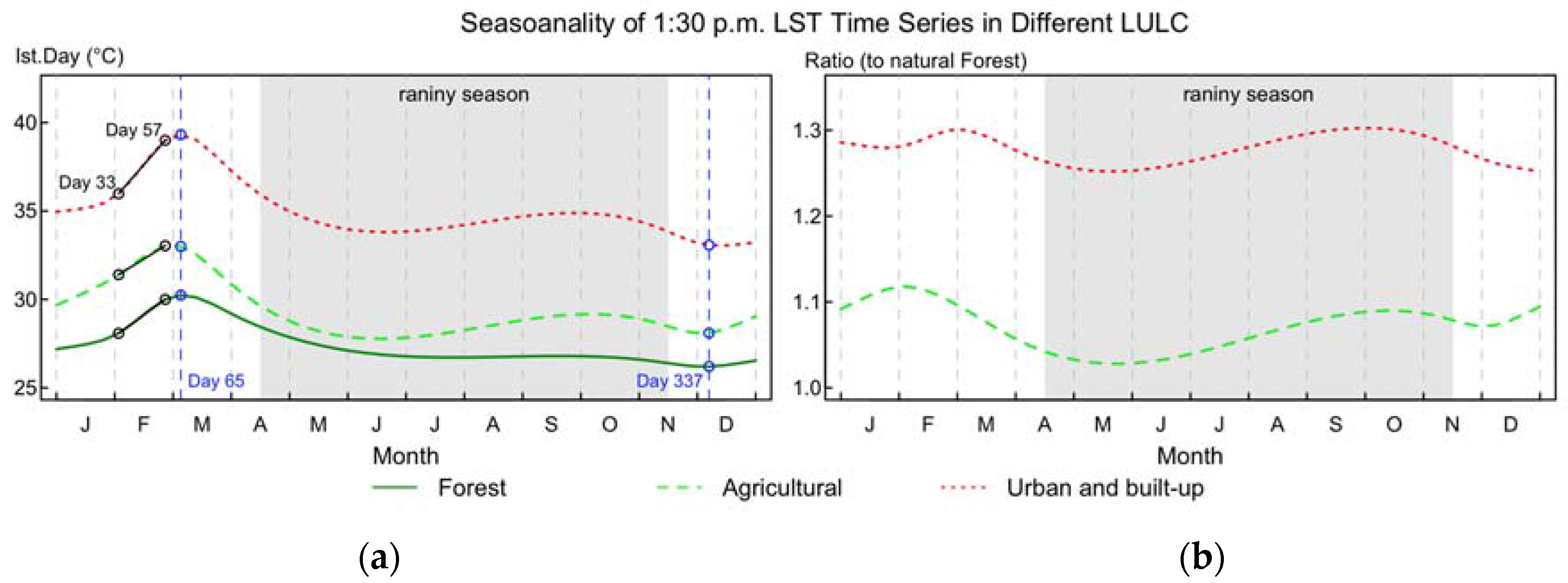
3.2. Annual Seasonal Patterns of LST Time Series
3.3. Application to Daytime MODIS LST Data
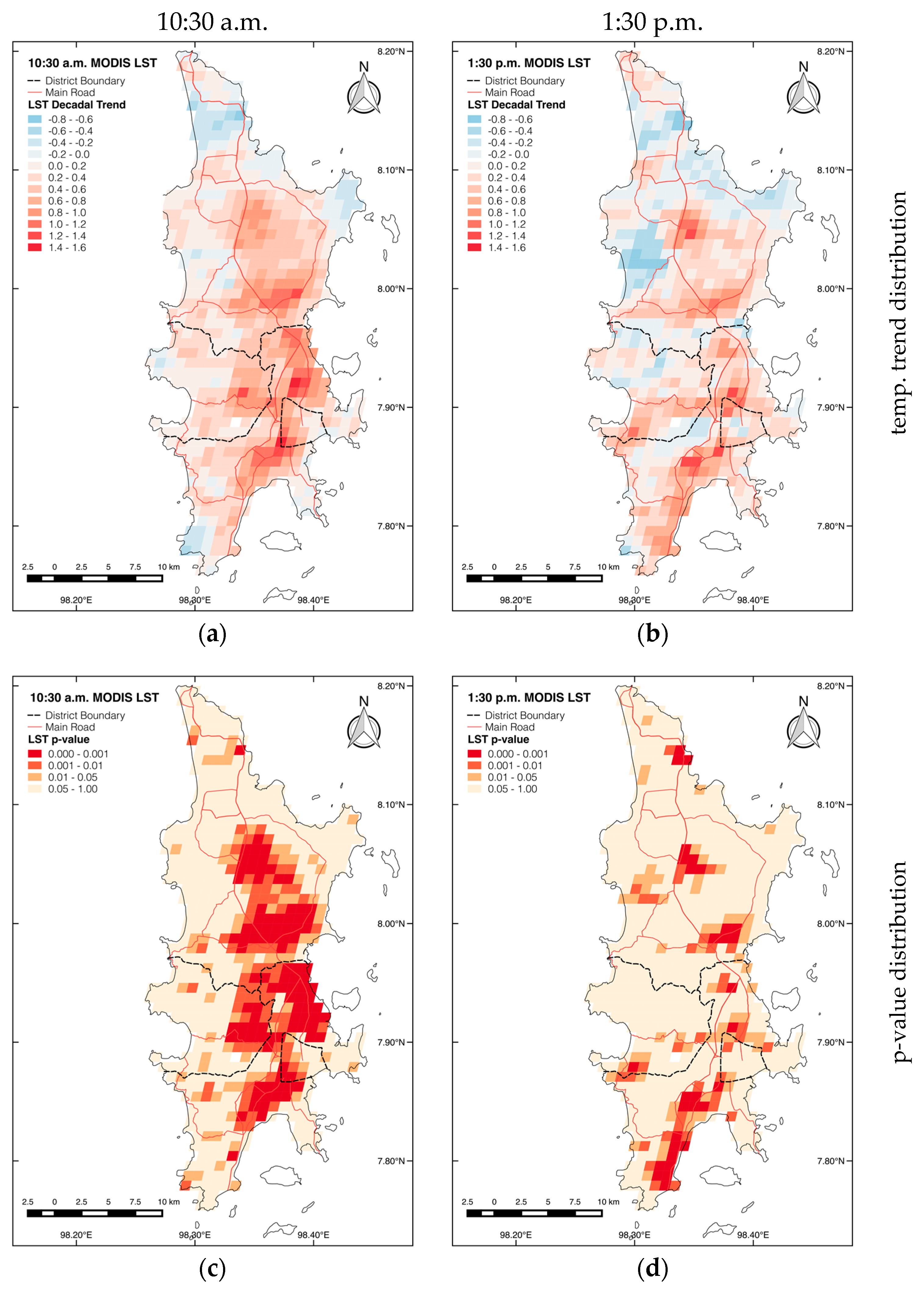
3.3.1. Spatial Distribution of Daytime LST Trends
3.3.2. Trend of Daytime LST in Different LULC Types
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Scarino, B.; Minnis, P.; Palikonda, R.; Reichle, R.H.; Morstad, D.; Yost, C.; Shan, B.; Liu, Q. Retrieving clear-sky surface skin temperature for numerical weather prediction application from geostationary satellite data. Remote Sens. 2013, 5, 342–366. [Google Scholar] [CrossRef]
- Cho, A.-R.; Suh, M.-S. Evaluation of land surface temperature operationally retrieved from Korean geostationary satellite (COMS) data. Remote Sens. 2013, 5, 3951–3970. [Google Scholar] [CrossRef]
- Li, Z.-L.; Wu, H.; Wang, N.; Qiu, S.; Sobrino, J.A.; Wan, Z.; Tang, B.-H.; Yan, G. Land surface emissivity retrieval from satellite data. Int. J. Remote Sens. 2013, 34, 3084–3127. [Google Scholar] [CrossRef]
- Stroppiana, D.; Antoninetti, M.; Brivio, P. A. Seasonality of MODIS LST over Southern Italy and correlation with land cover, topography and solar radiation. Eur. J. Remote Sens. 2014, 47, 133–152. [Google Scholar] [CrossRef]
- Wan, Z. Collection-6 MODIS Land Surface Temperature Products Users’ Guide. December 2013. Available online: https://icess.eri.ucsb.edu/modis/LstUsrGuide/usrguide.html (accessed on 1 September 2017).
- Frey, C.M.; Kuenzer, C. Land-surface temperature dynamics in the Upper Mekong Basin derived from MODIS time series. Int. J. Remote Sens. 2014, 35, 2780–2798. [Google Scholar] [CrossRef]
- Frey, C.M.; Kuenzer, C. Analysing a 13 Years MODIS Land Surface Temperature Time Series in the Mekong Basin. In Remote Sensing Time Series; Kuenzer, C., Dech, S., Wagner, W., Eds.; Springer: Cham, Switzerland, 2015; Volume 22, pp. 119–140. ISBN 978-3-31-915966-9. [Google Scholar] [CrossRef]
- Zhao, G.; Dong, J.; Liu, J.; Zhai, J.; Cui, Y.; He, T.; Xiao, X. Different patterns in daytime and nighttime thermal effects of urbanization in Beijing-Tianjin-Hebei urban agglomeration. Remote Sens. 2017, 9, 121. [Google Scholar] [CrossRef]
- Jin, M.S.; Kessomkiat, W.; Pereira, G. Satellite-observed urbanization characters in Shanghai, China: Aerosols, urban heat island effect, and land–atmosphere interactions. Remote Sens. 2011, 3, 83–99. [Google Scholar] [CrossRef]
- Yao, R.; Wang, L.; Huang, X.; Niu, Z.; Liu, R.; Wang, Q. Temporal trends of surface urban heat islands and associated determinants in major Chinese cities. Sci. Total Environ. 2017, 609, 742–754. [Google Scholar] [CrossRef] [PubMed]
- Neteler, M. Estimating daily land surface temperatures in mountainous environments by reconstructed MODIS LST data. Remote Sens. 2010, 2, 333–351. [Google Scholar] [CrossRef]
- Crosson, W.L.; Al-Hamdan, M.Z.; Hemmings, S.N.J.; Wade, G.M. A daily merged MODIS Aqua–Terra land surface temperature data set for the conterminous United States. Remote Sens. Environ. 2012, 119, 315–324. [Google Scholar] [CrossRef]
- Benali, A.; Carvalho, A.C.; Nunes, J.P.; Carvalhais, N.; Santos, A. Estimating air surface temperature in Portugal using MODIS LST data. Remote Sens. Environ. 2012, 124, 108–121. [Google Scholar] [CrossRef]
- Metz, M.; Rocchini, D.; Neteler, N. Surface temperatures at the continental scale: Tracking changes with remote sensing at unprecedented detail. Remote Sens. 2014, 6, 3822–3840. [Google Scholar] [CrossRef]
- Yu, W.; Nan, Z.; Wang, Z.; Chen, H.; Wu, T.; Zhao, L. An effective interpolation method for MODIS land surface temperature on the Qinghai–Tibet plateau. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4539–4550. [Google Scholar] [CrossRef]
- Duan, S.-B.; Li, Z.-L.; Leng, P. A framework for the retrieval of all-weather land surface temperature at a high spatial resolution from polar-orbiting thermal infrared and passive microwave data. Remote Sens. Environ. 2017, 195, 107–117. [Google Scholar] [CrossRef]
- Wan, Z. New refinements and validation of the collection-6 MODIS land-surface temperature/emissivity product. Remote Sens. Environ. 2014, 140, 36–45. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen–Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Global Subsets Tool: MODIS Collection 6 Land Products. Available online: https://modis.ornl.gov/cgi-bin/MODIS/global/subset.pl (accessed on 15 July 2017).
- Duan, S.-B.; Li, Z.-L.; Cheng, J.; Leng, P. Cross-satellite comparison of operational land surface temperature products derived from MODIS and ASTER data over bare soil surfaces. ISPRS J. Photogramm. Remote Sens. 2017, 126, 1–10. [Google Scholar] [CrossRef]
- Wahba, G. Spline Models for Observational Data; CBMS-NSF Regional Conference Series in Applied Mathematics; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 1990; pp. 1–20. [Google Scholar] [CrossRef]
- Wold, S. Spline function in data analysis. Technometrics 1974, 16, 1–11. [Google Scholar] [CrossRef]
- Smith, R.E.; Price, J.M.; Howser, L.M. A Smoothing Algorithm Using Cubic Spline Functions; Technical Note: NASA TN D-7397; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 1974.
- Graham, N.Y. Smoothing with periodic cubic splines. Bell Syst. Tech. J. 1983, 62, 101–110. [Google Scholar] [CrossRef]
- Feng, G. Data smoothing by cubic spline filters. IEEE T. Signal Proces. 1998, 46, 2790–2796. [Google Scholar] [CrossRef]
- Ferrer-Arnau, L.; Reig-Bolaño, R.; Marti-Puig, P.; Manjabacas, A.; Parisi-Baradad, V. Efficient cubic spline interpolation implemented with FIR filters. Int. J. Comput. Inf. Syst. Ind. Manag. Appl. 2013, 5, 98–105. [Google Scholar]
- Hou, H.; Andrews, H. Cubic splines for image interpolation and digital filtering. IEEE T. Acoust. Speech. 1978, 26, 508–517. [Google Scholar] [CrossRef]
- Wüst, S.; Wendt, V.; Linz, R.; Bittner, M. Smoothing data series by means of cubic splines: Quality of approximation and introduction of a repeating spline approach. Atmos. Meas. Tech. 2017, 10, 3453–3462. [Google Scholar] [CrossRef]
- Zhang, H.; Pu, R.; Liu, X. A New Image Processing Procedure Integrating PCI-RPC and ArcGIS-Spline Tools to Improve the Orthorectification Accuracy of High-Resolution Satellite Imagery. Remote Sens. 2016, 8, 827. [Google Scholar] [CrossRef]
- Chen, S.; Hu, X.; Peng, S.; Zhou, Z. Denoising of hyperspectral imagery by cubic smoothing spline in the wavelet domain. High Technol. Lett. 2014, 20, 54–62. [Google Scholar] [CrossRef]
- Yu, G.; Di, L.; Yang, Z.; Chen, Z.; Zhang, B. Crop condition assessment using high temporal resolution satellite images. In Proceedings of the 2012 First International Conference on Agro-Geoinformatics, Shanghai, China, 2–4 August 2012. [Google Scholar] [CrossRef]
- Singh, R.K.; Liu, S.; Tieszen, L.L.; Suyker, A.E.; Verma, S.B. Estimating seasonal evapotranspiration from temporal satellite images. Irrig. Sci. 2012, 30, 303–313. [Google Scholar] [CrossRef]
- Mao, F.; Li, X.; Du, H.; Zhou, G.; Han, N.; Xu, X.; Liu, Y.; Chen, L.; Cui, L. Comparison of two data assimilation methods for improving MODIS LAI time series for bamboo forests. Remote Sens. 2017, 9, 401. [Google Scholar] [CrossRef]
- Kimball, B.A. Smoothing Data with Cubic Splines. Agron. J. 1976, 68, 126–129. [Google Scholar] [CrossRef]
- Jamrozik, J.; Bohmanova, J.; Schaeffer, L.R. Selection of locations of knots for linear splines in random regression test-day models. J. Anim. Breed. Genet. 2010, 127, 87–92. [Google Scholar] [CrossRef] [PubMed]
- Wan, Z.; Zhang, Y.; Zhang, Q.; Li, Z.L. Quality assessment and validation of the MODIS global land surface temperature. Int. J. Remote Sens. 2004, 25, 261–274. [Google Scholar] [CrossRef]
- Molinari, N.; Durand, J.; Sabatier, R. Bounded optimal knots for regression splines. Comput. Stat. Data Anal. 2004, 45, 159–178. [Google Scholar] [CrossRef]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the 14th International Joint Conference on Artificial Intelligence (IJCAI), Montreal, QC, Canada, 20–25 August 1995. [Google Scholar]
- Lukas, M.A.; Hoog, F.R.; Anderssen, R.S. Efficient algorithms for robust generalized cross-validation spline smoothing. J. Comput. Appl. Math. 2010, 235, 102–107. [Google Scholar] [CrossRef]
- Jin, M.; Dickinson, R.E. Land surface skin temperature climatology: Benefitting from the strengths of satellite observations. Environ. Res. Lett. 2010, 5, 044004. [Google Scholar] [CrossRef]
- Huang, R.; Zhang, C.; Huang, J.; Zhu, D.; Wang, L.; Liu, J. Mapping of daily mean air temperature in agricultural regions using daytime and nighttime land surface temperatures derived from TERRA and AQUA MODIS data. Remote Sens. 2015, 7, 8728–8756. [Google Scholar] [CrossRef]
- Noi, P.T.; Kappas, M.; Degener, J. Estimating daily maximum and minimum land air surface temperature using MODIS land surface temperature data and ground truth data in northern Vietnam. Remote Sens. 2016, 8, 1002. [Google Scholar] [CrossRef]
- Zeng, L.; Wardlow, B.D.; Tadesse, T.; Shan, J.; Hayes, M.J.; Li, D.; Xiang, D. Estimation of daily air temperature based on MODIS land surface temperature products over the Corn Belt in the US. Remote Sens. 2015, 7, 951–970. [Google Scholar] [CrossRef]
- Vancutsem, C.; Ceccato, P.; Dinku, T.; Connor, S.J. Evaluation of MODIS land surface temperature data to estimate air temperature in different ecosystems over Africa. Remote Sens. Environ. 2010, 114, 449–465. [Google Scholar] [CrossRef]
- Breiman, L. Fitting additive models to regression data. Comput. Stat. Data Anal. 1993, 15, 13–46. [Google Scholar] [CrossRef]
- Gunnip, J. Analyzing Aggregated AR(1) Processes. Master’s Thesis, University of Utah, Salt Lake City, UT, USA, 2006. [Google Scholar]
- Brockwell, P.J.; Davis, R.A. Introduction to Time Series and Forecasting, 2nd ed.; Springer: New York, NY, USA, 2002; ISBN 038-7-95-351-5. [Google Scholar]
- Miao, C.; Ni, J. Implement of filter to remove the autocorrelation’s influence on the Mann-Kendall test: A case in hydrological series. J. Food Agric. Environ. 2010, 8, 1241–1246. [Google Scholar]
- Ballinger, G.A. Using generalized estimating equations for longitudinal data Analysis. Organ. Res. Methods 2004, 7, 127–150. [Google Scholar] [CrossRef]
- Wang, M. Generalized Estimating Equations in Longitudinal Data Analysis: A Review and Recent Developments. Adv. Statist. 2014, 2014. [Google Scholar] [CrossRef] [PubMed]
- Liang, K.; Zeger, S.L. Longitudinal data analysis using generalized linear models. Biometrika 1986, 73, 13–22. [Google Scholar] [CrossRef]
- Ackerman, S.A.; Strabala, K.I.; Menzel, W.P.; Frey, R.A.; Moeller, C.C.; Gumley, L.E. Discriminating clear sky from clouds with MODIS. J. Geophys. Res. Atmos. 1998, 103, 32141–32157. [Google Scholar] [CrossRef]
- Swets, D.L.; Reed, B.C.; Rowland, J.D.; Marko, S.E. A weighted least-squares approach to temporal NDVI smoothing. In Proceedings of the 1999 ASPRS Annual Conference: From Image to Information, Portland, OR, USA, 17–21 May 1999. [Google Scholar]
- Chen, J.; Jönsson, P.; Tamurab, M.; Gua, Z.; Matsushitab, B.; Eklundhd, L. A simple method for reconstructing a highquality NDVI time-series data set based on the Savitzky–Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
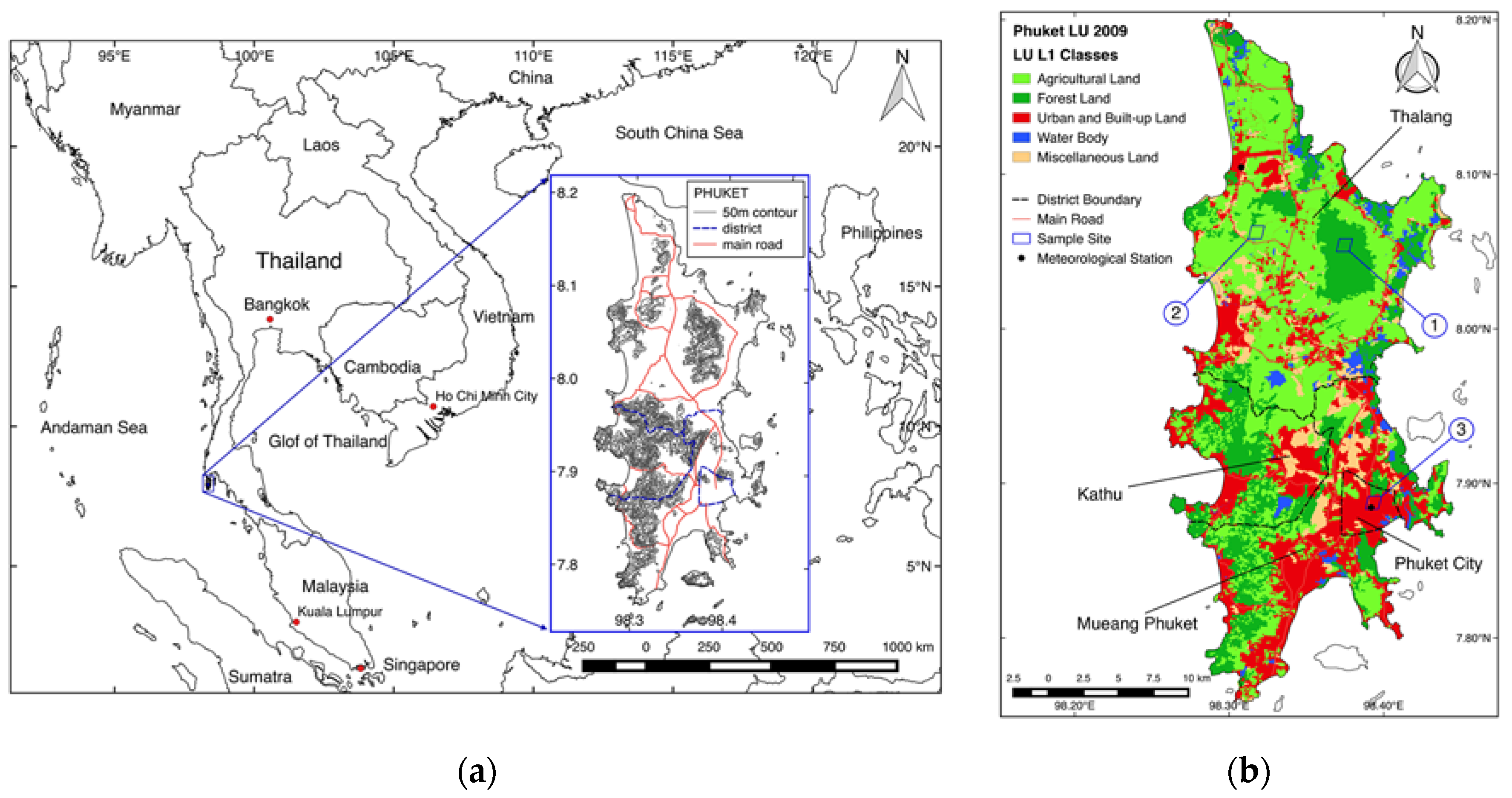
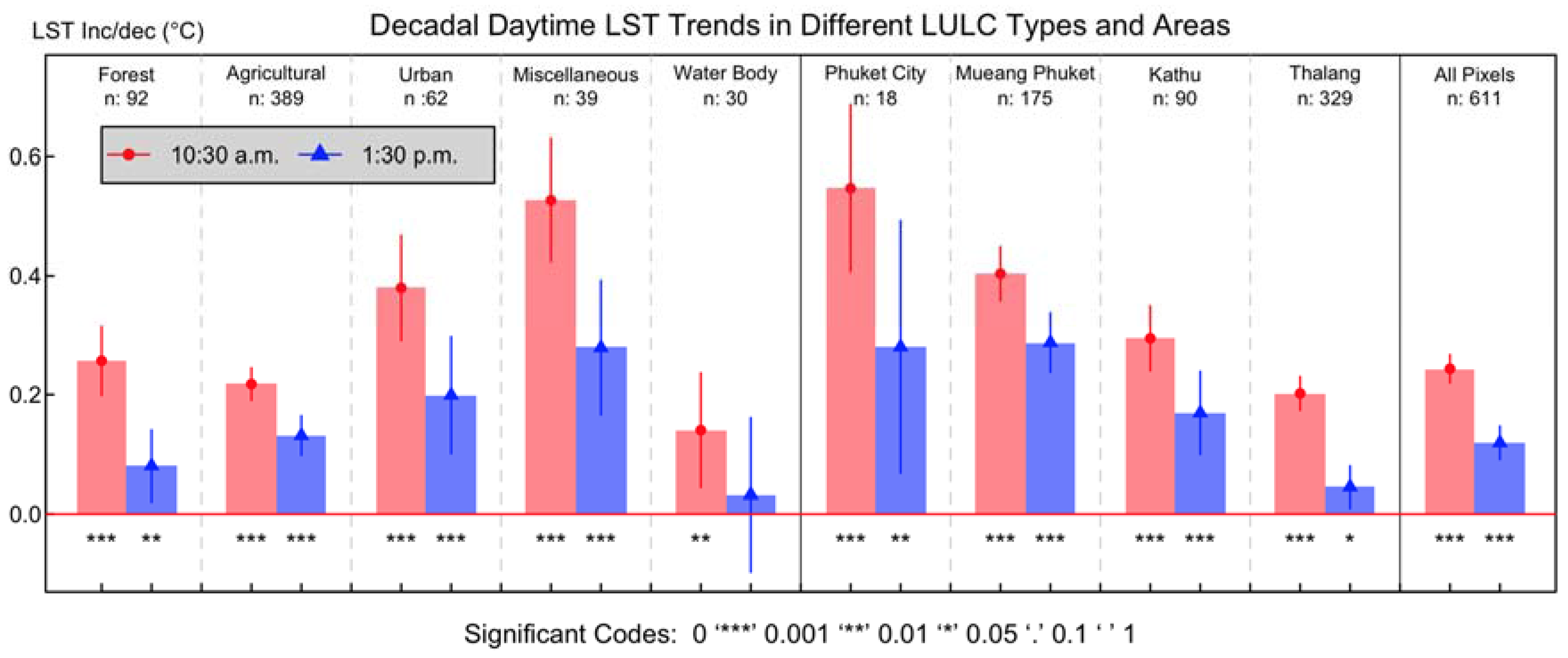
| District | Area: km2 | Lowland: km2 (%) * | LULC 2009: km2 (%) | ||||
|---|---|---|---|---|---|---|---|
| F | A | U | M | W | |||
| Phuket City | 13.6 | 12.6 (92.6) | 0.7 (5.2) | 1.2 (8.8) | 10.8 (79.4) | 0.6 (4.4) | 0.3 (2.2) |
| Mueang Phuket | 151.8 | 102.6 (67.6) | 37.5 (24.6) | 41.4 (27.3) | 58.6 (38.6) | 12.6 (8.4) | 1.6 (1.1) |
| Kathu | 80.2 | 26.0 (32.4) | 28.0 (34.9) | 22.7 (28.3) | 23.8 (29.7) | 4.5 (5.6) | 1.2 (1.5) |
| Thalang | 284.4 | 212.8 (74.8) | 53.8 (18.9) | 165.7 (58.3) | 40.3 (14.2) | 19.7 (6.9) | 4.9 (1.7) |
| Total | 530.0 | 354.0 (66.8) | 120.0 (22.6) | 231.0 (43.6) | 133.5 (25.2) | 37.5 (7.1) | 8.0 (1.5) |
| Site | Average Elevation | LULC 2009 | MODIS Sinusoidal Project Tile System | Latitude, Longitude (Middle of Pixel) |
|---|---|---|---|---|
| 1 | 275.2 m | Forest (F) | V: 8, H: 27, S: 800, L: 233 | 8.054167, 98.374528 |
| 2 | 53.1 m | Agricultural (A) * | V: 8, H: 27, S: 881, L: 232 | 8.062500, 98.317638 |
| 3 | 14.6 m | Urban and built-up (U) | V: 8, H: 27, S: 895, L: 253 | 7.887500, 98.393357 |
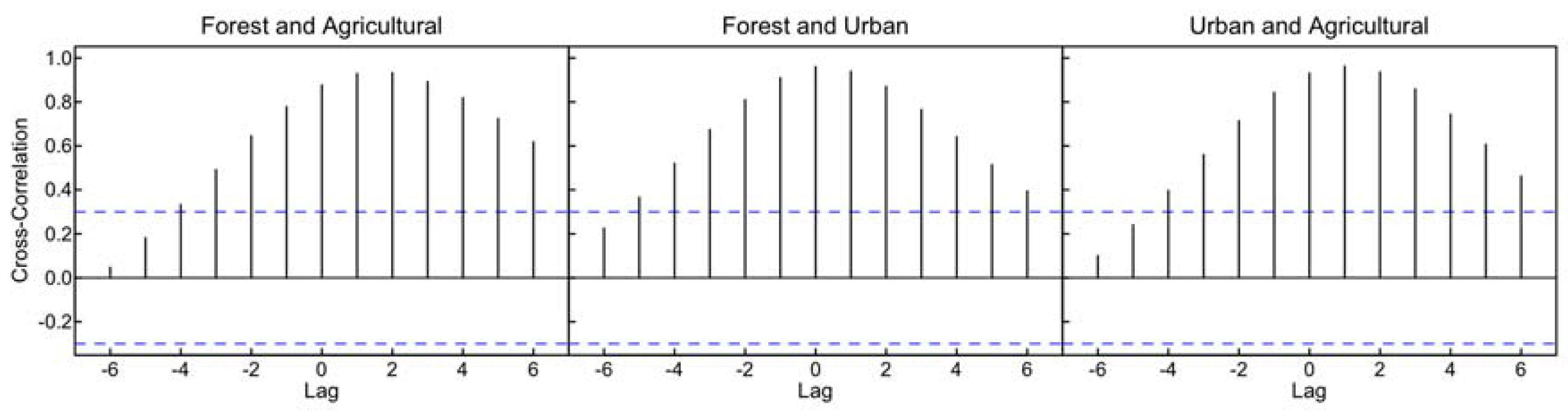
| Cross-Correlation | Lag | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| Forest vs. Agric. | 0.047 | 0.182 | 0.333 | 0.492 | 0.645 | 0.778 | 0.877 | 0.929 | 0.933* | 0.892 | 0.819 | 0.724 | 0.618 |
| Forest vs. Urban | 0.225 | 0.366 | 0.520 | 0.674 | 0.810 | 0.910 | 0.960* | 0.939 | 0.870 | 0.765 | 0.641 | 0.514 | 0.395 |
| Urban vs. Agric. | 0.101 | 0.241 | 0.397 | 0.560 | 0.714 | 0.843 | 0.931 | 0.963* | 0.936 | 0.859 | 0.744 | 0.607 | 0.462 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wongsai, N.; Wongsai, S.; Huete, A.R. Annual Seasonality Extraction Using the Cubic Spline Function and Decadal Trend in Temporal Daytime MODIS LST Data. Remote Sens. 2017, 9, 1254. https://doi.org/10.3390/rs9121254
Wongsai N, Wongsai S, Huete AR. Annual Seasonality Extraction Using the Cubic Spline Function and Decadal Trend in Temporal Daytime MODIS LST Data. Remote Sensing. 2017; 9(12):1254. https://doi.org/10.3390/rs9121254
Chicago/Turabian StyleWongsai, Noppachai, Sangdao Wongsai, and Alfredo R. Huete. 2017. "Annual Seasonality Extraction Using the Cubic Spline Function and Decadal Trend in Temporal Daytime MODIS LST Data" Remote Sensing 9, no. 12: 1254. https://doi.org/10.3390/rs9121254
APA StyleWongsai, N., Wongsai, S., & Huete, A. R. (2017). Annual Seasonality Extraction Using the Cubic Spline Function and Decadal Trend in Temporal Daytime MODIS LST Data. Remote Sensing, 9(12), 1254. https://doi.org/10.3390/rs9121254