Improving Jason-2 Sea Surface Heights within 10 km Offshore by Retracking Decontaminated Waveforms
Abstract
1. Introduction
2. Materials and Study Regions
2.1. Jason-2 Altimeter Data
2.2. Study Regions
3. Methodologies
3.1. Recapitulation of the WM Technique
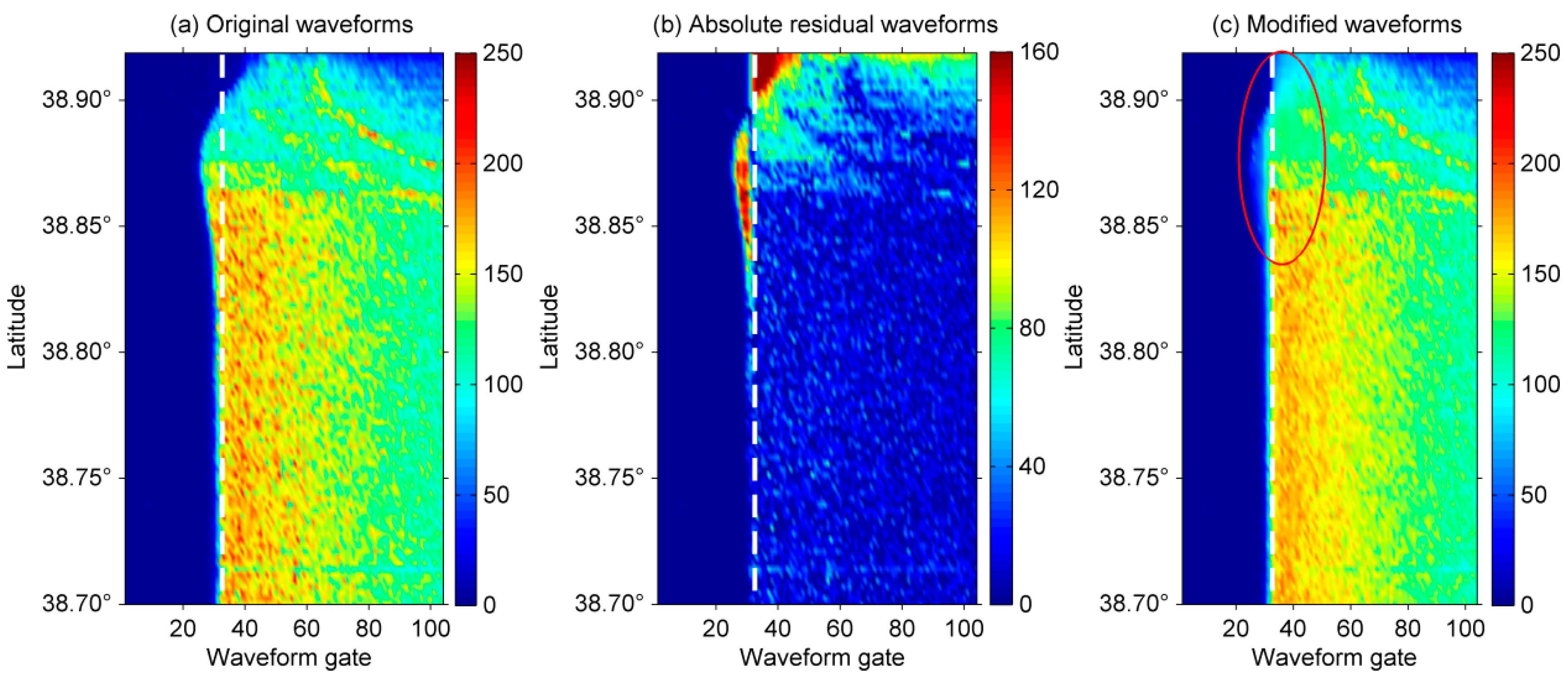
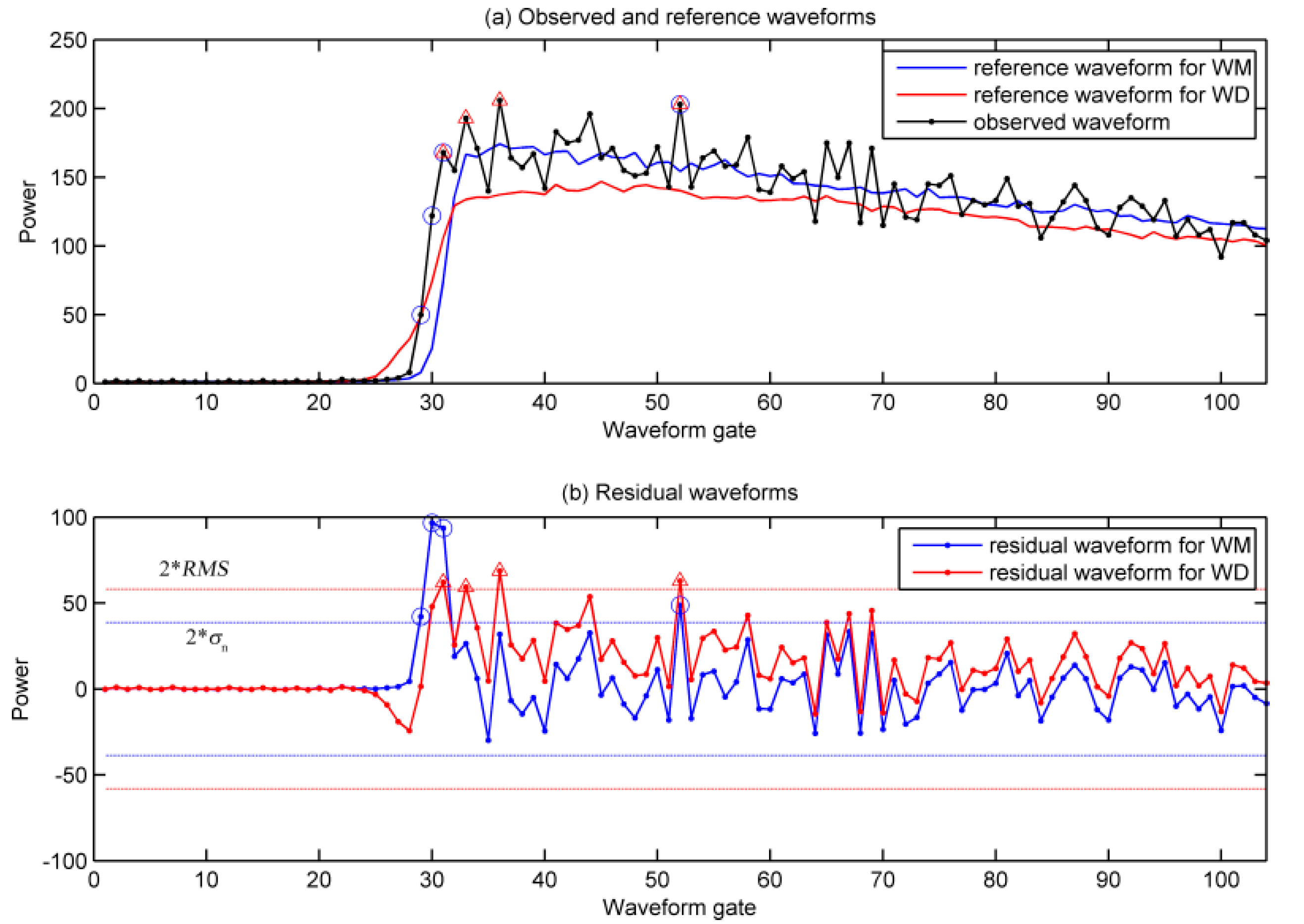
3.2. Waveform Decontamination
3.3. Computation and Evaluation of the Retracked SSHs
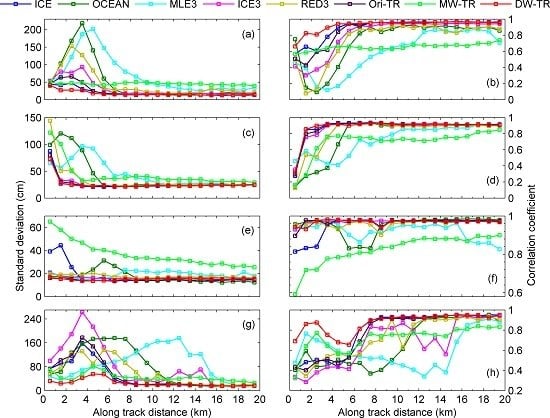
4. Results
4.1. Comparison to Geoid
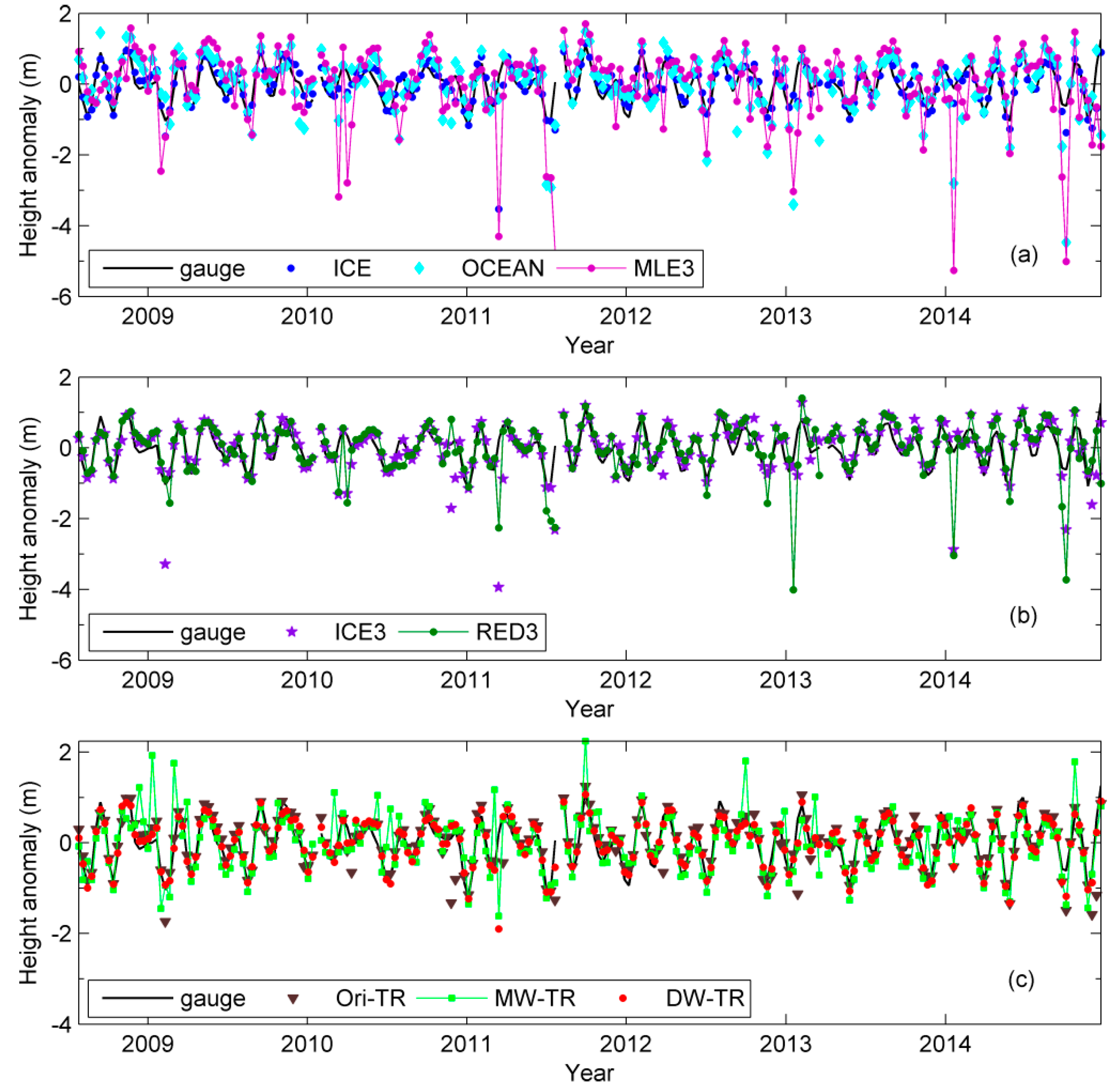
4.2. Comparison to Tide Gauge Data
5. Discussion
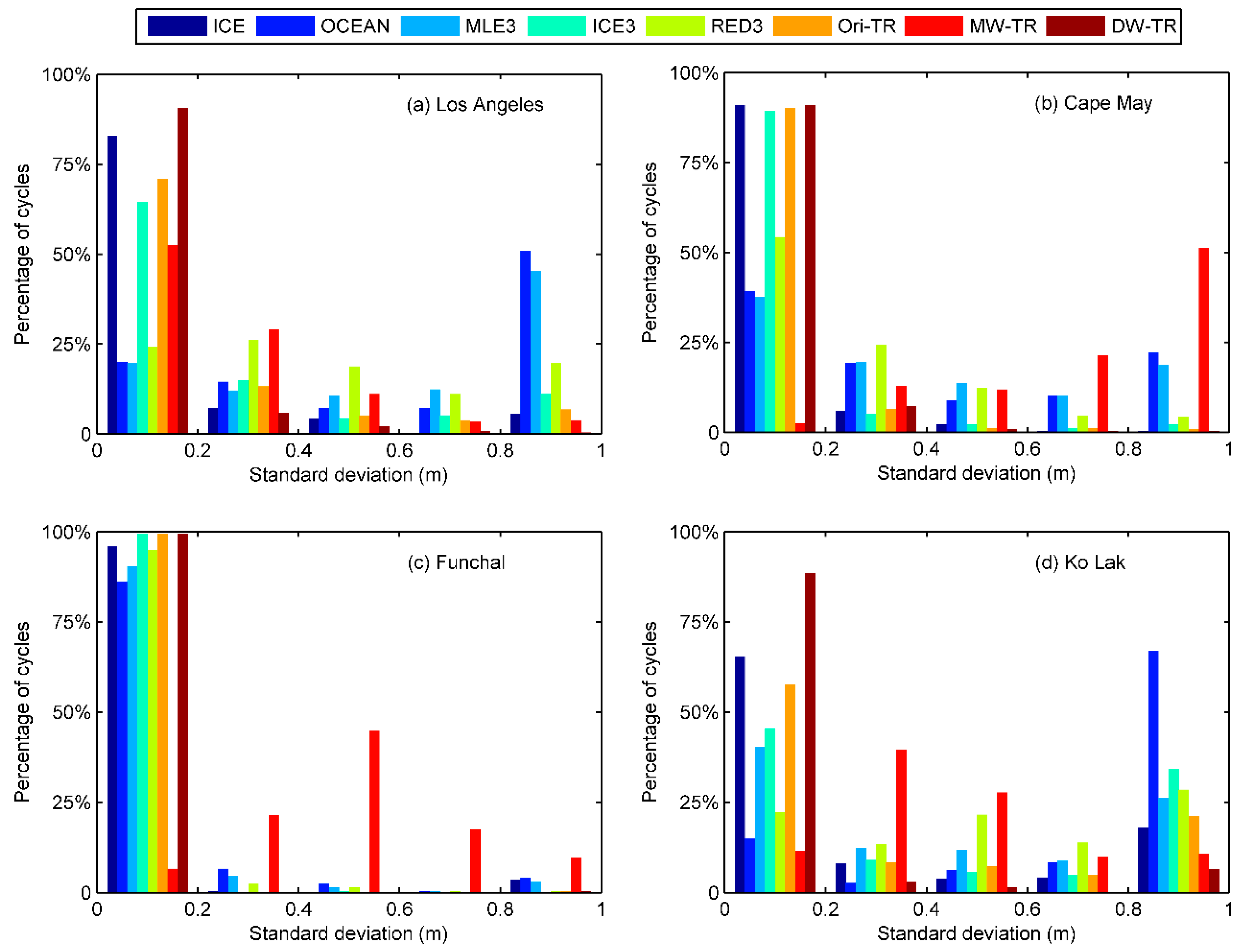
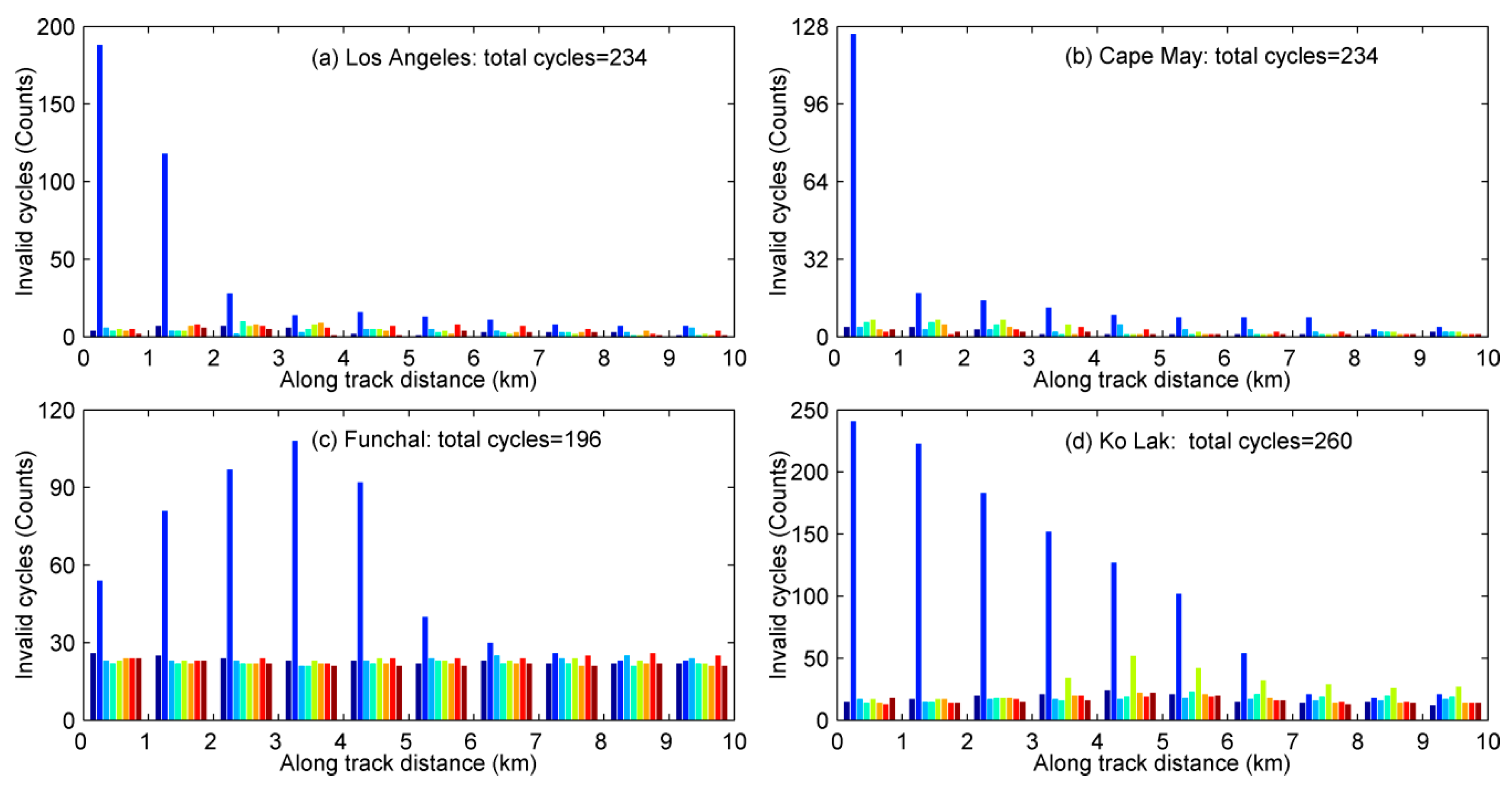
5.1. Negative Effects of Contaminations in Coastal Waveforms on Retrackers
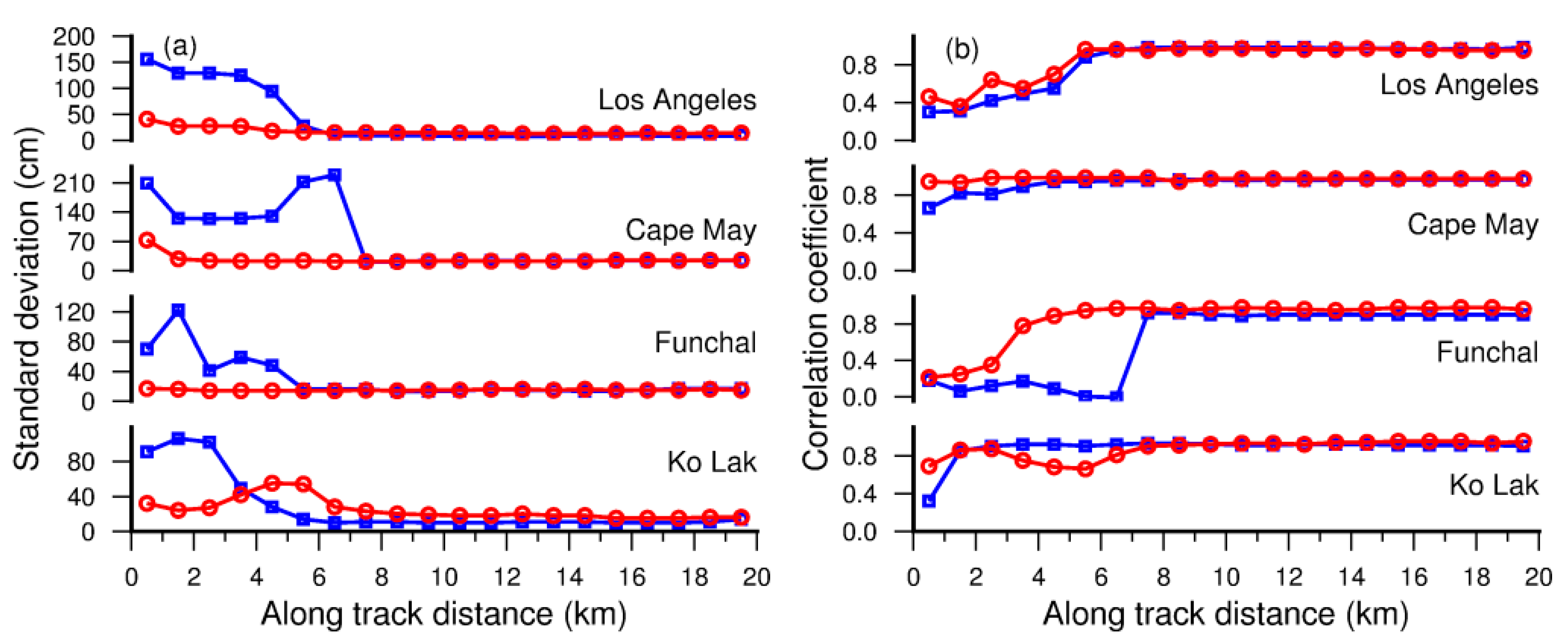
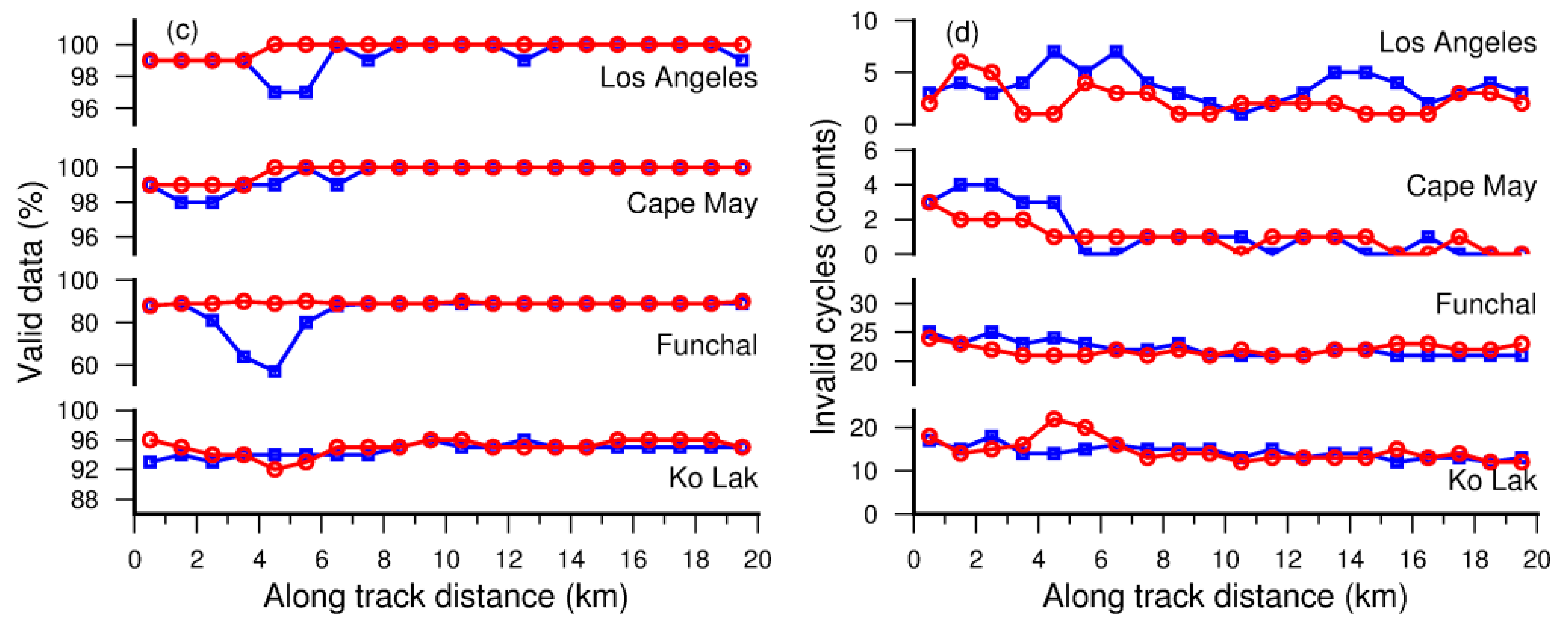
5.2. Improvement of the WD with Respect to the WM
5.3. Bias Analysis
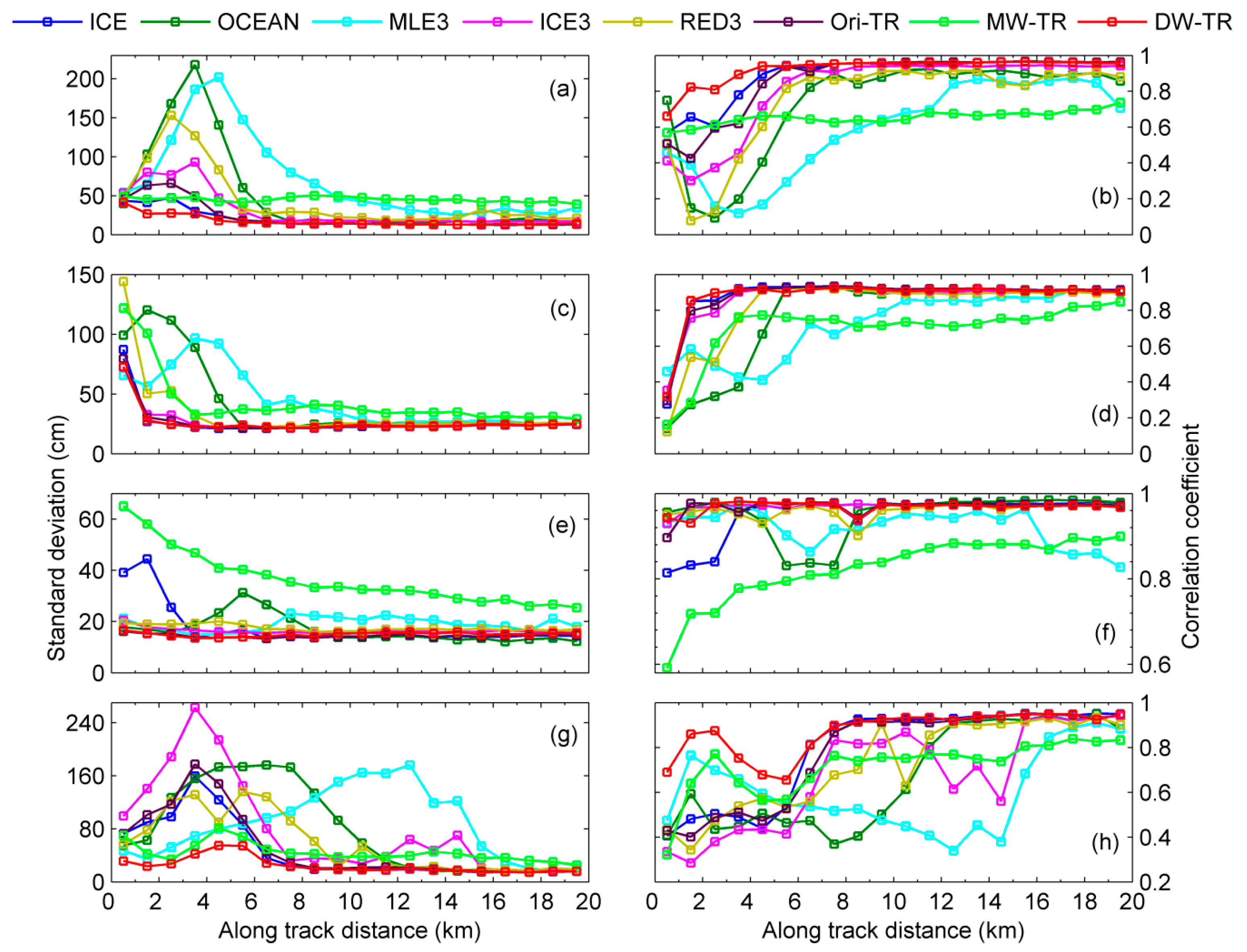
5.4. Test for Tracks Paralleling or Crossing Intricate Coastlines
5.5. Issues for Further Research
6. Conclusions and Recommendations
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fu, L.L.; Cazenave, A. Satellite Altimetry and Earth Sciences: A Handbook of Techniques and Applications; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Deng, X.; Featherstone, W.E.; Hwang, C.; Berry, P.A.M. Estimation of contamination of ERS-2 and POSEIDON satellite radar altimetry close to the coast of Australia. Mar. Geodesy 2002, 25, 249–271. [Google Scholar] [CrossRef]
- Vignudelli, S.; Cipollini, P.; Roblou, L.; Lyard, F.; Gasparini, G.P.; Manzella, G.; Astraldi, M. Improved satellite altimetry in coastal systems: Case study of the Corsica Channel (Mediterranean Sea). Geophys. Res. Lett. 2005, 32, L07608. [Google Scholar] [CrossRef]
- Gómez-Enri, J.; Cipollini, P.; Passaro, M.; Vignudelli, S.; Tejedor, B.; Coca, J. Coastal altimetry products in the Strait of Gibralta. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5455–5466. [Google Scholar] [CrossRef]
- Deng, X. Improvement of Geodetic Parameter Estimation in Coastal Regions from Satellite Radar Altimetry. Ph.D. Thesis, Curtin University of Technology, Perth, Australia, 2004. [Google Scholar]
- Halimi, A.; Mailhes, C.; Tourneret, J.Y.; Thibaut, P.; Boy, F. Parameter estimation for peaky altimetric waveforms. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1568–1577. [Google Scholar] [CrossRef]
- Anderson, O.B.; Scharroo, R. Range and geophysical corrections in coastal regions: And implications for mean sea surface determination. In Coastal Altimetry; Vignudelli, S., Kostianoy, A.G., Cipollini, P., Benveniste, J., Eds.; Springer: Berlin, Germany, 2011; pp. 103–145. [Google Scholar]
- Feng, H.; Vandemark, D. Altimeter data evaluation in the coastal gulf of Maine and Mid-Atlantic bight regions. Mar. Geodesy 2011, 34, 340–363. [Google Scholar] [CrossRef]
- Idris, N.H.; Deng, X.L.; Anderson, O.B. The importance of coastal altimetry retracking and detiding: A case study around the Great Barrier Reef, Australia. Int. J. Remote Sens. 2014, 35, 1729–1740. [Google Scholar] [CrossRef]
- Vignudelli, S.; Snaith, H.M.; Lyard, F.; Cipollini, P.; Venuti, F.; Birol, F.; Bouffard, J.; Roblou, L. Satellite radar altimetry from open ocean to coasts: Challenges and perspectives. In Proceedings of the 5th Asia-Pacific Remote Sensing Symposium, Goa, India, 13–17 November 2006; Volume 6406, pp. 1–12. [Google Scholar]
- Reale, F.; Dentale, F.; Pugliese Carratelli, E.; Torrisi, L. Remote sensing of small-scale storm variations in coastal seas. J. Coast. Res. 2014, 30, 130–141. [Google Scholar] [CrossRef]
- Vincent, P.; Steunou, N.; Caubet, E.; Phalippou, L.; Rey, L.; Thouvenot, E.; Verron, J.; AltiKa, A. Ka-band altimetry payload and system for operational altimetry during the GMES period. Sensors 2006, 6, 208–234. [Google Scholar] [CrossRef]
- Raney, R.K. The delay/Doppler radar altimeter. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1578–1588. [Google Scholar] [CrossRef]
- Halimi, A.; Mailhes, C.; Tourneret, J.Y.; Boy, F.; Moreau, T. Including antenna mispointing in a semi-analytical model for delay/Doppler altimetry. IEEE Trans. Geosci. Remote Sens. 2015, 53, 598–608. [Google Scholar] [CrossRef]
- Lowe, S.T.; Zuffada, C.; Chao, Y.; Kroger, P.; Young, L.E.; LaBrecque, J.L. 5-cm-precision aircraft ocean altimetry using GPS reflections. Geophys. Res. Lett. 2002, 29, 131–134. [Google Scholar] [CrossRef]
- Allan, T. The story of GANDER. Sensors 2006, 6, 249–259. [Google Scholar] [CrossRef]
- Enjolras, V.; Vincent, P.; Souyris, J.C.; Rodriguez, E.; Phalippou, L.; Cazenave, A. Performances study of interferometric radar altimeters: From the instrument to the global mission definition. Sensors 2006, 6, 164–192. [Google Scholar] [CrossRef]
- Anzenhofer, M.; Shum, C.K.; Rentsh, M. Coastal Altimetry and Applications; Report No. 464; Geodetic Science and Surveying, The Ohio State University: Columbus, OH, USA, 1999. [Google Scholar]
- Bouffard, J.; Vignudelli, S.; Cipollini, P.; Menard, Y. Exploiting the potential of an improved multimission altimetric data set over the coastal ocean. Geophys. Res. Lett. 2008, 35, L10601. [Google Scholar] [CrossRef]
- Cipollini, P.; Calafat, F.M.; Jevrejeva, S.; Melet, A.; Prandi, P. Monitoring sea level in the coastal zone with satellite altimetry and tide gauges. Surv. Geophys. 2016, 38, 33–57. [Google Scholar] [CrossRef]
- Mercier, F.; Rosmorduc, V.; Carrere, L.; Thibaut, P. Coastal and Hydrology Altimetry Product (PISTACH) Handbook. CLS-DOS-NT-10-246, SALP-MU-P-OP-16031-CN 01/00. 2010. Available online: https://www.aviso.altimetry.fr/fileadmin/documents/data/tools/hdbk_Pistach.pdf (accessed on 23 October 2017).
- Cipollini, P.; Susana Barbosa, S.; Caparrini, M.; Challenor, P.; Coelho, H.; Dinardo, S.; Fernandes, S.; Gleason, S.; Gómez-Enri, J.; Gommenginger, C.; et al. COASTALT Project’s contribution to the development and dissemination of coastal altimetry. In Proceedings of the 20 Years of Progress in Radar Altimetry Symposium, Venice, Italy, 24–29 September 2012. [Google Scholar]
- Birol, F.; Fuller, N.; Lyard, F.; Cancet, M.; Nino, F.; Delebecque, C.; Léger, F. Coastal applications from nadir altimetry: Example of the X-TRACK regional products. Adv. Space Res. 2017, 59, 936–953. [Google Scholar] [CrossRef]
- Vignudelli, S.; Kostianoy, A.G.; Cipollini, P.; Benveniste, J. Coastal Altimetry; Springer: Berlin, Germany, 2011. [Google Scholar]
- Tran, N.; Vandemark, D.; Chapron, B.; Labroue, S.; Feng, H.; Beckley, B.; Vincent, P. New models for satellite altimeter sea state bias correction developed using global wave model data. J. Geophys. Res. 2006, 111, C09009. [Google Scholar] [CrossRef]
- Feng, H.; Yao, S.; Li, L.; Tran, N.; Vandemark, D.; Labroue, S. Spline-based nonparametric estimation of the altimeter sea-state bias correction. IEEE Geosci. Remote Sens. Lett. 2010, 7, 577–581. [Google Scholar] [CrossRef]
- Tran, N.; Vandemark, D.; Labroue, S.; Feng, H.; Chapron, B.; Tolman, H.L.; Lambin, J.; Picot, N. Sea state bias in altimeter sea level estimates determined by combining wave model and satellite data. J. Geophys. Res. 2010, 115, C03020. [Google Scholar] [CrossRef]
- Pires, N.; Fernandes, M.; Gommenginger, C.; Scharroo, R. A Conceptually Simple Modeling Approach for Jason-1 Sea State Bias Correction Based on 3 Parameters Exclusively Derived from Altimetric Information. Remote Sens. 2016, 8, 576. [Google Scholar] [CrossRef]
- Reale, F.; Dentale, F.; Pugliese Carratelli, E. Numerical simulation of whitecaps and foam effects on satellite altimeter response. Remote Sens. 2014, 6, 3681–3692. [Google Scholar] [CrossRef]
- Brown, G. The average impulse response of a rough surface and its applications. IEEE Trans. Antennas Propag. 1977, 25, 67–74. [Google Scholar] [CrossRef]
- Davis, C.H. A robust threshold retracking algorithm for measuring ice-sheet surface elevation change from satellite radar altimeters. IEEE Trans. Geosci. Remote Sens. 1997, 35, 974–979. [Google Scholar] [CrossRef]
- Hwang, C.; Guo, J.Y.; Deng, X.L.; Hsu, H.Y.; Liu, Y.T. Coastal gravity anomalies from retracked Geosat/GM altimetry: Improvement, limitation and the role of airborne gravity data. J. Geodesy 2006, 80, 204–216. [Google Scholar] [CrossRef]
- Lee, H.; Shum, C.K.; Emery, W.; Calmant, S.; Deng, X.; Kuo, C.Y.; Roesler, C.; Yi, Y.C. Validation of Jason-2 altimeter data by waveform retracking over California coastal ocean. Mar. Geodesy 2010, 33, 304–316. [Google Scholar] [CrossRef]
- Guo, J.; Gao, Y.; Hwang, C.; Sun, J. A mutli-subwaveform parametric retracker of the radar satellite altimetric waveform and recovery of gravity anomalies over coastal oceans. Sci. China Earth Sci. 2010, 53, 610–616. [Google Scholar] [CrossRef]
- Yang, Y.; Hwang, C.; Hsu, H.J.; Dongchen, E.; Wang, H. A subwaveform threshold retracker for ERS-1 altimetry: A case study in the Antarctic Ocean. Comp. Geosci. 2012, 41, 88–98. [Google Scholar] [CrossRef]
- Yang, L.; Lin, M.; Liu, Q.; Pan, D. A coastal altimetry retracking strategy based on waveform classification and subwaveform extraction. Int. J. Remote Sens. 2012, 33, 7806–7819. [Google Scholar] [CrossRef]
- Idris, N.H.; Deng, X. The retracking technique on multi-peak and quasi-specular waveforms for Jason-1 and Jason-2 missions near the coast. Mar. Geodesy 2012, 35, 217–237. [Google Scholar] [CrossRef]
- Passaro, M.; Cipollini, P.; Vignudelli, S.; Quartly, G.D.; Snaith, H.M. ALES: A multi-mission adaptive subwaveform retracker for coastal and open sea altimetry. Remote Sens. Environ. 2014, 145, 173–189. [Google Scholar] [CrossRef]
- Gómez-Enri, J.; Vignudelli, S.; Quartly, G.D.; Gommenginger, C.P.; Cipollini, P.; Challenor, P.G.; Benveniste, J. Modeling ENVISAT RA-2 waveforms in the coastal zone: Case study of calm water contamination. IEEE Geosci. Remote Sens. Lett. 2010, 7, 474–478. [Google Scholar] [CrossRef]
- Deng, X.; Featherstone, W. A coastal retracking system for satellite radar altimeter waveforms: Application to ERS-2 around Australia. J. Geophys. Res. 2006, 111, C06012. [Google Scholar] [CrossRef]
- Wang, H.H.; Luo, Z.C.; Yang, Y.D.; Zhong, B.; Zhou, H. An adaptive retracking method for coastal altimeter data based on waveform classification. Acta Geodesy Cartogr. Sin. 2012, 41, 729–734. [Google Scholar]
- Khakia, M.; Forootan, E.; Sharifi, M.A. Satellite radar altimetry waveform retracking over the Caspian Sea. Int. J. Remote Sens. 2014, 35, 6329–6356. [Google Scholar] [CrossRef]
- Tseng, K.H.; Shum, C.K.; Yi, Y.C.; Emery, W.J.; Kuo, C.Y.; Wang, H.H. The improved retrieval of coastal sea surface heights by retracking modified radar altimetry waveforms. IEEE Trans. Geosci. Remote Sens. 2014, 52, 991–1001. [Google Scholar] [CrossRef]
- Desjonquères, J.D.; Carayon, G.; Steunou, N.; Lambin, J. Poseidon-3 radar altimeter: New modes and in-flight performances. Mar. Geodesy 2010, 33, 53–79. [Google Scholar] [CrossRef]
- AVISO+ CNES. Available online: https://www.aviso.altimetry.fr/en/missions/current-missions/jason-2/index.html (accessed on 20 May 2017).
- Lambin, L.; Morrow, R.; Fu, L.L.; Willis, J.; Bonekamp, H.; Lillibridge, J.; Perbos, J.; Zaouche, G.; Vaze, P.; Bannoura, W.; et al. The OSTM/Jason-2 mission. Mar. Geodesy 2010, 33, 4–25. [Google Scholar] [CrossRef]
- Chelton, D.B.; Ries, J.C.; Haines, B.J.; Fu, L.-L.; Callahan, P.S. Satellite Altimetry. In Satellite Altimetry and Earth Sciences: A Handbook of Techniques and Applications; Fu, L.-L., Cazenave, A., Eds.; Academic Press: San Diego, CA, USA, 2001; pp. 1–131. [Google Scholar]
- Dumont, J.-P.; Rosmordue, V.; Picot, N.; Desai, S.; Bonekamp, H.; Figa, J.; Lillibridge, J.; Sharroo, R. OSTM/Jason-2 Products Handbook. CNES: SALP-MU-M-OP-15818-CN; EUMETSAT: EUM/OPS-JAS/MAN/08/0041; JPL: OSTM-29–1237; NOAA/NESDIS: Polar Series/OSTM J400; 2011; Available online: https://www.aviso.altimetry.fr/fileadmin/documents/data/tools/hdbk_j2.pdf (accessed on 23 October 2017).
- Wingham, D.J.; Rapley, C.G.; Griffiths, H. New techniques in satellite altimeter tracking systems. In Proceedings of the 1986 International Geoscience and Remote Sensing Symposium on Remote Sensing: Today’s Solutions for Tomorrow’s Information Needs, Noordwijk, The Netherlands, 8– 11September 1986; Volume 3, pp. 1339–1344. [Google Scholar]
- Gommenginger, C.; Thibaut, P.; Fenoglio-Marc, L.; Quartly, G.; Deng, X.; Gómez-Enri, J.; Challenor, P.; Gao, Y. Retracking altimeter waveforms near the coasts. In Coastal Altimetry; Vignudelli, S., Kostianoy, A.G., Cipollini, P., Benveniste, J., Eds.; Springer: Berlin, Heidelberg, 2011; pp. 61–102. [Google Scholar]
- Becker, J.J.; Sandwell, D.T.; Smith, W.H.F.; Braud, J.; Binder, B.; Depner, J.; Fabre, D.; Factor, J.; Ingalls, S.; Kim, S.H.; et al. Global bathymetry and elevation data at 30 arc seconds resolution: SRTM30_PLUS. Mar. Geodesy 2009, 32, 355–371. [Google Scholar] [CrossRef]
- Caldwell, P.C.; Merrfield, M.A.; Thompson, P.R. Sea Level Measured by Tide Gauges from Global Oceans—The Joint Archive for Sea Level Holdings (NCEI Accession 0019568), Version 5.5. NOAA National Centers for Environmental Information, Dataset. 2015. Available online: https://uhslc.soest.hawaii.edu/datainfo/ (accessed on 23 October 2017).
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. 2012, 117, B04406. [Google Scholar] [CrossRef]
- Wang, X.; Ichikawa, K. Coastal waveform retracking for Jason-2 altimeter data based on along-track echograms around the Tsushima Islands in Japan. Remote Sens. 2017, 9, 762. [Google Scholar] [CrossRef]
- Thibaut, P.; Poisson, J.C.; Bronner, E.; Picot, N. Relative performance of the MLE3 and MLE4 retracking algorithms on Jason-2 altimeter waveforms. Mar. Geodesy 2010, 33, 317–335. [Google Scholar] [CrossRef]
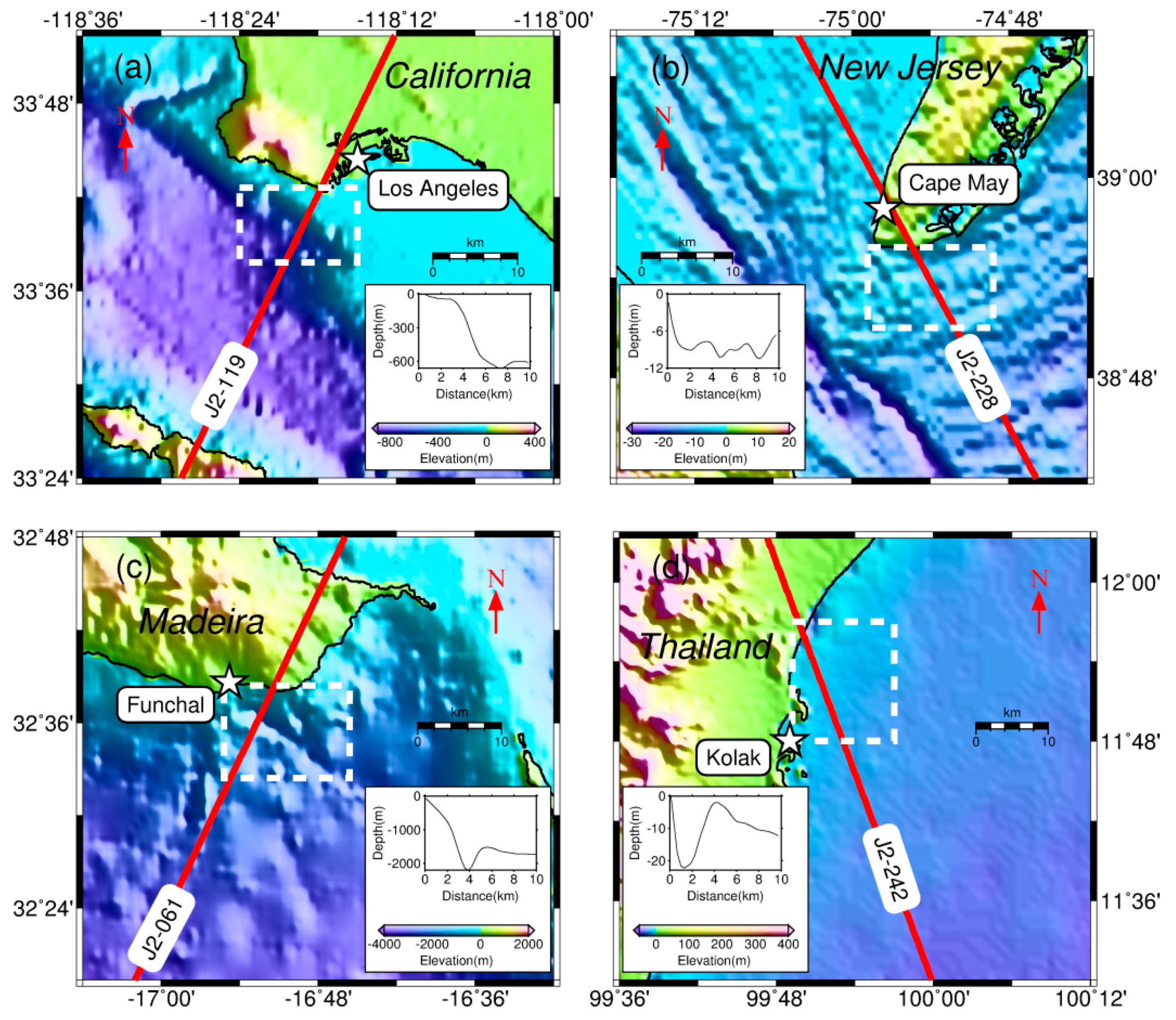

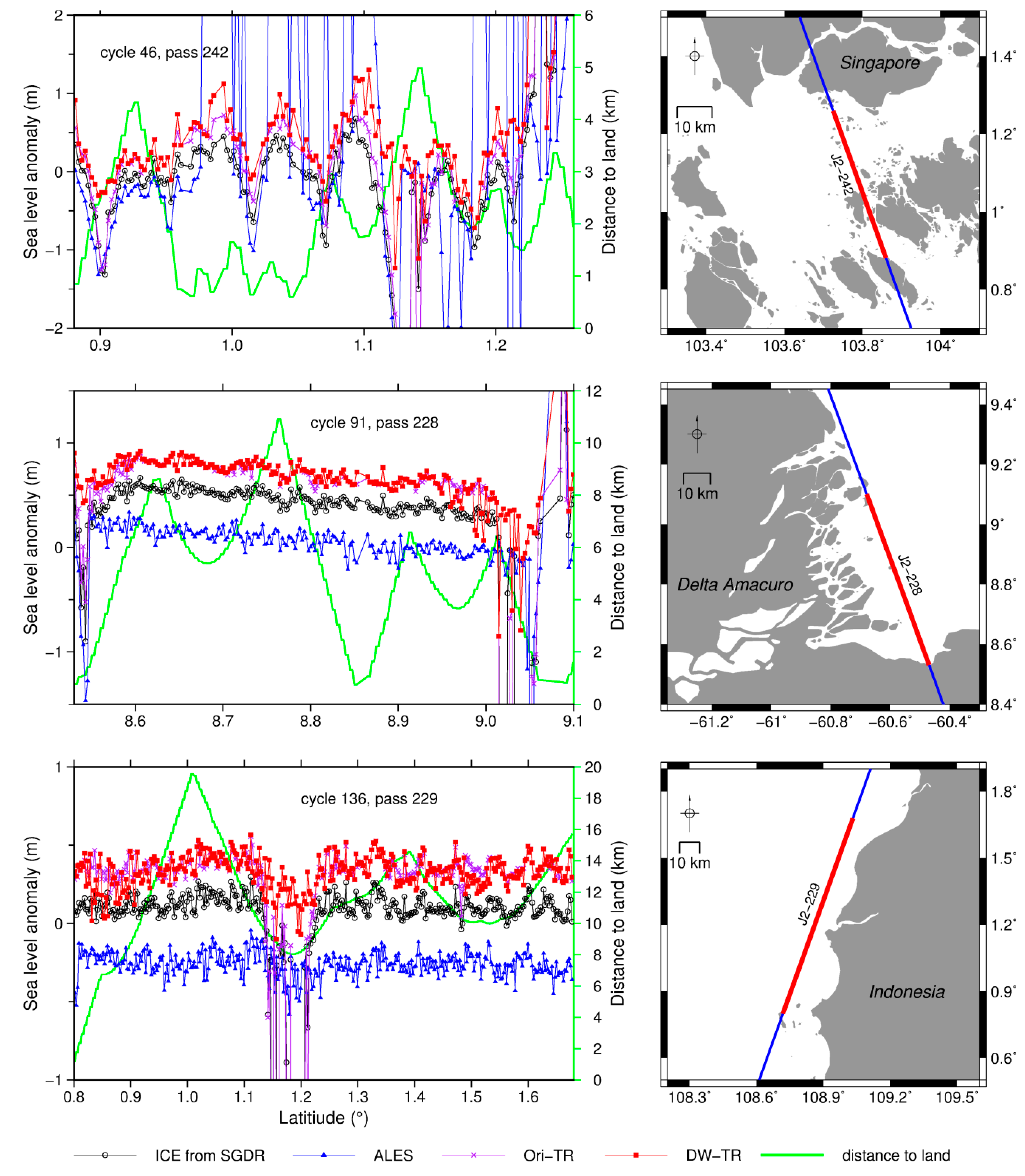
| Region | Pass | Cycle 1 | Time Span | Direction |
|---|---|---|---|---|
| Los Angeles, USA | 119 | 2-238(234) | July 2008–December 2014 | Ascending, approaching land |
| Cape May, USA | 228 | 2-238(234) | July 2008–December 2014 | Descending, leaving land |
| Funchal, Portugal | 061 | 2-202(196) | July 2008–December 2013 | Ascending, approaching land |
| Ko Lak, Thailand | 242 | 2-262(260) | July 2008–December 2014 | Descending, leaving land |
| Region | 20 Hz Data (pt) | Ocean Waveform (%) | Retracker (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ICE | OCEAN | MLE3 | ICE3 | OCE3 | RED3 | Ori-TR | MW-TR | DW-TR | |||
| Los Angeles | 8082 | 57 | 100 | 92 | 100 | 99 | 57 | 97 | 100 | 100 | 100 |
| Cape May | 8265 | 74 | 100 | 97 | 100 | 100 | 74 | 99 | 100 | 100 | 100 |
| Funchal | 6746 | 53 | 100 | 70 | 100 | 100 | 52 | 100 | 100 | 100 | 100 |
| Ko Lak | 8569 | 30 | 100 | 66 | 100 | 99 | 30 | 88 | 100 | 100 | 100 |
| Mean | 7916 | 54 | 100 | 81 | 100 | 99 | 54 | 96 | 100 | 100 | 100 |
| Region (a): Los Angeles | ||||||||
| Retracker | ICE | OCEAN | MLE3 | ICE3 | RED3 | Ori-TR | MW-TR | DW-TR |
| SD (cm)/IMP (%) | 32/68 | 128/−28 | 120/−20 | 56/44 | 94/6 | 46/54 | 39/61 | 25/75 |
| Cal. SD (cm)/IMP (%) | 20/79 | 109/−15 | 103/−8 | 35/63 | 63/34 | 29/69 | 35/63 | 18/81 |
| Valid data (%) | 96 | 77 | 97 | 94 | 92 | 95 | 99 | 97 |
| Invalid cycle | 5 | 2 | 5 | 9 | 7 | 8 | 1 | 1 |
| Region (b): Cape May | ||||||||
| Retracker | ICE | OCEAN | MLE3 | ICE3 | RED3 | Ori-TR | MW-TR | DW-TR |
| SD (cm)/IMP (%) | 36/82 | 85/58 | 64/68 | 31/85 | 59/71 | 32/84 | 117/42 | 31/85 |
| Cal. SD (cm)/IMP (%) | 15/92 | 64/67 | 56/71 | 16/92 | 34/82 | 17/91 | 94/51 | 17/91 |
| Valid data (%) | 97 | 85 | 98 | 96 | 93 | 97 | 97 | 97 |
| Invalid cycle | 1 | 3 | 2 | 5 | 2 | 2 | 1 | 1 |
| Region (c): Funchal | ||||||||
| Retracker | ICE | OCEAN | MLE3 | ICE3 | RED3 | Ori-TR | MW-TR | DW-TR |
| SD (cm)/IMP (%) | 30/68 | 26/73 | 21/78 | 10/89 | 17/82 | 14/85 | 64/33 | 14/85 |
| Cal. SD (cm)/IMP (%) | 10/89 | 18/81 | 14/85 | 9/90 | 13/86 | 9/90 | 61/34 | 9/90 |
| Valid data (%) | 96 | 69 | 96 | 99 | 97 | 99 | 99 | 99 |
| Invalid cycle | 6 | 6 | 6 | 1 | 5 | 1 | 1 | 1 |
| Region (d): Ko Lak | ||||||||
| Retracker | ICE | OCEAN | MLE3 | ICE3 | RED3 | Ori-TR | MW-TR | DW-TR |
| SD (cm)/IMP (%) | 77/60 | 135/30 | 71/63 | 118/39 | 107/45 | 86/55 | 71/63 | 35/82 |
| Cal. SD (cm)/IMP (%) | 49/74 | 127/33 | 60/68 | 93/51 | 72/62 | 56/70 | 57/70 | 16/92 |
| Valid data (%) | 95 | 53 | 97 | 96 | 84 | 94 | 96 | 94 |
| Invalid cycle | 9 | 3 | 6 | 4 | 11 | 10 | 8 | 14 |
| Average over Four Regions | ||||||||
| Retracker | ICE | OCEAN | MLE3 | ICE3 | RED3 | Ori-TR | MW-TR | DW-TR |
| SD (cm)/IMP (%) | 44/70 | 94/33 | 69/47 | 54/64 | 69/51 | 45/70 | 73/50 | 26/82 |
| Cal. SD (cm)/IMP (%) | 24/84 | 80/42 | 58/54 | 38/74 | 46/66 | 28/80 | 62/55 | 15/89 |
| Valid data (%) | 96 | 71 | 97 | 96 | 92 | 96 | 98 | 97 |
| Invalid cycle | 5.3 | 3.5 | 4.8 | 4.8 | 6.3 | 5.3 | 2.8 | 4.3 |
| Region (a): Los Angeles | ||||||||
| Retracker | ICE | OCEAN | MLE3 | ICE3 | RED3 | Ori-TR | MW-TR | DW-TR |
| SD (cm)/IMP (%) | 34/65 | 69/31 | 103/−4 | 55/44 | 58/41 | 41/59 | 46/53 | 22/78 |
| Cal. SD (cm)/IMP (%) | 21/76 | 55/37 | 76/13 | 35/60 | 34/61 | 24/72 | 37/57 | 17/81 |
| Valid data (%) | 98 | 76 | 97 | 95 | 92 | 98 | 98 | 97 |
| Invalid cycles | 3 | 4 | 6 | 6 | 7 | 6 | 6 | 1 |
| Correlation | 0.89 | 0.6 | 0.43 | 0.77 | 0.75 | 0.82 | 0.7 | 0.95 |
| Region (b): Cape May | ||||||||
| Retracker | ICE | OCEAN | MLE3 | ICE3 | RED3 | Ori-TR | MW-TR | DW-TR |
| SD (cm)/IMP (%) | 33/56 | 88/−19 | 82/−10 | 41/45 | 71/4 | 36/51 | 50/32 | 35/53 |
| Cal. SD (cm)/IMP (%) | 22/63 | 46/23 | 44/26 | 24/60 | 26/57 | 23/62 | 39/35 | 22/63 |
| Valid data (%) | 97 | 85 | 97 | 97 | 93 | 97 | 97 | 97 |
| Invalid cycles | 1 | 1 | 3 | 2 | 1 | 1 | 1 | 1 |
| Correlation | 0.92 | 0.65 | 0.69 | 0.9 | 0.89 | 0.92 | 0.73 | 0.92 |
| Region (c): Funchal | ||||||||
| Retracker | ICE | OCEAN | MLE3 | ICE3 | RED3 | Ori-TR | MW-TR | DW-TR |
| SD (cm)/IMP (%) | 51/36 | 39/51 | 24/69 | 16/80 | 17/78 | 27/66 | 41/48 | 14/82 |
| Cal. SD (cm)/IMP (%) | 18/68 | 19/65 | 15/72 | 16/71 | 16/71 | 13/76 | 35/37 | 13/76 |
| Valid data (%) | 98 | 76 | 97 | 95 | 92 | 98 | 98 | 97 |
| Invalid cycles | 25 | 24 | 24 | 22 | 23 | 22 | 24 | 22 |
| Correlation | 0.9 | 0.93 | 0.93 | 0.97 | 0.97 | 0.98 | 0.83 | 0.98 |
| Region (d): Ko Lak | ||||||||
| Retracker | ICE | OCEAN | MLE3 | ICE3 | RED3 | Ori-TR | MW-TR | DW-TR |
| SD (cm)/IMP (%) | 89/6 | 143/−51 | 94/1 | 133/−41 | 122/−29 | 94/0 | 56/41 | 49/49 |
| Cal. SD (cm)/IMP (%) | 57/36 | 113/−27 | 75/15 | 104/−17 | 56/36 | 58/34 | 36/60 | 27/70 |
| Valid data (%) | 91 | 51 | 94 | 91 | 81 | 91 | 92 | 92 |
| Invalid cycles | 20 | 15 | 17 | 17 | 20 | 21 | 18 | 18 |
| Correlation | 0.67 | 0.47 | 0.61 | 0.58 | 0.72 | 0.64 | 0.76 | 0.84 |
| Average over Four Regions | ||||||||
| Retracker | ICE | OCEAN | MLE3 | ICE3 | RED3 | Ori-TR | MW-TR | DW-TR |
| SD (cm)/IMP (%) | 52/41 | 85/3 | 76/14 | 61/32 | 67/24 | 50/44 | 48/44 | 30/66 |
| Cal. SD (cm)/IMP (%) | 30/61 | 58/25 | 53/32 | 45/44 | 33/56 | 30/56 | 37/47 | 20/73 |
| Valid data (%) | 96 | 72 | 96 | 95 | 90 | 96 | 96 | 96 |
| Invalid cycles | 12.3 | 11 | 12.5 | 11.8 | 12.8 | 12.5 | 12.3 | 10.5 |
| Correlation | 0.85 | 0.66 | 0.67 | 0.81 | 0.83 | 0.84 | 0.76 | 0.92 |
| Region (a) | Region (b) | Region (c) | Region (d) | |
|---|---|---|---|---|
| DW-TR–OCEAN (cm) | 72.6 ± 11.9 | 73 ± 6.5 | 78 ± 11.8 | 65.7 ± 6.9 |
| Ori-TR–OCEAN (cm) | 72.9 ± 11.7 | 71.9 ± 6.3 | 77.6 ± 10.8 | 65 ± 8.2 |
| DW-TR–Ori-TR (cm) | 0.2 ± 1.1 | 1.4 ± 1.2 | 0.5 ± 1.7 | 1.3 ± 1.9 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Wang, H.; Luo, Z.; Shum, C.K.; Tseng, K.-H.; Zhong, B. Improving Jason-2 Sea Surface Heights within 10 km Offshore by Retracking Decontaminated Waveforms. Remote Sens. 2017, 9, 1077. https://doi.org/10.3390/rs9101077
Huang Z, Wang H, Luo Z, Shum CK, Tseng K-H, Zhong B. Improving Jason-2 Sea Surface Heights within 10 km Offshore by Retracking Decontaminated Waveforms. Remote Sensing. 2017; 9(10):1077. https://doi.org/10.3390/rs9101077
Chicago/Turabian StyleHuang, Zhengkai, Haihong Wang, Zhicai Luo, C. K. Shum, Kuo-Hsin Tseng, and Bo Zhong. 2017. "Improving Jason-2 Sea Surface Heights within 10 km Offshore by Retracking Decontaminated Waveforms" Remote Sensing 9, no. 10: 1077. https://doi.org/10.3390/rs9101077
APA StyleHuang, Z., Wang, H., Luo, Z., Shum, C. K., Tseng, K.-H., & Zhong, B. (2017). Improving Jason-2 Sea Surface Heights within 10 km Offshore by Retracking Decontaminated Waveforms. Remote Sensing, 9(10), 1077. https://doi.org/10.3390/rs9101077