Vis-NIR Spectroscopy and PLS Regression with Waveband Selection for Estimating the Total C and N of Paddy Soils in Madagascar
Abstract
1. Introduction
2. Materials and Methods
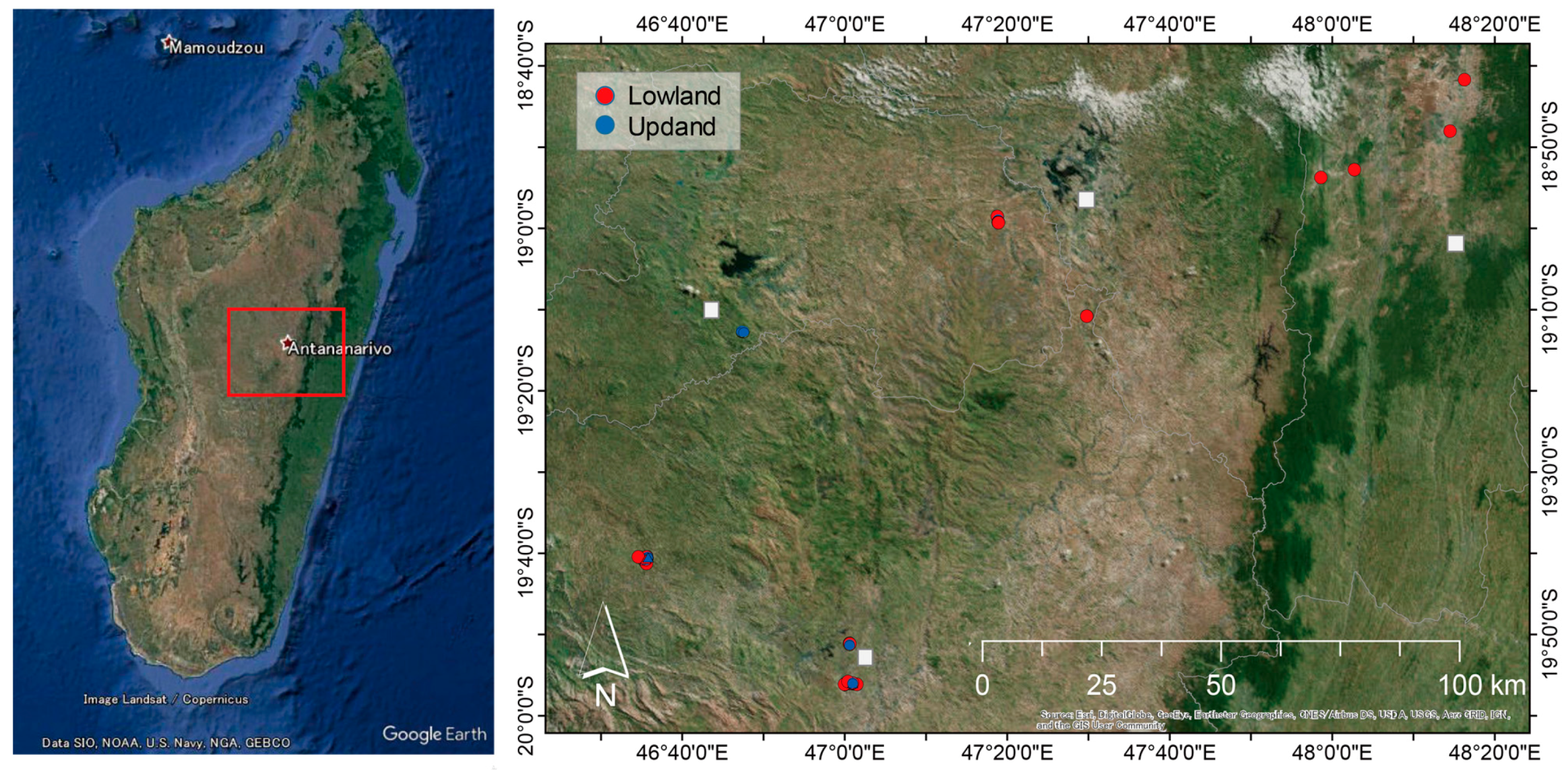
2.1. Study Site and Soil Sampling and Chemical Analyses
2.2. Soil Chemical Analyses
2.3. Vis-NIR Diffuse Reflectance Measurement
2.4. Preprocessing of Spectral Data
2.5. Standard Full-Spectrum Partial Least Sqares (FS-PLS) Regression
2.6. Iterative Stepwise Elimination Partial Least Squares (ISE-PLS) Regression
2.7. Predictive Ability of the PLS Models
3. Results and Discussion
3.1. Soil Properties (TC and TN) and Their Correlations with Each Waveband
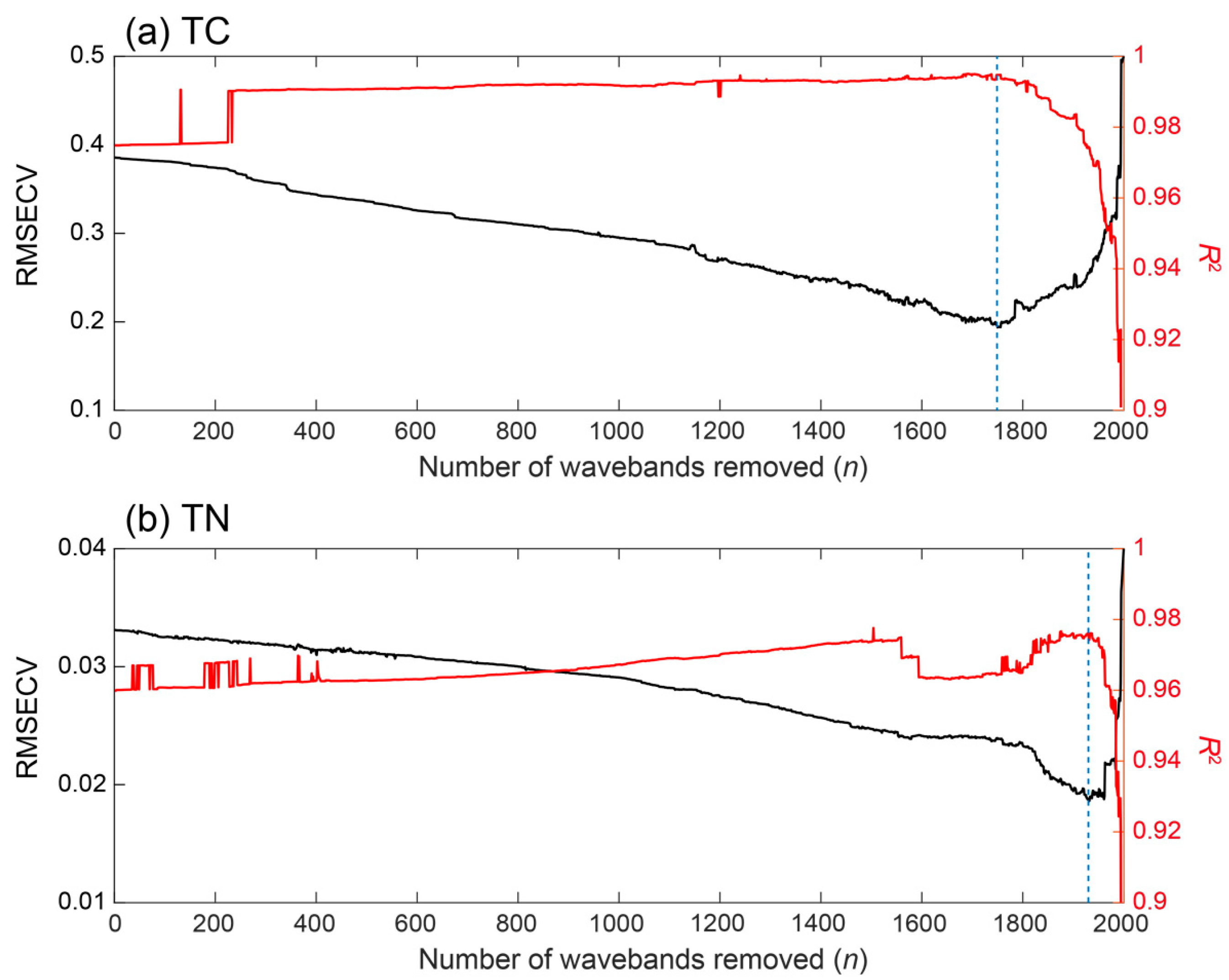
3.2. Comparison between FS-PLS and ISE-PLS Models
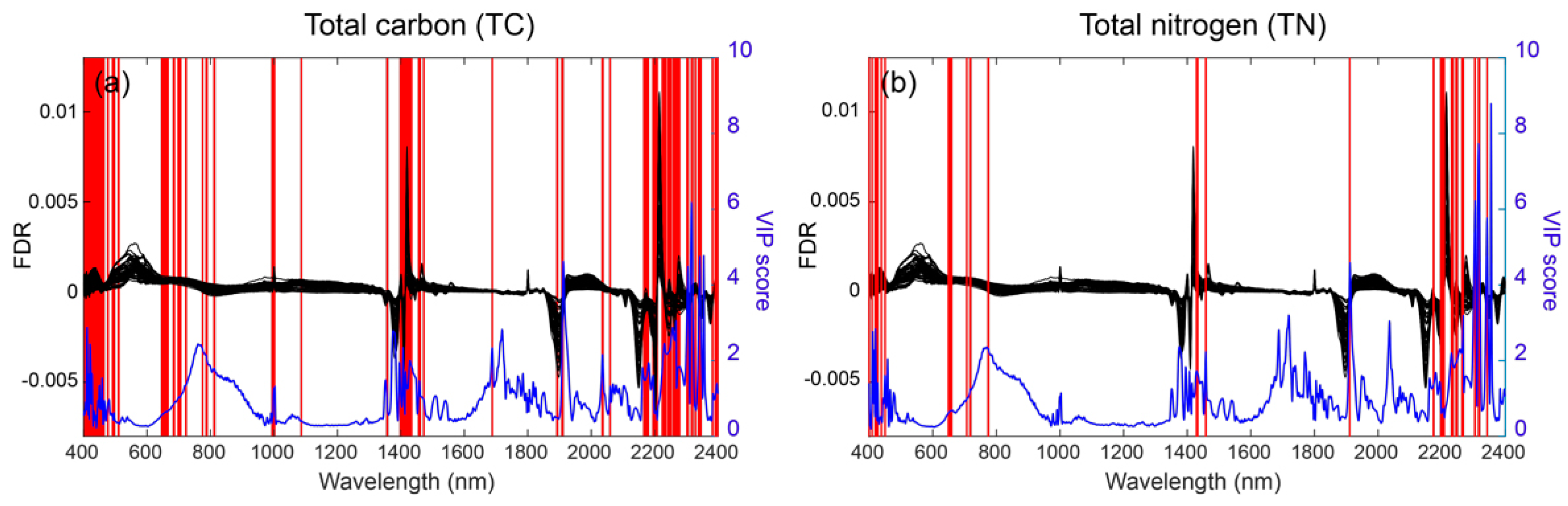
3.3. Selected Wavebands from ISE-PLS Models
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Weil, R.; Magdoff, F. Significance of soil organic matter to soil quality and health. In Soil Organic Matter in Sustainable Agriculture; Mangdoff, E., Weil, R.R., Eds.; CRC Press: Boca Raton, FL, USA, 2004; p. 412. [Google Scholar]
- Lal, R. Soil carbon sequestration to mitigate climate change. Geoderma 2004, 123, 1–22. [Google Scholar] [CrossRef]
- Mouazen, A.M.; Maleki, M.R.; De Baerdemaeker, J.; Ramon, H. On-line measurement of some selected soil properties using a vis–nir sensor. Soil Tillage Res. 2007, 93, 13–27. [Google Scholar] [CrossRef]
- Conant, R.T.; Ogle, S.M.; Paul, E.A.; Paustian, K. Measuring and monitoring soil organic carbon stocks in agricultural lands for climate mitigation. Front. Ecol. Environ. 2011, 9, 169–173. [Google Scholar] [CrossRef]
- Sinfield, J.V.; Fagerman, D.; Colic, O. Evaluation of sensing technologies for on-the-go detection of macro-nutrients in cultivated soils. Comput. Electron. Agric. 2010, 70, 1–18. [Google Scholar] [CrossRef]
- Conforti, M.; Castrignanò, A.; Robustelli, G.; Scarciglia, F.; Stelluti, M.; Buttafuoco, G. Laboratory-based vis–NIR spectroscopy and partial least square regression with spatially correlated errors for predicting spatial variation of soil organic matter content. Catena 2015, 124, 60–67. [Google Scholar] [CrossRef]
- Islam, K.; Singh, B.; McBratney, A. Simultaneous estimation of several soil properties by ultra-violet, visible, and near-infrared reflectance spectroscopy. Soil Res. 2003, 41, 1101–1114. [Google Scholar] [CrossRef]
- Miller, C.E. Chemical principles of near-infrared technology. In Near Infrared Technology in the Agricultural and Food Industries, 2nd ed.; Williams, P.C., Horris, K.H., Eds.; American Association of Cereal Chemists: St. Paul, MN, USA, 2001; pp. 19–37. [Google Scholar]
- Viscarra Rossel, R.A.; Walvoort, D.J.J.; McBratney, A.B.; Janik, L.J.; Skjemstad, J.O. Visible, near infrared, mid infrared or combined diffuse reflectance spectroscopy for simultaneous assessment of various soil properties. Geoderma 2006, 131, 59–75. [Google Scholar] [CrossRef]
- Mouazen, A.M.; Kuang, B.; De Baerdemaeker, J.; Ramon, H. Comparison among principal component, partial least squares and back propagation neural network analyses for accuracy of measurement of selected soil properties with visible and near infrared spectroscopy. Geoderma 2010, 158, 23–31. [Google Scholar] [CrossRef]
- Kuang, B.; Mouazen, A.M. Calibration of visible and near infrared spectroscopy for soil analysis at the field scale on three european farms. Eur. J. Soil Sci. 2011, 62, 629–636. [Google Scholar] [CrossRef]
- Fystro, G. The prediction of C and N content and their potential mineralisation in heterogeneous soil samples using vis–nir spectroscopy and comparative methods. Plant Soil 2002, 246, 139–149. [Google Scholar] [CrossRef]
- 13 D’Acqui, L.P.; Pucci, A.; Janik, L.J. Soil properties prediction of western mediterranean islands with similar climatic environments by means of mid-infrared diffuse reflectance spectroscopy. Eur. J. Soil Sci. 2010, 61, 865–876. [Google Scholar] [CrossRef]
- Yang, H.; Kuang, B.; Mouazen, A.M. Quantitative analysis of soil nitrogen and carbon at a farm scale using visible and near infrared spectroscopy coupled with wavelength reduction. Eur. J. Soil Sci. 2012, 63, 410–420. [Google Scholar] [CrossRef]
- Vohland, M.; Ludwig, M.; Thiele-Bruhn, S.; Ludwig, B. Determination of soil properties with visible to near- and mid-infrared spectroscopy: Effects of spectral variable selection. Geoderma 2014, 223, 88–96. [Google Scholar] [CrossRef]
- Inoue, Y.; Sakaiya, E.; Zhu, Y.; Takahashi, W. Diagnostic mapping of canopy nitrogen content in rice based on hyperspectral measurements. Remote Sens. Environ. 2012, 126, 210–221. [Google Scholar] [CrossRef]
- Bolster, K.L.; Martin, M.E.; Aber, J.D. Determination of carbon fraction and nitrogen concentration in tree foliage by near infrared reflectance: A comparison of statistical methods. Can. J. For. Res. 1996, 26, 590–600. [Google Scholar] [CrossRef]
- Kawamura, K.; Watanabe, N.; Sakanoue, S.; Lee, H.-J.; Inoue, Y.; Odagawa, S. Testing genetic algorithm as a tool to select relevant wavebands from field hyperspectral data for estimating pasture mass and quality in a mixed sown pasture using partial least squares regression. Grassl. Sci. 2010, 56, 205–216. [Google Scholar] [CrossRef]
- Kawamura, K.; Watanabe, N.; Sakanoue, S.; Lee, H.-J.; Lim, J.; Yoshitoshi, R. Genetic algorithm-based partial least squares regression for estimating legume content in a grass-legume mixture using field hyperspectral measurements. Grassl. Sci. 2013, 59, 166–172. [Google Scholar] [CrossRef]
- Wang, Z.; Kawamura, K.; Sakuno, Y.; Fan, X.; Gong, Z.; Lim, J. Retrieval of chlorophyll-a and total suspended solids using iterative stepwise elimination partial least squares (ISE-PLS) regression based on field hyperspectral measurements in irrigation ponds in higashihiroshima, Japan. Remote Sens. 2017, 9, 264. [Google Scholar] [CrossRef]
- Fan, W.; Shan, Y.; Li, G.; Lv, H.; Li, H.; Liang, Y. Application of competitive adaptive reweighted sampling method to determine effective wavelengths for prediction of total acid of vinegar. Food Anal. Meth. 2012, 5, 585–590. [Google Scholar] [CrossRef]
- Cramer, J.A.; Kramer, K.E.; Johnson, K.J.; Morris, R.E.; Rose-Pehrsson, S.L. Automated wavelength selection for spectroscopic fuel models by symmetrically contracting repeated unmoving window partial least squares. Chemom. Intell. Lab. Syst. 2008, 92, 13–21. [Google Scholar] [CrossRef]
- Kawamura, K.; Watanabe, N.; Sakanoue, S.; Inoue, Y. Estimating forage biomass and quality in a mixed sown pasture based on pls regression with waveband selection. Grassl. Sci. 2008, 54, 131–146. [Google Scholar] [CrossRef]
- Boggia, R.; Forina, M.; Fossa, P.; Mosti, L. Chemometric study and validation strategies in the structure-activity relationships of new cardiotonic agents. Quant. Struct.-Act. Relatsh. 1997, 16, 201–213. [Google Scholar] [CrossRef]
- Centner, V.; Massart, D.L.; de Noord, O.E.; de Jong, S.; Vandeginste, B.M.; Sterna, C. Elimination of uninformative variables for multivariate calibration. Anal. Chem. 1996, 68, 3851–3858. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Liang, Y.; Xu, Q.; Cao, D. Key wavelengths screening using competitive adaptive reweighted sampling method for multivariate calibration. Anal. Chim. Acta 2009, 648, 77–84. [Google Scholar] [CrossRef] [PubMed]
- Nørgaard, L.; Saudland, A.; Wagner, J.; Nielsen, J.P.; Munck, L.; Engelsen, S.B. Interval partial least-squares regression (iPLS): A comparative chemometric study with an example from near-infrared spectroscopy. Appl. Spectrosc. 2000, 54, 413–419. [Google Scholar] [CrossRef]
- Jiang, J.H.; Berry, R.J.; Siesler, H.W.; Ozaki, Y. Wavelength interval selection in multicomponent spectral analysis by moving window partial least-squares regression with applications to mid-infrared and near-infrared spectroscopic data. Anal. Chem. 2002, 74, 3555–3565. [Google Scholar] [CrossRef] [PubMed]
- Leardi, R. Application of a genetic algorithm to feature selection under full validation conditions and to outlier detection. J. Chemom. 1994, 8, 65–79. [Google Scholar] [CrossRef]
- Yoshida, H.; Leardi, R.; Funatsu, K.; Varmuza, K. Feature selection by genetic algorithms for mass spectral classifiers. Anal. Chim. Acta 2001, 446, 483–492. [Google Scholar] [CrossRef]
- Xiaobo, Z.; Jiewen, Z.; Povey, M.J.W.; Holmes, M.; Hanpin, M. Variables selection methods in near-infrared spectroscopy. Anal. Chim. Acta 2010, 667, 14–32. [Google Scholar] [CrossRef] [PubMed]
- GriSP (Global Rice Science Partnership). Rice Almanac, 4th ed.; International Rice Research Institute: Los Banos, Philippines, 2013; p. 298. [Google Scholar]
- Tsujimoto, Y.; Horie, T.; Randriamihary, H.; Shiraiwa, T.; Homma, K. Soil management: The key factors for higher productivity in the fields utilizing the system of rice intensification (SRI) in the central highland of madagascar. Agric. Syst. 2009, 100, 61–71. [Google Scholar] [CrossRef]
- Grinand, C.; Maire, G.L.; Vieilledent, G.; Razakamanarivo, H.; Razafimbelo, T.; Bernoux, M. Estimating temporal changes in soil carbon stocks at ecoregional scale in madagascar using remote-sensing. Int. J. Appl. Earth Obs. Geoinf. 2017, 54, 1–14. [Google Scholar] [CrossRef]
- Ramifehiarivo, N.; Brossard, M.; Grinand, C.; Andriamananjara, A.; Razafimbelo, T.; Rasolohery, A.; Razafimahatratra, H.; Seyler, F.; Ranaivoson, N.; Rabenarivo, M.; et al. Mapping soil organic carbon on a national scale: Towards an improved and updated map of madagascar. Geoderma Reg. 2017, 9, 29–38. [Google Scholar] [CrossRef]
- Razakamanarivo, R.H.; Grinand, C.; Razafindrakoto, M.A.; Bernoux, M.; Albrecht, A. Mapping organic carbon stocks in eucalyptus plantations of the Central Highlands of Madagascar: A multiple regression approach. Geoderma 2011, 162, 335–346. [Google Scholar] [CrossRef]
- Andriamananjara, A.; Hewson, J.; Razakamanarivo, H.; Andrisoa, R.H.; Ranaivoson, N.; Ramboatiana, N.; Razafindrakoto, M.; Ramifehiarivo, N.; Razafimanantsoa, M.-P.; Rabeharisoa, L.; et al. Land cover impacts on aboveground and soil carbon stocks in malagasy rainforest. Agric. Ecosyst. Environ. 2016, 233, 1–15. [Google Scholar] [CrossRef]
- Asner, G.P.; Mascaro, J.; Muller-Landau, H.C.; Vieilledent, G.; Vaudry, R.; Rasamoelina, M.; Hall, J.S.; van Breugel, M. A universal airborne lidar approach for tropical forest carbon mapping. Oecologia 2012, 168, 1147–1160. [Google Scholar] [CrossRef] [PubMed]
- IUSS Working Group WRB. World Reference Base for Soil Resources 2014, Update 2015 International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; World Soil Resources Reports No. 106; FAO: Rome, Italy, 2015. [Google Scholar]
- Soil Survey Staff. Keys to Soil Taxonomy, 12th ed.; USDA-Natural Resources Cnservation Service: Washington, DC, USA, 2014. [Google Scholar]
- Brunet, D.; Barthès, B.G.; Chotte, J.-L.; Feller, C. Determination of carbon and nitrogen contents in alfisols, oxisols and ultisols from africa and brazil using nirs analysis: Effects of sample grinding and set heterogeneity. Geoderma 2007, 139, 106–117. [Google Scholar] [CrossRef]
- Reeves, J.; McCarty, G.; Mimmo, T. The potential of diffuse reflectance spectroscopy for the determination of carbon inventories in soils. Environ. Pollut. 2002, 116, S277–S284. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Forina, M.; Lanteri, S.; Oliveros, M.C.C.; Millan, C.P. Selection of useful predictors in multivariate calibration. Anal. Bioanal. Chem. 2004, 380, 397–418. [Google Scholar] [CrossRef] [PubMed]
- Williams, P.C. Implementation of near-infrared technology. In Near-Infrared Technology in the Agricultural and Food Industries, 2nd ed.; Williams, P.C., Norris, K.H., Eds.; American Association of Cereal Chemists Inc.: St. Paul, MN, USA, 2001; pp. 145–169. [Google Scholar]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Chong, I.-G.; Jun, C.-H. Performance of some variable selection methods when multicollinearity is present. Chemom. Intell. Lab. Syst. 2005, 78, 103–112. [Google Scholar] [CrossRef]
- Li, B.; Liew, O.W.; Asundi, A.K. Pre-visual detection of iron and phosphorus deficiency by transformed reflectance spectra. J. Photochem. Photobiol. B 2006, 85, 131–139. [Google Scholar] [CrossRef] [PubMed]
- Ben-Dor, E.; Inbar, Y.; Chen, Y. The reflectance spectra of organic matter in the visible near-infrared and short wave infrared region (400–2500 nm) during a controlled decomposition process. Remote Sens. Environ. 1997, 61, 1–15. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; Lark, R.M. Improved analysis and modelling of soil diffuse reflectance spectra using wavelets. Eur. J. Soil Sci. 2009, 60, 453–464. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; Fouad, Y.; Walter, C. Using a digital camera to measure soil organic carbon and iron contents. Biosyst. Eng. 2008, 100, 149–159. [Google Scholar] [CrossRef]
- Whiting, M.L.; Li, L.; Ustin, S.L. Predicting water content using gaussian model on soil spectra. Remote Sens. Environ. 2004, 89, 535–552. [Google Scholar] [CrossRef]
- Ben Dor, E.; Irons, J.R.; Epema, J.F. Soil reflectance. In Manual of Remote Sensing: Remote Sensing for the Earth Sciences; John Wiley & Sons: New York, NY, USA, 1999; Volume 3, pp. 111–188. [Google Scholar]
- Yang, H. Spectroscopic calibration for soil N and C measurement at a farm scale. Proc. Environ. Sci. 2011, 10, 672–677. [Google Scholar] [CrossRef]
- Martin, P.D.; Malley, D.F.; Manning, G.; Fuller, L. Determination of soil organic carbon and nitrogen at the field level using near-infrared spectroscopy. Can. J. Soil Sci. 2002, 82, 413–422. [Google Scholar] [CrossRef]
- Chang, C.-W.; Laird, D.A. Near-infrared reflectance spectroscopic analysis of soil C and N. Soil Sci. 2002, 167, 110–116. [Google Scholar] [CrossRef]
- Chang, C.W.; Laird, D.; Mausbach, M.J.; Hurburgh, C.R.J. Nearinfrared reflectance spectroscopy-principal components regression analyses of soil properties. Soil Sci. Soc. Am. J. 2001, 65, 480–490. [Google Scholar] [CrossRef]
- Saiano, F.; Oddo, G.; Scalenghe, R.; La Mantia, T.; Ajmone-Marsan, F. DRIFTS sensor: Soil carbon validation at large scale (Pantelleria, Italy). Sensors 2013, 13, 5603–5613. [Google Scholar] [CrossRef] [PubMed]


| Soil Parameters | n | Min | Max | Mean | SD | CV |
|---|---|---|---|---|---|---|
| TC (%) | 59 | 0.65 | 6.02 | 2.18 | 1.16 | 53.35 |
| TN (%) | 59 | 0.06 | 0.44 | 0.17 | 0.08 | 48.08 |
| Soil Parameter | Regression Method | Calibration | Cross-validation | NW | NW% | ||||
|---|---|---|---|---|---|---|---|---|---|
| NLV | R2 | RMSEC | R2 | RMSECV | RPD | ||||
| Total carbon | FS-PLS | 14 | 0.996 | 0.076 | 0.893 | 0.379 | 3.064 | 252 | 12.59 |
| (TC, %) | ISE-PLS | 12 | 0.995 | 0.084 | 0.972 | 0.194 | 5.995 | ||
| Total nitrogen | FS-PLS | 9 | 0.960 | 0.016 | 0.837 | 0.033 | 2.480 | 71 | 3.55 |
| (TN, %) | ISE-PLS | 7 | 0.974 | 0.013 | 0.949 | 0.019 | 4.416 | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kawamura, K.; Tsujimoto, Y.; Rabenarivo, M.; Asai, H.; Andriamananjara, A.; Rakotoson, T. Vis-NIR Spectroscopy and PLS Regression with Waveband Selection for Estimating the Total C and N of Paddy Soils in Madagascar. Remote Sens. 2017, 9, 1081. https://doi.org/10.3390/rs9101081
Kawamura K, Tsujimoto Y, Rabenarivo M, Asai H, Andriamananjara A, Rakotoson T. Vis-NIR Spectroscopy and PLS Regression with Waveband Selection for Estimating the Total C and N of Paddy Soils in Madagascar. Remote Sensing. 2017; 9(10):1081. https://doi.org/10.3390/rs9101081
Chicago/Turabian StyleKawamura, Kensuke, Yasuhiro Tsujimoto, Michel Rabenarivo, Hidetoshi Asai, Andry Andriamananjara, and Tovohery Rakotoson. 2017. "Vis-NIR Spectroscopy and PLS Regression with Waveband Selection for Estimating the Total C and N of Paddy Soils in Madagascar" Remote Sensing 9, no. 10: 1081. https://doi.org/10.3390/rs9101081
APA StyleKawamura, K., Tsujimoto, Y., Rabenarivo, M., Asai, H., Andriamananjara, A., & Rakotoson, T. (2017). Vis-NIR Spectroscopy and PLS Regression with Waveband Selection for Estimating the Total C and N of Paddy Soils in Madagascar. Remote Sensing, 9(10), 1081. https://doi.org/10.3390/rs9101081







