An Inter-Comparison Study of Multi- and DBS Lidar Measurements in Complex Terrain
Abstract
:1. Introduction
2. Materials and Methods
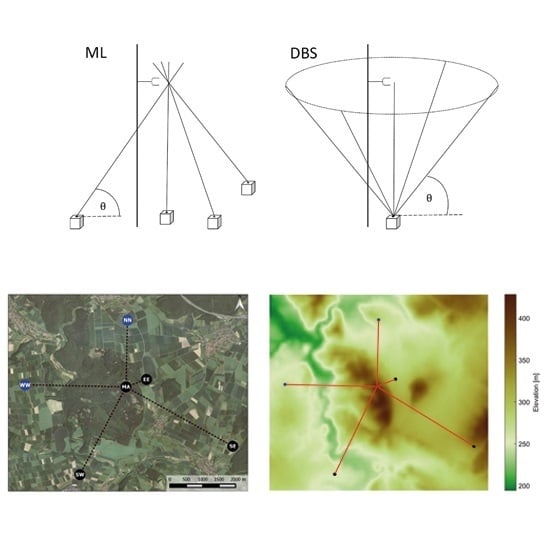
2.1. Wind Vector Reconstruction and Scanning Strategies
2.2. Second-Order Statistics of
2.3. Second-Order Statistics from Multiple Lidar (ML) Beams
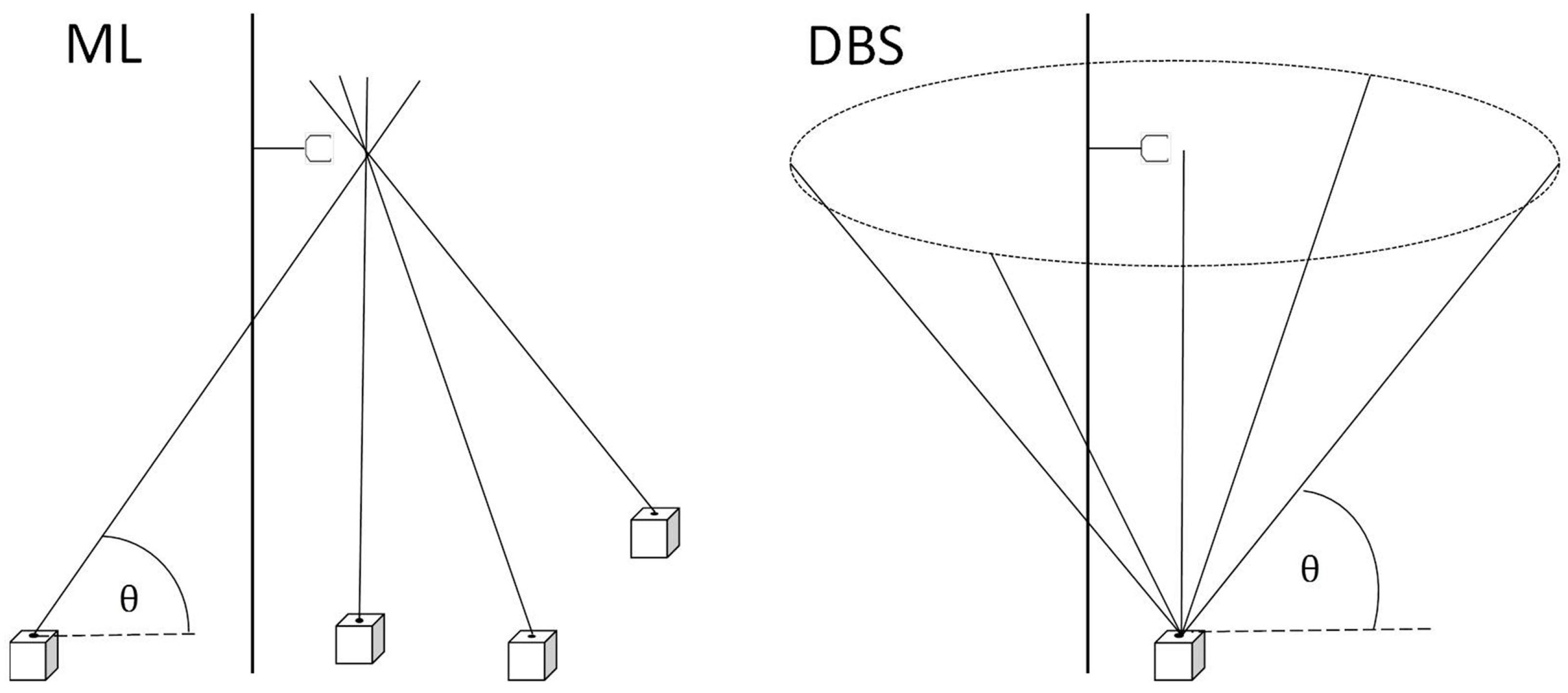
2.4. Experimental Setup: The Kassel 2014 Experiment
2.5. Data Treatment, Quality Control and Coordinate Systems
3. Results and Discussion
3.1. Radial Velocity Components
3.1.1. First-Order Statistics
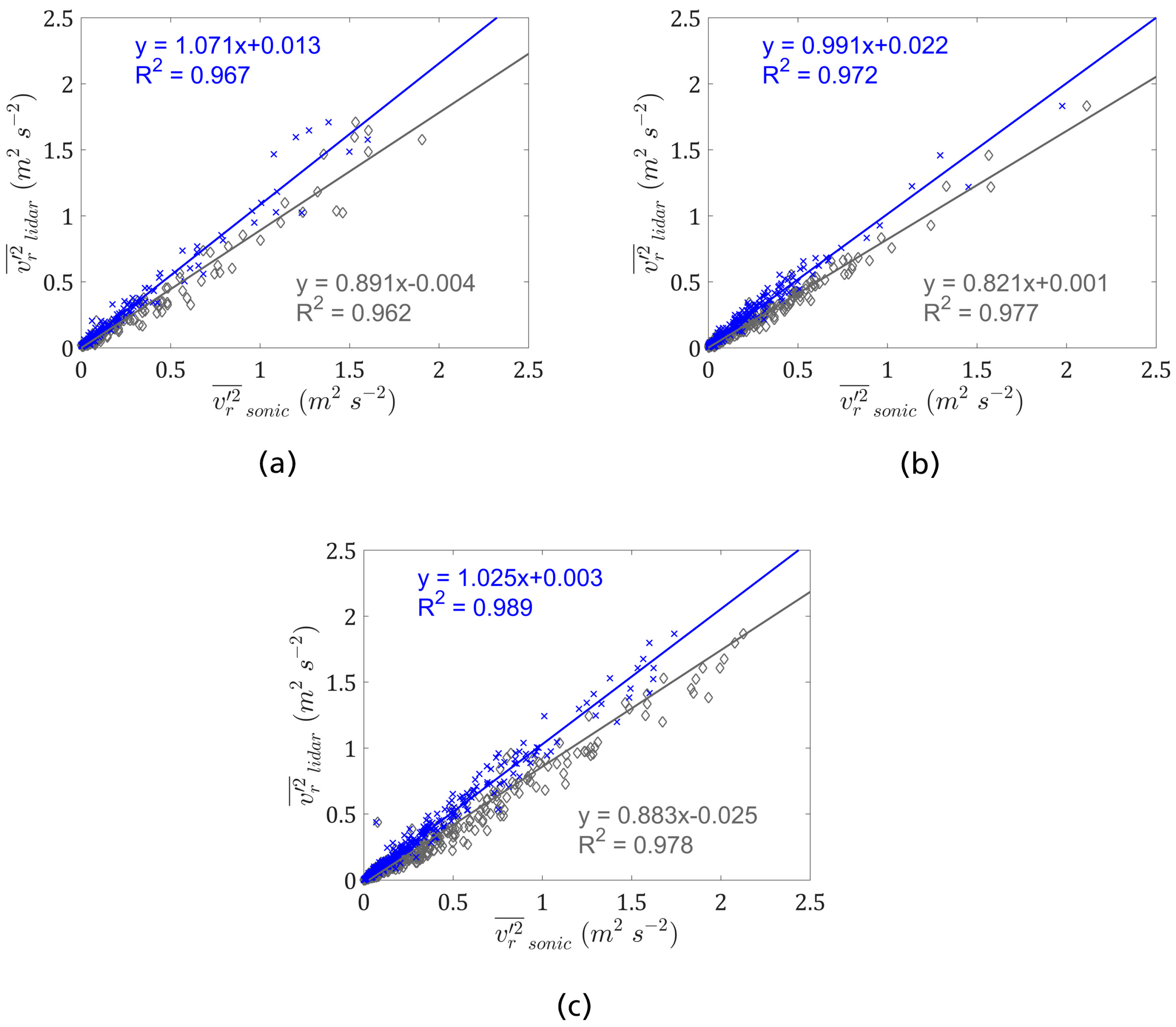
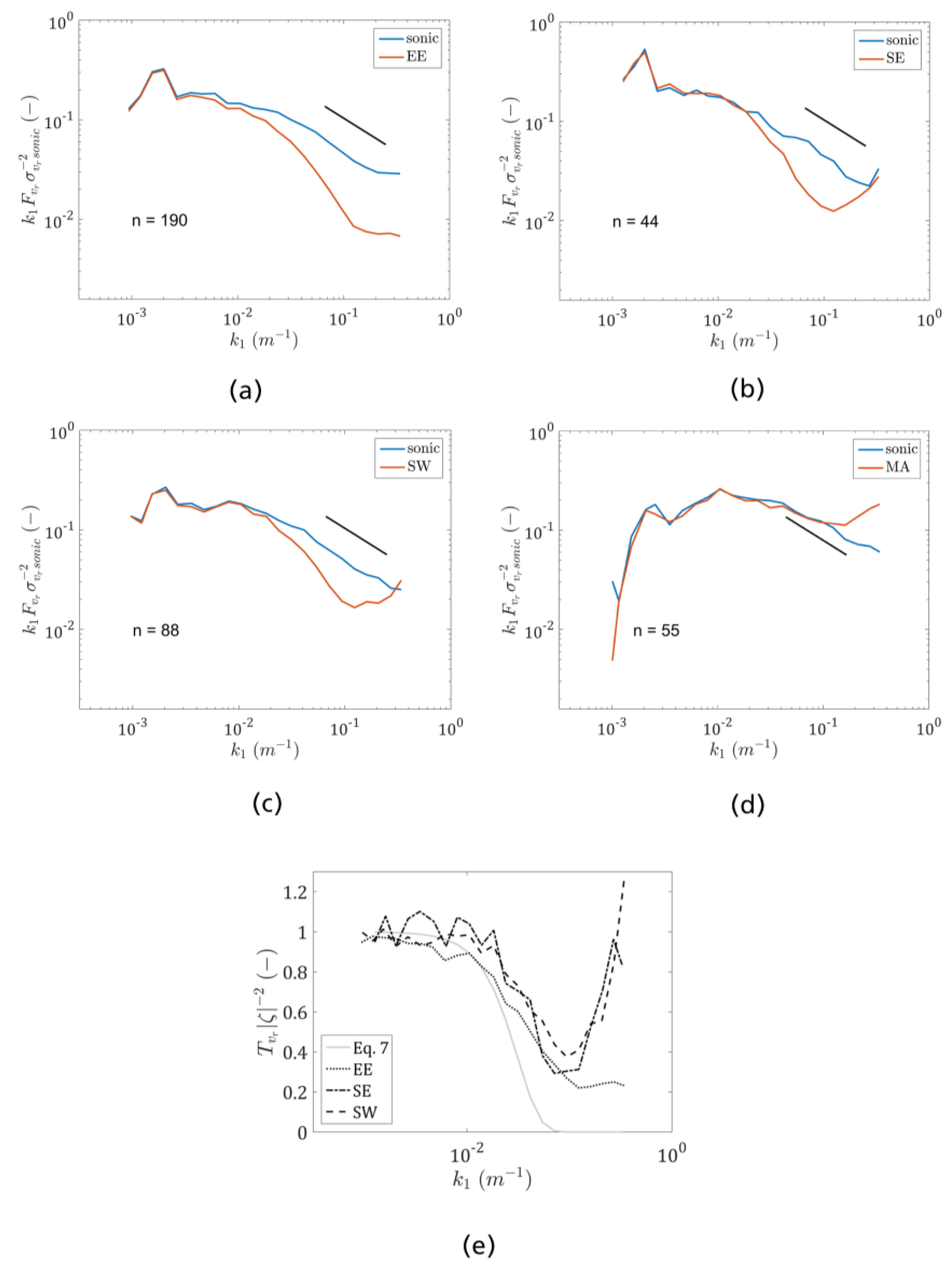
3.1.2. Second-Order Statistics
3.2. Horizontal Wind-Speed Statistics from the ML and Doppler Beam Swinging (DBS) Technique
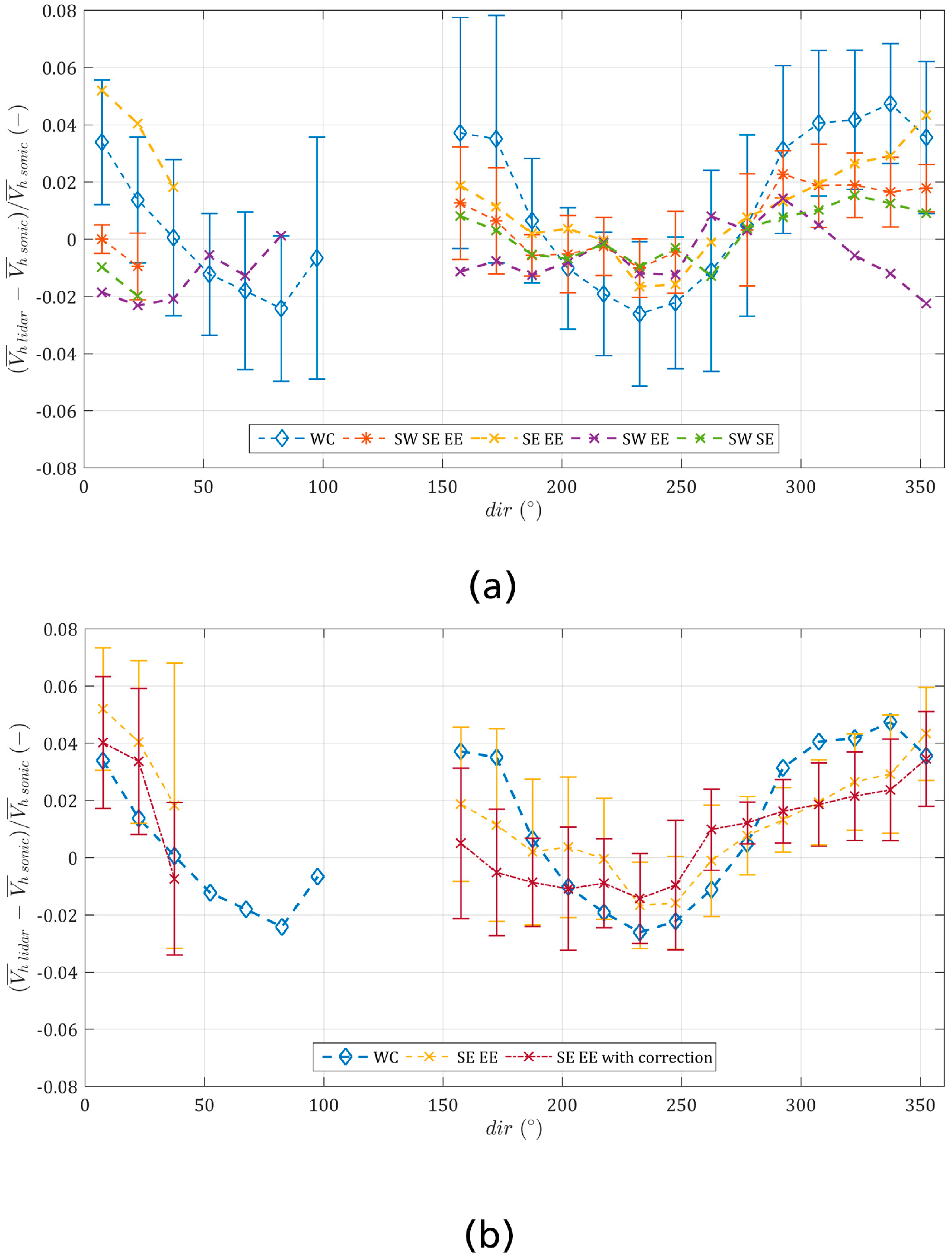
3.2.1. First-Order Statistics of the Horizontal Wind Speed
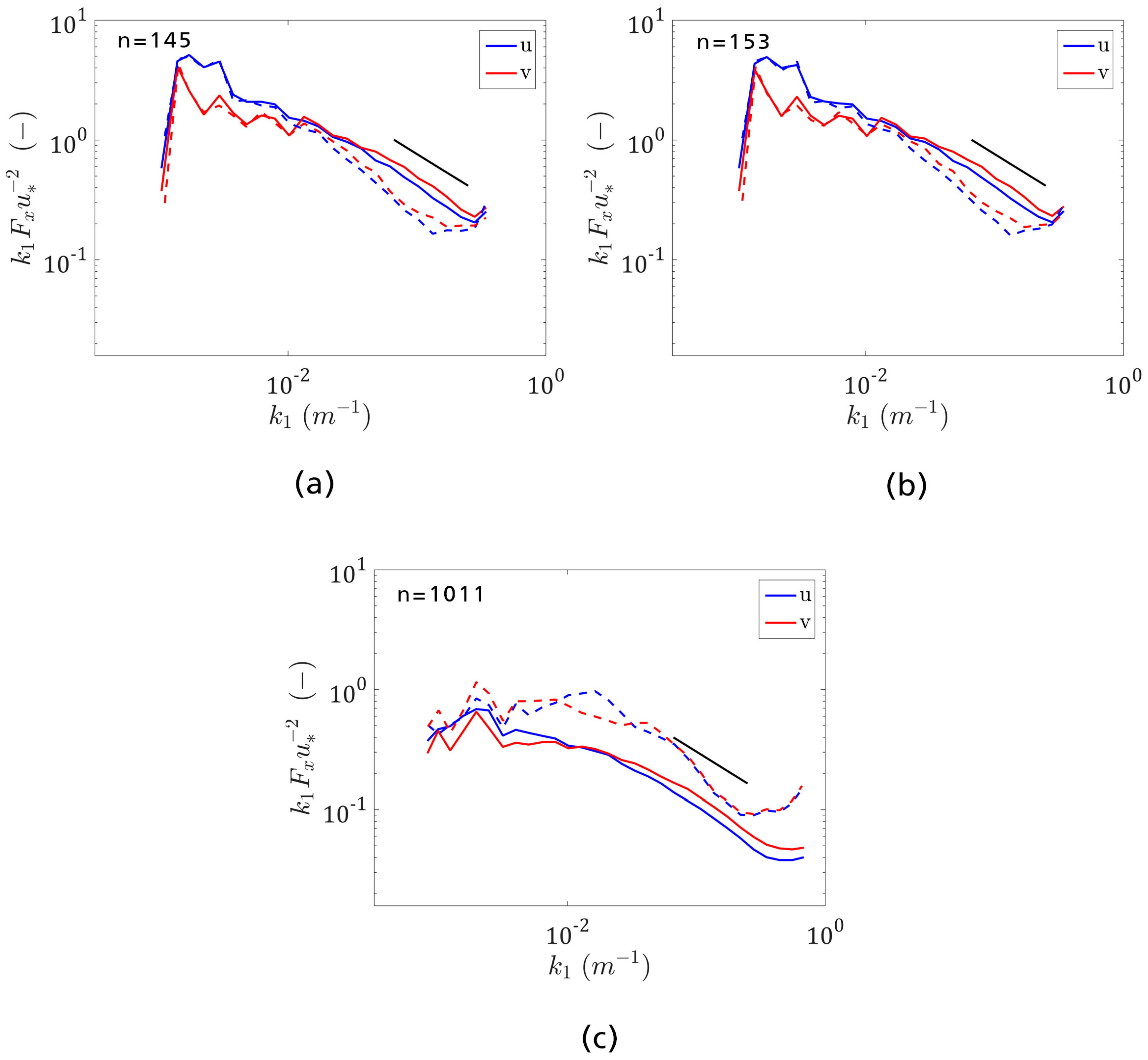
3.2.2. Second-Order Statistics of the Horizontal Wind Vector Components
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| CNR | Carrier-to-noise ratio |
| DBS | Doppler beam swinging |
| lidar | Light detection and ranging |
| ML | Multi-lidar |
| FWHM | Full width at half maximum |
| RMSD | Root-mean-square deviation |
| VAD | Velocity azimuth display |
References
- Gottschall, J.; Courtney, M.S.; Wagner, R.; Jørgensen, H.E.; Antoniou, I. Lidar profilers in the context of wind energy—A verification procedure for traceable measurements. Wind Energy 2012, 15, 147–159. [Google Scholar] [CrossRef]
- International Electrotechnical Commission. IEC 61400-12 Wind Turbines—Part 12-1: Power Performance Measurements of Electricity Producing Wind Turbines (2nd Committee Draft), 2nd ed.; International Electrotechnical Commission: Geneva, Switzerland, 2013. [Google Scholar]
- Fördergesellschaft Windenergie und andere Erneuerbare Energien e.V. (FGW). TR6 Bestimmung von Windpotenzial und Energieerträgen. Available online: http://www.wind-fgw.de/TR.html (accessed on 20 September 2016).
- Bingöl, F.; Mann, J.; Foussekis, D. Conically scanning lidar error in complex terrain. Meteorol. Z. 2009, 18, 189–195. [Google Scholar] [CrossRef]
- Bradley, S.; Strehz, A.; Emeis, S. Remote sensing winds in complex terrain—A review. Meteorol. Z. 2015, 24, 547–555. [Google Scholar]
- Klaas, T.; Pauscher, L.; Callies, D. Lidar-mast deviations in complex terrain and their simulation using CFD. Meteorol. Z. 2015, 24, 591–603. [Google Scholar]
- Sathe, A.; Mann, J. A review of turbulence measurements using ground-based wind lidars. Atmos. Meas. Tech. 2013, 6, 3147–3167. [Google Scholar] [CrossRef]
- Sathe, A.; Banta, R.; Pauscher, L.; Vogstad, K.; Schlipf, D.; Wylie, S. Estimating Turbulence Statistics and Parameters from Ground- and Nacelle-Based Lidar Measurements; IEA Wind Expert Report; DTU Wind Energy: Roskilde, Denmark, 2015. [Google Scholar]
- Sathe, A.; Mann, J.; Gottschall, J.; Courtney, M.S. Can wind lidars measure turbulence? J. Atmos. Ocean. Technol. 2011, 28, 853–868. [Google Scholar] [CrossRef]
- Sathe, A.; Mann, J. Measurement of turbulence spectra using scanning pulsed wind lidars. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Newman, J.F.; Klein, P.M.; Wharton, S.; Sathe, A.; Bonin, T.A.; Chilson, P.B.; Muschinski, A. Evaluation of three lidar scanning strategies for turbulence measurements. Atmos. Meas. Tech. 2016, 9, 1993–2013. [Google Scholar] [CrossRef]
- Sathe, A.; Mann, J.; Vasiljevic, N.; Lea, G. A six-beam method to measure turbulence statistics using ground-based wind lidars. Atmos. Meas. Tech. 2015, 8, 729–740. [Google Scholar] [CrossRef]
- Eberhard, W.L.; Cupp, R.E.; Healy, K.R. Doppler lidar measurement of profiles of turbulence and momentum flux. J. Atmos. Ocean. Technol. 1989, 6, 809–819. [Google Scholar] [CrossRef]
- Mann, J.; Cariou, J.-P.; Courtney, M.S.; Parmentier, R.; Mikkelsen, T.; Wagner, R.; Lindelöw, P.; Sjöholm, M.; Enevoldsen, K. Comparison of 3D turbulence measurements using three staring wind lidars and a sonic anemometer. Meteorol. Z. 2009, 18, 135–140. [Google Scholar] [CrossRef]
- Vasiljevic, N. A Time-Space Synchronization of Coherent Doppler Scanning Lidars for 3D Measurements of Wind Fields. Ph.D. Thesis, Technical University of Denmark, Roskilde, Denmark, 2014. [Google Scholar]
- Fuertes, F.C.; Iungo, G.V.; Porté-Agel, F. 3D turbulence measurements using three synchronous wind lidars: Validation against Sonic Anemometry. J. Atmos. Ocean. Technol. 2014, 31, 1549–1556. [Google Scholar] [CrossRef]
- Berg, J.; Vasiljevíc, N.; Kelly, M.; Lea, G.; Courtney, M. Addressing spatial variability of surface-layer wind with long-range WindScanners. J. Atmos. Ocean. Technol. 2015, 32, 518–527. [Google Scholar] [CrossRef]
- Mann, J. The spatial structure of neutral atmospheric surface-layer turbulence. J. Fluid Mech. 1994, 273, 141–168. [Google Scholar] [CrossRef]
- Newman, J.F.; Bonin, T.A.; Klein, P.M.; Wharton, S.; Newsom, R.K. Testing and validation of multi-lidar scanning strategies for wind energy applications. Wind Energy 2016. [Google Scholar] [CrossRef]
- Mann, J.; Angelou, N.; Arnqvist, J.; Callies, D.; Cantero, E.; Chávez Arroyo, R.; Courtney, M.; Cuxart, J.; Dellwik, E.; Gottschall, J.; et al. Complex terrain experiments in the New European Wind Atlas. Philos. Trans. R. Soc. A 2016. in review. [Google Scholar]
- Tatarskii, V.I.; Muschinski, A. The difference between Doppler velocity and real wind velocity in single scattering from refractive index fluctuations. Radio Sci. 2001, 36, 1405–1423. [Google Scholar] [CrossRef]
- Huffaker, R.M.; Hardesty, R.M. Remote sensing of atmospheric wind velocities using solid-state and CO2 coherent laser systems. Proc. IEEE 1996, 84, 181–204. [Google Scholar] [CrossRef]
- Frehlich, R. Effects of wind turbulence on coherent Doppler lidar performance. J. Atmos. Ocean. Technol. 1997, 14, 54–75. [Google Scholar] [CrossRef]
- Lindelöw, P.J.P.; Mohr, J.J.; Peucheret, C.; Feuchter, T.; Christensen, E.L. Fiber Based Coherent Lidars for Remote Wind Sensing; Technical University of Denmark, DTU: Kgs. Lyngby, Denmark, 2008. [Google Scholar]
- Banakh, V.A.; Smalikho, I.N. Estimation of the turbulence energy dissipation rate from the pulsed Doppler lidar data. Atmos. Ocean. Opt. 1997, 10, 957–965. [Google Scholar]
- Kaimal, J.C.; Wyngaard, J.C.; Haugen, D.A. Deriving power spectra from a three-component sonic anemometer. J. Appl. Meteorol. 1968, 7, 827–837. [Google Scholar] [CrossRef]
- Cariou, J.-P.; Leopshere, Paris, France. Personal communication, 2016.
- International Electrotechnical Commission. IEC 61400-1 Wind Turbines—Part 1: Design Requirements; International Electrotechnical Commission: Geneva, Switzerland, 2005. [Google Scholar]
- Veers, P.S. Three-Dimensional Wind Simulation; Sandia National Laboratories: Albuquerque, NM, USA, 1988. [Google Scholar]
- Mann, J. Wind field simulation. Probab. Eng. Mech. 1998, 13, 269–282. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef]
- Vasiljevic, N.; Lea, G.; Hansen, P.; Jensen, H.M. Mobile Network Architecture of the Long-Range WindScanner System; DTU Wind Energy: Roskilde, Denmark, 2016. [Google Scholar]
- Kaimal, J.C.; Finnigan, J.J. Atmospheric Boundary Layer Flows: Their Structure and Measurement; Oxford University Press: New York, NY, USA, 1994. [Google Scholar]
- Foken, T.; Leuning, R.; Oncley, S.R.; Mauder, M.; Aubinet, M. Corrections and data quality control. In Eddy Covariance: A Practical Guide to Measurement and Data Analysis; Aubinet, M., Vesala, T., Papale, D., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 2012; pp. 85–131. [Google Scholar]
- Mauder, M.; Oncley, S.P.; Vogt, R.; Weidinger, T.; Ribeiro, L.; Bernhofer, C.; Foken, T.; Kohsiek, W.; de Bruin, H.; Liu, H. The energy balance experiment EBEX-2000. Part II: Intercomparison of eddy-covariance sensors and post-field data processing methods. Bound. Lay Meteorol. 2007, 123, 29–54. [Google Scholar] [CrossRef]
- Angelou, N.; Mann, J.; Sjöholm, M.; Courtney, M. Direct measurement of the spectral transfer function of a laser based anemometer. Rev. Sci. Instrum. 2012, 83, 033111. [Google Scholar] [CrossRef] [PubMed]
- Sjöholm, M.; Mikkelsen, T.; Mann, J.; Enevoldsen, K.; Courtney, M. Spatial averaging-effects on turbulence measured by a continuous-wave coherent lidar. Meteorol. Z. 2009, 18, 281–287. [Google Scholar] [CrossRef]
- Stawiarski, C.; Träumner, K.; Knigge, C.; Calhoun, R. Scopes and challenges of dual-Doppler lidar wind measurements — an error analysis. J. Atmos. Ocean. Technol. 2013, 30, 2044–2062. [Google Scholar] [CrossRef]
- Bradley, S.; Perrott, Y.; Behrens, P.; Oldroyd, A. Corrections for wind-speed errors from sodar and lidar in complex terrain. Bound. Lay. Meteorol. 2012, 143, 37–48. [Google Scholar] [CrossRef]
- Newsom, R.K.; Berg, L.K.; Shaw, W.J.; Fischer, M.L. Turbine-scale wind field measurements using dual-Doppler lidar. Wind Energy 2015, 18, 219–235. [Google Scholar] [CrossRef]
- Canadillas, B.; Bégué, A.; Neumann, T. Comparison of turbulence spectra derived from Lidar and sonic measurements at the offshore platform FINO1. In Proceedings of the 10th German Wind Energy Conference (DEWEK 2010), Bremen, Germany, 17–18 November 2010.
- Moore, C.J. Frequency response corrections for eddy correlation systems. Bound. Lay. Meteorol. 1986, 37, 17–35. [Google Scholar] [CrossRef]
- Hogan, R.J.; Grant, A.L.M.; Illingworth, A.J.; Pearson, G.N.; O’Connor, E.J. Vertical velocity variance and skewness in clear and cloud-topped boundary layers as revealed by Doppler lidar. Q. J. R. Meteorol. Soc. 2009, 135, 635–643. [Google Scholar] [CrossRef]
- Barlow, J.F.; Halios, C.H.; Lane, S.E.; Wood, C.R. Observations of urban boundary layer structure during a strong urban heat island event. Environ. Fluid Mech. 2015, 15, 373–398. [Google Scholar] [CrossRef]
- Smalikho, I.; Köpp, F.; Rahm, S. Measurement of atmospheric turbulence by 2-μm Doppler lidar. J. Atmos. Ocean. Technol. 2005, 22, 1733–1747. [Google Scholar] [CrossRef]
- Mann, J.; Peña, A.; Bingöl, F.; Wagner, R.; Courtney, M.S. Lidar scanning of momentum flux in and above the atmospheric surface layer. J. Atmos. Ocean. Technol. 2010, 27, 959–976. [Google Scholar] [CrossRef]

| MA | EE | SE | SW | WC | |
|---|---|---|---|---|---|
| Instrument type | WLS 200S V2 | WLS 200S | WLS 200S | WLS 200S V2 | WINDCUBE WLS7 V2 |
| Altitude (m) | 387.7 | 294.6 | 346.6 | 258.3 | 387.7 |
| Latitude (m) | 5,690,182.6 | 5,690,409.1 | 5,688,371.9 | 5,687,503.8 | 5,690,181.2 |
| Longitude (m) | 513,590.5 | 514,213.3 | 516,843.2 | 512,185.9 | 513,593.1 |
| (°) | 90 | 23.3 | 3.5 | 6.0 | 62, 90 |
| (°) | - | 250.6 | 299.3 | 27.4 | 8, 98, 188, 278, - |
| Dist. to mast (m) | 2 | 732 | 3740 | 3047 | 3 |
| Pulse length FWHM (ns) | 100 | 400 | 400 | 400 | 175 |
| Gate length FWHM (ns) | 74 | 150 | 150 | 150 | 58 |
| (m) | 6.4 | 25.5 | 25.5 | 25.5 | 11.1 |
| (m) | 9.5 | 19.1 | 19.1 | 19.1 | 7.4 |
| Accumulation time (s) | 2 | 2 | 2 | 2 | ~1.12 (~5.62 for full circle) |
| MA | EE | SE | SW | |
|---|---|---|---|---|
| No 10 min periods | 503 | 2592 | 1419 | 1278 |
| Mean | ||||
| m | 1.045 | 0.992 | 1.005 | 0.993 |
| b (m·s−1) | 0.056 | −0.036 | 0.018 | 0.055 |
| R2 | 0.858 | 0.999 | 0.998 | 1.000 |
| RMSD (m·s−1) | 0.087 | 0.104 | 0.116 | 0.079 |
| Variance | ||||
| m | 0.970 | 0.829 | 0.836 | 0.819 |
| b (m·s−1) | 0.017 | −0.025 | −0.018 | 0.001 |
| R2 | 0.969 | 0.968 | 0.952 | 0.970 |
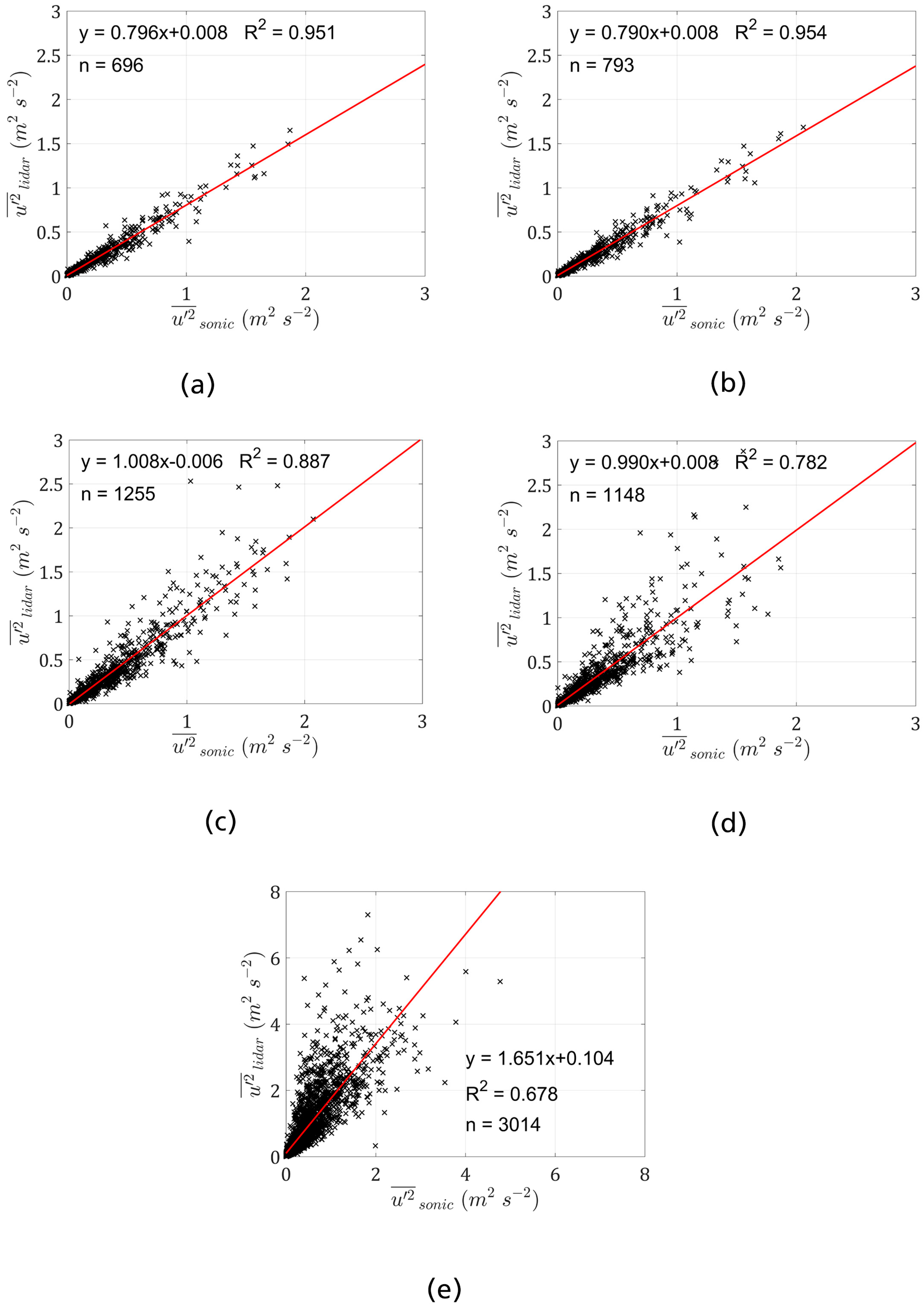
| SE SW EE | SW SE | SE EE | SW EE | WC | |
|---|---|---|---|---|---|
| m | 0.796 (0.829) | 0.790 (0.816) | 1.008 (1.026) | 0.990 (0.916) | 1.651 (1.531) |
| b (m·s−1) | 0.008 (0.006) | 0.008 (0.009) | −0.006 (-0.011) | 0.008 (0.006) | 0.104 (0.070) |
| R2 | 0.951 (0.963) | 0.954 (0.967) | 0.887 (0.896) | 0.782 (0.865) | 0.678 (0.796) |
| m | 0.825 (0.800) | 0.822 (0.800) | 0.884 (0.861) | 0.883 (0.890) | 1.822 (1.731) |
| b (m·s−1) | 0.003 (0.008) | 0.004 (0.009) | -0.006 (-0.007) | 0.020 (0.018) | 0.076 (0.038) |
| R2 | 0.962 (0.963) | 0.966 (0.966) | 0.903 (0.930) | 0.861 (0.901) | 0.689 (0.737) |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pauscher, L.; Vasiljevic, N.; Callies, D.; Lea, G.; Mann, J.; Klaas, T.; Hieronimus, J.; Gottschall, J.; Schwesig, A.; Kühn, M.; et al. An Inter-Comparison Study of Multi- and DBS Lidar Measurements in Complex Terrain. Remote Sens. 2016, 8, 782. https://doi.org/10.3390/rs8090782
Pauscher L, Vasiljevic N, Callies D, Lea G, Mann J, Klaas T, Hieronimus J, Gottschall J, Schwesig A, Kühn M, et al. An Inter-Comparison Study of Multi- and DBS Lidar Measurements in Complex Terrain. Remote Sensing. 2016; 8(9):782. https://doi.org/10.3390/rs8090782
Chicago/Turabian StylePauscher, Lukas, Nikola Vasiljevic, Doron Callies, Guillaume Lea, Jakob Mann, Tobias Klaas, Julian Hieronimus, Julia Gottschall, Annedore Schwesig, Martin Kühn, and et al. 2016. "An Inter-Comparison Study of Multi- and DBS Lidar Measurements in Complex Terrain" Remote Sensing 8, no. 9: 782. https://doi.org/10.3390/rs8090782
APA StylePauscher, L., Vasiljevic, N., Callies, D., Lea, G., Mann, J., Klaas, T., Hieronimus, J., Gottschall, J., Schwesig, A., Kühn, M., & Courtney, M. (2016). An Inter-Comparison Study of Multi- and DBS Lidar Measurements in Complex Terrain. Remote Sensing, 8(9), 782. https://doi.org/10.3390/rs8090782