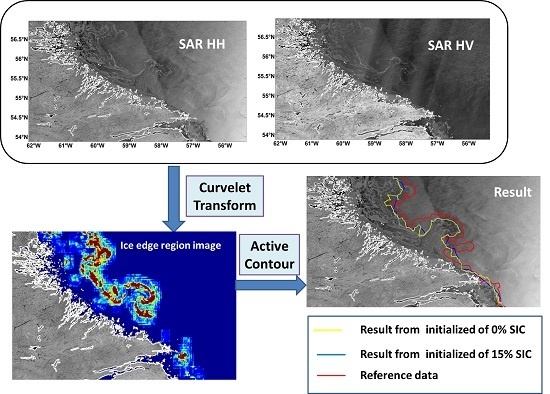
Automatic Detection of the Ice Edge in SAR Imagery Using Curvelet Transform and Active Contour
Abstract
:1. Introduction
2. Curvelet Transform and Active Contour
2.1. Curvelet Transform
- Coarse scale (),
- Middle scale (), and,
- Fine scale ().
2.2. Active Contour
3. Data
3.1. RADARSAT-2 SAR Images
3.2. Passive Microwave Sea Ice Concentration
3.3. Image Analysis Chart
4. Method
4.1. Overview of the Method
4.2. Ice Edge Region Image Generation by Curvelet Transform
4.3. Active Contours
- The external energy requires no absolute threshold, rather is trying to maximize a gradient, whether that found gradient is large or small.
- Active contours, particularly the variant used here [35], can be noise robust and can ignore mistakenly included noisy windows.
4.4. Description of Experiments
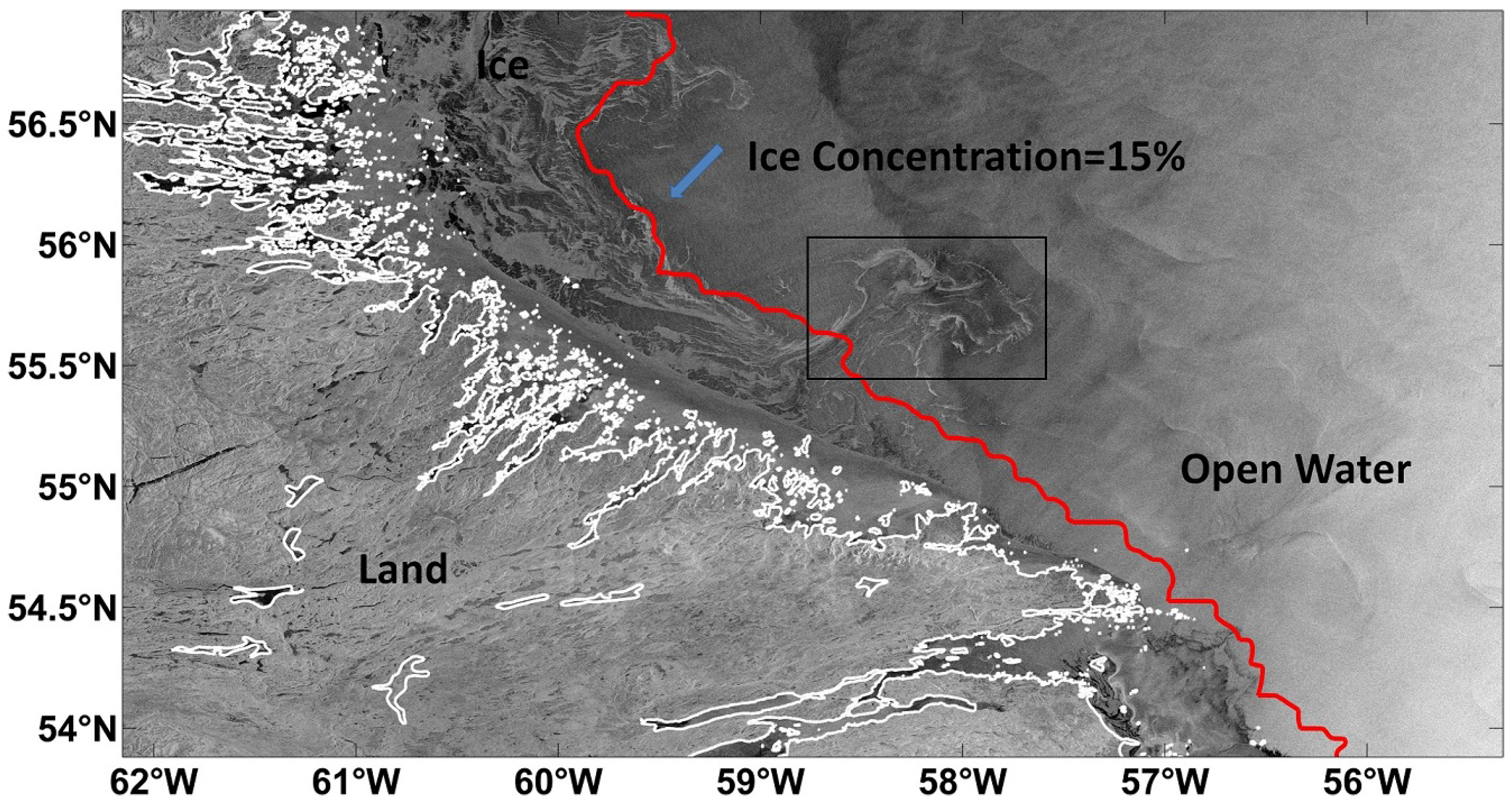
5. Results and Discussion
5.1. Qualitative Analysis of Results
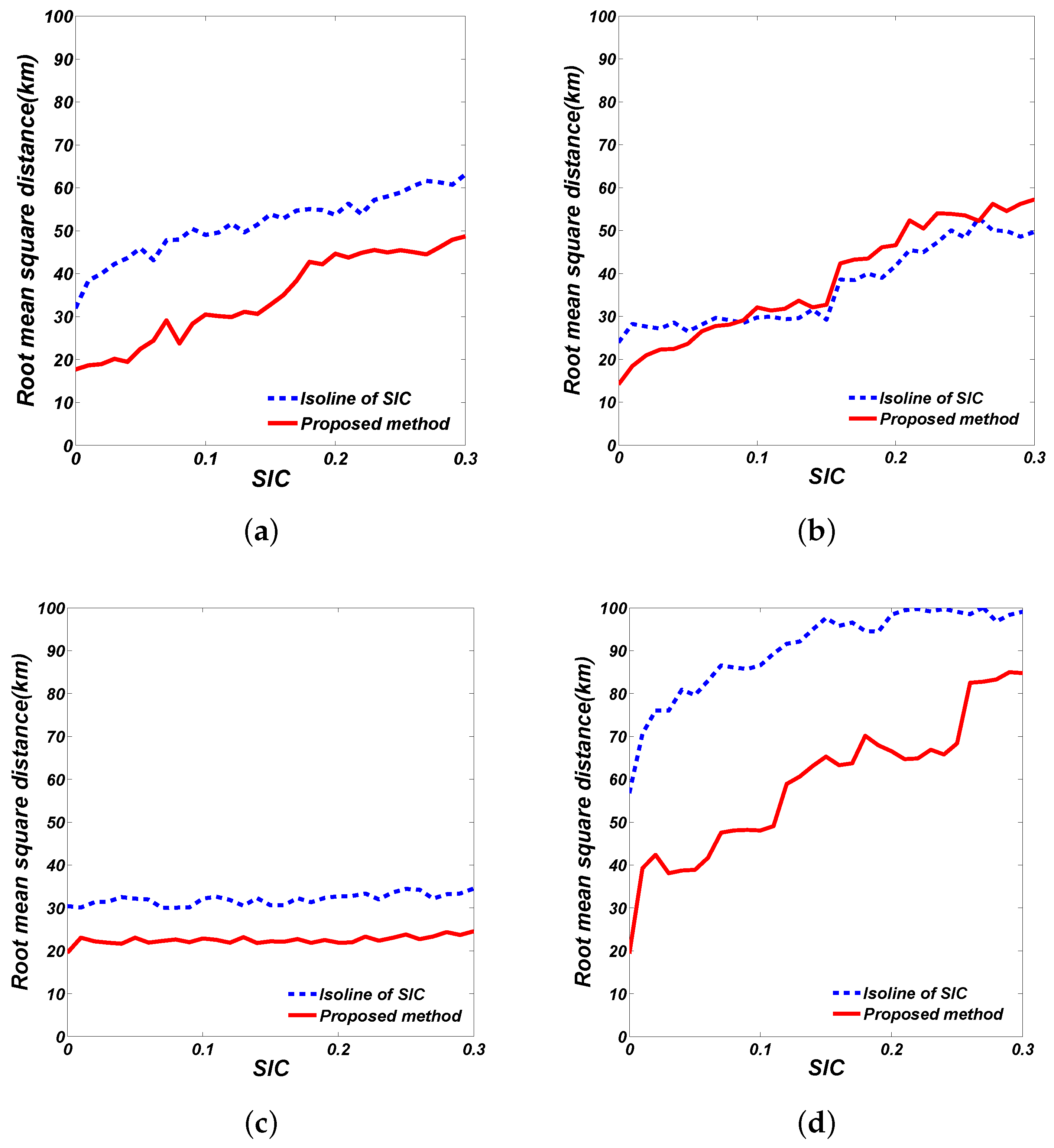
5.1.1. Results for 20 February 2011
5.1.2. Result for 16 February 2011
5.1.3. Results for 13 February and 5 April 2011
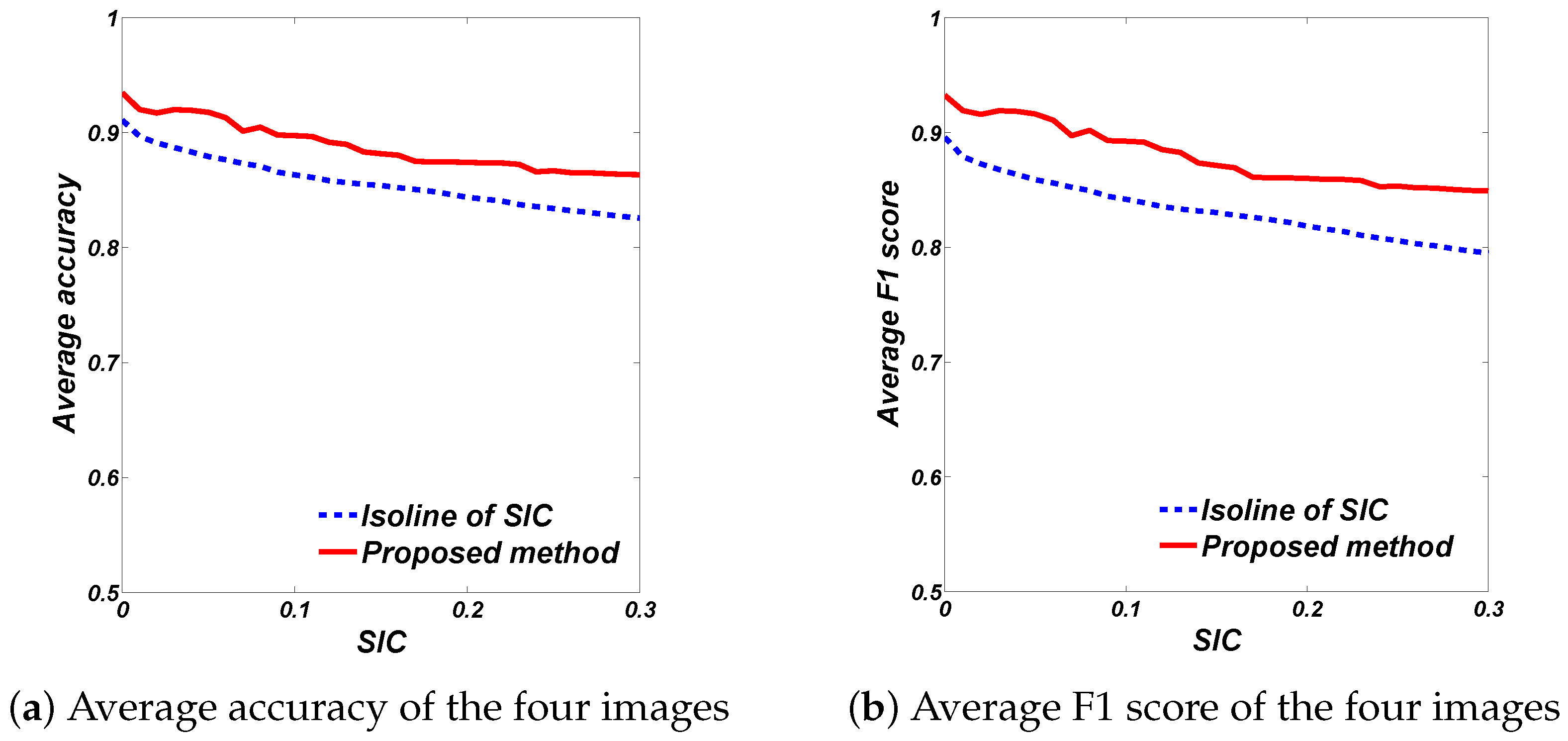
5.2. Quantitative Comparison
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Perrette, M.; Yool, A.; Quartly, G.; Popova, E. Near-ubiquity of ice-edge blooms in the Arctic. Biogeosciences 2011, 8, 515–524. [Google Scholar] [CrossRef]
- Strong, C. Atmospheric influence on Arctic marginal ice zone position and width in the Atlantic sector, February–April 1979–2010. Clim. Dyn. 2012, 39, 3091–3102. [Google Scholar] [CrossRef]
- Johannessen, J.A.; Johannessen, O.M.; Sevendsen, E.; Shuchman, R.; Manley, T.; Campbell, W.J.; Josberger, E.O.; Sandven, S.; Gascard, J.C.; Olaussen, T.; et al. Mesoscale eddies in the fram strait marginal ice zone during the 1983 and 1984 Marginal Ice Zone Experiments. J. Geophys. Res. Atmos. 1987, 92, 6754–6772. [Google Scholar] [CrossRef]
- Strong, C.; Rigor, I.G. Arctic marginal ice zone trending wider in summer and narrower in winter. Geophys. Res. Lett. 2013, 40, 4864–4868. [Google Scholar] [CrossRef]
- Brigham, L. Marine protection in the Arctic cannot wait. Nature 2011, 478, 157. [Google Scholar] [CrossRef] [PubMed]
- Pizzolato, L.; Howell, S.E.L.; Derksen, C.; Dawson, J.; Copland, L. Changing sea ice conditions and marine transportation activity in Canadian Arctic Waters between 1990 and 2012. Clim. Chang. 2014, 123, 161–173. [Google Scholar] [CrossRef]
- Anderson, H.E. Polar shipping, the forthcoming polar code and implications for the polar environments. J. Marit. Law Commer. 2012, 43, 59–84. [Google Scholar]
- Su, H.; Wang, Y.; Xiao, J.; Yan, X.H. Classification of MODIS images combining surface temperature and texture features using the support vector machine method for estimation of the extent of sea ice in the Frozen Bohai Bay, China. Int. J. Remote Sens. 2015, 36, 2734–2750. [Google Scholar]
- Meier, W.N.; Fetterer, F.; Stewart, S.J.; Helfrich, S. How do sea-ice concentrations from operational data compare with passive microwave estimates? Implications for improved model evaluations and forecasting. Ann. Glaciol. 2015, 69, 332–340. [Google Scholar] [CrossRef]
- Heinrichs, J.F.; Cavalieri, D.J.; Markus, T. Assessment of the AMSR-E ice concentration product at the ice edge using RADARSAT-1 and MODIS imagery. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3070–3079. [Google Scholar] [CrossRef]
- Agnew, T.; Howell, S. The use of operational ice charts for evaluating passive microwave ice concentration data. Atmos. Ocean 2003, 41, 317–331. [Google Scholar] [CrossRef]
- Cavalieri, D.J.; Crawford, J.P.; Drinkwater, M.R.; Eppler, D.T.; Farmer, L.D.; Jentz, R.R.; Wackerman, C.C. Aircraft active and passive microwave validation of sea ice concentration from the Defense Meteorological Satellite Program special sensor microwave imager. J. Geophys. Res. Oceans 1991, 96, 21989–22008. [Google Scholar] [CrossRef]
- Shuchman, R.A.; Onstott, R.G.; Johannessen, O.M.; Sandven, S.; Johannessen, J.A. Processes at the Ice Edge—The Arctic; SAR Marine Users Manual; US National Oceanic and Atmospheric Administration: Silver Spring, MD, USA, 2004; pp. 373–395.
- Peterson, I.K.; Prinsenberg, S.J.; Holladay, J.S. Observations of sea ice thickness, surface roughness and ice motion in Amundsen Gulf. J. Geophys. Res. Atmos. 2008, 113, 205–210. [Google Scholar] [CrossRef]
- Vachon, P.W.; Dobson, F.W. Wind retrieval from RADARSAT SAR images: Selection of a suitable C-band HH polarization wind retrieval model. Can. J. Remote Sens. 2000, 26, 306–313. [Google Scholar] [CrossRef]
- Beaven, S.G.; Gogineni, S.P.; Shanableh, M. Radar backscatter signatures of thin sea ice in the central arctic. Int. J. Remote Sens. 1994, 15, 1149–1154. [Google Scholar] [CrossRef]
- Scheuchl, B.; Flett, B.D.; Caves, R.; Cumming, I. Potential of RADARSAT-2 for operational sea ice monitoring. Can. J. Remote Sens. 2004, 30, 448–461. [Google Scholar] [CrossRef]
- Leigh, S.; Wang, Z.; Clausi, D.A. Automated ice-water classification using dual polarization SAR satellite imagery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5529–5539. [Google Scholar] [CrossRef]
- Scott, K.A.; Ashouri, Z. Assimilation of SAR data in the marginal ice zone. In Proceedings of the IEEE Radar Conference, Ottawa, ON, Canada, 29 April–3 May 2013; pp. 1–5.
- Mäkynen, M.P.; Manninen, A.T.; Similä, M.H.; Karvonen, J.A.; Hallikainen, M.T. Incidence angle dependence of the statistical properties of C-band HH-polarization backscattering signatures of the baltic sea ice. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2593–2605. [Google Scholar] [CrossRef]
- Ochilov, S.; Clausi, D. Operational SAR sea-ice image classification. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4397–4408. [Google Scholar] [CrossRef]
- Karnoven, J.; Simila, M.; Makynen, M. Open water detection from Baltic Sea ice Radarsat-1 SAR imagery. IEEE Trans. Geosci. Remote Sens. 2005, 2, 275–179. [Google Scholar]
- Haarpainter, J.; Solbo, S. Automatic Ice-Ocean Discrimination in SAR Imagery; Norut: Tromsø, Norway, 2007. [Google Scholar]
- Schmidt, R.; Hunewinke, T. Compatibility of sea ice edges detected in ERS-SAR images and SSMI/I data. In Proceedings of the 1997 IEEE International Geoscience and Remote Sensing, IGARSS ’97, Remote Sensing—A Scientific Vision for Sustainable Development, Singapore, 3–8 August 1997; Volume 1, pp. 417–419.
- Liu, A.; Martin, S.; Kwok, R. Tracking of ice edges and ice floes by wavelet analysis of SAR images. J. Atmos. Sci. Technol. 1997, 14, 1187–1198. [Google Scholar] [CrossRef]
- Gill, R. Operational detection of sea ice edges and icebergs using SAR. Can. J. Remote Sens. 2011, 27, 411–432. [Google Scholar] [CrossRef]
- Candès, E.J.; Donoho, D.L. Curvelets—A surprisingly effective non-adaptive representation for objects with edges. In Curve and Surface Fitting: Saint-Malo; Cohen, A., Rabut, C., Schumaker, L.L., Eds.; Vanderbilt University Press: Nashville, TN, USA, 1999. [Google Scholar]
- Candès, E.J.; Donoho, D.L. New tight frames of curvelets and optimal representations of objects with C2 singularities. Commun. Pure Appl. Math. 2004, 57, 219–266. [Google Scholar] [CrossRef]
- Zhou, G.Y.; Gui, Y.; Chen, Y.L.; Yang, J.; Rashvand, H.F. SAR image edge detection using curvelet transform and Duda operator. Int. J. Electron. Lett. 2010, 46, 167–169. [Google Scholar] [CrossRef]
- Candès, E.J.; Demanet, L.; Donoho, D.L.; Ying, L. Fast Discrete Curvelet Transforms. Multiscale Model. Simul. 2005, 5, 861–899. [Google Scholar] [CrossRef]
- Menaka, R.; Chellamuthu, C.; Karthik, R. Efficient feature point detection in CT images using Discrete Curvelet Transform. J. Sci. Ind. Res. 2013, 72, 312–315. [Google Scholar]
- Chopra, A.; Dandu, B.R. Image segmentation using active contour model. Int. J. Comput. Eng. Res. 2012, 2, 819–822. [Google Scholar]
- Jing, Y.; An, J.; Liu, Z. A novel edge detection algorithm based on global minimization active contour model for oil slick infrared aerial image. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2005–2013. [Google Scholar] [CrossRef]
- Arbelaez, P.; Maire, M.; Fowlkes, C. Contour detection and hierarchical image segmentation. IEEE Trans. Pattern Anal. 2011, 33, 898–916. [Google Scholar] [CrossRef] [PubMed]
- Gawish, A.; Fieguth, P. Forces for active contours using the undecimated wavelet transform. In Proceedings of the International Conference on Image Processing, Quebec City, QC, Canada, 27–30 September 2015; pp. 1453–1457.
- Gawish, A.; Fieguth, P.; Marschall, S.; Bizheva, K. Undecimated hierachical active contours for OCT image segmentation. In Proceedings of the International Conference on Image Processing, Paris, France, 27–30 October 2014; pp. 882–886.
- Kass, M.; Witkin, A.; Terzopoulos, D. Snakes: Active contour models. Int. J. Comput. Vision. 1988, 1, 321–331. [Google Scholar] [CrossRef]
- Chan, T.F. Active Contours Without Edges. IEEE Trans. Image Process. 2001, 10, 266–277. [Google Scholar] [CrossRef] [PubMed]
- Canadian Space Agency. Satellite Characteristics. Available online: asc-csa.gc.ca/eng/satellites/radarsat/radarsat-tableau.asp (accessed on 1 October 2015).
- Kaleschke, L.; Heygster, G.; Lupkes, C.; Bochert, A.; Hartmann, J.; Haarpaintner, J.; Vihma, T. SSM/I sea ice remote sensing for mesoscale ocean-atmosphere interaction analysis. Remote Sens. 2001, 27, 526–573. [Google Scholar] [CrossRef]
- Spreen, G.; Kaleschke, L.; Heygster, G. Sea ice remote sensing using AMSR-E 89 GHz channels. J. Geophys. Res. Atmos. 2008, 113, C02S03. [Google Scholar] [CrossRef]
- Institute of Environmental Physics, University of Bremen. Sea Ice Concentration Archive Calculated with the ARTIST Sea Ice (ASI) Algorithm Using AMSR-E Data. Available online: http://iup.physik.uni-bremen.de:8084/amsredata/ (accessed on 1 October 2015).
- Crocker, G. Canadian Ice Service Digital Archive-Regional Charts: History, Accuracy and Caveats; Canadian Ice Service: Ottawa, ON, Canada, 2006. [Google Scholar]
- Donoho, D.L.; Johnstone, J.M. Ideal spatial adaptation by wavelet shrinkage. Biometrika 1994, 81, 425–455. [Google Scholar] [CrossRef]
- Comiso, J.C. Abrupt decline in the arctic winter sea ice cover. Geophys. Res. Lett. 2006, 33, 488–506. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C. A universal image quality index. IEEE Signal Proc. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Powers, D. Evaluation: From precision, recall and F-Measure to ROC, informedness, markedness & correlation. J. Mach. Learn. Technol. 2011, 2, 37–63. [Google Scholar]

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Scott, K.A.; Gawish, A.; Fieguth, P. Automatic Detection of the Ice Edge in SAR Imagery Using Curvelet Transform and Active Contour. Remote Sens. 2016, 8, 480. https://doi.org/10.3390/rs8060480
Liu J, Scott KA, Gawish A, Fieguth P. Automatic Detection of the Ice Edge in SAR Imagery Using Curvelet Transform and Active Contour. Remote Sensing. 2016; 8(6):480. https://doi.org/10.3390/rs8060480
Chicago/Turabian StyleLiu, Jiange, K. Andrea Scott, Ahmed Gawish, and Paul Fieguth. 2016. "Automatic Detection of the Ice Edge in SAR Imagery Using Curvelet Transform and Active Contour" Remote Sensing 8, no. 6: 480. https://doi.org/10.3390/rs8060480
APA StyleLiu, J., Scott, K. A., Gawish, A., & Fieguth, P. (2016). Automatic Detection of the Ice Edge in SAR Imagery Using Curvelet Transform and Active Contour. Remote Sensing, 8(6), 480. https://doi.org/10.3390/rs8060480