Abstract
Recent satellite observations yield estimates of the distribution of sea ice thickness across the entire Arctic Ocean. While these sensors were only placed in operation within the last few years, information from other sensors may assist us with estimating the distribution of sea ice thickness in the Arctic beginning in the 1980s. A previous study found that the age of sea ice is correlated to sea ice thickness from 2003 to 2006, but an extension of the temporal analysis is needed to better quantify this relationship and its variability from year to year. Estimates of the ice age/thickness relationship may allow the thickness record to be extended back to 1985, the beginning of our ice age dataset. Comparisons of ice age and thickness estimates derived from both ICESat (2004–2008) and IceBridge (2009–2015) reveal that the relationship between age and thickness differs between these two campaigns, due in part to the difference in area of coverage. Nonetheless, sea ice thickness and age exhibit a direct relationship when compared on pan-Arctic or regional spatial scales.
1. Introduction
The area of the Arctic covered by sea ice has been decreasing since 1979, when satellites began regularly observing the spatial distribution of Artic sea ice. Linear trends in Arctic ice extent are negative for all calendar months, with the weakest trends in winter and the strongest in September, at the end of the melt season [1]. While a linear fit is usually used to quantify overall changes in September ice extent, the trend has accelerated in recent years. Through 2001, the linear trend in September ice extent over the satellite record was about –7.0% per decade. Through 2015, it is –13.4% per decade and the nine lowest September extents in the satellite record have all occurred in the past nine years [2,3]. Decreased summer sea ice extent has been accompanied by large reductions in winter sea ice thicknesses [4] that are primarily explained by changes in the ocean’s coverage of multiyear ice (MYI) [5,6,7,8].
A sea ice age product [9] tracks how long ice survives within the Arctic using satellite-derived ice motion to determine when older sea ice disappears. It provides not only a distinction between seasonal first-year (FYI) and MYI, but also estimates of the age of the MYI pack. In the mid-1980s, MYI accounted for 70% of total winter ice extent, whereas by the end of 2012 it had dropped to less than 20% [2,5,6]. At the same time, the fraction of ice five years or older dropped from 20% to less than 5%. Models suggest that as FYI replaces MYI as the dominant ice type, the Arctic Ocean becomes more vulnerable to natural climate variability, initiating feedbacks that have the potential to promote a rapid transition towards a seasonally ice-free Artic [10].
Two efforts at validating the ice age product have found that the estimated age of the ice roughly corresponds with ice thickness. In the first approach [6], ice age data was mapped to the same grid as data from the Ice, Cloud, and land Elevation Satellite (ICESat) Geoscience Laser Altimeter System thickness fields [11]. Results revealed high correlation between ice age and thickness from 2003 to 2006, with the mean thickness increasing linearly with age at a rate of 0.19 m/year (correlation coefficient R = 0.96).
The use of an ice model provides a similar comparison but using an approach that is independent of remotely-sensed or buoy data. Age versus thickness within the CICE climate-scale sea ice model [12] yields a strong correlation between the ice age-derived thicknesses and the model-derived age. The strong and significant relationships seen in these two analyses suggest that the ice age record may be useful as a proxy for sea ice thickness during time periods with limited thickness measurements.
However, while changes in sea ice age may reflect clear changes in ice thickness, it is unclear if the relationship identified in [6] has remained valid as the ice cover has continued to shrink and thin in recent years, or how it can help us understand ice thickness during years before the ICESat time period. It is likely that the relationship previously identified [6] has changed post-2007, when a large amount of solar heating of the ocean resulted in large basal and lateral melt of the multiyear ice [13], and since 2007, the Arctic has been dominated by low summer ice extent minima. In this study, we perform our own analysis to compare the ICESat ice thickness data to ice age, which is estimated using our sea ice age product [9]. We also compare ice thickness to age by incorporating sea ice thickness estimates derived from NASA’s Operation IceBridge campaign [14].
2. Materials and Methods
2.1. Ice Age Product
Using satellite and buoy data, individual sea ice parcels are tracked as they form, move on the Arctic Ocean surface and disappear (through melt or transport out of the Arctic) at 12.5 km spatial resolution in Equal Area Scalable Earth (EASE) grid [15]. The approach is based on ice motion vectors derived using a cross-correlation technique applied to sequential, daily satellite images acquired by the Scanning Multichannel Microwave Radiometer (SMMR), the Special Sensor Microwave Imager (SSM/I), the SSM/I Sounder (SSMIS), and the Advanced Microwave Scanning Radiometer—Earth Observing System (AMSR-E) sensors. These motion vectors are then blended via optimal interpolation with drifting-buoy vectors from the International Arctic Buoy Program (IABP) and wind vectors generated from the NCEP/NCAR Reanalysis to produce a daily sea ice motion product [16].
The sea ice age product [9] builds on this sea ice motion product. Each week, sea ice extent is determined by applying the NASA Team algorithm [17] to passive microwave brightness temperatures. Ice is considered present if the calculated sea ice concentration is at least 15%. Each year when the Arctic sea ice is at its minimum extent, the age of each sea ice parcel is incremented by one year. The evolution of the location of that season's ice is calculated by applying the average weekly ice motion to the location of each ice parcel, effectively treating each parcel as a Lagrangian particle. Ice parcels are tracked independently and can merge or diverge with other parcels as the ice motions are applied to them. The ice age is the age of the oldest parcel in each grid cell. At any point in the model evolution, the age of the grid cell is the age of the oldest ice parcel at the grid cell's location. If a parcel ever finds itself in a location where the ice concentration is below 15%, the parcel is considered to have melted. If no MYI parcel is present in a grid cell, but the ice extent indicates that ice exists there, that ice is considered FYI.
Age is therefore assigned on a yearly basis, with the age incremented by one year if the ice survives summer melt and stays within the Arctic domain. In the model, the ice age is binned from 1 to 10 years, though for analysis, we combine ice older than 5 years in a “5+” age category, as the relationship between thickness and age levels off for much older ice. In other words, there was little difference between the thickness of 6-, 7-, 8-, 9-, and 10-year-old ice. The procedure to estimate ice age is essentially a middle-of-the-road approach between the direct use of satellite data to estimate coverage of first-year and multiyear ice, as is done using passive microwave brightness temperatures or radar backscatter [7,18], and the comparable age calculations that rely entirely on buoy drift tracks [19]. The ice age data set spans 1979 to present, although we consider the first six years a “spin-up” period for the model since no age distribution is assumed when the model is initialized, and therefore start the product in 1985. Note that age is assigned such that ice classified as 1 year old is at most 1 year old, an ice age of 2 years is between 1 and 2 years old, etc.
In addition to the approximation of ice advection with Lagrangian parcels, two other aspects of this methodology introduce sources of uncertainty: (1) uncertainties associated with errors in the true ice drift trajectories versus actual drift tracks and (2) uncertainties introduced with the land masking process, since ice motion is not computed near the coast. Accuracy of daily motion estimates depends on the source imagery. Higher spatial resolution generally results in higher accuracy. Passive microwave imagery at 25 km resolution (e.g., from the 37 GHz channel on SSMIS) can provide daily motions with a root-mean-square (RMS) accuracy of ~6–7 km/day when using oversampling techniques; 12.5 km resolution imagery (e.g., from the 91 GHz channel on SSMIS) can provide daily motions with an RMS accuracy of ~4–5 km/day. An optimal interpolation scheme is used to take advantage of the spatial correlation of neighboring motion estimates to create gridded fields with uncertainties of 3–4 km/day. While the daily RMS errors are fairly high, they are uncorrelated with each other so there is little or no bias in the longer-term motion estimates, so averaging daily vectors into weekly estimates reduces the RMS error. A study [20] that compared ice motion estimated from ERS-1 synthetic aperture radar (SAR) to this motion product resulted in an error of 1.0 to 1.8 cm/s (0.86 to 1.56 km/day). However, this error is not necessarily cumulative, as annual displacement errors have been found to be on the order of 50–100 km [21].
2.2. Thickness Data Sets
Laser altimetry measures the elevation of a target below the instrument by emitting a signal in nadir direction and measuring the echo reflected from the surface. The time it takes for the signal to return is used to determine the surface height. Since the laser signal is reflected off the air-snow interface, the thickness of the ice can be computed after estimating the sea ice freeboard—the height of the ice above the water surface minus the depth of snow on top of the ice, which is typically estimated using RADAR. Assuming hydrostatic equilibrium allows for the conversion of freeboard into sea ice thickness according to:
where hi is the ice thickness, hs the snow depth, fs the snow plus ice freeboard, and ρw, ρs and ρi are the densities of water, snow and ice, respectively.
hi = [fsρw + hs (ρs − ρw)]/(ρw − ρi)
In this study, we examine ice thickness fields from ICESat based on this methodology [8], providing five years (2004–2008) of data up to 86°N. ICESat satellite tracks have a resolution of ~170 m in the along-track direction, with several kilometers separating the individual tracks. Estimated uncertainty in the mean thickness is 0.5 m for each 25 km grid cell [8].
NASA’s Operation IceBridge is an airborne mission that provides an ice thickness product during March and April from 2009 to 2015 [22], with plans for future campaigns in place as well. The IceBridge aircraft has overflown sea ice of varying ages, with numerous flight lines over sea ice in the Western Arctic. The IceBridge Sea Ice Freeboard, Snow Depth, and Thickness L4 Version 1 dataset is available at NSIDC [22]. Thickness in this product is determined by estimating the freeboard using an airborne LIDAR (called the Airborne Topographic Mapper) to deduce the level of the snow-atmosphere interface and a snow radar for the position of the ice/snow interface. Retrieval methods for ice thickness are discussed in [22,23]. The IceBridge ice thickness data has 1 m resolution with ~200 m swath, averaged to give a mean for 40 m segments of the flight line, so that each latitude/longitude point in the data set represents a ~40 m by ~200 m area.
We use published values of ice thickness for ICESat and IceBridge. There are significant differences in the methodologies between these two data sets. In particular, snow depth and snow and ice density are processed differently, and may have a significant impact on the thickness retrieval. For example, one study [24] found that the choice of ice density used when converting sea ice freeboard to ice thickness has a large impact on the mean ice thickness, while snow depth plays a large role in year-to-year variability. This presents challenges in creating a consistently processed sea ice thickness time-series with which to compare the ice age dataset.
2.3. Method
2.3.1. ICESat
To determine if there is a relationship between sea ice thickness and age, co-registered thickness and age fields are needed. The ICESat-derived ice thickness fields, provided by Dr. R. Kwok [25], represent the average thickness of the Arctic sea ice cover for a six-week period in the spring. These fields are re-gridded to the 12.5 km EASE grid using a drop-in-the-bucket averaging.
An initial investigation of the relationship between ICESat thickness estimates and ice age has been reported [6]. Since then, three additional years of ICESat data have become available. However, ICESat data from the spring of 2003 and 2009 are not used in our analysis, due to poor data quality and the subsequent recommendation for exclusion by the provider, Dr. R. Kwok. Our methodology varies slightly from that of the previous study [6] in that we not only use additional years, but we include FYI and bin all ice ages older than 4 years into a single “5 years or older” age category, due to the relatively small number of observations of 6th-year and older ice. We note the effect of this difference in the results section.
Because the gridded ICESat fields are estimates of thicknesses over time periods of 4 to 6 weeks (i.e., each year averages over a different time period), several weekly ice age fields exist for each ICESat thickness field. We compare the spring ICESat thickness field with each of the weekly ice age fields for the period of the ICESat coverage and use all these comparisons in our age/thickness distribution.
2.3.2. IceBridge
In contrast to the gridded ICESat product, the IceBridge ice thickness data has higher spatial resolution than the ice age data. An example of the distribution of observed ice thickness in a single 12.5 km ice age grid cell is shown in Figure 1. The age-thickness relationship for IceBridge is computed by averaging all valid IceBridge thickness measurements contained in each ice age grid cell. Only IceBridge thickness measurements with a freeboard uncertainty less than 5 cm and an ice concentration of >90% are used. Furthermore, only grid cells that contain a minimum of 100 IceBridge thickness measurements are included in the calculations. The mean IceBridge ice thickness is calculated for each grid cell of the 12.5 km EASE grid used for the ice age product. We also investigated the age/thickness relationship using the modal thickness values for each grid cell. For example, in Figure 1, the modal value would be 1.2 m. However, we found that the wide range of ice thicknesses used to compute the mean thickness were not sufficiently dense to create a thickness histogram that resolved mode thicknesses between grid cells, so we conducted our analysis using mean thicknesses.
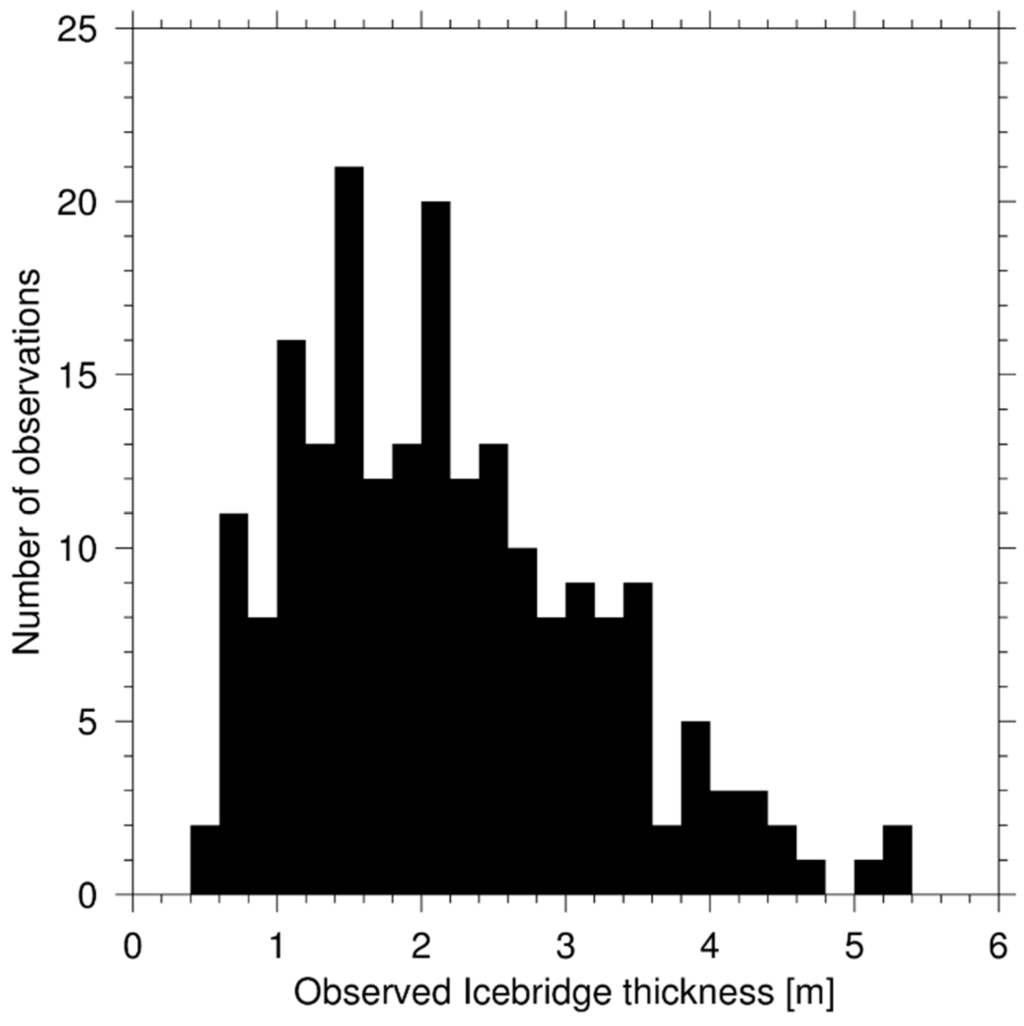
Figure 1.
IceBridge ice thickness data points for one ice age parcel.
By calculating the mean thickness for each ice age category, we obtain ice thickness values that can be heavily influenced by ice deformation. For example, the ice age grid cell in Figure 1, which has an age of 1–2 years (second-year ice, which is referred to as ice of age 2 years in the age product), contains an ice distribution ranging from 0.5 m to 5.5 m. Deformed ice likely accounts for the ice in the thickest ice bins. In this cell, ice deformation may have occurred for ice thicker than ~3.5 m.
Using co-located grids of the ICESat, IceBridge and Ice Age datasets, we compute the relationship between age and thickness for each year and for the entire data record for the two ice thickness products. We calculate the mean ice thickness, as well as the 25th and 75th percentile, for each age category (1, 2, 3, 4, 5+ years). We also calculate the correlation coefficient, R, in two distinct ways. The correlation coefficient Rm is computed using only the mean value for each ice age category, so we are correlating the age and thickness for the five mean points. We also compute the correlation using all data points for each ice age category, Ra. As expected, Ra typically is much smaller than Rm, given the spread of ice thickness values for each age category.
For 2014–2015, we use the IceBridge “quick-look” thickness dataset [26]. We include these data, although this thickness dataset is considered “experimental” and may have more error than the IceBridge L4 ice thickness datasets for 2009–2013 [23].
3. Results
3.1. ICESat
Figure 2 summarizes the mean 2004–2008 ice age/thickness relationship using the ICESat ice thickness dataset [25]. For the entire 2004–2008 period (bottom right), there is a general increase in ice thickness with age of 0.36 m/year, with Rm = 0.97 and Ra = 0.48. First-year ice has a five-year mean thickness of 1.56 m, increasing for each class up to ~3.0 m for fifth-year and older ice. The mean ice thickness for the Arctic over this period was about 2.6 m. We note that 5+ year ice had the same thickness as 4th–year ice during spring 2008, with a mean of 2.52 m for both distributions. This phenomenon was observed in an earlier study [8], which observed that a decline of 0.6 m in the mean sea ice thickness from 2004–2008 was entirely explained by the thinning of thick multiyear ice.
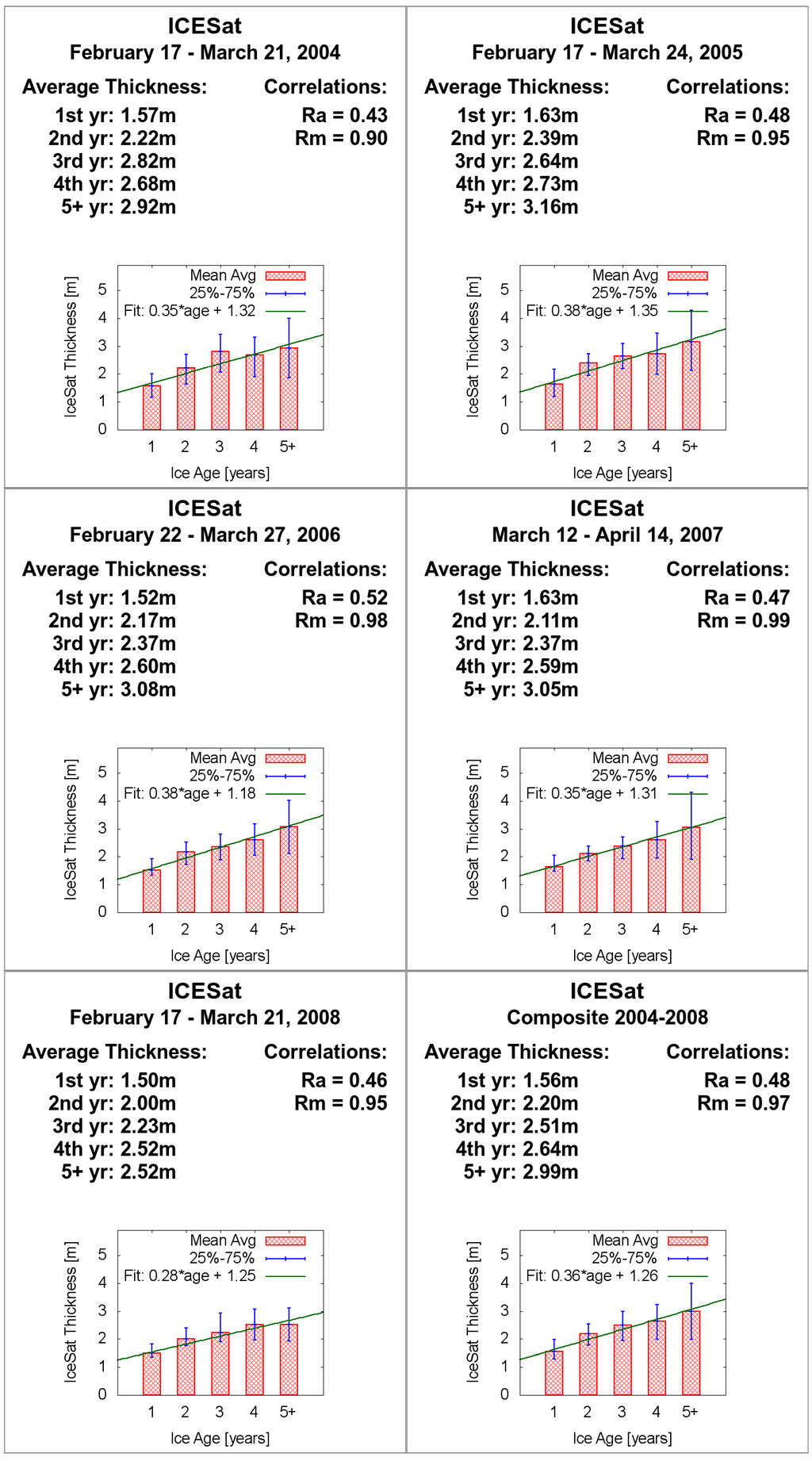
Figure 2.
ICESat sea ice thickness vs. ice age.
The age vs. thickness relationships found for spring 2004 (~0.35 m/year), 2005 (~0.38 m/year), and 2006 (~0.38 m/year) were higher than found previously [6], where computed slopes of 0.15 m/year, 0.24 m/year, and 0.17 m/year for 2004–2006, respectively were found. This is partly due to our technique of averaging together all ice at least 5 years or older into one ice age category, compared to the previous method of using ice categories up to 10 years old. A larger impact on the difference in age/thickness relationships between our study and the previous one is that the previous study’s authors reported slopes that excluded first-year ice [6]. In 2004, the slope for ice aged 2–4 years in the previous ICESat results is ~0.18 m/year, and we compute 0.18 m/year for this same segment. The results are also similar for 2005 (0.29 vs. 0.28 m/year) and 2006 (0.21 to 0.25 m/year).
We note that the slope of the age/thickness line of best fit decreased from ~0.35 m/year in 2007 to ~0.28 m/year in 2008. There was therefore less thickness difference between younger and older ice in 2008 than in 2007. As noted previously, there was also a leveling off of ice thickness for ice four years and older in 2008. This change in the age/thickness relationship may in part reflect the extensive melt in 2007 that led to enhanced basal melting of the ice cover [14]. While the data scatter is large, these results hint at a fundamental change in the thickness of the oldest ice in the year following the 2007 minimum.
3.2. IceBridge
The overall age/thickness relationships for 2009–2015, as well as for individual years, along with the IceBridge flight segments where ice thickness data was computed, are shown in Figure 3. We find a more gradual slope for the age/thickness relationship in the IceBridge data than for ICESat: a 2009–2015 mean 0.15-m/year increase (Rm = 0.95, Ra = 0.24).
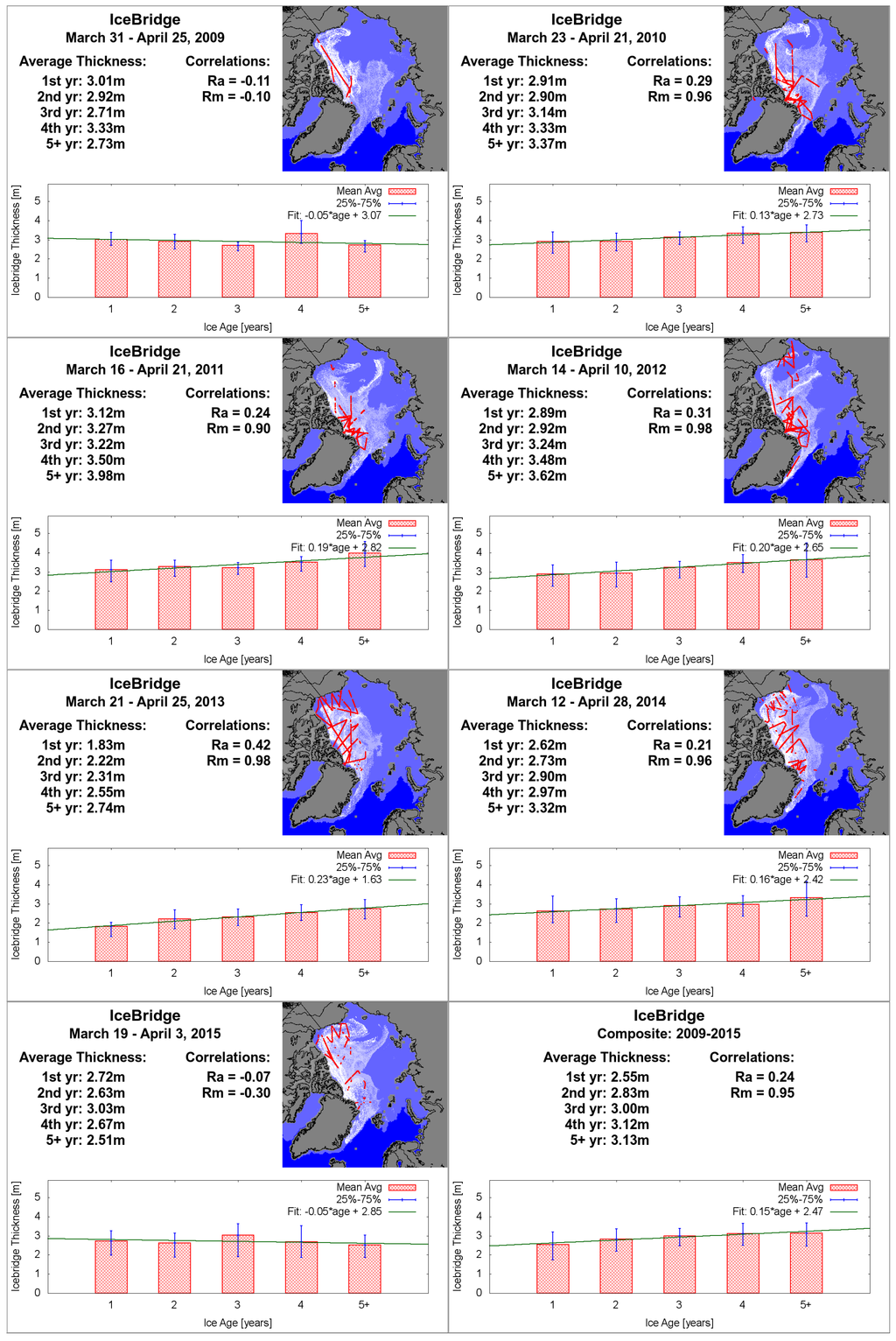
Figure 3.
Operation IceBridge sea ice thickess vs. ice age.
From 31 March–25 April 2009, five IceBridge flights were conducted over sea ice off the coast of Northern Greenland, and two flights were focused on sea ice in the Beaufort Sea, which served as a limited sample in the inaugural campaign. We do not find a sea ice thickness/age relationship for this year. While this was an interesting initial campaign to view sea ice properties, the limited set of flights did not adequately sample all the ice age classes, with less than forty ice age cells overflown for each age class, significantly less than subsequent years (Table 1). We also note that most of the thickness data was obtained over older ice near the Canadian Archipelago.

Table 1.
Number of IceBridge 12.5 km ice age grid cells used for age/thickness comparison, and mean ice thickness for all sampled IceBridge observations.
For the spring 2010 campaign there were eight IceBridge flights over the Arctic ice pack from 23 March–21 April. This campaign’s flight tracks covered significantly more of the Arctic than the previous year, overflying a substantial number of grid cells (Table 1) for all ice age classes. We observe a relationship between ice age and thickness up through ice 5+ years old with an increase of about 0.13 m/year (Rm = 0.96, Ra = 0.29). We note that first and second-year ice thickness means are about the same (2.9 m), as are fourth-year and fifth-year and older ice (~3.3 m).
In 2011, nine IceBridge flights took place from 17–28 March. The results show an age/thickness relationship of 0.19 m/year (Rm = 0.90, Ra = 0.25). We see in Figure 2 that most of the sea ice flights acquired altimetry data near the coast of Greenland and the Northeast Canadian Archipelago, where ice tends to pile up and persist. For example, there were many more second-year and third-year ice pixels overflown, compared to first-year ice (Table 1). Much of the first-year ice in this area was likely heavily deformed, as first-year ice thickness was computed up to 8 m [23].
During 2012, there were 12 IceBridge flights over sea ice from 14 March to 10 April. We note an ice thickness vs. age relationship of ~0.20 m/year (Rm = 0.98, Ra = 0.31), with first and second-year ice having about the same thickness as in 2010. The 2012 results span more sea ice over different regions than previous years (Figure 2), which may contribute to the improved correlation in the mean (Rm) over the correlation found for 2011. Furthermore, 2012 had the most ice age grid cells sampled, although 5+ year ice was sampled significantly less than younger age classes (Table 1).
In 2013, 9 IceBridge flights were conducted over sea ice from 21–27 March. The age vs. thickness relationship is found to be ~0.23 m/year (Rm = 0.98 and Ra = 0.42) although the difference in means for 2nd and 3rd year ice is minimal. Note again that regions bordering Alaska, Canada, and Greenland are sampled (Figure 2), and that ice of each age is highly sampled (Table 1). First-year ice is prevalent in the Beaufort and Chukchi Seas, and we note that the first-year ice thickness is considerably lower (~2.0 m) than in 2012 (2.8 m) and previous years. Furthermore, the 2013 overall mean thickness is nearly 80 cm thinner than the previous year. This likely relates in part to the chosen IceBridge flight paths, but may also reflect a thinning of the ice cover following the record September 2012 sea ice minimum [27]. Thicknesses are dependent on specific flight tracks, which may or may not sample representative data for the entire Arctic. Furthermore, these thicknesses are from the quick-look dataset, which will be undergoing further quality control before final release. However, it is interesting and may be significant as a snapshot of the changing Arctic ice cover.
For 2014, 15 IceBridge flights, from 12 March to 28 April, overflew sea ice, obtaining a sufficient number of ice thickness observations to utilize 861 ice age grid cells (Table 1). Ice thickness for all age classes exhibit a small variation, with an age/thickness relationship of only 0.16 m/year, with Rm = 0.96 and Ra = 0.21. However, we do note that the thickness does increase with age for each age class. In 2015, we do not observe a positive age/thickness relationship. We do note from Table 1 that most age classes, except for fifth-year and older ice, were not highly sampled.
4. Discussion
For IceBridge thickness vs. age distributions, we note that the best-defined relationships occur during campaigns when a larger number of ice age grid cells for each age class were sampled, which is expected. In general, ice age sample sizes of at least 100 ice thickness data points per ice age parcel produce the best age vs. thickness correlation for a particular year (Table 1).
We note that the younger ice classes are much thicker in the IceBridge dataset than in the ICESat set, while 5+ year ice thickness is about the same for each dataset. The difference between these relationships is likely associated with the area of sampling. ICESat ice thickness is estimated throughout the Arctic, and IceBridge has sampled ice in a region closer to the Greenland, Canadian, and Alaska coasts, where thick, perennial multiyear ice is present. Further consequences of this sampling are that the younger ice classes are much thicker in the IceBridge dataset than in the ICESat set because of strong ice convergence in this region associated with the Beaufort Gyre, while 5+ year ice thickness is about the same for each dataset. Thus, we expect more ridging of the younger ice in the IceBridge area of coverage, where thicker ice can accumulate and exert more lateral pressure on the ice with convergence. These forces are weaker in other areas of the Arctic, such as the Trans-polar drift stream, so first-year ice there would expected to be thinner. An investigation [28] found thicker ice and a longer tail in ice thickness distribution in multi-year ice northwest of the Canadian Archipelago in end of summer 2013.
We also observe that, for ICESat, the 5+ year ice was thinner than 4th-year ice in 2008 (Figure 2). This absence of or minimal increasing thickness between these two age classes is also evident in the IceBridge distribution for 2009 (although this year is under-sampled), as well as 2010 and 2015 (with under-sampling likely), but most significantly, for the collective 2009–2015 distribution. This phenomena provides some evidence of the recent thinning of old ice in the Beaufort Sea, since the oldest ice is not significantly thicker than fourth-year, or, for that matter, third-year ice.
It is important to recall that the nature of this shift may also be affected in part by the distribution of ice age in each ice thickness cell. Recall that the age of the ice is the oldest age in each grid cell. Therefore many ice age cells will likely also contain ice that is younger than the designated age for that cell. It may be that many old (5+ year ice) grid cells have a lower concentration of that ice type than in previous years. It is nonetheless interesting that the ice pack observed by IceBridge does not consistently exhibit increasing mean thickness with age for every year. Furthermore, some of the oldest ice has previously been observed to be rotten and very weathered in the Canadian Archipelago [29].
Each year of our study period had unique conditions preceding and during the spring observation periods, as noted in NSIDC’s Arctic Sea Ice News and Analysis [27]. 2009 had a fairly warm winter, with temperatures 1–2 °C above normal, with a high percentage of first-year ice noted. In 2010, there was a surge of first-year ice growth in March. 2011 saw a markedly high temperature (7–9 °C) over the Chukchi Sea in March, and had the second-lowest ice extent on record. Sea ice extent was higher in March 2012 than in the previous few years, although the overall trend of ice extent decrease continued. The Arctic Oscillation (AO) exhibited an extreme negative phase in March of 2013, which led to wind patterns that increased fracturing of the ice cover in the Beaufort and Chukchi Seas.
An increase in multiyear ice was observed in March of 2014 (Figure 4). For March 2015, the age fractions were similar to the previous year. The ice age distribution from 1985–2015 has fundamentally changed, with a significant increase in first-year ice fraction (50% in 1985, 70% in 2015). Furthermore, there has been a profound loss of older (4 years and older) ice, from 20% in March 1985 to only 3% in March 2015. First-year ice fraction increased markedly in March 2013, but multiyear ice (>one year old) fraction increased from 25%–30% from March 2013 to the same month in 2014 and 2015 [30].
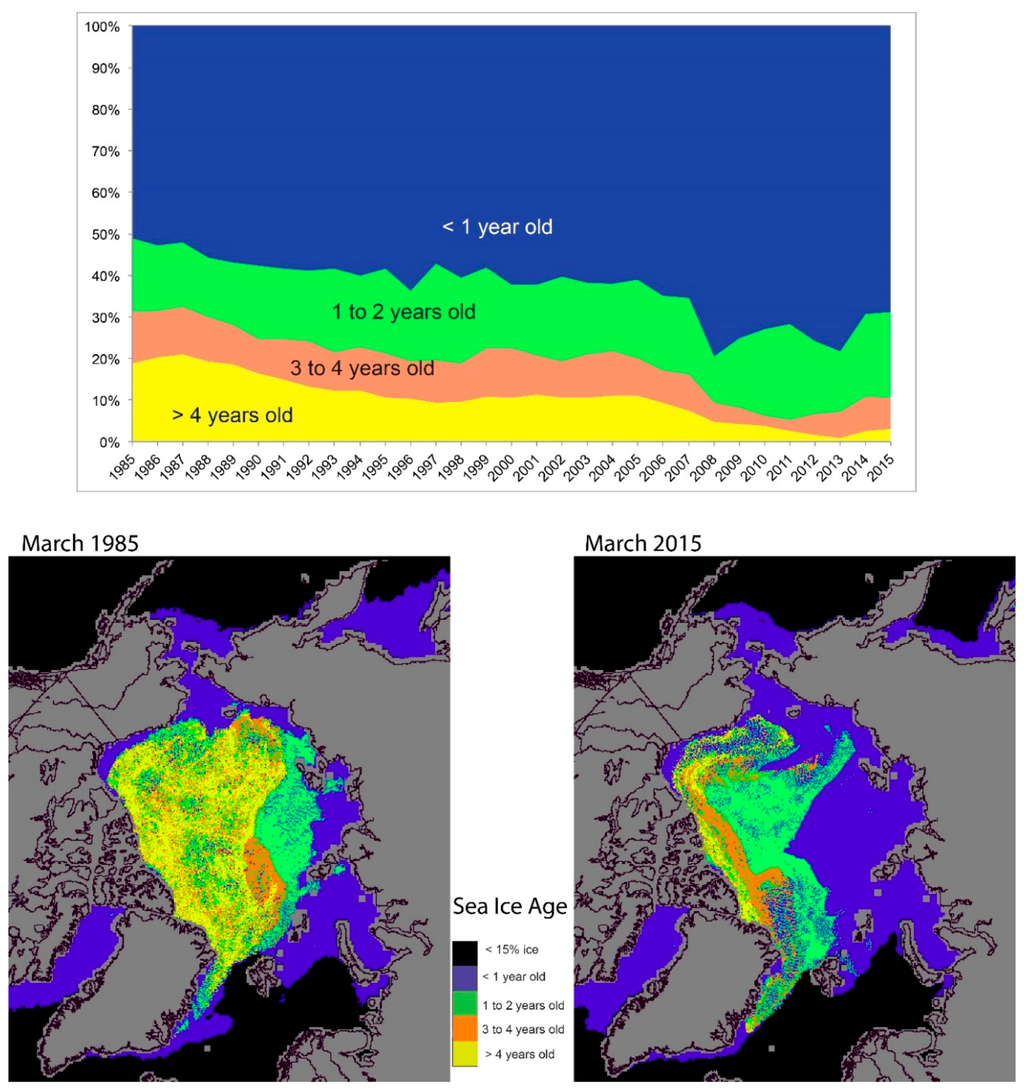
Figure 4.
Sea ice age fraction for March 1985–2015 (top), and maps for March 1985 and 2015 (bottom) from the Univ. of CO sea ice age product (NSIDC, 2015). Figure by J. Maslanik, in the sea ice section of the Arctic Report Card, 2015 [30].
5. Conclusions
We observe relationships between ice age and ICESat- and IceBridge-derived thickness when including all years of observations, suggesting that the ice age product could be used as a proxy for thickness when thickness cannot be directly measured. The composite relationship between the ice age product and mean IceBridge ice thickness, for years 2009–2015, exhibits an increase in ice thickness of ~0.15 m/year (Rm = 0.95, Ra = 0.24) compared to 0.36 m/year (Rm = 0.97 and Ra = 0.48) in the 2004–2008 time period for ICESat. This large discrepancy does make selection of a proxy conversion value difficult. But a direct correlation between age and thickness would allow for an ice volume estimate for the entire Arctic, using a relationship on the order of the ICESat result, or for volume calculation of ice within a few hundred kilometers of the Greenland, Canadian, and Alaska coasts, using the IceBridge age/thickness relationship.
We should consider the relationships derived in this study to be a first look at the observed differences of sea ice thickness within different age classes. In the current age algorithm, we define the age of each 12.5 km grid cell to be the oldest age within that cell. Improvements to this algorithm would retain the fractional coverage of all age categories within the grid cell, allowing for a more accurate determination of age relationships with thickness. It is likely that the magnitude of the age/thickness relationship may change with this algorithm update, as a larger fraction of younger ice age categories may occupy a grid cell categorized as old ice.
While we use published values of ice thickness, we must acknowledge that the IceBridge and ICESat thickness estimates are not necessarily consistent with each other. Radar and laser technologies use different wavelengths, have different footprints and different techniques with which to recover ice thickness from ice draft and surface elevation measurements. This creates challenges in creating a consistent sea ice thickness time-series with which to compare to the ice age dataset. Recent retrieval of ice thickness by satellite, such as thickness derived from CryoSat-2 [31], will allow for future age/thickness relationships to be evaluated, along with ice thickness estimates from ICESat-2 after launch. We also plan to utilize a modeled ice thickness for comparison with ice age, to better elucidate a fixed age/thickness value that could be applied to estimate past age thickness and volume using our age product as a basis. Furthermore, improvement of the ice age product [9] to include a distribution of ice age within each grid cell would allow for an improved estimate of the ice age/thickness distribution. This and other improvements to this product are planned and pending support.
Acknowledgments
The authors wish to thank the reviewers who helped improve the quality of this manuscript.
Author Contribution
Mark Tschudi analyzed the results of the age vs. thickness comparisons, and wrote the majority of this paper. J. Scott Stewart wrote and ran computer programs to ingest the data, perform calculations, and produce the ice age vs. thickness plots, and provided descriptions of his algorithms for this paper. Julienne Stroeve performed some initial data analysis and contributed text to the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AMSR-E | Advanced Microwave Scanning Radiometer - Earth Observing System |
| CICE | The Los Alamos sea ice model |
| EASE | Equal Area Scalable Earth grid |
| FYI | First-year ice |
| ICESat | Ice, Cloud, and land Elevation Satellite |
| IABP | International Arctic Buoy Program |
| LIDAR | Light Detection and Ranging |
| MYI | Multi-year ice |
| NCAR | National Center for Atmospheric Research |
| NCEP | National Centers for Environmental Prediction |
| NSIDC | National Snow and Ice Data Center |
| Ra | Correlation coefficient using all ice thickness data points |
| Rm | Correlation coefficient using only mean ice thickness data points for each ice age class |
| RADAR | RAdio Detection And Ranging |
| RMS | root-mean-square |
| SMMR | Scanning Multichannel Microwave Radiometer |
| SSM/I | Special Sensor Microwave Imager |
| SSMIS | SSM/I Sounder |
References
- Serreze, M.C.; Holland, M.M.; Stroeve, J. Perspectives on the Arctic’s shrinking sea-ice cover. Science 2007, 315, 1533–1536. [Google Scholar] [CrossRef] [PubMed]
- Stroeve, J.C.; Serreze, M.C.; Holland, M.M.; Kay, J.E.; Maslanik, J.; Barrett, A.P. The Arctic’s rapidly shrinking sea ice cover: A research synthesis. Clim. Chang. 2012, 110, 1005–1027. [Google Scholar] [CrossRef]
- Serreze, M.C.; Stroeve, J. Arctic sea ice trends, variability and implications for seasonal ice forecasting. Phil. Trans. R. Soc. A 2015, 373. [Google Scholar] [CrossRef] [PubMed]
- Kwok, R.; Rothrock, D.A. Decline in Arctic sea ice thickness from submarine and ICESat records. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Maslanik, J.A.; Stroeve, J.; Fowler, C.; Emery, W. Distribution and trends in Arctic sea ice age through spring 2011. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Maslanik, J.A.; Fowler, C.; Stroeve, J.; Drobot, S.; Zwally, J.; Yi, D.; Emery, W. A younger, thinner Arctic ice cover: Increased potential for rapid, extensive sea-ice loss. Geophys. Res. Lett. 2007, 34, L24501. [Google Scholar] [CrossRef]
- Nghiem, S.V.; Rigor, G.; Perovich, D.K.; Clemente-Colón, P.; Weatherly, J.W.; Neumann, G. Rapid reduction of Arctic perennial sea ice. Geophys. Res. Lett. 2006, 34. [Google Scholar] [CrossRef]
- Kwok, R.; Cunningham, G.F. ICESat over Arctic sea ice: Estimation of snow depth and ice thickness. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Tschudi, M.; Fowler, C.; Maslanik, J. EASE-Grid Sea Ice Age, Version 2; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2015; Available online: http://dx.doi.org/10.5067/1UQJWCYPVX61 (accessed on 1 November 2015).
- Holland, M.M.; Bitz, C.M.; Tremblay, B. Future abrupt reductions in the summer Arctic sea ice. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Kwok, R.; Zwally, H.J.; Yi, D. ICESat observations of Arctic sea ice: A first look. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Bitz, C.M.; Holland, M.M.; Weaver, A.J.; Eby, M. Simulating the ice-thickness distribution in a coupled climate model. J. Geophys. Res. 2001, 106, 2441–2463. [Google Scholar] [CrossRef]
- Perovich, D.K.; Richter-Menge, J.A.; Jones, K.F.; Light, B. Sunlight, water, and ice: Extreme Arctic sea ice melt during the summer of 2007. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Studinger, M.; Koenig, L.; Martin, S.; Sonntag, J. Operation icebridge: Using instrumented aircraft to bridge the observational gap between Icesat and Icesat-2. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July2010; pp. 1918–1919.
- Meier, W.N.; Maslanik, J.A.; Fowler, C.W. Error analysis and assimilation of remotely sensed ice motion within an Arctic sea ice model. J. Geophys. Res. 2000, 105, 3339–3356. [Google Scholar] [CrossRef]
- Fowler, C.; Maslanik, J.; Emery, W.; Tschudi, M. Polar Pathfinder Daily 25 km EASE-Grid Sea Ice Motion Vectors, Version 2; National Snow and Ice Data Center: Boulder, CO, USA, 2013. [Google Scholar]
- Cavalieri, D.J.; Gloersen, P.; Campbell, W.J. Determination of sea ice parameters with the NIMBUS 7 scanning multichannel microwave radiometer. J. Geophys. Res. 1984, 89, 5355–5369. [Google Scholar] [CrossRef]
- Comiso, J.C. A rapidly declining perennial sea ice cover in the Arctic. Geophys. Res. Lett. 2002, 29. [Google Scholar] [CrossRef]
- Rigor, I.G.; Wallace, J.M. Variations in the age of Arctic sea-ice and summer sea-ice extent. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Sumata, H.; Kwok, R.; Gerdes, R.; Kauker, F.; Karcher, M. Uncertainty of Arctic summer ice drift assessed by high-resolution SAR data. J. Geophys. Res. Oceans. 2015. [Google Scholar] [CrossRef]
- Tschudi, M.A.; Fowler, C.; Maslanik, J.A.; Stroeve, J. Tracking the movement and changing surface characteristics of Arctic sea ice. IEEE J. Sel. Top. Earth Obs. Remote Sens. 2010. [Google Scholar] [CrossRef]
- Kurtz, N.; Farrell, S.L.; Studinger, M.; Galin, N.; Harbeck, J.P.; Lindsay, R.; Onana, V.D.; Panzer, B.; Sonntag, J.G. Sea ice thickness, freeboard, and snow depth products from operation IceBridge airborne data. Cryosphere 2012, 6, 4771–4827. [Google Scholar] [CrossRef]
- Kurtz, N.; Studinger, M.S.; Harbeck, J.; Onana, V.; Yi, D. IceBridge L4 Sea Ice Freeboard, Snow Depth, and Thickness, Version 1; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2015. [Google Scholar]
- Zygmuntowska, M.; Rampal, P.; Ivanova, N.; Smedsrud, L.H. Uncertainties in Arctic sea ice thickness and volume: New estimates and implications for trends. Cryosphere 2014, 8, 705–720. [Google Scholar] [CrossRef]
- Kwok, R. ICESat: Sea Ice Thickness and Freeboard. Available online: http://rkwok.jpl.nasa.gov/icesat/download.html (accessed on 12 December 2015).
- NSIDC. Available online: https://nsidc.org/data/docs/daac/icebridge/evaluation_products/sea-ice-freeboard-snowdepth-thickness-quicklook-index.html (accessed on 17 October 2015).
- NSIDC. March 2009–2015: Arctic Sea Ice News and Analysis. Available online: https://nsidc.org/arcticseaicenews/ (accessed on 23 February 2016).
- Tilling, R.L.; Ridout, A.; Shepherd, A.; Wingham, D.J. Increased Arctic sea ice volume after anomalously low melting in 2013. Nat. Geosci. 2015, 8, 643–646. [Google Scholar] [CrossRef]
- Galley, R.; Hwang, B.J.; Barber, D.; Key, E.; Ehn, J.K. Spatial and temporal variability of sea ice in the CASES study region: 1980–2004. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Perovich, D.; Meier, W.; Tschudi, M.; Farrell, S.; Gerland, S.; Hendricks, S. Arctic Report Card: Update for 2015, Sea Ice. Available online: http://www.arctic.noaa.gov/reportcard/sea_ice.html (accessed on 24 February 2016).
- Laxon, S.W.; Giles, K.A.; Ridout, A.L.; Wingham, D.J.; Willatt, R.; Cullen, R.; Kwok, R.; Schweiger, A.; Zhang, J.; Haas, C.; et al. CryoSat-2 estimates of Arctic sea ice thickness and volume. Geophys. Res. Lett. 2013, 40. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).