1. Introduction
Airborne laser scanning (ALS) is used today as a tool for forest applications, both for research purposes as well as in operational settings. Productive forest has in many places been the main target, but ALS can also be applied in other types of forest. The very frontiers of the forests have in many places gradually expanded into alpine areas [
1], and this expansion is believed to be caused by several factors, with reduced grazing by domestic livestock and climate changes as two dominating causes. Expansion of forests into areas such as the forest-tundra ecotone will influence carbon sequestration, but will also in many places have a direct effect on the climate through the so-called “albedo-effect”. The darker-colored trees will reflect less of the solar radiation than bare ground, especially in the winter when the ground is covered with snow. The net effect of this phenomenon is warming [
2].
It is therefore of interest to map and monitor possible changes taking place in the vegetation structure of the forest-tundra ecotone, such as the appearance of pioneer trees and the migration of the tree line. ALS has through several studies been proposed and tested as a tool for this task [
3,
4,
5,
6,
7,
8]. Several of these studies investigate and document the potential for discriminating between echoes reflected from trees and echoes reflected from other objects using metrics derived from ALS data, such as the height above the modeled terrain surface, the backscatter intensity of the echoes and the properties of the spatial distribution of echoes. There is, however, a need to apply this knowledge and further develop methods to derive quantitative properties such as tree numbers, crown coverage or tree size distributions to enable the establishment of efficient monitoring methodologies. A segmentation and identification of single trees from the ALS data would be one possible way of deriving such properties. Numerous studies have already proposed and tested methods to derive single-tree segments from ALS data [
9,
10,
11,
12,
13]. An introduction to tree segmentation and an overview of these methods can be found in Koch
et al. [
14]. Common to all of these studies are that they are focused on mature forests, with an emphasis on trees considerably larger than those typically found in the forest-tundra ecotone. We did not consider any of the described methods to be directly applicable to the task of deriving single-tree information for smaller trees in the forest-tundra ecotone because with an average point density of, for example, 5–10 points per m
2, the number of echoes from each individual tree will typically range from one single echo up to less than 100 in most cases.
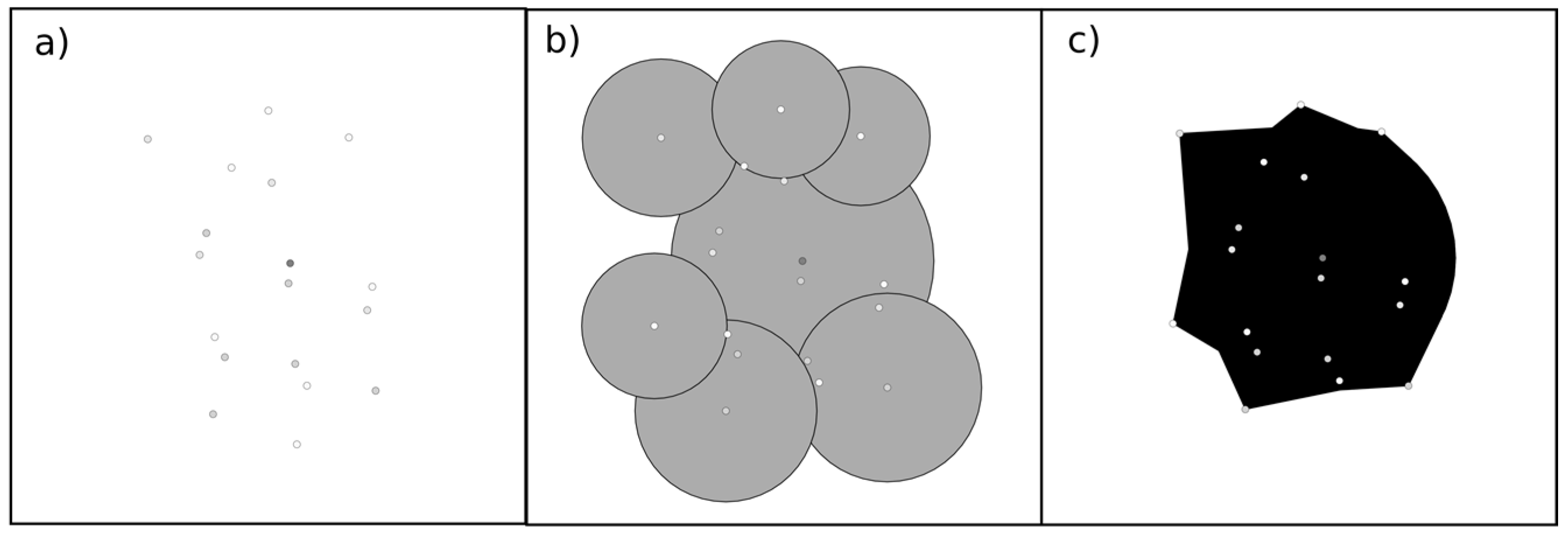
Many of the existing segmentation methods involve interpolation of the ALS point cloud to a raster or to a three-dimensional voxel space [
14]. However, such methods typically assume a choice of a fixed pixel—or voxel—size. This pixel size will be closely linked to the range of tree sizes which can be detected. A large pixel size will smooth out the information inherent in the ALS point cloud and therefore make the detection of small trees harder, whereas smaller pixels will likely cause over-segmentation of echoes from larger trees. With these existing methods one is, in practice, faced with a choice of detecting trees within a limited size range, through the choice of a fixed pixel size. The chosen pixel size and the level of smoothing applied will also determine the spatial extent of each segmented tree crown. The extent of the segmented tree crowns is typically represented by pixels, which could limit the ability to accurately represent the crown of small trees. We wanted a method that could detect trees ranging from small to medium in size, and rather than modifying any of the existing methods, we developed a simple and novel segmentation procedure. Thus, the proposed segmentation procedure was specifically tailored to the detection of small trees, with as few as only one laser echo. It should be noted that its area of application could be wider than just small trees in the forest-tundra ecotone, including, for example, the monitoring of seedlings in forest stands planted after final fellings in managed boreal forests, or the detection and monitoring of small trees in afforested areas in the tropics.
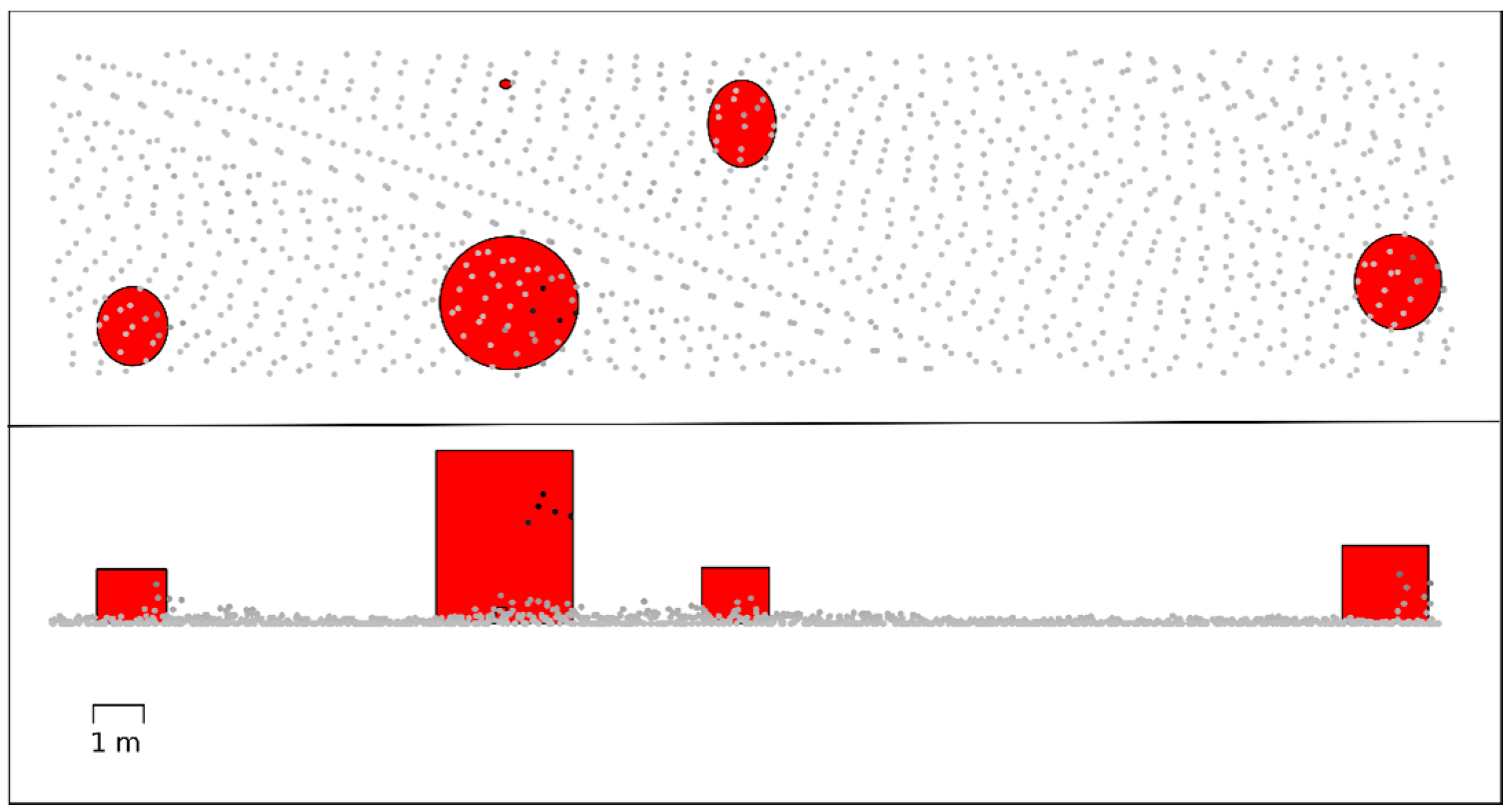
The objectives of the present study were (1) to develop a procedure for automatic detection and segmentation of small trees using ALS data and (2) to assess the accuracy of the method by comparing the results with field reference data. We consider small trees in this context to be trees with heights up to 7 m and crown diameters up to 6 m. We further wanted to assess the suitability for monitoring purposes by testing the stability of the method across two separate ALS acquisitions for the same study area.
4. Discussion
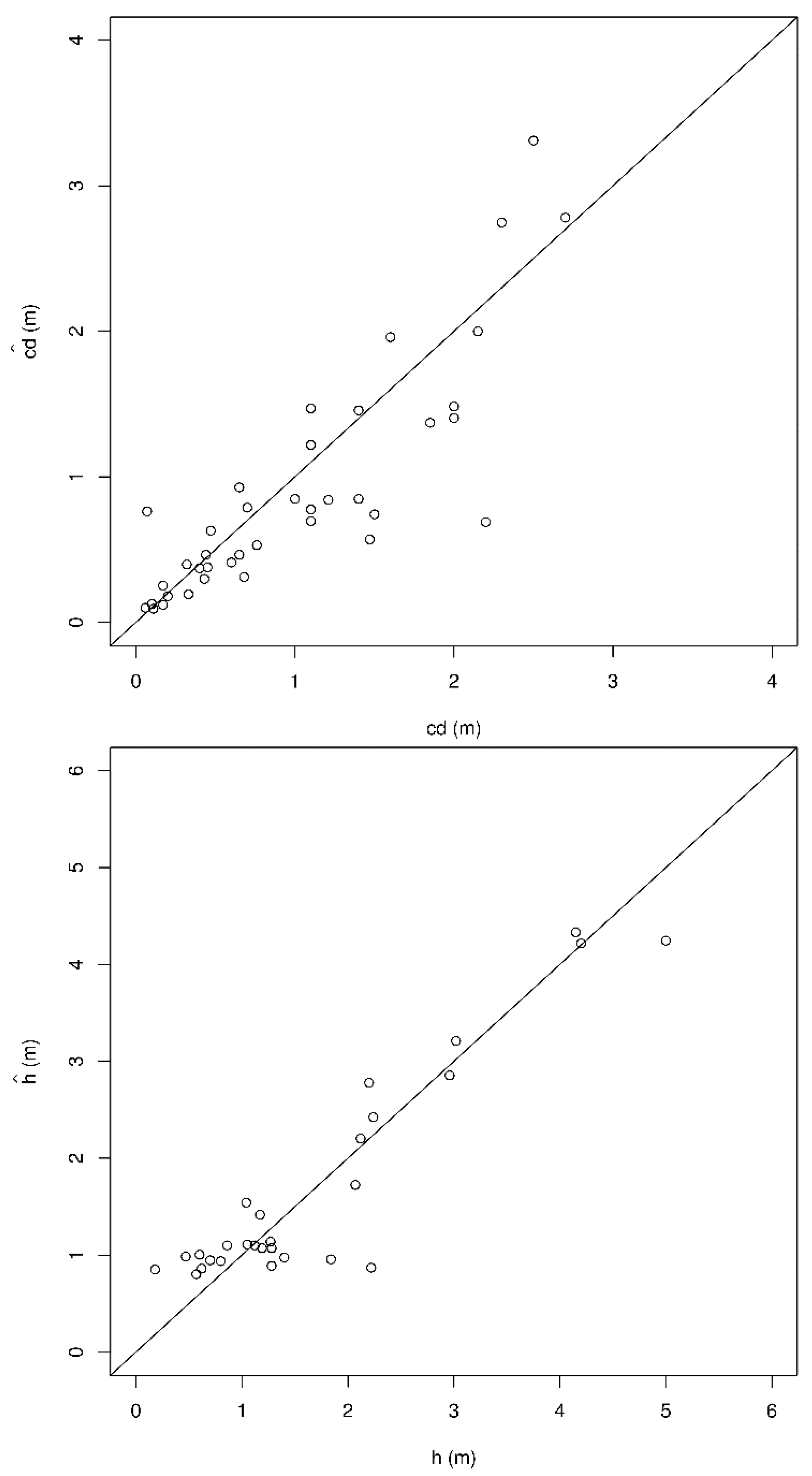
Over all the four height classes, 46.2% of the trees were correctly segmented by the proposed method. A higher proportion of the larger trees were correctly segmented and the detection rate decreased with the decreasing tree size. There are few directly comparable studies, since previous studies typically targeted trees that are larger than in the present study. Vauhkonen
et al. [
21] compared six single-tree detection algorithms in different types of mature forests. The average detection rates for the different forest types reported by Vauhkonen
et al. varied between 54% and 91%. These detection rates were, however, calculated using the plot-wise total number of tree segments in relation to the number of field-measured trees. They cannot be directly compared to the detection rates in the present study, which were calculated based on the linking field and ALS-derived trees. Vauhkonen
et al. report a corresponding number called “treetop candidates linked to field trees”, and this varied between 42% and 60%. The mean tree diameter at the different sites in the data material used by Vauhkonen
et al. was 18.5–35.8 cm, and the ALS point density was 1.5–30 per m
2. The detection rates observed for trees with
h < 1 m in the present study were considerably lower than the rates reported by Vauhkonen
et al. [
21]. These trees are, however, much smaller than any tree in the data material used in that study. For the trees with
h > 1 m, the proportion of detected field trees in the present study seems to be within the range reported in Vauhkonen
et al. [
21], as well as in recent studies by Liu
et al. [
26], and Mongus and Zalik [
27].
The advantage of the proposed method is that it is simple, and can be implemented using models developed from a limited number of sample trees. A disadvantage is the need for these sample trees, as well as the detection errors discussed in the following.
From the current study it is evident that direct detection of all individual trees by ALS is not possible when the properties of the ALS data are similar to those of the current study. Omission errors will occur, caused by two different factors: firstly, due to limitations in the data material itself; ALS can be viewed as measuring distances from the aircraft to the ground, with the distance to only some particular spots on the ground being acquired. In the present study the average density of laser pulses was eight pulses per m2, and given the footprint size together with the non-uniform spatial distribution of the laser pulses, this means that some trees will not be hit at all. The fraction of the trees that is not hit by any laser pulse will depend on a range of factors, such as the pulse density, the pulse footprint size and the degree of unevenness in the spatial distribution of the pulses on the ground. It is, however, clear that the size of a tree directly affects the probability for it to be hit by a laser pulse, so smaller trees are less likely to be hit than larger trees. The trees which are not hit by any laser pulses cannot be directly detected using the ALS data, and it is hence a definite limit to direct detection of individual trees inherent in the data material itself. There is, under such conditions, not enough information in the data material to directly detect all trees, and omission errors are unavoidable if all trees, even the smallest ones, are considered. The chance of being hit by a laser pulse increases with the tree size, but even an echo reflected from the tree is in itself not sufficient to ensure a successful detection. To be able to separate it from the surrounding terrain, the echo must have a positive above-ground height.
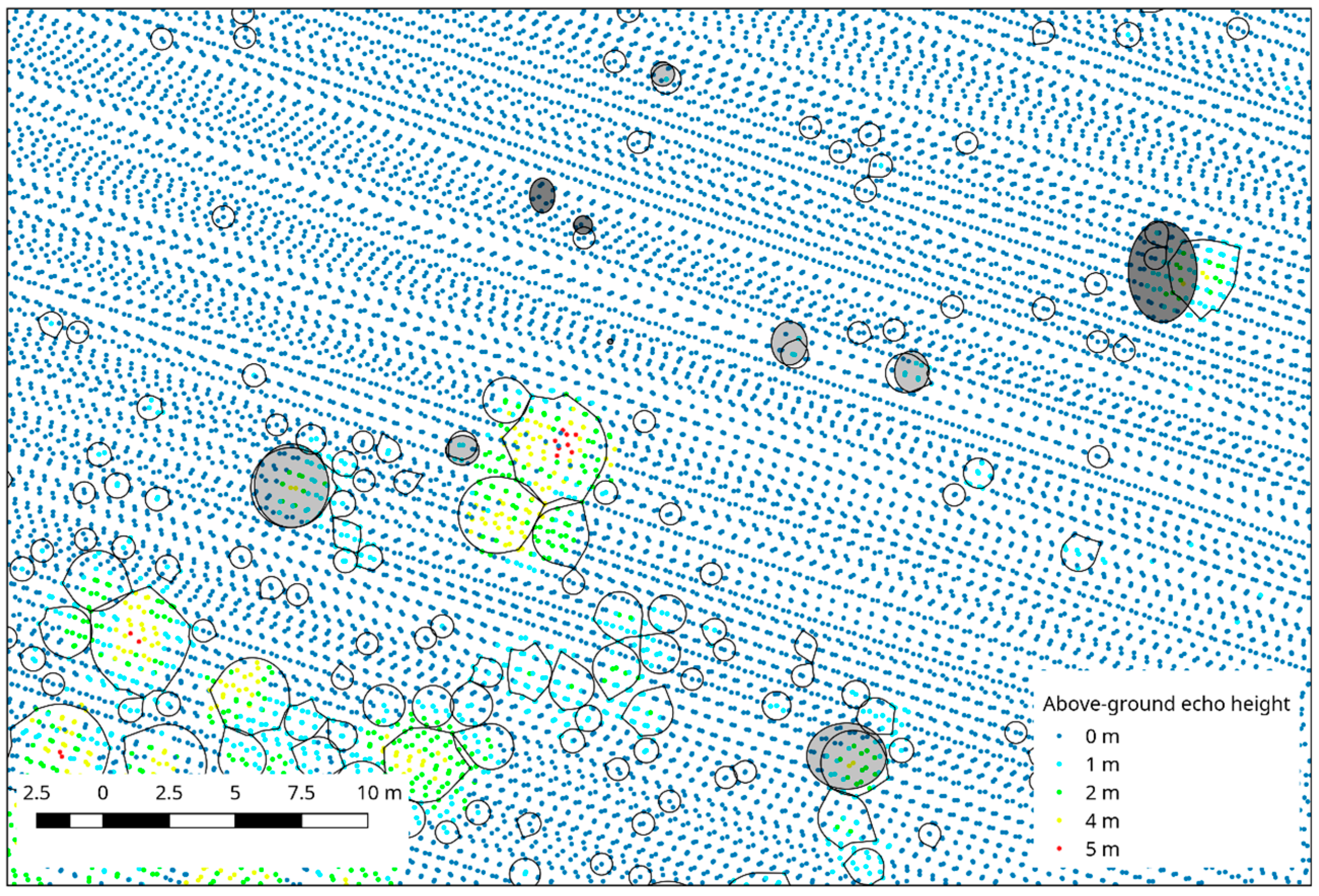
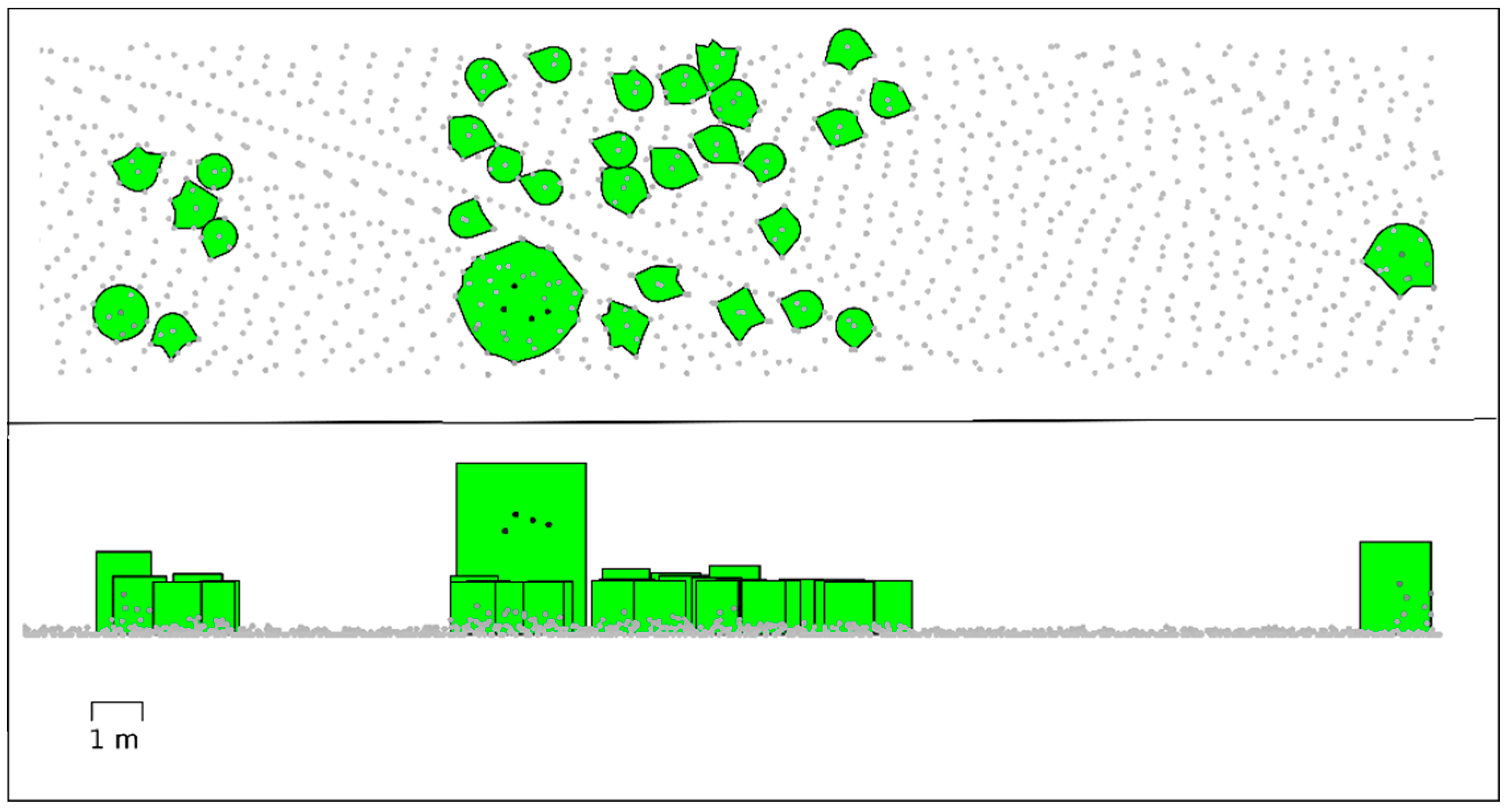
The second cause of omission errors is in the segmentation procedure, which in some cases will fail to produce a segment that matches that of the tree on the ground. This can be seen in
Figure 6, at the rightmost field-measured tree. The ALS-derived segment is, in this case, not similar enough to be considered a correct segmentation. The reason can be measurement errors, neighboring trees or other factors affecting how the echoes are being reflected from that particular tree. Segments from multiple trees can also be erroneously merged, and thus lead to omissions. How the procedure merges segments is controlled by the
s parameter, and this is discussed later in this section.
All echoes with a positive above-ground height will, however, not be reflected from trees, which is one out of two types of commission errors. Objects such as rocks, hummocks and bushes may all result in positive above-ground heights, and thus result in falsely detected trees. The intensity value of the echoes could, however, hold some information that can be used to distinguish between trees and the surrounding terrain and vegetation, and some studies have found a positive contribution from the intensity values when classifying tree and non-tree echoes [
7].
The second type of commission error is over-segmentation, which means detecting several trees from the echoes reflected from a single tree. Due to the design of the field work in which only a sample of the trees was measured, we were not able to fully assess these commission errors. The parameter s controls how the segmentation procedure merges initially overlapping segments, and the number of segments will increase as s increases. So with s = 1 all initial segments are kept as separate segments, whereas with s = 0 all overlapping segments are merged, i.e., no final segments overlap. Since tree crowns sometimes do overlap, a reasonable value of s should be somewhere between the two extremes. The detection rates in the present study varied, however, very little for the different tested values of s. This can be attributed to several factors, first of all that changing the value of s will only affect segments that initially overlapped. Furthermore, it is clear that the presence of small segments at the edge of larger segments does not have a large influence on either detection or omission errors. So even with some small segments overlapping, the larger segment will still be connected with the field tree. These small segments will, on the other hand, directly influence the commission errors, and this is the type of error we were unable to control in the present study. Further research is needed in order to find an optimal value for s, and to fully assess the commission errors. It should be noted that the study area, as well as other transition zones between forest and alpine areas, is, in parts, sparsely populated with trees. In more dense forests, a larger proportion of the trees will have overlapping crowns, which will affect the performance of the proposed segmentation procedure, as well as the optimal value of the s parameter.
The initial processing of ALS data for most applications related to forests or trees involves a choice of algorithms and corresponding parameter values. In the current study, this involves the echo classification as well as the computation of the above-ground heights. This choice of algorithm and parameter values will most likely influence further use of the data in, for example, single tree detection. The widely used classification algorithm based on the principles described by Axelsson [
18,
28] is used in the present study. This algorithm requires parameter values for “iteration angle” and “iteration distance”. The effect of the iteration angle on echoes reflected from small trees in the forest-tundra ecotone was investigated by Næsset [
3]. In that study, an increase in omission errors and a decrease in commission errors were observed when the iteration angle was increased from six to 12 degrees. A tree was, in that study, regarded as detected if it yielded at least one echo with a positive above-ground height, and the terms omission and commission error refer to that definition. A conclusive suggestion on an optimal iteration angle was, however, not given based on those results. The use of a model-chain as in the proposed algorithm will cause errors to propagate and add up through the chain. Errors in the allometric model given by Equation (2) will, for example, affect the results from applying the model given in Equation (1), and finally the resulting single-tree segments.
When evaluating single-tree detection algorithms, the obtained tree segments will deviate from the field measurements. The process of choosing and defining the detection criteria will inevitably involve subjectivity. The choice of detection criteria will affect the detection rates, and the effect of detection criteria should be incorporated in the evaluation of segmentation algorithms.
In the case of a change assessment in which an identical detection method is applied at two points in time, omission and commission errors should theoretically be of less consequence. Given that these errors occur with the same magnitude in each of the two segmentations, actual changes on the ground between two ALS acquisitions should lead to corresponding differences in the two sets of segmented trees. The stability of the ALS-derived variables plays a role in this case. The amount of variation that is due to the scanning and the segmentation process itself will determine the magnitude of the vegetation changes that can be reliably detected for a given area. The results from the present study indicate that for the proposed segmentation procedure, some variation must be expected for smaller areas. The magnitude of the changes that can be reliably detected using the proposed method could be further investigated. The spatial distribution of the laser echoes on the ground and in the vegetation will differ from one acquisition to another. We assessed, in the present study, the influence of these differences on the resulting single-tree segments by using two separate acquisitions from the same sensor. The use of different sensors in multi-temporal data acquisition will further contribute to differences between the two sets of data. Expected effects and possible calibration methods to mitigate these could be subject to further research.