Abstract
A new approach for three-dimensional (3-D) reconstruction of building roofs from airborne light detection and ranging (LiDAR) data is proposed, and it includes four steps. Building roof points are first extracted from LiDAR data by using the reversed iterative mathematic morphological (RIMM) algorithm and the density-based method. The corresponding relations between points and rooftop patches are then established through a smoothness strategy involving “seed point selection, patch growth, and patch smoothing.” Layer-connection points are then generated to represent a layer in the horizontal direction and to connect different layers in the vertical direction. Finally, by connecting neighboring layer-connection points, building models are constructed with the second level of detailed data. The key contributions of this approach are the use of layer-connection points and the smoothness strategy for building model reconstruction. Experimental results are analyzed from several aspects, namely, the correctness and completeness, deviation analysis of the reconstructed building roofs, and the influence of elevation to 3-D roof reconstruction. In the two experimental regions used in this paper, the completeness and correctness of the reconstructed rooftop patches were about 90% and 95%, respectively. For the deviation accuracy, the average deviation distance and standard deviation in the best case were 0.05 m and 0.18 m, respectively; and those in the worst case were 0.12 m and 0.25 m. The experimental results demonstrated promising correctness, completeness, and deviation accuracy with satisfactory 3-D building roof models.
1. Introduction
The three-dimensional (3-D) reconstruction of building models is an important means of obtaining 3-D structural information of urban scenes. Such reconstructions are applicable in fields such as urban planning, change detection research, and solar mapping [1,2,3]. The 3-D modeling solutions enable users to rapidly construct 3-D maps of surrounding areas that are suitable for professional visualization systems. As the most important and challenging task in digital city construction, the 3-D reconstruction of building models has received considerable attention over the past few decades [4,5]. Traditionally, photogrammetry is the primary approach used for deriving geo-spatial information, and it is implemented through the use of single or multiple optical images; often, aerial stereo images have been used for 3-D building model reconstruction. Some detailed reviews of the techniques for building reconstruction from aerial imagery have been published in the literature [6]. However, considerable manual assistance is required, which results in a low degree of automation.
Airborne light detection and ranging (LiDAR) technology has developed rapidly, and has been found useful for many applications in various fields [7,8,9,10]. In particular, airborne LiDAR technology presents a new avenue for the 3-D reconstruction of building models [11], and relevant methods have been reviewed in the literature [12]. Tomljenovic et al. [13] provided an overview of building extraction approaches applied to airborne LiDAR data from several aspects, such as dataset area, accuracy measures, reference data for accuracy assessment, and the use of auxiliary data. Presently, detailed 3-D information about the ground surface can be obtained by the airborne LiDAR equipment with a high degree of automation; however, the massive number of irregularly distributed points brings new challenges for the reconstruction work. Therefore, full utilization of the advantages of LiDAR points for high-quality building model reconstruction remains an important research topic.
Most previous approaches related to building model reconstruction with airborne LiDAR data can be divided into the following two categories: model-driven (parametric or top-down strategy) and data-driven (non-parametric or bottom-up strategy) methods. The benefits and drawbacks of the model- and data-driven methods have been discussed in a previous study [14]. In the model-driven methods, a predefined catalog of roof shapes is prescribed (e.g., flat, hip, gambrel). One of the advantages of model-driven methods is that the final roof shape is always topologically correct according to the predefined shapes. However, failure is possible when reconstructing complex building characteristics and building models that are excluded in the predefined shapes [12]. In addition, the level of detail in the reconstructed buildings is compromised as the input models usually consist of rectangular footprints and the current level of automation is comparatively low. In contrast to model-driven methods, data-driven approaches are more flexible and do not require prior knowledge, in which a building roof is reassembled from roof parts found by a segmentation algorithm. A challenging feature of these methods is to identify the relationship between the neighboring rooftop patches; for example, coplanar patches, intersection lines, or step edges between neighboring planes. The main advantage of these methods is that polyhedral buildings of arbitrary shape may be reconstructed [15]. The main drawback of data-driven methods is their susceptibility to the point density of the point clouds.
In the past studies, much of the work on the reconstruction of building models using airborne LiDAR data focuses on the extraction of rooftop contours [11,16]. Cheng et al. [17] combined airborne LiDAR data and optical remotely sensed images for the reconstruction of 3-D building models. They developed an integration mechanism that incorporates the segmented roof points and two-dimensional (2-D) lines extracted from optical multi-view aerial images to enable 3-D step line determination, from which 3-D roof models could be reconstructed. Similarly, Susaki [18] achieved 3-D building model reconstruction through a combination of airborne LiDAR data and high-spatial resolution aerial images. Verma et al. [19] introduced a new method for the detection and reconstruction of complex building models in which no a priori hypotheses are required; with this method, the topology of complex roof shapes is determined by using the roof-topology graph. Sohn et al. [20] used a binary space partitioning tree to reconstruct the global geometric topology of polyhedral buildings from adjacent linear features by using airborne LiDAR data. Zhang et al. [21] derived the building footprints through the combination of a region-growing algorithm and a boundary extraction method before building model reconstruction. Kada and McKinley [22] proposed an approach for decomposition of footprint with an additional generalization of the footprint. The building models were reconstructed by assembling building blocks from a library of parameterized standard shapes. Further, Vallet et al. [23] introduced an approach where the footprint decomposition is triggered by a digital surface model derived from the laser points. However, the reconstruction of 3-D building models with rooftop contours extracted from airborne LiDAR data is usually difficult. This is because the topological relationship between rooftop contours of different roof layers is difficult to confirm and, additionally, the extraction of rooftop contours is strongly affected by noise.
The extraction of rooftop patches, a prerequisite of plane-based methods, is another way to obtain building models from airborne LiDAR data. Common methods of extracting rooftop patches include the 3-D Hough transformation [24,25], the region growing technique [26,27], and application of the random sample consensus (RANSAC) algorithm [28,29]. Fan et al. [30] proposed the hierarchical decomposition of ridge lines for rooftop patch extraction. Awrangjeb and Fraser [31] classified original airborne LiDAR points into ground points and non-ground points. Coplanarity and local characteristics of each point were then used to segment the building rooftops from the non-ground points. Chen et al. [32] conducted a sequential process of morphological filtering, region growing, and adaptive RANSAC algorithm calculations to segment the rooftop points, whereas Kim and Shan [33] considered the optimization of an energy function and introduced a global segmentation strategy for rooftop patches that guaranteed the topological consistency of the extracted patches. Sampath and Shan [34] applied a fuzzy k-means algorithm to cluster the rooftop points to each patch and distinguished parallel and coplanar patches based on distance and connectivity. The 3-D building models were then obtained by using an adjacency matrix. Although the rooftop patches can be segmented well by using the above mentioned methods, the patches are not fit to construct 3-D building models directly. This is because the airborne LiDAR points representing these rooftop patches are usually irregularly distributed. Therefore, some researchers considered combining the model- and data-driven methods to reconstruct building roofs from airborne LiDAR data. This hybrid approach, also known as the global strategy, exhibits both model- and data-driven characteristics. For example, Satari et al. [35] applied the data-driven method to reconstruct cardinal planes and the model-driven method to reconstruct dormers. Lafarge et al. [36] presented a structural approach for building reconstruction from a single DSM, which treats buildings as an assemblage of simple urban structures extracted from a library of 3D parametric blocks. The Gibbs model and the Bayesian decision approach were used to control the block assemblage and to find the optimal configuration of 3-D blocks. To reflect the orientation and placement similarities between planar elements in building structures, Zhou and Neumann [37] emphasized global regularity during the construction of planar rooftops. This approach improved the reliability of the final results and decreased the complexity of the building models. Similarly, Zhang et al. [38] proposed a novel method that represents building roofs by geometric primitives and constructs a cost function for the final 3-D model reconstruction. In addition, Chen et al. [39] used a multiscale grid method for the detection and reconstruction of building roofs from airborne LiDAR data. Although it is beneficial to the plane-based methods that LiDAR data provide a high density of 3-D points, the discrete and irregular distribution of these points may lead to low geometrical accuracy for building models. Especially, it is difficult to determine accurate boundaries and the connection relationships among roof faces with a height jump [34,40].
Here, we present a new point-based approach for 3-D reconstruction of building roofs from airborne LiDAR data. The overall idea is as follows.
1. Smoothness-oriented rooftop patch extraction. For airborne LiDAR points of buildings, rooftop patches are segmented by using a region growing approach. To reduce noise interference and eliminate the effect of irregularly- distributed points, the rooftop points are smoothed before the building roofs are reconstructed.
2. Determination of layer-connection points and calculations for building roof reconstruction. Layer-connection points are generated from a 2-D grid to guarantee consistency between the boundary footprints of different roof layers. Building roofs are then reconstructed by connecting neighboring layer-connection points. The generation of layer-connection points helps to establish the relationships among different rooftop patches effectively and efficiently.
2. Methodology
The proposed approach for 3-D building roof reconstruction from airborne LiDAR data consists of four steps. These four steps are as follows.
1. Preprocessing. Building rooftop points are extracted from airborne LiDAR data by using the reversed iterative mathematic morphological (RIMM) algorithm and the density-based method.
2. Smoothness-oriented rooftop patch extraction. A strategy of “seed point selection, patch growth, and patch smoothing” is introduced during the rooftop patch extraction to smooth the building rooftop points.
3. Generation of layer-connection points. Layer-connection points are generated from a 2-D grid, thus guaranteeing consistency between the boundary footprints of different roof layers.
4. Building model reconstruction. By connecting neighboring layer-connection points together, the building roofs are reconstructed.
2.1. Extraction of Building Rooftop Points
As a precondition for 3-D building roof reconstruction, building roof points need to be detected and extracted from airborne LiDAR data. We applied Cheng’s RIMM algorithm to extract the building points [41]. The RIMM method first employs a morphological opening operation, and this opening operation is iterated by gradually decreasing the window size at a fixed step length (3 m). The elevation difference between two adjacent iterations is then compared, and parts with elevation differences exceeding the minimum building height (3 m in this study) are regarded as building point clouds. However, in the detected building point clouds, there may be some dense tree points, and the tree points are removed by using a threshold roughness value (we set this to 0.8 m), i.e., the standard deviation of height values of LiDAR points. The algorithm has been described in detail in the literature [41].
Airborne laser scanners not only acquire the laser measurements from building roofs, but also obtain partial reflected pulses from building walls. Therefore, wall points still exist in the building point clouds obtained by the RIMM algorithm. In order to retain only the rooftop points, we used Awrangjeb’s method to remove wall points [42]. The experimental results demonstrated that the wall points were eliminated by this method effectively.
2.2. Smoothness-Oriented Rooftop Patch Segmentation
Once we have extracted the building roof LiDAR points from the raw data, the different rooftop patches must be determined, i.e., rooftop patches must be segmented. The segmentation process follows a strategy of seed point selection, patch growth, and patch smoothing.
2.2.1. Rooftop Patch Segmentation
The input for the rooftop patch segmentation algorithm was implemented based on the classified individual buildings, and for this, the region growing segmentation algorithm proposed by Sun and Salvaggio [26] was used in our study; this algorithm uses the point normals and their curvatures. First, the normal and curvature values of each LiDAR point are calculated and the point with the smallest curvature value is selected as the seed point. Within a small neighborhood of this seed point, the direction of the normal vector of any other point with the normal direction of this seed point are compared. If the directional difference is larger than a predetermined threshold, the point being examined does not belong to the group initiated by the seed point, and otherwise, it does. In those points that have been grouped together by the seed point, points with curvature values lower than a predetermined threshold are chosen as future seed points. The procedure is iteratively executed until all LiDAR points have been visited.
2.2.2. Smoothness-Oriented Rooftop Patch Optimization
Rooftop patch optimization involves (1) smoothing of the rooftop patch points and (2) eliminating the interference of omissive LiDAR points.
The red box in Figure 1a contains a number of protuberant points (i.e., a small number of points above a large rooftop patch); however, these protuberant points were not seen in the rooftop patch segmentation results (Figure 1b). If these protuberant points are directly discarded before building roof reconstruction, some holes will appear on the building roofs. As these points are usually distributed above the real rooftop patches, we set a distance threshold (2 m) to recognize them. After all the protuberant points have been found, they are projected to the corresponding segmented rooftop patch by using the plane equation calculated by the RANSAC algorithm [29].
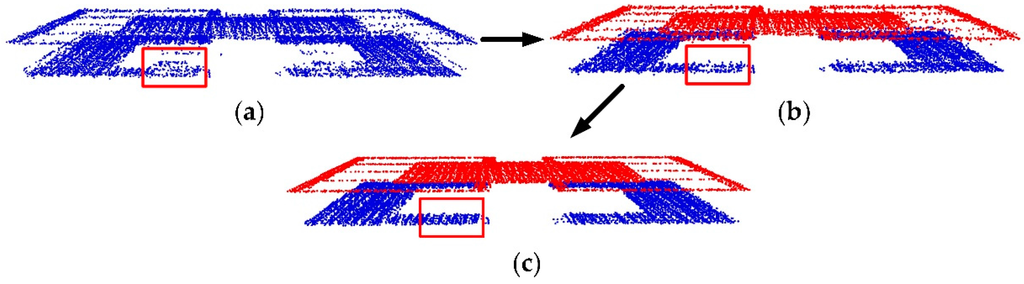
Figure 1.
Smoothing of building rooftop points: (a) original points; (b) segmented points; and (c) smoothed points.
Furthermore, even if such points belong to the same rooftop patch, they may not be precisely distributed on the same plane. Hence, a smoothing operation must be conducted prior to the building roofs being reconstructed. Here, for each segmented rooftop patch, the RANSAC algorithm was applied to fit a virtual plane from the candidate points, and then the points were forced to move on to this estimated plane in order to assign a perfect flatness property to each surface. The smoothing procedures described above were conducted iteratively for all rooftop patches. Figure 1c illustrates the point clouds after smoothing.
2.3. Generation of Layer-Connection Points
According to the derived rooftop patches, contour-based approaches are usually used for the reconstruction of 3-D building roofs. However, some major flaws impede the use of 3-D contours in building model reconstruction. These limitations are as follows: (1) the fitting of 3-D contours is strongly affected by noise; (2) the extraction of 3-D contours demands a large number of points, so the 3-D contours may be broken when not enough points are provided; and (3) the topological relationships of 3-D contours among different roof layers are difficult to confirm.
Therefore, a point-based method for 3-D building roof reconstruction is proposed here. The core objective of this method is to generate points to represent and connect roof layers (see Figure 2), which are named as layer-connection points, for a building rooftop. Layer-connection points have two purposes, namely, to represent a roof layer in the horizontal direction and to connect different roof layers in the vertical direction. In the horizontal direction, as shown in Figure 2a,b, yellow points represent the first layer (ground), blue points represent the second layer, and red points represent the third layer. These points with different colors are defined as layer-points. In the vertical direction, as shown in Figure 2c, a yellow point and red point form a line to connect the corresponding local region of the first layer and the third layer. These two layer-points, which have the same x–y coordinates but different z values, as a whole, are called a layer-connection point. Similarly, in Figure 2d, a yellow point and blue point form a line to connect the first layer and the second layer. Moreover, in Figure 2e, a yellow point, blue point, and red point form a line to connect the first layer, the second layer, and the third layer. These three layer-points, as a whole, are also called a layer-connection point.
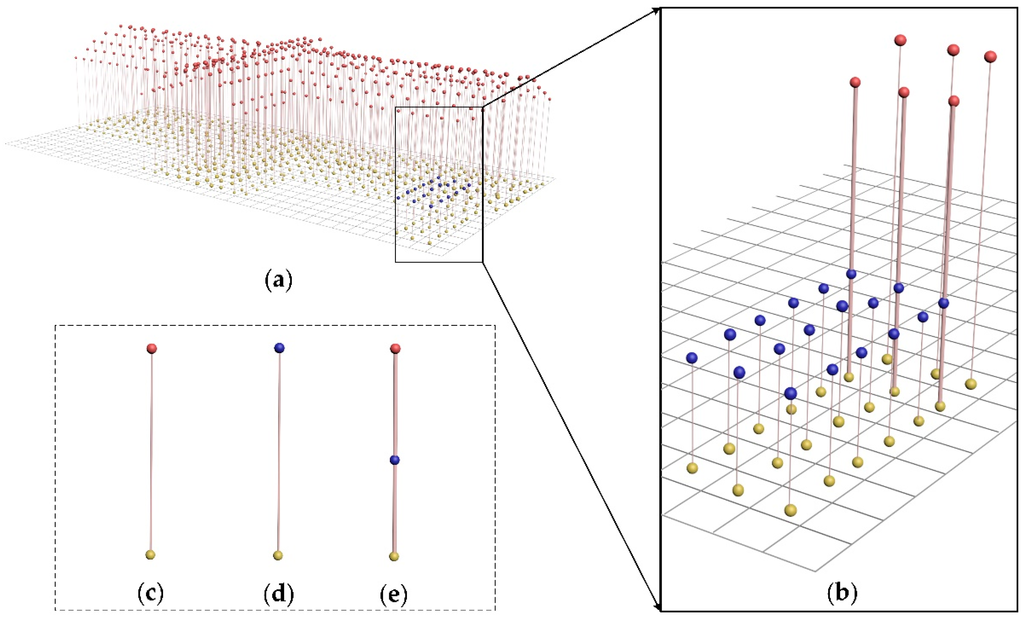
Figure 2.
An example of layer-connection points: (a) yellow points represent the first layer (ground), blue points represent the second layer, and red points represent the third layer; (b) an enlarged view; (c); (d) lines to connect points from two layers; and (e) line to connect points from three layers.
Before calculation of layer-connection points, we need to merge the rooftop patches into several roof layers. First, we give a clear definition of the roof layer. A roof layer is defined as being made up of several rooftop patches, which are adjacent and intersected with one another. For example, in Figure 2a, the red points represent the third layer, but the layer has four different rooftop patches, and, therefore, the four rooftop patches should be merged into a roof layer. Airborne LiDAR points corresponding to different rooftop patches are used as source data for merging. Here, we first introduce the principles for merging rooftop patches. The principles include whether there is an intersection line and an adjacent relationship between two rooftop patches. For example, in Figure 3a, there are two rooftop patches, i.e., S1 (red points in Figure 3a) and S2 (yellow points in Figure 3a). When S1 and S2 have an intersection line (blue line in Figure 3a), and the two rooftop patches have an adjacent relationship, they can be merged into the same roof layer. After the completion of judgments for all rooftop patches in accordance with the above principles, we can obtain the final merging results, as illustrated in Figure 3b. After the merging of rooftop patches, the layer-connection points can be calculated.

Figure 3.
Example of merging rooftop patches into a layer. (a) Points with different colors represent different rooftop patches; the blue line represents the intersection line between S1 and S2; and (b) red points and blue points represent a roof layer.
2.3.1. Construction of the 2-D Grid System
Before calculating the layer-connection points, we need to create a 2-D grid system. Thus, the scale and grid cell size of the 2-D grid system need to be determined. The scale of the grid system is set according to the maximum and minimum values of the point clouds in the X and Y directions. To guarantee that a reasonable number of points lie inside each grid cell, the grid cell size is set to 2–3 times the average point spacing (we set it to 1.0 m in this study). The grid cells record the serial numbers of each LiDAR point within them, and a cell with no points is said to be empty. For each LiDAR point, we record the row and column number of its corresponding cell to construct a two-way index. The index of a point with coordinates (x, y, z) can be obtained from the following formula:
where i and j represent the number of row and column of a grid cell, respectively, (xmin, ymin) represents the minimum coordinates of the building points, and Gridsize represents the size of a grid cell.
2.3.2. Calculation of Layer-Connection Points
During the calculation of layer-connection points, a center cell and its neighboring four cells are taken into consideration. Aforementioned layer results are used to determine whether the LiDAR points in the neighboring four cells are on the same roof layer with that in the center cell. There are five potential situations.
In the first situation, as illustrated in Figure 4a, where all LiDAR points belong to the same roof layer, the center cell (red box in Figure 4a) does not contain any connections between different roof layers. In this situation, the cell will only generate a layer-point for the layer connection. The coordinates of this cell’s center (blue rectangle in Figure 4a) are set as the x–y coordinates of this layer-point, and the average height value of all LiDAR points inside the center cell is set as its height.
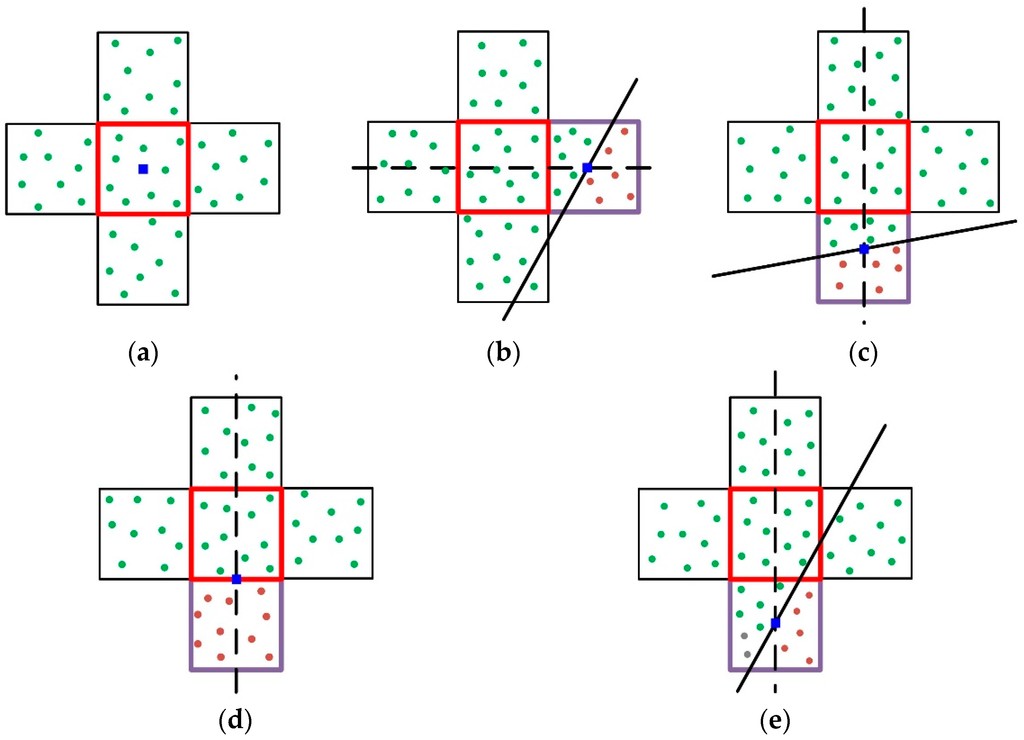
Figure 4.
Calculation of layer-connection points, points with different colors representing different roof layers, and the blue rectangle representing the x–y coordinates of the derived layer-connection point: (a) the points inside the five cells belonging to the same roof layer; and (b), (c), (d), (e) the points inside the five cells belonging to different roof layers.
In the second situation, as illustrated in Figure 4b, where the LiDAR points inside the center cell and four neighboring cells do not belong to the same roof layer, the violet cell may contain connections between different roof layers. A line splitting different roof layers can be calculated on which a point to connect different layers can be located. If the cell (violet box in Figure 4b) with LiDAR points from different roof layers lies to the left or right of the center cell (red box in Figure 4b), a black dotted horizontal line is generated to intersect the splitting line (black solid line in Figure 4b). The point of intersection (blue rectangle in Figure 4b) is taken as the x–y coordinates of the layer-connection point. Simultaneously, the cell containing the planimetric coordinates of the intersection point is confirmed and the LiDAR points in it are selected. Based on these points, height values of each layer-point are determined by the average height of the LiDAR points of the corresponding roof layer.
In the third situation, as illustrated in Figure 4c, if the cell (violet box in Figure 4c) with LiDAR points from different roof layers lies above or below the center cell (red box in Figure 4c), a black dotted vertical line is generated to intersect with the splitting line (black solid line in Figure 4c). The point of intersection (blue rectangle in Figure 4c) gives the x–y coordinates of the layer-connection point. Similarly, the cell containing the planimetric coordinates of the intersection point is confirmed and height values of each layer-point is determined by the average height of the LiDAR points of the corresponding roof layer.
In the fourth situation, as illustrated in Figure 4d, if the x–y coordinates of the layer-connection point are exactly on the boundary of the center cell (red box in Figure 4d), a black dotted vertical line intersecting the boundary gives the x–y coordinates of the layer-connection point (blue rectangle in Figure 4d). Again, height values of each layer-point are set according to the average height value of the LiDAR points (red and violet cells) of the corresponding roof layer.
In the fifth situation, as illustrated in Figure 4e, if the LiDAR points inside a cell (violet box in Figure 4e) come from more than two roof layers, the number of points from each roof layer is counted, and only two major groups of points are used to determine the x–y coordinates. The subsequent calculations are the same as those used in situation two, three, or four.
2.3.3. Optimization of Layer-Connection Points
There are a number of layer-connection points distributed along building contours. If these layer-connection points are directly connected, a series of zigzag contours will be produced. Thus, the layer-connection points along building contours need to be smoothed. We applied Zhou’s method [43], in which the principal orientations are derived from boundary points, and the points are iteratively fitted to a line running along the principal orientations.
2.4. Building Model Reconstruction
Figure 5a shows a sample of the layer-connection points generated by the proposed approach. As shown in Figure 5a, a building model can be obtained by connecting neighboring layer-connection points.
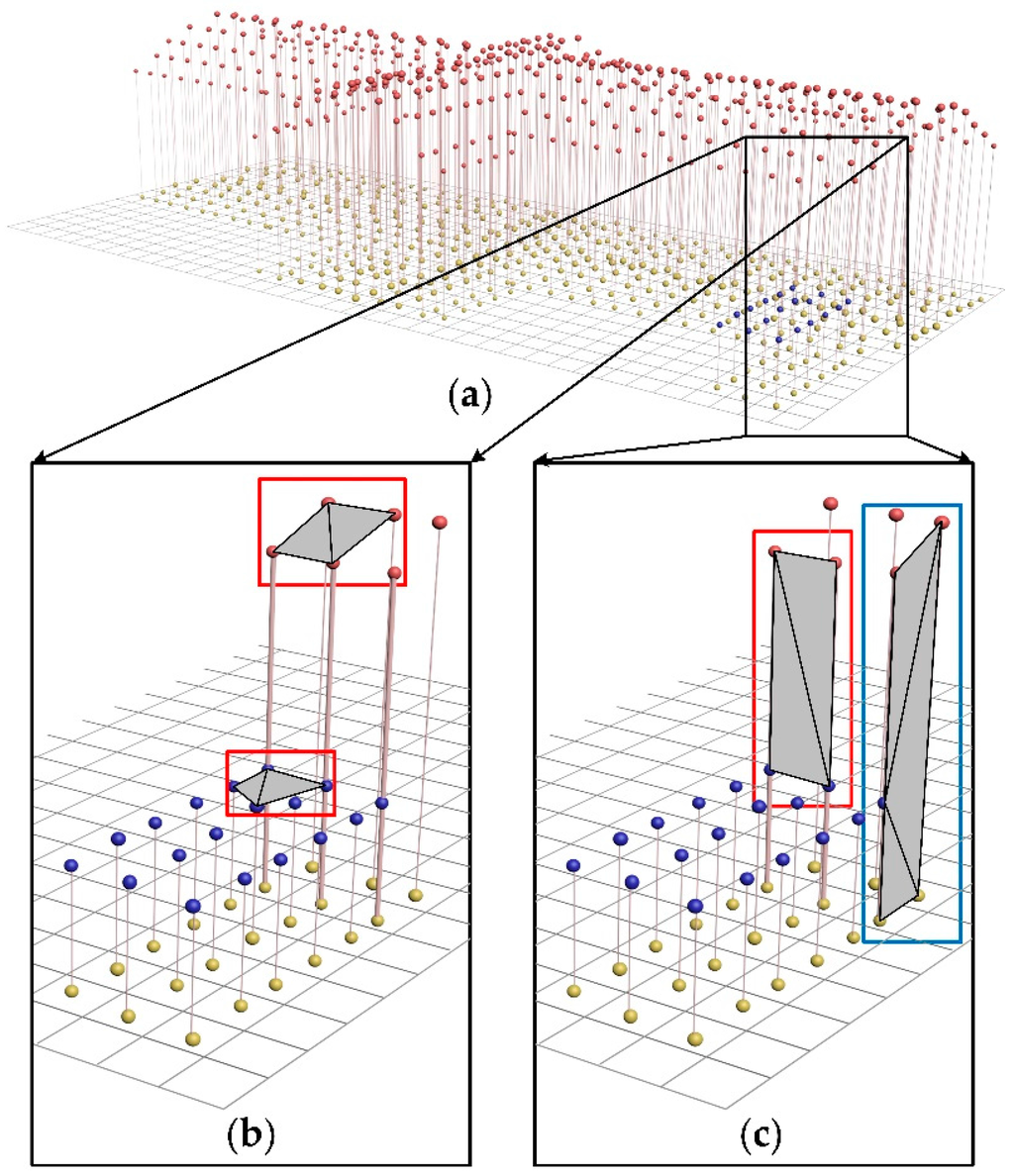
Figure 5.
An example of building model reconstruction: (a) layer-connection points; (b) rooftop construction; and (c) wall construction.
For building roof reconstruction, the three neighboring cells should be searched, which correspond to three layer-connection points. If the layer-points of the layer-connection points inside the three neighboring cells are located on the same roof layer, these layer-points are connected to construct a triangle mesh (red box in Figure 5b). By traversing all of the cells, the construction of rooftops can be completed.
This paper only focuses on building roof reconstruction. Therefore, building walls are replaced with vertical planes. A similar operation is performed to construct the building walls. Briefly, layer-connection points including multiple layer-points inside neighboring or diagonally adjacent cells indicate the existence of a building wall. By connecting the layer-points belonging to different roof layers (red box in Figure 5c), this building wall can be obtained. In addition, the layer-connection points located on the boundary of a building must be connected to enable the construction of whole building walls (blue box in Figure 5c).
2.5. Sensitivity Analysis of the Key Parameters
Given that a few parameters were used in this study, a summary of the setting procedures used for the associated key thresholds is necessary. The setting basis of these thresholds involved two types of information; namely, the data source and empirical results. The term “data source” means that a threshold is set according to the real data. If this method is applied to some other 3-D building model reconstruction, the “data source” thresholds can be determined easily, which increases the applicability of the proposed method. The term “empirical” means that the thresholds are set empirically, and in most cases, they can be set directly as we have proposed here.
During the process of extracting building rooftop points, the RIMM algorithm is employed. The parameters used during this step are shown in Table 1. The initial window size Iw and the height difference Th were set according to the data source, and these values usually refer to the length of the largest building (106 m) and the height of the lowest building (3 m) in the experimental area, respectively. The fixed step length Lc, and roughness value Rv were, respectively, set to 3 m and 0.8 m, empirically. Two sets of different values (in meters) were tested while setting the values for the two parameters Lc and Rv. For Lc the test values were 1, 3, 5, 7 m; for Rv the test values were 0.4, 0.6, 0.8, 1.0, and 1.2 m. According to the completeness and correctness of the segmented rooftop patches, we found that the smaller Lc and the larger Rv could lead to that the extracted building point clouds contained some tree LiDAR points. Conversely, there could be some missing building points if Lc was too large and Rv was too small. The optimal extraction results were observed at Lc = 3 m and Rv = 0.8 m.

Table 1.
Key parameters in the proposed approach.
In the process of smoothness-oriented rooftop patch segmentation, an extraction method based on region growth and rooftop patch optimization is used. The key parameters are shown in Table 1. As we can see, all parameters used in this step can be set empirically. The search radius Rs and the number of inner points N are related to the input LiDAR data. To guarantee that there were more than ten points to calculate the normal of each LiDAR point, Rs is suitable for 2–3 times average of point spacing. Elaborate consideration was given to the value of N as follows. We assumed that the area of a minimum rooftop patch that could be detected was 4 m2, i.e., 2 m × 2 m. According to the point density of LiDAR data, a threshold for N can then be calculated easily. The distance threshold Td were set to 0.2, 0.3, 0.4, 0.5, and 0.6 m to find the optimal value. In the process of patch optimization, the phenomenon of over-smoothing will be occurred, if Td is set too large. At Td = 0.5 m the effect of smoothing is moderate. The probability is a minimum probability of finding at least one good set of observations in all iterative procedures. It usually lies between 0.90 and 0.99. In our experiments, the probability was set to 0.98. During the generation of layer-connection points, a grid-based method is introduced, and the cell size is set empirically.
3. Experiments and Analysis
3.1. Experimental Data
The airborne LiDAR data used in this paper were collected over Nanjing City, China, by using an Optech ALTM Gemini laser scanning system from a flying altitude of about 1000 m on 26 November 2011. The average point density was about 10 points per m2, its average point spacing is about 0.25 m, and data had a vertical accuracy of 0.15 m and a horizontal accuracy of 0.20 m. We used the campus of Nanjing University, China, as the experimental Region 1 (Figure 6); this region covered an area of about 900 m × 500 m and contained 4.2 million LiDAR points. Figure 6a,b shows the aerial orthophotos with 0.3 m resolution and the LiDAR data from a side view, respectively. Figure 6c shows no-data areas where very sparse LiDAR points (one point in 30 m2) were collected as a result of the particular color and special structures of the corresponding building tops. The buildings in these no-data areas were not involved in the 3-D reconstruction process. The experimental Region 2 (Figure 7) was a residential area in the Jianye district, Nanjing City, China; this region covered an area of about 900 m × 600 m and contained 4.5 million LiDAR points. Figure 7a,b shows the aerial orthophotos and the LiDAR data, respectively. There were many buildings with various sizes and spatial distributions in Region 2.
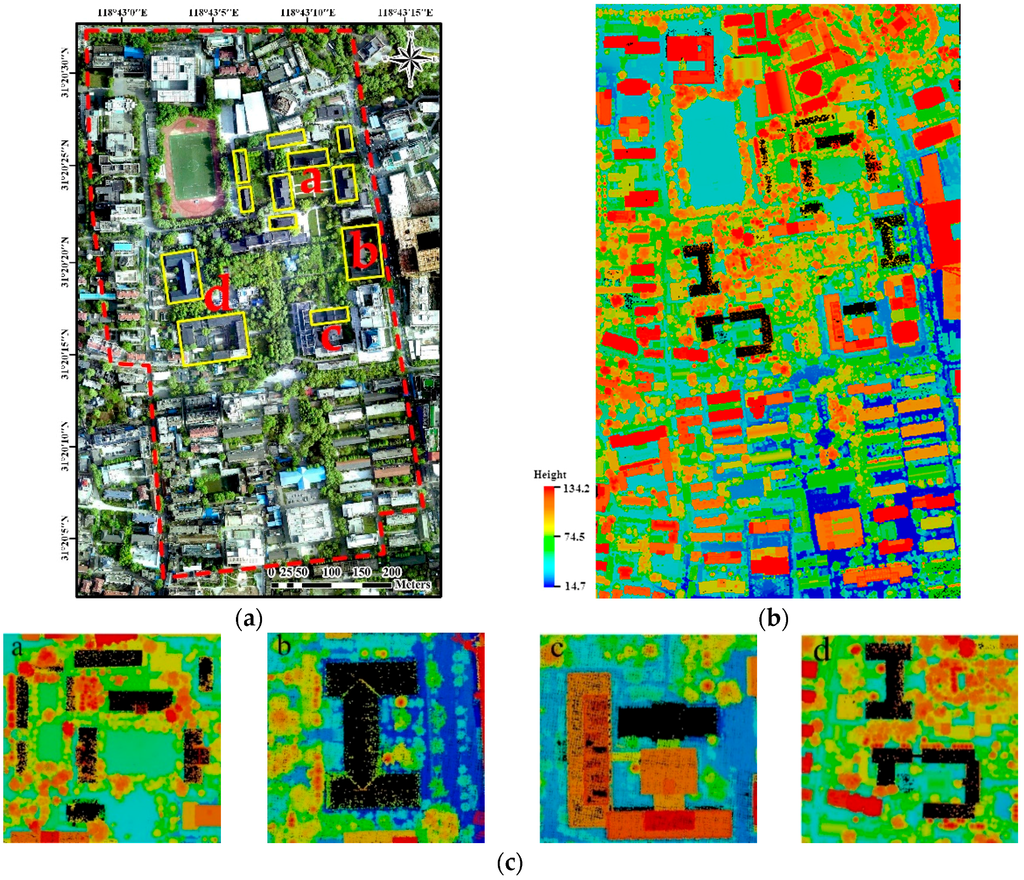
Figure 6.
Experimental Region 1: (a) aerial orthophotos with 0.3 m resolution (no-data areas are shown by yellow boxes); (b) airborne LiDAR data; and(c) no-data areas (black), corresponding the yellow boxes in (a) with letters.

Figure 7.
Experimental Region 2: (a) aerial orthophotos with 0.3 m resolution; and (b) airborne LiDAR data.
3.2. Experimental Results
Figure 8a and Figure 9a demonstrate the reconstructed 3-D building roof models in Regions 1 and 2, respectively. Details of the roof models in Region 1 can be seen in Figure 8b–d. Several building models were selected to illustrate the details of the roofs in Region 2 (see Figure 9b–d). In Figure 8 and Figure 9, the building roofs with different structures, different directions, and different levels of complexity were well-built and the results were satisfactory.
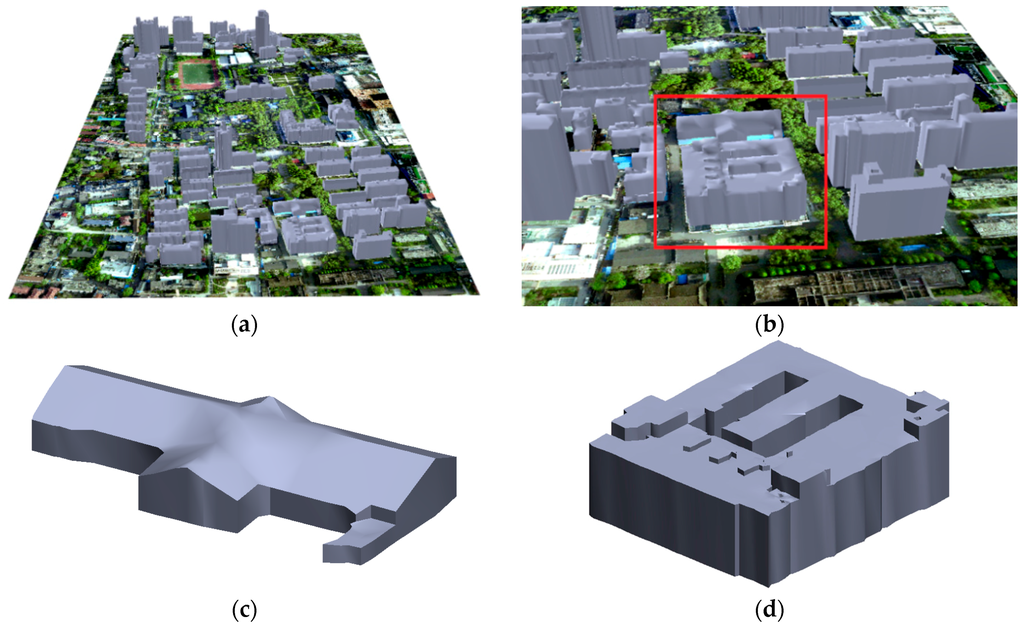
Figure 8.
Reconstruction results in Region 1: (a) an overview; (b) a side view of the local reconstructed roof models; and (c) and (d), building roof models for the red box in (b).
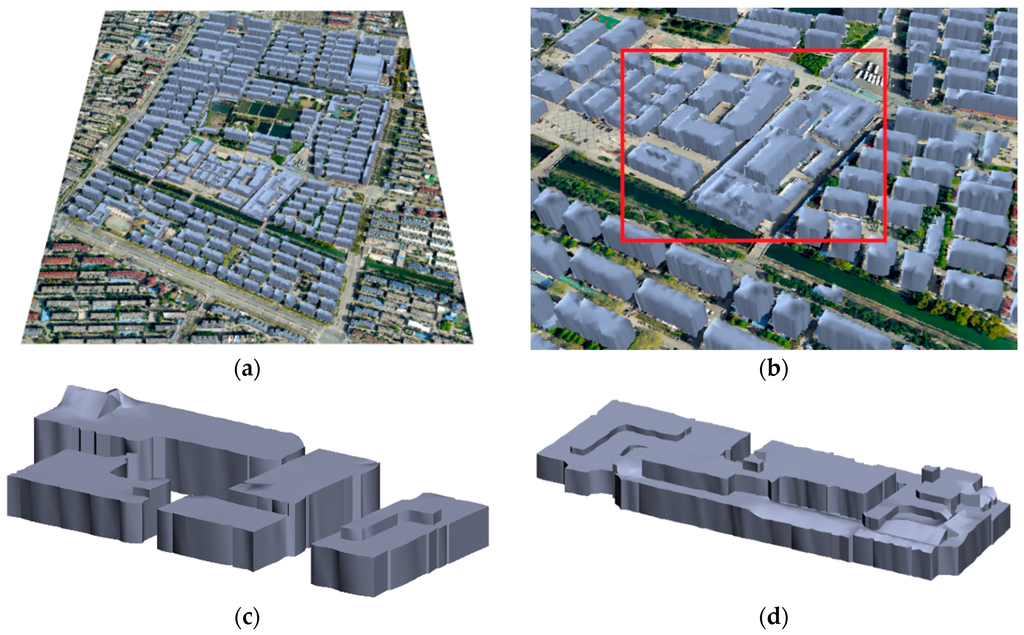
Figure 9.
Reconstruction results in Region 2: (a) an overview; (b) a side view of the local reconstructed roof models; and (c) and (d), building roof models for the red box in (b).
3.3. Experimental Analysis
Evaluation of the experimental results was conducted according to (1) correctness and completeness of the reconstruction results and (2) deviation distances between model points and their nearest points in the laser data. These assessment criteria have been widely used in previous studies to analyze the reconstruction performance of building models [39,44,45,46].
3.3.1. Correctness and Completeness
This section employs the correctness and completeness information to quantitatively evaluate the quality of the 3-D reconstructions. The LiDAR point clouds, which contain building points, and the aerial orthophotos were used as reference data. Here, the unit of evaluation were the rooftop patches of the buildings. The rooftop patches in the reference data were extracted manually according to the airborne LiDAR building point clouds and aerial orthophotos. When the area of a rooftop patch was more than 2 m, the rooftop patch was determined and extracted. The correctness and completeness of the experimental results were evaluated from two aspects; namely, the number of rooftop patches (called the number evaluation) and the area of rooftop patches (called the area evaluation). For the aspect of number evaluation, the reconstructed results and the reference data were then put together as follows: (1) overlaid rooftop patches, in which the ratio of the overlapping area was more than 80%, were taken as correct reconstructions; (2) rooftop patches only existing in the reference data were taken as missing reconstructions; and (3) rooftop patches only existing in the reconstructed results, or rooftop patches whose ratios of the overlapping areas were less than 20%, were taken as wrong reconstructions. For the aspect of area evaluation, the accuracy is computed by the accumulated statistics on the correct, missing, and wrong areas of the reconstructed rooftop patches.
where TP (true positives) represents the number or area of correct reconstructions for rooftop patches, FN (false negatives) represents the number or area of missing reconstructions for rooftop patches, and FP (false positives) represents the number or area of wrong reconstructions for rooftop patches.
Table 2 lists the detailed evaluation values. The evaluation results demonstrate that the proposed method has high correctness and completeness. In regards to the number evaluation, the completeness and correctness of Region 1 were 89.39% and 97.12%, respectively, and the completeness and correctness of Region 2 were 90.37% and 95.42%, respectively. In regards to the area evaluation, the completeness and correctness of Region 1 were 90.64% and 97.19%, respectively, and the completeness and correctness of Region 2 were 91.85% and 93.26%, respectively. As can be seen from the results of the experimental evaluation, the correctness was higher than the completeness. This was mainly due to the use of a point-based method in the proposed approach whereby it is difficult to produce erroneous commissions. The missing building rooftop patches were mainly caused by the fact that some small building rooftop patches were not extracted during the process of segmentation because the number of LiDAR points representing them was less than the pre-set threshold.

Table 2.
Correctness and completeness of the reconstructed buildings’ rooftop patches.
3.3.2. Deviation Analysis of the Reconstructed Building Roofs
The deviation analysis of the reconstructed building roofs was performed by calculating the deviation distances between the reconstructed building roofs and the corresponding airborne LiDAR data. The airborne LiDAR points of buildings were used as reference data for the quantitative evaluation of the reconstructed building roofs’ accuracy. In the reconstructed building model M, we selected a point Ri from reference data R and searched for the most neighboring triangular polygon Mi by using a method that has been described previously in the literature [47]. Then, the deviation distance between each LiDAR point and its corresponding patch was calculated. The statistical results of the deviation distances for Regions 1 and 2 were computed based on the validation point set (as shown in Figure 10a,b).
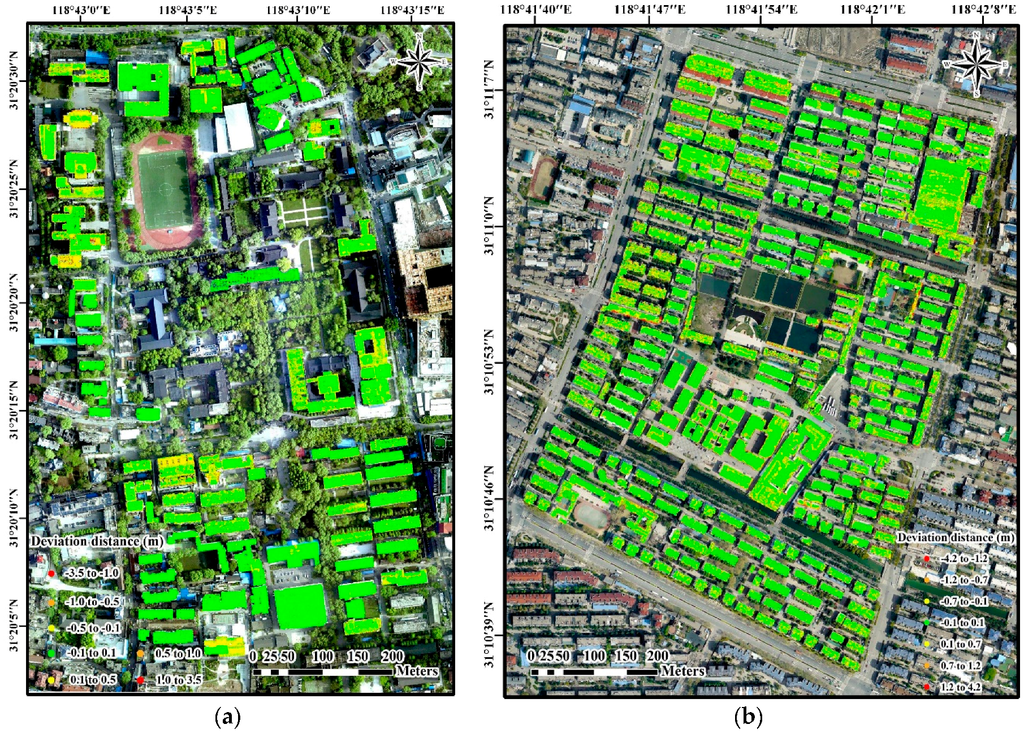
Figure 10.
Deviation distances between the reconstructed building roof models and the LiDAR-derived validation data, as represented by points with different colors: (a), (b) Region 1 and Region 2, respectively.
Table 3 lists the statistical results of the deviation analysis for Regions 1 and 2. The average deviation distance and standard deviation (abbreviated as Std. Dev. in Table 3) of all reconstructed building roofs in Region 1 were 0.05 m and 0.18 m, respectively. The average deviation distance and standard deviation of all roofs in Region 2 were 0.12 m and 0.25 m, respectively. Compared with Region 1, Region 2 had a larger average deviation distance and a higher standard deviation, which was due to the fact that the roof structures of residential buildings were irregular and contained some small objects. Overall, the evaluation results demonstrated that the reconstructed building roofs were well matched with the reference data. Certainly, the deviation distances were mainly concentrated at the average value. For example, in Region 1, about 96.61% points of the deviation distances are distributed in the range from 0 to 0.3 m, and in Region 2, about 93.28% of the points are distributed in the range from 0 to 0.3 m. The points with large deviation distances were mainly distributed in the contour regions of buildings or in air conditioning and chimney areas.

Table 3.
Deviation distances of the reconstructed building roofs.
3.3.3. Influence of Elevation to 3-D Roof Reconstruction
This study also analyzed the influence of elevation on the reconstructed building roofs. First, the airborne LiDAR points of buildings were divided into different groups according to the elevation value (the elevation interval was set to 1 m). Afterward, we calculated the deviation distance under each elevation range. The statistical results of Regions 1 and 2 are shown in Figure 11a,b, where the solid squares in the figures represent the average values of the deviation distances under each elevation range and the error bars represent the positive and negative deviations of each average value. From Figure 11a,b, we can draw some conclusions. First, most of the average values of the deviation distances were located in the range from −0.05 m to 0.05 m. Second, in regards to different ranges of elevations, when the elevation was more than the height of a specific value (80 m in Region 1; 37 m in Region 2), fluctuations of the average values and standard deviations were larger than those where the elevation was less than a specific value (70 m in Region 1; 33 m in Region 2). The reason for this phenomenon is that for modern high-rise buildings, there are many central air conditioning units on the building roofs, but there are not reflected in the reconstructed building roofs. Therefore, the average values and standard deviations are more sensitive to the presence of modern high-rise buildings.

Figure 11.
Evaluation of the building roofs’ deviations under different elevations, where the solid squares in the figures represent the average values of the deviation distances under each elevation range, and the error bars represent the positive and negative deviations of each average value: (a), (b) Region 1 and Region 2, respectively.
3.4. Experimental Discussion
To further verify the effectiveness and reliability of the proposed method, several analysis processes were conducted from two aspects of evaluation from the ISPRS test project and comparison with other methods.
3.4.1. Evaluation from the ISPRS Test Project
The ISPRS benchmark test on urban object detection and reconstruction offers a unique possibility to compare state-of-the-art methods [48,49]. Therefore, we used the test data provided by the ISPRS benchmark test to evaluate the proposed method. The airborne LiDAR data for Vaihingen Areas 1, 2, and 3 were selected. The focus of the evaluation is on the quality of the roof plane segmentation and on the geometrical accuracy of the roof polygons. The properties of datasets and the evaluation metrics have been described in literature [48,50]. For the purpose of comparison with the state-of-the-art methods, six different approaches from the ISPRS test project were selected [16,20,51,52,53], and the overview of these methods is showed in Table 4, in which the proposed method is abbreviated as NUC.

Table 4.
Overview of the reconstruction methods. ID: Identifier of the method used in this paper. Researcher/Affiliation: name and affiliation of the person submitting the results. Reference: a reference where the method is described.
The evaluation of the building reconstruction results for Vaihingen Areas 1–3 are summarized in Table 5. The quality metrics are explained in literature [48]. For Area 1, the completeness and the correctness of the extracted roof planes by using the proposed method were 73.6% and 99.2%, respectively; the completeness and the correctness of the roof planes covering an area of at least 10 m2 were 75.5% and 99.0%, respectively. For Area 2, the completeness and the correctness of the extracted roof planes by using the proposed method were 71.0% and 100.0%, respectively; the completeness and the correctness of the roof planes covering an area of at least 10 m2 were 89.6% and 100.0%, respectively. For Area 3, the completeness and the correctness of the extracted roof planes were 74.9% and 100.0%, respectively; the completeness and the correctness of the roof planes covering an area of at least 10 m2 were 85.5% and 100.0%, respectively. Although there was a clear difference between the quality metrics for all planes and for roof planes larger than 10 m2, the reconstruction quality of the proposed method could reach about or above the average accuracy of the six state-of-the-art methods. In addition, the geometrical errors (RMS, RMSZ) caused by the proposed approach were also in the range of the six previous methods. Therefore, the proposed method produced a good reconstructions for Areas 1–3.

Table 5.
Evaluation of building reconstruction results in Areas 1, 2, and 3. The best values per column are printed in bold font.
Compared to Area 2, Areas 1 and 3 was more difficult to reconstruct roofs because various buildings with gabled roofs and small superstructures were present in the scene [50]. There was more under-segmentation in Areas 1 and 3, which might be explained by a large number of small attachments to the houses that were erroneously merged with neighboring roof planes.
3.4.2. Comparison with other Methods
We conducted a comparative experiment on six buildings, i.e., Buildings 1–6, which were covered with all the rooftop types of the experimental regions. One innovation of the proposed method is that it smooths segmented rooftop patches before reconstructing the building roofs. Therefore, this experiment compared the proposed approach (Approach A) with the ordinary building reconstruction approach (Approach B). In Approach B, the segmented rooftop patches along with the region growing algorithm were directly used for the reconstruction task without smoothing the irregularly distributed rooftop points and eliminating the interference of omissive LiDAR points. Furthermore, a grid-based approach (Approach C) was selected to compare with the proposed method. Details regarding Approach C can be found in the literature [39]. Figure 12 and Figure 13 show the six building roof models reconstructed by use of Approaches A, B, and C.
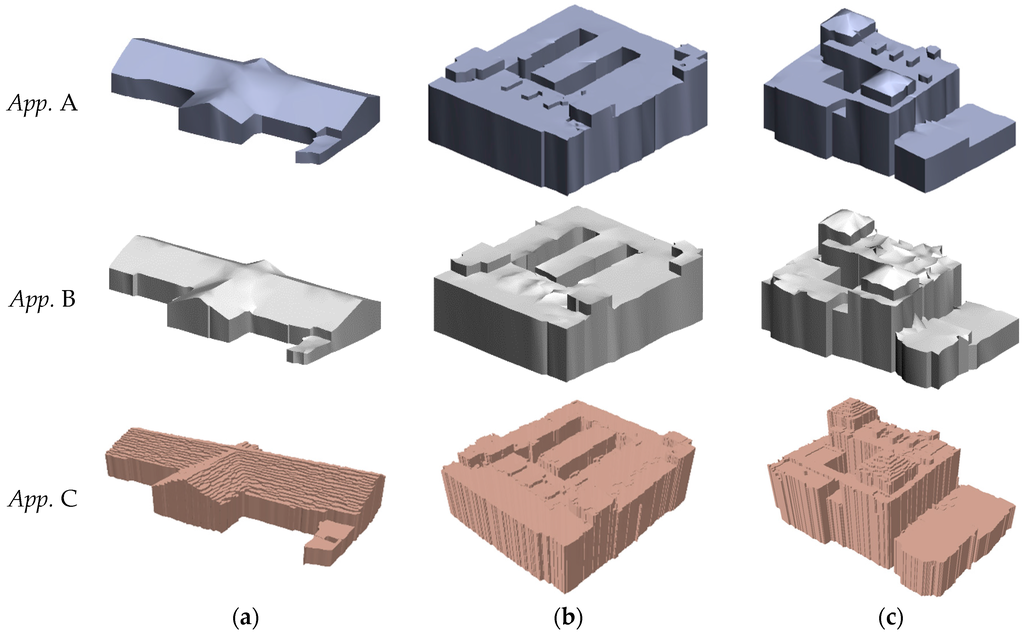
Figure 12.
Comparison of Approaches (abbreviated as App.) A, B, and C: (a), (b), and (c) the reconstructed roof models of Buildings 1, 2, and 3, respectively.

Figure 13.
Comparison of Approaches (abbreviated as App.) A, B, and C: (a), (b), and (c) The reconstructed roof models of Buildings 4, 5, and 6, respectively.
From the visual perspective, the reconstructed models of Building 1 that were obtained by using Approaches A and B had similar reconstruction accuracies (see Figure 12a). The other building roof models reconstructed by using the proposed approach were obviously superior to those reconstructed by using Approach B, thus demonstrating the importance of smoothing before model reconstruction. The superior behavior of Approach A is understandable because, as mentioned previously, even if points belong to the same rooftop patch, small projections usually exist. If layer-connection points are generated directly from the rough points, the reconstructed results will be fractured. In particular, when it comes to interference information, the building roof models will be incoherent and unable to accurately reflect the roofs of the buildings. Here, we must notice that the reconstruction of sloped roofs with Approach C was unsatisfactory. This was mainly due to the fact that stair-step shapes were created during the segmentation of depth imagery. For flat roofs, Approach C can guarantee satisfactory reconstruction results, except irregular boundaries still exist in the roof models. The difficulty of determining the optimal segmentation scale limits the application of the grid-based method for 3-D reconstruction of building roofs with complex top structures in large urban areas. However, some small mistakes were encountered in the model of Building 4 reconstructed by the proposed approach (see Figure 13a); in particular, there was a lack of building fences. The reason for these errors lies in the point spacing of the acquired LiDAR data. The width of the fence pickets was only a few tens of centimeters, and the average point spacing was about 0.4 m. Thus, only one or two points could be acquired along the fences, which made it difficult to accurately reconstruct them.
To quantitatively evaluate the modeling accuracy of the different approaches, Table 6 lists the comparison results of the deviation distances for Buildings 1–6. The statistical results demonstrate that the performance of building roof models reconstructed by Approach A was superior to those reconstructed by Approaches B and C. Approach A was associated with smaller average deviation distances (less than 0.14 m) and lower standard deviations than those derived from the other approaches. Specifically, the average deviation distances and standard deviations of the six building roof models from Approaches B and C were larger than those from Approach A. This situation illustrates that the roof models reconstructed by the latter two methods are unstable. For Buildings 1 and 2, Approaches A and B had similar average deviation distances and standard deviations, thus indicating that the distribution of original airborne LiDAR data was smooth. When there were sloped roof structures on building roofs, the average deviation distances and standard deviations from Approach C were higher than those from Approaches A and B. For example, the average deviation distance and standard deviation of Building 1 reconstructed by Approach C were 0.28 m and 0.56 m, respectively. However, the average deviation distance and standard deviation of Building 1 reconstructed by Approach A were only 0.02 m and 0.11 m.

Table 6.
Comparison of deviation distances for Buildings 1–6 reconstructed by Approaches A, B, and C.
From Figure 12 and Figure 13, we found that the building roof models reconstructed by using Approach B were much rougher than those reconstructed by using Approach A. To quantitatively analyze the experimental results of the two approaches, we calculated the roughness for each building. However, because the roughness of a roof model cannot be calculated directly, we had to resample the roof model to a high density point cloud (200 points/m2 in this paper) as replacement data. First, the roughness, i.e., standard deviation, needs to be calculated for each point p. In the process of determining roughness, the neighboring points (20 points in this paper) of point p are defined. Then, the roughness of point p can be determined based on Euclidean distances from all neighboring points to the fitted plane. Finally, the roughness of each building can be derived according to the calculated roughness of each point.
Table 7 presents the roughness comparisons for Buildings 1–6. Generally speaking, the roughness of building roof models reconstructed by using Approach A was about 0.005 m. Ideally, the roughness values of all building roof models should be zero, as the rooftop patches are strict planes. However, during the process of resampling roof models and calculating roughness, the loss of sampled data accuracy may not lead to a roughness value of zero. As a comparison, the roughness values of building roof models reconstructed by using Approach B were in the range of 0.10 m to 0.25 m. From Table 7, we can see that the roughness values of Building 1 reconstructed by using the two approaches were almost the same. This was because the roof of Building 1 contained no interference information, and the original LiDAR point cloud was relatively smooth. Figure 14 shows the specific distribution of roughness for Buildings 4 and 6, which supports the experimental analysis in Table 7. Therefore, we can conclude that the building roof models reconstructed by using the proposed approach, which were associated with smaller fluctuations and better smoothness, were superior to those reconstructed by using Approach B. Thus, the importance of smoothing before model reconstruction is further verified here.

Table 7.
Roughness comparison of building roof models for Approaches A and B.
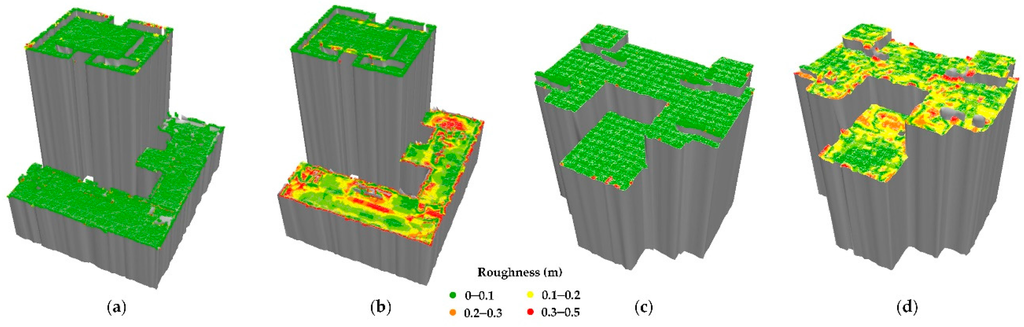
Figure 14.
Roughness comparison between Approaches A and B: (a), (c) roughness of roof models reconstructed using Approach A for Buildings 4 and 6; (b), (d) roughness of roof models reconstructed using Approach B for Buildings 4 and 6, respectively. Data are represented by points with different colors.
4. Conclusions
This paper has presented a new approach involving a layer connection and smoothness strategy for the reconstruction of building roof models from airborne LiDAR data. The proposed approach consists of building rooftop point extraction, smoothness-oriented rooftop patch extraction, layer-connection point generation, and building model reconstruction. The main contributions of the proposed approach are as follows. (1) During the rooftop patch extraction, a “seed point selection, patch growth, and patch smoothing” strategy is used to smooth building points, eliminate interference information, and ensure the integrity of the point cloud data; and (2) layer-connection points are proposed to guarantee consistency between the boundary footprints of different roof layers. By connecting neighboring layer-connection points, the building roofs are reconstructed. Through the calculation of layer-connection points, different roof layers are connected in a simple and fast way. In the two experimental regions used in this paper, the completeness and correctness of the reconstructed rooftop patches were about 90% and 95%, respectively. For the deviation accuracy, the average deviation distance and standard deviation in the best case were 0.05 m and 0.18 m, respectively, and those in the worst case were 0.12 m and 0.25 m. Our experiments prove that this method has good applicability for model reconstruction of buildings in urban environments.
However, too many types of geometric shapes may exist on building roofs, such as artistic sculptures, curved surfaces, and so forth. Therefore, there could be some phenomena of over-smoothing for not-flat roofs by using the proposed method. To reconstruct building roofs with very complex structures, further investigations will be necessary. In addition, small mistakes can persist in certain tiny structures such as fences, air conditioning vents, and chimneys. The proposed method cannot deal with roof overhangs, which are also difficult to reconstruct by the most previous methods. In our future work, we will consider to reconstruct these roof parts with the aid of the auxiliary data (e.g., terrestrial LiDAR data). This paper has concentrated on the reconstruction of building roofs from airborne LiDAR data, and little work was done for the subtle reconstruction of building façades. To achieve the reconstruction of complete building models, further work is needed to allow for the subtle reconstruction of façade models from terrestrial LiDAR data.
Acknowledgments
The authors thank the anonymous reviewers and members of the editorial team for their comments and contributions. We also thank M. Gerke (University of Twente) and U. Breitkopf (University Hannover) for the accuracy analysis of the building reconstruction results of the ISPRS benchmark test project. This work was supported by the National Natural Science Foundation of China (NSFC) Project (Grant Nos. 41071244 and 41371017).
Author Contributions
Hao Xu proposed and developed the research design, collected airborne LiDAR data. Yongjun Wang performed the data analysis, results interpretation. Yajun Wang assisted with developing the research design. Nan Xia and Yong Tang assisted with the experimental result analysis. Liang Cheng and Yanming Chen assisted with refining the research design. Manchun Li checked the manuscript. All authors contributed to manuscript writing.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Groger, G.; Plumer, L. CityGML—Interoperable semantic 3D city models. ISPRS J. Photogramm. Remote Sens. 2012, 71, 12–33. [Google Scholar] [CrossRef]
- Qin, R.J. Change detection on LOD 2 building models with very high resolution spaceborne stereo imagery. ISPRS J. Photogramm. Remote Sens. 2014, 96, 179–192. [Google Scholar] [CrossRef]
- Santos, T.; Gomes, N.; Freire, S.; Brito, M.; Santos, L.; Tenedório, J. Applications of solar mapping in the urban environment. Appl. Geogr. 2014, 51, 48–57. [Google Scholar] [CrossRef]
- Volk, R.; Stengel, J.; Schultmann, F. Building Information Modeling (BIM) for existing buildings—Literature review and future needs. Autom. Constr. 2014, 38, 109–127. [Google Scholar] [CrossRef]
- Yue, H.; Chen, W.; Wu, X.; Liu, J. Fast 3D modeling in complex environments using a single Kinect sensor. Opt. Laser Eng. 2014, 53, 104–111. [Google Scholar] [CrossRef]
- Remondino, F.; El-Hakim, S. Image-based 3D modelling: A review. Photogramm. Rec. 2006, 21, 269–291. [Google Scholar] [CrossRef]
- Cheng, L.; Wu, Y.; Wang, Y.; Zhong, L.S.; Chen, Y.M.; Li, M.C. Three-dimensional reconstruction of large multilayer interchange bridge using airborne LiDAR data. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 691–708. [Google Scholar] [CrossRef]
- Lu, Z.Y.; Im, J.; Rhee, J.; Hodgson, M. Building type classification using spatial and landscape attributes derived from LiDAR remote sensing data. Landsc. Urban Plan. 2014, 130, 134–148. [Google Scholar] [CrossRef]
- Xu, H.; Cheng, L.; Li, M.C.; Chen, Y.M.; Zhong, L.S. Using octrees to detect changes to buildings and trees in the urban environment from airborne LiDAR data. Remote Sens. 2015, 7, 9682–9704. [Google Scholar] [CrossRef]
- Shayeganrad, G. On the remote monitoring of gaseous uranium hexafluoride in the lower atmosphere using LiDAR. Opt. Laser Eng. 2013, 51, 1192–1198. [Google Scholar] [CrossRef]
- Kabolizade, M.; Ebadi, H.; Mohammadzadeh, A. Design and implementation of an algorithm for automatic 3D reconstruction of building models using genetic algorithm. Int. J. Appl. Earth Observ. 2012, 19, 104–114. [Google Scholar] [CrossRef]
- Haala, N.; Kada, M. An update on automatic 3D building reconstruction. ISPRS J. Photogramm. Remote Sens. 2010, 65, 570–580. [Google Scholar] [CrossRef]
- Tomljenovic, I.; Höfle, B.; Tiede, D.; Blaschke, T. Building extraction from airborne laser scanning data: An analysis of the state of the art. Remote Sens. 2015, 7, 3826–3862. [Google Scholar] [CrossRef]
- Tarsha-Kurdi, F.; Landes, T.; Grussenmeyer, P.; Koehl, M. Model-driven and data-driven approaches using LiDAR data: Analysis and comparison. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Syst. 2007, 36, 87–92. [Google Scholar]
- Awrangjeb, M.; Zhang, C.; Fraser, C.S. Automatic extraction of building roofs using LiDAR data and multispectral imagery. ISPRS J. Photogramm. Remote Sens. 2013, 83, 1–18. [Google Scholar] [CrossRef]
- Dorninger, P.; Pfeifer, N. A comprehensive automated 3D approach for building extraction, reconstruction, and regularization from airborne laser scanning point clouds. Sensors 2008, 8, 7323–7343. [Google Scholar] [CrossRef]
- Cheng, L.; Tong, L.H.; Chen, Y.M.; Zhang, W.; Shan, J.; Liu, Y.X.; Li, M.C. Integration of LiDAR data and optical multi-view images for 3D reconstruction of building roofs. Opt. Laser Eng. 2013, 51, 493–502. [Google Scholar] [CrossRef]
- Susaki, J. Knowledge-based modeling of buildings in dense urban areas by combining airborne LiDAR data and aerial images. Remote Sens. 2013, 5, 5944–5968. [Google Scholar] [CrossRef]
- Verma, V.; Kumar, R.; Hsu, S. 3D building detection and modeling from aerial LiDAR data. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 17–22 June 2006; pp. 2213–2220.
- Sohn, G.; Huang, X.F.; Tao, V. Using a binary space partitioning tree for reconstructing polyhedral building models from airborne LiDAR data. Photogramm. Eng. Remote Sens. 2008, 74, 1425–1438. [Google Scholar] [CrossRef]
- Zhang, K.; Yan, J.H.; Chen, S.C. Automatic construction of building footprint's from airborne LiDAR data. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2523–2533. [Google Scholar] [CrossRef]
- Kada, M.; McKinley, L. 3D building reconstruction from LiDAR based on a cell decomposition approach. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2009, 38, 47–52. [Google Scholar]
- Vallet, B.; Pierrot-Deseilligny, M.; Boldo, D.; Bredif, M. Building footprint database improvement for 3D reconstruction: A split and merge approach and its evaluation. ISPRS J. Photogramm. Remote Sens. 2011, 66, 732–742. [Google Scholar] [CrossRef]
- Vosselman, G.; Dijkman, S. 3D building model reconstruction from point clouds and ground plans. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2001, 34, 37–44. [Google Scholar]
- Sumer, E.; Turker, M. Automated extraction of photorealistic facade textures from single ground-level building images. Int. J. Pattern Recogn. 2014, 28, 1455007. [Google Scholar] [CrossRef]
- Sun, S.H.; Salvaggio, C. Aerial 3D building detection and modeling from airborne LiDAR point clouds. IEEE J. Sel Top. Appl. Earth Observ. Remote Sens. 2013, 6, 1440–1449. [Google Scholar] [CrossRef]
- Vo, A.V.; Truong-Hong, L.; Laefer, D.F.; Bertolotto, M. Octree-based region growing for point cloud segmentation. ISPRS J. Photogramm. Remote Sens. 2015, 104, 88–100. [Google Scholar] [CrossRef]
- Henn, A.; Groger, G.; Stroh, V.; Plumer, L. Model driven reconstruction of roofs from sparse LiDAR point clouds. ISPRS J. Photogramm. Remote Sens. 2013, 76, 17–29. [Google Scholar] [CrossRef]
- Tarsha-Kurdi, F.; Landes, T.; Grussenmeyer, P. Extended RANSAC algorithm for automatic detection of building roof planes from LiDAR data. Photogramm. J. Finl. 2008, 21, 97–109. [Google Scholar]
- Fan, H.C.; Yao, W.; Fu, Q. Segmentation of sloped roofs from airborne LiDAR point clouds using ridge-based hierarchical decomposition. Remote Sens. 2014, 6, 3284–3301. [Google Scholar] [CrossRef]
- Awrangjeb, M.; Fraser, C.S. Automatic segmentation of raw LiDAR data for extraction of building roofs. Remote Sens. 2014, 6, 3716–3751. [Google Scholar] [CrossRef]
- Chen, D.; Zhang, L.Q.; Li, J.; Liu, R. Urban building roof segmentation from airborne LiDAR point clouds. Int. J. Remote Sens. 2012, 33, 6497–6515. [Google Scholar] [CrossRef]
- Kim, K.; Shan, J. Building roof modeling from airborne laser scanning data based on level set approach. ISPRS J. Photogramm. Remote Sens. 2011, 66, 484–497. [Google Scholar] [CrossRef]
- Sampath, A.; Shan, J. Segmentation and reconstruction of polyhedral building roofs from aerial LiDAR point clouds. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1554–1567. [Google Scholar] [CrossRef]
- Satari, M.; Samadzadegan, F.; Azizi, A.; Maas, H.G. A multi-resolution hybrid approach for building model reconstruction from LiDAR data. Photogramm. Rec. 2012, 27, 330–359. [Google Scholar] [CrossRef]
- Lafarge, F.; Descombes, X.; Zerubia, J.; Pierrot-Deseilligny, M. Structural approach for building reconstruction from a single DSM. IEEE Trans. Pattern. Anal. 2010, 32, 135–147. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Q.Y.; Neumann, U. 2.5D building modeling by discovering global regularities. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 326–333.
- Zhang, W.; Wang, H.; Chen, Y.; Yan, K.; Chen, M. 3D building roof modeling by optimizing primitive’s parameters using constraints from LiDAR data and aerial imagery. Remote Sens. 2014, 6, 8107–8133. [Google Scholar] [CrossRef]
- Xiong, B.; Jancosek, M.; Oude Elberink, S.; Vosselman, G. Flexible building primitives for 3D building modeling. ISPRS J. Photogramm. Remote Sens. 2015, 101, 275–290. [Google Scholar] [CrossRef]
- Chen, Y.M.; Cheng, L.; Li, M.C.; Wang, J.C.; Tong, L.H.; Yang, K. Multiscale grid method for detection and reconstruction of building roofs from airborne LiDAR data. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 4081–4094. [Google Scholar] [CrossRef]
- Cheng, L.; Zhao, W.; Han, P.; Zhang, W.; Shan, J.; Liu, Y.X.; Li, M.C. Building region derivation from LiDAR data using a reversed iterative mathematic morphological algorithm. Opt. Commun. 2013, 286, 244–250. [Google Scholar] [CrossRef]
- Awrangjeb, M.; Lu, G.; Fraser, C. Automatic building extraction from LiDAR data covering complex urban scenes. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 1, 25–32. [Google Scholar] [CrossRef]
- Zhou, Q.Y.; Neumann, U. Fast and extensible building modeling from airborne LiDAR data. In Proceedings of the 16th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Irvine, CA, USA, 5–7 November 2008; pp. 1–8.
- Zhu, L.; Lehtomäki, M.; Hyyppä, J.; Puttonen, E.; Krooks, A.; Hyyppä, H. Automated 3D scene reconstruction from open geospatial data sources: Airborne laser scanning and a 2D topographic database. Remote Sens. 2015, 7, 6710–6740. [Google Scholar] [CrossRef]
- Awrangjeb, M.; Fraser, C.S. An automatic and threshold-free performance evaluation system for building extraction techniques from airborne LiDAR data. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 4184–4198. [Google Scholar] [CrossRef]
- Elberink, S.O.; Vosselman, G. Quality analysis on 3D building models reconstructed from airborne laser scanning data. ISPRS J. Photogramm. Remote Sens. 2011, 66, 157–165. [Google Scholar] [CrossRef]
- Besl, P.J.; Mckay, N.D. A method for registration of 3D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Rottensteiner, F.; Sohn, G.; Jung, J.; Gerke, M.; Baillard, C.; Benitez, S.; Breitkopf, U. ISPRS benchmark on urban object classification and 3D building reconstruction. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 1, 293–298. [Google Scholar] [CrossRef]
- Web Site of the ISPRS Test Project on Urban Classification and 3D Building Reconstruction. Available online: http://www2.isprs.org/commissions/comm3/wg4.html (accessed on 28 February 2016).
- Rottensteiner, F.; Sohn, G.; Gerke, M.; Wegner, J.D.; Breitkopf, U.; Jung, J. Results of the ISPRS benchmark on urban object detection and 3D building reconstruction. ISPRS J. Photogramm. Remote Sens. 2014, 93, 256–271. [Google Scholar] [CrossRef]
- Rau, J.-Y.; Lin, B.-C. Automatic roof model reconstruction from ALS data and 2D ground planes based on side projection and the TMR algorithm. ISPRS J. Photogramm. Remote Sens. 2011, 66, s13–s27. [Google Scholar] [CrossRef]
- Oude Elberink, S.; Vosselman, G. Building reconstruction by target based graph matching on incomplete laser data: Analysis and limitations. Sensors 2009, 9, 6101–6118. [Google Scholar] [CrossRef] [PubMed]
- Xiong, B.; Oude Elberink, S.; Vosselman, G. A graph edit dictionary for correcting errors in roof topology graphs reconstructed from point clouds. ISPRS J. Photogramm. Remote Sens. 2014, 93, 227–242. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).