Abstract
The error in satellite precipitation-driven complex terrain flood simulations is characterized in this study for eight different global satellite products and 128 flood events over the Eastern Italian Alps. The flood events are grouped according to two flood types: rain floods and flash floods. The satellite precipitation products and runoff simulations are evaluated based on systematic and random error metrics applied on the matched event pairs and basin-scale event properties (i.e., rainfall and runoff cumulative depth and time series shape). Overall, error characteristics exhibit dependency on the flood type. Generally, timing of the event precipitation mass center and dispersion of the time series derived from satellite precipitation exhibits good agreement with the reference; the cumulative depth is mostly underestimated. The study shows a dampening effect in both systematic and random error components of the satellite-driven hydrograph relative to the satellite-retrieved hyetograph. The systematic error in shape of the time series shows a significant dampening effect. The random error dampening effect is less pronounced for the flash flood events and the rain flood events with a high runoff coefficient. This event-based analysis of the satellite precipitation error propagation in flood modeling sheds light on the application of satellite precipitation in mountain flood hydrology.
1. Introduction
The potential of high-resolution satellite precipitation estimation in hydrological applications has been investigated for more than two decades [1,2,3,4,5]. The main advantage to the conventional ground-based measurements is that precipitation estimation from space-borne sensors is uninhibited by topography, and thus can provide coherent global-scale estimates at high space (0.25°) and time (3 h) resolution [6,7,8]. This provides a potential solution for measuring precipitation over complex terrain basins where ground-based measurement networks are sparsely distributed or unavailable. However, precipitation estimates from satellite sensors are associated with errors that propagate to the prediction of hydrologic variables through the rainfall-runoff modeling [3,5,9,10,11]. It has been argued that the performance of satellite precipitation estimates and its driven simulation largely depend on the regional rainfall properties (e.g., types, magnitudes, space-time pattern, etc.), the geomorphology of the area (e.g., surface inclination, basin scales, etc.), the basin conditions (e.g., soil moisture, existence of snow cover, etc.), the choice of modeling complexity and, finally, the interactions between all of these factors [10,11,12,13,14,15].
Mei et al. [16] classified 3249 storm events from 13 varying-sized basins (200 km2 to 4200 km2) according to their rain volume and storm type (i.e., convective vs. organized frontal systems). Their results showed that satellite precipitation estimates are more biased in frontal precipitation events. On the other hand, it was shown that the error has a higher degree of variability for short-duration events, which were associated with low rain accumulations over small basin scales. Similar results were exhibited for satellite-driven hydrologic simulations by Wu et al. [14], who showed that the performance of hydrologic simulations improved with flood duration. Vergara et al. [10] and Maggioni et al. [9] conducted separate satellite precipitation error propagation analyses over mild-slope-terrain basins with results revealing that the satellite precipitation error variance is buffered by the rainfall-runoff process and that this dampening effect exhibits basin-scale dependence. Two other hydrologic evaluation studies of satellite products [11,12] have shown terrain elevation dependence on the performance of satellite precipitation estimation. Furthermore, Yong et al. [13,17] have shown that the existence of snow cover and mixed-phase precipitation over complex terrain basins can significantly affect satellite precipitation uncertainty and the satellite precipitation-driven simulations.
The majority of studies on satellite precipitation error propagation presented in the literature rely on pixel-based evaluation or long-term basin-averaged time series. Few studies have focused on storm events at the catchment scale, which represents the physical aspect of the rainfall-runoff transformation process [2,3,5]. Nikolopoulos et al. [3] showed that the volumetric error in rainfall is linearly translated to the error in the simulated runoff for the steep-slope topography of their study region. Furthermore, Nikolopoulos et al. [15], for a major flash flood event in the same region, showed that linearity in error translation appears for wet soil moisture conditions while for dry antecedent conditions, error propagation was nonlinear. Several of the studies also revealed that the magnitude of error in rainfall and runoff are reduced with increasing the satellite product resolution and basin scale [2,5,15,18]; these dependencies of error vary seasonally and across climate regions [5,18]. Apart from the magnitude of error in hydrologic response, the timing error is another important source of error with particular significance in satellite-based flood predictions. Hossain and Anagnostou [2] showed that the time-to-peak error depends on various factors (e.g., duration of event, magnitude of rainfall rate, etc.).
The event-based error analysis studies discussed above relied on a small number of flood events and were focused on the error magnitude in rainfall or simulated runoff, missing other important event properties (e.g., overall shape of hydrograph or hyetograph). Accurate representation of the hydrographs is important for a number of flood-risk operations such as reservoir operation and timely emergency response. This study focuses on the analysis of satellite precipitation error propagation in flood simulations, expanding on two main aspects: (i) evaluating a relatively large number of flood events that occurred over mountainous basins; (ii) examining error propagation for different flood types and with respect to several characteristics of flood response (i.e., timing and magnitude). Thus, we believe this study will provide new insights on the hydrologic implications of satellite precipitation error propagation.
Previous studies over the Upper Adige region have investigated the uncertainty of satellite precipitation products and their propagation in hydrologic simulations [11,16]. This study renders the focus on the assessment of satellite precipitation for the prediction of flood events. Eight satellite precipitation products and 128 flood events that occurred in the period of May to November between 2002 and 2010 over nine sub-basins of the region are used to support this study. The satellite precipitation retrieval and flood modeling errors are defined with respect to reference rainfall and reference rainfall–based simulations to directly make a connection between the error in quantifying the basin-average rainfall and the corresponding error in satellite-driven runoff prediction. Events from the cold season months (December to April) where precipitation in the region is dominated by snow and the satellite products are significantly subjected to detection issues (typically non-detecting light precipitation) were not considered [11]. It is noted that flood events occurring during the cold period in the study area are typically triggered by rain falling on snow-covered areas or snowmelt processes [19]. The study is organized as follows: Section 2 provides a description of the study area, the hydrologic model used for flood simulations, the satellite and reference precipitation data, and the flood events database. Section 3 introduces the method used to identify and match satellite events with reference events and the error metrics used to quantify the event-based satellite product and flood simulation error at the basin scale. Results and discussions are presented in Section 4 and Section 5. Conclusions are summarized in Section 6.
2. Study Area, Data and Hydrologic Model
2.1. Study Area
The study focuses on nine catchments of the Upper Adige river basin closed at Bronzolo (6967 km2) and located in the Eastern Italian Alps (Figure 1). This is a mountainous area characterized by high elevation from 200 to 3900 meters above sea level (m a.s.l.), steep slopes and a sharp hydro-climatic gradient [20]. The nine selected study sub-basins (located on the west and north part of the Upper Adige basin) have mean basin elevations above 1800 m a.s.l. and small drainage areas (50 to 600 km2) (Table 1). This region is influenced by the Meridional South and Southeast circulation patterns and western Atlantic airflows causing heavy precipitation events and associated flash floods and debris flows in the August to November period. The late October to April period is typically dominated by snow and widespread-type precipitation, which increases the cumulative snow depth. The following late spring snow melting increases the soil moisture; precipitation and large snow melt episodes may cause floods from June to early August [20,21,22].
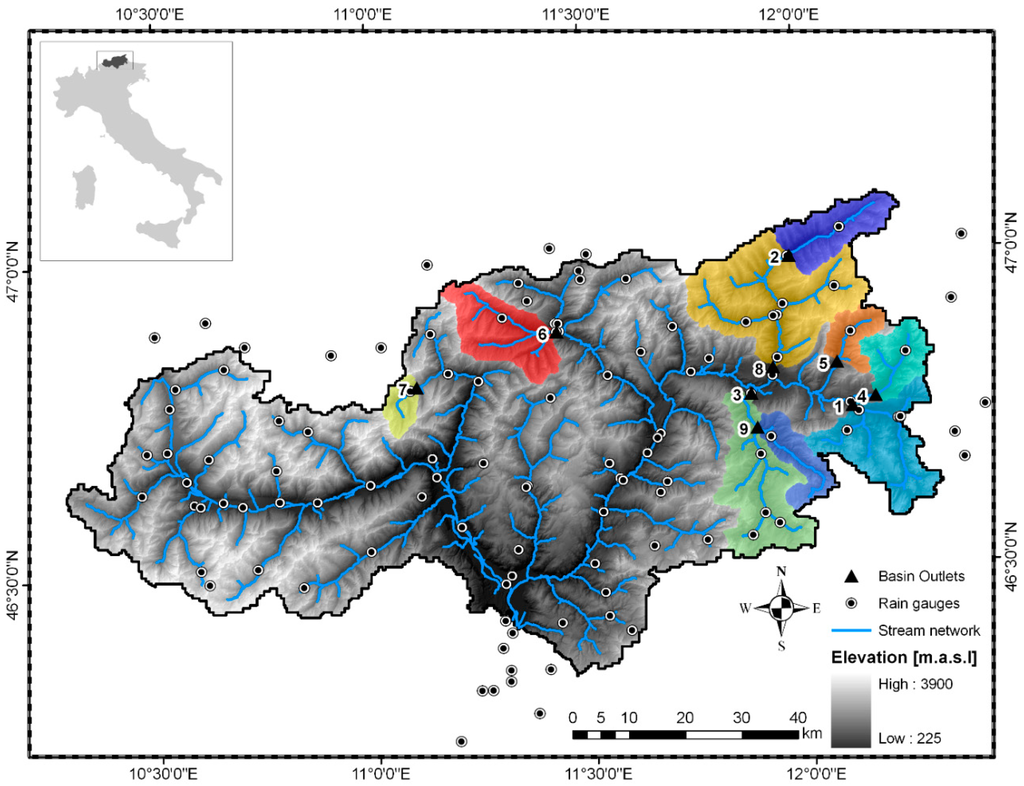
Figure 1.
Location and topography of the sub-basins.

Table 1.
Information of the study sub-basins.
2.2. Precipitation Data
Eight quasi-global satellite precipitation products are evaluated. The first two products, named 3B42-CCA and 3B42-V7 (hereafter named TR and aTR), are from the National Aeronautics and Space Administration Tropical Rainfall Measuring Mission Multi-satellite Precipitation Analysis (TMPA). The 3B42-CCA and 3B42-V7 products are corrected versions of the near-real-time 3B42 where the 3B42-CCA is adjusted according to the climatological correction algorithm (CCA) and the other is the post-processing gauge-adjusted product [23,24]. The next two products are the Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks (PERSIANN, hereafter named PE) [25] and its bias-adjusted version based on the GPCP (Global Precipitation Climatology Project) product and the 2.5°/monthly PERSIANN estimates (hereafter named aPE) [26,27]. The National Oceanic and Atmospheric Administration Climate Prediction Center morphing (CMORPH, abbreviated as CM) technique [28] and a recently available gauge-adjusted version (named hereafter as aCM) based on daily gauge estimates from 30,000 gauges worldwide are also investigated [29]. These six products are 0.25°/3-hourly. We also included two high-resolution products available at 0.073° and hourly space-time scale. These two products are the Kalman Filter-based CMORPH and, similarly, its gauge-corrected counterpart (named as hC and ahC hereafter). The Kalman Filter–based CMORPH incorporates additional infrared-based information and the integration of all passive microwave- and infrared-based information from the original CMORPH to produce accurate estimations of precipitation [30].
A network of 108 rain gauges distributed across the entire Upper Adige river basin represents an untypically high density network (~1 gauge per 65 km2) for a mountainous area. The hourly rain gauge record used in this study spans a nine-year period from 2002 to 2010. Rain gauge data were interpolated, using the nearest neighbor method, which is the procedure used by the hydrologic model to convert rain gauge data to basin averages; this interpolation method is consistent with previous satellite precipitation error studies in the area [11,16]. Gauge and satellite precipitation fields are then averaged at the sub-basin scale using areal weighting to produce the basin-average precipitation time series for the nine study catchments. These time series were used to force the hydrologic model, which is discussed next.
2.3. Hydrologic Simulations
In this study we applied the Integrated Catchment Hydrological Model (ICHYMOD), which is an off-line version of the operational modeling scheme of the Adige River Flood Forecasting System. ICHYMOD involves a semi-distributed conceptual rainfall-runoff model that consists of a snow routine, a soil moisture routine and a flow routine model. The soil moisture component of the ICHYMOD follows the structure of the probability-distributed moisture model [31,32]. Snow accumulation and melting is modeled based on temporally variable distribution functions which exploit a combined radiation index degree-day concept originally developed by Cazorzi and Dalla Fontana [33]; potential evapotranspiration is estimated by the Hargreaves method [34]. The model is applied in a semi-distributed way by dividing the study area into sub-basins. At the sub-basin scale, runoff is routed by using a cascade of two linear conceptual reservoirs. Hydrographs are routed through the river network by means of the Muskingum-Cunge method [35]. Application of the model requires specification of 14 parameters for the snow routine, the runoff generation module and the runoff propagation module [36]. The calibration procedure for determining the model parameters is detailed in Borga et al. [37]. In our analysis, we adopt the same modeling parameters for our simulations to allow results to be directly related to an existing flood forecasting application. This also helps to exclude the effect of model uncertainty isolating the effect of precipitation error propagation, which is the focus of our study.
The input precipitation forcing is aggregated at the sub-basin scale, accordingly with the procedure reported in the previous section. Given the dense rain gauge coverage, sub-basin scale rainfall estimates obtained by using the ground stations are considered as the ground reference for inter-comparison in this work. Analogously, the gauge precipitation-driven hydrological simulations are used as the reference for comparison with the satellite precipitation-driven hydrological simulations. Hydrological simulations are carried out by using rain gauge-derived precipitation for the nine study basins from 2002 to 2010, thus providing the reference discharge time series. The accuracy of the simulations was qualified by using the Nash-Sutcliffe Index (NSI) [38]. The mean of the NSI determined between the gauge-driven simulated stream flows and measured stream flows for the selected basins and period of simulation is 0.66 (Table 1). We notice low model efficiency for basins 3 and 9, which is partially attributed to the difficulties in simulating responses from a karst aquifer-dominated catchment. The flood periods in the observed streamflow data are well captured by the model, whereas recession periods are less reliably represented. The hourly runoff simulations for all satellite products were run for the May to November period of each study year to avoid mixing satellite estimation errors for rainfall and snowfall (snowfall dominates from December to April of the study area). Each simulation cycle (i.e., May–November per year) was initialized by the state variables (snow and soil moisture storage) obtained from the continuous gauge-based simulations.
2.4. Flood Events: Archive and Flood Types
The archive of observed flood events used in this study has been established based on the work of Zoccatelli et al. [19]. In this work, the archive of the three most intense floods observed over each year and over each study basin has been used to establish a flood-type classification based on a combination of a number of process indicators, including the timing of the floods, storm duration, rainfall depths, snowmelt, catchment state, runoff response dynamics, and spatial coherence [39]. In Zoccatelli et al. [19] the flood-type classification scheme is based on data from 33 basins distributed along a North-South Alpine transect (including the nine basins used in the current study), with a focus which permits us to analyze the changes in flood types along an altitudinal and climatic gradient. The application of the ICHYMOD model over each basin allows retrieving variables such as catchment soil moisture conditions, and solid precipitation/snowmelt contribution to flood formation.
The analysis, carried out based on a cluster analysis, helped to determine three flood types:
- Snow-dominated floods: events in which the input from snowmelt dominates over liquid precipitation.
- Rain-dominated events: floods with time to flow peak exceeding 24 h and moderately intense rainfall uniformly distributed over the area.
- Flash flood events: events developing in smaller basins (mostly smaller than 200 km2) triggered by intense rainfall and with time to flow peak less than 24 h.
In the current work, we limited the analysis only to the warm season floods (May to November), which leads to the exclusion of the snow-dominated events. Thus, only two types of floods are used here: (i) long-rain flood (116 events) and flash floods (12 events).
The selected flood event properties are summarized in Table 2. It can be inferred that the flash flood events are characterized by more intense rainfall and flow rates, given the shorter durations and larger accumulations. The standard deviations (SDs) of the event hyetograph and hydrograph are also different between the two types of flood events, with higher values obtained for the flash floods. The above observations reveal the higher intensity and variability associated with flash floods relative to rain floods. The average values and ranges of the initial soil moisture and the runoff coefficient, for all the events analyzed, are also listed in the table. It is seen that although the mean of the initial soil moisture is similar between the two flood types (1% higher in flash flood cases), the event-based runoff coefficients (RC) are quite different between rain flood and flash flood events (22% vs. 35% average RC with a wider value range for rain vs. flash flood events).

Table 2.
Mean and range of event properties for rain flood and flash flood.
3. Methodology
3.1. Event Matching
The start time and duration of a rainfall event varies across the different rainfall dataset, which also results in varying temporal characteristics of simulated flood hydrographs. Therefore, event-based analysis requires matching each satellite rainfall event and its associated simulated flood events with the corresponding reference rainfall and flood events. In this section, we introduce the method utilized to identify and match the 128 events from the database with their corresponding counterparts from each of the flow simulations to form the “flood event pairs” used in the error analysis. A rainfall-runoff event is considered as a combination of the basin-average rainfall and the resulting flood event. Thus, matching a rainfall-runoff event required identifying the timing of both aspects. The method is separated into two parts; first, the timing of flood events is identified and matched with the database; second, rainfall events are identified for each product; and third, the rainfall events from various products are matched to the corresponding flood event based on the Characteristic Point Method (CPM, Mei and Anagnostou [40]). Inputs of the process are the timing of flood events from Zoccatelli et al. [19], and the corresponding time series of both satellite and rain gauge–based rainfall and simulated runoff. Outputs are the start/end time of matched gauge and satellite rainfall-runoff events pairs. The following steps applied to each satellite product are:
- (1)
- The start and end hour of each flood event are identified from the simulated flow time series of all the products according to the database.
- (2)
- Continuous periods of nonzero rainfall are identified based on the basin-average rainfall time series.
- (3)
- For each product match, rainfall periods from step 2 are matched with corresponding flood events using CPM. Details of the technical steps are documented in Section 3.2.3 of Mei and Anagnostou [40]. For each flood event, CPM identifies the associated rainfall period. If more than one rainfall event satisfy the conditions, they are jointed as one rainfall event and are considered as the inducing rainfall of the flood event. These rainfall and flood event pairs together form a rainfall-runoff event.
Two sample matched events derived from the above method are illustrated in Figure 2. As it is exhibited in the figure, the start/end time of event rainfall and runoff could be varied from different rainfall forcing. However, these differences are within relatively small extents, with hydrographs having reasonable shapes. These together verify the matching technique applied in this study.

Figure 2.
Example of two matched rainfall-runoff events for basins with ID 6 (left) and 8 (right). Basin-averaged rainfall time series (top) and simulated hydrographs (bottom) are shown for all precipitation products used.
3.2. Event Properties
We focus our error analysis on three event properties: the event cumulative rainfall or runoff depth (VX, in mm), the centroid of the hyetograph or hydrograph from the starting time of the event (CtX, in h) and the spreadness of the hyetograph or hydrograph (SdX, in h). The concept of event cumulative depth is defined as:
where X can be properties from either the rainfall or simulated flow aspect. Thus, X(t) is the precipitation or runoff time series for the satellite or reference (in mm/h) and TX is the duration of the rainfall or runoff event.
The concept of the centroid is often used as a surrogate of time to peak to account for the time series dynamic. It determines the arrival of the event mass center; it is the weighted average of time with respect to the temporal dynamics of rainfall (or runoff) time series:
Ctr defines the location of the event mass center with respect to the temporal variability of the time series.
The last event property analyzed is the spreadness (denoted as Sdx), which quantifies the temporal degree of dispersion of the event time series. It determines the variability of the event time (t) with respect to the temporal dynamics of the time series:
Typically, larger Sdx values are associated with a more dispersed shape of the time series around the centroid (i.e., high flow tends to locate on both the early and late phase of an event). For the same number of peaks in the hydrograph (e.g., mono-modal or bi-modal), this parameter can be surrogate to the peakedness of the time series.
3.3. Comparative Analysis
Comparison between reference- and satellite-based rainfall/runoff events has two main objectives. First, differences in event properties (e.g., magnitude, variability, etc.) are assessed to demonstrate the ability and limitations of satellite products in representing the characteristics of flood events. Second, propagation of error from rainfall to runoff is evaluated to understand how certain properties of error in rainfall translate into error in runoff. The error analysis is conducted based on metrics determined for the properties of “event pairs” described in the previous section. We use the Taylor diagram [41] to demonstrate the consistency between event properties calculated from the satellite products and those attained from the reference time series. The Taylor diagrams are produced for both rainfall and simulated flow. The metrics and statistics involved in the Taylor diagram are: the variance (σ2) of satellite and gauge event time series, the centered root mean square difference (CRMSD) and the correlation coefficient (ρ). Forms of these three metrics (illustrated for the cumulative depth property) are:
where n and N stand for the event index and the total number of events, and subscripts G and S represent the gauge and satellite hyetograph/hydrograph, respectively.
Our comparative analysis also includes the evaluation of systematic and random error determined from each event pair. The systematic error is quantified as the mean relative error (MRE) of event properties between satellite and reference. The MRE form illustrated for the cumulative depth property is:
Analogously, MRECt and MRESd are similarly defined by replacing V with Ct and Sd, respectively. A value of MRE greater/smaller than 0 indicates over-/under-estimation of the reference property for an event. The random error is calculated as the centered relative root mean square difference (CRRMSD) determined for the time series of the “event pairs”. As shown in Figure 2, the timing of the event time series of satellite products can be slightly different from the reference in terms of the beginning and ending hour. To remove timing issues, we take the common period for satellite and reference hydrographs/hyetographs before calculating the CRRMSD. The CRRMSD is calculated based on these new time series as:
where the asterisk (*) represents the time series with common period TX*. The CRRMSD quantifies the random error between the two time series as the smaller the value, the higher the degree of similarity between the two time series.
To quantify the error propagation through the rainfall-runoff process, we take the absolute ratio (γ) between error metrics (MRE and CRRMSD) for the flood and rainfall event. By taking the absolute value, γ is always greater than 0, while values higher (lower) than 1 indicate amplification (dampening) of the error magnitude. We further investigate the role of event-based RC (as a lumped indicator of the initial condition and interaction between rainfall and the various catchment processes) on error propagation by sorting the events to three thresholds: below 40th, 40th to 75th and above 75th percentile groups of the RC values.
4. Results
As a qualitative inspection of the error pattern, we show two sample events (after completion of the matching procedure) in Figure 2. In the first event, the CMORPH products, particularly the gauge-adjusted ones (aCM and ahC), are overestimating the gauge rainfall. This leads also to overestimation in the simulated flow. It is worth noting from this figure that, although the 3B42V7 product is underestimating the reference rainfall, its distinctly high initial flow condition yields overestimation of the gauge-simulated flood event (note that the initial condition for each product could be different since the simulations run continuously throughout each May–November period). For the rest of the satellite products, their underestimation relative to the gauge rainfall and relatively low initial flow rates resulted in strong underestimation of the reference flow simulations. For the second sample event, all the products are underestimating the gauge rainfall with similar initial flow rates. Thus, all of them are providing underestimation of the reference flood event. This shows that the higher initial flow rate to the reference may not always yield higher cumulative flow depth (implying overestimation) to the reference due to the difference in rainfall variability and its complex interaction with the catchment processes.
4.1. Event Properties Error Statistics
First, we present the Taylor diagrams, which integrate the statistics introduced in Equations (4) through (6) for the three event properties (cumulative depth, centroid and spreadness) in basin-average rainfall and simulated runoff time series. Results for cumulative rainfall and runoff depths for the two flood types are presented in Figure 3. As shown, the satellite products underestimate the variability of cumulative depth of the reference precipitation and simulated runoff, especially for the flash flood cases. Comparison between rain flood and flash flood events suggests that the σ2 of cumulative depths decreases noticeably for the two 3B42 and PERSIANN products and only slightly for the CMORPH and Kalman Filter-Based CMORPH. The CRMSD values exhibit distinct patterns between the two flood types and between rainfall and simulated runoff parameters. Lower CRMSD values are shown for the runoff-based event cumulative depth compared to the basin-average precipitation event parameters. Comparing the CRMSD of the two flood event types for 3B42 and PERSIANN shows that the flash flood events exhibit lower CRMSD values compared to the rain flood events on both the event rainfalls and their corresponding flow simulations; reversed trends are shown on the CMORPHs’ estimated cumulative rainfall depth. It is noted that the two gauge-adjusted CMORPHs exhibit similar (slightly decreased) CRMSD values with the corresponding unadjusted counterparts. The last aspect shown on the Taylor diagram is the correlation between the V values of each satellite product and reference. The correlation coefficients of cumulative event flow depth are higher than the basin-averaged precipitation ones for most of the products, pointing to the fact that the inclusion of the baseflow component in the cumulative depth parameter modulates the volumetric error. The ρ for the hydrograph ranges from 0.4 to 0.8; ρ for the hyetograph is located around 0.4. Also, similar ρ values are shown for the high-resolution Kalman Filter–Based CMORPH product compared to the original CMORPH product.

Figure 3.
Taylor diagram of the cumulative rainfall and flow depths for different products.
Results for the event centroid parameter are illustrated by the Taylor diagram in Figure 4. It is shown that all the points are relatively closely distributed to each other regardless of the flood types and rainfall or runoff. This is particularly seen for the rain flood hydrograph centroid cases. This means the values of σ2, CRMSD and ρ are, in general, almost identical for the eight products and the estimations on the reference flood event centroid are consistent. In other words, the effect of gauge adjustments or spatial aggregation has little influence on the arrival of the event mass center. In detail, the CRMSDs of runoff event centroids are closer to the reference compared to the rainfall ones, indicating a clear dampening effect in the random error of the event centroid. This dampening effect can be further confirmed by the less-than-one values of γMRE,Ct discussed in detail later in this section. The flash flood events in this case also exhibit lower CRMSD values in contrast to the rain flood counterparts. This is due to the shorter concentration time and duration (or equivalently shorter event centroid) of the flash flood event than the rain flood event. Observations on the correlation coefficients reveal that the flood event centroid parameter values derived from the satellite products are characterized with high correlation (above 0.95 and 0.8 for rain flood and flash flood, respectively). The correlation coefficient is reduced in the rainfall event cases where the ρ values for rain flood and flash flood are around 0.8 and 0.6, respectively.
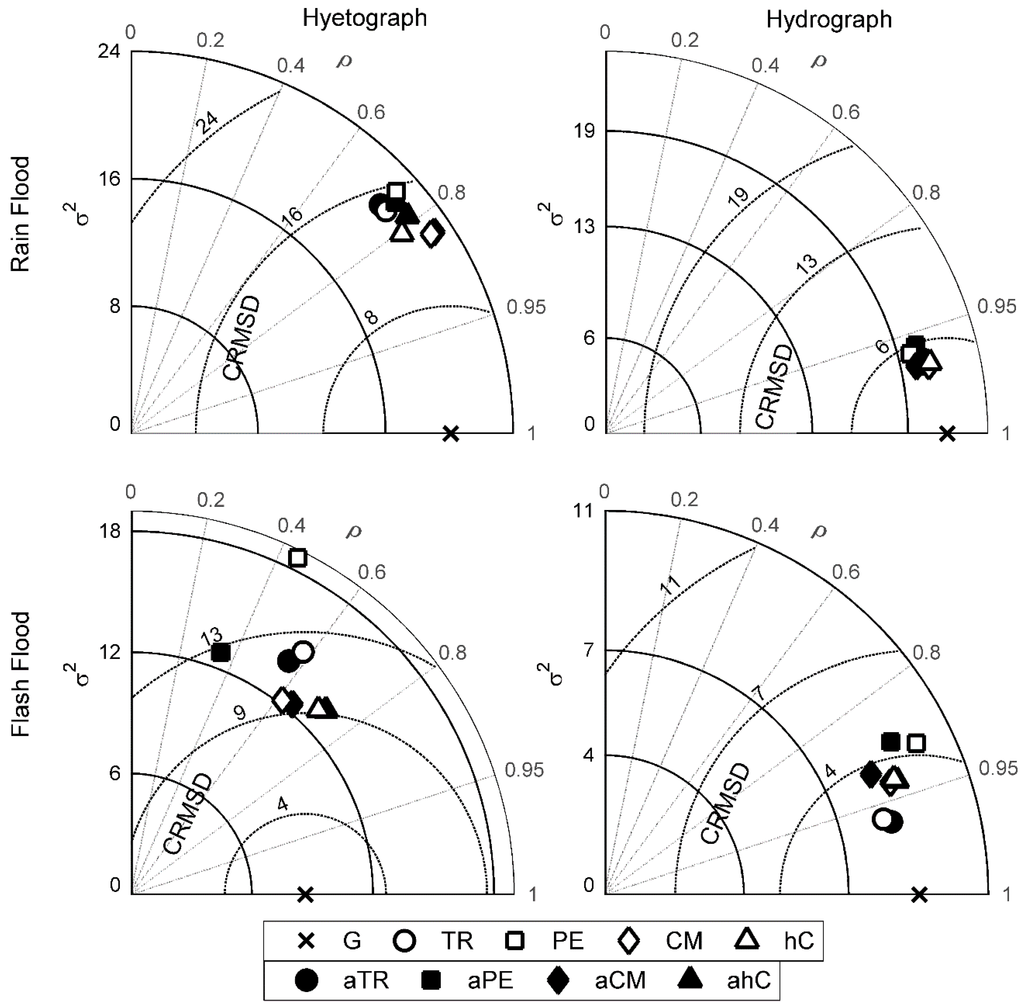
Figure 4.
Same as in Figure 3, but for the event centroid.
The error metrics for spreadness are integrated in the Taylor diagrams of Figure 5. The variance of reference spreadness is overestimated by nearly all of the satellite products. Similar to the results of the event centroid, the satellite estimations on the reference time series in terms of the spreadness reveal relatively low CRMSD. Meanwhile, the rain flood spreadness cases share fairly similar performances among products where all the points are closely located to each other. This states the insignificant influences from gauge adjustment and resolution to the spreadness parameter. The CRMSD values of the hydrographs for the two flood types show negligible change compared to the hyetograph ones, implying a small dampening effect in spreadness through the rainfall-runoff processes. This is also later suggested by the close-to-one median of the γMRE,Sd. A comparison between rain flood and flash flood reveals that the values of CRMSD are decreasing; this is because the spreadness of the flash flood is smaller than that of the rain flood and thus results in a lower degree of random error. Different from the CRMSD, the correlation values reveal improvements from the hyetograph to the hydrograph (from below to above 0.8 and below to above 0.4 for rain flood and flash flood, respectively).

Figure 5.
Same as in Figure 3, but for the spreadness.
The means of MRE determined based on the three properties of the study rainfall and flow event time series are reported in Table 3 for each product. It is seen that MREs in rainfall depth is not linearly related to those in the runoff depth, indicated by fairly low correlation coefficient (CC) values for most of the products. Results suggest that the total depth of rainfall is mostly underestimated; this leads also to underestimations for the event runoff. The MREs of runoff centroid and spreadness appear generally uncorrelated with the MRE of the rainfall centroid, which suggests that differences in the hyetographs are not linearly translated into differences in the shape of the hydrographs. A potential explanation for this is given by the fact that hydrograph shape is controlled, apart from rainfall temporal variability, by the space-time interaction between the generated flow and flow routing [42,43]. Most of the mean MRE magnitudes in event rainfall centroid and spreadness are larger than the event flow ones, indicating higher similarity in the shape of the hydrograph compared to the corresponding hyetograph. This reveals the filtering effect of the catchment which smooths the high frequency precipitation signal to a low frequency flow signal [44,45]. We show also the mean MRE of peak flow as a complement to the spreadness parameter. Generally, the mean peak flow MREs are negative (except for the CM case), indicating underestimation in the peak flow rate. The CC values demonstrate the positive relationship between MREs in peak flow and rainfall depth (except for CM and aCM). A product-wise comparison reveals that the gauge-adjusted products show improvements in the mean MRE of cumulative depth, in contrast to the cases of event centroid and spreadness which show no improvements. This is an expected observation since the gauge-adjustment algorithms for satellite products are monthly (i.e., the adjustment changes the cumulative volume of precipitation within the monthly period but maintains the space-time variability of precipitation fields).

Table 3.
Mean MRE for rainfall and runoff and the correlation coefficient between the biases.
The random errors quantified by the centered relative root mean square difference (CRRMSD) for each event pair are visualized as boxplots in Figure 6 for the two food types. As it is observed from the top and bottom panels, the medians and value ranges of event rainfall CRRMSD are almost 10 times (four times) of the runoff ones for the rain flood (flash flood) events. This represents a significant dampening of the random error component (in terms of the overall value and value variability) through the rainfall-runoff process. Dampening in random error through the hydrologic model is expected since the output flow signal is less dynamic relative to the rainfall forcing, which has been reported in several error propagation studies [3,9,10,11]. Comparing the two flood types reveals that the centered relative root mean square differences for both the event rainfall and runoff are closer for the flash flood cases, characterized by narrower value ranges. This could be attributed to the higher runoff coefficient condition in flash flooding, which leads to a more linear behavior in error translation. The magnitudes of CRRMSD between the near–real-time and gauge-adjusted products are fairly similar which, again, could be due to the nature of gauge-adjusted algorithms as stated in the previous paragraph.

Figure 6.
Boxplots of the centered relative root mean square difference. Cross corresponds to outlier and circles represent median.
4.2. Error Propagation
To further investigate the patterns of the error propagation of event properties from precipitation to runoff simulations, the ratios of MREs between rainfall and runoff are taken (denoted as γ). The γ values for all the events and products are rendered as boxplots in Figure 7. The upper panel of Figure 7 shows the ratio of MREs of cumulative depth for the two flood types. It is seen that the values are mostly around 1, indicating a weak dampening effect in the volumetric error when translating the event rainfall to runoff. This is consistent with the value magnitudes for mean MREs of rainfall and runoff exhibited in Table 3. The middle panel of Figure 7 displays the γMRE of event centroids (mostly from 0.01 to 10). A clear error buffering effect in the MRE of the event centroid is revealed by the smaller-than-one γMRE,Ct values, confirming the observation from Table 3. This means that with the various differences in the arrival of the rainfall event, the rainfall-runoff processes are able to mitigate these differences and give a closer estimation in the arrival of flood events. The event spreadness is demonstrated in the last panel, with results showing, again, a dampening effect as it is in Table 3 (25th and 75th quantiles of γMRE,Sd are distributed within 0.1 to 1). This could be anticipated since, in general, the shapes of the hydrograph (from different rainfall forcing) are much more alike with each other than those of the hyetograph. The gauge-adjustment is concluded to have a limited effect on the error in time series shape given the almost identical γMRE,Ct and γMRE,Sd between the near–real-time products and their corresponding gauge-adjusted counterparts. This is also explained by the same reason that gauge adjustment is not able to change the space-time dynamic of rainfall at event scales.

Figure 7.
Ratio of mean relative error for the depth (top panel); centroid (middle panel) and spreadness properties (bottom panel). Cross corresponds to outlier and circles represent median.
Similar to the MRE, the error propagation of CRRMSD is quantified by the γCRRMSD values shown in Figure 8. The CRRMSD ratio patterns are not very distinctive between products. The upper panel representing the two flood types further confirms the random error dampening effect (revealed in Figure 6) by giving γCRRMSD values lower than 1. The figure also demonstrates that the differences in random error dampening for the two flood types are not the same. The CRRMSD ratios of rain flood range from 0.05 to 0.2 for most of the event pairs (in terms of the 25th and 75th quantiles) while the flash flood counterparts are noticeably higher, distributed mostly from 0.1 to 0.4. This is ascribed to the stronger linear precipitation-to-runoff error translation for the flash flood events (due to the higher RC). The role of RC on the random error propagation is visualized in the lower panel of Figure 8. The boxplots indicate an increase in the γCRRMSD values with the event-based runoff coefficients but a decrease in their value ranges, indicating a positive relationship between RC and the degree of linearity [3,15]. Values of γCRRMSD for both gauge-adjusted and near–real-time products are almost identical because gauge adjustment changes the overall magnitude rather than the space-time organization of precipitation.

Figure 8.
Ratio of centered relative root mean square difference sorted according to flood type (top panel) and runoff coefficient (bottom panel). Cross corresponds to outlier and circles represent median.
5. Discussion
Overall, results from this study show that the satellite-derived cumulative depth deviates significantly from the gauge-based one while the satellite performance in estimating the centroid and spreadness is generally better (both in terms of rainfall and simulated runoff). Specifically, a lower degree of random error (CRMSD) with a higher temporal correlation (ρ) is found in the estimates from the hydrograph cases for the three event properties’ parameters. It is also noted that the gauge adjustments to the satellite products and spatial aggregation yield a similar degree of consistency in the event centroid and spreadness parameters described by the Taylor diagram statistics.
The systematic error in terms of MRE revealed mostly underestimation in the cumulative depth parameter. The MRE magnitudes for the shape parameters (centroid and spreadness) exhibited more pronounced significance for the hyetograph relative to the simulated runoff due to the dampening of error from rainfall to runoff. Systematic error of the cumulative depth and shape parameters in rainfall is uncorrelated with error in runoff depth. This is due to the fact that the volume and shape of the flood hydrograph is controlled not only by the volume and shape of the hyetograph but also by the space-time structure of runoff generation and routing. The magnitude of random error quantified by CRRMSD is found to be higher in the hyetograph. Also, rain flood events exhibited higher CRRMSD magnitudes than the flash flood events. Gauge adjustment in satellite products yielded improvement in the systematic error of cumulative depth, but the systematic error of shape parameters as well as the random error component remained unaffected.
Investigation of the propagation of precipitation error to runoff reveals a clear dampening effect in the MRE of the centroid and spreadness parameters, but not in the cumulative depth. The error propagation ratio of cumulative depth for most of the products is fairly close to one. These findings indicate that discrepancies in hyetograph shape can be smoothed out by the rainfall-runoff process at catchment scale, which acts as a space-time filter [45]. However, underestimation of rainfall volume remains a main issue in capturing flood magnitude. Finally, examination of the error propagation dependence on flood type and runoff coefficient showed a clear dependence to both factors. Specifically, a higher degree of linearity in error propagation is associated with flash flood events and events with higher runoff coefficients.
6. Conclusions
In this work, an event-based analysis of satellite rainfall estimation error and its propagation in streamflow simulations is conducted for a number of flood events over mountainous basins in the Eastern Italian Alps. Conclusions are summarized relative to two main aspects that include the error statistics of rainfall/runoff properties (cumulative depth, centroid, spreadness) and the propagation of error with reference to these properties. For the first aspect, it is concluded that compared to the volumetric parameter, the shape-related parameters of rainfall and simulated runoff are better captured by the satellite, indicated by lower random error and higher correlation in the Taylor diagram. Comparisons between error statistics of parameters for different products also suggest that the gauge adjustments have effects on the volumetric parameter but not on the shape-related parameters.
For the error propagation aspect, systematic error of the shape-related parameters and random error show, on average, a general decrease from rainfall to runoff, but this does not hold for the error in the volumetric parameter, which maintains a γ value close to 1. Results also reveal that higher linearity in error propagation is shown for events with a higher runoff coefficient.
We recognize that results from this analysis can mainly represent satellite applications over mountainous basins with hydroclimatic and geomorphologic characteristics similar to the Alpine environment. Besides, this study was conducted based on a relatively limited number of flood events, particularly for the flash flood event type given that the occurrence frequency of this flood event type is comparatively low. However, the results of our study highlight current challenges in using satellite-based precipitation for modeling flood response over complex topography. We believe that our findings will offer the end users (e.g., hydrologic agencies, civil protection, etc.) important indications on the associated sources and magnitude of uncertainty in satellite-based flood prediction, which can serve as guidance for a number of flood-risk operations and decision-making. Future studies should evaluate the potential of the newly available high-resolution (0.1°/hourly) Integrated Multi-satellitE Retrievals for GPM (IMERG) product by also including the snowmelt-driven floods, which, although available in the flooding database, were excluded from this study. Lastly, even though this study did not demonstrate a particular benefit from using the high-resolution CMORPH product, other higher-resolution products such as the PERSIANN-CCS (0.04°/hourly), GSMaP (0.1°/hourly) and the newly available IMERG should be examined to further understand the potential impact of product resolution in the error properties of satellite precipitation–driven runoff simulations.
Acknowledgments
This work was supported by the NASA Precipitation Measurement Mission (Award Number: NNX07AE31G). Efthymios Nikolopoulos was supported by the EU-funded EartH2Observe (ENVE.2013.6.3-3) project. We acknowledge and appreciate Roberto Dinale from the Province of Bolzano for making the gauge data available in this study.
Author Contributions
Yiwen Mei, Emmanouil N. Anagnostou and Efthymios I. Nikolopoulos developed the research framework. Yiwen Mei processed the satellite precipitation data, matched the satellite-suggested events with the reference one, analyzed the data and established the original manuscript. Efthymios I. Nikolopoulos processed the gauge precipitation data, ran the hydrologic simulation and contributed to the writing of the manuscript. Emmanouil N. Anagnostou contributed to the writing of the manuscript. Davide Zoccatelli and Marco Borga provided the flood event database and edited the manuscript. Overall this article is great deal of coordinated effort.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Guetter, A.K.; Georgakakos, K.P.; Tsonis, A.A. Hydrologic applications of satellite data: 2. Flow simulation and soil water estimates. J. Geophys. Res. 1996, 101, 26527–26538. [Google Scholar] [CrossRef]
- Hossain, F.; Anagnostou, E.N. Assessment of current passive-microwave- and infrared-based satellite rainfall remote sensing for flood prediction. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef]
- Nikolopoulos, E.I.; Anagnostou, E.N.; Hossain, F.; Gebremichael, M.; Borga, M. Understanding the Scale Relationships of Uncertainty Propagation of Satellite Rainfall through a Distributed Hydrologic Model. J. Hydrometeorol. 2010, 11, 520–532. [Google Scholar] [CrossRef]
- Siddique-E-Akbor, A.H.M.; Hossain, F.; Sikder, S.; Shum, C.K.; Tseng, S.; Yi, Y.; Turk, F.J.; Limaye, A. Satellite Precipitation Data–Driven Hydrological Modeling for Water Resources Management in the Ganges, Brahmaputra, and Meghna Basins. Earth Interact. 2014, 18, 1–25. [Google Scholar] [CrossRef]
- Seyyedi, H.; Anagnostou, E.N.; Beighley, E.; McCollum, J. Hydrologic Evaluation of Satellite and Reanalysis Precipitation Datasets over a Mid-Latitude Basin. Atmos. Res. 2015, 164–165, 37–48. [Google Scholar] [CrossRef]
- Arkin, P.A.; Ardanuy, P.E. Estimating Climatic-Scale Precipitation from Space: A Review. J. Clim. 1989, 2, 1229–1238. [Google Scholar] [CrossRef]
- Kidd, C.; Kniveton, D.R.; Todd, M.C.; Bellerby, T.J. Satellite Rainfall Estimation Using Combined Passive Microwave and Infrared Algorithms. J. Hydrometeorol. 2003, 4, 1088–1104. [Google Scholar] [CrossRef]
- Anagnostou, E.N.; Maggioni, V.; Nikolopoulos, E.I.; Meskele, T.; Hossain, F.; Papadopoulos, A. Benchmarking High-Resolution Global Satellite Rainfall Products to Radar and Rain-Gauge Rainfall Estimates. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1667–1683. [Google Scholar] [CrossRef]
- Maggioni, V.; Vergara, H.J.; Anagnostou, E.N.; Gourley, J.J.; Hong, Y.; Stampoulis, D. Investigating the Applicability of Error Correction Ensembles of Satellite Rainfall Products in River Flow Simulations. J. Hydrometeorol. 2013, 14, 1194–1211. [Google Scholar] [CrossRef]
- Vergara, H.J.; Hong, Y.; Gourley, J.J.; Anagnostou, E.N.; Maggioni, V.; Stampoulis, D.; Kirstetter, P.-E. Effects of Resolution of Satellite-Based Rainfall Estimates on Hydrologic Modeling Skill at Different Scales. J. Hydrometeorol. 2013, 15, 593–613. [Google Scholar] [CrossRef]
- Mei, Y.; Nikolopoulos, E.I.; Anagnostou, E.N.; Borga, M. Evaluating Satellite Precipitation Error Propagation in Runoff Simulations of Mountainous Basins. J. Hydrometeorol. 2015. In press. [Google Scholar] [CrossRef]
- Yong, B.; Ren, L.-L.; Hong, Y.; Wang, J.-H.; Gourley, J.J.; Jiang, S.-H.; Chen, X.; Wang, W. Hydrologic evaluation of Multisatellite Precipitation Analysis standard precipitation products in basins beyond its inclined latitude band: A case study in Laohahe basin, China. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Yong, B.; Hong, Y.; Ren, L.-L.; Gourley, J.J.; Huffman, G.J.; Chen, X.; Wang, W.; Khan, S.I. Assessment of evolving TRMM-based multisatellite real-time precipitation estimation methods andtheir impacts on hydrologic prediction in a high latitude basin. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Wu, H.; Adler, R.F.; Hong, Y.; Tian, Y.; Policelli, F. Evaluation of Global Flood Detection Using Satellite-Based Rainfall and a Hydrologic Model. J. Hydrometeorol. 2012, 13, 1268–1284. [Google Scholar] [CrossRef]
- Nikolopoulos, E.I.; Anagnostou, E.N.; Borga, M. Using High-resolution Satellite Rainfall Products to Simulate a Major Flash Flood Event in Northern Italy. J. Hydrometeorol. 2013, 14, 171–185. [Google Scholar] [CrossRef]
- Mei, Y.; Nikolopoulos, E.I.; Anagnostou, E.N.; Borga, M. Error Analysis of Satellite Rainfall Products in Mountainous Basins. J. Hydrometeorol. 2014, 15, 1778–1789. [Google Scholar] [CrossRef]
- Yong, B.; Liu, D.; Gourley, J.J.; Tian, Y.; Huffman, G.J.; Ren, L.-L.; Hong, Y. Global view of real-time TRMM Multi-satellite Precipitation Analysis: Implication to its successor Global Precipitation Measurement mission. Bull. Am. Meteor. Soc. 2014, 96, 283–296. [Google Scholar] [CrossRef]
- Yilmaz, K.K.; Adler, R.F.; Tian, Y.; Hong, Y.; Pierce, H.F. Evaluation of a satellite-based global flood monitoring system. Int. J. Remote Sens. 2010, 31, 3763–3782. [Google Scholar] [CrossRef]
- Zoccatelli, D.; Parajka, J.; Gaál, L.; Blöschl, G.; Borga, M. A process flood typology along an Alpine transect: analysis based on observations and modelling approaches. J. Hydrol. 2016. Submitted. [Google Scholar]
- Parajka, J.; Kohnová, S.; Bálint, G.; Marbuc, M.; Borga, M.; Claps, P.; Cheval, S.; Dumitrescu, A.; Gaume, É.; Hlavčová, K.; et al. Seasonal characteristics of flood regimes across the Alpine–Carpathian range. J. Hydrol. 2010, 394, 78–89. [Google Scholar] [CrossRef] [PubMed]
- Norbiato, D.; Borga, M.; Merz, R.; Blöschl, G.; Carton, A. Controls on event runoff coefficients in the eastern Italian Alps. J. Hydrol. 2009, 375, 312–325. [Google Scholar] [CrossRef]
- Frei, C.; Schär, C. A precipitation climatology of the Alps from high-resolution rain-gauge observations. Int. J. Climatol. 1998, 18, 873–900. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Nelkin, E.J. The TRMM Multi-Satellite Precipitation Analysis (TMPA). In Satellite Rainfall Applications for Surface Hydrology; Gebremichael, M., Hossain, F., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 2010; pp. 3–22. [Google Scholar]
- Sorooshian, S.; Hsu, K.-L.; Gao, X.; Gupta, H.V.; Iman, B.; Braithwaite, D. Evaluation of PERSIANN System Satellite–Based Estimates of Tropical Rainfall. Bull. Am. Meteor. Soc. 2000, 81, 2035–2046. [Google Scholar] [CrossRef]
- Adler, R.F.; Huffman, G.J.; Chang, A.; Ferraro, R.; Xie, P.-P.; Janowiak, J.; Rudolf, B.; Schneider, U.; Curtis, S.; Bolvin, D.; et al. The Version-2 Global Precipitation Climatology Project (GPCP) Monthly Precipitation Analysis (1979–Present). J. Hydrometeorol. 2003, 4, 1147–1167. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G. Improving the global precipitation record: GPCP Version 2.1. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method that Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Xie, P.; Yoo, S.-H.; Joyce, R.J.; Yarosh, Y. Bias-Corrected CMORPH: A 13-Year Analysis of High-Resolution Global Precipitation. In Proceedings of the 2011 EGU General Assembly, Vienna, Austria, 4–8 April 2011.
- Joyce, R.J.; Xie, P. Kalman Filter–Based CMORPH. J. Hydrometeorol. 2011, 12, 1547–1563. [Google Scholar] [CrossRef]
- Moore, R.J. The PDM rainfall-runoff model. Hydrol. Earth Syst. Sci. 2007, 11, 483–499. [Google Scholar] [CrossRef]
- Moore, R.J. The probability-distributed principle and runoff production at point and basin scales. Hydrol. Sci. J. 1985, 30, 273–297. [Google Scholar] [CrossRef]
- Cazorzi, F.; Dalla Fontana, G. Snowmelt modelling by combining air temperature and a distributed radiation index. J. Hydrol. 1996, 181, 169–187. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Estimating potential evapotranspiration. J. Irr. Drain. Div. 1982, 108, 225–230. [Google Scholar]
- Cunge, J.A. On The Subject of A Flood Propagation Computation Method (Musklngum Method). J. Hydraul. Res. 1969, 7, 205–230. [Google Scholar] [CrossRef]
- Norbiato, D.; Borga, M.; Dinale, R. Flash flood warning in ungauged basins by use of the flash flood guidance and model-based runoff thresholds. Met. Apps. 2009, 16, 65–75. [Google Scholar] [CrossRef]
- Borga, M.; Nikolopoulos, E.I.; Zoccatelli, D.; Marra, F. Extension of Adige River Flood Forecasting System for Debris Flow Forecasting, Simulation of Glacial Hydrology and Artificial Reservoir Storage Accounting. University of Padova. 2014. Available online: http://webcache.googleusercontent.com/search?q=cache:ZDL1lB2SSv0J:www.provinz.bz.it/zivilschutz/service/veroeffentlichungen.asp%3Fsomepubl_action%3D300%26somepubl_image_id%3D349342+&cd=1&hl=it&ct=clnk&gl=it (accessed on 9 January 2016).
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Merz, R.; Blöschl, G. A process typology of regional floods. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Mei, Y.; Anagnostou, E.N. A Hydrograph Separation Method Based on Information from Rainfall and Runoff Records. J. Hydrol. 2015, 523, 636–649. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Viglione, A.; Chirico, G.B.; Komma, J.; Woods, R.; Borga, M.; Blöschl, G. Quantifying space-time dynamics of flood event types. J. Hydrol. 2010, 394, 213–229. [Google Scholar] [CrossRef]
- Mei, Y.; Anagnostou, E.N.; Stampoulis, D.; Nikolopoulos, E.I.; Borga, M.; Vegara, H.J. Rainfall Organization Control on the Flood Response of Mild-slope Basins. J. Hydrol. 2014, 510, 565–577. [Google Scholar] [CrossRef]
- Skøien, J.O.; Blöschl, G.; Western, A.W. Characteristic space scales and timescales in hydrology. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Skøien, J.O.; Blöschl, G. Catchments as space-time filters—A joint spatio-temporal geostatistical analysis of runoff and precipitation. Hydrol. Earth Syst. Sci. 2006, 10, 645–662. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).