A New Global fAPAR and LAI Dataset Derived from Optimal Albedo Estimates: Comparison with MODIS Products
Abstract
:1. Introduction
1.1. Leaf Area Index (LAI)
Caveats: LAI
1.2. fAPAR: Fraction of Absorbed Photosynthetically Active Radiation
Caveats: fAPAR
2. Experimental Section
2.1. GlobAlbedo-Derived LAI and fAPAR
2.1.1. Two-Stream Model
2.1.2. Two-Stream Model Inversion
2.1.3. Spatial Resolution
2.1.4. Data Format
2.1.5. Time Period and Data Size
2.1.6. FLUXNET Sites Used for Site-Level Comparisons
- Grasslands
- Deciduous broadleaf
- Evergreen needleleaf
- Mixed forest
- Crop/natural
2.2. MODIS LAI and fAPAR
3. Results and Discussion
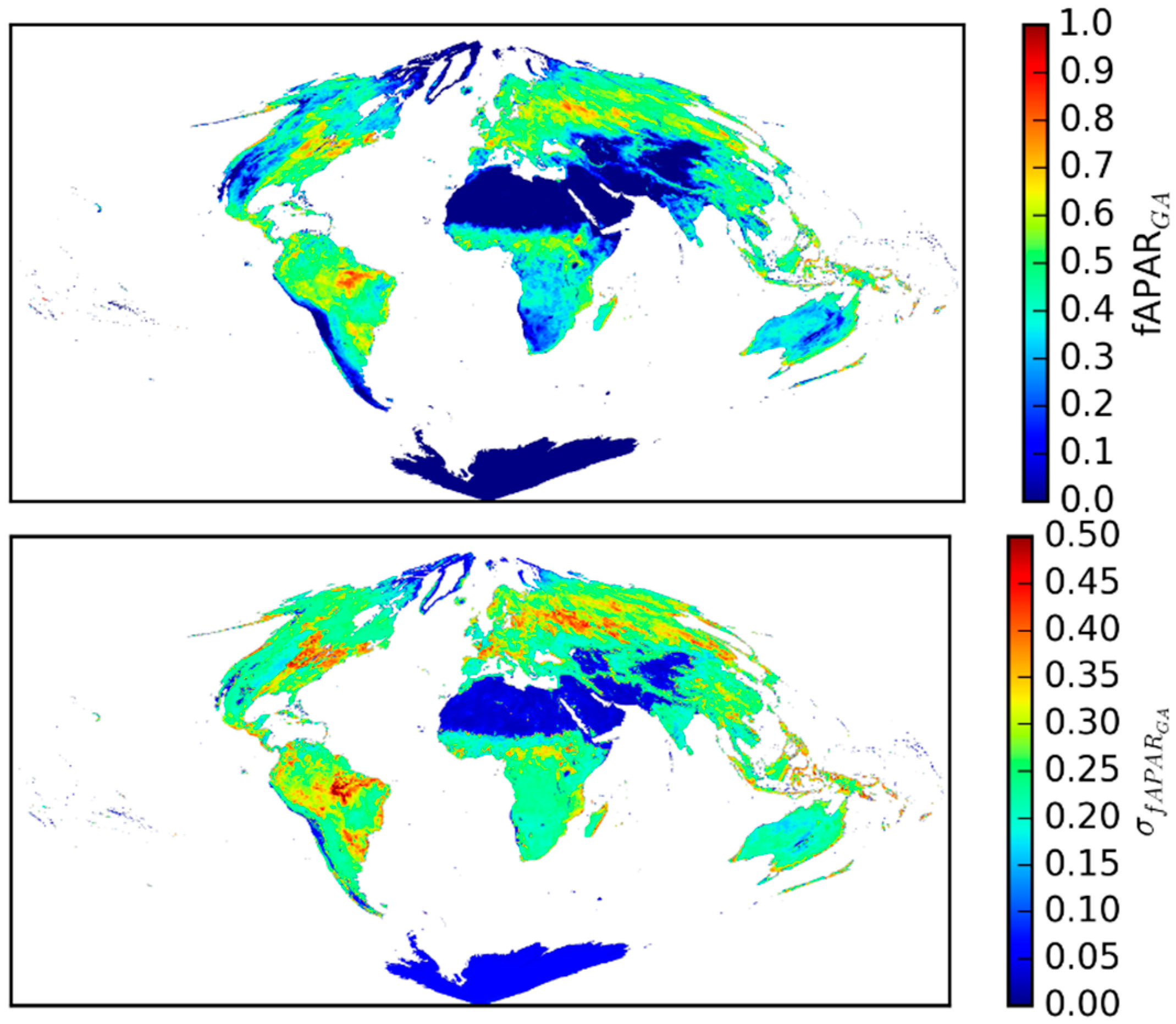
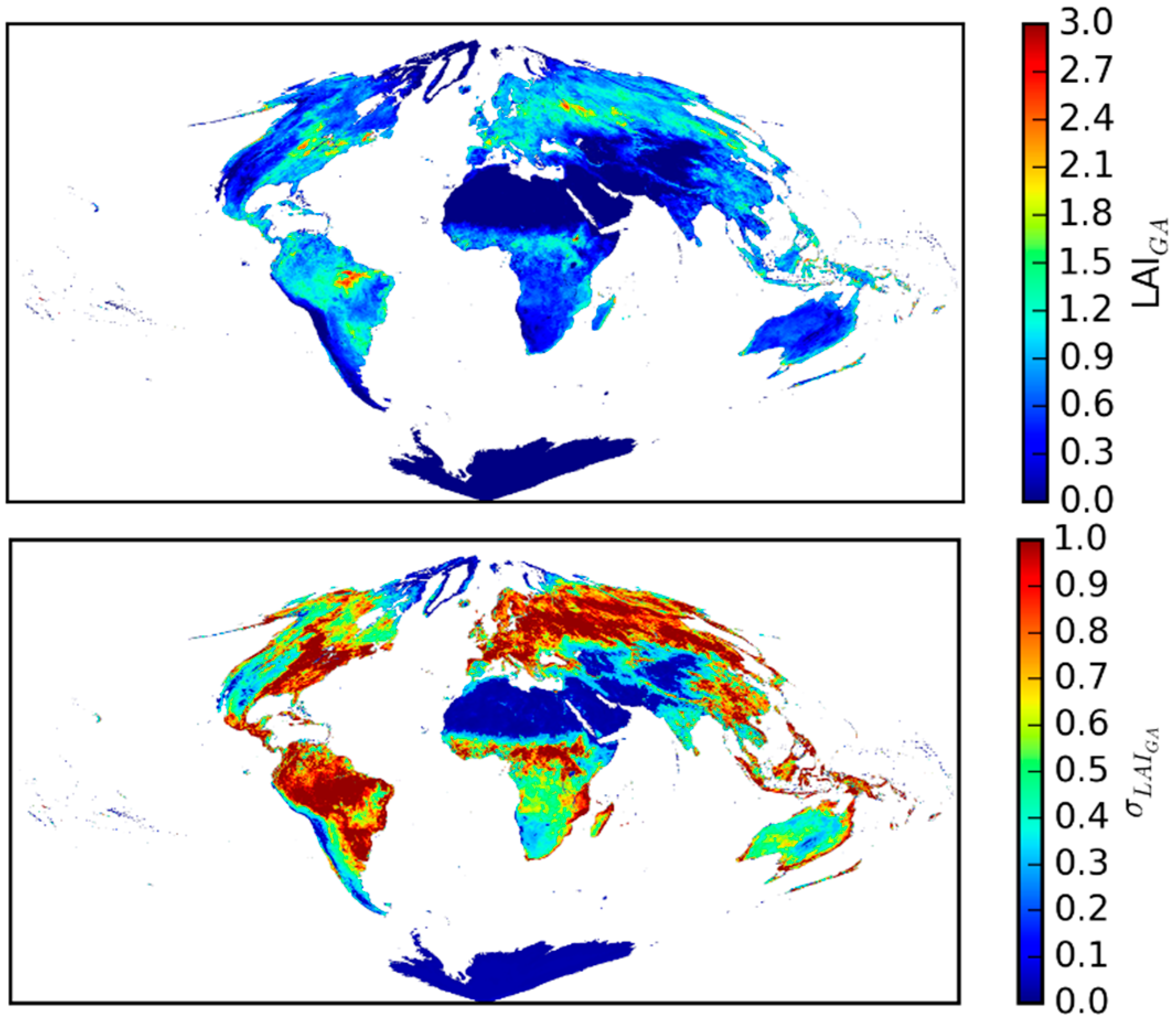
3.1. Global LAI and fAPAR Derived from GlobAlbedo
3.2. Site-Specific and Regional GlobAlbedo-Derived fAPAR and LAI
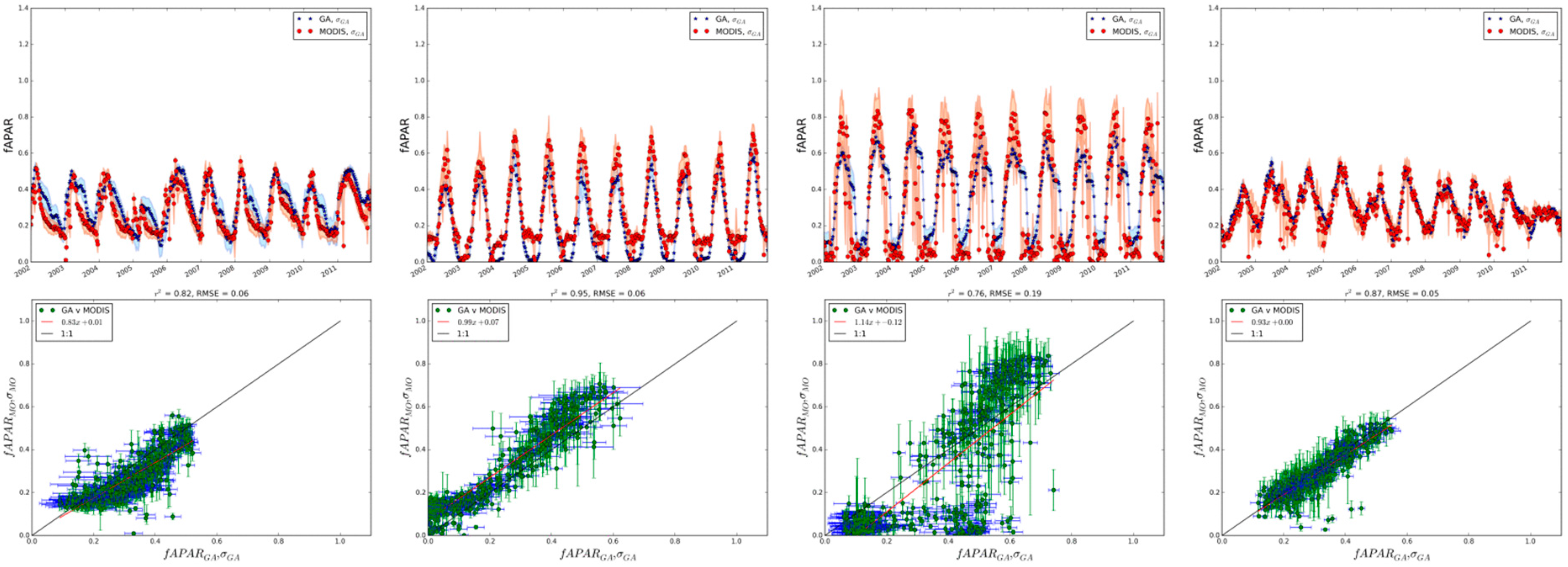
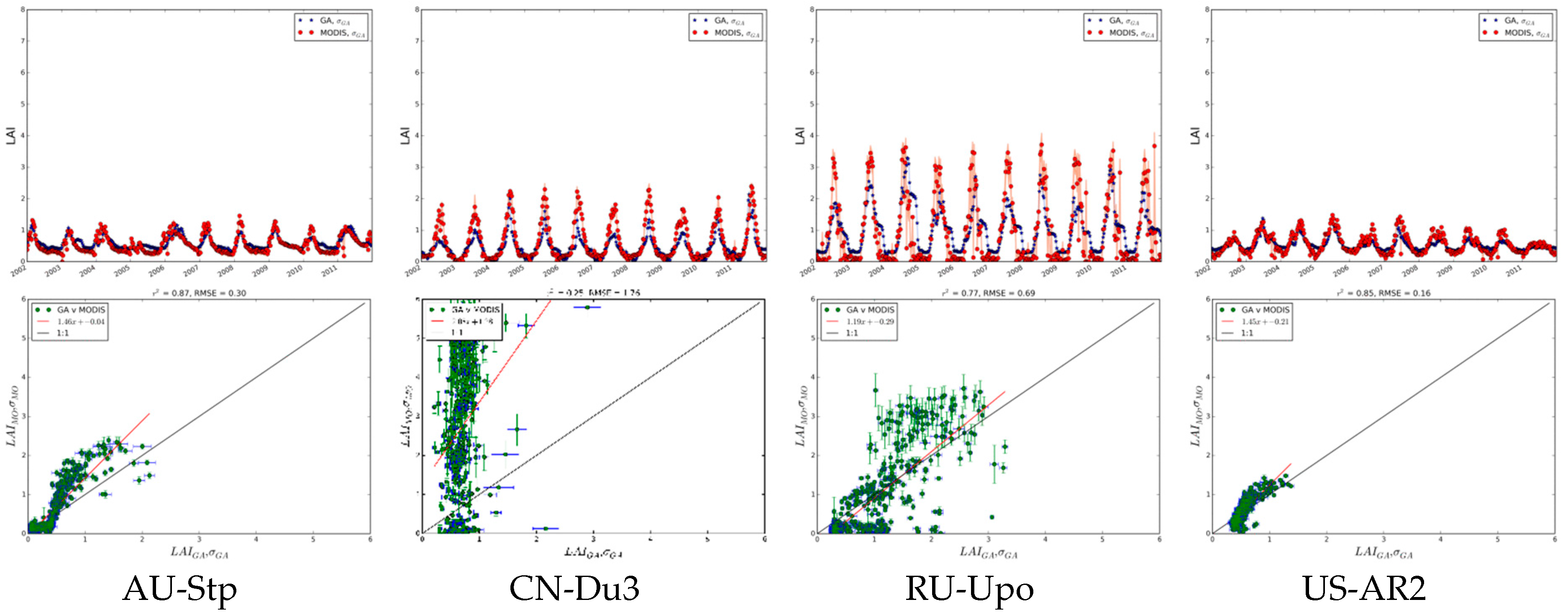
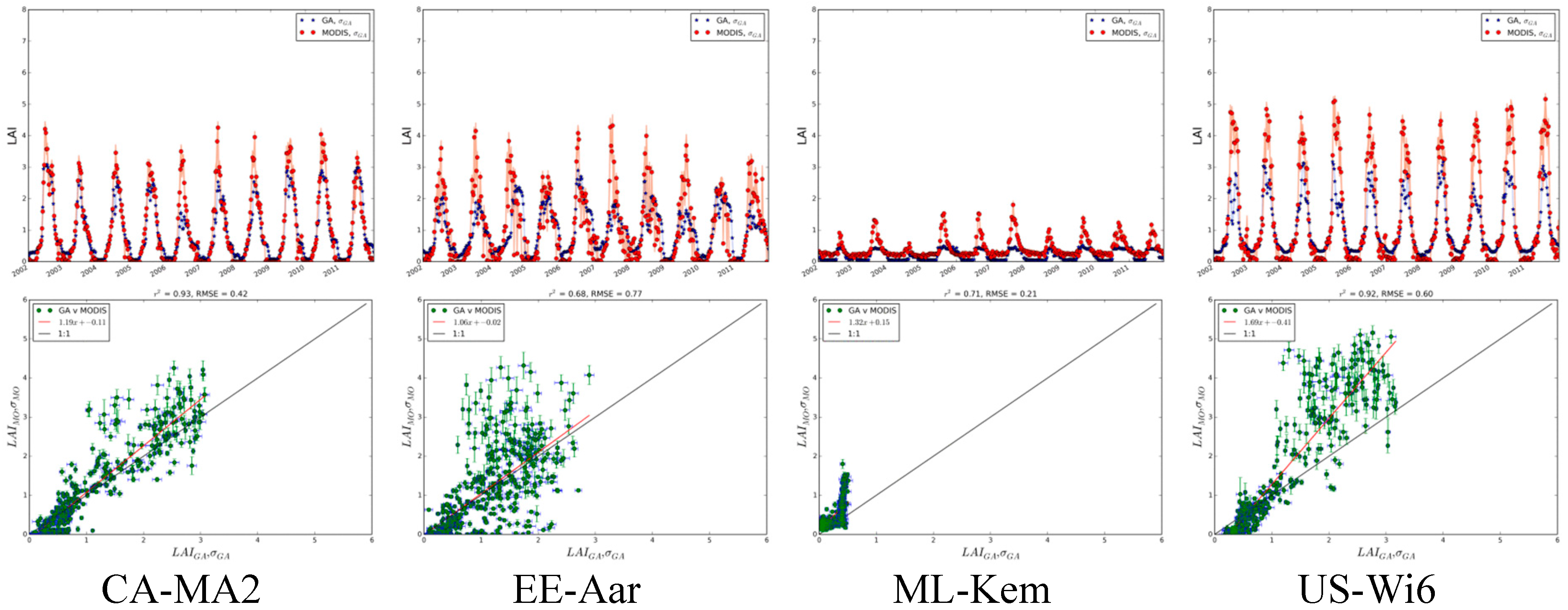
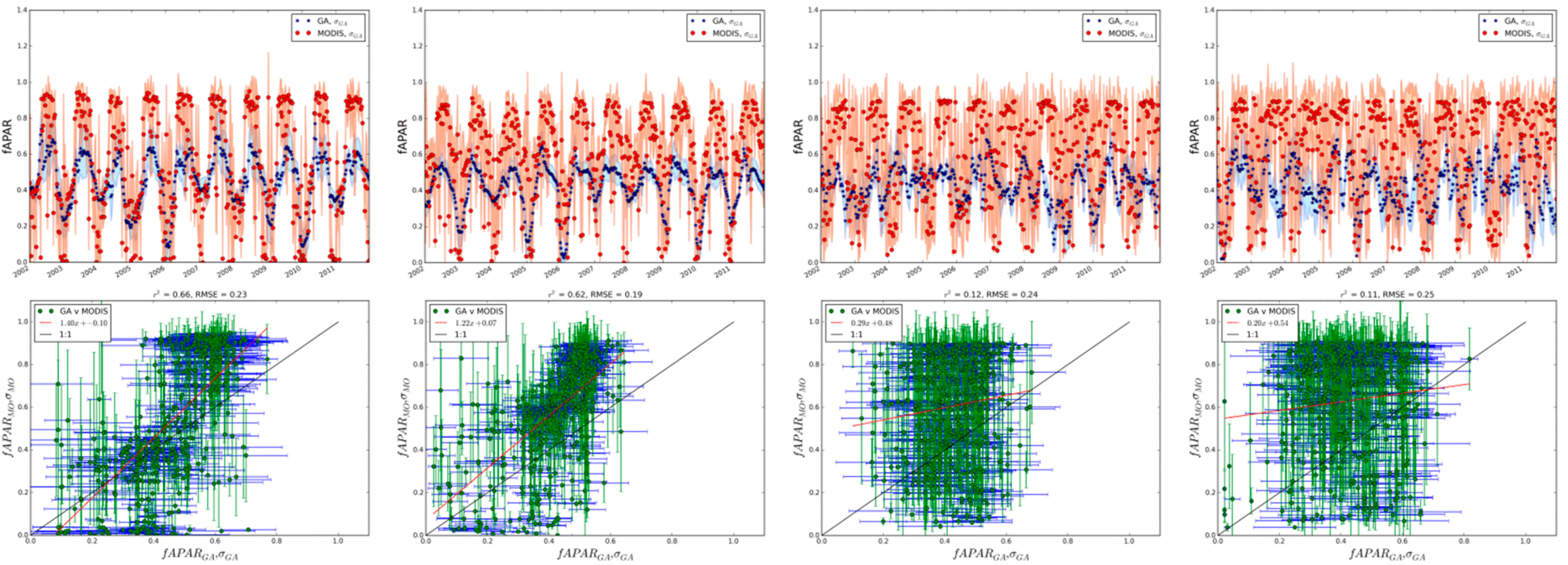
3.2.1. Flux Site Comparisons by Cover Type
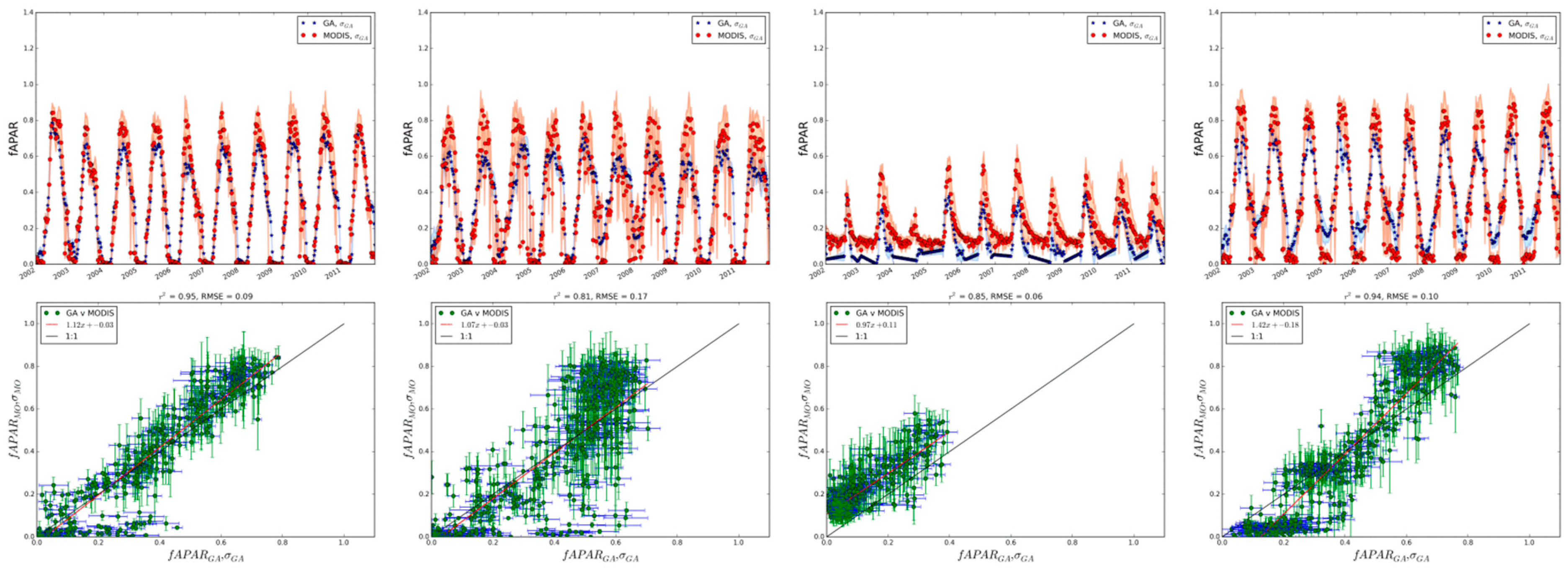
Grasslands
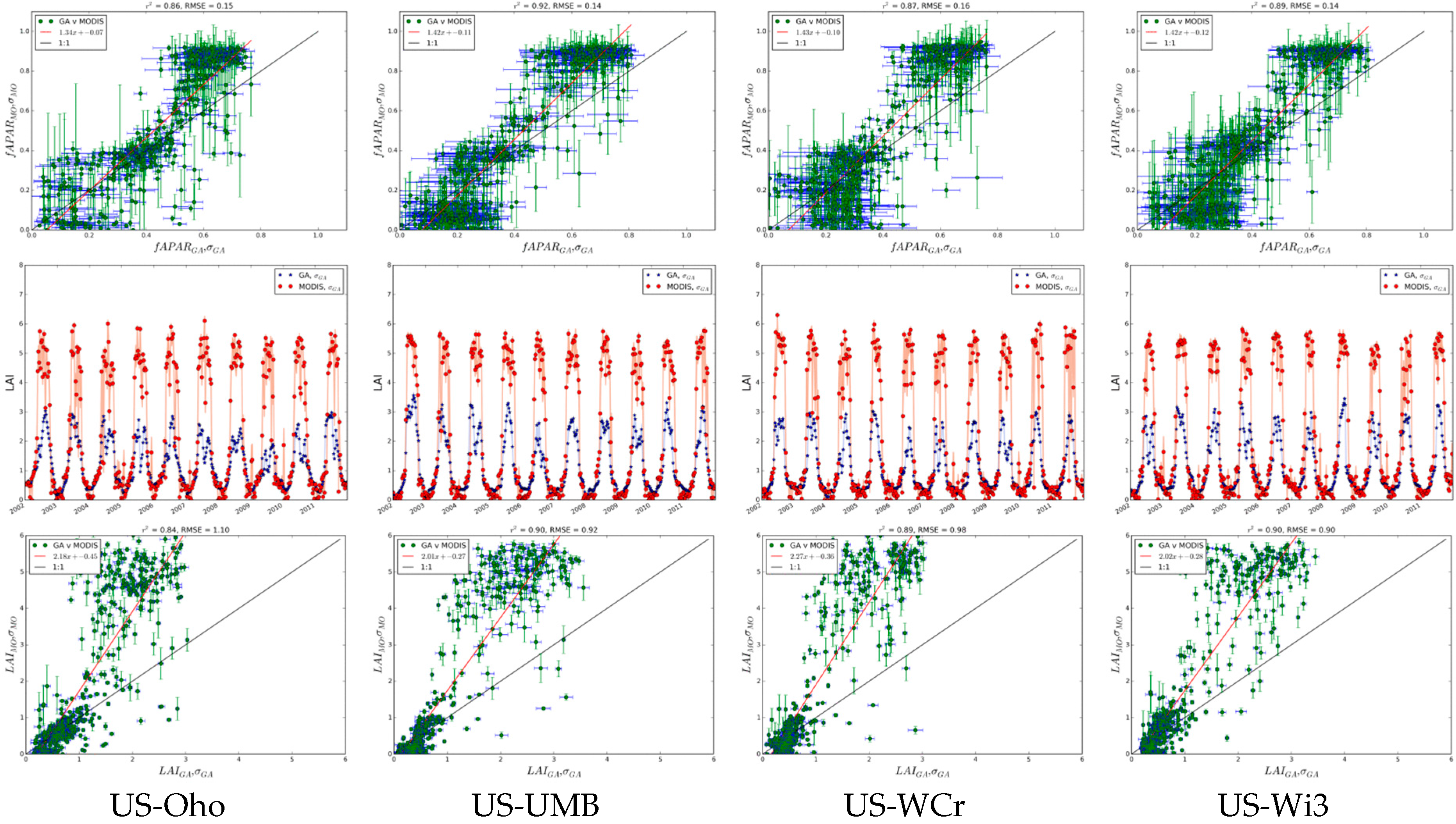
Deciduous Broadleaf Forest
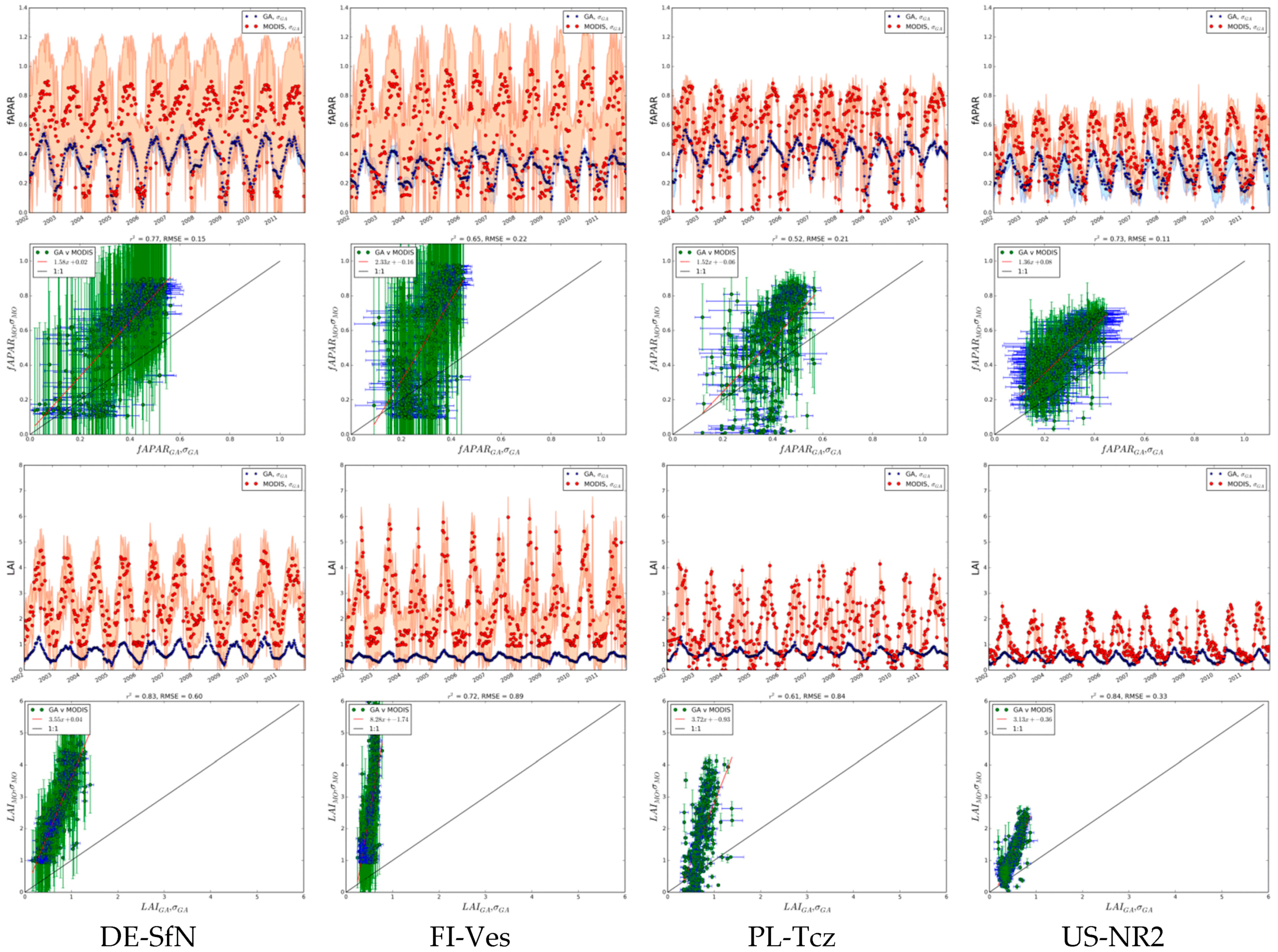
Evergreen Needleleaf Forest
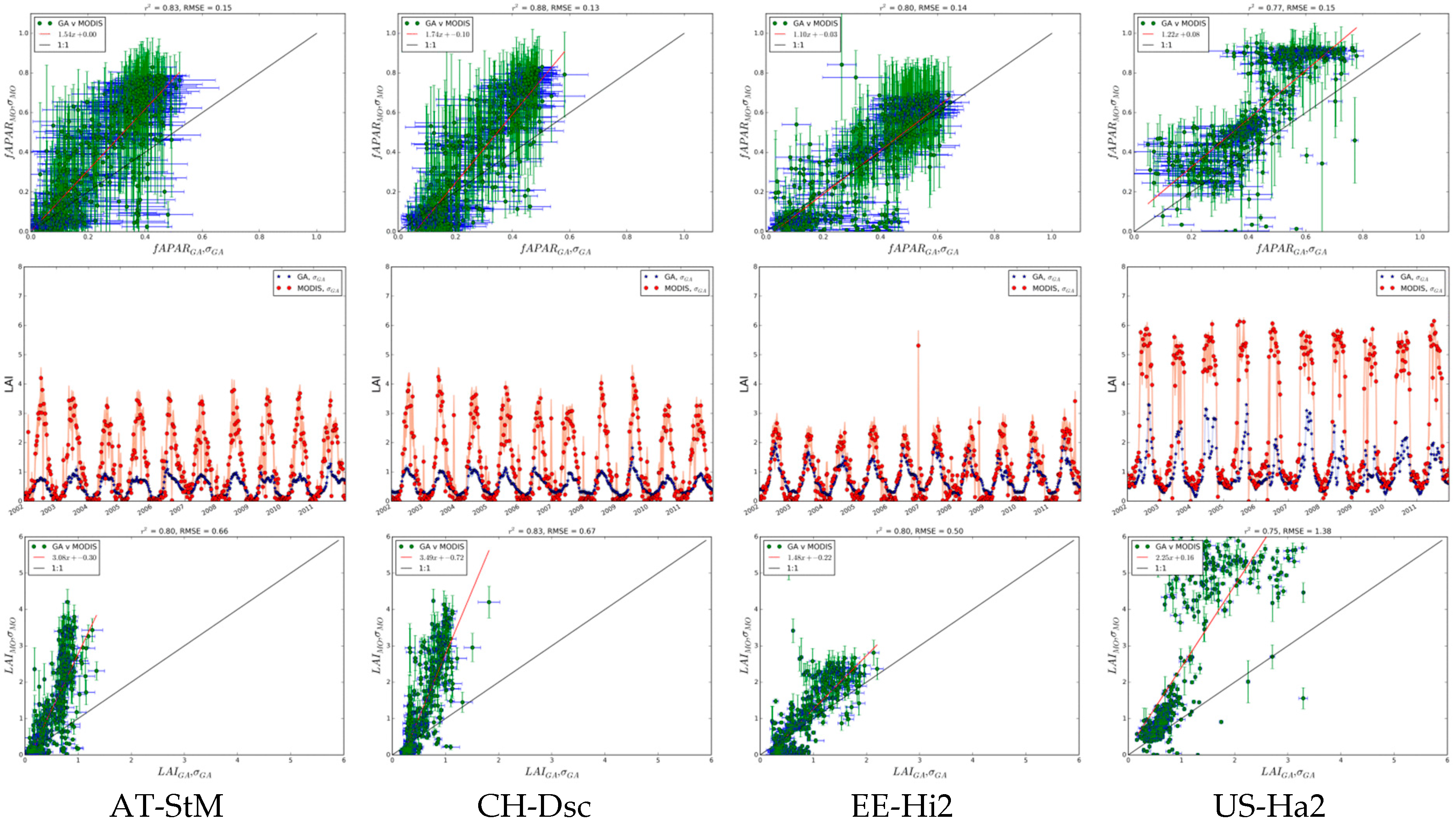
Mixed Forest
Crop/Natural
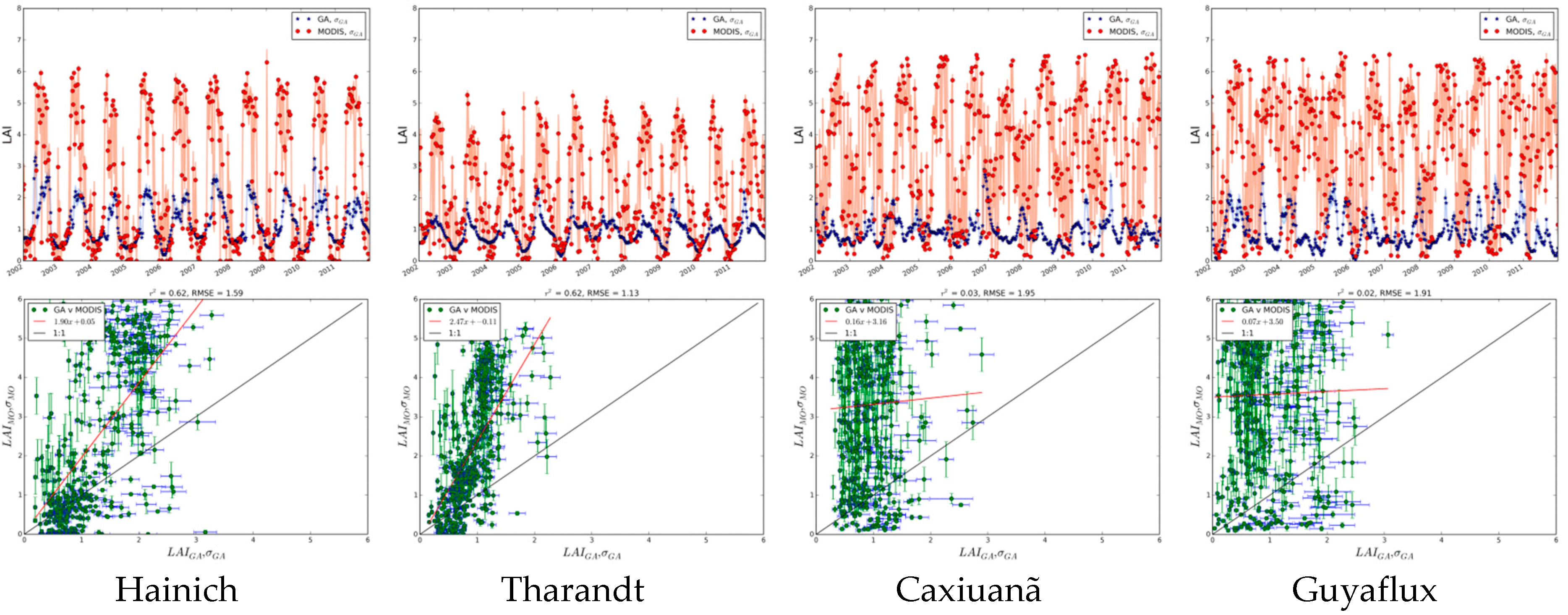
Miscellaneous
Summary of Site Comparisons
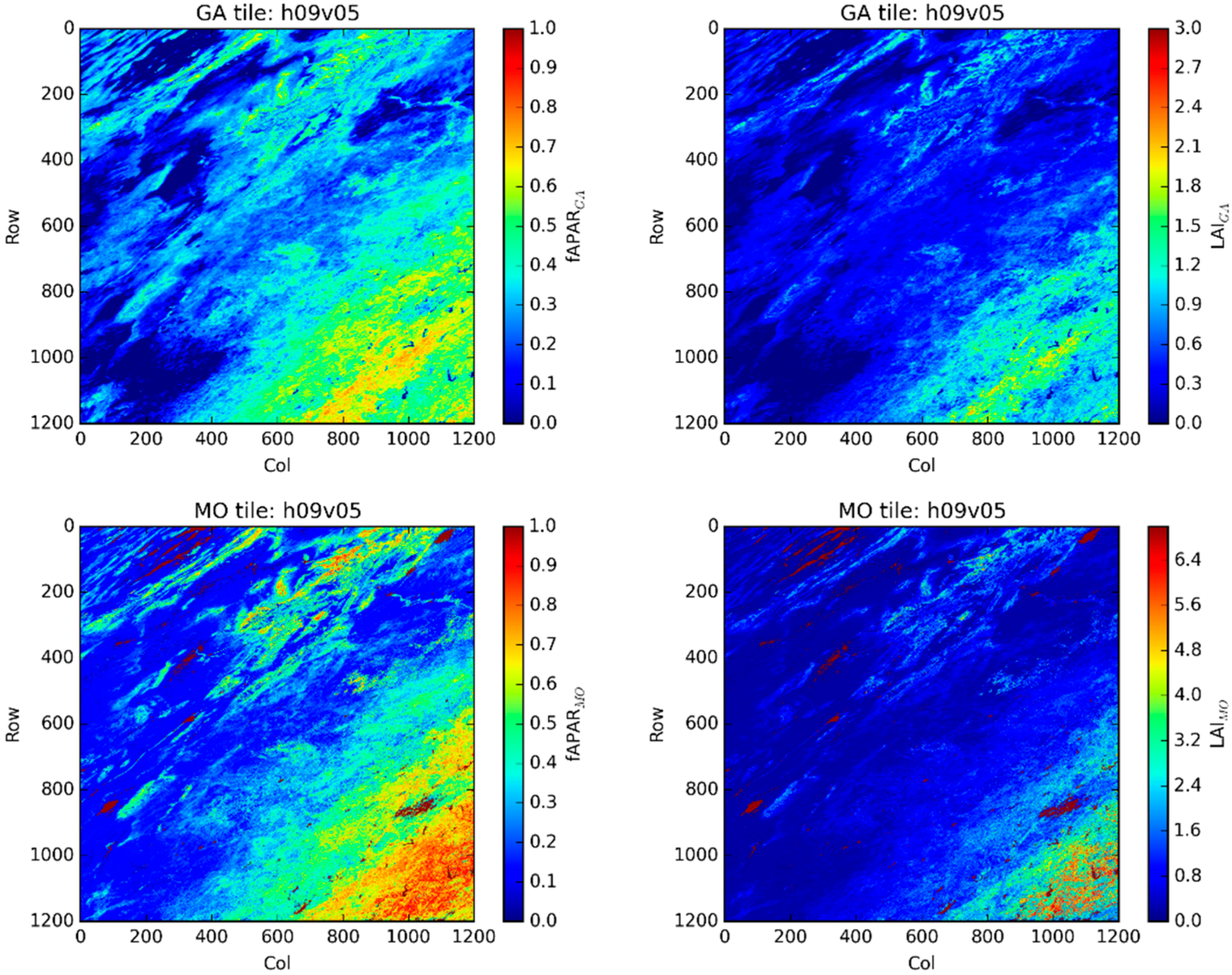
3.2.2. Regional Comparisons
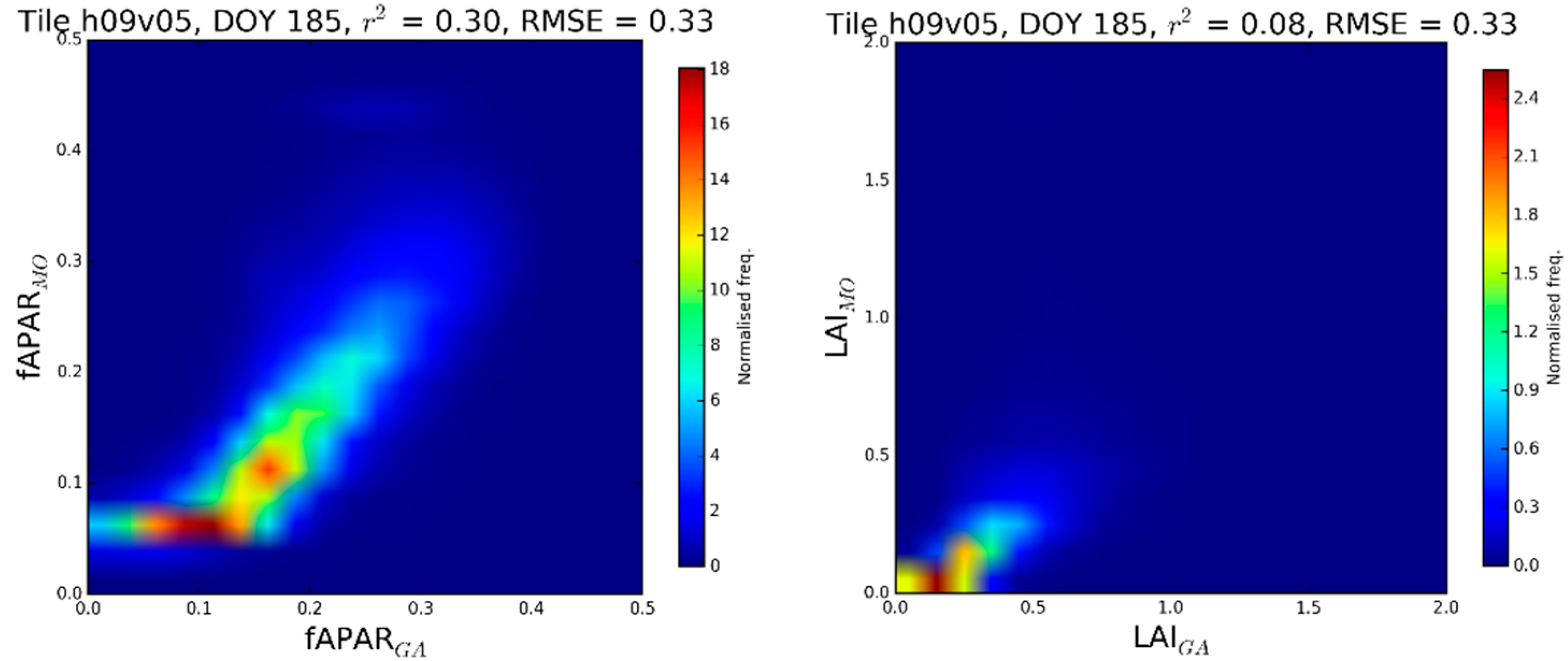
- h09v05: Central USA
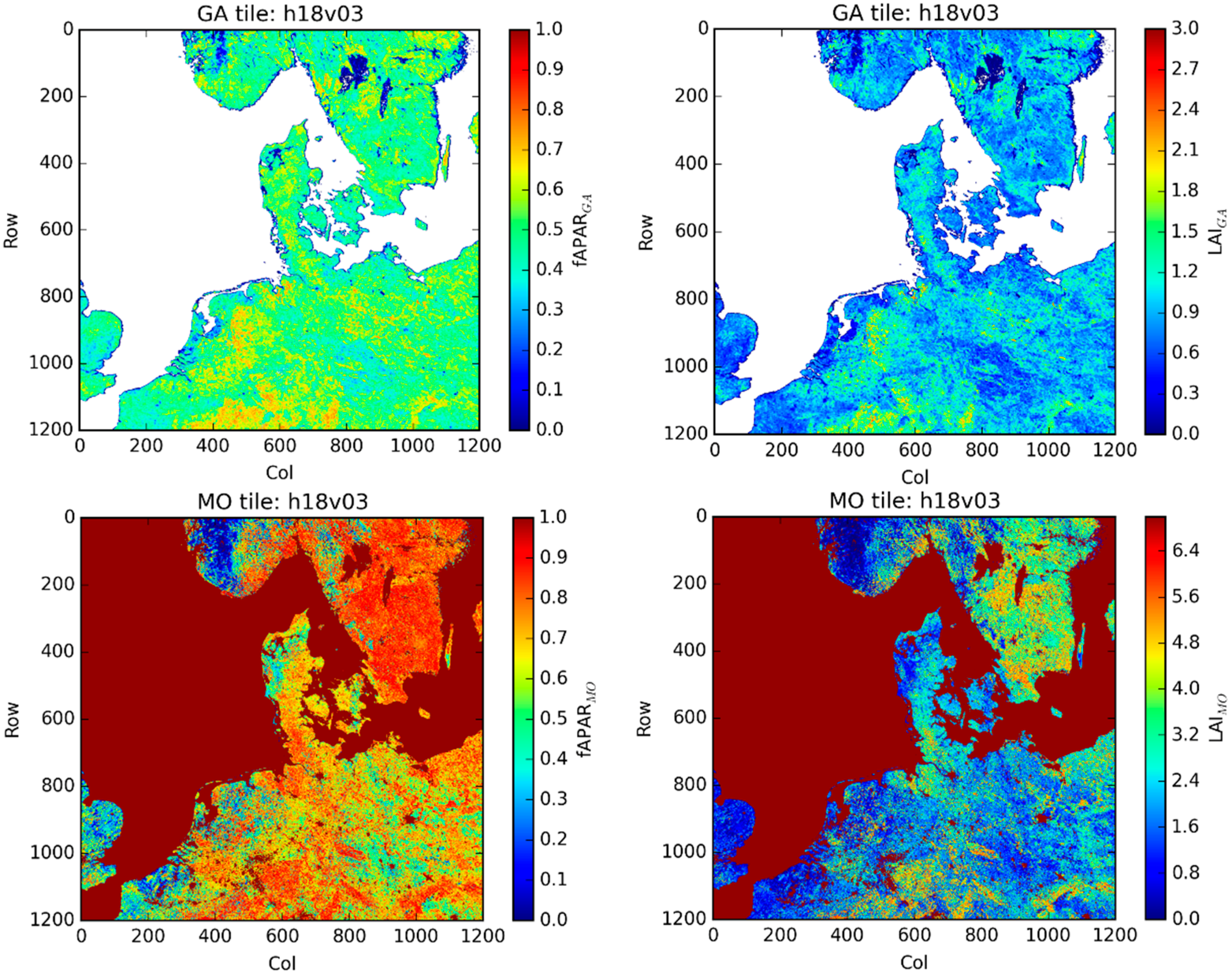
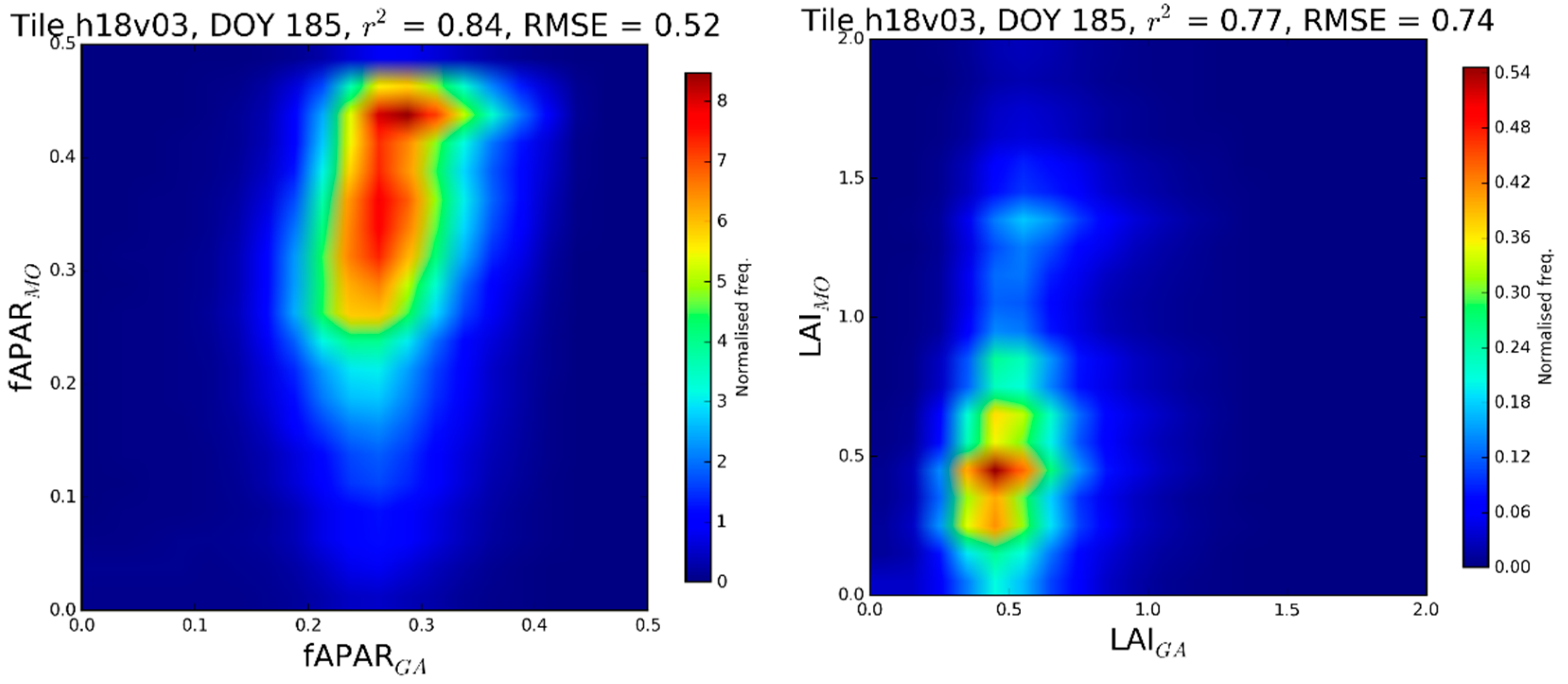
- h18v03: Western Europe
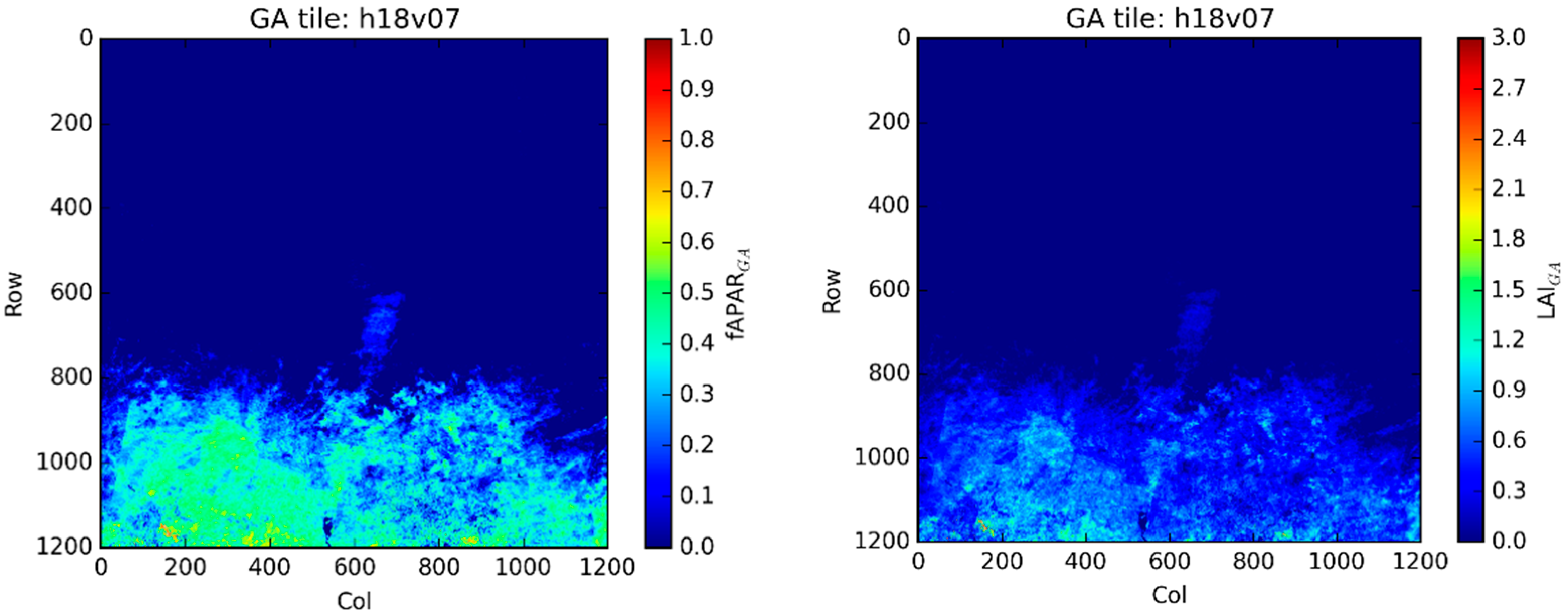
- h18v07: Central West Africa
- h29v12: South Australia
Central USA: Tile h09v05
Western Europe: Tile h18v03
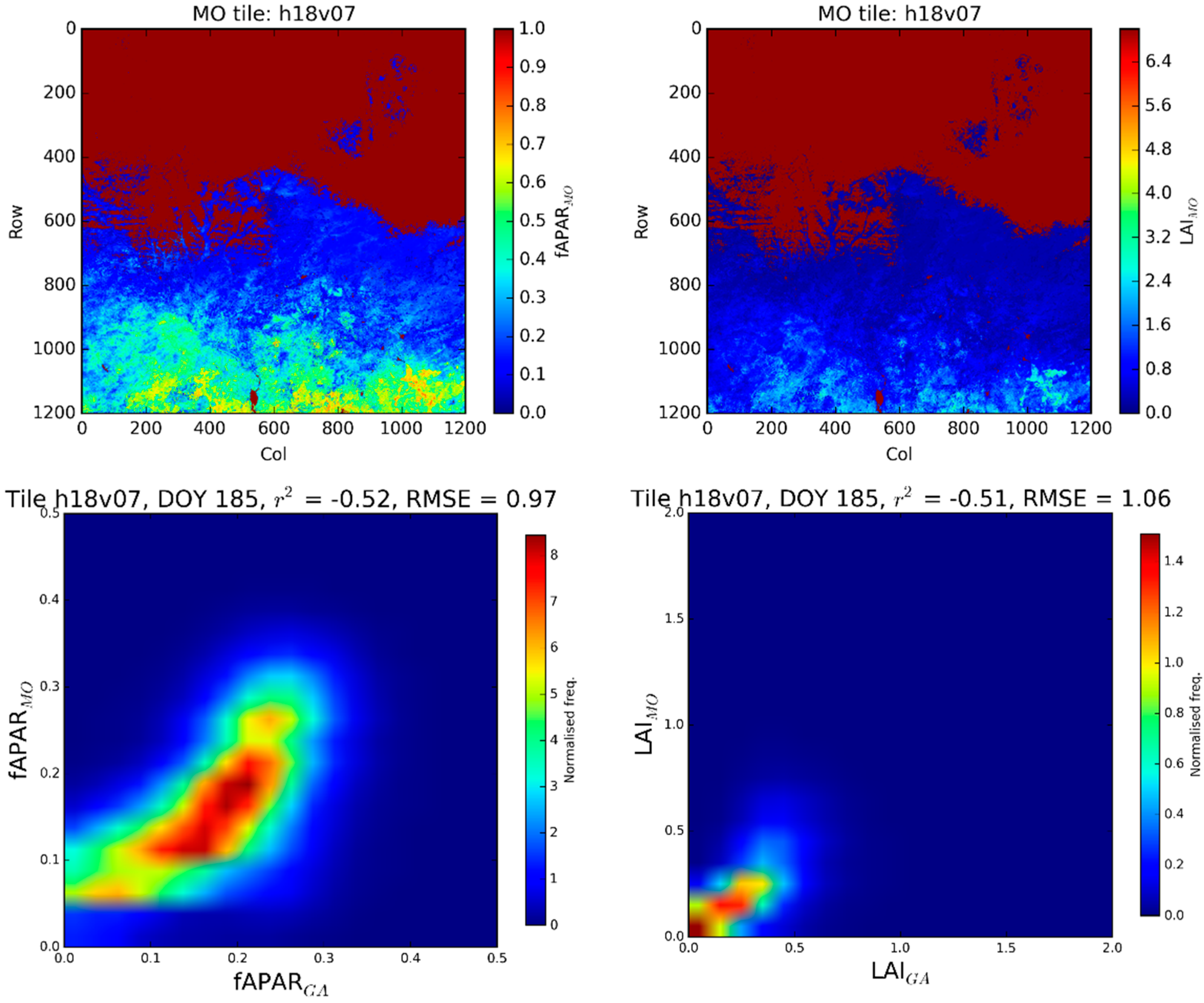
Central and West Africa: Tile h18v07
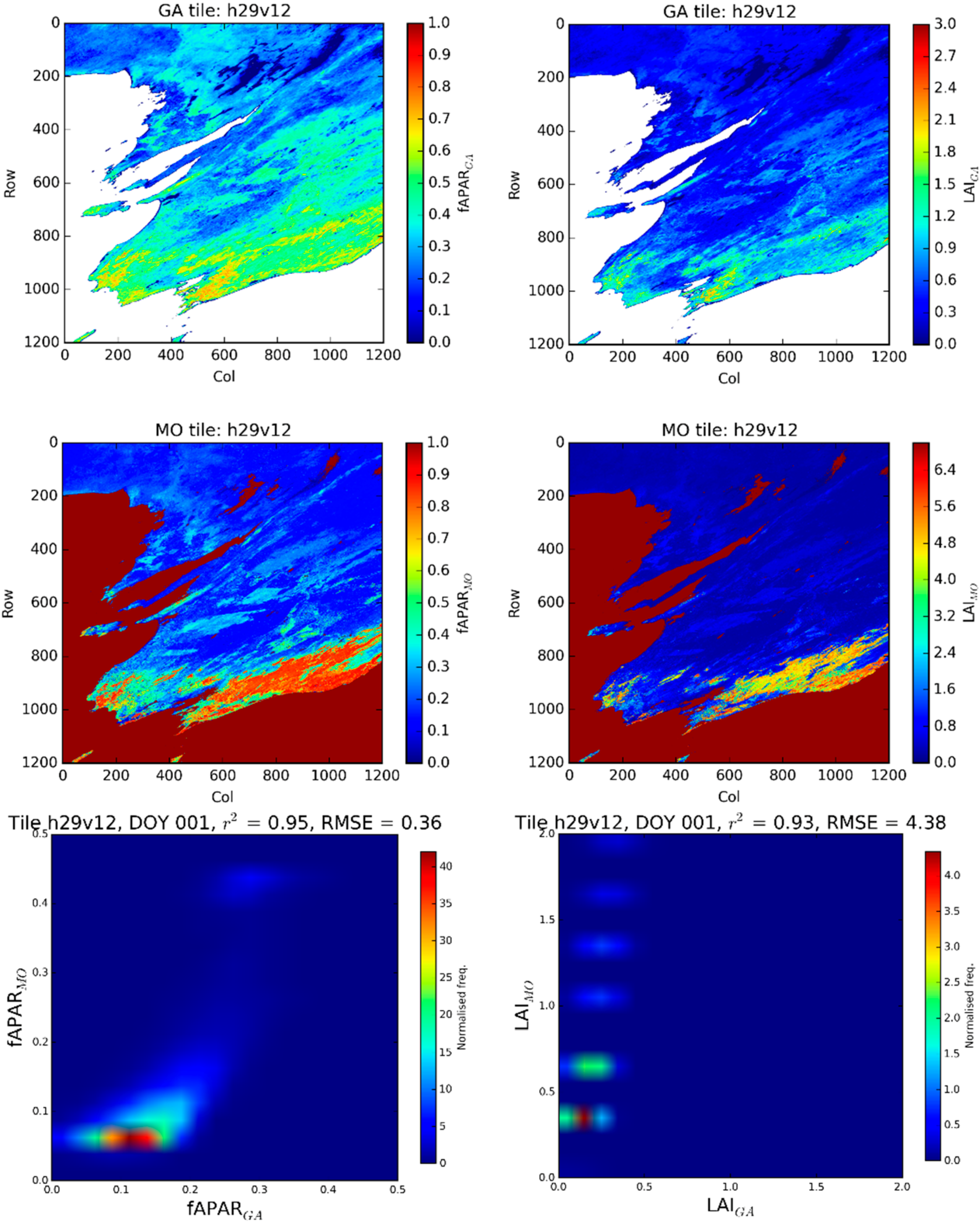
South Australia: Tile h29v12
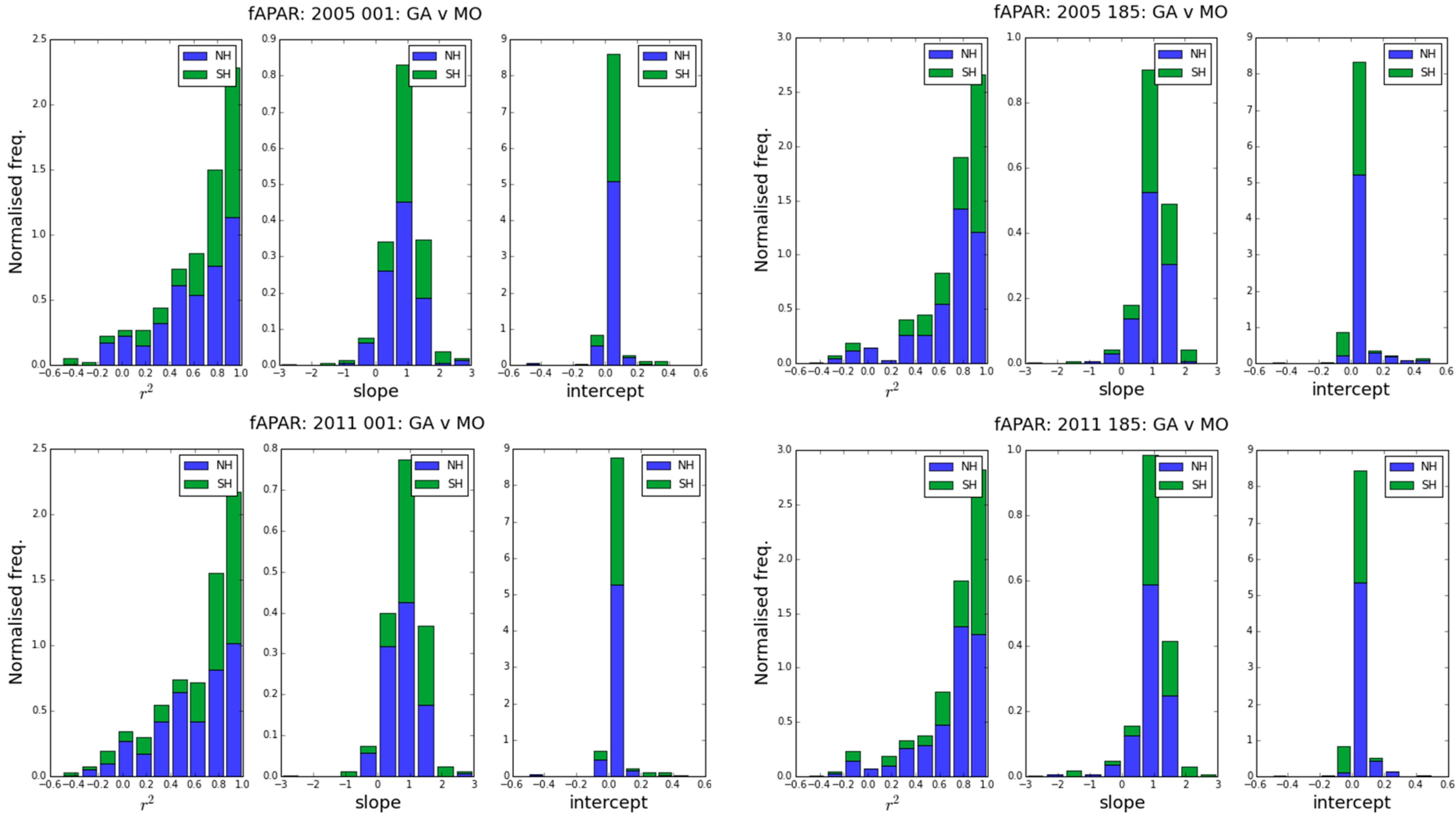
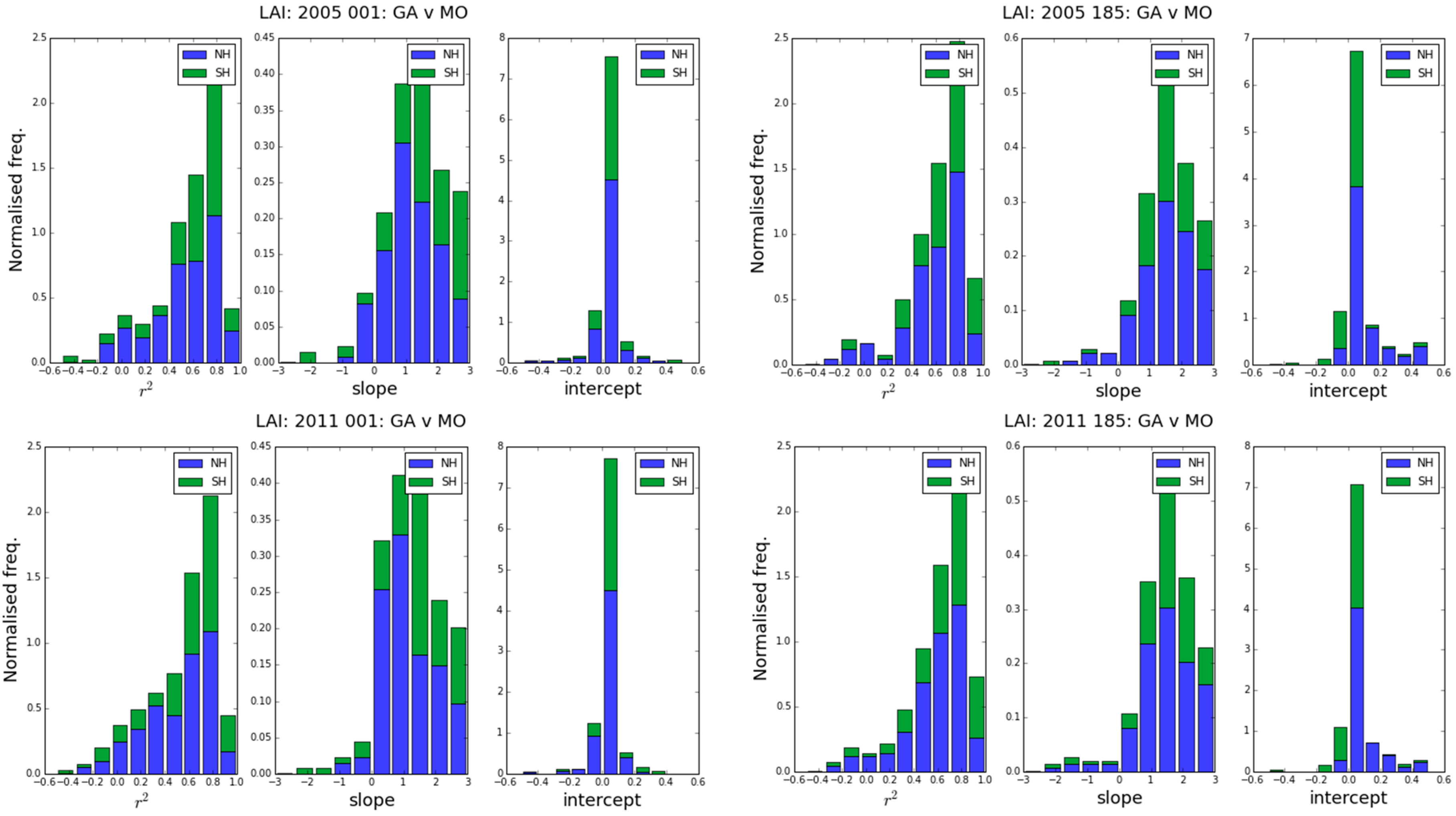
3.3. Whole-Hemisphere Comparisons
4. Discussion
- mean slope 1.01, σ = 0.78
- mean intercept 0.03, σ = 0.10
- mean slope 1.70, σ = 1.73
- mean intercept 0.15, σ = 0.58
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Verger, A.; Baret, F.; Weiss, M.; Filella, I.; Peñuelas, J. GEOCLIM: A global climatology of LAI, FAPAR, and FCOVER from VEGETATION observations for 1999–2010. Remote Sens. Environ. 2015, 166, 126–137. [Google Scholar] [CrossRef]
- Nemani, R.R.; Keeling, C.D.; Hashimoto, H.; Jolly, W.M.; Piper, S.C.; Tucker, C.J.; Myneni, R.B.; Running, S.W. Climate-driven increases in global terrestrial net primary production from 1982 to 1999. Science 2003, 300, 1560–1563. [Google Scholar] [CrossRef] [PubMed]
- Xia, J.; Chen, J.; Piao, S.; Ciais, P.; Luo, Y.; Wan, S. Terrestrial carbon cycle affected by non-uniform climate warming. Nat. Geosci. 2014, 7, 173–180. [Google Scholar] [CrossRef]
- Gamon, J.A.; Field, C.; Goulden, M.L.; Griffin, K.L.; Hartley, A.E.; Geeske, J.; Penuelas, J.; Valentini, R. (1995) Relationships between NDVI, canopy structure and photosynthesis in three Californian Vegetation Types. Ecol. Appl. 1995, 5, 28–41. [Google Scholar] [CrossRef]
- Myneni, R.B.; Nemani, R.R.; Running, S.W. Estimation of global leaf area index and absorbed PAR using radiative transfer models. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1380–1393. [Google Scholar] [CrossRef]
- Baret, F.; Hagolle, O.; Geiger, B.; Bicheron, P.; Miras, B.; Huc, M.; Berthelot, B.; Nino, F.; Weiss, M.; Samain, O.; et al. LAI, fAPAR and fCOVER CYLCOPES global products derived from VEGETATION: Part 1: Principles of algorithm. Remote Sens. Environ. 2007, 110, 275–286. [Google Scholar] [CrossRef]
- Knyazikhin, Y.; Martonchik, J.V.; Myneni, R.B.; Diner, D.J.; Running, S.W. Synergistic algorithm for estimating vegetation canopy leaf area index and fraction of absorbed photosynthetically active radiation from MODIS and MISR data. J. Geophys. Res. 1998, 103, 32257–32274. [Google Scholar] [CrossRef]
- Knyazikhin, Y.; Glassy, J.; Privette, J.L.; Tian, Y.; Lotsch, A.; Zhang, Y.; Wang, Y.; Morisette, J.T.; Votava, P.; Myneni, R.B.; et al. Running MODIS Leaf Area Index (LAI) and Fraction of Photosynthetically Active Radiation Absorbed by Vegetation (FPAR) Product (MOD15), Algorithm Theoretical Basis Document (ATBD) 1999. Available online: https://lpdaac.usgs.gov/products/modis_products_table/mcd15a2 and http://modis.gsfc.nasa.gov/data/atbd/atbd_mod15.pdf; (accessed on 3 August 2015).
- European Space Agency (ESA) GlobAlbedo Project. Available online: http://www.globalbedo.org (accessed on 8 January 2016).
- ESA Water Cycle Observation Multi-mission Strategy—EvapoTranspiration (WACMOS-II) Project. Available online: http://wacmoset.estellus.eu/ (accessed on 8 January 2016).
- Anser, G.P.; Scurlock, J.M.O.; Hicke, J.A. Global synthesis of leaf area index observations: Implications for ecological and remote sensing studies. Glob. Ecol. Biogeogr. 2003, 12, 191–205. [Google Scholar]
- Chen, J.M.; Black, T.A. Defining leaf area index for non-flat leaves. Plant Cell Environ. 1992, 15, 421–429. [Google Scholar] [CrossRef]
- Ross, J. The Radiation Regime and the Architecture of Plant Stands; W. Junk Publ: The Hague, The Netherlands, 1981. [Google Scholar]
- Liang, S. Quantitative Remote Sensing of Land Surfaces; ISBN 0-471-28166-2. John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2004. [Google Scholar]
- CEOS (2014) Committee on Earth Observation Satellites Working Group on Calibration and Validation: Land Product Validation Sub-Group, Global Leaf Area Index Product Validation: Good Practices. Fernandes, R.; Plummer, S.; Nightingale, J. (Eds.) . Available online: http://lpvs.gsfc.nasa.gov/documents.html (accessed on 3 August 2015).
- LI-COR LAI 2200c Plant Canopy Analyser. Available online: http://www.licor.com/env/products/leaf_area/LAI-2200/ (accessed on 8 January 2016).
- Delta-T SunScan Canopy Analysis System. Available online: http://www.delta-t.co.uk/product-display.asp?id=SS1%20Product&div=Plant%20Science (accessed on 8 January 2016).
- Jonckheere, I.; Fleck, S.; Nackaerts, K.; Muys, B.; Coppin, P.; Weiss, M.; Baret, F. Methods for leaf area index determination Part I: Theories, techniques and instruments. Agric. For. Meteorol. 2004, 121, 19–35. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Smith, G.J.; Jonckheere, I. Methods for in situ leaf area index measurement, Part II: From gap fraction to leaf area index: Retrieval methods and sampling strategies. Agric. For. Meteorol. 2004, 121, 17–53. [Google Scholar]
- Pinty, B.; Lavergne, T.; Dickinson, R.E.; Widlowski, J.-L.; Gobron, N.; Verstraete, M.M. Simplifying the Interaction of Land Surfaces with Radiation for Relating Remote Sensing Products to Climate Models. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Chen, J.M.; Menges, C.H.; Leblanc, S. Global derivation of the vegetation clumping index from multi-angular satellite data. Remote Sens. Environ. 2005, 97, 447–457. [Google Scholar] [CrossRef]
- Widlowski, J.-L.; Pinty, B.; Clerici, M.; Dai, Y.; De Kauwe, M.; de Ridder, K.; Kallel, A.; Kobayashi, H.; Lavergne, T.; Ni-Meister, W.; et al. RAMI4PILPS: An intercomparison of formulations for the partitioning of solar radiation in land surface models. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Widlowski, J.-L.; Pinty, B.; Lavergne, T.; Verstraete, M.M. Using 1-D models to interpret the reflectance anisotropy of 3-D targets: Issues and caveats. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2008–2017. [Google Scholar]
- Pfeifer, M.; Disney, M.I.; Quaife, T.; Marchant, R. Terrestrial ecosystems from space: A review of earth observation products for macroecology applications. Glob. Ecol. Biogeogr. 2012, 21, 603–624. [Google Scholar] [CrossRef]
- Liang, S. Numerical experiments on spatial scaling of land surface albedo and leaf area index. Remote Sens. Rev. 2000, 19, 225–242. [Google Scholar] [CrossRef]
- Stoy, P.; Williams, M.; Disney, M.I.; Prieto-Blanco, A.; Huntley, B.; Baxter, B.; Lewis, P. Upscaling as ecological information transfer: A simple framework with application to Arctic ecosystem carbon exchange. Landsc. Ecol. 2009, 24, 971–986. [Google Scholar] [CrossRef]
- Ceccherini, G.; Gobron, N.; Robustelli, M. Harmonization of Fraction of Absorbed Photosynthetically Active Radiation (FAPAR) from Sea-Viewing Wide Field-of-View Sensor (SeaWiFS) and Medium Resolution Imaging Spectrometer Instrument (MERIS). Remote Sens. 2013, 5, 3357–3376. [Google Scholar] [CrossRef]
- Bojinski, S.; Verstraete, M.M.; Peterson, T.C.; Simmons, A.; Zemp, M. The concept of Essential Climate Variables in support of climate research, applications, and policy. Bull. Am. Meteorol. Soc. 2014. [Google Scholar] [CrossRef]
- Pinty, B.; Lavergne, T.; Voßbeck, M.; Kaminski, T.; Aussedat, O.; Giering, R.; Gobron, N.; Taberner, M.; Verstraete, M.M.; Widlowski, J.-L. Retrieving surface parameters for climate models from MODIS and MISR albedo products. J. Geophys. Res. Atmos. 2007, 112, D10116. [Google Scholar] [CrossRef]
- Pinty, B.; Andredakis, I.; Clerici, M.; Kaminski, T.; Taberner, M.; Verstraete, M.M.; Gobron, N.; Plummer, S.; Widlowski, J.-L. Exploiting the MODIS albedos with the Two-stream Inversion Package (JRC-TIP) Part I: Effective Leaf Area Index, Vegetation and Soil properties. J. Geophys. Res. 2010, 116, D09106. [Google Scholar]
- Pinty, B.; Clerici, M.; Andredakis, I.; Kaminski, T.; Taberner, M.; Verstraete, M.M.; Gobron, N.; Plummer, S.; Widlowski, J.-L. Exploiting the MODIS albedos with the Two-stream Inversion Package JRC-TIP) Part II: Fractions of transmitted and absorbed fluxes in the vegetation and soil layers. J. Geophys. Res. 2010, 116, D09106. [Google Scholar]
- GlobAlbedo Algorithm Theoretical Basis Document (ATBD). Available online: http://www.globalbedo.org/docs/GlobAlbedo_Albedo_ATBD_V4.12.pdf (accessed on 7 January 2016).
- Voßbeck, M.; Clerici, M.; Kaminski, T.; Pinty, B.; Lavergne, T.; Giering, R. An inverse radiative transfer model of the vegetation canopy based on automatic differentiation. Inverse Probl. 2010, 26, 095003. [Google Scholar] [CrossRef]
- Voßbeck, M.; Giering, R.; Kaminski, T. Development and First Applications of TAC++. In Advances in Automatic Differentiation; Bischof, C., Bücker, H.M., Hovland, P.D., Naumann, U., Utke, J., Eds.; Springer: Berlin, Germany, 2008; pp. 187–197. [Google Scholar]
- Network Common Data Form (NetCDF). Available online: http://www.unidata.ucar.edu/software/netcdf/ (accessed on 7 January 2016).
- MODIS Grids. Available online: http://modis-land.gsfc.nasa.gov/MODLAND_grid.html (accessed on 7 January 2016).
- FLUXNET. Available online: http://fluxnet.ornl.gov/ (accessed on 7 January 2016).
- LP DAAC. Available online: https://lpdaac.usgs.gov/products/modis_products_table/mcd15a2 (accessed on 7 January 2016).
- GlobAlbedo Subsetting Tool. Available online: http://www.globalbedo.org/roi_v2.php (accessed on 7 January 2016).
- MODIS LAI, FPAR Collection 005 Changes. Available online: http://landweb.nascom.nasa.gov/QA_WWW/forPage/C005_Changes_LAI_FPAR.pdf (accessed on 7 January 2016).
- Quaife, T.; Lewis, P.; De Kauwe, M.; Williams, M.; Law, B.; Disney, M.I.; Bowyer, P. Assimilating Canopy Reflectance data into an Ecosystem Model with an Ensemble Kalman Filter. Remote Sens. Environ. 2008, 112, 1347–1364. [Google Scholar] [CrossRef]
- Lewis, P.; Gomez-Dans, J.; Kaminski, T.; Settle, J.; Quaife, T.; Gobron, N.; Styles, J.; Berger, M. An Earth Observation Land Data Assimilation System (EO-LDAS). Remote Sens. Environ. 2012, 120, 219–235. [Google Scholar] [CrossRef]
- Loew, A.; van Bodegom, P.M.; Widlowski, J.-L.; Otto, J.; Quaife, T.; Pinty, B.; Raddatz, T. Do we (need to) care about canopy radiation schemes in DGVMs? Caveats and potential impacts. Biogeosciences 2014, 11, 1873–1897. [Google Scholar] [CrossRef]
- MOD15 User Guide. Available online: https://lpdaac.usgs.gov/sites/default/files/public/product_documentation/mod15_user_guide.pdf (accessed on 22 March 2016).
- Mayr, M.J.; Samimi, C. Comparing the Dry Season In situ Leaf Area Index (LAI) Derived from High-Resolution RapidEye Imagery with MODIS LAI in a Namibian Savanna. Remote Sens. 2015, 5, 4834–4857. [Google Scholar] [CrossRef]
- Brandt, M.; Hiernaux, P.; Tagesson, T.; Verger, A.; Rasmussen, K.; Aziz Diouf, A.; Mbow, C.; Mougin, E.; Fensholt, R. Woody plant cover estimation in drylands from Earth Observation based seasonal metrics. Remote Sens. Environ. 2012, 120, 219–235. [Google Scholar] [CrossRef]
- Fang, H.; Li, W.; Myneni, R. The Impact of Potential Land Cover Misclassification on MODIS Leaf Area Index (LAI) Estimation: A Statistical Perspective. Remote Sens. 2013, 5, 830–844. [Google Scholar] [CrossRef]
- Knorr, W.; Kaminski, T.; Scholze, M.; Gobron, N.; Pinty, B.; Giering, R.; Mathieu, P.-P. Carbon cycle data assimilation with a generic phenology model. J. Geophys. Res. 2010, 115, G04017. [Google Scholar] [CrossRef]
- Kaminski, T.; Knorr, W.; Scholze, M.; Gobron, N.; Pinty, B.; Giering, R.; Mathieu, P.-P. Consistent assimilation of MERIS FAPAR and atmospheric CO2 into a terrestrial vegetation model and interactive mission benefit analysis. Biogeosciences 2012, 9, 3173–3184. [Google Scholar] [CrossRef]
- Schürmann, G.J.; Kaminski, T.; Köstler, C.; Carvalhais, N.; Voßbeck, M.; Kattge, J.; Giering, R.; Rödenbeck, C.; Heimann, M.; Zaehle, S. Constraining a land surface model with multiple observations by application of the MPI-Carbon Cycle Data Assimilation System. Geosci. Model Dev. 2016. [Google Scholar] [CrossRef]


| FLUXNET Code, Full Name | Location: Lat, Lon |
|---|---|
| Grassland | |
| AU-Stp: Australia, Stuart Plains | −17.15, 133.35 |
| CN-Du3: China, Doulun Degraded Meadow | 42.06, 116.28 |
| RU-Upo: Russia, Ust Pojeg | 61.93, 50.23 |
| US-AR2: ARM USDA UNL OSU Woodward Switchgrass 2 | 36.64, −99.60 |
| Deciduous broadleaf forest | |
| US-Oho: Ohio Oak Openings | 41.55, −83.84 |
| US-UMB: Univ. of Michigan Biological Station | 45.56, −84.71 |
| US-WCr: Willow Creek | 45.81, −90.08 |
| US-Wi3: Wisconsin Mature Hardwood | 46.63, −91.10 |
| Evergreen needleleaf forest | |
| DE-SfN: Schechenfilz Nord, Germany | 47.81, 11.33 |
| FI-Ves: Vesijako, Finland | 61.37, 25.11 |
| PL-Tcz: Tuczno, Poland | 53.19, 16.10 |
| US-NR2: Niwot Ridge, Colorado, US | 40.04, −105.55 |
| Mixed forest | |
| AT-StM: Stubai Meadow, Austria | 47.13, 11.31 |
| CH-Dsc: Dischma, Switzerland | 46.79, 9.86 |
| EE-Hi2: Hiiesoo, Estonia | 59.35, 27.10 |
| US-Ha2: Harvard Forest Hemlock, US | 42.54, −72.18 |
| Crop/Natural | |
| CA-MA2: Manitoba Agricultural Site 2, Canada | 50.17, −97.88 |
| EE-Aar: Aardlapalu, Estonia | 58.31, 26.74 |
| ML-Kem: Kelma, Mali | 15.22, −1.57 |
| US-Wi6: Wisconsin Pine Barrens, US | 46.62, −91.30 |
| Miscellaneous | |
| DE-Hai: Hainich, Germany (mixed forest) | 51.08, 10.45 |
| DE-Tha: Tharandt, Germany (evergreen needleleaf) | 50.96, 13.57 |
| BR-Cax: Caxiuanã Forest, Brazil (evergreen broadleaf) | −1.72, −51.46 |
| GF-Guy: Guyaflux, French Guiana (evergreen broadleaf) | 5.28, −52.92 |
| Biome | Slope (Lower, Upper) | Intercept (Lower, Upper) | ||
|---|---|---|---|---|
| fAPAR | LAI | fAPAR | LAI | |
| Grassland | 0.9, 1.1 | 1.2, 2.1 | −0.1, 0.07 | −0.3, 1.3 |
| Deciduous broadleaf forest | 1.3, 1.4 | 2, 2.3 | −0.1 | −0.5, −0.3 |
| Evergreen needleleaf forest | 1.4, 2.3 | 3.1, 8.3 | −0.2, 0.1 | −1.7, 0 |
| Mixed forest | 1.1, 1.7 | 1.5, 3.5 | −0.1, 0.1 | −0.7, 0.2 |
| Crop/natural | 1, 1.4 | 1.1, 1.6 | −0.2, 0.1 | −0.4, 0.2 |
| Miscellaneous | 0.2, 1.4 | 0.1, 2.5 | −0.1, 0.5 | −0.1, 3.5 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Disney, M.; Muller, J.-P.; Kharbouche, S.; Kaminski, T.; Voßbeck, M.; Lewis, P.; Pinty, B. A New Global fAPAR and LAI Dataset Derived from Optimal Albedo Estimates: Comparison with MODIS Products. Remote Sens. 2016, 8, 275. https://doi.org/10.3390/rs8040275
Disney M, Muller J-P, Kharbouche S, Kaminski T, Voßbeck M, Lewis P, Pinty B. A New Global fAPAR and LAI Dataset Derived from Optimal Albedo Estimates: Comparison with MODIS Products. Remote Sensing. 2016; 8(4):275. https://doi.org/10.3390/rs8040275
Chicago/Turabian StyleDisney, Mathias, Jan-Peter Muller, Said Kharbouche, Thomas Kaminski, Michael Voßbeck, Philip Lewis, and Bernard Pinty. 2016. "A New Global fAPAR and LAI Dataset Derived from Optimal Albedo Estimates: Comparison with MODIS Products" Remote Sensing 8, no. 4: 275. https://doi.org/10.3390/rs8040275
APA StyleDisney, M., Muller, J.-P., Kharbouche, S., Kaminski, T., Voßbeck, M., Lewis, P., & Pinty, B. (2016). A New Global fAPAR and LAI Dataset Derived from Optimal Albedo Estimates: Comparison with MODIS Products. Remote Sensing, 8(4), 275. https://doi.org/10.3390/rs8040275








