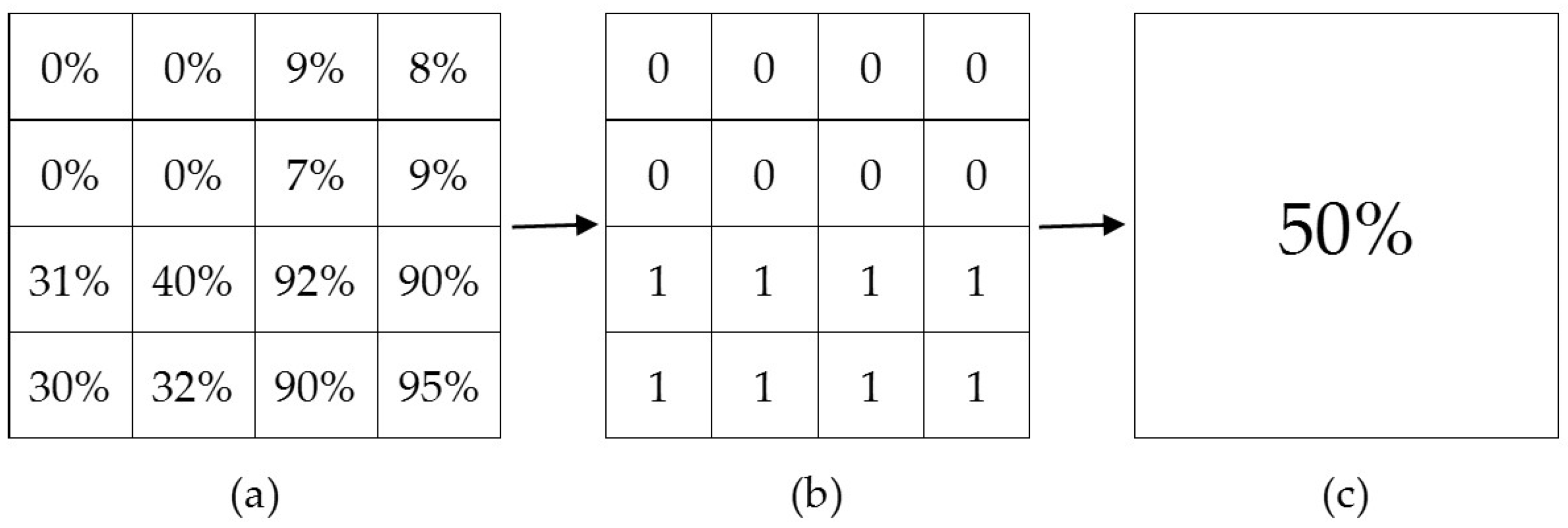
1. Introduction
Land cover maps provide useful information on the geographical distribution of different land cover types, as well as on land cover change over time. Land cover products are widely used as input data in various applications, such as climate change models, management of natural resources, environmental monitoring and comprehensive spatial quantification of ecosystems and landscapes, among many others [
1]. Maps of forest cover, in particular, provide valuable inputs to a diverse range of applications, including the modelling of forest growth and productivity, the assessment of bioenergy potentials, carbon flux monitoring and REDD+.
The last few decades have seen an increase in the number of land cover and forest datasets derived from remote sensing products. The overall trend has been towards higher spatial resolution, such as the 30-m maps of the percentage of forest cover, forest cover gain and loss by Hansen [
2] and the 30-m Globeland product [
3,
4]. These maps were developed from Landsat high resolution satellite imagery, which has only been made possible because this data stream has recently become freely available [
5]. However, higher resolution products are not always more accurate than maps with a coarser resolution [
6]. Hansen’s forest cover map could be considered an exception, as it is one of the most accurate global forest cover maps available for the year 2000 [
7]. Among global land cover products, the GLC2000 [
8], MODIS [
9] and GlobCover [
10], with a resolution of 1 km–300 m and an accuracy ranging from 68.5%–74.8%, have been widely used in different models to represent the basic land cover as an input. However, Fritz
et al. [
11] have shown that these maps disagree considerably over space when harmonised and compared, and they do not correspond to official land cover statistics at the national or regional level. Although new high resolution satellite imagery from Sentinel 2 [
12] may provide the basis for better land cover maps in the future, the methodology for developing land cover and forest products still requires further research in order to produce the most accurate information about global land cover, particularly for historical baseline periods.
Data fusion represents a powerful way of integrating individual sources of information to produce a better output than could be achieved by any of the individual sources on their own [
13]. These approaches have been used in many different domains, including remote sensing [
6,
14,
15,
16], e.g., to improve forest cover characterisation using a regression tree model [
16] or a Bayesian spatial statistical approach [
17]; to estimate forest inventory attributes by applying the k-nearest neighbour method [
18,
19],
etc. De’ath
et al. in their work [
20] showed that, in comparison with linear models, classification and regression trees are an easy-to-use and effective technique for different environmental tasks. Spatial analytical and statistical methods are also becoming widely used for data fusion. For example, See
et al. [
6] applied a geographically-weighted regression model (GWR) to develop a global land cover map by integrating different global land cover maps and crowdsourced data. Crowdsourcing and citizen science are increasingly being used to collect ground-based data across many fields of study, from ecology [
21] to astronomy [
22], which have become a valuable input to many applications [
23]. The relevance and importance of this new data stream is therefore increasing. Another example can be found in Schepaschenko
et al. [
7], where they combined diverse data sources to produce a single forest cover product utilizing GWR.
To date, there exist several studies on the empirical comparison of different data fusion methods of land cover products derived from remote sensing, e.g., [
24]. However, they do not directly relate to the problem of the integration of diverse sources of land cover information to increase the accuracy of land cover/forest products. An exception is the work by Clinton
et al. [
25], who compared nine methods to fuse three global land cover products produced in similar ways. The results show that the method of classification trees (J48) performed the best.
Based on the above review, it is clear that many different methods have been applied in the past with little intercomparison of methods. Moreover, the work of Clinton
et al. [
25] did not use crowdsourced data as an input to the data fusion process. With new and increasing sources of ground-based data becoming available through initiatives, such as Geo-Wiki [
26], it is not clear which data fusion method is relevant to apply in order to maximize the information content of this data source.
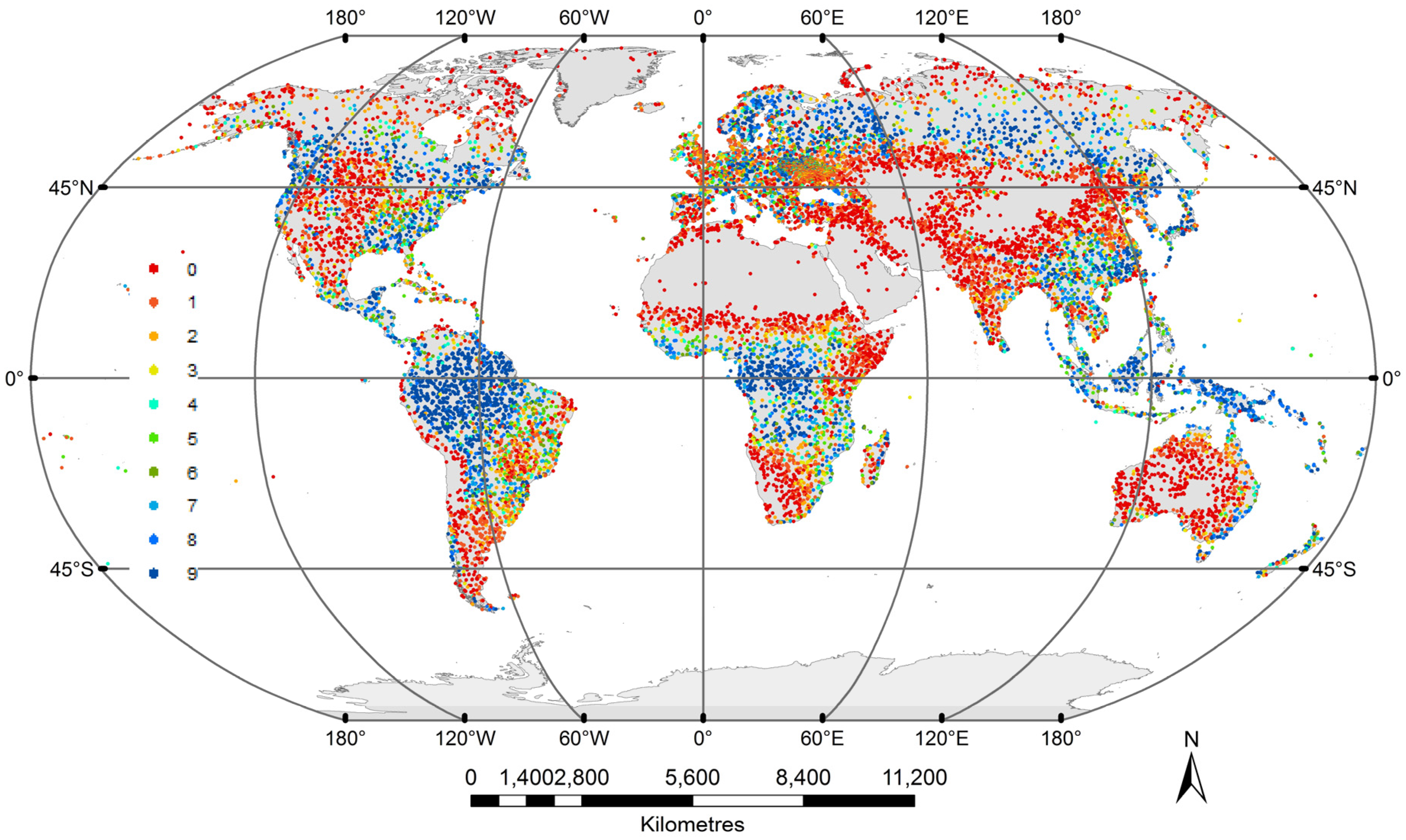
In this study, we extend the work of Schepaschenko
et al. [
7], who used only GWR to create their hybrid forest maps, by considering other commonly-used methods of data fusion for creating a global forest map. The input datasets used in the data fusion experiments are described in detail in
Section 2.1. For forest, we took the definition of The Food and Agriculture Organisation of the United Nations (FAO): “Land spanning more than 0.5 hectares with trees higher than 5 m and a canopy cover of more than 10 percent, or trees able to reach these thresholds
in situ” [
27] (p. 209). Due to the fact that it is difficult to derive tree plantations from remote sensing, we include them in the definition. The methods tested here include: nearest neighbour, the naive Bayes classifier, logistic and geographically-weighted logistic regression (GWR) and regression trees, as outlined in
Section 2.2. These methods were chosen because they are often used as data fusion approaches, although GWR has not been compared previously with other methods in terms of integrating land cover products. We consider various criteria in the comparison of approaches, such as apparent error rate, sensitivity and specificity.
4. Discussion
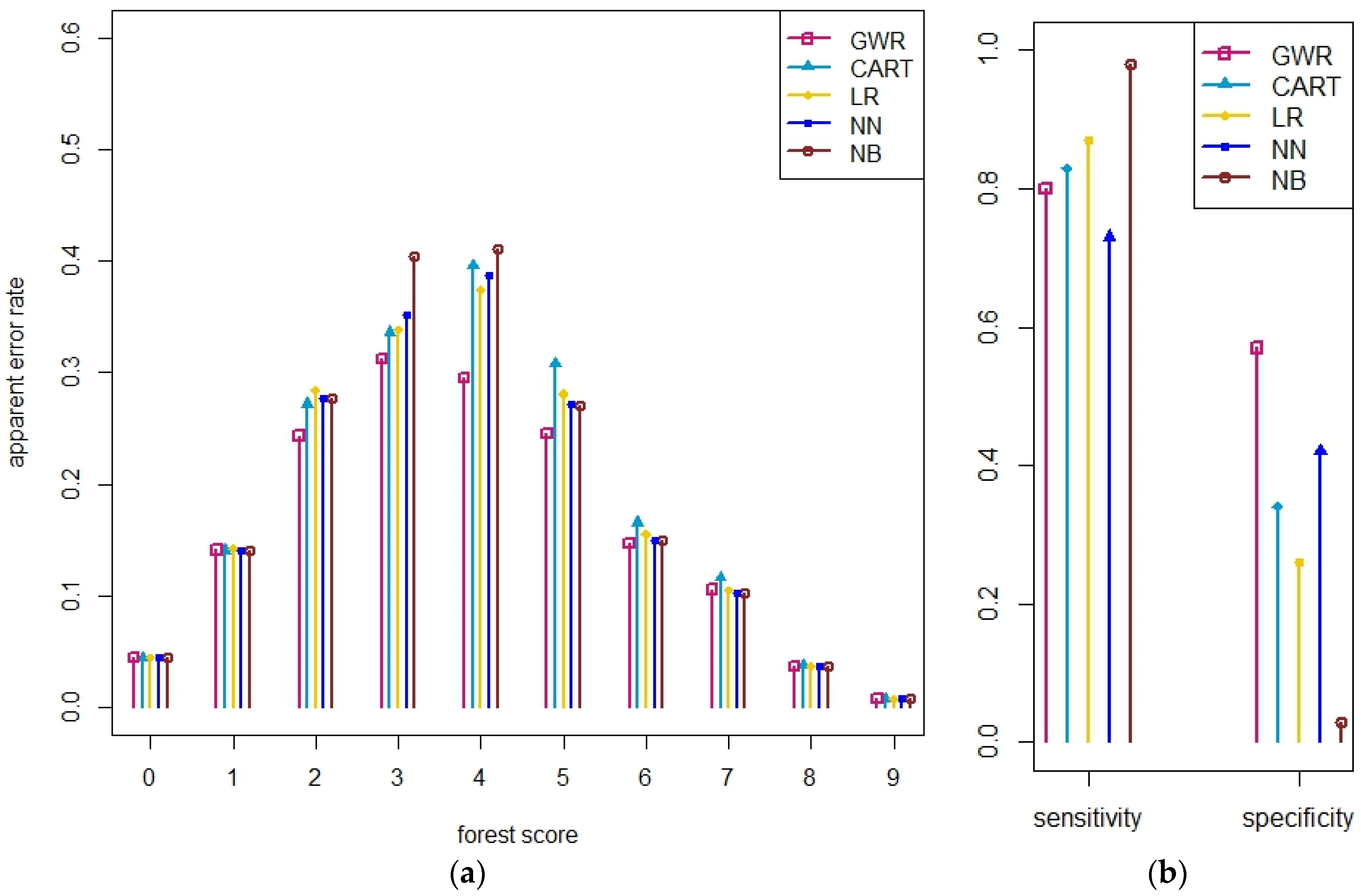
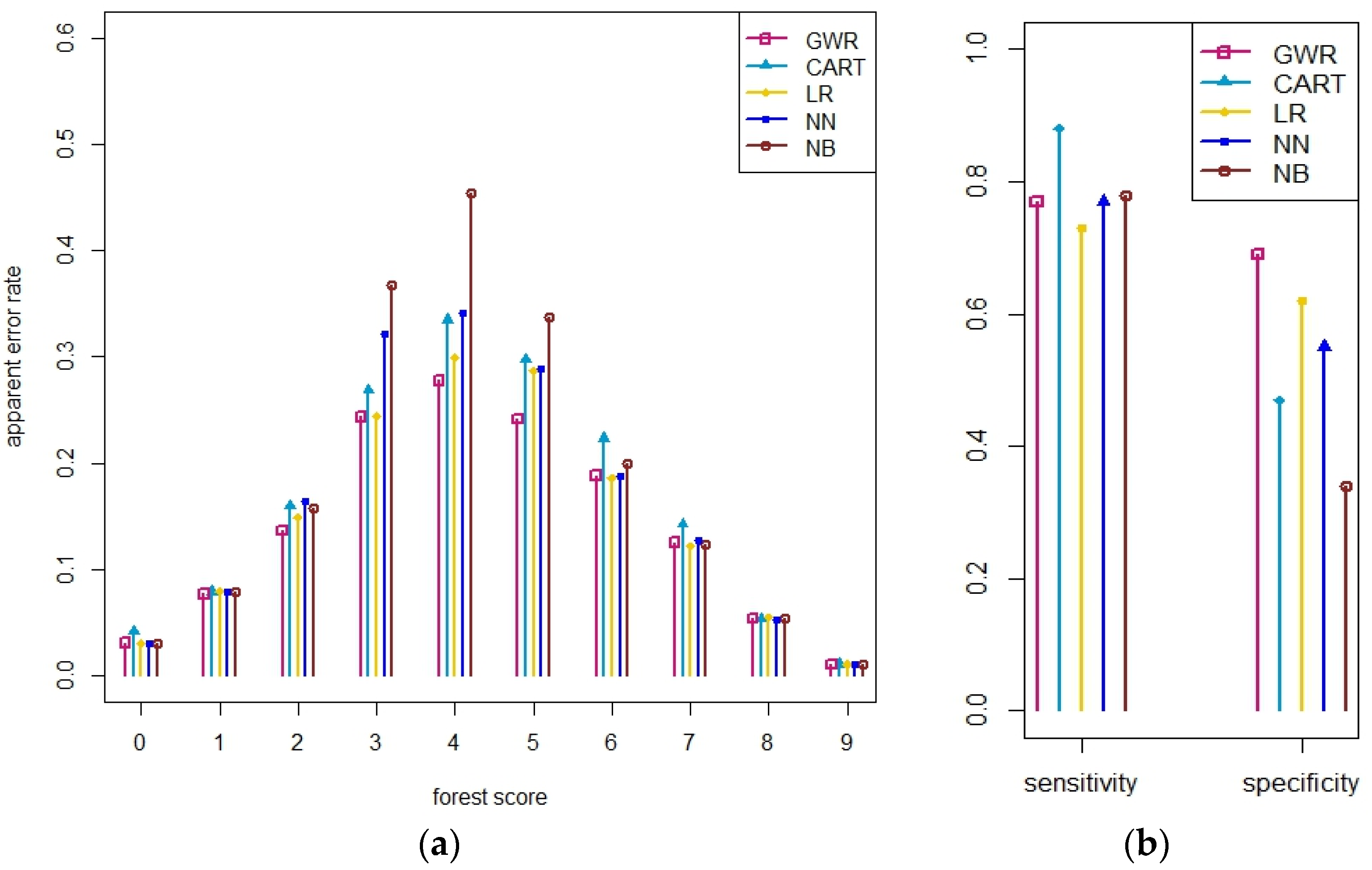
In this study, we have applied a variety of statistical methods to combine nine different forest cover maps with crowdsourced data from Geo-Wiki to produce a single hybrid forest cover map of high accuracy. The results show that using the percentage of forest cover (
Section 3.1, first experiment) rather than simple dichotomous presence/absence of forest cover (
Section 3.2, second experiment) as the input results in a more accurate hybrid map. We also show that for areas with high disagreement among input maps, all of the methods have high sensitivity and low specificity, but that NB considerably overestimates forest.
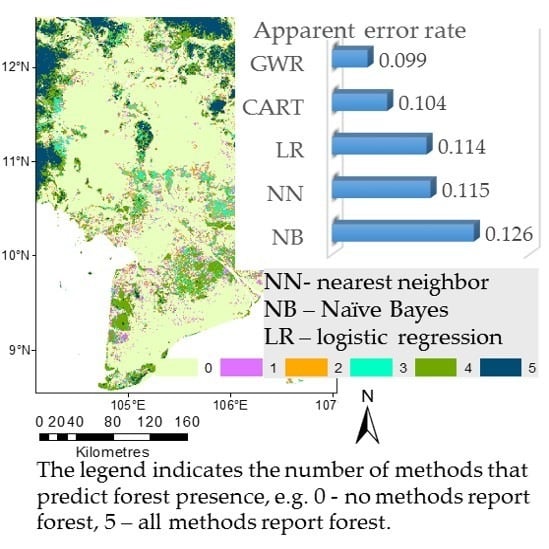
4.1. Performance of the Methods
In this study, the NN and the NB methods have not performed well in comparison with other, parametric methods. One of the possible reasons for this is the fact that the training dataset does not adequately represent all possible combinations of the product inputs. The crowdsourced data from Geo-Wiki campaigns were collected to capture a wide range of land cover information that could be further used in different applications. This sample was not originally chosen based on the combinations of input layers. In this study, we wanted to show which of the methods extracts the maximum information available from the crowdsourced data and the input maps. Therefore, NN and NB are not recommended here. However, when more crowdsourced information is acquired in the future, they may prove to be more useful. Alternatively, if a sampling design was implemented specifically for these approaches, they may also perform better.
In general, the CART methods and ordinary logistic regression provided good results for both the binary input data, as well as for the continuous data. In the second experiment, where logistic regression was used, the performance is slightly better. Both methods are easy to implement using widely available statistical software (e.g., packages in R). A recent study that examined different types of data fusion methods, referred to in the paper as geographical stacking [
25], showed that classification trees produced the best results when fusing different land cover datasets together, although the authors did not compare the methods with GWR.
By implementing NB for binary data, the method performed poorly for percentage input data in the areas of high disagreement,
i.e., when half of the input products identified the presence of forest while the other indicated absence. There have been many studies undertaken to examine the performance of this method [
53,
54,
55]; despite the assumption of the independence of the inputs, all of the studies showed that it gave good results in practice. However, this method still requires a deeper understanding of the data characteristics that affect its performance [
53].
In general, GWR performed marginally better than the other methods, but it is in areas with high disagreement between the input datasets that the results of the prediction by GWR were found to be much more accurate. One of the advantages of this method is that the estimates of the model coefficients vary in space. From this, we can conclude that GWR provides the best results for the prediction of land cover classes through combining different data sources. This gain in accuracy has a trade-off in that it is more computationally intensive than the other methods tested. Moreover, it is important to mention that GWR is not statistically proven as a method for the analysis of nonstationary data. Wheeler and Tiefelsdorf [
56] state that multicollinearities and pairwise correlations between sets of local coefficients do not provide appropriate model results. However, the method needs a more detailed study of its implementation for solving particular tasks, e.g., in the development of hybrid land cover maps.
We have also looked at the performance of the methods with different inputs to understand if the maps from different time periods, in particular the FAO map, decrease the performance of the final results. At the global level, there is no statistically-significant difference in the results when the FAO map is excluded. One of the reasons for this is that the apparent error rate of the forest products is higher than the relative change of forest area over time.
4.2. Accuracy Trade-Off
Table 8 presents the apparent error estimates of the input forest datasets. Some fusion methods were not able to outperform the accuracy of the individual input datasets. For example, NN and NB did not produce a map that is more accurate than Hansen’s tree cover (TC). However, the GWR resulted in improvements in forest map accuracy of around 2% compared to the most accurate input dataset of Hansen’s TC.
All of the differences in apparent error rates are statistically significant with high p-values equal to 0.001. Although the gain in accuracy is small, 1% of a land cover map is approximately 150 million hectares, which is a substantially-sized area, e.g., to place this in context, the area of Mongolia is around 155 million hectares In comparison with Hansen’s TC, a hybrid map better captures 2% of the land cover or approximately 300 M ha. These are territories that are very often found in the borders of forest land and where there are classification errors in the products (e.g., Hansen’s TC very often confuses wetlands with forest areas).
The results of comparing the methods show that for countries or bioclimatic zones where fragmentation of landscape structure is not high, in other words, the agreement areas of the input maps, there is little difference regarding which method to apply, e.g., tropical countries with rainforest. For regions with more complex landscape structures (e.g., Tanzania, Brazil), it is desirable to implement spatially-explicit methods (e.g., GWR) to develop a hybrid land cover map. As input data for these methods, it is crucial to collect as much training data of high quality as possible.
The geographically-weighted kernel used in GWR can also be implemented with other methods, including NB, CART and NN. With an increase in the amount of crowdsourced data or ground truth data and the development of new corresponding R packages, it will be interesting to compare the performance of spatially-explicit methods for building a hybrid land cover map. These will be the subject of further research.
In the paper on the development of a hybrid forest map for 2000 [
7], the authors have applied GWR for the integration of crowdsourced data and land cover products. However, the authors did not undertake a comparative analysis of the performance of other methods for solving this task. The results of our study are valuable because they show that the difference in implementing GWR and other data fusion methods is small. However, the improvements from GWR were shown to be statistically significant.
The results of the study have important practical implications for building land cover maps of different land cover types. As new land cover products appear, it is always possible to build a hybrid land cover map by applying one of the data fusion methods outlined in the paper.
5. Conclusions
This paper presents a comparison of selected data fusion methods in predicting forest cover by integrating land cover datasets and crowdsourced data from Geo-Wiki. The results have shown that continuous data (percentage of land cover classes in a pixel) are preferable to binary data as the results are improved. Of the methods tested, GWR was shown to be the best fusion method for predicting the presence/absence of forest in terms of accuracy. This was especially true in areas with high disagreement among the input data sources. The CART and ordinary logistic regression were found to be the second best in terms of prediction accuracy. In practice, for the regions with homogeneous landscapes, it matters very little which method is chosen. However, for territories with highly fragmented landscapes, we recommend implementing a spatially-explicit method, e.g., GWR, as a data fusion method for producing hybrid land cover maps. GWR, as any other spatially-explicit method, is more demanding in terms of computing resources than the other methods, but we would argue that the increase in accuracy, albeit small overall, is worth the effort.