Global and Regional Variability and Change in Terrestrial Ecosystems Net Primary Production and NDVI: A Model-Data Comparison
Abstract
:1. Introduction
2 Methods
2.1. NDVI Dataset
2.2. Ecosystem Models
2.3. Analysis
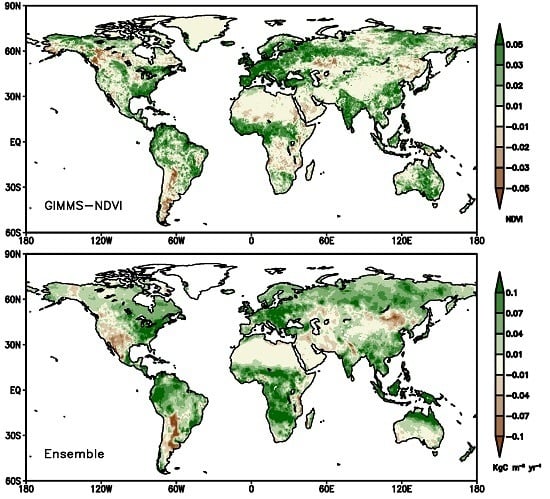
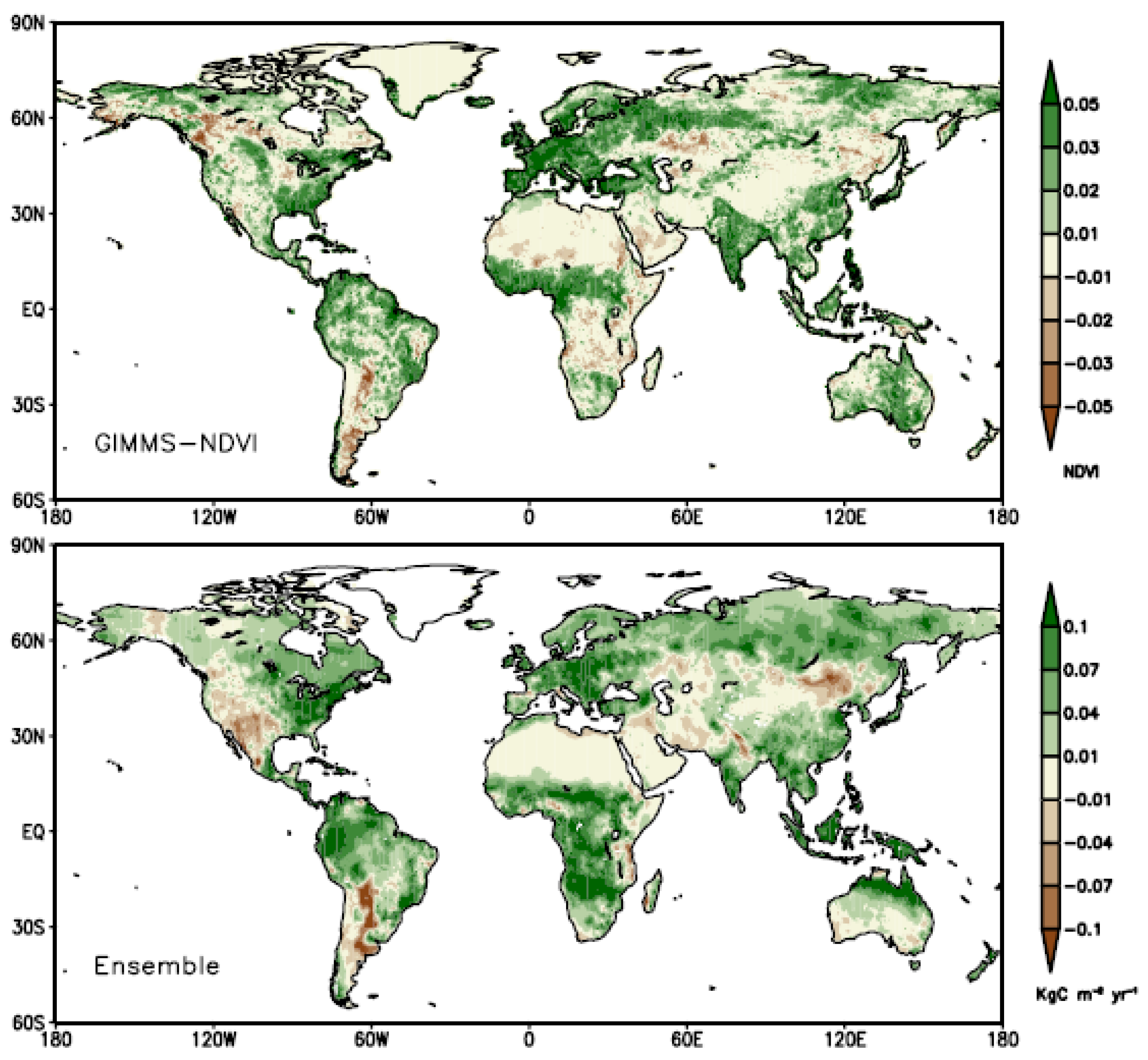
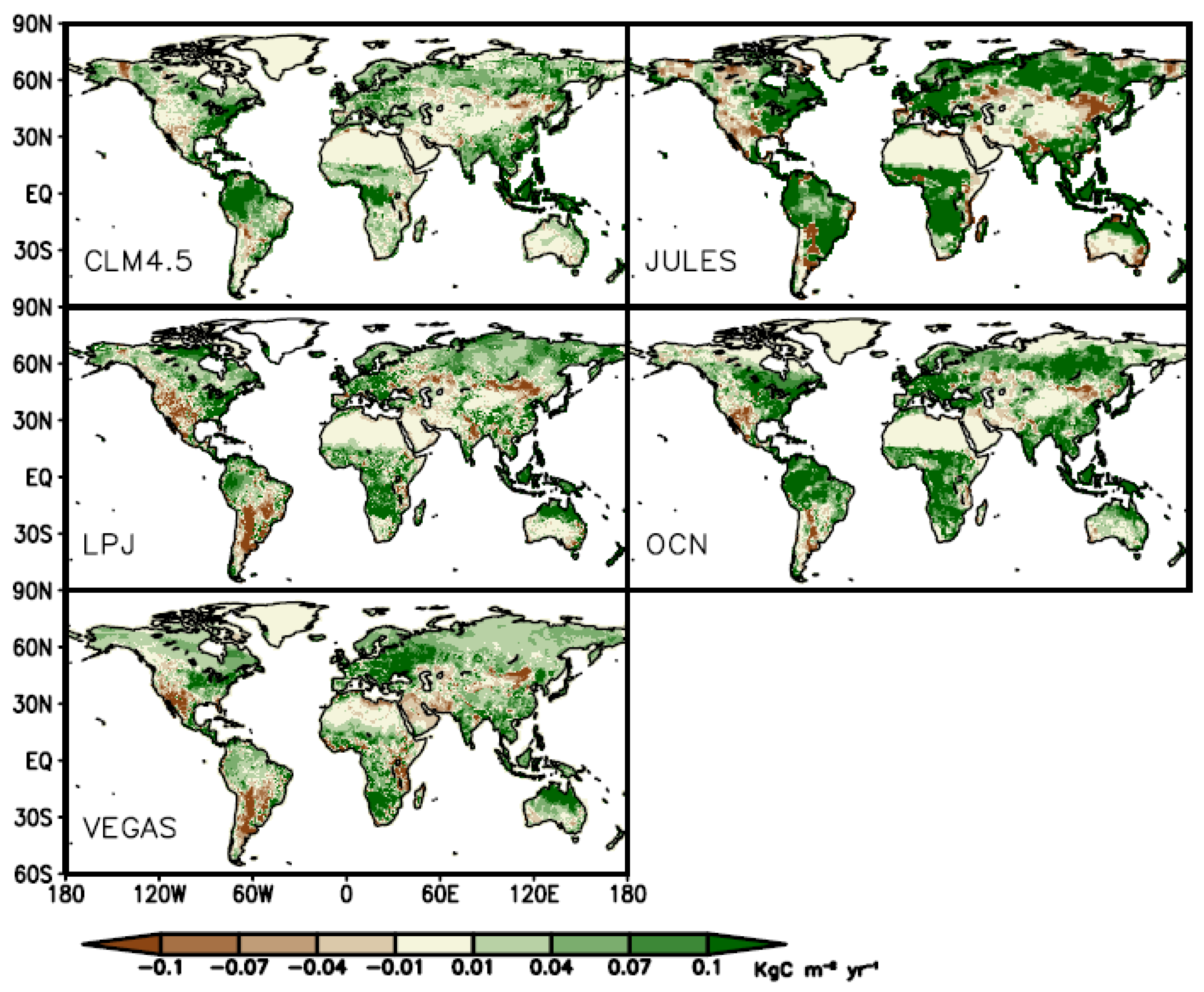
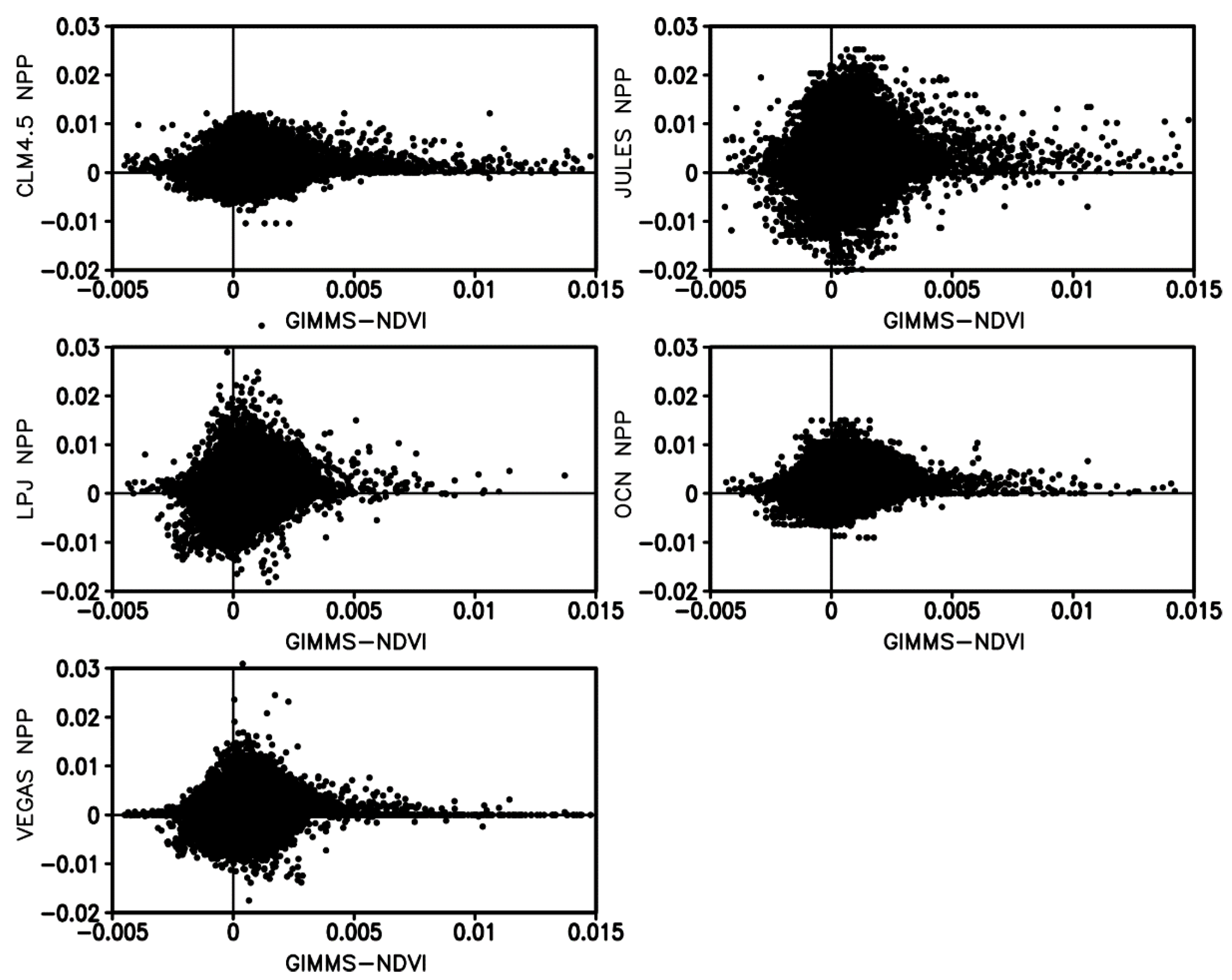
3. Results
3.1. Spatial Trends of Observed NDVI and Modeled NPP
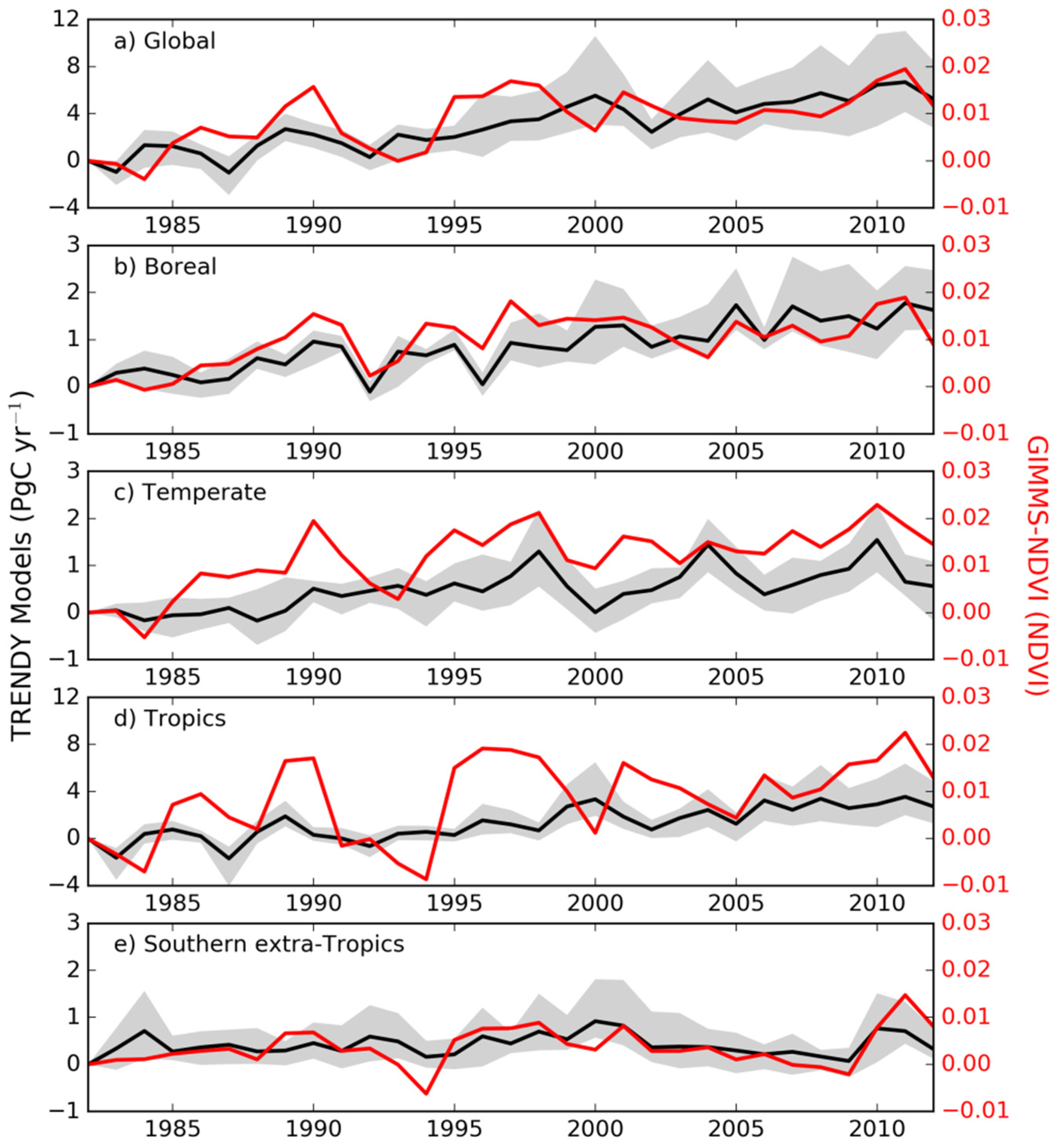
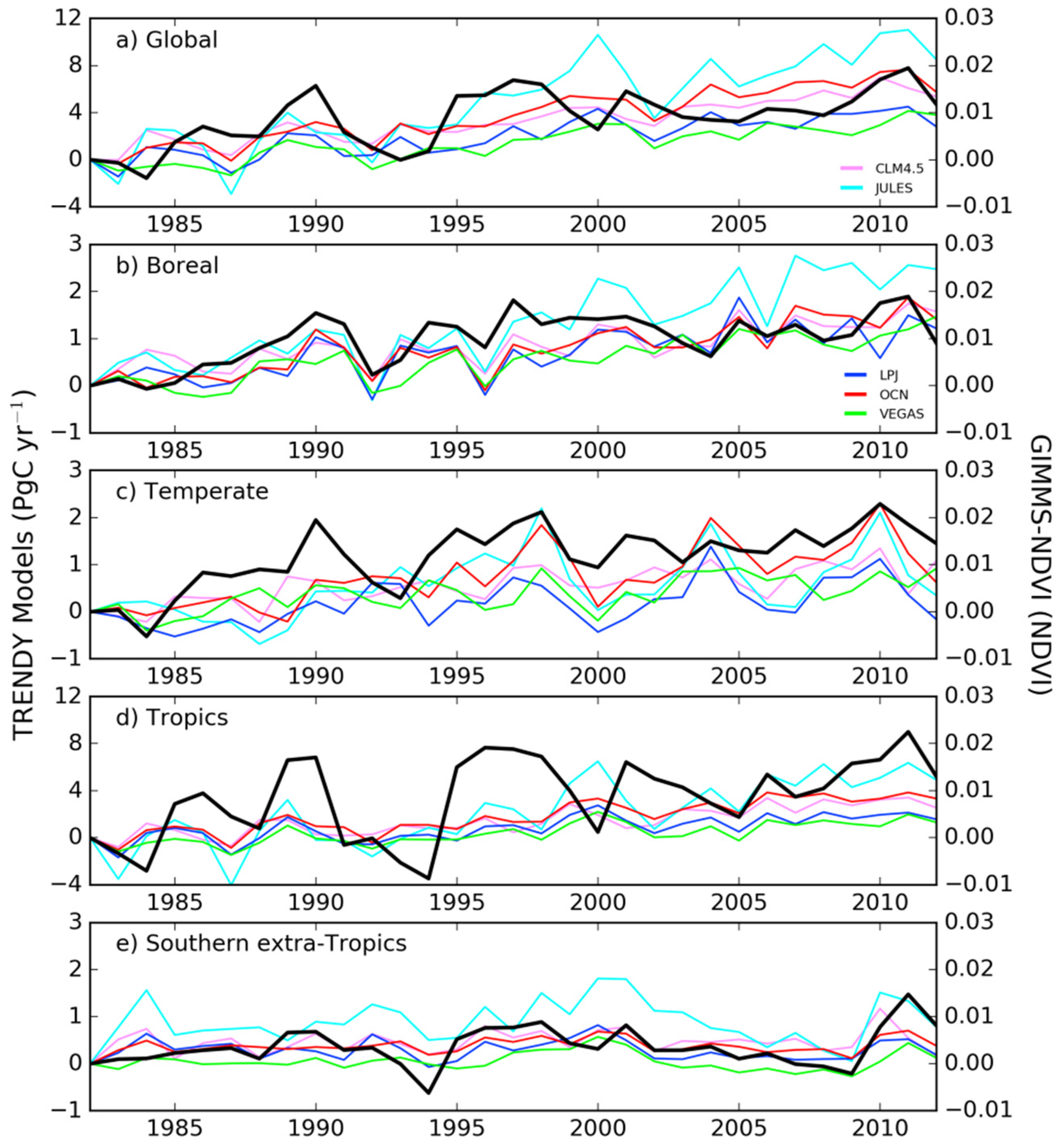
3.2. Temporal Trends of NDVI and Modeled NPP
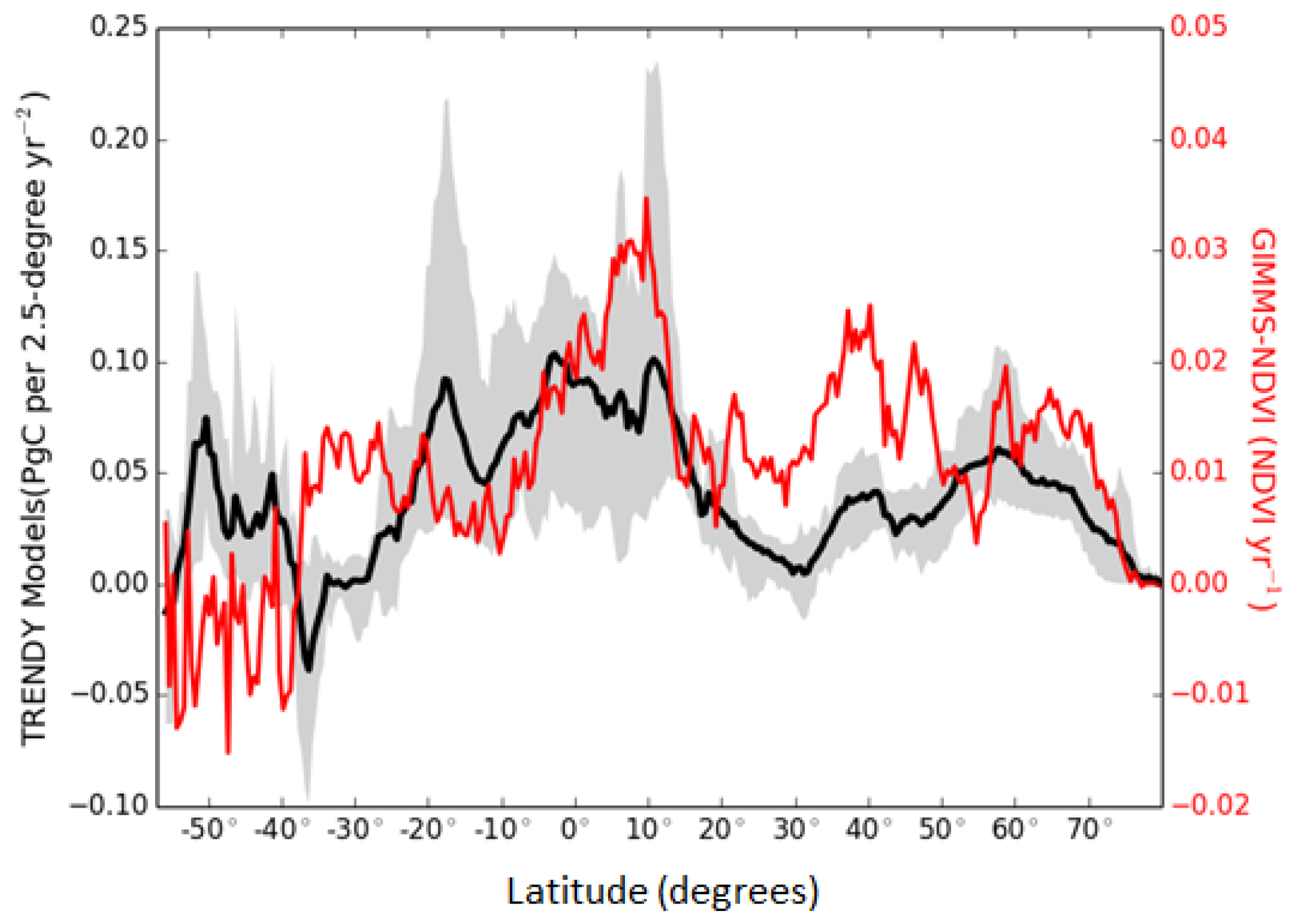
3.3. Latitudinal Trends of NDVI and Modeled NPP
4. Discussion
4.1. Potential Drivers of NDVI and NPP Trends
4.2. Uncertainties Related to NDVI-NPP Comparison
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lucht, W.; Prentice, C.; Myneni, R.B.; Sitch, S.; Friedlingstein, P.; Cramer, W.; Bousquet, P.; Buermann, W.; Smith, B. Climatic control of the high-latitude vegetation greening trend and pinatubo effect. Science 2002, 296, 1687–1689. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Bi, J.; Pan, Y.; Ganguly, S.; Anav, A.; Xu, L.; Samanta, A.; Piao, S.; Nemani, R.R.; Myneni, R.B. Global data sets of Vegetation Leaf Area Index (LAI)3g and Fraction of Photosynthetically Active Radiation (FPAR)3g derived from Global Inventory Modeling and Mapping Studies (GIMMS) Normalized Difference Vegetation Index (NDVI3g) for the period 1981 to 2011. Remote Sens. 2013, 5, 927–948. [Google Scholar]
- Fang, J.; Piao, S.; Field, C.B.; Pan, Y.; Guao, Q.; Zhou, L.; Peng, C.; Tao, S. Increasing net primary production in China from 1982 to 1999. Front. Ecol. Environ. 2003, 1, 293–297. [Google Scholar] [CrossRef]
- Zhou, L.; Tucker, C.T.; Kaufmann, R.K.; Slayback, D.; Shabanov, N.V.; Myneni, R.B. Variations in northern vegetation activity inferred from satellite data of vegetation index during 1981 to 1999. J. Geophys. Rese. Atmos. 2001, 106, 20069–20083. [Google Scholar] [CrossRef]
- Myneni, R.B.; Keeling, C.D.; Tucker, C.J.; Asrar, G.; Nemani, R.R. Increased plant growth in the northern high latitudes from 1981 to 1991. Nature 1997, 386, 698–702. [Google Scholar] [CrossRef]
- Higginbottom, T.; Symeonakis, E. Assessing land degradation and desertification using vegetation index data: Current frameworks and future directions. Remote Sens. 2014, 6, 9552–9575. [Google Scholar] [CrossRef]
- De Jong, R.; Schaepman, M.E.; Furrer, R.; de Bruin, S.; Verburg, P.H. Spatial relationship between climatologies and changes in global vegetation activity. Glob. Chang. Biol. 2013, 19, 1953–1964. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Lü, S.; Liu, Y.; Gao, Y.; Ao, Y. Variations and trends of terrestrial NPP and its relation to climate change in the 10 CMIP5 models. J. Earth Syst. Sci. 2015, 124, 395–403. [Google Scholar] [CrossRef]
- Forkel, M.; Carvalhais, N.; Verbesselt, J.; Mahecha, M.D.; Neigh, C.S.R.; Reichstein, M. Trend change detection in NDVI time series: Effects of inter-annual variability and methodology. Remote Sens. 2013, 5, 2113–2144. [Google Scholar] [CrossRef]
- Dan, L.; Ji, J.; He, Y. Use of ISLSCP II data to intercompare and validate the terrestrial net primary production in a land surface model coupled to a general circulation model. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Cao, M.; Prince, S.D.; Small, J.; Goetz, S.J. Remotely sensed interannual variations and trends in terrestrial net primary productivity 1981–2000. Ecosystems 2004, 7, 233–242. [Google Scholar] [CrossRef]
- Nemani, R.R.; Keeling, C.D.; Hashimoto, H.; Jolly, M.F.; Piper, S.C.; Tucker, C.J.; Myneni, R.B.; Running, S.W. Climate-Driven increases in global terrestrial net primary production from 1982 to 1999. Science 2003, 300, 1560–1563. [Google Scholar] [CrossRef] [PubMed]
- Friedlingstein, P.; Cox, P.; Betts, R.; Bopp, L.; Von Bloh, W.; Brovkin, V.; Cadule, P.; Doney, S.; Eby, M.; Fung, I.; et al. Climate-Carbon cycle feedback analysis: Results from the C4MIP model intercomparison. J. Clim. 2006, 19, 3337–3353. [Google Scholar] [CrossRef]
- Todd-Brown, K.E.O.; Randerson, J.T.; Post, W.M.; Hoffman, F.M.; Tarnocai, C.; Schuur, E.A.G.; Allison, S.D. Causes of variation in soil carbon simulations from CMIP5 Earth system models and comparison with observations. Biogeosciences 2013, 10, 1717–1736. [Google Scholar] [CrossRef]
- Sitch, S.; Huntingford, C.; Gedney, N.; Levy, P.E.; Lomas, M.; Piao, S.L.; Betts, R.; Ciais, P.; Cox, P.; Friedlingstein, P.; et al. Evaluation of the terrestrial carbon cycle, future plant geography and climate-carbon cycle feedbacks using five Dynamic Global Vegetation Models (DGVMs). Glob. Chang. Biol. 2008, 14, 2015–2039. [Google Scholar] [CrossRef]
- Bala, G.; Joshi, J.; Chatuvedi, R.K.; Gangamani, H.V.; Hashimoto, H.; Nemani, R. Trends and variability of AVHRR-derived NPP in India. Remote Sens. 2013, 5, 810–829. [Google Scholar] [CrossRef]
- Knorr, W.; Heimann, M. Uncertainties in global terrestrial biosphere modeling: 1. A comprehensive sensitivity analysis with a new photosynthesis and energy balance scheme. Glob. Biogeochem. Cycles 2001, 15, 207–225. [Google Scholar] [CrossRef]
- Gutman, G.G. On the use of long-term global data of land reflectances and vegetation indices derived from the advanced very high resolution radiometer. J. Geophys. Res. Atmos. 1999, 104, 6241–6255. [Google Scholar] [CrossRef]
- Zhang, P.; Anderson, B.; Tan, B.; Huang, D.; Myneni, R. Potential monitoring of crop production using a satellite-based Climate-Variability Impact Index. Agric. For. Meteorol. 2005, 132, 344–358. [Google Scholar] [CrossRef]
- Myneni, R.B.; Hall, F.G. The interpretation of spectral vegetation indexes. IEEE Trans. Geosci. Remote Sens. 1995, 33, 481–486. [Google Scholar] [CrossRef]
- Asrar, G.; Fuchs, M.; Kanemasu, E.T.; Hatfield, J.L. Estimating Absorbed Photosynthetic Radiation and Leaf Area Index from Spectral Reflectance in Wheat. Agron. J. 1984, 76, 300–306. [Google Scholar] [CrossRef]
- DeFries, R.; Hansen, M.; Townshend, J. Global discrimination of land cover types from metrics derived from AVHRR pathfinder data. Remote Sens. Environ. 1995, 54, 209–222. [Google Scholar] [CrossRef]
- Tucker, C.J.; Pinzon, J.E.; Brown, M.E.; Slayback, D.A.; Pak, E.W.; Mahoney, R.; Vermote, E.F.; El Saleous, N. An extended AVHRR 8-km NDVI dataset compatible with MODIS and SPOT vegetation NDVI data. Int. J. Remote Sens. 2005, 26, 4485–4498. [Google Scholar] [CrossRef]
- Pinzon, J.E.; Tucker, C.J. A non-stationary 1981–2012 AVHRR NDVI3g time series. Remote Sens 2014, 6, 6929–6960. [Google Scholar] [CrossRef]
- Peng, S.; Ciais, P.; Chevallier, F.; Peylin, P.; Cadule, P.; Sitch, S.; Piao, S.; Ahlström, A.; Huntingford, C.; Levy, P.; et al. Benchmarking the seasonal cycle of CO2 fluxes simulated by terrestrial ecosystem models. Glob. Biogeochem. Cycles 2015, 29, 46–64. [Google Scholar] [CrossRef]
- Shao, P.; Zeng, X.; Sakaguchi, K.; Monson, R.K.; Zeng, X. Terrestrial carbon cycle: Climate relations in eight CMIP5 Earth system models. J. Clim. 2013, 26, 8744–8764. [Google Scholar] [CrossRef]
- Mueller, T.; Dressler, G.; Tucker, C.J.; Pinzon, J.E.; Leimgruber, P.; Dubayah, R.O.; Hurtt, G.C.; Böhning-Gaese, K.; Fagan, W.F. Human land-use practices lead to global long-term increases in photosynthetic capacity. Remote Sens. 2014, 6, 5717–5731. [Google Scholar] [CrossRef]
- Piao, S.; Ciais, P.; Friedlingstein, P.; de Noblet-Ducoudre, N.; Cadule, P.; Viovy, N.; Wang, T. Spatiotemporal patterns of terrestrial carbon cycle during the 20th century. Glob. Biogeochem. Cycles 2009, 23. [Google Scholar] [CrossRef]
- Zhao, M.; Running, S.W. Drought-Induced reduction in global terrestrial net primary production from 2000 through 2009. Science 2010, 329, 940–943. [Google Scholar] [CrossRef] [PubMed]
- Sitch, S.; Friedlingstein, P.; Gruber, N.; Jones, S.D.; Murray-Tortarolo, G.; Ahlström, A.; Doney, S.C.; Graven, H.; Heinze, C.; Huntingford, C.; et al. Recent trends and drivers of regional sources and sinks of carbon dioxide. Biogeosciences 2015, 12, 653–679. [Google Scholar] [CrossRef]
- Chen, J.M.; Chen, B.; Higuchi, K.; Liu, J.; Chan, D.; Worthy, D.; Tans, P.; Black, A. Boreal ecosystems sequestered more carbon in warmer years. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Miranda-Aragón, L.; Treviño-Garza, E.J.; Jiménez-Pérez, J.; Aguirre-Calderón, O.A.; González-Tagle, M.A.; Pompa-García, M.; Aguirre-Salado, C.A. NDVI-rainfall relationship using hyper-temporal satellite data in a portion of North Central Mexico (2000–2010). Afr. J. Agric. Res. 2012, 7, 1023–1033. [Google Scholar]
- Zeng, N.; Zhao, F.; Collatz, G.J.; Kalnay, E.; Salawitch, R.J.; West, T.O.; Guanter, L. Agricultural Green Revolution as a driver of increasing atmospheric CO2 seasonal amplitude. Nature 2014, 515, 394–397. [Google Scholar] [CrossRef]
- Janssens, I.A.; Dieleman, W.; Luyssaert, S.; Subke, J.A.; Reichstein, M.; Ceulemans, R.; Ciais, P.; Dolman, A.J.; Grace, J.; Matteucci, G.; et al. Reduction of forest soil respiration in response to nitrogen deposition. Nat. Geosci. 2010, 3, 315–322. [Google Scholar] [CrossRef]
- Mann, C.C. Addicted to rubber. Science 2009, 325, 564–566. [Google Scholar] [CrossRef] [PubMed]
- Beck, P.S.; Goetz, S.J. Satellite observations of high northern latitude vegetation productivity changes between 1982 and 2008: Ecological variability and regional differences. Environ. Res. Lett. 2011, 6, 045501. [Google Scholar] [CrossRef]
- Allen, C.D.; Macalady, A.K.; Chenchouni, H.; Bachelet, D.; McDowell, N.; Vennetier, M.; Kitzberger, T.; Rigling, A.; Breshears, D.D.; Hogg, E.T.; et al. A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. For. Ecol. Manag. 2010, 259, 660–684. [Google Scholar] [CrossRef]
- Seaquist, J.W.; Hickler, T.; Eklundh, L.; Ardö, J.; Heumann, B.W. Disentangling the effects of climate and people on Sahel vegetation dynamics. Biogeosciences 2009, 6, 469–477. [Google Scholar] [CrossRef]
- Valentini, R.; Matteucci, G.; Dolman, A.J.; Schulze, E.D.; Rebmann, C.J.M.E.A.G.; Moors, E.J.; Granier, A.; Gross, P.; Jensen, N.O.; Pilegaard, K.; et al. Respiration as the main determinant of carbon balance in European forests. Nature 2000, 404, 861–865. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Li, X.; Hu, J.; Yang, X.; Sheng, S.; Liu, M. Evaluating the difference between the normalized difference vegetation index and net primary productivity as the indicators of vegetation vigor assessment at landscape scale. Environ. Monit. Assess. 2012, 184, 1275–1286. [Google Scholar] [CrossRef] [PubMed]
- Schloss, A.L.; Kicklighter, D.W.; Kaduk, J.; Wittenberg, U.; Intercomparison, T.; Model, P.O.T.P.N. Comparing global models of terrestrial net primary productivity (NPP): Comparison of NPP to climate and the Normalized Difference Vegetation Index (NDVI). Glob. Chang. Biol. 1999, 5 (Suppl. S1), 25–34. [Google Scholar] [CrossRef]
- Rafique, R.; Kumar, S.; Luo, Y.; Kiely, G.; Asrar, G. An algorithmic calibration approach to identify globally optimal parameters for constraining the DayCent model. Ecol. Model. 2015, 297, 196–200. [Google Scholar] [CrossRef]
- Diner, D.J.; Asner, G.P.; Davies, R.; Knyazilkhin, Y.; Muller, J.P.; Nolin, A.W.; Pinty, B.; Schaaf, C.B.; Stroeve, J. New directions in earth observing: Scientific applications of multiangle remote sensing. Bull. Am. Meteorol. Soc. 1999, 80, 2209–2228. [Google Scholar] [CrossRef]
- Huete, A.; Jackson, R. Soil and atmosphere influences on the spectra of partial canopies. Remote Sens. Environ. 1988, 25, 89–105. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Fang, Y.; Liu, C.; Huang, M.; Li, H.; Leung, L.R. Steady state estimation of soil organic carbon using satellite-derived canopy leaf area index. J. Adv. Model. Earth Syst. 2014, 6, 1049–1064. [Google Scholar] [CrossRef]
- Wullschleger, S.D.; Epstein, H.E.; Box, E.O.; Euskirchen, E.S.; Goswami, S.; Iversen, C.M.; Kattge, J.; Norby, R.J.; van Bodegom, P.M.; Xu, X. Plant functional types in Earth system models: Past experiences and future directions for application of dynamic vegetation models in high-latitude ecosystems. Ann. Bot. 2014, 114, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Kurz, W.A.; Stinson, G.; Rampley, G. Could increased boreal forest ecosystem productivity offset carbon losses from increased disturbances? Philos. Trans. R. Soc. B Biol Sci. 2008, 363, 2261–2269. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.; Tian, H.; Dangal, S.R.; Zhang, C.; Yang, J.; Tao, B.; Ouyang, Z.; Wang, X.; Lu, C.; Ren, W.; et al. Complex spatiotemporal responses of global terrestrial primary production to climate change and increasing atmospheric CO2 in the 21st century. PLoS ONE 2014, 9, e112810. [Google Scholar] [CrossRef] [PubMed]

| Models | Resolution (Degrees) | Period |
|---|---|---|
| CLM4.5 | 192 × 288 | 1860–2012 |
| JULES | 192 × 112 | 1860–2012 |
| LPJ | 720 × 360 | 1901–2012 |
| OCN | 360 × 150 | 1901–2012 |
| VEGAS | 720 × 360 | 1860–2013 |
| Models/Data | Fraction (%) > 0 | Fraction (%) < 0 | % of Statistically Significant Land Pixels (p < 0.05) |
|---|---|---|---|
| MME | 79.46 | 20.54 | 50 |
| CLM4.5 | 80.35 | 19.65 | 36 |
| JULES | 67.82 | 32.18 | 44 |
| LPJ | 71.66 | 28.34 | 30 |
| OCN | 83.35 | 16.65 | 48 |
| VEGAS | 78.82 | 21.18 | 58 |
| NDVI | 67.15 | 32.85 | 48 |
| Spatial Unit | Trend (NDVI·y−1) | SE |
|---|---|---|
| Global | 0.00041 ** | 0.03 |
| Boreal | 0.00038 ** | 0.03 |
| Temperate | 0.00052 ** | 0.03 |
| Tropics | 0.00048 ** | 0.03 |
| Extra Tropics | 0.00011 * | 0.04 |
| Global | |||
|---|---|---|---|
| Models | NPP (Pg C·y−1) | Trend (Pg C·y−1·y−1) | SE |
| MME | 62.90 | 0.214 ** | 0.03 |
| CLM4.5 | 64.75 | 0.184 ** | 0.02 |
| JULES | 72.4 | 0.359 ** | 0.05 |
| LPJ | 53.72 | 0.148 ** | 0.03 |
| OCN | 60.78 | 0.238 ** | 0.03 |
| VEGAS | 62.85 | 0.141 ** | 0.02 |
| Boreal (50 N–90 N) | |||
| MME | 9.68 | 0.051 ** | 0.06 |
| CLM4.5 | 9.39 | 0.038 ** | 0.06 |
| JULES | 11.42 | 0.080 ** | 0.08 |
| LPJ | 11.33 | 0.042 ** | 0.07 |
| OCN | 9.19 | 0.050 ** | 0.07 |
| VEGAS | 7.06 | 0.043 ** | 0.08 |
| Temperate (25 N–50 N) | |||
| MME | 13.55 | 0.034 ** | 0.05 |
| CLM4.5 | 14.04 | 0.032 ** | 0.04 |
| JULES | 14.16 | 0.037 ** | 0.08 |
| LPJ | 10.57 | 0.026 ** | 0.08 |
| OCN | 14.48 | 0.050 ** | 0.06 |
| VEGAS | 14.49 | 0.026 ** | 0.04 |
| Tropics (25 S–25 N) | |||
| MME | 36.24 | 0.126 ** | 0.05 |
| CLM4.5 | 37.74 | 0.109 ** | 0.04 |
| JULES | 42.8 | 0.237 ** | 0.08 |
| LPJ | 29.89 | 0.081 ** | 0.05 |
| OCN | 33.97 | 0.133 ** | 0.04 |
| VEGAS | 36.78 | 0.072 ** | 0.04 |
| Extra Tropics (25 S–90 S) | |||
| MME | 3.44 | 0.003 * | 0.13 |
| CLM4.5 | 3.58 | 0.006 * | 0.14 |
| JULES | 4.03 | 0.005 * | 0.23 |
| LPJ | 1.93 | −0.001 * | 0.23 |
| OCN | 3.15 | 0.005 * | 0.10 |
| VEGAS | 4.53 | 0.001 * | 0.09 |
| Spatial Unit | CLM4.5 | JULES | LPJ | OCN | VEGAS | MME |
|---|---|---|---|---|---|---|
| Global | 0.59 | 0.61 | 0.60 | 0.66 | 0.67 | 0.64 |
| Boreal | 0.64 | 0.64 | 0.63 | 0.71 | 0.68 | 0.69 |
| Temperate | 0.72 | 0.56 | 0.50 | 0.73 | 0.67 | 0.73 |
| Tropics | 0.42 | 0.49 | 0.50 | 0.49 | 0.50 | 0.50 |
| Extra Tropics | 0.44 | 0.50 | 0.48 | 0.67 | 0.57 | 0.59 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rafique, R.; Zhao, F.; De Jong, R.; Zeng, N.; Asrar, G.R. Global and Regional Variability and Change in Terrestrial Ecosystems Net Primary Production and NDVI: A Model-Data Comparison. Remote Sens. 2016, 8, 177. https://doi.org/10.3390/rs8030177
Rafique R, Zhao F, De Jong R, Zeng N, Asrar GR. Global and Regional Variability and Change in Terrestrial Ecosystems Net Primary Production and NDVI: A Model-Data Comparison. Remote Sensing. 2016; 8(3):177. https://doi.org/10.3390/rs8030177
Chicago/Turabian StyleRafique, Rashid, Fang Zhao, Rogier De Jong, Ning Zeng, and Ghassem R. Asrar. 2016. "Global and Regional Variability and Change in Terrestrial Ecosystems Net Primary Production and NDVI: A Model-Data Comparison" Remote Sensing 8, no. 3: 177. https://doi.org/10.3390/rs8030177
APA StyleRafique, R., Zhao, F., De Jong, R., Zeng, N., & Asrar, G. R. (2016). Global and Regional Variability and Change in Terrestrial Ecosystems Net Primary Production and NDVI: A Model-Data Comparison. Remote Sensing, 8(3), 177. https://doi.org/10.3390/rs8030177