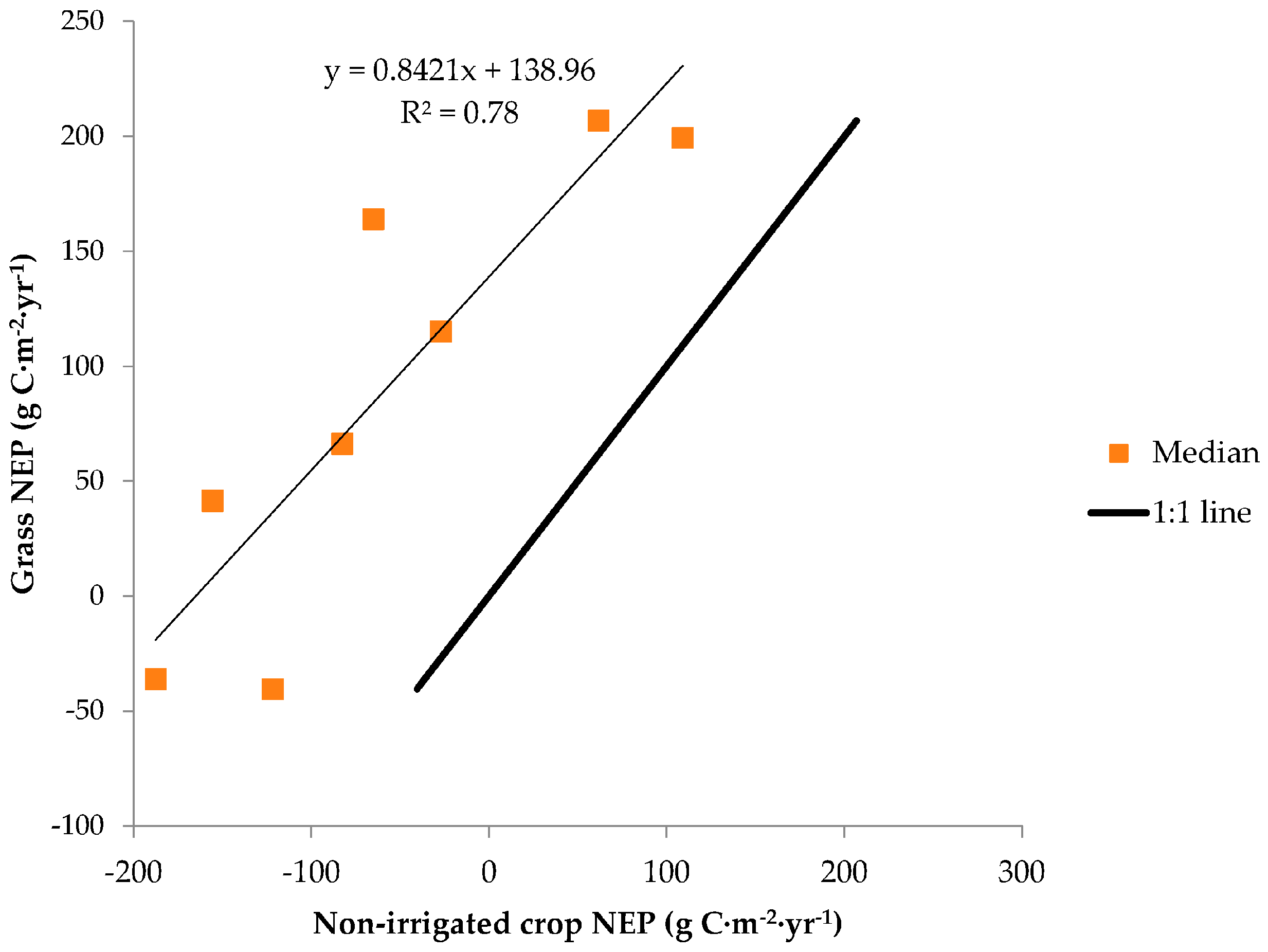1. Introduction
The far reaching effects and evidence of climate change, driven by increases in atmospheric greenhouse gas concentrations, motivated international mitigation focus at the 2015 United Nations Framework Convention on Climate Change Fifteenth Session of the Conference of the Parties [
1]. Regional syntheses of carbon flux tower data [
2,
3,
4] provide geographically referenced estimates from multiple flux towers and offer detailed summarization of carbon flux properties.
Throughout modern history, scientists have been developing models to formulate generalized algorithms to expand geographically and temporally sparse field observations to a much larger landscape means [
2,
3,
4] or to make up-scaled maps of the measured field characteristics [
5]. Understanding, mapping, and quantifying regional carbon flux magnitudes and variability of terrestrial non-point carbon sinks (removal of atmospheric carbon) and sources (emission of carbon to the atmosphere) is important in the promotion of ecosystem sustainability. Methodological and technological advances in the areas of remote sensing, environmental monitoring devices, data management, and computer-aided analytics have led the way to more innovative modeling. With these advancements, scientists have been able to apply these modeling methods to make estimates about discrete environmental characteristics, such as, atmospheric composition and below ground characteristics [
6,
7,
8,
9].
Remote sensing data [
5,
10,
11], light use efficiency modeling [
9,
12], data mining techniques [
5,
10,
11,
13,
14], process-base modeling [
15,
16], and greenhouse gas inventories [
17] have enhanced regional understanding and monitoring capabilities. Mapping efforts are sometimes at coarse resolutions, long time step intervals, have large (continental or global) study areas which may miss local detail, and can have highly automated or general gap filling strategies for temporary flux tower instrument failures.
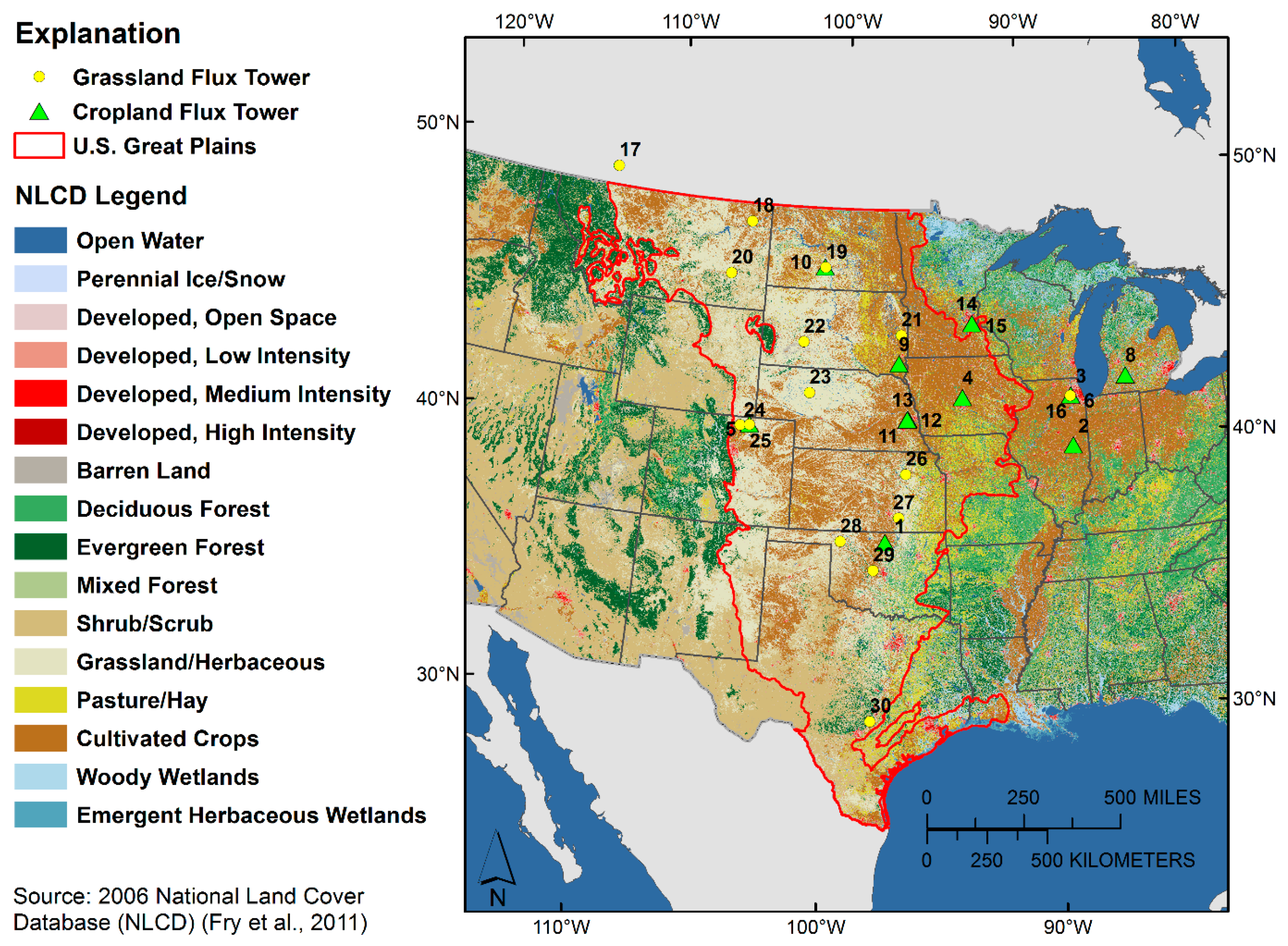
Our analysis focused on two primary large ecosystem classes in the U.S. Great Plains, cropland and grassland. We developed and applied our models at the 250 m spatial resolution and the weekly temporal resolution to retain the detailed temporal dynamics of carbon fluxes in the output maps. The primary objective of this study was to combine measurements acquired at flux towers with applicable remote sensing, weather, and other biogeophysical data to develop separate grassland and cropland ecologically-based net ecosystem production (NEP) models and derive mean daily NEP maps at a weekly time step from 2000 to 2008 for the study area of interest, the U.S. Great Plains (
Figure 1). Although a flux tower measures only its surrounding vicinity, numerous studies have shown that these recordings can be used in regional or land cover specific synthesis [
3,
4] or up-scaled to much greater levels through analyses of geospatial data relationships using computer modeling [
9,
13,
18]. Of particular interest is the use of data mining regression tree algorithms for carbon flux mapping [
5,
10,
11,
13,
14,
18]. An acute capability to address nonlinear relationships, deal with complex high order interactions, easily interpret results, and utilize both categorical and continuous variables, lends data mining regression tree [
10], which contrasts with process-based modeling approaches that are frequently heavily driven by precipitation, a difficult variable to map accurately, particularly in rural regions where weather stations are sparse. A vulnerability of regression tree approaches is a tendency of over fitting. However, this can be mitigated through cross validation [
19] and generalization of sequential dichotomous tests (trees) into generalized rules [
20]. Regional comparisons indicated a higher grassland carbon sink strength and a higher water use efficiency than non-irrigated crops across rainfall gradients in the Great Plains.
In addition to model development and map production, a secondary objective of this study was to perform a systematic comparative analysis of the grassland and cropland NEP results. Our hypothesis was that cropland ecosystems, being highly managed to optimize productivity of usually annual vegetation and often in a state of tilled (exposed) soil, vulnerable to respiration losses, would lean more towards the C sources. Conversely, grasslands with perennial vegetation, generally subject to little management and no tillage, would tend to perform as C equilibrium or sinks. Grassland and cropland make up approximately 85% of the total surface area of the U.S. Great Plains (48% grasslands or shrubs and 37% cultivated crops, pasture, or hay;
Figure 1), signifying the importance of understanding C fluxes in these two ecosystem classes. This spatial and temporal synthesis of Ameriflux, Agriflux, and independent flux tower data was performed with attention to the stated goals of the North American Carbon Program (NACP) [
22].
4. Discussion
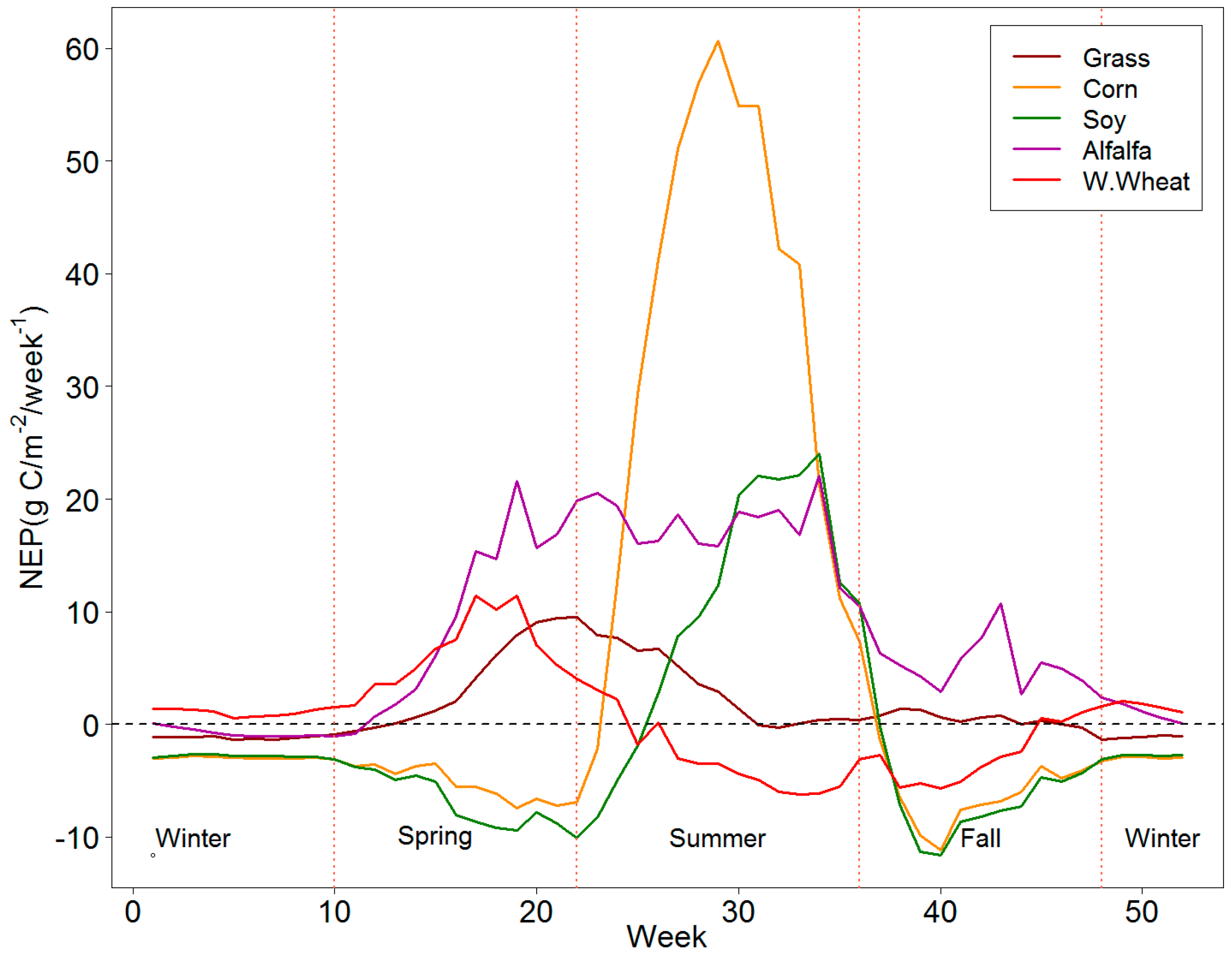
The most influential spatial variables in the NEP maps were typically those that were dynamic at the weekly time step (for example, NDVI, PAR, Week, and DOY). Precipitation (PCP), a major driver in many process-based models, had only moderate utilization in NEP modeling of 33% and 21% for grass and crop, respectively. The reduced usage or precipitation in the regression tree models may be related to the difficulty of extrapolating precipitation away from weather stations as regression tree models will only employ spatial inputs when and where they contribute to explaining the spatial or temporal variability of weekly NEP. Temperature inputs are much more reliably extrapolated away from weather stations but temperature inputs were more utilized in the crop model than the grass model. Incorporation of PAR and its high utilization in the grass model may have reduced the impact of the phenological variables (SOSN, SOST, AMP, MAXN, and EOST) relative to the crop model.
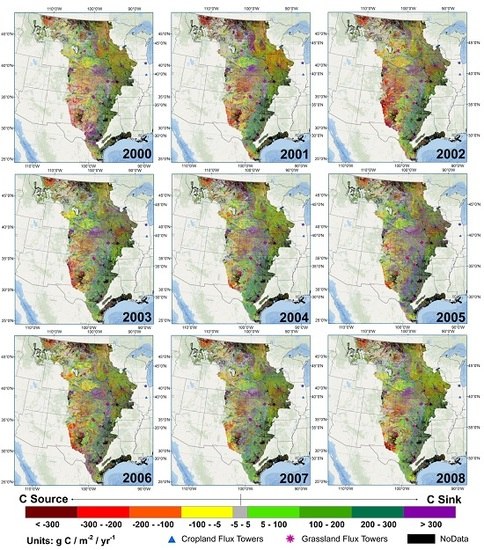
East to west moisture and productivity gradients were observed in annual and multiple year summaries (
Figure 5 and
Figure 7), agreeing with the general flux trends in other studies [
5,
11,
70]. These mapping approaches provide logical and useful means to reliably extend flux tower data across space and time. Currently, available flux towers grossly under sample the Great Plains ecosystems in both time and space relative to the mapped population (area × years) of this study. The 76 site years of flux tower data used to develop the NEP mapping models represented only 0.00003% of the space for time population that was mapped (28,817,873 pixels at 250 m resolution × 9 years). Particularly, limited flux tower representation occurs in cropland areas in the extreme northern, southern, and western portions of the U.S. Great Plains (
Figure 1), where high RMSE values were observed (
Figure 8). Crop flux towers are primarily located in either corn or soybean fields, with little or no data available for other crops, such as cotton, spring wheat, and sorghum. Grassland areas along the southwestern edge of the Great Plains are also deficient in flux tower representation [
70]. A focused expansion to the current flux tower network would improve the spatial mapping accuracies and help to ensure that extreme weather and environmental conditions are captured. Capturing extreme weather and environmental conditions with additional flux towers would result in more robust modeling results to better inform the carbon cycle science communities.
Referencing
Figure 5 and
Figure 7, areas with persistent high carbon sinks (>300 g C·m
−2·year
−1) mapped in this study aligned with: (1) the grassland-dominated Flint Hill ecoregion (9.4.4) primarily in eastern Kansas where shallow rocky soils have allowed native tallgrass prairie systems to persist; (2) the northwestern Central Great Plains ecoregion (9.4.2) which is a mix of grassland and cropland; and (3) the eastern portions of the Northwestern Glaciated Plains ecoregion (9.3.1), a grassland-dominated region with some cropland. Another notable high carbon sink region is the edges for the Prairie Coteau in northeastern South Dakota, where steep slopes have precluded crop expansion in these grasslands which are considered by many as tallgrass systems [
71].
Carbon source areas are generally aligned with the drier western edge of the Great Plains with small grain cropping in the central and western Northwestern Glaciated Plains ecoregion (9.3.1), primarily dry grasslands in the Southwestern Tablelands (9.43) and grassland and shrubland in the High Plains (9.41) ecoregion. Extreme carbon source areas (<−300 g C·m
−2·year
−1) tended to be in warmer southern croplands of the Great Plains in the southeastern High Plains (9.4.1), southwestern Central Great Plains (9.4.2), and southern croplands of the Western Gulf Coastal Plain (9.51) ecoregions. These extreme flux regions are distant from the nearest crop non-wheat flux tower (
Figure 1,
Table S1) and may have moderate to high flux mapping uncertainties (
Figure 8).
Corn production dominates the Western Corn Belt Plains ecoregion (9.2.3) transitioning from moderate carbon sinks (200 to 100 g C·m−2·year−1) in northern and central parts of this ecoregion to moderate sources (−200 to −100 g C·m−2·year−1) in the southern and eastern part of this ecoregion where pasture land use becomes more common in erodible soils and landscapes.
The productivity gradient analysis used regression intercept terms to quantify carbon sink advantages of grass over non-irrigated crop (
Figure 12), but equilibrium NEP discussed here is from 2000 to 2008, not a long-term NEP. Given that the long-term spatial and temporal weather variations and weather extremes (very wet to strong drought years) are high in the Great Plains [
72], 2000–2008 equilibrium NEP are expected to vary from the 30-year climate record (1981–2010 used in this study) and to future conditions. However, NEP productivity relationships with 30-year climate precipitation (
Table 7) can help quantify expected ecosystem service benefits and consequences related to grass and non-irrigated land cover changes. Extending the carbon flux mapping period forward in time and adding more dryland crop flux tower datasets would further improve these estimates.
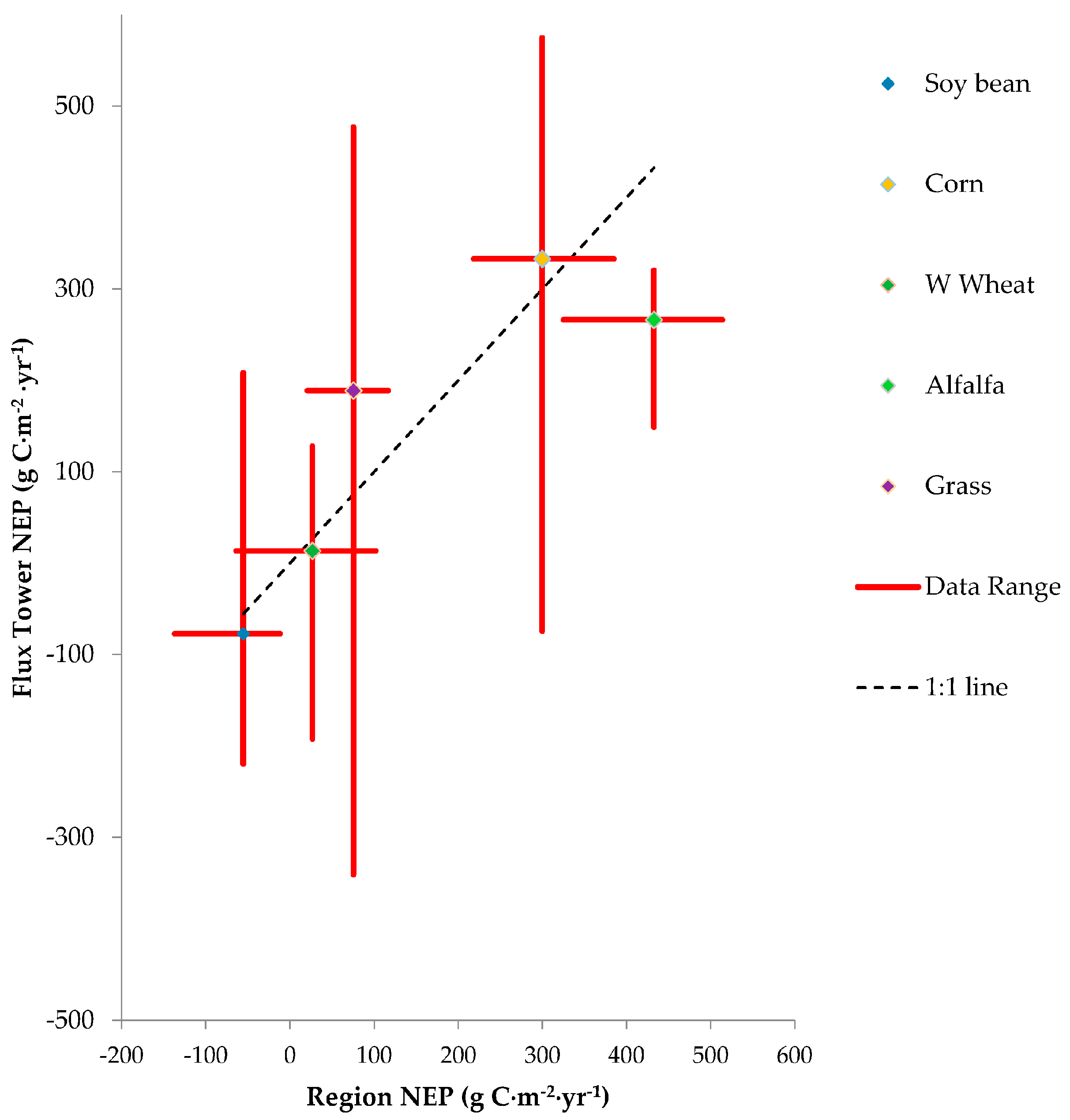
Regional Great Plains NEP means and minimum to maximum years for each majority land cover (
Figure S2) through the study period agreed well with published flux tower estimates with most crop types and grass estimates, with the possible exception of alfalfa (
Figure 13). Generally, individual flux tower site and year variability in NEP tended to be greater than the inter-annual variability in regional mean NEP through regional averaging and generalized fitting of the NEP mapping models for crops and grass not capturing all of the occasional flux variations. Corn-dominated regional flux means (218–385 g C·m
−2·year
−1), which likely included some soybean years in the crop rotations, encompassed the mean annual corn NEP from flux towers from Gilmanov et al. [
4] of 333 g C·m
−2·year
−1 (
Figure 13). The range of corn flux tower annual NEP observations was 121–548 g C·m
−2·year
−1. Soybean-dominated areas had a long-term NEP of −56 g C·m
−2·year
−1 and ranged from −137 to −12 g C·m
−2·year
−1. Soybean flux tower estimates from Gilmanov, et al. [
4] agreed closely with a mean NEP of −77 and a data range of −220–208 g C·m
−2·year
−1. Similarly, winter wheat mean NEP was consistent (27 and 13 g C·m
−2·year
−1) for regional and flux tower means, respectively. The range of annual flux estimates from regional yearly means and flux towers were comparable (−64–102 and −193–128 g C·m
−2·year
−1, respectively). Grassland flux tower mean NEP was greater than the regional inter-annual mean (189 versus 75 g C·m
−2·year
−1). The high variation in grass flux tower NEP is probably related to the inclusion of international grassland flux towers and because the maximum, minimum, and mean NEPs were estimated from a NEP frequency graph (Figure 11A in Gilmanov et al. [
2]). Regional grassland annual means averaged across moisture and latitudinal gradients in the Great Plains tended to minimize inter-annual regional variations relative to flux tower estimates. Only alfalfa regional means and inter-annual NEP data ranges were higher than the flux tower site-year observations (
Figure 13). The regional distributions of long-term alfalfa cropping are more prevalent along the drier western edge of the Great Plains and appear to be irrigation dependent due to proximities to major river systems (Arkansas, Platte, Yellowstone, and Milk Rivers,
Figure S2). Flux tower alfalfa NEP estimates (5 site years) included towers east of Mandan, ND and towers in moist ecosystems (Michigan, Pennsylvania, and Italy) [
3]. Recall also that alfalfa-mapped NEP was the average of the grass and crop NEP predictions (
Section 2.3), which could add uncertainty. The lowest alfalfa regional annual means were in 2000 and 2002, both drier than normal years (
Figure 5). Flux tower data on irrigated alfalfa in arid and semiarid ecosystems would be useful in quantifying alfalfa flux uncertainty and improving mapped NEP accuracy in these alfalfa-dominant areas.
Utilizing spatial, temporal, synoptic, remotely sensed, and ancillary digital map products to interpolate carbon fluxes through space and time is a strong approach. Our regression tree approach of using mapped versions of all input spatial variables in model development ensures that input variables are used only if prediction utility persists despite any mapping errors in the input drivers. Improved mapping of NEP fluxes would be realized with improved resolution and spatial accuracy of weather, climate, and soils information. Another limiting factor is the low density of carbon flux tower observations relative to the spatial and temporal area mapped. In particular, extreme events (droughts, wet years, early and late freezes, etc.) need to be captured to make the regression tree mapping model robust to expected and witnessed increased weather variability. Representation of major crops by flux towers is weak, particularly in non-irrigated dry environments. Regression tree mapping models should be assessed for possible over fitting or over fitting tendencies to help ensure better final map products.
Our experience has been that regression trees can be quite site specific as they are tuned to optimize prediction for a specific study area. Therefore, we do not recommend applying the Great Plains NEP mapping models in this manuscript (
Tables S2 and S3) to other areas. However, we have successfully applied regression trees to subsequent (newer) years with reasonable success.
Future plans include mapping of the partitioned carbon fluxes associated with GPP and RE, which allow more functional prediction of carbon fluxes through time and space [
2,
3,
4] than the direct mapping of the somewhat functionally confounded NEP. Further GPP and RE spatial and temporal maps would improve understanding of the causes of carbon sinks and sources. The authors intend to apply the GPP and Re mapping approach to grass and croplands across the conterminous U.S. by adding additional flux tower site years.
5. Conclusions
In this study, regression tree models were developed to estimate weekly mean daily NEP for grassland and cropland of the U.S. Great Plains for the period 2000–2008. In collecting applicable, supporting flux tower data for the study area and time frame, the final sample for mapping NEP across select grassland and cropland in the U.S. Great Plains consisted of 76 site years of flux tower data. The modeling methodology used in this study exhibited the capability for quantifying NEP at the regional level. However, a more robust flux tower network for model sampling would have been ideal for this study and several areas were identified as possible candidates for future flux tower development to better serve environmental model developers and the carbon cycle science community.
The models were applied to create weekly NEP maps at 250 m resolution for much of the cropland and grassland ecosystems in the U.S. Great Plains. Heavily used spatial inputs in the mapping models were weekly NDVI, weekly PAR, and time of year inputs (Week or DOY). The resulting map products were scaled and summarized at various temporal and spatial units and the two different land cover types were considered in a statistical, comparative analysis. Grass and cropland NEP magnitudes were similar when comparing inter-annual values. Corn and alfalfa had the strongest C stock of all the crops in this study. Grasslands showed stronger C sink tendencies (139 g·m−2·year−1) more at the 2000–2008 NEP equilibrium than non-irrigated croplands across the moisture and productivity gradients of the Great Plains. Grassland 2000–2008 equilibrium NEP was expected to occur near 373 mm of annual precipitation from the 30-year climate record. Non-irrigated crop 2000–2008 equilibrium NEP was expected at an annual 30-year climate precipitation of 629 mm. Typically, grasslands are subject to minimal management and the soil is generally left alone, apart from occasional weed control, animal grazing, and cutting. Croplands, meanwhile, are commonly managed to control pests and weeds from the time the seed is drilled into the soil until harvest, followed by tilling, and applications of fertilizer. Higher spring and fall C retention levels in cropland soils might be observed if a cover crop was introduced to minimize soil exposure and erosion.
The maps and statistics presented in this study provide a framework and basic overview of C fluctuations in the U.S. Great Plains throughout the 2000–2008 time frame. This effort is expected to be continued and to be expanded to include cropland and grassland for the entire conterminous U.S. and possibly include NEP estimates for additional years and/or other land cover types, such as forests and shrublands. Understanding and being able to visualize the carbon cycling as a function of land cover and land use will help drive decision making in the area of land management and promote natural resource sustainability.