Using Google Earth Surface Metrics to Predict Plant Species Richness in a Complex Landscape
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. Field Data
2.3. Image Processing
2.4. Statistical Analysis
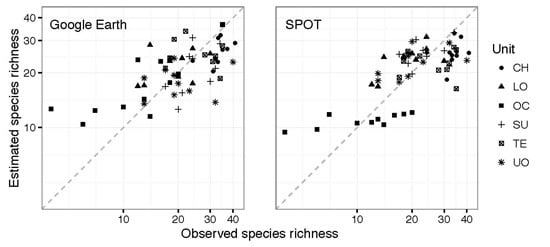
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Turner, W.; Spector, S.; Gardiner, N.; Fladeland, M.; Sterling, E.; Steininger, M. Remote sensing for biodiversity science and conservation. Trends Ecol. Evol. 2003, 18, 306–314. [Google Scholar] [CrossRef]
- Chambers, J.Q.; Asner, G.P.; Morton, D.C.; Anderson, L.O.; Saatchi, S.S.; Espírito-Santo, F.D.B.; Palace, M.; Souza, C. Regional ecosystem structure and function: Ecological insights from remote sensing of tropical forests. Trends Ecol. Evol. 2007, 22, 414–423. [Google Scholar] [CrossRef] [PubMed]
- Pitt, D.G.; Wagner, R.G.; Hall, R.J.; King, D.J.; Leckie, D.G.; Runesson, U. Use of Remote sensing for forest vegetation management: A problem analysis. For. Chron. 1997, 73, 459–477. [Google Scholar] [CrossRef]
- Franklin, S.E. Remote Sensing for Sustainable Forest Management; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Harris, G.M.; Jenkins, C.N.; Pimm, S.L. Refining biodiversity conservation priorities. Conserv. Biol. 2005, 19, 1957–1968. [Google Scholar] [CrossRef]
- Holl, K.D.; Aide, T.M. When and where to actively restore ecosystems? For. Ecol. Manag. 2011, 261, 1558–1563. [Google Scholar] [CrossRef]
- Wulder, M.A.; Masek, J.G.; Cohen, W.B.; Loveland, T.R.; Woodcock, C.E. Opening the archive: How free data has enabled the science and monitoring promise of Landsat. Remote Sens. Environ. 2012, 122, 2–10. [Google Scholar] [CrossRef]
- Asner, G.P.; Keller, M.; Pereira, R.; Zweede, J.C. Remote sensing of selective logging in Amazonia: Assessing limitations based on detailed field observations, Landsat ETM+, and textural analysis. Remote Sens. Environ. 2002, 80, 483–496. [Google Scholar] [CrossRef]
- Hu, Q.; Wu, W.; Xia, T.; Yu, Q.; Yang, P.; Li, Z.; Song, Q. Exploring the use of google earth imagery and object-based methods in land use/cover mapping. Remote Sens. 2013, 5, 6026–6042. [Google Scholar] [CrossRef]
- Barbosa, J.M.; Broadbent, E.N.; Bitencourt, M.D. Remote sensing of aboveground biomass in tropical secondary forests: A review. Int. J. For. Res. 2014, 2014, 1–14. [Google Scholar] [CrossRef]
- Ploton, P.; Pélissier, R.; Proisy, C.; Flavenot, T.; Barbier, N.; Rai, S.N.; Couteron, P. Assessing aboveground tropical forest biomass using Google Earth canopy images. Ecol. Appl. 2012, 22, 993–1003. [Google Scholar] [CrossRef] [PubMed]
- Schowengerdt, R.A. Remote Sensing: Models and Methods for Image Processing; Academic Press: San Diego, CA, USA, 2007. [Google Scholar]
- Pettorelli, N.; Vik, J.O.; Mysterud, A.; Gaillard, J.-M.; Tucker, C.J.; Stenseth, N.C. Using the satellite-derived NDVI to assess ecological responses to environmental change. Trends Ecol. Evol. 2005, 20, 503–510. [Google Scholar] [CrossRef] [PubMed]
- Haralick, R.M. Statistical and structural approaches to texture. Proc. IEEE 1979, 67, 786–804. [Google Scholar] [CrossRef]
- Rocchini, D.; Balkenhol, N.; Carter, G.A.; Foody, G.M.; Gillespie, T.W.; He, K.S.; Kark, S.; Levin, N.; Lucas, K.; Luoto, M.; et al. Remotely sensed spectral heterogeneity as a proxy of species diversity: Recent advances and open challenges. Ecol. Inform. 2010, 5, 318–329. [Google Scholar] [CrossRef]
- Couteron, P.; Pelissier, R.; Nicolini, E.A.; Paget, D. Predicting tropical forest stand structure parameters from Fourier transform of very high-resolution remotely sensed canopy images. J. Appl. Ecol. 2005, 42, 1121–1128. [Google Scholar] [CrossRef]
- Gallardo-Cruz, J.A.; Meave, J.A.; González, E.J.; Lebrija-Trejos, E.E.; Romero-Romero, M.A.; Pérez-García, E.A.; Gallardo-Cruz, R.; Hernández-Stefanoni, J.L.; Martorell, C. Predicting tropical dry forest successional attributes from space: Is the key hidden in image texture? PLoS ONE 2012, 7, e30506. [Google Scholar] [CrossRef] [PubMed]
- Siebe, C.; Arana-Salinas, L.; Abrams, M. Geology and radiocarbon ages of Tláloc, Tlacotenco, Cuauhtzin, Hijo del Cuauhtzin, Teuhtli, and Ocusacayo monogenetic volcanoes in the central part of the Sierra Chichinautzin, México. J. Volcanol. Geotherm. Res. 2005, 141, 225–243. [Google Scholar] [CrossRef]
- Siebe, C.; Rodríguez-Lara, V.; Schaaf, P.; Abrams, M. Radiocarbon ages of Holocene Pelado, Guespalapa, and Chichinautzin scoria cones, south of Mexico City: Implications for archaeology and future hazards. Bull. Volcanol. 2004, 66, 203–225. [Google Scholar] [CrossRef]
- INEGI (Instituto Nacional de Estadística y Geografía). Cuaderno Estadístico Municipal de Tepoztlán, Morelos. Available online: http://www.inegi.org.mx/est/contenidos/espanol/sistemas/cem03/estatal/mor/m020/index.html (accessed on 5 January 2010).
- Magurran, A.E. Measuring Biological Diversity; John Wiley & Sons: Oxford, UK, 2004. [Google Scholar]
- Huete, A.R.; Liu, H.Q.; Batchily, K.; VanLeeuwen, W. A comparison of vegetation indices over a global set of TM images for EOS-MODIS. Remote Sens. Environ. 1997, 5, 6026–6042. [Google Scholar] [CrossRef]
- Planetary Habitability Laboratory (PHL). Visible Vegetation Index (VVI). Available online: http://phl.upr.edu/projects/visible-vegetation-index-vvi (accessed on 24 August 2016).
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.’H. Textural features for image classification. Proc. IEEE 1973, 3, 610–621. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference; Springer: New York, NY, USA, 2002. [Google Scholar]
- Block, S.; Meave, J.A. Structure and diversity of oak forests in the El Tepozteco National Park (Morelos, Mexico). Bot. Sci. 2015, 93, 429–460. [Google Scholar] [CrossRef]
- Barbier, N.; Couteron, P.; Proisy, C.; Malhi, Y.; Gastellu-Etchegorry, J.-P. the variation of apparent crown size and canopy heterogeneity across lowland Amazonian forests. Glob. Ecol. Biogeogr. 2010, 19, 72–84. [Google Scholar] [CrossRef]
- Barbier, N.; Proisy, C.; Véga, C.; Sabatier, D.; Couteron, P. Bidirectional Texture function of high resolution optical images of tropical forest: An approach using LiDAR hillshade simulations. Remote Sens. Environ. 2011, 115, 167–179. [Google Scholar] [CrossRef]
- Chave, J.; Réjou-Méchain, M.; Búrquez, A.; Chidumayo, E.; Colgan, M.S.; Delitti, W.B.C.; Duque, A.; Eid, T.; Fearnside, P.M.; Goodman, R.C.; et al. Improved allometric models to estimate the aboveground biomass of tropical trees. Glob. Chang. Biol. 2014, 20, 3177–3190. [Google Scholar] [CrossRef] [PubMed]
- Lu, D.; Batistella, M. Exploring TM image texture and its relationships with biomass estimation in Rondônia, Brazilian Amazon. Acta Amazon. 2005, 35, 249–257. [Google Scholar] [CrossRef]
- Block, S. Heterogeneidad florística y estructural de los encinares del Parque Nacional El Tepozteco, México. Bachelor’s Thesis, National Autonomous University of Mexico, Mexico City, Mexico, 2013. [Google Scholar]

| Model Type | BA | COV | DEN | HEm | HEv | Scan | Stot | Hcan | Htot |
|---|---|---|---|---|---|---|---|---|---|
| Google Earth | |||||||||
| 3 | 0.580 | 0.343 | 0.039 | 0.587 | 0.628 | 0.939 | 0.519 | 0.508 | 0.135 |
| 7 | 0.888 | 0.743 | 0.088 | 0.865 | 0.958 | 0.664 | 0.002 | 0.611 | 0.407 |
| 7 | 0.481 | 0.431 | 0.170 | 0.250 | 0.285 | 0.715 | 0.018 | 0.799 | 0.093 |
| 5 | 0.557 | 0.725 | 0.065 | 1.000 | 0.711 | 0.811 | 0.002 | 0.391 | 0.109 |
| 9 | 0.807 | 0.809 | 0.067 | 0.752 | 0.793 | 0.156 | 0.004 | 0.717 | 0.232 |
| 8 | 0.695 | 0.729 | 0.186 | 0.624 | 0.659 | 0.916 | 0.007 | 0.604 | 0.197 |
| 10 | 0.778 | 0.837 | 0.136 | 0.955 | 0.703 | 0.532 | 0.004 | 0.352 | 0.154 |
| 6 | 0.374 | 0.306 | 0.195 | 0.304 | 0.388 | 0.813 | 0.019 | 0.694 | 0.196 |
| SPOT | |||||||||
| 3 | 0.486 | 0.108 | 0.585 | 0.002 | 0.034 | 0.943 | 0.001 | 0.844 | 0.001 |
| 7 | 0.711 | 0.162 | 0.092 | 0.002 | 0.189 | 0.795 | 0.002 | 0.988 | 0.002 |
| 4 | 0.521 | 0.106 | 0.567 | 0.002 | 0.180 | 0.784 | 0.001 | 0.776 | 0.004 |
| 5 | 0.853 | 0.294 | 0.334 | 0.004 | 0.530 | 0.679 | 0.001 | 0.982 | 0.001 |
| 9 | 0.298 | 0.378 | 0.593 | 0.009 | 0.239 | 0.925 | 0.011 | 0.952 | 0.039 |
| 8 | 0.661 | 0.218 | 0.332 | 0.003 | 0.530 | 0.915 | 0.001 | 0.918 | 0.001 |
| 10 | 0.793 | 0.520 | 0.424 | 0.010 | 0.410 | 0.772 | 0.002 | 0.959 | 0.001 |
| 6 | 0.518 | 0.119 | 0.424 | 0.004 | 0.238 | 0.764 | 0.002 | 0.743 | 0.002 |
| Vegetation Attribute | Image | x1 | x2 | Model Type | ΔAICc | R2 | R2CV |
|---|---|---|---|---|---|---|---|
| Total richness | SPOT | red.cc.mean | red.st.entro | y = β0 + β1x1 − β2x12 − β3x2 + β4x22 | 0 | 0.51 | 0.40 |
| red.st.mean | red.st.entro | y = β0 + β1x1 − β2x12 − β3x2 + β4x22 | 0.289 | 0.50 | 0.40 | ||
| red.st.entro | red.cc.mean | y = β0 − β1x1 + β2x12 + β3x2 | 1.585 | 0.47 | 0.39 | ||
| GE | red.cc.asm | vvi.cc.mean | y = β0 + β1x1 − β2x2 − β3x1x2 | 0 | 0.44 | 0.34 | |
| red.cc.asm | vvi.st.mean | y = β0 + β1x1 − β2x2 − β3x1x2 | 0.365 | 0.44 | 0.33 | ||
| Height mean | SPOT | ndvi.st.entro | red.cc.mean | y = β0 − β1x1 + β2x12 − β3x2 − β4x22 | 0 | 0.42 | 0.31 |
| red.st.dr | ndvi.st.mean | y = β0 + β1x1 + β2x2 | 0.493 | 0.37 | 0.31 | ||
| red.st.dr | ndvi.cc.mean | y = β0 + β1x1 + β2x2 | 0.632 | 0.37 | 0.31 | ||
| red.cc.mean | red.cc.hom | y = β0 − β1x1 − β2x12 − β3x2 + β4x22 | 0.661 | 0.41 | 0.25 | ||
| red.cc.mean | ndvi.st.entro | y = β0 − β1x1 − β2x2 + β3x1x2 | 0.704 | 0.39 | 0.28 | ||
| ndvi.st.entro | ndvi.st.mean | y = β0 − β1x1 + β2x12 + β3x2 − β4x22 | 0.914 | 0.41 | 0.32 | ||
| ndvi.st.entro | ndvi.cc.mean | y = β0 − β1x1 + β2x12 + β3x2 − β4x22 | 1.142 | 0.41 | 0.32 | ||
| ndvi.st.mean | red.st.dr | y = β0 + β1x1 − β2x12 + β3x2 | 1.147 | 0.39 | 0.31 | ||
| red.cc.mean | red.cc.diss | y = β0 − β1x1 − β2x12 − β3x2 + β4x22 | 1.307 | 0.41 | 0.26 | ||
| ndvi.cc.hom | red.cc.mean | y = β0 − β1x1 + β2x12 − β3x2 − β4x22 | 1.356 | 0.41 | 0.26 | ||
| ndvi.cc.mean | red.st.dr | y = β0 + β1x1 − β2x12 + β3x2 | 1.398 | 0.38 | 0.31 | ||
| ndvi.st.entro | red.st.mean | y = β0 − β1x1 + β2x12 + β3x2 + β4x22 | 1.483 | 0.41 | 0.29 | ||
| red.cc.mean | ndvi.cc.hom | y = β0 + β1x1 + β2x2 − β3x1x2 | 1.517 | 0.38 | 0.26 | ||
| red.st.mean | red.cc.hom | y = β0 + β1x1 − β2x12 − β3x2 + β4x22 | 1.522 | 0.40 | 0.24 | ||
| ndvi.st.mean | red.st.var | y = β0 + β1x1 − β2x12 + β3x2 | 1.917 | 0.38 | 0.31 | ||
| Shannon diversity | SPOT | red.st.entro | red.cc.mean | y = −β0 + β1x1 − β2x12 − β3x2 | 0 | 0.42 | 0.34 |
| red.st.entro | red.cc.mean | y = −β0 − β1x1 + β2x12 + β3x2 − β4x22 | 0.856 | 0.43 | 0.34 | ||
| red.st.entro | red.st.mean | y = −β0 + β1x1 − β2x12 − β3x2 | 1.918 | 0.42 | 0.34 | ||
| Density | GE | red.st.skew | y = β0 + β1x1 | 0 | 0.18 | 0.07 | |
| Height variance | SPOT | ndvi.st.mean | y = β0 + β1x1 | 0 | 0.16 | 0.10 | |
| ndvi.cc.mean | y = β0 + β1x1 | 0.183 | 0.15 | 0.09 | |||
| red.cc.mean | y = β0 − β1x1 | 1.918 | 0.13 | 0.07 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Block, S.; González, E.J.; Gallardo-Cruz, J.A.; Fernández, A.; Solórzano, J.V.; Meave, J.A. Using Google Earth Surface Metrics to Predict Plant Species Richness in a Complex Landscape. Remote Sens. 2016, 8, 865. https://doi.org/10.3390/rs8100865
Block S, González EJ, Gallardo-Cruz JA, Fernández A, Solórzano JV, Meave JA. Using Google Earth Surface Metrics to Predict Plant Species Richness in a Complex Landscape. Remote Sensing. 2016; 8(10):865. https://doi.org/10.3390/rs8100865
Chicago/Turabian StyleBlock, Sebastián, Edgar J. González, J. Alberto Gallardo-Cruz, Ana Fernández, Jonathan V. Solórzano, and Jorge A. Meave. 2016. "Using Google Earth Surface Metrics to Predict Plant Species Richness in a Complex Landscape" Remote Sensing 8, no. 10: 865. https://doi.org/10.3390/rs8100865
APA StyleBlock, S., González, E. J., Gallardo-Cruz, J. A., Fernández, A., Solórzano, J. V., & Meave, J. A. (2016). Using Google Earth Surface Metrics to Predict Plant Species Richness in a Complex Landscape. Remote Sensing, 8(10), 865. https://doi.org/10.3390/rs8100865